AA-LMM: Robust Accuracy-Aware Linear Mixture Model for Remote Sensing Image Registration
Abstract
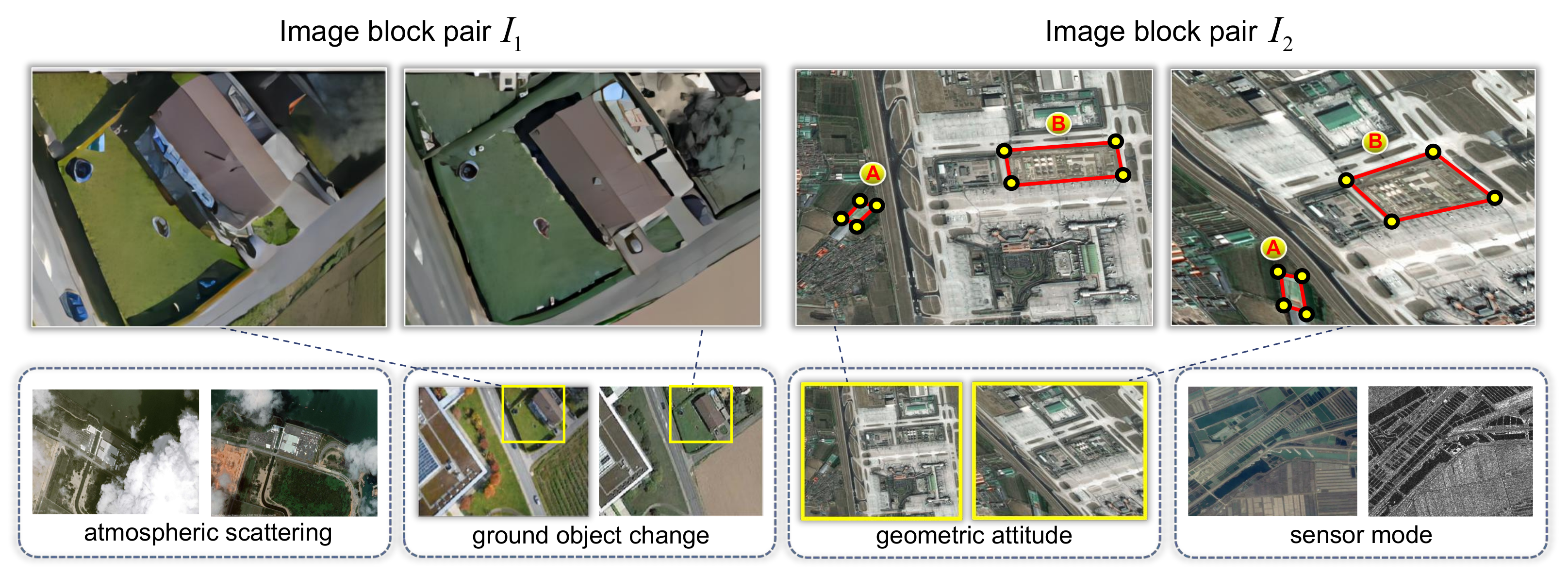
:1. Introduction
- An adaptive accuracy-aware mechanism is incorporated into the PSR framework to eliminate the discrepancies caused by degradation existing in the point sets, which makes the model focus more on the faithful points so that it estimates the non-rigid transformations more reliably and robustly;
- An effective iterative updating strategy is utilized to dynamically select suitable samples for the transformation estimation as iteration, which can improve the adaptation of the proposed model to a different point set with different degrees of degradation;
- We model the non-rigid spatial transformation as a sparse approximate problem in the RKHS, and a low rank kernel constraint is applied to fast select the best kernels for the approximation with a large number of points, which achieves a higher registration accuracy with a lower calculation expense.
2. Related Work
3. Methodology
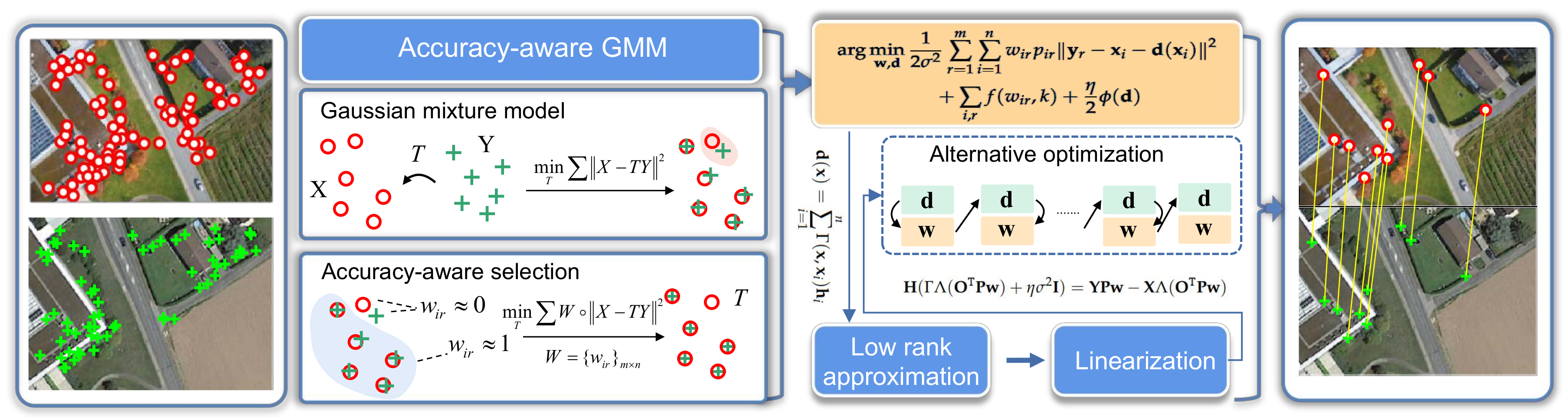
3.1. Gaussian Mixture Models
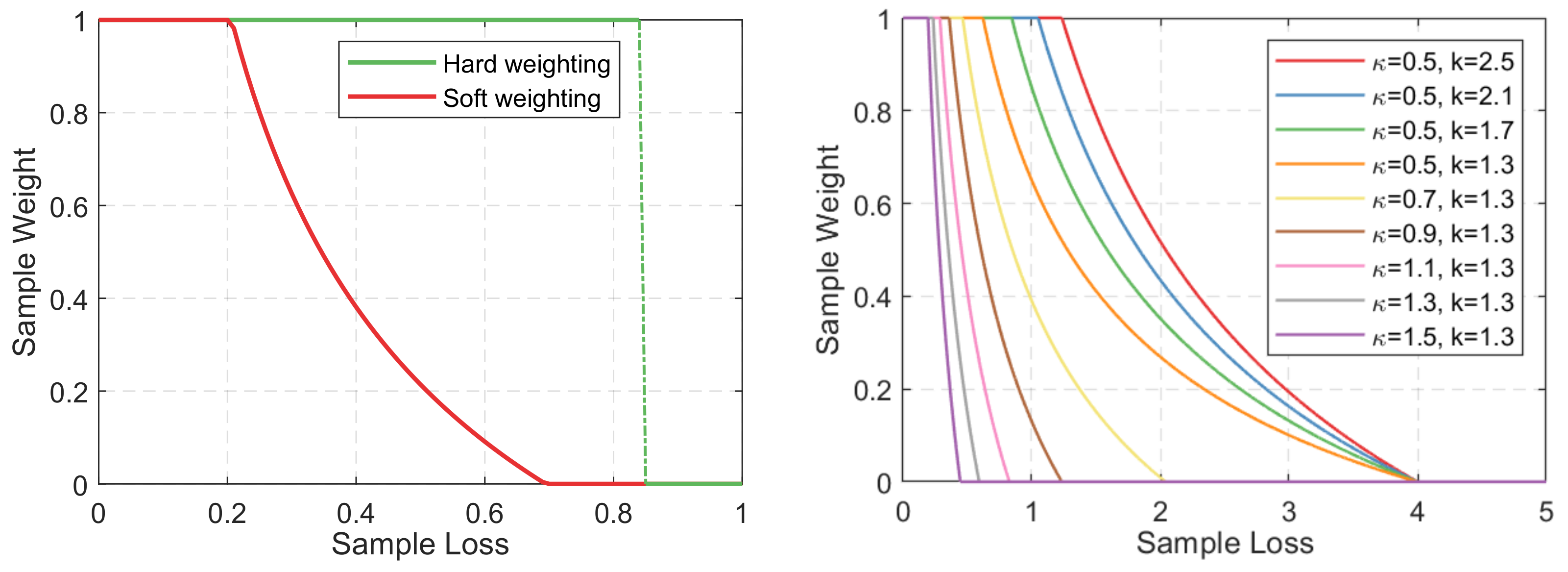
3.2. Accuracy-Aware Selection
3.3. Accuracy-Aware GMM
3.4. Accuracy-Aware Linear Mixture Model
3.5. Alternate Optimization
| Algorithm 1 Point alignment with accuracy-aware selection |
Input: Model and data points , , parameters , , , iteration number Output: Optimal transformation T
|
4. Experiments
4.1. Non-Rigid Shape Alignment
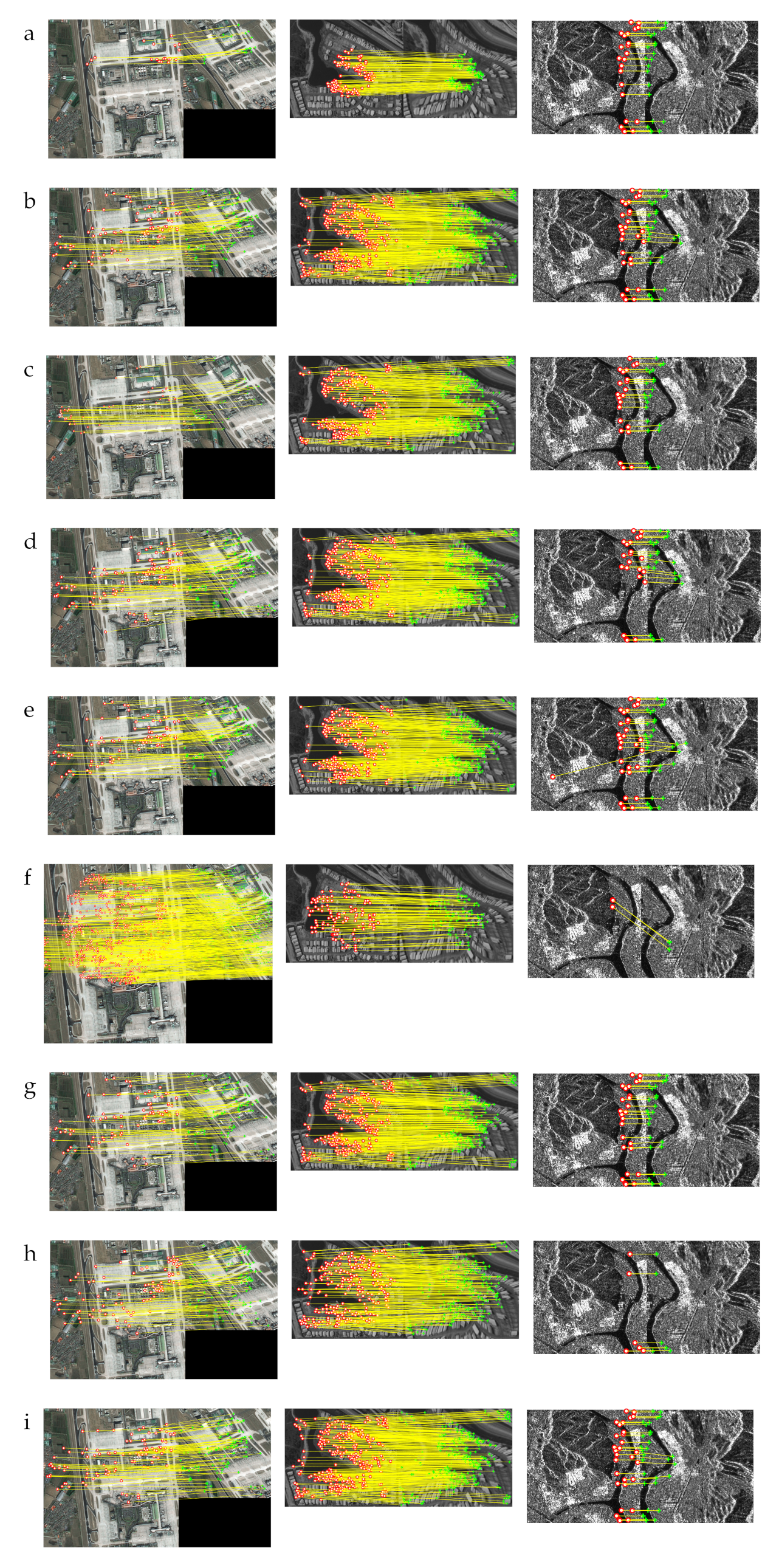
4.2. Remote Sensing Image Registration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SLAM | Simultaneous localization and mapping |
| PSR | Point set registration |
| GMMs | Gaussian Mixture Models |
| GMM | Gaussian Mixture Model |
| TPS | Thin plate spline |
| CPD | Coherent points drift |
| ICP | Iterative closest point |
| KC | Kernel correlation |
| UAV | Unmanned Aerial Vehicle |
| SAR | Synthetic aperture radar |
| HSI | Hyperspectral image |
| MSI | Multispectral image |
| RKHS | Reproducing kernel Hilbert space |
| RANSAC | Random sample consensus |
| SIFT | Scale-invariant feature transform |
| DA | Deterministic annealing |
| ED | Eigen-decomposition |
| EM | Expectation Maximization |
| RMSE | Root mean square error |
References
- Huang, C.; Mees, O.; Zeng, A.; Burgard, W. Visual language maps for robot navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, London, UK, 29 May–2 June 2023; pp. 10608–10615. [Google Scholar]
- Cattaneo, D.; Vaghi, M.; Valada, A. Lcdnet: Deep loop closure detection and point cloud registration for lidar slam. IEEE Trans. Robot. 2022, 38, 2074–2093. [Google Scholar] [CrossRef]
- Liu, Y.; Pang, C.; Zhan, Z.; Zhang, X.; Yang, X. Building change detection for remote sensing images using a dual-task constrained deep siamese convolutional network model. IEEE Geosci. Remote Sens. Lett. 2020, 18, 811–815. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; You, H. OS-SIFT: A robust SIFT-like algorithm for high-resolution optical-to-SAR image registration in suburban areas. IEEE Geosci. Remote Sens. 2018, 56, 3078–3090. [Google Scholar] [CrossRef]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.R.; Guttag, J.; Dalca, A.V. VoxelMorph: A learning framework for deformable medical image registration. IEEE Trans. Med. Imaging 2019, 38, 1788–1800. [Google Scholar] [CrossRef]
- Yang, K.; Pan, A.; Yang, Y.; Zhang, S.; Ong, S.H.; Tang, H. Remote sensing image registration using multiple image features. Remote Sens. 2017, 9, 581. [Google Scholar] [CrossRef]
- Shen, Z.; Han, X.; Xu, Z.; Niethammer, M. Networks for joint affine and non-parametric image registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Los Angeles, CA, USA, 16–20 June 2019; pp. 4224–4233. [Google Scholar]
- Liu, S.; Yang, B.; Wang, Y.; Tian, J.; Yin, L.; Zheng, W. 2D/3D multimode medical image registration based on normalized cross-correlation. Appl. Sci. 2022, 12, 2828. [Google Scholar] [CrossRef]
- Paul, S.; Pati, U.C. A comprehensive review on remote sensing image registration. Int. J. Remote Sens. 2021, 42, 5396–5432. [Google Scholar] [CrossRef]
- Han, L.; Xu, L.; Bobkov, D.; Steinbach, E.; Fang, L. Real-time global registration for globally consistent rgb-d slam. IEEE Trans. Robot. 2019, 35, 498–508. [Google Scholar] [CrossRef]
- Chui, H.; Rangarajan, A. A new point matching algorithm for non-rigid registration. Comput. Vis. Image Underst. 2003, 89, 114–141. [Google Scholar] [CrossRef]
- Maiseli, B.; Gu, Y.; Gao, H. Recent developments and trends in point set registration methods. J. Vis. Commun. Image Represent. 2017, 46, 95–106. [Google Scholar] [CrossRef]
- Jian, B.; Vemuri, B.C. Robust point set registration using gaussian mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1633–1645. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Yang, J.; Ai, D.; Xia, L.; Zhao, Y.; Gao, X.; Wang, Y. Convex hull indexed Gaussian mixture model (CH-GMM) for 3D point set registration. Pattern Recognit. 2016, 59, 126–141. [Google Scholar] [CrossRef]
- Yang, Y.; Ong, S.H.; Foong, K.W.C. A robust global and local mixture distance based non-rigid point set registration. Pattern Recognit. 2015, 48, 156–173. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Ma, Y.; Tian, J. Non-rigid visible and infrared face registration via regularized Gaussian fields criterion. Pattern Recognit. 2015, 48, 772–784. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, Q.; Chen, Y. Robust non-rigid point set registration using spatially constrained Gaussian fields. IEEE Trans. Image Process. 2017, 26, 1759–1769. [Google Scholar] [CrossRef]
- Tajdari, F.; Huysmans, T.; Song, Y. Non-rigid registration via intelligent adaptive feedback control. IEEE Trans. Vis. Comput. Graph. 2023, 1–17. [Google Scholar] [CrossRef]
- Schölkopf, B.; Herbrich, R.; Smola, A.J. A generalized representer theorem. In Proceedings of the International Conference on Computational Learning Theory, Amsterdam, The Netherlands, 16–19 July 2001; pp. 416–426. [Google Scholar]
- Guo, Y.; Zhao, L.; Shi, Y.; Zhang, X.; Du, S.; Wang, F. Adaptive weighted robust iterative closest point. Neurocomputing 2022, 508, 225–241. [Google Scholar] [CrossRef]
- Cao, L.; Zhuang, S.; Tian, S.; Zhao, Z.; Fu, C.; Guo, Y.; Wang, D. A Global Structure and Adaptive Weight Aware ICP Algorithm for Image Registration. Remote Sens. 2023, 15, 3185. [Google Scholar] [CrossRef]
- Ma, J.; Ma, Y.; Zhao, J.; Tian, J. Image feature matching via progressive vector field consensus. IEEE Signal Process. Lett. 2014, 22, 767–771. [Google Scholar] [CrossRef]
- Li, X.; Ma, Y.; Hu, Z. Rejecting mismatches by correspondence function. Int. J. Comput. Vis. 2010, 89, 1–17. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef]
- Tsin, Y.; Kanade, T. A correlation-based approach to robust point set registration. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 558–569. [Google Scholar]
- Tang, J.; Shao, L.; Zhen, X. Robust point pattern matching based on spectral context. Pattern Recognit. 2014, 47, 1469–1484. [Google Scholar] [CrossRef]
- Qu, H.B.; Wang, J.Q.; Li, B.; Yu, M. Probabilistic model for robust affine and non-rigid point set matching. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 371–384. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Zhao, J.; Yuille, A.L. Non-rigid point set registration by preserving global and local structures. IEEE Trans. Image Process. 2015, 25, 53–64. [Google Scholar]
- Wang, J.; Chen, J.; Xu, H.; Zhang, S.; Mei, X.; Huang, J.; Ma, J. Gaussian field estimator with manifold regularization for retinal image registration. Signal Process. 2019, 157, 225–235. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Fan, L.; Wu, Q.; Yuan, C. A systematic approach for cross-source point cloud registration by preserving macro and micro structures. IEEE Trans. Image Process. 2017, 26, 3261–3276. [Google Scholar] [CrossRef]
- Fan, J.; Cao, X.; Yap, P.T.; Shen, D. BIRNet: Brain image registration using dual-supervised fully convolutional networks. Med. Image Anal. 2019, 54, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Hansen, L.; Heinrich, M.P. GraphRegNet: Deep graph regularisation networks on sparse keypoints for dense registration of 3D lung CTs. IEEE Trans. Med. Imaging 2021, 40, 2246–2257. [Google Scholar] [CrossRef]
- Arar, M.; Ginger, Y.; Danon, D.; Bermano, A.H.; Cohen-Or, D. Unsupervised multi-modal image registration via geometry preserving image-to-image translation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–20 June 2020; pp. 13410–13419. [Google Scholar]
- Mok, T.C.; Chung, A. Fast symmetric diffeomorphic image registration with convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–20 June 2020; pp. 4644–4653. [Google Scholar]
- Goforth, H.; Lucey, S. GPS-denied UAV localization using pre-existing satellite imagery. In Proceedings of the International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 2974–2980. [Google Scholar]
- Papadomanolaki, M.; Christodoulidis, S.; Karantzalos, K.; Vakalopoulou, M. Unsupervised multistep deformable registration of remote sensing imagery based on deep learning. Remote Sens. 2021, 13, 1294. [Google Scholar] [CrossRef]
- Xu, Y.; Li, J.; Du, C.; Chen, H. NBR-Net: A nonrigid bidirectional registration network for multitemporal remote sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Horaud, R.; Forbes, F.; Yguel, M.; Dewaele, G.; Zhang, J. Rigid and articulated point registration with expectation conditional maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 587–602. [Google Scholar] [CrossRef]
- Yuille, A.L.; Grzywacz, N.M. A computational theory for the perception of coherent visual motion. Nature 1988, 333, 71–74. [Google Scholar] [CrossRef]
- Micchelli, C.A.; Pontil, M.; Bartlett, P. Learning the Kernel Function via Regularization. J. Mach. Learn. Res. 2005, 6, 1099–1125. [Google Scholar]
- Zheng, Y.; Doermann, D. Robust point matching for nonrigid shapes by preserving local neighborhood structures. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 643–649. [Google Scholar] [CrossRef]
- Nordstrøm, M.M.; Larsen, M.; Sierakowski, J.; Stegmann, M.B. The IMM Face Database—An Annotated Dataset of 240 Face Images; Technical University of Denmark: Lyngby, Denmark, 2004. [Google Scholar]
- Wu, F.; Zhang, H.; Wang, C.; Li, L.; Li, J.J.; Chen, W.R.; Zhang, B. SARBuD1.0: A SAR Building Dataset Based on GF-3 FSII Imageries for Built-up Area Extraction with Deep Learning Method. Natl. Remote Sens. Bull. 2022, 26, 620–631. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Ma, J.; Qiu, W.; Zhao, J.; Ma, Y.; Yuille, A.L.; Tu, Z. Robust L2E estimation of transformation for non-rigid registration. IEEE Trans. Signal Process. 2015, 63, 1115–1129. [Google Scholar] [CrossRef]
- Fan, A.; Ma, J.; Tian, X.; Mei, X.; Liu, W. Coherent point drift revisited for non-rigid shape matching and registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–23 June 2022; pp. 1424–1434. [Google Scholar]
- Efe, U.; Ince, K.G.; Alatan, A. Dfm: A performance baseline for deep feature matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 19–25 June 2021; pp. 4284–4293. [Google Scholar]
- Jiang, X.; Ma, J.; Fan, A.; Xu, H.; Lin, G.; Lu, T.; Tian, X. Robust feature matching for remote sensing image registration via linear adaptive filtering. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1577–1591. [Google Scholar] [CrossRef]
- Xia, Y.; Jiang, J.; Lu, Y.; Liu, W.; Ma, J. Robust feature matching via progressive smoothness consensus. ISPRS J. Photogramm. Remote Sens. 2023, 196, 502–513. [Google Scholar] [CrossRef]





| Methods | Def1 | Rot | Occ | Out1 | Def2 | Out2 |
|---|---|---|---|---|---|---|
| CPD | 0.2624 | 0.2673 | 0.0050 | 1.1379 | 1.5571 | 0.1267 |
| L2E | 0.0043 | 0.0129 | 0.0140 | 0.7895 | 0.6939 | 0.0306 |
| PR-LGS | 0.0166 | 0.0032 | 0.0046 | 0.6882 | 0.5259 | 0.0255 |
| GCPD | 0.0081 | 0.0040 | 0.0896 | 0.5153 | 0.5030 | 0.0151 |
| Ours | 0.0045 | 0.0010 | 0.0014 | 0.5053 | 0.4876 | 0.0097 |
| Method | Metrics | #Matches | ||||
|---|---|---|---|---|---|---|
| RANSAC | 1.4541 | 0.8198 | 0.3959 | 24 | 137 | 27 |
| CPD | 2.3980 | 0.9167 | 1.7119 | 86 | 349 | 30 |
| L2E | 2.5901 | 2.7353 | 2.9314 | 55 | 250 | 22 |
| PR-GLS | 2.2100 | 2.8341 | 1.5589 | 99 | 319 | 23 |
| GCPD | 2.4033 | 2.0786 | 2.6015 | 83 | 292 | 31 |
| DFM | 13.2901 | 4.893 | - | 861 | 124 | 3 |
| LAF | 4.3478 | 2.4255 | 2.5952 | 96 | 338 | 30 |
| PSC | 9.1314 | 2.465 | 0.2877 | 87 | 285 | 6 |
| Ours | 1.4465 | 0.7945 | 0.5135 | 106 | 369 | 31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Li, C.; Li, X. AA-LMM: Robust Accuracy-Aware Linear Mixture Model for Remote Sensing Image Registration. Remote Sens. 2023, 15, 5314. https://doi.org/10.3390/rs15225314
Yang J, Li C, Li X. AA-LMM: Robust Accuracy-Aware Linear Mixture Model for Remote Sensing Image Registration. Remote Sensing. 2023; 15(22):5314. https://doi.org/10.3390/rs15225314
Chicago/Turabian StyleYang, Jian, Chen Li, and Xuelong Li. 2023. "AA-LMM: Robust Accuracy-Aware Linear Mixture Model for Remote Sensing Image Registration" Remote Sensing 15, no. 22: 5314. https://doi.org/10.3390/rs15225314
APA StyleYang, J., Li, C., & Li, X. (2023). AA-LMM: Robust Accuracy-Aware Linear Mixture Model for Remote Sensing Image Registration. Remote Sensing, 15(22), 5314. https://doi.org/10.3390/rs15225314






