Abstract
The precise point positioning (PPP) technique generally takes tens of minutes to converge, severely limiting its use. This longer convergence time is mainly due to the slower variation of satellite geometry in space and the stronger correlation of unknown parameters to be estimated. Fortunately, the lower orbit altitude of Low Earth Orbit (LEO) satellites contributes to the fast variation of the satellites’ spatial geometry. In addition, high-precision atmospheric delay information has become readily available, which can help decrease unknown parameters’ correlation. This study proposes a double-augmentation PPP approach with accelerated convergence by tightly integrating the LEO/atmosphere-augmented information. The GNSS observations in both mid-latitude and low-latitude areas, and simulated LEO observations under a Walker/polar mixed constellation, are used to validate the double-augmentation PPP approach. Test results in both areas indicate that the double-augmentation PPP can converge within 0.8 min, improving the convergence time by over 73%, and over 83% compared to the LEO-only augmented PPP and atmosphere-only augmented PPP.
1. Introduction
The Global Navigation Satellite System (GNSS) precise point positioning (PPP) technique has been widely used due to its high accuracy, low cost, and flexible operation [1,2]. Nevertheless, its convergence time usually takes tens of minutes, which limits its applications, especially in the navigation field [3]. There are two main reasons for this slow convergence. On the one hand, GNSS satellites’ spatial geometry change is too slow due to higher GNSS orbit altitude [4]. On the other hand, atmospheric delay parameters need to be estimated due to a lack of accurate atmospheric delay corrections, leading to over-parameterization and simultaneously increasing the parameters’ correlation [5]. Although a dual-frequency ionosphere-free combination can be applied to remove most effects of the ionospheric delay instead of direct estimation as unknowns, it sacrifices the number of usable observations. Fortunately, the emergence of Low Earth Orbit (LEO) satellites provides an opportunity to speed up the PPP convergence. The orbit altitudes of the LEO satellites are typically between 300 and 2000 km [6], which facilitates the quick variation of the satellites’ geometric distribution [7]. Also, LEO satellites can increase the redundancy of observation data and improve the integrity of the navigation system [8]. In addition, regional GNSS tracking networks have become commonly available, which can be utilized to generate precise atmospheric delay information at the user station. Both the LEO- and atmosphere-augmented information contribute to speeding up the PPP convergence.
Recently, some LEO systems have been rapidly developing, like the Iridium system, SpaceX, OneWeb, Hongyun, and Hongyan systems [9]. In addition, some research institutions have attempted to launch LEO satellites, such as Luojia-1 from Wuhan University, China. LEO-augmented multi-GNSS PPP has been widely investigated in recent years. Ke et al. [10] performed the GPS/LEO combined PPP and concluded that LEO satellites can accelerate the PPP convergence and improve its accuracy. They also compared the GPS/LEO combination with the GPS/GLONASS combination, and the results demonstrate that the LEO satellites contribute more to improving the GPS PPP performance than the GLONASS satellites. Ge et al. [11,12,13] proposed the concept of the LEO-Enhanced Global Navigation Satellite System (LeGNSS), in which the LEO satellites receive GNSS signals and simultaneously transmit navigation signals to ground users. With the augmentation of a simulated Iridium constellation with 66 LEO satellites, the GNSS PPP convergence time can be reduced to 5 min. Ma et al. [4,14] pointed out that the hybrid LEO constellation outperformed a single LEO constellation in augmenting GNSS PPP, and the PPP convergence time can be reduced to less than 3 min when the LEO satellites approach a saturation number of 192. Xu et al. [15] comprehensively analyzed the effect of the LEO-augmented GNSS PPP in challenging environments, and the results show that the addition of the LEO satellites can significantly decrease the initial convergence and reconvergence time of GNSS PPP in complex environments.
The atmosphere-augmented PPP method has been widely applied in the PPP-RTK. Wabbena et al. [16] first proposed the concept of PPP-RTK, which combines the PPP and Real-Time Kinematic (RTK) technique and provides a centimeter-accuracy real-time positioning service. In the PPP-RTK, the reference station network infrastructure is used to extract precise atmospheric delay information at each station and then disseminate correction information to users, thus improving the positioning performance at the user station [17]. Nadar et al. [18] investigated the positioning performance of the multi-GNSS PPP-RTK using Curtin University’s PPP-RTK data processing platform, and the results indicated that the PPP-RTK technique based on a large network of reference stations can achieve a convergence time within 15 min. When the PPP-RTK is implemented based on a small network of reference stations, the convergence time can be reduced to less than 2 min. Although the PPP-RTK method can accelerate convergence, the stability of its positioning performance is quite dependent on the data service quality from the reference stations.
As stated above, the existing research mainly focuses on standalone LEO or atmosphere augmentation. Although the PPP convergence time has been significantly decreased by a single augmentation, the convergence performance still needs further improvement. Recently, Hong et al. [19] attempted to augment PPP-RTK with LEO satellites, and the results indicated that the first fixation time of the ambiguities in the PPP-RTK can be significantly shortened. Inspired by this, we propose a tightly combined LEO/atmosphere double-augmentation PPP approach to improve PPP convergence performance.
This paper is outlined as follows. The LEO/atmosphere double-augmentation PPP approach is presented in Section 2. The LEO constellation design and data simulation are presented in Section 3. The double-augmentation PPP approach is evaluated in Section 4. Finally, some conclusions are drawn in Section 5.
2. LEO/Atmosphere Double-Augmentation PPP Approach
In this section, a tightly combined LEO/atmosphere double-augmentation PPP approach is presented. In this approach, the atmosphere-augmented LEO and the atmosphere-augmented GNSS are integrated to perform PPP. The observation equations of the LEO/atmosphere double-augmentation PPP are expressed as follows:
where the superscripts and denote a GNSS satellite and an LEO satellite, respectively. and represent code and phase observations in meters, respectively. The subscript denotes the frequency number. is the geometric distance between the receiver and the satellite in meters. refers to the speed of light in meters per second. and are the receiver clock offset and the satellite clock offset in seconds, respectively. represents the inter-system bias (ISB) with respect to GPS. is the ionospheric delay on in meters. represents the zenith tropospheric delay, denotes the tropospheric mapping function. represents the carrier-phase ambiguity and is the carrier-phase wavelength. is the code hardware delay in meters at both the receiver and satellite sides. is the phase hardware delay at both the receiver and satellite sides. The equations of and denote the pseudo-observables of the zenith tropospheric delay and single-difference slant ionospheric delay between satellites, respectively. The right side of the equations represents the parameters to be estimated. is the coefficient matrix for ionospheric parameters.
To remove the hardware delay at the receiver side, the single-difference slant-path ionospheric delay between satellites is extracted using multiple reference stations [20]. Simultaneously, the zenith tropospheric delay is estimated at each reference station. Afterwards, the extracted ionospheric and tropospheric delays are interpolated to obtain precise atmospheric delay information at the user station using the Modifications Linear Combination Method (MLCM) [17]. The acquired single-difference ionospheric delay and zenith tropospheric delay for both GNSS and LEO satellites are used as pseudo-observables to constrain the atmospheric parameters in Equation (1).
After applying precise satellite orbit and clock corrections, the residual orbit and clock errors are considered as random errors. The hardware delay at the satellite side is corrected by the differential code bias (DCB) data, and the hardware delay at the receiver side is absorbed by the receiver clock offset, ambiguity parameters, and ionospheric parameters. The other errors that need to be considered in PPP have been well-described in kinds of literature such as Kouba and Héroux [2]. After linearizing in Equation (1), the unknown parameters include three-dimensional position coordinates, receiver clock offset, ISB, ambiguity, slant ionospheric delay, and zenith tropospheric delay. A Kalman filter is employed for parameter estimation in the LEO/atmosphere double-augmentation PPP. The GNSS code observation precision is set to 0.3 m, while the carrier-phase observation precision is set to 0.002 m. As for the LEO observation, a weight of 1:1 is assigned between GPS and LEO satellites. The precision for the pseudo-observables of ionospheric and tropospheric delays are set as 0.1 m and 0.03 m, respectively [21]. The receiver clock offset is modeled as white noise. The ISB, ionospheric delay, and tropospheric delay are modeled as random walk (RW) processes, while the ambiguity and static receiver coordinates are considered as constants [22,23].
3. LEO Constellation and Data Simulation
So far, most LEO constellations for navigation are still in the stage of feasibility demonstration or experimental verification [15]. As a typical representative, the Centispace LEO constellation has been designed and deployed by the Future Navigation company as a navigation augmentation system of BDS. The Centispace LEO constellation consists of 12 inclined Walker orbit planes and 3 polar orbit planes, with orbital altitudes of 975 km and 1200 km and inclinations of 55° and 85° to the equatorial plane, respectively [24]. Each orbit plane is evenly populated with 10 LEO satellites. To date, two test satellites have been successfully launched. The company expects to launch 150 LEO satellites and complete the ground infrastructure construction in the coming years. This study simulates a LEO constellation following the Centispace LEO design. The simulated LEO constellation is shown in Figure 1, where the red line represents the polar orbit and the green line represents the Walker orbit.
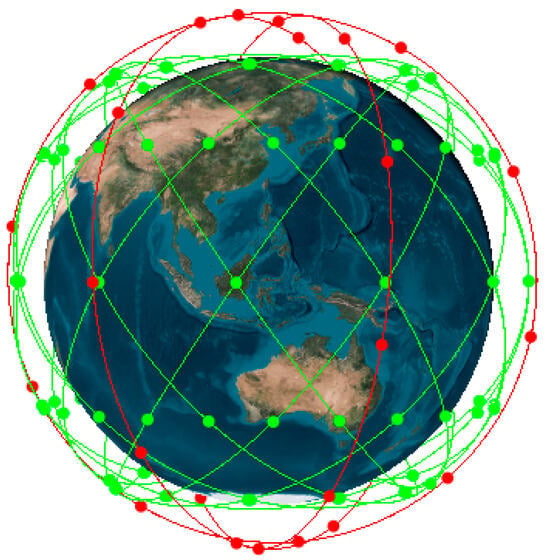
Figure 1.
Spatial configuration of simulated LEO constellation.
Due to the lack of precise LEO satellite orbit and clock offset data as well as ground observation data, this study simulates precise LEO data and observations. For the LEO satellite orbit simulation, the initial orbit elements of the LEO satellites are first determined according to the designed constellation configuration. Then, the daily orbit of the LEO satellites is obtained through dynamics integration. For the LEO satellite clock simulation, the GPS satellite clock offset products provided by the International GNSS Service (IGS) are used as the clock offsets of the LEO satellites. To make the simulated precise data more practical, different magnitudes of colored noises are added to the LEO satellites’ orbital components and clock offsets. As for the ground observation simulation, the geometric distance between the satellites and stations is first calculated, and then various errors are added to the distance value, such as the satellite orbital errors, satellite clock offsets, ionospheric and tropospheric delays, receiver clock offset, and the other errors that need to be specially considered in PPP [2]. Considering that most of the commonly used GNSS receivers can receive GPS L1 and L2 frequencies, the carrier frequencies of GPS L1 at 1575.42 MHz and L2 at 1227.60 MHz are used for the LEO satellites in this experiment. The ionospheric delay is extracted from the IGS global ionospheric maps (GIM) file. The tropospheric delay is simulated as a sum of the dry delay and the wet delay. The dry delay is generated using the Saastamoinen model [25], while the wet delay is from the parameter estimates in GNSS PPP. One can refer to Li et al. [4] for the specific error simulation methods. Given the complexity of practical observation, GPS code and phase observation residuals in PPP processing with actual observations are added to the simulated LEO observations. We summarize the scenario for simulating LEO observations in Table 1.

Table 1.
LEO observation simulation scenario.
4. Experimental Results and Analysis
In this section, the simulated LEO constellation is first used to evaluate the LEO-augmented PPP performance. Subsequently, GNSS stations in two areas are used to assess the LEO/atmosphere double-augmentation PPP performance.
4.1. LEO-Augmented GNSS PPP
To assess the LEO-augmented GNSS PPP performance, GNSS observations were collected on 21 October 2022 from 14 globally distributed MGEX (Multi-GNSS Experiment) stations, as shown in Figure 2. LEO observations are simulated at the same observation time as GNSS. Given the fast motion of LEO satellites, both GNSS and LEO observations are sampled at an interval of 1 s. The satellite elevation mask angle is set to 7°.
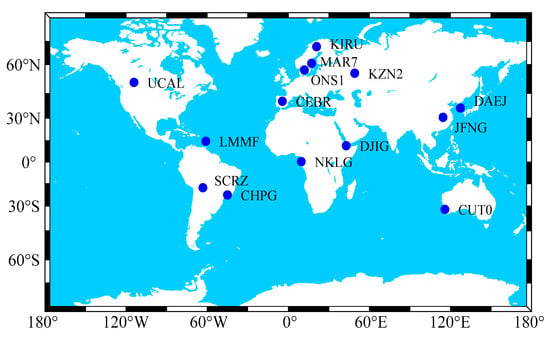
Figure 2.
Geographical distribution of GNSS stations.
The number of visible satellites and PDOP are important indices to determine the positioning performance. Figure 3 shows the satellite number of the LEO satellites in a global distribution, indicating that the simulated LEO constellation achieves a global quadruple coverage. Figure 4 illustrates the number of visible satellites and PDOP for a LEO-augmented GNSS. The top two subplots in Figure 4 represent the number of visible satellites for a quad-constellation GNSS of GPS, GLONASS, Galileo and BDS, and GNSS/LEO combination, respectively. The bottom two subplots in Figure 4 indicate the corresponding PDOP values. From Figure 4, the number of visible satellites and satellite geometry are significantly improved after adding the LEO constellation. Specifically, the average number of visible satellites increases from 28 to 36 and the PDOP decreases from 1.1 to 0.7.
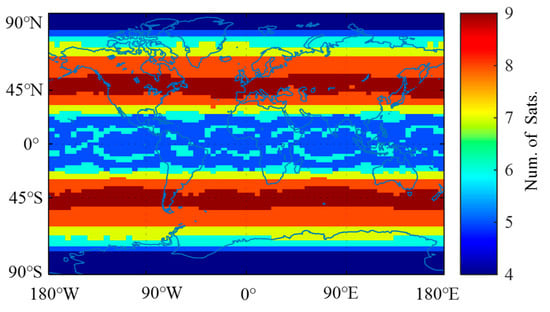
Figure 3.
Visible LEO satellite distribution.
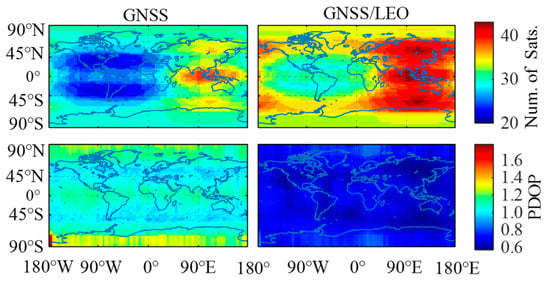
Figure 4.
Number of visible satellites and PDOP for LEO-augmented GNSS.
Five constellation combination scenarios, namely GPS, GPS/BDS, GPS/BDS/Galileo, GPS/GLONASS/BDS/Galileo, and GPS/GLONASS/BDS/Galileo/LEO are employed for PPP processing. Taking MAR7 and JFNG stations as an example, Figure 5 shows the positioning errors at a session length of two hours for the five combination scenarios. It can be found that the positioning accuracy and convergence time are improved, but at a slight degree, with the addition of GNSS constellations. By contrast, the inclusion of LEO satellites considerably accelerates the PPP convergence. In all cases, the LEO-augmented positioning solution converges to a stable value more quickly than the other scenarios, as seen from the magenta curves.
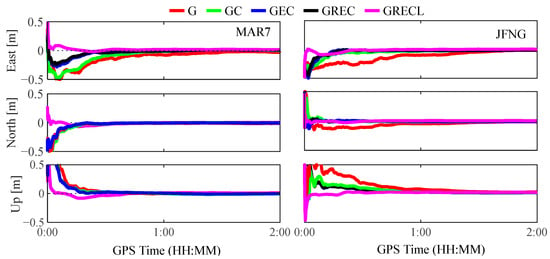
Figure 5.
LEO-augmented GNSS PPP errors at MAR7 and JFNG stations, ‘GRECL’ denotes GPS, GLONASS, Galileo, BDS, and LEO.
Table 2 reveals the RMS statistical results of the PPP convergence time and its positioning accuracy on 21 October 2022 for 168 datasets at 14 stations in 12 sessions, with a session length of 2 h. The convergence time is defined as the minimum time required for the 3D position errors to be less than 0.1 m and remain within 0.1 m for at least 10 min. Compared with GPS, the convergence time for quad-constellation GNSS is reduced from 27.5 min to 16.2 min. With LEO augmentation, the convergence time is further decreased to 3.5 min, indicating a significant gain from the LEO satellites.

Table 2.
Convergence time and positioning accuracy for LEO-augmented GNSS PPP.
4.2. LEO/Atmosphere Double-Augmentation PPP
4.2.1. Data Description
The LEO augmentation is different from the atmosphere augmentation. The former augments PPP by adding observation information, while the latter augments PPP by mitigating atmospheric errors. The double-augmentation approach proposed in this paper simultaneously uses observation information and atmospheric error-correction information to augment PPP. To evaluate the effectiveness of the double-augmentation PPP approach, three-day datasets at 14 stations were collected on 21–23 October 2022. Each day is divided into eight sessions with a session length of 3 h, and observations in a total of 24 sessions were processed. Among the 14 stations, seven stations are located in France, a mid-latitude area with a latitude range of 44°–46°, and the other seven stations are located in China, a low-latitude area with a latitude range of 27°–29°. The distribution of the GPS stations in the two areas is shown in Figure 6, in which five blue triangle points serve as reference stations for extracting atmospheric information in each area, while two red five-pointed star points are used as mobile stations to validate the double-augmentation PPP approach.
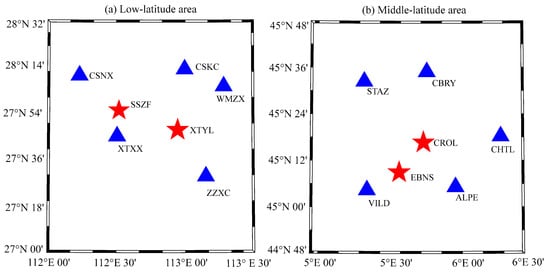
Figure 6.
Geographical distribution of regional GPS stations.
The average distances between stations in the mid-latitude and low-latitude areas were about 40 km and 50 km, respectively. Since multi-GNSS observations are unavailable in the two areas, only GPS data is used in this experiment. The LEO observations are simulated following the strategy depicted in Section 3. The sampling interval for all datasets is set to 1 s, and the satellite elevation mask angle is set to 7°. The reference station coordinates are calculated using Bernese 5.2 software by differential mode.
4.2.2. Results and Analysis
In the LEO/atmosphere double-augmentation PPP, the accuracy of the obtained ionospheric and tropospheric delay information at the user station is vital to determine the PPP convergence performance. Figure 7 shows the zenith tropospheric delay errors at the SSZF and EBNS stations, which are obtained through the interpolated tropospheric delay values from the reference station, minus the extracted tropospheric delay values at the mobile stations. It can be observed that the zenith tropospheric delay errors vary within 3 cm. Their RMS values at the SSZF and EBNS stations are 0.4 cm and 0.9 cm, respectively.
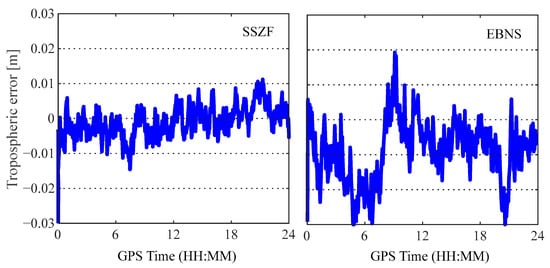
Figure 7.
Errors of the obtained tropospheric delay at mobile stations.
Similarly, Figure 8 displays the inter-satellite single-difference slant ionospheric delay errors for GPS and LEO satellites at the SSZF and EBNS stations. Different colors represent different satellites. The ionospheric delay errors vary within 0.2 m and are less than 0.1 m most of the time. The RMSs of ionospheric delay errors for GPS at SSZF and EBNS stations are 3.9 cm and 3.6 cm, respectively, while the RMSs of ionospheric delay errors for LEO at SSZF and EBNS stations are 3.5 cm and 3.1 cm, respectively. In summary, the obtained tropospheric and ionospheric delay accuracy at the mobile stations is comparable to the atmospheric accuracy level in PPP-RTK [19].
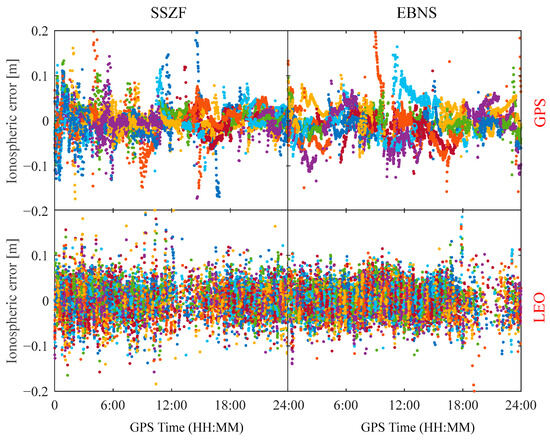
Figure 8.
Errors of the obtained slant ionospheric delay at mobile stations.
To validate the proposed tightly integrated double-augmentation PPP approach, we compare it with the loosely integrated double-augmentation PPP approach in which the atmospheric augmentation information is only applied to GNSS satellites. Figure 9 shows the positioning errors for the two double-augmentation PPP processing scenarios at SSZF and EBNS stations. The blue curves represent the tightly integrated scenario, while the red curves represent the loosely integrated scenario.
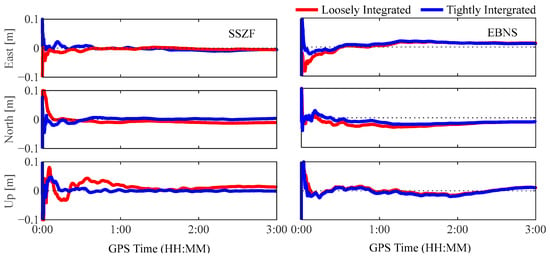
Figure 9.
Positioning errors for two different double-augmentation PPP processing scenarios.
As seen from the two curves, the blue curves are closer to the zero axis and vary more steadily, especially in the filter convergence phase, which suggests that the simultaneous GPS/LEO atmospheric corrections have a more significant augmentation effect with smaller positioning errors in the East, North, and Up coordinate components when compared to the GPS-only atmospheric augmentation. To provide a more specific illustration of the positioning performance of the two double-augmentation methods, Figure 9 is taken as an example to analyze the PPP convergence time and positioning accuracy. For the tightly integrated solution, the convergence can be achieved at 0.2 min with a 3D RMS error of 0.01 m after convergence. By contrast, the loosely integrated solution needs a slightly longer convergence time of 0.5 min, with a 3D RMS error of 0.015 m after convergence. It can be easily understood that the tightly integrated double-augmentation PPP outperforms the loosely integrated double-augmentation PPP, since the atmosphere augmentation is made for both GPS and LEO.
To further validate the advantage of the tightly integrated double-augmentation PPP, its positioning performance is evaluated by comparing it with atmosphere-only augmented-PPP and LEO-only augmented-PPP approaches. Figure 10 shows the positioning errors at the low-latitude station SSZF and mid-latitude station EBNS on 21 October 2022 for three different processing scenarios. The red, green, and blue curves represent the atmosphere-only, LEO-only, and atmosphere/LEO-augmented scenarios. All three augmented PPP solutions can reach stable values very quickly. Compared with the atmosphere-only or LEO-only augmented scenarios, the double-augmentation PPP solution shows smaller position errors, especially in the PPP convergence phase, and it converges more quickly in all three coordinate components at both stations. Figure 11 displays the statistical distribution of convergence time for the 48 datasets at the two stations over three days for each area. According to the statistical results, the double-augmentation PPP solutions, at a percentage of 68%, can converge within 1 min. By contrast, this percentage is much smaller when the atmosphere-only or the LEO-only augmentation is made.
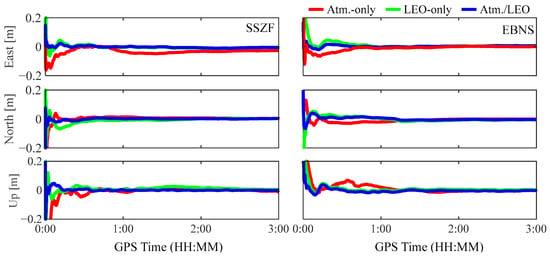
Figure 10.
Positioning errors for different PPP-processing scenarios on 21 October 2022.
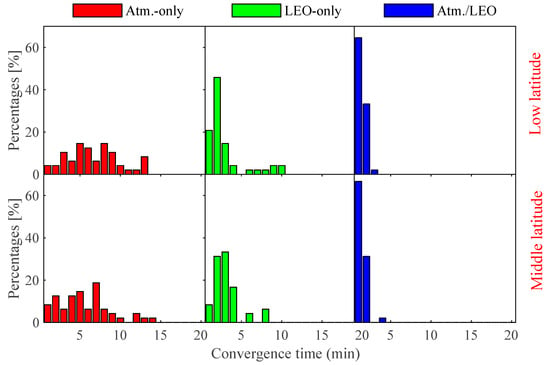
Figure 11.
Distribution of convergence time for different PPP-processing scenarios.
Table 3 provides the RMS statistical results of convergence time and positioning accuracy for three different processing scenarios. It is worth noting that the traditional GPS PPP convergence times without augmentations for the low- and mid-latitude regions are 22.4 min and 29.5 min, respectively. Compared to the traditional GPS PPP, all three augmentation strategies significantly improve the PPP performance. In the low- and mid-latitude areas, the atmosphere-only augmented PPP can converge within 5.1 min and 6.2 min, respectively, and the LEO-only augmented PPP can converge within 3.2 min and 2.9 min, respectively. By contrast, the double-augmentation PPP can converge within 0.8 min in both areas. Compared with the atmosphere-only and LEO-only augmentations, the convergence time is reduced by over 83% and 73% in both areas, respectively. In addition, the positioning accuracy also shows an obvious improvement in the three coordinate components. The maximum improvement in the horizontal directions can be up to 1.3 cm.

Table 3.
RMS statistics of the convergence time and positioning errors.
5. Conclusions
This study proposes a tightly integrated double-augmentation PPP approach with accelerated convergence by jointly using LEO/atmosphere augmentation information. Three-day GPS datasets at 14 stations in low- and mid-latitude areas, along with simulated LEO observations, are used to evaluate the effectiveness of the double-augmentation PPP approach. Experimental results indicate that the addition of LEO satellites can significantly reduce PPP convergence time on a global scale. In the low- and mid-latitude areas, the convergence time for the atmosphere-only augmented PPP is 5.1 min and 6.2 min, respectively, and the convergence time for the LEO-only augmented PPP is 3.2 min and 2.9 min, respectively. By contrast, the tightly integrated double-augmentation PPP method can further reduce the convergence time to 0.8 min. Compared to the atmosphere-only and LEO-only augmentation, the convergence time is reduced by over 83% and 73% in both areas, respectively. In addition, the positioning accuracy also shows an obvious improvement in the three coordinate components. It should be noted that the conclusions are drawn from experimental data analysis based on actual measured GNSS and simulated LEO datasets. Further validation is needed when the actual measured LEO observations are available.
Author Contributions
Formal analysis, B.H.; supervision, C.C. and L.P.; validation, B.H.; writing—original draft, B.H. and C.C.; writing—review and editing, B.H., C.C. and L.P. All authors have read and agreed to the published version of the manuscript.
Funding
The financial support from the National Key Research and Development Program of China (No. 2020YFA0713501), National Natural Science Foundation of China (No. 42174040), and State Key Laboratory of Geo-Information Engineering (No. SKLGIE2021-Z-2-1) is greatly appreciated.
Data Availability Statement
The precise GNSS satellite orbit and clock products as well as GNSS observation data are available at https://cddis.nasa.gov/archive/gnss/.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J.; Hérous, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Bahadur, B.; Nohutcu, M. Comparative analysis of MGEX products for post-processing multi-GNSS PPP. Measurement 2019, 145, 361–369. [Google Scholar] [CrossRef]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2019, 93, 749–764. [Google Scholar] [CrossRef]
- Wu, G.; Chen, J.; Wu, X.; Hu, J. Modeling and assessment of regional atmospheric corrections based on undifferenced and uncombined PPP-RTK. Acta Geod. Cartogr. Sin. 2020, 49, 1407. [Google Scholar]
- Zhang, X.; Ma, F. Review of the development of LEO navigation-augmented GNSS. Acta Geod. Cartogr. Sin. 2019, 48, 1073. [Google Scholar]
- Zhao, Q.; Pan, S.; Gao, C.; Gao, W.; Xia, Y. BDS/GPS/LEO triple-frequency uncombined precise point positioning and its performance in harsh environments. Measurement 2020, 151, 107216. [Google Scholar] [CrossRef]
- Joerger, M.; Gratton, L.; Pervan, B.; Cohen, C.E. Analysis of Iridium-augmented GPS for floating carrier phase positioning. Navigation 2010, 57, 137–160. [Google Scholar] [CrossRef]
- Su, M.; Su, X.; Zhao, Q.; Liu, J. BeiDou augmented navigation from low earth orbit satellites. Sensors 2019, 19, 198. [Google Scholar] [CrossRef]
- Ke, M.; Lv, J.; Chang, J.; Dai, W.; Tong, K.; Zhu, M. Integrating GPS and LEO to accelerate convergence time of precise point positioning. In Proceedings of the 7th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial assessment of precise point positioning with LEO enhanced global navigation satellite systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Ge, M.; Nie, L.; Shen, Y.; Schuh, H. LEO enhanced Global Navigation Satellite System (LeGNSS) for real-time precise positioning services. Adv. Space Res. 2019, 63, 73–93. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Nie, L.; Ge, M.; Schuh, H. LEO constellation optimization for LEO enhanced global navigation satellite system (LeGNSS). Adv. Space Res. 2020, 66, 520–532. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, X.; Li, X.; Cheng, J.; Guo, F.; Hu, J.; Pan, L. Hybrid constellation design using a genetic algorithm for a LEO-based navigation augmentation system. GPS Solut. 2020, 24, 62. [Google Scholar] [CrossRef]
- Li, M.; Xu, T.; Guan, M.; Gao, F.; Jiang, N. LEO-constellation-augmented multi-GNSS real-time PPP for rapid re-convergence in harsh environments. GPS Solut. 2022, 26, 29. [Google Scholar]
- Wabbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 2584–2594. [Google Scholar]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Nadarajah, N.; Khodabandeh, A.; Wang, K.; Choudhury, M.; Teunissen, P.J.G. Multi-GNSS PPP-RTK: From large-to small-scale networks. Sensors 2018, 18, 1078. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Tu, R.; Zhang, P.; Zhang, R.; Han, J.; Fan, L.; Wang, S.; Lu, X. GNSS rapid precise point positioning enhanced by low Earth orbit satellites. Satell. Navig. 2023, 4, 11. [Google Scholar] [CrossRef]
- Hong, J.; Tu, R.; Zhang, S.; Li, F.; Liu, M.; Lu, X. Inter-Satellite Single-Difference Ionospheric Delay Interpolation Model for PPP-RTK and Its Positioning Performance Verification. Remote Sens. 2022, 14, 4153. [Google Scholar] [CrossRef]
- Li, P.; Cui, B.; Hu, J.; Liu, X.; Zhang, X.; Ge, M.; Schuh, H. PPP-RTK considering the ionosphere uncertainty with cross-validation. Satell. Navig. 2022, 3, 10. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar]
- Cai, C.; Gao, Y.; Pan, L.; Zhu, J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar]
- Yang, L. The Centispace-1: A LEO Satellite-Based Augmentation System. In Proceedings of the 14th Meeting of the International Committee on Global Navigation Satellite Systems, Bengaluru, India, 8–13 December 2019. [Google Scholar]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).