Review of the Monothematic Series of Publications Concerning Research on Statistical Distributions of Navigation Positioning System Errors

Abstract

This review presents the main results of the author’s study, obtained as part of the post-doctoral (habilitation) dissertation entitled “Research on Statistical Distributions of Navigation Positioning System Errors”, which constitutes a series of five thematically linked scientific publications. The main scientific aim of this series is to answer the question of what statistical distributions follow the position errors of navigation systems, such as Differential Global Positioning System (DGPS), European Geostationary Navigation Overlay Service (EGNOS), Global Positioning System (GPS), and others. All of the positioning systems under study (Decca Navigator, DGPS, EGNOS, and GPS) are characterised by the Position Random Walk (PRW), which means that latitude and longitude errors do not appear randomly, being a feature of the normal distribution. The research showed that the Gaussian distribution is not an optimal distribution for the modelling of navigation positioning system errors. A higher fit to the 1D and 2D position errors was exhibited by such distributions as beta, gamma, and lognormal. Moreover, it was proven that the Twice the Distance Root Mean Square (2DRMS(2D)) measure, which assumes a priori normal distribution of position errors in relation to latitude and latitude, was smaller by 10–14% than the position error value from which 95% fixes were smaller (it is known as the R95(2D) measure).

1. Introduction

Positioning accuracy relates to the statistical degree of the determined coordinates with the real values or the values assumed to be actual. The position accuracy measure is its error that can be assessed in relation to any given dimension of plane or space. This is undoubtedly one of the main criteria for assessing navigation positioning systems, which determines, to a large extent, their quality [1].

In various types of navigation, a view has been formed that the measurement error distributions of instruments and systems have the normal (Gaussian) distribution. Obviously, this thesis also applies to position errors. The assumption that the navigation positioning system error distribution has the normal distribution is commonly found in scientific publications [2,3], books, and monographs [4,5,6], as well as in norms and standards [1,7,8,9,10,11,12]. A detailed analysis of the navigation literature also leads to the conclusion that many publications have ignored the issue of the consistency between the navigation positioning system errors and the normal distribution. One analysis was a publication by Frank van Diggelen [3], who concluded that the Global Positioning System (GPS) positioning accuracy, calculated based on the Twice the Distance Root Mean Square (2DRMS(2D)) measure, which assumes a priori normal distribution of position errors in relation to the latitude (φ) and longitude (λ), is lower by 10% than the position error value from which 95% fixes are smaller (it is known in the literature as the R95(2D) measure). Van Diggelen demonstrated that the R95 measure reflects the statistical nature of the navigation positioning system errors better than the 2DRMS measure. This author also formulated similar conclusions about the Differential Global Positioning System (DGPS) [3]. The studies I have conducted on different navigation positioning systems (DGPS, European Geostationary Navigation Overlay Service (EGNOS) and GPS) [13], multi-Global Navigation Satellite System (GNSS) solutions, and GNSS geodetic networks [14,15] confirm the existence of the discrepancies mentioned by van Diggelen, and, depending on the positioning solution, amount to 13–16%. In a 1993 document fundamental for the GPS [16], one can see that the statistical distributions of the φ, λ, and h (separately) error Probability Density Functions (PDF) differ significantly from the Gaussian statistic. One-dimensional error distributions are asymmetrical. Moreover, the concentration of errors is also noticeable in the vicinity of the average value that is clearly greater than for a formal distribution (Figure 1a–c) [17].

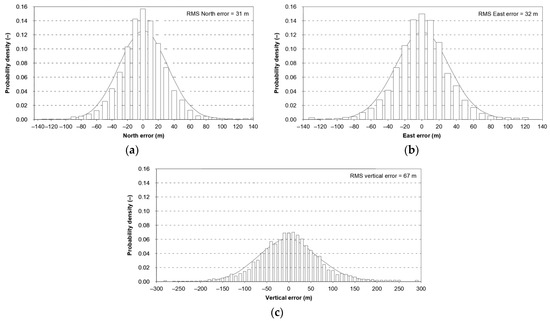
Figure 1. A comparison of the empirical data of the GPS error in the directions of N-S (a), E-W (b), and h (c) with the theoretical normal distribution [17].

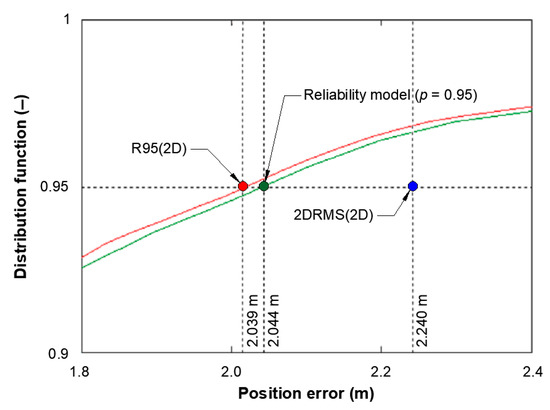
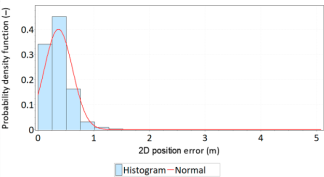
The differences in φ and λ error distributions in relation to normal distributions, presented in Figure 1a,b, undoubtedly lead to considerable differences in the consistency between the 2D position error and the chi-squared distribution, which is a commonly applied 2D position error distribution model for navigation systems [6,18]. The document [16] analysed the 2D position error that was determined in two ways (Figure 2). The theoretical value (83 m, p = 0.95) was calculated based on the 2DRMS measure (assuming that the normal distribution of φ and λ errors), while the empirical value (64 m, p = 0.95) was determined when searching for such an error value from which 95% fixes would be greater (R95 measure). It should be stressed that the difference in the same quantity (position error at p = 0.95), calculated by two different methods, amounted to 19 m. Hence, it is difficult to agree with the view that the application of the 2DRMS measure to assess the navigation positioning system accuracy is correct [17].

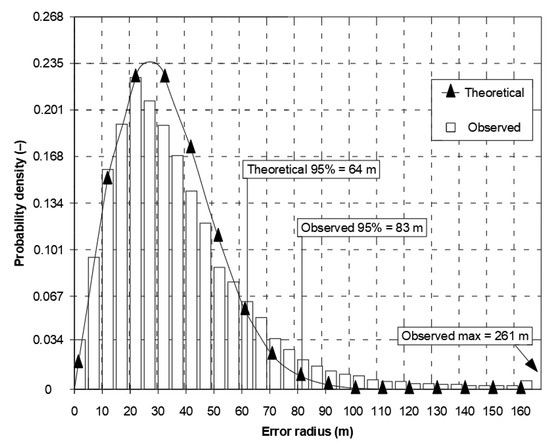
Figure 2. A comparison of the empirical data of the GPS 2D position error with the theoretical chi-squared distribution [17].

Therefore, before proceeding with the calculation of 1D and 2D position errors, it is necessary to conduct consistency analysis between empirical position errors and the normal distribution. Nevertheless, it should be noticed that for large measurement campaigns (at least one hundred thousand fixes), outliers will almost certainly emerge, which can result in the thesis about the consistency between the sample and normal distribution being rejected. This can also lead to the false assumption that position errors do not correspond to a Gaussian distribution. Hence, the determination of the sample size that will ensure high reliability in inferring whether the empirical data are consistent or not with the theoretical distribution is a crucial issue that has not been previously described in the navigation literature.

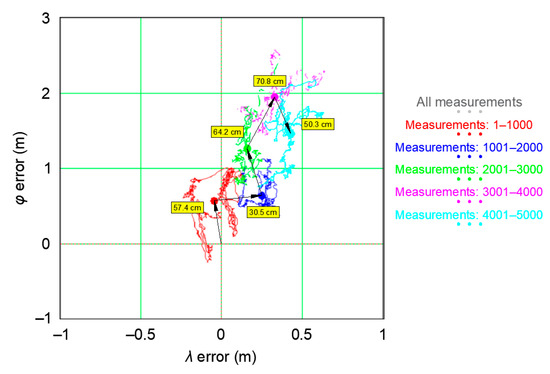
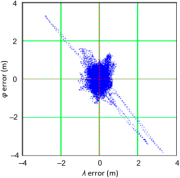
To make correct statistical inferences about a particular phenomenon, one needs to understand the nature of the phenomenon in depth. As regards the determination of coordinates in a navigation positioning system, one can observe the process of a position’s “wandering”. It manifests itself in the fact that the successive positions of a stationary receiver do not emerge in a random manner in relation to the average value (no intercorrelation of measurements), as is the case with the commonly applied normal distribution, but in close vicinity of the previous position. It seems by its very nature to resemble the random walk defined by Karl Pearson in 1905 [19]. A common feature of Pearson’s process and the process of positioning in navigation systems is the “random walk” of the position’s coordinates, which is why the term has been introduced into analyses. The process of a position’s “wandering” was defined in this series as the “Position Random Walk” (PRW). Its nature is best reflected in Figure 3, which shows position error distributions for three different navigation systems recorded by the receiver in static measurements.

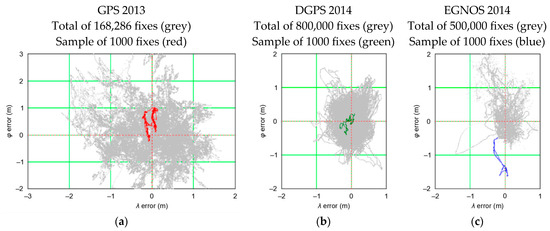
Figure 3. Examples of a position’s “wandering” for the system’s GPS (a), DGPS (b), and EGNOS (c) [20].

Figure 3 shows that the position coordinates recorded by navigation system receivers move along “paths”, which are not random in their nature. This means that the position coordinates do not “emerge” in a random manner around the average coordinate values (0,0). What is more, the process of a position’s “wandering” results in the position error value, calculated on the basis of a sample of 1000 fixes, differing significantly from the position error value determined for the whole population (grey colour). Hence, at this point, the obvious question arises: what length should the sample be in order for its results (position errors) to be consistent with the actual values for which the real accuracies of navigation positioning systems will be considered? In the context of the sample size, it will be reasonable to raise further research questions: is the size of the representative sample determined by the positioning system? Is it related to its accuracy? Is it constant for all positioning systems? It should be stressed that the world literature on navigation positioning systems has so far failed to provide answers to these questions [20].

Summarising the scientific reasons of this series of publications, it should be noted that they are derived from the following issues:

• Adopting a priori the normal distribution as the statistical model of 1D errors;
• The validity of the application of the 2DRMS measure to determine the navigation positioning system accuracy (2D);
• The occurrence, in the process of the position coordinate determination, of the PRW phenomenon resulting in the need to determine the length (number of measurements) of the representative sample;
• The determination of the representative sample length and its relationship with the positioning system type and its accuracy.

In view of the scientific doubts indicated, the following aims of the monothematic series of publications entitled “Research on Statistical Distributions of Navigation Positioning System Errors” [17,20,21,22,23] should be considered:

• The development of a method enabling the determination of the navigation positioning system representative sample length from the perspective of assessing its accuracy [20];
• The determination of consistency between empirical position errors for selected systems (GPS, DGPS, and EGNOS) and typical statistical distributions based on long-term measurement campaigns (1–2 million fixes) [17];
• The development of the author’s original method (reliability modelling of stationary processes with renewal) enabling the calculation of a navigation system position error value based on the empirical data [21];
• The determination of differences between the position accuracy measures calculated using the 2DRMS and R95 for the GPS [22];
• The performance of statistical analyses to determine the relation between the 2D position error and the Horizontal Dilution Of Precision (HDOP) values for the GPS.

The above-mentioned aims developed the logical and thematic structure for the successive articles in the series and had an effect on the selection of research methods. In the series of publications that constitute the post-doctoral (habilitation) dissertation, the following research methods were applied:

• Statistical testing of empirical data—employed to determine the statistical distributions with the best fit to the empirical data (navigation positioning systems’ 1D and 2D position errors) [17,21,22,23]. Moreover, the method was used to calculate selected measures of position error statistical distributions [17,21,22] and the HDOP [23];
• Mathematical modelling—enabled the determination of numerical measures describing the process of a position’s “wandering” occurring in navigation systems [20], the calculation of the length of the positioning system representative sample [20], the development of the author’s original method enabling the determination of the navigation system’s position error value with a probability of 0.95 [21], and the determination of differences between the accuracy measures (2DRMS and R95) for positioning systems [21,22];
• Experimental research—enabled the determination of position error statistics. The publication series used the results of seven long-term measurement campaigns: Decca Navigator 1993 [20], DGPS 2006 [17] and 2014 [20,21], EGNOS 2006 [17] and 2014 [20,21], as well as GPS 2013 [20,21] and 2021 [22,23]. It should be noted that the author personally participated in the surveys conducted in the years 2013, 2014, and 2021, while the results of archive measurements conducted in 1993 and 2006 are taken from research projects implemented at the Institute of Navigation and Marine Hydrography of the Polish Naval Academy in Gdynia under the supervision of Professor Zdzisław Kopacz. The results of these surveys were used with the permission of Professor Kopacz. All measurement campaigns were carried out in stationary mode, where the position coordinates of the fixed receiver were determined with centimetre accuracy using the geodetic method. In all surveys, position data were recorded as National Marine Electronics Association (NMEA) GGA messages with a frequency of 1 Hz. The receivers were set with a min. topocentric height amounting to 10° in order to prevent the multipath effect. Before processing the measurement data, erroneously recorded NMEA GGA messages were deleted. A single 1D or 2D position error was calculated as the difference between the coordinates recorded by the fixed receiver and those measured by the geodetic method;
• Interdependence analysis and inference—one of the main research methods applied in the publication series. The need for its use resulted from the range of the research questions raised, to which no comprehensive answers have been provided by the scientific literature on the subject. It should be stressed that despite the prior (before writing the first article) planning of the subject matter of individual publications in the series, it repeatedly appeared that the results obtained were surprising and inconsistent with the initial expectations. Therefore, based on the interdependence analysis and inference, it was necessary to modify the concept of the research and the subject of the successive articles.

This review presents the main results of the author’s study, obtained as part of the post-doctoral (habilitation) dissertation entitled “Research on Statistical Distributions of Navigation Positioning System Errors”, which constitutes a series of five thematically linked scientific publications. The main scientific aim of this series is to answer the question of what statistical distributions follow the position errors of navigation systems, such as DGPS, EGNOS, GPS, and others. It must be emphasised that the purpose of the whole series of publications is not to analyse the causes of PRW, such as ionospheric and tropospheric effects, multipath, and noise. The causes might be very complex and probably deserve a separate series of publications.

2. The Development of a Method Enabling the Determination of the Navigation Positioning System Representative Sample Length from the Perspective of Assessing Its Accuracy

This study used a two-day GPS measurement campaign of 2013, conducted at a frequency of 1 Hz using a stationary receiver located in Gdynia, Poland. During the surveys, 168,286 fixes were recorded. These data were used to assess the changes in the position coordinates resulting from the PRW process for five short sessions consisting of 1000 fixes. Each session was subjected to a separate statistical analysis. The distance calculated between the average 2D position coordinates from the successive sessions was adopted as the PRW process rate measure. Figure 4 shows four such distances marked with large dots. Moreover, the distance between the actual position of the stationary receiver and the average 2D position coordinate from the first session was marked.

Figure 4. Distances between the average 2D position coordinates $\overline{P}\left(S_N\right)$ calculated for five GPS sessions during the measurement campaign in 2013 [20].

Based on Figure 4, it can be concluded that the PRW phenomenon had an effect on the average 2D position coordinate ($\overline{P}\left(S_N\right)$) and the average latitude ($\overline{\phi }$) and longitude ($\overline{\lambda }$) calculated for each session. In relation with the fact, it makes sense to ask whether or not a session consisting of 1000 fixes is representative for drawing inferences about the measurement result dispersion. Hence, it was decided to compare the results of five sessions (1000 fixes) with the results of the whole campaign (168,286 fixes) (Table 1).

Table 1. Shift values in measurement results (φ and λ) and Root Mean Square (RMS) values for five sessions (1000 fixes) in relation to the results for the whole population (168,286 fixes) during the GPS measurement campaign in 2013 [20].

Measure	All Fixes (168,286)	S1—Red Session (1–1000)	S2—Blue Session (1001–2000)	S3—Green Session (2001–3000)	S4—Purple Session (3001–4000)	S5—Sky-Blue Session (4001–5000)	Mean from S1–S5
$\overline{\phi }$ shift	0.000 m	0.572 m	0.633 m	1.268 m	1.956 m	1.463 m	1.178 m
$\overline{\lambda }$ shift	0.000 m	−0.047 m	0.251 m	0.157 m	0.326 m	0.427 m	0.223 m
$\mathrm{Distance} \mathrm{of} \mathrm{point} \overline{P}\left(S_N\right)$ from the real coordinates (0, 0)	0.000 m	0.574 m	0.681 m	1.278 m	1.983 m	1.524 m	1.208 m
RMSφ	0.910 m	0.299 m	0.201 m	0.414 m	0.275 m	0.358 m	0.309 m
Session RMSφ vs. all measurements RMSφ (%)	100.00%	32.86%	22.12%	45.54%	30.26%	39.37%	34.03%
RMSλ	0.653 m	0.098 m	0.066 m	0.059 m	0.120 m	0.085 m	0.086 m
Session RMSλ vs. all measurements RMSλ (%)	100.00%	15.07%	10.09%	9.01%	18.36%	13.01%	13.11%

It should be noted that the standard deviation of 1D errors, calculated based on the sessions of 1000 fixes, was considerably smaller than those selected from the whole population (Table 1). Therefore, it should be concluded that survey sessions considerably underestimate the actual GPS position accuracy. The determination of the effect of 1D error standard deviations on the 2D position error with a probability of 0.68 (DRMS(p = 0.68)) can be expressed using the following formula:

$$DRMS\left(p=0.68\right)=\sqrt{RM{S}_{\phi }{}^2+RM{S}_{\lambda }{}^2}$$

(1)

where:

RMS_φ—RMS of the geodetic latitude;

RMS_λ—RMS of the geodetic longitude.

For example, if the values of RMS_φ and RMS_λ from five sessions (5000 fixes) were reduced by 65.97% (φ) and 86.89% (λ), respectively, in relation to the whole population (Table 1), then the DRMS value (p = 0.68) will decrease by:

$$DRMS\left(p=0.68\right)=\sqrt{{\left(65.97\%\right)}^2+{\left(86.89\%\right)}^2}=109.1\%$$

(2)

Therefore, it can be concluded that sessions comprising several thousand fixes are not representative of the determination of the GPS position accuracy.

Another question that clearly arises at this point is whether the PRW phenomenon occurs in other navigation positioning systems and what the distances are between the average 2D position coordinates for 1000 fixes. For the analyses, the surveys of the Decca Navigator and EGNOS were used. The detailed results of the study are presented in [20]. Based on these, it can be concluded that the more accurate the positioning system (EGNOS) is, the lower rate of the position’s “wandering” process will be.

Not only does the PRW process result in the lack of representativeness of short-term measurement sessions, but it also must call into question the statistical consistency between 1D errors and the theoretical normal distribution. For this reason, it was reasonable to conduct statistical testing on one of the samples (S₁) when using the Kolmogorov–Smirnov test (Table 2).

Table 2. Statistical testing of 1D errors from the sample S₁ for the GPS of 2013 [20].

Kolmogorov–Smirnov Test
φ Error	λ Error

The statistical testing demonstrated that the distributions of GPS 1D errors from sample S₁ were inconsistent with the normal distribution. Therefore, it should be concluded that making inferences about the GPS accuracy based on a session consisting of 1000 fixes yields false results. It is also worth asking an important question: how many measurements should a session take to make it representative? In order to answer this question, it was decided to conduct an experiment involving increasing the number of surveys, while simultaneously calculating the RMS and DRMS error values. A number of measurements will be sought for which the RMS and DRMS error values will be similar to the actual ones, i.e., those calculated from the entire campaign (168,286 fixes). Figure 5 presents standard deviations calculated by the cumulative method for the errors of latitude (RMS_φ), longitude (RMS_λ), and 2D position (DRMS(2D)). The session length increased from 1000 to 168,000 surveys, with an increment of 1000 fixes. Each of the RMS and DRMS curves is divided into areas. In the first of them, the RMS/DRMS value increases rapidly until stabilisation is achieved. The process of RMS_φ and DRMS(2D) curve stabilisation takes place at approx. 13,000 fixes, while the process of RMS_λ curve stabilisation takes place at approx. 78,000 fixes. This means that the GPS sessions comprising 78,000 fixes will be representative, which will allow reliable inferences to be made about its accuracy.

Figure 5. The process of stabilisation of the RMS_φ, RMS_λ, and DRMS(2D) measures for the GPS of 2013 [20].

It should be noted that after the stabilisation of the RMS and DRMS curves, temporary disturbances occur in their course due to the reduction in the positioning system accuracy. This reduction is related to the change in the HDOP value, which is affected by the number of satellites tracked. The hypothesis of the existence of two time frames (initial lack of stabilisation and stabilisation) of the RMS and DRMS values was positively verified based on the DGPS data from 2014 [20].

3. The Determination of Consistency between Empirical Distributions of Position Errors for Selected Systems (DGPS, EGNOS, and GPS) and Typical Statistical Distributions

This study used two long-term DGPS and EGNOS measurement campaigns conducted in 2006 and 2014 at a frequency of 1 Hz by stationary receivers located in Gdynia, Poland. During the surveys, 927,553 to 2,187,842 fixes were recorded [24,25,26]. These data were used to assess the consistency between the empirical distributions and the theoretical distributions. Statistical testing shall be carried out by the determination of distribution measures that enable the assessment of their asymmetry, central tendency, concentration, and dispersion. It must be stated that there is not a strictly specified set of statistical distribution measures used in navigation and that it depends on the variable under consideration [17]. Therefore, the assessment of the consistency between the empirical distributions and the theoretical distributions was conducted in two steps:

• The calculation of selected statistical distribution measures: arithmetic mean, asymmetry coefficient, kurtosis, median, range, standard deviation, and variance [27]. In addition, the 2DRMS(2D) and R95(2D) measures were determined;
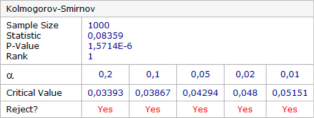
• Statistical testing using the Anderson–Darling [28], chi-squared [29], and Kolmogorov–Smirnov tests [30,31].

Before proceeding with the statistical testing, the following assumptions had to be made:

• The sample size for each positioning system under study was set at 900,000 fixes. Based on the research conducted in [20], this number of measurements should be regarded as representative;
• The determination of consistency between the 1D error distributions with the normal distribution was conducted based on 1000 randomly selected surveys using the Anderson–Darling, chi-squared, and Kolmogorov–Smirnov tests;
• In order to compare the empirical distributions of 1D and 2D position errors, the most popular theoretical distributions were used, i.e., beta, Cauchy, chi-square, exponential, gamma, Laplace, logistic, lognormal, normal, Pareto, Rayleigh, Student’s, and Weibull;
• The rankings of the statistical distributions best fitted to the empirical data were established based on the Kolmogorov–Smirnov statistics (D) for a significance level (α) of 0.05.

Firstly, the analysis of the 1D error distributions was conducted. Table 3 presents the results of the statistical analyses of distribution measures and tests of φ and λ errors, while Table 4 analyses the consistency between the 1D error empirical distribution and the theoretical distributions for the DGPS of 2014.

Table 3. Statistical analyses of the distribution measures and 1D error tests for the DGPS of 2014 [17].

Distribution Measure	φ Error	λ Error	PDF for φ Error		PDF for λ Error
Sample size	900,000
Arithmetic mean	−0.001 m	−0.001 m
Median	−0.013 m	0.010 m
Range	7.176 m	6.153 m
Variance	0.135 m	0.063 m
Standard deviation	0.368 m	0.251 m
Skewness	−0.114	0.216
Kurtosis	6.204	12.956
			Anderson–Darling	No reject	Anderson–Darling	Reject
			Chi-squared	Reject	Chi-squared	Reject
			Kolmogorov–Smirnov	No reject	Kolmogorov–Smirnov	Reject

Table 4. An analysis of the consistency between the 1D error empirical distributions and the theoretical distributions for the DGPS of 2014 [17].

Best Fit Distribution for φ Error		Best Fit Distribution for λ Error

From Table 3 and Table 4, it can be concluded that:

• Since the values of arithmetic means and skewness were close to zero, φ and λ error distributions can be considered symmetrical in the directions N-S and E-W;
• The latitude error standard deviation value was greater by approx. 1.5 times than that for the longitude error, despite the similar range values;
• One-dimensional error distributions were leptokurtic (Kurt > 0), which indicates that the intensity or extreme values was greater than that for the normal distribution;
• Anderson–Darling and Kolmogorov–Smirnov tests confirmed the consistency between the empirical φ error distribution and the Gaussian distribution. However, all the tests demonstrated no consistency between the empirical λ error distribution and the normal distribution;
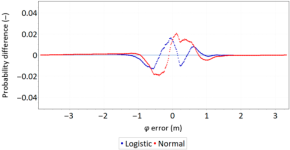
• The logistic distribution was the best fitted statistical distribution to the empirical data for 1D errors. The figures in Table 4 show the consistency (probability difference) between the 1D error empirical distributions and the theoretical distributions for the DGPS of 2014. It can be noted that there were approx. 0.01 greater probability differences across the entire error range for the third best fitted distribution (normal) than for the best fitted distribution (logistic). Statistical distributions classified in further positions were characterised by greater probability differences between the 1D error empirical distributions and the theoretical distributions.

Then, the analysis of the 2D position error distributions was conducted. Table 5 shows the results of statistical analyses of the 2D position error distributions, while Table 6 analyses the consistency between the 2D position error empirical distribution and the theoretical distributions for the DGPS of 2014.

Table 5. Statistical analyses of the 2D position error distribution measures for the DGPS of 2014 [17].

Distribution Measure	2D Position Error	PDF for 2D Position Error	2D Position Error Distribution
Sample size	900,000
Arithmetic mean	0.367 m
Median	0.330 m
Range	5.076 m
Variance	0.064 m
Standard deviation	0.252 m
Skewness	4.513
Kurtosis	54.192
2DRMS(2D)	0.885 m
R95(2D)	0.748 m

Table 6. An analysis of the consistency between the 2D position error empirical distributions and the theoretical distributions for the DGPS of 2014 [17].

Best Fit Distribution for 2D Position Error

From Table 5 and Table 6, it can be concluded that:

• The range value (5.076 m) suggests that there were no outliers during the tests. It indicates the high quality of the DGPS services;
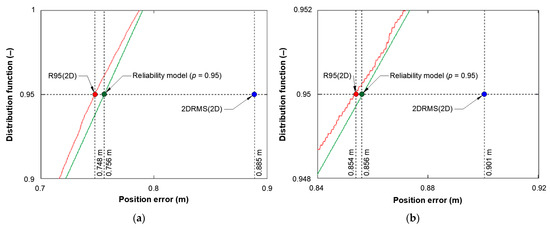
• The 2DRMS measure value (0.885 m) and the R95 measure value (0.748 m) were similar, and both amounted to less than 1 m, which indicated the high accuracy of the navigation positioning system;
• The graph of the 2D position error distribution might indicate that the empirical distribution exhibited a linear trend. But, in reality, it was not, because only 0.17% of the test sample (1496 fixes) had errors of more than 2 m;
• Beta, gamma, lognormal, Rayleigh, and Weibull distributions were the best fitted statistical distributions to the empirical data for the 2D position error. Statistical distributions were classified depending on the size of the probability difference between the 2D position error empirical distribution and the theoretical distribution.

Further on, it was decided to classify the statistical distributions in terms of their fit to the empirical data for the DGPS (Table 7). The distributions were assigned points from 1 to 10 in one of the three following categories: φ error, λ error, or 2D position error. The best fitting distribution as part of a particular category was assigned 10 points.

Table 7. Statistical distributions with the best fit to the empirical data for the DGPS [17].

Ranking of the Best Fit Distributions
φ Error		λ Error		2D Position Error
1. Logistic	10 pt	1. Logistic	10 pt	1. Weibull	10 pt
2. Lognormal (3P)	9 pt	2. Beta	9 pt	2. Lognormal (3P)	9 pt
3. Normal	8 pt	3. Normal	8 pt	3. Beta	8 pt
4. Beta	7 pt	4. Lognormal (3P)	7 pt	4. Gamma (3P)	7 pt
5. Gamma (3P)	6 pt	5. Gamma (3P)	6 pt	5. Rayleigh	6 pt
6. Laplace	5 pt	6. Weibull (3P)	5 pt	6. Weibull (3P)	5 pt
7. Cauchy	4 pt	7. Laplace	4 pt	7. Gamma	4 pt
8. Weibull (3P)	3 pt	8. Cauchy	3 pt	8. Lognormal	3 pt
9. Chi-square (2P)	2 pt	9. Rayleigh (2P)	2 pt	9. Rayleigh (2P)	2 pt
10. Rayleigh (2P)	1 pt	10. Chi-square (2P)	1 pt	10. Logistic	1 pt

Identical statistical analyses were also performed for the DGPS measurement campaign of 2006 and the EGNOS measurement campaigns conducted in 2006 and 2014. The detailed results of the study are presented in [17].

The research was culminated by the establishment of rankings of the best fitting statistical distributions within the three categories:

• The universal distribution of the 1D and 2D position errors. For the analyses, the results of the following campaigns were used: DGPS 2006 and 2014, as well as EGNOS 2006 and 2014;
• The best fitting distribution of the 1D errors. For the analyses, the results of the following campaigns were used: DGPS 2006 and 2014, as well as EGNOS 2014;
• The best fitting distribution of the 2D position errors. For the analyses, the results of the following campaigns were used: DGPS 2006 and 2014, as well as EGNOS 2014.

Under categories 2 and 3, the results of the 2006 EGNOS measurement campaign were not taken into account, as they exhibited low representativeness. The rankings of the best fitting statistical distributions are provided in Table 8. Points within each category were calculated as follows. For example, the best fit distribution in the category of the 1D errors (logistic) received 53 pt, including 16 pt from the DGPS 2006 campaign (7 pt for φ error and 9 pt for λ error), 20 pt from the DGPS 2014 campaign (10 pt for φ error and 10 pt for λ error), 0 pt from the EGNOS 2006 campaign, and 17 pt from the EGNOS 2014 campaign (7 pt for φ error and 10 pts for λ error). Points were calculated in a similar way for the remaining statistical distributions within one of the three categories.

Table 8. Statistical distributions with the best fit to the campaigns under analysis, depending on the position’s dimension (1D, 2D, or 1D and 2D) [17].

Ranking of the Best Fit Distributions
1D Error		2D Position Error		1D + 2D Position Errors
1. Logistic	53	1. Lognormal (3P)	26	1. Lognormal (3P)	93
2. Beta	51	2. Weibull	26	2. Beta	86
3. Lognormal (3P)	49	3. Beta	24	3. Gamma (3P)	75
4. Normal	44	4. Gamma (3P)	23	4. Logistic	69
5. Gamma (3P)	39	5. Weibull (3P)	15	5. Normal	56
6. Weibull (3P)	30	6. Gamma	14	6. Weibull (3P)	51
7. Laplace	25	7. Rayleigh	13	7. Laplace	42
8. Cauchy	21	8. Lognormal	13	8. Cauchy	42
9. Rayleigh (2P)	9	9. Rayleigh (2P)	7	9. Weibull	31
10. Chi-square (2P)	8	10. Normal	2	10. Lognormal	23

From Table 8, it can be concluded that:

• The lognormal distribution is a universal statistical distribution, as it approximates the best of both 1D and 2D position errors;
• Distributions: beta, gamma, logistic, and Weibull showed a slightly worse fit to the empirical data than the lognormal distribution;
• The normal distribution should only be applied for the analysis of navigation positioning system errors in the 1D dimension;
• The chi-squared distribution, which is suggested, particularly for the analysis of the 2D position errors, exhibited a slight similarity to the empirical data.

4. The Development of the Author’s Original Method (Reliability Modelling of Stationary Processes with Renewal) Enabling the Calculation of a Navigation System Position Error Value Based on the Empirical Data

No consistency between the position errors and the Gaussian distribution, which is commonly used in navigation [6,32], contributes to the search for other methods for determining the position error with a probability of 0.95. One such method is the reliability method proposed by Professor Cezary Specht [33]. The method is based on the fact that navigation system availability for the pre-set position error value is determined based on the fitness (life) and unfitness (failure) times, and not, as previously, using the measurement errors.

When considering a navigation system which determines a position with an error δ_n in time t, in order to be able to assess if it actually is in the life status or the failure status, it is necessary to specify the requirements for the positioning accuracy and availability, which are imposed on navigation applications [1,7,8,9,10,11,12,34,35,36]. Hence, for the purposes of the model, max position error values (p = 0.95) were introduced for navigation applications, which are denoted by the parameter U. It was later possible to determine whether the navigation positioning system was in the life status (δ_n ≤ U for the number of measurements (n) = 1, 2, …) or in the failure status (δ_n > U) [37].

Let us assume that X₁, X₂, … correspond to the durations of life times and Y₁, Y₂, … denote the durations of failure times, which are independent and have the same distributions. Changing the durations of life and failure times results in the change of the operational status of a positioning system (α(t)). Hence, $Z_n^{\prime } \hspace{0.33em}=X_1+Y_1+X_2+Y_2+\dots +Y_{n-1}{+\mathrm{X}}_n$ become the moments of failure, while $Z_n^{"} \hspace{0.33em}=Z_n^{\prime }{+\mathrm{Y}}_n$ are the moments of life (Figure 6) [37].

Figure 6. The fitness and unfitness statuses of a positioning system in accordance with the reliability method. Own study based on [37].

However, before doing so, it was necessary to define all the assumptions and designations related to the reliability model [38]. One of the main assumptions of the model is that the life (F(x)) and failure (G(y)) time distribution functions are right-continuous:

$$P\left(X_i\le x\right)=F\left(x\right)$$

(3)

$$P\left(Y_i\le y\right)=G\left(y\right) \mathrm{for} i=1,2,\dots$$

(4)

Moreover, the expected values and variances can be expressed as:

$$E\left(X_i\right)=E\left(x\right)$$

(5)

$$E\left(Y_i\right)=E\left(y\right)$$

(6)

$$V\left(X_i\right)={\sigma }_1^2$$

(7)

$$V\left(Y_i\right)={\sigma }_2^2 \mathrm{for} i=1,2,\dots$$

(8)

where:

E(X_i)—life time expected value;

E(X_i)—failure time expected value;

V(X_i)—life time variance;

V(Y_i)—failure time variance.

Formula (9) takes the logical value of “0”, when the sum of the two variances of the life and failure times, defined by the sum of the standard deviation squares, amounts to 0. This is a degenerate (deterministic) case which needs to be excluded from the calculations because it is not possible to determine the life and failure times with error-free accuracy:

$${\sigma }_1^2+{\sigma }_2^2>0$$

(9)

Based on the above assumptions, it is possible to determine the relationship between the δ_n and U parameters. Thanks to this, the operational status of a positioning system can be assigned as [37]:

$$U=\left\{\begin{array}{l}1 \mathrm{for} Z_n^{"}\le t<Z_{n+1}^{\prime }\\ 0 \mathrm{for} Z_{n+1}^{\prime }\le t<Z_{n+1}^{"}\end{array}\right. \mathrm{for} n=0,1,\dots$$

(10)

The availability of a navigation positioning system can be written as the probability of error δ_n occurrence (no greater than the U value) at any moment of time t [37]:

$$A\left(t\right)=P\left[\delta \left(t\right)\le U\right]$$

(11)

$$A\left(t\right)=1-F\left(t\right)+{\displaystyle \underset{0}{\overset{t}{\int }}\left[1-F\left(t-x\right)\right]d}{H}_{\Phi }\left(x\right)$$

(12)

where:

$$H_{\Phi }\left(x\right)={\displaystyle \sum _{n=1}^{\infty }{\Phi }_n\left(x\right)}$$

(13)

is the function of the navigation system operation renewal, while Φ_n(t) is the distribution function of the random variable $Z_n^{"}$.

It has been commonly adopted that the life and failure time distributions have exponential distributions in navigation. Hence, their distribution functions and the PDFs are determined based on the following relations [38]:

$$f\left(t\right)=\left\{\begin{array}{c}\lambda \cdot e^{-\lambda \cdot t} \mathrm{for} t>0\\ 0 \mathrm{for} t\le 0\end{array}\right.$$

(14)

$$g\left(t\right)=\left\{\begin{array}{c}\mu \cdot e^{-\mu \cdot t} \mathrm{for} t>0\\ 0 \mathrm{for} t\le 0\end{array}\right.$$

(15)

$$F\left(t\right)=\left\{\begin{array}{c}1-e^{-\lambda \cdot t} \mathrm{for} t>0\\ 0 \mathrm{for} t\le 0\end{array}\right.$$

(16)

$$G\left(t\right)=\left\{\begin{array}{c}1-e^{-\mu \cdot t} \mathrm{for} t>0\\ 0 \mathrm{for} t\le 0\end{array}\right.$$

(17)

where:

f(t)—life time PDF;

g(t)—failure time PDF;

λ—failure rate;

μ—renewal rate.

Based on the above assumptions, the final availability function can be written as [37]:

$$A_{\exp }\left(t\right)=\frac{\mu }{\lambda +\mu }+\frac{\lambda }{\lambda +\mu }\cdot e^{-\left(\lambda +\mu \right)\cdot t}$$

(18)

For the validation of the proposed reliability model, measurement campaigns of three navigation positioning systems were used: GPS 2013 (168,286 fixes), DGPS 2014 (900,000 fixes), and EGNOS 2014 (900,000 fixes). Additionally, in order to evaluate which of the two models, i.e., the classical model based on the 2DRMS(2D) measure or the reliability model, is closer to the actual value, it was decided to compare them with the R95(2D) measure value that is determined by sorting the errors from the smallest to the largest [13,14,15]. This should be considered the most reliable method for calculating the position error with a probability of 0.95, as it assumes no statistical distribution.

Figure 7 presents the distribution function of the sorted position errors (red curve), the distribution function calculated for the reliability model (green curve), and the R95(2D) measure value (blue dot) for the GPS of 2013 [21].

Figure 7. A comparison of the 2DRMS(2D) measure and the reliability model (p = 0.95) to the R95(2D) measure for the GPS of 2013 [21].

From Figure 7, it should be noticed that the position error value calculated using the reliability model with a probability of 0.95 (2.044 m) was considerably closer to the R95 measure value (2.039 m) than the 2DRMS measure value (2.240 m). To verify the results acquired for the GPS, it was decided to conduct identical statistical analyses for other navigation positioning systems, such as DGPS and EGNOS (Figure 8) [21].

Figure 8. A comparison of the 2DRMS(2D) measure and the reliability model (p = 0.95) to the R95(2D) measure for the systems DGPS (a) and EGNOS (b) [21].

From Figure 8, it should be observed that the differences between the R95 measure value and the position error value calculated using the reliability model with a probability of 0.95 amounted to 0.008 m for the DGPS and 0.002 m for the EGNOS. On the other hand, the differences between the R95 measure value and the 2DRMS measure value amounted to 0.137 m for the DGPS and 0.047 m for the EGNOS. Hence, it can be stated that similarly to the GPS, the position error value calculated using the reliability model with a probability of 0.95 was considerably closer to the R95 measure value than the 2DRMS measure values for both DGPS and EGNOS. It should be stressed that many authors have indicated the underestimation of the position error value calculated based on the 2DRMS measure [3].

5. The Determination of Differences between the Position Accuracy Measures Calculated Using the 2DRMS and R95 for the GPS

This study used two long-term GPS measurement campaigns conducted in 2021 at a frequency of 1 Hz by two GPS code receivers located in Gdynia, Poland. The parallel use of two receivers was aimed at determining the repeatability of results while conducting two sessions in succession enabled the assessment of the representativeness of statistics. The first of the survey sessions (main session) comprised 900,000 fixes, while during the second session (verification session), 237,000 fixes were recorded. These data were used to assess the consistency between the GPS 1D and 2D position errors and different statistical distributions, as well as selected measures of statistical distributions being calculated. Moreover, the differences between the position accuracy measures calculated using the 2DRMS and R95 were determined.

The main session tests demonstrated that the statistical distributions beta, logistic, lognormal, normal, and Student’s t best approximated φ errors (GPS 1 receiver), while the distributions beta, gamma, logistic, lognormal, and normal best described λ errors (GPS 1 receiver). What is more, based on the data recorded during the main session, it can be concluded that [22]:

• Statistical distribution measure values are similar for both GPS 1 and GPS 2 receivers;
• Differences between the arithmetic mean values for the GPS 1 and GPS 2 receivers, operating in parallel, amounted to 8 mm for φ and 22 mm for λ;
• The values of φ error standard deviations (1.067 m for GPS 1 and 1.117 m for GPS 2) were much greater than those for λ errors (0.796 m for GPS 1 and 0.818 m for GPS 2). Hence, it can be concluded that the latitude errors for the GPS were greater than the longitude errors. This thesis is also positively verified by the range value, which was considerably greater for φ error (11.495 m for GPS 1 and 11.115 m for GPS 2) than for λ error (7.668 m for GPS 1 and 7.342 m for GPS 2);
• Both coordinates showed a slight asymmetry (skewness) close to 0. For the latitude, it was negative (–0.166 for GPS 1 and –0.106 for GPS 2), while for the longitude, it was positive (0.022 for GPS 1 and 0.034 for GPS 2). The low arithmetic mean and skewness values for both receivers enabled the conclusion that the statistical distributions of 1D errors were symmetrical and exhibited consistency with the normal distribution.

Further on, the obtained results of the main session measurements against the verification session were verified, whose population size was four times smaller. On the basis of data from the verification session, it can be concluded that [22]:

• The values of the arithmetic means and standard deviations were similar to the results obtained during the main session;
• Latitude errors were greater than longitude errors, similar to the main session;
• One-dimensional error skewness values showed a slight skewness (asymmetry), which proved that the statistical distributions of these errors were symmetrical and consistent with the normal distribution.

The differences between the standard deviation values for φ and λ errors have an effect on the 2D position error value for the GPS. Based on the analysis of the GPS 2D position error, it can be stated that [22]:

• During the main session, the R95 measure values amounted to 2.393 m for the GPS 1 receiver and 2.488 m for the GPS 2 receiver. Therefore, they were similar to the R95 measure values obtained during the verification session (2.232 m for GPS 1 and 2.356 m for GPS 2). The difference between the R95 measure values was less than 10 cm during the main session, which proved that this session was representative. A slightly greater difference between the R95 measure values (12.4 cm) was obtained for the verification session, which may have resulted from the measurement session length;
• Statistical distributions beta, gamma, lognormal, and Weibull best approximated the 2D position errors both in the main and verification sessions;
• Based on the analysis of the Q-Q plot, it can be concluded that the beta distribution approximated the GPS position errors well in almost the entire probability range. This was due to the fact that the beta distribution described these errors well up to 3.7 m with a high probability of 0.997 (3σ) for the main session.

Latitude errors being considerably greater than longitude errors for the GPS must result in the values of the 2DRMS(2D) and R95(2D) measures considerably differing from each other. Therefore, the percentage value of the difference between the 2DRMS measure and the R95 measure (relative percentage error) was calculated in accordance with the following formula [22]:

$$RPE=\frac{R95(2D)-2DRMS(2D)}{R95(2D)}\cdot 100\%$$

(19)

Figure 9 presents the differences between the 2DRMS measure and the R95 measure for the GPS during the main session and the verification session, as well as the measurement campaign conducted in 2013.

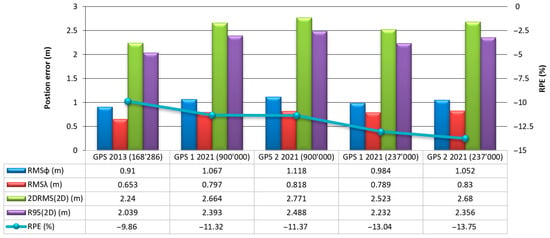
Figure 9. Differences between the 2DRMS measure and the R95 measure for the GPS of 2021.

Based on the statistical analyses, the following conclusions about the GPS position errors can be drawn [22]:

• Standard deviation values for φ errors were greater by 25–39% than those for λ errors. For the main session, these differences ranged from 33.88% (GPS 1 receiver) to 36.67% (GPS 2 receiver), while for the verification session, the differences concerned were slightly smaller and amounted to 24.71% (GPS 1 receiver) and to 26.75% (GPS 2 receiver). As regards the GPS measurement campaign of 2013, φ errors were greater by 39.36% than λ errors;
• The 2DRMS measure value was underestimated by 10–14% in relation to the R95 measure value that should be considered the actual value. Similar differences between the 2DRMS measure and the R95 measure are presented in [39,40];
• The 1D error skewness value decreased with an increase in the measurement session length, which resulted in the statistical distributions of these errors becoming increasingly symmetrical;
• Latitude errors had a kurtosis greater by 2–3 times (being more concentrated in relation to the average value) than longitude errors.

6. The Performance of Statistical Analyses to Determine the Relationship between the 2D Position Error and the HDOP Values for the GPS

This study used the main GPS measurement campaign conducted in 2021 (900,000 fixes) at a frequency of 1 Hz by a GPS code receiver located in Gdynia, Poland. These data were used to carry out statistical analyses aimed at determining a relation between the 2D position error and the HDOP. Moreover, this study determined the most frequently occurring values of the HDOP and what 2D position error distributions are subject to them. The relation between this coefficient and the number of satellites tracked was determined as well.

In the first step of the study, a statistical analysis was carried out of the HDOP values for the GPS main session of 2021. To this end, only the statistical measures (arithmetic mean, asymmetry coefficient, kurtosis, median, percentiles, range, standard deviation, and variance), which refer to the 2D position error, were used. Based on the statistical analyses, it can be concluded that [23]:

• The HDOP arithmetic average value was 0.781, with a small standard deviation of 0.113;
• The most frequently occurring HDOP values were 0.7 and 0.8;
• For more than 95% of measurements, the coefficient had a value of less than or equal to 1;
• The obtained HDOP values should be considered low, which was possible thanks to the optimal conditions for the GPS measurement performance due to the lack of field obstacles.

Then, it was decided to determine the percentage of time during which individual HDOP values occurred. Figure 10a shows the percentage of individual HDOP values in the entire session, while Figure 10b shows the population size of the sets containing the same HDOP value.

Figure 10. The percentage of the HDOP values in the entire session (a) and the population size of the sets containing the same HDOP value (b) for the main GPS measurement campaign of 2021 [23].

In the first step of the study, a statistical analysis was carried out of the HDOP values for the GPS main session of 2021. To this end, only the statistical measures (arithmetic mean, asymmetry coefficient, kurtosis, median, percentiles, range, standard deviation, and variance), which refer to the 2D position error, were used. Based on the statistical analyses, the following can be concluded [23]:

From Figure 10, it can be stated that [23]:

• The HDOP value ranged from 0.6 to 1.8 during the main session carried out under optimal conditions for the GPS measurement performance;
• HDOP values of 0.7 and 0.8 occurred 78.52% of the time;
• HDOP values of more than 1 occurred 2.77% of the time;
• Population sizes of the sets (32,221–389,007 fixes) for the HDOP values in the range from 0.6 to 1.0 should be considered fully representative, enabling further statistical analyses and inference as regards the 2D position errors. The population sizes of the sets (60–14,270 fixes) for the HDOP values in the range from 1.1 to 1.8 should be considered hardly representative, which prevents the performance of further statistical analyses.

Subsequently, the effect of the number of satellites tracked on the HDOP value falling within a range of 0.6–1.0 was assessed. Based on the statistical analyses, it can be concluded that [23]:

• In order to ensure the greatest HDOP value of 0.6, from 12 to 16 satellites were used. An average of 14.085 satellites were tracked;
• Obtaining the HDOP value of 0.7 was possible when using from 9 to 14 satellites. An average of 12.506 satellites were tracked;
• In order to obtain the most frequently occurring HDOP value of 0.8 (p = 0.432), from 8 to 14 satellites were used. An average of 11.336 satellites were tracked;
• For the HDOP values of 0.9 and 1.0, there was an evident decrease in the number of satellites tracked to 10.149 and 8.749, respectively.

Later on, a statistical analysis of the GPS 2D position error values was performed for specific HDOP values in the range from 0.6 to 1.0, and these values were compared to the results from the entire campaign (Table 9) [23].

Table 9. GPS 2D position error statistical measures for specific HDOP values in the range from 0.6 to 1.0 and for all the HDOP values in the range from 0.6 to 1.8 [23].

Descriptive Statistic	2D Position Error
	HDOP = 0.6	HDOP = 0.7	HDOP = 0.8	HDOP = 0.9	HDOP = 1.0	HDOP ∈ <0.6, 1.8>
Sample size	51,215	317,743	389,007	84,937	32,221	900 000
Availability	5.69%	35.30%	43.22%	9.44%	3.58%	100%
Arithmetic mean	0.988 m	1.16 m	1.151 m	1.168 m	1.353 m	0.875 m
Range	3.902 m	6.582 m	6.582 m	4.109 m	6.102 m	0.802 m
Variance	0.322 m	0.41 m	0.439 m	0.456 m	0.673 m	5.993 m
Standard deviation	0.568 m	0.641 m	0.663 m	0.675 m	0.82 m	2.448 m
R95	2.048 m	2.31 m	2.373 m	2.493 m	2.889 m	2.393 m

From Table 9, it can be stated that the 2D position error value (R95 measure) increased with an increase in the HDOP value, which was to be expected. The R95 measure value was calculated for all the HDOP values in the range from 0.6 to 1.8 was 2.393 m and was greater than the R95 measure values determined for specific HDOP values ranging from 0.6 to 0.8. The obtained coefficient values should be considered low, as only 2.77% of measurements had an HDOP value greater than 1. If gross or outlier errors did not appear in the sets for the HDOP values in the range from 1.1 to 1.8, they had no significant effect on the R95 measure value calculated for all of the HDOP values.

In the final step of work, GPS 2D position error PDFs were determined for specific HDOP values in the range from 0.6 to 1.0, and the R95 measure values were calculated for the selected HDOP values (Figure 11). For the approximation of the GPS 2D position error probability density function, the beta PDF [41], which exhibits a high degree of fit to the navigation system position errors, was used [23].

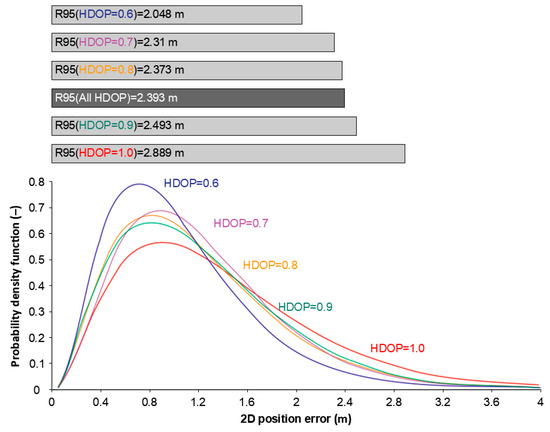
Figure 11. GPS 2D position error PDFs for specific HDOP values in the range from 0.6 to 1.0 and the R95 measure values calculated for the selected HDOP values [23].

In order to assess the relation between the 2D position error and the HDOP, it was necessary to compare the PDFs for the extreme values, i.e., for the HDOP of 0.6 and 1.0. The R95 measure value for HDOP = 0.6 was 2.048 m, accounting for 85.58% of the R95 measure value calculated for the whole campaign. What is more, the R95 measure value for HDOP = 1.0 was greater by almost 1 m than that for HDOP = 0.6, and greater by more than 50 cm than that for all the HDOP values in the range from 0.6 to 1.8. The reason for this was the average number of satellites tracked. For the HDOP value of 0.6, an average of 14.085 satellites were tracked. However, for the HDOP value of 1.0, there was an evident decrease in the number of satellites tracked to 8.749 [23].

7. Discussion

This review presents the main results of the author’s study, obtained as part of the post-doctoral (habilitation) dissertation entitled “Research on Statistical Distributions of Navigation Positioning System Errors”, which constitutes a series of five thematically linked scientific publications. The most important scientific achievements of this dissertation include:

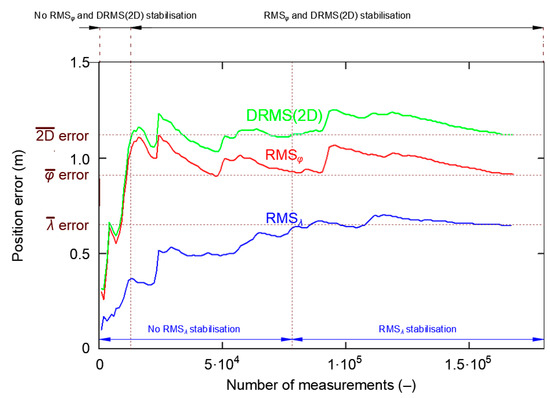
• The development of a method enabling the determination of the navigation positioning system representative sample length from the perspective of assessing its accuracy [20]. In the navigation systems under study (Decca Navigator, DGPS, EGNOS, and GPS), the PRW phenomenon occurred, and 1D errors did not appear in a random manner as in the normal distribution. Moreover, it was demonstrated that the extent of the “wandering” phenomenon of the position coordinates was determined by the navigation positioning system accuracy. A system with a lower accuracy (Decca Navigator) exhibited considerably greater changes in the successively recorded position coordinates than systems with higher accuracy (DGPS and EGNOS). Moreover, the length of the representative measurement campaign, which will enable reliable statistical inference about the navigation systems’ accuracy, was determined. This will be a session with such a length, for which the process of stabilisation of standard deviations calculated by the cumulative method for the measurement errors of the latitude (RMS_φ), longitude (RMS_λ), and 2D position (DRMS(2D)) will occur;
• The determination of consistency between empirical distributions of position errors for selected systems (DGPS, EGNOS, and GPS) and typical statistical distributions based on long-term measurement campaigns (1–2 million fixes) [17]. On the basis of data from the GPS measurement campaigns conducted in 2006 and 2014, as well as for the EGNOS of 2014, it can be concluded that the distributions of φ and λ errors are not always consistent with the Gaussian distribution. Moreover, this is not an optimal distribution for the modelling of navigation positioning systems’ errors. A higher fit to the 1D errors was exhibited by such distributions as beta, logistics, and lognormal. On the other hand, a considerably higher fit to the 2D position errors was exhibited by such distributions as beta, gamma, logistic, lognormal, and Weibull. Hence, it should be concluded that the normal distribution should only be applied for the analysis of navigation positioning system errors in the 1D dimension. Moreover, the chi-squared distribution, which is suggested in particular for the analysis of the 2D position errors, exhibited a slight similarity to the empirical data. Therefore, it should not be used for the modelling of the positioning systems’ navigation errors in the 2D dimension;
• The development of the author’s original method (reliability modelling of stationary processes with renewal) enabling the calculation of a navigation system position error value based on the empirical data [21]. The publication presented the author’s original method for determining the accuracy of navigation positioning systems, whose essence is based on the reliability model of stationary processes with renewal. The random variables in this method are the life and failure times of the position coordinate determination process and not position errors as in the classical model based on the 2DRMS(2D) measure. The author believes that the reliability method better reflects the nature of the navigation process (real-time process), which is based on time, and it can be effectively used in the assessment of the positioning system suitability for a specific navigation application. Based on the data recorded during the measurement campaigns of the following systems: GPS 2013, DGPS 2014, and EGNOS 2014, it can be concluded that the proposed reliability method ensures considerably more precise calculation of the accuracy of navigation positioning systems in comparison with the 2DRMS measure. Another advantage of this model is the non-complex computational algorithm;
• The determination of differences between the position accuracy measures calculated using the 2DRMS and R95 for the GPS [22]. On the basis of data from the GPS measurement campaigns conducted in 2013 and 2021, it can be concluded that φ errors are greater by 25–39% than λ errors. The differences between these 1D errors must result in the inconsistency between the 2D position error distribution and the chi-squared distribution. This study demonstrated that the 2DRMS(2D) measure value was underestimated by 10–14% in relation to the R95(2D) measure value that should be considered the actual value. It was also proven that the statistical distributions beta, logistic, lognormal, normal, and Student’s best approximate φ errors; the distributions beta, gamma, logistic, lognormal, and normal best describe λ errors; and the distributions beta, gamma, lognormal, and Weibull best approximate the 2D position errors;
• The performance of statistical analyses to determine the relation between the 2D position error and the HDOP values for the GPS [23]. On the basis of data from the GPS measurement campaign conducted in 2021, it can be concluded that the HDOP values fell within a range of 0.6–1.8, with the most frequently occurring quantities of 0.7 (p = 0.353) and 0.8 (p = 0.432). It should be noted that for 95% of surveys (2σ), the HDOP value was 0.973, and for 2.77% of measurements, the coefficient value was greater than 1. It was possible to obtain such low HDOP values thanks to the optimal conditions for the GPS measurement performance due to the lack of field obstacles. Moreover, this study demonstrated that, in order to ensure a low value of the HDOP, and thus a low value of the GPS 2D position error, a great average number of the tracked satellites (at least 12) with low variability are required.