Sequential Generation of Multi-GNSS Multi-Frequency PPP-RTK Products and Their Performance Using the EUREF Permanent GNSS Network
Abstract
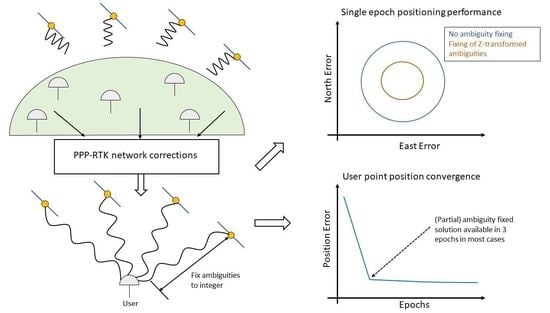
1. Introduction
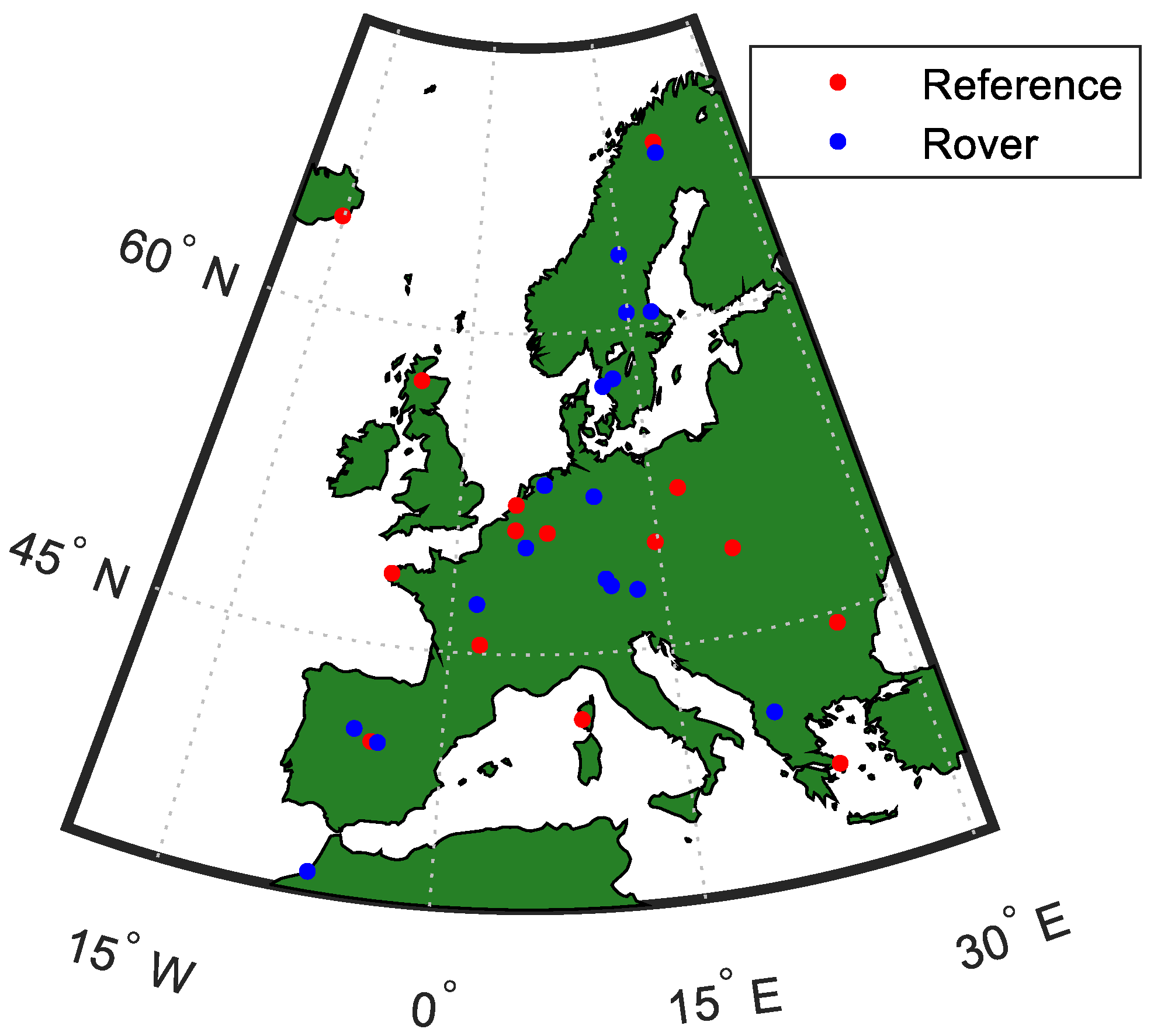
2. Data
3. Methods
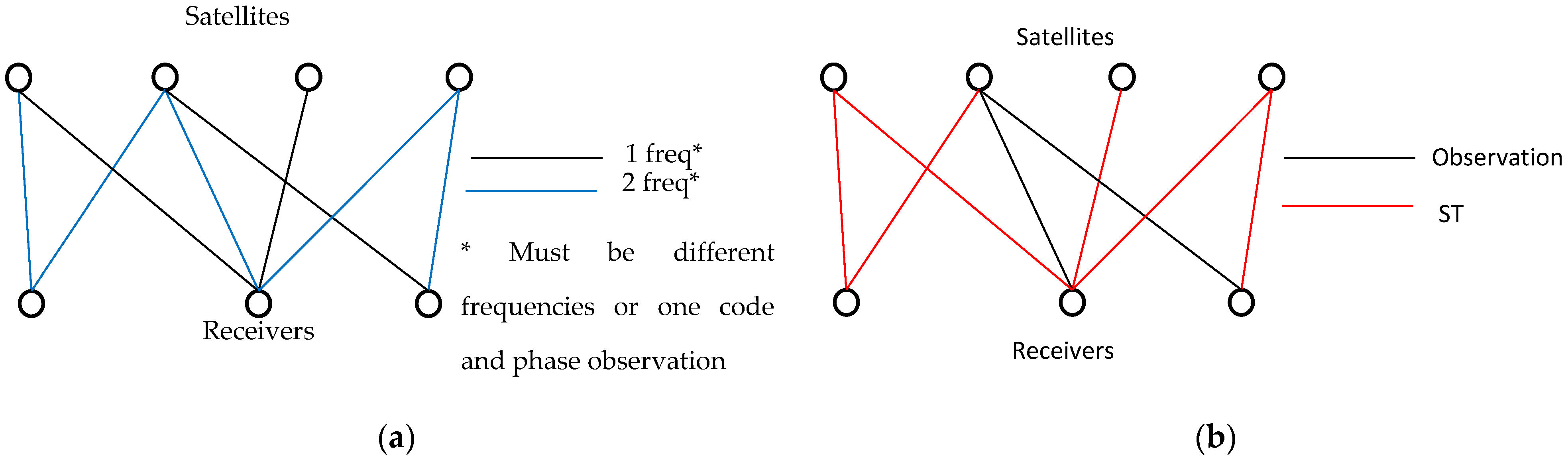
3.1. Functional Model
3.2. Network and User Processing
3.2.1. Time Update, Measurement Update
3.2.2. Ambiguity Resolution
| Item | Description | Item | Description |
|---|---|---|---|
| Observations and Corrections | |||
| Observations | Raw pseudo-range and carrier phase, signals and channels as listed in Table 1 | Loading Effects | Solid Earth Tide, Pole Tide corrected [26] Ocean Loading Model FES95.2 [27] |
| Observation weighting * | Relativistic Clock Effects | Shapiro Effect and orbit eccentricity corrected | |
| Elevation Mask | Station Coordinates | Network: Fixed to Reference Frame solution [15] | |
| Phase Center Offset & Variations | Corrected with IGS14.atx model [28] | Satellite Orbits | Fixed to final Code orbit [16] |
| Phase Wind-Up | Corrected [29] | Tropospheric Mapping, Hydrostatic Zenith Delay | GPT3 [30] |
| Satellite Attitude | Nominal Yaw-Steering [31] | Earth Rotation Parameters (ERP) | Final Code ERP [16] |
| Parameter Estimation ** and Process Noises | |||
| Receiver/Satellite Clocks | (“epoch-wise”) | Zenith Tropospheric Delay | |
| Receiver/Satellite Code Biases | Constant parameters | Ionospheric Slant Delays | (“epoch-wise”) |
| Receiver/Satellite Phase Biases | Constant or one reference phase clock (see Section 3.2.3) Reset in case of loss of ambiguity datum (see Section 3.2.3) GPS satellite L5 phase bias process noise in all cases | Ambiguities | Constant along one continuous satellite arc, reset when phase observation is detected as an outlier |
| Ambiguity resolution (Network) | Success Rate > 99%, Ratio Test < 0.5 using MLAMBDA for Integer Least Squares [23,24] | Ambiguity resolution (User) | Ratio Test Integer Aperture estimation [13], after wide-lane ambiguities are attempted to be fixed with Success Rate > 99% and Ratio Test < 0.5 |
3.2.3. Temporal Constraints on Phase Biases
- Phase Biases are estimated as constant parameters (constant phase biases);
- An epoch-wise reference phase clock is introduced. All other phase biases are assumed as constant parameters relative to it (reference phase clock).
4. Results
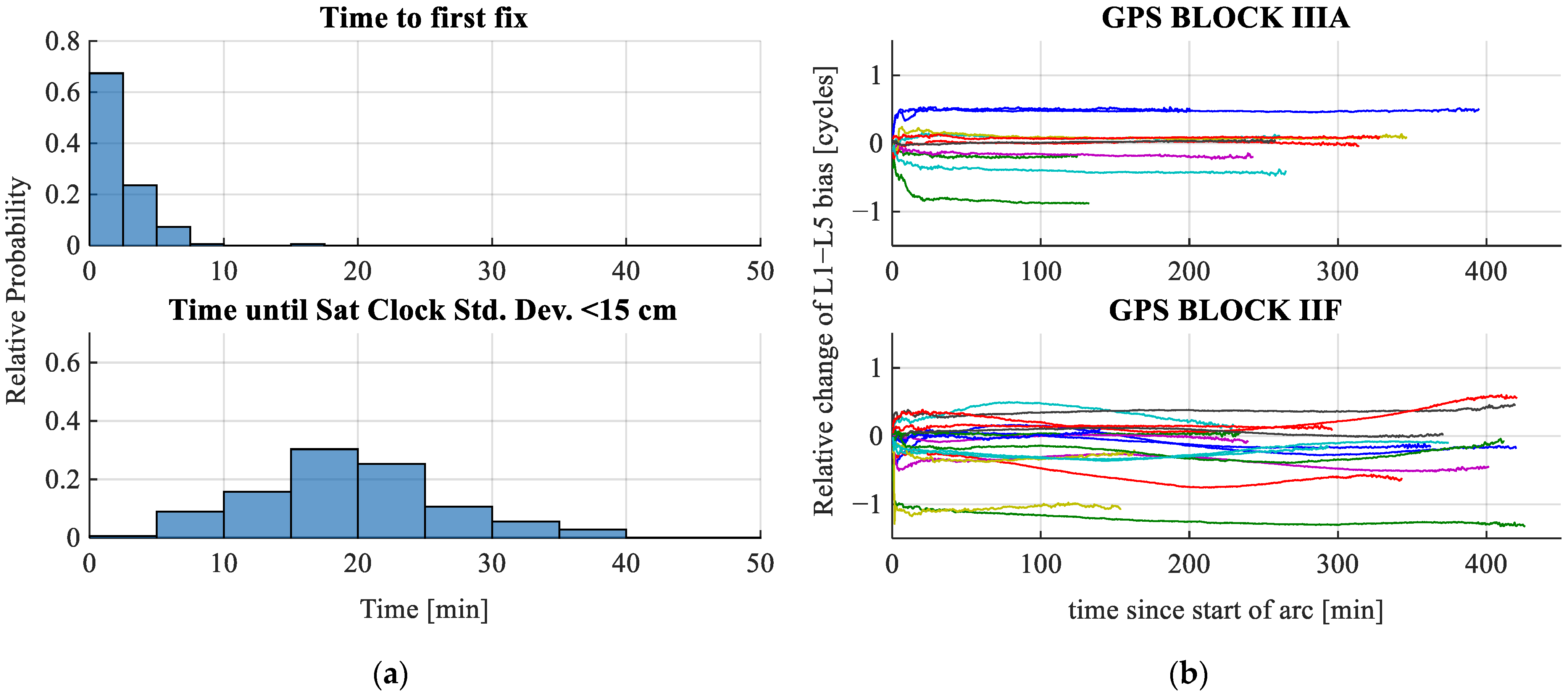
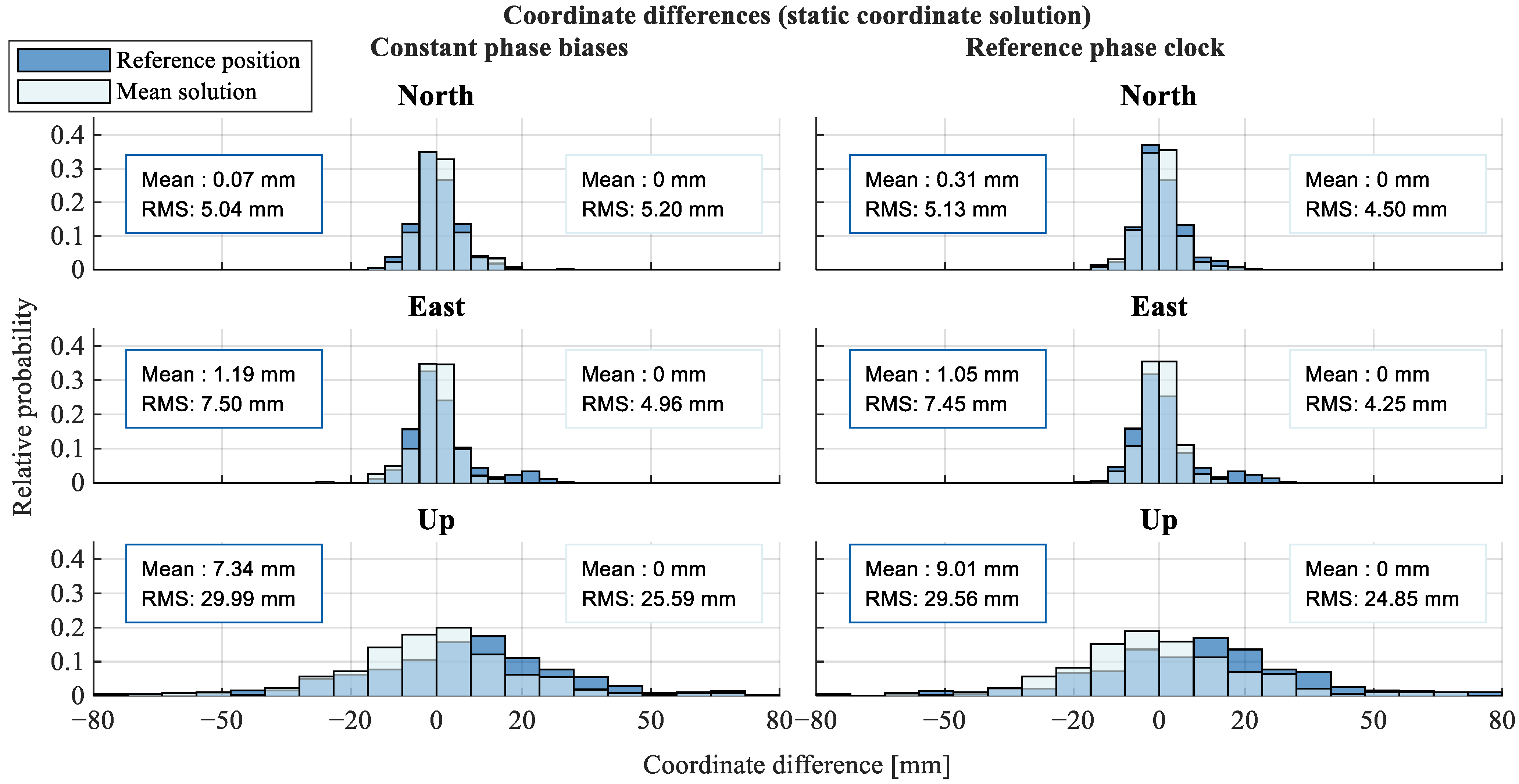
4.1. Network Results
4.2. User Results
4.2.1. Multi-Frequency
4.2.2. Dual-Frequency
5. Discussion and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teunissen, P.J.G.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2015, 90, 15–44. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A.H. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv. Space Res. 2011, 47, 1664–1673. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. A new GLONASS FDMA model. GPS Solut. 2019, 23, 100. [Google Scholar] [CrossRef]
- Brack, A.; Männel, B.; Schuh, H. GLONASS FDMA data for RTK positioning: A five-system analysis. GPS Solut. 2020, 25, 9. [Google Scholar] [CrossRef]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Geng, J.; Shi, C.; Ge, M.; Dodson, A.H.; Lou, Y.; Zhao, Q.; Liu, J. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning. J. Geod. 2011, 86, 579–589. [Google Scholar] [CrossRef]
- Geng, J.; Chen, X.; Pan, Y.; Zhao, Q. A modified phase clock/bias model to improve PPP ambiguity resolution at Wuhan University. J. Geod. 2019, 93, 2053–2067. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hugentobler, U.; Dach, R.; Steigenberger, P.; Hauschild, A. Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite. GPS Solut. 2012, 16, 303–313. [Google Scholar] [CrossRef]
- Yue, C.; Dang, Y.; Xue, S.; Wang, H.; Gu, S.; Xu, C. A Short-Term Forecasting Method of Inter-Frequency Clock Bias for GPS Block IIF Satellites. Remote Sens. 2022, 14, 4130. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Verhagen, S. On the Foundation of the Popular Ratio Test for GNSS Ambiguity Resolution. In Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2004), Long Beach, CA, USA, 21–24 September 2004; pp. 2529–2540. Available online: http://www.ion.org/publications/abstract.cfm?jp=p&articleID=5937 (accessed on 20 March 2023).
- Bruyninx, C.; Legrand, J.; Fabian, A.; Pottiaux, E. GNSS metadata and data validation in the EUREF Permanent Network. GPS Solut. 2019, 23, 106. [Google Scholar] [CrossRef]
- Legrand, J. EPN Multi-Year Position and Velocity Solution C2220; Royal Observatory of Belgium: Uccle, Belgium, 2022. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Prange, L.; Susnik, A.; Villiger, A.; Jäggi, A.; Villiger, A. CODE Final Product Series for the IGS [Datensatz]; Astronomical Institute, University of Bern: Bern, Switzerland, 2020; Available online: http://www.aiub.unibe.ch/download/CODE (accessed on 14 March 2023).
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer Science & Business Media: Boston, NY, USA, 2007. [Google Scholar]
- Kouba, J.; Lahaye, F.; Tétreault, P. Precise Point Positioning. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 723–751. [Google Scholar] [CrossRef]
- Teunissen, P. Zero Order Design: Generalized Inverses, Adjustment, the Datum Problem and S-Transformations. In Optimization and Design of Geodetic Networks; Grafarend, E.W., Sansò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 11–55. [Google Scholar] [CrossRef]
- Wilson, R.J. Introduction to Graph Theory; Longman: London, UK, 2010. [Google Scholar]
- Khodabandeh, A.; Teunissen, P.J.G. Integer estimability in GNSS networks. J. Geod. 2019, 93, 1805–1819. [Google Scholar] [CrossRef]
- Teunissen, P. The invertible GPS ambiguity transformations. Manuscr. Geod. 1995, 20, 489–497. [Google Scholar]
- Chang, X.-W.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Verhagen, S.; Li, B. LAMBDA Software Package: Matlab Implementation, Version 3.0; Delft University of Technology and Curtin University: Perth, Austraila, 2012. [Google Scholar]
- Cocard, M.; Bourgon, S.; Kamali, O.; Collins, P. A systematic investigation of optimal carrier-phase combinations for modernized triple-frequency GPS. J. Geod. 2008, 82, 555–564. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. (Eds.) IERS Technical Note, 36. In IERS Conventions (2010); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Le Provost, C.; Lyard, F.; Molines, J.M.; Genco, M.L.; Rabilloud, F. A hydrodynamic ocean tide model improved by assimilating a satellite altimeter-derived data set. J. Geophys. Res. Ocean. 1998, 103, 5513–5529. [Google Scholar] [CrossRef]
- Antenna. International GNSS Service. Available online: https://igs.org/wg/antenna/ (accessed on 20 March 2023).
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Manuscr. Geod. 1993, 18, 91–98. [Google Scholar]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Montenbruck, O.; Schmid, R.; Mercier, F.; Steigenberger, P.; Noll, C.; Fatkulin, R.; Kogure, S.; Ganeshan, A.S. GNSS satellite geometry and attitude models. Adv. Space Res. 2015, 56, 1015–1029. [Google Scholar] [CrossRef]
- Luo, X.; Mayer, M.; Heck, B.; Awange, J. A Realistic and Easy-to-Implement Weighting Model for GPS Phase Observations. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6110–6118. [Google Scholar] [CrossRef]
- Psychas, D.; Khodabandeh, A.; Teunissen, P.J.G. Impact and mitigation of neglecting PPP-RTK correctional uncertainty. GPS Solut. 2021, 26, 33. [Google Scholar] [CrossRef]
- Melbourne, W. The case for ranging in GPS-based geodetic systems. In Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Wübbena, G. Software Developments for Geodetic Positioning with GPS Using TI 4100 Code and Carrier Measurements. In Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; U.S. Department of Commerce: Washington, DC, USA, 1985; pp. 403–412. Available online: https://cir.nii.ac.jp/crid/1571698599798417280 (accessed on 20 January 2023).
- Prochniewicz, D.; Wezka, K.; Kozuchowska, J. Empirical Stochastic Model of Multi-GNSS Measurements. Sensors 2021, 21, 13. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Y.; Chen, J.; Wang, H. Improving the (re-)convergence of multi-GNSS real-time precise point positioning through regional between-satellite single-differenced ionospheric augmentation. GPS Solut. 2022, 26, 39. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Li, X.; Lyu, H.; Wang, B.; Xiong, Y.; Xie, W. Multi-constellation GNSS PPP instantaneous ambiguity resolution with precise atmospheric corrections augmentation. GPS Solut. 2021, 25, 107. [Google Scholar] [CrossRef]
- Re3data.Org. VMF Data Server. 2016. Available online: https://vmf.geo.tuwien.ac.at/ (accessed on 15 November 2022). [CrossRef]





| GNSS | Receiver Type A | Receiver Type B |
|---|---|---|
| GPS | *1C, *2W, *5Q | *1C, *2W, *5X |
| Galileo | *1Q, *5Q, *6C, *7Q, *8Q | *1X, *5X, *6X, *7X, *8X |
| BDS | *2I, *6I, *1P, *5P | *2I, *6I, *1X, *5X |
| S-Basis Restriction | Parameter | Condition |
|---|---|---|
| CC-R S-basis | ||
| Pivot Receiver Clock | ||
| Pivot Receiver Code, Phase Biases | ||
| Receiver IF Code Bias | ||
| Receiver GF Code Bias | ||
| Satellite IF Code Bias | For signals exclusive to receiver Type A | |
| Satellite GF Code Bias | For signals exclusive to receiver Type A | |
| Pivot Receiver Ambiguities * | ||
| Pivot Satellite Ambiguities * | ||
| CC-R S-basis Adaptations | ||
| Pivot Satellite Code Bias | (For satellite code biases not observed by pivot receiver) | |
| Satellite GF Code Bias | (For GNSS A where no common signal between Receiver Type A and B exists) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platz, H.D. Sequential Generation of Multi-GNSS Multi-Frequency PPP-RTK Products and Their Performance Using the EUREF Permanent GNSS Network. Remote Sens. 2023, 15, 2792. https://doi.org/10.3390/rs15112792
Platz HD. Sequential Generation of Multi-GNSS Multi-Frequency PPP-RTK Products and Their Performance Using the EUREF Permanent GNSS Network. Remote Sensing. 2023; 15(11):2792. https://doi.org/10.3390/rs15112792
Chicago/Turabian StylePlatz, Hans Daniel. 2023. "Sequential Generation of Multi-GNSS Multi-Frequency PPP-RTK Products and Their Performance Using the EUREF Permanent GNSS Network" Remote Sensing 15, no. 11: 2792. https://doi.org/10.3390/rs15112792
APA StylePlatz, H. D. (2023). Sequential Generation of Multi-GNSS Multi-Frequency PPP-RTK Products and Their Performance Using the EUREF Permanent GNSS Network. Remote Sensing, 15(11), 2792. https://doi.org/10.3390/rs15112792