Hyperspectral Anomaly Detection with Auto-Encoder and Independent Target
Abstract
:1. Introduction
- It develops a novel approach of constructing a low-rank space, formed by the encoder weight matrix in a designed AE network with m neurons in the latent layer, to represent BKG. The adaptive determination of network structure can potentially and consciously prefer the reconstruction of BKG. The proposed BKG representation approach combines the advantages of data-driven and network structure constraints, which is different from other AE-based HAD methods that utilize the reconstruction error or latent feature of the AE framework.
- It utilizes an independent target/endmember extracted from the sphered residual component, which is obtained by projecting original data into the BKG orthogonal subspace, to construct the anomaly space. For further reduction in the influence of noise, SC constraint is imposed on the anomaly component. The proposed sparse anomaly component construction method can effectively represent anomalies by dealing with BKG and noise.
- This paper explores the effect of different components on the detection performance and demonstrates the applicability of different component combinations, which serve as a reference for the construction of subsequent detectors.
2. Methodology
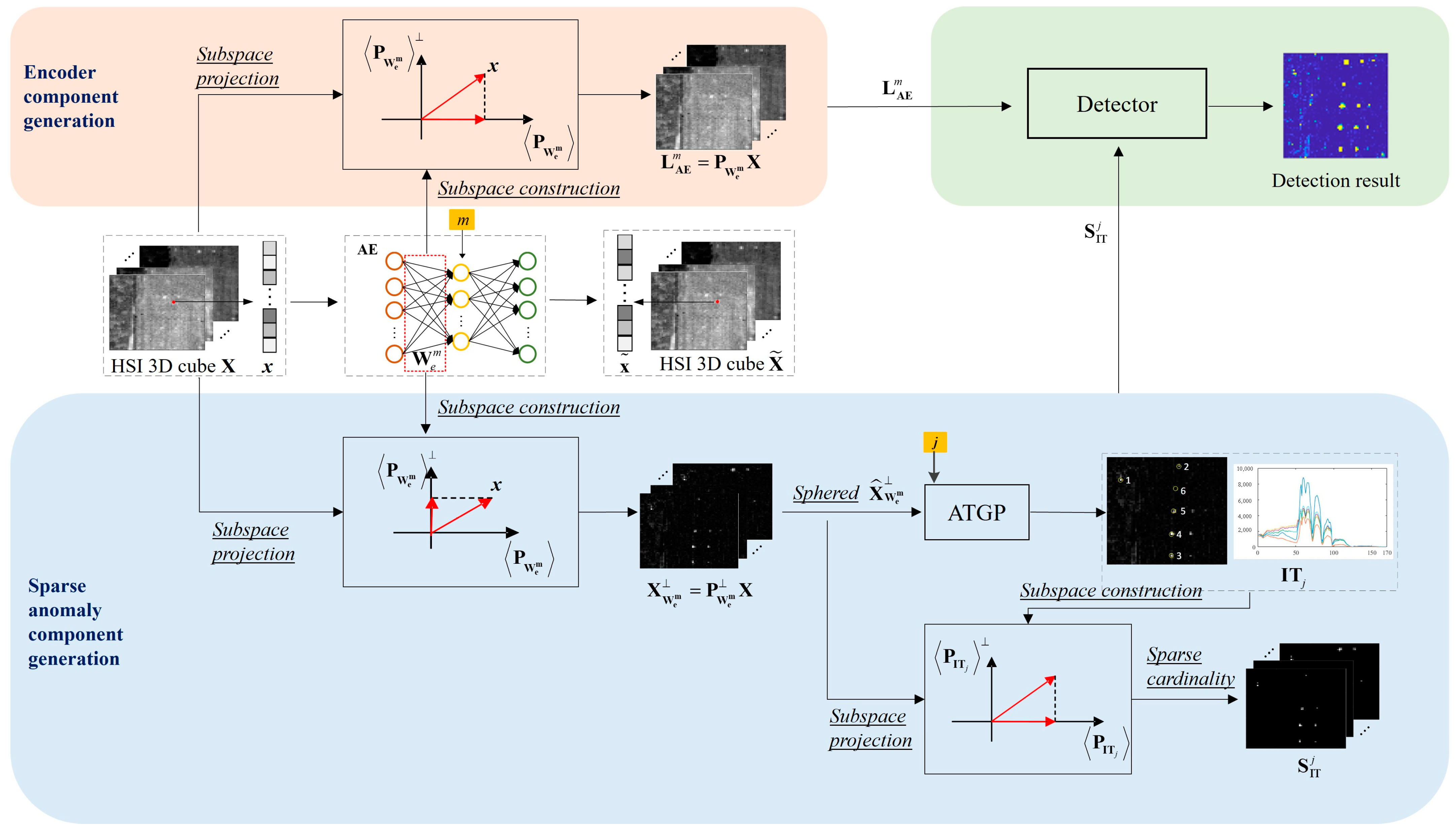
2.1. The LRaSMD Model with AE-IT
2.1.1. The BKG Component
2.1.2. The Anomaly Component
2.2. The Proposed AE-IT
| Algorithm 1: AE-IT Algorithm |
| 1. Initial conditions: m and j are determined by NWHFC and MX-SVD for original HSI 2. Use the designed AE to find encoder weight matrix . 3. Use (4) to find and ; 4. Find the sphered and find the first j target vectors by ATGP to form 5. Find in (6) and determine k for SC to obtain by (7) |
| Algorithm 2: MX-SVD |
| 1. Initial conditions: Let p be given and , i.e., . 2. Use SVD to find the first p principal left singular vectors (SV) of the data matrix , denoted by and let . 3. Let . Form . Use SVD to find the first principal left SVs, of the matrix and find 4. Repeat step 3 until . Continue 5. At this stage, calculate by |
2.3. The AE-IT for Different Anomalies by Correlating Multi-Components
3. Experiments and Results
3.1. Real Hyperspectral Images Used for Experiments
3.1.1. Dataset I: HYDICE Urban Scene
3.1.2. Dataset II: Pavia City Data
3.1.3. Dataset III: Hyperion Data
3.1.4. Dataset IV: San Diego Airport Scene
3.1.5. Dataset V: Gulfport Scene
3.2. Criteria
3.3. Parameter Settings
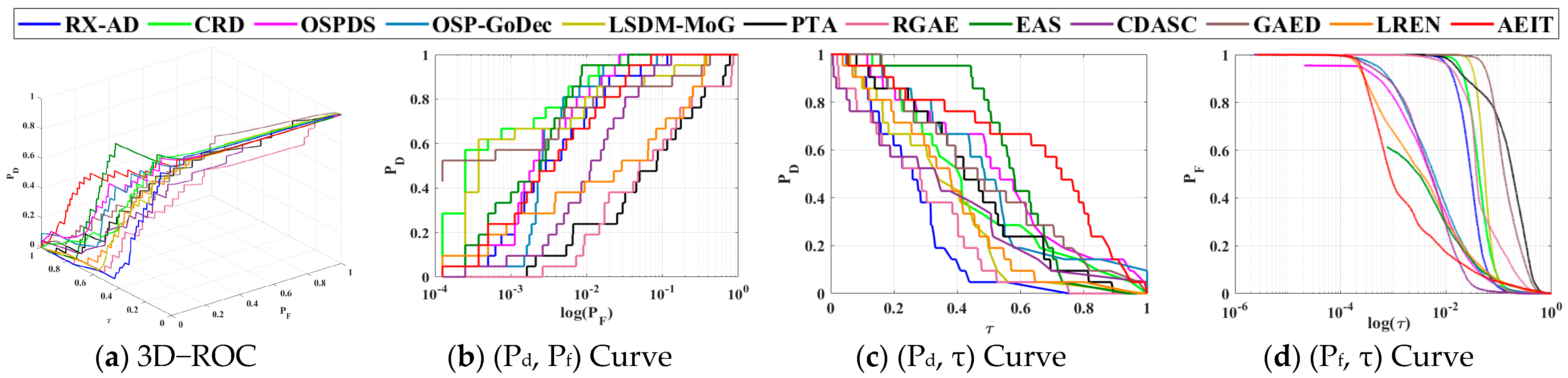
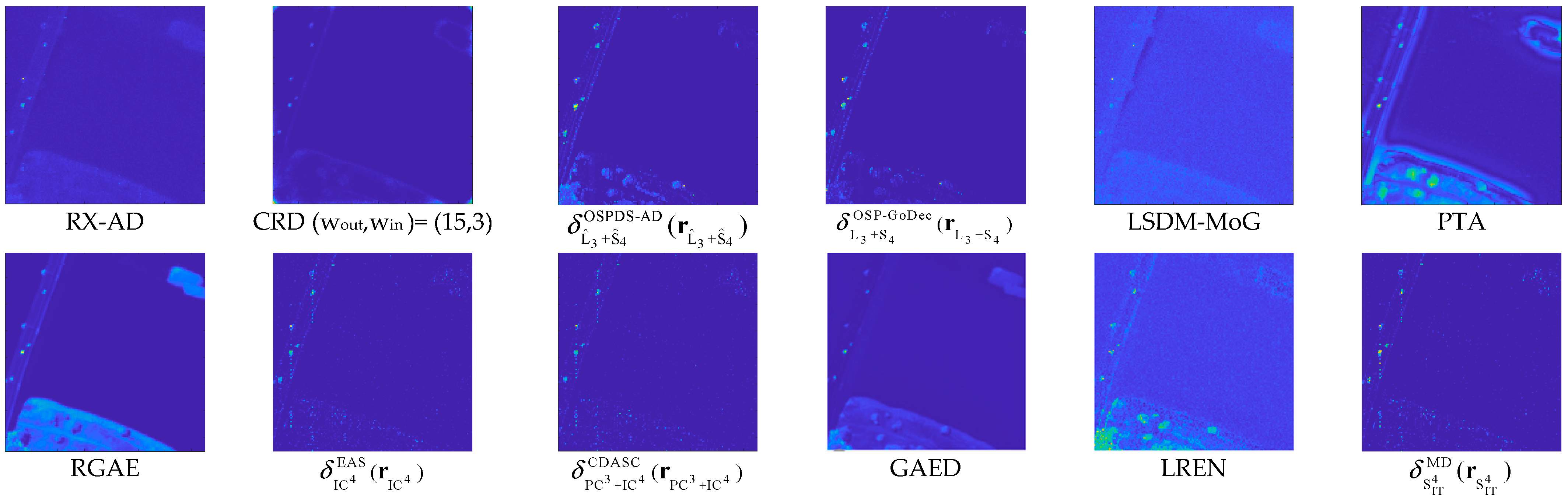
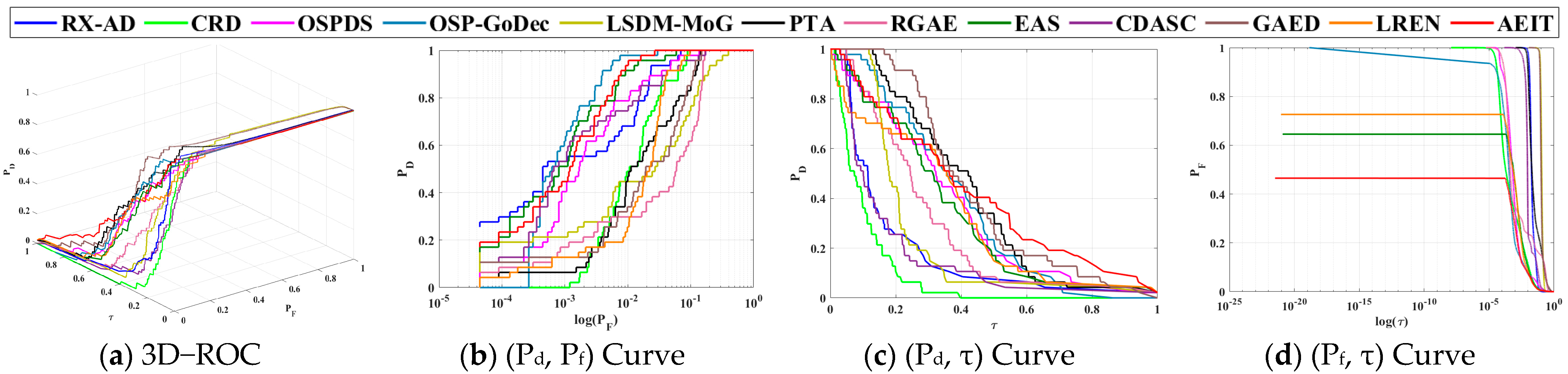
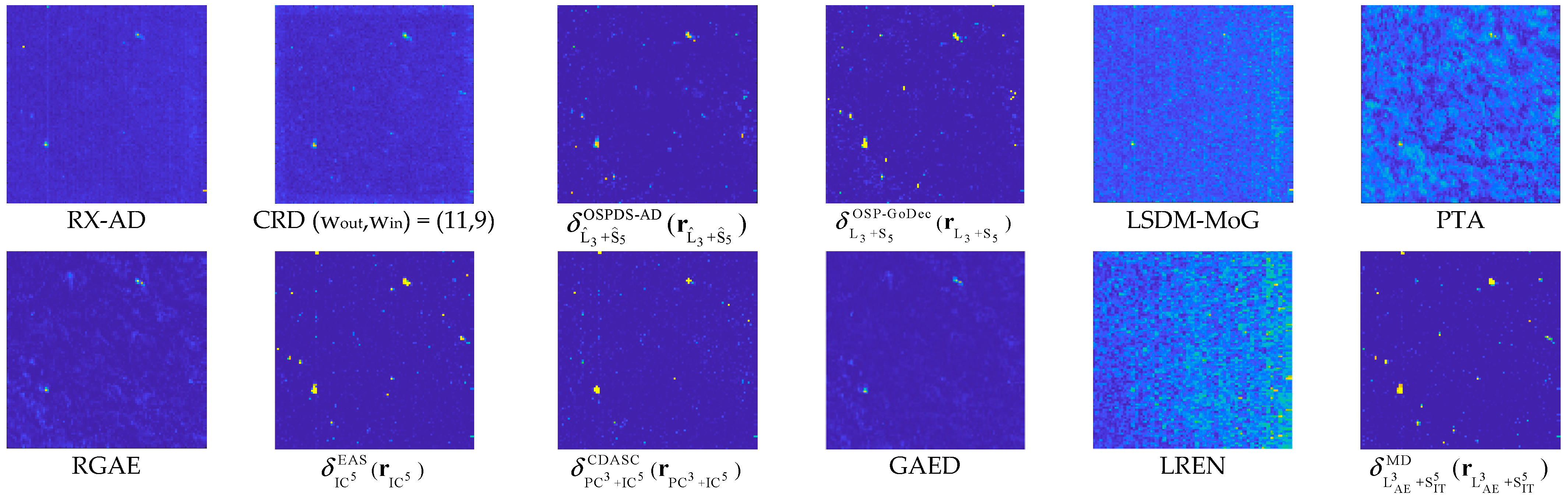
3.4. Results and Analysis
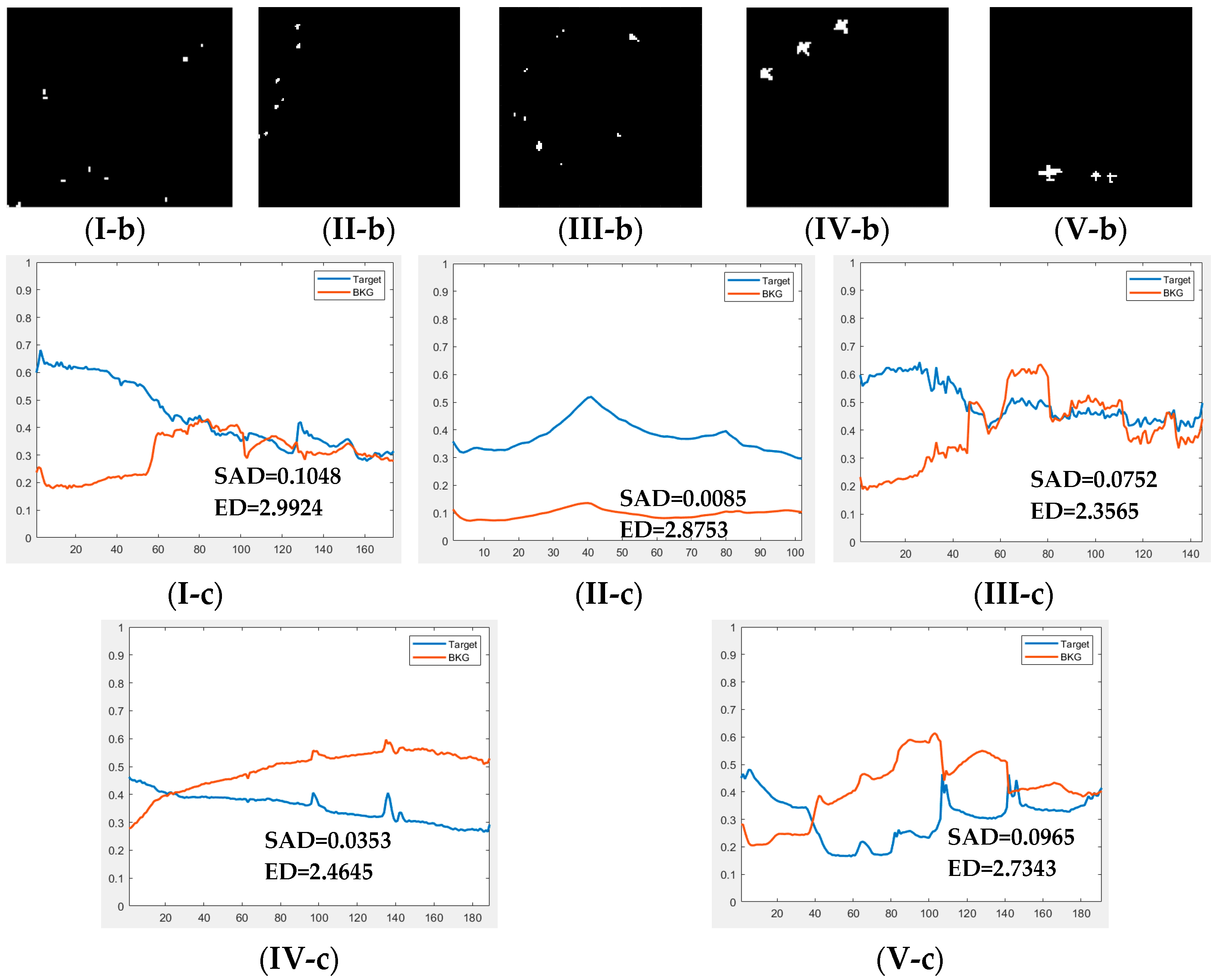
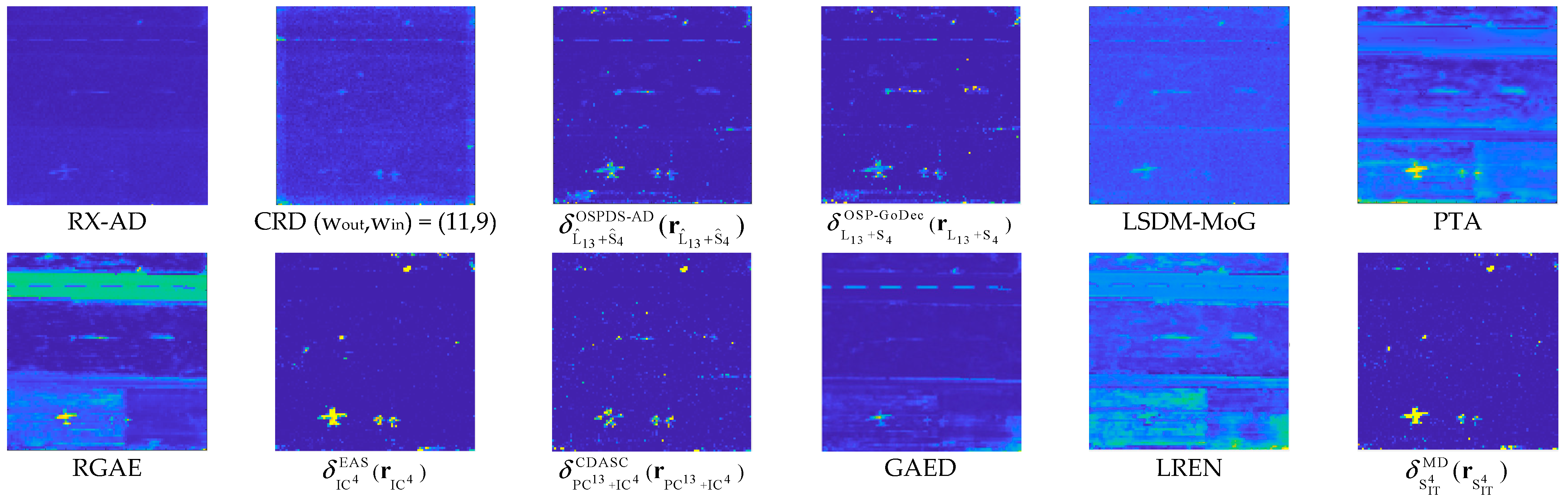
3.4.1. Experiments with Real Datasets
- HYDICE Urban Scene
- 2.
- Pavia City Scene
- 3.
- Hyperion Scene
- 4.
- San Diego Airport Scene
- 5.
- Gulfport Scene
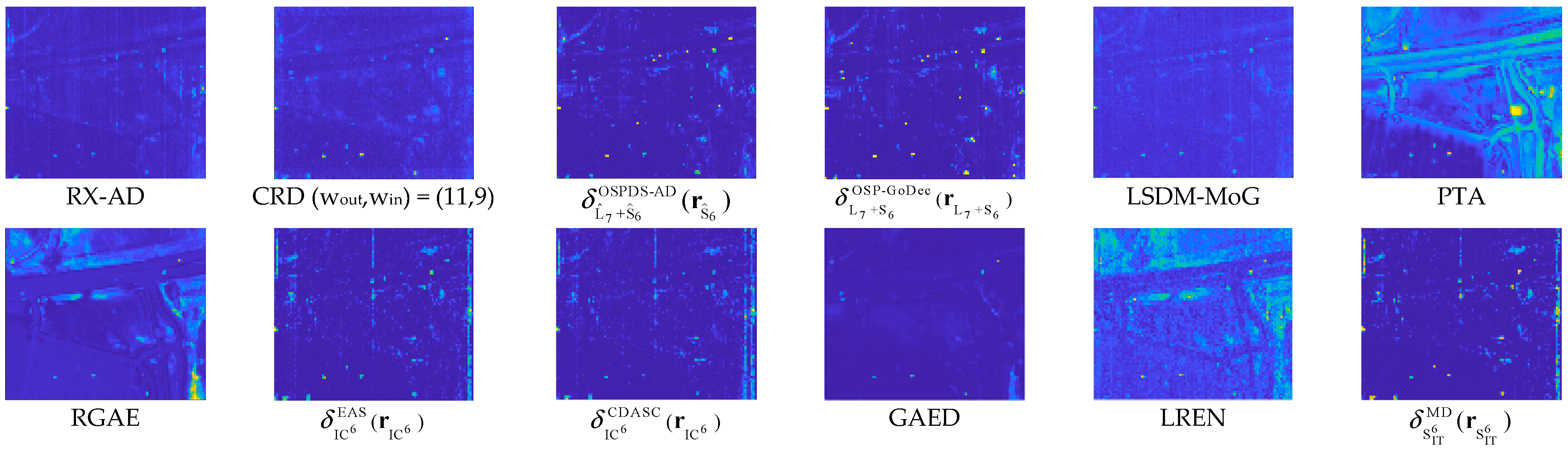
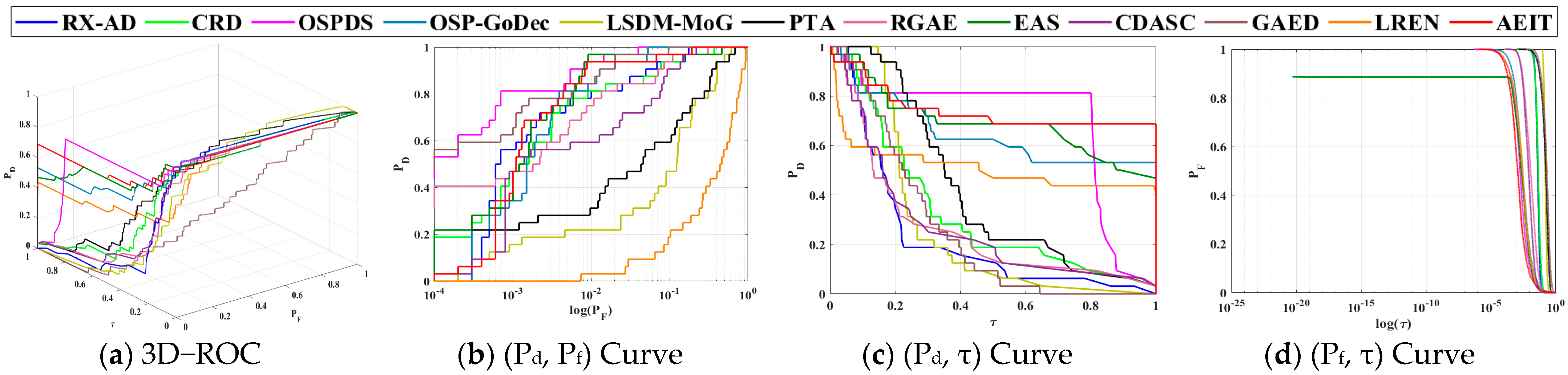
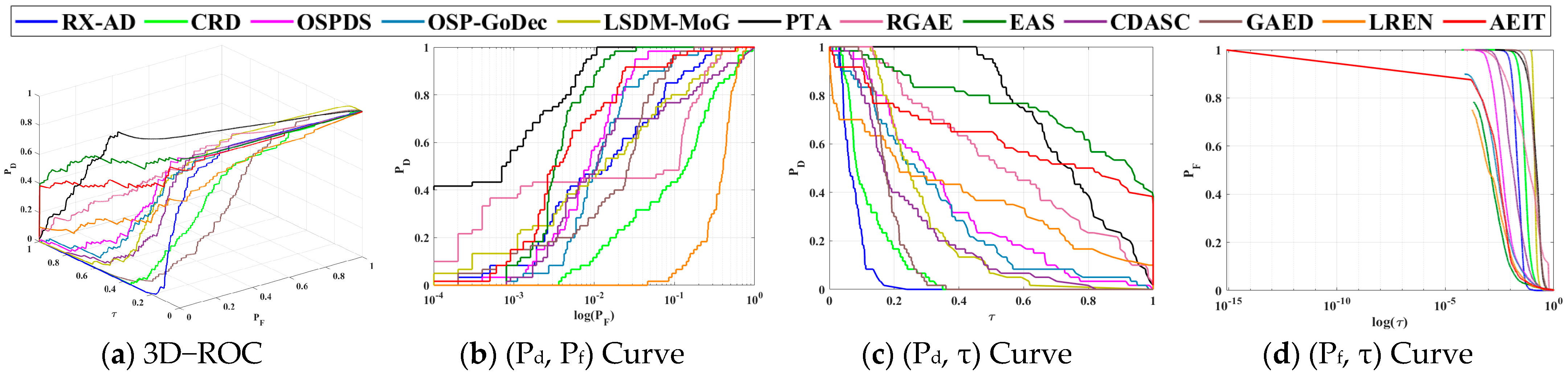
3.4.2. Comparative Analysis on Detection Performance
- HYDICE Urban Scene
- 2.
- Pavia Scene
- 3.
- Hyperion Scene
- 4.
- San Diego Airport Scene
- 5.
- Gulfport Scene
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, C.-I. Hyperspectral anomaly detection: A dual theory of hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511720. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Matteoli, S.; Veracini, T.; Diani, M.; Corsini, G. A locally adaptive background density estimator: An evolution for RX-based anomaly detectors. IEEE Geosci. Remote Sens. Lett. 2014, 11, 323–327. [Google Scholar] [CrossRef]
- Banerjee, A.; Burlina, P.; Diehl, C. A support vector method for anomaly detection in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2282–2291. [Google Scholar] [CrossRef]
- Wang, S.; Feng, W.; Quan, Y.; Bao, W.; Dauphin, G.; Gao, L.; Zhong, X.; Xing, M. Subfeature Ensemble-Based Hyperspectral Anomaly Detection Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5943–5952. [Google Scholar] [CrossRef]
- Yuan, S.; Shi, L.; Yao, B.; Li, F.; Du, Y. A hyperspectral anomaly detection algorithm using sub-features grouping and binary accumulation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6007505. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, J.; Wu, H.; Wang, J.; Sun, K. Self-adaptive low-rank and sparse decomposition for hyperspectral anomaly detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3672–3685. [Google Scholar] [CrossRef]
- Wu, Z.; Su, H.; Tao, X.; Han, L.; Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Hyperspectral anomaly detection with relaxed collaborative representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5533417. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1990–2000. [Google Scholar] [CrossRef]
- Cheng, T.; Wang, B. Graph and total variation regularized low-rank representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2019, 58, 391–406. [Google Scholar] [CrossRef]
- Feng, R.; Li, H.; Wang, L.; Zhong, Y.; Zhang, L.; Zeng, T. Local spatial constraint and total variation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5512216. [Google Scholar] [CrossRef]
- Zhao, C.; Li, C.; Feng, S.; Jia, X. Enhanced total variation regularized representation model with endmember background dictionary for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518312. [Google Scholar] [CrossRef]
- Candes, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2009, 58, 1027–1063. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, D. GoDec: Randomized low-rank & sparsity matrix decomposition in noisy case. In Proceedings of the 28th International Conference on Machine Learning, ICML 2011, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Chang, C.-I.; Cao, H.; Chen, S.; Shang, X.; Song, M.; Yu, C. Orthogonal subspace projection-based GoDec for low rank and sparsity matrix decomposition for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2403–2429. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Du, Q.; Tao, R. Low-rank and sparse decomposition with mixture of Gaussian for hyperspectral anomaly detection. IEEE Trans. Cybern. 2021, 51, 4363–4372. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Qu, Y.; Zhao, C.; Tao, R.; Du, Q. Prior-based tensor approximation for anomaly detection in hyperspectral imagery. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1037–1050. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z. Joint reconstruction and anomaly detection from compressive hyperspectral images using Mahalanobis distance-regularized tensor RPCA. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2919–2930. [Google Scholar] [CrossRef]
- Chang, C.-I.; Cao, H.; Song, M. Orthogonal subspace projection target detector for hyperspectral anomaly detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4915–4932. [Google Scholar] [CrossRef]
- Chen, S.; Chang, C.-I.; Li, X. Component Decomposition Analysis for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5516222. [Google Scholar] [CrossRef]
- Huyan, N.; Zhang, X.; Zhou, H.; Jiao, L. Hyperspectral anomaly detection via background and potential anomaly dictionaries construction. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2263–2276. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, M.; Cheng, X.; Wang, L.; Xu, M.; Wang, H. Hyperspectral anomaly detection via dual dictionaries construction guided by two-stage complementary decision. Remote Sens. 2022, 14, 1784. [Google Scholar] [CrossRef]
- Cheng, T.; Wang, B. Total variation and sparsity regularized decomposition model with union dictionary for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1472–1486. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, B. Kernel-Based Decomposition Model with Total Variation and Sparsity Regularizations via Union Dictionary for Nonlinear Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5542916. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, M.; Cheng, X.; Zhou, K.; Zhao, S.; Wang, H. Dual Collaborative Constraints Regularized Low-Rank and Sparse Representation via Robust Dictionaries Construction for Hyperspectral Anomaly Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 16, 2009–2024. [Google Scholar] [CrossRef]
- Su, H.; Wu, Z.; Zhu, A.X.; Du, Q. Low rank and collaborative representation for hyperspectral anomaly detection via robust dictionary construction. ISPRS J. Photogramm. Remote Sens. 2020, 169, 195–211. [Google Scholar] [CrossRef]
- Xiang, P.; Li, H.; Song, J.; Wang, D.; Zhang, J.; Zhou, H. Spectral–spatial complementary decision fusion for hyperspectral anomaly detection. Remote Sens. 2022, 14, 943. [Google Scholar] [CrossRef]
- Cheng, X.; Wen, M.; Gao, C.; Wang, Y. Hyperspectral anomaly detection based on wasserstein distance and spatial filtering. Remote Sens. 2022, 14, 2730. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, L. Spectral-spatial stacked autoencoders based on low-rank and sparse matrix decomposition for hyperspectral anomaly detection. Infrared Phys. Technol. 2018, 92, 166–176. [Google Scholar] [CrossRef]
- Fan, G.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Hyperspectral anomaly detection with robust graph autoencoders. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511314. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, L.; Zhong, Y. Auto-AD: Autonomous Hyperspectral Anomaly Detection Network Based on Fully Convolutional Autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5503314. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, L.; Zhong, Y. Deep Low-Rank Prior for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5527017. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y.; Xie, W.; Du, Q. Discriminative reconstruction constrained generative adversarial network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4666–4679. [Google Scholar] [CrossRef]
- Xiang, P.; Ali, S.; Jung, S.K.; Zhou, H. Hyperspectral anomaly detection with guided autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5538818. [Google Scholar] [CrossRef]
- Jiang, K.; Xie, W.; Lei, J.; Jiang, T.; Li, Y. LREN: Low-rank embedded network for sample-free hyperspectral anomaly detection. Proc. AAAI Conf. Artif. Intell. 2021, 35, 4139–4146. [Google Scholar] [CrossRef]
- Chang, C.-I. A review of virtual dimensionality for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1285–1305. [Google Scholar] [CrossRef]
- Chang, C.-I.; Xiong, W.; Wen, C.H. A theory of high order statistics-based virtual dimensionality for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 188–208. [Google Scholar] [CrossRef]
- Kuybeda, O.; Malah, D.; Barzohar, M. Rank estimation and redundancy reduction of high-dimensional noisy signals with preservation of rare vectors. IEEE Trans. Signal Process. 2007, 55, 5579–5592. [Google Scholar] [CrossRef]
- Chang, C.-I. An effective evaluation tool for hyperspectral target detection: 3D receiver operating characteristic curve analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5131–5153. [Google Scholar] [CrossRef]
- Chang, C.-I. Comprehensive Analysis of Receiver Operating Characteristic (ROC) Curves for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5541124. [Google Scholar] [CrossRef]
- Wei, L.; Qian, D. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar]
- Chang, C.-I. Effective anomaly space for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5526624. [Google Scholar] [CrossRef]
- Chang, C.-I. Target-to-anomaly conversion for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5540428. [Google Scholar] [CrossRef]
- Chang, C.-I.; Lin, C.Y.; Chung, P.C.; Hu, P.F. Iterative Spectral-Spatial Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5504330. [Google Scholar] [CrossRef]

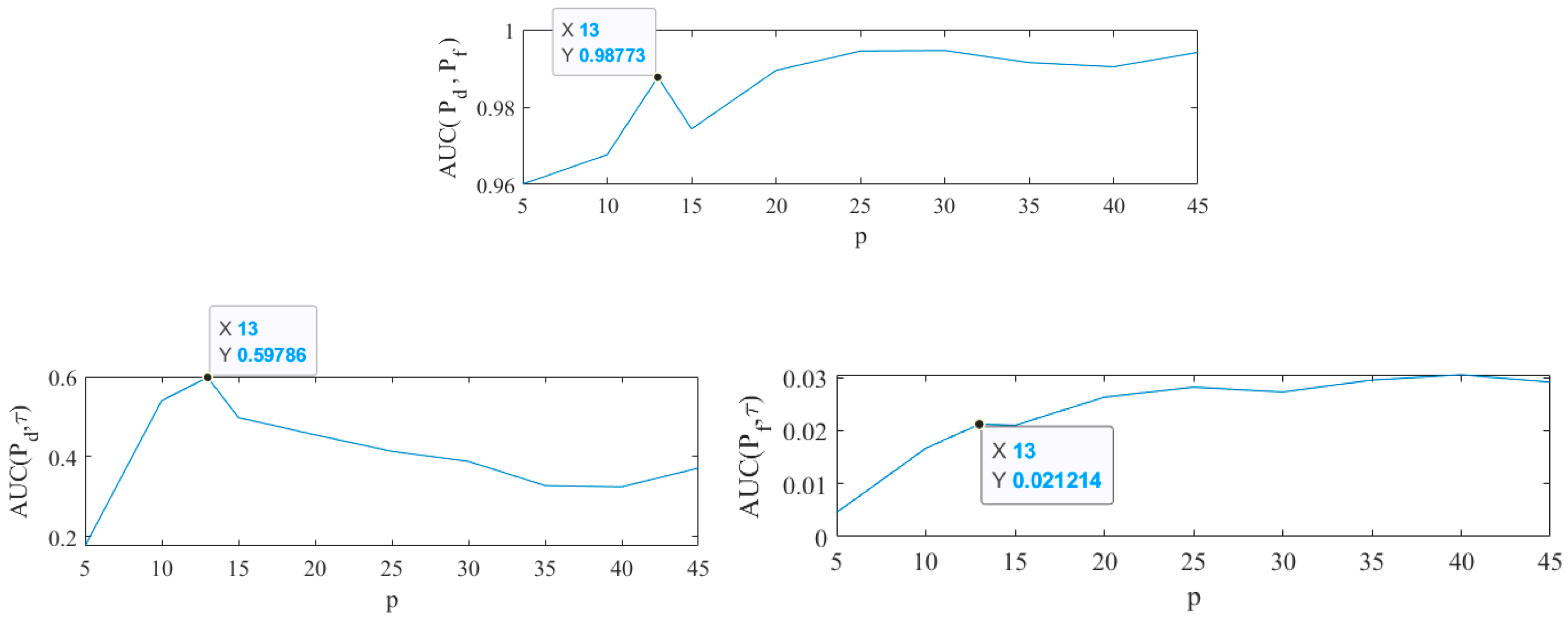







| Dataset | p | m | j | (wout, win) for CRD [42] |
|---|---|---|---|---|
| HYDICE Urban Scene | 13 | 7 | 6 | (wout,win) = (11,9) |
| Pavia City Scene | 7 | 3 | 4 | (wout,win) = (15,3) |
| Hyperion Scene | 8 | 3 | 5 | (wout,win) = (11,9) |
| San Diego Airport Scene | 11 | 2 | 9 | (wout,win) = (15,9) |
| Gulfport Scene | 17 | 13 | 4 | (wout,win) = (11,9) |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP |
|---|---|---|---|---|---|---|---|---|---|
| 0.9870 | 0.0210 | 0.6402 | 0.9790 | 1.6272 | 1.9660 | 1.6192 | 30.521 | 2.6062 | |
| 0.9651 | 0.0012 | 0.1042 | 0.9988 | 1.0693 | 1.9639 | 1.1030 | 85.920 | 2.0681 | |
| 0.9874 | 0.0208 | 0.6133 | 0.9792 | 1.6007 | 1.9666 | 1.5925 | 29.497 | 2.5799 | |
| 0.6599 | 0.1542 | 0.2078 | 0.8458 | 0.8677 | 1.5057 | 1.0537 | 1.3479 | 1.7135 | |
| 0.9850 | 0.0011 | 0.1031 | 0.9989 | 1.0881 | 1.9839 | 1.1019 | 90.846 | 2.0869 | |
| 0.9873 | 0.0210 | 0.6135 | 0.9790 | 1.6008 | 1.9663 | 1.5925 | 29.190 | 2.5798 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP |
|---|---|---|---|---|---|---|---|---|---|
| 0.9970 | 0.0040 | 0.4068 | 0.9960 | 1.4037 | 1.9930 | 1.4028 | 101.99 | 2.3997 | |
| 0.9763 | 0.0005 | 0.0711 | 0.9995 | 1.0474 | 1.9758 | 1.0705 | 140.41 | 2.0469 | |
| 0.9970 | 0.0040 | 0.4057 | 0.9960 | 1.4026 | 1.9930 | 1.4017 | 101.70 | 2.3986 | |
| 0.9560 | 0.0323 | 0.2892 | 0.9677 | 1.2452 | 1.9237 | 1.2569 | 8.9553 | 2.2129 | |
| 0.9753 | 0.0005 | 0.0713 | 0.9995 | 1.0466 | 1.9748 | 1.0708 | 140.21 | 2.0461 | |
| 0.9970 | 0.0040 | 0.4058 | 0.9960 | 1.4028 | 1.9930 | 1.4018 | 101.70 | 2.3988 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP |
|---|---|---|---|---|---|---|---|---|---|
| 0.9818 | 0.0065 | 0.7576 | 0.9935 | 1.7393 | 1.9753 | 1.7511 | 116.50 | 2.7328 | |
| 0.0870 | 0.1444 | 0.0870 | 0.8556 | 0.1740 | 0.9426 | 0.9426 | 0.6023 | 1.0296 | |
| 0.9794 | 0.0097 | 0.6229 | 0.9903 | 1.6023 | 1.9697 | 1.6132 | 64.304 | 2.5926 | |
| 0.9228 | 0.1817 | 0.4715 | 0.8183 | 1.3943 | 1.7411 | 1.2898 | 2.5951 | 2.2126 | |
| 0.9975 | 0.0023 | 0.1704 | 0.9977 | 1.1679 | 1.9952 | 1.1680 | 73.033 | 2.1655 | |
| 0.9913 | 0.0068 | 0.7581 | 0.9932 | 1.7495 | 1.9846 | 1.7514 | 111.98 | 2.7427 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP |
|---|---|---|---|---|---|---|---|---|---|
| 0.8532 | 0.0252 | 0.0907 | 0.9748 | 0.9439 | 1.8279 | 1.0654 | 3.5915 | 1.9186 | |
| 0.2816 | 0.2365 | 0.2254 | 0.7635 | 0.5070 | 1.0452 | 0.9889 | 0.9532 | 1.2706 | |
| 0.8534 | 0.0253 | 0.0905 | 0.9747 | 0.9438 | 1.8281 | 1.0652 | 3.5756 | 1.9185 | |
| 0.6688 | 0.1242 | 0.1715 | 0.8758 | 0.8403 | 1.5446 | 1.0473 | 1.3811 | 1.7161 | |
| 0.9013 | 0.0224 | 0.1633 | 0.9776 | 1.0646 | 1.8789 | 1.1408 | 7.2772 | 2.0422 | |
| 0.8584 | 0.0255 | 0.0912 | 0.9745 | 0.9496 | 1.8329 | 1.0657 | 3.5765 | 1.9241 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP |
|---|---|---|---|---|---|---|---|---|---|
| 0.9794 | 0.0135 | 0.6491 | 0.9865 | 1.6285 | 1.9659 | 1.6356 | 48.1138 | 2.6150 | |
| 0.9108 | 0.0006 | 0.0050 | 0.9994 | 0.9158 | 1.9102 | 1.0044 | 8.3738 | 1.9152 | |
| 0.9848 | 0.0141 | 0.5687 | 0.9859 | 1.5535 | 1.9707 | 1.5546 | 40.3545 | 2.5395 | |
| 0.6482 | 0.1597 | 0.2023 | 0.8403 | 0.8505 | 1.4885 | 1.0426 | 1.2668 | 1.6908 | |
| 0.9103 | 0.0006 | 0.0050 | 0.9994 | 0.9153 | 1.9097 | 1.0044 | 8.3603 | 1.9147 | |
| 0.9815 | 0.0143 | 0.6426 | 0.9857 | 1.6241 | 1.9672 | 1.6284 | 44.9524 | 2.6098 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP | Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| RX-AD | 0.9872 | 0.0361 | 0.2641 | 0.9639 | 1.2514 | 1.9511 | 1.2280 | 7.3144 | 2.2153 | 0.96 |
| CRD | 0.9978 | 0.0472 | 0.4739 | 0.9528 | 1.4716 | 1.9506 | 1.4267 | 10.039 | 2.4244 | 4.50 |
| OSPDS-AD | 0.9942 | 0.0182 | 0.5103 | 0.9818 | 1.5045 | 1.9760 | 1.4921 | 28.027 | 2.4863 | 570.33 |
| OSP-GoDec | 0.9921 | 0.0196 | 0.5005 | 0.9804 | 1.4926 | 1.9725 | 1.4809 | 25.502 | 2.4730 | 11.44 |
| LSDM-MoG | 0.9826 | 0.0546 | 0.2795 | 0.9454 | 1.2621 | 1.9280 | 1.2249 | 5.1181 | 2.2075 | 8.54 |
| PTA | 0.8175 | 0.2081 | 0.4478 | 0.7919 | 1.2653 | 1.6095 | 1.2397 | 2.1518 | 2.0572 | 12.77 |
| RGAE | 0.8148 | 0.0745 | 0.2697 | 0.9255 | 1.0845 | 1.7404 | 1.1952 | 3.6215 | 2.0100 | 58.91 |
| EAS | 0.9956 | 0.0232 | 0.5847 | 0.9768 | 1.5803 | 1.9724 | 1.5615 | 25.186 | 2.5571 | 0.78 |
| CDASC | 0.9758 | 0.0244 | 0.3658 | 0.9756 | 1.3417 | 1.9515 | 1.3415 | 15.012 | 2.3173 | 3.53 |
| GAED | 0.9535 | 0.0096 | 0.3324 | 0.9904 | 1.2859 | 1.9439 | 1.3228 | 34.6707 | 2.2763 | 41.83 |
| LREN | 0.8988 | 0.1698 | 0.4994 | 0.8302 | 1.3982 | 1.7289 | 1.3296 | 2.9404 | 2.2283 | 39.04 |
| AE-IT | 0.9873 | 0.0210 | 0.6135 | 0.9790 | 1.6008 | 1.9663 | 1.5925 | 29.190 | 2.5798 | 52.90 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP | Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| RX-AD | 0.9905 | 0.0233 | 0.1730 | 0.9767 | 1.1635 | 1.9672 | 1.1497 | 7.4149 | 2.1402 | 5.52 |
| CRD | 0.9794 | 0.0053 | 0.0979 | 0.9947 | 1.0773 | 1.9741 | 1.0926 | 18.607 | 2.0720 | 33.03 |
| OSPDS-AD | 0.9904 | 0.0077 | 0.4141 | 0.9923 | 1.4046 | 1.9827 | 1.4064 | 53.565 | 2.3968 | 1104.16 |
| OSP-GoDec | 0.9980 | 0.0041 | 0.3719 | 0.9959 | 1.3699 | 1.9939 | 1.3678 | 91.200 | 2.3658 | 38.31 |
| LSDM-MoG | 0.9318 | 0.0519 | 0.1570 | 0.9481 | 1.0888 | 1.8800 | 1.1051 | 3.0258 | 2.0369 | 12.97 |
| PTA | 0.9635 | 0.0590 | 0.3952 | 0.9410 | 1.3588 | 1.9045 | 1.3362 | 6.7001 | 2.2998 | 25.05 |
| RGAE | 0.9278 | 0.0383 | 0.2705 | 0.9617 | 1.1982 | 1.8894 | 1.2321 | 7.0548 | 2.1599 | 127.09 |
| EAS | 0.9957 | 0.0046 | 0.3238 | 0.9954 | 1.3196 | 1.9911 | 1.3192 | 69.894 | 2.3149 | 5.49 |
| CDASC | 0.9859 | 0.0043 | 0.3199 | 0.9957 | 1.3057 | 1.9816 | 1.3156 | 74.717 | 2.3014 | 34.55 |
| GAED | 0.9569 | 0.0186 | 0.1584 | 0.9814 | 1.1153 | 1.9383 | 1.1399 | 8.529 | 2.0967 | 91.81 |
| LREN | 0.9758 | 0.1210 | 0.4361 | 0.8790 | 1.4119 | 1.8549 | 1.3151 | 3.6055 | 2.2910 | 59.95 |
| AE-IT | 0.9970 | 0.0040 | 0.4068 | 0.9960 | 1.4037 | 1.9930 | 1.4028 | 101.99 | 2.3997 | 33.30 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP | Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| RX-AD | 0.9829 | 0.0435 | 0.2319 | 0.9565 | 1.2148 | 1.9395 | 1.1884 | 5.3358 | 2.1714 | 1.32 |
| CRD | 0.9574 | 0.0768 | 0.3678 | 0.9232 | 1.3252 | 1.8806 | 1.2910 | 4.7866 | 2.2484 | 10.87 |
| OSPDS-AD | 0.9949 | 0.0074 | 0.4203 | 0.9926 | 1.4152 | 1.9875 | 1.4129 | 56.6127 | 2.4078 | 1073.96 |
| OSP-GoDec | 0.9938 | 0.0099 | 0.6507 | 0.9901 | 1.6445 | 1.9839 | 1.6407 | 65.5467 | 2.6346 | 13.19 |
| LSDM-MoG | 0.8480 | 0.1861 | 0.2926 | 0.8139 | 1.1406 | 1.6619 | 1.1066 | 1.5727 | 1.9546 | 6.70 |
| PTA | 0.8676 | 0.1802 | 0.4063 | 0.8198 | 1.2739 | 1.6874 | 1.2260 | 2.2542 | 2.0937 | 13.70 |
| RGAE | 0.9777 | 0.0178 | 0.2460 | 0.9822 | 1.2237 | 1.9599 | 1.2282 | 13.7923 | 2.2059 | 74.97 |
| EAS | 0.9831 | 0.0082 | 0.6957 | 0.9918 | 1.6788 | 1.9749 | 1.6875 | 84.5472 | 2.6706 | 1.42 |
| CDASC | 0.9675 | 0.0082 | 0.5127 | 0.9918 | 1.4801 | 1.9593 | 1.5045 | 62.5347 | 2.4719 | 7.99 |
| GAED | 0.9942 | 0.0117 | 0.2565 | 0.9883 | 1.2507 | 1.9825 | 1.2448 | 22.0067 | 2.239 | 18.80 |
| LREN | 0.5525 | 0.2258 | 0.2551 | 0.7742 | 0.8077 | 1.3268 | 1.0294 | 1.1301 | 1.5819 | 87.39 |
| AE-IT | 0.9913 | 0.0068 | 0.7581 | 0.9932 | 1.7495 | 1.9846 | 1.7514 | 111.9838 | 2.7427 | 70.28 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP | Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| RX-AD | 0.8314 | 0.0453 | 0.0803 | 0.9547 | 0.9117 | 1.7861 | 1.0349 | 1.7708 | 1.8663 | 1.23 |
| CRD | 0.8177 | 0.0620 | 0.1142 | 0.9380 | 0.9319 | 1.7556 | 1.0522 | 1.8413 | 1.8699 | 29.00 |
| OSPDS-AD | 0.8775 | 0.0091 | 0.1396 | 0.9909 | 1.0171 | 1.8684 | 1.1305 | 15.3034 | 2.0080 | 1091.95 |
| OSP-GoDec | 0.9307 | 0.0140 | 0.1576 | 0.9860 | 1.0882 | 1.9167 | 1.1436 | 11.2881 | 2.0743 | 14.88 |
| LSDM-MoG | 0.8647 | 0.1197 | 0.2013 | 0.8803 | 1.0660 | 1.7450 | 1.0817 | 1.6823 | 1.9463 | 2.12 |
| PTA | 0.9846 | 0.1939 | 0.6914 | 0.8061 | 1.6761 | 1.7908 | 1.4976 | 3.5667 | 2.4822 | 17.18 |
| RGAE | 0.9014 | 0.0242 | 0.1547 | 0.9758 | 1.0560 | 1.8772 | 1.1305 | 6.3930 | 2.0318 | 79.49 |
| EAS | 0.8527 | 0.0198 | 0.0973 | 0.9802 | 0.9500 | 1.8329 | 1.0775 | 4.9113 | 1.9301 | 1.31 |
| CDASC | 0.9011 | 0.0210 | 0.1608 | 0.9790 | 1.0619 | 1.8801 | 1.1398 | 7.6697 | 2.0409 | 7.60 |
| GAED | 0.9438 | 0.0151 | 0.1626 | 0.9849 | 1.1064 | 1.9287 | 1.1475 | 10.7552 | 2.0913 | 81.34 |
| LREN | 0.7596 | 0.2880 | 0.4325 | 0.712 | 1.1921 | 1.4716 | 1.1446 | 1.5021 | 1.9041 | 33.77 |
| AE-IT | 0.9013 | 0.0224 | 0.1633 | 0.9776 | 1.0646 | 1.8789 | 1.1408 | 7.2772 | 2.0422 | 75.37 |
| Detector | AUC(D,F) | AUC(F,τ) | AUCADP = AUC(D,τ) | AUCBDP = 1 − AUC(F,τ) | AUCJAD | AUCJBS | AUCADBS | AUCSNPR | AUCOADP | Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| RX-AD | 0.9526 | 0.0248 | 0.0746 | 0.9752 | 1.0272 | 1.9278 | 1.0498 | 3.0074 | 2.0024 | 1.23 |
| CRD | 0.8052 | 0.0583 | 0.1201 | 0.9417 | 0.9253 | 1.7469 | 1.0618 | 2.0613 | 1.8670 | 4.67 |
| OSPDS-AD | 0.9844 | 0.0171 | 0.3515 | 0.9829 | 1.3359 | 1.9674 | 1.3344 | 20.5994 | 2.3189 | 1077.15 |
| OSP-GoDec | 0.9759 | 0.0160 | 0.3131 | 0.9840 | 1.2890 | 1.9599 | 1.2971 | 19.5484 | 2.2729 | 14.99 |
| LSDM-MoG | 0.9300 | 0.1395 | 0.2848 | 0.8605 | 1.2148 | 1.7905 | 1.1452 | 2.0409 | 2.0753 | 7.64 |
| PTA | 0.9979 | 0.1700 | 0.7327 | 0.8300 | 1.7306 | 1.8278 | 1.5627 | 4.3095 | 2.5606 | 17.23 |
| RGAE | 0.8951 | 0.1525 | 0.5483 | 0.8475 | 1.4435 | 1.7427 | 1.3959 | 3.5963 | 2.2910 | 79.50 |
| EAS | 0.9949 | 0.0117 | 0.7628 | 0.9883 | 1.7577 | 1.9832 | 1.7510 | 65.0084 | 2.7459 | 1.29 |
| CDASC | 0.8895 | 0.0130 | 0.3770 | 0.9870 | 1.2665 | 1.8765 | 1.3641 | 29.0926 | 2.2536 | 7.61 |
| GAED | 0.9671 | 0.0301 | 0.2414 | 0.9699 | 1.2084 | 1.937 | 1.2113 | 8.0225 | 2.1783 | 21.60 |
| LREN | 0.6105 | 0.1668 | 0.1825 | 0.8332 | 0.793 | 1.4436 | 1.0157 | 1.0939 | 1.6261 | 35.92 |
| AE-IT | 0.9794 | 0.0135 | 0.6491 | 0.9865 | 1.6285 | 1.9659 | 1.6356 | 48.1138 | 2.6150 | 71.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Li, X.; Yan, Y. Hyperspectral Anomaly Detection with Auto-Encoder and Independent Target. Remote Sens. 2023, 15, 5266. https://doi.org/10.3390/rs15225266
Chen S, Li X, Yan Y. Hyperspectral Anomaly Detection with Auto-Encoder and Independent Target. Remote Sensing. 2023; 15(22):5266. https://doi.org/10.3390/rs15225266
Chicago/Turabian StyleChen, Shuhan, Xiaorun Li, and Yunfeng Yan. 2023. "Hyperspectral Anomaly Detection with Auto-Encoder and Independent Target" Remote Sensing 15, no. 22: 5266. https://doi.org/10.3390/rs15225266
APA StyleChen, S., Li, X., & Yan, Y. (2023). Hyperspectral Anomaly Detection with Auto-Encoder and Independent Target. Remote Sensing, 15(22), 5266. https://doi.org/10.3390/rs15225266






