Abstract
This study assesses coastal flooding extension mapping based on two innovative approaches. The first is based on the coupling of two robust numerical models (SWASH and LISFLOOD); in this case, discharges were extracted from the wave overtopping results from SWASH 1D and set as boundary conditions for LISFLOOD on the crest of an existing seawall where overtopping typically occurs. The second, hereby called the ‘Tilted Bathtub Approach’ (TBTA), is based on wave run-up levels and buffering the affected area of a prior flooding event, adjusting it for expected sea states according to different return periods. The proposed approaches are applied to a case study on the Northern Portuguese coast, at Furadouro beach, in the municipality of Ovar, which has been facing multiple flooding episodes throughout recent years, including a dramatic storm in February 2014. This event was used as validation for the proposed methods. A 30-year-long hourly local wave climate time series was used both to perform an extreme value analysis in order to obtain expected sea states according to different return periods and also for performing a sensitivity test for established empirical formulas to estimate wave run-up in this particular case. Results indicate both approaches are valuable: they yield coherent flood extension predictions that align well with the real inundated area from the 2014 storm. The convergence of these findings underscores the potential for these methods in future coastal flood risk assessment, planning, and understanding of coastal responses under extreme weather conditions.
1. Introduction
The Portuguese coastal zone has one of the most energetic wave climates in the world, and it also faces intense anthropic pressure, with its main public and private infrastructures located in this area, as well as housing about 75% of the Portuguese population [1]. Therefore, it has been suffering from systematic coastal flooding episodes at several spots, with an increasing trend being observed in recent decades [2]. Although many of the occupied zones on the Portuguese coast are heavily modified with defence structures, such as groins, breakwaters, and artificial nourishment, it has been showing an insufficient capability of preventing such hazardous events, resulting in risk to the population and economic assets. The climate change scenario is likely to dramatically increase these risk situations within the next decades, with mean sea level rises and extreme events, which has already confirmed this concern with the recent increased episodes of coastal flooding.
Coastal flooding occurrence is not likely to depend on a single factor but a combination of variables, which makes it a so-called compound event [3]. While tides and waves are the more apparent variables, a multitude of others, including wind, currents, rainfall, erosion, storm surges, and river discharges, interplay and intensify the situation. Extreme weather conditions, especially with the increasing frequency and intensity of tropical and extra-tropical cyclones [4], further compound these interactions, exacerbating vulnerabilities in several coastal areas. Nonetheless, in Portugal, coastal flooding predominantly results from wave-induced events, correlating with high-energy storms in the North Atlantic, often originated by extra-tropical cyclones [5], that result in long-period waves, which have been found to be critical for wave overtopping situations, especially in harbour resonance and coastal defence structures [6,7]. Furthermore, shore retreat and unsuitable developments in vulnerable areas have also potentialised this scenario. Furadouro (N 40°53′2.0″, W 8°40′24.9″) is one of the hotspots for these episodes, and it will be assessed in this case study.
A robust approach to analyse wave-induced coastal flooding is through numerical models that are capable of solving the wave transformation process from off-shore to nearshore (e.g., SWAN [8]), coupled with techniques to estimate the flooded extension and intensity that can also be based on numerical models (e.g., LISFLOOD) or through GIS tools. However, most of the GIS-based tools are meant for continental floods [9], and despite the possibility of adaptation [10], they usually neglect the influence of waves [11], which, in the case of Portugal, are an essential part of coastal flooding assessment.
The ‘bathtub approach’, which is a static inundation method where areas hydraulic connected to the sea and below the maximum vertical elevation that waves can reach (wave run-up) are flooded, is a widely used approach due to its straightforwardness [12]. Despite accounting for wave contributions, the ‘bathtub approach’ often results in significant overestimations, particularly in coastal areas with low-lying terrain profiles beyond berm or dune crests. This method does not account for any form of dissipation or the temporal and spatial variability inherent to wave overtopping mechanisms [11]. A few adaptations of this approach can implement terrain roughness or permeability with a potential increase in its accuracy [12]. Alternatively, a reduction coefficient based on past flood observations derived from remote sensing can be implemented into the approach to bring more accuracy to the flood extension estimation.
This paper proposes an adaptation of the bathtub approach (BTA), called the Tilted Bathtub Approach (TBTA) [13], based on both in situ and remotely sensed observations of past flooding events to reduce the typical over-estimation from the method. In comparison, a robust approach based on the coupling of a non-hydrostatic model for wave propagation on shallow waters (SWASH, [14,15]) and a dynamic inundation model (LISFLOOD-FP, [16]) was also implemented to compare the results. Both approaches carve out innovative paths in flood modelling.
The coupling of SWASH and LISFLOOD-FP investigates a relatively unexplored convergence of these specific models, connecting nearshore wave modelling with a hydrological model. This coupling is a processes-based method that requires a certain level of computational capacity and modelling skills, combined with the need for data for validation. On the other hand, the TBTA provides a scarcely documented yet practically validated [13] method for refining flood prediction and management. Together, they introduce methodological innovations, bridging the gap between field-applicable models and theoretical research.
Study Site Description
Furadouro beach is located on the Council of Ovar, Aveiro’s district, and the initial stages of its occupation were connected to fishing activities by the century XVIII [17], but more recently, the area’s main economic activity was gradually becoming tourism, which today represents the most important activity. The first episodes of coastal flooding were reported in 1857, when a few local fishermen’s haystacks were damaged, similarly in 1863, 1887, 1889, and 1912, as well as in the early 1940s, when more urban structures were already in existence [18]. The anthropogenic push for tourism edification protection prompted authorities to act in 1958, when the first major intervention to alleviate this risk was carried out, consisting of a 600 m long seawall.
Later, in 1974, a more decisive intervention was carried out, consisting of fortifying the existing seawall up to 9 m high, but more critically, three groynes of approximately 200 m extension and 5.5 m height were built 350 m apart. One of them was buried in the late 1990s, but the other two have survived to this day with a few modifications. Following this intervention, occurrences appear to have been less hazardous since only four reports of damage were recorded in the 1990s, all of which reported damages only to defence structures [19].
However, in this century, incidents of wave overtopping have increased dramatically in frequency and intensity, particularly since 2010, when urban structures, both commercial and residential, were harmed. During this last decade, a succession of hazardous events occurred, with the years 2014 and 2018 being emphasised for having many incidents, with events in early 2014 producing the most severe damages so far (Figure 1), including one injured person, and the year 2018 presenting the most amount of number of occurrences [19]. Therefore, the pattern of impacts shifted from mild impacts in the 1980s and 1990s to severe material impacts in the last two decades, with a focus on damage to buildings, public places, and coastal protection systems [2].

Figure 1.
Location map of Furadouro, showcasing (A) an aerial view under mild summer conditions, (B,C) wave overtopping and overwash during a flooding event on 2 February 2014, (D) aftermath debris from the same event, and the delineated area reportedly affected (highlighted in dashed lines). Source: publico.pt and sapo.pt.
Between 2018 and 2020, the costs related to overtopping in Furadouro amounted to EUR 214,882.00. This could escalate to between EUR 2.5 and 3.7 million over the next 20 years. Factoring in the impacts of climate change, especially sea level rise, these costs could surge by approximately 2 to 7 times if no preventive measures are implemented [20,21,22]. Given the substantial financial implications and potential damage escalation due to climate change, a comprehensive understanding of the overtopping phenomenon in Furadouro is crucial. Moreover, its recent history, marked by recurrent interventions and intense episodes, underscores its suitability as an ideal location for such an investigation.
2. Materials and Methods
This study’s methodology is outlined in Figure 2. Data on wave climate, tides, topography, and observations of a significant storm (Hs = 5.67 m, Tp = 19.0 s, and Tide = 4.0 m) event at Furadouro were collected. In response to this event, local authorities have created a map depicting the impacted areas, which serves as a validation event for this study. Two approaches for assessing the flood extension were carried out, one based on robust numerical methods and another one based on an offset of the affected area of the validation event derived from wave run-up levels. An extreme values analysis was carried out in order to obtain expected values for wave heights and periods, and both methods were applied in order to estimate expected flooded areas according to them. The resulting flood maps were carried out using GIS tools.
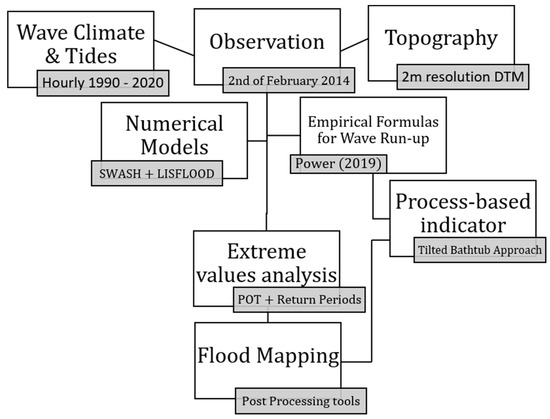
Figure 2.
Methodology scheme.
2.1. Oceanographic and Topographic Data
This study adopts an adaptation of the regional wave model introduced by [23], which encompasses the full expanse of the Portuguese coast. The computational domain spans approximately 115,000 km2 and employs a structured grid with a resolution of 2 m by 2 m. Wave boundary conditions are sourced from the Spanish State Port Authority (Puertos del Estado) via the SIMAR-44 data sets. These sets are derived from the synergy of the high-resolution atmospheric model REMO [24] and the spectral wave model WAM [25]. For the specific needs of this case study, the propagated sea states were extracted from the coordinates 40.81°N 8.73°W. These data have a time resolution of one hour and span a 30-year period from 1990 to 2020.
Additionally, sea level measurements were collected from an in-situ equipment located in a nearby port (Leixoes).
Local topography was obtained through the Program for Coastal Monitoring of Continental Portugal (COSMO), where it is possible to assess the beach slope, which is essential for the wave run-up evaluation, and the critical thresholds, i.e., the heights of points where flooding starts (dune crests or maximum height of defence structures). The topo-hydrographic survey with a 0.3 m resolution is the result of combining various acquisition techniques. An aerophotogrammetric survey was conducted in August 2018, with an initial resolution of 0.03 m and horizontal and vertical quadratic error of 0.053 m. Missing areas were interpolated using a geographic information system, with single-beam surveys and multi-beam surveys conducted at different depths. Hydrographic zero (ZH) was used as the reference plan, which is established 2.00 m below the mean sea level (MSL) in mainland Portugal, except for the port of Lisbon, where it is considered to be 2.08 m.
As this survey only accounts for the nearshore topography, an additional LIDAR survey was obtained through the Diretorio Nacional do Territorio (DGT) to assess the inland topography. The digital model of the terrain in the coastal zones of mainland Portugal was created in 2011 with a 2 m resolution. It includes both bathymetric and topographic information, roughly 400 m to land and 600 m to sea, and is in the PT-TM06/ETRS89 reference system with the altimetric datum of Cascais Helmert 38.
2.2. Numerical Models
This study uses two numerical models in its core, the LISFLOOD-FP to simulate the distribution of water volume from the wave overtopping process on dry land, and the SWASH non-hydrostatic was used to estimate the overtopping discharges as input for LISFLOOD.
2.2.1. SWASH
SWASH is a wave-flow model based on a Non-Linear Shallow Water equation with non-hydrostatic pressure terms, and in this case, in a 1D mode (flume-like). The decision for a 1D model was primarily motivated by the need for computational efficiency, taking into account the high resolution of the topographic data and relatively uniform cross sections of the nearshore topography. This uniformity is attributed to the presence of a permanent seawall installed along the study site.
The setup was modelled based on the procedures outlined by reference [14], which had been executed, calibrated, and verified in a study area with similar wave conditions and topographical surveys. Simulations were conducted using the SWASH model in one-dimensional mode with a computational period of 500 waves and a spin-up period of 15% of the computational period. The simulations used an initial time step of 0.008 s, an automatic time step control, and a maximum Courant number of 0.5 and a minimum of 0.1. Perpendicular wave conditions were considered for the simulations.
The mean overtopping discharge, represented by q, was identified at the critical point—specifically, the crest of the existing seawall—where wave overtopping typically occurs. This was achieved by simulating the instantaneous overtopping discharge at each time step using the DISCH command. The average overtopping discharge was computed by dividing the sum of individual discharges by the computational time, which corresponds to the total number of instantaneous discharges captured in the output. Maximum overtopping discharge was also assessed but found to be unrealistic due to an apparent overestimation when compared to the existing literature.
The boundary conditions consisted of a JONSWAP spectrum representing perpendicular irregular waves. This spectrum had a significant wave height (Hs) and wave peak period (Tp) mirroring the sea state observed in February 2014, which served as validation for this study. Subsequently, a bi-variate extreme values analysis was conducted to estimate the expected values of Hs and Tp for different return periods, specifically 5, 10, 25, 50, and 100 years. Therefore, this analysis consisted of six separate simulations. In each simulation, the sea level was set at 4 m, representing a typical spring high tide level observed in tide gauges’ time series near the study area.
2.2.2. LISFLOOD
The potentially flooded area was evaluated with the LISFLOOD-FP. The model LISFLOOD is a grid-based hydrological model that can distribute volumes of water on a topography, normally related to either rainfall or rivers, that can be adapted for coastal flooding assessment [26].The LISFLOOD-FP diffusive version was used [26], which considers a uniform flow and an adaptive time step, which is provided by
where is the time step of the model, is the water-free surface height, and z and represent the depth through which water can flow between two cells. The continuity equation was employed to simulate mass conservation [16], expressed as follows:
Here, represents the flow between cells, calculated at the cell faces using a centred difference scheme that is decoupled in the or directions. h denotes the water depth at the centre of each cell, is the width of the cell, and and are the spatial indices of the cell. However, there is a distinction in how is calculated at each face of a cell between the two hydraulic models. In LISFLOOD-FP, a uniform flow formula is employed to determine the flow over a time step between two faces.
where is the cell bed elevation, n is Manning’s roughness coefficient, and is the depth between cells through which water can flow [27].
In this case, the input discharges were extracted from the average wave overtopping outputs from SWASH 1D. The computational domain (Figure 3) covered an area of 0.5 km2 with a spatial resolution of 2 m. The flood model was forced with constant discharge imposed along the coastline boundary, characterised by the crest of a seawall of about 7 m in height. The fixed time-step 2D solver version was applied. The infiltration coefficient was set to the default values considering the characteristics of the urban area. The friction coefficient (i.e., Manning’s n value) was also default. The total simulation time was 432 s.
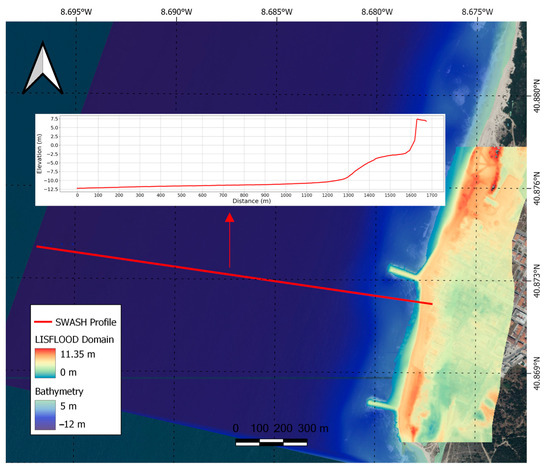
Figure 3.
SWASH 1D ‘raw’ profile (red), LISFLOOD domain, and nearshore bathymetry.
2.3. Observation
In an initial effort to evaluate prior coastal flooding events, especially the extent of the flooding, satellite images from prominent sources such as Sentinel 2, LandSat 7 and 8 were analysed. Nevertheless, it was concluded that those satellite images were unsuitable for this study due to limited resolution, weather-related constraints (clouds), and the unavailability of satellite imagery at the precise time of the flooding. However, it may be plausible to employ on-demand, paid satellite imagery as a valuable source for the evaluation of past coastal flooding events.
Alternatively, this study utilised a map detailing the affected areas, prepared by the Ovar Municipality, from the flooding event on 2 February 2014—the most destructive storm to date. The map was crafted after consulting the impacts of this event and the subsequent damages, delineating the perimeter of the area impacted by that specific coastal flooding episode, predominantly driven by waves. During this event, a total of 12 hectares were inundated, with the floodwaters extending up to 340 m inland from the beach. Numerous damages to both private and public properties were observed, including cafes, restaurants, hotels, and houses. Pathways were disrupted, and debris was scattered throughout the area.
It is likely that this event was potentialised by a previous hazardous event one month prior to this one, during the remarkable “Hercules” storm. This event has also caused great damage at Furadouro, although a smaller affected area was identified, as well as smaller damages [28].
2.4. Tilted Bathtub Approach
To evaluate inundation risk and severity, the bathtub approach is a common method used to define the flood-prone area. This technique posits that all coastal areas connected to the sea and lying below the total water level are susceptible to flooding. In the context of wave-induced coastal flooding, the total water level is often referred to as the wave run-up. This term signifies the highest vertical rise of the water level oscillating in the nearshore due to ocean waves. Nonetheless, this method tends to overestimate flooding predictions [12,29]. The primary cause of this overestimation stems from its disregard for wave dynamics, including temporal and spatial variations, due to its inherent static nature. The model presumes that the overtopping water volume uniformly fills the landscape below the peak run-up level, thereby neglecting the dynamic nature of the phenomenon.
An effective strategy to improve the representation of flooding involves modifying the bathtub approach by incorporating historical records of flooding. By considering the known maximum overwash extension and its correlation with corresponding run-up values at a particular event, a more accurate depiction of the affected area can be achieved for following events. This approach allows for potential expansion of the affected area based on higher wave-run-up values, introducing an offset to the flooding extension. Therefore, the run-up estimation is required.
2.4.1. Wave Run-Up Estimation
Wave run-up is evaluated by testing several of the most well-established empirical formulas available in the literature by comparing them with reports of wave overtopping in the last three decades [30,31,32,33,34,35,36,37].
Early laboratory experiments and studies [30,38] have provided evidence that the run-up phenomenon primarily relies on specific factors such as the significant wave height (H₀), wave period (T), wavelength (L₀), and the local beach slope or steepness (β). These variables are interrelated through a linear dispersion relationship, with the wave period playing a crucial role. Together, they contribute to the calculation of the Iribarren number (ξ). The Iribarren number serves as a critical dimensionless indicator of the wave transformation processes occurring on sloped beaches, particularly the nature of wave breaking, which can manifest as spilling, plunging, collapsing, or surging. Additionally, this relationship sheds light on the dynamic interaction between the beach profile and incoming waves, determining whether the beach exhibits a dissipative, intermediate, or reflective response.
Subsequent studies have extensively explored the relationship between these essential variables, incorporating empirical coefficients to account for roughness and permeability factors. These investigations have encompassed various coastal environments, including gravel, sand, and rocky beaches, as well as the presence of hard defence structures [30,31,32,33,39,40,41]. Consequently, multiple empirical formulas have been developed to estimate wave run-up, each tailored to specific environments and objectives. In this study, six of the most widely recognised empirical formulas were evaluated to identify the one that best fits the requirements of the case study. In the context of wave run-up, represents the elevation exceeded by the top 2% of wave run-up events, serving as a critical metric to assess the potential for wave-induced coastal inundation.
This study employed a 30-year hindcast of hourly wave climate data as inputs for the five selected empirical formulas. Additionally, the beach slope was derived from the aforementioned Digital Terrain Model (DTM); in this case, the representative beach slope has β = 0.04. A preliminary analysis was conducted to evaluate the performance of each formula, taking into account factors such as probability of occurrence and comparison with previous studies, including the work by [2]. Historical sea level was also incorporated in the calculations, although some lack of data for a few observations was identified. Most of the formulas only consider wave and topography parameters; however, reference [37] also considers a roughness, or friction, coefficient, which, in this case, r = 3 × 10−5 m (observed by [42]) for an asphalt bed.
To determine which formula most accurately represents Furadouro’s specific situation, a sensitivity test was performed. This involved examining whether the wave run-up results from the formulas surpassed the critical 10 m threshold, approximately the height of the existing seawall’s crown. Additionally, reviewing significant storm events from previous years in Portugal that caused extensive damage, as per references [2,28], made it possible to validate and compare the performance of each formula against actual events.
2.4.2. Flood Extension Estimation
Once the most representative formula was validated for the case study, an analysis of extreme values was conducted to determine the expected wave run-up values for different return periods, specifically 5, 10, 25, 50, and 100 years. The analysis utilised the Peak Over Threshold (POT) univariate sampling method, which involved identifying run-up values exceeding a critical threshold defined by the crest of the seawall in this particular scenario. Subsequently, a probabilistic curve was fitted to the data to estimate the expected values corresponding to the different return periods using a Generalised Pareto Distribution. Furthermore, the expected flood extension was estimated using the rules of triangle resemblance. This involved measuring the relationship between the observed flood extension and its corresponding characteristic run-up and extrapolating it to account for extreme run-up conditions, creating a sort of offset in the flooded area (Figure 4).
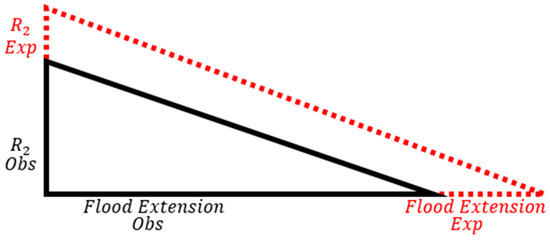
Figure 4.
Scheme of the Tilted Bathtub Approach, highlighting the relationship between observed flood extension and its wave run-up, as well as the expected flood extension (red) with its run-up value, respectively.
3. Results
3.1. Numerical Models
The mean overtopping discharges (q) simulated using SWASH exhibited a consistent order of magnitude in line with previous studies and experiments [40], ranging from 10−2 to 10−1 in squared meters per second. However, the maximum discharge peaks appeared to be overestimated, reaching values as high as 8.04 m3/s/m, an order of magnitude also found for peaks in [14]. Furthermore, the behaviour of these peaks did not follow a linear trend.
Interestingly, for waves characterised by larger height and period, respectively, for the return periods of 10, 25, and 50 years (Rp10, Rp25, Rp50), the maximum discharge values were comparatively smaller when compared to waves with smaller Hs and Tp. This observation aligns with the notion of strong non-linearity in wave overtopping events [40] and could be attributed to nearshore complex numerical–physical phenomena, such as wave breaking. In such cases, a larger wave may interact with the bottom earlier and break, resulting in a more significant dissipation of energy and subsequently leading to a smaller wave overtopping discharge.
Nevertheless, despite the aforementioned observations, the average discharge rate displayed a progressive increase as the wave characteristics were enhanced, with the exception of Rp10, which exhibited a higher discharge rate compared to Rp25. Notably, the February 2014 event, characterised by the greatest wave peak period, indicated a strong dependency between wave run-up, overtopping, and Tp. It exhibited a mean discharge rate equivalent to that of a storm with a 5-year return period, underscoring its significance. Results are shown in Table 1 and the time series for discharges in Figure 5.

Table 1.
Cases of February 2014 and different return periods, values for wave significant height, wave peak period, mean discharge rate, total discharge, and maximum discharge.
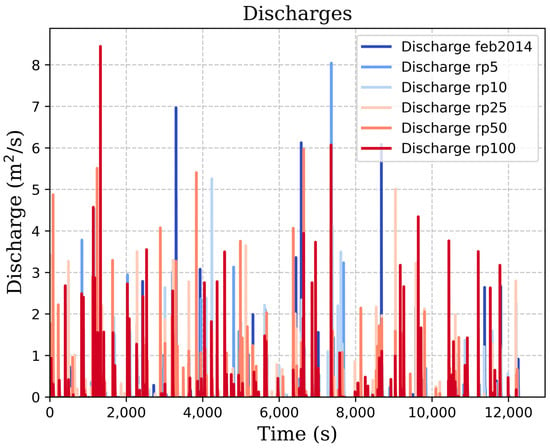
Figure 5.
Time series for discharge outputs from SWASH.
Inputting the mean q as fixed discharge points in the crest of the seawall, and therefore coupling SWASH with LISFLOOD, have resulted in the flood maps in Figure 6. The LISFLOOD outputs, which represented the flooded area, exhibited a commendable agreement with the reported damaged area provided by the municipality, particularly in the central region. However, an overestimation was observed in the southern part of the area. This discrepancy could be attributed to the absence of buildings in the Digital Terrain Model (DTM), which acts as a physical barrier obstructing the flow. The inclusion of a more comprehensive Digital Elevation Model (DEM) could potentially yield more accurate results in this regard since it could incorporate buildings and provide more realistic pathways for the waterflow. Additionally, changes in the nearshore topography specific to this section of the study area, which were not fully captured by the SWASH assessment, might contribute to an unrealistic representation of the flooded area in that particular region. It is crucial to note that the reliability of LISFLOOD heavily relies on the accurate estimation of discharges, indicating the need for further refinement in the estimation of wave overtopping discharge to enhance the overall reliability of the results.
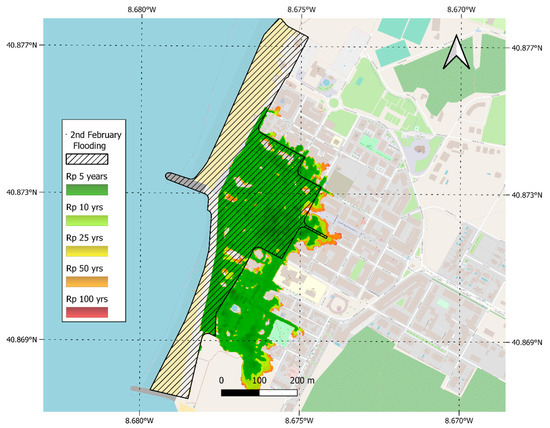
Figure 6.
Flood maps with the coupling SWASH + LISFLOOD.
Despite the substantial difference between the maximum mean discharge rate (for the 100-year return period) and the minimum (for the 5-year return period), there was not a significant increase in the extent of flooding and affected areas. This can be attributed to the local topography, which appears to create a low-lying zone a few meters beyond the seawall, followed by an elevation increase that acts as a barrier, trapping the flooded water. However, it is noteworthy that even for a storm with a 5-year return period, a considerable flooded area was observed. This highlights the importance of addressing recurrent events, as the potential risk remains high during considerably high-probability events.
3.2. Tilted Bathtub Approach
3.2.1. Run-Up Estimations
The empirical predictors, here named as NS, PW, HM, RG, VK, and ST, respectively, for Nielsen’s, Power’s, Holman’s, Ruggiero’s, and Vousdoukas’ formulas, are subsequently examined in relation to the run-up levels. For clarity and ease of visualisation, Figure 7 displays the maximum run-up value every three days, considering only values exceeding 3.5 m. A critical threshold of 10 m was adopted, approximately matching the height of the current coastal defence structure—a seawall aligned parallel to the shoreline. This evaluation is conducted using the range of formulas applied to the representative profile, the same as the SWASH setup.
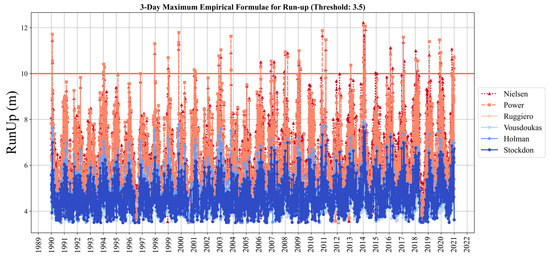
Figure 7.
Time series for 5 empirical predictors at the representative profile.
Among these formulas, VK, RG, HM, and ST formulas did not surpass the critical threshold level, indicating no occurrence of wave overtopping during the analysis period (1990–2021). Consequently, these formulas are deemed unsuitable for this specific case, given their underestimation. However, NS and PW formulas not only surpassed the critical threshold but also exhibited a relatively good agreement with observed overtopping events documented by [2,19,28]. Furthermore, the event on 2 February 2014 exhibited one of the highest run-up levels throughout the entire time series—11.28 m and 11.66 m for PW and NS, respectively. This serves as an indicator of appropriateness, given that this day was recognised as the most severe coastal flooding episode according to the municipality.
Both formulas seem apt for this case study as they yield results that closely match. However, NS tends to project higher estimations of run-up levels in milder sea states, while the PW formula generally produces more pronounced peaks during rough sea states with less run-up in average conditions (Figure 8). NS was developed based on measurements taken on sandy beaches along the New South Wales Coast in Australia. These beaches are typically flat, aligning with Rayleigh’s distribution for the maximum levels reached by individual waves. It was found that categorising beaches according to their steepness, between “steep” (β > 0.1) and “flat” (β < 0.1), can enhance the formula’s accuracy.
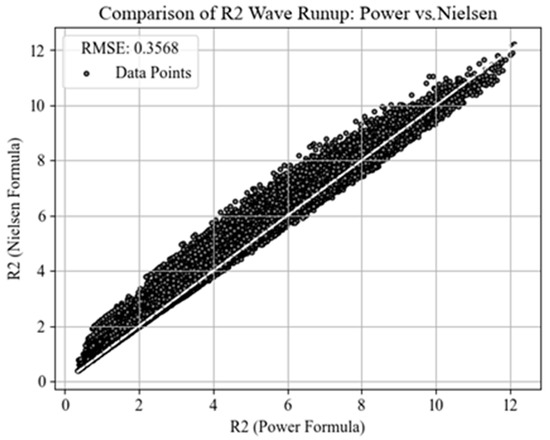
Figure 8.
Comparison of Nielsen’s and Power’s formulas, with Root Mean Squared Error displayed.
It is also worth noting that PW is a more recent study employing machine learning algorithms, specifically a genetic programming-based methodology that integrates datasets from various prior authors. Consequently, it is considered to be more robust in nature.
The return periods were then obtained through the extreme values analysis, providing wave run-up levels expected for return periods of 5, 10, 25, 50, and 100 years.
3.2.2. Flood Extension
The flood extensions expected for the different run-up values were determined across four sections (Table 2). These sections were chosen based on the affected perimeter and their distinct lengths, as certain streets exhibited more extensive flooding than others. The flooded area expansion was performed in the streets, preserving the blocks as they were impermeable, apart from the 100-year return period, which covered a whole new block limit. The maximum flood extent from the validation case was 325 m away from the crest of the seawall, which may be extended for up to 430 m for a storm with a 100-year return period. The projected flood extensions are visually presented in Figure 9. Overall, the offset has not presented a significant increase in the flooded area, which also aligns with the numerical models’ results. The expected wave run-up for a 5-year return period was less than the February 2014 event, which for run-up values was more similar to a 10-year return period storm.

Table 2.
Wave run-up values and matching flood extension at four cross sections.
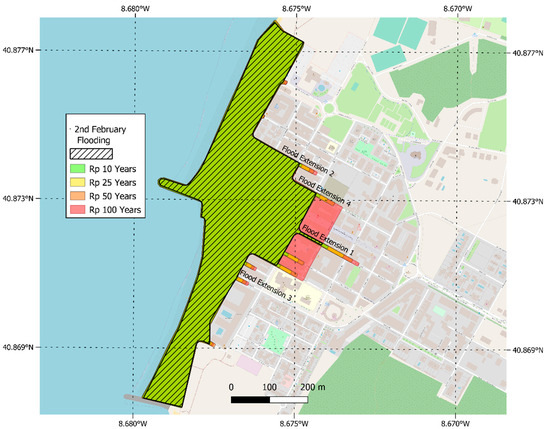
Figure 9.
Flood map with the TBTA for different return periods.
While several authors have advanced methods for assessing overwash-induced flood extensions in natural environments [13,43,44,45], many of these techniques rely on empirical assumptions or complex inputs like wave overtopping discharge, introducing significant uncertainty. The ‘Tilted Bathtub Approach’ is a proxy of flood extension that is a process-based indicator of flooding hazard [46], rooted in the observation of a previous hazardous event, ensuring a strong alignment with real-life applications. However, it introduces uncertainty when predicting potential future events, such as expected storms with varying return periods. Since every storm has its unique characteristics and the TBTA is based on a single observed event, this can lead to uncertainty when anticipating the nature of future storms. One potential solution to mitigate this limitation is to incorporate multiple validation events. This would provide a more comprehensive foundation for associating a variety of events with different storm intensities, with wave run-up being the primary variable in this context.
4. Discussion
This study has successfully presented and compared two approaches for coastal flood mapping: the Tilted Bathtub Approach (TBTA) based on run-up levels and an event of validation, as well as the coupling of the SWASH and LISFLOOD models. The results have demonstrated the potential of these approaches in accurately assessing the extent of wave-induced coastal flooding.
The TBTA provides a straightforward and simplistic method for estimating flood extension in potential wave-induced coastal flooding events. This approach offers several advantages over more complex numerical or physical models, as it is relatively simple to implement and understand. Moreover, compared to the conventional “bathtub” approach commonly used in such scenarios, the TBTA brings notable enhancements by incorporating additional factors derived from observation and validation events. This incorporation enhances the fidelity of the approach and improves its alignment with real-world conditions. Furthermore, the Tilted Bathtub Approach (TBTA) can serve as a streamlined tool for local authorities and coastal planners to easily assess potential flood extents under various sea state conditions, aiding in the development of resilient urban planning strategies and tailored community outreach and preparedness programs.
The coupling of SWASH and LISFLOOD models has been shown to offer significant advantages over traditional physical models in terms of simplicity, cost-effectiveness, and computational efficiency. By accounting for wave overtopping discharges, flow directions, and velocities, this approach provides a more comprehensive understanding of coastal flooding dynamics compared to static GIS-based methods. It can facilitate a thorough depiction and analysis of coastal flooding dynamics, which is pivotal for designing robust coastal protection structures and formulating actionable emergency response plans. In particular, these methods can assist in identifying vulnerable coastal sectors, thereby guiding the strategic placement of defence structures and ensuring optimal allocation of resources for repair and reinforcement activities.
However, it is important to acknowledge the limitations and areas for improvement identified in this study. The need for more accurate data, such as Digital Elevation Models, to better represent topographic features and obstacles in flood modelling has been highlighted. Additionally, incorporating multiple validation events with detailed mapping of affected areas, such as categorising impacts by hazard levels, could significantly enhance the results. Using multiple validation events rather than a singular one might lead to a more refined TBTA, employing a more robust statistical approach to correlate various flooding events with their respective wave setup characteristics. Further refinements on the SWASH implementation, for instance, incorporating 2D effects, such as wave obliquity and better representation of the wave reflection from the existing groyne, could increase the accuracy of the SWASH outputs.
While these methods emphasise wave run-up and overtopping-induced coastal flooding, they overlook other factors often present in hazardous coastal events in other coastal setups, such as river discharges, storm surges, tidal bores, rainfall, and wind. Consequently, their applicability might be restricted in coastal contexts vastly different from our study site, particularly where waves are not a major influence. Nonetheless, since coastal flooding in Portugal is predominantly wave-driven, and the data from the Furadouro case is widely available, these methods could be effectively applied to other Portuguese sites experiencing similar conditions.
5. Conclusions
Despite these limitations, the findings of this study contribute to the scientific understanding of wave-induced coastal flooding and provide valuable insights for coastal planners and stakeholders. The identified advantages of the coupled SWASH and LISFLOOD models, along with the potential for future advancements and refinements, make them promising tools for enhancing coastal risk assessment, informing decision-making processes, and implementing effective measures to mitigate the impacts of coastal flooding.
Further research directions should focus on replicating this validated method for extreme event scenarios and incorporating considerations of climate change, such as sea level rise. Moving forward, investigating the integration of real-time data for more accurate flood prediction and delving into the socio-economic impacts of coastal flooding within the study area could also be potential areas for improvement. By addressing these challenges and building upon the findings of this study, coastal communities can work towards resilience and develop sustainable strategies for managing coastal flooding risks.
Author Contributions
Conceptualisation, J.E.C.-B.; methodology, J.E.C.-B., T.F.-F. and T.A.P.; software, J.E.C.-B. and T.A.P.; validation, J.E.C.-B., T.A.P., T.F.-F., P.R.-S. and F.T.-P.; formal analysis, J.E.C.-B., T.F.-F., P.R.-S. and F.T.-P.; investigation, J.E.C.-B., T.A.P., T.F.-F., P.R.-S. and F.T.-P.; resources, J.E.C.-B., T.F.-F., P.R.-S. and F.T.-P.; data curation, J.E.C.-B.; writing—original draft preparation, J.E.C.-B.; writing—review and editing, J.E.C.-B., T.F.-F., P.R.-S. and F.T.-P.; visualisation, J.E.C.-B.; supervision, F.T.-P.; project administration, J.E.C.-B., T.F.-F., P.R.-S. and F.T.-P.; funding acquisition, J.E.C.-B. All authors have read and agreed to the published version of the manuscript.
Funding
The main author acknowledges funding in the form of a Ph.D. fellowship granted by the “la Caixa” Foundation (ID 100010434) within the Doctoral INPhINIT program (ID LCF/BQ/DI22/11940021).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to confidentiality and privacy concerns.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pereira, C.; Coelho, C. Mapas de Risco das Zonas Costeiras por Efeito da Ação Energética do Mar. Rev. De Gestão Costeira Integr. 2013, 13, 27–43. [Google Scholar] [CrossRef]
- Tavares, A.O.; Barros, J.L.; Freire, P.; Santos, P.P.; Perdiz, L.; Fortunato, A.B. A coastal flooding database from 1980 to 2018 for the continental Portuguese coastal zone. Appl. Geogr. 2021, 135, 102534. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; Van Den Hurk, B.J.J.M.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Stojanovic, M.; Gonçalves, A.; Sorí, R.; Vázquez, M.; Ramos, A.M.; Nieto, R.; Gimeno, L.; Liberato, M.L.R. Consecutive Extratropical Cyclones Daniel, Elsa and Fabien, and Their Impact on the Hydrological Cycle of Mainland Portugal. Water 2021, 13, 1476. [Google Scholar] [CrossRef]
- Gao, J.; Shi, H.; Zang, J.; Liu, Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Booji, N.; Holthuijsen, L.H.; Ris, R.C. The SWAN wave model for shallow water. In Proceedings of the 25th International Confer-ence on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; pp. 668–676. [Google Scholar]
- Dottori, F.; Martina, M.; Figueiredo, R. A methodology for flood susceptibility and vulnerability analysis in complex flood scenarios. J. Flood Risk Manag. 2016, 11, S632–S645. [Google Scholar] [CrossRef]
- Breilh, J.F.; Chaumillon, E.; Bertin, X.; Gravelle, M. Assessment of static flood modeling techniques: Application to contrasting marshes flooded during Xynthia (western France). Nat. Hazards Earth Syst. Sci. 2013, 13, 1595–1612. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Mentaschi, L.; Dottori, F.; Giardino, A.; Bouziotas, D.; Bianchi, A.; Salamon, P.; Feyen, L. Developments in large-scale coastal flood hazard mapping. Nat. Hazards Earth Syst. Sci. 2016, 16, 1841–1853. [Google Scholar] [CrossRef]
- Williams, L.L.; Lück-Vogel, M. Comparative assessment of the GIS based bathtub model and an enhanced bathtub model for coastal inundation. J. Coast. Conserv. 2020, 24, 23. [Google Scholar] [CrossRef]
- van Dongeren, A.; Ciavola, P.; Martinez, G.; Viavattene, C.; Bogaard, T.; Ferreira, O.; Higgins, R.; McCall, R. Introduction to RISC-KIT: Resilience-increasing strategies for coasts. Coast. Eng. 2017, 134, 2–9. [Google Scholar] [CrossRef]
- Manz, A.; Zózimo, A.C.; Garzon, J.L. Application of SWASH to Compute Wave Overtopping in Ericeira Harbour for Operational Purposes. J. Mar. Sci. Eng. 2022, 10, 1881. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Bates, P.; De Roo, A. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Martins, A.R.S. Avaliação da Hidrodinâmica e dos Níveis de Galgamento na Praia do Furadouro: Análise Comparativa da Situação atual e com a construção de Quebramares Destacados. Master’s Thesis, Faculdade de Arquitectura da Universidade do Porto, Porto, Portugal, 2016. [Google Scholar]
- dos Reis, A.R.A. Dicotomia Entre a Zona Piscatória e a Zona Balnear. Ph.D. Thesis, Universidade de Coimbra, Coimbra, Portugal, 2015. [Google Scholar]
- Pinto, I.M.P. Galgamentos e Inundações Costeiras na Frente Urbana do Furadouro—Concelho de Ovar. Master’s Thesis, Faculdade de Letras da Universidade do Porto, Porto, Portugal, 2022. [Google Scholar]
- Lima, M.; Coelho, C.; Jesus, F. Wave Overtopping and Flooding Costs in the Pre-Design of Longitudinal Revetments. Water 2023, 15, 1434. [Google Scholar] [CrossRef]
- Almar, R.; Ranasinghe, R.; Bergsma, E.W.J.; Diaz, H.; Melet, A.; Papa, F.; Vousdoukas, M.; Athanasiou, P.; Dada, O.; Almeida, L.P.; et al. A global analysis of extreme coastal water levels with implications for potential coastal overtopping. Nat. Commun. 2021, 12, 3775. [Google Scholar] [CrossRef] [PubMed]
- Rentschler, J.; Avner, P.; Marconcini, M.; Su, R.; Strano, E.; Vousdoukas, M.; Hallegatte, S. Global evidence of rapid urban growth in flood zones since 1985. Nature 2023, 622, 87–92. [Google Scholar] [CrossRef]
- Ramos, V.; López, M.; Taveira-Pinto, F.; Rosa-Santos, P. Influence of the wave climate seasonality on the performance of a wave energy converter: A case study. Energy 2017, 135, 303–316. [Google Scholar] [CrossRef]
- Jacob, D.; Podzun, R. Sensitivity studies with the regional climate model REMO. Meteorol. Atmospheric Phys. 1997, 63, 119–129. [Google Scholar] [CrossRef]
- Group, T.W. The WAM Model—A Third Generation Ocean WAve Prediction Model. Am. Meteorol. Soc. 1988, 6, 128. [Google Scholar] [CrossRef]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, M.G. An adaptive time step solution for raster-based storage cell modelling of floodplain inundation. Adv. Water Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Fewtrell, T.; Budimir, M.; Bates, P.; Mason, D. Evaluating a new LISFLOOD-FP formulation with data from the summer 2007 floods in Tewkesbury, UK. J. Flood Risk Manag. 2011, 4, 88–95. [Google Scholar] [CrossRef]
- APA. Registo das Ocorrências No Litoral; Technical Report; APA: Lisbon, Portugal, 2014. [Google Scholar] [CrossRef]
- Didier, D.; Baudry, J.; Bernatchez, P.; Dumont, D.; Sadegh, M.; Bismuth, E.; Bandet, M.; Dugas, S.; Sévigny, C. Multihazard simulation for coastal flood mapping: Bathtub versus numerical modelling in an open estuary, Eastern Canada. J. Flood Risk Manag. 2018, 12, 12505. [Google Scholar] [CrossRef]
- Holman, R. Extreme value statistics for wave run-up on a natural beach. Coast. Eng. 1986, 9, 527–544. [Google Scholar] [CrossRef]
- Nielsen, P.; Hanslow, D.J. Wave runup distributions on natural beaches. J. Coast. Res. 1991, 7, 1139–1152. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Wziatek, D.; Almeida, L.P. Coastal vulnerability assessment based on video wave run-up observations at a mesotidal, steep-sloped beach. Ocean Dyn. 2011, 62, 123–137. [Google Scholar] [CrossRef]
- Didier, D.; Bernatchez, P.; Marie, G.; Boucher-Brossard, G. Wave runup estimations on platform-beaches for coastal flood hazard assessment. Nat. Hazards 2016, 83, 1443–1467. [Google Scholar] [CrossRef]
- Poate, T.G.; McCall, R.T.; Masselink, G. A new parameterisation for runup on gravel beaches. Coast. Eng. 2016, 117, 176–190. [Google Scholar] [CrossRef]
- Dodet, G.; Leckler, F.; Sous, D.; Ardhuin, F.; Filipot, J.F.; Suanez, S. Wave Runup Over Steep Rocky Cliffs. J. Geophys. Res. Oceans 2018, 123, 7185–7205. [Google Scholar] [CrossRef]
- Power, H.E.; Gharabaghi, B.; Bonakdari, H.; Robertson, B.; Atkinson, A.L.; Baldock, T.E. Prediction of wave runup on beaches using Gene-Expression Programming and empirical relationships. Coast. Eng. 2018, 144, 47–61. [Google Scholar] [CrossRef]
- Hunt, I.A. Design of Seawalls and Breakwaters. J. Waterw. Harb. Div. 1959, 85, 123–152. [Google Scholar] [CrossRef]
- Ruggiero, P.; Komar, P.D.; McDougal, W.G.; Marra, J.J.; Beach, R.A. Wave Runup, Extreme Water Levels and the Erosion of Proper-ties Backing Beaches. J. Coast. Res. 2001, 17, 407–419. [Google Scholar]
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application. Report 2016, pp. 264. Available online: http://www.overtopping-manual.com/assets/downloads/EurOtop_II_2018_Final_version.pdf (accessed on 14 April 2023).
- Da Silva, P.G.; Coco, G.; Garnier, R.; Klein, A.H.F. On the prediction of runup, setup and swash on beaches. Earth Sci. Rev. 2020, 204, 103148. [Google Scholar] [CrossRef]
- Howe, D. Bed Shear Stress under Wave Runup on Steep Slopes. Ph.D. Thesis, School of Civil and Environmental Engineering, UNSW, Kennington, NSW, Australia, 2016. [Google Scholar] [CrossRef]
- Ferreira, O.; Viavattene, C.; Jiménez, J.; Bolle, A.; das Neves, L.; Plomaritis, T.; McCall, R.; van Dongeren, A. Storm-induced risk assessment: Evaluation of two tools at the regional and hotspot scale. Coast. Eng. 2018, 134, 241–253. [Google Scholar] [CrossRef]
- Plomaritis, T.A.; Ferreira, Ó.; Costas, S. Regional assessment of storm related overwash and breaching hazards on coastal barriers. Coast. Eng. 2018, 134, 124–133. [Google Scholar] [CrossRef]
- Donnelly, C.; Wamsley, T.V.; Kraus, N.C.; Larson, M.; Hanson, H. Morphologic classification of coastal overwash. In Proceedings of the 30th International Conference, Atlanta, GA, USA, 17–19 June 2013; pp. 2805–2817. [Google Scholar]
- Ferreira, Ó.; Plomaritis, T.A.; Costas, S. Process-based indicators to assess storm induced coastal hazards. Earth-Sci. Rev. 2017, 173, 159–167. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).