Reconfigurable Intelligent Surface-Assisted Radar Deception Electronic Counter-Countermeasures

Abstract

A reconfigurable intelligent surface (RIS) is a promising technology for wireless communication and radar detection, owing to its superior ability to realize smart radio environments. Inspired by previous studies on RISs, this study deals with the use of RISs for radar electronic counter-countermeasures (ECCMs) in deception jamming scenarios. At first, a RIS was applied to a monostatic radar, constructing a virtual multi-radar system combined with multi-beam receiving technology. Then, a data-fusion-based deception ECCM method for the proposed virtual multi-radar system was studied to discriminate the active false targets generated by deception jamming. A theoretical analysis of the target discrimination probability was derived. Because the location of RISs is the key to determining the target discrimination ability, the location optimization of the RIS was considered based on the theoretical analysis. Simulation results corroborate the deception ECCM ability of the proposed RIS-assisted virtual multi-radar system, enhancing the survivability of a radar system in a complex electromagnetic environment.

1. Introduction

Reconfigurable intelligent surfaces (RISs), which are composed of a massive number of low-cost and passive reflection elements that can reflect the incident signal with an adjustable phase and/or amplitude shift, have attracted great attention in the recent past. Different from a specular reflector, a RIS can effectively control the propagation channel, as its elements can be individually controlled by a low-power external logic to redirect the incident electromagnetic wave towards an arbitrary direction or a specific location. As a nearly passive low-cost planar structure, the RIS can be easily deployed in the environment and allows for smart radio environments to be realized [1,2].

Motivated by these preferable features, RISs were firstly introduced into wireless communications [3,4,5], and it has been shown that with the assistance of a RIS, the performance of wireless communication systems can be significantly improved. In [6], RISs were introduced to alleviate communication channel fading and improve the signal-to-noise ratio. A RIS-assisted single-cell wireless system was studied by the authors in [7], and it was verified that a RIS can enhance the spectrum and energy efficiency as well as reduce the implementation cost of future wireless communication systems. Luo. et al. considered the spatial modulation for the uplink communication of a RIS-assisted system [8], which investigates the transmit spatial modulation scheme and jointly optimizes the RIS reflection coefficients to achieve a lower symbol error rate (SER) and enhance the system reliability. Ref. [9] instead considered the downlink multiuser communication in a single-cell network, and the RIS phase offsets were optimized to increase the system energy efficiency. In [10], the RIS was employed to cope with the non-line-of-sight paths, which resulted in significant gains to the system sum rate to meet the challenge of enabling large-scale access for Internet of things (IoT) devices. In [11,12], passive beamforming and trajectory optimization was considered for a RIS-assisted unmanned aerial vehicle (UAV) secure communication scheme to maximize the average secrecy rate. Moreover, radio localization with the aid of RISs has been researched by the authors in [13,14,15]. Owing to the potential of RIS in mitigating multiuser interference (MUI), the RIS-assisted dual-function radar-communication (DFRC) system has been investigated. In [16], the minimization of MUI under the strict beampattern constraint by jointly optimizing the DFRC waveform and RIS phase shift matrix was studied. A double-RIS-assisted coexistence system was considered by the authors in [17], and the beamforming of RISs and radar were optimized to maximize communication performance while maintaining radar detection performance.

More recently, researchers have started to investigate the RIS benefits of RIS-assisted radar systems. Traditionally, the propagation channels between the radar and the targets have been passively adopted, which limits the performance of the radar. By exploiting the potential of RISs in achieving smart radio environments, the author in [18] first incorporated the radar system with the RIS technique to improve the target detection performance. The RIS-assisted MIMO radar was considered [19,20], where RIS phase shifts were designed to improve the detection performance. In [21], the authors dealt with the use of RISs for radar surveillance in non-line-of-sight (N-LOS) scenarios. Zhang et al. extended the application to the multi-target scenario by jointly optimizing both radar waveforms and RIS phase shifts to improve the multi-target detection performance [22]. In addition to target detection performance, parameter estimation is also of concern. Grossi et al. studied the joint detection and localization of a prospective target with the receiver assisted by a RIS [18], and the DOA-based target positioning in a RIS-assisted MIMO radar system was considered by the authors in [23]. The available studies have focused on the design of the phase shifts of RIS elements, which optimizes the channel conditions between the radar and the targets to improve the target detection and/or location performance of the radar systems.

However, this has not been applied in radar electronic counter-countermeasures (ECCMs). The practical radar systems always work with exposure to complicated electromagnetic environments, and radar ECCM ability is of great significance for their survival and operation performance in electronic warfare [24,25,26]. Among electronic countermeasure (ECM) techniques, active deception jamming is an important jamming pattern faced by radar. The radar ECCM ability of monostatic radar is limited due to its single view angle. A distributed multi-radar fusion system is an important development trend, benefiting from the advantages of multiple-view detection and information fusion [27,28]. Deception jamming cancellation methods proposed in a multi-radar system can be divided into data-fusion-based and signal-fusion-based methods. Data-fusion-based methods discriminate the deception jamming from the local measurements obtained, exploiting the difference in spatial location aggregation characteristics of true and false targets [29,30,31]. Signal-fusion-based methods counter the deception jamming by fusing the target amplitude or the original echo signals from the local sites [32,33,34], exploiting their differences in target spatial scattering characteristics [35,36].

Although a multi-radar system can exhibit excellent anti-jamming performance, its construction conditions are harsh, especially in the case of complex electromagnetic jamming. Firstly, each radar is usually responsible for different tasks, and the overlapping monitoring area is small, so it is difficult or costly to realize simultaneous detection. However, for the built multi-radar system, the system is always faced with destruction, such as damage to the sites or the breakdown of communication links. Therefore, the ECCM ability of monostatic radar will still directly determine the radar survivability, and the key to improving it is to realize the distributed target detection for monostatic radar.

Therefore, we are motivated to introduce the RIS technique into the radar ECCM system. Its excellent characteristics in controlling the propagation channel provide a new method of assisting monostatic radar to construct distributed detection conditions, which is a very promising research direction. By applying the RIS to monostatic radar, a virtual multi-radar system was constructed, combined with the multi-beam receiving technology. Then, the data-fusion-based deception ECCM method was studied to effectively discriminate the deception targets. The theoretical analysis for the discrimination probability of the proposed deception ECCM method is given, followed by the location optimization of RISs. Simulation results corroborate the deception ECCM ability of the proposed RIS-assisted virtual multi-radar system.

The rest of this paper is organized as follows: In Section 2, the target and deception jamming system model of the constructed virtual multi-radar system is given. In Section 3, the data-fusion-based deception ECCM method is provided to discriminate the active false targets. In Section 4, the theoretical analysis of the discrimination probability and the location optimization of RISs are studied. The simulation results are provided in Section 5. And the discussions are given in Section 6. Finally, the conclusions are drawn in Section 7.

2. System Model

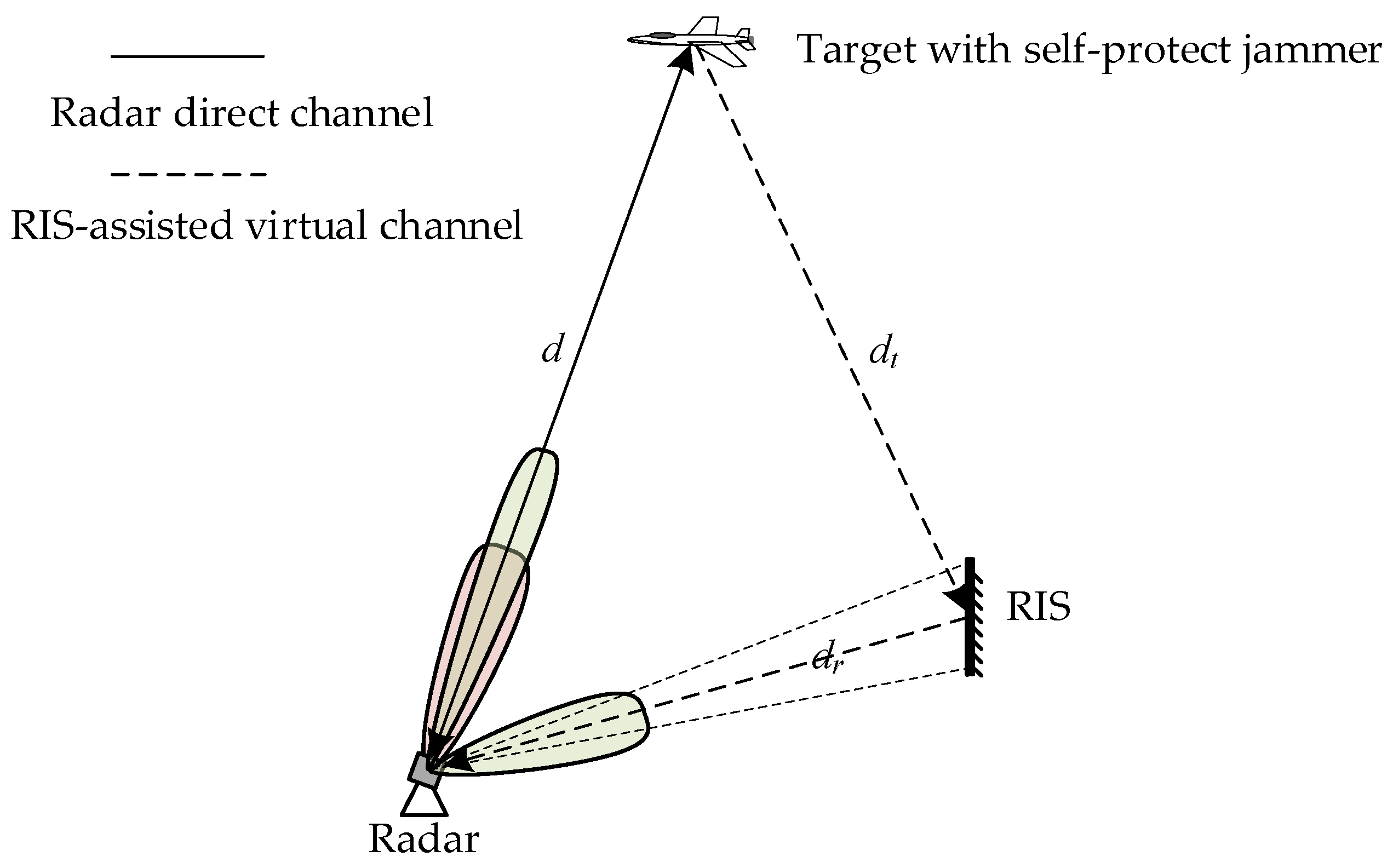
Consider a radar deception ECCM problem where the radar is assisted by RISs. In Figure 1, a radar with one RIS is shown as an example. The target is illuminated by the radar-transmitted signal, and its echoes are collected by the radar and the RIS. In the radar, the multi-beam receiving technology is applied, and multiple receiving beams are directed at the target and the RIS to receive target direct echoes and the reflected echoes from the RIS, respectively. Then, a multi-view detection of the target is realized by introducing the RIS to the radar. In the direct channel, the target echo is received by the radar. In the RIS-assisted virtual channels, the target echo is reflected by the RIS, and the reflected signal is then received by the radar. To protect the target, a self-protect jammer implements deception jamming to the radar through both the direct and the virtual receiving channels. Obviously, a virtual multi-radar system is constructed here by taking advantage of the ability of the RIS to reconstruct the signal propagation environment, which will provide more freedom to significantly improve the anti-jamming ability of the monostatic radar.

For cooperative anti-jamming, the received and reflected beams of the RIS should be controlled by adjusting the phases of the RIS reflectors, which is designed by the radar station through the transmission link. The reflected beam of the RIS should point to the radar in the virtual multi-radar system. The received beam of the RIS should be followed by the transmitting beam of the radar and should scan all the detected areas for every transmitting beam. This is because the radar serves as the only transmitting station, and the RIS-assisted virtual channels detect the target by receiving the target echo reflected by the RIS.

However, for the reliable anti-jamming ability of the virtual multi-radar system, the RIS station should be distributed from the radar to ensure a sufficient target detection angle difference among the direct and virtual receiving channels.

The radar waveform is assumed to be narrowband, and the impinging wavefield can be approximated as a plane wave in the paths between the radar and the target, the target and the RIS, and the radar and each element of the RIS. As is shown in Figure 1, $d$, $d_t$, and $d_r$ refer to the range between the radar and the target, the target and the RIS, and the radar and the center of the RIS.

• Target signal model

In the radar direct channel, the target echo $r_0(t)$ is

$$r_0(t)=\alpha s(t-t_0)+w_0(t)$$

(1)

where $\alpha$ is the target amplitude; $s(t)$ is the radar transmitted signal; $t_0=2d/\mathrm{c}$ refers to the time delay; $\mathrm{c}$ is the speed of light; and $w_0(t)$ is the channel noise following the Gaussian distribution.

In the RIS-assisted virtual channel, the target echo $r_1(t)$ is

$$r_1(t)={\displaystyle \sum _{l=1}^L{\alpha }_{r,l}}{e}^{\mathrm{j}({\psi }_{t,l}+{\varphi }_l+{\psi }_{r,l})}s(t-t_1)+w_1(t)$$

(2)

where $l=1,2,\dots ,L$; L is the number of sub-$\lambda$-sized surface elements of the RIS; ${\alpha }_{r,l}$ is the target amplitude from the l-th element of the RIS; ${\psi }_{t,l}$ and ${\psi }_{r,l}$ are the target phases of the target–RIS and RIS–radar channels, respectively; and ${\varphi }_l$ is the adjustable RIS phase of the l-th reflecting element of the RIS. To achieve the highest SNR for the under-test resolution cell, ${\varphi }_l=-{\psi }_{t,l}-{\psi }_{r,l}$. $t_1=(d+d_t+d_r)/\mathrm{c}$ refers to the time delay in the RIS-assisted virtual channel. Gaussian noise $w_1(t)$ is independent from $w_0(t)$.

• Deception jamming model

In the radar direct channel, the received deception jamming $j_0(t)$ can be written as

$$j_0(t)={\alpha }_J{e}^{\mathrm{j}{\beta }_J}J(t-\mathsf{\Delta }t-t_{J0})+w_0(t)$$

(3)

where ${\alpha }_J$, ${\beta }_J$, and $\mathsf{\Delta }t$ are the signal amplitude, phase, and deceptive time delay, respectively. The one-way time delay $t_{J0}=d/\mathrm{c}$. $J(t)$ is the transmitted deception jamming signal, which is usually the same signal as $s(t)$.

In the RIS-assisted virtual channel, the received deception jamming $j_1(t)$ can be written as

$$j_1(t)={\displaystyle \sum _{l=1}^L{\alpha }_{J,l}}{e}^{\mathrm{j}({\psi }_{J,l}+{\varphi }_l+{\psi }_{r,l})}J(t-\mathsf{\Delta }t-t_{J1})+w_1(t)$$

(4)

where ${\alpha }_{J,l}$ is the jamming amplitude from the l-th element of the RIS. The phase ${\psi }_{J,l}$, ${\psi }_{r,l}$, and ${\varphi }_l$ remain the same. The one-way time delay $t_{J1}=(d_t+d_r)/\mathrm{c}$.

The problem is discriminating the false target generated by the jammer by exploiting the additional received signals available in the RIS-assisted virtual channel.

3. Deception ECCM Method

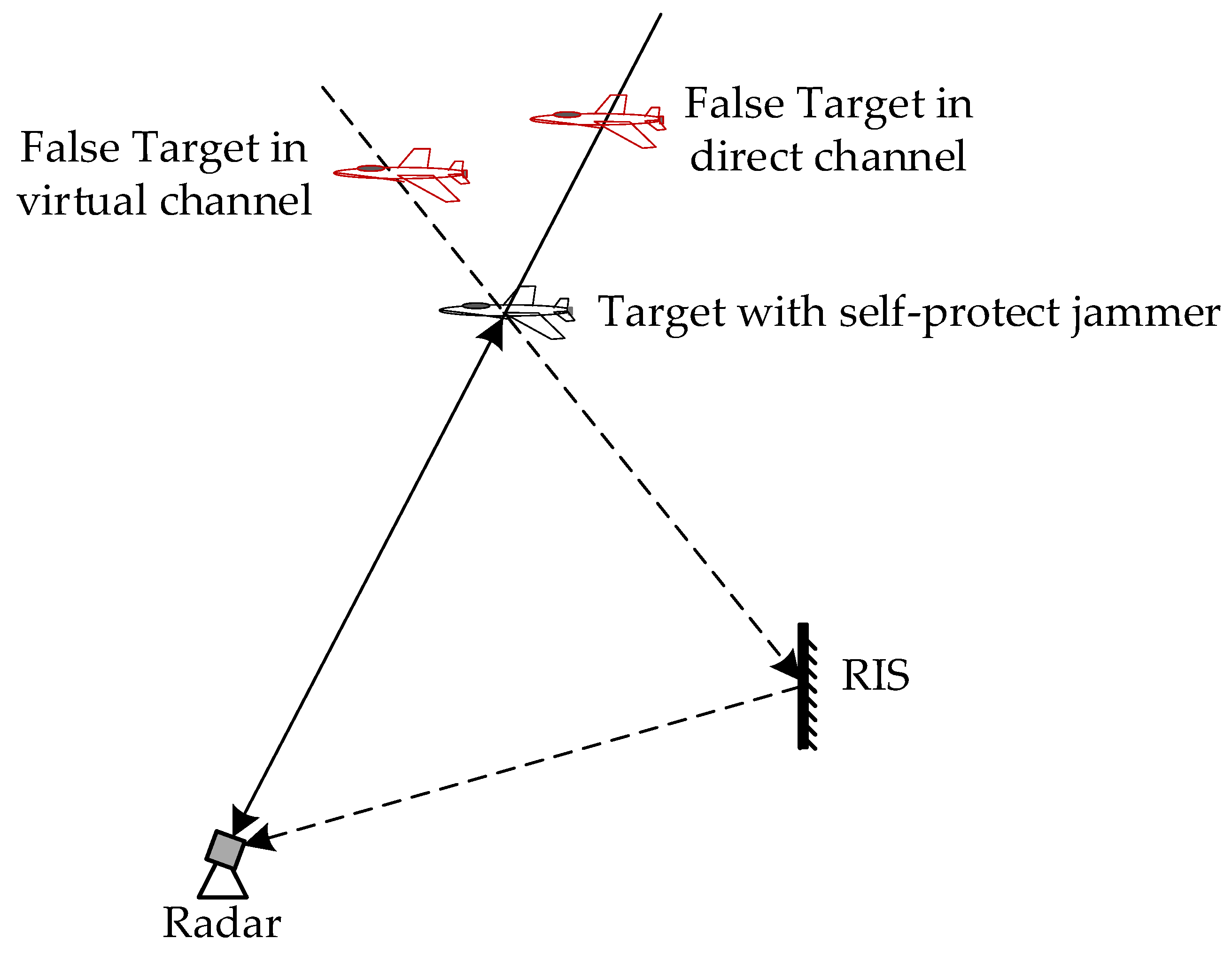
The theoretical basis of the data-fusion-based deception ECCM method is the difference between true and false targets in the spatial dispersion of the location, as shown in Figure 2. For the true target, which has the characteristics of spatial aggregation, its measurements in different detection channels are relatively concentrated after being converted to the unified coordinate system and they exist in an error ellipse determined by the measurement errors.

Active false targets are generated by the self-protect jammer by modulating and delaying the transmission signal of the received radar. Due to the difficulty of angle deception, the false targets generated by the jammer are located on the extension line between the jammer and the receiving station. In the direct channel, the false target is located on the extension line between the jammer and the radar, and its distance to the jammer is the deception range. In the RIS-assisted virtual channel, the false target is located on the extension line of the incident beam of the RIS pointing to the jammer. The false targets generated by deception jamming in the direct and virtual channels do not coincide in terms of their spatial positions; therefore, the location results of false targets obtained in different channels are relatively dispersed in the unified coordinate system. According to this difference, the target measurements can be used to discriminate the false targets.

In the constructed architecture in Figure 1, the target measurements can be obtained in the radar direct and RIS-assisted virtual channels.

3.1. Radar Direct Channel

The target measurement is the same as for the normal radar, including the range and angle measurements. Taking the two-coordinate radar, for example, the target measurement includes the range $r_d$ and angle ${\theta }_d$, and the measurement vector is $Z_d={[r_d,{\theta }_d]}^{\mathrm{T}}$, where ${[\cdot ]}^{\mathrm{T}}$ represents the matrix transpose. Then, the target would be located at ${\mathit{X}}_d={[x_d,y_d]}^{\mathrm{T}}$,

$$\left\{\begin{array}{l}{x}_d=r_d\cos ({\theta }_d)+x_{\mathrm{R}}\\ y_d=r_d\sin ({\theta }_d)+y_{\mathrm{R}}\end{array}\right.$$

(5)

with $[x_{\mathrm{R}},y_{\mathrm{R}}]$ being the radar location. The location error can be described by the location covariance matrix $R_d=\mathrm{E}[\mathrm{d}{\mathit{X}}_d\mathrm{d}{\mathit{X}}_d^T]$, and $\mathrm{E}[\cdot ]$ stands for taking expectation. By the approximate linearization of (5), $\mathrm{d}{\mathit{X}}_d$ can be written as $\mathrm{d}{\mathit{X}}_d=T_d^{}\cdot \mathrm{d}{Z}_d$, and the transition matrix $T_d^{}$ is

$${\mathit{T}}_d^{}=\left[\begin{array}{cc}\partial x_d/\partial r_d& \partial x_d/\partial {\theta }_d\\ \partial y_d/\partial r_d& \partial y_d/\partial {\theta }_d\end{array}\right]=\left[\begin{array}{cc}\cos ({\theta }_d)& -r_d\sin ({\theta }_d)\\ \sin ({\theta }_d)& r_d\cos ({\theta }_d)\end{array}\right]$$

(6)

Then, the location covariance matrix $R_d$ is

$$R_d=\mathrm{E}[\mathrm{d}{\mathit{X}}_d\mathrm{d}{\mathit{X}}_d^T]=\mathrm{E}[(T_d^{}\mathrm{d}{Z}_d){(T_d^{}\mathrm{d}{Z}_d)}^T]=T_d^{}{\Lambda }_d{T}_d^T$$

(7)

where ${\Lambda }_d=\mathrm{E}[\mathrm{d}{Z}_d\mathrm{d}{Z}_d^T]=\mathrm{diag}({\sigma }_r^2,{\sigma }_{\theta }^2)$, and ${\sigma }_r^{}$ and ${\sigma }_{\theta }^{}$ are the radar measurement errors of the range and angle, respectively.

3.2. RIS-Assisted Virtual Channel

The target range can also be measured by estimating the time delay in the RIS-assisted virtual channel, which corresponds to the range sum of the path from the radar to the target, then to the RIS, and finally, to the radar. By cutting off the known range between the radar and the RIS, the measured range sum can be equitably considered as a bistatic range measurement with the radar as a transmitter and the RIS as a receiver. In the RIS-assisted virtual channel, the received beam of the radar points to the RIS, and the angle of the target cannot be measured directly in the radar. Because the cooperative anti-jamming is realized by the beam scanning of the received beam of the RIS, the RIS sensing signal can be reconstructed by the radar station with the RIS phases ${\{{\varphi }_l\}}_{l=1}^L$, and the angle of the target relative to the RIS can be measured using the maximum amplitude method.

Let $r_v$ be the measured range sum, which is the estimation of the range sum of the path from the radar to the target and then to the RIS. The measured angle of the target relative to the RIS is denoted as ${\theta }_v$. With the measurement vector $Z_v={[r_v,{\theta }_v]}^{\mathrm{T}}$, the target would be located at ${\mathit{X}}_v={[x_v,y_v]}^{\mathrm{T}}$,

$$\left\{\begin{array}{l}{x}_v=x_{\mathrm{RIS}}+r_{\mathrm{RIS}}\cos ({\theta }_v)\\ y_v=y_{\mathrm{RIS}}+r_{\mathrm{RIS}}\sin ({\theta }_v)\end{array}\right.$$

(8)

$r_{\mathrm{RIS}}$ is the range from the target to the RIS,

$$r_{\mathrm{RIS}}=\frac{r_v^2-[{(x_{\mathrm{RIS}}-x_0)}^2+{(y_{\mathrm{RIS}}-y_0)}^2]}{2[r_v^{}+(x_{\mathrm{RIS}}-x_0)\cos ({\theta }_R)+(y_{\mathrm{RIS}}-y_0)\sin ({\theta }_R)]}$$

(9)

with $[x_{\mathrm{RIS}},y_{\mathrm{RIS}}]$ being the location of the RIS. Similar to the derivation of the location error in the direct channel, the location error of ${\mathit{X}}_v$, measured by its location error covariance matrix $R_v$, can also be obtained by the approximate linearization,

$$R_v=\mathrm{E}[\mathrm{d}{\mathit{X}}_v\mathrm{d}{\mathit{X}}_v^T]=\left[\begin{array}{cc}{\sigma }_x^2& {\sigma }_{xy}^{}\\ {\sigma }_{xy}^{}& {\sigma }_y^2\end{array}\right]$$

(10)

where

$${\sigma }_x^2=\frac{1}{{\left|C\right|}^2}\left[\frac{{\cos }^2{\theta }_v}{r_{\mathrm{RIS}}^2}{\sigma }_{r_v}^2+{(c_{R2}+c_{T2})}^2{\sigma }_{{\theta }_v}^2\right]$$

(11)

$${\sigma }_{xy}^{}=\frac{1}{{\left|C\right|}^2}\left[\frac{\sin (2{\theta }_v)}{2r_{\mathrm{RIS}}^2}{\sigma }_{r_v}^2+(c_{R1}+c_{T1})(c_{R2}+c_{T2}){\sigma }_{{\theta }_v}^2\right]$$

(12)

$${\sigma }_y^2=\frac{1}{{\left|C\right|}^2}\left[\frac{{\sin }^2{\theta }_v}{r_{\mathrm{RIS}}^2}{\sigma }_{r_v}^2+{(c_{R1}+c_{T1})}^2{\sigma }_{{\theta }_v}^2\right]$$

(13)

$$\left|C\right|=\frac{(c_{R1}+c_{T1})\cos {\theta }_v}{r_{\mathrm{RIS}}^{}}+\frac{(c_{R2}+c_{T2})\sin {\theta }_v}{r_{\mathrm{RIS}}^{}}$$

(14)

$$c_{R1}=\cos {\theta }_v,c_{T1}=\cos {\theta }_R,c_{R2}=\sin {\theta }_v,c_{T2}=\sin {\theta }_R$$

(15)

${\sigma }_{r_v}^{}$ and ${\sigma }_{{\theta }_v}^{}$ are the measurement errors of $r_v$ and ${\theta }_v$, respectively. ${\theta }_R$ is the angle of the target relative to the radar.

3.3. Discrimination of Deception Targets

For the virtual multi-radar system, true targets have spatial aggregation characteristics, and active false targets have spatial dispersion characteristics. With the redundant measurements in the RIS-assisted virtual channel, the target discrimination statistics are designed, and the problem of discriminating a detected target as a true or false target can be formulated as a binary hypothesis testing problem.

Under the null hypothesis (H₀), it is assumed that the detection target corresponds to a true target. Under the alternative hypothesis (H₁), it is instead assumed that the target is generated by deception jamming.

The difference in the target locations in the radar direct channel ${\mathit{X}}_d$ and the RIS-assisted virtual channel ${\mathit{X}}_v$ is defined as the location difference $\mathsf{\Delta }\mathit{X}={\mathit{X}}_d-{\mathit{X}}_v$. To make an optimized decision, the discrimination is inferred from the location difference $\mathsf{\Delta }\mathit{X}$ in a probabilistic framework. Due to the location errors, $\mathsf{\Delta }\mathit{X}$ is a random vector following a normal distribution,

$$\mathsf{\Delta }\mathit{X}~N(\mathsf{\Omega },R_{\mathsf{\Delta }})$$

(16)

where $R_{\mathsf{\Delta }}=R_d+R_v$. Under $H_0$, the mean value $\mathsf{\Omega }={\mathbf{0}}_{2\times 1}$, due to the spatial aggregation characteristics of the true targets. Under $H_1$, the mean value $\mathsf{\Omega }$ is non-zero due to the spatial dispersion characteristics of false targets, as shown in Figure 2. Therefore, with the constant probability of missing alarms, the discrimination statistic is chosen as the Mahalanobis distance,

$$d=\mathsf{\Delta }{\mathit{X}}^{\mathrm{T}}{R}_{\mathsf{\Delta }}\mathsf{\Delta }\mathit{X}$$

(17)

The optimal discrimination algorithm is designed as

$$d_{}\underset{H_0}{\overset{H_1}{\begin{array}{c}>\\ <\end{array}}}\eta$$

(18)

If the threshold is exceeded, the detected target would be discriminated against as a false target. Otherwise, a true target is declared. The threshold η is set to ensure the required constant probability of missing alarms $P\{H_1\left|H_0\right.\}$. For the case with one RIS, the significance of the hypothesis testing $\alpha =P\{H_1\left|H_0\right.\}$. Because $d\sim {\chi }_2^2$ under $H_0$, $\eta =F_{{\chi }_2^2}^{-1}\left(1-\alpha \right)$, where ${\chi }_2^2$ is the chi-square distribution with two degrees of freedom, and $F_{{\chi }_2^2}^{-1}\left(\cdot \right)$ is the inverse cumulative distribution function of ${\chi }_2^2$.

Here, the proposed deception ECCM method is given in the virtual multi-radar with one RIS-assisted virtual channel as an example. It is then extended to the virtual multi-radar with multiple RIS-assisted virtual channels. The multiple RIS-assisted radar can be treated as multiple direct–virtual channel pairs, and multiple discrimination results can be synthesized with a certain fusion rule (such as ‘and’, ‘or’, KM rule) to obtain more reliable discrimination results.

4. Theoretical Performance Analysis and Location Optimization

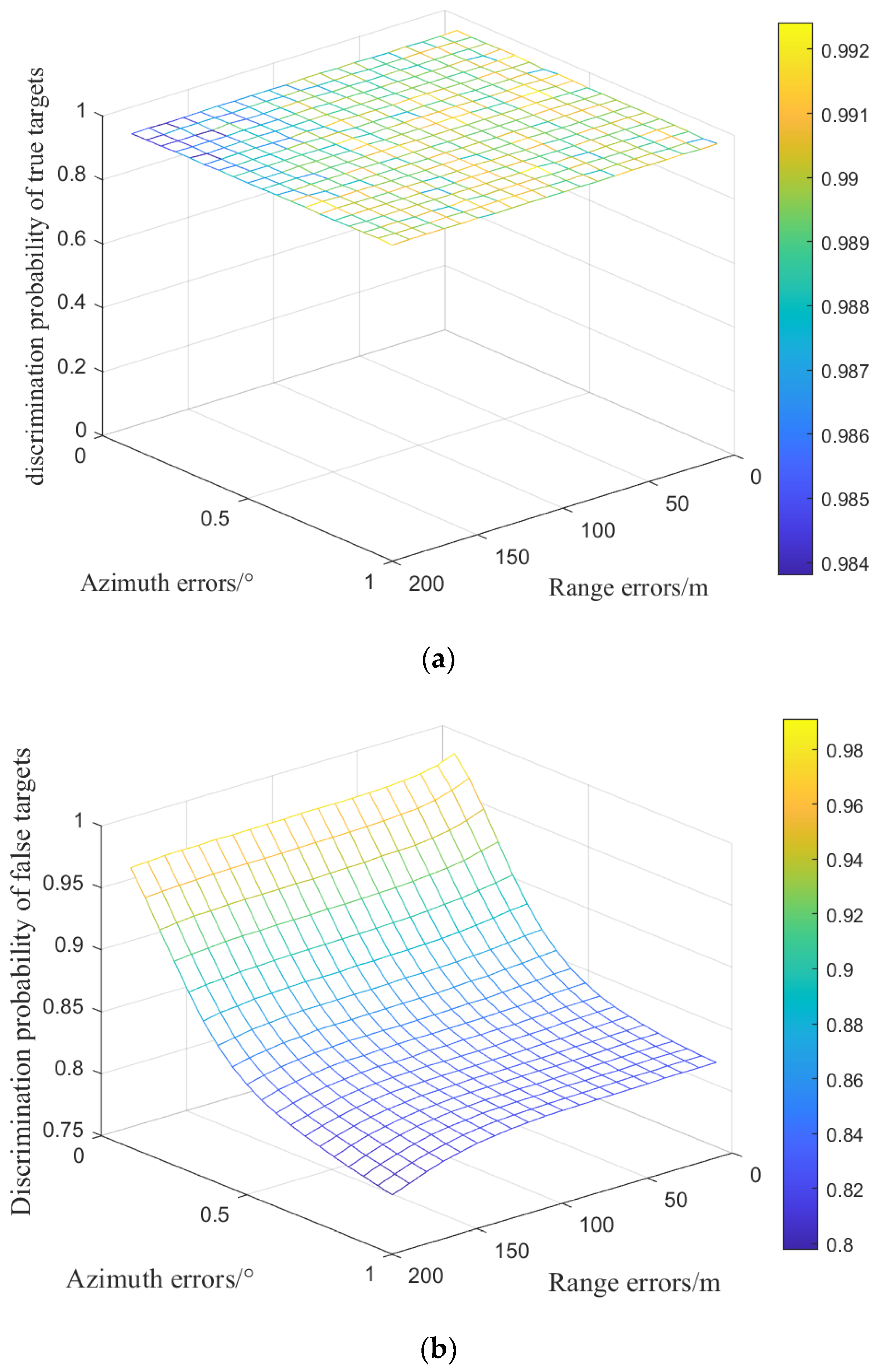
In this section, the theoretical performance analysis of the proposed discrimination method is given. And, based on the derived discrimination probability, the locations of RISs in the virtual multi-radar system are optimized to ensure the best discrimination performance.

4.1. Theoretical Performance Analysis

The discrimination performance is measured by the total discrimination probability of true targets $P_{\mathrm{true}}$ and the total misjudgment probability of false targets $P_{\mathrm{false}}$ (i.e., the deception probability of the virtual multi-radar). For a virtual multi-radar with M assisted RISs, the total discrimination result is synthesized by M local discrimination results. Hence, the total discrimination probability is determined by the local discrimination performance of each direct–virtual channel pair, which is derived first.

For each direct–virtual channel pair, the location difference $\mathsf{\Delta }\mathit{X}$ between the direct channel and the indirect channel is a random vector following a normal distribution due to the location errors, as shown in Equation (16). Under $H_0$, the mean value $\mathsf{\Omega }={\mathbf{0}}_{2\times 1}$ due to the spatial aggregation characteristics of true targets. Under $H_1$, the mean value $\mathsf{\Omega }$ is non-zero, which can be written as $\mathit{E}={[u_x,u_y]}^{\mathrm{T}}$. Hence, the distribution of $\mathsf{\Delta }\mathit{X}$ can be given as

$$\mathsf{\Delta }\mathit{X}~\left\{\begin{array}{l}N({\mathbf{0}}_{2\times 1},{\mathit{R}}_{\mathsf{\Delta }}),\hspace{1em}{H}_0\hfill \\ N(\mathit{E},{\mathit{R}}_{\mathsf{\Delta }}),\hspace{1em}\hspace{1em}{H}_1\hfill \end{array}\right.$$

(19)

where $R_{\mathsf{\Delta }}$ is the error covariance matrix of the location errors $\mathsf{\Delta }\mathit{X}$. $R_{\mathsf{\Delta }}$ is a symmetric matrix and can be defined as

$${\mathit{R}}_{\mathsf{\Delta }}=\left[\begin{array}{cc}{\xi }_{11}& {\xi }_{12}\\ {\xi }_{12}& {\xi }_{22}\end{array}\right]=\left[\begin{array}{cc}{\delta }_x^2& \rho {\delta }_x{\delta }_y\\ \rho {\delta }_x{\delta }_y& {\delta }_y^2\end{array}\right]$$

(20)

where ${\delta }_x=\sqrt{{\xi }_{11}}$ and ${\delta }_y=\sqrt{{\xi }_{22}}$ represent the accuracy of the x-axis and y-axis location differences, respectively. $\rho ={\xi }_{12}/({\delta }_x{\delta }_y)$ represents the correlation coefficient of the location difference between the x-axis and the y-axis.

Under $H_0$, the discrimination statistic (Mahalanobis distance) $d=\mathsf{\Delta }{\mathit{X}}^{\mathrm{T}}{R}_{\mathsf{\Delta }}\mathsf{\Delta }\mathit{X}~{\chi }_2^2$, and the discrimination threshold $\eta =F_{{\chi }_2^2}^{-1}\left(1-\alpha \right)$. The proposed data-fusion-based deception ECCM method can discriminate the false targets under the condition of ensuring that the misjudgment probability of true targets is equal to $\alpha$. Therefore, the local discrimination probability of true targets $P(H_0\left|H_0\right.)$ is

$$P(H_0\left|H_0\right.)=1-\alpha$$

(21)

Under $H_1$, the mean value $\mathit{E}$ of the location difference $\mathsf{\Delta }\mathit{X}$ is jointly determined by the radar location ${\mathit{X}}_{\mathrm{R}}=[x_{\mathrm{R}},y_R]$, the RIS location ${\mathit{X}}_{\mathrm{RIS}}=[x_{\mathrm{RIS}},y_{\mathrm{RIS}}]$, the location of the true target ${\mathit{X}}_{\mathrm{T}}=[x_{\mathrm{T}},y_{\mathrm{T}}]$, and the deception distance $\mathsf{\Delta }d$.

The location of the false target measured in the direct channel is $[x_f^{},y_f^{}]$, and

$$\left\{\begin{array}{c}{x}_f^{}=(r+\mathsf{\Delta }d)\cos (\theta )+x_R\\ y_f^{}=(r+\mathsf{\Delta }d)\sin (\theta )+y_R\end{array}\right.$$

(22)

where $[r,\theta ]$ are the coordinates of the true target in the radar polar coordinate system in the direct channel, with $r=\sqrt{{(x_{\mathrm{T}}-x_{\mathrm{R}})}^2+{(y_{\mathrm{T}}-y_R)}^2}$ and $\theta =\arctan \left((y_{\mathrm{T}}-y_R)/(x_{\mathrm{T}}-x_R)\right)$.

The location of the false target measured in the indirect channel is $[{x^{\prime }}_f^{},{y^{\prime }}_f^{}]$, and

$$\left\{\begin{array}{c}{x^{\prime }}_f^{}={r^{\prime }}_{\mathrm{RIS}}\cos (\phi )+x_{\mathrm{RIS}}\\ {y^{\prime }}_f^{}={r^{\prime }}_{\mathrm{RIS}}\sin (\phi )+y_{\mathrm{RIS}}\end{array}\right.$$

(23)

$${r^{\prime }}_{\mathrm{RIS}}=\frac{{\left(d_{\mathrm{sum}}^{}+2\mathsf{\Delta }d\right)}^2-\left[{\left(x_{\mathrm{RIS}}-x_{\mathrm{R}}\right)}^2+{\left(y_{\mathrm{RIS}}-y_{\mathrm{R}}\right)}^2\right]}{2\left[\left(d_{\mathrm{sum}}^{}+2\mathsf{\Delta }d\right)+\left(x_{\mathrm{RIS}}-x_{\mathrm{R}}\right)\cos \phi +\left(y_{\mathrm{RIS}}-y_{\mathrm{R}}\right)\sin \phi \right]}$$

(24)

where $d_{\mathrm{sum}}^{}=\sqrt{{(x_{\mathrm{T}}-x_{\mathrm{R}})}^2+{(y_{\mathrm{T}}-y_{\mathrm{R}})}^2}+\sqrt{{(x_{\mathrm{T}}-x_{\mathrm{RIS}})}^2+{(y_{\mathrm{T}}-y_{\mathrm{RIS}})}^2}$ is the distance sum of the target in the indirect channel, and its corresponding azimuth is $\phi =\arctan ((y_{\mathrm{T}}-y_{\mathrm{RIS}})/(x_{\mathrm{T}}-x_{\mathrm{RIS}}))$.

According to Equations (22) and (23), the mean value $\mathit{E}$ of $\mathsf{\Delta }\mathit{X}$ can be obtained as

$$\mathit{E}={[u_x,u_y]}^{\mathrm{T}}={[x_f^{}-{x^{\prime }}_f^{},y_f^{}-{y^{\prime }}_f^{}]}^{\mathrm{T}}$$

(25)

Then, the two-dimensional probability density function of $\mathsf{\Delta }\mathit{X}$ can be written as

$$f(x,y)=\frac{1}{2\mathsf{\pi }{\delta }_x{\delta }_y\sqrt{1-{\rho }^2}}\exp \left\{\frac{-1}{2(1-{\rho }^2)}\left[\frac{{(x-u_x)}^2}{{\delta }_x^2}-2\rho \frac{(x-u_x)(y-u_y)}{{\delta }_x{\delta }_y}+\frac{{(y-u_y)}^2}{{\delta }_y^2}\right]\right\}$$

(26)

The discrimination statistic $d=\mathsf{\Delta }{\mathit{X}}^{\mathrm{T}}{R}_{\mathsf{\Delta }}\mathsf{\Delta }\mathit{X}$ can be further simplified as

$$\begin{array}{ll}\hfill d& =\mathsf{\Delta }{\mathit{X}}^{\mathrm{T}}{R}_{\mathsf{\Delta }}\mathsf{\Delta }\mathit{X}=[x,y]\left[\begin{array}{cc}{\delta }_x^2& \rho {\delta }_x{\delta }_y\\ \rho {\delta }_x{\delta }_y& {\delta }_y^2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\hfill \\ & =K({\delta }_y^2{x}^2-2\rho {\delta }_x{\delta }_{y}xy+{\delta }_x^2{y}^2)\hfill \\ & =K^{\prime }\left({(\frac{x}{{\delta }_x})}^2-2\rho (\frac{x}{{\delta }_x})(\frac{y}{{\delta }_y})+{(\frac{y}{{\delta }_y})}^2\right)\hfill \end{array}$$

(27)

where $K=\frac{1}{{\delta }_x^2{\delta }_y^2(1-{\rho }^2)}$ and $K^{\prime }=\frac{1}{1-{\rho }^2}$.

According to the hypothesis testing model in Equation (19), it can be seen that the misjudgment probability of false targets $P(H_0\left|H_1\right.)$ can be given as

$$P(H_0\left|H_1\right.)=P(d\le \eta \left|H_1\right.)$$

(28)

Substitute Equation (27) into (28),

$$P(H_0\left|H_1\right.)=P(d\le \eta \left|H_1\right.)=P\left(\left.K^{\prime }\left({(\frac{x}{{\delta }_x})}^2-2\rho (\frac{x}{{\delta }_x})(\frac{y}{{\delta }_y})+{(\frac{y}{{\delta }_y})}^2\right)\le \eta \right|H_1\right)$$

(29)

Hence, the misjudgment probability of false targets $P(H_0\left|H_1\right.)$ can be expressed as the double integral of the probability density function $f(x,y)$ of $\mathsf{\Delta }\mathit{X}$ on the integration area $\mathsf{\Omega }$,

$$P(H_0\left|H_1\right.)={\displaystyle \underset{\mathsf{\Omega }}{\iint }f(x,y)\mathrm{d}x\mathrm{d}y}$$

(30)

$$\mathsf{\Omega }=\left\{K^{\prime }\left({(\frac{x}{{\delta }_x})}^2-2\rho (\frac{x}{{\delta }_x})(\frac{y}{{\delta }_y})+{(\frac{y}{{\delta }_y})}^2\right)\le \eta \right\}$$

(31)

Equation (30) can be simplified as

$$P(H_0\left|H_1\right.)={\displaystyle {\int }_{-\sqrt{\delta }\cdot {\sigma }_x}^{\sqrt{\delta }\cdot {\sigma }_x}{\displaystyle {\int }_{g_{low}(x)}^{g_{up}(\mathrm{x})}f(x,y)}dxdy}$$

(32)

$$g_{up}(\mathrm{x})={\delta }_y\left[\sqrt{\left(\eta -{\left(\frac{x}{{\delta }_x}\right)}^2\right)\left(1-{\rho }^2\right)}+\rho \left(\frac{x}{{\delta }_x}\right)\right]$$

(33)

$$g_{low}(x)={\delta }_y\left[-\sqrt{\left(\eta -{\left(\frac{x}{{\delta }_x}\right)}^2\right)\left(1-{\rho }^2\right)}+\rho \left(\frac{x}{{\delta }_x}\right)\right]$$

(34)

For a virtual multi-radar with M assisted RISs, if the total discrimination result is synthesized by M local discrimination results with the rule of ‘and’, that is, the target is discriminated against as being true unless all M local discrimination results indicate that it is a true target, the total discrimination probability of true targets $P_{\mathrm{true}}$ is

$$P_{\mathrm{true}}={\displaystyle \prod _{m=1,2,\dots ,M}{P}_m(H_0\left|H_0\right.)}={(1-\alpha )}^M$$

(35)

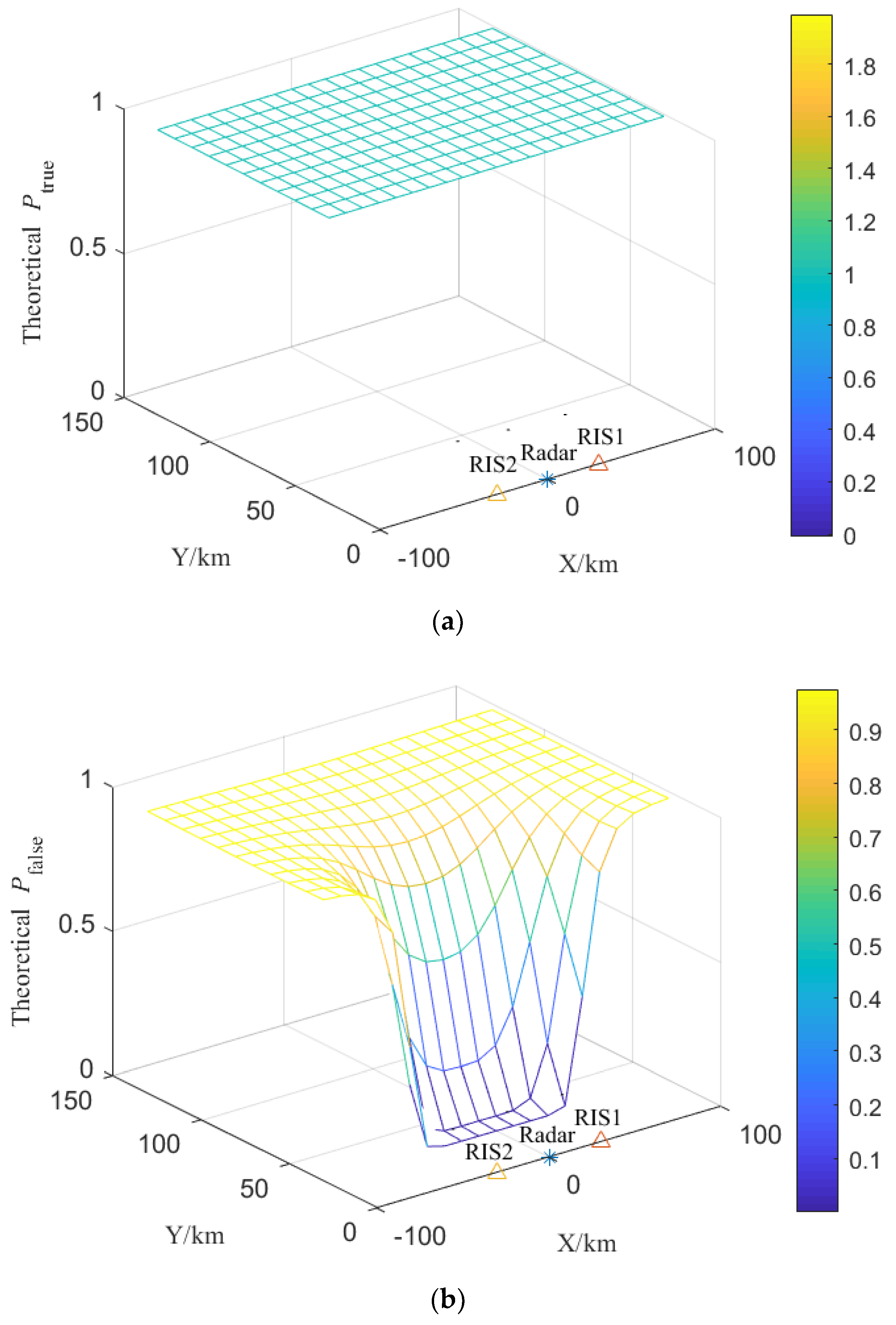
From Equation (35), to ensure the required constant probability of missing alarms being $P\{H_1\left|H_0\right.\}$, the total discrimination probability of true targets $P_{\mathrm{true}}=1-P\{H_1\left|H_0\right.\}$. Then, the significance of each hypothesis testing should be $\alpha =1-\sqrt[M]{1-P\{H_1\left|H_0\right.\}}$ for the fusion rule of ‘and’.

And the deception probability of the virtual multi-radar $P_{\mathrm{false}}$ is

$$P_{\mathrm{false}}={\displaystyle \prod _{m=1,2,\dots ,M}{P}_m(H_0\left|H_1\right.)}$$

(36)

where $P_m(H_0\left|H_0\right.)$ and $P_m(H_0\left|H_1\right.)$ are the local discrimination probability of true targets and the misjudgment probability of false targets in the direct–virtual channel pair with the m-th RIS, which can be obtained by (21) and (32), respectively.

4.2. Location Optimization of RISs

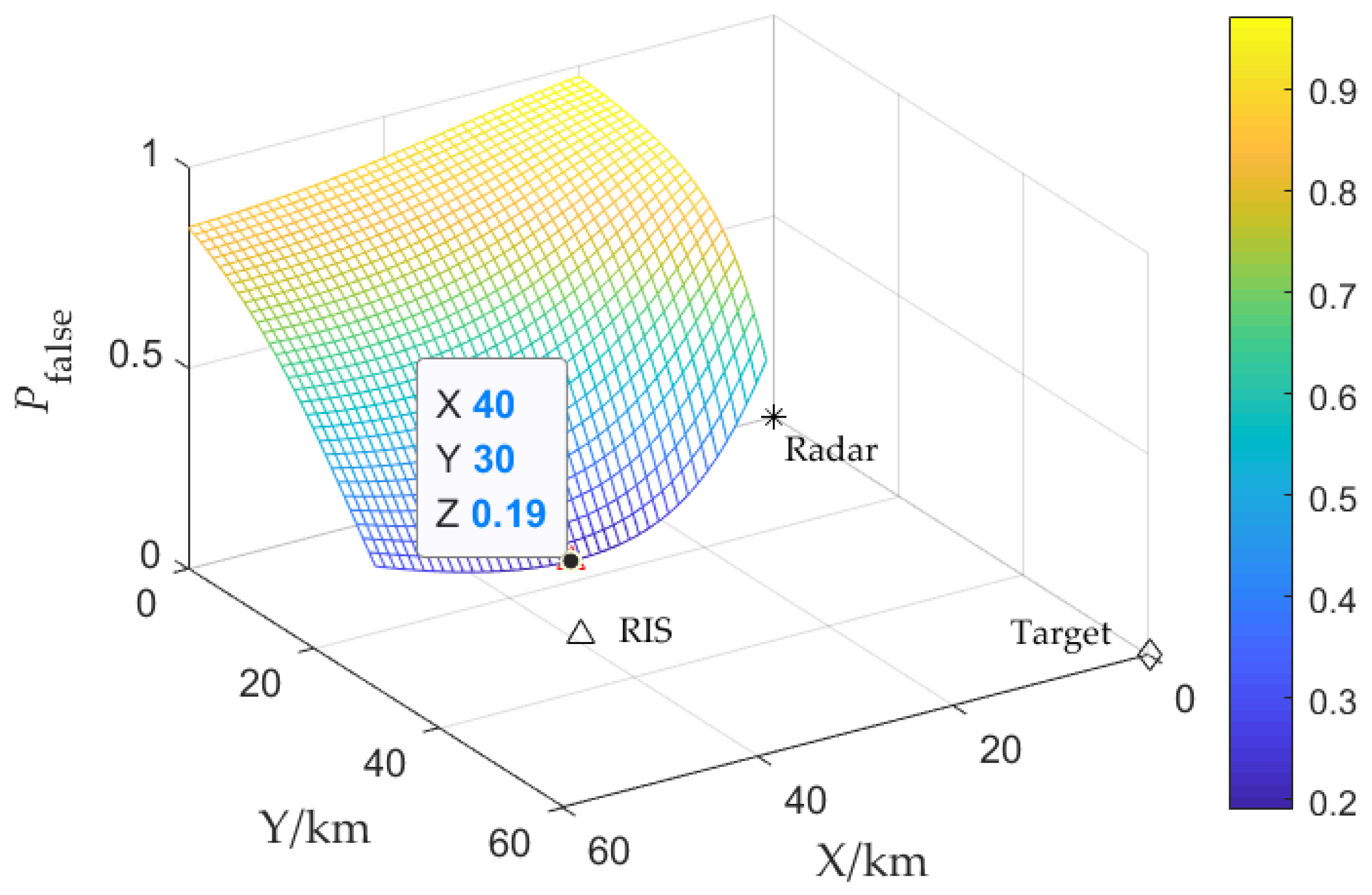
From the above theoretical analysis, the deception probability of the virtual multi-radar $P_{\mathrm{false}}$ is related to the location of RISs relative to the radar and the target. Therefore, the radar deception probability can be minimized by optimizing the location of the RISs, which is discussed in the subsection.

If the distance between the RISs and the radar is greater, the path loss in the RIS-assisted indirect channel is greater, and the target signal-to-noise ratio (SNR) obtained by the indirect channel is lower, which would reduce the target measurement accuracy. If the RISs are located closer to the radar, the difference in the target detection angle between the indirect channel and the direct channel is smaller, and the spatial location dispersion of the active false target becomes worse. This will reduce the difference between true and false targets, leading to the deterioration of the discrimination probability of false targets. Therefore, the optimal location of RISs is a joint optimization problem.

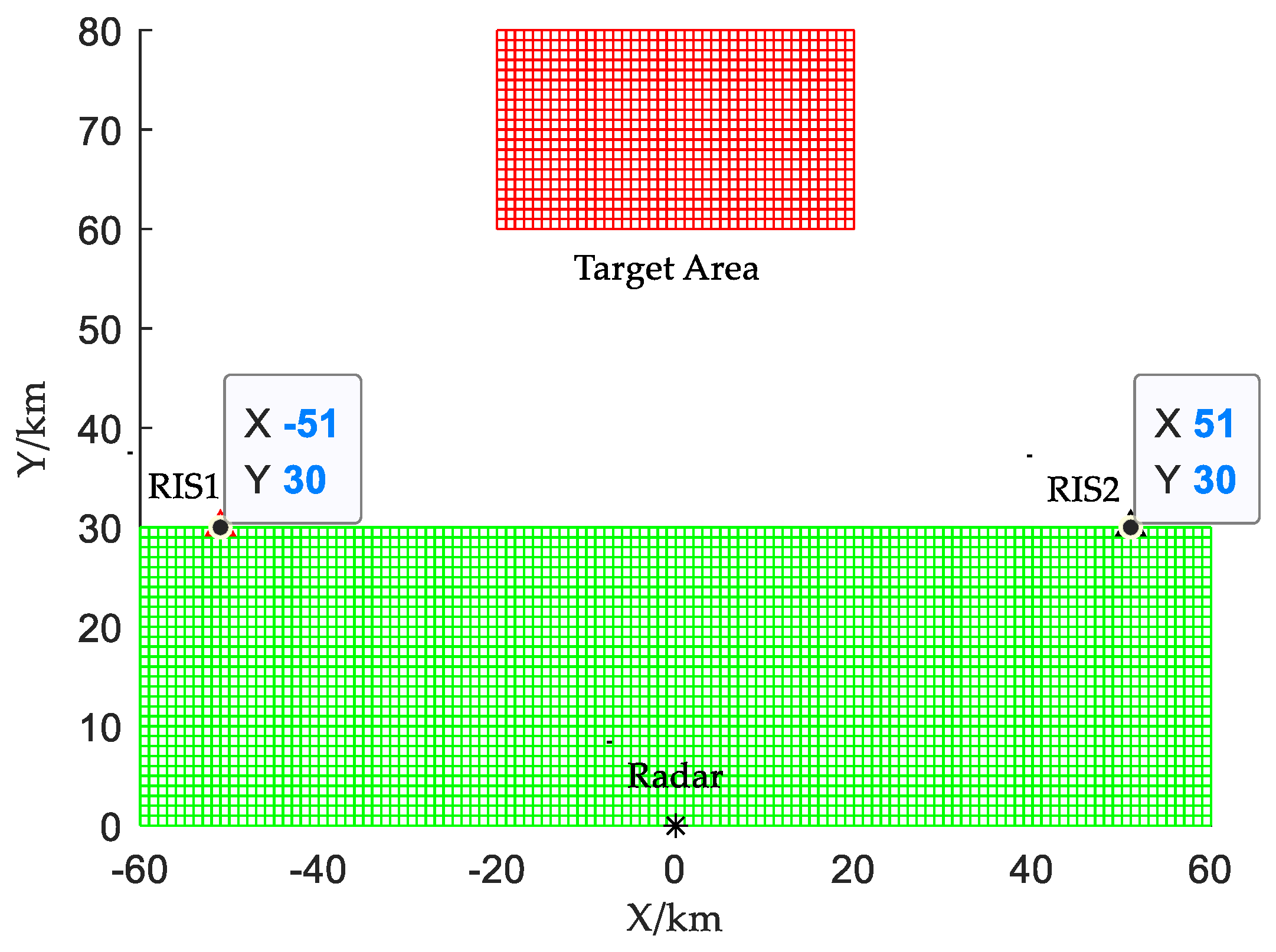
For a detection area ${\mathsf{\Omega }}_D$, the location of M RISs is optimized to minimize the average deception probability for all targets in the detection area. There are certain restrictions on the optimal location of RISs. First of all, in order to ensure the advantages of multiple perspectives and a certain angle difference, the distance between the radar and the RISs should be greater than a threshold value $‖{\mathit{X}}_{\mathrm{R}}-{\mathit{X}}_{\mathrm{RIS}}^m‖\ge R_{\min }$, where ${\mathit{X}}_{\mathrm{RIS}}^m$ is the location of the m-th RIS, m = 1, 2, …, M. Secondly, the redundant detection of the virtual multi-radar should be ensured for the target discrimination, which requires that the detection area ${\mathsf{\Omega }}_D$ is within the detection range of the system, i.e., $‖{\mathit{X}}_{\mathrm{R}}-{\mathit{X}}_{\mathrm{T}}^{}‖+‖{\mathit{X}}_{\mathrm{T}}^{}-{\mathit{X}}_{\mathrm{RIS}}^m‖+‖{\mathit{X}}_{\mathrm{RIS}}^m-{\mathit{X}}_{\mathrm{R}}‖\le 2R_{\max }$, $\forall {\mathit{X}}_{\mathrm{T}}\in {\mathsf{\Omega }}_D$, where $R_{\max }$ is the detection range in the direct channel.

It is assumed that the location range of the RISs is $\mathsf{\Psi }$, and the optimization problem of the location of the RISs can be formulated as

$$\begin{array}{ll}\underset{{\mathit{X}}_{\mathrm{RIS}}^m}{\min }& \frac{1}{N}{\displaystyle \sum _{n=1}^N{P}_{\mathrm{false}}^n}\\ \mathrm{s}.\mathrm{t}.& ‖{\mathit{X}}_{\mathrm{R}}-{\mathit{X}}_{\mathrm{T}}^n‖+‖{\mathit{X}}_{\mathrm{T}}^n-{\mathit{X}}_{\mathrm{RIS}}^m‖+‖{\mathit{X}}_{\mathrm{RIS}}^m-{\mathit{X}}_{\mathrm{R}}‖\le 2R_{\max },\forall {\mathit{X}}_{\mathrm{T}}^n\in {\mathsf{\Omega }}_D\\ & ‖{\mathit{X}}_{\mathrm{R}}-{\mathit{X}}_{\mathrm{RIS}}^m‖\ge R_{\min },‖{\mathit{X}}_{\mathrm{RIS}}^m-{\mathit{X}}_{\mathrm{RIS}}^{m^{\prime }}‖\ge R_{\min },m\ne m^{\prime }\\ & {\mathit{X}}_{\mathrm{RIS}}^m\in \mathsf{\Psi }\end{array}$$

(37)

where ${\mathit{X}}_{\mathrm{T}}^n$, n = 1, 2, …, N is the location of the n-th RIS in the detection area ${\mathsf{\Omega }}_D$, and $P_{\mathrm{false}}^n$ is the deception probability of the virtual multi-radar when the target is located at ${\mathit{X}}_{\mathrm{T}}^n$, which can be obtained by Equation (36). For the formulated optimization problem, we can resort to the genetic algorithm.

5. Simulation Results

First, a RIS-assisted virtual multi-radar is simulated to indicate the feasibility and effectiveness of the algorithm, and the discrimination performance versus the radar measurement errors are covered. Secondly, the discrimination probability of the virtual multi-radar is simulated and compared with the derived theoretical formula in Equations (35) and (36) to prove the validity of the theoretical performance analysis. Finally, the results for the location optimization of RISs are given.

5.1. Feasibility Analysis

A radar assisted by one RIS is considered. The radar, the RIS, and the target are located at $[0,0]$ km, $[15,0]$ km, and $[80,70]$ km. The radar measurement errors in the radar direct channel are ${\sigma }_r^{}=30$ m and ${\sigma }_{\theta }^{}={0.05}^{°}$. The radar measurement errors in the RIS-assisted virtual channel are ${\sigma }_{r_v}^{}={\sigma }_r^{}$ and ${\sigma }_{{\theta }_v}^{}={0.15}^{°}$. The expected probability of missing alarms is set as $P\{H_1\left|H_0\right.\}=0.01$; therefore, the significance of the hypothesis testing should be $\alpha =0.01$.

Self-protect jamming is performed, and eight false targets are generated by the deception jamming with the deception ranges of ±600 m, ±1200 m, ±1800 m, and ±2400 m. The radar dots in direct and virtual channels are reported in Figure 3a. The proposed data-fusion-based deception ECCM method is applied to discriminate the false targets. With the false targets removed, the residual dots and the fusion dots are shown in Figure 3b. It is shown that all the false targets have been discriminated against on the premise of the remaining the true targets, which verifies the feasibility of the discrimination method and the ECCM ability of the RIS-assisted virtual multi-radar system. In addition, the location accuracy can be improved by the dot fusion of two detection channels.

With the deception range of 600 m, the discrimination probability of true and false targets versus the radar measurement errors ${\sigma }_r^{}$ and ${\sigma }_{\theta }^{}$ are given in Figure 4, where the discrimination probability is calculated by Monto Carlo simulation with 10⁵ run times. Obviously, the discrimination probability of true targets is approximately 0.99, which coincides with the pre-set probability of missing alarms. The discrimination probability of false targets is inversely proportional to the measurement errors, because larger measurement errors will lead to an increase in the discrimination threshold for the constant probability of missing alarms, bringing a decrease in the discrimination probability of false targets. However, the influence of angle error on the discrimination probability is greater than that of the distance error.

5.2. Simulation for Theoretical Analysis

A radar assisted by two RISs is considered, and the total discrimination result is synthesized by two local discrimination results with the rule of ‘and’. The location of the first RIS is [0, 30] km, and the second RIS is located at [−30, 0] km. The remainder of the simulation parameters of the virtual multi-radar are the same as in Section 5.1. To ensure that the expected probability of missing alarms is 0.01, the total discrimination probability of true targets $P_{\mathrm{true}}={(1-\alpha )}^2=0.99$; therefore, the significance of each hypothesis testing should be $\alpha =1-\sqrt{0.99}=0.005$.

Because the target location affects the discrimination performance, the discrimination probability for different target locations is simulated. For each target located in the detection area of $[-100,100]\times [30,130]$ km, the total discrimination probability of true targets $P_{\mathrm{true}}$ and the deception probability of the virtual multi-radar $P_{\mathrm{false}}$ are obtained by Monto Carlo simulation with 10⁵ run times. The simulation results are given in Figure 5.

For each target located in the detection area of $[-100,100]\times [30,130]$ km, the theoretical total discrimination probability of true targets $P_{\mathrm{true}}$ and the deception probability of the virtual multi-radar $P_{\mathrm{false}}$ are calculated using Equations (35) and (36). The results are shown in Figure 6.

As is shown in Figure 6a, the theoretical $P_{\mathrm{true}}$ is equal to 0.99 for the arbitrary target location, which coincides with the pre-set probability of missing alarms. The simulated discrimination probability $P_{\mathrm{true}}$ in Figure 5a, which is approximately 0.99, is consistent with the theoretical results. The theoretical deception probability $P_{\mathrm{false}}$ shown in Figure 6b is lower when the target is located closer to the radar. When the target becomes further away from the virtual multi-radar, the deception probability $P_{\mathrm{false}}$ increases. This is because the angle difference between the indirect and direct channels becomes smaller, leading to the deterioration of the discrimination probability of false targets. Compared with the results in Figure 5b, the simulated probability $P_{\mathrm{false}}$ is approximately the same as the theoretical probability in terms of the values and variation trends, which indicates the correctness of the performance analysis.

5.3. Simulation for RIS Location Optimization

A radar assisted by one RIS is first considered. The peak power of the radar is 1 MW. The operating frequency is 1 GHz. The antenna gain is 45 dB; an effective noise temperature is 290 K; and the radar loss and the noise coefficients are 3 dB. The radar bandwidth is 400 kHz, and the target radar cross section (RCS) is 1 m². The coordinates of the target location are [0, 60] km, the deception distance is 2 km, and the location area of the RIS is $[20,60]\times [0,30]$ km. The optimization results are shown in Figure 7 (‘*’ denotes the radar location, ‘△’ denotes the RIS location, and ‘◊’ denotes the target location).

It can be seen from Figure 7 that the optimal RIS is located at [30, 40] km for the target at [0, 60] km, and the deception probability of the radar is minimized to be 0.19.

For a target detection area of $[-20,20]\times [60,80]$ km, the optimization results are shown in Figure 8, where the average deception probability is minimized. The optimal RIS is located at [30, 51] km for the target located in the specified detection area, and the minimum value is 0.54. The average deception probability is much higher than the minimum deception probability for the target at [0, 60] km, because [0, 60] km is located closest to the virtual multi-radar system and has the lowest deception probability in the detection area.

The optimization results in Figure 7 and Figure 8 show that the optimal location of the RISs can be realized to minimize the deception probability of the virtual multi-radar.

Then, the location optimization of two RISs are considered. The location area of the RIS is $[-60,60]\times [0,30]$ km. When the target is located at [0, 60] km, the optimized locations are shown in Figure 9. When the target is located in the detection area of $[-20,20]\times [60,80]$ km, the optimized locations are shown in Figure 10.

As is shown in Figure 9, when two RISs are located at [−38, 30] km and [30, 38] km, the deception probability of the RIS-assisted radar is the lowest. For the optimized locations, the minimum deception probability is 0.11. In Figure 10, the optimal locations of two RISs are [51, 30] km and [−51, 30] km for the target area of $[-20,20]\times [60,80]$ km, when the average deception probability is minimized. For the optimized locations, the minimum average deception probability is 0.41. Comparing the deception probability with the minimum values in Figure 7 and Figure 8 with one RIS, it can be seen that the deception probability becomes lower with more RISs; therefore, the anti-jamming ability of the virtual multi-radar system can be improved by increasing the number of RISs.

6. Discussion

Assisted by the RISs, monostatic radar can collect the target echoes in distributed directions, forming a virtual multi-radar system. Based on the above analysis, the data-fusion-based deception ECCM method can be used in the proposed system to discriminate the false targets, and its deception ECCM ability is affected by multiple factors, such as radar measurement errors, deception range, target location, the number and locations of the RISs, etc.

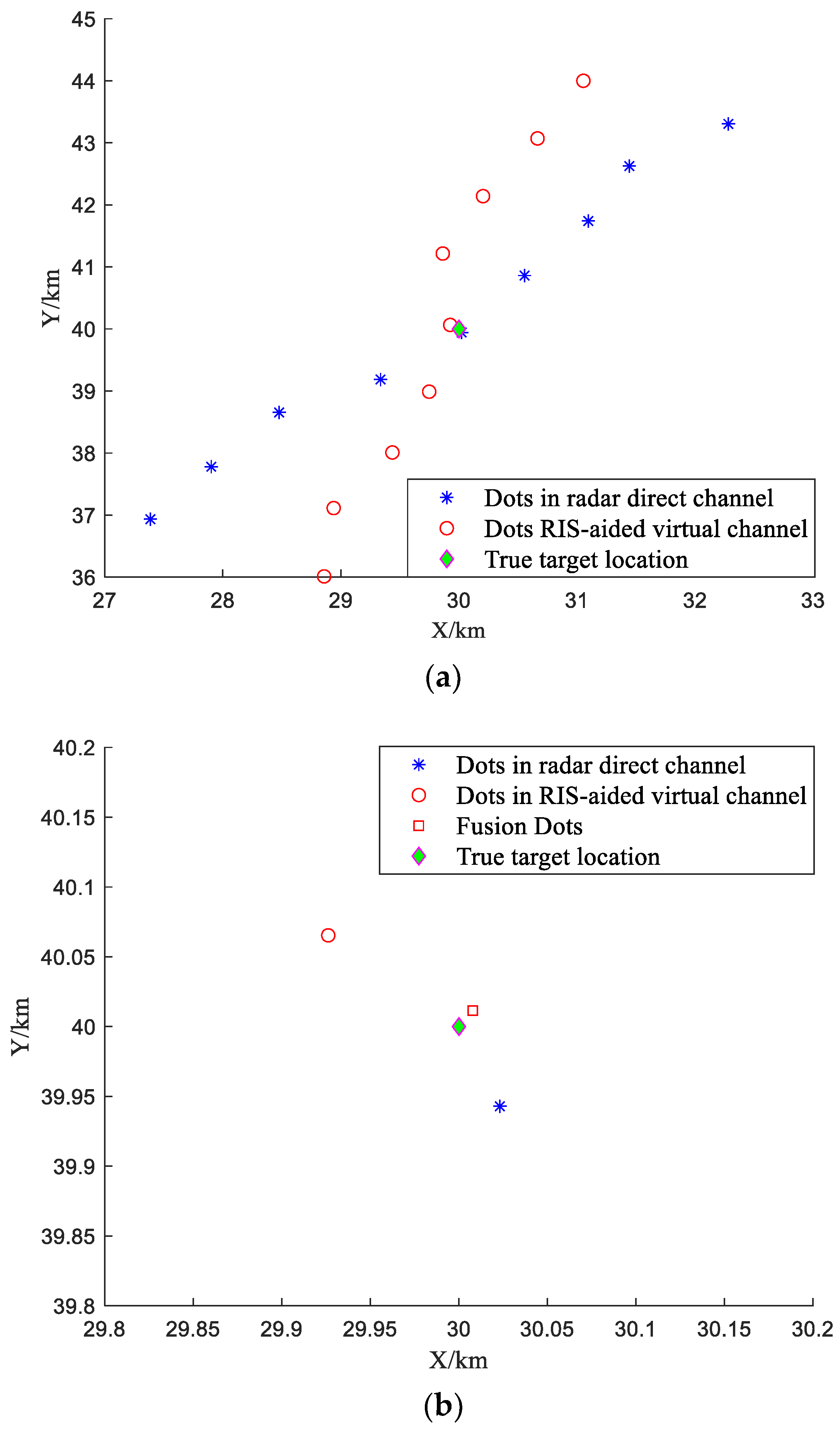
In addition, the proposed discrimination method essentially utilizes the differences in the spatial aggregation characteristics of true and false targets. It is valid for the false targets generated by any type of deception jamming, which is not limited to the range of deception false targets mentioned in Figure 2. Because the RIS, as an auxiliary receiving platform, is silent in the direction of the target area, the jammer cannot obtain the location of the RIS to generate false targets that match the spatial location of the direct channel in the RIS-assisted virtual channel. Therefore, it is impossible to implement cooperative deception jamming on the virtual multi-radar system with the silent RIS. The spatial dispersion characteristics of false targets are always established, and the proposed data-fusion-based deception ECCM method always works.

In this section, the differences and similarities between the RIS-assisted virtual multi-radar system and the practical multi-radar system are discussed, which are summarized below.

• The discrimination algorithms adopted by the two systems are similar. The discrimination statistics are both based on the Mahalanobis distance, and the discrimination methods are based on hypothesis testing algorithms. However, the target measurement in the RIS-assisted virtual channel is different from the practical multi-radar system, which makes the derivation of its location error covariance matrix $R_v$ complicated.
• The proposed discrimination algorithm applies data fusion to discriminate true and false targets with the target measurements from different detection channels. As a high-level information fusion strategy, data fusion requires minimal computational complexity. Compared with the deception ECCM algorithm in practical multi-static radar, their computational complexities are similar.
• Measurement error, deception distance, and target position have the same effect on the discrimination performance of both systems, essentially because the basic principle of discriminating active false targets is the same. Both systems make use of the difference between true and false targets in the spatial dispersion of the locations from different observation channels.
• Simulation results have shown that the discrimination probability increases with the increase in the number of RISs, which is in accordance with the effect of the radar number on the discrimination performance of the practical system. In contrast to the practical system, however, the number of RISs cannot be increased indefinitely to improve its performance. This is because the number of RISs is limited by the maximum number of multiple beams that the monostatic radar can achieve.
• Location optimization of the RISs is different from that of the practical multi-radar system. The layout of a practical system is optimized to ensure the maximum radar aperture. As a result of this, the difference in the observation directions of the target is maximized. However, in addition to the maximum observation aperture, the location optimization of the RISs should also consider the influence of the target signal-to-noise ratio (SNR) in the RIS-assisted virtual channel on its measurement error. This, in turn, affects the target discrimination performance.

The deception ECCM ability of the RIS-assisted radar was first discussed, and the data-fusion-based algorithm was extended to the RIS-assisted radar to indicate its excellent anti-jamming ability. As a low-cost passive device, the introduction of the RIS greatly improves the effectiveness and cost ratio of the radar in a complex electronic warfare environment.

7. Conclusions

This paper introduces a RIS to a monostatic radar to improve its deception ECCM ability. By exploiting the excellent characteristics of the RIS in reconstructing a signal propagation environment, a virtual multi-radar system was constructed, and a data-fusion-based deception ECCM method was used to discriminate active false targets. The theoretical discrimination probability of the proposed virtual multi-radar system was derived, and the location optimization of the RIS was discussed to maximize target discrimination performance. A simulation was conducted to verify its excellent ECCM ability. However, it is noted that the ECCM method presented in this paper did not include signal-fusion-based methods in the RIS-assisted radar. Subsequent studies should focus on the design of the phase shifts of RIS elements for signal-fusion-based methods.