A Review of GAN-Based Super-Resolution Reconstruction for Optical Remote Sensing Images
Abstract
:1. Introduction
- We offer a thorough overview of the super-resolution process based on GANs, which covers the working mechanism of GANs, the reconstruction process for SR, and the GAN application in super-resolution reconstruction. This provides the detailed background knowledge for this paper.
- We present pertinent datasets of both natural and remotely sensed images, metrics for assessing image quality, and techniques for inducing degradation in imagery.
- We present the model of GANs on super-resolution reconstruction. We categorize them as blind super-resolution models and non-blind super-resolution models based on whether or not the blurred kernel is assumed to be known and applied to the image. We compare performance on natural images and remote sensing imagery.
- We examine the issues and challenges surrounding SR reconstruction of remote sensing imagery from various perspectives. Additionally, we provide an overview and forecast of the SR reconstruction methodologies based on GAN.
2. Background
2.1. GAN and SR
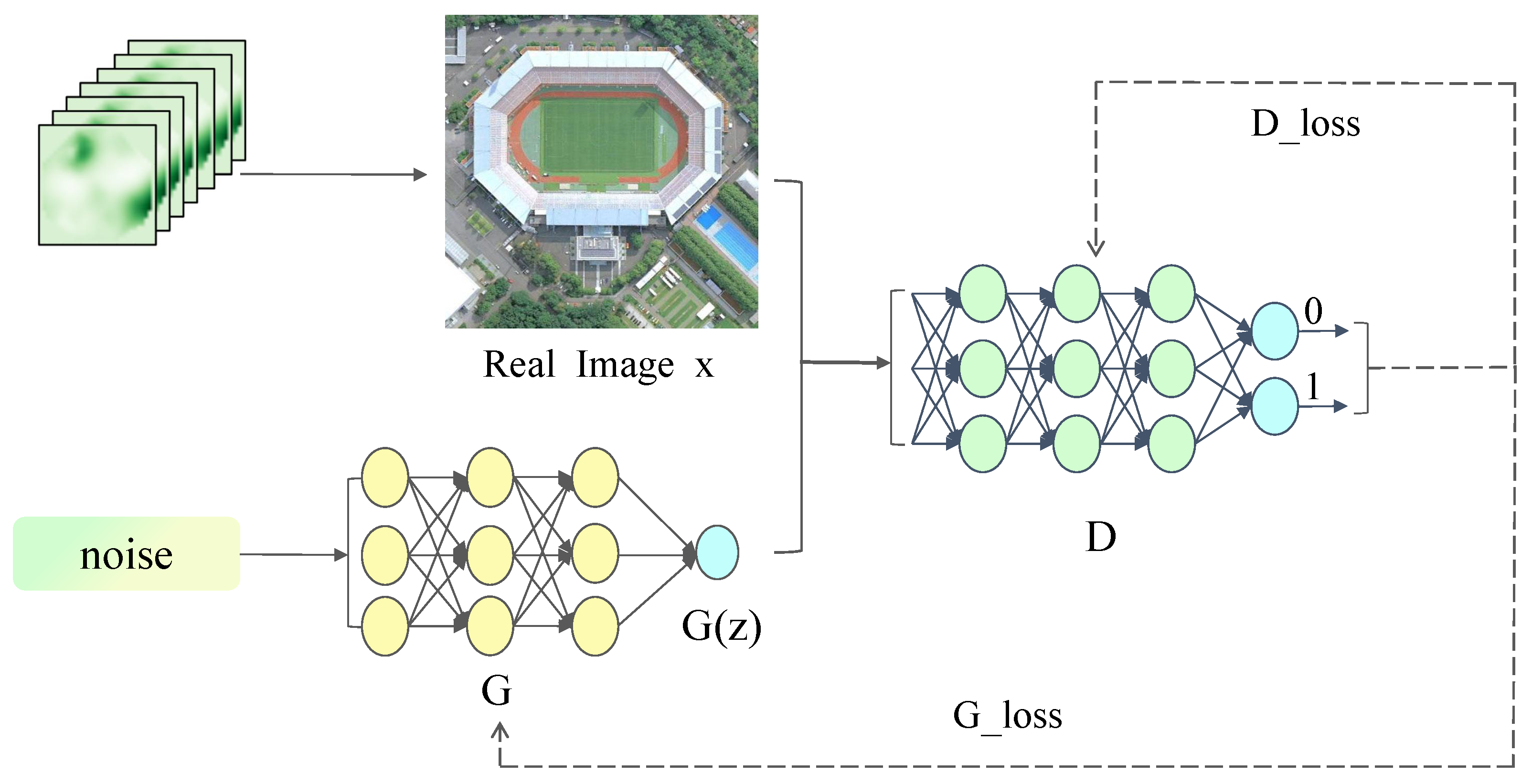
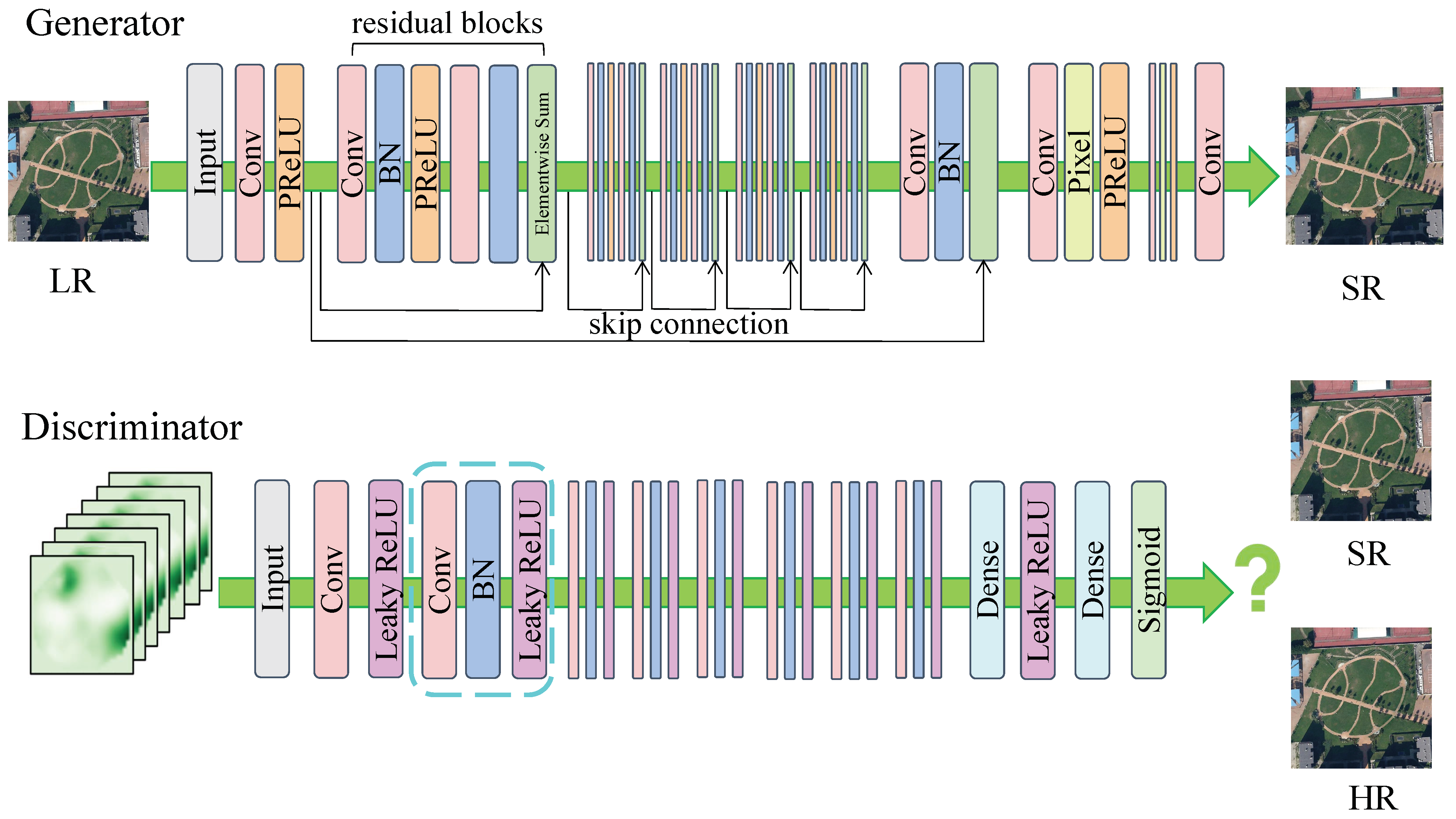
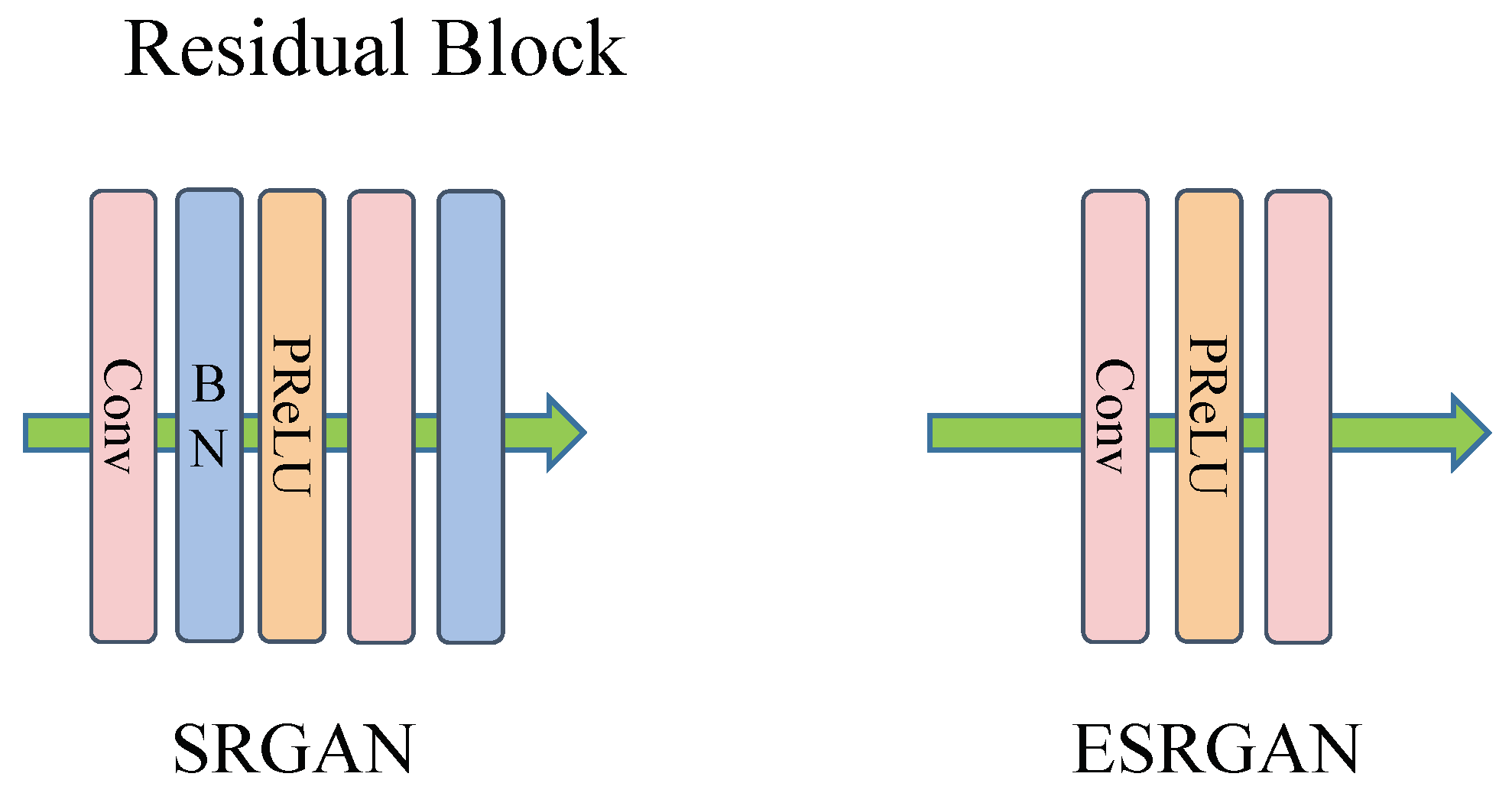
2.1.1. Generating Adversarial Networks
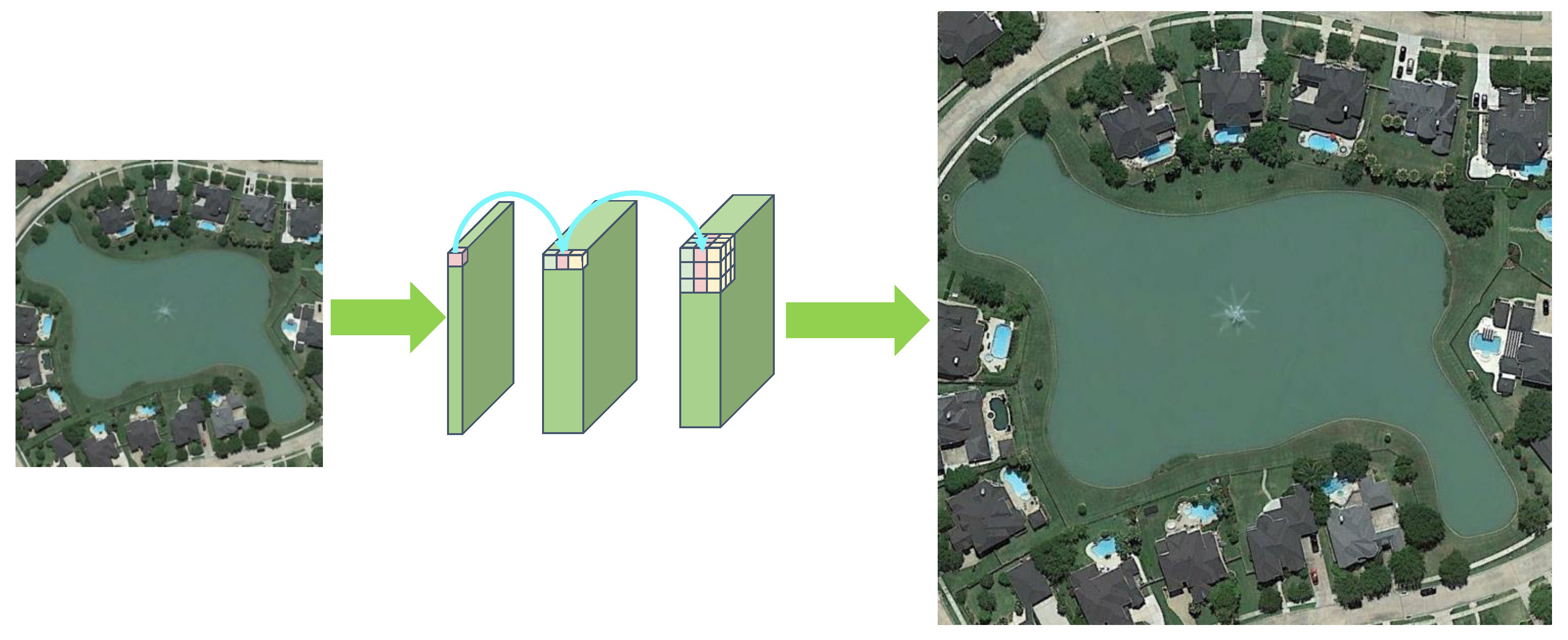
2.1.2. Super-Resolution Reconstruction
2.2. Loss Function
2.2.1. Perceptual Loss
2.2.2. Pixel Loss
2.2.3. GAN Loss
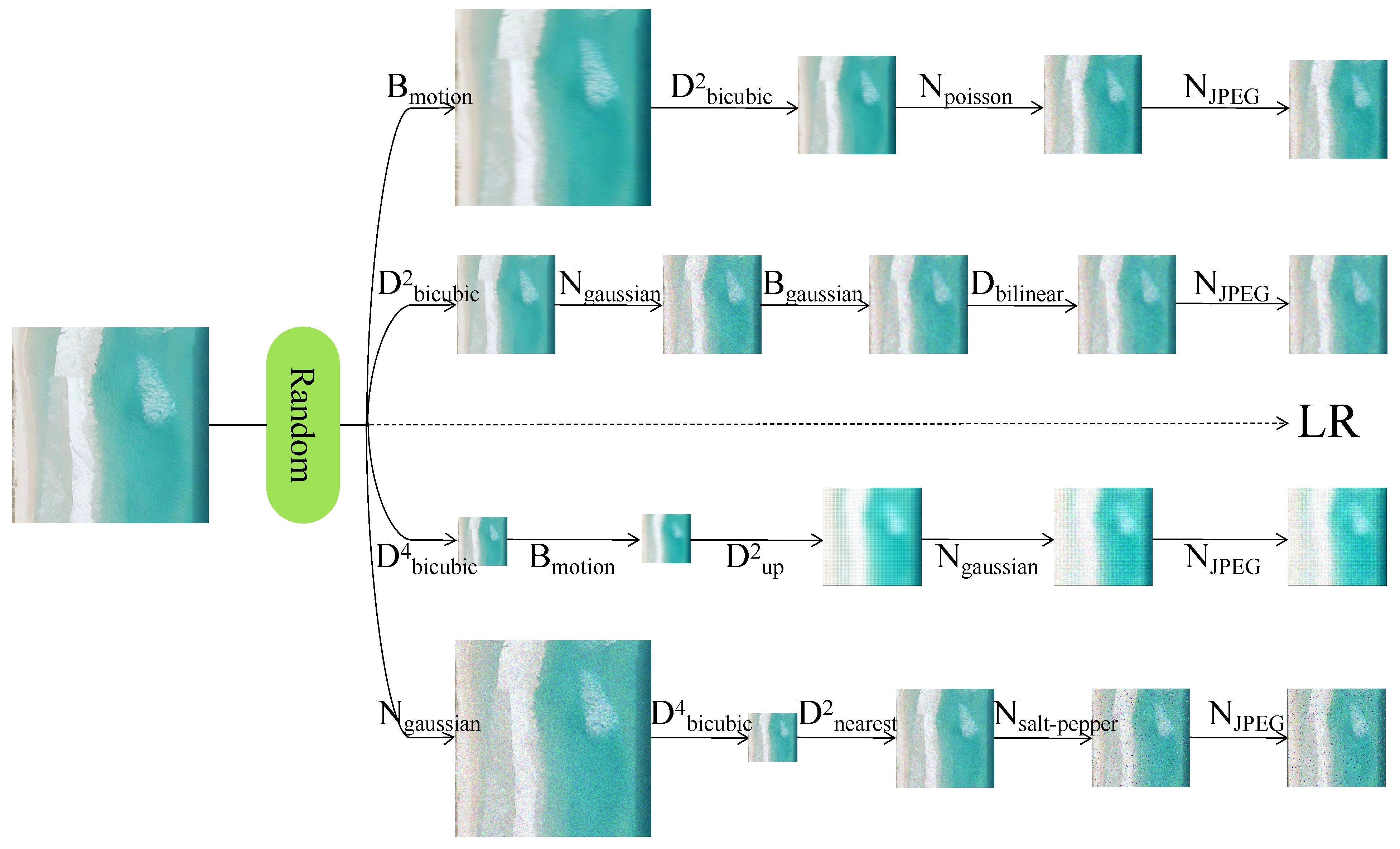
2.3. Image Degradation
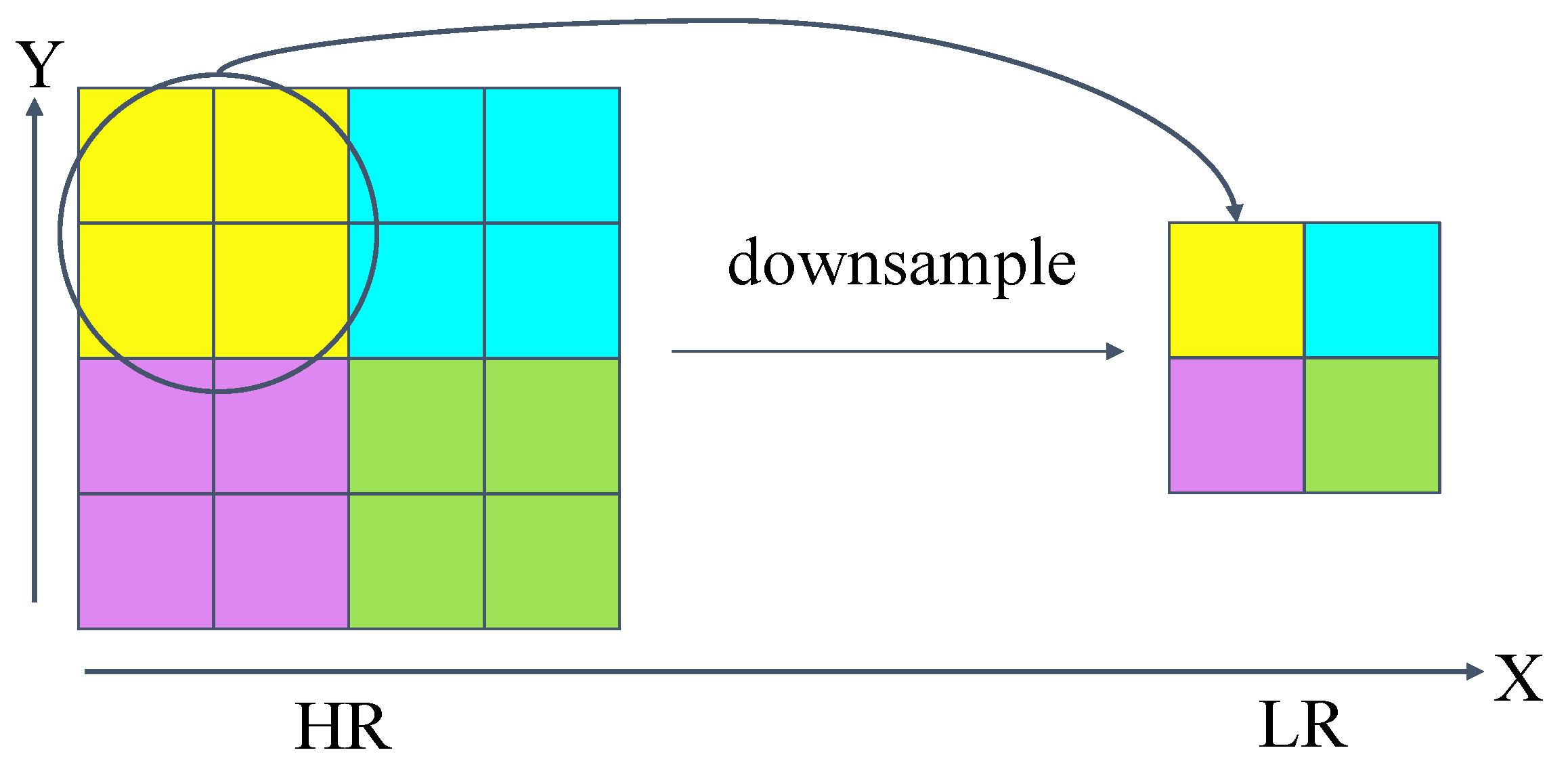
2.3.1. Bicubic Interpolation
2.3.2. BSR Degradation
2.3.3. Degradation of Higher Order
2.4. Traditional Super-Resolution Reconstruction Model
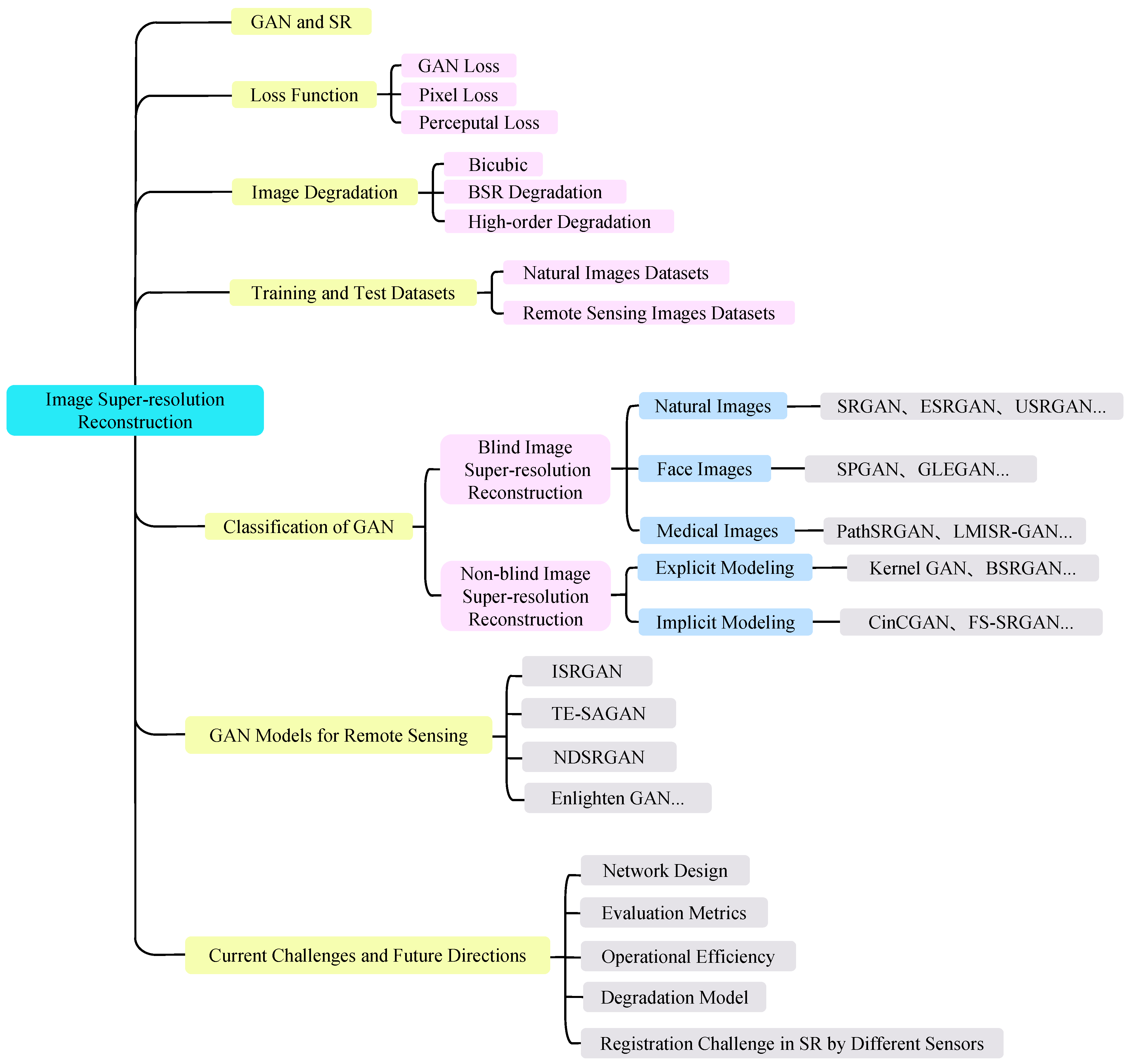
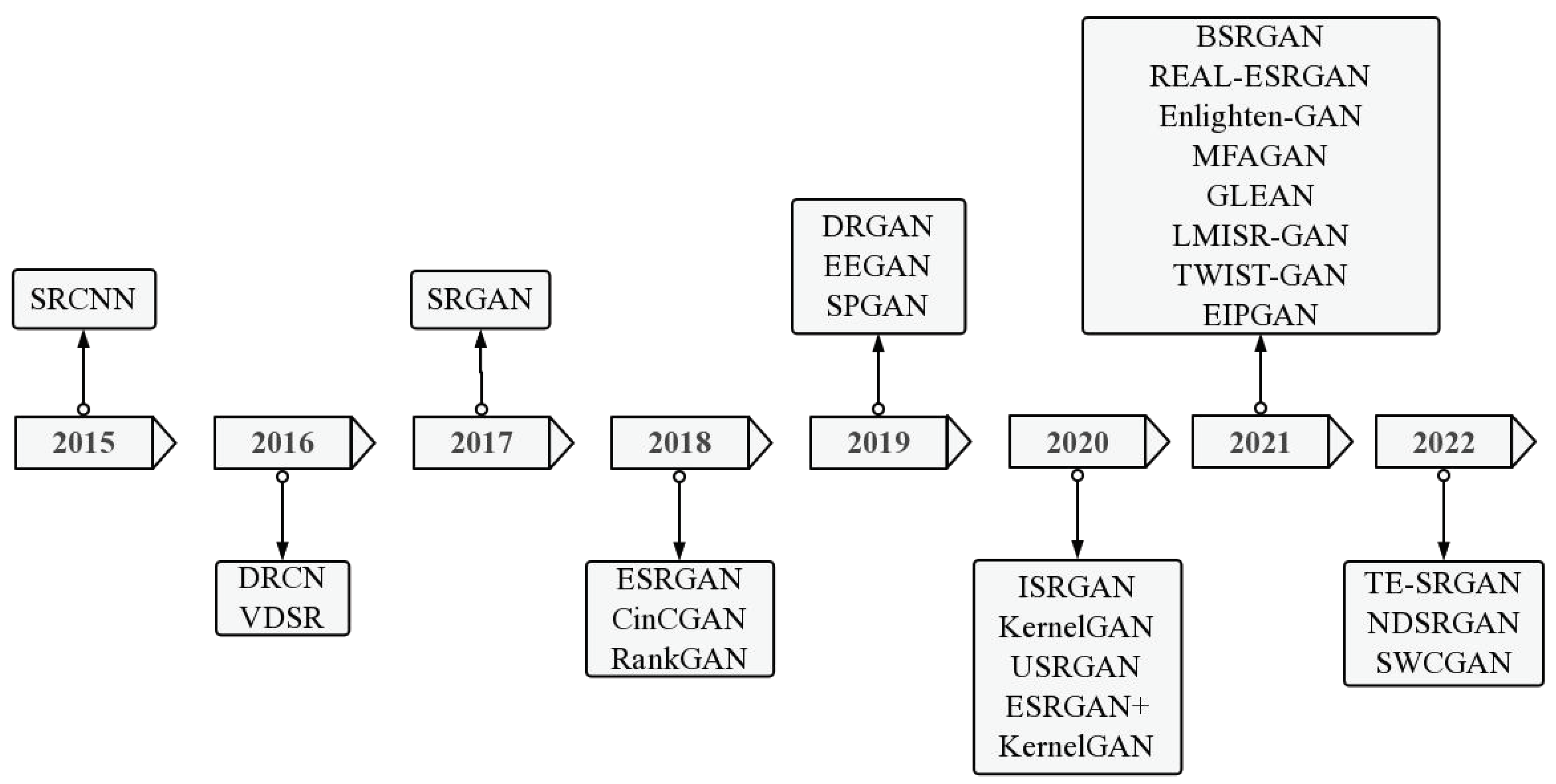
3. State of the Classification of Super-Resolution GAN Models
3.1. Super-Resolution Model Classification
3.2. Non-Blind Super-Resolution Reconstruction Models
3.2.1. Natural Images
3.2.2. Face Images
3.2.3. Medical Images
3.3. Blind Super-Resolution Reconstruction Models
3.3.1. Explicit Modeling
3.3.2. Implicit Modeling
4. GAN Models for Remote Sensing
4.1. The Effect of Noise in Remote Sensing Images
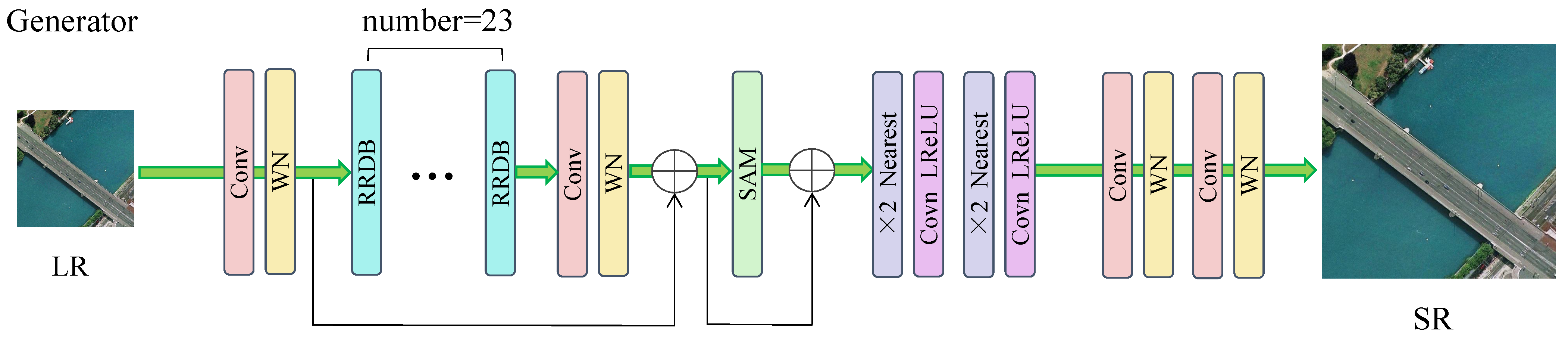
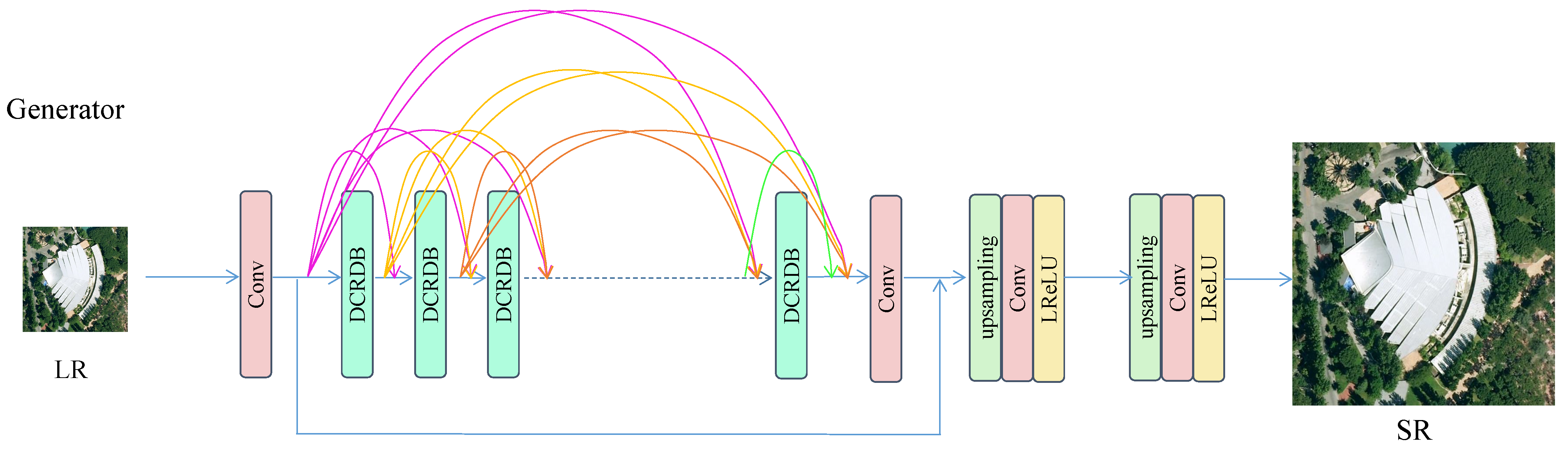
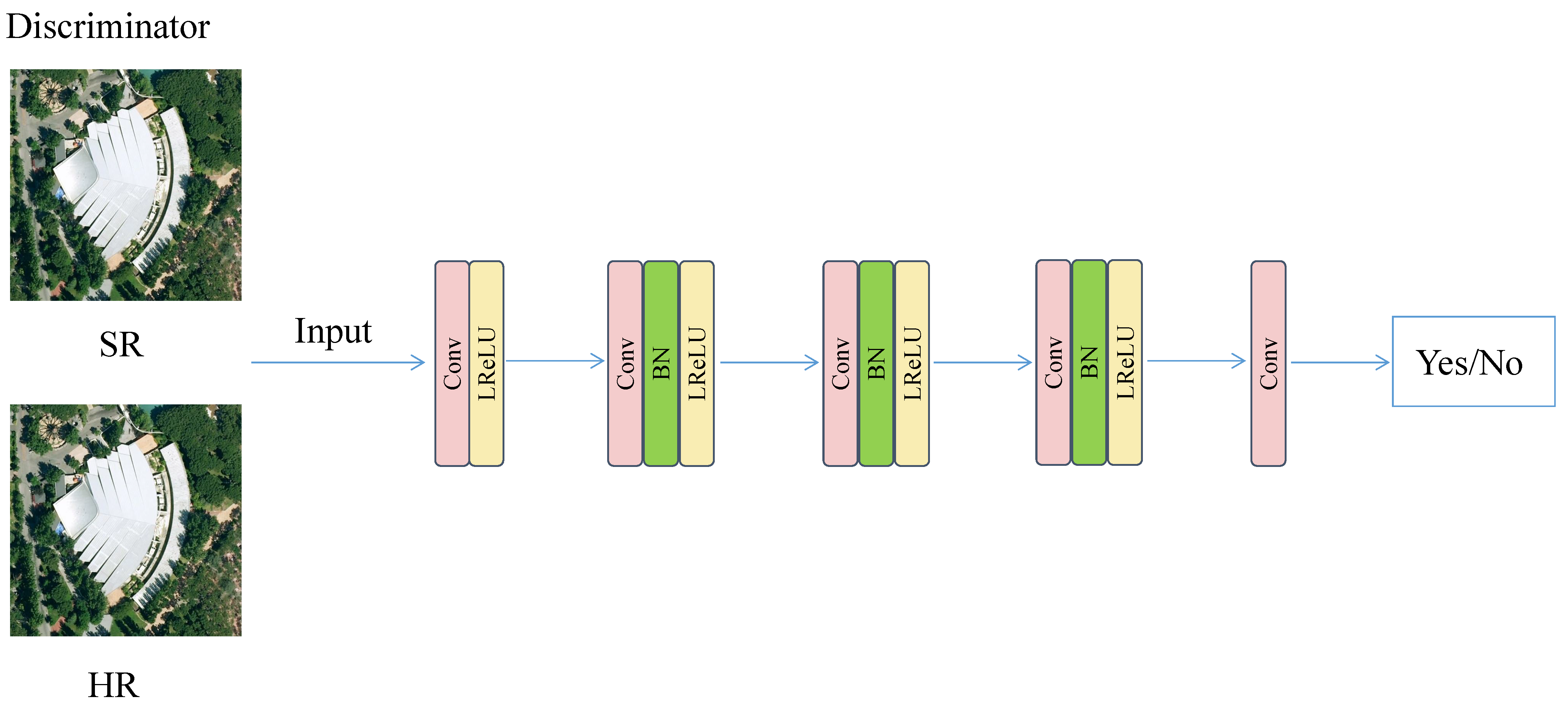
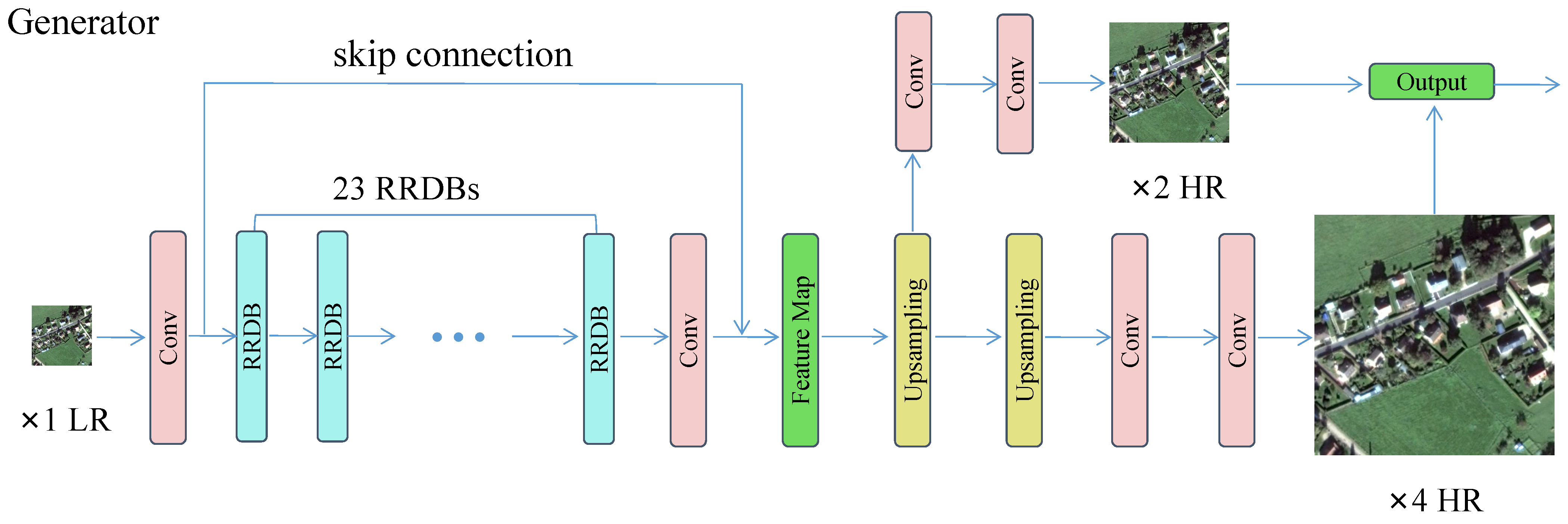
4.2. GAN-Based Super-Resolution Reconstruction Model for Remote Sensing Images
4.3. The Applications of SR Based on Remote Sensing
5. Datasets and Evaluation Metrics
5.1. Datasets
- Washington DC dataset [117]: The Washington DC data refer to an aerial hyperspectral image acquired by the HYDICE sensor. The data size is 1208 × 307. Categories of features include roofs, streets, graveled roads, grassy areas, etc.
- The Berlin–Urban–Gradient dataset [118] contains HyMap hyperspectral imagery at different resolutions and simulated EnMap hyperspectral imagery. The real MyMap data contain 111 bands. The dataset with a spatial resolution of 3.6 m has dimensions of 6895 × 1803, and the data with a spatial resolution of 9 m is 2722 × 732.
- Airborne hyperspectral datasets [119] contain 128 bands ranging from 343 to 1018 nanometers. There are 19 categories of features, all-encompassing in both urban and rural areas.
5.2. Evaluation Metrics
5.2.1. Peak Signal-to-Noise Ratio (PSNR)
5.2.2. Structural Similarity (SSIM)
5.2.3. Mean Opinion Score (MOS)
6. Comparison and Analysis of State-of-Art Models on Remote Sensing Image
6.1. Comparison and Analysis of Remote Sensing Image Models Using the Same Degradation Method
6.2. Comparison and Analysis of Remote Sensing Image Models Using the Different Degradation Method
7. Current Challenges and Future Directions
7.1. Challenges of Super-Resolution and Major Concerns
7.2. Future Directions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harris, J.L. Diffraction and resolving power. J. Opt. Soc. Am. 1964, 54, 931–936. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3365–3387. [Google Scholar] [CrossRef] [PubMed]
- Greenspan, H. Super-resolution in medical imaging. Comput. J. 2009, 52, 43–63. [Google Scholar] [CrossRef]
- Isaac, J.S.; Kulkarni, R. Super resolution techniques for medical image processing. In Proceedings of the 2015 International Conference on Technologies for Sustainable Development (ICTSD), Mumbai, India, 4–6 February 2015; pp. 1–6. [Google Scholar]
- Thornton, M.W.; Atkinson, P.M.; Holland, D. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super-resolution pixel-swapping. Int. J. Remote Sens. 2006, 27, 473–491. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Super-resolution for remote sensing images via local–global combined network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Lucas, A.; Lopez-Tapia, S.; Molina, R.; Katsaggelos, A.K. Generative adversarial networks and perceptual losses for video super-resolution. IEEE Trans. Image Process. 2019, 28, 3312–3327. [Google Scholar] [CrossRef]
- Fessler, J.A. Model-based image reconstruction for MRI. IEEE Signal Process. Mag. 2010, 27, 81–89. [Google Scholar] [CrossRef]
- Zhu, D.; Qiu, D. Residual dense network for medical magnetic resonance images super-resolution. Comput. Methods Progr. Biomed. 2021, 209, 106330. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Y.; Zhang, T.; Zou, X. Channel splitting network for single MR image super-resolution. IEEE Trans. Image Process. 2019, 28, 5649–5662. [Google Scholar] [CrossRef]
- Domínguez, C.; Heras, J.; Pascual, V. IJ-OpenCV: Combining ImageJ and OpenCV for processing images in biomedicine. Comput. Biol. Med. 2017, 84, 189–194. [Google Scholar] [CrossRef]
- Ševo, I.; Avramović, A. Convolutional neural network based automatic object detection on aerial images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 740–744. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, M.; Yu, L.; Li, Y. Image super-resolution reconstruction based on sparse representation and deep learning. Signal Process. Image Commun. 2020, 87, 115925. [Google Scholar] [CrossRef]
- Gilani, S.Z.; Mian, A.; Eastwood, P. Deep, dense and accurate 3D face correspondence for generating population specific deformable models. Pattern Recognit. 2017, 69, 238–250. [Google Scholar] [CrossRef]
- Yang, Y.; Bi, P.; Liu, Y. License plate image super-resolution based on convolutional neural network. In Proceedings of the 2018 IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, 27–29 June 2018; pp. 723–727. [Google Scholar]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech, Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Parker, J.A.; Kenyon, R.V.; Troxel, D.E. Comparison of interpolating methods for image resampling. IEEE Trans. Med. Imaging 1983, 2, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Mori, T.; Kameyama, K.; Ohmiya, Y.; Lee, J.; Toraichi, K. Image resolution conversion based on an edge-adaptive interpolation kernel. In Proceedings of the 2007 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, BC, Canada, 22–24 August 2007; pp. 497–500. [Google Scholar]
- Han, J.W.; Kim, J.H.; Sull, S.; Ko, S.J. New edge-adaptive image interpolation using anisotropic Gaussian filters. Digit. Signal Process. 2013, 23, 110–117. [Google Scholar] [CrossRef]
- Thévenaz, P.; Blu, T.; Unser, M. Image interpolation and resampling. In Handbook of Medical Imaging, Processing and Analysis; Elsevier: Amsterdam, The Netherlands, 2000; Volume 1, pp. 393–420. [Google Scholar]
- Irani, M.; Peleg, S. Improving resolution by image registration. CVGIP Graph. Model. Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Zhou, D.; Yang, R. An improved iterative back projection algorithm based on ringing artifacts suppression. Neurocomputing 2015, 162, 171–179. [Google Scholar] [CrossRef]
- Tekalp, A.M.; Ozkan, M.K.; Sezan, M.I. High-resolution image reconstruction from lower-resolution image sequences and space-varying image restoration. In Proceedings of the ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; Volume 3, pp. 169–172. [Google Scholar]
- Patti, A.J.; Altunbasak, Y. Artifact reduction for set theoretic super resolution image reconstruction with edge adaptive constraints and higher-order interpolants. IEEE Trans. Image Process. 2001, 10, 179–186. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, D.; Yang, J.; Han, W.; Huang, T. Deep networks for image super-resolution with sparse prior. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 370–378. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Peleg, T.; Elad, M. A statistical prediction model based on sparse representations for single image super-resolution. IEEE Trans. Image Process. 2014, 23, 2569–2582. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, L.; Shi, G.; Wu, X. Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization. IEEE Trans. Image Process. 2011, 20, 1838–1857. [Google Scholar] [CrossRef] [PubMed]
- Baker, S.; Kanade, T. Limits on super-resolution and how to break them. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1167–1183. [Google Scholar] [CrossRef]
- Arel, I.; Rose, D.C.; Karnowski, T.P. Deep machine learning-a new frontier in artificial intelligence research [research frontier]. IEEE Comput. Intell. Mag. 2010, 5, 13–18. [Google Scholar] [CrossRef]
- Haut, J.M.; Fernandez-Beltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A new deep generative network for unsupervised remote sensing single-image super-resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, T.; Li, J.; Jiang, S.; Zhang, Y. Single-Image Super Resolution of Remote Sensing Images with Real-World Degradation Modeling. Remote Sens. 2022, 14, 2895. [Google Scholar] [CrossRef]
- Arefin, M.R.; Michalski, V.; St-Charles, P.L.; Kalaitzis, A.; Kim, S.; Kahou, S.E.; Bengio, Y. Multi-image super-resolution for remote sensing using deep recurrent networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 206–207. [Google Scholar]
- Salvetti, F.; Mazzia, V.; Khaliq, A.; Chiaberge, M. Multi-image super resolution of remotely sensed images using residual attention deep neural networks. Remote Sens. 2020, 12, 2207. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Shen, H. A super-resolution reconstruction algorithm for hyperspectral images. Signal Process. 2012, 92, 2082–2096. [Google Scholar] [CrossRef]
- Liebel, L.; Körner, M. Single-Image Super Resolution For Multispectral Remote Sensing Data Using Convolutional Neural Networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 883–890. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Fudenberg, D.; Tirole, J. Game Theory; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Liang, J.; Wei, J.; Jiang, Z. Generative adversarial networks GAN overview. J. Front. Comput. Sci. Technol. 2020, 14, 1–17. [Google Scholar]
- Tian, C.; Zhang, X.; Lin, J.C.W.; Zuo, W.; Zhang, Y.; Lin, C.W. Generative adversarial networks for image super-resolution: A survey. arXiv 2022, arXiv:2204.13620. [Google Scholar]
- Wang, K.; Gou, C.; Duan, Y.; Lin, Y.; Zheng, X.; Wang, F.Y. Generative adversarial networks: Introduction and outlook. IEEE/CAA J. Autom. Sin. 2017, 4, 588–598. [Google Scholar] [CrossRef]
- Johnson, J.; Alahi, A.; Li, F.-F. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 694–711. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. Memnet: A persistent memory network for image restoration. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4539–4547. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Zhang, K.; Liang, J.; Van Gool, L.; Timofte, R. Designing a practical degradation model for deep blind image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 4791–4800. [Google Scholar]
- Hou, H.; Andrews, H. Cubic splines for image interpolation and digital filtering. IEEE Trans. Acoust. Speech, Signal Process. 1978, 26, 508–517. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 1905–1914. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhang, K.; Gool, L.V.; Timofte, R. Deep unfolding network for image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 3217–3226. [Google Scholar]
- Zhang, M.; Ling, Q. Supervised pixel-wise GAN for face super-resolution. IEEE Trans. Multimed. 2020, 23, 1938–1950. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, S.; Zhang, J.; Zhang, Y.; Dong, C.; Lin, L. Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 701–710. [Google Scholar]
- Bell-Kligler, S.; Shocher, A.; Irani, M. Blind super-resolution kernel estimation using an internal-gan. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Rakotonirina, N.C.; Rasoanaivo, A. ESRGAN+: Further improving enhanced super-resolution generative adversarial network. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3637–3641. [Google Scholar]
- Cheng, W.; Zhao, M.; Ye, Z.; Gu, S. Mfagan: A compression framework for memory-efficient on-device super-resolution gan. arXiv 2021, arXiv:2107.12679. [Google Scholar]
- Shamsolmoali, P.; Zareapoor, M.; Wang, R.; Jain, D.K.; Yang, J. G-GANISR: Gradual generative adversarial network for image super resolution. Neurocomputing 2019, 366, 140–153. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Dong, C.; Qiao, Y. Ranksrgan: Generative adversarial networks with ranker for image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3096–3105. [Google Scholar]
- Chan, K.C.; Wang, X.; Xu, X.; Gu, J.; Loy, C.C. Glean: Generative latent bank for large-factor image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14245–14254. [Google Scholar]
- Indradi, S.D.; Arifianto, A.; Ramadhani, K.N. Face image super-resolution using inception residual network and gan framework. In Proceedings of the 2019 7th International Conference on Information and Communication Technology (ICoICT), Kuala Lumpur, Malaysia, 24–26 July 2019; pp. 1–6. [Google Scholar]
- Cai, J.; Han, H.; Shan, S.; Chen, X. FCSR-GAN: Joint face completion and super-resolution via multi-task learning. IEEE Trans. Biom. Behav. Identity Sci. 2019, 2, 109–121. [Google Scholar] [CrossRef]
- Ko, S.; Dai, B.R. Multi-laplacian GAN with edge enhancement for face super resolution. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 3505–3512. [Google Scholar]
- Cao, M.; Liu, Z.; Huang, X.; Shen, Z. Research for face image super-resolution reconstruction based on wavelet transform and SRGAN. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; Volume 5, pp. 448–451. [Google Scholar]
- Wang, Y.; Hu, Y.; Yu, J.; Zhang, J. Gan prior based null-space learning for consistent super-resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 2724–2732. [Google Scholar]
- Ma, J.; Yu, J.; Liu, S.; Chen, L.; Li, X.; Feng, J.; Chen, Z.; Zeng, S.; Liu, X.; Cheng, S. PathSRGAN: Multi-supervised super-resolution for cytopathological images using generative adversarial network. IEEE Trans. Med. Imaging 2020, 39, 2920–2930. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Liu, Y.; Gu, J.; Qiao, Y.; Dong, C. Blind image super-resolution: A survey and beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5461–5480. [Google Scholar] [CrossRef]
- Ren, H.; Kheradmand, A.; El-Khamy, M.; Wang, S.; Bai, D.; Lee, J. Real-world super-resolution using generative adversarial networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 436–437. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Bulat, A.; Yang, J.; Tzimiropoulos, G. To learn image super-resolution, use a gan to learn how to do image degradation first. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 185–200. [Google Scholar]
- Zhou, Y.; Deng, W.; Tong, T.; Gao, Q. Guided frequency separation network for real-world super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 428–429. [Google Scholar]
- Zhao, T.; Ren, W.; Zhang, C.; Ren, D.; Hu, Q. Unsupervised degradation learning for single image super-resolution. arXiv 2018, arXiv:1812.04240. [Google Scholar]
- Xu, J.; Feng, G.; Fan, B.; Yan, W.; Zhao, T.; Sun, X.; Zhu, M. Landcover classification of satellite images based on an adaptive interval fuzzy c-means algorithm coupled with spatial information. Int. J. Remote Sens. 2020, 41, 2189–2208. [Google Scholar] [CrossRef]
- Ma, W.; Pan, Z.; Yuan, F.; Lei, B. Super-resolution of remote sensing images via a dense residual generative adversarial network. Remote Sens. 2019, 11, 2578. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L.; Xue, Y.; Jiang, C.; Wang, J.; Sun, K.; Ma, H. FeNet: Feature enhancement network for lightweight remote-sensing image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Kang, X.; Li, J.; Duan, P.; Ma, F.; Li, S. Multilayer degradation representation-guided blind super-resolution for remote sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Wang, Y.; Bashir, S.M.A.; Khan, M.; Ullah, Q.; Wang, R.; Song, Y.; Guo, Z.; Niu, Y. Remote sensing image super-resolution and object detection: Benchmark and state of the art. Expert Syst. Appl. 2022, 197, 116793. [Google Scholar] [CrossRef]
- Xiong, Y.; Guo, S.; Chen, J.; Deng, X.; Sun, L.; Zheng, X.; Xu, W. Improved SRGAN for remote sensing image super-resolution across locations and sensors. Remote Sens. 2020, 12, 1263. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, W.; Hu, A.; Xie, Z.; Xie, X.; Tao, L. TE-SAGAN: An improved generative adversarial network for remote sensing super-resolution images. Remote Sens. 2022, 14, 2425. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, Z.; Liu, H.; Huang, Y. Ndsrgan: A novel dense generative adversarial network for real aerial imagery super-resolution reconstruction. Remote Sens. 2022, 14, 1574. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, L.; Zhang, J. SD-GAN: Saliency-discriminated GAN for remote sensing image superresolution. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1973–1977. [Google Scholar] [CrossRef]
- Gong, Y.; Liao, P.; Zhang, X.; Zhang, L.; Chen, G.; Zhu, K.; Tan, X.; Lv, Z. Enlighten-GAN for super resolution reconstruction in mid-resolution remote sensing images. Remote Sens. 2021, 13, 1104. [Google Scholar] [CrossRef]
- Dharejo, F.A.; Deeba, F.; Zhou, Y.; Das, B.; Jatoi, M.A.; Zawish, M.; Du, Y.; Wang, X. TWIST-GAN: Towards wavelet transform and transferred GAN for spatio-temporal single image super resolution. ACM Trans. Intell. Syst. Technol. (TIST) 2021, 12, 1–20. [Google Scholar] [CrossRef]
- Wang, J.; Shao, Z.; Huang, X.; Lu, T.; Zhang, R.; Ma, J. Enhanced image prior for unsupervised remoting sensing super-resolution. Neural Netw. 2021, 143, 400–412. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Y.; Zhang, X.; Xu, D.; Wang, X. An unsupervised remote sensing single-image super-resolution method based on generative adversarial network. IEEE Access 2020, 8, 29027–29039. [Google Scholar] [CrossRef]
- Tu, J.; Mei, G.; Ma, Z.; Piccialli, F. SWCGAN: Generative adversarial network combining swin transformer and CNN for remote sensing image super-resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5662–5673. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-enhanced GAN for remote sensing image superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, Y.; Chen, F.; Shang, E.; Yao, W.; Zhang, S.; Yang, J. SA-GAN: A Second Order Attention Generator Adversarial Network with Region Aware Strategy for Real Satellite Images Super Resolution Reconstruction. Remote Sens. 2023, 15, 1391. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.H.; Zhang, L. Ntire 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 114–125. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision. ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 898–916. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M.L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the 23rd British Machine Vision Conference (BMVC), Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the Curves and Surfaces: 7th International Conference, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Cai, J.; Zeng, H.; Yong, H.; Cao, Z.; Zhang, L. Toward real-world single image super-resolution: A new benchmark and a new model. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3086–3095. [Google Scholar]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Dai, D.; Yang, W. Satellite image classification via two-layer sparse coding with biased image representation. IEEE Geosci. Remote Sens. Lett. 2010, 8, 173–176. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, X.; Dai, W.; Fu, K.; Ye, Q.; Jiao, J. Orientation robust object detection in aerial images using deep convolutional neural network. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3735–3739. [Google Scholar]
- Zhao, L.; Tang, P.; Huo, L. Feature significance-based multibag-of-visual-words model for remote sensing image scene classification. J. Appl. Remote Sens. 2016, 10, 035004. [Google Scholar] [CrossRef]
- Zou, Q.; Ni, L.; Zhang, T.; Wang, Q. Deep learning based feature selection for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2321–2325. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Zhu, Q.; Zhong, Y.; Zhao, B.; Xia, G.S.; Zhang, L. Bag-of-visual-words scene classifier with local and global features for high spatial resolution remote sensing imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 747–751. [Google Scholar] [CrossRef]
- Yang, M.Y.; Liao, W.; Li, X.; Rosenhahn, B. Deep learning for vehicle detection in aerial images. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 3079–3083. [Google Scholar]
- Li, K.; Wan, G.; Cheng, G.; Meng, L.; Han, J. Object detection in optical remote sensing images: A survey and a new benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 159, 296–307. [Google Scholar] [CrossRef]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3974–3983. [Google Scholar]
- Fujimoto, A.; Ogawa, T.; Yamamoto, K.; Matsui, Y.; Yamasaki, T.; Aizawa, K. Manga109 dataset and creation of metadata. In Proceedings of the 1st International Workshop on Comics Analysis, Processing and Understanding, Cancun, Mexico, 4 December 2016; pp. 1–5. [Google Scholar]
- Wang, X.; Yu, K.; Dong, C.; Loy, C.C. Recovering realistic texture in image super-resolution by deep spatial feature transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 606–615. [Google Scholar]
- Everingham, M.; Eslami, S.A.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes challenge: A retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3730–3738. [Google Scholar]
- Baumgardner, M.F.; Biehl, L.L.; Landgrebe, D.A. 220 band aviris hyperspectral image data set: June 12, 1992 indian pine test site 3. Purdue Univ. Res. Repos. 2015, 10, 991. [Google Scholar]
- Okujeni, A.; van der Linden, S.; Hostert, P. Berlin-urban-gradient dataset 2009—An EnMAP preparatory flight campaign. In EnMAP Flight Campaigns Technical Report; GFZ Data Services: Potsdam, Germany, 2016; p. 9. [Google Scholar] [CrossRef]
- Yokoya, N.; Iwasaki, A. Airborne Hyperspectral Data over Chikusei; Technical Report SAL-2016-05-27; Space Application Laboratory, The University of Tokyo: Tokyo, Japan, 2016; Volume 5, p. 5. [Google Scholar]
- Wang, X.; Yi, J.; Guo, J.; Song, Y.; Lyu, J.; Xu, J.; Yan, W.; Zhao, J.; Cai, Q.; Min, H. A review of image super-resolution approaches based on deep learning and applications in remote sensing. Remote Sens. 2022, 14, 5423. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, C.; Yang, W.; Liu, J.; Guo, Z. Blind visual quality assessment for image super-resolution by convolutional neural network. Multimed. Tools Appl. 2018, 77, 29829–29846. [Google Scholar] [CrossRef]
- Jiang, Q.; Liu, Z.; Gu, K.; Shao, F.; Zhang, X.; Liu, H.; Lin, W. Single image super-resolution quality assessment: A real-world dataset, subjective studies, and an objective metric. IEEE Trans. Image Process. 2022, 31, 2279–2294. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhao, T.; Chen, W.; Niu, Y.; Hu, J. SPQE: Structure-and-Perception-Based Quality Evaluation for Image Super-Resolution. arXiv 2022, arXiv:2205.03584. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Yang, D.; Li, Z.; Xia, Y.; Chen, Z. Remote sensing image super-resolution: Challenges and approaches. In Proceedings of the 2015 IEEE international conference on digital signal processing (DSP), Singapore, 21–24 July 2015; pp. 196–200. [Google Scholar]
- Cheng, J.; Kuang, Q.; Shen, C.; Liu, J.; Tan, X.; Liu, W. ResLap: Generating high-resolution climate prediction through image super-resolution. IEEE Access 2020, 8, 39623–39634. [Google Scholar] [CrossRef]
- Elfadaly, A.; Attia, W.; Lasaponara, R. Monitoring the environmental risks around Medinet Habu and Ramesseum Temple at West Luxor, Egypt, using remote sensing and GIS techniques. J. Archaeol. Method Theory 2018, 25, 587–610. [Google Scholar] [CrossRef]
- Tatem, A.J.; Lewis, H.G.; Atkinson, P.M.; Nixon, M.S. Super-resolution target identification from remotely sensed images using a Hopfield neural network. IEEE Trans. Geosci. Remote Sens. 2001, 39, 781–796. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Y.; Ding, M.; Ghanem, B. Sod-mtgan: Small object detection via multi-task generative adversarial network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 206–221. [Google Scholar]
- Rabbi, J.; Ray, N.; Schubert, M.; Chowdhury, S.; Chao, D. Small-object detection in remote sensing images with end-to-end edge-enhanced GAN and object detector network. Remote Sens. 2020, 12, 1432. [Google Scholar] [CrossRef]








| Dataset | Format | Number | Resolution | Category |
|---|---|---|---|---|
| DIV2K [93] | PNG | 1000 | (1972, 1437) | people, scenery, animal, decoration, etc. |
| Flickr2K [94] | PNG | 2650 | (2048, 1080) | people, animal, flower, etc. |
| BSD300 [95] | JPG | 300 | (435, 367) | animal, scenery, decoration, plant, etc. |
| BSD500 [96] | JPG | 500 | (432, 370) | animal, scenery, decoration, plant, etc. |
| T91 [26] | PNG | 91 | (264, 204) | fruit, people, flower, etc. |
| Set5 [98] | PNG | 5 | (313, 336) | baby, butterfly, bird, head, woman |
| Set14 [99] | PNG | 14 | (492, 446) | pepper, zebra, coastguard, foreman, etc. |
| BSD100 [95] | JPG | 100 | (481, 321) | animal, scenery, plant, etc. |
| Urban100 [100] | PNG | 100 | (984, 797) | building, architecture, scenery, etc. |
| AID [102] | JPG | 10,000 | (600, 600) | airport, desert, farmland, pond, etc. |
| WHU-RS19 [103] | JPG | 1005 | (600, 600) | beach, bridge, forest, parking, etc. |
| UCAS-AOD [105] | PNG | 910 | (1280, 659) | car, airplane |
| RSC11 [106] | TIF | 1232 | (512, 512) | denseforest, grassland, roads, etc. |
| NWPU-RESISC45 [104] | PNG | 31,500 | (256, 256) | commercial area, harbor, island, etc. |
| RSSCN7 [107] | JPG | 2800 | (400, 400) | parking lots, residential areas, lakes, etc. |
| UC Merced [108] | PNG | 2100 | (256, 256) | farmland, bushes, highways, overpasses, etc. |
| SIRI-WHU [109] | TIF | 2400 | (200, 200) | agriculture, industrial, river, etc. |
| ITCVD [110] | JPG | 135 | (5616, 3744) | vehicles, buildings, etc. |
| DIOR [111] | JPG | 23,463 | (800, 800) | stadiums, bridges, dams, ports, etc. |
| DOTA [112] | PNG | 2806 | (800, 4000) | swimming pool, bridge, plane, ship, etc. |
| Bicubic PSNR/SSIM | SRGAN PSNR/SSIM | ESRGAN PSNR/SSIM | RankGAN PSNR/SSIM | BSRGAN PSNR/SSIM | |
|---|---|---|---|---|---|
| denseforest | 25.77/0.5288 | 26.66/0.5080 | 25.38/0.4106 | 24.73/0.3894 | 25.19/0.4398 |
| grassland | 24.22/0.4355 | 26.28/0.4577 | 26.05/0.4361 | 25.35/0.3971 | 27.57/0.5507 |
| harbor | 17.46/0.4169 | 18.76/0.4264 | 17.92/0.3649 | 17.89/0.3349 | 17.78/0.4094 |
| highbuildings | 19.52/0.4423 | 21.87/0.5612 | 20.62/0.4759 | 21.35/0.5056 | 20.68/0.5790 |
| lowbuildings | 18.72/0.3568 | 20.87/0.4777 | 20.11/0.4470 | 20.34/0.4177 | 20.07/0.4969 |
| overpass | 19.54/0.3797 | 21.43/0.4586 | 20.44/0.3893 | 20.39/0.3669 | 20.58/0.4502 |
| railway | 19.93/0.3703 | 22.45/0.4697 | 21.43/0.4186 | 21.51/0.3928 | 21.71/0.4905 |
| residentialarea | 19.76/0.4064 | 20.61/0.4398 | 19.96/0.3981 | 19.50/0.3514 | 19.55/0.4186 |
| roads | 19.94/0.4115 | 22.31/0.5031 | 21.25/0.4420 | 21.37/0.4325 | 21.12/0.4866 |
| sparseforest | 23.10/0.3627 | 24.67/0.3813 | 23.37/0.3041 | 23.60/0.3236 | 24.61/0.3806 |
| stroagetanks | 18.90/0.3764 | 20.62/0.4538 | 19.75/0.4053 | 19.96/0.3944 | 19.76/0.4629 |
| Bicubic PSNR/SSIM | SRGAN PSNR/SSIM | ESRGAN PSNR/SSIM | RankSRGAN PSNR/SSIM | BSRGAN PSNR/SSIM | |
|---|---|---|---|---|---|
| Airport | 18.71/0.3662 | 26.27/0.7180 | 25.20/0.6576 | 25.14/0.6300 | 22.08/0.5507 |
| BareLand | 19.22/0.3204 | 32.18/0.8011 | 29.33/0.6849 | 31.48/0.7075 | 27.00/0.6718 |
| BaseballField | 20.92/0.4611 | 27.74/0.7553 | 26.27/0.6673 | 26.82/0.6721 | 23.51/0.6194 |
| Beach | 19.83/0.4054 | 29.54/0.7762 | 28.41/0.7258 | 29.38/0.7273 | 25.23/0.6835 |
| Bridge | 21.29/0.4974 | 28.35/0.7729 | 26.95/0.7192 | 27.14/0.7174 | 23.80/0.6497 |
| Center | 18.38/0.3911 | 24.51/0.6750 | 23.86/0.6310 | 23.74/0.6018 | 20.51/0.5095 |
| Church | 18.03/0.3816 | 21.88/0.5924 | 21.66/0.5557 | 21.19/0.5113 | 19.01/0.4103 |
| Commercial | 19/15/0.4390 | 25.36/0.6962 | 23.80/0.6023 | 23.58/0.5699 | 20.80/0.4654 |
| DenseResidential | 17.85/0.3779 | 22.24/0.6044 | 21.20/0.5189 | 21.17/0.5010 | 18.49/0.3568 |
| Desert | 18.52/0.2883 | 32.87/0.8360 | 31.89/0.7989 | 34.66/0.8186 | 30.47/0.8014 |
| Farmland | 21.98/0.4387 | 30.89/0.7701 | 29.47/0.7099 | 29.93/0.7037 | 26.92/0.6669 |
| Forest | 22.56/0.4284 | 26.56/0.6031 | 22.69/0.3757 | 24.41/0.4678 | 22.80/0.3242 |
| Industrial | 18.12/0.3761 | 24.70/0.6790 | 23.43/0.5999 | 23.32/0.5743 | 20.24/0.4531 |
| Meadow | 23.32/0.4351 | 30.56/0.6824 | 28.06/0.5241 | 28.50/0.5345 | 28.36/0.5984 |
| MediumResidential | 19.83/0.4032 | 24.86/0.6316 | 23.66/0.5457 | 23.99/0.5327 | 21.00/0.4270 |
| Mountain | 20.82/0.4369 | 27.01/0.6874 | 24.40/0.4992 | 24.85/0.5176 | 22.16/0.4137 |
| Park | 20.07/0.4404 | 26.03/0.6894 | 24.06/0.5691 | 24.22/0.5508 | 21.73/0.4647 |
| Parking | 17.25/0.3817 | 22.67/0.7014 | 21.93/0.6512 | 21.96/0.6079 | 18.35/0.4941 |
| Playground | 20.36/0.4458 | 27.97/0.7531 | 26.39/0.6833 | 27.22/0.6921 | 23.27/0.6163 |
| Pond | 21.80/0.4966 | 27.79/0.7419 | 26.22/0.6679 | 26.64/0.6734 | 24.13/0.6180 |
| Port | 19.06/0.4847 | 24.64/0.7510 | 23.71/0.7195 | 23.60/0.6937 | 20.60/0.6256 |
| RailwayStation | 18.99/0.3883 | 25.72/0.6822 | 24.29/0.5935 | 24.22/0.5732 | 21.17/0.4388 |
| Resort | 18.91/0.4112 | 25.38/0.6890 | 23.74/0.5930 | 24.18/0.5872 | 20.98/0.4875 |
| River | 21.64/0.4448 | 28.26/0.7058 | 25.94/0.5785 | 26.57/0.5881 | 24.38/0.5355 |
| School | 19.06/0.4367 | 24.58/0.6774 | 23.06/0.5773 | 23.27/0.5669 | 20.18/0.4503 |
| SparseResidential | 21.27/0.3773 | 24.71/0.5649 | 22.95/0.4223 | 23.24/0.4302 | 21.73/0.3343 |
| Square | 18.90/0.4124 | 26.08/0.7068 | 24.59/0.6290 | 25.08/0.6186 | 21.17/0.5121 |
| Stadium | 18.69/0.4245 | 24.97/0.7011 | 24.19/0.6520 | 24.15/0.6320 | 20.70/0.5352 |
| StorageTanks | 18.71/0.3871 | 24.20/0.6511 | 23.49/0.5915 | 23.30/0.5620 | 20.55/0.4821 |
| Viaduct | 19.57/0.4066 | 25.47/0.6656 | 24.13/0.5750 | 24.17/0.562 | 21.24/0.4380 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Sun, L.; Chehri, A.; Song, Y. A Review of GAN-Based Super-Resolution Reconstruction for Optical Remote Sensing Images. Remote Sens. 2023, 15, 5062. https://doi.org/10.3390/rs15205062
Wang X, Sun L, Chehri A, Song Y. A Review of GAN-Based Super-Resolution Reconstruction for Optical Remote Sensing Images. Remote Sensing. 2023; 15(20):5062. https://doi.org/10.3390/rs15205062
Chicago/Turabian StyleWang, Xuan, Lijun Sun, Abdellah Chehri, and Yongchao Song. 2023. "A Review of GAN-Based Super-Resolution Reconstruction for Optical Remote Sensing Images" Remote Sensing 15, no. 20: 5062. https://doi.org/10.3390/rs15205062
APA StyleWang, X., Sun, L., Chehri, A., & Song, Y. (2023). A Review of GAN-Based Super-Resolution Reconstruction for Optical Remote Sensing Images. Remote Sensing, 15(20), 5062. https://doi.org/10.3390/rs15205062








