An Unsupervised CNN-Based Pansharpening Framework with Spectral-Spatial Fidelity Balance
Abstract
1. Introduction
2. Materials and Methods
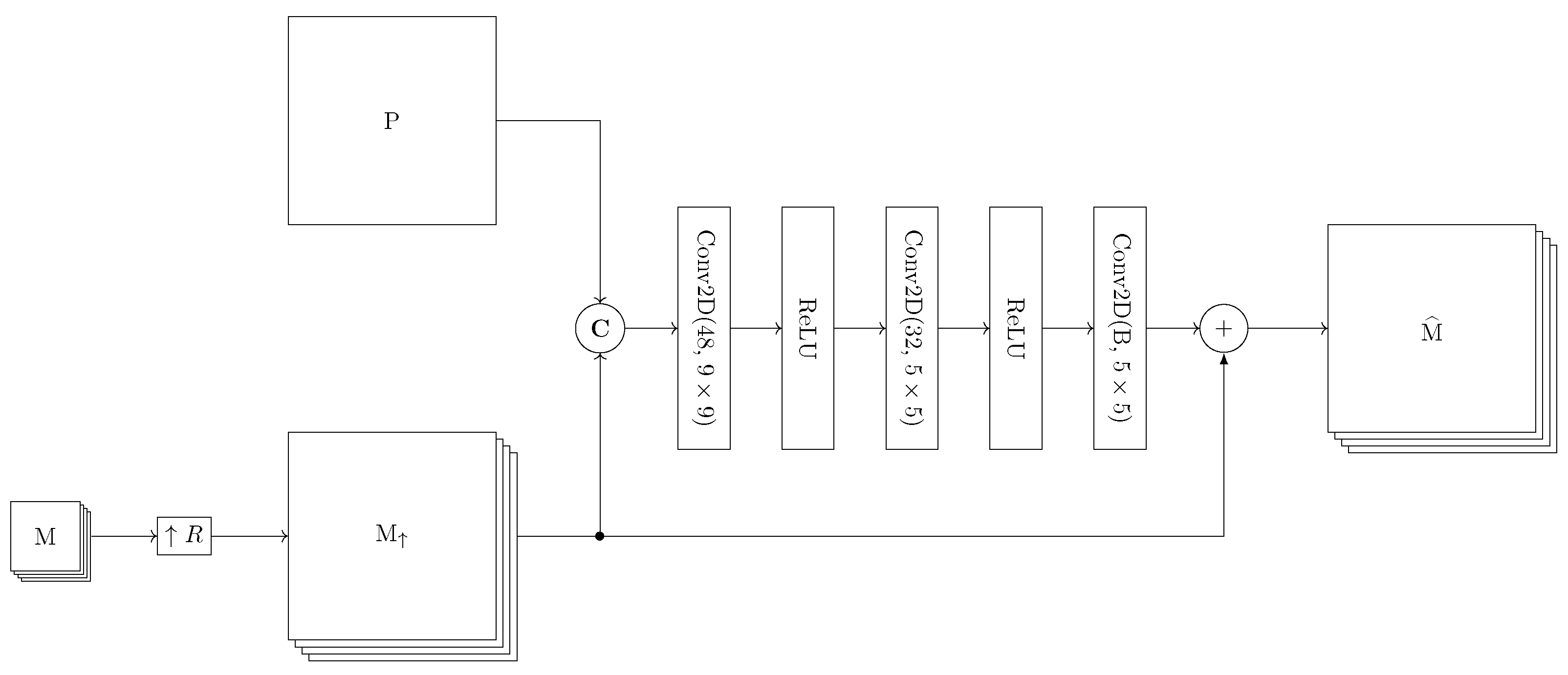
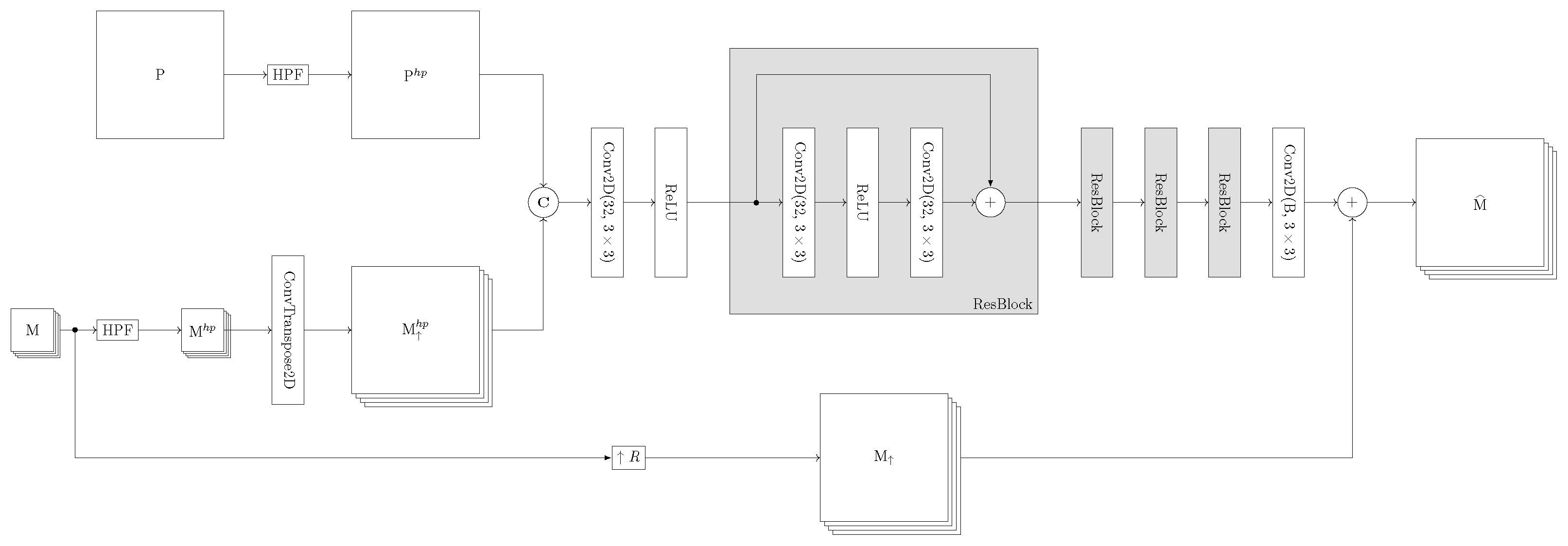
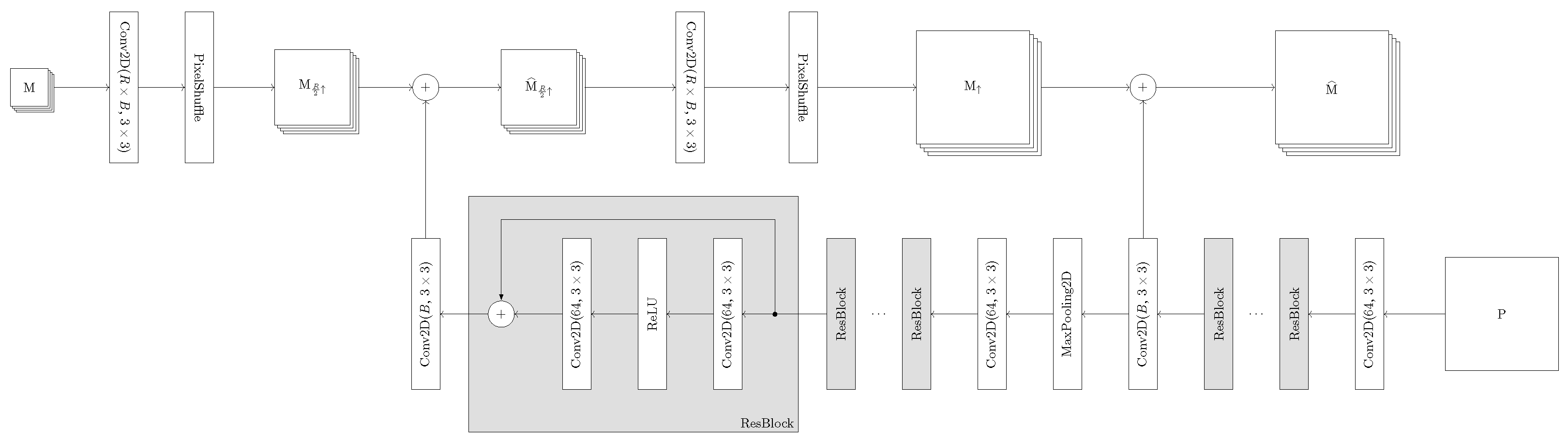
2.1. Unsupervised Losses for Pansharpening
2.2. Proposed Framework with Balanced Spectral-Spatial Loss
3. Results
3.1. Experimental Setup
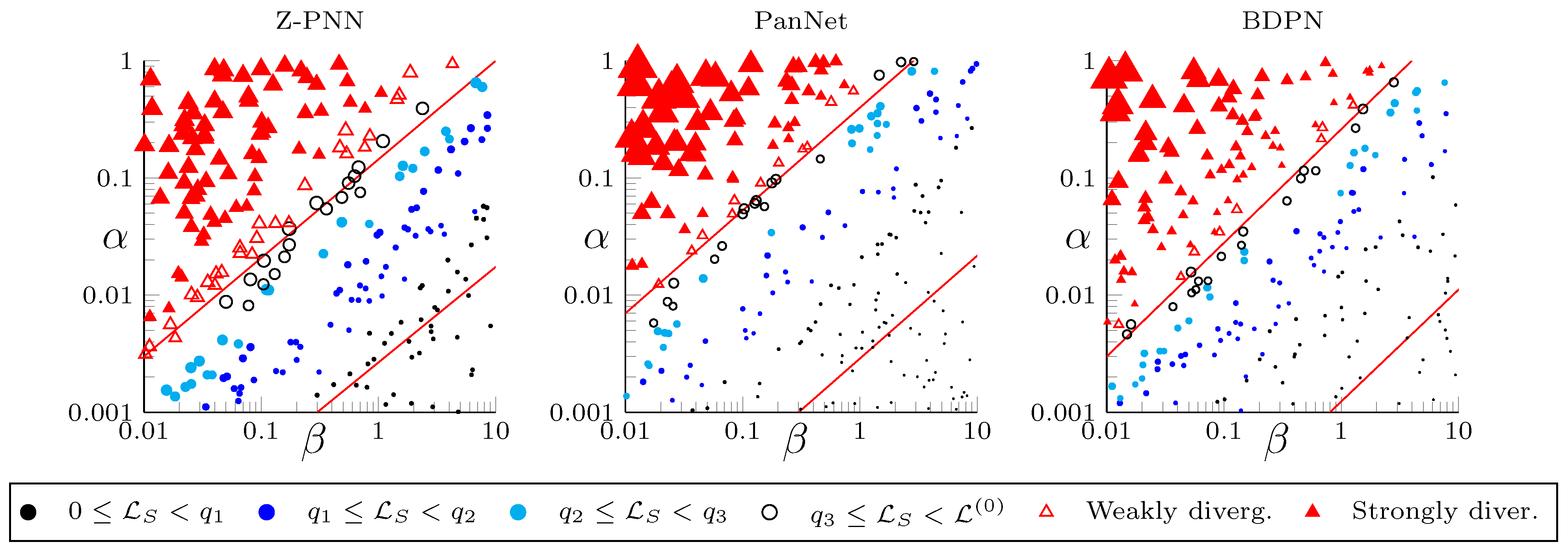
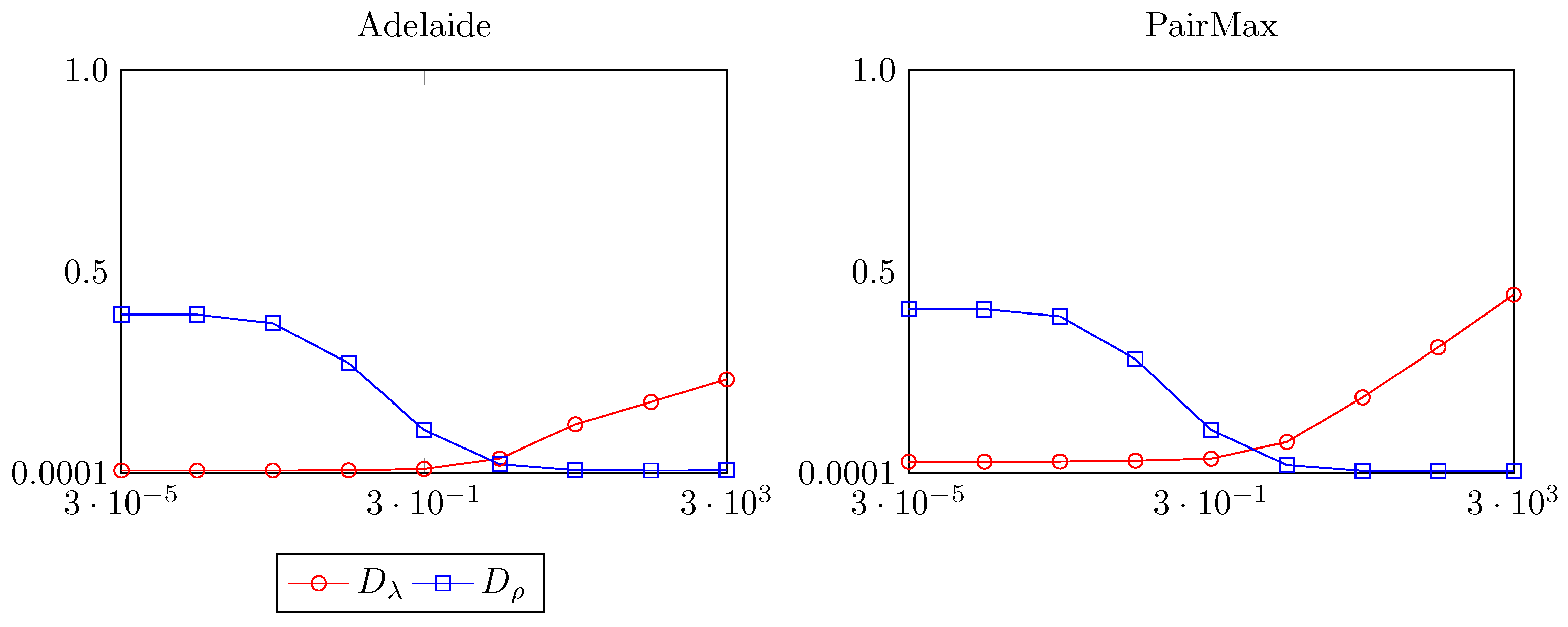
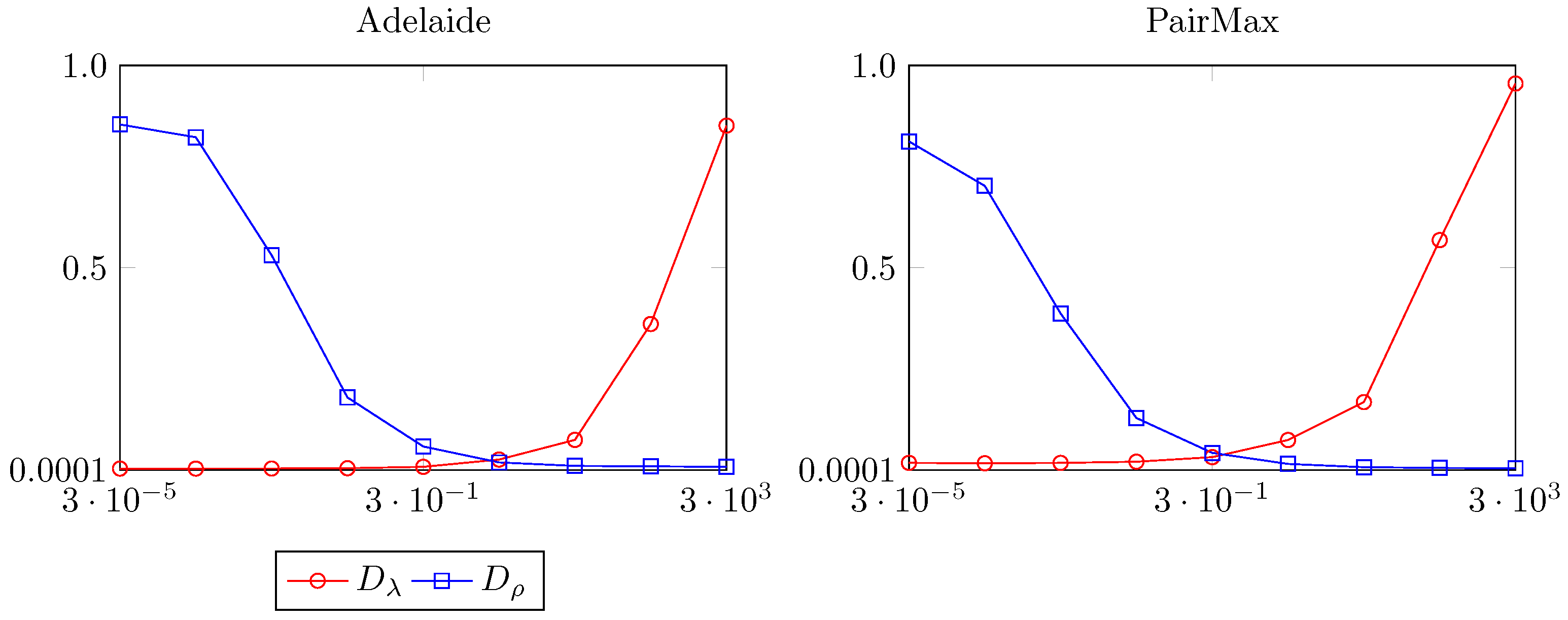
3.2. Finding the Correct Balance
3.3. Comparative Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.O.; Alparone, L.; Chanussot, J. A New Benchmark Based on Recent Advances in Multispectral Pansharpening: Revisiting Pansharpening With Classical and Emerging Pansharpening Methods. IEEE Geosci. Remote Sens. Mag. 2021, 9, 53–81. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS+Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Lolli, S.; Alparone, L.; Garzelli, A.; Vivone, G. Haze Correction for Contrast-Based Multispectral Pansharpening. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2255–2259. [Google Scholar] [CrossRef]
- Vivone, G. Robust Band-Dependent Spatial-Detail Approaches for Panchromatic Sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Otazu, X.; González-Audícana, M.; Fors, O.; Núñez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Intersensor Statistical Matching for Pansharpening: Theoretical Issues and Practical Solutions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4682–4695. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. A regression-based high-pass modulation pansharpening approach. IEEE Trans. Geosci. Remote Sens. 2017, 56, 984–996. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A New Pansharpening Algorithm Based on Total Variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Wang, T.; Fang, F.; Li, F.; Zhang, G. High-Quality Bayesian Pansharpening. IEEE Trans. Image Process. 2019, 28, 227–239. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. CNN-based Pansharpening of Multi-Resolution Remote-Sensing Images. In Proceedings of the Joint Urban Remote Sensing Event 2017, Dubai, United Arab Emirates, 6–8 March 2017. [Google Scholar]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A Deep Network Architecture for Pan-Sharpening. In Proceedings of the ICCV 2017, Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Jin, C.; Chanussot, J. Detail injection-based deep convolutional neural networks for pansharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6995–7010. [Google Scholar] [CrossRef]
- Chavez, P.S.; Kwarteng, A.W. Extracting spectral contrast in Landsat thematic mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 339–348. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6011875, 4 January 2000. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II. Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Tu, T.M.; Huang, P.S.; Hung, C.L.; Chang, C.P. A fast intensity hue-saturation fusion technique with spectral adjustment for IKONOS imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Ranchin, T.; Wald, L. Fusion of high spatial and spectral resolution images: The ARSIS concept and its implementation. Photogramm. Eng. Remote Sens. 2000, 66, 49–61. [Google Scholar]
- Khan, M.M.; Chanussot, J.; Condat, L.; Montanvert, A. Indusion: Fusion of Multispectral and Panchromatic Images Using the Induction Scaling Technique. IEEE Geosci. Remote Sens. Lett. 2008, 5, 98–102. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Restaino, R.; Mura, M.D.; Vivone, G.; Chanussot, J. Context-Adaptive Pansharpening Based on Image Segmentation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 753–766. [Google Scholar] [CrossRef]
- Vivone, G.; Simões, M.; Dalla Mura, M.; Restaino, R.; Bioucas-Dias, J.M.; Licciardi, G.A.; Chanussot, J. Pansharpening Based on Semiblind Deconvolution. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1997–2010. [Google Scholar] [CrossRef]
- Vicinanza, M.R.; Restaino, R.; Vivone, G.; Mura, M.D.; Chanussot, J. A Pansharpening Method Based on the Sparse Representation of Injected Details. IEEE Geosci. Remote Sens. Lett. 2015, 12, 180–184. [Google Scholar] [CrossRef]
- Palsson, F.; Ulfarsson, M.O.; Sveinsson, J.R. Model-Based Reduced-Rank Pansharpening. IEEE Geosci. Remote Sens. Lett. 2020, 17, 656–660. [Google Scholar] [CrossRef]
- Vitale, S.; Ferraioli, G.; Pascazio, V. A New Ratio Image Based CNN Algorithm for SAR Despeckling. In Proceedings of the IGARSS 2019, Yokohama, Japan, 28 July–2 August 2019; pp. 9494–9497. [Google Scholar] [CrossRef]
- Fayad, I.; Ienco, D.; Baghdadi, N.; Gaetano, R.; Alvares, C.A.; Stape, J.L.; Ferraço Scolforo, H.; Le Maire, G. A CNN-based approach for the estimation of canopy heights and wood volume from GEDI waveforms. Remote Sens. Environ. 2021, 265, 112652. [Google Scholar] [CrossRef]
- Nyborg, J.; Pelletier, C.; Lefèvre, S.; Assent, I. TimeMatch: Unsupervised cross-region adaptation by temporal shift estimation. ISPRS J. Photogramm. Remote Sens. 2022, 188, 301–313. [Google Scholar] [CrossRef]
- Vitale, S.; Ferraioli, G.; Pascazio, V. Analysis on the Building of Training Dataset for Deep Learning SAR Despeckling. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4015005. [Google Scholar] [CrossRef]
- Haq, M.A. CNN based automated weed detection system using UAV imagery. Comput. Syst. Sci. Eng. 2022, 42, 837–849. [Google Scholar]
- Belmouhcine, A.; Burnel, J.C.; Courtrai, L.; Pham, M.T.; Lefèvre, S. Multimodal Object Detection in Remote Sensing. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 1245–1248. [Google Scholar] [CrossRef]
- Haq, M.A.; Hassine, S.B.H.; Malebary, S.J.; Othman, H.A.; Tag-Eldin, E.M. 3D-CNNHSR: A 3-Dimensional Convolutional Neural Network for Hyperspectral Super-Resolution. Comput. Syst. Sci. Eng. 2023, 47, 2689–2705. [Google Scholar]
- Guarino, G.; Ciotola, M.; Vivone, G.; Scarpa, G. Band-Wise Hyperspectral Image Pansharpening Using CNN Model Propagation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5500518. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by Convolutional Neural Networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A Multiscale and Multidepth Convolutional Neural Network for Remote Sensing Imagery Pan-Sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Liu, Q. Psgan: A Generative Adversarial Network for Remote Sensing Image Pan-Sharpening. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 873–877. [Google Scholar]
- Shao, Z.; Cai, J. Remote Sensing Image Fusion With Deep Convolutional Neural Network. IEEE J. Sel. Topics Appl. Earth Observ. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Scarpa, G.; Vitale, S.; Cozzolino, D. Target-Adaptive CNN-Based Pansharpening. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5443–5457. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Sun, M.; Ou, Y. Pan-Sharpening Using an Efficient Bidirectional Pyramid Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5549–5563. [Google Scholar] [CrossRef]
- He, L.; Rao, Y.; Li, J.; Chanussot, J.; Plaza, A.; Zhu, J.; Li, B. Pansharpening via Detail Injection Based Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1188–1204. [Google Scholar] [CrossRef]
- Guarino, G.; Ciotola, M.; Vivone, G.; Poggi, G.; Scarpa, G. PCA-CNN Hybrid Approach for Hyperspectral Pansharpening. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5511505. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, H.; Xu, H.; Tian, X.; Ma, J. Multipatch Progressive Pansharpening With Knowledge Distillation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5401115. [Google Scholar] [CrossRef]
- Gong, M.; Ma, J.; Xu, H.; Tian, X.; Zhang, X.P. D2TNet: A ConvLSTM Network With Dual-Direction Transfer for Pan-Sharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5409114. [Google Scholar] [CrossRef]
- Kumar, D.G.; Joseph, C.; Subbarao, M.V. An Efficient PAN-sharpening of Multispectral Images using Multi-scale Residual CNN with Sparse Representation. In Proceedings of the 2024 International Conference on Integrated Circuits and Communication Systems (ICICACS), Raichur, India, 23–24 February 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Deng, L.j.; Vivone, G.; Paoletti, M.E.; Scarpa, G.; He, J.; Zhang, Y.; Chanussot, J.; Plaza, A. Machine Learning in Pansharpening: A benchmark, from shallow to deep networks. IEEE Geosci. Remote Sens. Mag. 2022, 10, 279–315. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolution: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Luo, S.; Zhou, S.; Feng, Y.; Xie, J. Pansharpening via Unsupervised Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4295–4310. [Google Scholar] [CrossRef]
- Ciotola, M.; Vitale, S.; Mazza, A.; Poggi, G.; Scarpa, G. Pansharpening by Convolutional Neural Networks in the Full Resolution Framework. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5408717. [Google Scholar] [CrossRef]
- Ciotola, M.; Poggi, G.; Scarpa, G. Unsupervised Deep Learning-Based Pansharpening With Jointly Enhanced Spectral and Spatial Fidelity. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5405417. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Chen, C.; Liang, P.; Guo, X.; Jiang, J. Pan-GAN: An unsupervised pan-sharpening method for remote sensing image fusion. Inf. Fusion 2020, 62, 110–120. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Q.; Wang, Y. PGMAN: An Unsupervised Generative Multiadversarial Network for Pansharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6316–6327. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Dai, H.; Kang, X.; Plaza, A.; Zu, W. Mun-GAN: A Multiscale Unsupervised Network for Remote Sensing Image Pansharpening. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5404018. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Q.; Weng, D.; Wang, Y. Unsupervised Cycle-Consistent Generative Adversarial Networks for Pan Sharpening. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5408814. [Google Scholar] [CrossRef]
- Qu, Y.; Baghbaderani, R.K.; Qi, H.; Kwan, C. Unsupervised Pansharpening Based on Self-Attention Mechanism. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3192–3208. [Google Scholar] [CrossRef]
- Ni, J.; Shao, Z.; Zhang, Z.; Hou, M.; Zhou, J.; Fang, L.; Zhang, Y. LDP-Net: An Unsupervised Pansharpening Network Based on Learnable Degradation Processes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5468–5479. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, P.; Bai, Y.; Li, Y. MetaPan: Unsupervised Adaptation With Meta-Learning for Multispectral Pansharpening. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5513505. [Google Scholar] [CrossRef]
- Ciotola, M.; Scarpa, G. Fast Full-Resolution Target-Adaptive CNN-Based Pansharpening Framework. Remote Sens. 2023, 15, 319. [Google Scholar] [CrossRef]
- Uezato, T.; Hong, D.; Yokoya, N.; He, W. Guided deep decoder: Unsupervised image pair fusion. In Proceedings of the European Conference on Computer Vision 2020, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 87–102. [Google Scholar]
- Xiong, Z.; Liu, N.; Wang, N.; Sun, Z.; Li, W. Unsupervised Pansharpening Method Using Residual Network With Spatial Texture Attention. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5402112. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Processing Letters 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)—interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Scarpa, G.; Ciotola, M. Full-Resolution Quality Assessment for Pansharpening. Remote Sens. 2022, 14, 1808. [Google Scholar] [CrossRef]
- Khan, M.M.; Alparone, L.; Chanussot, J. Pansharpening Quality Assessment Using the Modulation Transfer Functions of Instruments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3880–3891. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F. Hypercomplex Quality Assessment of Multi/Hyperspectral Images. IEEE GRSL 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Scarpa, G.; Gargiulo, M.; Mazza, A.; Gaetano, R. A CNN-Based Fusion Method for Feature Extraction from Sentinel Data. Remote Sens. 2018, 10, 236. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Pacifici, F. A Benchmarking Protocol for Pansharpening: Dataset, Preprocessing, and Quality Assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6102–6118. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Garzelli, A. Pansharpening of Multispectral Images Based on Nonlocal Parameter Optimization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2096–2107. [Google Scholar] [CrossRef]
- Choi, J.; Yu, K.; Kim, Y. A New Adaptive Component-Substitution-Based Satellite Image Fusion by Using Partial Replacement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 295–309. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full Scale Regression-Based Injection Coefficients for Panchromatic Sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef] [PubMed]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S Data-Fusion Contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Restaino, R.; Vivone, G.; Dalla Mura, M.; Chanussot, J. Fusion of Multispectral and Panchromatic Images Based on Morphological Operators. IEEE Trans. Image Process. 2016, 25, 2882–2895. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Yuan, Q.; Shen, H.; Zhang, L. Boosting the Accuracy of Multispectral Image Pansharpening by Learning a Deep Residual Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1795–1799. [Google Scholar] [CrossRef]





| Symbol | Description |
|---|---|
| R | resolution ratio |
| B | number of multispectral bands |
| M, P | original multispectral and panchromatic components |
| I | simulated P obtained by linearly combining M components |
| pansharpened image | |
| () downscaled version of | |
| () upscaled version of M | |
| low-pass filtered versions of | |
| high-pass filtered versions of P and | |
| expanded panchromatic component | |
| spectral, spatial and total loss | |
| Binary Cross-Entropy loss | |
| spatial and spectral average | |
| ∇ | image gradient operation |
| local correlation coefficient | |
| suitably estimated pixel/band-wise upper-bound for | |
| step function |
| Loss Name | ||||
|---|---|---|---|---|
| [45] | 1.00 | 1.00 | ||
| [49] | 2.00 | 1.00 | ||
| [48] | 1.00 | 5.00 | ||
| [56] | 0.10 | 1.00 | ||
| [57] | 0.79 | 0.20 | ||
| [46] | 1.00 | 0.36 | ||
| [47] | 1.25 | 3.75 |
| WorldView-3 (GSD at Nadir: 0.31 m) | |||
|---|---|---|---|
| Dataset | Training | Validation | Test |
| (PAN Size) | (512 × 512) | (512 × 512) | (2048 × 2048) |
| Fortaleza | 32 | 8 | - |
| Mexico City | 32 | 8 | - |
| Xian | 32 | 8 | - |
| Adelaide | - | 24 | 3 |
| Munich (PairMax) | - | - | 3 |
| Component Substitution (CS) |
|---|
| BT-H [3], BDSD [66], C-BDSD [67], BDSD-PC [4], GS [14], GSA [2], C-GSA [20], PRACS [68] |
| Multiresolution Analysis (MRA) |
| AWLP [5], MTF-GLP [6], MTF-GLP-FS [69], MTF-GLP-HPM [6], MTF-GLP-HPM-H [3], |
| MTF-GLP-HPM-R [7], MTF-GLP-CBD [70], C-MTF-GLP-CBD [20], MF [71] |
| Variational Optimization (VO) |
| FE-HPM [21], SR-D [22], TV [8] |
| Supervised Deep Learning-based |
| PNN [32], A-PNN [36], A-PNN-TA [36], BDPN [37], DiCNN [38], DRPNN [72], |
| FusionNet [12], MSDCNN [33], PanNet [11] |
| Unsupervised Deep Learning-based |
| QSS [45], GDD [56], PanGan [48], Z-PNN [46], -PNN [47] |
| Method | Adelaide | PairMax | ||||||
|---|---|---|---|---|---|---|---|---|
| R-SAM | R-ERGAS | R-SAM | R-ERGAS | |||||
| EXP | 0.0724 | 5.1446 | 4.6528 | 0.8441 | 0.0637 | 2.6788 | 3.9106 | 0.8542 |
| BT-H | 0.0652 | 5.1339 | 4.4104 | 0.0757 | 0.0793 | 2.9367 | 4.1615 | 0.0487 |
| BDSD | 0.0969 | 6.3726 | 5.3757 | 0.1219 | 0.1198 | 3.3852 | 5.5961 | 0.0749 |
| C-BDSD | 0.1198 | 6.6654 | 6.1608 | 0.1822 | 0.1370 | 3.9009 | 6.7313 | 0.1128 |
| BDSD-PC | 0.0802 | 5.7458 | 4.8476 | 0.0885 | 0.1075 | 3.3266 | 5.4472 | 0.0585 |
| GS | 0.0854 | 5.3908 | 4.8940 | 0.0934 | 0.1281 | 3.5500 | 5.0121 | 0.0722 |
| GSA | 0.0612 | 5.5015 | 4.4211 | 0.0739 | 0.0754 | 3.8093 | 4.4156 | 0.0507 |
| C-GSA | 0.0614 | 5.6468 | 4.4500 | 0.1299 | 0.0782 | 3.7375 | 4.4110 | 0.0603 |
| PRACS | 0.0602 | 5.1321 | 4.2519 | 0.1715 | 0.0628 | 2.9408 | 3.9187 | 0.1953 |
| AWLP | 0.0493 | 5.1313 | 3.9130 | 0.1028 | 0.0432 | 2.5507 | 3.0784 | 0.0793 |
| MTF-GLP | 0.0493 | 5.1570 | 3.9348 | 0.0842 | 0.0416 | 2.4502 | 2.9481 | 0.0556 |
| MTF-GLP-FS | 0.0513 | 5.1646 | 3.9989 | 0.1090 | 0.0428 | 2.4565 | 2.9792 | 0.0672 |
| MTF-GLP-HPM | 0.0492 | 5.2024 | 3.9451 | 0.0891 | 0.0479 | 2.9681 | 3.3831 | 0.0605 |
| MTF-GLP-HPM-H | 0.0488 | 5.2352 | 3.9550 | 0.0813 | 0.0425 | 2.5682 | 2.9528 | 0.0492 |
| MTF-GLP-HPM-R | 0.0510 | 5.1782 | 3.9988 | 0.1209 | 0.0423 | 2.4742 | 2.9861 | 0.0711 |
| MTF-GLP-CBD | 0.0515 | 5.1643 | 4.0069 | 0.1124 | 0.0432 | 2.4588 | 2.9950 | 0.0701 |
| C-MTF-GLP-CBD | 0.0565 | 5.1537 | 4.1845 | 0.2081 | 0.0468 | 2.6051 | 3.2540 | 0.1628 |
| MF | 0.0444 | 5.1306 | 3.7584 | 0.1128 | 0.0424 | 2.4981 | 3.0371 | 0.0780 |
| FE-HPM | 0.0503 | 5.1766 | 4.0367 | 0.1115 | 0.0427 | 2.5400 | 3.1030 | 0.0728 |
| SR-D | 0.0557 | 5.3438 | 4.2833 | 0.3014 | 0.0340 | 2.3290 | 2.7768 | 0.1857 |
| TV | 0.0352 | 4.1076 | 3.3427 | 0.2149 | 0.0403 | 1.7289 | 2.8877 | 0.1684 |
| PNN | 0.1059 | 7.2978 | 6.5981 | 0.4612 | 0.4163 | 8.0292 | 9.1146 | 0.4754 |
| A-PNN | 0.0598 | 5.2748 | 4.2779 | 0.5144 | 0.1693 | 3.5492 | 4.3984 | 0.6649 |
| A-PNN-FT | 0.0558 | 5.1300 | 4.1730 | 0.3087 | 0.0845 | 2.5642 | 3.5205 | 0.3352 |
| BDPN | 0.1229 | 5.8025 | 5.7712 | 0.1624 | 0.2944 | 6.5828 | 7.6926 | 0.3107 |
| DiCNN | 0.1207 | 6.4165 | 5.9754 | 0.3957 | 0.2169 | 4.9339 | 6.0772 | 0.4101 |
| DRPNN | 0.1168 | 5.8407 | 5.6579 | 0.1945 | 0.1981 | 4.9018 | 6.5979 | 0.1861 |
| FusionNet | 0.0730 | 5.4970 | 4.7655 | 0.4133 | 0.2382 | 4.5529 | 5.3020 | 0.3402 |
| MSDCNN | 0.1349 | 6.1317 | 5.8902 | 0.2005 | 0.3923 | 7.6591 | 6.6639 | 0.3484 |
| PanNet | 0.0554 | 5.0563 | 4.1737 | 0.3403 | 0.0609 | 2.5416 | 3.3221 | 0.2970 |
| QSS | 0.0590 | 5.2782 | 4.2730 | 0.2853 | 0.0828 | 3.1963 | 3.5671 | 0.2843 |
| PanGan | 0.6586 | 14.6330 | 13.7631 | 0.7134 | 0.3816 | 15.0563 | 17.5895 | 0.1317 |
| GDD | 0.1949 | 11.2320 | 7.4459 | 0.6440 | 0.3044 | 9.9670 | 8.6931 | 0.5867 |
| Z-PNN | 0.0374 | 4.8544 | 3.2925 | 0.0946 | 0.0919 | 3.5759 | 3.7666 | 0.1012 |
| -PNN | 0.0203 | 3.7631 | 2.5363 | 0.0574 | 0.0341 | 2.3690 | 2.6606 | 0.0515 |
| Balanced Z-PNN | 0.0194 | 3.4759 | 2.3798 | 0.1084 | 0.0415 | 2.1883 | 2.5103 | 0.1126 |
| Balanced PanNet | 0.0170 | 3.3167 | 2.2524 | 0.0592 | 0.0332 | 2.0381 | 2.4103 | 0.0435 |
| Balanced BDPN | 0.0412 | 5.3797 | 3.3833 | 0.1025 | 0.0934 | 3.3760 | 3.5132 | 0.0884 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciotola, M.; Guarino, G.; Scarpa, G. An Unsupervised CNN-Based Pansharpening Framework with Spectral-Spatial Fidelity Balance. Remote Sens. 2024, 16, 3014. https://doi.org/10.3390/rs16163014
Ciotola M, Guarino G, Scarpa G. An Unsupervised CNN-Based Pansharpening Framework with Spectral-Spatial Fidelity Balance. Remote Sensing. 2024; 16(16):3014. https://doi.org/10.3390/rs16163014
Chicago/Turabian StyleCiotola, Matteo, Giuseppe Guarino, and Giuseppe Scarpa. 2024. "An Unsupervised CNN-Based Pansharpening Framework with Spectral-Spatial Fidelity Balance" Remote Sensing 16, no. 16: 3014. https://doi.org/10.3390/rs16163014
APA StyleCiotola, M., Guarino, G., & Scarpa, G. (2024). An Unsupervised CNN-Based Pansharpening Framework with Spectral-Spatial Fidelity Balance. Remote Sensing, 16(16), 3014. https://doi.org/10.3390/rs16163014









