Annual and Interannual Variability in the Diffuse Attenuation Coefficient and Turbidity in Urbanized Washington Lake from 2013 to 2022 Assessed Using Landsat-8/9
Abstract
1. Introduction
1.1. Background
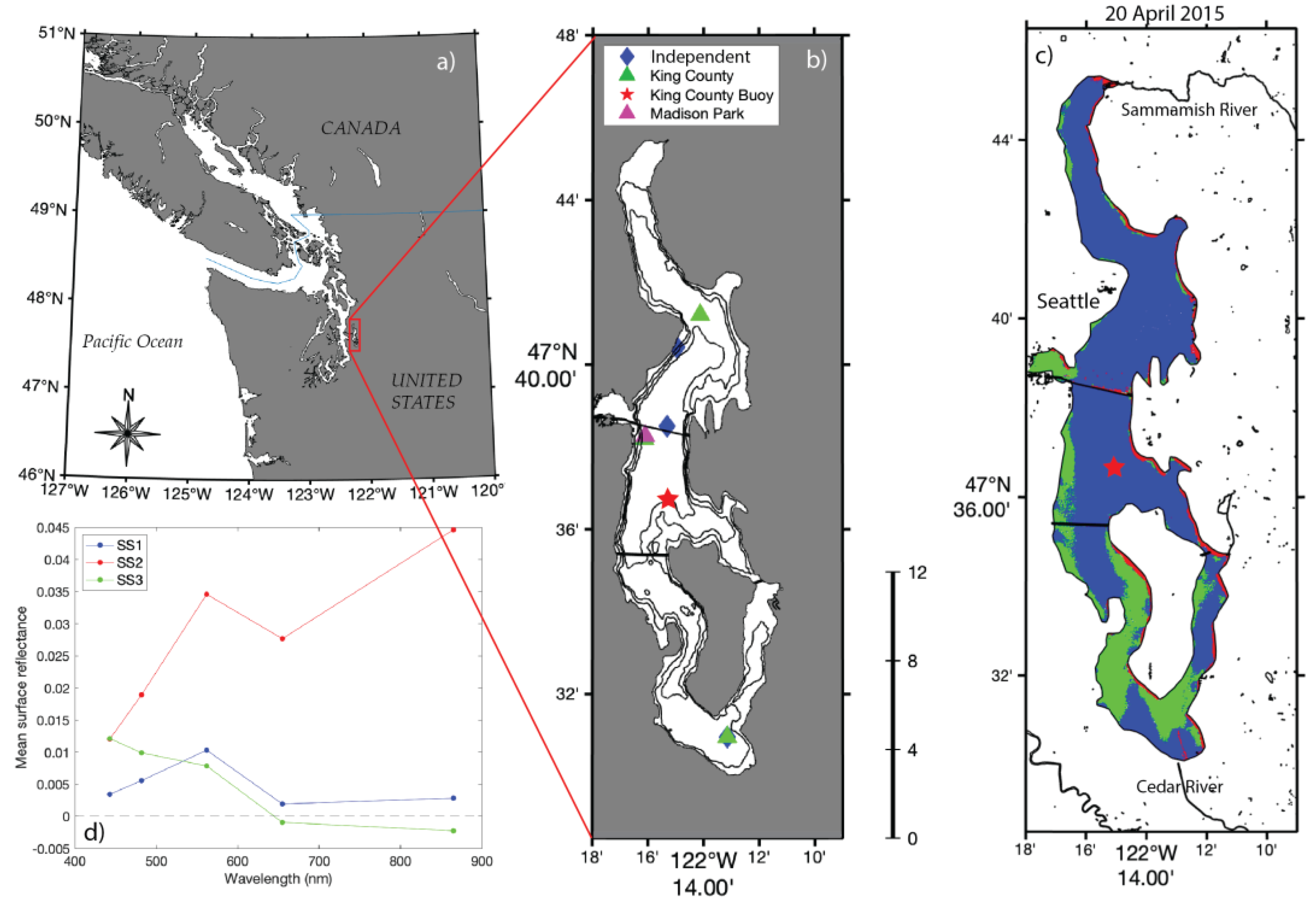
1.2. Study Area
2. Materials and Methods
2.1. Datasets
2.1.1. In-Situ Kd
2.1.2. In-Situ Turbidity
2.1.3. In-Situ Surface Reflectance
2.1.4. Landsat-8/9
2.1.5. Additional Datasets
2.2. IOP-Based Algorithms for Deriving Kd and Turbidity
2.2.1. QAA-v6 Lee-Kd(PAR) Algorithm
2.2.2. Nechad Turbidity Algorithm
2.3. Derivation of Regional Models for Turbidity
2.4. Performance Metrics
2.5. Trend Statistics
3. Results
3.1. In Situ Surface Reflectance
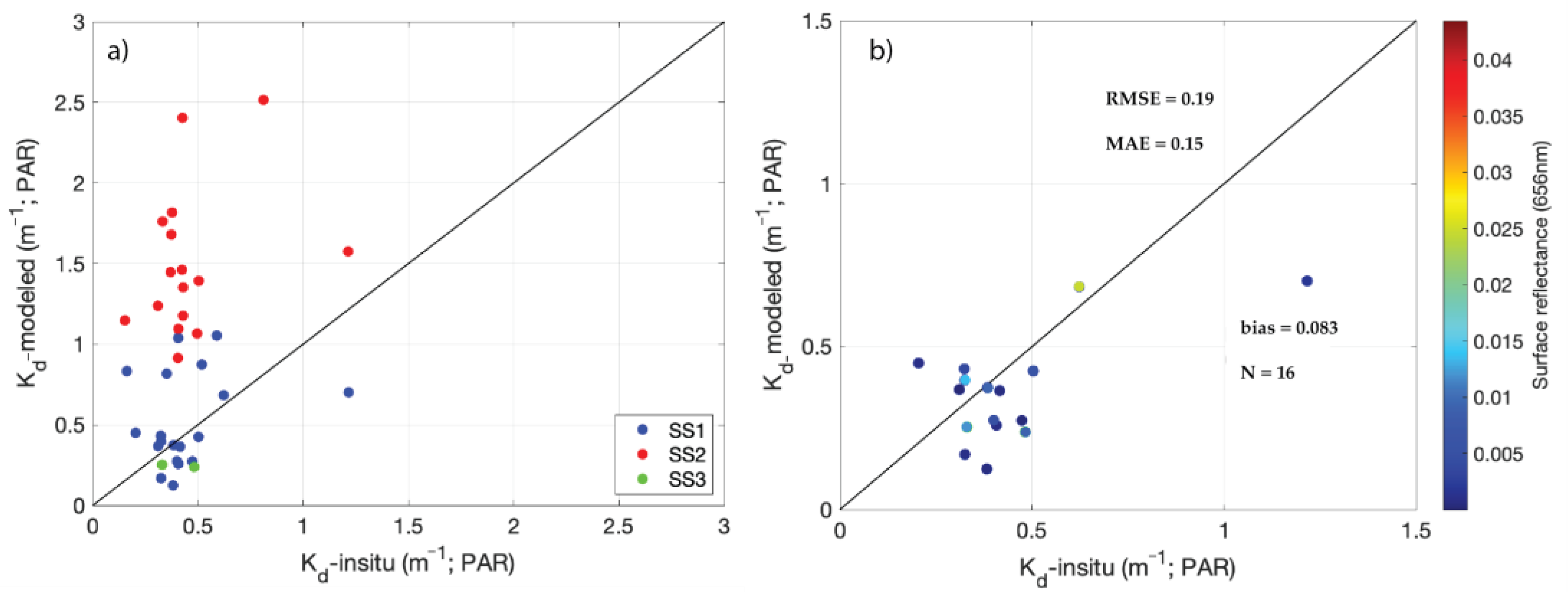
3.2. Performance of Semi-Analytical Models
3.2.1. QAA-v6 Lee-Kd(PAR)
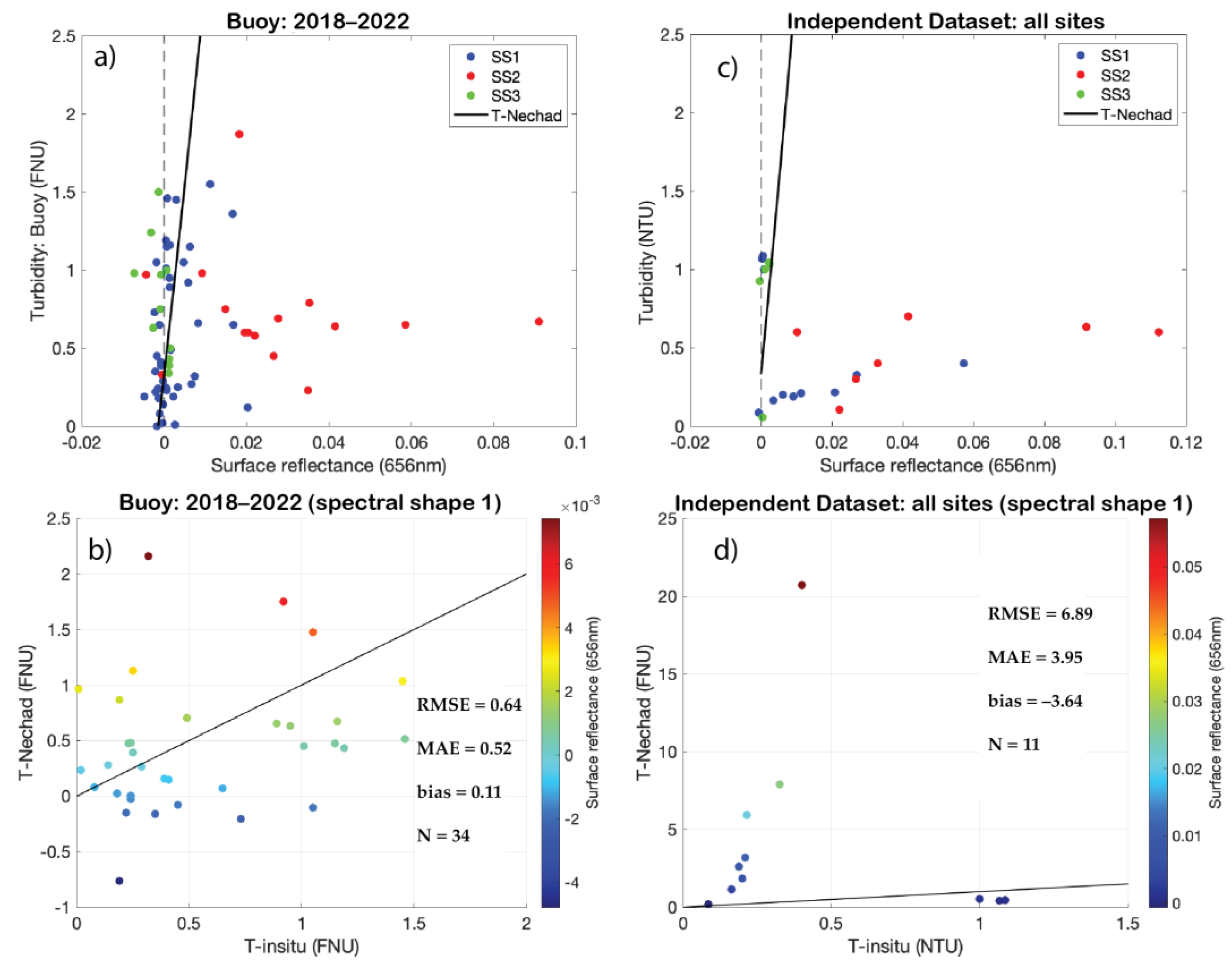
3.2.2. Nechad Turbidity
3.3. Regional Turbidity Algorithm
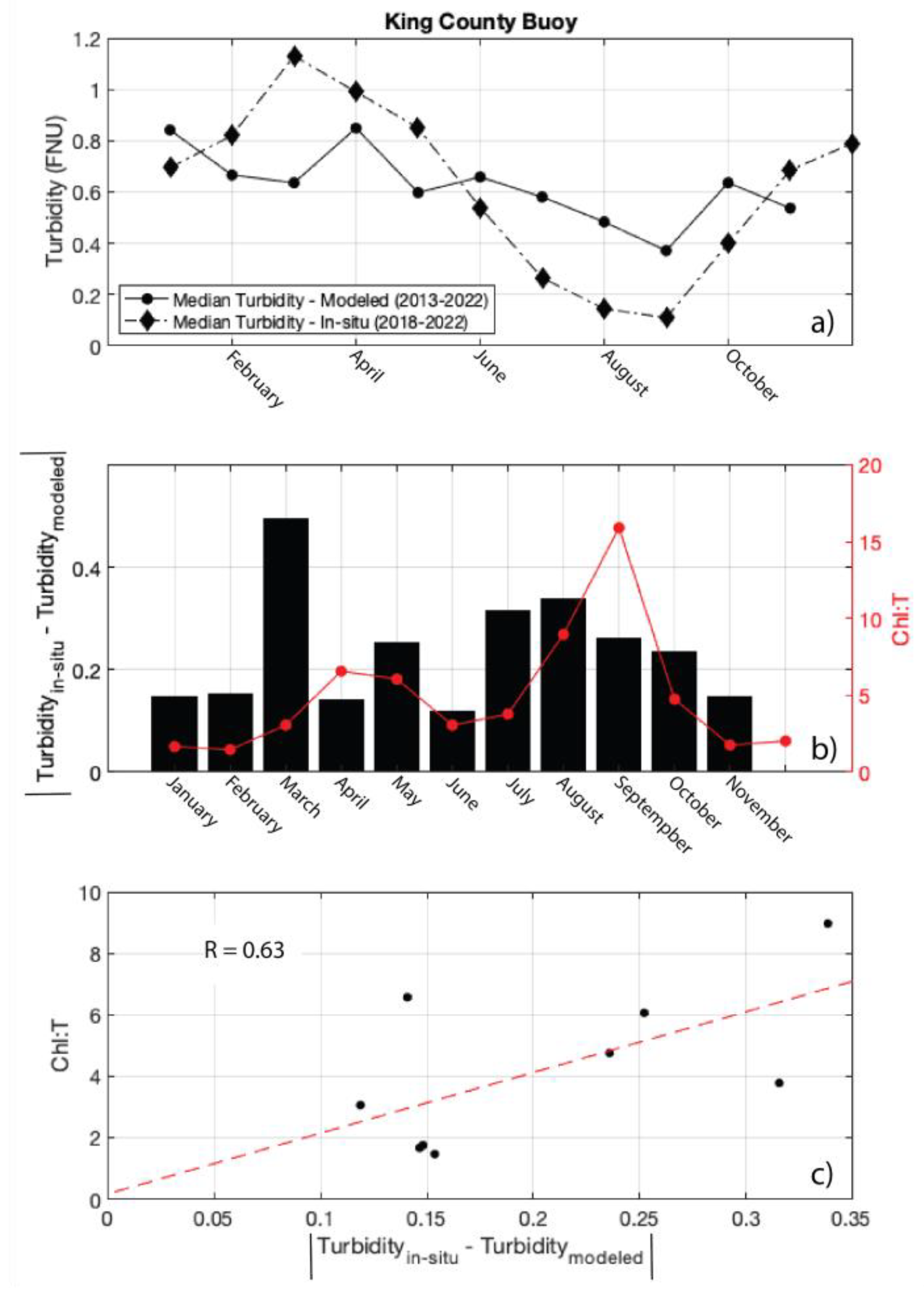
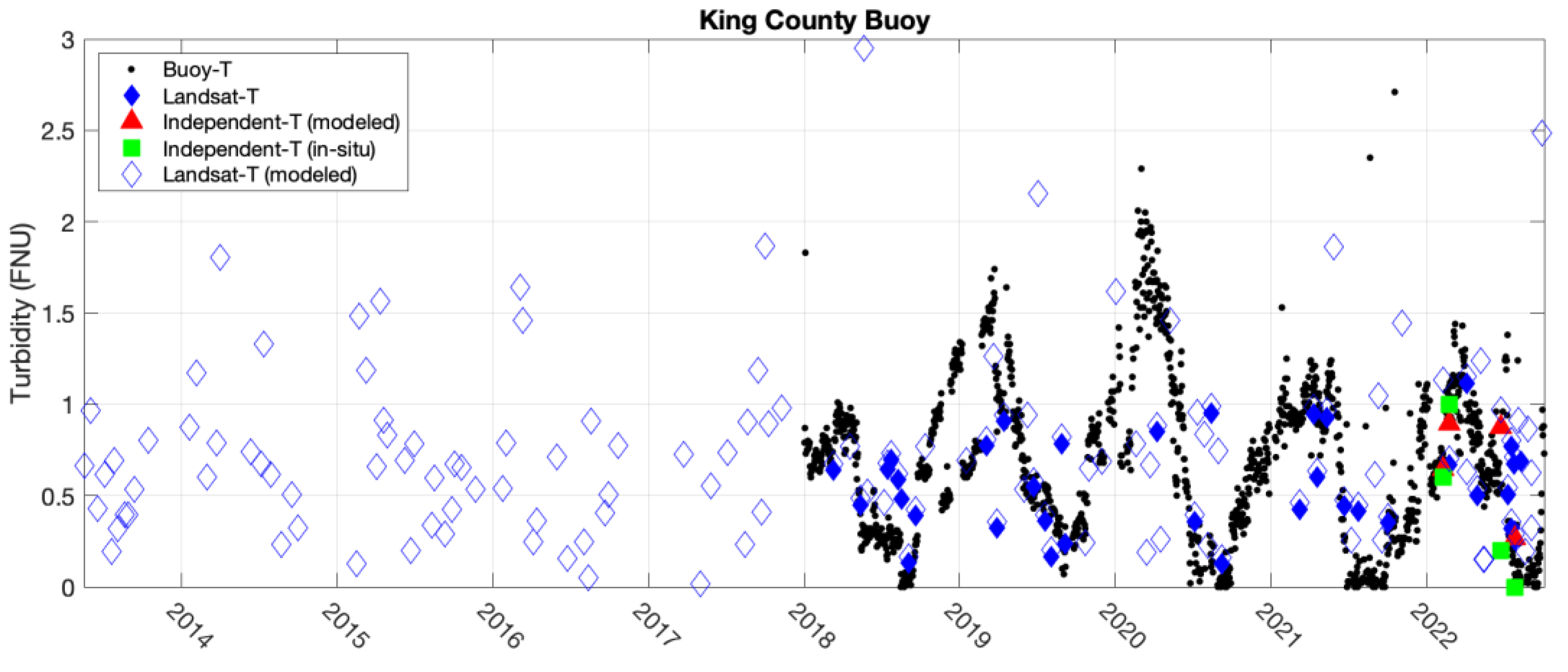
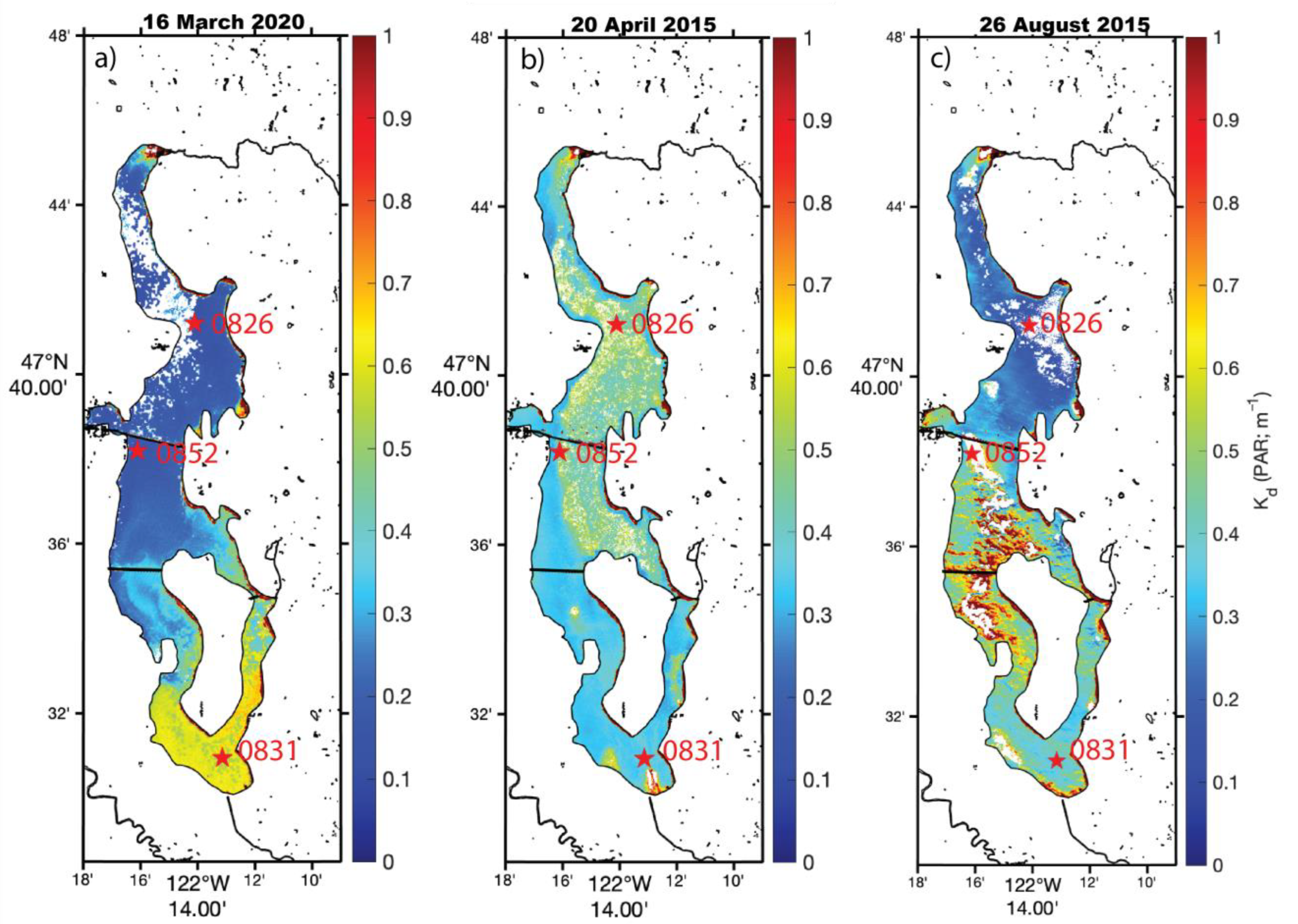
3.4. Spatiotemporal Water Clarity Variability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ISO 7027-1:2016; Water quality-determination of turbidity. ISO: Geneva, Switzerland, 2016.
- Davies-Colley, R.J.; Smith, D.G. Turbidity, suspended sediment, and water clarity: A review. J. Am. Water Resour. Assoc. 2001, 37, 1085–1101. [Google Scholar] [CrossRef]
- Turner, J.S.; Fall, K.A.; Friedrichs, C.T. Clarifying water clarity: A call to use metrics best suited to corresponding research and management goals in aquatic ecosystems. Limnol. Oceanogr. Lett. 2022, 8, 388–397. [Google Scholar] [CrossRef]
- Levy, D.A. Sensory mechanism and selective advantage for diel vertical migration in juvenile sockeye salmon, Oncorhynchus nerka. Can. J. Fish. Aquat. Sci. 1990, 47, 1796–1802. [Google Scholar] [CrossRef]
- Beauchamp, D.A.; Baldwin, C.M.; Vogel, J.L.; Gubala, C.P. Estimating diel, depth-specific foraging with a visual encounter rate model for pelagic piscivores. Can. J. Fish. Aquat. Sci. 1999, 56 (Suppl. S1), 128–139. [Google Scholar] [CrossRef]
- Bunnell, D.B.; Ludsin, S.A.; Knight, R.L.; Rudstam, L.G.; Williamson, C.E.; Höök, T.O.; Collingsworth, P.D.; Lesht, B.M.; Barbiero, R.P.; Scofield, A.E.; et al. Consequences of changing water clarity on the fish and fisheries of the Laurentian Great Lakes. Can. J. Fish. Aquat. Sci. 2021, 78, 1524–1542. [Google Scholar] [CrossRef]
- Jamet, C.; Loisel, H.; Dessailly, D. Retrieval of the spectral diffuse attenuation coefficient Kd(λ) in open and coastal ocean waters using a neural network inversion: Retrieval of Diffuse Attenuation. J. Geophys. Res. Ocean. 2012, 117, C10023. [Google Scholar] [CrossRef]
- Begouen Demeaux, C.; Boss, E. Validation of Remote-Sensing Algorithms for Diffuse Attenuation of Downward Irradiance Using BGC-Argo Floats. Remote Sens. 2022, 14, 4500. [Google Scholar] [CrossRef]
- Rubin, H.J.; Lutz, D.A.; Steele, B.G.; Cottingham, K.L.; Weathers, K.C.; Ducey, M.J.; Palace, M.; Johnson, K.M.; Chipman, J.W. Remote Sensing of Lake Water Clarity: Performance and Transferability of Both Historical Algorithms and Machine Learning. Remote Sens. 2021, 13, 1434. [Google Scholar] [CrossRef]
- Lee, Z.; Du, K.; Arnone, R.; Liew, S.; Penta, B. Penetration of solar radiation in the upper ocean: A numerical model for oceanic and coastal waters. J. Geophys. Res. Ocean. 2005, 110, C09019. [Google Scholar] [CrossRef]
- Lee, Z.; Hu, C.; Shang, S.; Du, K.; Lewis, M.; Arnone, R.; Brewin, R. Penetration of UV-visible solar radiation in the global oceans: Insights from ocean color remote sensing. J. Geophys. Res. Ocean. 2013, 118, 4241–4255. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Yin, Z.; Li, J.; Liu, Y.; Xie, Y.; Zhang, F.; Wang, S.; Sun, X.; Zhang, B. Water clarity changes in Lake Taihu over 36 years based on Landsat TM and OLI observations. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102457. [Google Scholar] [CrossRef]
- Rodríguez-López, L.; González-Rodríguez, L.; Duran-Llacer, I.; García, W.; Cardenas, R.; Urrutia, R. Assessment of the diffuse attenuation coefficient of photosynthetically active radiation in a Chilean Lake. Remote Sens. 2022, 14, 4568. [Google Scholar] [CrossRef]
- Keith, D.J.; Salls, W.; Schaeffer, B.A.; Werdell, P.J. Assessing the suitability of lakes and reservoirs for recreation using Landsat 8 Water Clarity. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.G.; Neukermans, G. September. Calibration and validation of a generic multisensor algorithm for mapping of turbidity in coastal waters. In Remote Sensing of the Ocean, Sea Ice, and Large Water Regions 2009; SPIE: Bellingham, WA, USA, 2009; Volume 7473, pp. 161–171. [Google Scholar]
- Dogliotti, A.I.; Ruddick, K.G.; Nechad, B.; Doxaran, D.; Knaeps, E. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sens. Environ. 2015, 156, 157–168. [Google Scholar] [CrossRef]
- Potes, M.; Costa, M.J.; Salgado, R. Satellite remote sensing of water turbidity in Alqueva reservoir and implications on lake modelling. Hydrol. Earth Syst. Sci. 2012, 16, 1623–1633. [Google Scholar] [CrossRef]
- Hossain, A.A.; Mathias, C.; Blanton, R. Remote sensing of turbidity in the Tennessee River using Landsat 8 satellite. Remote Sens. 2021, 13, 3785. [Google Scholar] [CrossRef]
- Edmondson, W.T. Sixty years of Lake Washington: A curriculum vitae. Lake Reserv. Manag. 1994, 10, 75–84. [Google Scholar] [CrossRef]
- Arhonditsis, G.; Brett, M.T.; Frodge, J. Environmental control and limnological impacts of a large recurrent spring bloom in Lake Washington, USA. Environ. Manag. 2003, 31, 0603–0618. [Google Scholar] [CrossRef]
- Fresh, K.L. Lake Washington fish: A historical perspective. Lake Reserv. Manag. 1994, 9, 148–151. [Google Scholar] [CrossRef][Green Version]
- Kendall, N.W.; Quinn, T.P.; Beauchamp, D.A.; Fresh, K.; Volk, C.; Unrein, J. Life-cycle model reveals sensitive life stages and evaluates recovery options for a dwindling Pacific salmon population. N. Am. J. Fish. Manag. 2022, 43, 203–230. [Google Scholar] [CrossRef]
- Vogel, J.L.; Beauchamp, D.A. Effects of light, prey size, and turbidity on reaction distances of lake trout (Salvelinus namaycush) to salmonid prey. Can. J. Fish. Aquat. Sci. 1999, 56, 1293–1297. [Google Scholar] [CrossRef]
- Mazur, M.M.; Beauchamp, D.A. A comparison of visual prey detection among species of piscivorous salmonids: Effects of light and low turbidities. Environ. Biol. Fishes 2003, 67, 397–405. [Google Scholar] [CrossRef]
- Utne-Palm, A.C. Visual feeding of fish in a turbid environment: Physical and behavioral aspects. Mar. Freshw. Behav. Physiol. 2002, 35, 111–128. [Google Scholar] [CrossRef]
- Fiksen, Ø.; Aksnes, D.L.; Flyum, M.H.; Giske, J. The influence of turbidity on growth and survival of fish larvae: A numerical analysis. In Proceedings of the Sustainable Increase of Marine Harvesting: Fundamental Mechanisms and New Concepts: Proceedings of the 1st Maricult Conference held in Trondheim, Norway, 25–28 June 2000; Springer: Dordrecht, The Netherlands, 2002; pp. 49–59. [Google Scholar]
- Hansen, A.G.; Beauchamp, D.A.; Schoen, E.R. Visual prey detection responses of piscivorous trout and salmon: Effects of light, turbidity, and prey size. Trans. Am. Fish. Soc. 2013, 142, 854–867. [Google Scholar] [CrossRef]
- Beauchamp, D.A.; Stewart, D.J.; Thomas, G.L. Corroboration of a bioenergetics model for sockeye salmon. Trans. Am. Fish. Soc. 1989, 118, 597–607. [Google Scholar] [CrossRef]
- Hovel, R.A.; Thorson, J.T.; Carter, J.L.; Quinn, T.P. Within-lake habitat heterogeneity mediates community response to warming trends. Ecology 2017, 98, 2333–2342. [Google Scholar] [CrossRef] [PubMed]
- Hansen, A.G.; Beauchamp, D.A. Effects of prey abundance, distribution, visual contrast and morphology on selection by a pelagic piscivore. Freshw. Biol. 2014, 59, 2328–2341. [Google Scholar] [CrossRef]
- Thomas, Z.R.; Beauchamp, D.A.; Clark, C.P.; Quinn, T.P. Seasonal shifts in diel vertical migrations by lake-dwelling coastal cutthroat trout, Oncorhynchus clarkii clarkii, reflect thermal regimes and prey distributions. Ecol. Freshw. Fish 2023, 32, 842–851. [Google Scholar] [CrossRef]
- Kitano, J.; Mori, S.; Peichel, C.L. Divergence of male courtship displays between sympatric forms of anadromous threespine stickleback. Behaviour 2008, 145, 443–461. [Google Scholar]
- Quinn, T.P.; Sergeant, C.J.; Beaudreau, A.H.; Beauchamp, D.A. Spatial and temporal patterns of vertical distribution for three planktivorous fishes in Lake Washington. Ecol. Freshw. Fish 2012, 21, 337–348. [Google Scholar] [CrossRef]
- Hansen, A.G.; Beauchamp, D.A. Latitudinal and photic effects on diel foraging and predation risk in freshwater pelagic ecosystems. J. Anim. Ecol. 2015, 84, 532–544. [Google Scholar] [CrossRef]
- Patmont, C.R.; Davis, J.I.; Swartz, R.G. Aquatic Plants in Selected Waters of King County: Distribution and Community Composition of Macrophytes; Municipality of Metropolitan Seattle, Water Quality Division: Seattle, WA, USA, 1981. [Google Scholar]
- Olden, J.D.; Tamayo, M. Incentivizing the public to support invasive species management: Eurasian milfoil reduces lakefront property values. PLoS ONE 2014, 9, e110458. [Google Scholar] [CrossRef]
- Parsons, J.K.; Marx, G.E.; Divens, M. A study of Eurasian watermilfoil, macroinvertebrates and fish in a Washington lake. J. Aquat. Plant Manag. 2011, 49, 71–82. [Google Scholar]
- Frodge, J.D.; Thomas, G.L.; Pauley, G.B. Effects of canopy formation by floating and submergent aquatic macrophytes on the water quality of two shallow Pacific Northwest lakes. Aquat. Bot. 1990, 38, 231–248. [Google Scholar] [CrossRef]
- Frodge, J.D.; Marino, D.A.; Pauley, G.B.; Thomas, G.L. Mortality of largemouth bass (Micropterus salmoides) and steelhead trout (Oncorhynchus mykiss) in densely vegetated littoral areas tested using in situ bioassay. Lake Reserv. Manag. 1995, 11, 343–358. [Google Scholar] [CrossRef]
- Sound, I.P. Recommended Guidelines for Sampling Marine Sediment, Water Column, and Tissue; Puget Sound Water Quality Action Team: Olympia, WA, USA, 1997. [Google Scholar]
- King County Environmental Laboratory (KCEL). Standard Operating Procedure for SBE 25 Plus SeaLogger CTD. SOP # 220v5; KCEL, Water and Land Resources Division: Seattle, WA, USA, 2017. [Google Scholar]
- Zaneveld, J.R.V.; Barnard, A.H.; Boss, E. Theoretical derivation of the depth average of remotely sensed optical parameters. Opt. Express 2005, 13, 9052–9061. [Google Scholar] [CrossRef] [PubMed]
- King County: Lakes. Available online: https://green2.kingcounty.gov/lake-buoy/Data.aspx. (accessed on 10 October 2022).
- YSI Turbidity Sensors. Available online: https://www.ysi.com/filelibrary/documents/technicalnotes/t627_turbidity_units_and_calibration_solutions.pdf. (accessed on 1 September 2023).
- Mueller, J.L.; Pietras, C.; Hooker, S.B.; Austin, R.W.; Miller, M.; Knobelspiesse, K.D.; Frouin, R.; Holben, B.; Voss, K. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 5. Volume V: Biogeochemical and Bio-Optical Measurements and Data Analysis Protocols; Goddard Space Flight Space Center: Greenbelt, MD, USA, 2003; pp. 1–43, (NASA/TM-2003-). [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.L.; Qin, B.; van der Woerd, H.J.; Li, J.; Li, Y. Modeling Remote-Sensing Reflectance and Retrieving Chlorphyll-a Concentration in Extremely Turbid Case-2 Waters (Lake Taihu, China). IEEE Trans. Geosci. Remote Sens. 2009, 47, 1937–1948. [Google Scholar] [CrossRef]
- EarthExplorer. Available online: earthexplorer.usgs.gov. (accessed on 12 July 2022).
- Landsat Collection-2 Level-2 Science Products. Available online: https://www.usgs.gov/landsat-missions/landsat-collection-2-level-2-science-products. (accessed on 12 July 2022).
- Franz, B.A.; Bailey, S.W.; Kuring, N.; Werdell, P.J. Ocean color measurements with the Operational Land Imager on Landsat-8: Implementation and evaluation in SeaDAS. J. Appl. Remote Sens. 2015, 9, 096070. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Advantages of high quality SWIR bands for ocean colour processing: Examples from Landsat-8. Remote Sens. Environ. 2015, 161, 89–106. [Google Scholar] [CrossRef]
- King County Environmental Laboratory (KCEL). Standard Operating Procedure for Attended YSI EXO Multiprobe Operations. SOP#:245v1; King County Environmental Laboratory: Seattle, WA, USA, 2018. [Google Scholar]
- National Water Information System USGS 12119000 Cedar River at Renton, WA. Available online: https://waterdata.usgs.gov/nwis/dv?referred_module=sw&site_no=12119000 (accessed on 14 April 2023).
- Bogorov, V.G. To the methods of the zooplankton processing. Russ. Hydrobiol. J. 1927, 6, 193–198. [Google Scholar]
- Update of the Quasi-Analytical Algorithm (QAA-v6). Available online: https://www.ioccg.org/groups/Software_OCA/QAA_v6_2014209.pdf. (accessed on 8 March 2023).
- Nechad, B.; Ruddick, K.G.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Fatichi, S. Mann-Kendall Modified Test. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/25533-mann-kendall-modified-test (accessed on 10 August 2023).
- Chen, M.; Xiao, F.; Wang, Z.; Feng, Q.; Ban, X.; Zhou, Y.; Hu, Z. An Improved QAA-Based Method for Monitoring Water Clarity of Honghu Lake Using Landsat TM, ETM+ and OLI Data. Remote Sens. 2022, 14, 3798. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Edmondson, W.T.; Litt, A.H. Daphnia in lake Washington 1. Limnol. Oceanogr. 1982, 27, 272–293. [Google Scholar] [CrossRef]
- Phytoplankton Pigments in Oceanography: Guidelines to Modern Methods; Wright, S.W., Jeffrey, S.W., Mantoura, R.F.C., Eds.; Unesco Pub.: Paris, France, 2005. [Google Scholar]
- Courtemanche, B.; Levac, E. Low-cost profiling buoys to assess the effect of Eurasian watermilfoil density on dissolved oxygen in the water column. In Proceedings of the AGU Fall Meeting 2022, Chicago, IL, USA, 12–16 December 2022; p. H22W-1149. [Google Scholar]
- COSEWIC. COSEWIC Assessment and Status Report on the Sockeye Salmon Oncorhynchus nerka (Cultus Population) in Canada; Committee on the Status of Endangered Wildlife in Canada: Ottawa, ON, Canada, 2003. [Google Scholar]
- Codd-Downey, R.; Jenkin, M.; Dey, B.B.; Zacher, J.; Blainey, E.; Andrews, P. Monitoring re-growth of invasive plants using an autonomous surface vessel. Front Robot AI 2021, 7, 583416. [Google Scholar] [CrossRef]
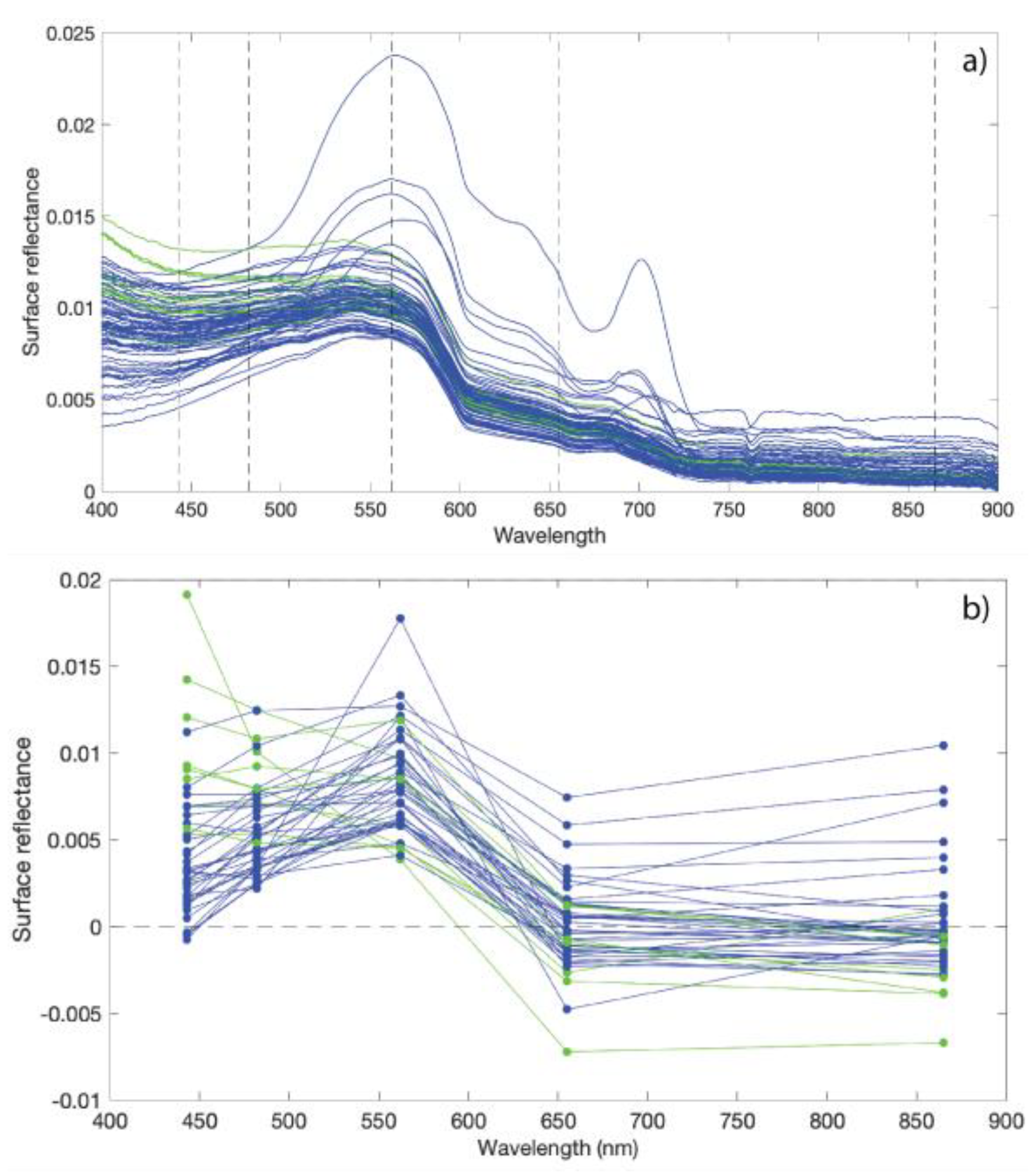
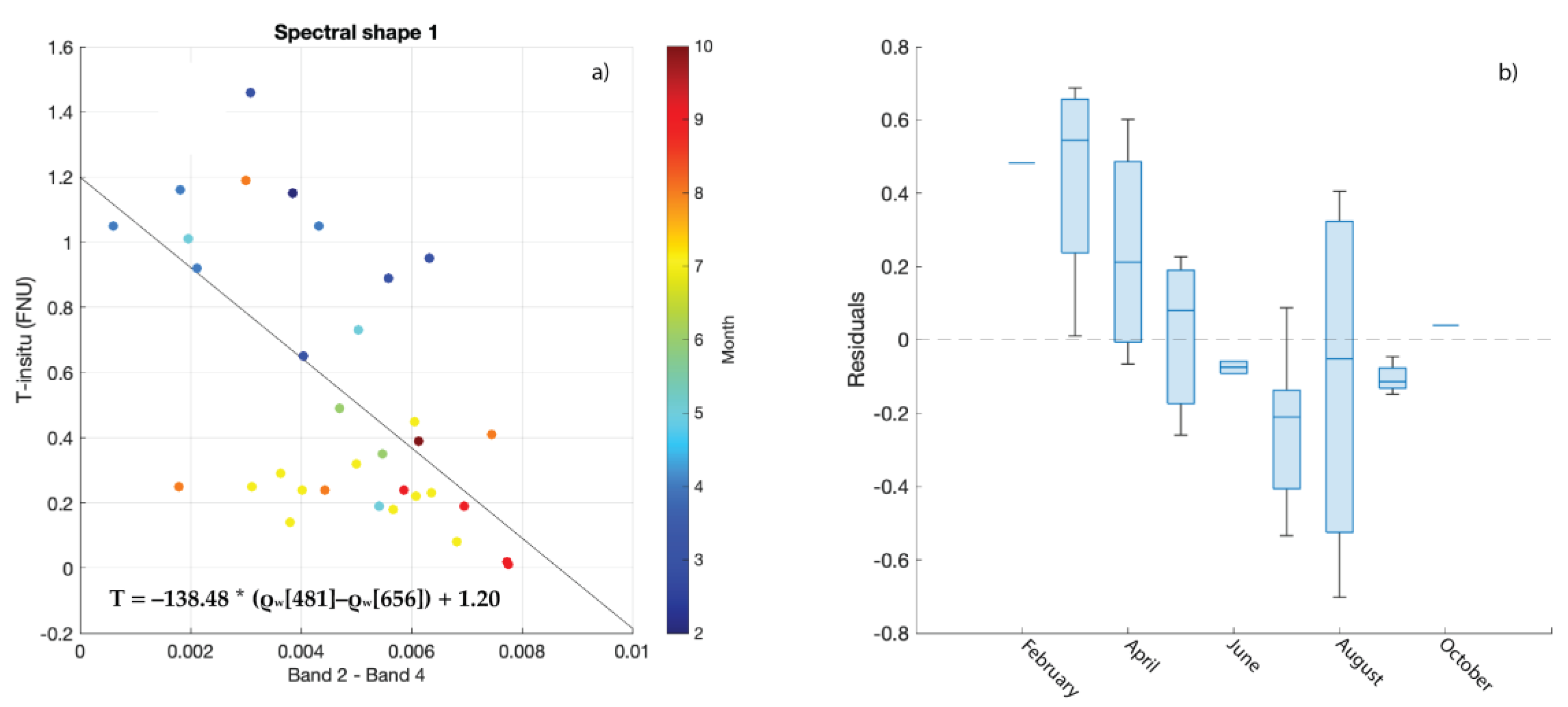



| B4-B1 | B4-B2 | B4-B3 | B3-B2 | B3-B1 | B2-B1 | Height B3 | |
|---|---|---|---|---|---|---|---|
| SS1 | 0.50 | 0.60 | 0.46 | −0.026 | 0.072 | 0.20 | −0.27 |
| SS3 | −0.080 | −0.011 | 0.27 | −0.25 | −0.21 | −0.15 | −0.42 |
| Spectral Shape | RMSE | MAE | Bias | N * | p-Value |
|---|---|---|---|---|---|
| 1 | 0.34 | 0.27 | −3.4 × 10−16 | 34 | 0.00019 |
| 2 | NA | NA | NA | 15 | NA |
| 3 | NA | NA | NA | 9 | NA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schulien, J.A.; Code, T.; DeGasperi, C.; Beauchamp, D.A.; Tonus Ellis, A.; Litt, A.H. Annual and Interannual Variability in the Diffuse Attenuation Coefficient and Turbidity in Urbanized Washington Lake from 2013 to 2022 Assessed Using Landsat-8/9. Remote Sens. 2023, 15, 5055. https://doi.org/10.3390/rs15205055
Schulien JA, Code T, DeGasperi C, Beauchamp DA, Tonus Ellis A, Litt AH. Annual and Interannual Variability in the Diffuse Attenuation Coefficient and Turbidity in Urbanized Washington Lake from 2013 to 2022 Assessed Using Landsat-8/9. Remote Sensing. 2023; 15(20):5055. https://doi.org/10.3390/rs15205055
Chicago/Turabian StyleSchulien, Jennifer A., Tessa Code, Curtis DeGasperi, David A. Beauchamp, Arielle Tonus Ellis, and Arni H. Litt. 2023. "Annual and Interannual Variability in the Diffuse Attenuation Coefficient and Turbidity in Urbanized Washington Lake from 2013 to 2022 Assessed Using Landsat-8/9" Remote Sensing 15, no. 20: 5055. https://doi.org/10.3390/rs15205055
APA StyleSchulien, J. A., Code, T., DeGasperi, C., Beauchamp, D. A., Tonus Ellis, A., & Litt, A. H. (2023). Annual and Interannual Variability in the Diffuse Attenuation Coefficient and Turbidity in Urbanized Washington Lake from 2013 to 2022 Assessed Using Landsat-8/9. Remote Sensing, 15(20), 5055. https://doi.org/10.3390/rs15205055







