Particle Size Distributions and Extinction Coefficients of Aerosol Particles in Land Battlefield Environments
Abstract
:1. Introduction
2. Methods
2.1. Aerosol Particle Sampling
2.2. PSD Measurement
2.3. Fitting and Evaluation of PSD Functions
2.4. Extinction Coefficient Calculation
3. Results and Discussion
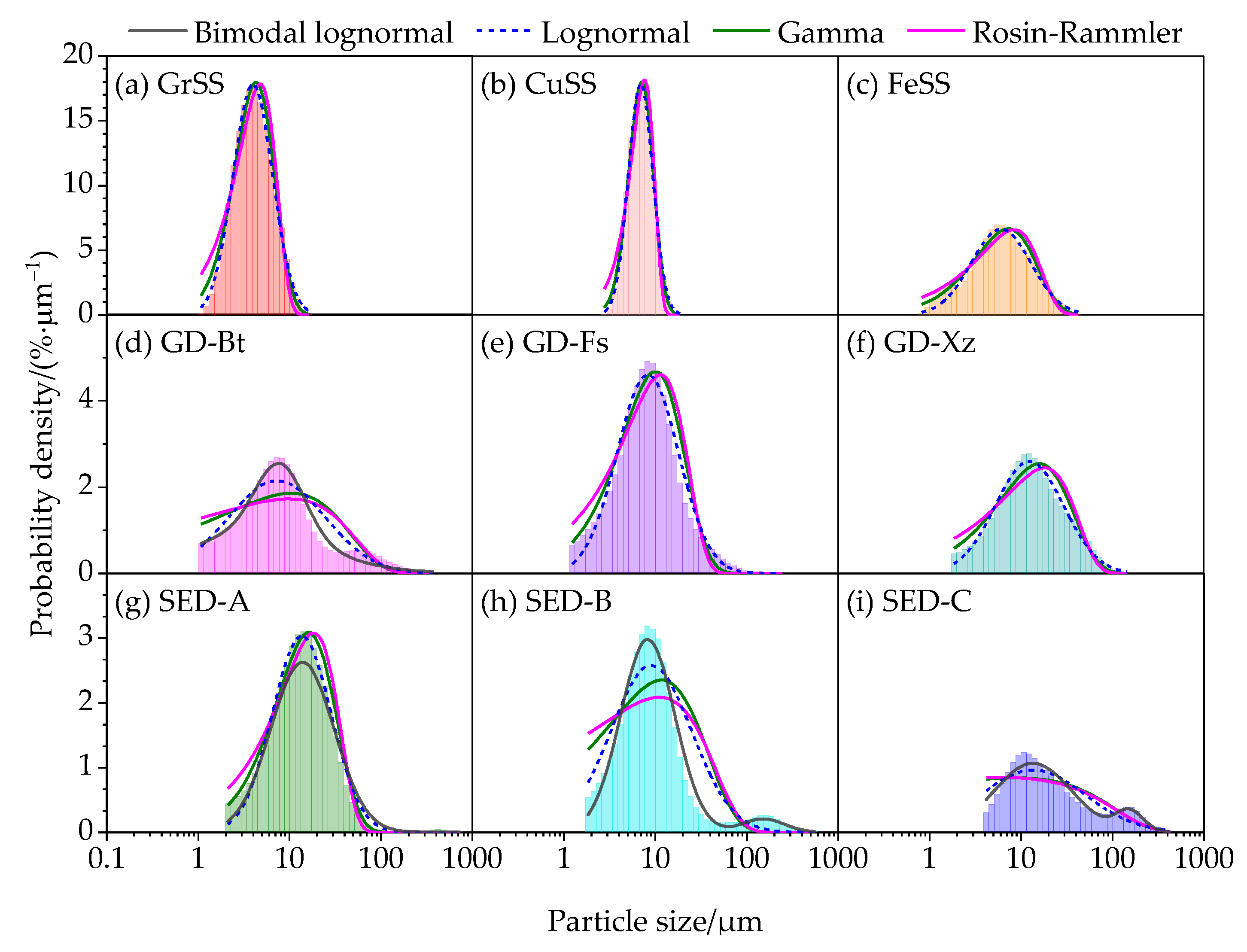
3.1. PSDs of Aerosol Particles
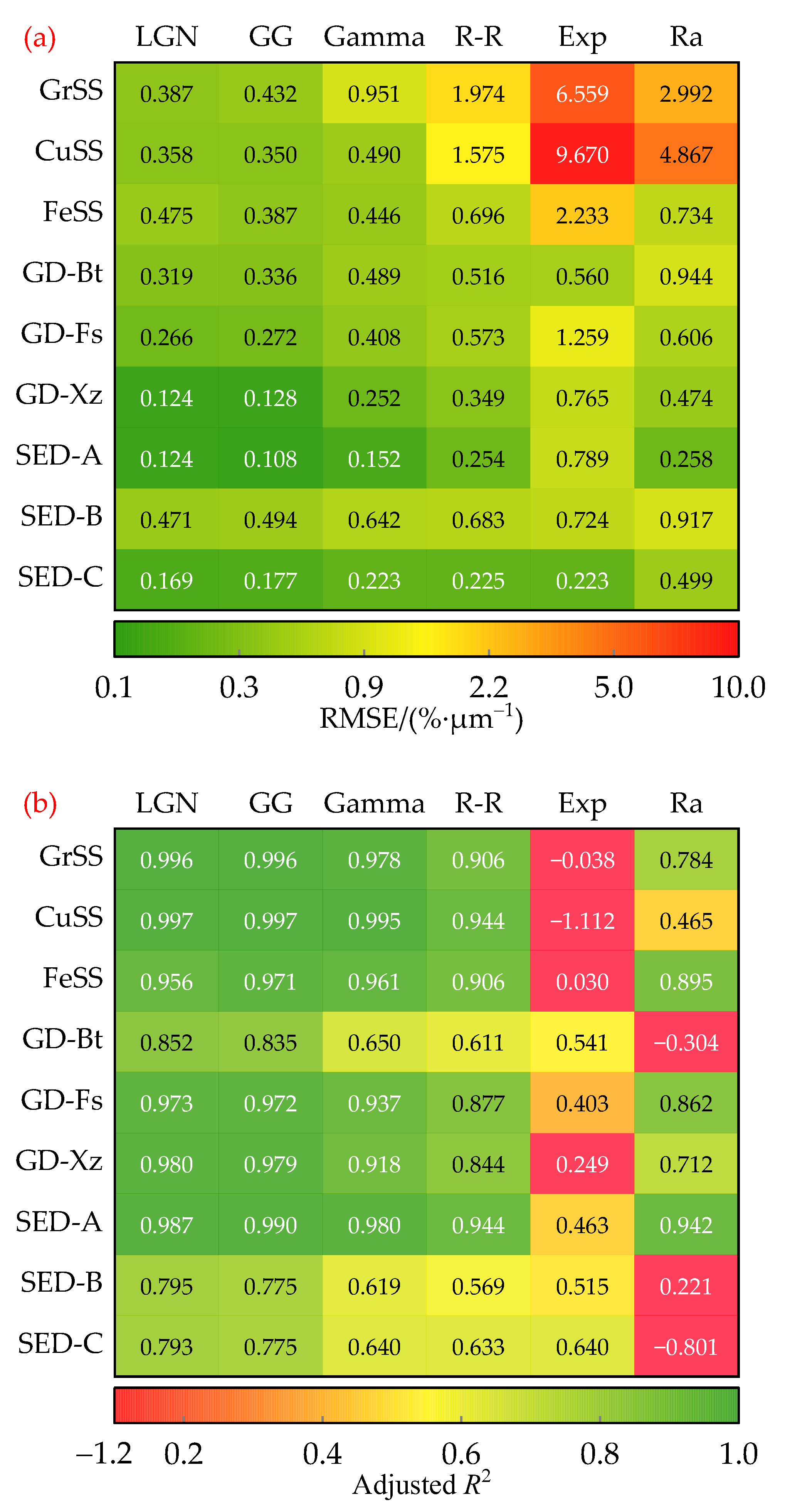
3.2. Goodness of Fit of PSD Functions
3.3. Extinction Coefficients of Aerosol Particles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Zhang, J.; Wu, S.; Gao, J.; Hao, Z.; Li, C. Study on laser scattering depolarization characteristics of typical aerosol particles. Opt. Commun. 2022, 518, 128183. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Mohsin, M.; Ali, S.M.Z. Survey and technological analysis of laser and its defense applications. Def. Technol. 2021, 17, 583–592. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Applications of lasers for tactical military operations. IEEE Access 2017, 5, 20736–20753. [Google Scholar] [CrossRef]
- Verhoeven, G. Imaging the invisible using modified digital still cameras for straightforward and low-cost archaeological near-infrared photography. J. Archaeol. Sci. 2008, 35, 3087–3100. [Google Scholar] [CrossRef]
- Scafutto, R.; de Souza Filho, C. Detection of methane plumes using airborne midwave infrared (3–5 µm) hyperspectral data. Remote Sens. 2018, 10, 1237. [Google Scholar] [CrossRef]
- Gao, L.; Chen, H.; Wang, F.; Yang, S.; Lu, C.; Ma, C.; Qi, B.; Deng, J. Study on the graphite smoke echo characteristics of pulsed laser fuze. Proc. SPIE 2020, 11562, 253–261. [Google Scholar]
- Song, C.; Cui, Y.; Liu, B. FMCW laser fuze multiple scattering model and accurate fixed-distance algorithm in a smoke environment. Sensors 2020, 20, 2604. [Google Scholar] [CrossRef]
- Zeng, J.; Bian, A.; Chen, A.; Xu, W.; Cheng, W.; Yan, S.; Wang, S.; Deng, T. A miniaturized aerosol sizing sensor using light-scattering angular spectrum. Opt. Lasers Eng. 2023, 160, 107257. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Huang, Z.; Ma, C. Fog backscattering interference suppression algorithm for FMCW laser fuze based on normalized frequency spectrum threshold. Optik 2017, 131, 188–193. [Google Scholar] [CrossRef]
- Gao, L.; Lien, F.-S.; Chen, H.; Chen, G.; Yang, S.; Deng, J. Backscattering echo intensity characteristics of laser in soil explosion dust. Sensors 2023, 23, 5638. [Google Scholar] [CrossRef] [PubMed]
- Okuda, T. Measurement of the specific surface area and particle size distribution of atmospheric aerosol reference materials. Atmos. Environ. 2013, 75, 1–5. [Google Scholar] [CrossRef]
- Zhao, X.; Hu, Y.; Gu, Y.; Chen, X.; Wang, X.; Wang, P.; Dong, X. A comparison of infrared extinction performances of bioaerosols and traditional smoke materials. Optik 2019, 181, 293–300. [Google Scholar] [CrossRef]
- Yang, S.; Chen, H.; Gao, L.; Qi, B.; Guo, P.; Deng, J. Study of spatial distribution characteristics for dust raised by vehicles in battlefield environments using CFD. IEEE Access 2021, 9, 48023–48038. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, H. Backscattering attenuation characteristics of multi-sized dust particles to pulsed laser. Optik 2019, 180, 738–744. [Google Scholar] [CrossRef]
- Fedorova, A.A.; Montmessin, F.; Rodin, A.V.; Korablev, O.I.; Määttänen, A.; Maltagliati, L.; Bertaux, J.-L. Evidence for a bimodal size distribution for the suspended aerosol particles on Mars. Icarus 2014, 231, 239–260. [Google Scholar] [CrossRef]
- Yi, B.; Hsu, C.N.; Yang, P.; Tsay, S.C. Radiative transfer simulation of dust-like aerosols: Uncertainties from particle shape and refractive index. J. Aerosol Sci. 2011, 42, 631–644. [Google Scholar] [CrossRef]
- Liang, Y.; Che, H.; Wang, H.; Zhang, W.; Li, L.; Zheng, Y.; Gui, K.; Zhang, P.; Zhang, X. Aerosols direct radiative effects combined ground-based lidar and sun-photometer observations: Cases comparison between haze and dust events in Beijing. Remote Sens. 2022, 14, 266. [Google Scholar] [CrossRef]
- Xiao, D.; Wang, N.; Shen, X.; Landulfo, E.; Zhong, T.; Liu, D. Development of ZJU high-spectral-resolution lidar for aerosol and cloud: Extinction retrieval. Remote Sens. 2020, 12, 3047. [Google Scholar] [CrossRef]
- Li, L. Optimal inversion of conversion parameters from satellite AOD to ground aerosol extinction coefficient using automatic differentiation. Remote Sens. 2020, 12, 492. [Google Scholar] [CrossRef]
- Ghasemy, A.; Rahimi, E.; Malekzadeh, A. Introduction of a new method for determining the particle-size distribution of fine-grained soils. Measurement 2019, 132, 79–86. [Google Scholar] [CrossRef]
- Ryżak, M.; Bieganowski, A. Methodological aspects of determining soil particle-size distribution using the laser diffraction method. J. Plant Nutr. Soil Sci. 2011, 174, 624–633. [Google Scholar] [CrossRef]
- Lyu, F.; Thomas, M.; Hendriks, W.H.; van der Poel, A.F.B. Size reduction in feed technology and methods for determining, expressing and predicting particle size: A review. Anim. Feed Sci. Technol. 2020, 261, 114347. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Z.; Yan, W. Identification and characteristic analysis of powder ejected from a lithium ion battery during thermal runaway at elevated temperatures. J. Hazard. Mater. 2020, 400, 123169. [Google Scholar] [CrossRef]
- Kiche, J.; Oscar, N.; George, O. On generalized gamma distribution and its application to survival data. Int. J. Stat. Probab. 2019, 8, 85–102. [Google Scholar]
- Lin, T.-H.; Chang, K.-E.; Chan, H.-P.; Hsiao, T.-C.; Lin, N.-H.; Chuang, M.-T.; Yeh, H.-Y. Potential approach for single-peak extinction fitting of aerosol profiles based on in situ measurements for the improvement of surface PM2.5 retrieval from satellite AOD product. Remote Sens. 2020, 12, 2174. [Google Scholar] [CrossRef]
- Lecompte, M.; Dumouchel, C. On the capability of the Generalized Gamma function to represent spray drop-size distribution. Part. Part. Syst. Charact. 2008, 25, 154–167. [Google Scholar] [CrossRef]
- Dumouchel, C.; Blaisot, J.B.; Ngo, V.D. On the adequacy between the laser diffraction diameter distribution and the 3-parameter Generalized-Gamma function. Chem. Eng. Sci. 2012, 79, 103–111. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Huang, Z. Research on the characteristics of fog backscattering signals for frequency modulated continuous wave laser fuze. Optik 2016, 127, 9046–9055. [Google Scholar] [CrossRef]
- Brouwers, H.J.H. Packing fraction of particles with a Weibull size distribution. Phys. Rev. E 2016, 94, 12905. [Google Scholar] [CrossRef]
- Zhang, Z.; Lan, X.; Wen, G.; Long, Q.; Yang, X. An experimental study on the particle size and shape distribution of coal drill cuttings by dynamic image analysis. Geofluids 2021, 2021, 5588248. [Google Scholar] [CrossRef]
- Ahmed, A.S.; Ali, A.A.; Alhaider, M.A. Measurement of atmospheric particle size distribution during sand/duststorm in Riyadh, Saudi Arabia. Atmos. Environ. 1987, 21, 2723–2725. [Google Scholar] [CrossRef]
- Kumar, A.; Ghosh, S.K. Size distribution analysis of wear particles in the transmission system of mining equipment. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 921–926. [Google Scholar] [CrossRef]
- Bao, J.; Zha, B.; Xu, C.; Zhang, H. Study of a laser echo in an inhomogeneous dust environment with a continuous field Monte Carlo radiative transfer model. Opt. Express 2021, 29, 17976–17996. [Google Scholar] [CrossRef]
- He, Z.; Qi, H.; Yao, Y.; Ruan, L. An effective inversion algorithm for retrieving bimodal aerosol particle size distribution from spectral extinction data. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 117–127. [Google Scholar] [CrossRef]
- Li, T.; Mu, T.; Liu, G.; Yang, X.; Zhu, G.; Shang, C. A method of soil moisture content estimation at various soil organic matter conditions based on soil reflectance. Remote Sens. 2022, 14, 2411. [Google Scholar] [CrossRef]
- Mitra, S.; Ahmad, A.; Biswas, S.; Das, A.K. A machine learning approach to predict the structural and magnetic properties of Heusler alloy families. Comput. Mater. Sci. 2023, 216, 111836. [Google Scholar] [CrossRef]
- Turner, R.E.; Eitner, P.G.; Leonard, C.D.; Snyder, D.G. Battlefield Environment Obscuration Handbook: Volume I; ADA102822; Science Applications Inc.: Ann Arbor, MI, USA, 1980. [Google Scholar]
- Horvath, H. Spectral extinction coefficients of rural aerosol in southern Italy—A case study of cause and effect of variability of atmospheric aerosol. J. Aerosol Sci. 1996, 27, 437–453. [Google Scholar] [CrossRef]
- Jung, C.H.; Kim, Y.P. Theoretical study on the change of the particle extinction coefficient during the aerosol dynamic processes. J. Aerosol Sci. 2008, 39, 904–916. [Google Scholar] [CrossRef]
- Louedec, K.; Dagoret-Campagne, S.; Urban, M. Ramsauer approach to Mie scattering of light on spherical particles. Phys. Scr. 2009, 80, 35403. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; Dover Publications, Inc.: New York, NY, USA, 1981. [Google Scholar]
- Mätzler, C. MATLAB Functions for Mie Scattering and Absorption; Institut für Angewandte Physik: Bern, Switzerland, 2002. [Google Scholar]
- Wiscombe, W.J. Improved Mie scattering algorithms. Appl. Opt. 1980, 19, 1505–1509. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, M.D.; Bui, K.T.T.; Prakash, I.; Chapi, K.; Bui, D.T. A novel artificial intelligence approach based on Multi-layer Perceptron Neural Network and Biogeography-based Optimization for predicting coefficient of consolidation of soil. Catena 2019, 173, 302–311. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Meng, Z.; Yang, P.; Kattawar, G.W.; Bi, L.; Liou, K.N.; Laszlo, I. Single-scattering properties of tri-axial ellipsoidal mineral dust aerosols: A database for application to radiative transfer calculations. J. Aerosol Sci. 2010, 41, 501–512. [Google Scholar] [CrossRef]
- Querry, M.R. Optical Constants; Defense Technical Information Center: Kansas City, MO, USA, 1985. [Google Scholar]
- Fu, Q.; Thorsen, T.J.; Su, J.; Ge, J.M.; Huang, J.P. Test of Mie-based single-scattering properties of non-spherical dust aerosols in radiative flux calculations. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1640–1653. [Google Scholar] [CrossRef]
- Yan, J.; Wang, F.; Li, Y.; Liu, H.; Gao, Y.; Li, Z. Research on the Effect of Extinction Characteristics of Coal Dust on Visibility. ACS Omega 2022, 7, 28293–28303. [Google Scholar] [CrossRef] [PubMed]






| Classification | Wavelength Range/µm | Typical Laser Wavelength/µm | |
|---|---|---|---|
| Ultraviolet (UV) | 0.249~0.38 | 0.249 | |
| Visible light (VIS) | 0.38~0.75 | 0.532, 0.694 | |
| Infrared (IR) | Near-infrared (NIR) | 0.75~1.4 | 0.905, 1.06 |
| Short-wave infrared (SWIR) | 1.4~3 | 1.55, 2 | |
| Mid-wave infrared (MWIR) | 3~6 | 4.6 | |
| Long-wave infrared (LWIR) | 6~12 | 10.6 | |
| Function Name | Probability Density Function | Scale Parameter | Shape Parameter | Shape or Location Parameter |
|---|---|---|---|---|
| Generalized Gamma | ||||
| Gamma | ||||
| Rosin–Rammler | ||||
| Exponential | ||||
| Rayleigh | ||||
| Lognormal |
| Sample | Characteristic | /µm | /µm | /µm | /µm | /µm | Span |
|---|---|---|---|---|---|---|---|
| GrSS | Unimodal | 5.87 | 5.56 | 2.70 | 5.09 | 9.16 | 1.27 |
| CuSS | Unimodal | 8.82 | 6.95 | 5.12 | 7.60 | 10.96 | 0.77 |
| FeSS | Unimodal | 15.17 | 10.63 | 4.07 | 10.42 | 22.42 | 1.76 |
| GD-Bt | Bimodal | 11.56, 88.58 | 69.71 | 6.74 | 49.84 | 168.81 | 3.25 |
| GD-Fs | Unimodal | 13.25 | 26.36 | 5.71 | 14.85 | 57.43 | 3.48 |
| GD-Xz | Unimodal | 44.94 | 32.82 | 8.69 | 26.26 | 66.54 | 2.20 |
| SED-A | Bimodal | 26.11, 517.20 | 70.34 | 9.10 | 23.14 | 271.85 | 11.35 |
| SED-B | Bimodal | 13.25, 200.00 | 106.57 | 7.20 | 63.60 | 261.35 | 4.00 |
| SED-C | Bimodal | 34.25, 174.62 | 112.28 | 14.10 | 104.43 | 226.48 | 2.03 |
| Aerosol Particle | Lognormal | Generalized Gamma | Gamma | Rosin–Rammler |
|---|---|---|---|---|
| GrSS | (1.63, 0.50) | (138.49, 0.17, 2.23 × 10−12) | (4.91, 1.10) | (2.57, 5.78) |
| CuSS | (2.03, 0.31) | (137.65, 0.28, 1.72 × 10−7) | (11.47, 0.68) | (3.91, 8.22) |
| FeSS | (2.36, 0.75) | (7.140.4, 0.550.1, 0.330.8) | (2.63, 4.47) | (1.88, 12.53) |
| GD-Bt | (3.46, 1.22) | [139.63, 0.07, (2.90 × 10−29)0.01] | (1.36, 29.22) | (1.20, 43.45) |
| GD-Fs | (2.71, 0.77) | [136.580.1, 0.11, (1.99 × 10−18)0.8] | (2.54, 6.49) | (1.83, 17.60) |
| GD-Xz | (3.25, 0.86) | (139.66, 0.10, 1.40 × 10−20) | (2.17, 13.53) | (1.66, 31.57) |
| SED-A | (3.15, 0.74) | [17.46, 0.35, (6.36 × 10−3)0.6] | (2.73, 9.35) | (1.92, 27.02) |
| SED-B | (3.24, 1.02) | [138.26, 0.09, (1.73 × 10−24)0.6] | (1.61, 19.06) | (1.29, 35.26) |
| SED-C | (4.30, 1.30) | [141.03, 0.07, (1.68 × 10−31)0.7] | (1.10, 89.38) | (1.05, 102.6) |
| Aerosol Particle | |||||
|---|---|---|---|---|---|
| GD-Bt | 0.25 | 2.45 | 0.62 | 4.48 | 1.76 |
| SED-A | 1.00 | 3.26 | 0.80 | 6.25 | 0.01 |
| SED-B | 0.54 | 2.58 | 0.68 | 5.30 | 0.52 |
| SED-C | 0.55 | 3.53 | 0.96 | 5.16 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Chen, H.; Chen, G.; Deng, J. Particle Size Distributions and Extinction Coefficients of Aerosol Particles in Land Battlefield Environments. Remote Sens. 2023, 15, 5038. https://doi.org/10.3390/rs15205038
Gao L, Chen H, Chen G, Deng J. Particle Size Distributions and Extinction Coefficients of Aerosol Particles in Land Battlefield Environments. Remote Sensing. 2023; 15(20):5038. https://doi.org/10.3390/rs15205038
Chicago/Turabian StyleGao, Lijuan, Huimin Chen, Guang Chen, and Jiahao Deng. 2023. "Particle Size Distributions and Extinction Coefficients of Aerosol Particles in Land Battlefield Environments" Remote Sensing 15, no. 20: 5038. https://doi.org/10.3390/rs15205038
APA StyleGao, L., Chen, H., Chen, G., & Deng, J. (2023). Particle Size Distributions and Extinction Coefficients of Aerosol Particles in Land Battlefield Environments. Remote Sensing, 15(20), 5038. https://doi.org/10.3390/rs15205038




