Optimized Deep Learning Model for Flood Detection Using Satellite Images
Abstract
:1. Introduction
- Cubic chaotic map weighted based k-means clustering is proposed for the segmentation process.
- Hybrid classification combining CNN and deep ResNet is proposed with a CHHSSO-based training process via tuning the optimal weights of the hybrid model.
2. Literature Review
- (1)
- Training an ensemble method of multiple U-Net frameworks through a high-confidence hand-labeled dataset given;
- (2)
- Filtering out poorly generated labels;
- (3)
- Combining the generated labels with an early-obtainable, strong-confidence hand-labeled dataset.
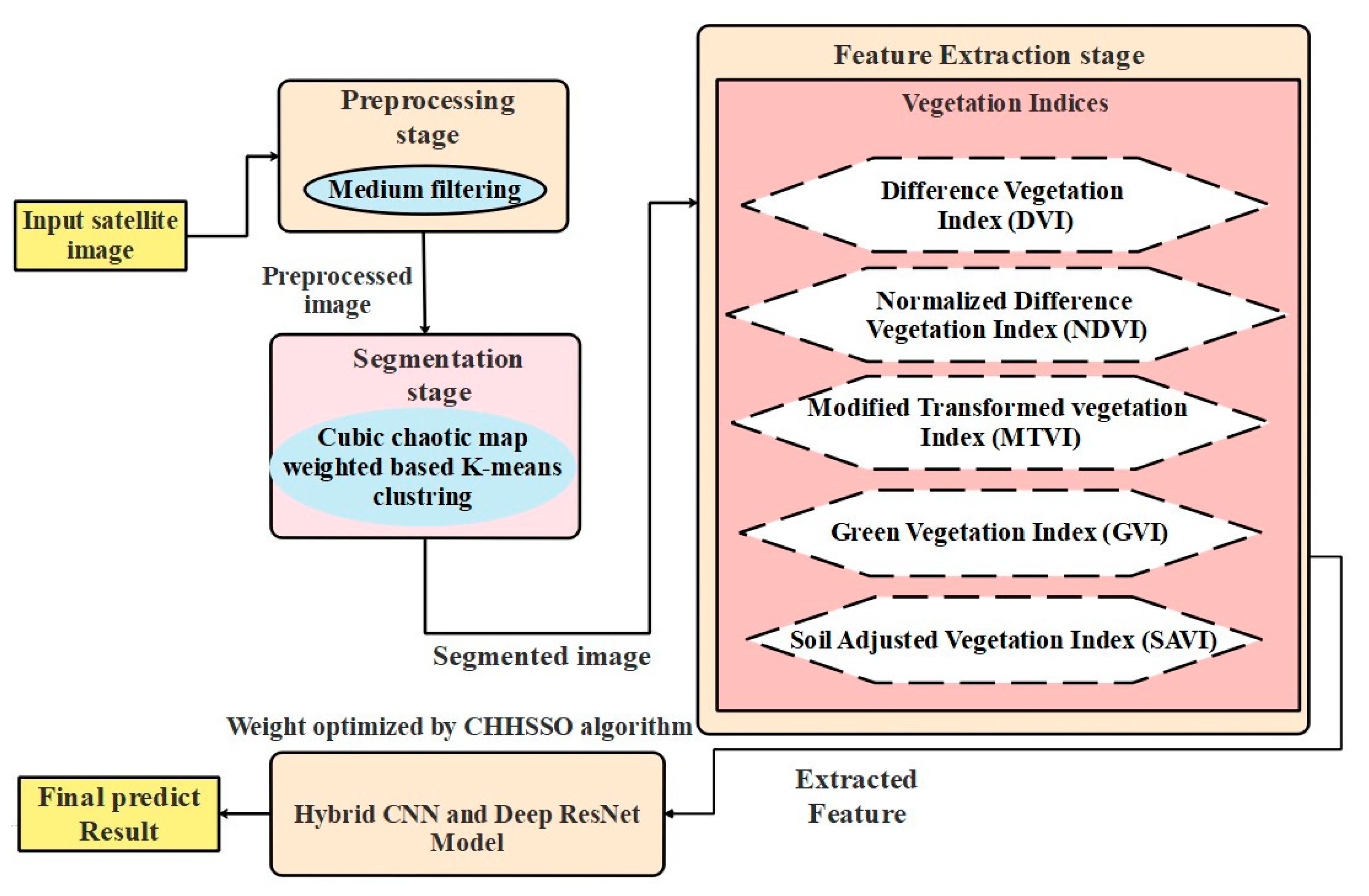
3. Proposed Deep Hybrid Model for Flood Prediction with CHHSSO-Based Training (DHMFP) Algorithm
3.1. Dataset Description
3.2. Preprocessing: Input Image
3.3. Cubic Chaotic Map Weighted Based k-Means Clustering for Segmentation
3.4. Vegetation Index-Based Feature Extraction
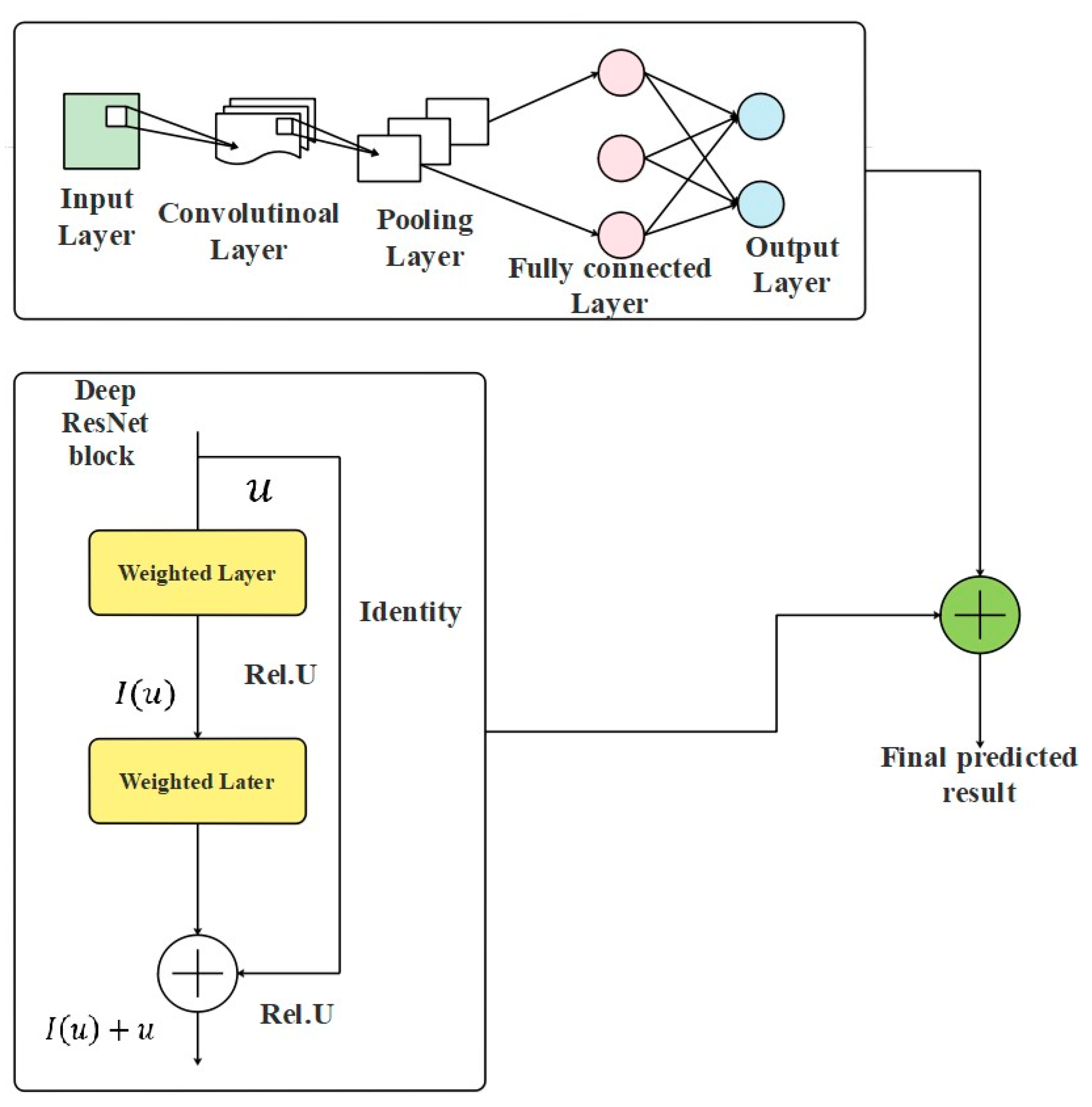
3.5. Hybrid Model for Flood Prediction
3.5.1. CNN Model
3.5.2. Deep ResNet Model
4. Training Phase: Combined Harris Hawks Shuffled Shepherd Optimization (CHHSSO) Algorithm
4.1. Proposed Exploration Phase
4.2. Proposed Transition from Exploration to Exploitation
4.3. Exploitation Phase
- soft besiege;
- hard besiege;
- soft besiege having progressive fast dives;
- hard besiege having progressive fast dives.
4.3.1. Soft Besiege
4.3.2. Hard Besiege
4.3.3. Soft Besiege: Having Progressive Fast Dives
4.3.4. Hard Besiege Having Progressive Fast Dives
| Algorithm 1: Pseudocode of CHHSSO |
| Input: and |
| Output: and (Optimal weights) |
| Initialize: |
| While end step is not reached do |
| Compute hawks’ fitness value |
| Assign as prey position (best position) |
| for each hawk do |
| Update jump strength as well as initial energy |
| , |
| Update as per the proposed Equation (17) with logistic map randomization |
| Update vector position using Equation (13), with new calculation |
| if then |
| if and |
| Update vector position by Equation (19) |
| end if |
| end if |
| else if and then |
| Update vector position by Equation (22) as per CHHSSO |
| else if and |
| Update vector position by Equation (26) |
| else if and then |
| Update vector position by Equation (27) |
| end if |
| end if |
| end if |
| end for |
| end while |
| Return |
5. Results and Discussion
- type of network: CNN and deep ResNet models.
- learning percentage: 60, 70, 80, and 90.
- Bands: coastal aerosol, blue, green, red, vegetation red edge, vegetation red edge, vegetation red edge, NIR, vegetation red edge, water vapour, SWIR-curris, SWIR, and SWIR.
- Batch parameter: 32.
- Epochs parameter: 50.
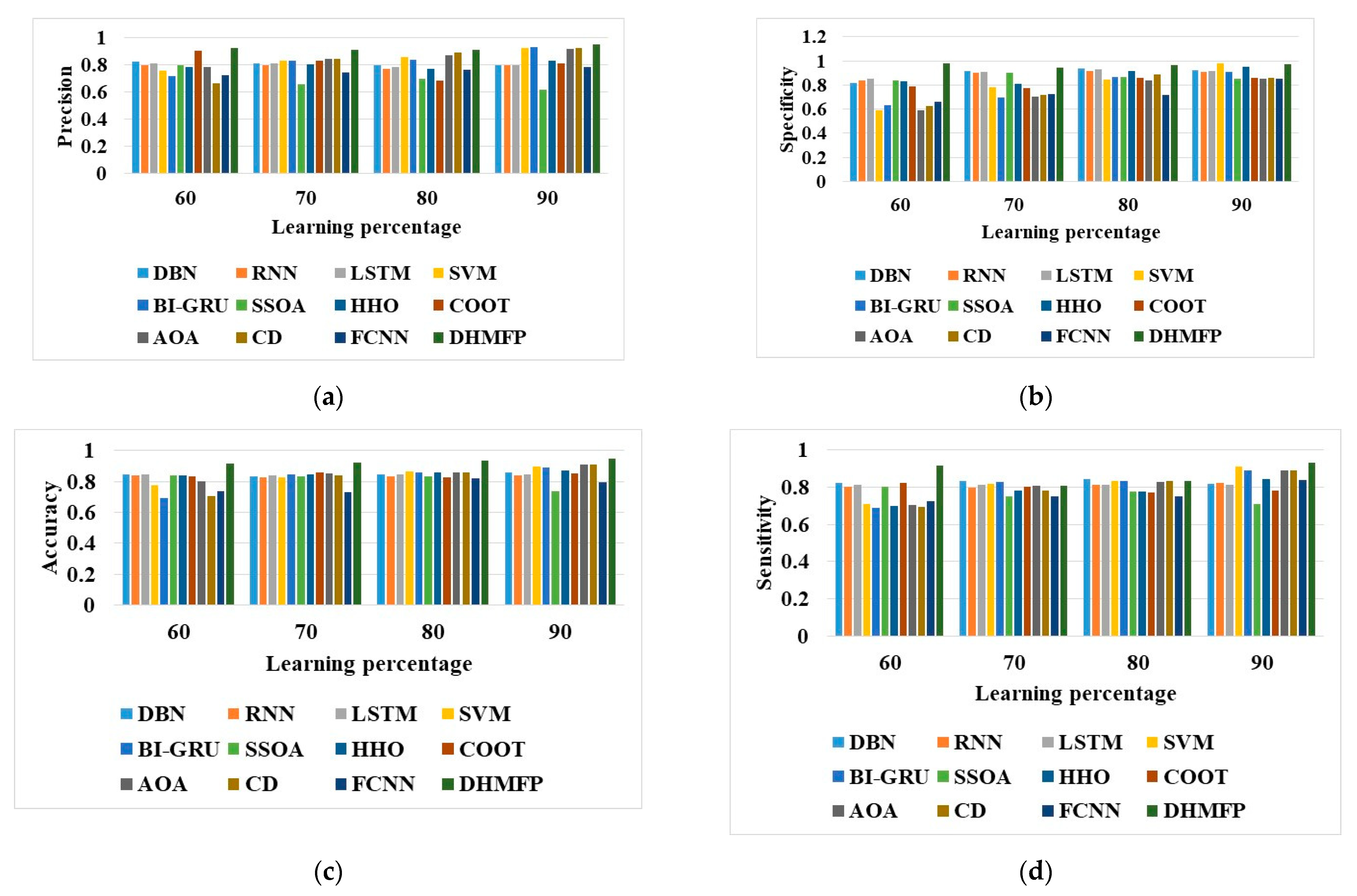
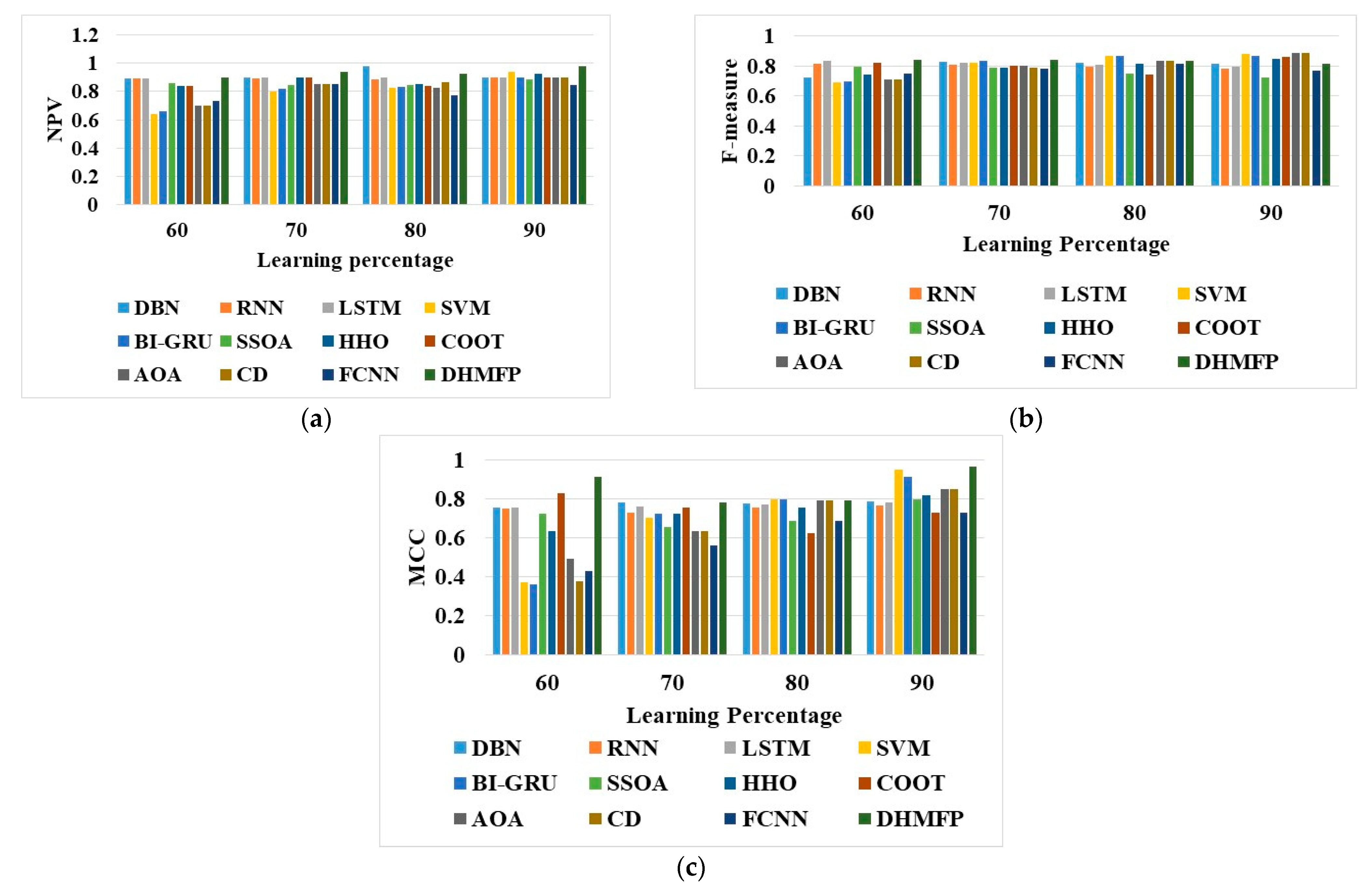
5.1. Analysis of DHMFP with Regard to Positive Measures
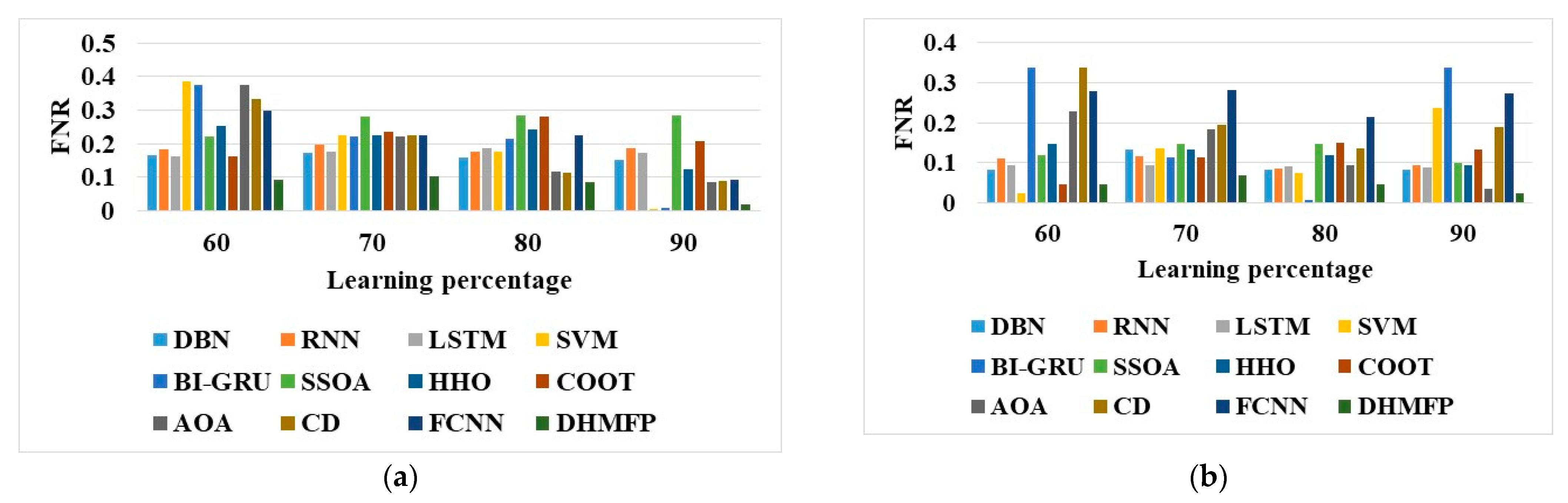
5.2. Analysis of DHMFP with Regard to Negative Measures
5.3. Analysis of DHMFP with Regard to Other Measures
5.4. Ablation Study DHMFP
5.5. Prediction Error Statistics on the Performance of DHMFP over Traditional Systems
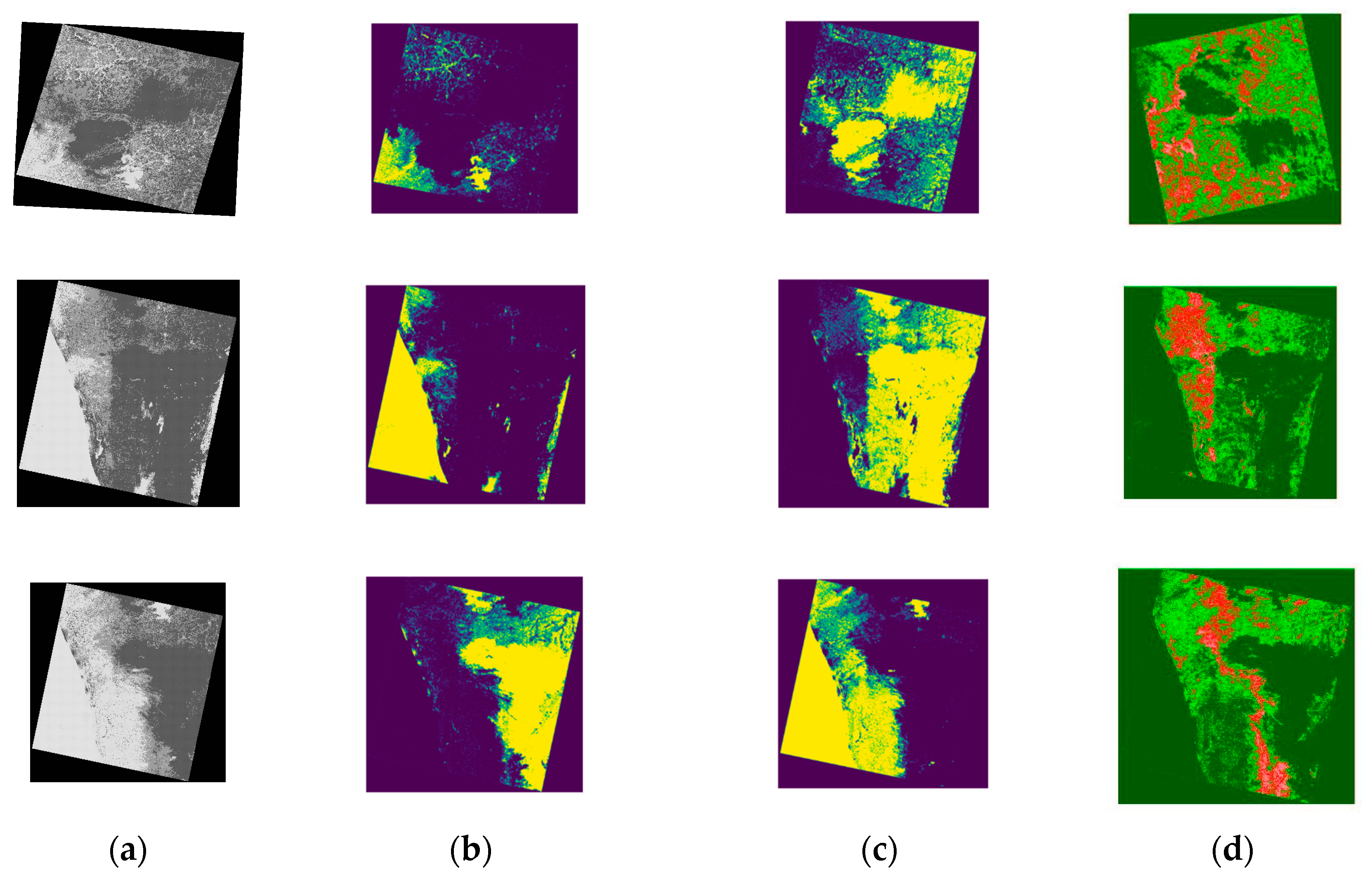
5.6. Assessment of Segmentation Performance
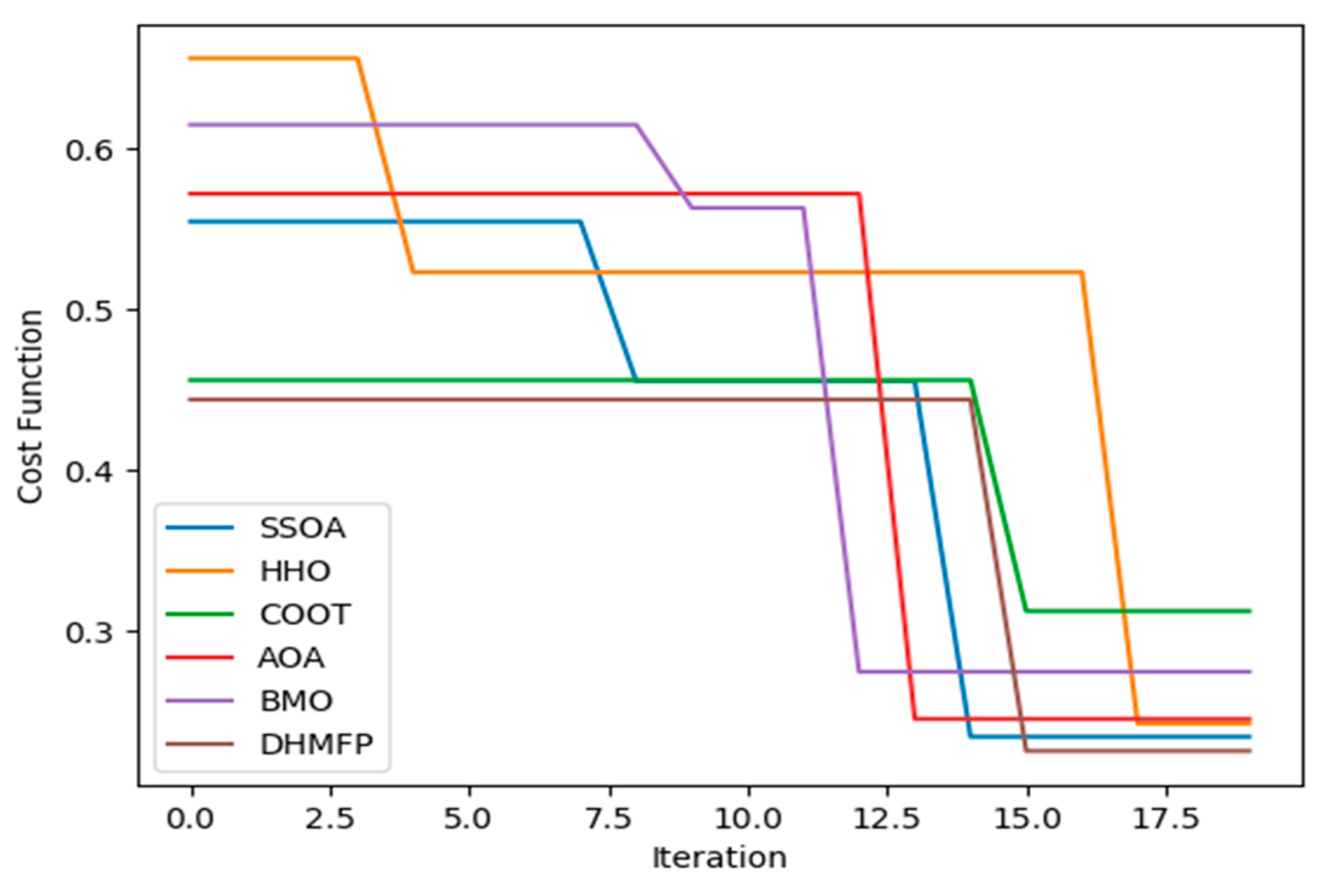
5.7. Convergence Analysis
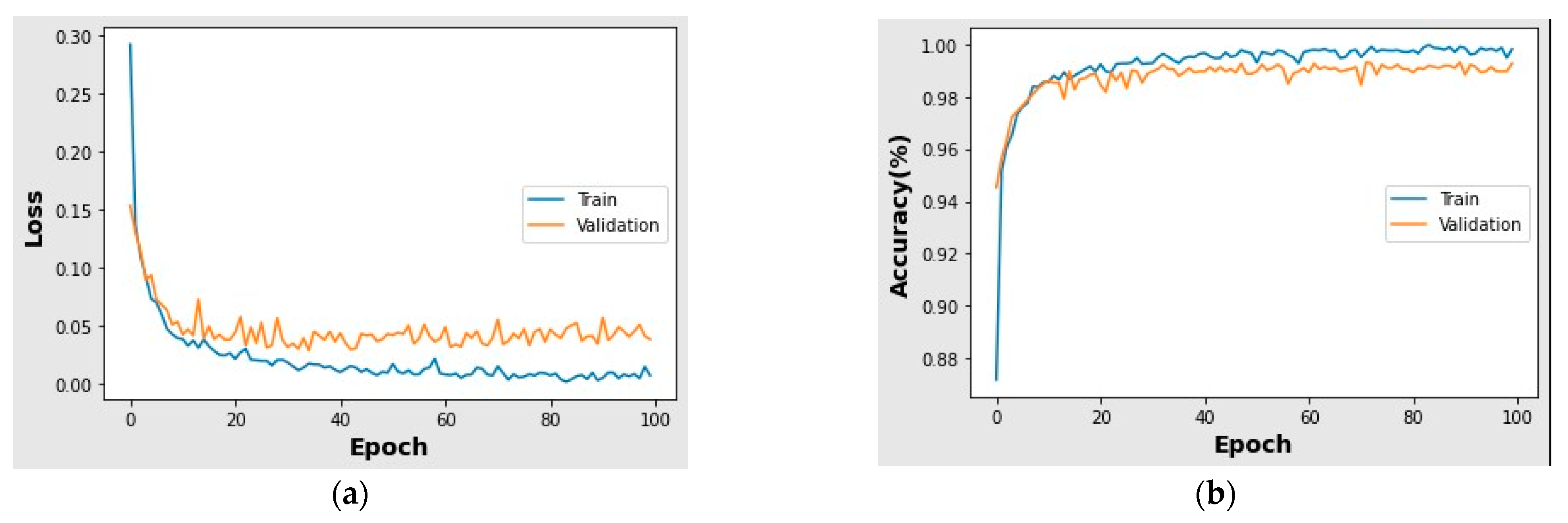
5.8. Analysis of Training and Validation Losses
5.9. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luis, C.; Alvarez, M.; Puertas, J. Estimation of flood-exposed population in data-scarce regions combining satellite imagery and high resolution hydrological-hydraulic modelling: A case study in the Licungo basin (Mozambique). J. Hydrol. Reg. Stud. 2022, 44, 101247. [Google Scholar]
- Mohammed Sarfaraz, G.A.; Siam, Z.S.; Kabir, I.; Kabir, Z.; Ahmed, M.R.; Hassan, Q.K.; Rahman, R.M.; Dewan, A. A novel framework for addressing uncertainties in machine learning-based geospatial approaches for flood prediction. J. Environ. Manag. 2023, 326, 116813. [Google Scholar]
- Roberto, B.; Isufi, E.; NicolaasJonkman, S.; Taormina, R. Deep Learning Methods for Flood Mapping: A Review of Existing Applications and Future Research Directions. Hydrol. Earth Syst. Sci. 2022, 26, 4345–4378. [Google Scholar]
- Kim, H.I.; Han, K.Y. Data-Driven Approach for the Rapid Simulation of Urban Flood Prediction. KSCE J. Civ. Eng. 2020, 24, 1932–1943. [Google Scholar] [CrossRef]
- Kim, H.I.; Kim, B.H. Flood Hazard Rating Prediction for Urban Areas Using Random Forest and LSTM. KSCE J. Civ. Eng. 2020, 24, 3884–3896. [Google Scholar] [CrossRef]
- Keum, H.J.; Han, K.Y.; Kim, H.I. Real-Time Flood Disaster Prediction System by Applying Machine Learning Technique. KSCE J. Civ. Eng. 2020, 24, 2835–2848. [Google Scholar] [CrossRef]
- Thiagarajan, K.; Manapakkam Anandan, M.; Stateczny, A.; Bidare Divakarachari, P.; Kivudujogappa Lingappa, H. Satellite image classification using a hierarchical ensemble learning and correlation coefficient-based gravitational search algorithm. Remote Sens. 2021, 13, 4351. [Google Scholar] [CrossRef]
- Jagannathan, P.; Rajkumar, S.; Frnda, J.; Divakarachari, P.B.; Subramani, P. Moving vehicle detection and classifi-cation using gaussian mixture model and ensemble deep learning technique. Wirel. Commun. Mob. Comput. 2021, 2021, 5590894. [Google Scholar] [CrossRef]
- Simeon, A.I.; Edim, E.A.; Eteng, I.E. Design of a flood magnitude prediction model using algorithmic and mathematical approaches. Int. J. Inf. Tecnol. 2021, 13, 1569–1579. [Google Scholar] [CrossRef]
- Aarthi, C.; Ramya, V.J.; Falkowski-Gilski, P.; Divakarachari, P.B. Balanced Spider Monkey Optimization with Bi-LSTM for Sustainable Air Quality Prediction. Sustainability 2023, 15, 1637. [Google Scholar] [CrossRef]
- Huynh, H.X.; Loi, T.T.T.; Huynh, T.P.; Van Tran, S.; Nguyen, T.N.T.; Niculescu, S. Predicting of Flooding in the Mekong Delta Using Satellite Images. In Context-Aware Systems and Applications, and Nature of Computation and Communication; Vinh, P., Rakib, A., Eds.; Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer: Cham, Switzerland, 2019; p. 298. [Google Scholar] [CrossRef]
- Mitchell, D.G.; Li, S.; Lindsey, D.T.; Sjoberg, W.; Zhou, L.; Sun, D. Mapping, Monitoring, and Prediction of Floods Due to Ice Jam and Snowmelt with Operational Weather Satellites. Remote Sens. 2020, 12, 1865. [Google Scholar] [CrossRef]
- Anastasia, M.; Bakratsas, M.; Andreadis, S.; Karakostas, A.; Gialampoukidis, I.; Vrochidis, S.; Kompatsiaris, I. Flood detection with Sentinel-2 satellite images in crisis management systems. In Proceedings of the 17th ISCRAM Conference, Blacksburg, VA, USA, 24–27 May 2020. [Google Scholar]
- Du, J. Satellite Flood Inundation Assessment and Forecast Using SMAP and Landsat. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6707–6715. [Google Scholar] [CrossRef] [PubMed]
- Mateo-Garcia, G.; Veitch-Michaelis, J.; Smith, L.; Oprea, S.V.; Schumann, G.; Gal, Y.; Baydin, A.G.; Backes, D. Towards global flood mapping onboard low-cost satellites with machine learning. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Sayak, P.; Ganju, S. Flood Segmentation on Sentinel-1 SAR Imagery with Semi-Supervised Learning. arXiv 2021, arXiv:2107.08369. [Google Scholar]
- Löwe, R.; Böhm, J.; Jensen, D.G.; Leandro, J.; Rasmussen, S.H. U-FLOOD—Topographic deep learning for predicting urban pluvial flood water depth. J. Hydrol. 2021, 603, 126898. [Google Scholar] [CrossRef]
- Motta, M.; de Castro Neto, M.; Sarmento, P. A mixed approach for urban flood prediction using Machine Learning and GIS. Int. J. Disaster Risk Reduct. 2021, 56, 102154. [Google Scholar] [CrossRef]
- Panahi, M.; Jaafari, A.; Shirzadi, A.; Shahabi, H.; Rahmati, O.; Omidvar, E.; Lee, S.; Bui, D.T. Deep learning neural networks for spatially explicit prediction of flash flood probability. Geosci. Front. 2021, 12, 101076. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Flood stage forecasting using machine-learning methods: A case study on the Parma River (Italy). Water 2021, 13, 1612. [Google Scholar] [CrossRef]
- Lei, X.; Chen, W.; Panahi, M.; Falah, F.; Rahmati, O.; Uuemaa, E.; Kalantari, Z.; Ferreira, C.S.; Rezaie, F.; Tiefenbacher, J.P.; et al. Urban flood modeling using deep-learning approaches in Seoul, South Korea. J. Hydrol. 2021, 601, 126684. [Google Scholar] [CrossRef]
- Drakonakis, G.I.; Tsagkatakis, G.; Fotiadou, K.; Tsakalides, P. OmbriaNet—Supervised flood mapping via convolutional neural networks using multitemporal sentinel-1 and sentinel-2 data fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2341–2356. [Google Scholar] [CrossRef]
- Anzhelika, T.K.; Kuznetsova, I.A.; Levin, E.L. Prediction of the flooding area of the northeastern Caspian Sea from satellite images. Geod. Geodyn. 2022, 14, 191–200. [Google Scholar]
- Ahad Hasan, T.; McRae, C.B.; Tavakol-Davani, H.; Goharian, E. Flood Detection in Urban Areas Using Satellite Imagery and Machine Learning. Water 2022, 14, 1140. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of flow based on a CNN-LSTM combined deep learning approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Before and after the Kerala Floods. Available online: https://earthobservatory.nasa.gov/images/92669/before-and-after-the-kerala-floods (accessed on 2 February 2023).
- Yuqin, S.; Liu, J. An improved adaptive weighted median filter algorithm. IOP Conf. Ser. J. Phys. Conf. Ser. 2019, 1187, 042107. [Google Scholar] [CrossRef]
- Saptarshi, C.; Paul, D.; Das, S.; Xu, J. Entropy Weighted Power k-Means Clustering. In Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics (AISTATS) 2020, Palermo, Italy, 26–28 August 2020; p. 108. [Google Scholar]
- Moghimi, A.; Khazai, S.; Mohammadzadeh, A. An improved fast level set method initialized with a combination of k-means clustering and Otsu thresholding for unsupervised change detection from SAR images. Arab. J. Geosci. 2017, 10, 1–8. [Google Scholar] [CrossRef]
- Ghosh, A.; Mishra, N.S.; Ghosh, S. Fuzzy clustering algorithms for unsupervised change detection in remote sensing images. Inf. Sci. 2011, 181, 699–715. [Google Scholar] [CrossRef]
- Hui, L.; Wang, X.; Fei, Z.; Qiu, M. The Effects of Using Chaotic Map on Improving the Performance of Multiobjective Evolutionary Algorithms. Hindawi Publ. Corp. Math. Probl. Eng. 2014, 2014, 924652. [Google Scholar] [CrossRef]
- Broadband Greenness. Available online: https://www.l3harrisgeospatial.com/docs/broadbandgreenness.html (accessed on 2 February 2023).
- Driss, H.; Millera, J.R.; Pattey, E.; Zarco-Tejadad, P.J.; Ian, B.S. Hyperspectral Vegetation Indices and Novel Algorithms for Predicting Green LAI of Crop Canopies: Modeling and Validation in the Context of Precision Agriculture; Elsevier Inc.: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Martinez, J.C.; De Swaef, T.; Borra-Serrano, I.; Lootens, P.; Barrero, O.; Fernandez-Gallego, J.A. Comparative leaf area index estimation using multispectral and RGB images from a UAV platform. In Proceedings of the Autonomous Air and Ground Sensing Systems for Agricultural Optimization and Phenotyping VIII, Orlando, FL, USA, 13 June 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12539, pp. 56–67. [Google Scholar]
- Zijie, J.W.; Turko, R.; Shaikh, O.; Park, H.; Das, N.; Hohman, F.; Kahng, M.; Horng, D. CNN EXPLAINER: Learning Convolutional Neural Networks with Interactive Visualization. arXiv 2020, arXiv:2004.15004v3. [Google Scholar]
- Ramayanti, S.; Nur, A.S.; Syifa, M.; Panahi, M.; Achmad, A.R.; Park, S.; Lee, C.W. Performance comparison of two deep learning models for flood susceptibility map in Beira area, Mozambique. Egypt. J. Remote Sens. Space Sci. 2022, 25, 1025–1036. [Google Scholar] [CrossRef]
- Aiden, N.; He, Z.; Wollersheim, D. Pulmonary nodule classification with deep residual networks. Int. J. Comput. Assist. Radiol. Surg. 2017, 10, 1799–1808. [Google Scholar] [CrossRef]
- Liu, J.; Liu, K.; Wang, M. A Residual Neural Network Integrated with a Hydrological Model for Global Flood Susceptibility Mapping Based on Remote Sensing Datasets. Remote Sens. 2023, 15, 2447. [Google Scholar] [CrossRef]
- Jackson, J.; Yussif, S.B.; Patamia, R.A.; Sarpong, K.; Qin, Z. Flood or Non-Flooded: A Comparative Study of State-of-the-Art Models for Flood Image Classification Using the FloodNet Dataset with Uncertainty Offset Analysis. Water 2023, 15, 875. [Google Scholar] [CrossRef]
- Hamzeh, M.A.; Alarabiat, D.; Abualigah, L.; Asghar Heidari, A. Harris hawks’ optimization: A comprehensive review of recent variants and applications. Neural Comput. Appl. 2021, 33, 8939–8980. [Google Scholar] [CrossRef]
- Ali, K.; Zaerreza, A.; Milad Hosseini, S. Shuffled Shepherd Optimization Method Simplified for Reducing the Parameter Dependency. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 15, 1397–1411. [Google Scholar] [CrossRef]
- Parsa, P.; Naderpour, H. Shear strength estimation of reinforced concrete walls using support vector regression improved by Teaching–learning-based optimization, Particle Swarm optimization, and Harris Hawks Optimization algorithms. J. Build. Eng. 2021, 44, 102593. [Google Scholar] [CrossRef]
- Murlidhar, B.R.; Nguyen, H.; Rostami, J.; Bui, X.; Armaghani, D.J.; Ragam, P.; Mohamad, E.T. Prediction of flyrock distance induced by mine blasting using a novel Harris Hawks optimization-based multi-layer perceptron neural network. J. Rock Mech. Geotech. Eng. 2021, 13, 1413–1427. [Google Scholar] [CrossRef]
| Index | Definition | Equation | |
|---|---|---|---|
| DVI [32] | This index can differentiate between vegetation and soil, but it cannot distinguish between radiance and reflectance that result from atmospheric factors or shadows. DVI is calculated in Equation (5). | (5) | |
| NDVI [32] | NDVI is robust in a variety of situations due to the normalized difference formulations it uses, together with the maximum reflectance and absorption areas of chlorophyll. The NDVI is a metric of rich, healthy vegetation that is calculated using Equation (6). | (6) | |
| MTVI [33] | By substituting the wavelength of 750 nm with 800 nm because reflectance is impacted by variations in leaf and canopy patterns, the MTVI index in Equation (7) renders TVI acceptable for LAI calculations. | (7) | |
| GVI [34] | The GVI index in Equation (8) reduces the impact of the background soil while highlighting the presence of green vegetation. In order to create new modified bands, it employs global coefficients that balance the pixel values. Where refers to thematic mapper. | (8) | |
| SAVI [32] | The SAVI index in Equation (9) is comparable to NDVI but handles the impact of soil pixels. It makes use of a canopy background adjusting factor , which depends on vegetation density and frequently needs to know how much vegetation is present. | (9) | |
| Flood Prediction without CHHSSO | Flood Prediction with Cubic Chaotic Map Weighted Based k-Means Clustering Algorithm | Flood Prediction with CHHSSO–DHMFP | |
|---|---|---|---|
| Sensitivity | 0.861 | 0.854 | 0.932 |
| FPR | 0.105 | 0.136 | 0.036 |
| NPV | 0.832 | 0.793 | 0.906 |
| Precision | 0.892 | 0.877 | 0.937 |
| F-measure | 0.859 | 0.823 | 0.869 |
| Specificity | 0.828 | 0.806 | 0.977 |
| MCC | 0.724 | 0.754 | 0.868 |
| Accuracy | 0.895 | 0.873 | 0.952 |
| FNR | 0.172 | 0.165 | 0.0858 |
| Methods | Best | Median | Standard Deviation | Worst | Mean |
|---|---|---|---|---|---|
| DBN | 0.113 | 0.057 | 0.003 | 0.113 | 0.109 |
| RNN | 0.132 | 0.072 | 0.004 | 0.132 | 0.127 |
| LSTM | 0.119 | 0.071 | 0.004 | 0.119 | 0.113 |
| SVM | 0.124 | 0.059 | 0.077 | 0.103 | 0.044 |
| Bi-GRU | 0.144 | 0.010 | 0.104 | 0.107 | 0.044 |
| SSOA | 0.170 | 0.049 | 0.022 | 0.177 | 0.134 |
| HHO | 0.131 | 0.012 | 0.035 | 0.134 | 0.079 |
| COOT | 0.153 | 0.039 | 0.019 | 0.151 | 0.128 |
| AOA | 0.123 | 0.044 | 0.067 | 0.118 | 0.044 |
| CD | 0.163 | 0.010 | 0.100 | 0.146 | 0.044 |
| FCNN | 0.226 | 0.018 | 0.043 | 0.229 | 0.176 |
| DHMFP | 0.034 | 0.086 | 0.009 | 0.033 | 0.022 |
| Performance Measures | Improved k-Means | Conventional k-Means | FCM | OmbriaNet–CNN [22] |
|---|---|---|---|---|
| Dice Score | 0.863 | 0.676 | 0.787 | N/A |
| Jaccard Coefficient | 0.889 | 0.732 | 0.739 | N/A |
| Segmentation Accuracy | 0.894 | 0.785 | 0.654 | 0.865 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stateczny, A.; Praveena, H.D.; Krishnappa, R.H.; Chythanya, K.R.; Babysarojam, B.B. Optimized Deep Learning Model for Flood Detection Using Satellite Images. Remote Sens. 2023, 15, 5037. https://doi.org/10.3390/rs15205037
Stateczny A, Praveena HD, Krishnappa RH, Chythanya KR, Babysarojam BB. Optimized Deep Learning Model for Flood Detection Using Satellite Images. Remote Sensing. 2023; 15(20):5037. https://doi.org/10.3390/rs15205037
Chicago/Turabian StyleStateczny, Andrzej, Hirald Dwaraka Praveena, Ravikiran Hassan Krishnappa, Kanegonda Ravi Chythanya, and Beenarani Balakrishnan Babysarojam. 2023. "Optimized Deep Learning Model for Flood Detection Using Satellite Images" Remote Sensing 15, no. 20: 5037. https://doi.org/10.3390/rs15205037
APA StyleStateczny, A., Praveena, H. D., Krishnappa, R. H., Chythanya, K. R., & Babysarojam, B. B. (2023). Optimized Deep Learning Model for Flood Detection Using Satellite Images. Remote Sensing, 15(20), 5037. https://doi.org/10.3390/rs15205037









