Cooperative Navigation Algorithm of Extended Kalman Filter Based on Combined Observation for AUVs
Abstract
1. Introduction
2. Theoretical Basis of Multi-AUV Cooperative Navigation
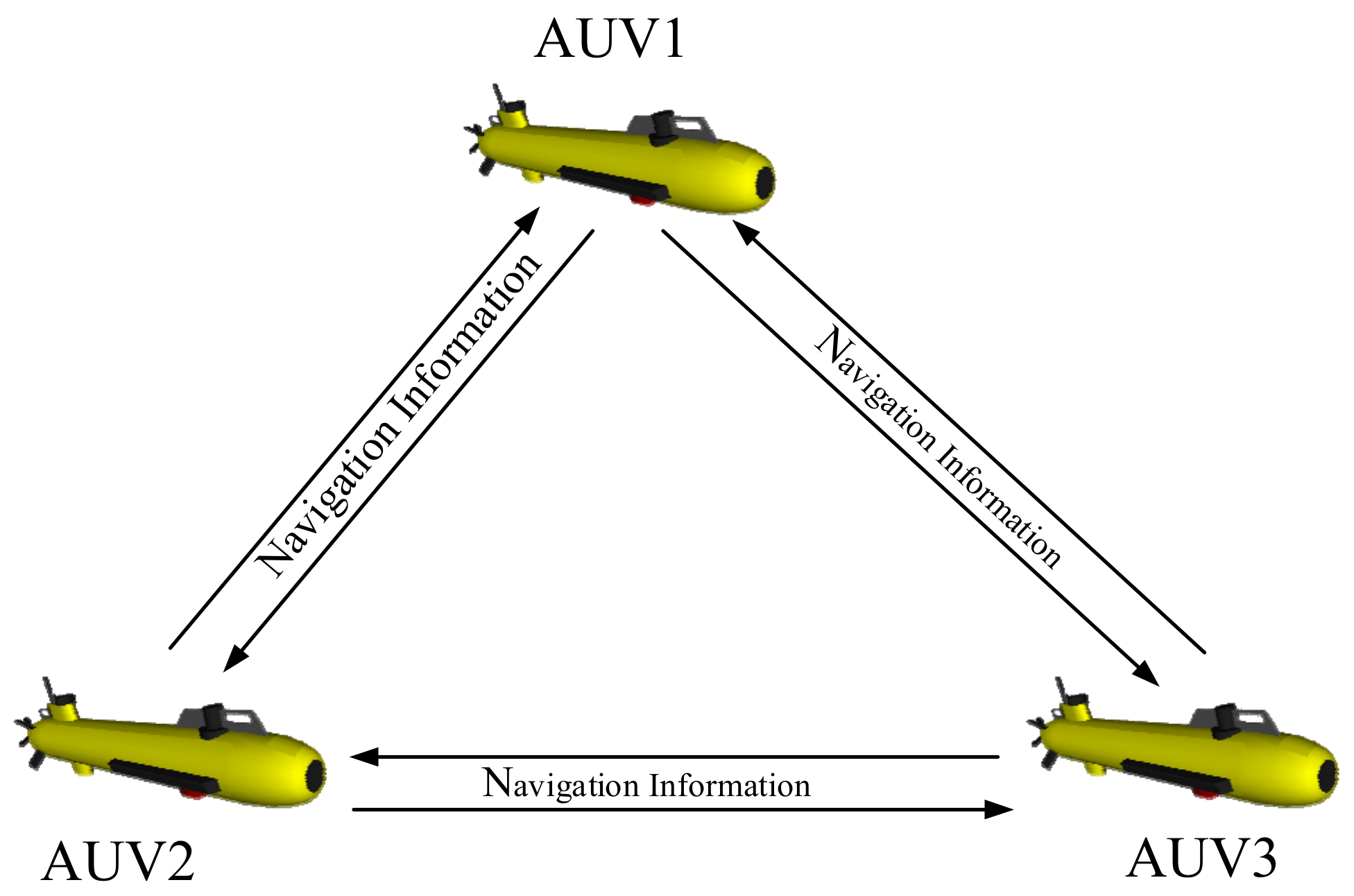
2.1. Principles of AUV Cooperative Navigation
2.2. Multi-AUV Motion Model
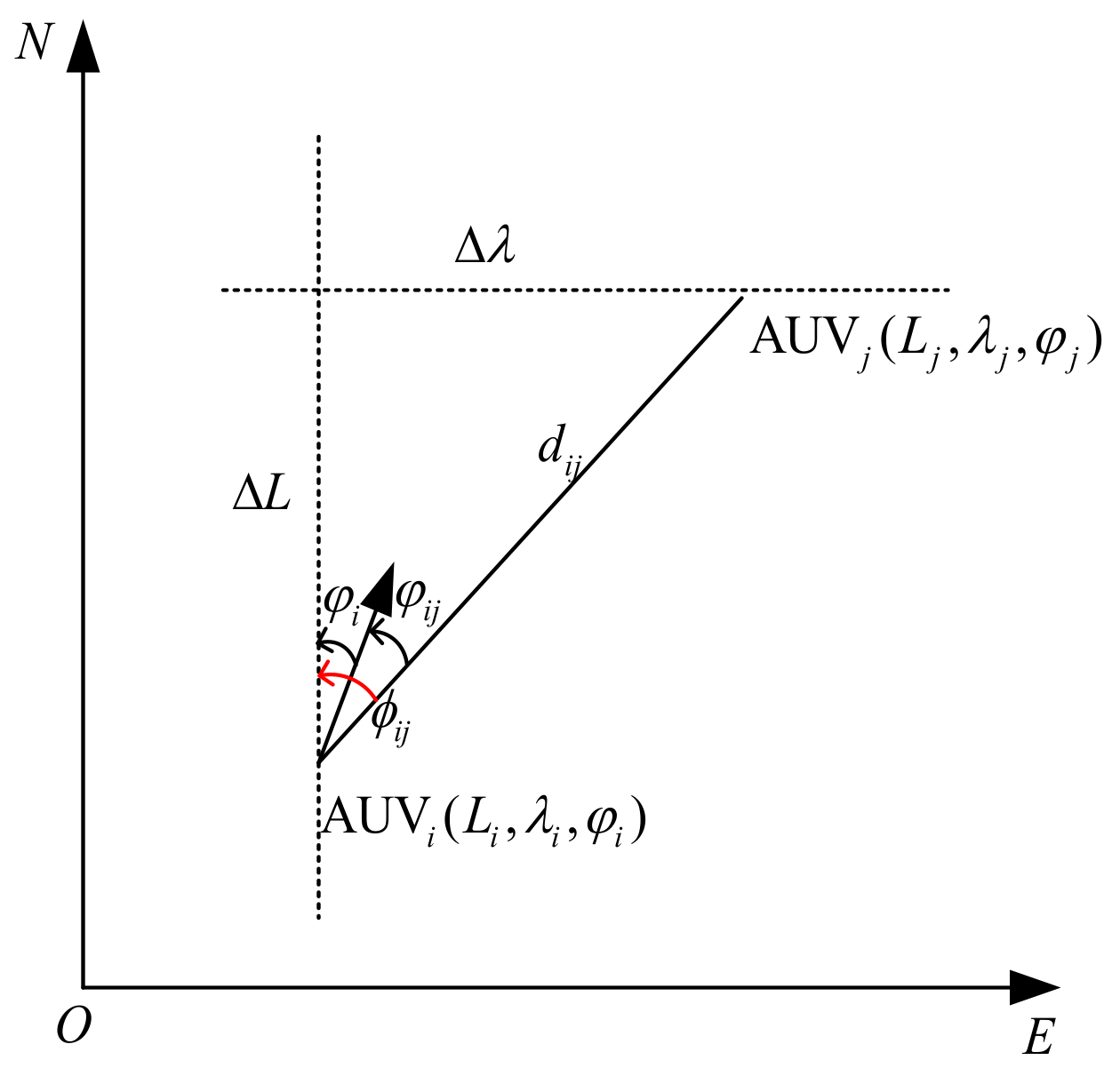
2.3. Measurement Update Model
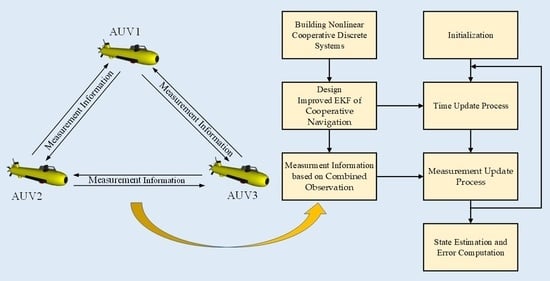
3. Derivation of EKF Based on Combined Observation of Cooperative Navigation
3.1. Scheme of Common EKF
3.2. Scheme of Improved EKF Based on Combined Observation
3.3. The Combined-Observation EKF of Multi-AUV Cooperative Navigation
4. Experimental Validation and Discussion
4.1. Simulation Test
4.1.1. Test Setting
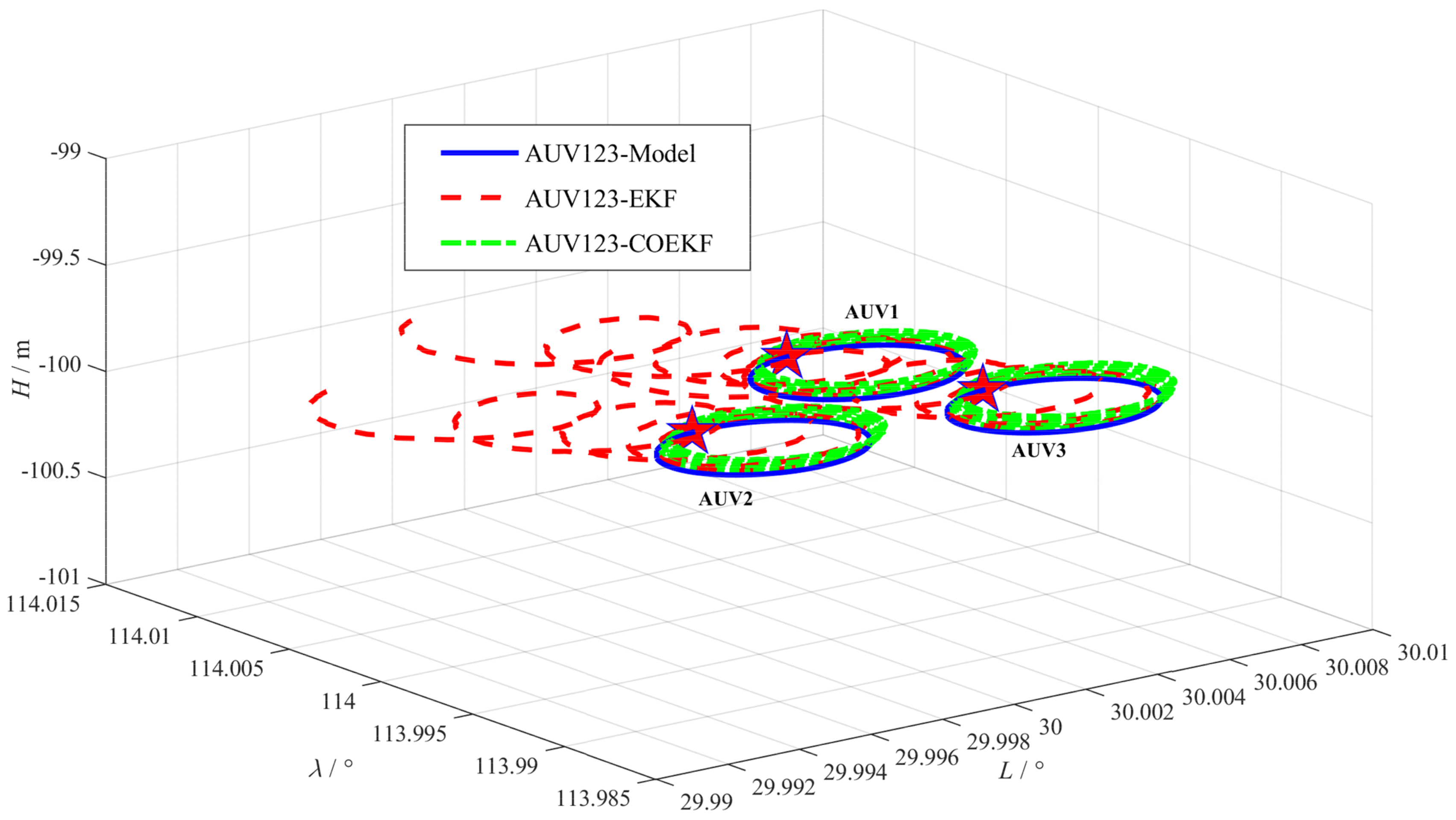
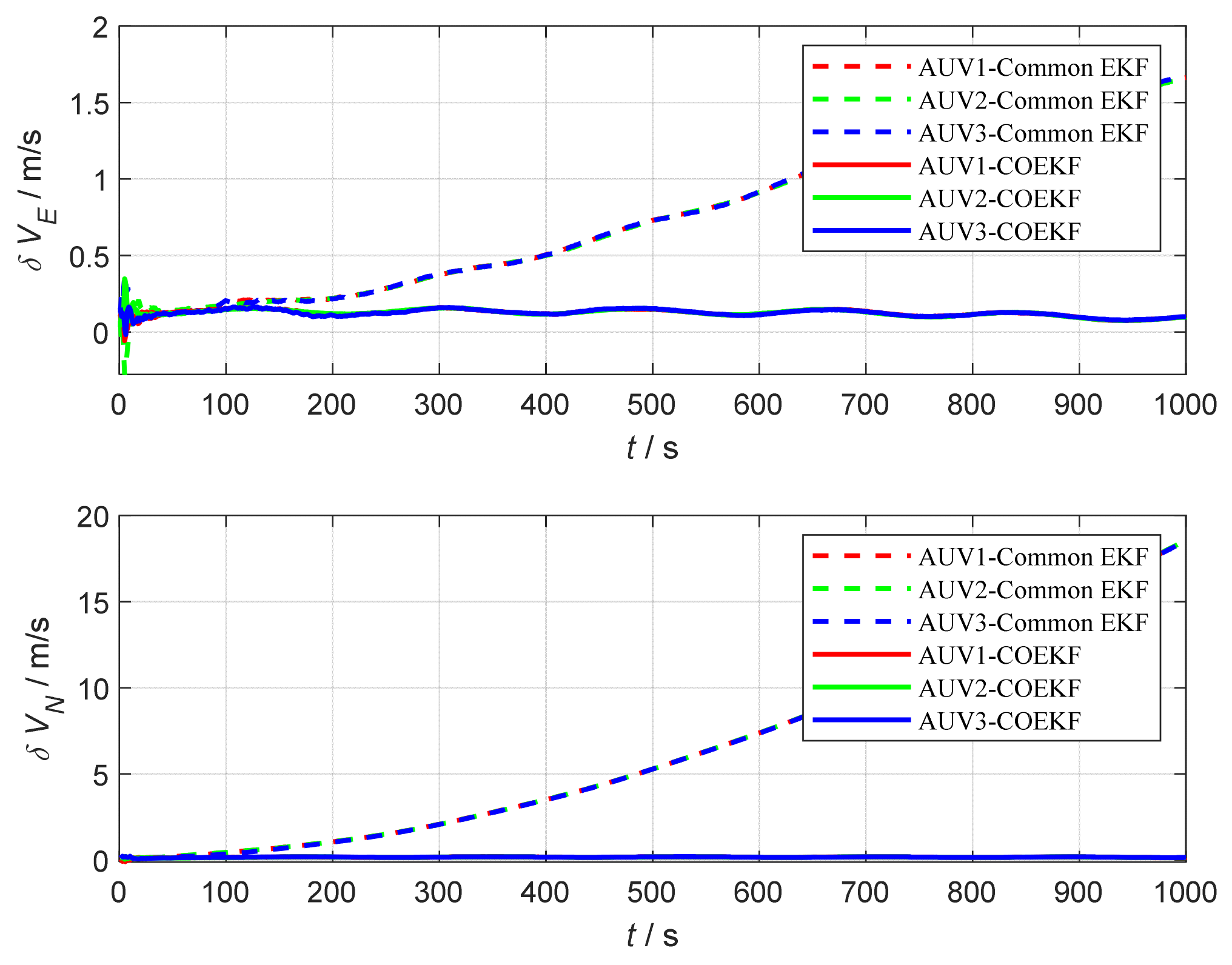
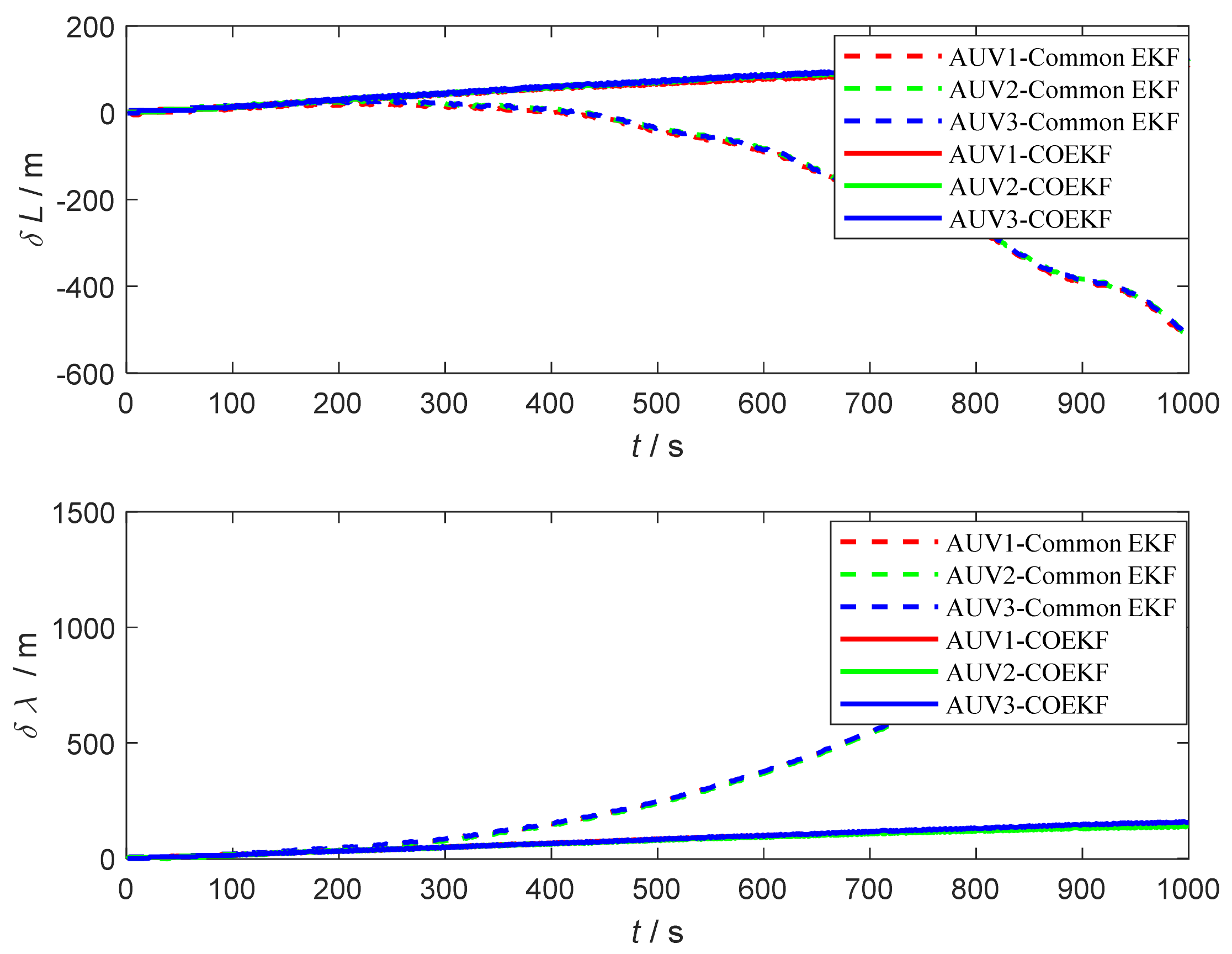
4.1.2. Results of the Test
4.2. Lake Experiments
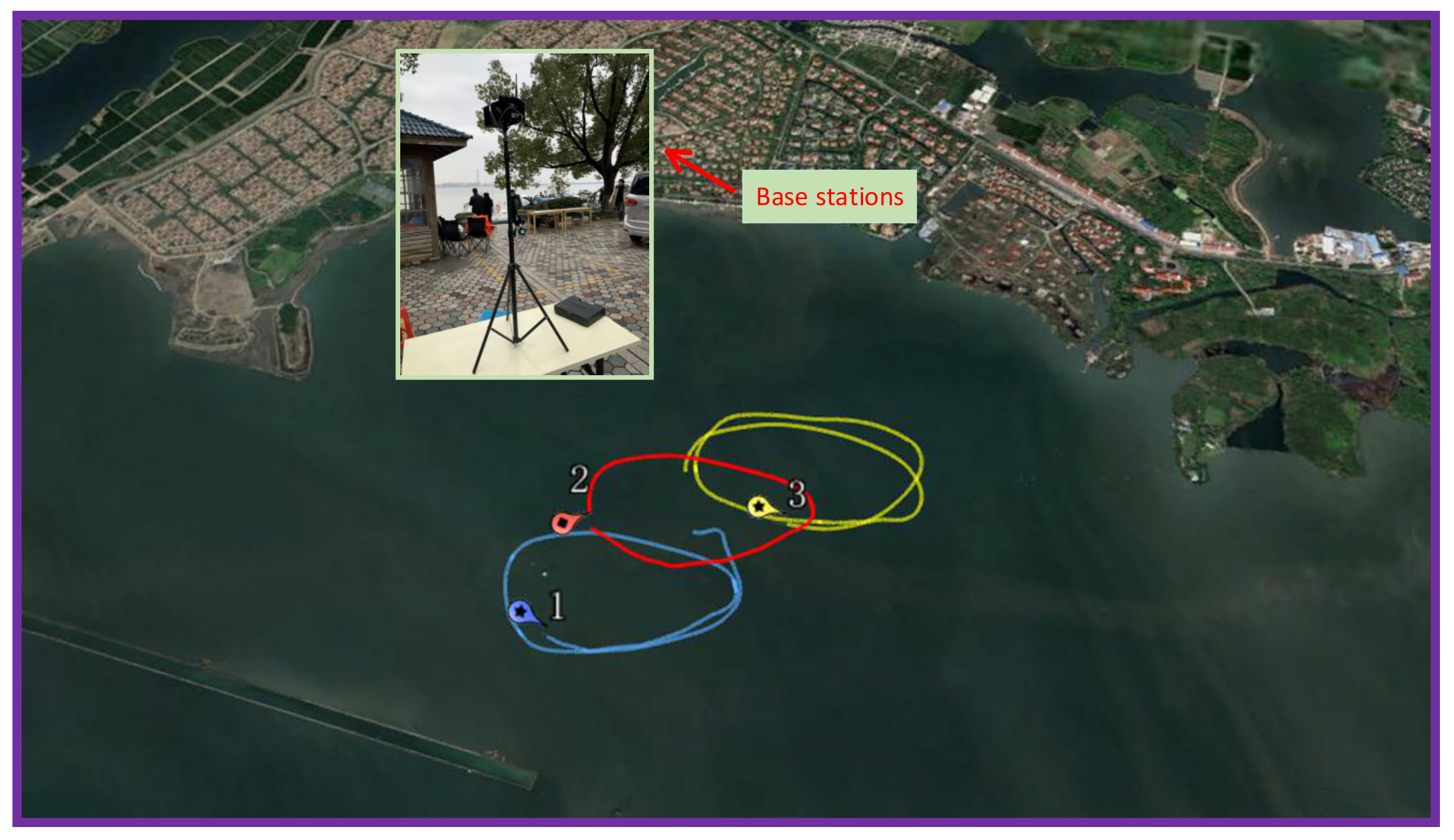
4.2.1. Experiment Setting
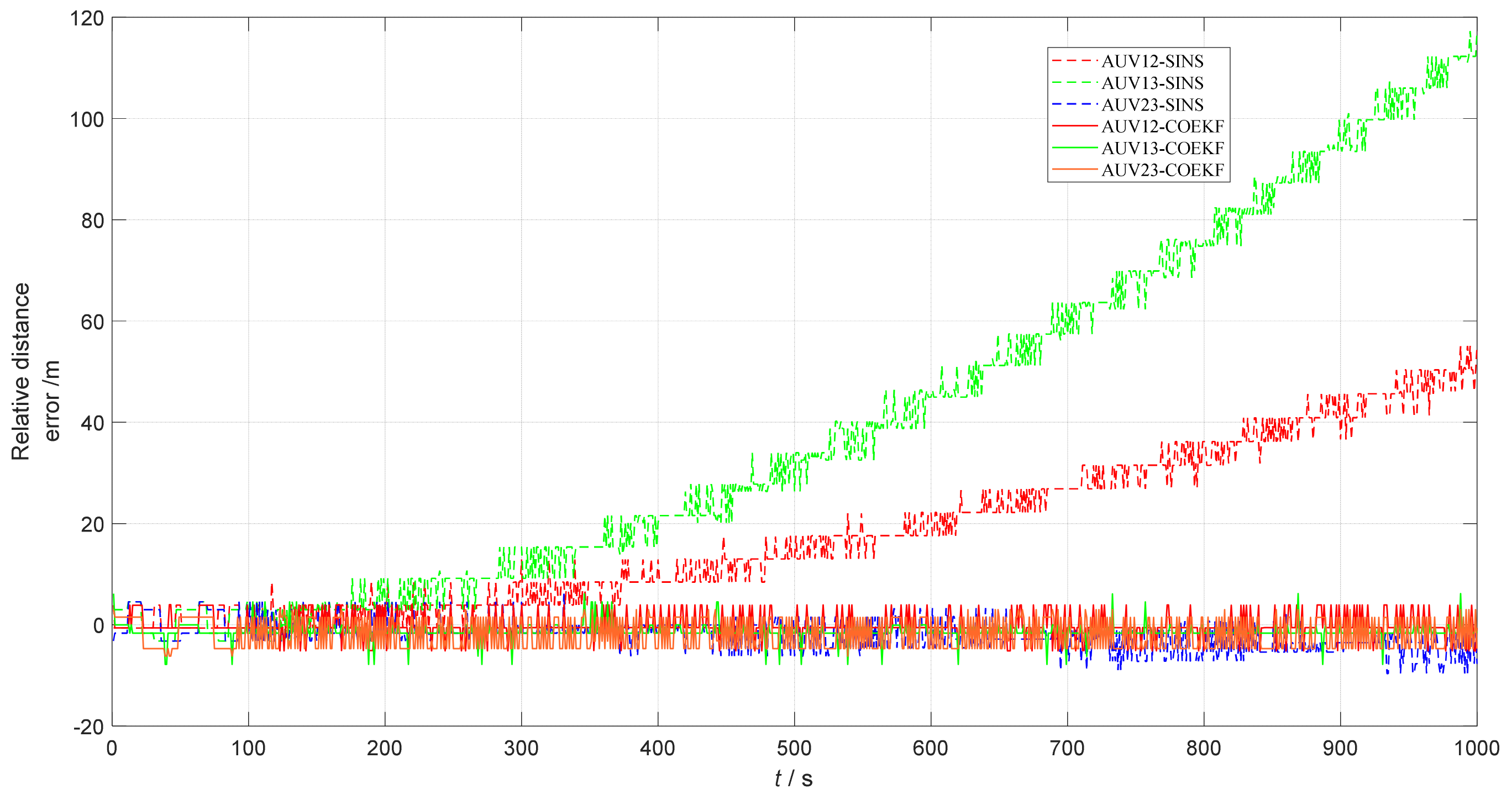
4.2.2. Results of the Lake Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AUV | autonomous underwater vehicle |
| RADNAV | radio navigation |
| GNSS | global navigation satellite system |
| SINS | strapdown inertial navigation system |
| KF | Kalman filter |
| EKF | extended Kalman filter |
| UKF | unscented Kalman filter |
| COEKF | combined-observation EKF |
| RTK | real-time kinematic |
| DVL | Doppler velocity log |
| TAN | terrain-assisted navigation |
| MCP | magnetic compass pilot |
| 2D | two-dimensional |
| 3D | three-dimensional |
References
- Ma, X.; Liu, X.; Li, C.; Liu, J.; Wu, X. A novel Rauch–Tung–Streibel smoothing scheme based on the factor graph for auto omous underwater vehicles. Rev. Sci. Instrum. 2020, 91, 075109. [Google Scholar] [CrossRef] [PubMed]
- Villa, J.; Aaltonen, J.; Virta, S.; Koskinen, K.T. A Co-Operative Autonomous Offshore System for Target Detection Using Multi-Sensor Technology. Remote Sens. 2020, 12, 4106. [Google Scholar] [CrossRef]
- Ross, J.; Lindsay, J.; Gregson, E.; Moore, A.; Patel, J.; Seto, M. Collaboration of multi-domain marine robots towards above and below-water characterization of floating targets. In Proceedings of the 2019 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Ottawa, ON, Canada, 17–18 June 2019; pp. 1–7. [Google Scholar]
- Klinger, W.B.; Bertaska, I.R.; von Ellenrieder, K.D.; Dhanak, M.R. Control of an unmanned surface vehicle with uncertain displacement and drag. IEEE J. Ocean. Eng. 2016, 42, 458–476. [Google Scholar] [CrossRef]
- Manderson, T.; Higuera, J.C.G.; Wapnick, S. Vision-based goal-conditioned policies for underwater navigation in the presence of obstacles. arXiv 2020, arXiv:2006.16235. [Google Scholar]
- Huang, H.; Tang, J.; Zhang, B.; Chen, J.C.; Zhang, J.J.; Song, X. A novel nonlinear algorithm for non-Gaussian noises and measurement information loss in underwater navigation. IEEE Access 2020, 8, 118472–118484. [Google Scholar] [CrossRef]
- Liu, P.; Wang, B.; Deng, Z.; Meng, Y.F. INS/DVL/PS tightly coupled underwater navigation method with limited DVL measurements. IEEE Sens. J. 2018, 18, 2994–3002. [Google Scholar] [CrossRef]
- Chang, L.; Di, J.; Qin, F. Inertial based integration with transformed INS mechanization in Earth frame. IEEE/ASME Trans. Mechatron. 2022, 27, 1738–1749. [Google Scholar] [CrossRef]
- Bobkov, V.A.; Kudryashov, A.P.; Mel’Man, S.V.; Shcherbatyuk, A.F. Autonomous underwater navigation with 3D environment modeling using stereo images. Gyroscopy Navig. 2018, 9, 67–75. [Google Scholar] [CrossRef]
- González-García, J.; Gómez-Espinosa, A.; Cuan-Urquizo, E.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Escobedo Cabello, J.A. Autonomous underwater vehicles: Localization, navigation, and communication for collaborative missions. Appl. Sci. 2020, 10, 1256. [Google Scholar] [CrossRef]
- Qu, J.; Sun, G.; Zhang, J. Optimality analysis for formation of Multi-AUV cooperative positioning based on genetic algorithm. In Proceedings of the 2021 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Datong, China, 17–22 July 2021; pp. 578–583. [Google Scholar]
- Ling, H.; Zhu, T.; He, W.; Zhang, Z.; Luo, H. Cooperative search method for multiple AUVs based on target clustering and path optimization. Nat. Comput. 2021, 20, 3–10. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Luo, M.; Zhou, Y. Cooperative localization for multiple AUVs based on the rough estimation of the measurements. Appl. Soft Comput. 2020, 91, 106197. [Google Scholar] [CrossRef]
- Chang, L.; Qin, F.; Xu, J. Strapdown inertial navigation system initial alignment based on group of double direct spatial isometries. IEEE Sens. J. 2022, 22, 803–818. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Shen, H.; Li, P.; Zhang, T. Self-aided SINS for spiral-diving human-occupied vehicle in midwater. Assem. Autom. 2021, 41, 106–115. [Google Scholar] [CrossRef]
- Xanthidis, M.; Karapetyan, N.; Damron, H.; Rahman, S.; Johnson, J.; O’Connell, A.; O’Kane, J.M.; Rekleitis, I. Navigation in the presence of obstacles for an agile autonomous underwater vehicle. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 892–899. [Google Scholar]
- Barker, L.D.; Jakuba, M.V.; Bowen, A.D.; German, C.R.; Maksym, T.; Mayer, L.; Boetius, A.; Dutrieux, P.; Whitcomb, L.L. Scientific challenges and present capabilities in underwater robotic vehicle design and navigation for oceanographic exploration under-ice. Remote Sens. 2020, 12, 2588. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Wang, L. SINS/DVL Integrated System with Current and Misalignment Estimation for Midwater Navigation. IEEE Access 2021, 9, 51332–51342. [Google Scholar] [CrossRef]
- Salavasidis, G.; Munafò, A.; Fenucci, D. Terrain-aided navigation for long-range AUVs in dynamic under-mapped environments. J. Field Robot. 2021, 38, 402–428. [Google Scholar] [CrossRef]
- Ge, H.; Chen, G.; Xu, G. Multi-AUV cooperative target hunting based on improved potential field in a surface-water environment. Appl. Sci. 2018, 8, 973. [Google Scholar] [CrossRef]
- Cao, X.; Sun, H.; Jan, G.E. Multi-AUV cooperative target search and tracking in unknown underwater environment. Ocean Eng. 2018, 150, 1–11. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.; Meng, D. Multi-UAV cooperative localization for marine targets based on weighted subspace fitting in SAGIN environment. IEEE Internet Things J. 2021, 9, 5708–5718. [Google Scholar] [CrossRef]
- Herlambang, T.; Nurhadi, H. Estimation of UNUSAITS AUV position of motion using extended Kalman filter (EKF). In Proceedings of the 2019 International Conference on Advanced Mechatronics, Intelligent Manufacture and Industrial Automation (ICAMIMIA), Batu, Indonesia, 9–10 October 2019; pp. 334–339. [Google Scholar]
- Zhang, F.; Wu, X.; Ma, P. Consistent Extended Kalman Filter-Based Cooperative Localization of Multiple Autonomous Underwater Vehicles. Sensors 2022, 22, 4563. [Google Scholar] [CrossRef]
- Xu, C.; Xu, C.; Wu, C.; Qu, D.; Liu, J.; Wang, Y.; Shao, G. A novel self-adapting filter based navigation algorithm for autonomous underwater vehicles. Ocean Eng. 2019, 187, 106146. [Google Scholar] [CrossRef]
- Wang, C.N.; Yang, F.C.; Vo, N.T.; Nguyen, V.T.T. Wireless Communications for Data Security: Efficiency Assessment of Cybersecurity Industry—A Promising Application for UAVs. Drones 2022, 6, 363. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Yuan, R. AUV Path Following Formation Control Based on Extended Kalman Filter. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; pp. 12–16. [Google Scholar]
- Causa, F.; Opromolla, R.; Fasano, G. Cooperative navigation and visual tracking with passive ranging for UAV flight in GNSS-challenging environments. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 1538–1547. [Google Scholar]
- Rego, F.; Pascoa, A. Cooperative single-beacon multiple AUV navigation under stringent communication bandwidth constraints. IFAC-PapersOnLine 2021, 54, 216–223. [Google Scholar] [CrossRef]
- Munafo, A.; Ferri, G. An acoustic network navigation system. J. Field Robot. 2017, 34, 1332–1351. [Google Scholar] [CrossRef]
- Farahi, F.; Yazdi, H.S. Probabilistic Kalman filter for moving object tracking. Signal Process. Image Commun. 2020, 82, 115751. [Google Scholar] [CrossRef]
- Ullah, I.; Shen, Y.; Su, X.; Esposito, C.; Choi, C. A localization based on unscented Kalman filter and particle filter localization algorithms. IEEE Access 2019, 8, 2233–2246. [Google Scholar] [CrossRef]
- Bai, M.; Huang, Y.; Chen, B.; Yang, L.; Zhang, Y. A novel mixture distributions-based robust Kalman filter for cooperative localization. IEEE Sens. J. 2020, 20, 14994–15006. [Google Scholar] [CrossRef]
- Hajiyev, C.; Vural, S.Y.; Hajiyeva, U. Adaptive Fading Kalman Filter with Q-adaptation for estimation of AUV dynamics. In Proceedings of the 20th Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, 3–6 July 2012; pp. 697–702. [Google Scholar]
- Liu, X.; Qu, H.; Zhao, J. Maximum Correntropy Unscented Kalman Filter for Spacecraft Relative State Estimation. Sensors 2016, 16, 1530. [Google Scholar] [CrossRef] [PubMed]
- Sheng, G.; Liu, X.; Wang, Z.; Pu, W.; Wu, X.; Ma, X. A transfer alignment algorithm based on combined double-time observation of velocity and attitude. Assem. Autom. 2022, 42, 542–551. [Google Scholar] [CrossRef]
- Ansari, K. Cooperative position prediction: Beyond vehicle-to-vehicle relative positioning. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1121–1130. [Google Scholar] [CrossRef]
- EI-Sheimy, N.; Youssef, A. Inertial sensors technologies for navigation applications: State of the art and future trends. Satell. Navig. 2020, 1, 1–21. [Google Scholar]
- Chang, L.; Qin, F.; Jiang, S. Strapdown inertial navigation system initial alignment based on modified process model. IEEE Sens. J. 2019, 19, 6381–6391. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, X.; Song, W. A Vision Aided Initial Alignment Method of Strapdown Inertial Navigation Systems in Polar Regions. Sensors 2022, 22, 4691. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, Y.; Wang, G.; Gao, W. A New Variational Bayesian Adaptive Extended Kalman Filter for Cooperative Navigation. Sensors 2018, 18, 2538. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Liu, X.; Li, C.; Wu, X.; Zhang, Y. Multiple Autonomous Underwater Vehicles Cooperative Localization Based on Asynchronous Relative Observation. In Proceedings of the 2021 International Mobile, Intelligent, and Ubiquitous Computing Conference (MIUCC), Cairo, Egypt, 26–27 May 2021; pp. 3–8. [Google Scholar]
- Liu, L.; Wu, B.; Yang, P. Orbit Precision Determination & Self-Calibration Technique of Spacecraft; National Defense Industry Press: Beijing, China, 2005. [Google Scholar]
- Jian, M.; Qi, Q.; Yu, H.; Dong, J.; Cui, C.; Nie, X.; Zhang, H.; Yin, Y.; Lam, K.M. The extended marine underwater environment database and baseline evaluations. Appl. Soft Comput. 2019, 80, 425–437. [Google Scholar] [CrossRef]
- Xu, B.; Li, S.; Razzaqi, A.A. Cooperative localization in Harsh underwater environment based on the MC-ANFIS. IEEE Access 2019, 7, 55407–55421. [Google Scholar] [CrossRef]
- Kim, J. Cooperative localization and unknown currents estimation using multiple autonomous underwater vehicles. IEEE Robot. Autom. Lett. 2020, 5, 2365–2371. [Google Scholar] [CrossRef]
- Ma, Y.; Tian, C.; Jiang, Y. A multitag cooperative localization algorithm based on weighted multidimensional scaling for passive UHF RFID. IEEE Internet Things J. 2019, 6, 6548–6555. [Google Scholar] [CrossRef]
- Bouffaut, L. Detection and Classification in Passive Acoustic Contexts: Application to Blue Whale Low-Frequency Signals. Ph.D. Thesis, Institut de Recherche de l’Ecole Navale, Brest, France, 2019. [Google Scholar]
- Ben, Y.; Zang, X.; Li, Q.; He, J. A dual-state filter for a relative velocity aiding Strapdown Inertial Navigation System. IEEE Trans. Instrum. Meas. 2020, 70, 1000215. [Google Scholar] [CrossRef]
- Kim, T.; Park, T.H. Extended Kalman filter (EKF) design for vehicle position tracking using reliability function of radar and lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Z.; Du, S.; Li, Y.; Zhang, Y. A high-accuracy GPS-aided coarse alignment method for MEMS-based SINS. IEEE Trans. Instrum. Meas. 2020, 69, 7914–7932. [Google Scholar] [CrossRef]

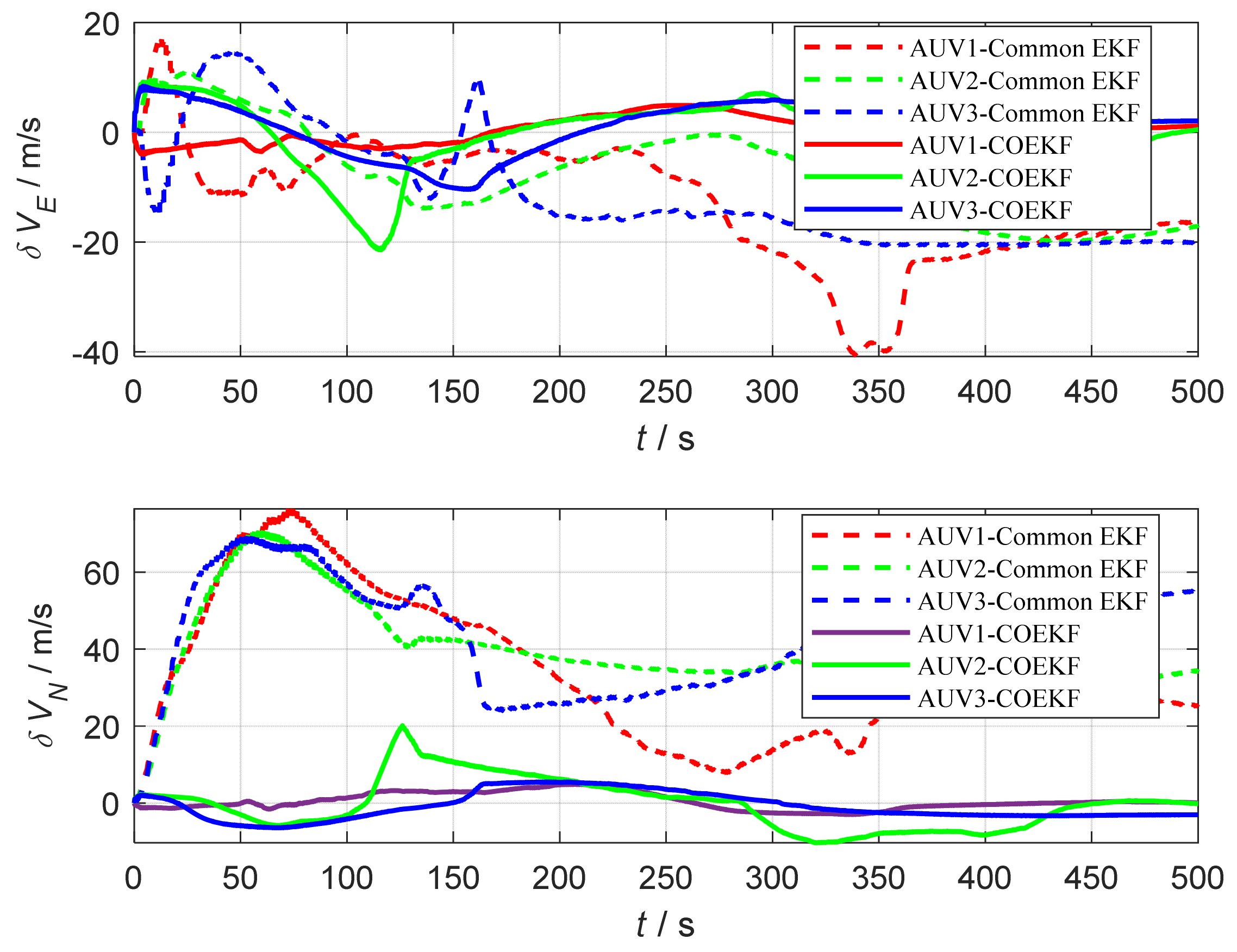
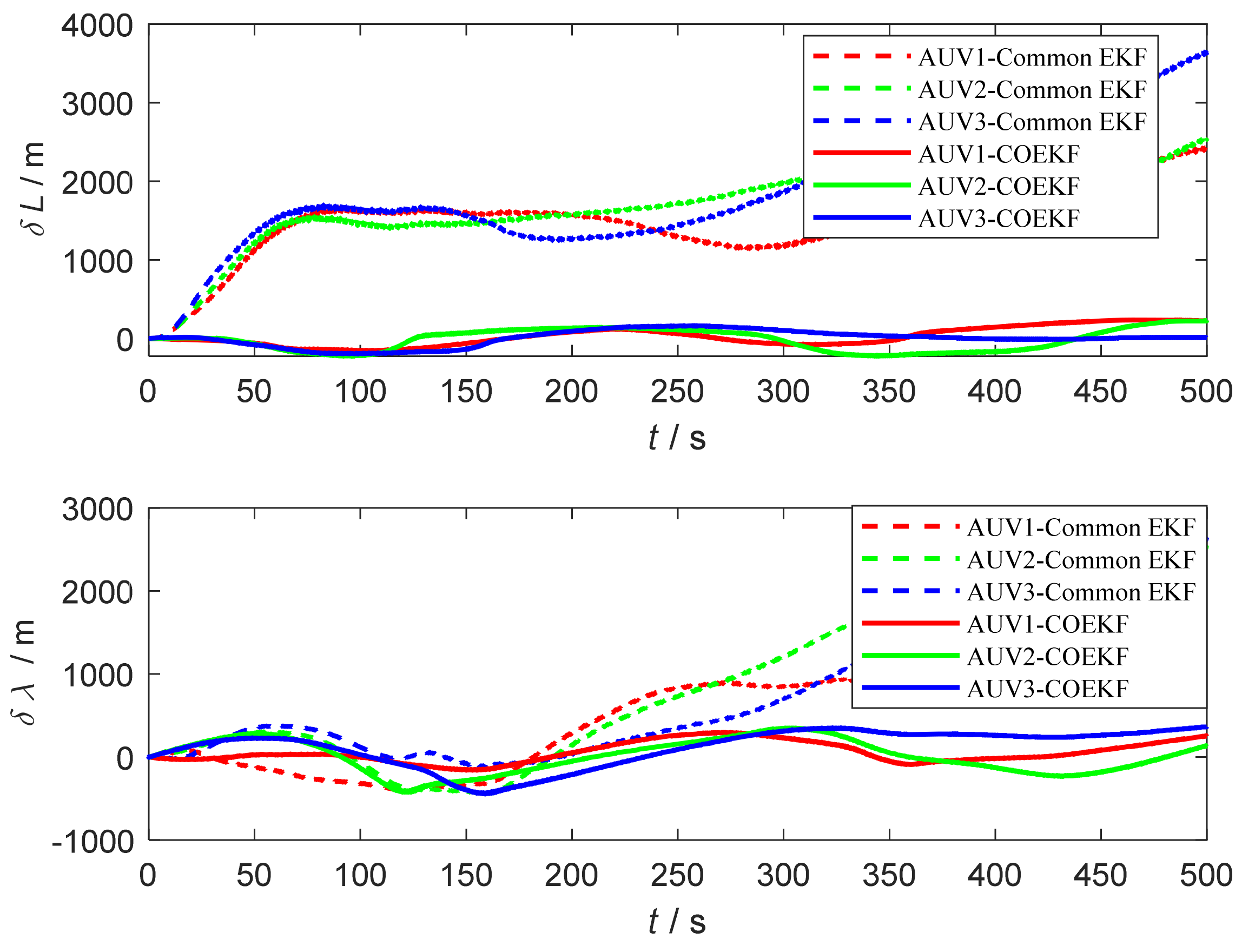
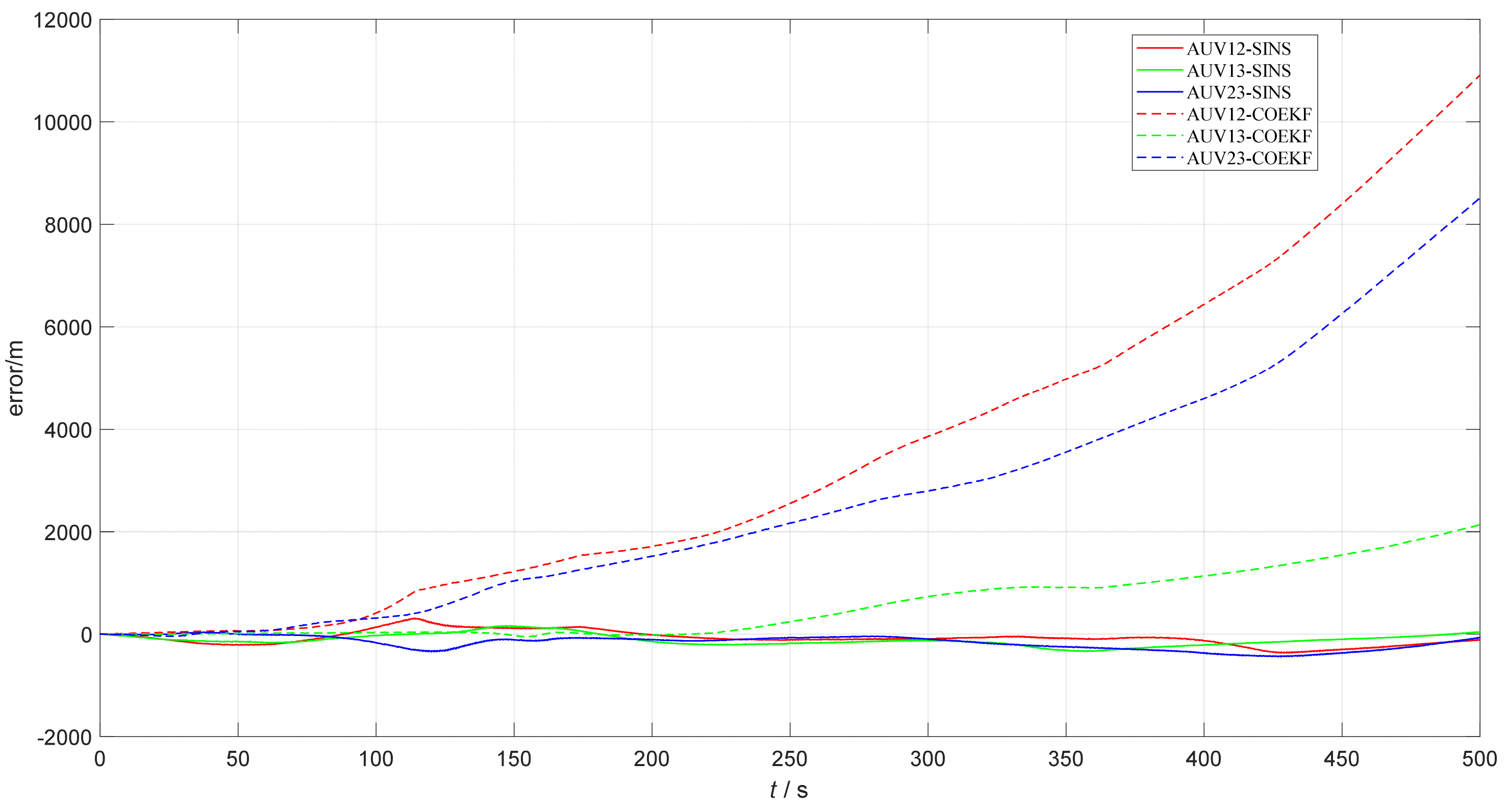
| Content | AUV12 | AUV13 | AUV23 |
|---|---|---|---|
| RMSE/m | 2.1449 | 1.9012 | 2.6130 |
| AME/m | 1.4524 | 1.4372 | 2.2626 |
| Gyro | Accelerometer | ||
|---|---|---|---|
| Constant | Random | Constant | Random |
| <0.02 | <0.01 | <500 | <500 |
| Content | AUV12 | AUV13 | AUV23 |
|---|---|---|---|
| RMSE/m | 15.6219 | 15.7213 | 20.9426 |
| AME/m | 13.2191 | 13.6113 | 16.1552 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, G.; Liu, X.; Sheng, Y.; Cheng, X.; Luo, H. Cooperative Navigation Algorithm of Extended Kalman Filter Based on Combined Observation for AUVs. Remote Sens. 2023, 15, 533. https://doi.org/10.3390/rs15020533
Sheng G, Liu X, Sheng Y, Cheng X, Luo H. Cooperative Navigation Algorithm of Extended Kalman Filter Based on Combined Observation for AUVs. Remote Sensing. 2023; 15(2):533. https://doi.org/10.3390/rs15020533
Chicago/Turabian StyleSheng, Guangrun, Xixiang Liu, Yehua Sheng, Xiangzhi Cheng, and Hao Luo. 2023. "Cooperative Navigation Algorithm of Extended Kalman Filter Based on Combined Observation for AUVs" Remote Sensing 15, no. 2: 533. https://doi.org/10.3390/rs15020533
APA StyleSheng, G., Liu, X., Sheng, Y., Cheng, X., & Luo, H. (2023). Cooperative Navigation Algorithm of Extended Kalman Filter Based on Combined Observation for AUVs. Remote Sensing, 15(2), 533. https://doi.org/10.3390/rs15020533