Abstract
A uniformity index for the axis ratios (Uar) derived from dual polarization weather radar data is proposed for raindrop area identification and analysis. The derivation of this new parameter is based on radar scattering simulations and assumptions. Uar is between 0 and 1 and can be calculated from the differential reflectivity (ZDR) and the copolar correlation coefficient (ρhv), which reflects the uniformity of the axis ratio (r) of the particle group. For raindrops, Uar is close to 1 under ideal conditions, but is clearly different from that of ice particles whose value is close to 0. Studies conducted during two convective weather events observed by X-band and S-band radar are presented to show the Uar features. In convective areas, high Uar presents a U-shaped vertical structure. One branch corresponds to the ZDR column, while the other branch is located at the rear of the convective cloud zone and is lower in altitude, representing the process of ice particles melting into raindrops and then being transported upward by a strong updraft. In stratiform cloud areas, a more than 95% overall identification ratio is obtained when the threshold of Uar is set to 0.2~0.3 for discriminating rain layers.
1. Introduction
The distribution and variation characteristics of the phase state (liquid, ice, mixed phase, etc.) of hydrometeors in clouds are extremely important issues in precipitation physics. Dual polarization weather radar obtains polarimetric variables, such as the horizontal/vertical reflectivity factor (ZH/ZV), differential reflectivity (ZDR), copolar correlation coefficient (ρhv) and differential propagation phase shift (KDP), which are closely related to the microphysical properties of hydrometeors in clouds [1,2,3]. For example, large raindrops show a flat shape and a corresponding high ZDR value when under air resistance [4]. This is clearly different from the various shapes of tumbling hail and graupel, which make it possible to roughly distinguish liquid and solid particles in the high ZH region [5]. Furthermore, lower ZH appears in snow and ice crystals due to the lower dielectric constant, while lower ρhv appears in mixed phase particles and sometimes in ice phase particles due to the variation of dielectric constant, shape and orientation [3,6]. Since different kinds of particles are not easily and directly identified due to the overlapping of the range of polarization parameters, a hydrometeor classification algorithm (HCA) based on the fuzzy logic algorithm [6] is the most feasible solution to obtain a general qualitative result. This kind of algorithm has been developed and improved over the past 20 years [7,8,9,10,11,12,13,14,15,16]. However, the HCA still has limitations in terms of subjectivity and experience [16]. Thus, its results cannot be regarded as absolutely accurate or the only microphysical analysis results, nor can the HCA completely replace the analysis of the original observed variables and other analysis methods. In particular, an additional input temperature profile is needed in most of the methods above, which means that the original polarimetric observables still cannot completely identify the hydrometeor phase independently.
Another principle algorithm that can distinguish the phase state of hydrometeor particles in clouds involves identifying the melting layer (ML) so that the part below the ML is identified as the rain area. In stratiform mixed phase clouds, the ML exhibits a ZH peak in the vertical direction [17,18], known as the bright band (BB) in radar meteorology. There is also a ZDR peak and a valley of ρhv in the ML. These dual polarization weather radar signals are closely related to changes in the dielectric constant, particle density, size and shape during the falling of ice phase particles [3]. Weather radar mostly adopts the polar coordinate volume scanning mode, where automatic ML detection algorithms are mainly built based on radar image features, including the gradient and extreme of ZH in a vertical profile of reflectivity (VPR) [18,19,20], the boundary of high ρhv [21], the thresholds or gradient of ZH, ZDR and ρhv [22,23,24,25], and the matching degree with the ideal model [26]. Automatic ML detection results can reduce contamination in radar quantitative precipitation estimation (QPE). Furthermore, ML is helpful for studying cloud and precipitation physical processes such as the ML sinking due to the riming or coalescence of snow [3,27,28]. However, such ML features mainly exist in large-scale stable stratiform precipitation and are difficult to be identified in convective clouds with severe temporal and spatial variability. Hence, the current algorithms above are not easily applied to the study of the melting or freezing processes within convective clouds. In addition, the accuracy of these algorithms mostly also depends on the additional input temperature profile, and it is usually necessary to summarize the thresholds of multiple variables. Therefore, it is still meaningful to find a more accurate and reliable method or some variables based on weather radar data to identify the hydrometeor phase.
In this study, a new parameter involving the microphysical characteristics of hydrometeor particles is proposed. The new parameter is derived from existing polarimetric radar observables and is found to reflect the uniformity of precipitation particles’ axial ratio. By this parameter alone, a simpler method for identifying raindrop areas is presented by setting a threshold. The derivation and demonstration of the new parameter will aim at the S-band (wavelength 10 cm) and X-band (wavelength 3.2 cm), which are commonly used in weather radars. The S-band is the most common band of operational weather radar, which has little rain attenuation and a long detection distance. X-band radar often has a smaller antenna and is easy to deploy in mobile platforms, and it is sensitive to weak precipitation.
The process of establishing the new parameter is described in Section 2. Section 3 shows and discusses the typical vertical structure characteristics of the new parameter in terms of radial height indicator (RHI) data from X-band radar and the performance and simple application of the new parameter in S-band weather radar volume scan data. The limitations of the new parameter are discussed in Section 4. A summary is given in Section 5.
2. Axis Ratio Uniformity Index
2.1. Approximate Relationship between the Reflectivity Ratio, Dielectric Properties and Axial Ratio
In this section, an approximate relationship between the reflectivity ratio, dielectric properties and axial ratio is proposed for the derivation of the new parameter presented in Section 2.3. When the scattering amplitude of ellipsoidal particles is calculated using the Rayleigh–Gans formula [1], both the axis ratio of the particle (r) and the dielectric constant (ε) exist in a nonlinear form, and these two parameters are not easily separated to form independent product terms. In previous studies, dielectric parameters were often regarded as fixed values according to the phase state of the particles, and then the approximate relationship of other parameters was discussed. For example, KDP can be approximated as the product of the rain content, mass-weighted axial ratio of the raindrop, and a constant term containing the given ε [29]. However, for mixed phase clouds, the phase state of particles needs to be considered as a variable since they are not fully known in advance.
The dielectric property parameters of particles are one of the key parameters that determine the scattering ability of particles. These parameters are usually considered to be related to the material of the object, incident wavelength and ambient temperature. There are two equivalent descriptions of dielectric properties: the complex dielectric constant ε = εr + iεi and the complex refractive index m = mr + imi, where εr and εi denote the real and imaginary parts of ε, mr and mi denote the real and imaginary parts of m, respectively, and i2 = −1. The conversion relationships between ε and m are as follows:
For different hydrometeor phase states, the Ray scheme [30] is used to calculate the dielectric parameters ε of pure water and pure ice. For an ice water mixture and spongy ice (mixture of ice and air), the overall dielectric constant is calculated according to the mass fraction method, and the Debye scheme [31] is selected as follows:
where ε(1) and ε(2) are the complex dielectric constants of the two components, ε(mix) is the overall complex dielectric constant of the mixture, and f is the volume fraction of the first component. The comparison of different schemes [31] shows that although the scheme of Equation (3) is not the most accurate scheme, the difference is very small compared with the best Maxwell–Garnett scheme, and the constraint conditions are the least accurate.
Some typical phases of hydrometeor particles in clouds and their corresponding dielectric properties are listed to find a simplified representation. The dielectric properties of pure water (clouds and raindrops) and pure ice (solid graupel and hail) are set according to the corresponding material. Mixtures of ice and water with f = 0.5 are used to characterize particles that are melting or freezing. Mixtures of ice and air (aggregated snow and ice crystals) with f = 0.1 and 0.5 are used to characterize spongy ice particles. For pure water, ambient temperatures of 0, 10, and 20 °C are selected to reflect the effect of temperature change on the dielectric properties. Since the dielectric properties of ice vary little with temperature, pure ice and other mixtures are set to 0 °C. Another problem is that εr and εi may vary differently with temperature, which leads to two variables of comparable magnitudes that need to be discussed. Note that mr is clearly larger than mi (Equations (1) and (2)); thus, only mr is taken as a dielectric characteristic parameter in the following attempts to characterize different phases.
Figure 1a gives mr at different phases and temperatures. The mr of water increases slightly with temperature in the X-band, while in the S-band, it decreases slightly or can be considered as undergoing little change. However, when water transitions to an ice/water mixture or ice, mr decreases, which generally has both nonlinear and nonmonotonic characteristics that are not easily used to form a simple model. However, if the reciprocal of mr is taken, it can be found that the mr−1 of spongy ice, pure ice, an ice/water mixture and pure water decrease somewhat linearly (Figure 1b). The different temperatures have little effect on mr−1 at this time. Therefore, mr−1 can be used as an available parameter to characterize the dielectric properties of the different phases.
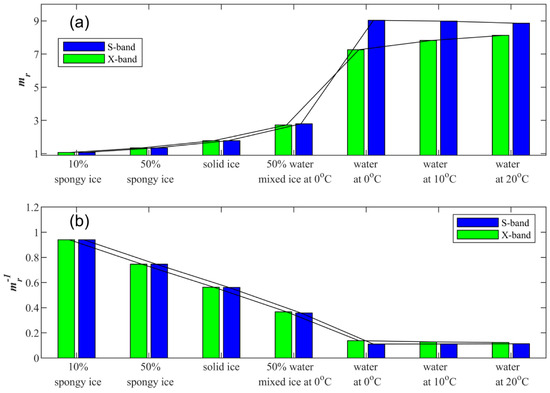
Figure 1.
Dielectric property parameters: (a) mr and (b) mr−1 of hydrometeors at different phases and temperatures.
The reflectivity variables are calculated using the T-matrix method [32]. For raindrops, the relevant theoretical calculation schemes of reflectivity variables [1] are as follows:
where Zh (or Zv), with lowercase subscripts, have linear units (mm6/m3), ZH (or ZV), with uppercase subscripts, are in log units (dBZ), and H or V represent horizontal or vertical polarization, respectively. ZDR is in log units (dB). Zdr is the dimensionless reflectivity ratio. Kw is associated with the dielectric property (Kw = (ε − 1)/(ε + 2)). λ (unit: m) is the wavelength of the radar. Shh,vv is the backscattering amplitude of a single hydrometeor particle in a horizontal or vertical channel. D is the equivalent spherical diameter of a particle, and N(D) is the particle number concentration density. Dmin and Dmax are the lower and upper limits of the drop size distribution, respectively.
A common problem in the simulation of particle scattering properties is that there are many dimensions that can be discussed, such as phase, shape, axis ratio and size distribution. Here, an individual particle is first discussed, trying to find some available laws that are less affected by particle size. To avoid confusion with the Zdr of the particle group, the reflectivity ratio of a single particle is represented by the symbol ηdr. Taking an ellipsoidal particle with r = 2 as an example, the effect of different phases on ηdr is analyzed (Figure 2). Note that r here is defined as the ratio of the horizontal scale to the vertical scale of the particle relative to the polarization direction of the radar beam, which is contrary to the definition of the raindrop axis ratio used in previous studies [33,34,35,36]. Figure 2 shows that ηdr increases as the phase of the particles becomes closer to pure water. For D greater than approximately 5 mm (in the S-band) and 2.5 mm (in the X-band), the ηdr of the pure water particle shows large oscillations due to the effect of Mie scattering. For the mixed phase, ηdr increases slightly with D. However, the general rule is still that the phase corresponding to mr−1 can amplify the value of ηdr. Therefore, we can use this relationship between the phase and ηdr of a single particle as an available approximation and the Mie scattering effect caused by the change in D as a potential error factor leading to the inaccuracy of this approximation. For example, based on this approximation, raindrops with a particle size greater than 6 mm in the S-band will introduce uncertainty, while particles of 3 to 4 mm in the X-band will lead to overestimation of the axial ratio. Considering that the actual radar detection variable is an integral of a group of particles, the above error factors will not always dominate.
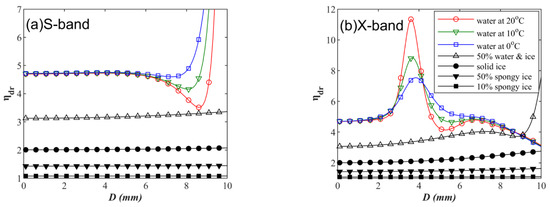
Figure 2.
Variation of ηdr with the spherical equivalent diameter D for a single ellipsoid water particle with an axial ratio r = 2 under different phase conditions. (a): S-band, (b): X-band. ηdr represents the Zdr of a single particle.
Then, if there is an available relationship with ηdr, phase and r can be discussed by ignoring the effect of D on ηdr, provided that the r is fixed, and D is fixed to 1 mm in the simulations. Figure 3 shows that the contribution of r also amplifies ηdr. However, this is not easily applied since ηdr changes along both r and phase. Hence, an approximate significant linear relationship is proposed here, taking X = mr−1 as an independent variable and Y = (ηdr0.5)/(r − 1) as a dependent variable to form the linear regression Y = a1X + a0 (Figure 4).
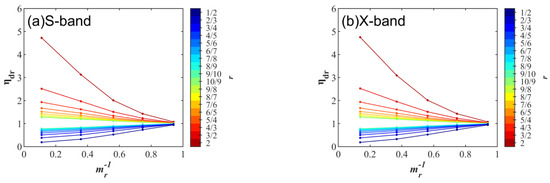
Figure 3.
Variation of ηdr with mr−1 for a single ellipsoidal water particle with different axial ratios (colors of the lines) when D = 1 mm. (a) S-band, (b) X-band.
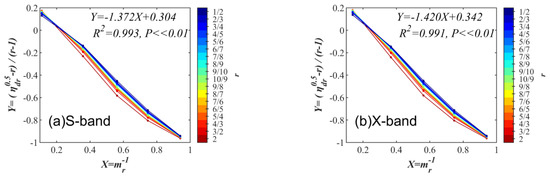
Figure 4.
Linear approximation between mr, ηdr and r of a single ellipsoidal particle. (R2 is the goodness of fit, and P is the significance of the linear fit. (a) S-band, (b) X-band.
According to the slope a1 and intercept a0 obtained by the linear fit shown in Figure 4, a new particle phase parameter E is defined instead of mr to characterize the phase state:
Furthermore, for a single ellipsoidal particle, a simple relationship between ηdr, E and r can be obtained, as shown in Equation (9):
Three points also need to be noted:
(1) The approximate linear relationship in Figure 4 is not the most accurate approximation. If r is logarithmic, an approximation with less error can be constructed. However, the approximate linear relationship shown in Figure 4 and Equation (9) is now more readily available for deriving the new index presented below. Therefore, Equation (9) is still used.
(2) The process of eliminating E will be shown in Section 2.3; thus, the values of E, a1, and a0 in Equation (8) are no longer discussed in the following sections.
(3) The effects of radar scanning elevation, particle orientation and nonellipsoidal shape are not considered here. Therefore, r should be considered as the flattening or narrowing of the particle in the horizontal and vertical polarization directions as detected by the radar.
2.2. Approximate Relationship between ρhv and Reflectivity
In this section, an approximate relationship between ρhv and the reflectivity variables is proposed for the derivation of the new parameter presented in Section 2.3. According to the principles involved in dual polarization radar detection, ρhv itself reflects the uniformity of the particle shape in the detection volume, but it is also affected by the radar observation system and noise [37,38]. Referring to the basic definition of ρhv, the ideal ρhv formula [3] is shown in Equation (10):
where <...> represents the volumetric average. The Shh,vv values are complex, and the molecular component included in Equation (10) requires conjugate multiplication, which makes it difficult to establish numerical connections with known parameters. For this reason, an approximate ρhv is proposed here as Equation (11):
where bh and bv reflect the contribution of a single particle to Zh and Zv, respectively, as follows:
In this way, the relationship between ρhv and the reflectivity of a single particle is established.
To verify the hypothetical approximation of Equation (11), a particle size distribution is necessary since ρhv is based on a particle group and is calculated by an integral or volumetric average. The range of the axial ratio and size distribution of ice particles may be too large and random, which is not easily resolved in a representative enumeration study; thus, a simpler raindrop size distribution (RSD) model is taken. By enumerating some typical RSDs, the difference between the ideal and approximate ρhv in different cases can be compared. A common RSD model can be expressed by a gamma distribution with three parameters [1] as follows:
where NT is the number concentration of particles, D0 is the spherical equivalent volume median diameter, and μ is the shape parameter of the RSD. When considering the “shape size” (D with r) model of raindrops, since the trends of D with r are not much different in previous models using fixed parameters [33,35,36], the scheme presented in [36] is taken as a typical case. Another key issue is the setting of Dmax. In common rainfall, raindrops larger than 6 mm are rare, but in severe convective rainfall, large raindrops of approximately 10 mm are often observed. Choosing a different Dmax may result in a large difference in the variables after integration according to RSD, thus Dmax values of 6 and 10 mm are both taken to represent common and typical severe rainfall cases, respectively. D is from 0.1 to Dmax with a 0.1 mm interval.
When enumerating different sets of RSD parameters, NT is not enumerated since ρhv does not involve the absolute number of particles. D0 starts from 0.1 mm with a 0.1 interval, and its upper limit is determined according to the constraint relation Dmax/D0 ≥ 2.5 [39] to limit the truncation error. μ is from −0.8 to 16 with a 0.2 interval to represent exponential shape (μ ≤ 0) and single peak shape (larger μ) distributions. By the combination of different Dmax, D0 and μ, RSD parameters in wide value ranges are enumerated to cover possible real conditions of raindrops.
The difference between the approximate ρhv and the ideal ρhv is evaluated by common statistics, including the correlation coefficient (R), mean absolute error (MAE) and mean relative error (MRE, see Appendix for definitions). The results are shown in Figure 5. For general rainfall in the S-band (Figure 5a), the approximate ρhv can be considered to be consistent with the ideal ρhv. In other cases, the approximate ρh is larger than the ideal ρh, but the deviation is generally limited. The largest deviation appears in the case of severe rainfall in the X-band (Figure 5b), but the MRE is only 0.13%. Therefore, the approximate ρhv in Equation (11) is considered basically consistent with the ideal ρhv for rainfall cases.
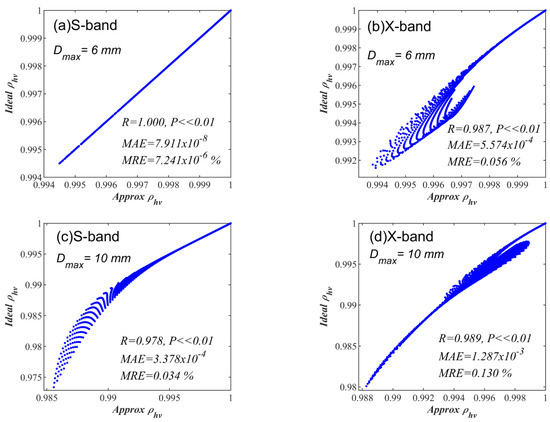
Figure 5.
Relationships between approximate ρhv in this study and ideal ρhv in raindrops. (The values of D0 are from 0.1 mm to Dmax in 0.1 mm intervals. The values of μ range from −0.8 to 16 in intervals of 0.2. R is the correlation coefficient between the approximate ρhv and ideal ρhv enumerated samples, and P is the significance of R. MAE is the mean absolute error, and MRE is the mean relative error. See Appendix). (a) S-band and Dmax = 6 mm, (b) X-band and Dmax = 6 mm, (c) S-band and Dmax = 10 mm, (d) X-band and Dmax = 10 mm.
2.3. Construction of the New Parameter
In this section, the derivation of the new parameter is proposed based on the approximations obtained in the previous two sections. First, according to the provisions of bh and bv (Equation (12)), Equation (9) can be transformed into Equations (14) and (15):
The above still applies to a single particle. When considering an integrated particle group, a new weighted average axial ratio is defined as Equation (16):
The here is actually the “vertical reflectivity weighted average axial ratio” and can be considered to reflect the overall average axial ratio of the particle group. Then, combining Equations (9) and (14) and the definition mode of Equation (16), is further defined as follows:
Then, the Zdr of a particle group can be written as a relation of E, and as Equation (18):
The E here is eventually moved outside the summation sign from Equations (19) to (20), where it represents the general phase of a particle group (which may be a mixture) and ignores the differences caused by the different phases of each particle. Furthermore, combining Equations (11), (14) and (18), Zdr and ρhv can be written as the relation between E and , as shown in Equation (19):
Thus far, there are two radar variables (Zdr and ρhv) that are used, while there are three unknowns: E, and . Although absolute quantities such as total concentration and water content are avoided, there is still no way to solve all unknowns. To this end, a solution is proposed here that eliminates E by a combination of Zdr and ρhv to finally obtain a relationship between and :
Note that Equation (24) can reflect the uniformity of r relative to 1 for a particle group. For example, the shape and orientation of ice particles may differ greatly, resulting in a large denominator and small molecule component in Equation (24), which eventually leads to the value of Equation (24) being close to 0. However, for raindrops, r is greater than 1 for most particles. This results in a value of Equation (24) between 0 and 1 and close to 1. In addition, the elimination of E between Equations (23) and (24) is equivalent to the elimination of the impact of phase on amplifying ηdr or Zdr. Finally, only one descriptive quantity for the axial ratio distribution uniformity of the particle group is obtained, and it is named the “axis ratio uniformity index” (Uar):
where the dimensionless Zdr can be transformed by Zdr = 10ZDR, and ZDR (in dB) is observed by radar. Therefore, Uar is a variable that can be calculated from radar measurements ZDR and ρhv.
The numerical distribution of Uar is shown in Figure 6, which is based on the same enumerated ranges of RSD as in Section 2.2. In the S-band, Uar values are mostly concentrated between 0.8 and 0.9, mostly above 0.7. In the X-band, the value distribution of Uar is more dispersed, but most values are more than 0.6. Less than 10% of the data have Uar values less than 0.1, and the relationship between Uar, D0, and μ is further examined (Figure 7). Uar rapidly decreased to 0 when D0 was less than 0.5 mm, i.e., indicating that Uar does not have the ability to distinguish particles in the ice phase from raindrop groups with small particle diameters. However, since the case in which D0 is less than 0.5 mm rarely appears in previous joint observation and retrieval studies based on weather radar and RSD [29,40,41], it can be considered that Uar can show a value close to 1 for raindrops, which is obviously different from the value close to 0 for most ice phase particles.
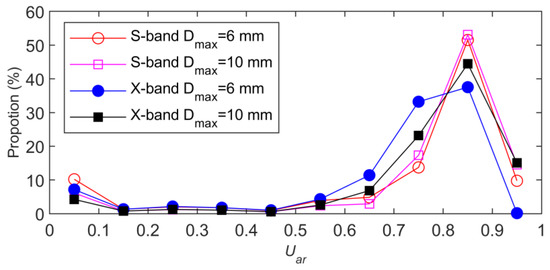
Figure 6.
Distribution of Uar within the enumeration range of the RSD parameters. (The values of D0 and μ are the same as those in Figure 5).
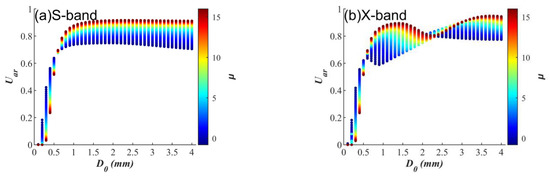
Figure 7.
Relationships of Uar versus D0 and μ when Dmax=10 mm. (Dmax = 10 mm. The values of D0 and μ are the same as those in Figure 5). (a) S-band, (b) X-band.
In summary, Uar has the potential to identify rain areas. However, the Uar probability distribution shown in Figure 6 is not the probability distribution considered for actual detection, and none of the above discussions include noise in ρhv. The practical application effect of Uar will be discussed below.
3. Performance of Uar on Real Observations
3.1. Typical Features of Vertical Structures of Uar on X-Band RHI Radar Data
3.1.1. Overview of RHI Data during a Convective Event
In this section, the vertical distribution characteristics of Uar are discussed using RHI data obtained by X-band dual polarization radar. The selected case is a convective event in Beijing that occurred during 18:00–19:30 (Local Standard Time (LST), GMT+8) on 7 September 2016. The radar is a 714XDP-A type X-band dual polarization mobile radar belonging to the Key Laboratory of Cloud-Precipitation Physics and Severe Storms (LACS), Institute of Atmospheric Physics (IAP), Chinese Academy of Sciences (CAS). That radar was deployed for field observations at the Beijing Olympic Water Park (116.68°E, 40.18°N) during the summer from 2015 to 2019. The main characteristics of this radar are listed in Table 1. Other information, including quality control and attenuation correction methods, can be seen in [42,43]. The vertical temperature profile used for the analysis was derived from the neighboring sounding station at 08:00 LST (station number: 54511, 116.28°E, 39.93°N). For the observation mode, plan position indicator (PPI) and RHI scans were switched manually in these observations. The PPI at 4° elevation was scanned first, followed by an RHI scan that aimed at the strong convection center, forming a cycle to track the evolution of the vertical structure of the severe convective cell. Figure 8 shows the convective system to the southwest of the radar moving southeastward.

Table 1.
Characteristics of the X-band dual polarization radar used in this paper.
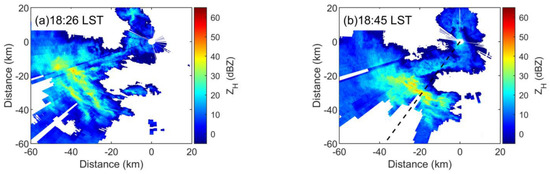
Figure 8.
Sample PPI observations of ZH. (The elevation of the PPI is 4°. The azimuth of the dashed line in Figure 8b is 212°. The data collection time is 7 September 2016). (a) 18:26 LST, (b) 18:45 LST.
Figure 9a–d show radar data at the RHI of 212° azimuth. The KDP is not shown here since it is not discussed in this paper. There is a stratiform cloud area from 0 to 25 km in the horizontal direction, and the BB characteristics of the ML are found below the 0 °C layer among ZH, ZDR and ρhv. The ML, at a horizontal distance of approximately 20 km, has a sinking feature, which may be related to the rapid fall caused by the riming or coalescence of snow [3,27,28]. In the convective cloud region, the convective core is located at a horizontal distance of 35 km (Figure 9a), and there is a distinct ZDR column [44] feature (Figure 9b). The value of ρhv in the lower layer and 40 km away is less than 0.4 (Figure 9c), which should be attributed to invalid observations caused by attenuation and noise. The corresponding ZH and ZDR values at such areas are automatically masked during the quality control process, despite some of the ZDR values remaining abnormally low at the rear of the radar beams. The Doppler radial velocity (VR, Figure 9d) shows convergence below 6 km at the convective core, while divergence appears at a height of approximately 10 km, indicating a strong updraft. Figure 9e shows the Uar proposed in this paper. In addition, a hydrometeor classification (HC) result is shown in Figure 9f as a reference for the particle phase, using the scheme from the work of Feng et al. [45], which is an ensemble and improved version from previous studies [9,10,11,12].
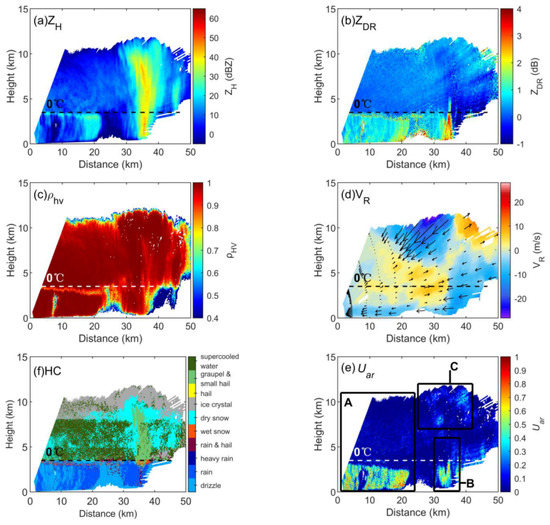
Figure 9.
Sample RHI observations and retrievals of the convective system from the X-band dual polarization weather radar. (The time is 18:46:30 LST. The azimuth is the same as the dashed line in Figure 8b. The maximum elevation is 44°). (a) ZH, (b) ZDR, (c) ρhv, (d) VR, (f) HC, (e) Uar.
The following focuses on the three regions shown in Figure 9e, where region A is a stratiform cloud area, region B is the lower area of the convective cloud, and region C is the upper area of the convective cloud.
In region A, Uar suddenly appears as a whole layer with values larger than approximately 0.5 from a certain distance below the 0 °C layer to the ground (Figure 9e), while the HC result shows wet snow corresponding to the ML, and then rain and drizzle below. These results show that HC and Uar are basically consistent in terms of identifying rainy areas. Moreover, the top of the high-value area of Uar exhibits a sinking feature consistent with ML.
In region B, there is an obvious difference between HC and Uar. The high value areas of Uar show a clear ‘U’-shaped spatial distribution, while HC shows a very narrow range of heavy rain, grauples and hail mixing with rain in other locations.
In region C, Uar has a high value area with the maximum value approaching 0.4 at the divergence area of VR, corresponding to dry snow in the HC results. This phenomenon may be explained by the fact that strong horizontal winds contributed to the formation of high-level snow clustering and the maintenance of quasi-horizontal orientation. However, since the spatial scope of that feature is limited, the value of Uar is not so large, and ice habits are not a focus of this study, there is no further discussion of it in the following sections. In Section 3.1.2 and Section 3.1.3 below, only areas A and B are discussed.
3.1.2. Analysis of the Stratiform Cloud Area
Average vertical profiles of polarimetric variables in region A are counted and shown in Figure 10. There are notable ML features with extreme values and strong gradients, where ZH has a peak and ρhv has a valley from the 0 °C level (3.48 km) down to approximately 9 °C (2.37 km). ZDR also shows a small peak in this ML. However, Uar is close to 0 in the cold cloud area and changes in the ML, mutating into an average of more than 0.4 below the ML. This result apparently shows that Uar is a step-like mutation signal in a three-layered cold cloud, which is unlike conventional variables (such as ZH, ZDR and ρhv) that exhibit extreme values in ML.
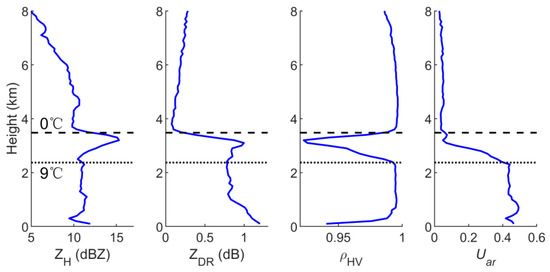
Figure 10.
Mean vertical profile in area A. (Statistics by data points with ZH > 0 dBZ).
The threshold value of Uar used for determining the raindrop areas should be given according to the Ua probability distribution statistics below the ML. If the data below the ML where ZH is larger than 0 dBZ are counted (Figure 11a), Uar is concentrated between 0.4 and 0.5, but there is a certain distribution from 0 to 1 that makes it difficult to select a threshold. If the statistics are performed in areas with a slightly stronger reflectivity, such as 20 dBZ, which is generally considered to have obvious rainfall, Uar values range, at most, from 0.6 to 0.7 (Figure 11b), and more than 90% are above 0.4. Therefore, it is possible to identify raindrop areas easily only by setting a Uar threshold and without temperature input instead of determining the boundaries of ML first. Further quantitative analysis of the threshold is presented in Section 3.3.
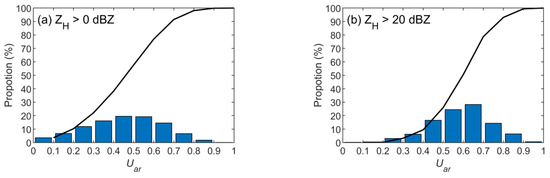
Figure 11.
Proportions of Uar values in the warm layer (below 2.37 km, warmer than 9 °C) of area A: (a) points with ZH > 0 dBZ and (b) points with ZH > 20 dBZ. The bars are the proportions within given ranges, and the black lines are the accumulated proportions.
3.1.3. Analysis of a Convective Cloud Area in the Lower Levels
Figure 12 shows the enlarged vertical structure of variables in region B. The divergence of VR is added (Figure 12c) to better diagnose the distribution of vertical airflow in the cloud, which is defined as dVR/ds, where s is the radial distance of a radar beam. Strong convergence (dVR/ds < 0) extends from the ground to a height of 5 km and reaches a maximum above the 0 °C layer, which indicates a deep and strong updraft here that is consistent with the position of the ZDR column shown in Figure 12b. The ZDR column is a phenomenon in which the high ZDR region extends above the 0 °C height [45] and is thought to be closely related to the transport of large raindrops and strong updrafts in the supercooled layer [46,47,48,49,50]. The right branch of the U-shape of Uar corresponds to the ZDR column and the strong convergence of VR, which indicates that the corresponding raindrops are transported upward by the updraft. The upper bound of the right branch of that U-shape crosses the 0 °C layer, indicating that the raindrops freeze after being transported to the supercooled layer. The left branch of the U-shape is 500 m lower than the right branch and is deflected away from the strong convergence area, which can be inferred as raindrops formed by the falling and melting of high-level ice particles.
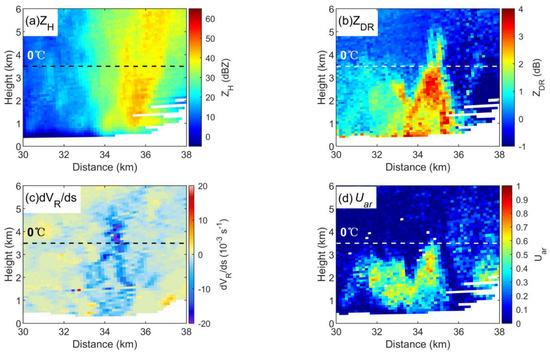
Figure 12.
Variables in area B with the ZDR column. (a) ZH, (b) ZDR, (c) dVR/ds, (d) Uar.
In the analysis of the above features that change with time, due to the large amount of low-level occlusion during the period preceding what is shown in Figure 9 and Figure 12, a later time is selected to track the change in the convective cell. Figure 13 shows PPI data 7 min later and RHI data 9 min later, where the RHI is obtained by tracking the horizontal movement of the ZH core. Figure 14 shows an enlarged view of the convective core at a low level, which is similar to Figure 12. The divergence of VR (dVR/ds > 0, Figure 14c) below 1 km indicates the dominating downdraft caused by rainfall. The ZDR column no longer exists (Figure 14b), which may be the result of deep updrafts disappearing. At the same time, Uar no longer displays a U-shape (Figure 14d). The upper bound of the large value of Uar is approximately 1 km below the 0 °C layer, showing the characteristics of large-scale melting of ice particles into raindrops. In summary, it can be inferred that the left and right branches of the U-shaped Uar in the lower troposphere correspond to rain formed by the melting of ice particles and rain transported upward by the updraft, respectively. This set of processes is very similar to Conway and Zrnic’s explanation of the formation mechanism of the ZDR column [46]. Therefore, the study presented here can not only be used as evidence to support previous studies but can also expand the means of future research on the ZDR column.
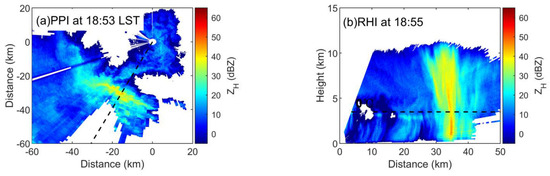
Figure 13.
PPI and RHI of ZH at subsequent time intervals. (a) PPI at 18:53 LST, (b) RHI at 18:55.
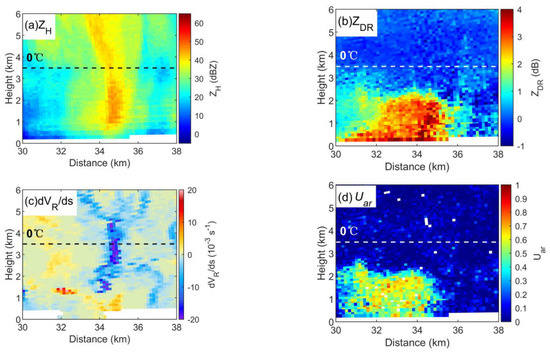
Figure 14.
Variables after the ZDR column disappeared. (a) ZH, (b) ZDR, (c) dVR/ds, (d) Uar.
3.2. Performance of Uar on S-Band Volume Scans Radar Data
In this section, S-band operational dual polarization radar volume scan data are used to evaluate the application of Uar. The involved case is a severe convective event that occurred in Shandong Province, China, during the evening on 17 May 2020. The radar is a dual polarization radar upgraded from CINRAD-SA type radar (station number: Z9532, 120.23°E, 35.99°N). The main characteristics of this radar are listed in Table 2. This radar performs a volume scan containing nine elevations from 0.5° to 19.5° (commonly called VCP-21 mode) in approximately 6 min. The vertical temperature profile used for the analysis was derived from the neighboring sounding station at 20:00 LST (station number: 54857, 120.33°E, 36.06°N).

Table 2.
Characteristics of the S-band dual polarization radar used in this paper.
The mid-late stage data regarding the convective system development are selected, where there is a large range of stratiform cloud areas behind the convection line. PPI data with obvious ML features are shown in Figure 15. The BB signal in ZH is not obvious (Figure 15a), while ZDR and ρhv both have a ring area with extreme values and rough texture, indicating that the ML is between 0 and 11 °C (Figure 15b,c). For the high ZH area, which is approximately 50 dBZ in the ML, it is noted that there is a negative ZDR area on the east side (higher), which is consistent with the characteristics of snow riming in previous studies [27,28]. The Uar shows an appearance similar to that of the X-band in Section 3.1, where a wide range of large values appears mostly just below the ML. This result indicates that Uar also has the ability to identify raindrop areas in S-band volume scan data.
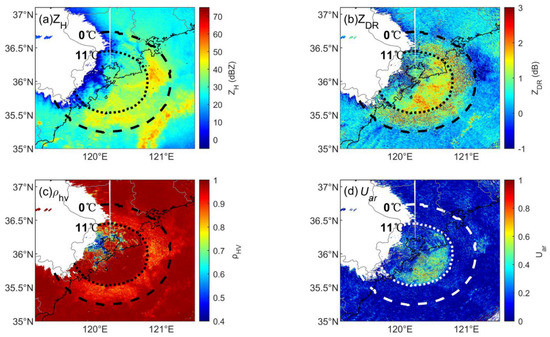
Figure 15.
Sample PPI observations with BB from the S-band dual polarization weather radar. (The data time is 17 May 2020 23:51 LST. The elevation is 2.4°, which is the third level of a volume scan). (a) ZH, (b) ZDR, (c) ρhv, (d) Uar.
To be further compared with the vertical structure in Section 3.1, a composite RHI is derived by interpolation, which covers both convective and stratiform areas (Figure 16). In the stratiform cloud area (distance from 0 to 60 km), the ML is visually estimated by the BB in ZH, ZDR and ρhv, whose bottom is at the height of 11 °C, and the high Uar appears below the ML. The ZDR column at a distance of 100 km also corresponds to a high value area of Uar. An approximate U-shaped vertical structure of Uar, whose two branches are at 70 and 100 km distances (Figure 16d), is more difficult to identify compared with that in X-band RHI data (Figure 12d). This may be due to the low elevation resolution of the volume scans. However, the general performances in the X-band and S-band are similar, regardless of the scanning mode.
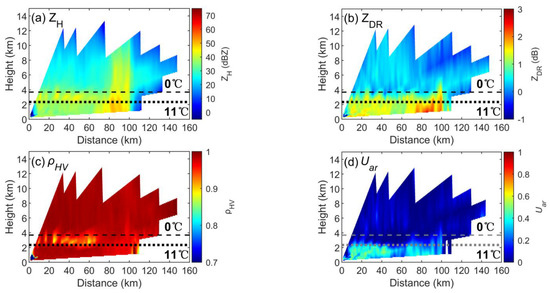
Figure 16.
Composite RHI at 130° azimuth from the S-band dual polarization weather radar. (The data time is 17 May 2020 23:51 LST, the same as Figure 15. The radial data are smoothed by 10-point median filtering, and triple linear interpolation is used to derive this composite result). (a) ZH, (b) ZDR, (c) ρhv, (d) Uar.
3.3. Identification Ratio of Raindrops in Stratiform Cloud Areas
One inevitable question is how accurate it is to use Uar to identify raindrops. However, the accurate phase state of particles in clouds is not easy to obtain, especially in convective areas, which is also the key and difficult point in the study of weather radar remote sensing. After all, there is not always a cloud-penetrating detection by aircraft to make a space–time continuous observation. Therefore, a relatively reliable method is selected. Aiming at stratiform areas with ML, the bottom height of the visual ML boundary is selected as the dividing line. Parts below the ML bottom are divided into rain layers, while other parts are divided into nonrain layers (mixed and ice phases), so that the identification results can be examined quantitatively. The data in Figure 10 (Section 3.1) are selected as Case 1, with the height of 9 °C as the dividing line; the data in Figure 16 (Section 3.2) are selected as Case 2, with the height of 11 °C as the dividing line. Weak echoes with ZH less than 20 dBZ are ignored in the statistics. The identification ratio of rain layers (Srain), nonrain layers (Snonrain) and overall ratio (Stotal) are defined as follows:
where Nr is data count in rain layers; Ni is data count in nonrain layers; Tr is data count of the correct identification of the rain layer, where a data point has a Uar larger than the given threshold and is located in rain layers; Ti is data count of correct identification of nonrain layer, where a data point has a Uar equal to or less than the given threshold and is located in nonrain layers.
The results (Table 3) show that Srain decreases as the Uar threshold increases, probably because small raindrops have a smaller Uar and cannot be identified, while the trend in Snonrain is the opposite. This results in a maximum value for Stotal, where Uar = 0.3 for Case 1 and Uar = 0.2 for Case 2. In general, a more than 95% overall identification accuracy can be obtained when Uar is set to 0.2~0.3.

Table 3.
Identification ratio of rain and nonrain layers using different thresholds of Uar.
3.4. Using Uar as a Mask to Compute Composite Reflectivity
Composite reflectivity (CR) is a common data product of weather radar volume scan data and is a two-dimensional image derived from the ZH maximum at the same horizontal position in each PPI for different elevations. By using the CR, the horizontal spatial distribution of the strong reflectivity population can be quickly observed, and a preliminary judgment of precipitation can be made, where it can avoid missing information caused by a partial occlusion in a single PPI or the uncertainty of the height of the reflectivity core. Using the same case in Section 3.2, Figure 17a shows a CR, where there is a severe convective line over 60 dBZ and a large-scale stratiform cloud area at the rear (northwest side). However, due to the high value and uneven horizontal distribution of ZH in the ML, some spots in the ML may be misjudged as convective clouds, which would lead to misinterpretations of the precipitation situation. To avoid this, the CR must be recalculated after removing the effects of ML signals.
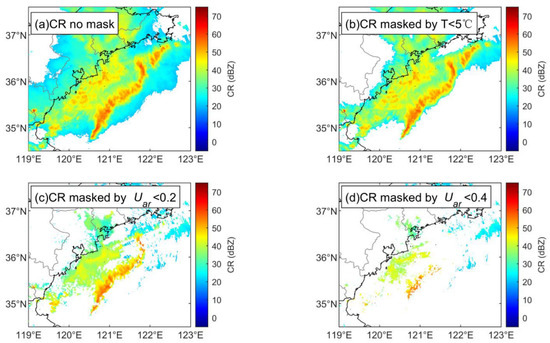
Figure 17.
CR with different reflectivity masks. (The points are with ZH > 20 dBZ. The time is the same as Figure 15. (a) CR no mask, (b) CR masked by T < 5 °C, (c) CR masked by Uar < 0.2, (d) CR masked by Uar < 0.4.
First, there is an example in which ML signals are not successfully removed. Suppose the lower bound temperature of the ML is 5 °C by assuming some experience that is not applicable to this case. After masking data with temperatures below 5 °C, a new CR is derived (Figure 17b), where the high ZH spots still exist in the stratiform area since the ML signal is not completely removed from the original PPI. This problem can certainly be solved if the lower bound of the ML in this example is accurately obtained at 11 °C. However, inaccuracies in the temperature profile and ML boundary detection can make a difference.
Next, Uar is taken as a mask template from ZH in each PPI. The ZH is masked where the Uar is less than a certain value, and then, the CR is calculated, which is equivalent to calculating the CR of raindrop areas. A loose threshold is applied first by taking Uar < 0.2 as the mask template to form the new CR (Figure 17c). The intensity of the CR in the stratiform cloud region to the northwest of the strong convective line is obviously smaller and more uniform and is basically not more than 45 dBZ, which is consistent with the common features of stratiform rainfall. If a stricter threshold is used, such as by taking Uar < 0.4 as the mask template (Figure 17d), the entire convective system becomes fragmented, and only part of the stratiform cloud region remains. The parts masked in Figure 17d may contain both smaller raindrops and particles, such as graupel and hail, that are likely to exist in the convective line. However, due to the need for other ground observation instruments to verify the identification of graupel and hail, such content is not discussed in this paper. In general, taking a loose Uar threshold as a mask (e.g., Uar < 0.2) to calculate CR can preserve the horizontal spatial distribution characteristics of most precipitation systems while masking ML signals. Furthermore, this approach is more convenient and efficient than traditional methods that require temperature input and multithreshold management to first detect the ML.
4. Discussion on Limitations of Uar
There are also some limitations of using Uar that were found in the course of this study. Here are three points to consider.
(1) If the ZDR of the X-band does not undergo quality control (QC) and attenuation correction, there may be a large area of small ZDR anomalies in the lower troposphere away from the radar side due to attenuation (Figure 18a). In addition, in the area where the signal-to-noise ratio is theoretically low at the end of the radar beam, there may be an abnormally large or small ZDR value due to noise. These can result in a larger value and overestimate Uar (Figure 18b), which inevitably affects the results of raindrop area identification. One solution is to set Uar to 0 when ZDR is less than 0 dB. Thus, a rough location of the raindrop areas can be obtained without waiting for a time-consuming quality control and attenuation correction process when collecting data.
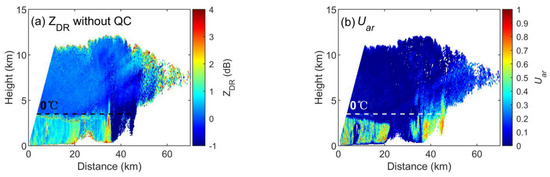
Figure 18.
Sample of the impact on the Uar calculation without data quality control and attenuation correction for ZDR in the X-band. (a) ZDR without QC, (b) Uar.
(2) If there is a systematic bias in the ZDR detected by the radar, it may cause Uar to be unavailable. A test in which a 0.3 dB systematic bias is artificially added to ZDR (Figure 19a) shows that Uar in the stratiform area no longer exhibits mutation features as shown in Figure 10, but rather displays a valley band feature (Figure 19b) similar to ρhv in the ML and loses the capability to identify raindrop areas. This suggests that the premise of using Uar is that the systematic deviation of ZDR needs to be controlled within 0.3 dB. For these reasons, attention should be given to the calibration of dual polarization radars, especially for mobile X-band radars, when conducting field observation experiments.
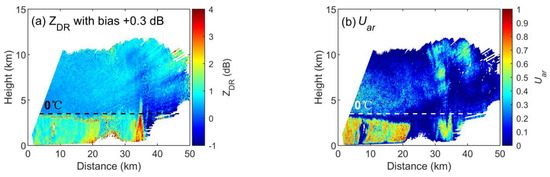
Figure 19.
Sample of the impact on the Uar calculation when there is a +0.3 dB systematic deviation in ZDR at the X-band. (a) ZDR with bias +0.3 dB, (b) Uar.
(3) The premise of using Uar is to eliminate or at least reduce the influence of the phase state and only to retrieve and utilize the axial ratio distribution characteristics of the particle group. However, there must be some extreme cases where the ice or snow particles exhibit a pronounced horizontal orientation under the action of the dominant wind. This could also lead to large values of Uar, which could be confused with the raindrop area. However, there is no good example to illustrate this expected extreme situation, and this work needs to be carried out in depth in the future. In addition, the cases presented in this paper involve relatively low elevations, and observations at high elevations will result in a smaller ZDR in the raindrop area and would need to be corrected. The impact of these factors on Uar also needs to be explored in more cases.
5. Conclusions and Summary
A uniformity index for hydrometeor axis ratios (Uar) derived from dual polarization weather radar data is proposed in this paper. Backscattering numerical simulations are used to find available relationships to derive Uar and show its theoretical features for the identification of raindrops. Then, observation data from X-band and S-band radar are used to show and examine the performance of Uar under real conditions and carry out initial applications. The main conclusions are as follows.
(1) Uar is close to 0 for ice particles with varying shapes and orientations and is close to 1 for raindrops theoretically, which gives Uar the ability to identify raindrop areas.
(2) In the real observations, Uar is basically consistent with its theoretical feature above. A more than 95% overall identification ratio can be obtained in stratiform cloud areas when the threshold of Uar is set to 0.2~0.3. Thus, the raindrop area can be more easily identified instead of identifying ML first by inputting a temperature profile and setting multiple thresholds.
(3) In the demonstration using X-band radar RHI data, high Uar in the convective areas presents a U-shaped vertical structure, which indicates the process of ice particles melting into raindrops and then being transported upward by strong updraft and provides evidence for the formation mechanism of the ZDR column.
(4) In the CR calculation demonstration using S-band radar, the impact of the ML signal on CR can be eliminated by setting Uar < 0.2 as a mask template to avoid misjudging stratiform clouds at the rear of the convective line as convective clouds.
The application of Uar still requires more in-depth research in the future. Due to the spatiotemporal limitations of RHI and volume scanning, the change process of the ZDR column may not be fully captured. Thus, more studies are needed to better summarize the evolution of Uar and other variables. Additionally, it is necessary to further evaluate and expand the application of Uar methods in hydrometeor classification and in the quantitative retrieval of microphysical features.
Author Contributions
Conceptualization, Y.S.; methodology, Y.S.; software, L.F. and W.S.; validation, Y.S. and L.F.; formal analysis, Y.S.; investigation, Y.S.; resources, H.X., H.C. and H.Y. (Han Yao); data curation, H.Y. (Han Yao); writing—original draft preparation, Y.S.; writing—review and editing, H.X., H.C. and H.Y. (Huiling Yang); visualization, W.S.; supervision, H.X.; project administration, H.X.; funding acquisition, Y.S. and H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Key Research and Development Plan of China (grant no. 2019YFC1510304), the National Natural Science Foundation of China (grant no. 42105127), and the Special Research Assistant Project of Chinese Academy of Sciences.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In Section 2.2 (Figure 5), R, MAE and MRE are used to evaluate the difference between and , which are defined as follows:
where X is , Y is , Cov(...) denotes the covariance and Var(...) indicates the variance.
References
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Zhang, G. Weather Radar Polarimetry; CRC Press, Inc.: Boca Raton, FL, USA, 2016. [Google Scholar]
- Ryzhkov, A.V.; Zrnic, D.S. Radar Polarimetry for Weather Observations; Springer Nature Switzerland AG: Cham, Switzerland, 2019. [Google Scholar]
- Seliga, T.A.; Bringi, V.N. Differential reflectivity and differential phase-shift-applications in radar meteorology. Radio Sci. 1978, 13, 271–275. [Google Scholar] [CrossRef]
- Aydin, K.; Seliga, T.A.; Balaji, V. Remote-sensing of hail with a dual linear-polarization radar. J. Appl. Meteorol. Climatol. 1986, 25, 1475–1484. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zrnic, D.S.; Ellis, S.M.; Oye, R.; Ryzhkov, A.V.; Straka, J. Cloud microphysics retrieval using S-band dual-polarization radar measurements. Bull. Am. Meteorol. Soc. 1999, 80, 381–388. [Google Scholar] [CrossRef]
- Straka, J.M.; Zrnic, D.S.; Ryzhkov, A.V. Bulk hydrometeor classification and quantification using polarimetric radar data: Synthesis of relations. J. Appl. Meteorol. 2000, 39, 1341–1372. [Google Scholar] [CrossRef]
- Liu, H.P.; Chandrasekar, V. Classification of hydrometeors based on polarimetric radar measurements: Development of fuzzy logic and neuro-fuzzy systems, and in situ verification. J. Atmos. Oceanic Technol. 2000, 17, 140–164. [Google Scholar] [CrossRef]
- Zrnic, D.S.; Ryzhkov, A.; Straka, J.; Liu, Y.D.; Vivekanandan, J. Testing a procedure for automatic classification of hydrometeor types. J. Atmos. Oceanic Technol. 2001, 18, 892–913. [Google Scholar] [CrossRef]
- Park, H.; Ryzhkov, A.V.; Zrnic, D.S.; Kim, K.E. The Hydrometeor Classification Algorithm for the Polarimetric WSR-88D: Description and Application to an MCS. Weather Forecast. 2009, 24, 730–748. [Google Scholar] [CrossRef]
- Dolan, B.; Rutledge, S.A. A Theory-Based Hydrometeor Identification Algorithm for X-Band Polarimetric Radars. J. Atmos. Oceanic Technol. 2009, 26, 2071–2088. [Google Scholar] [CrossRef]
- Snyder, J.C.; Bluestein, H.B.; Zhang, G.F.; Frasier, S.J. Attenuation Correction and Hydrometeor Classification of High-Resolution, X-band, Dual-Polarized Mobile Radar Measurements in Severe Convective Storms. J. Atmos. Oceanic Technol. 2010, 27, 1979–2001. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Kumjian, M.R.; Ganson, S.M.; Khain, A.P. Polarimetric Radar Characteristics of Melting Hail. Part I: Theoretical Simulations Using Spectral Microphysical Modeling. J. Appl. Meteorol. Climatol. 2013, 52, 2849–2870. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Kumjian, M.R.; Ganson, S.M.; Zhang, P.F. Polarimetric Radar Characteristics of Melting Hail. Part II: Practical Implications. J. Appl. Meteorol. Climatol. 2013, 52, 2871–2886. [Google Scholar] [CrossRef]
- Ortega, K.L.; Krause, J.M.; Ryzhkov, A.V. Polarimetric Radar Characteristics of Melting Hail. Part III: Validation of the Algorithm for Hail Size Discrimination. J. Appl. Meteorol. Climatol. 2016, 55, 829–848. [Google Scholar] [CrossRef]
- Zhang, G.F.; Mahale, V.N.; Putnam, B.J.; Qi, Y.C.; Cao, Q.; Byrd, A.D.; Bukovcic, P.; Zrnic, D.S.; Gao, J.D.; Xue, M.; et al. Current Status and Future Challenges of Weather Radar Polarimetry: Bridging the Gap between Radar Meteorology/Hydrology/Engineering and Numerical Weather Prediction. Adv. Atmos. Sci. 2019, 36, 571–588. [Google Scholar] [CrossRef]
- White, A.B.; Gottas, D.J.; Strem, E.T.; Ralph, F.M.; Neiman, P.J. An automated brightband height detection algorithm for use with Doppler radar spectral moments. J. Atmos. Oceanic Technol. 2002, 19, 687–697. [Google Scholar] [CrossRef]
- Sanchez-Diezma, R.; Zawadzki, I.; Sempere-Torres, D. Identification of the bright band through the analysis of volumetric radar data. J. Geophys. Res. Atmos. 2000, 105, 2225–2236. [Google Scholar] [CrossRef]
- Zhang, J.; Langston, C.; Howard, K. Brightband Identification Based on Vertical Profiles of Reflectivity from the WSR-88D. J. Atmos. Oceanic Technol. 2008, 25, 1859–1872. [Google Scholar] [CrossRef]
- Zhang, J.; Qi, Y.C. A Real-Time Algorithm for the Correction of Brightband Effects in Radar-Derived QPE. J. Hydrometeorol. 2010, 11, 1157–1171. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Clark, K.A.; Kingsmill, D.E. A polarimetric radar approach to identify rain, melting-layer, and snow regions for applying corrections to vertical profiles of reflectivity. J. Appl. Meteorol. Climatol. 2007, 46, 154–166. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Krause, J.M.; Ryzhkov, A.V. Automatic designation of the melting layer with a polarimetric prototype of the WSR-88D radar. J. Appl. Meteorol. Climatol. 2008, 47, 1354–1364. [Google Scholar] [CrossRef]
- Boodoo, S.; Hudak, D.; Donaldson, N.; Leduc, M. Application of Dual-Polarization Radar Melting-Layer Detection Algorithm. J. Appl. Meteorol. Climatol. 2010, 49, 1779–1793. [Google Scholar] [CrossRef]
- Wolfensberger, D.; Scipion, D.; Berne, A. Detection and characterization of the melting layer based on polarimetric radar scans. Q. J. R. Meteorol. Soc. 2016, 142, 108–124. [Google Scholar] [CrossRef]
- Allabakash, S.; Lim, S.H.; Jang, B.J. Melting Layer Detection and Characterization based on Range Height Indicator-Quasi Vertical Profiles. Remote Sens. 2019, 11, 2848. [Google Scholar] [CrossRef]
- Brandes, E.A.; Ikeda, K. Freezing-level estimation with polarimetric radar. J. Appl. Meteorol. 2004, 43, 1541–1553. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Mishra, S.; Giangrande, S.E.; Toto, T.; Ryzhkov, A.V.; Bansemer, A. Polarimetric radar and aircraft observations of saggy bright bands during MC3E. J. Geophys. Res. Atmos. 2016, 121, 3584–3607. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zhang, P.F.; Reeves, H.; Kumjian, M.; Tschallener, T.; Tromel, S.; Simmer, C. Quasi-Vertical Profiles-A New Way to Look at Polarimetric Radar Data. J. Atmos. Oceanic Technol. 2016, 33, 551–562. [Google Scholar] [CrossRef]
- Gorgucci, E.; Chandrasekar, V.; Bringi, V.N.; Scarchilli, G. Estimation of raindrop size distribution parameters from polarimetric radar measurements. J. Atmos. Sci. 2002, 59, 2373–2384. [Google Scholar] [CrossRef]
- Ray, P.S. Broad-band complex refractive indexes of ice and water. Appl. Opt. 1972, 11, 1836–1844. [Google Scholar] [CrossRef]
- Bohren, C.F.; Battan, L.J. Radar backscattering by inhomogeneous precipitation particles. J. Atmos. Sci. 1980, 37, 1821–1827. [Google Scholar] [CrossRef]
- Mishchenko, M.I. Calculation of the amplitude matrix for a nonspherical particle in a fixed orientation. Appl. Opt. 2000, 39, 1026–1031. [Google Scholar] [CrossRef]
- Pruppach, H.; Beard, K.V. A wind tunnel investigation of internal circulation and shape of water drops falling at terminal velocity in air. Q. J. R. Meteorol. Soc. 1970, 96, 247–256. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.F.; Vivekanandan, J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment. J. Appl. Meteorol. 2002, 41, 674–685. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.F.; Vivekanandan, J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment (Corrigendum). J. Appl. Meteorol. 2005, 44, 186. [Google Scholar] [CrossRef]
- Tang, Q.; Xiao, H.; Guo, C.W.; Feng, L. Characteristics of the raindrop size distributions and their retrieved polarimetric radar parameters in northern and southern China. Atmos. Res. 2014, 135, 59–75. [Google Scholar] [CrossRef]
- Liu, L.; Bringi, V.N.; Chandrasekar, V.; Mueller, E.A.; Mudukutore, A. Analysis of the copolar correlation-coefficient between horizontal and vertical polarizations. J. Atmos. Oceanic Technol. 1994, 11, 950–963. [Google Scholar] [CrossRef]
- Schuur, T.; Ryzhkov, A.V.; Heinselman, P.L.; Zrnic, D.S.; Scharfenberg, K.A. Observations and Classification of Echoes with the Polarimetric WSR-88D radar. In Proceedings of the Report of the National Severe Storms Laboratory, Norman, OK, USA, 1 October 2003. [Google Scholar]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.F.; Vivekanandan, J. Comparison of polarimetric radar drop size distribution retrieval algorithms. J. Atmos. Oceanic Technol. 2004, 21, 584–598. [Google Scholar] [CrossRef]
- Anagnostou, M.N.; Anagnostou, E.N.; Vivekanandan, J.; Ogden, F.L. Comparison of two raindrop size distribution retrieval algorithms for X-band dual polarization observations. J. Hydrometeorol. 2008, 9, 589–600. [Google Scholar] [CrossRef]
- Feng, L.; Xiao, H.; Wen, G.; Li, Z.F.; Sun, Y.; Tang, Q.; Liu, Y.N. Rain Attenuation Correction of Reflectivity for X-Band Dual-Polarization Radar. Atmosphere 2016, 7, 164. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, H.; Yang, H.L.; Feng, L.; Chen, H.N.; Luo, L. An Inverse Mapping Table Method for Raindrop Size Distribution Parameters Retrieval Using X-band Dual-Polarization Radar Observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7611–7632. [Google Scholar] [CrossRef]
- Hall, M.P.M.; Cherry, S.M.; Goddard, J.W.F.; Kennedy, G.R. Rain drop sizes and rainfall rate measured by dual-polarization radar. Nature 1980, 285, 195–198. [Google Scholar] [CrossRef]
- Feng, L.; Xiao, H.; Sun, Y. A Study on Hydrometeor Classification and Application Based on X-band Dual-polarization Radar Measurements. Clim. Environ. Res. 2018, 23, 366–386. (In Chinese) [Google Scholar]
- Conway, J.W.; Zrnic, D.S. A study of embryo production and hail growth using dual-doppler and multiparameter radars. Mon. Weather Rev. 1993, 121, 2511–2528. [Google Scholar] [CrossRef]
- Brandes, E.A.; Vivekanandan, J.; Tuttle, J.D.; Kessinger, C.J. A study of thunderstorm microphysics with multiparameter radar and aircraft observations. Mon. Weather Rev. 1995, 123, 3129–3143. [Google Scholar] [CrossRef]
- Bringi, V.N.; Knupp, K.; Detwiler, A.; Liu, L.; Caylor, I.J.; Black, R.A. Evolution of a Florida thunderstorm during the convection and precipitation/electrification experiment: The case of 9 August 1991. Mon. Weather Rev. 1997, 125, 2131–2160. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ganson, S.M.; Ryzhkov, A.V. Freezing of Raindrops in Deep Convective Updrafts: A Microphysical and Polarimetric Model. J. Atmos. Sci. 2012, 69, 3471–3490. [Google Scholar] [CrossRef]
- van Lier-Walqui, M.; Fridlind, A.M.; Ackerman, A.S.; Collis, S.; Helmus, J.; MacGorman, D.R.; North, K.; Kollias, P.; Posselt, D.J. On Polarimetric Radar Signatures of Deep Convection for Model Evaluation: Columns of Specific Differential Phase Observed during MC3E. Mon. Weather Rev. 2016, 144, 737–758. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).