Abstract
In this study, we focus on the Multi-robot Coverage Path Planning (MCPP) problem for maritime Search And Rescue (SAR) missions using a multiple Autonomous Underwater Vehicle (AUV) system, with the ultimate purpose of efficiently and accurately discovering the target from sonar images taken by Side-Scan Sonar (SSS) mounted on the AUVs. Considering the specificities of real maritime SAR projects, we propose a novel MCPP method, in which the MCPP problem is transformed into two sub-problems: Area partitioning and single-AUV coverage path planning. The structure of the task area is first defined using Morse decomposition of the spike pattern. The area partitioning problem is then formulated as an AUV ordering problem, which is solved by developing a customized backtracking method to balance the workload and to avoid segmentation of the possible target area. As for the single-AUV coverage path planning problem, the SAR-A* method is adopted, which generates a path that preferentially visits the possible target areas and reduces the number of turns to guarantee the high quality of the resulting sonar images. Simulation results demonstrate that the proposed method can maintain the workload balance and significantly improve the efficiency and accuracy of discovering the target. Moreover, our experimental results indicate that the proposed method is practical and the mentioned specificities are useful for discovering targets.
1. Introduction
In maritime Search And Rescue (SAR) missions, it is common to employ Autonomous Underwater Vehicles (AUVs) equipped with the Side-Scan Sonar (SSS) to cover the task area and discover the target from the obtained sonar images [1,2]. To improve the efficiency and robustness, multiple AUV systems have shown clear advantages [3,4]. In this context, Multi-robot Coverage Path Planning (MCPP) technology is needed to generate multi-AUV paths to cooperatively cover the task area [5].
1.1. Related Works
MCPP technology has been applied in many applications, such as terrain monitoring [6], SAR [7], data sampling [8], floor cleaning [9], and surface painting [10], among others. Currently, some MCPP methods are real-time cooperative MCPP methods which require reliable communication, while others are extended from single-robot CPP methods.
The MCPP methods in the first category directly generate multi-robot paths without the task assignment. Wei et al. designed an artificially weighted spanning tree coverage (AWSTC) algorithm [11], in which the spanning tree of each robot grew toward the uncovered area and kept away from the trees of other robots. This AWSTC method relies heavily on real-time communication. Kapanoglu et al. proposed a genetic algorithm based MCPP method [12] that decomposed the task area into disks whose assignment and order are determined by a pattern-based genetic algorithm. This method mainly focused on minimizing the coverage completion time and ignored the quality of the collected data. Luo et al. put forward a neural dynamic approach where each AUV was treated as a neuron [13]. During the task, the dynamics of robots were considered and other robots were treated as moving obstacles for avoidance. In this method, reliable communication was assumed for the entire task.
For the MCPP methods extended from the single-robot CPP method, the coverage task is divided into several subtasks and allocated to multi-robots in advance. A type of MCPP method first generates an overall tour and then assign segments to each robot. Considering the energy constraints, the task allocation of MCPP can be formulated as the capacitated arc routing problem (CARP), which aims to optimally select the weighted edges of a graph-based environment. In [14], a novel CARP algorithm is presented for narrow environments which is based on a modified Ulusoy’s algorithm [15]. The sensor-based coverage method presented in [16] applied another modified Ulusoy’s algorithm (MUA) to plan a dynamic approach. In [17], considering the strong currents in a fixed direction, the proposed MCPP method first generated the global path using the lawn-mower method and then broke it into segments for a fleet of Autonomous Surface Vehicles (ASV) to balance the workload. In summary, they are suitable for known environments which stay unchanged during the task.
Another type of task allocation method for the MCPP problem is area partitioning, which splits into two sub-problems: area partitioning and single-robot coverage path planning [11,18,19,20,21]. This type of method is particularly suitable for the tasks employed the SSS, since the interference between two close SSS is adverse to the discovery of the target. In [18], an area segment algorithm named DARP was proposed, based on the initial positions of robots, where the minimum Spanning Tree Coverage (STC) algorithm is used to generate the coverage paths for each robot. Nair et al. presented a Geodesic–Manhattan Voronoi Partition-based Coverage method (GM-VPC) [19]. Then, the boustrophedon method and the STC method are used to cover their assigned task areas. In the majority of MCPP methods, the task area is divided according to the current or calculated initial positions. Popular area partitioning methods include the Generalized Voronoi Diagram (GVD) [20], Constrained Delaunay Triangulation (CDT) [21], and Boustrophedon Cellular Decomposition (BCD) [22]. However, all AUVs start from a fixed initial position, which makes the existing methods inapplicable. Moreover, commonly used single-robot coverage algorithms include the STC algorithm, the Lawn-Mower(LM) method [23], and the grid-based coverage method [24]. Unfortunately, the existing single-robot coverage algorithms used for MCPP methods generate a lot of turns in paths, which can seriously decrease the sonar image quality.
1.2. Motivation
Upon analyzing the previous MCPP methods, we found that previous methods can not be well-applied to maritime SAR missions. Various aspects need to be considered in order to perform the MCPP for maritime SAR missions. Typically, the specificities of a real project have a direct effect on the performance of an algorithm [8]. The general specificities of maritime SAR missions using multi-AUV equipped with the SSS are as follows:
- (a)
- There is usually prior target information predicted by rescue specialists [25,26], offering the probability that a target exists in each position, which is helpful for determining AUV paths [27].
- (b)
- According to the usage of the SSS, the target is discovered by interpreting sonar images of sub-areas one by one after completing the task [28]. Hence, concentrating the possible target areas on a few sub-tasks and first interpreting the sonar images containing the possible target areas can help to discover the target quickly.
- (c)
- All the AUVs start from the same initial position, limited by the AUV deployment mode. Instead, most MCPP methods assume that the initial position of robots can be placed anywhere [18].
- (d)
- With regard to the characteristics of the SSS, the fewer turns that the AUV makes, the higher the quality of obtained sonar image [24,29] and less energy wastage [30]. Therefore, fewer turns in the path facilitate accurately discovering the target.
- (e)
- The workload balancing guarantees the robustness of the multi-AUV system as usual MCPP cases [18,31,32].
However, to the best of our knowledge, few published studies have systematically considered all the specificities mentioned above. The usage of prior target information and the same initial position of robots are never mentioned in existing MCPP research. Motivated by the above problem, it is necessary to formulate a new constrained MCPP problem and develop a MCPP method that can be well-applied in maritime SAR missions.
1.3. Contribution
Considering the aforementioned specificities, we formulate a MCPP problem including prior target information. Accordingly, we propose a novel MCPP method that includes a customized area partitioning method and a single-AUV coverage path planning method. The area partitioning method specifies responsible sub-areas for the AUVs, while the single-robot coverage path planning method generates their final paths to cover the assigned sub-areas.
As for the area partitioning method, Morse decomposition of the spike pattern is introduced to define the structure of the task area, considering specificity (c). Aiming at specificities (b) and (e), a customized backtracking method is utilized to determine the split lines and obtain optimal sub-areas. The result sub-areas can keep the workload balanced and reduce the number of AUVs assigned to the possible target area.
As for the single-robot coverage path planning method, the SAR-A* method, which we proposed previously [33], is employed to plan the AUV paths. For the discrete task area, the SAR-A* method generates a path through iteratively selecting optimal waypoints. The waypoint selection criteria include the distance, the probability of discovering the target, and the number of turns, in order to guarantee the resulting path meets the requirements of specificities (a) and (d).
The main novelty of the proposed method is to make full use of the real specificities to aid in the target discovery of maritime SAR missions. The specificities (c) and (f) help the planned path conform to the usage of the equipment. The specificities (a), (b) and (e) are conducive to further improve the effectiveness and efficiency of the maritime SAR mission.
The main contributions of this study can be summarized as follows:
- This research summarizes the specificities of real maritime SAR projects using multi-AUV equipped with SSS. This lays the foundation for future research related to maritime SAR missions.
- Considering the specificities, this research formulates a novel constrained MCPP problem and proposed a customized MCPP method. The multi-AUV paths generated by the proposed method facilitate discovering the target quickly and accurately and balancing multi-AUV workload.
- For the proposed area partitioning method, a variable conversion transforms the deflection angles of the split lines to the AUV sequences. It helps to simplify the solving process and reduce the solution space.
The remainder of this paper is organized as follows: In Section 2, we provide the definitions, assumptions, and objectives of the two sub-problems (i.e., the area partitioning problem and the single-robot coverage path planning problem). In Section 3, we present the process of the proposed area partitioning method and briefly describe the SAR-A* method. Next, simulation and experiment results are described, in order to demonstrate the performance of the proposed method, in Section 4. A discussion of the simulation and experimental results is provided in Section 5. Finally, the conclusion and directions for future work are stated in Section 6.
2. Problem Definition
For maritime SAR missions, this study addresses a multi-robot path planning problem to determine paths of AUVs to cover the task area. The MCPP problem is decomposed into two subproblems, i.e. the area partitioning and the single-AUV CPP. In the area partitioning, the task division is obtained by partitioning the task area. In the single-AUV CPP, each AUV covers its subtask area with a single-AUV coverage path. Combining the solutions of two subproblems, paths of all AUVs are obtained, which are expected to facilitate the target discovery in maritime SAR missions using AUVs equipped with SSS.
The task scenario is depicted in Figure 1. Additionally, after analyzing real SAR projects, we noticed that there are usually specificities, including the prior target information and characteristics of the equipment. Considering such specificities, an area partitioning problem and a single-AUV CPP problem with additional constraints are formulated.
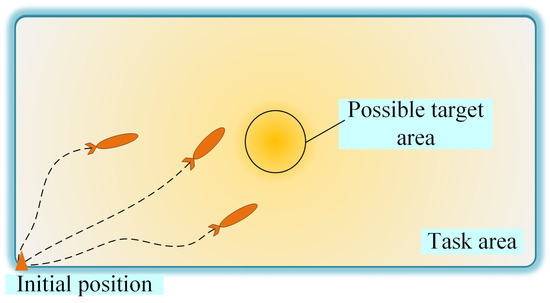
Figure 1.
Task scenario of maritime SAR missions.
2.1. MCPP Problem for Maritime SAR Mission
In the maritime SAR missions, a task area A assumed to be an open and flat sea area without obstacles, which must be covered. There exists a potential target whose likely position is simulated by rescue specialists. Due to both the target prediction and AUV navigation are with inevitable errors, the task area to be covered must be larger than the prior target information. Hence, the task area is to be covered by AUVs to confirm the exact target position.
According to assumed prior target information, the probabilistic map of target presence () is given [34]. Furthermore, the possible target area Z is defined as the zones within the task area where the probability of target presence is higher than a threshold:
where and , respectively, indicate the minimum and maximum values of target presence probability , and is a coefficient (with default value of 0.5). A multi-AUV system is assigned to cover the task area cooperatively. The AUVs are denoted as , , where stands for the total number of AUVs and r is the identifier of a given AUV. It is assumed that the AUVs can overcome the dynamic ocean environment and accurately follow the specified path. Task information is assigned to AUVs in advance, and the communication among AUVs is unnecessary while performing the task. All AUVs are equipped with the same load including the SSS and sensors. During the task, the available energy of each AUV can be different. Let be the energy capacity of , ranging from 1 (for full battery capacity) to 0 (for complete depletion).
This study focuses on planning paths for AUVs that are expected to cover the task area and facilitate the identification of targets. To solve the problem, the MCPP is split into two stages, i.e., the area partitioning and the single-AUV CPP. As for the area partitioning, the task area A is divided into subareas and assigned to AUVs. As for the single-AUV coverage path planning, the paths of each AUV are generated to cover the assigned subareas. Hence, the mathematical model of the MCPP problem is formulated as
where denotes the ith waypoint of , expresses the total number of waypoints of AUV . Combining solutions of the above two subproblems, the whole area is completely covered by the multi-AUV system. Details about the two subproblems are given which include the definitions and objectives. Table 1 lists the notations of all important parameters in the proposed MCPP method.

Table 1.
Main Notations.
2.2. Area Partitioning Problem
The area partitioning problem aims to divide the task area into subareas for AUVs. There are two basic principles: workload balance and avoiding the segmentation of the possible target area.
The workload in area partitioning is expressed as the area of , expressed by
where is the area of the task area A.
To describe the main objectives and constraints, the area partitioning problem is formulated as
where denotes the number of possible target areas before area partitioning ( by default), and and , respectively, represent the number of possible target areas and the real area of after area partitioning.
In Equation (5), the first objective function measures the segmentation of the possible target area (specificity (b)). In other words, possible target areas should be assigned to fewer AUVs, which is achieved by minimizing . The second objective indicates the deviation of AUV workloads (specificity (e)). By minimizing , AUVs can be assigned optimal workloads.
The constraints in Equation (5) are as follows: (1) the union of all sub-areas covers the original task area, and (2) the sub-areas are non-overlapping. For this step, the multi-robot coverage task for the whole task area is transformed into single AUV coverage tasks.
2.3. Single-AUV Coverage Path Planning Problem
Each AUV takes responsibility for its sub-area and covers the sub-area following an appropriate path. During this task, all AUVs move in a 2D plane with fixed speed and altitude. The SSS is used to generate sub-sea sonar images along the track, and the nadir of the SSS is considered negligible.
In the single-AUV coverage path planning problem, a path consisting of a set of waypoints is required to fully cover the sub-area. According to specificities (a) and (d), the possible target area should be first visited and turns in the path should be avoided, in order to discover the target efficiently and accurately.
3. Method
In this section, to solve the MCPP problem for maritime SAR mission using multi-AUV systems, a novel two-stage MCPP method is proposed, consisting of area partitioning and a single-robot coverage path planning. Figure 2 depicts the whole process of the proposed method to clearly show the main framework and the elaborate steps. In the area partitioning stage, the structure of the task area is defined using Morse decomposition of the spike pattern. A customized backtracking method is then proposed, in order to generate the sub-areas. In the single-AUV coverage path planning stage, the minimum circumscribed rectangle sub-area is given first. Then, this minimum circumscribed rectangle sub-area is decomposed into hexagonal cells. Next, the waypoints to be visited are defined as the centers of hexagonal cells within the subareas. Finally, the SAR-A* method is used to determine the final coverage path.
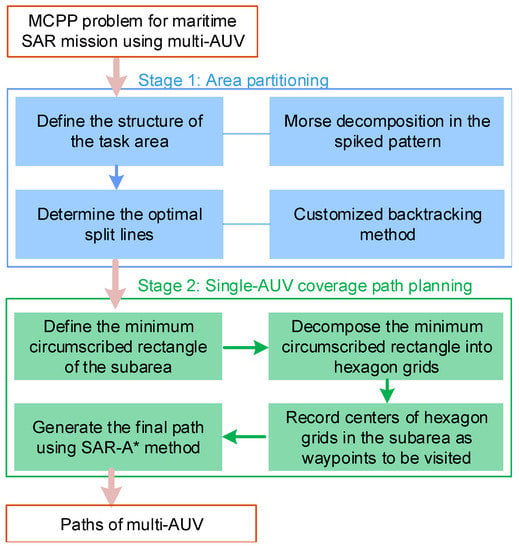
Figure 2.
Whole process of the proposed MCPP method.
3.1. Area Partitioning Method
The proposed area partitioning aims to balance the workload and avoid segmentation of the possible target area. First, Morse decomposition of the spike pattern is applied to define the structure of the task area. Then, the optimal split line is determined according to the order of the AUVs, which is solved using a customized backtracking method.
3.1.1. Spatial Structure of the Task Area
Morse decomposition provides a general framework to define the structure of the task area [35], which is used in existing coverage path planning studies [36,37,38]. The key idea is to scan the task region in different directions using slices of different shapes. Figure 3 shows four examples of Morse decomposition, using different slices and directions. The slices can be treated as split lines to partition the task area. In the case of task areas with special zones, such as obstacles, Morse decomposition is particularly suitable.
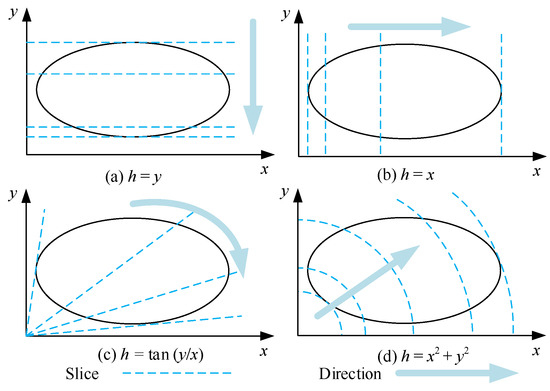
Figure 3.
Morse decomposition examples with different slices and directions.
In this study, Morse decomposition of the spike pattern (see Figure 3c) is adopted to define the structure of the task area. The reason for choosing the spike pattern is that all robots start from one position (specificity (c)). Hence, we wish to reduce the distance between the start position and the assigned sub-areas.
To distinctly display the Morse decomposition in the spike pattern, Figure 4 provides the definitions and notations of the task area. The slice is defined as a ray from the initial position. Let be the deflection angle from y-axis to slice (see in Figure 4), then the split lines are determined by the set of deflection angles . Thus, the area partitioning problem is transformed into finding the optimal angles .
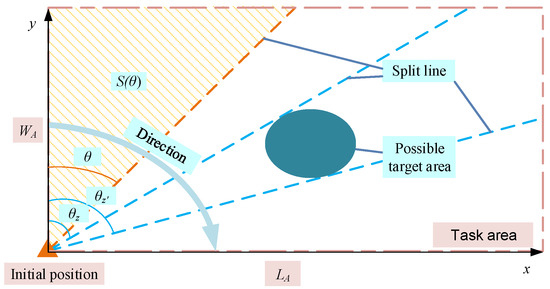
Figure 4.
Definitions and symbols of the spiked Morse decomposition.
3.1.2. Variable Conversion under the Structure
In this part, the optimal deflection angles are solved by changing the order of AUVs. The main idea is to assign the task area according to the expected area of , such that . The minimal is achieved by avoiding the split lines passing the possible target area. The variable conversion subtracts the objective functions , which helps to reduce the computational burden.
The optimal angles of split lines are expressed as . Let denote the area of the subarea determined by (see the yellow area in Figure 4) and be the mapping from to S; then, determined by can be expressed as
Then, let be the inverse function of (i.e., ), The can be obtained as
Thus, given the expected area from Equation (4), the optimal angle can be deduced.
Further, let be the order of AUVs, where records the identifier of the AUV to be assigned sub-area. As shown in Figure 5, taking as an example, is the second subarea to be assigned. Then, for Equation (7), replacing r in with O, is changed according to the AUV order O.
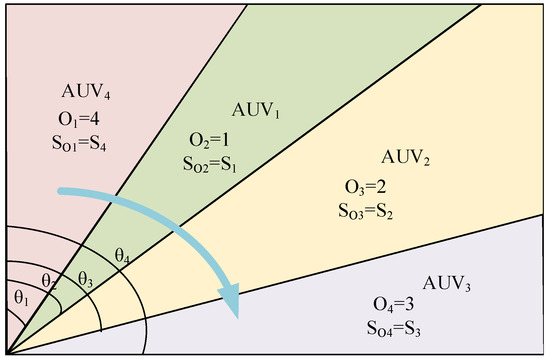
Figure 5.
With , as an example, the relationships between are displayed.
3.1.3. Determination of Optimal Split Lines
The area partitioning problem is transformed to determine the optimal order of AUVs, similar to the N-Queen problem. Traditionally, the purpose of the N-Queen problem is to determine the positions of N queens to avoid attacks [39,40].
In this study, a customized backtracking method is proposed to determine the order of AUVs. As a depth-first search method, the main idea of the backtracking method is to continuously try each possible position until the positions of all queens are settled. To find the order O such that satisfies Equation (8), we modified the traditional N-Queen problem by removing the attacks in diagonal and adding constraints on .
The details about the customized backtracking method are described in Figure 6. The core idea is the process of continuously determining whether an AUV is available for the position. The available function is described to test if there is no split line across the possible target area using the current solution (see Algorithm A2 in the Appendix B). If all candidate AUVs are unavailable, the AUV at the position is changed to another candidate AUV. The termination condition is all positions have an available AUV. With the optimal order , the optimal angles are determined.The region partitioning enables the most reasonable assignment of workloads, with possible target regions being assigned to fewer AUVs. The related pseudocode is given as Algorithm A1 in the Appendix A.
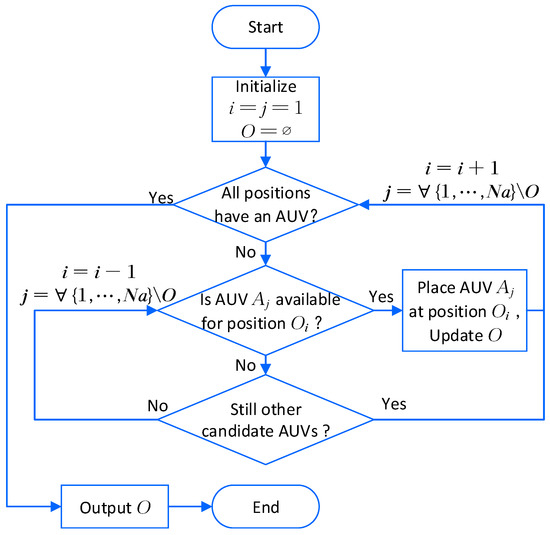
Figure 6.
The flowchat of the customized backtracking method.
3.2. Single-AUV Coverage Path Planning Method
After assigning designated areas for the AUVs, the coverage path is required to completely cover the sub-areas. There are available existing methods for this purpose, such as the lawnmower method [41,42], the spanning tree coverage method [43], and so on. However, considering the prior target information, we adopt our previously proposed SAR-A* [33], which is specifically designed for coverage path planning for AUVs equipped with SSS.
Using the SAR-A* method, the first step is to decompose the task area into hexagonal grids, the centers of which are treated as waypoints. Figure 7 shows a partitioned task area and their minimum circumscribed rectangles. Taking the first sub-area as an example, Figure 8 presents the hexagon decomposition. The hexagonal cells in the sub-area (red points) are retained, and other cells (blue points) are discarded. Thus, sub-area coverage is achieved by visiting all red waypoints within the subarea. The hexagon decomposition has the advantage of allowing for more candidate directions and having equal distances among neighboring grids [44]. If is the width of the SSS, the radius of the hexagonal grid elements should be .
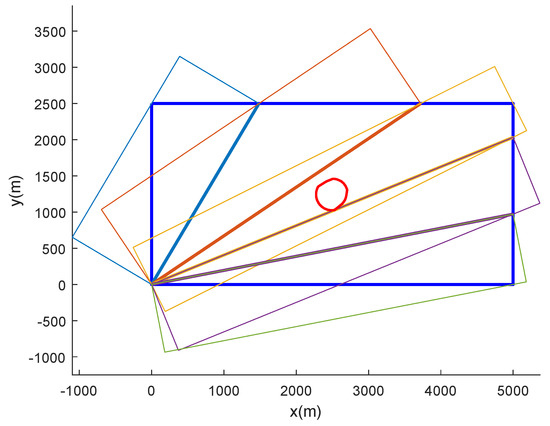
Figure 7.
Minimum circumscribed rectangles of the sub-areas generated by the area partitioning method.
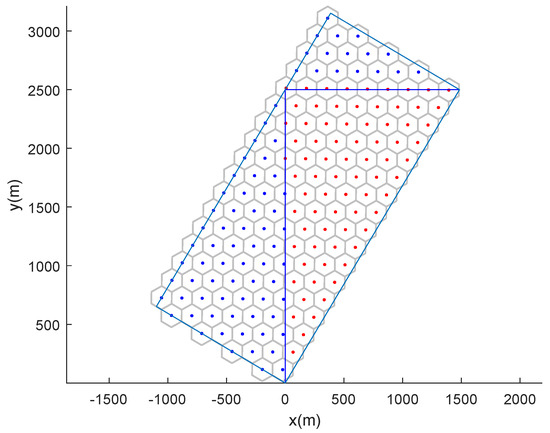
Figure 8.
The first sub-area in Figure 7 decomposed into hexagonal cells. The waypoints to be visited are marked with red points.
After determining all of the waypoints to visit, the SAR-A* method iteratively selects the most appropriate one as the next waypoint. According to specificities (a) and (d), the next waypoint selection strategy prefers waypoints with a shorter distance, a higher probability of discovering the target, and a smaller turning angle. Considering both the prior target information and the detection capability at cell , the probability of discovering the target is
where stands for the probability of detecting the target. Hence, preferentially visiting waypoints with high will help to find the target quickly. The resulting path is generated when all waypoints are visited. The paths generated by the SAR-A* method not only preferentially visit valuable areas, but also guarantee high-quality sonar images to easily identify the target from images.
3.3. Computational Complexity Analysis
The proposed method has two stages, i.e., area partitioning and single-AUV coverage path planning. For the area partitioning stage, the customized backtracking method is the main computational cost. The upper bound of the computational price of the backtracking method is which occurs for all AUVs’ sequences making the possible target area divided. For the single-AUV coverage path planning, the computation complexity is according to [33], where denotes the number of grids for . Hence, for the whole process of the proposed method, the worst computational load is .
4. Results
To test the performance of the proposed MCPP method, simulations and an experiment in a lake environment were conducted. The simulations included two parts: Coverage path results using different numbers of AUVs and comparisons with existing MCPP methods. Additionally, the field experiment was performed in a lake, in order to cover an area with a preset target. The details and results are elaborated in this section.
4.1. Simulations
In the simulation part, a rectangular area of 5000 m × 2500 m was to be covered, including regions with different SSS detection capabilities due to inhomogeneous hydrological conditions. As shown in Figure 9, the areas in blue and yellow are those with strong and poor detection capabilities, respectively. The sub-area in the red circle represents a possible target area. The blue dotted lines are the boundaries of the possible target area. Based on the prior target information, the target presence probability distribution is shown in Figure 10.
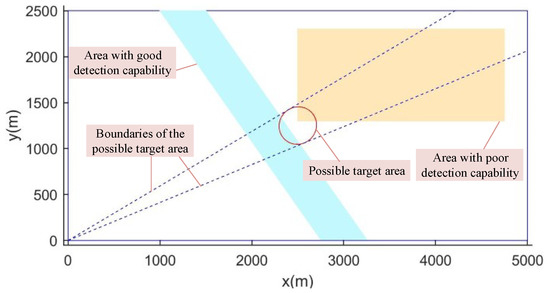
Figure 9.
Task area in a plane view. The target is assumed to be in the center of the task area. The possible target area and areas with different detection capabilities are marked.
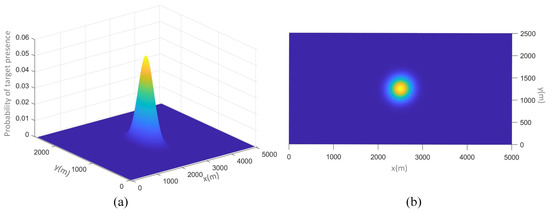
Figure 10.
The probabilistic distribution of the target presence, in (a) 3D and (b) 2D views.
4.1.1. Simulations with Different Numbers of AUVs
To cover the task area, multiple AUVs equipped with SSS were deployed from the point (0,0). The range of the SSS was 200 m. To test the performance with different numbers of AUVs, we considered the results for . The energy capacities were set as . If , the considered the first elements.
The customized backtracking method was used to partition the task area. Table 2 lists the numerical results of the customized backtracking method, including the optimal order and angles .

Table 2.
The area partitioning results of the proposed method.
Figure 11 shows that the task area was partitioned into sub-areas, according to the numerical results in Table 2 for . In the figure, the sub-areas are separated by thick lines. Additionally, the minimum circumscribed rectangles of the partitioned sub-regions are also shown in Figure 11. It can be seen that the possible target area was not divided when AUVs were used; that is, the proposed area partitioning method could assign the possible target area to fewer AUVs.
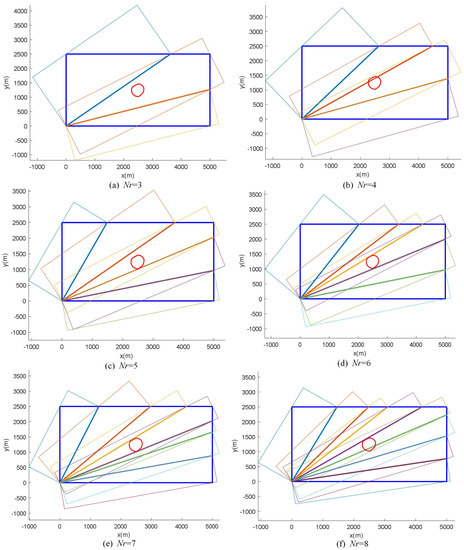
Figure 11.
Area partitioning result and corresponding minimum circumscribed rectangles.
The final paths generated by the proposed MCPP method are shown in Figure 12, where the number of AUVs ranged from 3 to 8. The paths of the AUVs are colored differently. As can be seen from the figure, all AUVs started from the original point and covered the task area completely. Obviously, there were few turns in the possible target area, even in the sub-areas, thus guaranteeing high-quality sonar images in the valuable area. Additionally, the waypoints with high possibility of discovering the target were preferentially visited.
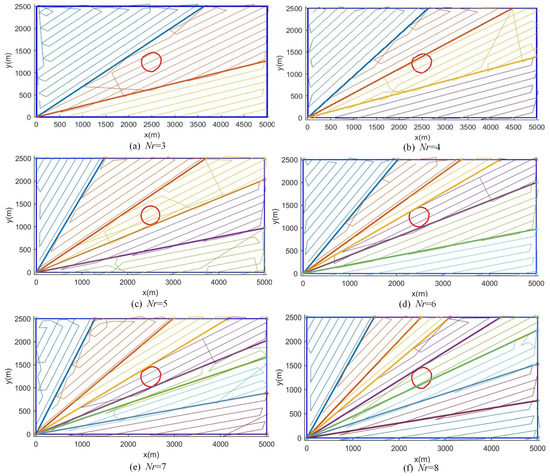
Figure 12.
AUV paths generated by the proposed method.
4.1.2. Comparison with Existing MCPP Methods
In order to verify the advance of the proposed method, we compared it with other current MCPP methods, taking five AUVs covering the task area as an example. The performances of the DARP method [18] and the BoB method [22] are given for comparison. The DARP method consists of a partitioning method based on the initial positions of the robots and the STC algorithm. As an alternative method for comparison, the BoB method is based on boustrophedon and backtracking mechanisms, which continuously moves to the unvisited areas incrementally through boustrophedon motions. Workload balancing was also addressed in the BoB method.
To describe the performance, we chose the following three indicators: (1) The first was the number of turns, which counts the number of turning angles greater than 0. Fewer turns implies higher quality of the resulting sonar image. (2) The second was the cumulative probability of discovering the target [45], which is calculated by the following formula:
where s denotes the step number. A rapidly increasing cumulative probability of discovering the target means that a target can be found quickly. (3) The third was the difference in workload () between the real and expected workloads. Unlike the workload in area partitioning, the final workload of an AUV is measured by the length of the coverage path . Hence, the difference in workload is given by
A smaller indicates better workload balancing performance.
Table 3 lists the final number of turns using the DARP method, the BoB method, and the proposed method. There were 31 turns in the whole path of the proposed method, while the other two methods presented 84 and 102 turns in the generated path, respectively. These results suggest that the quality of the sonar images obtained by the proposed method is higher, which helps discover the target from sonar images.

Table 3.
The number of turns in the final paths of the three methods.
Figure 13 compares the proposed method with the two other MCPP methods in terms of the cumulative probability of discovering the target. Apparently, the cumulative probability of discovering the target for the proposed method increased more rapidly, compared with the other two methods. This indicates that the proposed method is able to discover the target within the shortest time.
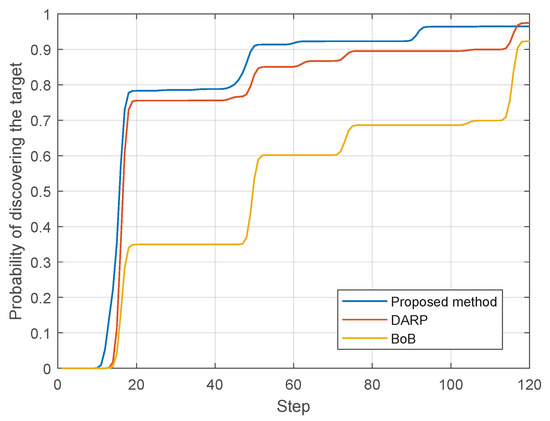
Figure 13.
Cumulative probabilities of discovering the target using three methods.
Figure 14 displays the difference in workload (i.e., the indicator given in Equation (11)) between the three methods. Overall, for the proposed method, the value of all AUVs varied between 0.1 and 1, lower than those of the other two methods. This means that the proposed method has the best capability for workload-balancing, compared to the DARP and BoB methods.
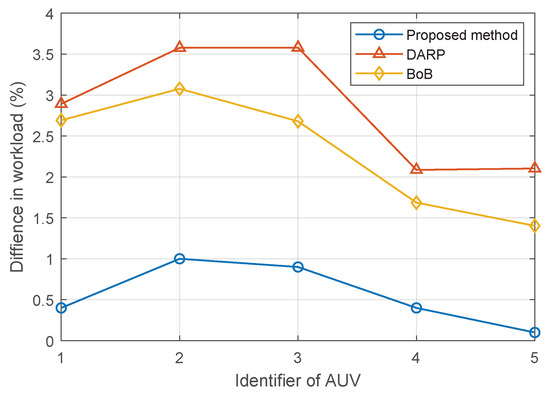
Figure 14.
Difference in workload for the three methods.
To further compare with existing methods, the time consumption of the compared methods is given. Taking 5 AUVs as an example, the time consumptions of the proposed method, the DARP method and the BoB method are 88.325 s, 90.103 s and 59.272 s. As can be seen, the running time of the proposed method is similar to the other two methods. By the way, all methods were run on an AMD Ryzen 7-4800U CPU @ 1.8 GHz with eight cores.
In summary, the proposed method dominated the DARP and BoB methods, in terms of the growth of the cumulative probability of discovering the target, the number of turns, and the workload balance. The proposed method has thus been theoretically shown to perform well in maritime SAR missions using multiple AUVs equipped with SSS. Field experiments were further conducted to verify the performance in a real-world environment.
4.2. Experiments
To verify the performance of the proposed method in practice, a field experiment was conducted. In this experiment, the employed multi-AUV system contained three AUVs, each equipped with a pair of SSS. The ultimate aim of the experiment was to cover the whole area and find the target from sonar images generated along the AUV trajectories by SSS.
The field experiment was carried out in Apr. 2022 in Liquan Lake, Shaanxi, China. Figure 15 depicts the general task scenario, with the task area, the start position, and the pre-placed target being marked. In the task area (600 m × 330 m), a metal cylinder target with a height of 1 m and a diameter of 0.5 m was placed as the target. The target location and the corresponding probability of target presence are presented in Figure 16.
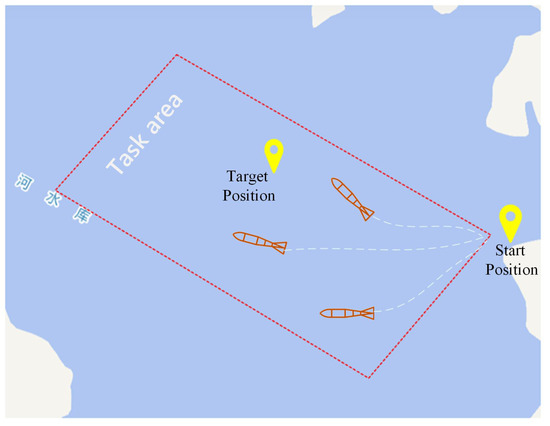
Figure 15.
Experimental scenario, including the task area, the start position, the target position, and the three AUVs.
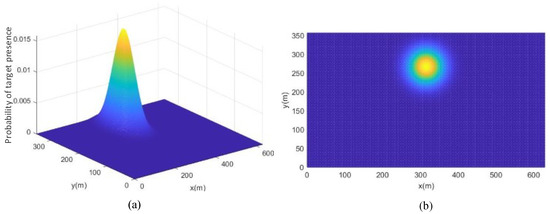
Figure 16.
Probability maps of target presence (a) and the target location (b).
Three AUVs developed by the Xi’an Tianhe Maritime Technology Co. were employed to cooperatively perform the coverage task. Table 4 lists the parameters of the employed small model AUVs and the equipped SSS. The AUV weighs 15 kg and is 1.53 m long. The maximum depth and maximum underwater speed are 50 m and 8 knots respectively. The navigation accuracy and turning radius are 5 m. During the experiment, all AUVs started from the Start Position shown in Figure 15, and moved at an altitude of 5 m and a speed of 2 knots. The equipped SSS worked at 330 kHz with a 30 m range and a beam width of 1.8 by 60. As the task area was relatively small, the detection capability of the SSS was neglected, such that the probability of target presence was numerically equal to the probability of discovering the target. Figure 17 displays the experimental scenario. The launching process is shown in Figure 17a,b, which further validates that AUVs start from the same position. In Figure 17c,d, AUVs are performing the coverage task following the planned paths.

Table 4.
The parameters of the employed equipment.

Figure 17.
Experimental scenarios.
Figure 18 shows the real trajectories of the three AUVs in different colors. While performing the task, AUVs obtained their position by the dead reckoning which continuously calculates the current position using the distance and direction of movement. The real trajectory is read from the AUV log file which records the calculated positions throughout the task. We can see that the task area was fully covered and the possible target area was preferentially visited by the three paths. It was concluded that the proposed method can assign the coverage task to multiple AUVs and generate feasible paths, such that the task area is successfully covered.
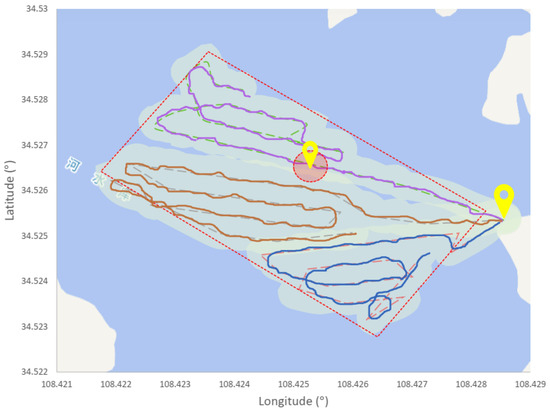
Figure 18.
Real trajectories of the three AUVs. The target location and the start position are marked with yellow icons. The possible target area is marked with a red circle.
Figure 19 displays the sonar image with the target found in the sonar images obtained by . It can be seen that the obtained sonar image was clear enough to identify the target. The main reason for guaranteeing the image quality is the consideration of avoiding turns in the SAR-A* method.

Figure 19.
The obtained high-quality sonar image containing the target (marked with a red circle).
By analyzing the experimental results (Figure 18 and Figure 19), the proposed method enabled the three AUVs to complete the coverage task with a possible target area. Areas with a higher probability of discovering the target are preferentially visited, such that the target can be found quickly. Moreover, the sonar images of the SSS are of superior quality and the target can more easily be identified.
5. Discussion
Motivated by the design of a customized MCPP method for maritime SAR missions using multi-AUV systems, this study takes into account the specificities regarding device usage and prior information. The proposed method balanced the workload of the multiple AUVs. Moreover, the generated paths guided AUVs preferentially cover the possible target area. Besides, the quality of sonar image along the generated paths are improved by reducing the number of turns. The possible target area was allocated to fewer AUVs for efficient object discovery from sonar images. The strong practicality and good performance of the proposed method have been demonstrated in both simulations and experiments. All above results are beneficial to efficiently and accurately discovering the target.
This study fills the gap where the existing MCPP methods do not work well for maritime SAR missions using multi-AUV systems. The results of the study revealed that the mentioned specificities play a vital role in discovering the target.
Unfortunately, we aware that the computation burden of our MCPP method may increase with the number of AUVs. The principle reason is the usage of the backtracking method which find feasible solutions by exhaustion. This problem can be solved by employing heuristic methods such as genetic algorithm to determine the AUVs’ sequence.
6. Conclusions
This study addressed the multi-robot coverage path planning problem with prior target information for maritime SAR missions using multiple AUVs equipped with SSS. Considering the specificities of the task scenario and the employed equipment, we proposed a novel MCPP method to assign the coverage task and generate feasible paths for multiple AUVs. The efficiency of discovering the target was improved by preferentially interpreting sonar images with respect to a possible target area and visiting waypoints with a high probability of discovering the target. The target discovery accuracy was enhanced by reducing the number of turns in path planning. The proposed method is the first MCPP method that simultaneously takes into account the effect of the potential target and the equipment. Furthermore, the proposed method is practical and significant, allowing for improvement of the efficiency of maritime SAR missions, as it takes into account the specificities of real maritime SAR projects.
Author Contributions
Conceptualization, C.C. and J.C.; methodology, C.C.; validation, C.C. and F.L.; writing—original draft preparation, C.C.; writing—review and editing, J.C. and Q.Y.; supervision, J.C.; funding acquisition, Q.Y. and F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 62071383.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors acknowledge editors and reviewers for comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
| Algorithm A1 Customized Backtracking Method |
| Input:, , |
| Output:,, O |
| 1: = = ∞; i = 1; j = 1;//initialization |
| 2: whiledo |
| 3: while do |
| 4: calculate (j,, ) |
| 5: if is Available then |
| 6: ; |
| 7: break |
| 8: else |
| 9: ; |
| 10: ; |
| 11: compare and record = min ; |
| 12: = argmin ; |
| 13: end if |
| 14: end while |
| 15: if then |
| 16: |
| 17: else |
| 18: BACKTRACKING; |
| 19: end if |
| 20: if all elements in are settled then |
| 21: calculate ; |
| 22: = min(); O = argmin ; |
| 23: end if |
| 24: end while |
| 25: if O is then |
| 26: |
| 27: |
| 28: calculate (O ) |
| 29: end if |
Appendix B
| Algorithm A2 Available Function |
| Input: |
| Output: |
| 1: ; |
| 2: calculate according to O; |
| 3: if then |
| 4: |
| 5: end if |
References
- Grza̧dziel, A. Results from developments in the use of a scanning sonar to support diving operations from a rescue ship. Remote Sens. 2020, 12, 693. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, J.; Gong, Q.; Huang, C.; Zheng, G.; Ma, J. Real-time underwater maritime object detection in side-scan sonar images based on transformer-YOLOv5. Remote Sens. 2021, 13, 3555. [Google Scholar] [CrossRef]
- Yang, T.; Jiang, Z.; Sun, R.; Cheng, N.; Feng, H. Maritime search and rescue based on group mobile computing for unmanned aerial vehicles and unmanned surface vehicles. IEEE Trans. Ind. Inform. 2020, 16, 7700–7708. [Google Scholar] [CrossRef]
- Cho, S.W.; Park, H.J.; Lee, H.; Shim, D.H.; Kim, S.Y. Coverage path planning for multiple unmanned aerial vehicles in maritime search and rescue operations. Comput. Ind. Eng. 2021, 161, 107612. [Google Scholar] [CrossRef]
- Almadhoun, R.; Taha, T.; Seneviratne, L.; Zweiri, Y. A survey on multi-robot coverage path planning for model reconstruction and mapping. SN Appl. Sci. 2019, 1. [Google Scholar] [CrossRef]
- Popović, M.; Vidal-Calleja, T.; Hitz, G.; Chung, J.J.; Sa, I.; Siegwart, R.; Nieto, J. An informative path planning framework for UAV-based terrain monitoring. Auton. Robot. 2020, 44, 889–911. [Google Scholar] [CrossRef]
- Rajan, R.; Otte, M.; Sofge, D. Optimizing multiagent area coverage using dynamic global potential fields. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018. [Google Scholar] [CrossRef]
- Tsiogkas, N.; Lane, D.M. An evolutionary algorithm for online, resource-constrained, multivehicle sensing mission planning. IEEE Robot. Autom. Lett. 2018, 3, 1199–1206. [Google Scholar] [CrossRef]
- Lakshmanan, A.K.; Mohan, R.E.; Ramalingam, B.; Le, A.V.; Veerajagadeshwar, P.; Tiwari, K.; Ilyas, M. Complete coverage path planning using reinforcement learning for Tetromino based cleaning and maintenance robot. Autom. Constr. 2020, 112, 103078. [Google Scholar] [CrossRef]
- Hassan, M.; Liu, D. Simultaneous area partitioning and allocation for complete coverage by multiple autonomous industrial robots. Auton. Robot. 2017, 41, 1609–1628. [Google Scholar] [CrossRef]
- Dong, W.; Liu, S.; Ding, Y.; Sheng, X.; Zhu, X. An artificially weighted spanning tree coverage algorithm for decentralized flying robots. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1689–1698. [Google Scholar] [CrossRef]
- Kapanoglu, M.; Alikalfa, M.; Ozkan, M.; Yazıcı, A.; Parlaktuna, O. A pattern-based genetic algorithm for multi-robot coverage path planning minimizing completion time. J. Intell. Manuf. 2010, 23, 1035–1045. [Google Scholar] [CrossRef]
- Luo, C.; Yang, S.X.; Li, X.; Meng, M.Q.H. Neural-dynamics-driven complete area coverage navigation through cooperation of multiple mobile robots. IEEE Trans. Ind. Electron. 2017, 64, 750–760. [Google Scholar] [CrossRef]
- Sipahioglu, A.; Kirlik, G.; Parlaktuna, O.; Yazici, A. Energy constrained multi-robot sensor-based coverage path planning using capacitated arc routing approach. Robot. Auton. Syst. 2010, 58, 529–538. [Google Scholar] [CrossRef]
- Ulusoy, G. The fleet size and mix problem for capacitated arc routing. Eur. J. Oper. Res. 1985, 22, 329–337. [Google Scholar] [CrossRef]
- Yazici, A.; Kirlik, G.; Parlaktuna, O.; Sipahioglu, A. A dynamic path planning approach for multirobot sensor-based coverage considering energy constraints. IEEE Trans. Cybern. 2014, 44, 305–314. [Google Scholar] [CrossRef] [PubMed]
- Kim, J. Multi-robot global sonar survey in the presence of strong currents. Ocean Eng. 2019, 188, 106316. [Google Scholar] [CrossRef]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. DARP: Divide areas algorithm for optimal multi-robot coverage path planning. J. Intell. Robot. Syst. 2017, 86, 663–680. [Google Scholar] [CrossRef]
- Nair, V.G.; Guruprasad, K.R. GM-VPC: An algorithm for multi-robot coverage of known spaces using generalized voronoi partition. Robotica 2019, 38, 845–860. [Google Scholar] [CrossRef]
- Alitappeh, R.J.; Jeddisaravi, K. Multi-robot exploration in task allocation problem. Appl. Intell. 2021, 52, 2189–2211. [Google Scholar] [CrossRef]
- Balampanis, F.; Maza, I.; Ollero, A. Area partition for coastal regions with multiple UAS. J. Intell. Robot. Syst. 2017, 88, 751–766. [Google Scholar] [CrossRef]
- Viet, H.H.; Dang, V.H.; Choi, S.; Chung, T.C. BoB: An online coverage approach for multi-robot systems. Appl. Intell. 2014, 42, 157–173. [Google Scholar] [CrossRef]
- Choset, H. Coverage of known spaces: The boustrophedon cellular decomposition. Auton. Robot. 2000, 9, 247–253. [Google Scholar] [CrossRef]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. Sensor-driven online coverage planning for autonomous underwater vehicles. IEEE/ASME Trans. Mechatron. 2013, 18, 1827–1838. [Google Scholar] [CrossRef]
- Akbari, A.; Eiselt, H.A.; Pelot, R. A maritime search and rescue location analysis considering multiple criteria, with simulated demand. INFOR Inf. Syst. Oper. Res. 2017, 56, 92–114. [Google Scholar] [CrossRef]
- OTOTE, D.A.; Li, B.; Ai, B.; Gao, S.; Xu, J.; Chen, X.; Lv, G. A decision-making algorithm for maritime search and rescue plan. Sustainability 2019, 11, 2084. [Google Scholar] [CrossRef]
- Yao, P.; Qiu, L.; Qi, J.; Yang, R. AUV path planning for coverage search of static target in ocean environment. Ocean Eng. 2021, 241, 110050. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, X.; Chu, Z.; Yang, Y.; Shi, J. Active learning for recognition of shipwreck target in side-scan sonar image. Remote Sens. 2019, 11, 243. [Google Scholar] [CrossRef]
- Chen, E.; Guo, J. Real time map generation using sidescan sonar scanlines for unmanned underwater vehicles. Ocean Eng. 2014, 91, 252–262. [Google Scholar] [CrossRef]
- Muthugala, M.V.J.; Samarakoon, S.B.P.; Elara, M.R. Toward energy-efficient online Complete Coverage Path Planning of a ship hull maintenance robot based on Glasius Bio-inspired Neural Network. Expert Syst. Appl. 2022, 187, 115940. [Google Scholar] [CrossRef]
- Collins, L.; Ghassemi, P.; Esfahani, E.T.; Doermann, D.; Dantu, K.; Chowdhury, S. Scalable Coverage Path Planning of Multi-Robot Teams for Monitoring Non-Convex Areas. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar] [CrossRef]
- Dutta, A.; Bhattacharya, A.; Kreidl, O.P.; Ghosh, A.; Dasgupta, P. Multi-robot informative path planning in unknown environments through continuous region partitioning. Int. J. Adv. Robot. Syst. 2020, 17, 172988142097046. [Google Scholar] [CrossRef]
- Cai, C.; Chen, J.; Yan, Q.; Liu, F.; Zhou, R. A prior information-based coverage path planner for underwater search and rescue using autonomous underwater vehicle (auv) with side-scan sonar. IET Radar Sonar Navig. 2022. [Google Scholar] [CrossRef]
- Krout, D.; Fox, W.; El-Sharkawi, M. Probability of target presence for multistatic sonar ping sequencing. IEEE J. Ocean Eng. 2009, 34, 603–609. [Google Scholar] [CrossRef]
- Acar, E.U.; Choset, H.; Rizzi, A.A.; Atkar, P.N.; Hull, D. Morse decompositions for coverage tasks. Int. J. Robot. Res. 2002, 21, 331–344. [Google Scholar] [CrossRef]
- Guastella, D.C.; Cantelli, L.; Giammello, G.; Melita, C.D.; Spatino, G.; Muscato, G. Complete coverage path planning for aerial vehicle flocks deployed in outdoor environments. Comput. Electr. Eng. 2019, 75, 189–201. [Google Scholar] [CrossRef]
- Balampanis, F.; Maza, I.; Ollero, A. Area decomposition, partition and coverage with multiple remotely piloted aircraft systems operating in coastal regions. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016. [Google Scholar] [CrossRef]
- Acar, E.; Choset, H.; Lee, J.Y. Sensor-based coverage with extended range detectors. IEEE Trans. Robot. 2006, 22, 189–198. [Google Scholar] [CrossRef]
- Priestley, H.; Ward, M. A multipurpose backtracking algorithm. J. Symb. Comput. 1994, 18, 1–40. [Google Scholar] [CrossRef][Green Version]
- Guldal, S.; Baugh, V.; Allehaibi, S. N-Queens solving algorithm by sets and backtracking. In Proceedings of the SoutheastCon 2016, Norfolk, VA, USA, 30 March–3 April 2016. [Google Scholar] [CrossRef]
- Vasquez-Gomez, J.I.; Marciano-Melchor, M.; Valentin, L.; Herrera-Lozada, J.C. Coverage path planning for 2d convex regions. J. Intell. Robot. Syst. 2019, 97, 81–94. [Google Scholar] [CrossRef]
- Yordanova, V.; Gips, B. Coverage path planning with track spacing adaptation for autonomous underwater vehicles. IEEE Robot. Autom. Lett. 2020, 5, 4774–4780. [Google Scholar] [CrossRef]
- Gabriely, Y.; Rimon, E. Spanning-tree based coverage of continuous areas by a mobile robot. In Proceedings of the Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation, Seoul, Republic of Korea, 21–26 May 2001. [Google Scholar] [CrossRef]
- Azpúrua, H.; Freitas, G.M.; Macharet, D.G.; Campos, M.F.M. Multi-robot coverage path planning using hexagonal segmentation for geophysical surveys. Robotica 2018, 36, 1144–1166. [Google Scholar] [CrossRef]
- Ai, B.; Jia, M.; Xu, H.; Xu, J.; Wen, Z.; Li, B.; Zhang, D. Coverage path planning for maritime search and rescue using reinforcement learning. Ocean Eng. 2021, 241, 110098. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).