Decentralized Approach for Translational Motion Estimation with Multistatic Inverse Synthetic Aperture Radar Systems
Abstract
:1. Introduction
- Velocity and acceleration () components for translation motion while in contrast, at the most, a single sensor could allow us to estimate the radial velocity and the modulus of the cross-range velocity (i.e., indeterminate sign).
- Roll, pitch, and yaw rates for rotation motion while only the overall effective rotation rate, or at the most, the vertical and horizontal rotation components could be estimated by single-sensor techniques.
- (a)
- (b)
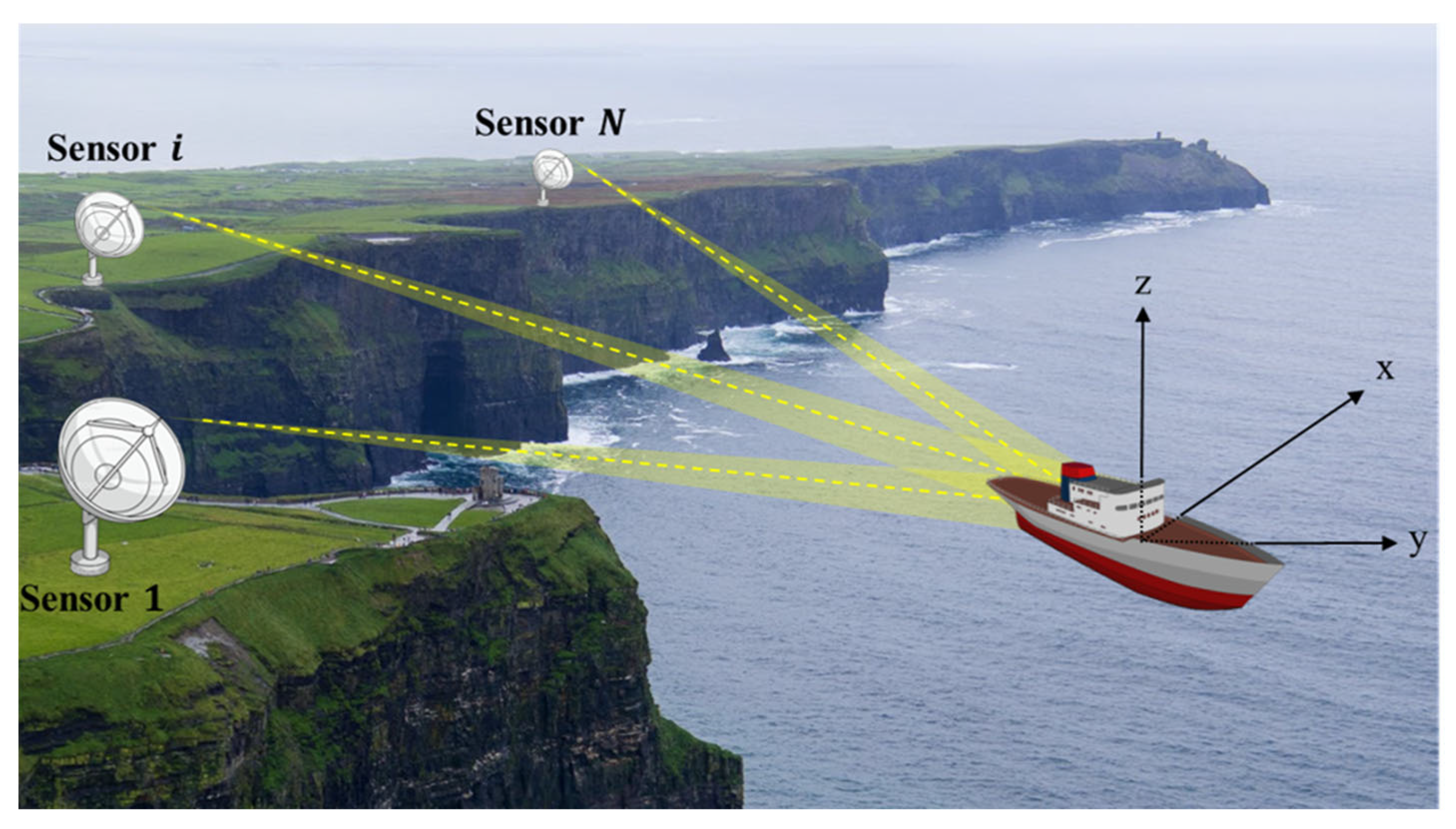
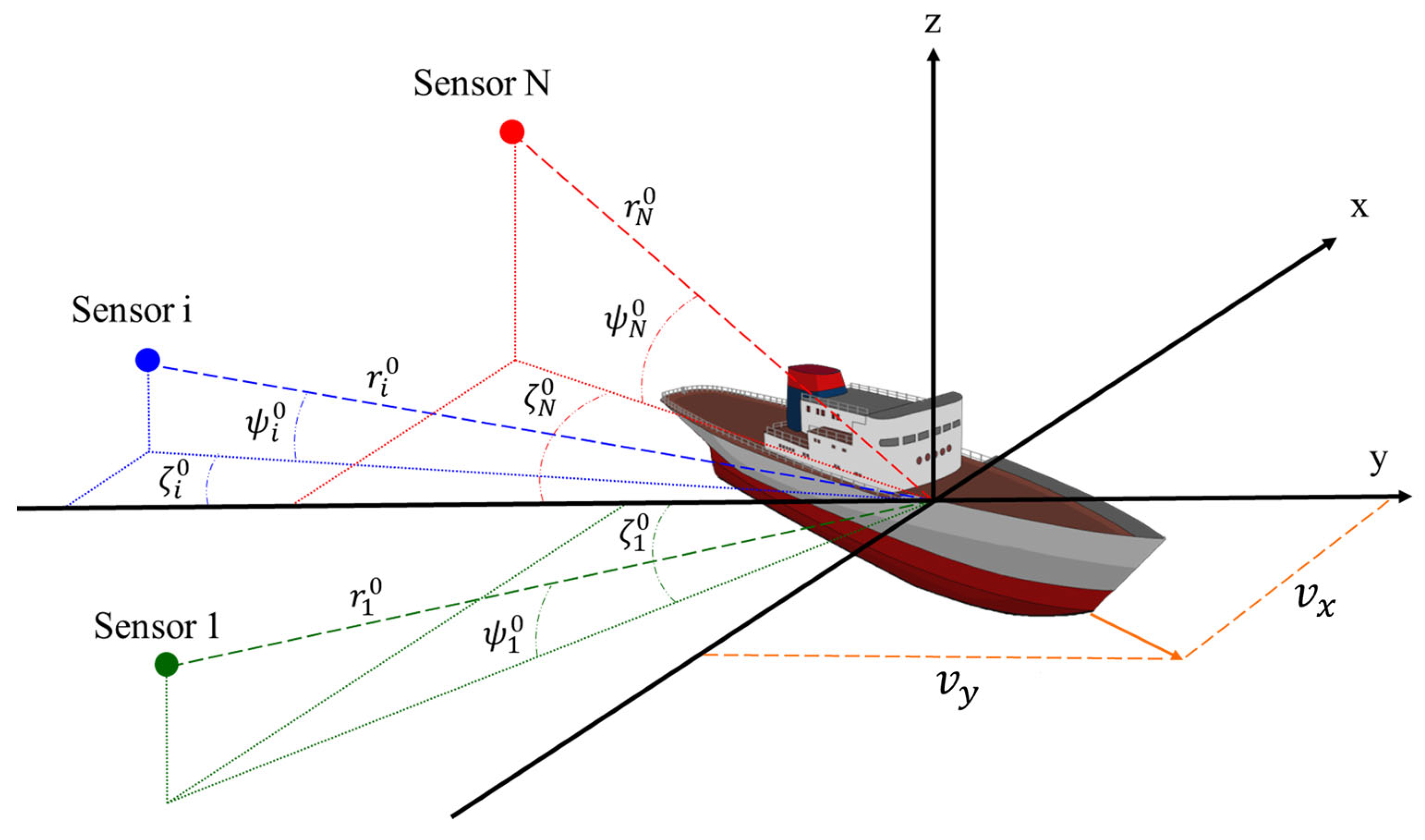
2. Geometry and Signal Model
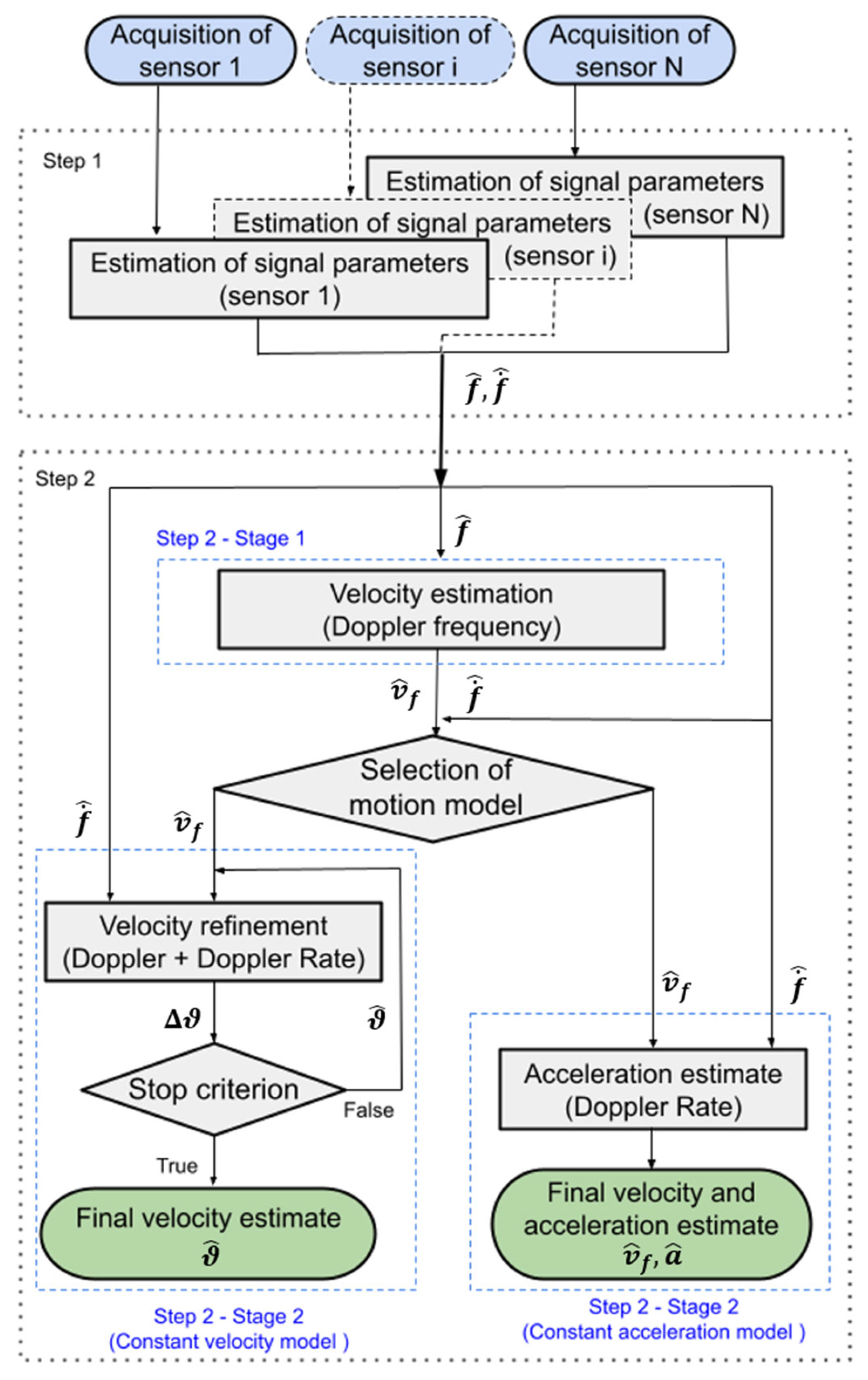
3. Multistatic Translational Motion Estimation Technique
- Step 1: The first step is aimed at estimating the signal parameters (basically Doppler centroid and Doppler rate) at the single-sensor level;
- Step 2: The second step is aimed at estimating the target motion parameters by inverting their analytical relationship with the target signal parameters. This step comprises two possibilities as the specific analytical relation depends on the assumed model for the target motion (the choice between the two is driven by a proper target motion model selection criterion).
3.1. Single-Sensor Signal Parameters Estimation Technique
3.2. Kinematic Parameters Estimation Technique
3.2.1. Kinematic Parameters Estimation Technique—Stage 1
3.2.2. Kinematic Parameters Estimation Technique—Stage 2
3.3. Automatic Motion Model Selection Criterion
4. Theoretical Performance Analysis
4.1. Theoretical Performance Analysis—Step 1: Single-Sensor Signal Parameters
4.2. Theoretical Performance Analysis for Step 2
4.2.1. Step 2—Stage 1: Velocity Estimation
4.2.2. Step 2—Stage 2: Velocity Refinement
4.2.3. Step 2—Stage 2: Acceleration Estimation
4.3. Automatic Motion Model Selection
5. Performance Assessment
5.1. Performance Assessment with Respect to SNR Conditions and Spatial Diversity
5.2. Performance Assessment with Respect to Extended Targets
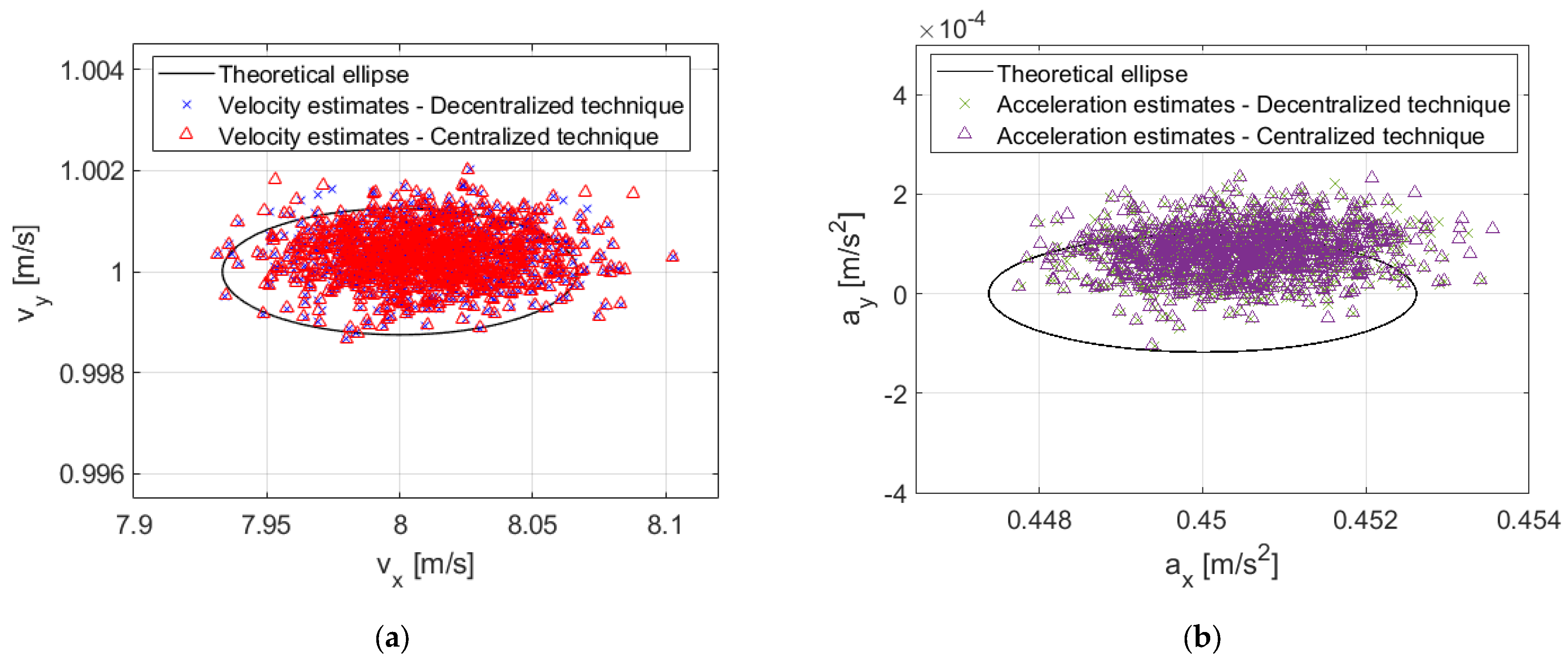
5.3. Performance Assessment with Respect to Centralized Approach
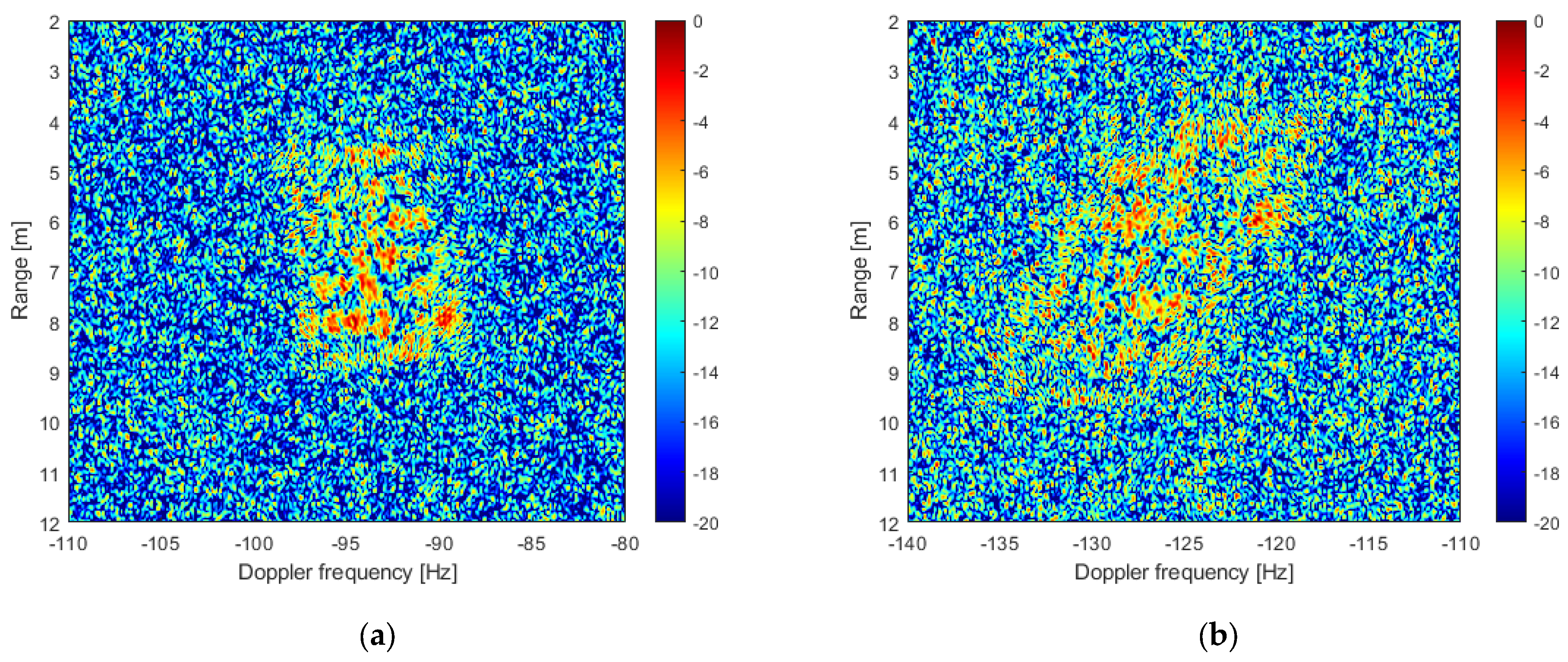
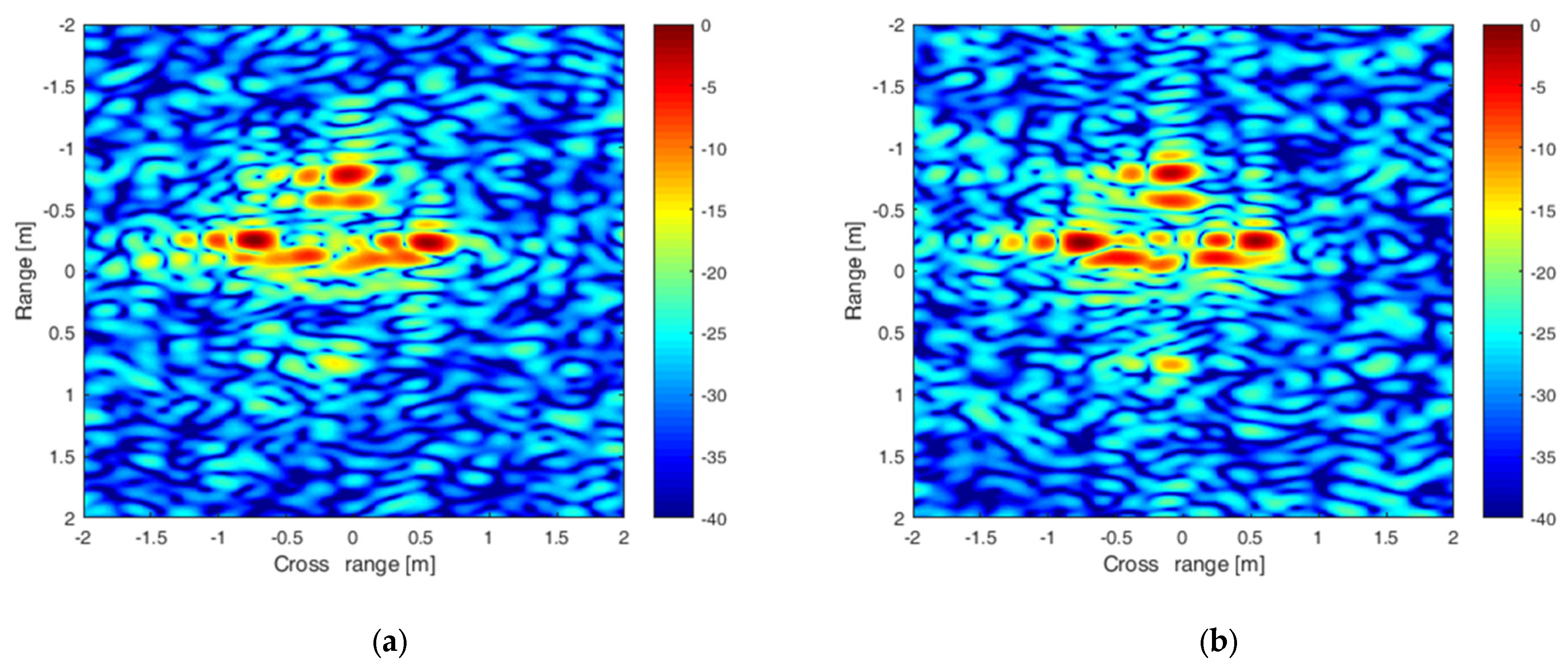
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Analytical Derivation of Single-Sensor Target Signal Parameters Accuracy
Appendix B. Analytical Derivation of Stage 2 Estimated Velocity and Acceleration Covariance Matrices
References
- Walker, J.L. Range-Doppler imaging of rotating objects. IEEE Trans. Aerosp. Electron. Syst. 1980, 16, 23–52. [Google Scholar] [CrossRef]
- Wehner, D.R. High-Resolution Radar, 2nd ed.; Artech House: Boston, MA, USA, 1992. [Google Scholar]
- Xu, X.; Narayanan, R.M. Three-dimensional interferometric ISAR imaging for target scattering diagnosis and modeling. IEEE Trans. Image Process. 2001, 10, 1094–1102. [Google Scholar] [PubMed]
- Rong, J.; Wang, Y.; Han, T. Interferometric ISAR Imaging of Maneuvering Targets With Arbitrary Three-Antenna Configuration. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1102–1119. [Google Scholar] [CrossRef]
- Vehmas, R.; Neuberger, N. Inverse Synthetic Aperture Radar Imaging: A Historical Perspective and State-of-the-Art Survey. IEEE Access 2021, 9, 113917–113943. [Google Scholar] [CrossRef]
- Pastina, D.; Bucciarelli, M.; Lombardo, P. Multistatic and MIMO Distributed ISAR for Enhanced Cross-Range Resolution of Rotating Targets. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3300–3317. [Google Scholar] [CrossRef]
- Zhu, Y.; Su, Y.; Yu, W. An ISAR Imaging Method Based on MIMO Technique. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3290–3299. [Google Scholar]
- Pastina, D.; Santi, F.; Bucciarelli, M. MIMO Distributed Imaging of Rotating Targets for Improved 2-D Resolution. IEEE Geosci. Remote Sens. Lett. 2015, 12, 190–194. [Google Scholar] [CrossRef]
- Brisken, S.; Matthes, D.; Mathy, T.; Worms, J.G. Spatially diverse ISAR imaging for classification performance enhancement. Int. J. Electron. Telecom. 2011, 57, 15–21. [Google Scholar] [CrossRef]
- Santi, F.; Bucciarelli, M.; Pastina, D. Multi-sensor ISAR technique for feature-based motion estimation of ship targets. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014; pp. 1–5. [Google Scholar]
- Santi, F.; Pastina, D.; Bucciarelli, M. Estimation of Ship Dynamics with a Multiplatform Radar Imaging System. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2769–2788. [Google Scholar] [CrossRef]
- Brisken, S.; Martorella, M.; Mathy, T.; Wasserzier, C.; Worms, J.G.; Ender, J.H.G. Motion estimation and imaging with a multistatic ISAR system. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1701–1714. [Google Scholar] [CrossRef]
- Brisken, S.; Martorella, M. Multistatic ISAR autofocus with an image entropy-based technique. IEEE Aerosp. Electron. Syst. Mag. 2014, 29, 30–36. [Google Scholar] [CrossRef]
- Bucciarelli, M.; Pastina, D.; Errasti-Alcala, B.; Braca, P. Multi-sensor ISAR technique for translational motion estimation. In Proceedings of the OCEANS 2015—Genova, Genova, Italy, 18–21 May 2015; pp. 1–5. [Google Scholar]
- Bucciarelli, M.; Pastina, D.; Errasti-Alcala, B.; Braca, P. Translational velocity estimation by means of bistatic ISAR techniques. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1921–1924. [Google Scholar]
- Goodman, N.A.; Bruyere, D. Optimum and decentralized detection for multistatic airborne radar. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 806–813. [Google Scholar] [CrossRef]
- Testa, A.; Santi, F.; Pastina, D. Translational motion estimation with multistatic ISAR systems. In Proceedings of the 2021 21st International Radar Symposium (IRS), Berlin, Germany, 21–22 June 2021; pp. 1–8. [Google Scholar]
- Testa, A.; Pastina, D.; Santi, F. Comparing decentralized and centralized approaches for translational motion estimation with multistatic ISAR systems. In Proceedings of the 2022 23rd International Radar Symposium (IRS), Gdansk, Poland, 12–14 September 2022; pp. 447–452. [Google Scholar]
- Raney, R.K. Synthetic aperture imaging radar and moving target. IEEE Trans. Aerosp. Electron. Syst. 1971, 7, 499–505. [Google Scholar] [CrossRef]
- Martorella, M.; Berizzi, F.; Haywood, B. Contrast maximisation based technique for 2-D ISAR autofocusing. IEE Proc. Radar Sonar Navig. 2005, 152, 253–262. [Google Scholar] [CrossRef]
- Xi, L.; Guosui, L.; Ni, J. Autofocusing of ISAR images based on entropy minimization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1240–1252. [Google Scholar] [CrossRef]
- Peleg, S.; Porat, B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase. IEEE Trans. Signal Process. 1991, 39, 749–752. [Google Scholar] [CrossRef]
- Pastina, D. Rotation motion estimation for high resolution ISAR and hybrid SAR/ISAR target imaging. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 3rd ed.; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Bucciarelli, M.; Pastina, D. Multi-grazing ISAR for side-view imaging with improved cross-range resolution. In Proceedings of the 2011 IEEE RadarCon (RADAR), Kansas City, MO, USA, 23–27 May 2011; pp. 939–944. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Opt. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Green, J.F.; Oliver, C.J. The limits on autofocus accuracy in SAR. Int. J. Remote Sens. 1992, 13, 2623–2641. [Google Scholar] [CrossRef]

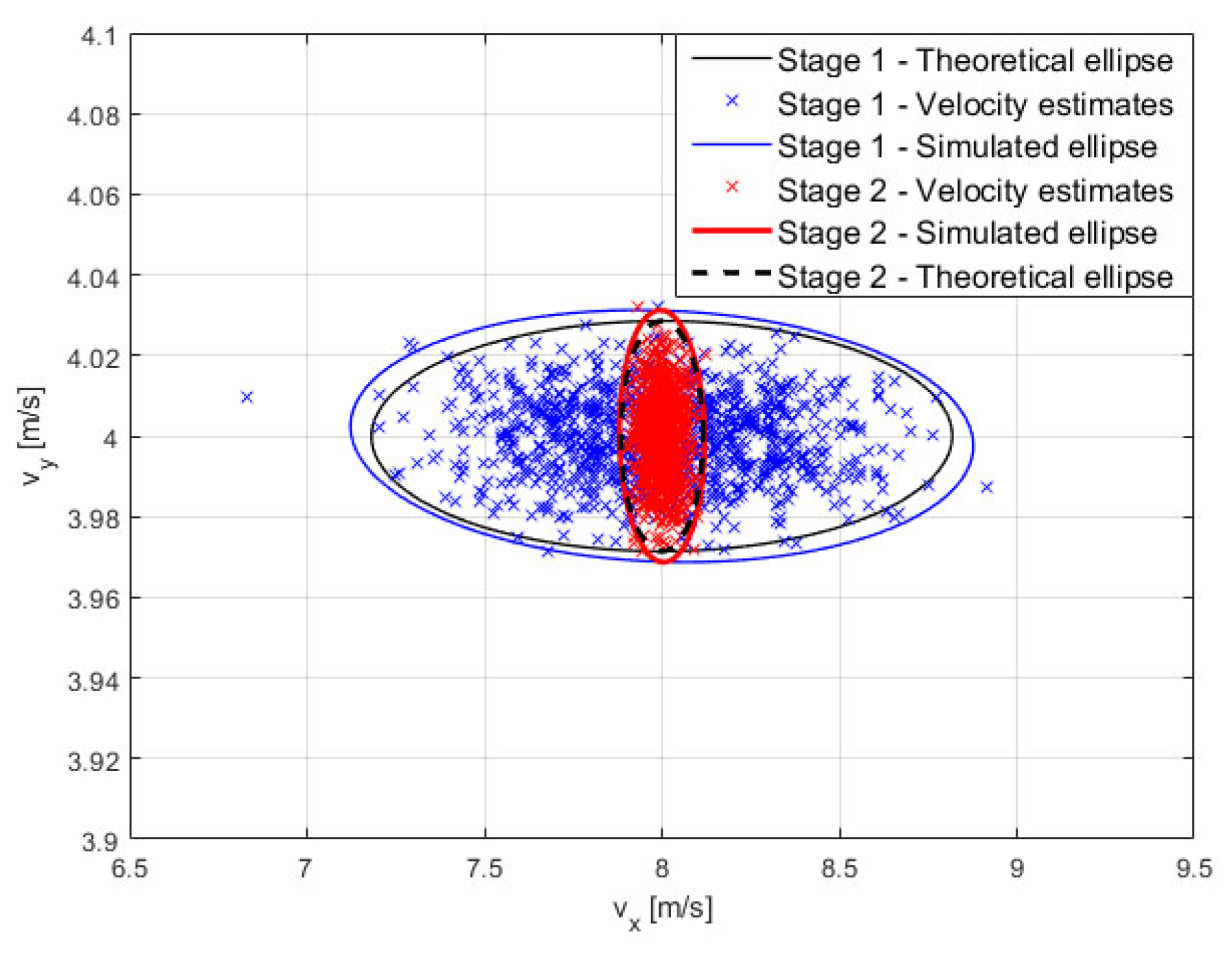
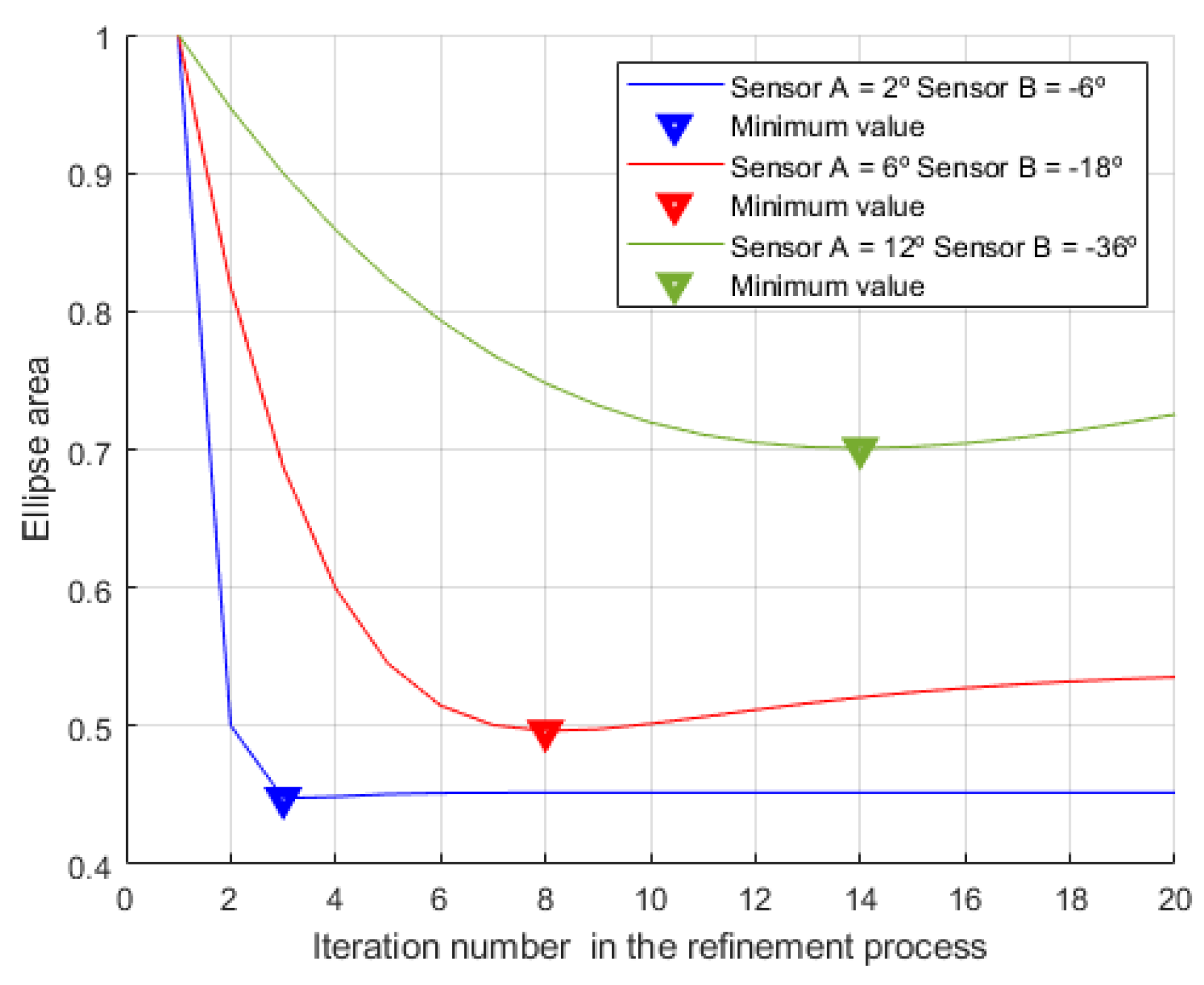
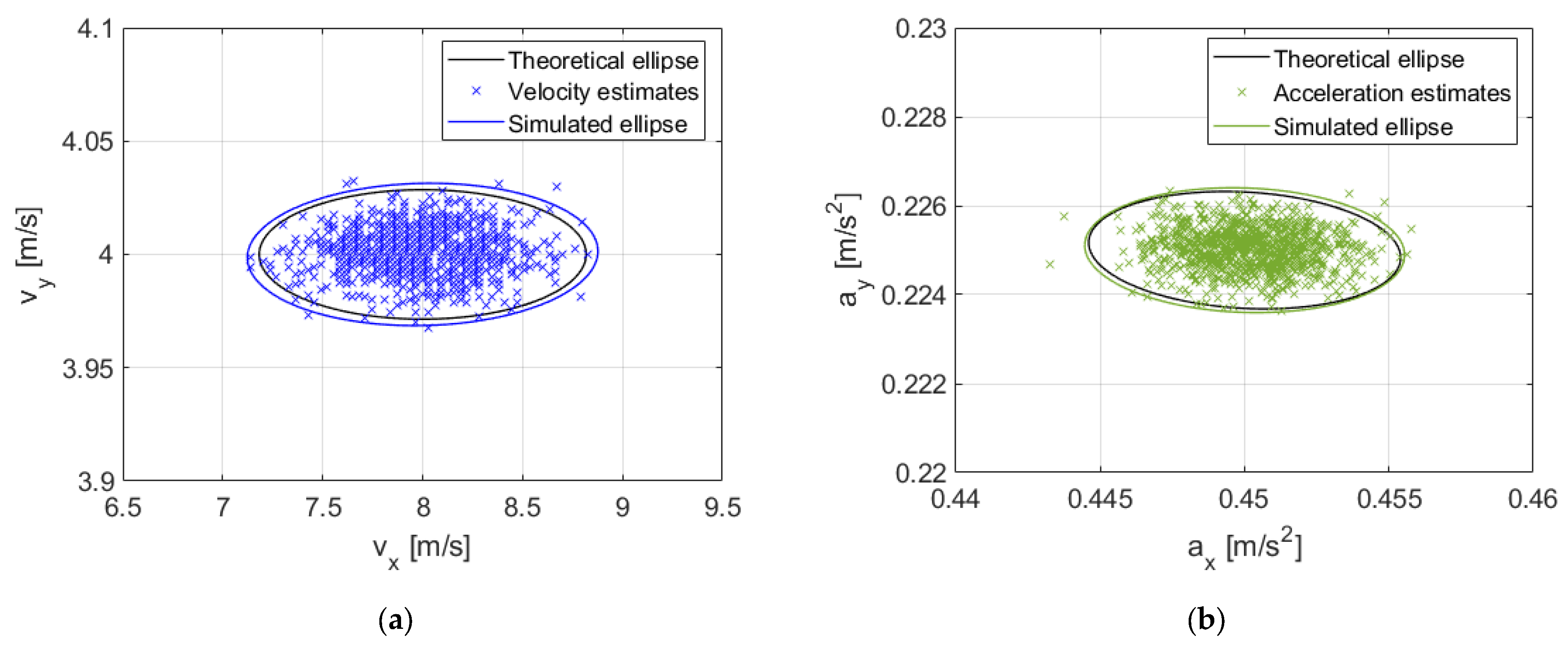

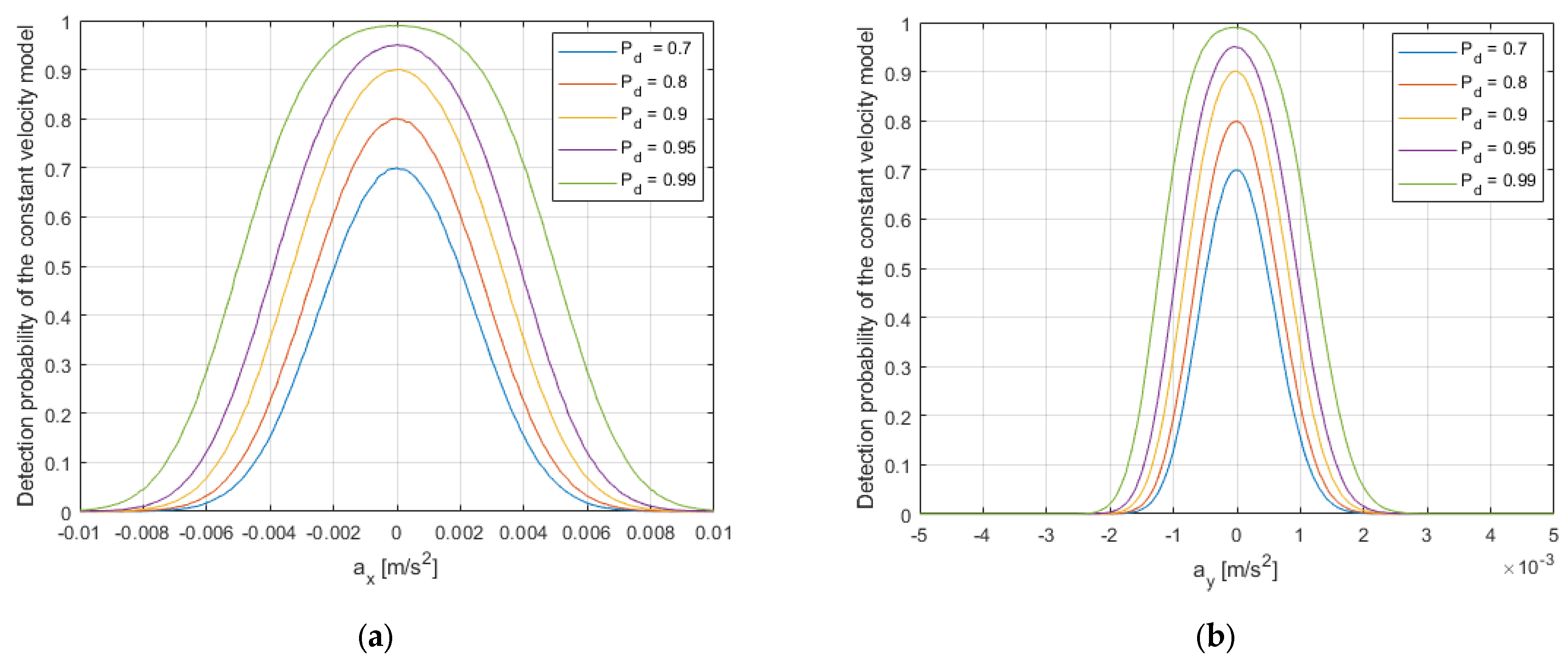
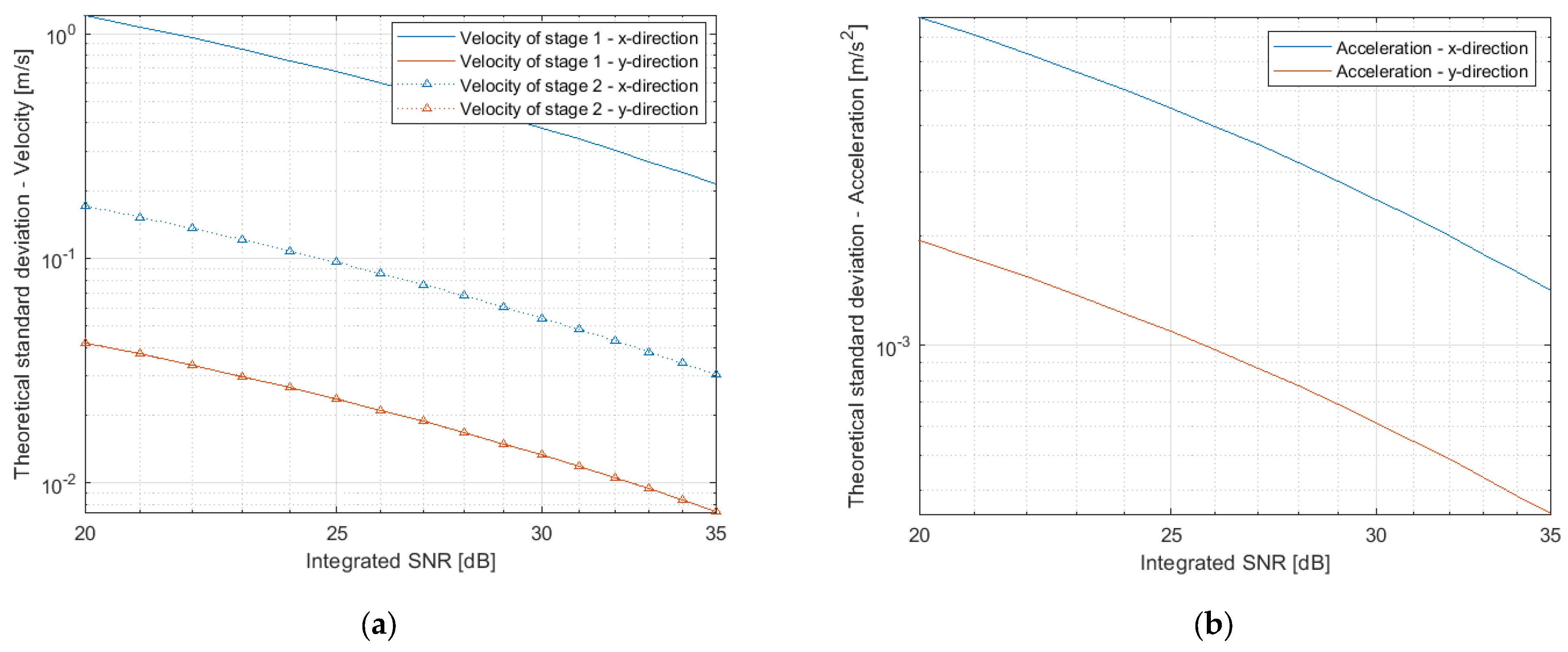
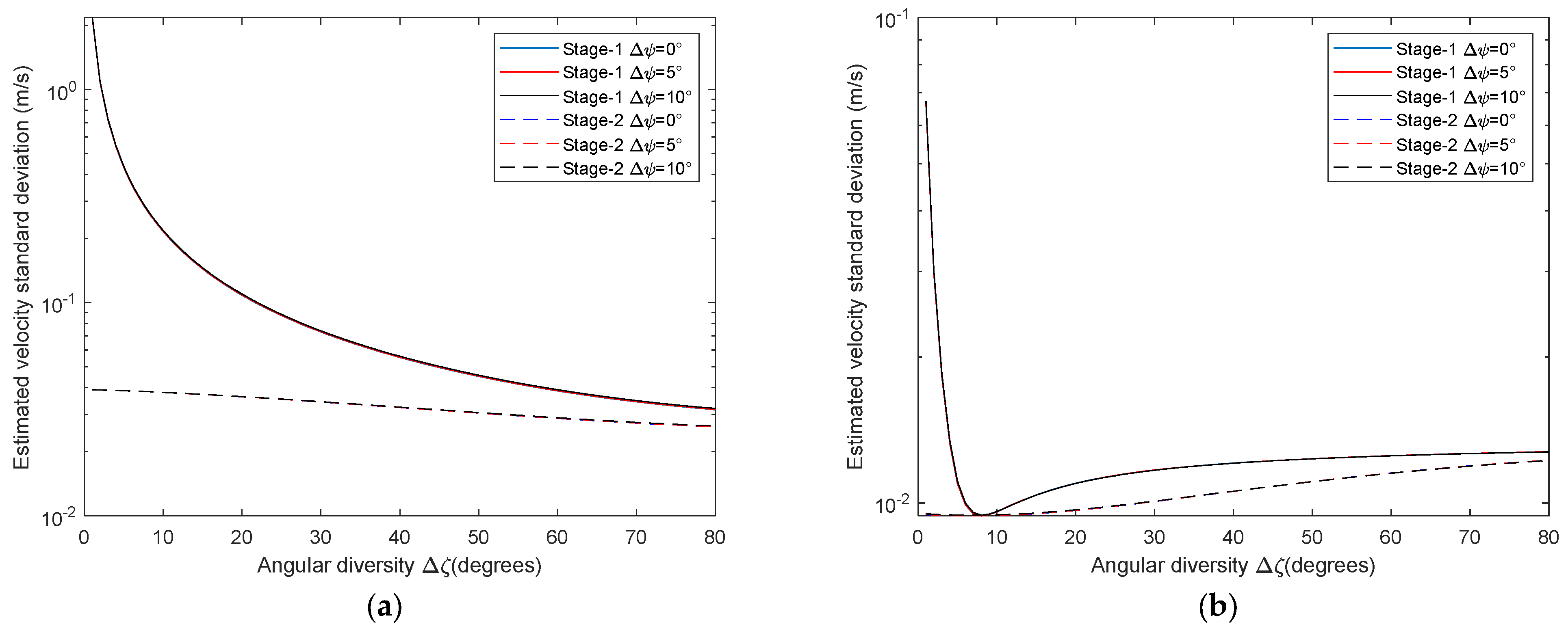
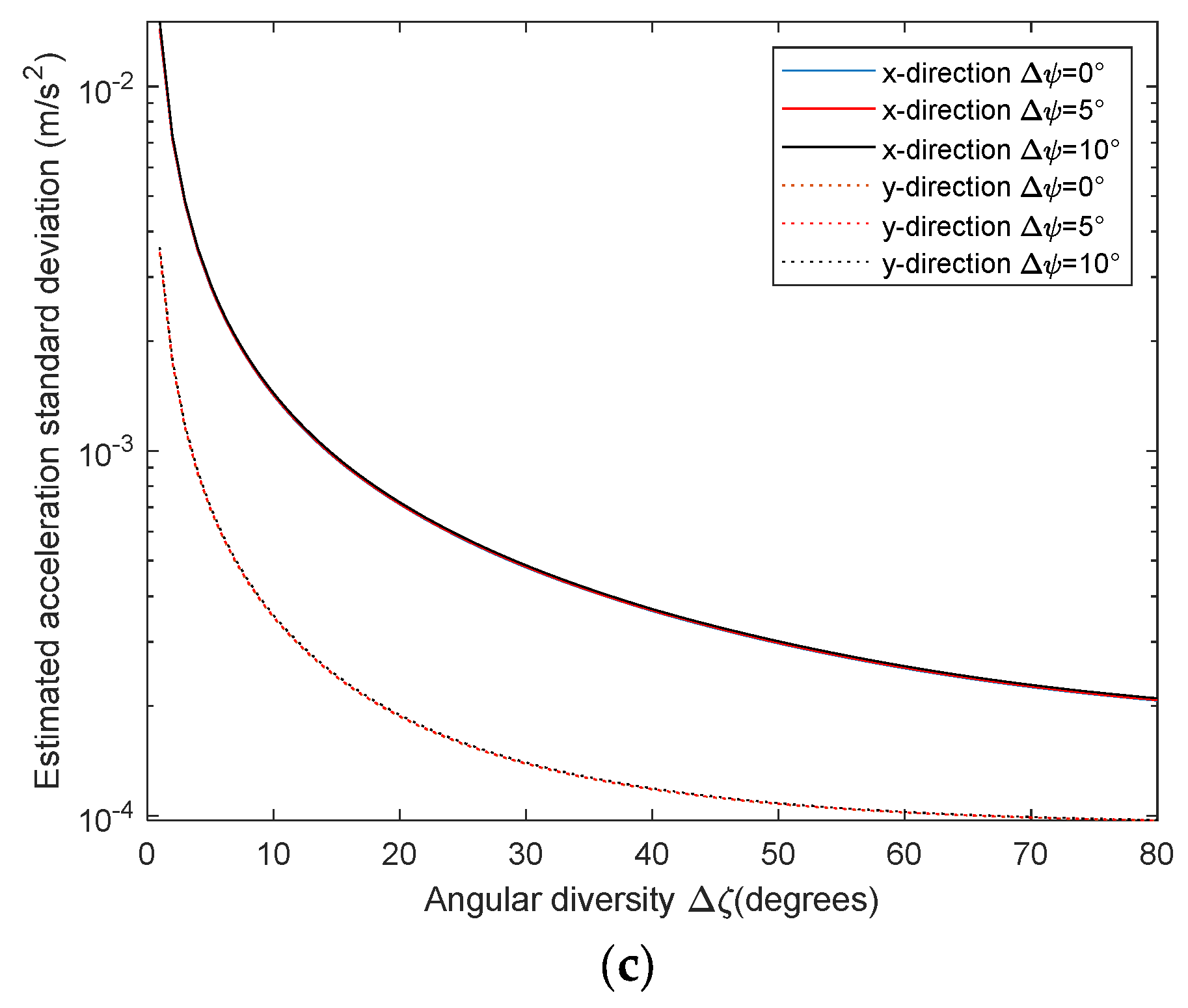
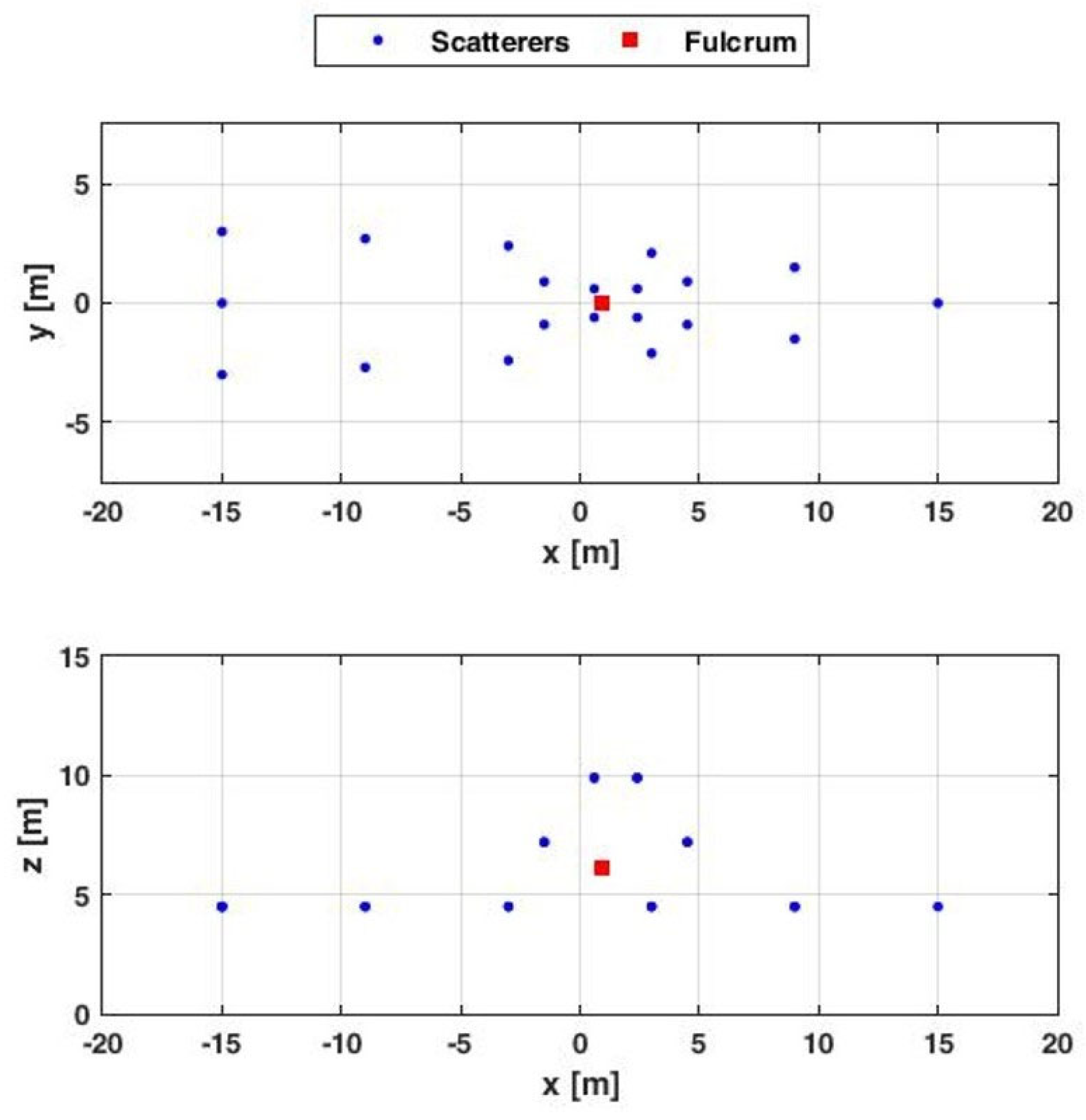
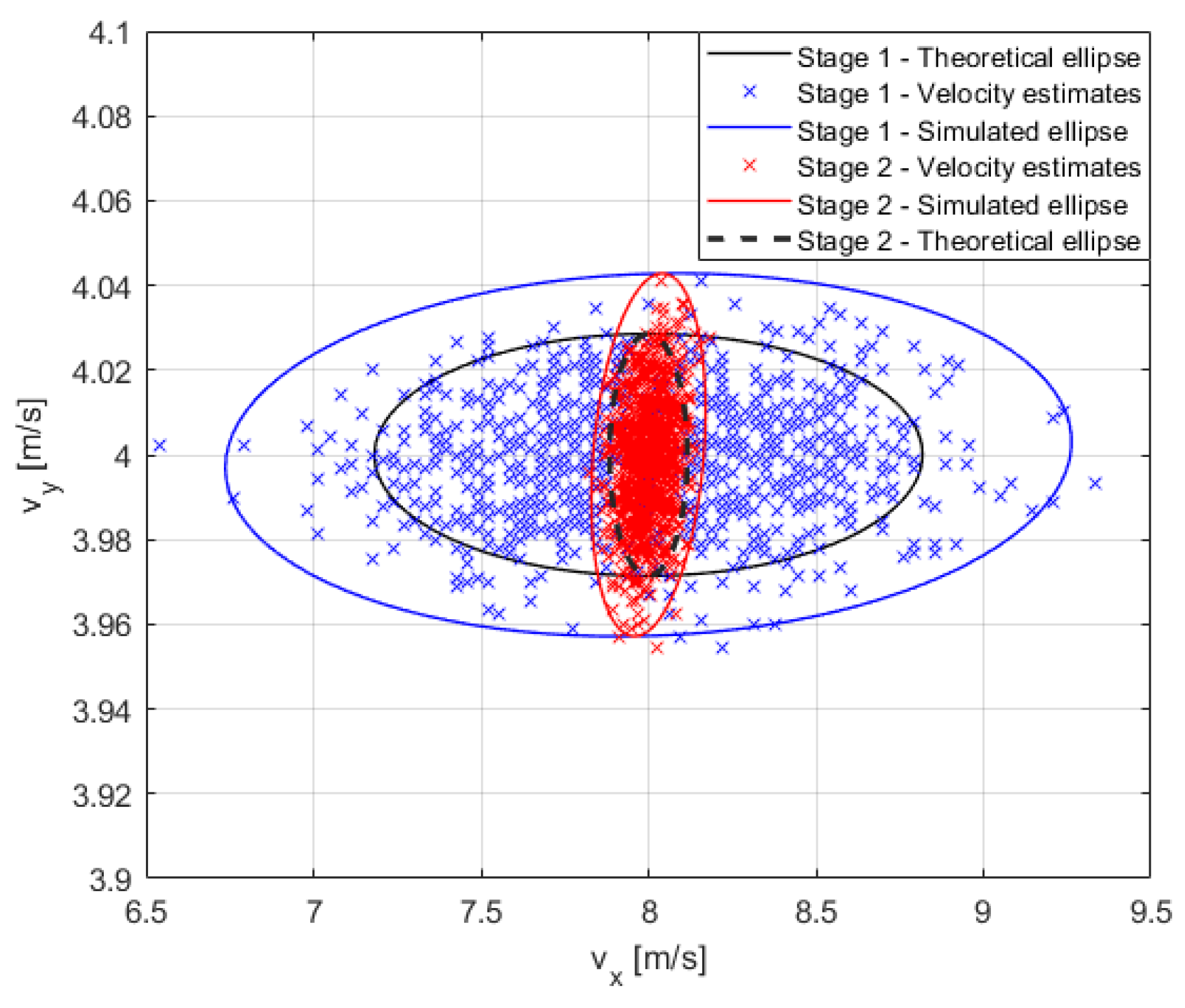



| Statistics | Target Kinematic Parameters | Theoretical Values | Decentralized Approach Estimates |
|---|---|---|---|
| mean | 8.000 | 8.001 | |
| 4.000 | 3.999 | ||
| std | 0.269 | 0.289 | |
| 0.009 | 0.010 |
| Statistics | Target Kinematic Parameters | Theoretical Values | Decentralized Approach Estimates |
|---|---|---|---|
| mean | 8.000 | 8.001 | |
| 4.000 | 3.999 | ||
| std | 0.038 | 0.040 | |
| 0.009 | 0.010 |
| Statistics | Target Kinematic Parameters | Theoretical Values | Decentralized Approach Estimates |
|---|---|---|---|
| mean | 8.000 | 7.986 | |
| 4.000 | 4.001 | ||
| 0.450 | 0.450 | ||
| 0.225 | 0.225 | ||
| std | 0.269 | 0.289 | |
| 0.009 | 0.010 | ||
| 0.002 | 0.002 | ||
| 0.000 | 0.000 |
| Statistics | Target Kinematic Parameters | Stage 1 Velocity | Stage 2 Velocity | ||||
|---|---|---|---|---|---|---|---|
| Theoretical Values (Point like Target) | Simulated (Extended Target with Constant Yaw Rotation) | Simulated (Extended Target with 3D Rotation) | Theoretical Values (Point like Target) | Simulated (Extended Target with Constant Yaw Rotation) | Simulated (Extended Target with 3D Rotation) | ||
| mean | 8.000 | 8.009 | 7.689 | 8.000 | 8.001 | 8.047 | |
| 4.000 | 3.999 | 4.033 | 4.000 | 3.999 | 4.033 | ||
| std | 0.269 | 0.416 | 0.403 | 0.038 | 0.056 | 0.071 | |
| 0.009 | 0.014 | 0.014 | 0.009 | 0.014 | 0.014 | ||
| Statistics | Target Kinematic Parameters | Theoretical Values | Decentralized Approach Estimates (Extended Target with Constant Yaw Rotation) | Decentralized Approach Estimates (Extended Target with 3D Rotation) |
|---|---|---|---|---|
| mean | 8.000 | 8.007 | 7.611 | |
| 4.000 | 3.999 | 4.025 | ||
| 0.450 | 0.451 | 0.448 | ||
| 0.225 | 0.225 | 0.226 | ||
| std | 0.269 | 0.373 | 0.397 | |
| 0.009 | 0.013 | 0.014 | ||
| 0.002 | 0.002 | 0.003 | ||
| 0.000 | 0.001 | 0.001 |
| Statistics | Target Kinematic Parameters | Narrow Angular Separation-NAS | Wide Angular Separation-WAS | ||||
|---|---|---|---|---|---|---|---|
| Centralized Approach (Random Initial Points) | Centralized Approach (Real Value Initial Point) | Decentralized Approach | Centralized Approach (Random Initial Points) | Centralized Approach (Real Value Initial Point) | Decentralized Approach | ||
| mean | 8.007 | 8.007 | 8.007 | 7.953 | 7.950 | 7.950 | |
| 3.999 | 3.999 | 3.999 | 4.007 | 4.007 | 4.007 | ||
| 0.451 | 0.451 | 0.451 | 0.450 | 0.450 | 0.450 | ||
| 0.225 | 0.225 | 0.225 | 0.225 | 0.225 | 0.225 | ||
| std | 0.376 | 0.376 | 0.374 | 0.815 | 0.078 | 0.078 | |
| 0.013 | 0.013 | 0.013 | 0.143 | 0.014 | 0.014 | ||
| 0.002 | 0.002 | 0.002 | 0.021 | 0.001 | 0.001 | ||
| 0.001 | 0.001 | 0.001 | 0.005 | 0.000 | 0.000 | ||
| Statistics | Target Parameters | Theoretical Values | Decentralized Approach Estimates |
|---|---|---|---|
| mean | −93.535 | −93.565 | |
| −126.489 | −126.544 | ||
| 0.221 | 0.211 | ||
| −1.629 | −1.641 | ||
| std | 0.064 | 0.083 | |
| 0.064 | 0.078 | ||
| 0.003 | 0.003 | ||
| 0.003 | 0.003 |
| Statistics | Target Kinematic Parameters | Aircraft Target | ||
|---|---|---|---|---|
| Theoretical Values | Centralized Approach (Real Value Initial Point) | Decentralized Approach | ||
| mean | 8.000 | 8.006 | 8.006 | |
| 1.000 | 1.000 | 1.000 | ||
| 0.450 | 0.450 | 0.450 | ||
| 0.000 | 9 × 10−5 | 9 × 10−5 | ||
| std | 0.022 | 0.028 | 0.028 | |
| 4 × 10−4 | 5 × 10−4 | 5 × 10−4 | ||
| 9 × 10−4 | 1 × 10−3 | 1 × 10−3 | ||
| 4 × 10−5 | 5 × 10−5 | 5 × 10−5 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Testa, A.; Pastina, D.; Santi, F. Decentralized Approach for Translational Motion Estimation with Multistatic Inverse Synthetic Aperture Radar Systems. Remote Sens. 2023, 15, 4372. https://doi.org/10.3390/rs15184372
Testa A, Pastina D, Santi F. Decentralized Approach for Translational Motion Estimation with Multistatic Inverse Synthetic Aperture Radar Systems. Remote Sensing. 2023; 15(18):4372. https://doi.org/10.3390/rs15184372
Chicago/Turabian StyleTesta, Alejandro, Debora Pastina, and Fabrizio Santi. 2023. "Decentralized Approach for Translational Motion Estimation with Multistatic Inverse Synthetic Aperture Radar Systems" Remote Sensing 15, no. 18: 4372. https://doi.org/10.3390/rs15184372
APA StyleTesta, A., Pastina, D., & Santi, F. (2023). Decentralized Approach for Translational Motion Estimation with Multistatic Inverse Synthetic Aperture Radar Systems. Remote Sensing, 15(18), 4372. https://doi.org/10.3390/rs15184372






