1. Introduction
ISAR emits electromagnetic waves to obtain high-resolution two-dimensional images of non-cooperative targets in all-day, all-weather conditions, offering critical support for target recognition [
1]. Therefore, it can be applied in military and civilian [
2,
3]. At present, ISAR imaging technology is widely used in the microwave band. However, the microwave band radar is limited by the bandwidth, resulting in low imaging resolution and low recognition rate. By contrast, the THz radar owns the higher carrier frequency and the more extensive bandwidth to achieve high-resolution imaging by the shorter observation time [
4,
5].
THz wave is also called a sub-millimeter wave, and its frequency range from 0.1 THz~10 THz. At the same time, some of the characteristics of microwave and infrared, are due to the THz wave between the microwave and infrared band. In the early stage, limited by the hardware such as the THz Source design, the range, and field of view of THz radar are severely limited. Therefore, THz radar was mainly used for near-field imaging and measuring THz targets’ scattering characteristics. [
6,
7,
8]. With the advancement of technology, THz radar is gradually developing in the SAR / ISAR imaging field. In 2012, the UESTC successfully implemented a 220 GHz terahertz radar imaging system based on solid-state electronic sources. It used this system to perform ISAR imaging experiments on aircraft target models [
9]. In the same year, to further apply THz radar technology to longer-range detection and to take advantage of its high frame rate imaging characteristics, DARPA launched the Video Synthetic Aperture Radar (ViSAR) project. The ViSAR project successfully built a one-transmitter four-receiver terahertz radar system. It obtained high-resolution and high-frame rate SAR images of ground-moving targets at a range of 4 km through experiments in 2017 [
10]. This result confirmed the feasibility of terahertz radar for long-range applications. In 2022, Emidio Marchetti et al. from the University of Birmingham in the United Kingdom proposed the concept of spaceborne sub-THz-ISAR space situational awareness. In space, the range of THz radar is no longer restricted by atmospheric absorption. At the same time, terahertz waves can sense diffuse echoes from rough surfaces of extended targets due to their short wavelength. Terahertz radar can achieve the ultra-high resolution of less than 1 cm, allowing the inversion of the fine structure of space targets due to its high carrier frequency and large bandwidth. These characteristics of THz radar give it significant advantages and potential for the component-level recognition and interpretation of ISAR images of space targets [
11,
12,
13].
Although THz radar has the potential to generate ISAR images with high-precision, high-resolution, and high frame rates, it also puts forward higher requirements for imaging processing algorithms. The conventional ISAR imaging process mainly consists of envelope alignment and initial phase correction. Researchers have proposed several methods for these two imaging steps to refine the ISAR imaging technique further. Currently, two main approaches are usually used to achieve envelope alignment: the cross-correlation method and the alignment criterion based on image quality [
14,
15]. After the envelope alignment is completed, the range units of each echo are aligned, but the initial phase correction is needed before the final imaging. Research related to initial phase error correction in the microwave band is well established. Such algorithms are divided into two main categories: the first one is based on the dominant scatterer and the second one is based on image quality. The first class of algorithms is based on the main scatterer algorithm which first selects the main scatterer by a criterion such as minimum variance, and compensates for the initial phase by using the phase of the strong scattering point as a reference. Relevant algorithms include the dominant scatterer algorithm (DSA) and phase gradient algorithm (PGA) [
16,
17]. The second class of algorithms is based on global image quality optimization. The initial phase error of the echo is compensated through iterative optimization by selecting image quality criteria such as image entropy, image contrast, and image sharpness. Such algorithms include the minimum entropy algorithm (MEA) [
18] and the maximum contrast algorithm (MCA) [
19].
The traditional two-step compensation method can no longer meet the demand for high-resolution imaging to obtain a focused ISAR image. The range offset and phase error generated during rotational motion will seriously affect the ISAR imaging quality. Moreover, the range offset and phase error are high-order quantities that cannot be corrected by traditional motion compensation algorithms. Therefore, KT is proposed to solve the FRM. The algorithm realizes frequency resampling by linear interpolation and can remove the FRM without parameters [
20].
In this way, the rotation-induced range offset is eliminated. However, in practical processing, the second-order space-varying range migration generated by the increased resolution of terahertz radar can no longer be ignored, which is rarely considered in conventional frequency bands [
21]. After the range migration correction is completed, the high-order space-varying phase error introduced by rotation will lead to Doppler broadening, and this broadening phenomenon becomes particularly serious due to the short THz wavelength. Compensation for higher-order space-varying phase errors must estimate the rotational parameters of the target, such as rotation velocity and rotation center.
The estimation of the rotational parameters algorithm is mainly divided into two categories: image-driven and data-driven. Among them, the image-driven algorithm directly estimates the rotation angle of two ISAR images by matching the images and then calculates the target rotational velocity, but the error is large. The second class of data-driven algorithms is also divided into two, one is based on parameter estimation, where the quadratic phase coefficients of the strong scattering points in the one-dimensional range profile are estimated by means of parameter estimation, and then fitted to obtain the target’s rotation velocity and rotation center. This algorithm requires multiple strong scattering points and good alignment of the range profile envelope. Another algorithm is based on the image quality criterion. However, terahertz radar is unable to ignore the effect of second-order range offsets, which will severely affect the estimation of rotational speed. Another algorithm is based on image quality criteria. This type of algorithm uses the rotation velocity and the rotation center of the required solution, constructs a phase compensation matrix and uses the image quality as an optimization criterion to finally obtain the rotational parameters of the required solution. This type of algorithm is robust but also requires a one-dimensional range profile envelope to be well aligned. Outside, a rotational velocity estimation method is proposed based on maximizing the envelope sharpness. Since a quantitative relationship exists between the second-order range bending and the rotational velocity, the correct rotational velocity can be obtained when the range profile envelope sharpness is maximized by correcting the SRM using the rotational velocity. However, this method fails at low SNR and the accuracy of the resulting rotational velocity is not high. And the algorithm subsequently needs to estimate the center of rotation to compensate for the phase error [
21]. Therefore, achieving high-order space-varying phase compensation and high-accuracy rotational parameters estimation in the presence of severe second-order space-varying range migration remains a challenging problem.
To solve the above problems, a THz-ISAR processing flow and algorithm are proposed in this paper. Firstly, the KT is performed on the echo signal after the translation compensation to correct the first-order space-varying range migration. Combined with the ME-MN, the rotation velocity and center are preliminarily estimated. Because the requirement for range migration correction accuracy is related to the range resolution, while the requirement for phase error compensation accuracy is related to the wavelength [
22]. The first estimated rotation velocity corrects the second-order space-varying range migration, and the range profile envelope has been aligned. Finally, the first estimated rotation velocity and center are taken as the initial values, and the ME-MN is used again for the echo after the SRM correction to perform accurate parameter estimation and phase error compensation. The main contributions of this paper are as follows:
The influence of range migration and phase error caused is analyzed in the terahertz band. It shows that THz-ISAR imaging must consider the second-order space-varying range migration correction problem.
The ME-MN is used to accurately estimate the target’s rotation velocity and center to achieve second-order space-varying range migration correction and second-order space-varying phase compensation. Two iterations of the algorithm give more accurate results and allow parameters such as rotation velocity and center to be solved. In addition, azimuthal scaling of the target can be achieved using the estimated rotation velocity
A modified Newton method is used to modify the step size and the Hessian matrix, avoiding the problem that the Newton method fails when the Hessian matrix is not positive. At the same time, the method also enables fast estimation of the rotational parameters.
This paper is arranged as follows:
Section 2 introduces the THz-ISAR signal model, and the influence of range migration and phase error on imaging is analyzed.
Section 3 gives the THz-ISAR imaging process and the derivation of the proposed method. In
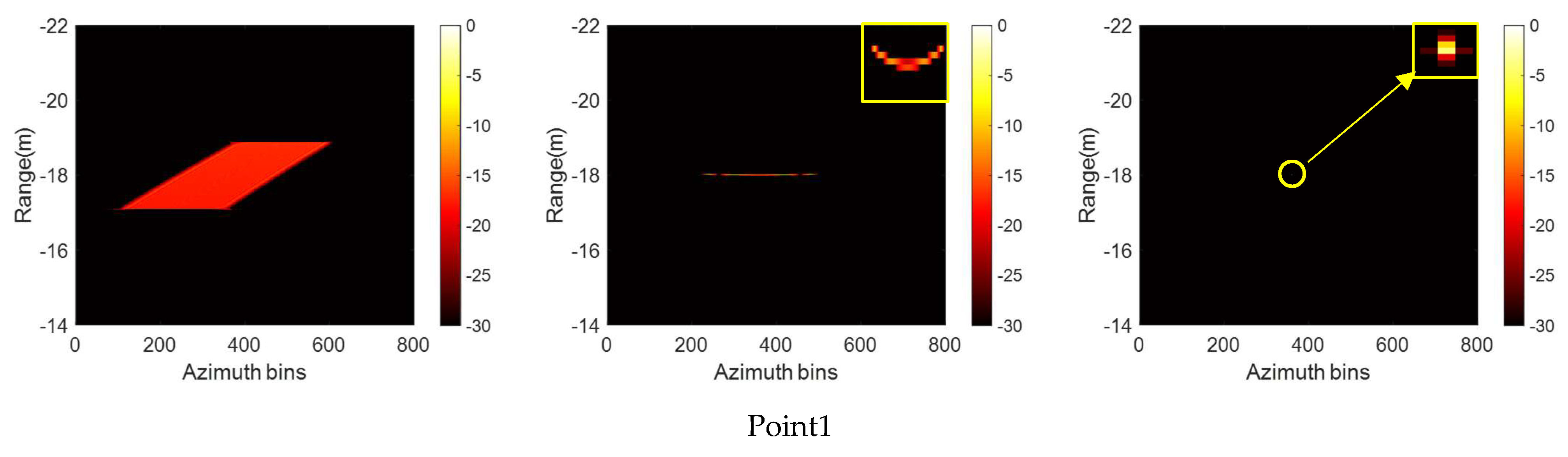
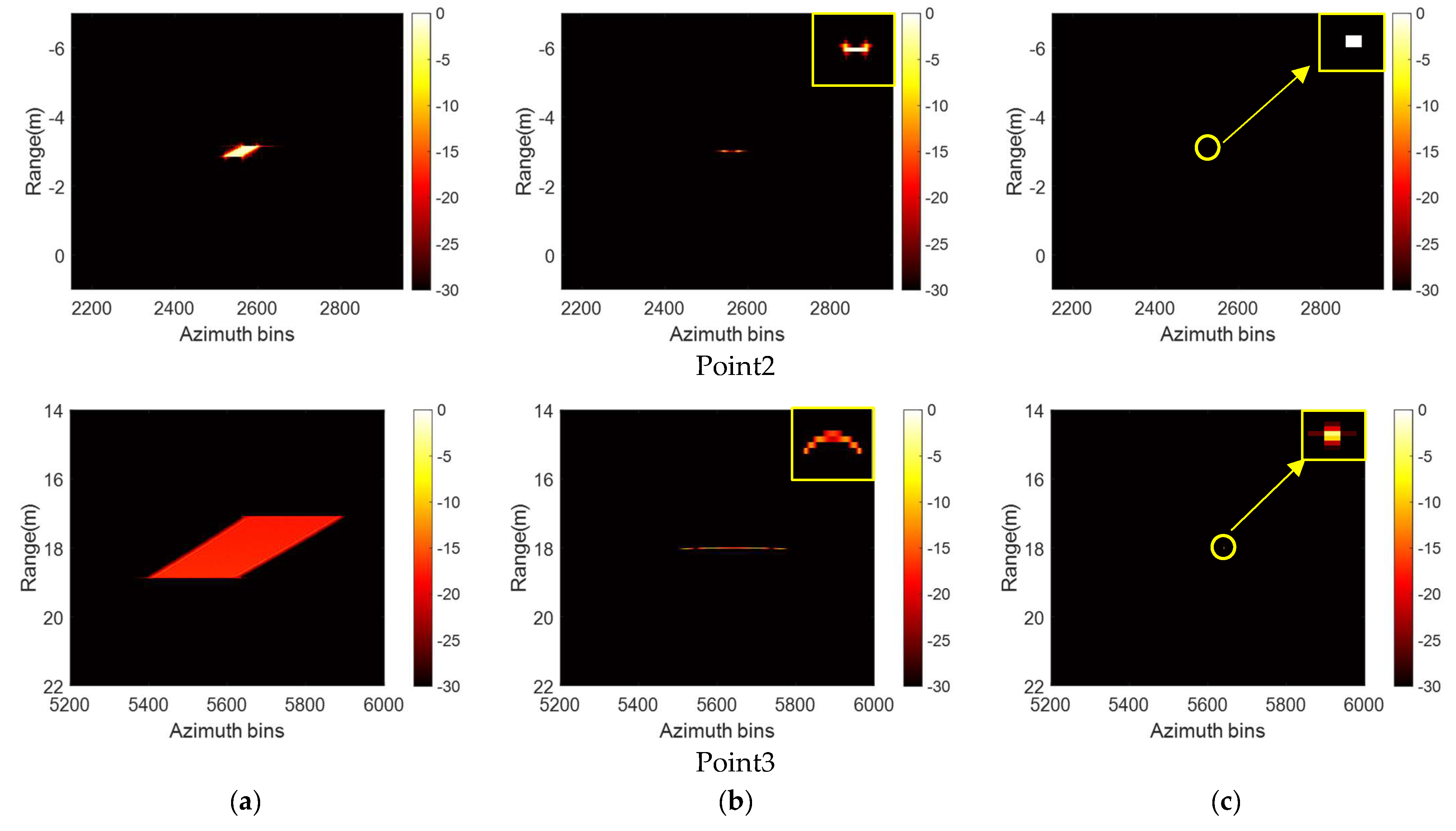
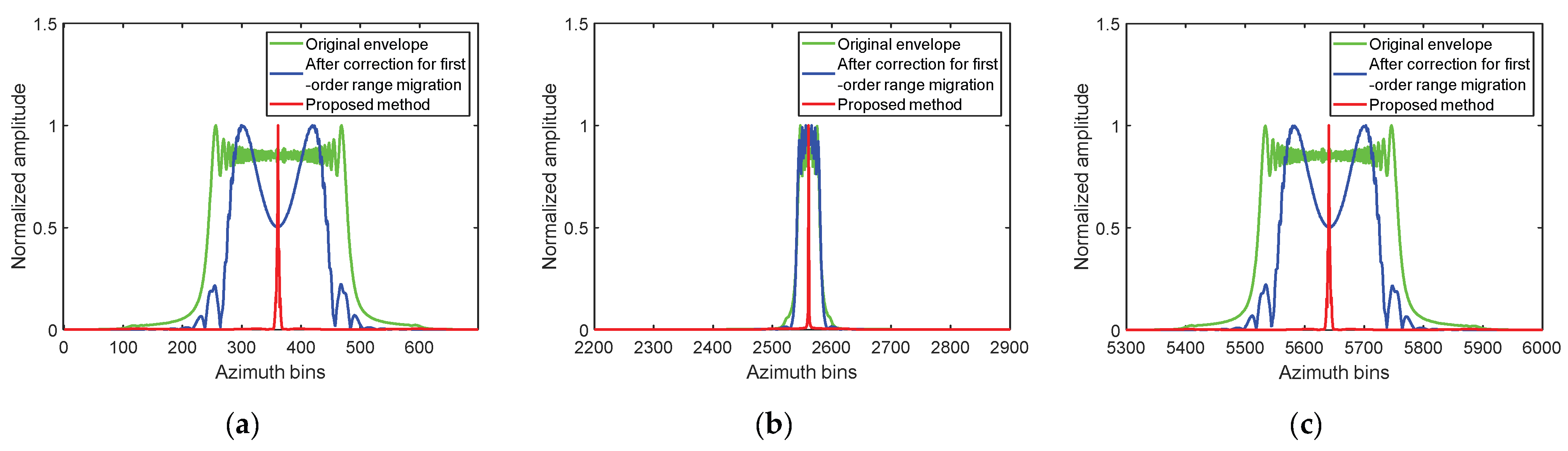
Section 4, the effectiveness of the proposed algorithm is verified by the simulation and the electromagnetic calculation.
Section 5 gives a conclusion and future research directions.
2. THz-ISAR Signal Model
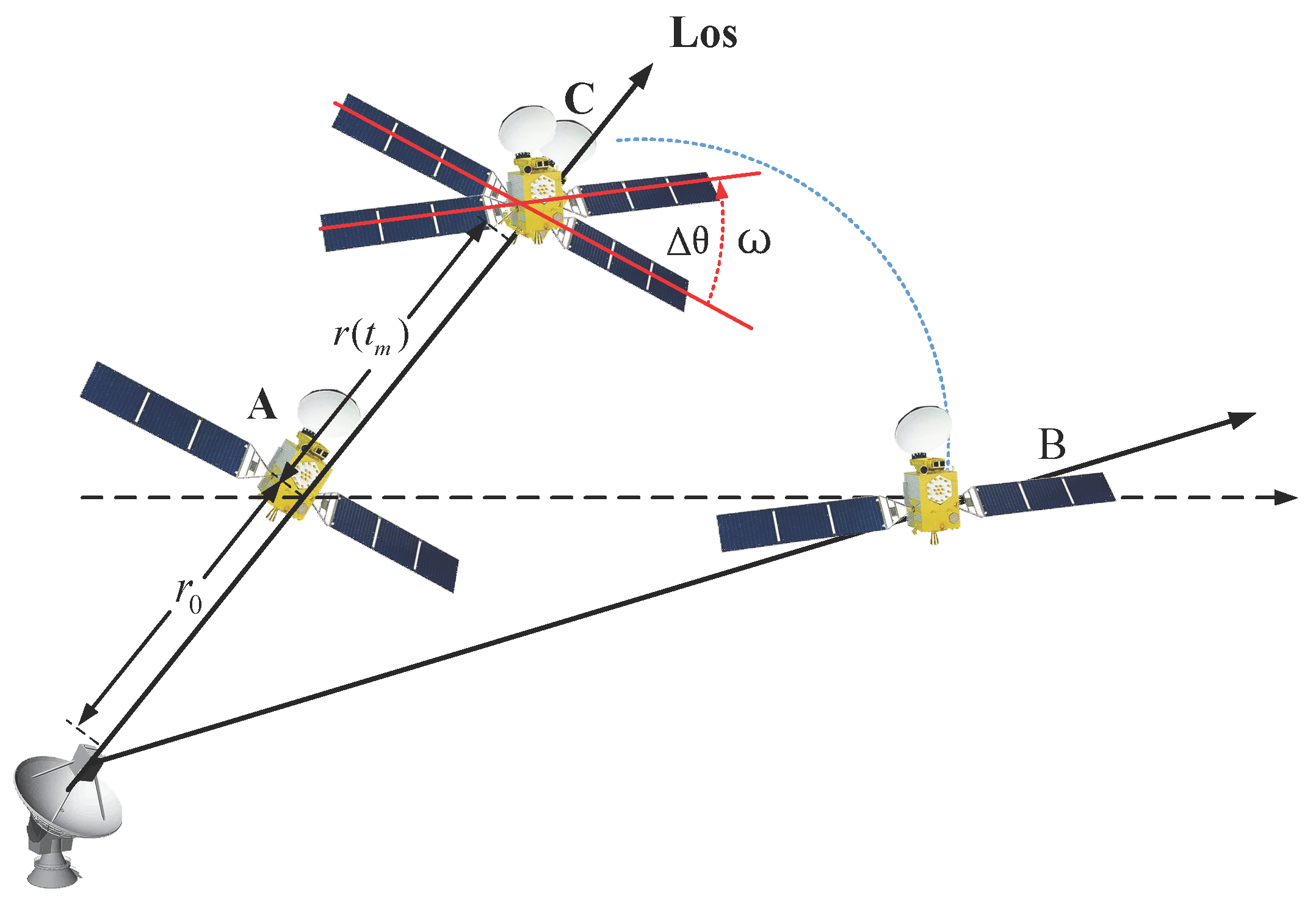
Because THz-ISAR is suitable for applications in space, the object considered is the space target. As shown in
Figure 1, in the geometric model of THz-ISAR imaging, the target moves from A to B. According to the far-field assumption, the motion process is decomposed into three parts. Firstly, point A is translated to point C along the radar line of sight. In this process, all scattering points move the same, and the generated Doppler is the same, so it is called translation. Secondly, at point C, the target rotates around the center of rotation. Because of the rotation, the range from different scattering points to the radar varies inconsistently. The generated Doppler can be used to distinguish different scattering points and provide azimuth resolution. Finally, the target moves in a circular motion from C to B with the radar at its center. During this process, all scattering points remain at the same distance from the radar, which does not affect the imaging results. Therefore, Thus, the motion of the target with respect to the radar can be independently decomposed into translational and rotational components. Considering the initial slant distance and the instantaneous change in slant distance due to translational motion, the slant range
of scattering point i can be expressed as
where
is the slow time,
is the initial slant range, and
is the slant range of the target rotation center changing with the slow time. Assuming that the radar transmits a linear frequency modulation (LFM) signal:
After the time delay
the obtained echo signal is
where
is the pulse width,
is the carrier frequency, and
is the frequency modulation of the LFM signal. Perform dechirp and pulse compression on the echo signal:
The above echoes are compensated for translation to remove the phase and migration effects produced by
, the echoes can be expressed as:
After the translation compensation, the effect of migration and phase errors on imaging in the THz bands will be quantitatively analyzed below. The trigonometric function in Equation (6) is Taylor expanded as follows:
Each term in Equation (7) produces range migration and phase error. The literature [
23] states that when the following inequalities hold, the effect of the corresponding terms on the range migration and phase error is negligible.
where
is the accumulation angle of imaging,
and
are the maximum size of target range-dimension and azimuth-dimension respectively, and
is the range resolution. The above equation describes the range migration and phase error caused by rotation. In Equation (8),
and
are the FRM and the SRM, respectively. And the third-order range migration (TRM)
can usually be ignored, which will also be obtained later in the analysis. When the migration momentum exceeds the distance resolving unit, it leads to the defocusing of the range dimension.
and
are range space-varying second-order phase error and azimuth space-varying third-order error, respectively. When two are greater than
, it will cause azimuth to defocus. The following numerical simulations are used to quantify the distance migration at different rotation angles, bandwidths and phase error at different rotation angles, and frequencies. Assuming that Da and Dr are 15 m,
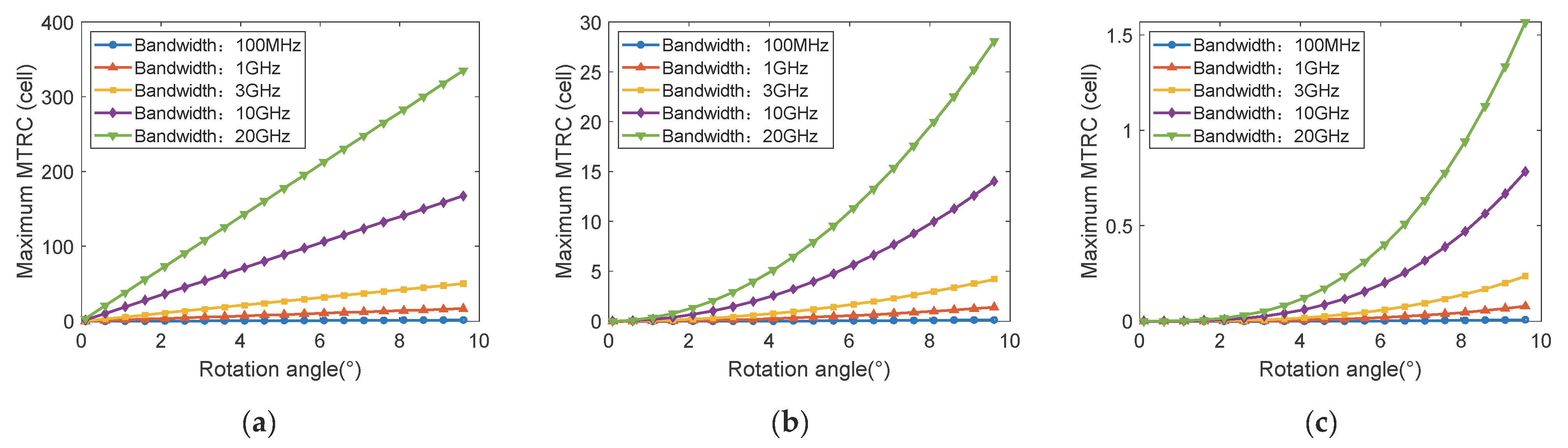
Figure 2 is the curve of the FRM, SRM and TRM with rotation angles under different bandwidths.
Figure 2a shows that the FRM changes linearly with time. As the bandwidth increases, FRM must be considered.
Figure 2b shows the variation curves of SRM with rotation angle under different bandwidths. From the diagram, we can see that with the increase in bandwidth, the SRM neglected in conventional radar must also be considered.
Figure 2c is the TRM.
Figure 3b shows that the TRM will not affect the imaging in most cases and can be generally ignored. As shown in
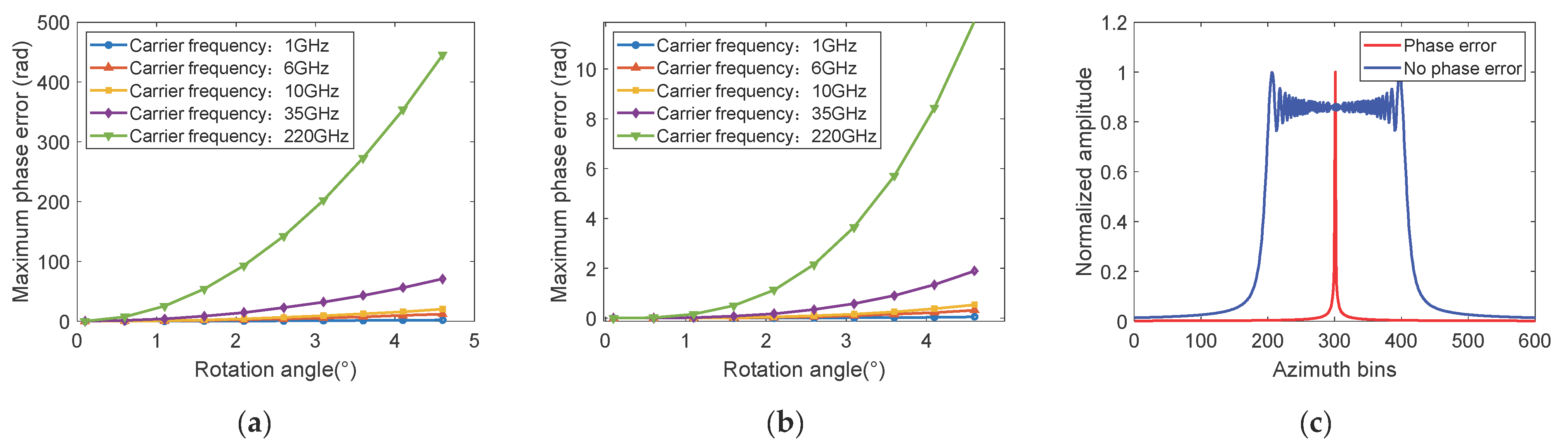
Figure 3, we analyze the high-order phase errors generated by different carrier frequencies.
Figure 3a,b are the second-order and third-order phase errors, respectively. In general, the third-order phase error is negligible for a limited target size and rotation angle. The results from
Figure 2a show that the second-order phase error becomes larger as the carrier frequency increases.
Figure 3c compares the azimuth profile with and without second-order phase error when the carrier frequency is 220 GHz, Dr = Da = 15 m, and the rotation angle is 5°. It can be illustrated that the second-order phase error in the THz band results in more severe azimuthal-defocusing compared to the conventional band. However, the severe azimuthal-defocus is favourable for the estimation of rotational parameters.
3. THz-ISAR Algorithm and Derivation
According to the analysis in
Section 2, terahertz-ISAR imaging has a non-negligible SRM in addition to FRM. For the FRM, we can use KT to correct it. The correction of the SRM involves the rotational velocity. In addition, THz-ISAR has more serious second-order space-varying phase errors compared with microwave bands. Although the more serious phase error will bring a huge impact on the imaging, facilitates the estimation of the target rotational velocity. Similarly, under the influence of range migration, it is difficult to perform effective phase compensation for the unaligned envelope. To address the above problems, a THz-ISAR imaging method is proposed in this paper. The specific steps are as follows:
- (1)
KT is applied to remove the FRM of echoes after translational compensation.
- (2)
The ME-MN is used to estimate the rotation velocity and rotation center.
- (3)
Because the envelope alignment accuracy is comparable to the resolution, the SRM is corrected utilizing the rotational velocity information obtained in step (2) to obtain an aligned envelope. This process can be implemented using the Chirp-Z transform (CZT).
- (4)
The rotation velocity and center estimated in the second step are used as the initial values, and the ME-MN is used again for accurate parameter estimation of the envelope-aligned echoes. At the same time, cross-range scaling is implemented.
- (5)
Using the rotation parameters obtained in step 4, the phase compensation matrix is constructed, and the Fourier transform is performed along the azimuthal dimension after compensating for the echo. A well-focused THz-ISAR image is finally acquired.
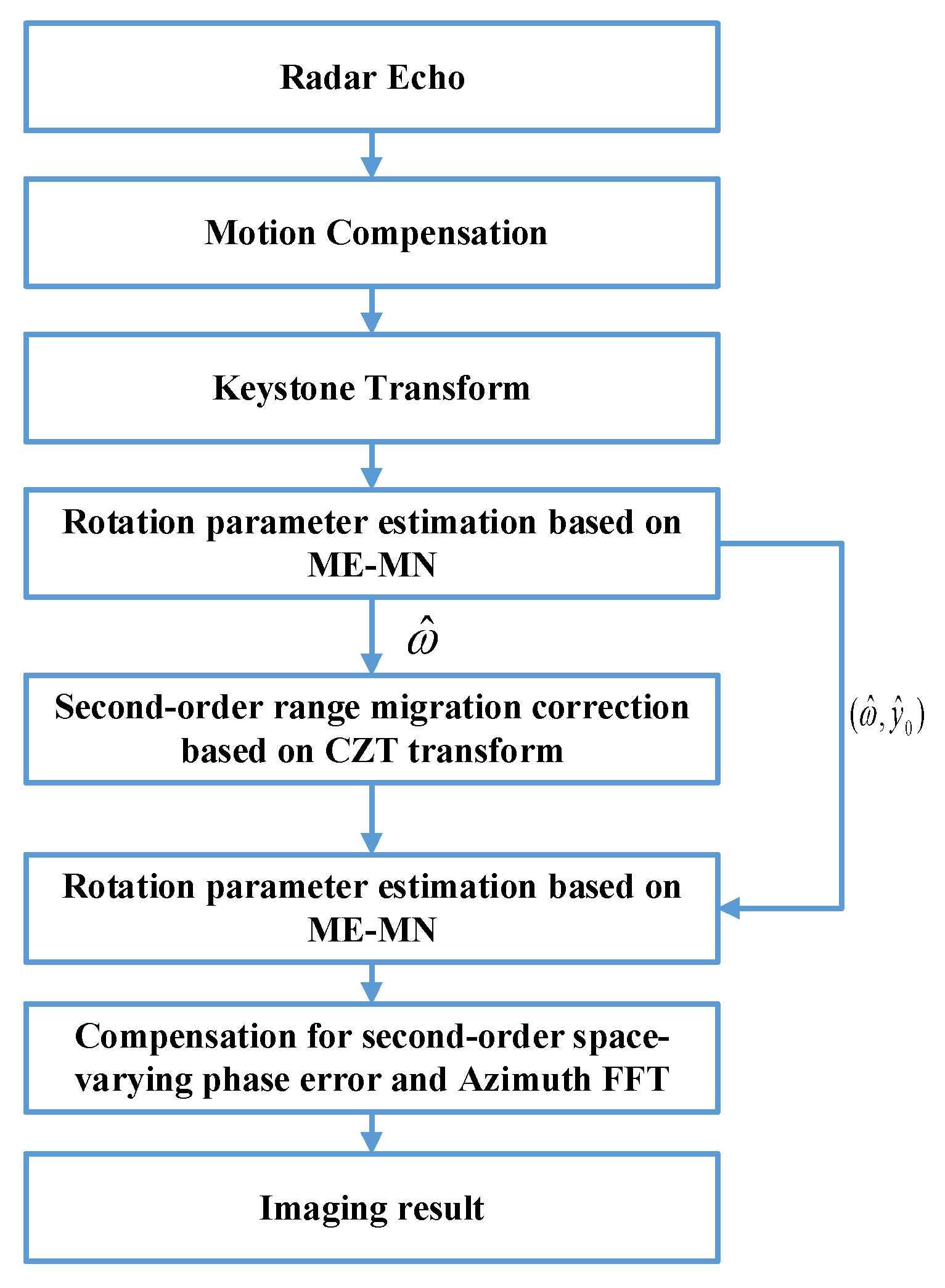
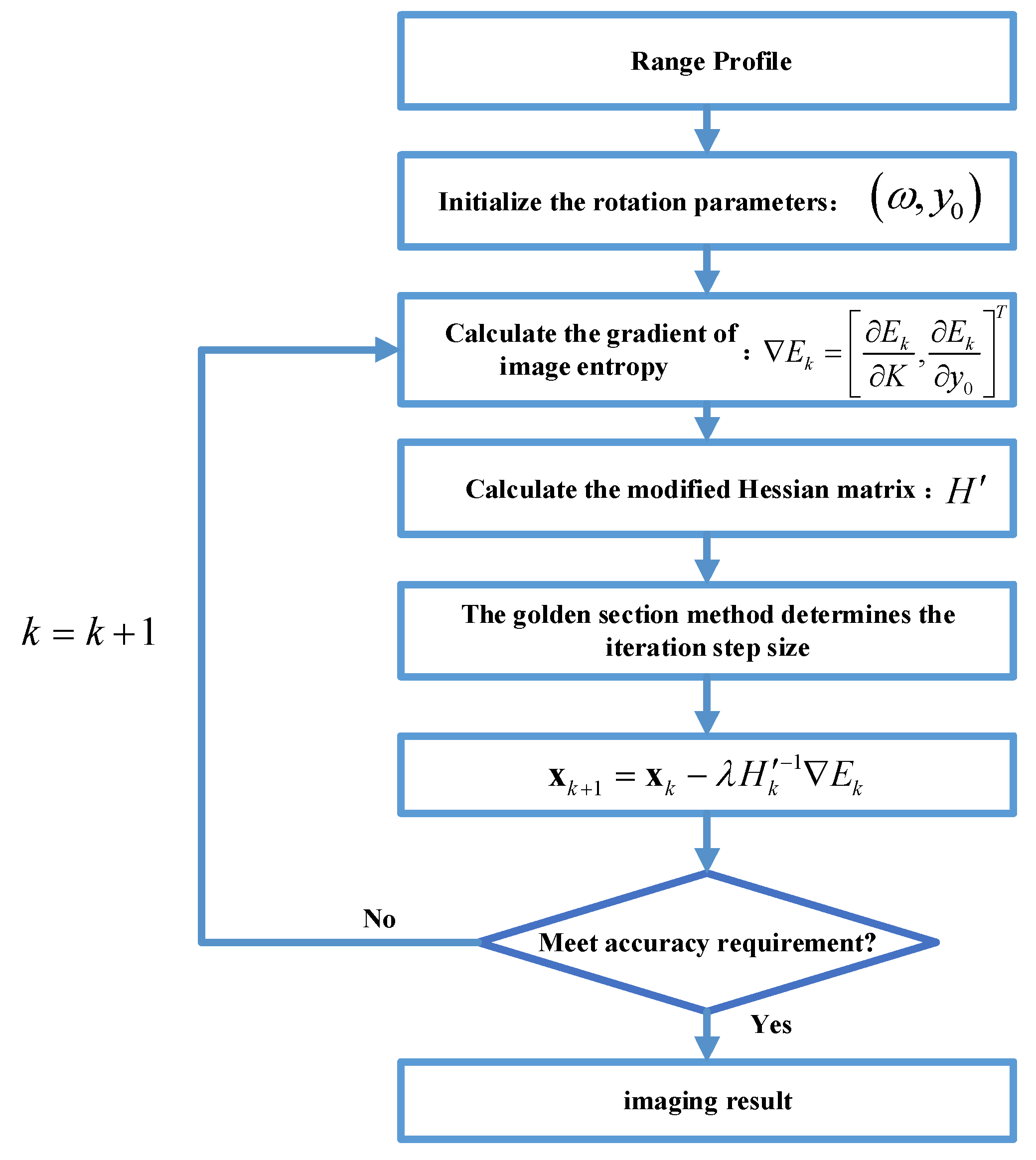
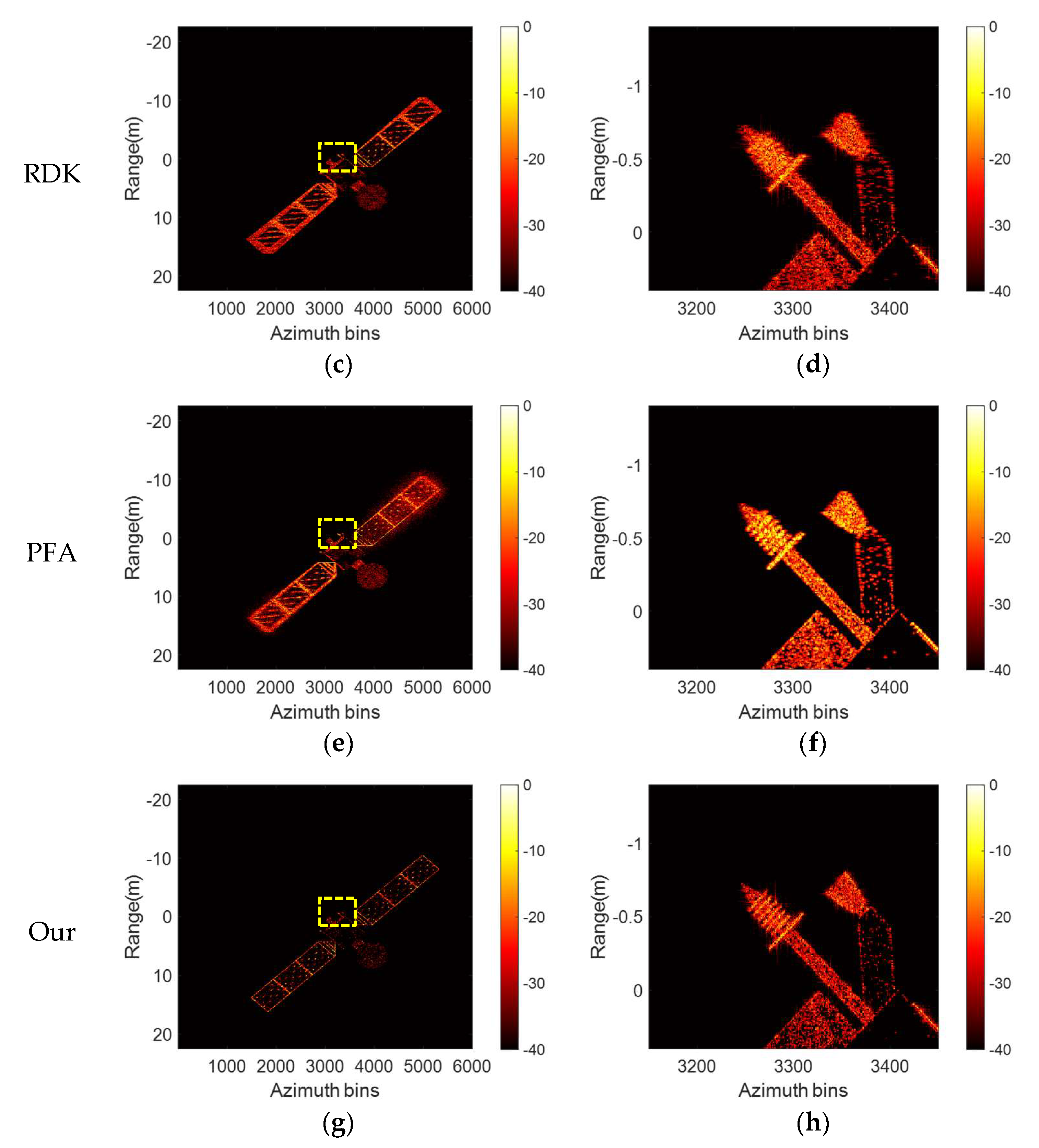
The proposed processing flowchart is shown in
Figure 4. Subsequent sections are specific to the implementation details of the proposed algorithmic process.
3.1. Correcting First-Order Range Migration by KT
Substituting Equation. (7) into Equation (6), after the range dimension IFFT transformation, Equation (5) is discretized to obtain
The KT, also known as keystone remapping, corrects linear range shifts in SAR/ISAR imaging by linearly interpolating to realign the time axis of each frequency cell with the expression
Equation (9) is approximated by the KT as
Converting Equation (10) to the range-frequency domain:
In the above equation, the difference between terahertz radar and conventional band radar is the consideration of an additional term: . This item leads to the SRM. And from the equation, it can be illustrated that the SRM is related to the rotation velocity and the coordinate: The larger the coordinate axis is, the larger the range migration is, which shows the characteristic of space-varying, so it cannot be corrected uniformly as the translational compensation. And compensating for the SRM requires the acquisition of rotational velocity.
3.2. Rotation Estimation Based on ME-MN
From the analysis in
Section 3.1, the rotational velocity must be estimated to calibrate the SRM. Therefore, this section will present a method for estimating the rotational velocity. The previous
Section 1 describes methods for rotational velocity estimation, including image-based and data-based [
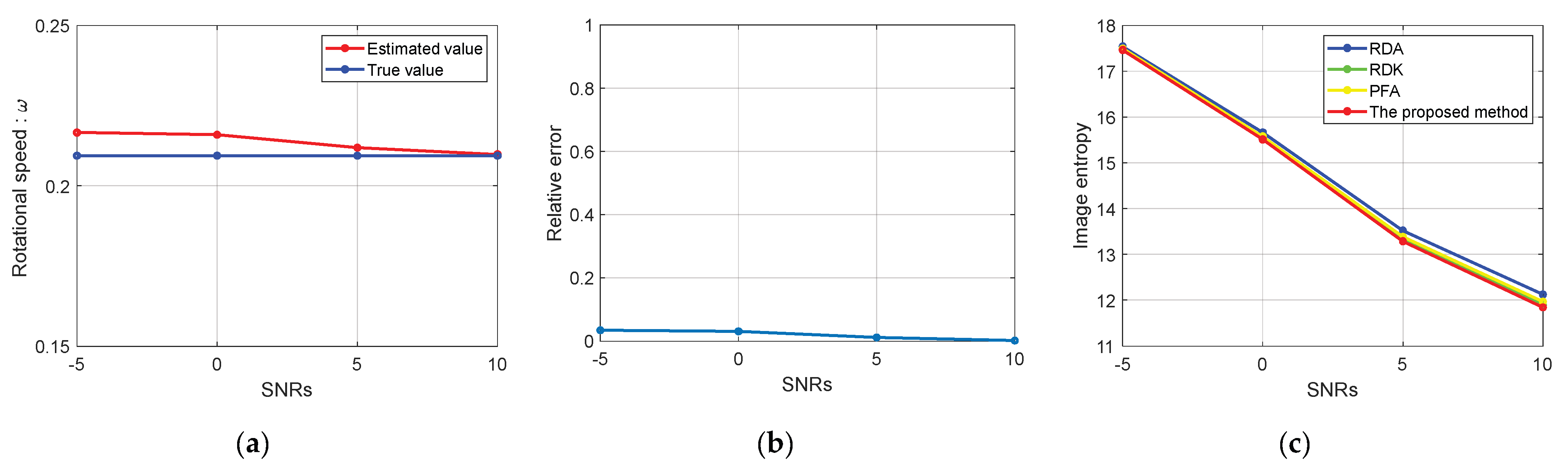
24], and also explains the advantages and disadvantages of these methods. The image-based method mainly performs image rotation and matching to estimate the rotation angle by extracting strong scattering points in the image. This type of algorithm requires high image quality and requires multiple images. However, the imaging quality of terahertz radar can be severely degraded due to the second-order phase, leading to the failure of such methods. The second method is based on the data-driven method, which estimates the rotational velocity by estimating the quadratic phase coefficient in the signal. Azimuth frequency modulation estimation and iterative solutions based on image quality optimization are mainly used in practice. Azimuth frequency modulation estimation needs to select the range cell where the dominant scatterer is located, and the envelope needs to be completely aligned, so the robustness is weaker than the rotational velocity estimation method based on image quality. In this paper, the ME-MN is used to estimate the rotational velocity with the image entropy as the iterative optimization criterion. Image entropy (IE) is commonly used to measure the focusing performance of ISAR imaging. The smaller the IE value, the more well-focused the image is.
Assuming
is the equivalent center of rotation, and the scattering points at the same range cell have the same y-coordinate, then
. The echo
is multiplied by the phase-compensated term:
. Finally, the azimuthal-dimensional FFT is applied to the phase-compensated echo to obtain the ISAR image
:
where let
,
, The optimal parameters are obtained by minimizing the cost function:
In Equation (14),
is the estimated value of
,
is the IE of
, which is defined as:
In Equation (15), represents the total energy of the image. The IE: is independent of the phase error: , according to the Parseval theorem, so is a constant.
The more effective methods for the above two-dimensional optimization problems are the gradient descent method(GDM) and the Newton method(NM). However, the traditional NM belongs to the unconstrained optimization problem and has the characteristics of fast convergence speed. In this paper, the NM is used to solve the optimization problem.
The gradient of the objective function to is
where
The Hessian matrix of the cost function
in
is derived below
In the above equation,
, so Hessian is a symmetric matrix. After obtaining the
and Hessian matrix, the iterative equation can be expressed as
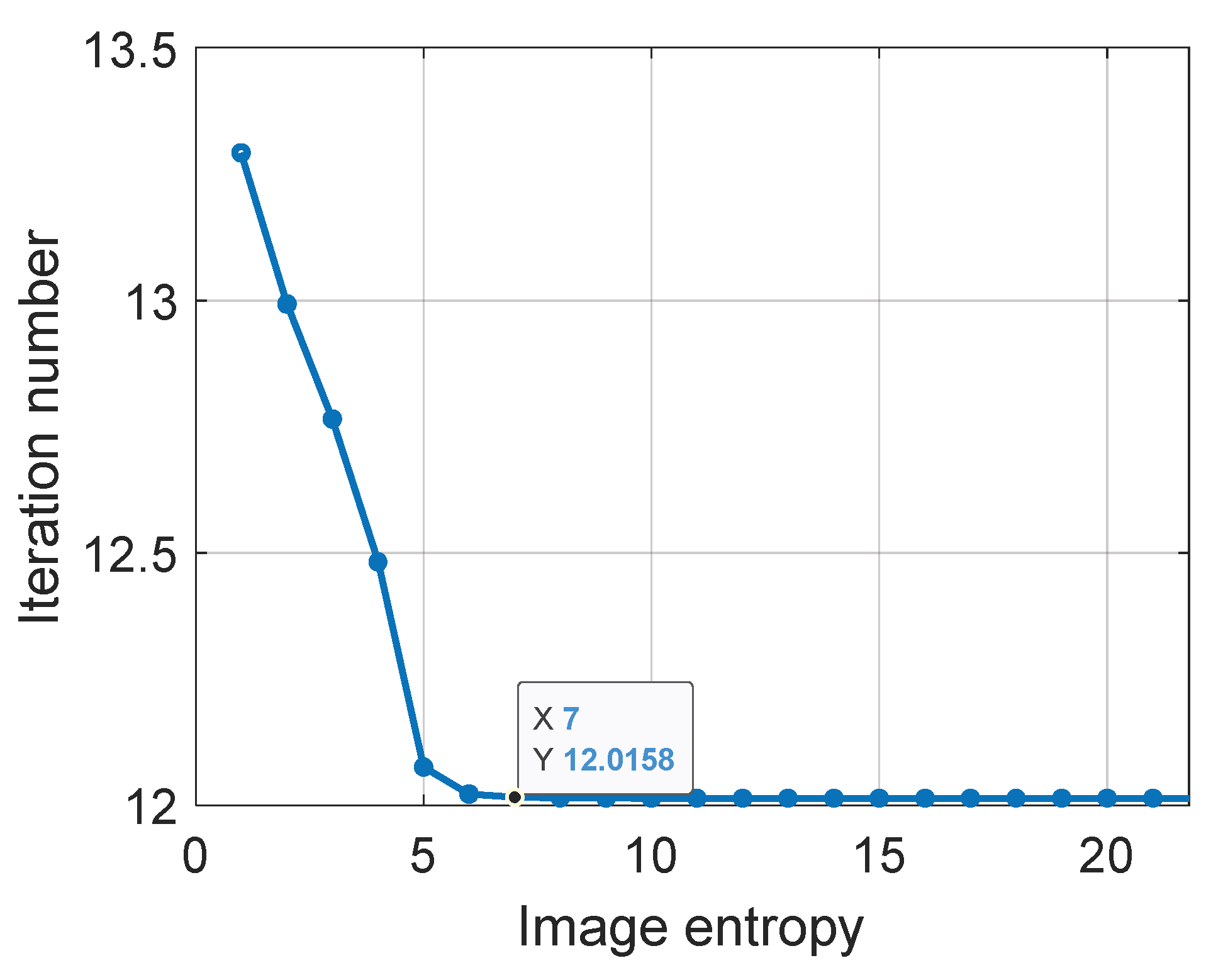
The above equation is the step of the traditional Newton iteration method. In the actual processing process, the IE of the imaging result has many local optimal points, as shown in
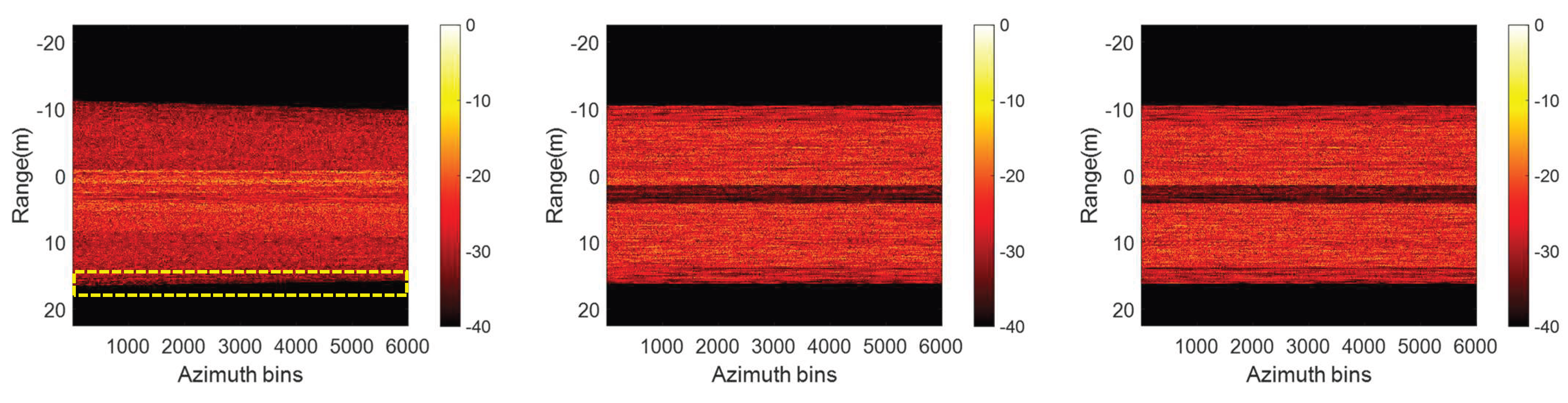
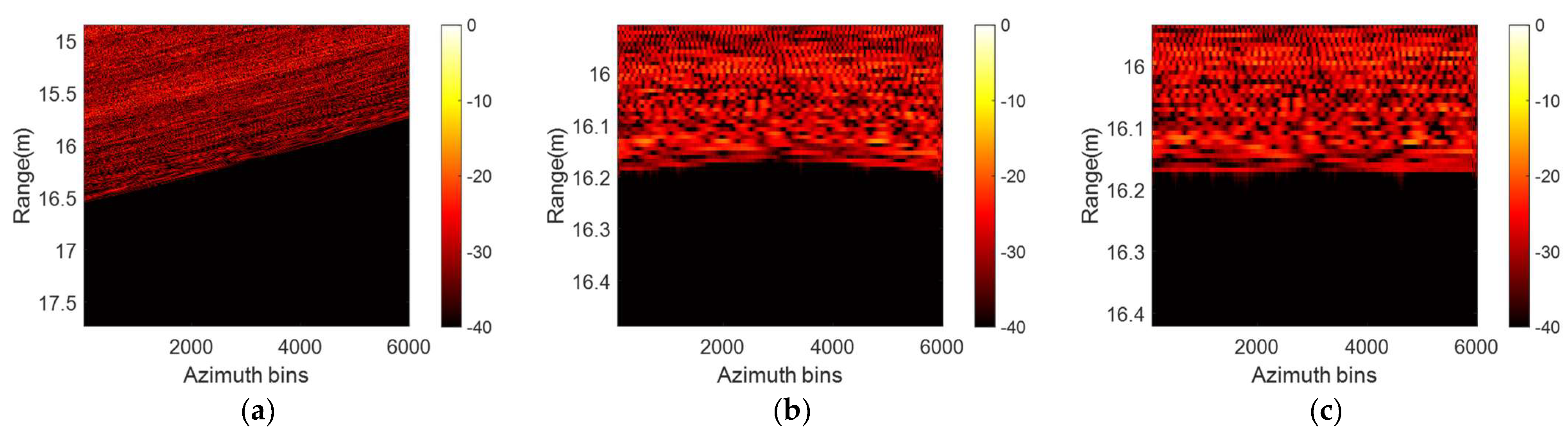
Figure 5.
At the same time, when the initial starting point is chosen far from the optimal solution, the Hessian matrix is not necessarily positive definite, which leads to the Hessian matrix not being invertible or the direction of the computed update being the direction that increases the objective function. At this moment, the NM fails, so the traditional NM should be modified and improved. The modified Newton method (MN) can be expressed as:
Equation (21) contains two modifications to NM. The first is the step size factor. The step size coefficients can be used to prevent the objective function from falling into a local optimum by using a linear search method (e.g., the golden section method). Secondly, when the Hessian matrix is not positive, it is modified to be
where
is the unit array. Distinguishing the step
, the eigenvalues of the Hessian matrix are
,
, ……, e, Then, the choice of
needs to be satisfied
i.e.,
is modified to remain positive at all times.
The processing flow of the rotational velocity estimation algorithm based on ME-MN is shown in
Figure 6.
3.3. Second-Order Space-Varying Range Migration Correction
Through the method in
Section 3.2, after the rotational velocity is obtained, the second-order space-varying range migration correction is performed below. Because different scattering point signals are superimposed in the range time domain, it is impossible to compensate the echo with a unified phase to eliminate the second-order range curvature. The frequency is resampled to correct the second-order range curvature by referring to the KT principle. This process can also be realized by CZT transform. The specific implementation process is as follows:
Finally, Equation (25) can be written as
The above equation is compensated for the quadratic phase and then an azimuthal FFT is performed. The final imaging result is obtained.