Improving the Estimation of Canopy Fluorescence Escape Probability in the Near-Infrared Band by Accounting for Soil Reflectance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulated Datasets
2.1.1. SCOPE Model Simulations
2.1.2. DART Model Simulations
2.2. Field Dataset
2.2.1. Field-Measured Dataset
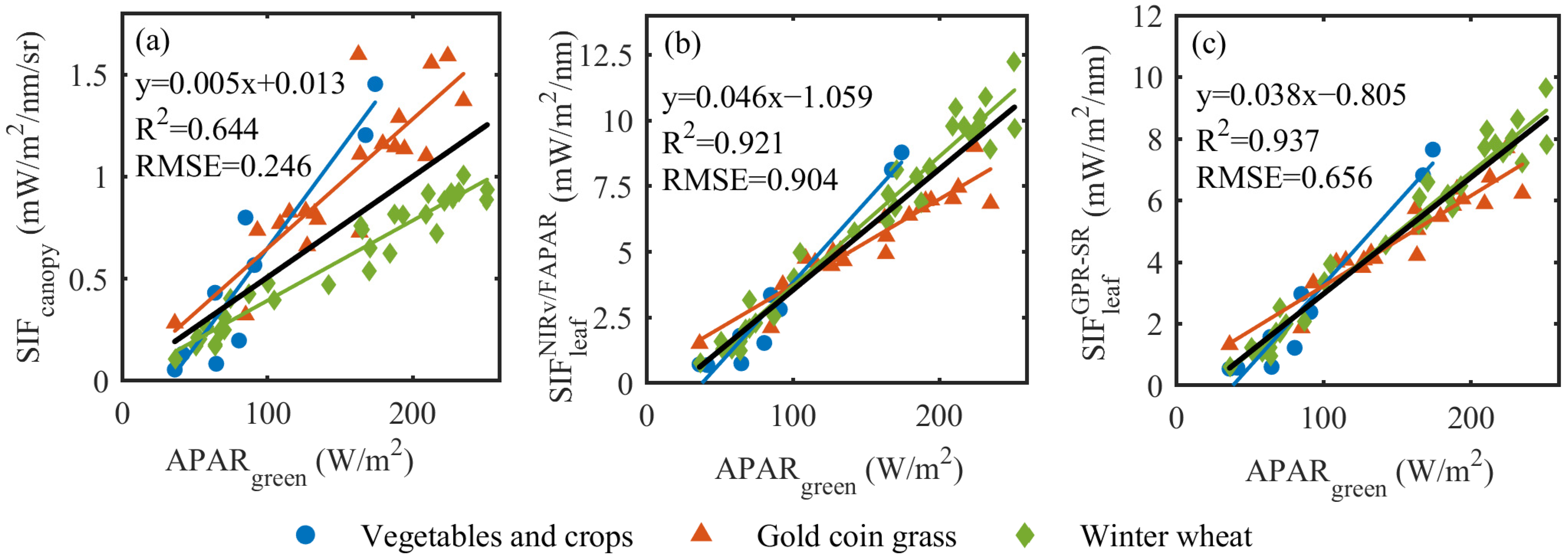
2.2.2. SIF Retrieval
2.2.3. Estimation of APARgreen
2.3. Correction Factor Accounting for Soil Reflectance
3. Results
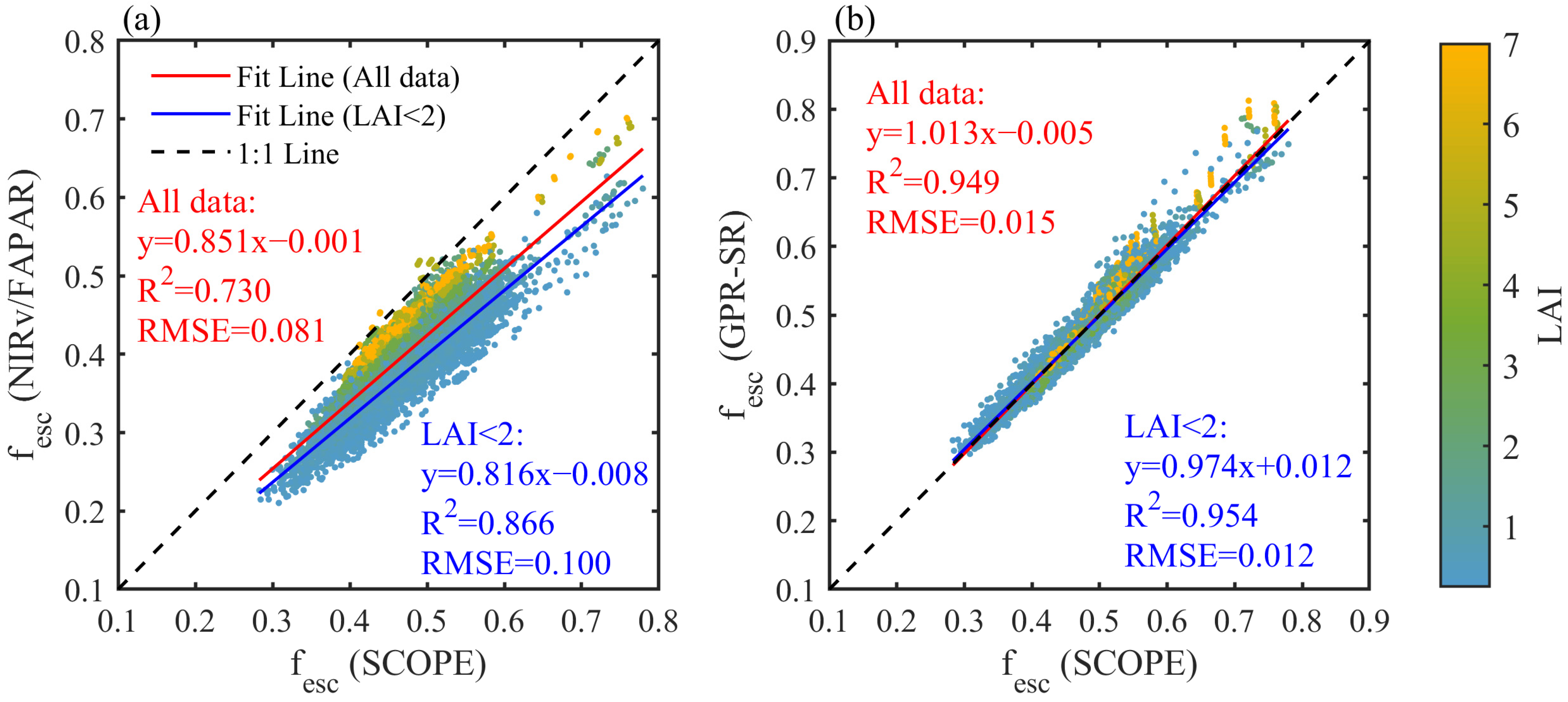
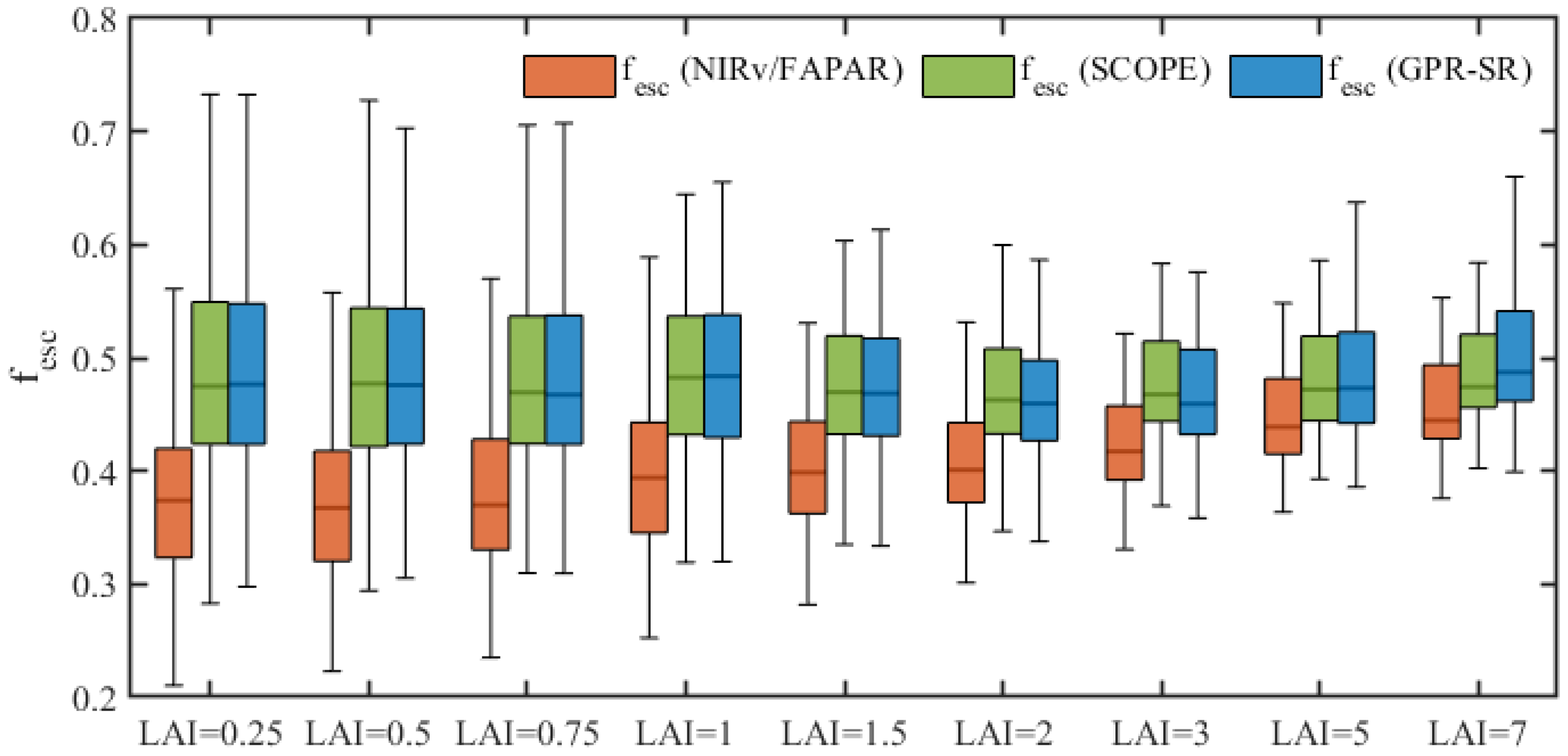
3.1. Performance of Different Correction Factors for fesc Estimation
3.2. Evaluation of the fesc_GPR-SR Model Using Simulated Data
3.2.1. Validation of the fesc_GPR-SR Model Using SCOPE Simulations
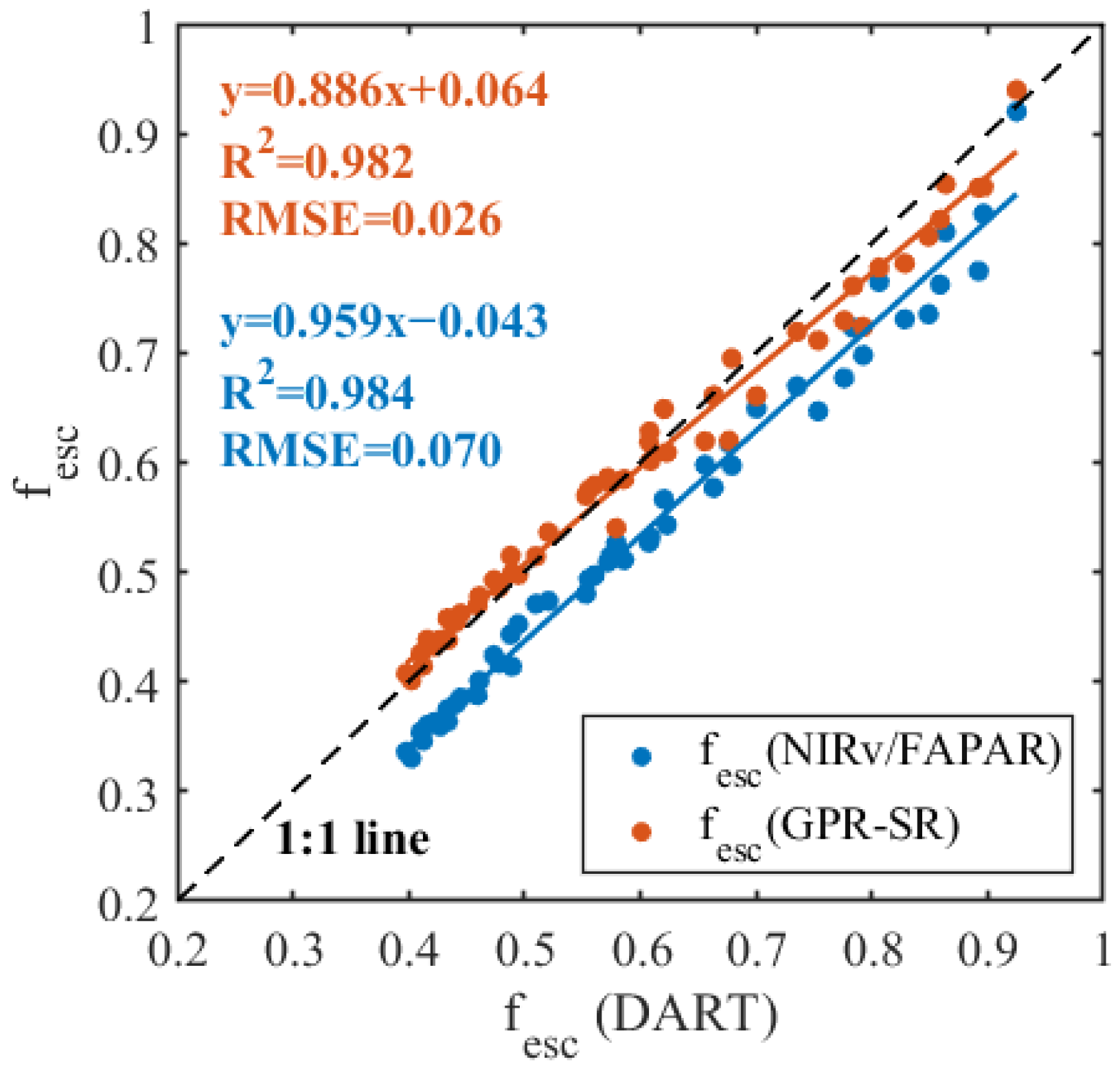
3.2.2. Validation of the fesc_GPR-SR Model Using DART Simulations
3.3. Evaluation of the fesc_GPR-SR Model Using Field-Measured Data
4. Discussion
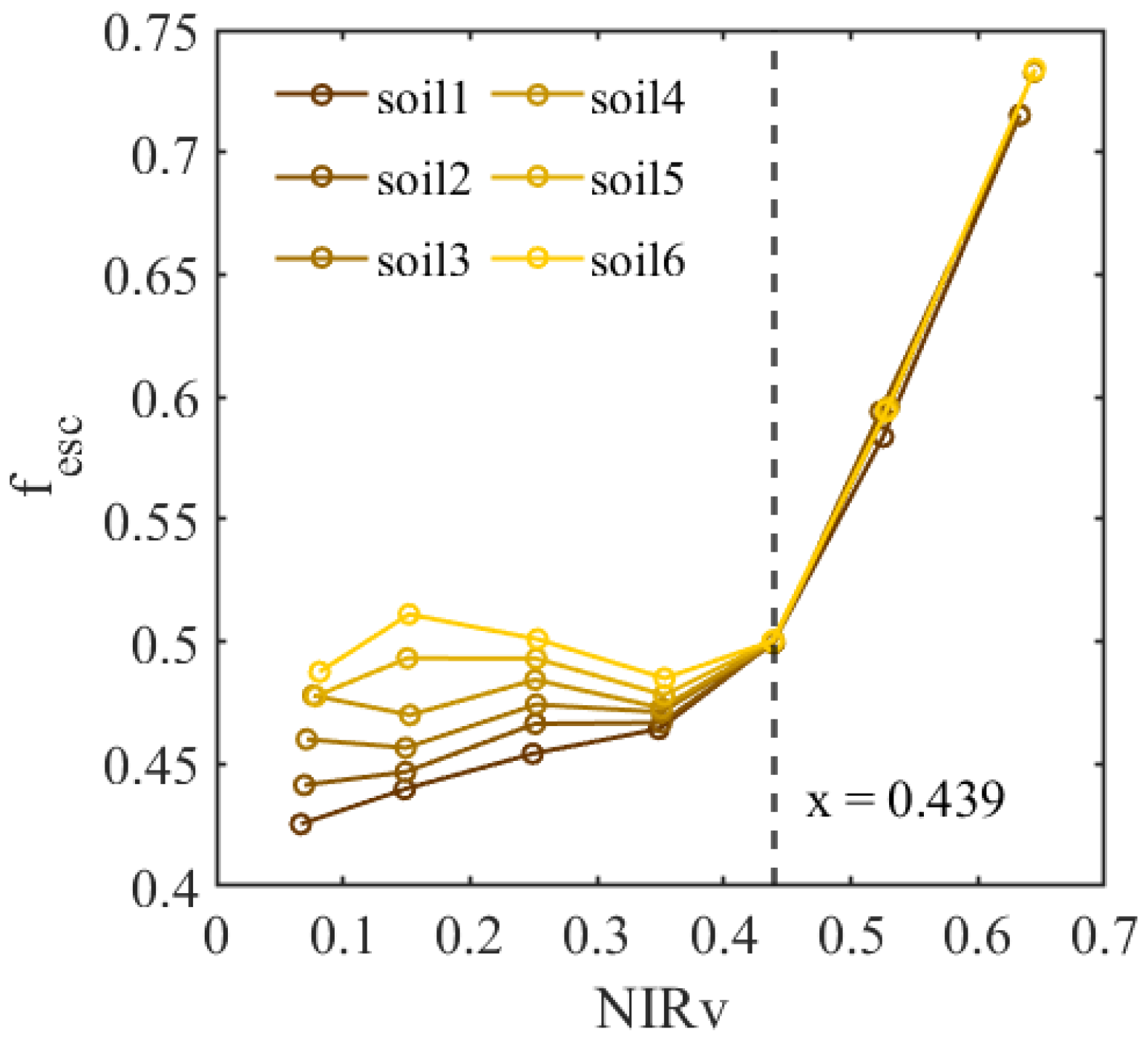
4.1. Effect of Soil Reflectance on Estimating fesc
4.2. Superiority of the fesc_GPR-SR Model
4.3. Uncertainties of the fesc_GPR-SR Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Magney, T.S.; Bowling, D.R.; Logan, B.A.; Grossmann, K.; Stutz, J.; Blanken, P.D.; Burns, S.P.; Cheng, R.; Garcia, M.A.; Köhler, P.; et al. Mechanistic evidence for tracking the seasonality of photosynthesis with solar-induced fluorescence. Proc. Natl. Acad. Sci. USA 2019, 116, 11640–11645. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; Van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Magney, T.; Dutta, D.; Yin, Y.; Köhler, P.; Grossmann, K.; Stutz, J.; Dold, C.; Hatfield, J.; Guan, K. From the ground to space: Using solar-induced chlorophyll fluorescence to estimate crop productivity. Geophys. Res. Lett. 2020, 47, e2020GL087474. [Google Scholar] [CrossRef]
- Kimm, H.; Guan, K.; Burroughs, C.H.; Peng, B.; Ainsworth, E.A.; Bernacchi, C.J.; Moore, C.E.; Kumagai, E.; Yang, X.; Berry, J.A.; et al. Quantifying high-temperature stress on soybean canopy photosynthesis: The unique role of sun-induced chlorophyll fluorescence. Glob. Chang. Biol. 2021, 27, 2403–2415. [Google Scholar] [CrossRef]
- Migliavacca, M.; Perez-Priego, O.; Rossini, M.; El-Madany, T.S.; Moreno, G.; Van der Tol, C.; Rascher, U.; Berninger, A.; Bessenbacher, V.; Burkart, A. Plant functional traits and canopy structure control the relationship between photosynthetic CO2 uptake and far-red sun-induced fluorescence in a Mediterranean grassland under different nutrient availability. New Phytol. 2017, 214, 1078–1091. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.S.; Jung, M.; Guanter, L.; Drewry, D.T.; Verma, M.; Porcar-Castell, A.; Griffis, T.J.; et al. OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence. Science 2017, 358, eaam5747. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, F.; Liu, X.; Yu, Q.; Wang, Y.; Peng, X.; Cai, H.; Lu, X. Direct estimation of photosynthetic CO2 assimilation from solar-induced chlorophyll fluorescence (SIF). Remote Sens. Environ. 2022, 271, 112893. [Google Scholar] [CrossRef]
- Mohammed, G.H.; Colombo, R.; Middleton, E.M.; Rascher, U.; Zarco-Tejada, P.J. Remote sensing of solar-induced chlorophyll fluorescence (SIF) in vegetation: 50 years of progress. Remote Sens. Environ. 2019, 231, 111177. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Malenovský, Z.; Magney, T.S.; Van Wittenberghe, S.; Fernández-Marín, B.; Maignan, F.; Zhang, Y.; Maseyk, K.; Atherton, J.; Albert, L.P.; et al. Chlorophyll a fluorescence illuminates a path connecting plant molecular biology to Earth-system science. Nat. Plants 2021, 7, 998–1009. [Google Scholar] [CrossRef]
- Frankenberg, C.; O’Dell, C.; Berry, J.; Guanter, L.; Joiner, J.; Köhler, P.; Pollock, R.; Taylor, T.E. Prospects for chlorophyll fluorescence remote sensing from the Orbiting Carbon Observatory-2. Remote Sens. Environ. 2014, 147, 1–12. [Google Scholar] [CrossRef]
- Gu, L.; Han, J.; Wood, J.D.; Chang, C.Y.Y.; Sun, Y. Sun-induced Chl fluorescence and its importance for biophysical modeling of photosynthesis based on light reactions. New Phytol. 2019, 223, 1179–1191. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Liu, X.; Chen, J.; Liu, L. Prospects for Solar-Induced Chlorophyll Fluorescence Remote Sensing from the SIFIS Payload Onboard the TECIS-1 Satellite. J. Remote Sens. 2022, 2022, 9845432. [Google Scholar] [CrossRef]
- Frankenberg, C.; Berry, J.; Guanter, L.; Joiner, J. Remote sensing of terrestrial chlorophyll fluorescence from space. SPIENewsroom 2013, 2–5, 4725. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.-E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38, L17706. [Google Scholar] [CrossRef]
- Liu, X.; Guanter, L.; Liu, L.; Damm, A.; Malenovský, Z.; Rascher, U.; Peng, D.; Du, S.; Gastellu-Etchegorry, J.-P. Downscaling of solar-induced chlorophyll fluorescence from canopy level to photosystem level using a random forest model. Remote Sens. Environ. 2019, 231, 110772. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Q.; Li, J.; Yang, X.; Wu, Y.; Zhang, Z.; Wang, S.; Wang, H.; Zhang, Y. Solar-induced chlorophyll fluorescence and its link to canopy photosynthesis in maize from continuous ground measurements. Remote Sens. Environ. 2020, 236, 111420. [Google Scholar] [CrossRef]
- Hao, D.; Zeng, Y.; Qiu, H.; Biriukova, K.; Celesti, M.; Migliavacca, M.; Rossini, M.; Asrar, G.R.; Chen, M. Practical approaches for normalizing directional solar-induced fluorescence to a standard viewing geometry. Remote Sens. Environ. 2021, 255, 112171. [Google Scholar] [CrossRef]
- Siegmann, B.; Cendrero-Mateo, M.P.; Cogliati, S.; Damm, A.; Gamon, J.; Herrera, D.; Jedmowski, C.; Junker-Frohn, L.V.; Kraska, T.; Muller, O. Downscaling of far-red solar-induced chlorophyll fluorescence of different crops from canopy to leaf level using a diurnal data set acquired by the airborne imaging spectrometer HyPlant. Remote Sens. Environ. 2021, 264, 112609. [Google Scholar] [CrossRef]
- van der Tol, C.; Rossini, M.; Cogliati, S.; Verhoef, W.; Colombo, R.; Rascher, U.; Mohammed, G. A model and measurement comparison of diurnal cycles of sun-induced chlorophyll fluorescence of crops. Remote Sens. Environ. 2016, 186, 663–677. [Google Scholar] [CrossRef]
- Berry, J.A.; Frankenberg, C.; Wennberg, P.; Baker, I.; Bowman, K.W.; Castro-Contreas, S.; Cendrero-Mateo, M.P.; Damm, A.; Drewry, D.; Ehlmann, B. New Methods for Measurement of Photosynthesis from Space. Geophys. Res. Lett. 2012, 38, L17706. [Google Scholar]
- Liu, L.; Guan, L.; Liu, X. Directly estimating diurnal changes in GPP for C3 and C4 crops using far-red sun-induced chlorophyll fluorescence. Agric. For. Meteorol. 2017, 232, 1–9. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Hu, J.; Guan, L. Assessing the wavelength-dependent ability of solar-induced chlorophyll fluorescence to estimate the GPP of winter wheat at the canopy level. Int. J. Remote Sens. 2017, 38, 4396–4417. [Google Scholar] [CrossRef]
- Wieneke, S.; Ahrends, H.; Damm, A.; Pinto, F.; Stadler, A.; Rossini, M.; Rascher, U. Airborne based spectroscopy of red and far-red sun-induced chlorophyll fluorescence: Implications for improved estimates of gross primary productivity. Remote Sens. Environ. 2016, 184, 654–667. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wolf, S.; Wu, J.; Wu, X.; Gioli, B.; Wohlfahrt, G.; Cescatti, A.; Van der Tol, C.; Zhou, S. Spatio-temporal convergence of maximum daily light-use efficiency based on radiation absorption by canopy chlorophyll. Geophys. Res. Lett. 2018, 45, 3508–3519. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Zhang, Y.; Gobron, N.; Frankenberg, C.; Wang, S.; Li, Z. The potential of satellite FPAR product for GPP estimation: An indirect evaluation using solar-induced chlorophyll fluorescence. Remote Sens. Environ. 2020, 240, 111686. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L.; Hu, J.; Guo, J.; Du, S. Improving the potential of red SIF for estimating GPP by downscaling from the canopy level to the photosystem level. Agric. For. Meteorol. 2020, 281, 107846. [Google Scholar] [CrossRef]
- Yang, P.; van der Tol, C. Linking canopy scattering of far-red sun-induced chlorophyll fluorescence with reflectance. Remote Sens. Environ. Interdiscip. J. 2018, 209, 456–467. [Google Scholar] [CrossRef]
- Zeng, Y.; Badgley, G.; Dechant, B.; Ryu, Y.; Berry, J.A. A practical approach for estimating the escape ratio of near-infrared solar-induced chlorophyll fluorescence. Remote Sens. Environ. 2019, 232, 111209. [Google Scholar] [CrossRef]
- Yang, P.; van der Tol, C.; Campbell, P.K.E.; Middleton, E.M. Fluorescence Correction Vegetation Index (FCVI): A physically based reflectance index to separate physiological and non-physiological information in far-red sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2020, 240, 111676. [Google Scholar] [CrossRef]
- van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Qian, X.; Liu, L.; Chen, X.; Zhang, X.; Chen, S.; Sun, Q. The global leaf chlorophyll content dataset over 2003–2012 and 2018–2020 derived from MERIS/OLCI satellite data (GLCC): Algorithm and validation. Earth Syst. Sci. Data Discuss. 2022, 2022, 1–21. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Martin, E.; Gascon, F. DART: A 3D model for simulating satellite images and studying surface radiation budget. Int. J. Remote Sens. 2004, 25, 73–96. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P.; Lauret, N.; Yin, T.; Landier, L.; Kallel, A.; Malenovský, Z.; Al Bitar, A.; Aval, J.; Hmida, S.B.; Qi, J.; et al. DART: Recent Advances in Remote Sensing Data Modeling With Atmosphere, Polarization, and Chlorophyll Fluorescence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2640–2649. [Google Scholar] [CrossRef]
- Maier, S.W.; Günther, K.; Stellmes, M. Sun-Induced Fluorescence: A New Tool for Precision Farming; ASA: Madison, WI, USA; Monroe, MI, USA, 2003. [Google Scholar]
- Damm, A.; Erler, A.; Hillen, W.; Meroni, M.; Schaepman, M.E.; Verhoef, W.; Rascher, U. Modeling the impact of spectral sensor configurations on the FLD retrieval accuracy of sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2011, 115, 1882–1892. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Hu, J. Effects of spectral resolution and SNR on the vegetation solar-induced fluorescence retrieval using FLD-based methods at canopy level. Eur. J. Remote Sens. 2015, 48, 743–762. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote estimation of fraction of radiation absorbed by photosynthetically active vegetation: Generic algorithm for maize and soybean. Remote Sens. Lett. 2018, 10, 283–291. [Google Scholar] [CrossRef]
- Liu, L.; Peng, D.; Hu, Y.; Jiao, Q. A novel in situ FPAR measurement method for low canopy vegetation based on a digital camera and reference panel. Remote Sens. 2013, 5, 274–281. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Richardsons, A.J.; Wiegand, A. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Jin, H.; Chen, X.; Wang, Y.; Zhong, R.; Zhao, T.; Liu, Z.; Tu, X. Spatio-temporal distribution of NDVI and its influencing factors in China. J. Hydrol. 2021, 603, 127129. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- van der Tol, C.; Berry, J.A.; Campbell, P.K.E.; Rascher, U. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. J. Geophys. Res. Biogeosci. 2014, 119, 2312–2327. [Google Scholar] [CrossRef]
- Liu, W.; Luo, S.; Lu, X.; Atherton, J.; Gastellu-Etchegorry, J.-P. Simulation-based evaluation of the estimation methods of far-red solar-induced chlorophyll fluorescence escape probability in discontinuous Forest canopies. Remote Sens. 2020, 12, 3962. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, J.M.; Guanter, L.; He, L.; Zhang, Y. From canopy-leaving to total canopy far-red fluorescence emission for remote sensing of photosynthesis: First results from TROPOMI. Geophys. Res. Lett. 2019, 46, 12030–12040. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Badgley, G.; Damm, A.; Rascher, U.; Ryu, Y.; Johnson, J.; Krieger, V.; Wu, S.; Qiu, H.; et al. Estimating near-infrared reflectance of vegetation from hyperspectral data. Remote Sens. Environ. 2021, 267, 112723. [Google Scholar] [CrossRef]
- Ma, C.; Zhang, H.H.; Wang, X. Machine learning for Big Data analytics in plants. Trends Plant Sci. 2014, 19, 798–808. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E.; Williams, C.K. Gaussian processes in machine learning. Lect. Notes Comput. Sci. 2004, 3176, 63–71. [Google Scholar]
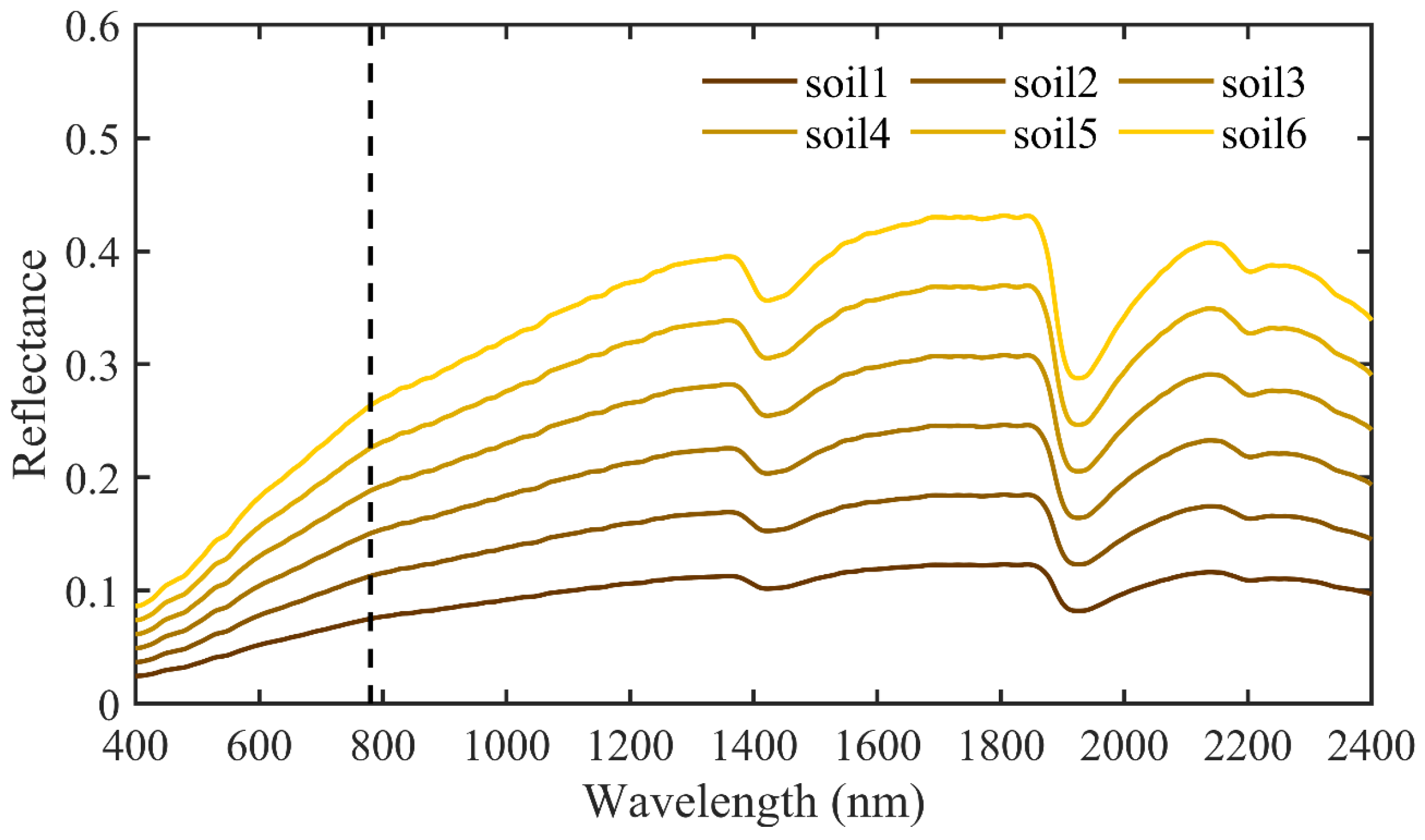
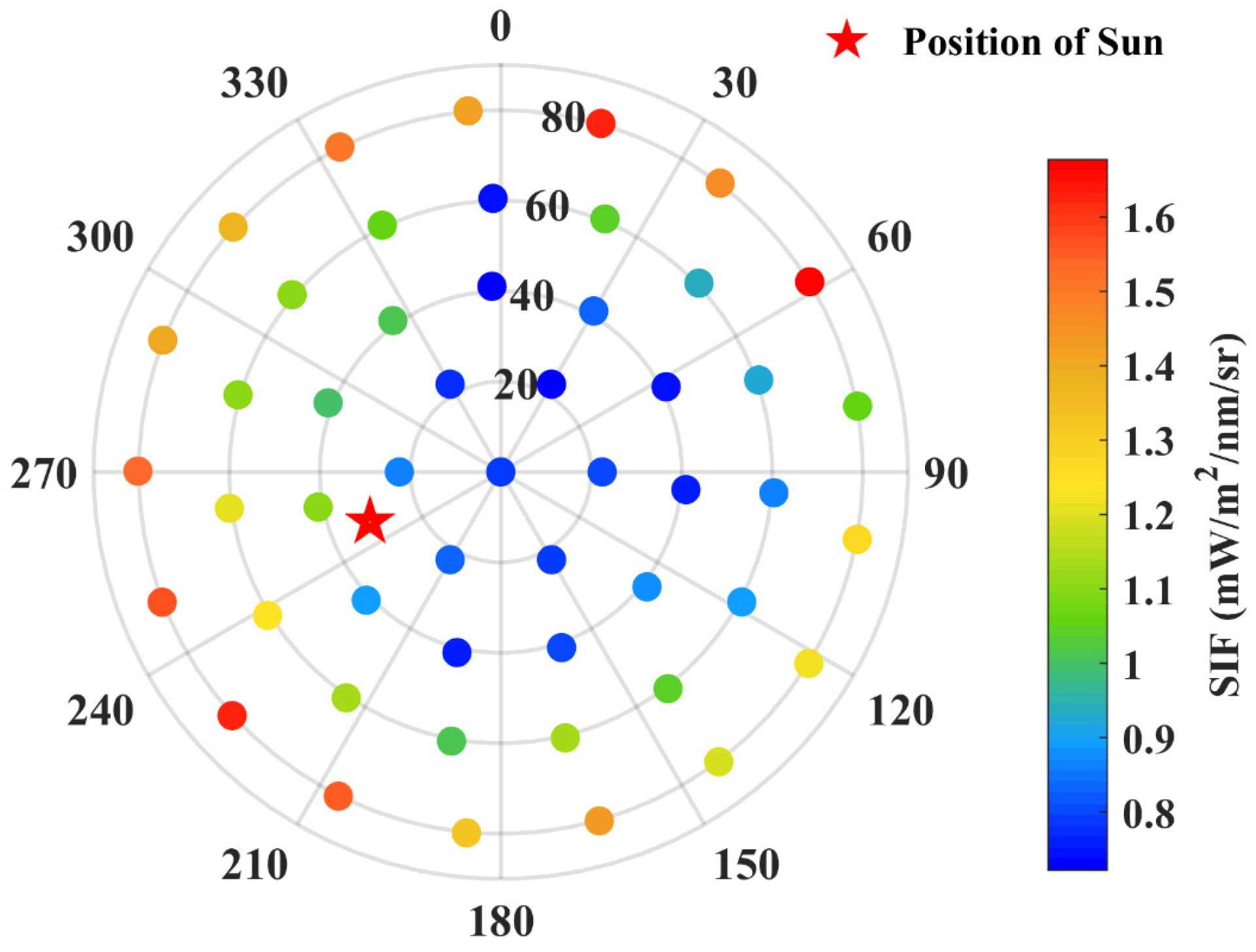




| Variables | Definition | Values | Unit |
|---|---|---|---|
| Cab | Leaf chlorophyll a and b content | 20, 40, 60, 80 | μg/cm2 |
| LAI | Leaf area index | 0.25, 0.5, 0.75, 1, 1.5, 2, 3, 5, 7 | m2/m2 |
| LIDFa | Leaf inclination parameter | 1, 0, 0, −0.35, 0 | − |
| LIDFb | Bimodality parameter | 0, −1, 1, −0.15, 0 | − |
| SZA | Solar zenith angle | 20, 30, 40, 50, 60 | Degree |
| VZA | Viewing zenith angle | 0, 15, 30, 45, 60 | Degree |
| RAA | Relative azimuth angle | 0, 90, 180 | Degree |
| Soil spectra | Soil reflectance | Six soil spectra | − |
| Variables | Definition | Values | Unit |
|---|---|---|---|
| Vegetation type | Vegetation type | Maize | − |
| N | Structure coefficient | 1.5 | − |
| Cab | Leaf chlorophyll a and b content | 58 | μg/cm2 |
| Yield PSI | Fluorescence quantum yield for photosystem I | 0.002 | − |
| Yield PSII | Fluorescence quantum yield for photosystem II | 0.008 | − |
| LAI | Leaf area index | 2 | m2/m2 |
| Canopy height | Canopy height | 1.5 | m |
| Soil spectra | Soil reflectance | loam_gravelly_brown_dark | − |
| SZA | Solar zenith angle | 30.9303 | Degree |
| SAA | Solar azimuth angle | 249.1069 | Degree |
| VZA | Viewing zenith angle | 0–90 | Degree |
| VAA | Viewing azimuth angle | 0–360 | Degree |
| Sites | Xiaotangshan Farm | Xiaotangshan Farm | Nanbin Farm | Sanya Station |
|---|---|---|---|---|
| Location | 40°11′N 116°27′E | 40°11′N 116°27′E | 18°22′N 109°10′E | 18°18′N 109°18′E |
| Dates in 2016 | 8, 9, 18 April | 8 December | 18 December | 18 December |
| Species | Winter wheat | Winter wheat | Vegetables and crops | Gold coin grass |
| Fractional vegetation cover (FVC) | 0.72–0.79 | 0.21–0.63 | 0.28–0.91 | 0.67 |
| Soil reflectance in NIR band * | 0.12–0.17 | 0.13–0.16 | 0.09–0.16 | 0.11–0.13 |
| VIs | References |
|---|---|
| [41] | |
| [42] | |
| [43] | |
| [44] |
| Inputs for Models | R2 | RMSE | MAE | R2 (LAI < 2) | RMSE (LAI < 2) | MAE (LAI < 2) |
|---|---|---|---|---|---|---|
| Refsoil, NDVI | 0.85 | 0.0391 | 0.0311 | 0.69 | 0.0438 | 0.0348 |
| Refsoil, SR | 0.85 | 0.0396 | 0.0315 | 0.68 | 0.0441 | 0.0350 |
| Refsoil, EVI2 | 0.84 | 0.0403 | 0.0313 | 0.65 | 0.0467 | 0.0372 |
| Refsoil, PVI | 0.82 | 0.0433 | 0.0334 | 0.62 | 0.0484 | 0.0385 |
| Vegetables and Crops | Gold Coin Grass | Winter Wheat | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| 0.883 | 0.187 | 0.750 | 0.195 | 0.944 | 0.071 | |
| 0.955 | 0.709 | 0.891 | 0.612 | 0.966 | 0.683 | |
| 0.950 | 0.646 | 0.901 | 0.518 | 0.970 | 0.511 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, M.; Liu, X.; Du, S.; Guan, L.; Chen, R.; Liu, L. Improving the Estimation of Canopy Fluorescence Escape Probability in the Near-Infrared Band by Accounting for Soil Reflectance. Remote Sens. 2023, 15, 4361. https://doi.org/10.3390/rs15184361
Qi M, Liu X, Du S, Guan L, Chen R, Liu L. Improving the Estimation of Canopy Fluorescence Escape Probability in the Near-Infrared Band by Accounting for Soil Reflectance. Remote Sensing. 2023; 15(18):4361. https://doi.org/10.3390/rs15184361
Chicago/Turabian StyleQi, Mengjia, Xinjie Liu, Shanshan Du, Linlin Guan, Ruonan Chen, and Liangyun Liu. 2023. "Improving the Estimation of Canopy Fluorescence Escape Probability in the Near-Infrared Band by Accounting for Soil Reflectance" Remote Sensing 15, no. 18: 4361. https://doi.org/10.3390/rs15184361
APA StyleQi, M., Liu, X., Du, S., Guan, L., Chen, R., & Liu, L. (2023). Improving the Estimation of Canopy Fluorescence Escape Probability in the Near-Infrared Band by Accounting for Soil Reflectance. Remote Sensing, 15(18), 4361. https://doi.org/10.3390/rs15184361






