A UAV Path Planning Method for Building Surface Information Acquisition Utilizing Opposition-Based Learning Artificial Bee Colony Algorithm
Abstract
:1. Introduction
- A target information entropy ratio (IER) model based on observation angles is established. Considering the constraints on flight, IER is an index of information loss, which is a function of observation angles.
- An opposition-based learning ABC algorithm is proposed. By introducing the concept of vague opposition-based learning into the ABC algorithm, the algorithm is able to search a larger solution space with high-quality solutions preserved.
- The activation mechanism of the scout bees has been upgraded. The novel mechanism is based on the individual’s relative position to the population, allowing the scout bees to adaptively abandon the individual.
2. Problem Definition
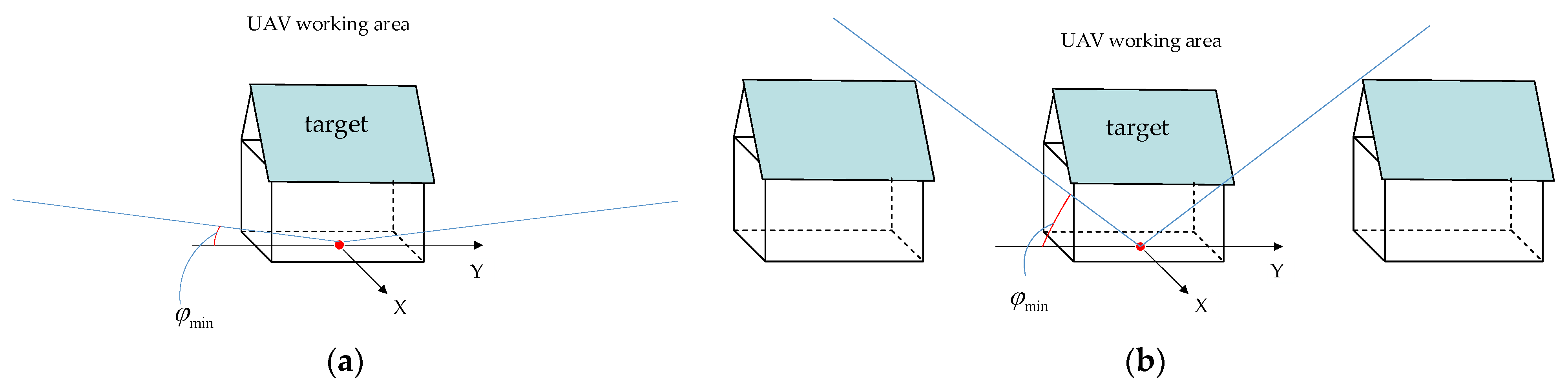
2.1. Definition of Drone Observation Angles
2.2. Analysis of Constraints for UAV Observations
2.2.1. Constraints on RDA
2.2.2. Constraints on RAA
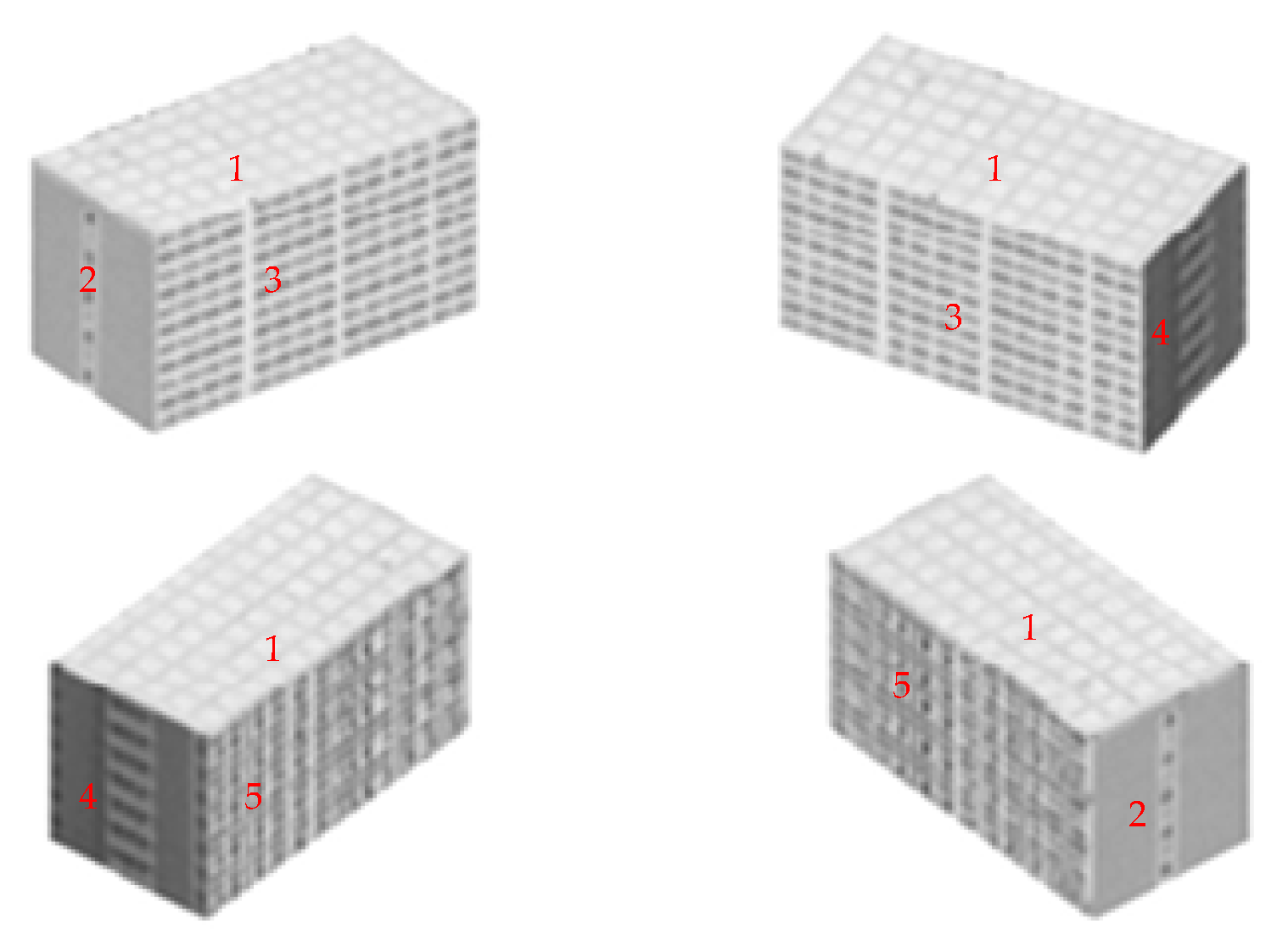
2.3. A Multi-Angle Target Information Acquisition Model
3. Proposed Method
3.1. Artificial Bee Colony Algorithm
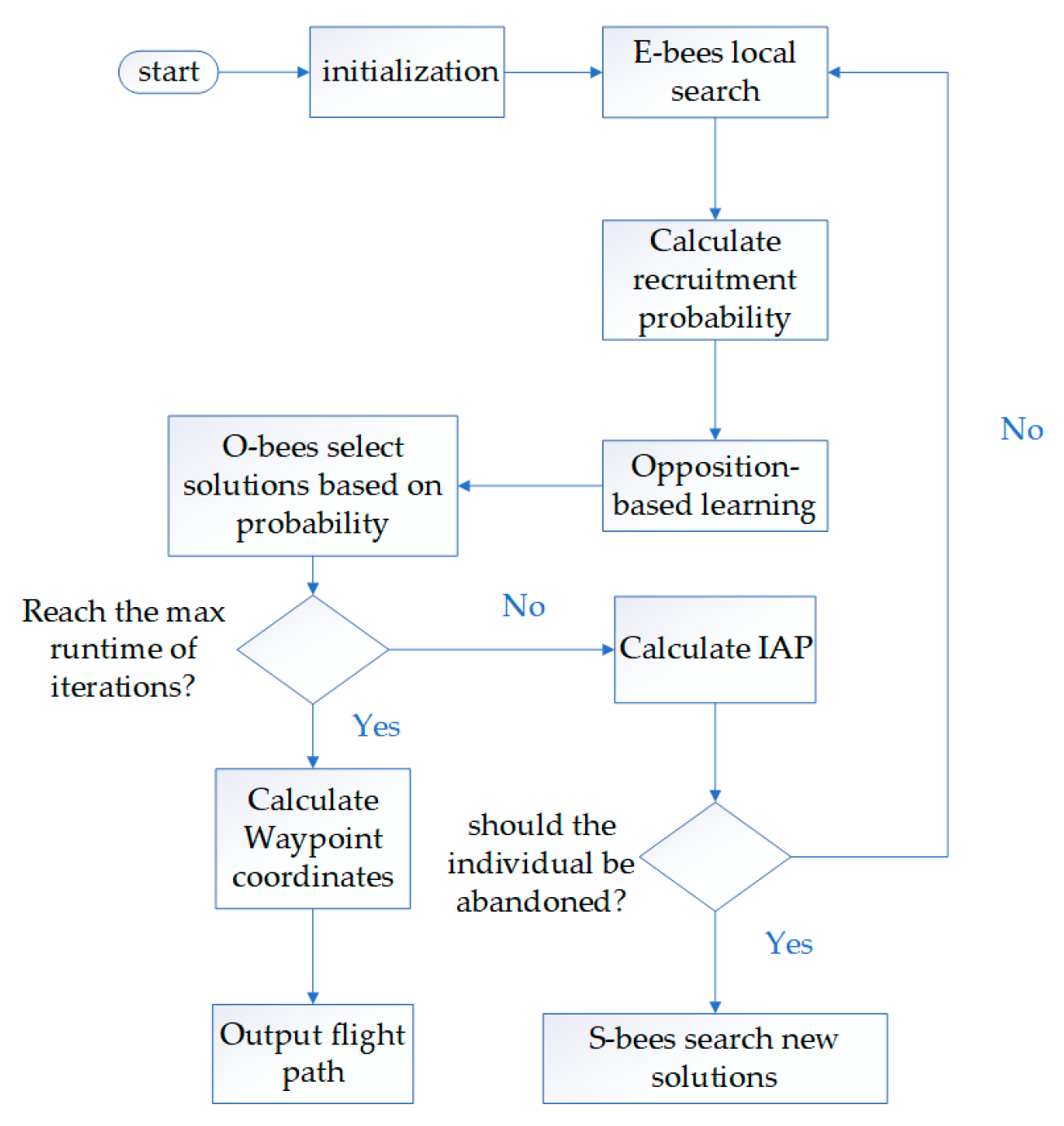
3.2. Opposition-Based Learning Artificial Bee Colony Algorithm
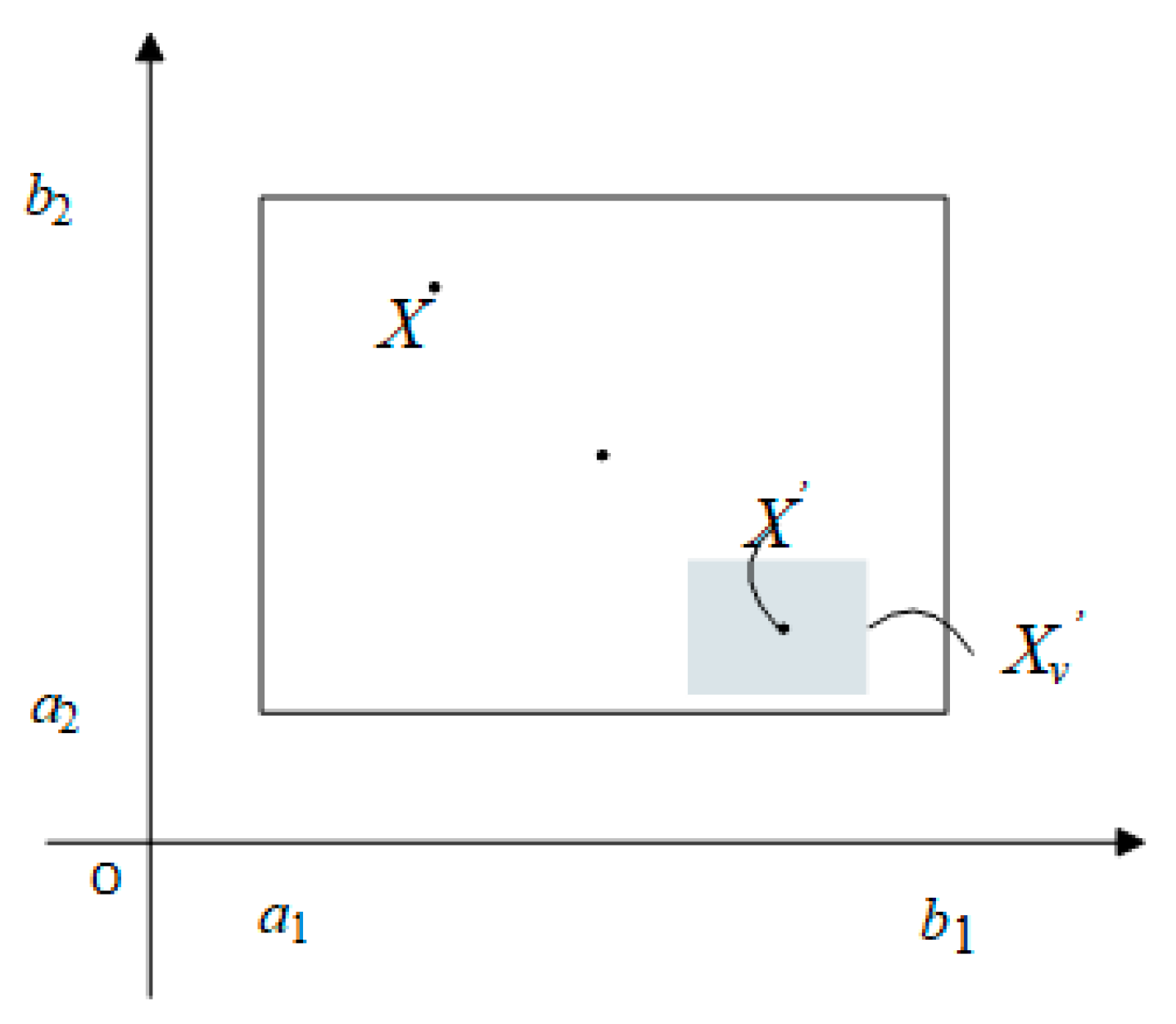
3.2.1. Opposition-Based Learning Mechanism
3.2.2. Improved S-Bee Search Mechanism
4. Experiment
4.1. Controlled Experiment
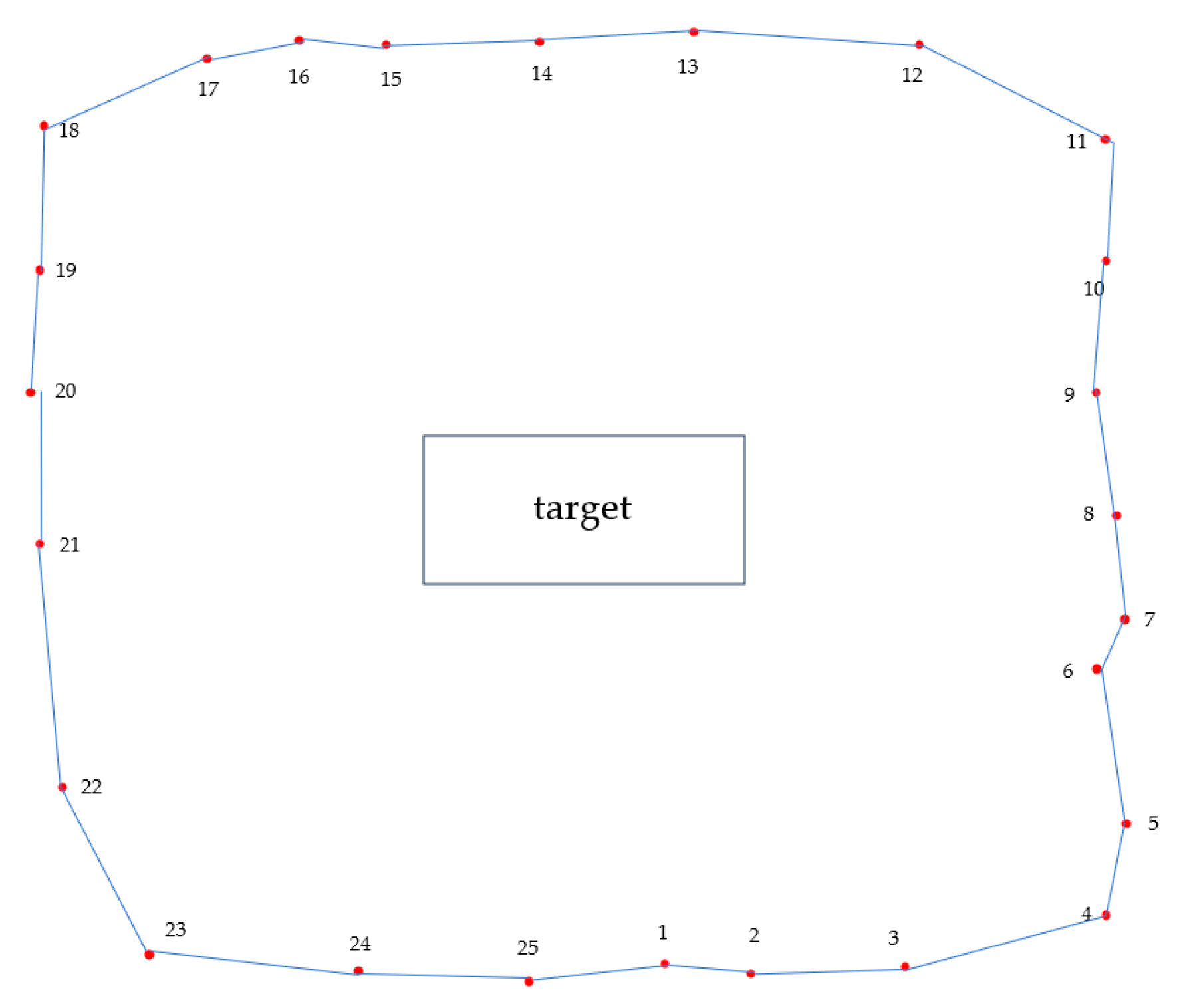
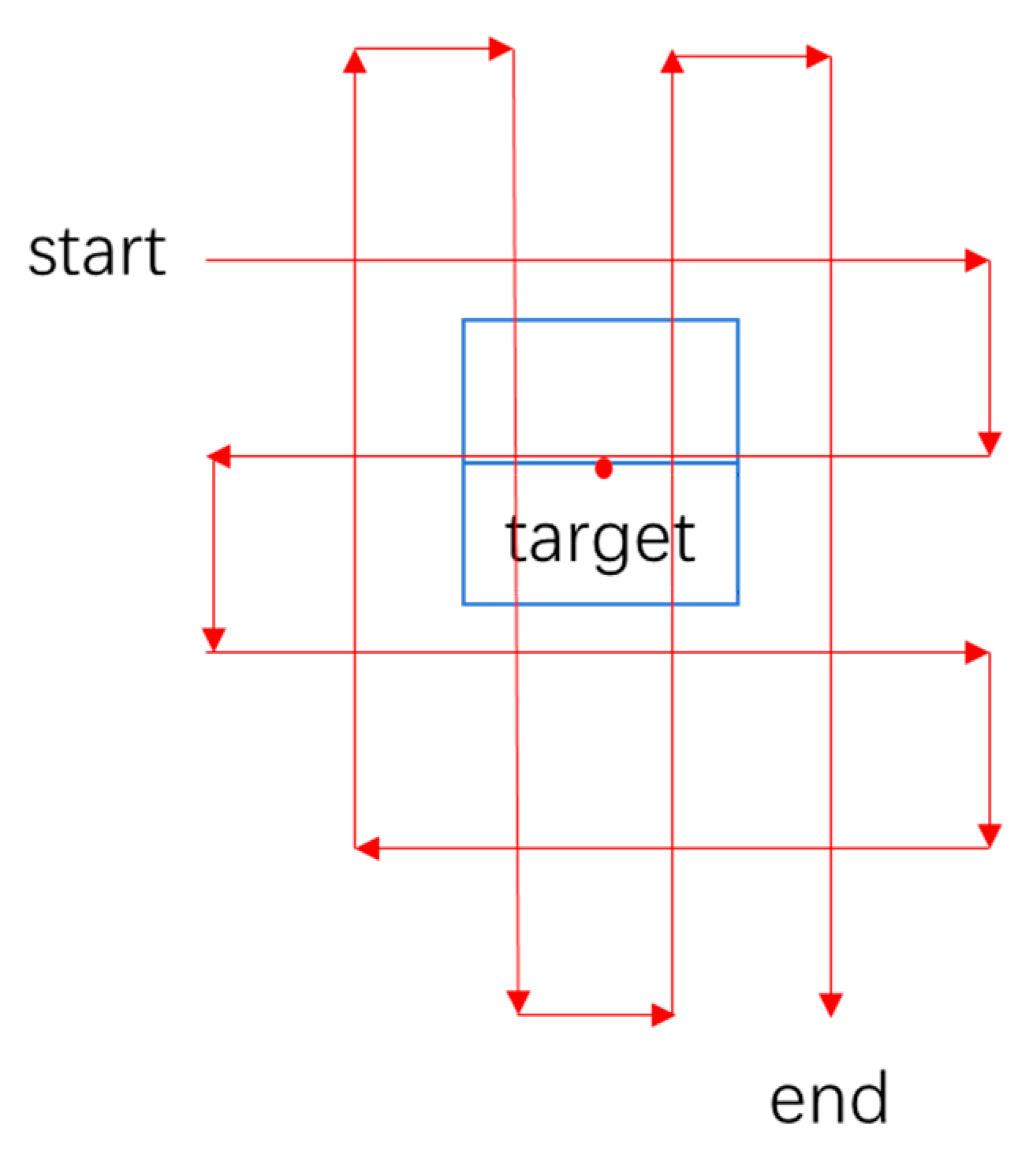
4.1.1. Experiment Design
4.1.2. Experiment Results
4.2. 3D Reconstruction Experiment
4.2.1. Experiment Design
4.2.2. Visual Comparison of Models
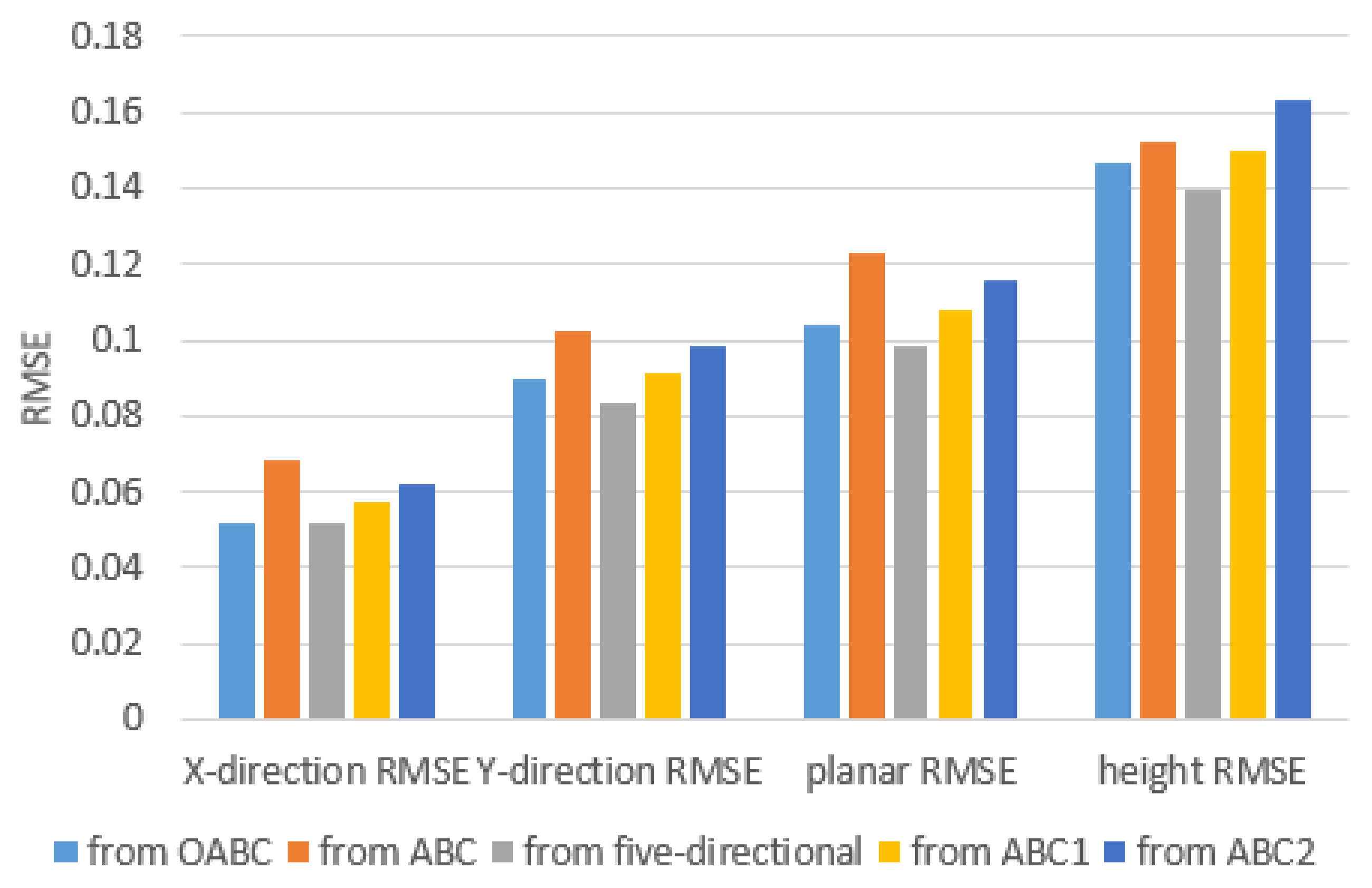
4.2.3. Quantitative Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, P.; Mou, L.; Xia, G.-S.; Zhu, X.X. Anomaly Detection in Aerial Videos with Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5628213. [Google Scholar] [CrossRef]
- Triantafyllia-Maria, P.; Antonios, M.; Dimitrios, T.; Georgios, M. Water Surface Level Monitoring of the Axios River Wetlands, Greece, Using Airborne and Space-Borne Earth Observation Data. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: Toulouse, France, 2022; pp. 6205–6208. [Google Scholar]
- Jhan, J.-P.; Kerle, N.; Rau, J.-Y. Integrating UAV and ground panoramic images for point cloud analysis of damaged building. IEEE Geosci. Remote Sens. Lett. 2021, 19, 6500805. [Google Scholar] [CrossRef]
- Zhan, P.; Song, C.; Luo, S.; Liu, K.; Ke, L.; Chen, T. Lake level reconstructed from DEM-based virtual station: Comparison of multisource DEMs with laser altimetry and UAV-LiDAR measurements. IEEE Geosci. Remote Sens. Lett. 2021, 19, 6502005. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y. Dynamic view planning by effective particles for three-dimensional tracking. IEEE Trans. Syst. Man Cybern. (Cybern.) 2008, 39, 242–253. [Google Scholar] [CrossRef]
- Xia, Z.; Du, J.; Wang, J.; Jiang, C.; Ren, Y.; Li, G.; Han, Z. Multi-agent reinforcement learning aided intelligent UAV swarm for target tracking. IEEE Trans. Veh. Technol. 2021, 71, 931–945. [Google Scholar] [CrossRef]
- Yao, A.; Huang, M.; Qi, J.; Zhong, P. Attention mask-based network with simple color annotation for UAV vehicle re-identification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 8014705. [Google Scholar] [CrossRef]
- Chang, J.; Dong, N.; Li, D.; Ip, W.H.; Yung, K.L. Skeleton Extraction and Greedy-Algorithm-Based Path Planning and its Application in UAV Trajectory Tracking. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4953–4964. [Google Scholar] [CrossRef]
- Ding, Y.; Xin, B.; Dou, L.; Chen, J.; Chen, B.M. A memetic algorithm for curvature-constrained path planning of messenger UAV in air-ground coordination. IEEE Trans. Autom. Sci. Eng. 2021, 19, 3735–3749. [Google Scholar] [CrossRef]
- Yu, Z.; Sun, F.; Lu, X.; Song, Y. Overview of research on 3d path planning methods for rotor uav. In Proceedings of the 2021 International Conference on Electronics, Circuits and Information Engineering (ECIE), Zhengzhou, China, 22–24 January 2021; IEEE: Toulouse, France, 2021; pp. 368–371. [Google Scholar]
- Liu, H. A Novel Path Planning Method for Aerial UAV based on Improved Genetic Algorithm. In Proceedings of the 2023 Third International Conference on Artificial Intelligence and Smart Energy (ICAIS), Coimbatore, India, 2–4 February 2023; IEEE: Toulouse, France, 2023; pp. 1126–1130. [Google Scholar]
- Zhu, Z.; Qian, Y.; Zhang, W. Research on UAV Searching Path Planning Based on Improved Ant Colony Optimization Algorithm. In Proceedings of the 2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Changsha, China, 20–22 October 2021; IEEE: Toulouse, France, 2021; pp. 1319–1323. [Google Scholar]
- Luo, Q.; Wang, H.; Zheng, Y.; He, J. Research on path planning of mobile robot based on improved ant colony algorithm. Neural Comput. Appl. 2020, 32, 1555–1566. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, J. Improved ant colony algorithm for path planning of fixed wing unmanned aerial vehicle. In Proceedings of the 2021 International Conference on Physics, Computing and Mathematical (ICPCM2021), MATEC Web of Conferences, Xiamen, China, 29–30 December 2021; EDP Sciences: Les Ulis, France, 2022; p. 03002. [Google Scholar]
- Bao, S.; Lu, Y.; Li, K.; Xu, P. Research on path planning of UAV based on ant colony algorithm with angle factor. J. Phys. Conf. Ser. 2020, 1627, 012008. [Google Scholar] [CrossRef]
- Shao, S.; Peng, Y.; He, C.; Du, Y. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 2020, 97, 415–430. [Google Scholar] [CrossRef]
- Panda, M.; Das, B.; Pati, B.B. Grey wolf optimization for global path planning of autonomous underwater vehicle. In Proceedings of the Proceedings of the Third International Conference on Advanced Informatics for Computing Research, Shimla, India, 15–16 June 2019; ACM: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Mishra, M.; An, W.; Sidoti, D.; Han, X.; Ayala, D.F.M.; Hansen, J.A.; Pattipati, K.R.; Kleinman, D.L. Context-aware decision support for anti-submarine warfare mission planning within a dynamic environment. IEEE Trans. Syst. Man Cybern. Syst. 2017, 50, 318–335. [Google Scholar] [CrossRef]
- Hong, K.R.; O, S.I.; Kim, R.H.; Kim, T.S.; Kim, J.S. Minimum dose path planning for facility inspection based on the discrete Rao-combined ABC algorithm in radioactive environments with obstacles. Nucl. Sci. Tech. 2023, 34, 50. [Google Scholar] [CrossRef]
- Tan, L.; Shi, J.; Gao, J.; Wang, H.; Zhang, H.; Zhang, Y. Multi-UAV path planning based on IB-ABC with restricted planned arrival sequence. Robotica 2023, 41, 1244–1257. [Google Scholar] [CrossRef]
- Han, Z.; Chen, M.; Zhu, H.; Wu, Q. Ground threat prediction-based path planning of unmanned autonomous helicopter using hybrid enhanced artificial bee colony algorithm. Def. Technol. 2023. [Google Scholar] [CrossRef]
- Saeed, R.A.; Omri, M.; Abdel-Khalek, S.; Ali, E.S.; Alotaibi, M.F. Optimal path planning for drones based on swarm intelligence algorithm. Neural Comput. Appl. 2022, 34, 10133–10155. [Google Scholar] [CrossRef]
- Shen, L.; Hou, Y.; Yang, Q.; Lv, M.; Dong, J.-X.; Yang, Z.; Li, D. Synergistic path planning for ship-deployed multiple UAVs to monitor vessel pollution in ports. Transp. Res. Transp. Environ. 2022, 110, 103415. [Google Scholar] [CrossRef]
- Li, B.; Gong, L.-G.; Yang, W.-L. An improved artificial bee colony algorithm based on balance-evolution strategy for unmanned combat aerial vehicle path planning. Sci. World J. 2014, 2014, 232704. [Google Scholar] [CrossRef]
- Li, G.; Niu, P.; Xiao, X. Development and investigation of efficient artificial bee colony algorithm for numerical function optimization. Appl. Soft Comput. 2012, 12, 320–332. [Google Scholar] [CrossRef]
- Lu, C.; Lv, Y.; Su, Y.; Liu, L. UAV Swarm Collaborative Path Planning Based on RB-ABC. In Proceedings of the 2022 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, China, 4–6 November 2022; IEEE: Toulouse, France, 2022; pp. 627–632. [Google Scholar]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Peng, H.; Deng, C.; Wu, Z. Best neighbor-guided artificial bee colony algorithm for continuous optimization problems. Soft Comput. 2019, 23, 8723–8740. [Google Scholar] [CrossRef]
- Guo, P.; Cheng, W.; Liang, J. Global artificial bee colony search algorithm for numerical function optimization. In Proceedings of the 2011 Seventh International Conference on Natural Computation, Shanghai, China, 26–28 July 2011; IEEE: Toulouse, France, 2011; pp. 1280–1283. [Google Scholar]
- Xiang, W.-L.; Meng, X.-L.; Li, Y.-Z.; He, R.-C.; An, M.-Q. An improved artificial bee colony algorithm based on the gravity model. Inf. Sci. 2018, 429, 49–71. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, Q.; Yang, Z.; Yu, X.; Jia, B. A novel artificial bee colony algorithm for structural damage detection. Adv. Civ. Eng. 2020, 2020, 3743089. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M. Opposition-based differential evolution. IEEE Trans. Evol. Comput. 2008, 12, 64–79. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, Z.; Deng, C.; Peng, H. Enhancing artificial bee colony algorithm with generalized opposition-based learning. Int. J. Comput. Sci. Math. 2015, 6, 297–309. [Google Scholar] [CrossRef]
- Han, Y.; Zhou, S.; Xia, P.; Zhao, Q. Research on fine 3D modeling technology of tall buildings based on UAV Photogrammetry. In Proceedings of the 2022 3rd International Conference on Geology, Mapping and Remote Sensing (ICGMRS), Zhoushan, China, 22–24 April 2022; IEEE: Toulouse, France, 2022; pp. 349–353. [Google Scholar]
- Marichal-Hernandez, J.G.; Nava, F.P.; Rosa, F.; Restrepo, R.; Rodriguez-Ramos, J.M. An Integrated System for Virtual Scene Rendering, Stereo Reconstruction and Accuracy Estimation. In Proceedings of the Geometric Modeling and Imaging—New Trends (GMAI’06), London, UK, 5–7 July 2006; IEEE: Toulouse, France, 2006; pp. 121–126. [Google Scholar]
- Hwang, J.-T.; Weng, J.-S.; Tsai, Y.-T. 3D modeling and accuracy assessment-a case study of photosynth. In Proceedings of the 2012 20th International Conference on Geoinformatics, Hong Kong, China, 15–17 June 2012; IEEE: Toulouse, France, 2012; pp. 1–6. [Google Scholar]
- Krichen, M.; Adoni, W.Y.H.; Mihoub, A.; Alzahrani, M.Y.; Nahhal, T. Security challenges for drone communications: Possible threats, attacks and countermeasures. In Proceedings of the 2022 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; IEEE: Toulouse, France, 2022; pp. 184–189. [Google Scholar]
- Ko, Y.; Kim, J.; Duguma, D.G.; Astillo, P.V.; You, I.; Pau, G. Drone secure communication protocol for future sensitive applications in military zone. Sensors 2021, 21, 2057. [Google Scholar] [CrossRef] [PubMed]




| Population Size | Algorithm | Mean | Std | Time (s) |
|---|---|---|---|---|
| 10 | EA | 3.6854 | 0.1352 | 56.17 |
| ACO | 1.9787 | 0.0368 | 53.18 | |
| ABC | 1.5870 | 0.0358 | 51.33 | |
| ABC1 | 1.3406 | 0.0271 | 53.01 | |
| ABC2 | 1.2696 | 0.0289 | 48.62 | |
| OABC | 1.2313 | 0.0154 | 46.98 | |
| 20 | EA | 3.425 | 0.1277 | 87.59 |
| ACO | 1.8390 | 0.0423 | 71.63 | |
| ABC | 1.4135 | 0.0312 | 73.88 | |
| ABC1 | 1.3048 | 0.0229 | 73.94 | |
| ABC2 | 1.2501 | 0.0247 | 79.16 | |
| OABC | 1.2309 | 0.0124 | 66.51 | |
| 30 | EA | 3.1183 | 0.1049 | 123.88 |
| ACO | 1.7581 | 0.0364 | 121.68 | |
| ABC | 1.3537 | 0.0291 | 127.80 | |
| ABC1 | 1.2425 | 0.0119 | 126.36 | |
| ABC2 | 1.2310 | 0.0202 | 124.97 | |
| OABC | 1.2309 | 0.0103 | 104.32 | |
| 50 | EA | 2.8609 | 0.1124 | 348.98 |
| ACO | 1.6872 | 0.0387 | 215.08 | |
| ABC | 1.3431 | 0.0272 | 226.95 | |
| ABC1 | 1.2356 | 0.0119 | 209.64 | |
| ABC2 | 1.2309 | 0.0182 | 199.02 | |
| OABC | 1.2310 | 0.0112 | 175.94 | |
| 100 | EA | 2.5439 | 0.0847 | 580.61 |
| ACO | 1.4598 | 0.0301 | 422.50 | |
| ABC | 1.2315 | 0.0243 | 450.13 | |
| ABC1 | 1.2310 | 0.0089 | 426.98 | |
| ABC2 | 1.2309 | 0.0104 | 412.52 | |
| OABC | 1.2308 | 0.0092 | 384.39 |
| Population Size | Algorithm | Mean | Std | Time (s) |
|---|---|---|---|---|
| 10 | EA | 2.1192 | 0.1488 | 59.64 |
| ACO | 0.9463 | 0.0618 | 53.49 | |
| ABC | 0.7732 | 0.0472 | 52.97 | |
| ABC1 | 0.7763 | 0.0366 | 49.32 | |
| ABC2 | 0.6289 | 0.0291 | 47.40 | |
| OABC | 0.6051 | 0.0209 | 47.96 | |
| 20 | EA | 1.8970 | 0.1358 | 89.84 |
| ACO | 0.9234 | 0.0589 | 81.06 | |
| ABC | 0.7156 | 0.0433 | 82.58 | |
| ABC1 | 0.6949 | 0.0315 | 77.20 | |
| ABC2 | 0.6593 | 0.0256 | 75.98 | |
| OABC | 0.6050 | 0.0182 | 73.44 | |
| 30 | EA | 1.2312 | 0.1586 | 178.48 |
| ACO | 0.8865 | 0.0378 | 137.29 | |
| ABC | 0.6954 | 0.0395 | 142.65 | |
| ABC1 | 0.6617 | 0.0292 | 126.89 | |
| ABC2 | 0.6201 | 0.0226 | 102.76 | |
| OABC | 0.6049 | 0.0136 | 102.88 | |
| 50 | EA | 0.9873 | 0.0973 | 354.36 |
| ACO | 0.7839 | 0.0423 | 229.10 | |
| ABC | 0.6723 | 0.0250 | 262.16 | |
| ABC1 | 0.6130 | 0.0217 | 218.22 | |
| ABC2 | 0.6050 | 0.0127 | 194.61 | |
| OABC | 0.6049 | 0.0129 | 173.20 | |
| 100 | EA | 0.9857 | 0.0925 | 572.65 |
| ACO | 0.6982 | 0.0247 | 461.60 | |
| ABC | 0.6154 | 0.0187 | 484.73 | |
| ABC1 | 0.6050 | 0.0151 | 462.53 | |
| ABC2 | 0.6049 | 0.0130 | 377.52 | |
| OABC | 0.6048 | 0.0127 | 343.85 |
| Surface 1 | Surface 2 | Surface 3 | Surface 4 | |
|---|---|---|---|---|
| OABC |  |  |  |  |
| ABC |  |  |  |  |
| ABC1 |  |  |  |  |
| ABC2 |  |  |  |  |
| Five-directional flight |  |  |  |  |
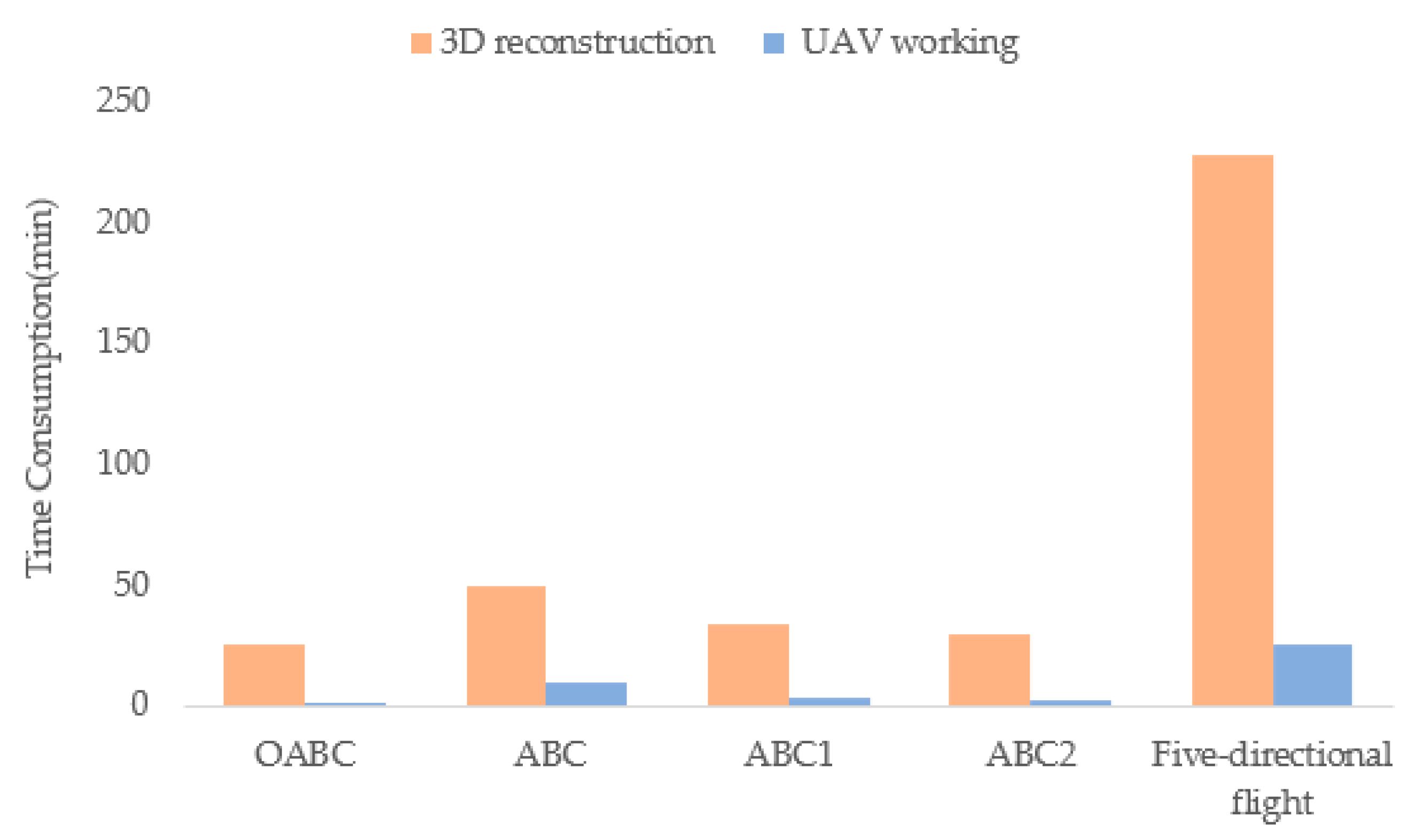
| Number of Images | Time Consumption of UAV Working | Time Consumption of 3D Reconstruction | |
|---|---|---|---|
| OABC | 25 | 2 min 10 s | 25 min 46 s |
| ABC | 52 | 10 min 13 s | 50 min 20 s |
| ABC1 | 30 | 3 min 21 s | 34 min 02 s |
| ABC2 | 28 | 2 min 43 s | 30 min 27 s |
| Five-Directional Flight | 89 | 25 min 46 s | 3 h 48 min |
| 3D Models | X-Direction RMSE | Y-Direction RMSE | Planar RMSE | Height RMSE |
|---|---|---|---|---|
| From OABC | 0.0515 | 0.0898 | 0.1036 | 0.1470 |
| From ABC | 0.0683 | 0.1023 | 0.1230 | 0.1522 |
| From ABC1 | 0.0576 | 0.0917 | 0.1083 | 0.1497 |
| From ABC2 | 0.0618 | 0.0984 | 0.1162 | 0.1633 |
| From Five-Directional Flight | 0.0521 | 0.0835 | 0.0984 | 0.1395 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Liang, Y.; Meng, X. A UAV Path Planning Method for Building Surface Information Acquisition Utilizing Opposition-Based Learning Artificial Bee Colony Algorithm. Remote Sens. 2023, 15, 4312. https://doi.org/10.3390/rs15174312
Chen H, Liang Y, Meng X. A UAV Path Planning Method for Building Surface Information Acquisition Utilizing Opposition-Based Learning Artificial Bee Colony Algorithm. Remote Sensing. 2023; 15(17):4312. https://doi.org/10.3390/rs15174312
Chicago/Turabian StyleChen, Hao, Yuheng Liang, and Xing Meng. 2023. "A UAV Path Planning Method for Building Surface Information Acquisition Utilizing Opposition-Based Learning Artificial Bee Colony Algorithm" Remote Sensing 15, no. 17: 4312. https://doi.org/10.3390/rs15174312
APA StyleChen, H., Liang, Y., & Meng, X. (2023). A UAV Path Planning Method for Building Surface Information Acquisition Utilizing Opposition-Based Learning Artificial Bee Colony Algorithm. Remote Sensing, 15(17), 4312. https://doi.org/10.3390/rs15174312





