Dynamic Order Picking Method for Multi-UAV System in Intelligent Warehouse
Abstract
1. Introduction
- The proposed method uses dynamic allocation based on interventionist order picking, and uses an efficient order picking method compared to previous logistics algorithms to achieve a smaller completion time. Through this, the warehouse operation’s performance is improved.
- The proposed HC strategy uses similarity information between orders allocated to the UAV and has a smaller average travel distance than previous algorithms. Through this, it contributes to increasing the operating time of each UAV compared to the charging time of the UAV.
- By applying the k-opt-based DTSP solving algorithm to the logistics environment, the proposed method can quickly calculate the task sequence for the order. Through this, the sequence is changed in real time even when the order is frequently changed in the picking list of the UAV, and the optimal path is guaranteed.
2. Related Works
2.1. Dynamic Order Picking
2.2. Method of Dynamic Order Picking
2.2.1. Dynamic Order Batching
2.2.2. Dynamic Pick Lists
2.3. Interventionist Order Picking Strategy
- 1.
- Interventionist—accept all (IAA): This method waits in the warehouse’s depot until new order arrives. If N orders arrive, they are assigned to a picker to start picking. The picker in operation is assigned a new order until the capacity conditions allow. This method increases the processing time of orders that were already on the pick list. Therefore, both the task completion time and the travel distance increase.
- 2.
- Interventionist—order completion time (IOCT): This method, like the IAA, waits in the warehouse’s depot until new order arrives. If N orders arrive, they are assigned to a picker to start picking. It is a method that adds a new order if the capacity condition is satisfied and the completion time increased by additional orders does not exceed a certain threshold. In this method, in order to obtain the completion time, it is necessary to find the optimal travel path in advance, and this computational cost increases the computation of the algorithm.
- 3.
- Interventionist—re-batching (IRB): This method also waits for N orders. When a new order comes in, a new batch is created with either (1) orders that have been assigned to the picker but have not been picked yet or (2) orders that have not been assigned yet. Although it is possible in various ways, it requires a lot of computation time even for a single picker.
2.4. DTSP
2.5. Multi-UAV Task Allocation
3. Problem Definition
- i: Index of an item
- P: Number of items present in the logistics warehouse
- : Location of item i
- k: Index of orders
- : An index set of items belonging to the kth order
- : Number of initial customer orders
- : Total orders, last customer orders
- : The number of items that the kth order has
- S: Maximum number of items a customer’s order can have
- : Order growth rate
- : Number of orders arriving per cycle
- : Number of depots
- : Minimum number of orders for order batch creation
- : The number of UAVs
- u: The index of a UAV
- : Current location of UAV u
- : The speed of the UAV
- : Load capacity of orders currently held by the UAV
- : Maximum order load on the UAV
- : Current picking list of UAV u
- : List of items that have not yet passed through within the current pickup list of UAV u
- 1.
- Each item is independent of other items and orders.
- 2.
- The speed of the UAV is constant.
- 3.
- The UAV has the ability to pick each item by itself.
- 4.
- The aisle is wide enough to prevent collisions between UAVs.
- 5.
- UAVs are equally assigned to each depot.
- 6.
- Each UAV starts from the depot, picks up the item on the picking list, and then moves to the starting depot.
- 7.
- It is assumed that the picking time of the UAV is constant. Therefore, no matter which algorithm is applied, the entire pickup time is the same, so the pickup time is ignored in the entire execution time of the algorithm.
- 8.
- UAVs are assigned orders and order sequences from the WMS. Each UAV calculates an optimal path along this sequence and then autonomously flies between shelves.
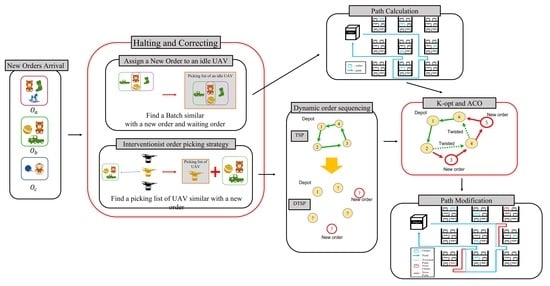
4. Proposed Method
4.1. Multi-UAV Task Allocation and Sequencing Strategy for Dynamic Order Picking
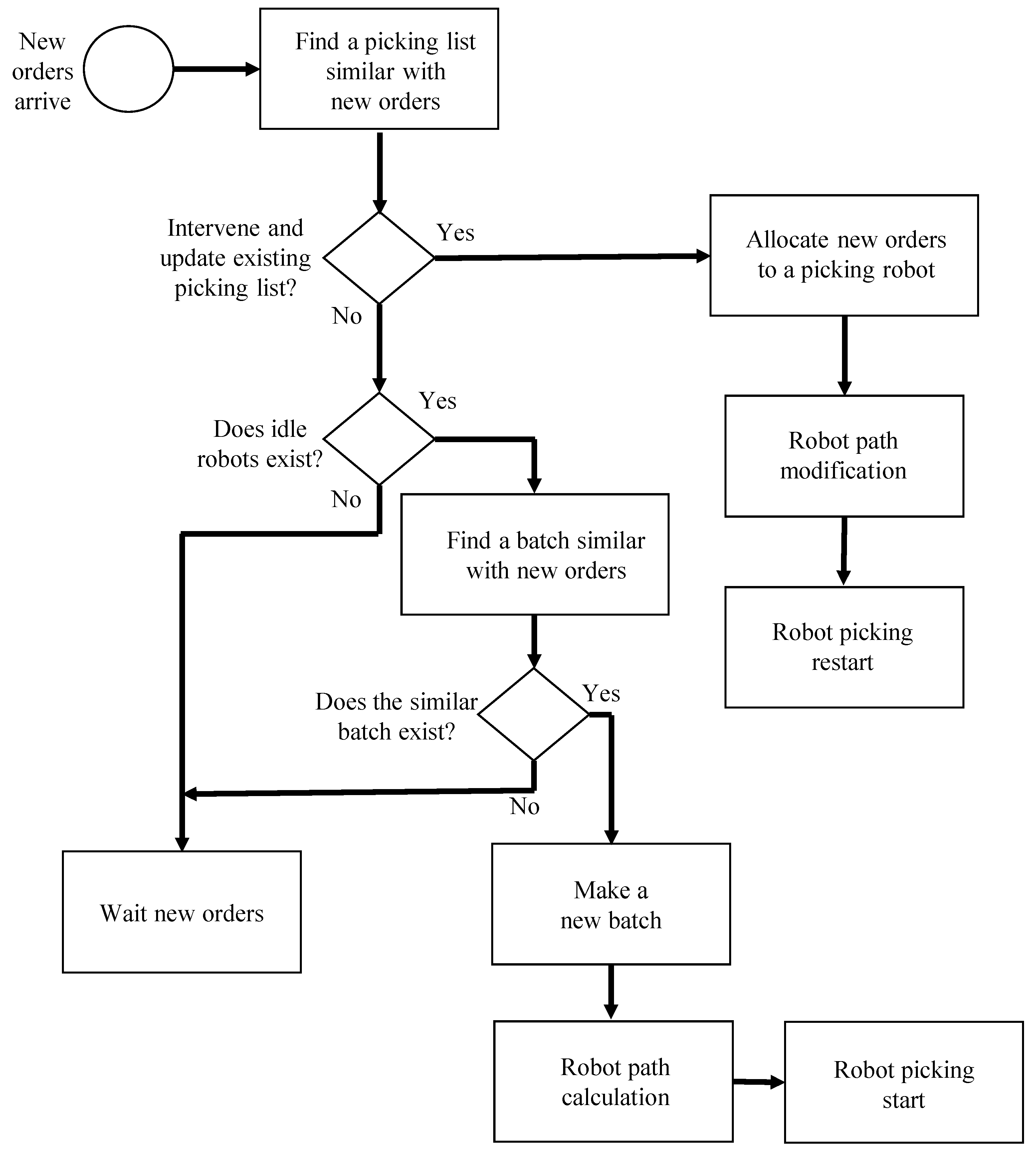
4.2. Halting and Correcting Strategy
4.2.1. Finding a Picking List Similar with New Orders
4.2.2. Constructing the Batch Similar to New Orders
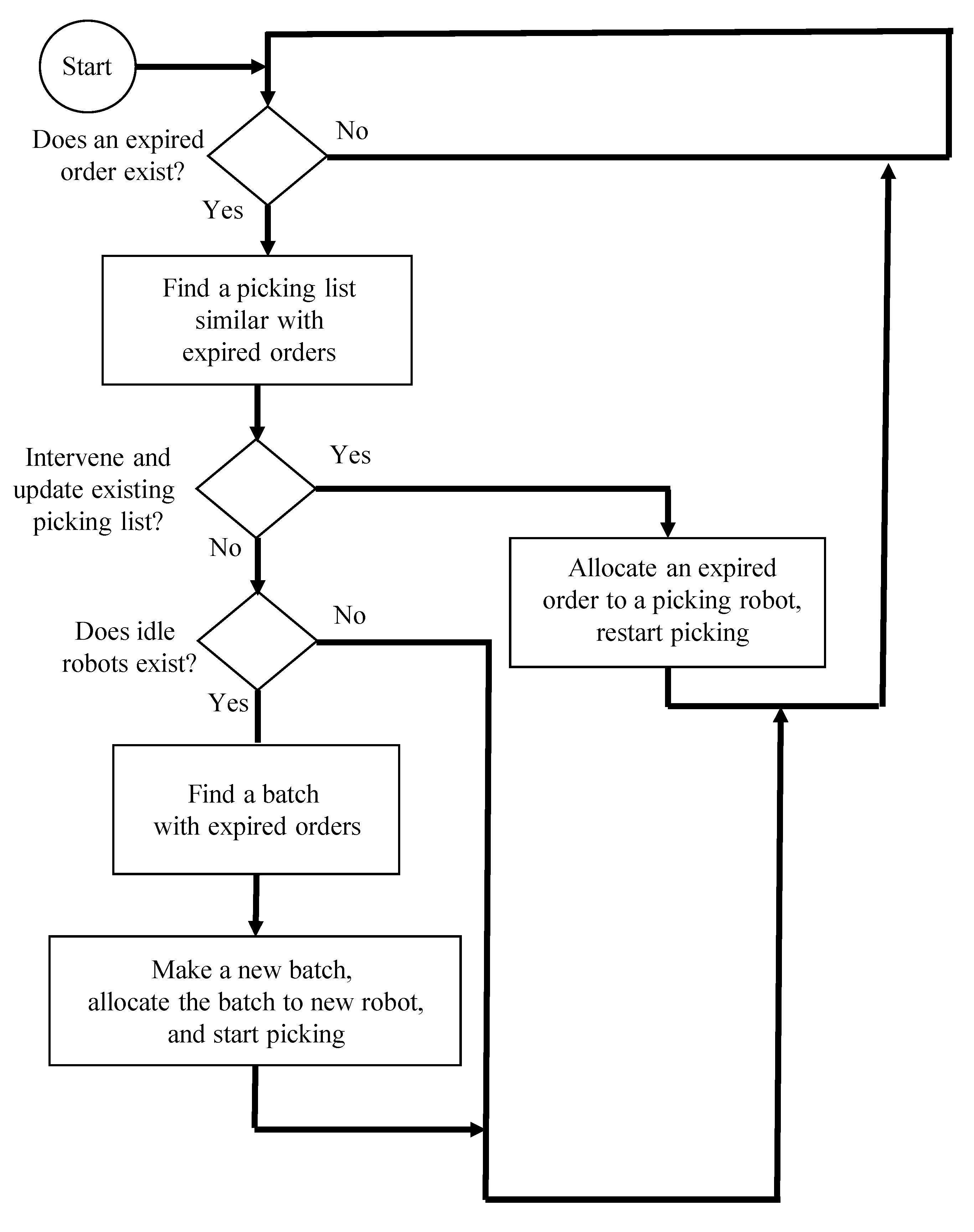
4.2.3. Processing Waiting Orders with Expired Time
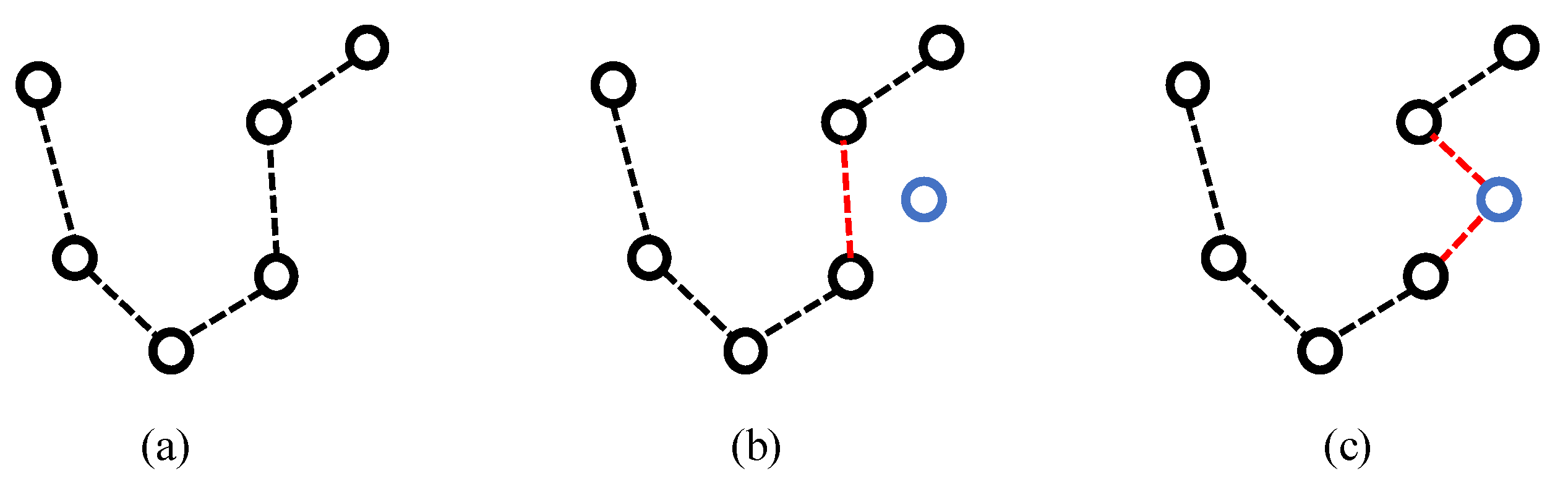
4.3. Order Sequencing
4.3.1. Normal Order Sequencing
4.3.2. Dynamic Order Sequencing
| Algorithm 1 Proposed method. |
Input: path R, allocated tasks V Output: Best path
|
5. Experiment
5.1. Experiment Design
5.2. Experiment Result
5.2.1. The Performance of Algorithms for Order Arrival Rates and Expired Time in Simulation
- 1.
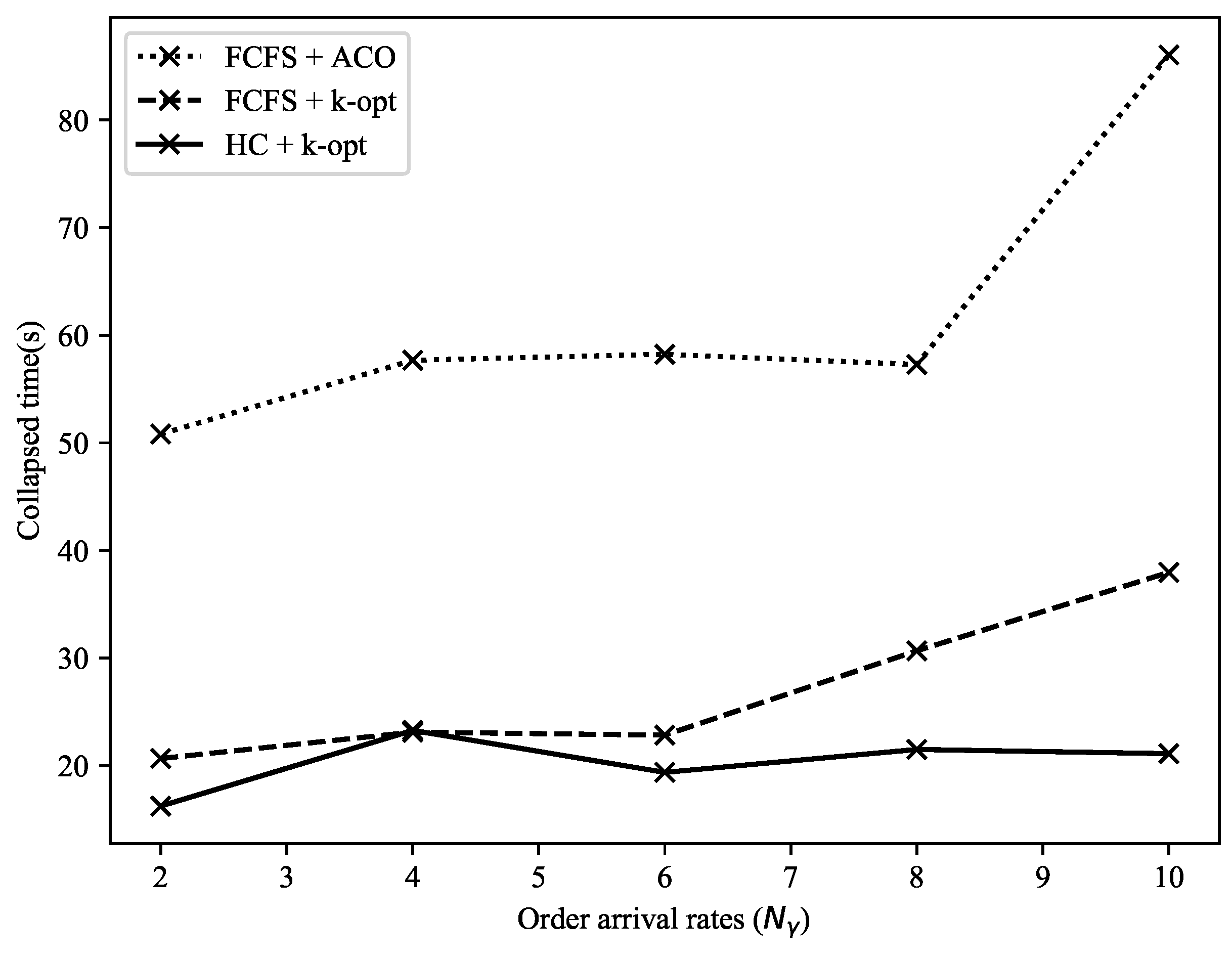
- Because the HC strategy creates a new batch through waiting rather than frequently applying k-opt every time a new order arrives, the convergence time and the number of executions for the algorithm to find the optimal solution are reduced.
- 2.
- Orders added to the picking list in the HC strategy are likely to have the same item composition as the existing picking list. Since this means a decrease in the number of nodes added in the TSP algorithm, the number of algorithm executions will be reduced.
5.2.2. The Performance of Algorithms for Number of UAVs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Almalki, F.A.; Albraikan, A.A.; Soufiene, B.O.; Ali, O. Utilizing artificial intelligence and lotus effect in an emerging intelligent drone for persevering solar panel efficiency. Wirel. Commun. Mob. Comput. 2022, 2022, 7741535. [Google Scholar] [CrossRef]
- Takechi, H.; Aragaki, S.; Irie, M. Differentiation of river sediments fractions in UAV aerial images by convolution neural network. Remote Sens. 2021, 13, 3188. [Google Scholar] [CrossRef]
- Padmanabhan, M.; Suresh, G.R. Coalition formation and task allocation of multiple autonomous robots. In Proceedings of the International Conference on Signal Processing, Communication and Networking (ICSCN), Chennai, India, 26–28 March 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Lee, B. Blockchain-Empowered multi-robot collaboration to fight COVID-19 and future pandemics. IEEE Access 2021, 9, 44173–44197. [Google Scholar] [CrossRef] [PubMed]
- Wurman, P.R.; D’Andrea, R.; Mountz, M. Coordinating hundreds of cooperative, autonomous vehicles in warehouses. AI Mag. 2008, 29, 9. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Ma, O.; Ansari, M.S.; Almalki, F.A. Survey on collaborative smart drones and internet of things for improving smartness of smart cities. IEEE Access 2019, 7, 128125–128152. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multiple UAV systems: A survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar] [CrossRef]
- Shakeri, R.; Al-Garadi, M.A.; Badawy, A.; Mohamed, A.; Khattab, T.; Al-Ali, A.K.; Harras, K.A.; Guizani, M. Design challenges of multi-UAV systems in cyber-physical applications: A comprehensive survey and future directions. IEEE Commun. Surv. Tutor. 2019, 21, 3340–3385. [Google Scholar] [CrossRef]
- Malmborg, C.J.; Al-Tassan, K. An integrated performance model for orderpicking systems with randomized storage. Appl. Math. Model. 2000, 24, 95–111. [Google Scholar] [CrossRef]
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Tang, L.C.; Chew, E.P. Order picking systems: Batching and storage assignment strategies. Comput. Ind. Eng. 1997, 33, 817–820. [Google Scholar] [CrossRef]
- Tompkins, J.A.; White, J.A.; Bozer, Y.A.; Tanchoco, J.M.A. Facilities Planning; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- ElGibreen, H.; Youcef-Toumi, K. Dynamic task allocation in an uncertain environment with heterogeneous multi-agents. Auton. Robot. 2019, 43, 1639–1664. [Google Scholar] [CrossRef]
- Gong, Y.; De Koster, R. A polling-based dynamic order picking system for online retailers. IIE Trans. 2008, 40, 1070–1082. [Google Scholar] [CrossRef]
- Rubrico, J.I.; Higashi, T.; Tamura, H.; Ota, J. Online rescheduling of multiple picking agents for warehouse management. Robot. Comput.-Integr. Manuf. 2011, 27, 62–71. [Google Scholar] [CrossRef]
- Giannikas, V.; Lu, W.; Robertson, B.; McFarlane, D. An interventionist strategy for warehouse order picking: Evidence from two case studies. Int. J. Prod. Econ. 2017, 189, 63–76. [Google Scholar] [CrossRef]
- Ran, W.; Liu, S.; Zhang, Z. A polling-based dynamic order-picking system considering priority orders. Complexity 2020, 2020, 4595316. [Google Scholar] [CrossRef]
- Ramanathan, R.; George, J.; Ramanathan, U. The role of logistics in e-commerce transactions: An exploratory study of customer feedback and risk. In Supply Chain Strategies, Issues and Models; Springer: Berlin/Heidelberg, Germany, 2014; pp. 221–233. [Google Scholar] [CrossRef]
- Le-Duc, T.; De Koster, R.M. Travel time estimation and order batching in a 2-block warehouse. Eur. J. Oper. Res. 2007, 176, 374–388. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Chan, F.T.; Ruan, J. On-line order batching and sequencing problem with multiple pickers: A hybrid rule-based algorithm. Appl. Math. Model. 2017, 45, 271–284. [Google Scholar] [CrossRef]
- Van Nieuwenhuyse, I.; de Koster, R.B. Evaluating order throughput time in 2-block warehouses with time window batching. Int. J. Prod. Econ. 2009, 121, 654–664. [Google Scholar] [CrossRef]
- Henn, S. Algorithms for on-line order batching in an order picking warehouse. Comput. Oper. Res. 2012, 39, 2549–2563. [Google Scholar] [CrossRef]
- Stodola, P.; Michenka, K.; Nohel, J.; Rybanskỳ, M. Hybrid algorithm based on ant colony optimization and simulated annealing applied to the dynamic traveling salesman problem. Entropy 2020, 22, 884. [Google Scholar] [CrossRef]
- Strąk, Ł.; Skinderowicz, R.; Boryczka, U.; Nowakowski, A. A self-adaptive discrete PSO algorithm with heterogeneous parameter values for dynamic TSP. Entropy 2019, 21, 738. [Google Scholar] [CrossRef] [PubMed]
- Simões, A.; Costa, E. Extended virtual loser genetic algorithm for the dynamic traveling salesman problem. In Proceedings of the Annual Conference on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 869–876. [Google Scholar]
- Guntsch, M.; Middendorf, M. Pheromone modification strategies for ant algorithms applied to dynamic TSP. In Proceedings of the Workshops on Applications of Evolutionary Computation, Como, Italy, 18–20 April 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–222. [Google Scholar]
- Mavrovouniotis, M.; Yang, S. Ant colony optimization with immigrants schemes for the dynamic travelling salesman problem with traffic factors. Appl. Soft Comput. 2013, 13, 4023–4037. [Google Scholar] [CrossRef]
- Melo, L.; Pereira, F.; Costa, E. Multi-caste ant colony algorithm for the dynamic traveling salesperson problem. In Proceedings of the International Conference on Adaptive and Natural Computing Algorithms, Lausanne, Switzerland, 4–6 April 2013; pp. 179–188. [Google Scholar] [CrossRef]
- Boryczka, U.; Strąk, Ł. A hybrid discrete particle swarm optimization with pheromone for dynamic traveling salesman problem. In Proceedings of the International Conference on Computational Collective Intelligence, Ho Chi Minh City, Vietnam, 28–30 November 2012; pp. 503–512. [Google Scholar] [CrossRef]
- Saravanan, S.; Ramanathan, K.C.; Ramya, M.M.; Janardhanan, M.N. Review on state-of-the-art dynamic task allocation strategies for multiple-robot systems. Ind. Robot 2020, 47, 929–942. [Google Scholar] [CrossRef]
- Sariel-Talay, S.; Balch, T.R.; Erdogan, N. Multiple traveling robot problem: A solution based on dynamic task selection and robust execution. IEEE/ASME Trans. Mechatron. 2009, 14, 198–206. [Google Scholar] [CrossRef]
- Nunes, E.; Manner, M.; Mitiche, H.; Gini, M. A taxonomy for task allocation problems with temporal and ordering constraints. Robot. Auton. Syst. 2017, 90, 55–70. [Google Scholar] [CrossRef]
- Setter, T.; Egerstedt, M. Energy-Constrained Coordination of Multi-Robot Teams. IEEE Trans. Control Syst. Technol. 2017, 25, 1257–1263. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, Y.; Che, L.; Zhou, M. Moving-Distance-Minimized PSO for Mobile Robot Swarm. IEEE Trans. Cybern. 2022, 52, 9871–9881. [Google Scholar] [CrossRef]
- Chen, F.; Wang, H.; Xie, Y.; Qi, C. An ACO-Based online routing method for multiple order pickers with congestion consideration in warehouse. J. Intell. Manuf. 2016, 27, 389–408. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Choe, K. Aisle-Based order pick systems with batching, zoning, and sorting. In School of Industrial and Systems Engineering; Georgia Institute of Technology: Atlanta, GA, USA, 1990. [Google Scholar]
- Sttzle, T. MAX-MIN ant system. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Aboelfotoh, A.; Singh, M.; Suer, G. Order Batching Optimization for Warehouses with Cluster-Picking. Procedia Manuf. 2019, 39, 1464–1473. [Google Scholar] [CrossRef]
- Fibrianto, H.Y.; Hong, S. Dynamic order batching in bucket brigade order picking systems with consecutive batch windows and non-identical pickers. Int. J. Prod. Res. 2019, 57, 6552–6568. [Google Scholar] [CrossRef]

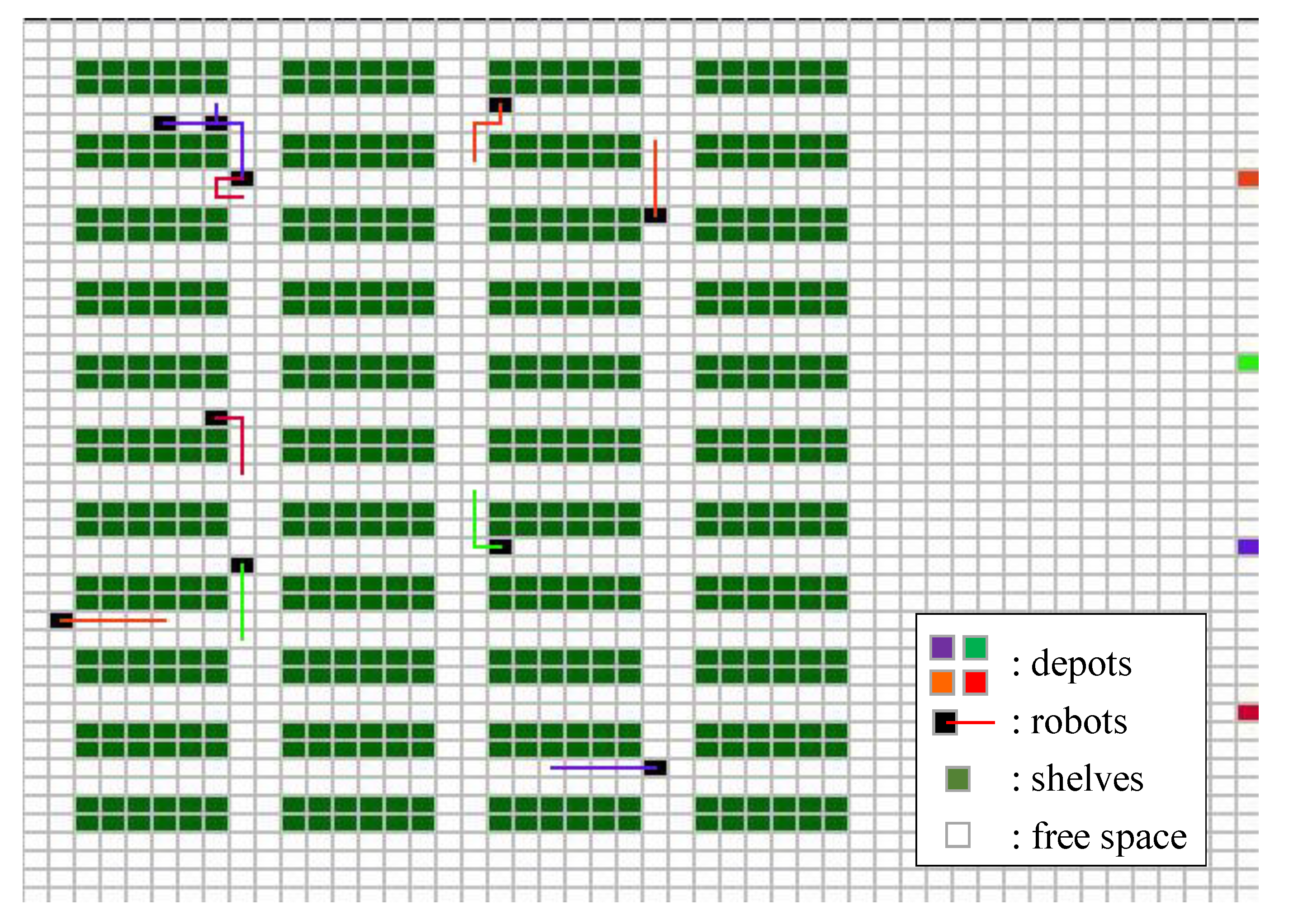



| Nieuwenhuyse et al. (2009) [21] | Henn et al. (2012) [22] | Rubrico et al. (2011) [15] | Gong et al. (2008) [14] | Giannikas et al. (2017) [16] | Proposed | |
|---|---|---|---|---|---|---|
| Method type | Dynamic order batch | Dynamic order batch | Dynamic pick lists | Dynamic pick lists | Dynamic pick lists | Dynamic pick lists |
| Picker type | Multiple | Single | Multiple | Multiple | Single | Multiple |
| Item size of order | Variable | Variable | One | Variable | Variable | Variable |
| Allow to change picking list | No | No | Yes | Yes | Yes | Yes |
| Allow to change picker’s route | No | No | Yes | No | Yes | Yes |
| 2 | 4 | 6 | 8 | 10 | ||
|---|---|---|---|---|---|---|
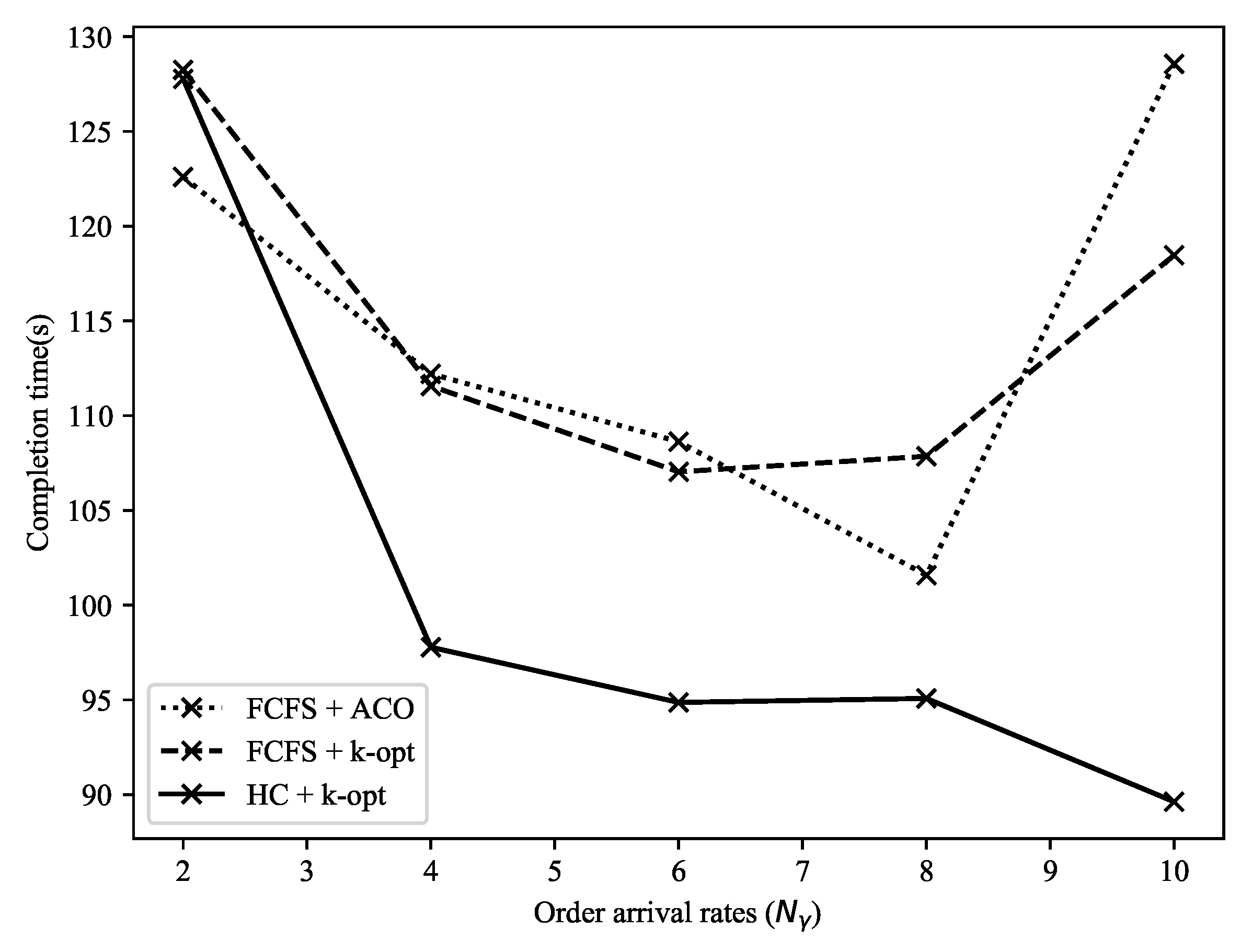
| Completion Time [s] | FCFS + ACO | 122.60 | 112.21 | 108.63 | 101.58 | 128.57 |
| FCFS + k-opt | 128.25 | 111.57 | 107.04 | 107.86 | 118.47 | |
| HC + k-opt | 127.78 | 97.78 | 94.87 | 95.08 | 89.63 | |
| Dif. | 4.23% | % | % | % | % | |
| Median of Travel Distance ( = 10) [m] | FCFS + ACO | 892.50 | 868.50 | 759.00 | 765.00 | 874.50 |
| FCFS + k-opt | 937.00 | 830.00 | 834.00 | 814.00 | 824.00 | |
| HC + k-opt | 666.00 | 705.50 | 644.00 | 667.50 | 579.50 | |
| Dif. | % | % | % | % | % | |
| Collapsed Time [s] | FCFS + ACO | 50.81 | 57.67 | 58.23 | 57.28 | 86.04 |
| FCFS + k-opt | 20.66 | 23.11 | 22.83 | 30.67 | 37.96 | |
| HC + k-opt | 16.24 | 23.27 | 19.37 | 21.50 | 21.11 | |
| Dif. | % | % | % | % | % |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Completion Time [s] | ACO | 1.60 | 1.57 | 1.50 | 1.46 | 1.57 | 1.28 | 1.40 | 1.22 | 1.27 | 1.10 |
| Proposed | 0.30 | 0.31 | 0.32 | 0.32 | 0.35 | 0.38 | 0.28 | 0.36 | 0.38 | 0.40 | |
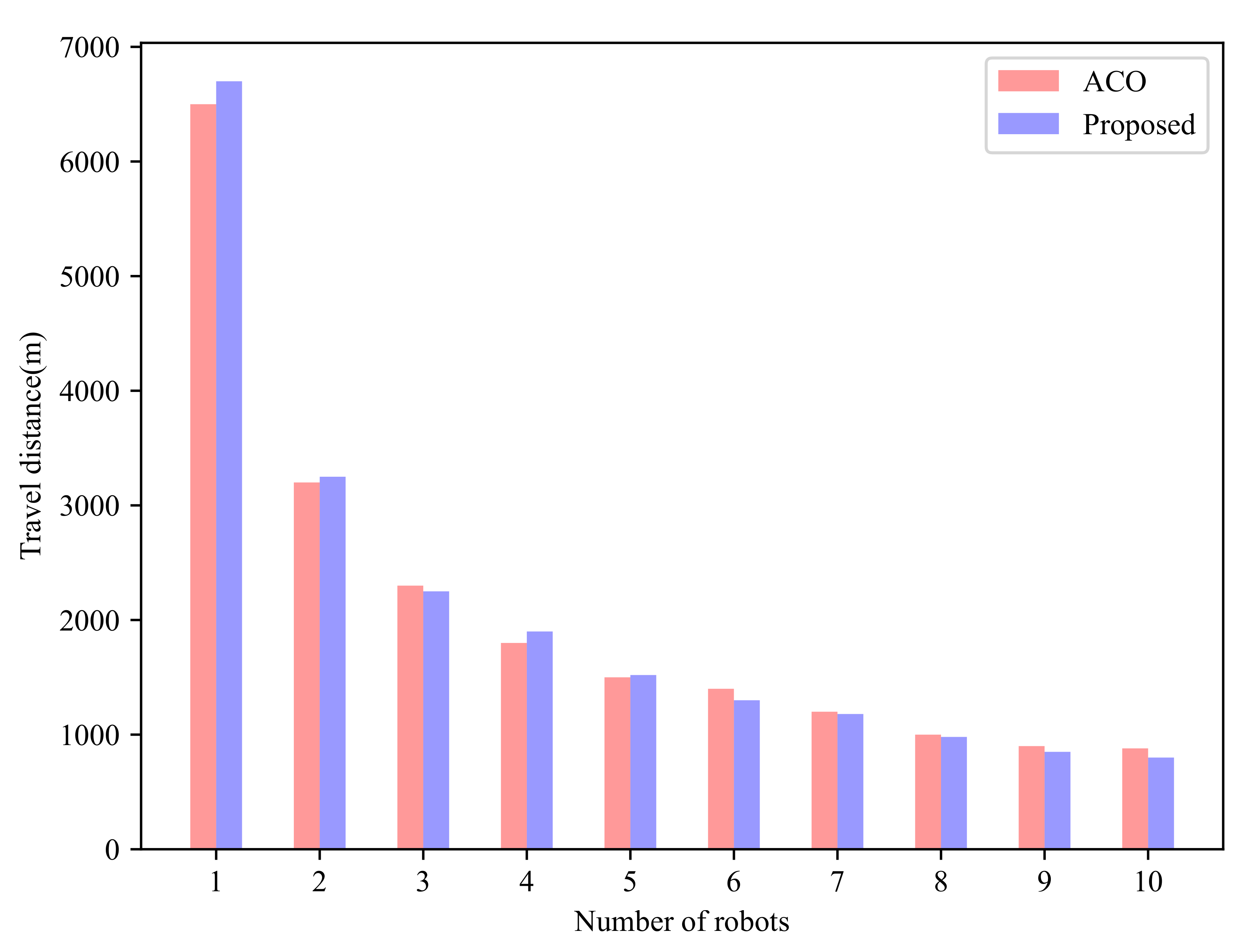
| Travel Distance [m] | ACO | 6512 | 3205 | 2298 | 1811 | 1480 | 1402 | 1222 | 998 | 887 | 868 |
| Proposed | 6712 | 3254 | 2256 | 1905 | 1528 | 1311 | 1187 | 982 | 852 | 807 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Jeon, H.; Oh, J.; Lee, H. Dynamic Order Picking Method for Multi-UAV System in Intelligent Warehouse. Remote Sens. 2022, 14, 6106. https://doi.org/10.3390/rs14236106
Han C, Jeon H, Oh J, Lee H. Dynamic Order Picking Method for Multi-UAV System in Intelligent Warehouse. Remote Sensing. 2022; 14(23):6106. https://doi.org/10.3390/rs14236106
Chicago/Turabian StyleHan, Changwan, Hyeongjun Jeon, Junghyun Oh, and Heungjae Lee. 2022. "Dynamic Order Picking Method for Multi-UAV System in Intelligent Warehouse" Remote Sensing 14, no. 23: 6106. https://doi.org/10.3390/rs14236106
APA StyleHan, C., Jeon, H., Oh, J., & Lee, H. (2022). Dynamic Order Picking Method for Multi-UAV System in Intelligent Warehouse. Remote Sensing, 14(23), 6106. https://doi.org/10.3390/rs14236106