Abstract
As more than 75% of the global population is expected to live in urban areas by 2050, there is an urgent need to assess the risk of natural hazards through a future-focused lens so that adequately informed spatial planning decisions can be made to define preventive risk policies in the upcoming decades. The authors propose an innovative methodology to assess the future multi-hazard exposure of urban areas based on remote sensing technologies and statistical and spatial analysis. The authors, specifically, applied remote sensing technologies combined with artificial intelligence to map the built-up area automatically. They assessed and calibrated a transferable Binary Logistic Regression Model (BLRM) to model and predict future urban growth dynamics under different scenarios, such as the business as usual, the slow growth, and the fast growth scenarios. Finally, considering specific socioeconomic exposure indicators, the authors assessed each scenario’s future multi-hazard exposure in urban areas. The proposed methodology is applied to the Municipality of Rende. The results revealed that the multi-hazard exposure significantly changed across the analyzed scenarios and that urban socioeconomic growth is the main driver of risk in urban environments.
Keywords:
exposure; risk; urban growth; prediction; logistic regression; remote sensing; geospatial analysis 1. Introduction
As more than 75% of the global population is expected to live in urban areas by 2050 [1], there is an urgent need to assess the risk of natural hazards through a future-focused lens so that adequately informed spatial planning decisions can be made to define preventive risk policies in the upcoming decades.
Disaster risk [2] is defined as the combination of three determinants, such as hazard, exposure, and vulnerability [3,4,5,6]. These three components change over time due to natural and human influences impacting future risk levels. Among them, exposure is the most important because it represents the elements that can be affected by a particular hazard in a specific area.
Exposure is defined as “the people, property, systems, or other elements present in hazard zones subject to potential losses” [7]. Exposure analysis is fundamental (i) to organize emergency response and relief to people affected or potentially affected; (ii) to provide information to decision-makers and the crisis management operators that manage resources and logistical infrastructure to support reconstruction and rehabilitation; and (iii) to reduce potential future hazard impact through disaster risk reduction strategies, by taking more risk-informed decisions.
Therefore, assessing exposure levels is a topic of great interest among scientists and researchers. Exposure to natural hazards has been evaluated using different methods and tools. Some authors used traditional technologies, while others applied new remote sensing technologies and techniques.
In the study developed by Duan et al. [8], aimed at assessing the waterlogging risk, the authors combined multi-criteria decision analysis and geographic information systems to determine, among other components, such as hazard, vulnerability, and emergency response and recovery capability, the exposure level to that risk. Boni et al. [9] developed a remote-sensing-based procedure to update the population exposed to natural hazards assessment quickly. A relationship between satellite nightlight intensity and urbanization density from globally available cartography is assessed and used to extrapolate urbanization data at different time steps, updating exposure each time. To test the reliability of the proposed methodology, the number of people exposed to riverine floods in Italy is assessed, deriving a probabilistic relationship between defense meteorological program nightlight intensity and urbanization density from the global urban footprint database for the year 2011. In another scientific work, Geiß et al. [10] combined a supervised remote sensing model, such as rotation forest, and open street map data for the automatic estimation of crucial exposure components, such as the number of buildings and population, with a high level of spatial detail referring to the tsunami hazard. Bhuyan et al. [11] applied a deep learning method, the ResUNet model, to detect the footprints of the buildings and used auxiliary open data to examine their exposure to floods in two areas in Kerala, India. Ehrlich et al. [12] combined the global built-up area and the global population density data with five global hazard maps to produce global layers of built-up area and population exposure to every single hazard for the epochs 1975, 1990, 2000, and 2015 to assess changes in exposure to each hazard over forty years. Freire et al. [13] evaluated and characterized the worldwide population distribution from 1975 to 2015 concerning the volcanism phenomenon using the population grids produced in the Global Human Settlement Layer project frame. Torres et al. [14] proposed a scalable and transferable procedure to assess urban exposure and vulnerability to seismic risk by integrating remote sensing technologies and machine learning techniques. Jitt-Aer et al. [15] applied a multi-stage spatial interpolation in the ArcGIS software to determine the population exposed to a tsunami impact in Patong (Phuket, Thailand).
All these existing studies on urban exposure to natural hazards rely on past or static observation. Therefore, they do not consider the evolutionary nature of risk, confirming what was stated by the authors of the reference [16]. Although the need to consider the long-term implications of natural hazards is widely recognized by organizations such as the United Nations, the European Union [17], and the World Bank [18], exposure applications focused on that issue are still rare. In the meantime, the emphasis of scientific works on disaster risk reduction is still on individual hazards. Even if it is clearly defined by the Sendai Framework 2015–2030 [19] that it is essential to promote comprehensive multi-risk analyses, only some studies consider combining more hazards.
Multi-risk methodology integrates multiple hazards and assesses their potential impacts on a specific area. It comprehensively explains the risks of specific land use and cover (LULC) patterns. LULC plays a crucial role in determining the vulnerability and exposure of an area to different hazards. Land use refers to the human activities and purposes for which land is employed (such as residential, commercial, industrial, agricultural, or recreational purposes); land cover refers to the physical and biological cover of the Earth’s surface, including forests, wetlands, urban areas, water bodies, and agricultural fields.
Land use choices are the main drivers of future exposure to natural hazards [20]. In disaster management planning, future exposure to natural risks is typically related to analyzing and predicting the effect of urban growth and LULC changes [21,22] regarding built-up area development and population growth. These analyses on land use changes are a valuable means to determine the impact of urbanization on disaster risk reduction policies.
Many methods to assess land use transformations have been developed recently, especially using remote sensing and geographic information systems (GIS) technologies. This analysis reached significant consideration in different fields, including defining rural and urban plans [23], identifying biodiversity hotspot landscapes [24], desertification dynamics, and the management planning process.
Future land cover transformations can be assessed by applying different LULC models. These are generally characterized by defined operational phases, such as data collection, calibration, simulation, validation, and prediction [25]. The data collection consists of deriving raw data about the historical LULC transformation and the driving factors data. LULC data can be retrieved from different sources, such as orthoimages, satellite imagery, and LULC change surveys, or can be obtained from the application of image classification techniques, both traditional and innovative. Driving factors data represent bio-physical, proximity, demographic, socio-economic, economic, and institutional factors, which can be defined as being responsible for the land cover changes over time. These data are available in public and administrative datasets. The calibration of the prediction model based on the LULC data and driving variable values at different time points is needed to parameterize the model. This latter is then applied to simulate future changes by generating the transition probability maps. The model validation phase estimates the model accuracy in predicting the LULC changes. This phase compares the LULC prediction with the LULC data available at a specific time. After checking the model prediction accuracy and validation, the last stage of LULC modeling consists of predicting future LULC.
According to the scientific literature, these LULC prediction models can accurately predict LULC changes for a short time, such as twenty or thirty years, because they depend on historical patterns. Different LULC prediction models have been developed in the scientific literature over time. Each model has specific characteristics.
The statistical models are the LULC prediction models based on a mathematical relationship between the LULC historical data and explanatory variables, defined as driving factors. These models generate transition probability maps, representing the suitability of specific areas to change. The most popular statical models are logistic regression [26], generalized additive models [27], and stochastic models, such as Markov chains [28,29,30]. These models are characterized by their easy implementation and generalization. However, they could perform better if stakeholder perception about land cover changes is considered.
The spatial dynamics of land cover change models, based on defined transition rules obtained considering neighborhood interaction effects or expert knowledge, are cellular automata (CA). These models simulate spatial analysis changes by generating suitability maps and are helpful for decision-making. Nevertheless, they lag in the temporal dynamic of change. Some examples of CA models employed to predict LULC changes are CLUES [31,32], CA [33,34], Slope, Land cover, Excluded region, Urban land cover, Transportation and Hillshade (SLEUTH) [35,36,37,38,39,40], and GEOMOD [41].
Another family of LULC simulation models is agent-based (ABMs). These models consent to simulate the LULC changes by considering the stakeholders’ considerations and elicitations as they are characterized by an environment through which decision-making entities can interact to define the relationship between them and their environment [42,43,44]. Due to this characteristic, the low generalizability of these models represents their main limitation.
All these models are often combined to strengthen the potentiality and overcome the limitations of each one. An example of an integrated model is CA-Markov [45,46,47]. These models generally well predict land cover changes but are challenging to implement and validate.
Land cover prediction modeling generates credible information about the LULC changes and provides valuable information about future urban development patterns. This is crucial for the sustainable urban planning of cities and disaster management planning in the uncertainty of tomorrow’s future. Therefore, the accurate geospatial modeling of urbanization to assess the multi-hazard exposure of urban areas is a fundamental prerequisite for enhancing urban resilience and disaster risk reduction.
Moving from this background, the authors provide a disaster management planning method to predict future land use changes and assess, through a census analysis, the future exposure of urban areas considering different hazards. To this end, after applying remote sensing technologies to map built-up areas, the authors predicted future urban growth dynamics, considering the main driving factors under different scenarios through a single averaged binary logistic regression model (BLRM). Based on the prediction results, the authors assessed the future multi-hazard exposure of urban areas by evaluating indicators related to the built-up area and socio-economic conditions. They applied the proposed methodology to the municipality of Rende (Calabria, Italy) to test and validate it.
The main objectives of this research are to (i) propose an innovative and transferable methodology that, using innovative methods and models connected to remote sensing and GIS techniques, could analyze the pattern of urban growth for a determined period and predict its trends by considering different driving factors; and to (ii) develop a decision support system able to predict the effects of territorial land use planning scenarios on the exposure to multiple natural hazards.
By employing this method, urban planners and decision-makers can model, predict, and quantify the future impact of risk from natural multi-hazards, according to which proper disaster management policies for tomorrow’s world can be defined.
The structure of this research includes five sections. The first section covers the introduction and the literature review. The second section presents the study area and the dataset used in the research, while the third section presents the overall methodology. The fourth section includes the results of the research. The fifth section discusses the results, while the sixth section gives the research conclusions.
2. Study Area and Dataset
2.1. Study Area
The proposed method is tested on an urban area in southern Italy: the municipality of Rende (Figure 1). Rende covers a surface of 55 km2 and has a population of 36,123 inhabitants. Rende is characterized by different settlement areas, such as Roges, Commenda, Quattromiglia, Arcavacata-Santo Stefano, Saporito, and Surdo.
Figure 1.
Location of the study area.
Rende experienced urban development from 1960 onwards, and, from a peripheral area, it became a modern metropolitan area, defined as the most dynamic of the province of Cosenza. Many infrastructural projects have been developed since the beginning of 1960, such as the construction of the Strada Statale 19 delle Calabrie, which represents one of the leading transportation infrastructures of the entire province of Cosenza, the construction of the railway system as well as the realization of the A2 Mediterraneo highway. Besides these essential infrastructural projects, construction works for completing the University of Calabria (UNICAL) in Arcavacata di Rende also started in 1960. The realization of the UNICAL campus, whose construction is inspired by American campuses and whose aim was to develop an environmentally sound cultural ecosystem, contributed to radically transforming the urban area of Rende as it represents the main engine of its social, economic, and environmental development.
Population data over time confirms the development trend of this urban area, showing the increase and the high presence of people less than 24 years of age as well as many residence transfers.
The territorial context of Rende is characterized by many vulnerabilities and critical factors connected to natural hazards. Many analyses of the territory by experts and decision-makers confirmed that only predicting potential natural risk effects could effectively contribute to defining organic urban land use planning policies.
Due to its geomorphological conformation, the municipality of Rende is mainly threatened by hydrogeological and seismic risks. Considering the landslide risk, 20.45% of the municipality territory is interested in landslide-risk areas. Many settlement areas, primarily located in the hilly part of the municipality, such as Arcavacata and the historical center of Rende, are characterized by landslide areas.
Looking at the hydraulic risk, the main hydraulic criticalities are the many streams that cross the entire municipality, such as Campagnano, Crati, Emoli, and Surdo. On these rivers, the Basin Authority of the Calabria Region conducted sector studies confirming their hazardous potential.
Another type of risk that needs to be considered in the urban context of Rende is the seismic risk. The entire territory is characterized by many active faults, meaning a high seismic risk characterizes the municipality. Despite seismic hazards representing a significant threat to Rende, only studies at the territorial level related to the seismic risk have been performed. Other specific studies, such as seismic microzonation, are not available.
For these reasons, the hazards considered for the proposed case study are landslide and hydraulic.
2.2. Dataset
Remote sensing, geospatial, and alphanumeric data from different sources have been combined to investigate the study area’s urban growth dynamics and future multi-hazard exposure (Table 1). The authors employed many data sources as, in Italy, a general open database containing centralized information about the territory does not exist.

Table 1.
Dataset details.
Orthophotos and satellite images are employed to detect the built-up area changes for the study area. First, to identify the built area relating to the year 2000, the orthophotos of the Calabria Region Cartographic Center [48] are used, with a pixel size of 1 m, and the Gauss-Boaga East—Monte Mario Italy 2 reference system. Unfortunately, for 2022, it was impossible to use the orthoimages as the last flight of the Military Geographical Institute dates to 2008. Therefore, for the year 2022, orthophotos are not available. For 2022, the cloud computing platform Google Earth Engine (GEE) is employed. GEE provides high computing power and accessibility to dense time series and various satellite data and satellite-derived products through its data catalog [49,50,51] (https://code.earthengine.google.com/6e61e10b6c5254694e20e01c8c9ec025 (accessed on 14 April 2023)). In particular, the authors accessed Sentinel-2 (S-2) products that provide high temporal resolution data, short revisit time, and a rich spectral configuration, making them appropriate sources for time series feature extraction [52,53]. The satellite images are characterized by 10 m/pixel resolution and refer to the period from 1 to 31 May 2022. The projected coordinate system employed is WGS84/UTM 33 N. Moreover, geo-topographic data produced by the Italian National Synthesis Database (DBSN) [54] on the national land use cover is used as the ground truth dataset to assess the accuracy of the classification and segmentation of the built-up area.
Shapefiles, raster, and alphanumerical data were used to assess the driving factors selected for the proposed analysis. The Digital Terrain Model (DTM), with national coverage, is used to calculate the study area’s altitude and average slope. It derives from interpolating the orographic data from the Military Geographical Institute (IGM) cartography [55]. The resulting product is a regular step matrix of 20 m, whose elements (pixels) report the values of the dimensions. The national territory is divided into units (tiles) of 10 km ×10 km. Shapefiles of roads, railway stations, water bodies, and higher educational services are derived from the OpenStreetMap (OSM) database [56]. The population and the services and industrial employees’ data are derived from the national population census conducted by the Italian National Institute of Statistics (ISTAT) [57].
The dataset on the population and employees are also employed to assess the future multi-hazard exposure in combination with the shapefiles containing the areas subject to landslide risk and hydraulic risk. The data about the landslide and hydraulic risk are retrieved from the Hydrogeological Structure Plan (PAI), which includes the actions and rules planned and programmed aimed at the conservation, defense, and valorization of the soil in the areas of danger and risk linked to geomorphological processes [58].
3. Methodology
3.1. Methodological Framework
Applying a quantitative methodology (Figure 2), the authors assessed the future multi-hazard exposure of urban areas under different socioeconomic growth scenarios by predicting the expected built-up area development through a single averaged BLRM calibrated considering the urban growth dynamics during a past reference period. In the proposed study, the authors applied the methodology to the case study described in Section 2, considering 2000–2022 as the past reference period to identify the urban growth patterns and 2040 as the future time point associated with the future urban growth prediction. The authors analyzed a 20-year observation period as the most significant territorial transformations linked to planning policies generally occur within 15/20 years.
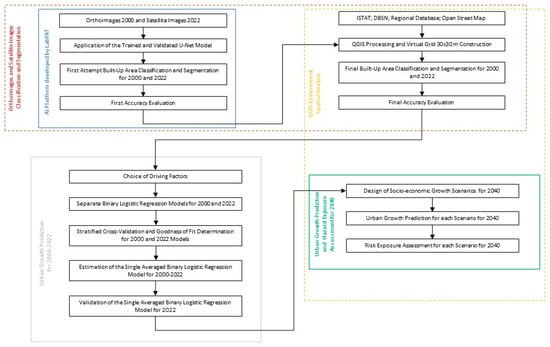
Figure 2.
The methodological workflow.
The authors obtained the built-up cover dynamics between 2000 and 2022 from the land use information detected by applying remote sensing and GIS technologies. Specifically, the authors employed the experimental Artificial Intelligence (AI) platform developed by the Laboratory of Environmental and Territorial Planning (LabPAT) of the Department of Civil Engineering of the University of Calabria. This experimental AI platform is based on the U-Net model. It is trained and validated to classify and segment the built-up area from satellite and aerial images. The results obtained from the AI platform are then refined manually by dividing the study area into a grid system of approximately 60,000 cells of 30 m × 30 m resolution to improve the accuracy of the prediction results.
After selecting the driving factors that potentially determined the urban growth dynamic, the grid system is used to perform the BLRM, obtaining the transition probability map for 2000 and 2022 and, therefore, to evaluate the coefficients’ driving factors values for the two years and the model’s goodness of fit.
Then, the authors evaluated a single averaged BLRM valid for 2000–2022 by averaging the coefficients’ value to the inverse of the respective variances and selecting only the transferable coefficients by performing a transferability test. The authors assessed the accuracy of the single averaged BLRM by comparing the results obtained from its application to 2022 and the actual built-up area pattern detected through the application of the AI platform, and the following refinement of the results using the grid system. The single averaged BLRM prediction accuracy is quantitatively assessed through the Kappa coefficient.
Once the accuracy of the built-up area prediction through the single averaged BLRM is demonstrated, the authors employed it to predict future urban growth patterns. Specifically, the single averaged BLRM is employed to predict urban growth in 2040 by considering different socioeconomic growth scenarios: business as usual (BAU), slow, and fast socio-economic growth. The prediction of the single averaged BLRM for these different scenarios in 2040 is combined with the socio-economic data and the hazard maps to assess future multi-hazard exposure at the census level by generating a future exposure map for each hazard.
3.2. Image Classification and Segmentation
A multistage procedure is applied to identify the urban growth dynamics of the study area from 2000 to 2022 through the classification and segmentation of built-up areas for each year.
First, the orthoimages referred to 2000 and S-2 satellite images for 2022 are processed employing the experimental AI platform, which combines Deep Learning (DL) technologies to classify and segment building heritage from satellite and orthoimages, with GIS techniques to import, use, and process its output to analyze the urban growth over time [59,60].
The experimental AI platform uses a U-Net model. The U-Net model is trained and validated for classifying and segmenting six different classes of features as buildings, vegetation, land, roads, water, and unlabeled. For this study, only buildings are considered. The platform is implemented using Python language using Pytorch with a TensorFlow backend.
A RELU activation function is used for the U-Net model, and the loss function considered is the IoU-based loss function. Adam model optimizer, with an initial learning rate of 0.001 and default hyper-parameters β1 = 0.9 and β2 = 0.999, is used. The validation task is carried out during the training stage, and its loss is calculated and monitored. The training is stopped to prevent overfitting if the validation loss does not improve within 100 epochs. The U-Net model is trained and validated using the “Semantic Segmentation of aerial imagery” [61], reaching an F1-Score of 0.72. The training and validation tasks are carried out on the Google Colaboratory Pro Plus Environment, using 52 GB of RAM and the GPU NVIDIA Tesla P100. The NVIDIA Tesla P100 Graphics Card provides 3584 CUDA cores and 16 GB of HBM2 vRAM linked via a 4096-bit interface. Moreover, the performance is 9.3 TFLOPS at single precision, 18.7 TFLOPS at half precision, and 4.7 TFLOPS at double precision.
The AI platform is employed to detect the built-up coverage in 2000 and 2022. The output of the DL model is imported into the GIS environment, which, in this case, coincides with the open-source QGIS software [62], obtaining an initial classification and segmentation of the built-up area cover changes in the 2000–2022 period. The accuracy of this first attempt to identify the built-up area cover is assessed by comparing the classification and segmentation obtained for 2022 with the information on land use land cover available from the DBSN. The accuracy level of the classification and segmentation through the AI platform is demonstrated through the F1-Score.
Then, the authors improved the accuracy of the results obtained automatically with the AI platform for each reference year. Specifically, the authors divided the study area into a grid of approximately 60,000 cells of 30 m × 30 m dimensions inside the QGIS environment. They manually refined the results obtained from the DL classification and segmentation of the built-up area, employing the orthoimages and the satellite images.
Therefore, the built-up and non-built-up cells are identified by exploiting the potential of remote sensing, artificial intelligence algorithms, and GIS tools through a two-step semi-automatic procedure.
After identifying the built-up area in 2000 and 2022, the authors calibrated a BLRM for each reference year, determining the influence of a selected cluster of driving factors on the urban growth dynamics of the study area for each year.
3.3. Selection and Assessment of Driving Factors
The urban growth driving factors widely used in the scientific literature are mainly related to the environmental conditions of the study area, the specification of its urban environment attributes, and the socio-economic condition of the resident population [63,64,65]. The consideration of these driving factors varies according to the geographic conditions and their relevance to the specific context where the method is applied [66].
For the environmental conditions, many studies considered terrain factors [67], such as slope, elevation, and aspect, and climate factors, such as temperature, precipitation, and moisture. Considering urban environment attributes, the most popular driving factors considered in the scientific literature are related to proximity to transportation services, such as roads, highways, railways, and public transportation infrastructures [68], proximity to urban and territorial services, such as hospitals, institutions, and proximity to job opportunities, such industrial, agricultural, farmland, and business areas [69]. Socioeconomic conditions include population density, household number, job density, employment rate, and gross domestic product per capita [70].
The authors considered nine driving factors in this study. The driving factors selected for this study include terrain factors, such as slope and elevation; socio-economic data, such as population and employees; and proximity factors, such as distance to the main roads, distance to railway stations, distance to main rivers, distance to built-up areas, and distance to territorial services. In the proposed study, the authors considered the university campus as a territorial service for higher education because of its presence in the study area. The authors selected these driving factors because they consider them to have the main explanatory power for built-up area changes and because of their easy calculation linked to their general availability in public and accessible datasets.
The authors assessed each driving factor employing the 30 × 30 m grid system. Indeed, they retrieved driving factors data and reclassified them using QGIS software functions. Slope and elevation values for each grid cell are derived from resampling the 20 × 20 m DTM. Population and employee data retrieved from the ISTAT census are associated with the grid system via the QGIS software. The authors evaluated the proximity to the main urban environment attributes by assessing the distance of each grid cell to the roads, railway stations, water streams, university, and buildings geometry. This analysis is performed through the tool “Distance to the nearest hub” from the QGIS Processing Toolbox. Giving the source point layer and the destination hub layer, which correspond to centroids of 30 × 30 m cells and the hub of destinations, respectively, this tool generates the lines to the hubs layer, indicating the nearest destination hub to each source point. The attribute linked to each line is the distance to the hub value. It represents the distance from the source point to the destination hub. The authors considered the centroid of every polygonal geometry for railway stations, higher education services, and built-up areas as destination hub layers. For main roads and water streams, the authors considered discretized hubs every 30 m along the line of these elements.
After assessing the driving factor values, the authors calibrated the BLRM for 2000 and 2022.
3.4. Binary Logistic Regression Model
The BLRM is used when the dependent variable is binary and the independent variables are continuous and categorical [71,72]. The main characteristic of the binary dependent variable in a logistic regression model is that it takes the value of 1 and 0 as the probability that a certain event happens or not, respectively [73].
The authors applied a BLRM to assess the probability of urban growth in a specific spatial location. The urban growth probability (P) follows the logistic curve and can be estimated through the mathematical expression of Equation (1).
In Equation (1), P is the probability of the dependent variable; X represents the independent variable; is a constant; is the correlation coefficient of the explaining variable and explained variable; and is the odds ratio (OR), which represents the odds that the event will occur given a particular condition compared to the odds of the event occurring in the absence of that condition.
Considering the built-up condition as the dependent variable and the driving factors values as the independent variables, the authors analyzed the relationship between urban growth and the driving factors following Equation (2).
Transforming Equation (2), the authors obtained Equation (3).
In Equation (3), P is the probability of a cell to built-up; Xi is the i-th driving factor of the urban growth; β0 is a constant; and βi is the correlation coefficient between the i-th driving factor and urban growth.
The authors performed the BLRM for 2000 and 2022 using the grid system and changing the value of driving factors according to the environmental, built environment, and socioeconomic conditions for each reference year. The BLRM for each year and, therefore, the estimation of the coefficient values is performed in SPSS [74].
3.5. Stratified Cross-Validation
In this research, the authors employed cross-validation for the accuracy evaluation of BLRMs calibrated for 2000 and 2022. Repeated stratified cross-validation is a valid technique recommended as a standard procedure for evaluating model accuracy by several studies [75,76,77,78,79,80,81,82,83,84,85] because it provides a stable and reliable estimate with low bias. The main advantage of this method over regular cross-validation is that it can provide a less biased estimate of the model skill.
The employed cross-validation method is a 10-fold cross-validation, especially useful in studies where the dataset is imbalanced such as in the present study. The first step in 10-fold cross-validation is randomly dividing the dataset into 10 equal parts. If the dataset contains 1000 instances, each fold will have 100 instances. Stratification ensures that each fold represents the whole dataset well and maintains the same distribution of class labels in each fold as in the entire dataset. For each of the ten folds, a single fold is retained as the validation data, and the remaining folds are used as training data. The regression model is trained using the nine training folds and validated on the remaining fold. The process is repeated ten times, with each of the ten folds used precisely once as validation data. After running the cross-validation loop, three different performance scores are obtained, providing an insight into how well the model might perform on unseen data. As score values of 10-fold cross-validation, Kappa statistic, mean absolute error, and Root mean squared error are used.
3.6. Goodness of Fit of the Binary Logistic Regression Model
Estimating the coefficient values of the BLRM is followed by assessing the model’s appropriateness, adequacy, and usefulness. The importance of each explanatory variable is evaluated by carrying out statistical tests of the significance of the coefficients. After, the overall goodness of fit of the models is tested.
To test the significance of each coefficient, the Wald statistic expressed by Equation (4) is calculated.
In Equation (4), βi is the estimated coefficient value, and σ(βi) is the estimated coefficient value Standard Error (SE).
Each calculated Wald statistic is compared with a one-degree-of-freedom χ2 distribution. Although Wald statistics are easy to calculate, the standard error could be inflated for datasets that produce large coefficient estimates, resulting in a lower Wald statistic. This condition identifies an explanatory variable that could be incorrectly assumed to be unimportant in the model.
Another suitable indicator to determine the impact of each driving factor on urban growth is the OR. This indicator is the predicted change in odds for a unit increase in the predictor. When this value is less than one, an increase in variable values corresponds to decreased odds of the event’s occurrence. Instead, when this value is greater than one, an increase in variable values corresponds to the increased odds of the event’s occurrence.
Once the significance and the impact of coefficients for 2000 and 2022 are assessed, the authors determined the goodness of fit of the BLRMs performed for each time point to measure how well the coefficient values predicted by the BLRM for each year are close to the observed values.
The Cox and Snell and the Nagelkerke R2 statistics are frequently used for assessing a model’s goodness of fit. These statistics determine the explained variation of the model. The maximum value of Cox and Snell R2 is less than 1. The Nagelkerke R2, instead, assumes values inside the full range interval from 0 to 1 and represents an adjusted version of the Cox and Snell R2, and, for these reasons, it is often preferred.
3.7. Estimation of the Single Averaged Binary Logistic Regression Model Coefficients and Assessment of Their Transferability
Once the significance of coefficients and the goodness of fit of the performed BLRM for 2000 and 2022 are assessed, the obtained BLRM coefficients estimated for 2000 and 2022 have been averaged to obtain a single averaged BLRM.
Model averaging is a widespread technique in statistical applications to identify the best model from a set of models according to a defined criterion. It consents to have a good prediction of the future outcomes [86], such as the future urban growth patterns, which is the purpose of this study.
In the proposed study, the coefficients of the single BLRM are estimated as the average of the obtained values from the application of the BLRM for 2000 and 2022, weighted to the inverse of the respective variances, according to Equation (5).
The variance of βm (j) results to be expressed by Equation (6).
Then, the authors carried out a transferability test of the estimated coefficients of the single BLRM [87] to assess if the single averaged BLRM can be applicable to predict future urban growth patterns. Employing this test, it can be verified whether the parameters of models estimated in 2000 and 2022 are systematically different or can be considered sample fluctuations of the single “true” averaged BLRM.
To test the null hypothesis E[βi] = βm for i = 1, …, k, where E[βi] represents the mean of the coefficients βi and K is the coefficient number corresponding to the i-th variable of BLRM, the likelihood ratio test expressed in Equation (7) is used.
The statistic of the TRANSF test, in the case of validity of the null hypothesis, results are distributed as a χ2 variable with a number of degrees of freedom equal to the number of periods minus one.
3.8. Validation of the Single Averaged Binary Logistic Regression Model
Before applying the BLRM to simulate future urban growth scenarios, the authors assessed the accuracy prediction of the single averaged BLRM. The built-up area distribution for 2022 is predicted by applying the single averaged BLRM considering the driving factors value for the 2022 reference period. The accuracy of the single averaged BLRM is evaluated through Cohen’s Kappa coefficient by comparing the 2022 built-up area map obtained from the two-step semi-automatic procedure described in Section 3.2, with the built-up area simulated by the single averaged BLRM. The Kappa coefficient is selected to measure the prediction accuracy as it considers the possibility of the agreement due to chance [88].
The Kappa coefficient is assessed employing Equation (8).
Po is the proportion of the observed total agreement between the real and the predicted, and Pe is the proportion of the expected total agreement between the real and the predicted due to chance. The Kappa statistic puts the measure of agreement on a scale ranging from 0 to 1, where 0 indicates agreement being no better than chance, while 1 represents perfect agreement. A typical interpretation of a Cohen’s Kappa result is that values from 0 to 0.2 represent slight agreement, values from 0.2 to 0.4 correspond to fair agreement, values from 0.4 to 0.6 indicate moderate agreement, values from 0.6 to 0.8 coincide with a substantial agreement situation, and values from 0.8 up to 1 demonstrate almost perfect agreement [89,90].
The future urban growth scenarios are simulated once the prediction accuracy is assessed, and the model with the estimated coefficients is validated.
3.9. Definition of the Urban Growth Scenarios
This study’s reference period for predicting future urban growth patterns is 2040. The authors simulated urban growth for this time, considering the BAU, slow, and fast socio-economic growth scenarios [91,92]. These are defined by considering the different growth rates of the population and employees in the industrial and service sectors in 2022, which is considered the baseline period. The authors synthesized specifications for the different scenarios in Table 2.

Table 2.
Urban growth scenarios definition.
Analyzing the growth rate of the population and of the employees in the industrial and service sectors that occurred during the period 2000–2022, the BAU scenario (S0) foresees for 2040 a growth rate of the population and employees in the industry and services sectors equal to the one that characterizes the period from 2000 to 2022.
The slow socioeconomic growth condition consists of scenarios S1, S2, and S3. S1, S2, and S3 foresee an increase in the population and employees in the industry and services sectors equal to 50%, 75%, and 100% of the growth rate occurred during the 2000–2022 period.
The fast socioeconomic growth condition comprises scenarios S5, S6, and S7. These scenarios foresee a significant growth of the population and employees in the industry and services sectors. Specifically, the authors assumed an increase in the population and of the services and industrial employees equal to the 50%, 75%, and 100%, compared to 2022.
The authors assessed the urban growth prediction for each defined scenario by applying the single averaged BLRM.
3.10. Future Multi-Hazard Exposure Assessment
Once the urban growth patterns in 2040 for each scenario are identified, the authors assessed the future multi-hazard socio-economic exposure at the census level, considering defined socio-economic exposure indicators and the hazard maps that, in this study, are related to the landslide and hydraulic hazards.
The exposure levels of urban systems depend on the presence of material and immaterial urban features as they represent urban risk hotspots that can be potentially affected by hazards. The level of exposure of these elements can be analyzed through specific indicators, which, in most cases, are related to the distribution, density, and quantity of these exposed elements.
In the literature, different methodologies to assess socioeconomic exposure using standard measures exist [93,94,95,96,97]. The measures widely used to assess natural hazard exposure levels are the built-up area [98], the gross domestic product [99], and the population density [100,101]. These essential variables assess natural hazard impact as they represent human activities and, in general, society [102].
Moving from this background, the authors employed these three indicators (Table 3) to assess the future exposure of urban areas to natural hazards. Specifically, the future socio-economic exposure is analyzed in this study by determining the built-up area density, the population density, and the number of employees exposed to hazards. The gross domestic product indicator, mainly used for economic exposure evaluation, is replaced with the number of employees exposed to hazards as this indicator can be retrieved more easily in public and official databases at the census level.

Table 3.
Exposure indicators.
The future socioeconomic exposure is performed at the census level as they are the minor sampling units recognized at the national and international levels by employing GIS techniques within the QGIS environment.
The built-up area density exposed to natural hazards is evaluated by intersecting for each scenario the built-up area predicted by the single averaged BLRM with the map of the hazards. The ratio between the built-up area crossed by the hazard map and the total area of the census tract is evaluated.
The population density is assessed according to the population growth rate defined in Section 3.9. The authors evaluated the population at the census level, then averaged the population data according to the built-up area intersected by the hazard and divided it by this latter. The same procedure is carried out for the number of employees affected by hazards.
After calculating the indicators in their unit of measurement, the authors normalized them using the minimum-maximum standardization method. This standardization method allows for the normalizing of raw values, obtaining a measurement scale between 0 and 1. The lowest values of this scale correspond to lower values of built-up area density, population, and number of employees exposed to hazards. The highest values correspond to higher levels of built-up area density, population, and employees exposed to hazards. The normalization step makes indicators comparable and facilitates aggregation operations. The aggregation phase is performed by summing the normalized values, obtaining a variation of the level of exposure ranging from 0 to 3.
The authors performed these steps within the QGIS software. The authors repeated these steps for all the defined scenarios. The result is an exposure map for each scenario and hazard in which the exposure value varies from 0 to 3. To provide a variation measure on the exposure level from one census tract to the other, the authors defined ten levels of value variation equal to 0.3.
4. Results
4.1. Built-Up Area Detection from Image Classification and Segmentation
From the application of the experimental AI software platform for the classification and segmentation of the Rende built-up area in 2000 and 2022, the authors assessed the accuracy of the results model by evaluating the F1-Score for 2022. The F1-Score for this timepoint equals 0.69, showing a good model level to classify and build up segment areas from orthoimages. As stated in the methodological section, the authors defined a square grid cell characterized by a dimension of 30 × 30 m to refine the segmentation of the built-up area retrieved from applying the DL model and to perform future urban growth predictions. By refining the results, the authors reached an F1-Score of 0.87.
The built-up area detected by the semiautomatic procedure equals 13.13 km2 in 2000 and 16.01 km2 in 2022. Therefore, the built-up area change detected for the study area during 2000–2022 revealed an increase of 2.88 km2. This built-up area change is related to the realization of residential and services buildings in Commenda, Roges, and Quattromiglia settlements, as well as the completion of supporting structures for the UNICAL campus, such as new residential buildings for students (San Gennaro, Chiodo, Monaci) and new services, such as the University Sports Center (CUS). The main driver of the increase in the built-up area during this period was the presence of the UNICAL campus, which determined the development of settlement areas next to it in terms of new buildings and urban services. On the contrary, the urban areas far from the university and the main center, such as the historical center of Rende and Nogiano, did not experience urban development during this period. Instead, they are characterized by many abandoned buildings and areas that need to be regenerated.
4.2. Binary Logistic Regression Models for 2000 and 2022
The authors calibrated the BLRM to assess the urban development prediction for 2000 and 2022, investigating the impact of the selected driving factors on the urban growth dynamics. For each cell in which the study area is divided, the dependent variable is binary and assumes values 1 and 0 in the case of built-up or not built-up cells. As stated in the methodological section, nine independent factors are examined in the BLRM to estimate the influence of each factor on urban growth. The coefficients of independent factors identified the nature of the correlation between urban growth and these driving factors for the municipality of Rende. If the coefficient value is positive, the probability of urban growth increases. Otherwise, the urban growth probability decreases if the coefficient value is negative. Table 4 and Table 5 show the values and the statistics of the nine independent factors for 2000 and 2022, respectively.

Table 4.
Estimated nine factor coefficients for 2000.

Table 5.
Estimated nine factor coefficients for the year 2022.
For 2000, considering the Wald statistic and the significance test, the coefficients related to the elevation and the distance to water are not significant for the model. The significance values, indeed, in both cases, are more than 0.05, while the Wald is low. Thus, except for these two variables, the other seven factors’ values have remarkable significance, indicating that these factors are statistically significant for urban growth. Looking at the significant variables, the authors found that three positively influence urban growth, while the other four negatively influence it. The driving factors that have a positive influence are population, employees, and distance to the university campus. Slope, distance to buildings, distance to main roads, and distance to railway stations have negative influence. Population and employees have the same impact on the urban growth dynamic. Their OR values indicate a greater probability of urban growth related to increased population and employees. Also, the probability of urban growth is higher for urban areas far from the university campus. Considering the slope, the distance to the main roads, and the distance to railway stations, the OR values indicate that the impact of the slope is more significant concerning the other factors on urban growth for the reference year. The probability of urban growth is higher for areas with lower slopes and areas near the main roads and railway stations. Moreover, urban areas tend to grow near existing buildings. Indeed, the OR value is 0.812, meaning that the probability of urban growth near already urbanized areas is estimated to be 1.23 times larger than the predicted expansion in an area far from these areas. The assessment of the model’s goodness of fit revealed that the Nagelkerke R2 statistic assumes a value of 0.83, meaning the BLRM explains about 83% of the total variance. To confirm that, Cox and Snell’s statistic also reaches a value of 0.51. These values indicate the high capability of the model to predict the observed values.
Regarding the results of the BLRM calibrated for 2022, the overall goodness of fit of the model indicates the high capability of the model to predict the observed values, with a Nagelkerke R2 value of 0.83 and a Cox and Snell statistic value of 0.55. Reading the significance test and Wald statistics of the driving factors, the elevation is not significant for urban growth. Contrary to what is determined for 2000, the distance to water is significant for the model. Also, for 2022, the other seven factors’ coefficients are significant. Population, employees, and distance to the university have a positive influence, while slope, distance to water, distance to buildings, distance to main roads, and distance to railway stations have a negative influence. As for 2000, the driving factor with the most significant influence on urban growth is the distance to buildings. The OR is 0.816 for this factor, meaning that the predicted expansion around existing urban areas is estimated to be 1.22 times more than the predicted expansion in an area far from urbanized areas. Similarly to what happened in 2000, the OR values indicate that the slope has a more significant impact concerning the distance to the main roads and the distance to railway stations, whose contribution to urban growth is similar. From OR values, it can be noted that the probability of urban growth is 1.02 times more likely in flat areas. Urban growth tended to occur near the main roads, the railway stations, and the water bodies. Also, for 2022, the probability of urban growth is higher far away from the university campus, although it has a small impact, as demonstrated by its OR values. The population and employment presence contribute almost the same to urban growth patterns. Specifically, the probability of urban growth increases slowly with the population and employees since the OR value for these variables is a little higher than 1.
4.3. Results of the Stratified Cross-Validation for 2000 and 2022 Models
The results of the 10-fold cross-validation analysis are reported in Table 6. The results for 2000 and 2022 are promising, providing stable and reliable estimations with low bias. For 2000, the number of totally correctly classified instances exceeds 95%, reaching Kappa Statistic, Mean Absolute Error, and Root Mean Squared Error values, respectively, of 0.85, 0.073, and 0.19. Also, for 2022, the results are promising, with 94.22% of correctly classified instances and Kappa Statistic, Mean Absolute Error, and Root Mean Squared Error values of 0.84, 0.09, and 0.21. The employed cross-validation method provides a less biased estimate of the models’ skills.

Table 6.
Stratified cross-validation results for 2000 and 2022.
4.4. Definition of the Single Averaged Binary Logistic Regression Model
As can be seen from the results obtained by calibrating the BLRMs for the years 2000 and 2022, the impact of the driving factors on the urban growth phenomenon is almost the same in both models, with excellent response in the levels of the goodness of fit between the predicted and observed values. For this reason, the authors verified whether the parameters of models estimated in different periods are systematically different or can be considered sample fluctuations of a single true model. If this condition is verified, it is possible to consider a single averaged predictive model valid and transferable to subsequent analysis periods.
The coefficient relating to elevation was excluded from the test as it is not significant in both reference years. However, the coefficient relating to the driving factor distance to water is included in the test as it is strongly significant in 2022.
By applying the methodology described in the methodological section, the results in Table 7 are obtained.

Table 7.
Transferability test for models’ 2000 and 2022 coefficients.
The hypothesis of the statistical theory of transferability can be accepted at a level of significance of 0.05 for all the coefficients. Respecting this limitation, the value of TRANSF does not exceed the value of 3.841 to satisfy each coefficient’s transferability condition. As shown in Table 4, the TRANSF value for all the significant driving factors is less than 3.841, demonstrating that all are transferable for 2000–2022. Therefore, the average coefficient value of each driving factor is considered to define the single averaged BLRM, which simulates the changes that occurred in a past timeline and represents the best model to predict future outcomes.
4.5. Model Validation Assessment
Before employing the single averaged BLRM to predict the 2040 urban growth dynamics under different socioeconomic growth scenarios, the authors validated the single averaged BLRM by comparing the urban growth dynamics obtained for 2022 employing the single averaged BLRM and the actual built-up area patterns.
First, the authors applied the single averaged BLRM to simulate the built-up area patterns for 2022. This result is represented in Figure 3, where orange and grey represent the built-up and non-built-up areas, respectively.
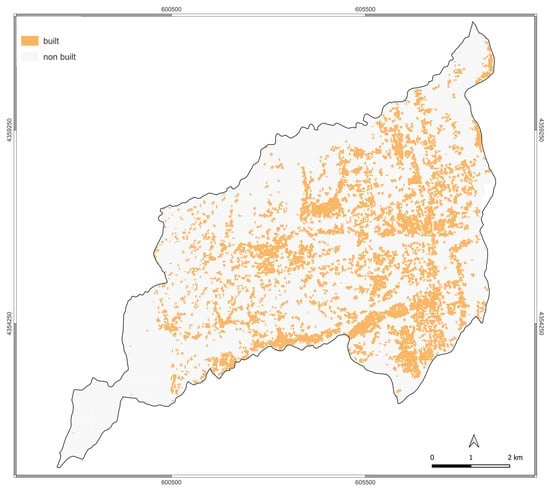
Figure 3.
Predicted built-up area for 2022.
The prediction is, then, compared to the actual built-up area pattern identified by the application of the AI platform and the refining operations. The accuracy level of the prediction is assessed by evaluating Cohen’s Kappa coefficient. For the 2022 time point, the Kappa coefficient is equal to 0.84, demonstrating a great level of accuracy of the single averaged BLRM. The real and the predicted built-up area patterns showed an observed agreement proportion of 0.94 and a proportion of probable agreement occurrences rate due to chance equal to 0.64. This result revealed that the calibrated logistic regression model predicts the built-up area changes well.
4.6. Built-Up Area Prediction for 2040 Based on Urban Growth Scenarios
After validating the single averaged BLRM, the authors predicted the future urban growth patterns in 2040 according to the scenarios defined in the methodological section. The predicted urban growth for the defined scenarios is represented in Figure 4, where the grey color represents the non-built-up area, the orange color the built-up area in 2022, and the brown color the built-up area changes compared to 2022.
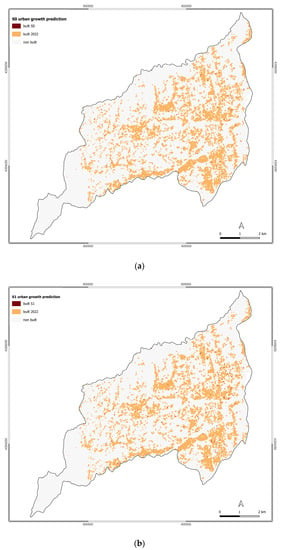
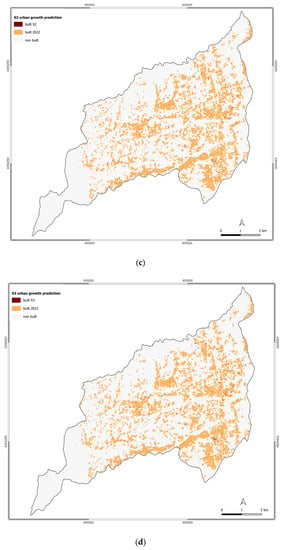
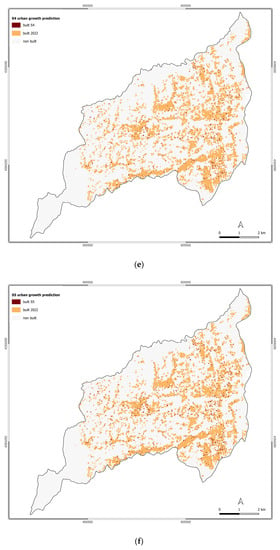
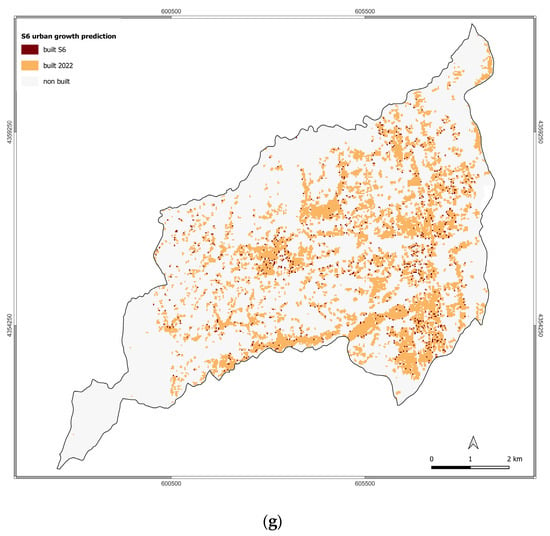
Figure 4.
Urban growth prediction for the scenarios: (a) S0; (b) S1; (c) S2; (d) S3; (e) S4; (f) S5; (g) S6.
The spatial distribution and the changes in the built-up area in 2040 for the different scenarios are synthesized in Table 8.

Table 8.
Built-up area changes in 2040 for defined scenarios compared to 2022.
The BAU scenario determined slight modifications compared to 2022. Indeed, the change in built-up area is equal to 0.07 km2, which represents an increase rate of 0.44%. This increase in the built-up area is mainly located within the consolidated part of Rende, which corresponds to the Roges and Villaggio Europa settlements, by occupying the vacant land in this urban context. Other built-up area changes for this scenario are located in the industrial zone of Rende.
For S1 and S2, the built-up area changes are equal to 16.14 and 16.15 km2 for an increasing rate of 0.81% and 0.87%, respectively. Regarding the localization of built-up area changes, S1 and S2 follow the BAU scenario as the changes are mainly distributed in Rende’s urban consolidated and industrial area. The changes in the Arcavacata and Santo Stefano settlements represent some exceptions.
Under S3, the Rende municipality will experience an increase in the built-up area following a densification process of the already existing settlements. The main changes will interest Roges, Santo Stefano, and the industrial area. S3 will determine an increase in the built-up area of 0.18 km2 compared to 2022 for a rate of 1.12%.
Considering the fast growth scenarios, the authors found that S4 determines a widespread build-up area increase. Indeed, the built-up area changes compared to 2022 registered for this scenario is 0.51 km2, corresponding to a rate of 3.19%.
S5 determines an increase in the built-up area of 0.73 km2. It means an increased rate of 4.56% compared to 2022. These built-up area changes are mainly located in the Roges and Commenda settlements area. Moreover, these changes are in the industrial zone of Rende and in the development area of Quattromiglia. Another significant built-up area change occurs near the university campus UNICAL, within the Arcavacata and Santo Stefano settlement areas, while others are in the Saporito di Rende.
The built-up area change found for S6 follows the pattern changes registered for S5 with an increase in the built-up area compared to 2022 equal to 0.99 km2, corresponding to a rate of 6.18% of the built-up area more than the baseline year. Also, in this case, significant changes interest Quattromiglia, Commenda, Rogers, Saporito, Arcavacata, Santo Stefano, and Arcavacata settlement areas. For this scenario, significant changes also occur within the Rocchi area, the urban settlement behind the UNICAL campus bordering the Montalto municipality.
The analyzed scenarios revealed that significant changes will occur in the case of the fast growth scenarios. Despite this, looking at the built-up area changes that occurred over time for the analyzed case study, the authors consider the slow growth condition as the most probable urban growth forecast in 2040.
4.7. Future Multi-Hazard Exposure Prediction for 2040 based on Urban Growth Scenarios
After assessing the urban growth prediction, the future multi-hazard exposure is evaluated for the defined scenarios. The authors analyzed the indicators for the hydraulic and landslide hazards in the methodological section. Using the census tracts, the authors analyzed the main urban features exposed to the aforementioned hazards through QGIS software and assessed the exposure indicators defined in Section 3.10.
The exposure to the hydraulic hazard over the different scenarios is represented in Figure 5. Over the different scenarios, significant changes in the exposure can be observed.
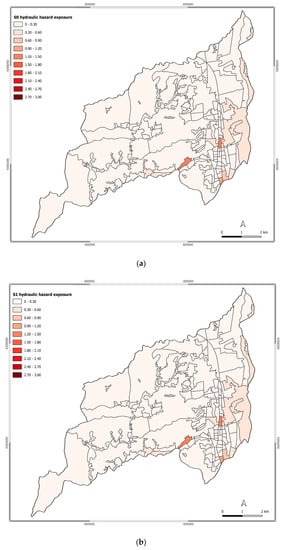
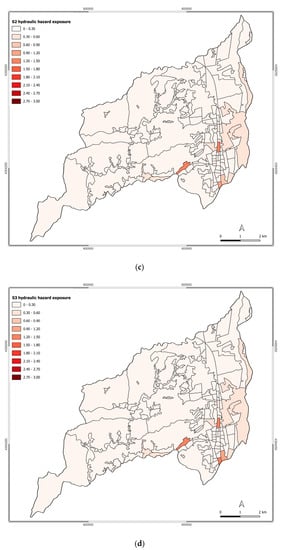
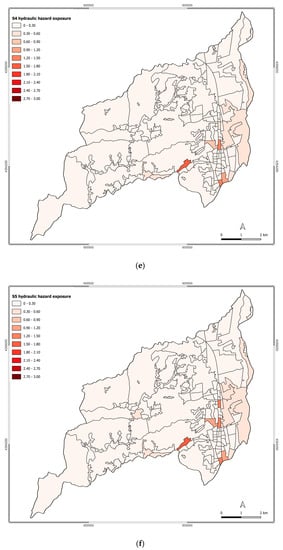
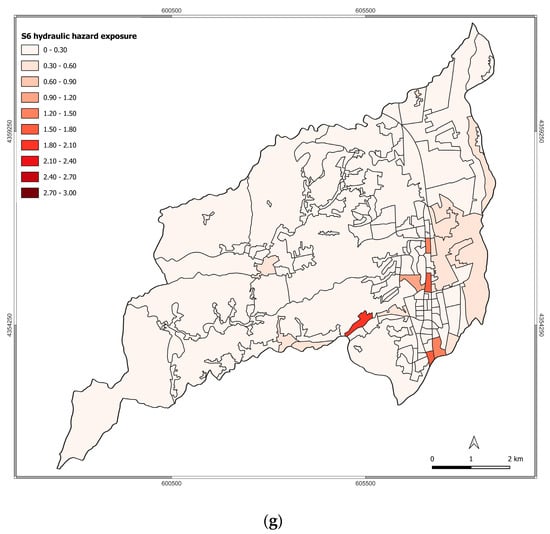
Figure 5.
Exposure to hydraulic hazard for scenarios: (a) S0; (b) S1; (c) S2; (d) S3; (e) S4; (f) S5; (g) S6.
As the main threats regarding the hydraulic hazard are represented by the rivers Campagano, Crati, Emoli, and Surdo, the main exposure changes occurred in the census tracts facing the attention areas of these two rivers. Specifically, over the analyzed scenario, the main changes in the exposure level are registered for the Saporito, Commenda, Roges, and Santo Stefano settlements.
In Figure 6, the exposure level to landslide hazard of Rende’s census tracts is represented across the different scenarios. Also, in this case, the exposure level of Rende increases over the different scenarios.
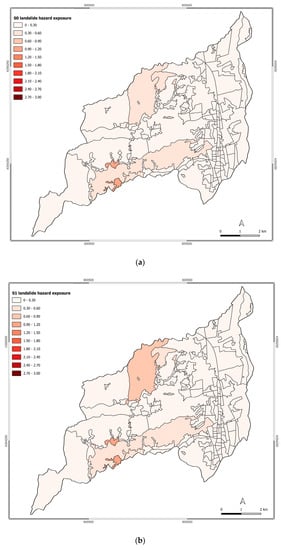
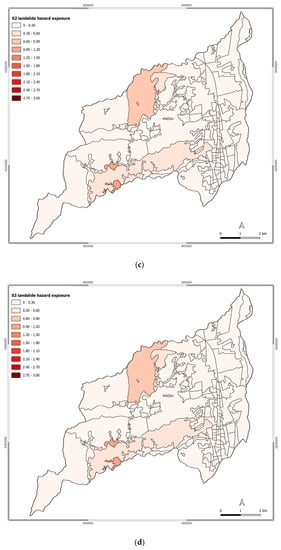
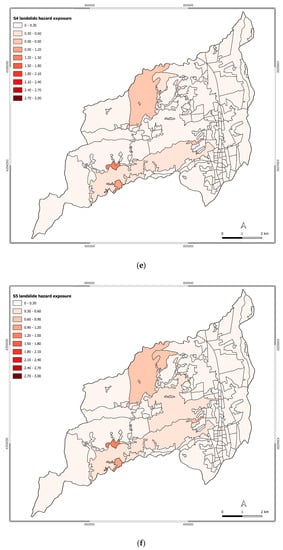
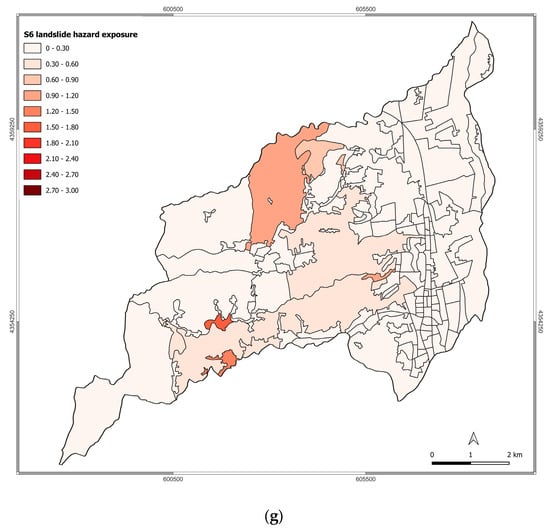
Figure 6.
Exposure to landslide hazard for scenarios: (a) S0; (b) S1; (c) S2; (d) S3; (e) S4; (f) S5; (g) S6.
Due to the geomorphological characteristics of the municipality of Rende and the differences in the urban elements exposed to landslide hazard across the analyzed scenario, the main changes in the exposure level are mainly noticed in the historical center of Rende, Malavitani, Dattoli, and Surdo.
5. Discussions
An analysis of the outcomes of this study reveals meaningful research insights.
As stated in reference [103], DL algorithms applied to orthoimages and satellite images can obtain a detailed land cover classification and discriminate among classes of interest with promising results. These results demonstrate that new classification methods can improve the capabilities of performing land cover maps from remote sensing information. Despite the expanding amount of satellite images and land cover data provided by spatial agencies, these are affected by an excessive aggregation level and, often, the satellite images do not have the required spatial and temporal resolution. Therefore, creating an AI platform based on DL algorithms interfaced with GIS systems allows several advantages, including automated data analysis, improved accuracy, scalability, data integration and interoperability, and real-time processing and predictions. The applied methodology using satellite and aerial images from Unmanned Aircraft System (UAS) flights planned ad hoc can guarantee higher spatial resolution than most land cover maps provided by space agencies, often based on aggregated data from various sources.
The results revealed that the single averaged BLRM calibrated to determine the urban growth dynamics and patterns by considering the output of the semi-automatic procedure to classify and segment satellite and aerial imageries as the dependent variable, and nine driving factors as the independent variables have a great level of accuracy, as demonstrated by the Kappa statistic employed to perform the model validation assessment. Indeed, despite the accuracy of the semi-automatic procedure to determine the dependent variable, which, in this case, consisted of the application of an experimental AI platform that uses the U-Net model to classify and segment the built-up area from satellite and aerial imageries and the following refinement performed manually by the authors has a quite good level of accuracy in the identification of built-up features, the urban growth seems to be well predicted. The accuracy of the single averaged BLRM is also linked to the good calibration of the BLRM relating to 2000 and 2022. The goodness of fit of these two models was equal to 0.83, greater than that of the BLRMs calibrated to simulate urban growth dynamics in other research work [104]. Moreover, the use of the single averaged BLRM, which is calibrated to analyze the changes that occurred between 2000 and 2022 and to predict the future urban growth dynamics, could help to overcome the limitation of considering only one specific BLRM calibrated for a single time point or a single period, as carried out by reference [105]. The transferability test employed to assess the validity of each driving factor over time consented to define a single averaged BLRM for predicting better future urban growth dynamics. The benefit of calibrating a single averaged BLRM that considers the transferability of the impact of each driving factor is also demonstrated by the accuracy of the model prediction.
From the analysis of the impact of the selected driving factors on the urban growth dynamics for the 2000 and 2022 time points, the results showed that the proximity to existing buildings represents the dominant driving factor estimating a predicted expansion around existing urban centers greater than the predicted expansion in areas far from urban centers. This result is consistent with the other published studies about urban growth dynamics analyzed employing BLRMs in other case studies, even if they are mostly related to big cities, such as Atlanta [106] and Bucharest [107]. In these cases, the negative impact of the distance to existing buildings or existing built-up is major. The OR in these studies is equal to 0.38 and 0.14, while it is equal to 0.82 in the proposed study. The difference between the extension and the complexity of the study area can determine this difference. Calibrating the proposed single averaged BLRM to another case study could confirm this thesis. As a result of this study, urban growth probability is higher for areas with lower slopes. This result confirms that urban growth dynamics occurred in the analyzed territorial context over the years, tending to increase the built-up area in areas characterized by flat topography. Population, employees in the industry and services sectors, and the distance to territorial services have the same impact on the urban growth dynamic. A greater probability of urban growth is related to increased population and employees. The authors, moreover, found that urban growth probability is greater near the main roads, railway stations, and water. This result is in line with other scientific studies [108,109]. This latter scientific study also revealed that the influence of the proximity to higher education, such as a university, is not influential to the phenomenon as the obtained OR is equal to 1. Within the proposed study, the OR related to the distance to the university campus is slightly greater than 1, confirming that its impact could be more influential. Starting from these considerations, it can be highlighted how urban growth in the territory of Rende, even if less evident than in other large cities, is guided by the need to access better economic opportunities and services, mainly linked to infrastructures and services.
The prediction of urban growth dynamics in 2040, assessed considering the different socio-economic growth scenarios, revealed that a more substantial urban growth may occur in the fastest socio-economic growth conditions. Indeed, the cells that from non-built became built are more prevalent in these scenarios than the BAU and the slow socio-economic growth scenarios. The urban growth patterns in slow socio-economic growth conditions are areas closest to the existing buildings where the population, the economy, and the services are more concentrated. As the population and the number of employees in the services and industries sector grow, the diffusion of urban cells increases in correspondence with the already consolidated areas, such as Quattromiglia, the high-density settlements of Roges, and, lastly, the peripheral areas of Saporito, Surdo, Arcavacata, and Santo Stefano of Rende. The prediction model results applied in this study provide valuable insights for the future urban planning of Rende. Planning policies should promote a balance between the expansion phenomena along the valley axis, which connects the South (near Cosenza) to the North (near Montalto) part of the study area, and the transverse directions. As demonstrated in this study, the valley part of the study area has a higher urban growth probability than the other part of the city. These latter areas, such as Surdo, and Saporito, experience urban growth only if fast socio-economic growth conditions occur. It happens because they are marginal areas concerning the new urban center characterized by degraded and abandoned neighborhoods. These areas do not need to be expanded but require regeneration actions oriented to an improvement in existing settlement quality. These integrated regeneration interventions could involve the physical and functional recovery of buildings and the redevelopment of the adjacent spaces. These smaller-scale interventions should be combined with wider-scale interventions, enhancing infrastructure connections between the center and the periphery and strengthening the services offered to residents.
The results obtained from the future multi-hazard exposure assessment based on predicting future built-up areas, population density, and employees for industrial and services exposed to hazards showed the areas potentially affected by these hazards. These elements are the main variables that provide an initial measure and spatial pattern of the exposed urban features, population, and employees linked to the urban growth phenomenon. The exposure geography obtained by assessing the future exposure of built environments to natural hazards reveals that land use management and policies need to be optimized to minimize hazard damages. Strong and context-fitted disaster management tools can guide future urban growth localization outside current and, if defined, future hazard areas. The proposed method fits well with this necessity as it can be employed as a valuable support for urban and disaster management planners in evaluating planning scenarios considering their impact on risk. Indeed, urban planners can define robust strategies for the entire urban area and context-related specific interventions for neighborhoods [110].
The proposed research addresses different novelties in this research area. First, the study presents an innovative quantitative and transferable methodology that guarantees a high level of precision in urban growth prediction. The calibrated BLRM is characterized by a high level of stability in the assessment of each driving factor determining the predicted urban growth. The level of detail contributes to determining slight differences in built-up area changes determined by the changes in driving factors. This contributes to evaluating the effects of these changes in hazard impacts. The assessment of changes in exposure level considering different scenarios is an effective means to define proper planning strategies aimed at enhancing the resilience of the urban environment and making urban settlements safer and more resilient. Furthermore, the main challenge of this research was the harmonization of data from different sources caused by the complexity of the proposed method, which involved the geospatial processing of different data formats, such as orthoimages, aerial imageries, shapefiles, raster, and alphanumerical data.
Despite its strength and novelty, the study has limitations as well. The accuracy in predicting the built-up area through the AI platform should be improved to avoid the two-step semiautomatic procedure. Also, the accuracy of predicting urban growth patterns through the single average BLRM could be further demonstrated by calibrating and employing the single averaged BLRM in another context. This would demonstrate if the single averaged BLRM works well for other areas. A useful test would be applying the single averaged BLRM to big cities or metropolises and comparing the results with existing research work. Moreover, the calibration and use of other models to predict future urban growth patterns and their comparison could help identify the best predictive model in terms of result and accuracy. In this study, the authors employed nine driving factors. The integration of other driving factors could be considered in future research to improve prediction accuracy. For the definition of scenarios, better results and research insights could be obtained if the land use planning scenarios defined in urban plans were analyzed to predict future urban growth patterns. Considering the future multi-hazard exposure, in this research, the authors assessed the future exposure to hazards by evaluating the current hazard maps available at the regional scale. Multisectoral and multidisciplinary studies would overcome this limitation by defining future hazard maps, which, combined with this study, could define the future overall risk of urban areas. Additionally, the authors are aware that only the built-up area density, population, and employees variables do not give a broad measure of exposure. For example, considering the built-up area, a more precise assessment of the future multi-hazard exposure would require information about its specific characteristics, such as the use destination, physical characteristics, and volume. For this kind of investigation, having precise information about this data could be addressed in the future development of this research.
6. Conclusions
This research proposed an innovative methodology to assess the future multi-hazard exposure of urban areas based on remote sensing technologies and statistical and spatial analysis. The authors, specifically, applied remote sensing technologies combined with artificial intelligence to map the built-up area automatically. Then, they assessed and calibrated a transferable BLRM to model and predict future urban growth dynamics under different scenarios, such as the business as usual, the slow growth, and the fast growth scenarios. Finally, considering specific socioeconomic exposure indicators, the authors assessed each scenario’s future multi-hazard exposure of urban areas.
The results revealed that the multi-hazard exposure significantly changed across the analyzed scenarios and that urban growth is the main driver of risk in urban environments. The resulting multi-hazard analysis provides a better understanding of the disaster management policies to implement in urban areas. Indeed, employing this method makes it possible to identify the settlement areas more prone to natural hazards and, therefore, define preventive risk mitigation measures.
This research represents the first study to assess the future multi-hazard exposure of urban areas. This methodology could be applied in other urban contexts with rising natural hazards. It could represent a valuable method for assessing future built-up area changes under different scenarios and multi-hazard exposure. Therefore, it could help urban planners to define better urban policies by considering the effects of urban planning scenarios in the face of natural hazards. This would help to determine suitable mitigation measures for contrasting economic, social, and environmental losses from natural hazards. The proposed methodology helps to estimate the future urban exposure to natural hazards, representing a valuable tool for policymakers, urban planners, and disaster management planners to better understand tomorrow’s risk.
Author Contributions
Conceptualization, C.S. and A.V.; methodology, C.S. and A.V.; software, A.V.; validation, C.S.; formal analysis, C.S. and A.V.; data curation, C.S. and A.V.; writing—original draft preparation, C.S. and A.V.; writing—review and editing, C.S. and A.V.; visualization, C.S. and A.V.; supervision, C.S. and A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The “semantic segmentation dataset” employed in the training and validation tasks is available by registering at https://humansintheloop.org/semantic-segmentation-dataset (accessed on 14 March 2023). The orthoimages of the study area are available by registering at: http://geoportale.regione.calabria.it/ (accessed on 10 April 2023). Sentinel-2 Missions satellite images are available at https://sentinel.esa.int/web/sentinel/missions/sentinel-2 (accessed on 14 April 2023). The Italian National Synthesis Database is available online at https://www.igmi.org/it/dbsn-database-di-sintesi-nazionale (accessed on 19 April 2023). The Shapefiles of roads, railway stations, water bodies, and higher educational services derived from the OpenStreetMap database are available at https://www.openstreetmap.org/#map=6/42.088/12.564 (accessed on 19 April 2023). The Digital Terrain Model is available online at https://www.igmi.org/it/descrizione-prodotti/cartografia-digitale/dtm-digital-terrain-model (accessed on 19 April 2023). Population data are available online at http://www.istat.it/it/censimento-popolazione/censimento-popolazione-2011 accessed on 19 April 2023). The data about the landslide and hydraulic risks are available online at https://www.distrettoappenninomeridionale.it/index.php/elaborati-di-piano-menu/ex-adbcalabria-menu (accessed on 19 April 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABM | Agent-Based Model |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| BAU | Business As Usual |
| BLRM | Binary Logistic Regression Model |
| CA | Cellular Automata |
| CUS | University Sport Center |
| DBSN | Italian National Database |
| DRR | Disaster Risk Reduction |
| DTM | Digital Terrain Model |
| GEE | Google Earth Engine |
| GIS | Geographical Information System |
| IGM | Military Geographical Institute |
| ISTAT | Italian National Institute of Statistics |
| LULC | Land Use and Land Cover |
| NDVI | Normalized Difference Vegetation Index |
| OR | Odds Ratio |
| OSM | Open Street Map |
| PAI | Hydrogeological Structure Plan |
| S-2 | Sentinel-2 |
| SE | Standard Error |
| UAS | Unmanned Aircraft System |
| UNICAL | University of Calabria |
References
- United Nations Department of Economic and Social Affairs (UNDESA), Population Division. World Urbanization Prospects: The 2018 Revision; Technical Report; ST/ESA/SER.A/420; United Nations: New York, NY, USA, 2019. [Google Scholar]
- United Nations Office for Disaster Risk Reduction (UNISDR). Global Assessment Report 2015; United Nations: Geneva, Switzerland, 2015. [Google Scholar]
- United Nations Office for Disaster Risk Reduction (UNISDR). Making Development Sustainable: The Future of Disaster Risk Management, Global Assessment Report on Disaster Risk Reduction; United Nations: Geneva, Switzerland, 2015. [Google Scholar]
- Birkmann, J.; Welle, T. Assessing the risk of loss and damage: Exposure, vulnerability and risk to climate-related hazards for different country classifications. Int. J. Glob. Warm. 2015, 8, 191–212. [Google Scholar] [CrossRef]
- Erdik, M. Earthquake risk assessment. Bull. Eart. Eng. 2017, 15, 5055–5092. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; van den Hurk, B.; Seneviratne, S.; Ward, P.; Pitman, A.; AghaKouchak, A.; Bresch, D.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- United Nations International Strategy for Disaster Reduction (UNISDR). Terminology on Disaster Risk Reduction; United Nations: Geneva, Switzerland, 2009; Available online: https://www.unisdr.org/files/7817_UNISDRTerminologyEnglish.pdf (accessed on 12 February 2023).
- Duan, C.; Zhang, J.; Chen, Y.; Lang, Q.; Zhang, Y.; Wu, C.; Zhang, Z. Comprehensive Risk Assessment of Urban Waterlogging Disaster Based on MCDA-GIS Integration: The Case Study of Changchun, China. Remote Sens. 2022, 14, 3101. [Google Scholar] [CrossRef]
- Boni, G.; De Angeli, S.; Taramasso, A.C.; Roth, G. Remote Sensing-Based Methodology for the Quick Update of the Assessment of the Population Exposed to Natural Hazards. Remote Sens. 2020, 12, 3943. [Google Scholar] [CrossRef]
- Geiß, C.; Schauß, A.; Riedlinger, T.; Dech, S.; Zelaya, C.; Guzmán, N.; Hube, M.A.; Arsanjani, J.J.; Taubenböck, H. Joint use of remote sensing data and volunteered geographic information for exposure estimation: Evidence from Valparaíso, Chile. Nat. Hazards 2017, 86 (Suppl. 1), 81–105. [Google Scholar] [CrossRef]
- Bhuyan, K.; Van Westen, C.; Wang, J.; Meena, S.R. Mapping and characterising buildings for flood exposure analysis using open-source data and artificial intelligence. Nat. Hazards 2022, 1–31. [Google Scholar] [CrossRef]
- Ehrlich, D.; Melchiorri, M.; Florczyk, A.J.; Pesaresi, M.; Kemper, T.; Corbane, C.; Freire, S.; Schiavina, M.; Siragusa, A. Remote Sensing Derived Built-Up Area and Population Density to Quantify Global Exposure to Five Natural Hazards over Time. Remote Sens. 2018, 10, 1378. [Google Scholar] [CrossRef]
- Freire, S.; Florczyk, A.J.; Pesaresi, M.; Sliuzas, R. An Improved Global Analysis of Population Distribution in Proximity to Active Volcanoes, 1975–2015. ISPRS Int. J. Geo-Inf. 2019, 8, 341. [Google Scholar] [CrossRef]
- Torres, Y.; Arranz, J.J.; Gaspar-Escribano, J.M.; Haghi, A.; Martínez-Cuevas, S.; Benito, B.; Ojeda, J.C. Integration of LiDAR and multispectral images for rapid exposure and earthquake vulnerability estimation. Application in Lorca, Spain. Int. J. Appl. Earth Obs. Geoinf. 2019, 81, 161–175. [Google Scholar] [CrossRef]
- Jitt-Aer, K.; Wall, G.; Jones, D.; Teeuw, R. Use of GIS and dasymetric mapping for estimating tsunami-affected population to facilitate humanitarian relief logistics: A case study from Phuket, Thailand. Nat. Hazards 2022, 113, 185–211. [Google Scholar] [CrossRef]
- Gallina, V.; Torresan, S.; Critto, A.; Sperotto, A.; Glade, T.; Marcomini, A. A review of multi-risk methodologies for natural hazards: Consequences and challenges for a climate change impact assessment. J. Environ. Manag. 2016, 168, 123–132. [Google Scholar] [CrossRef]
- European Commission, Directorate-General for European Civil Protection and Humanitarian Aid Operations. Overview of Natural and Man-Made Disaster Risks the European Union May Face: 2020 Edition; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Fraser, S.; Jongman, B.; Balog, S.; Simpson, A.; Saito, K.; Himmelfarb, A. The Making of a Riskier Future: How Our Decisions Are Shaping Future Disaster Risk; Global Facility for Disaster Reduction and Recovery: Washington, DC, USA, 2016. [Google Scholar]
- United Nations Office for Disaster Risk Reduction (UNISDR). Sendai Framework for Disaster Risk Reduction 2015–2030; United Nations: Geneva, Switzerland, 2015. [Google Scholar]
- Santini, M.; Valentini, R. Predicting hot-spots of land use changes in Italy by ensemble forecasting. Reg. Environ. Chang. 2011, 11, 483–502. [Google Scholar] [CrossRef]
- Cremen, G.; Galasso, C.; McCloskey, J. Modelling and quantifying tomorrow’s risks from natural hazards. Sci. Total Environ. 2022, 817, 152552. [Google Scholar] [CrossRef]
- Song, Y.; Chen, B.; Kwan, M.P. How does urban expansion impact people’s exposure to green environments? A comparative study of 290 Chinese cities. J. Clean. Prod. 2020, 246, 119018. [Google Scholar] [CrossRef]
- Theobald, D.M.; Spies, T.; Kline, J.; Maxwell, B.; Hobbs, N.T.; Dale, V.H. Ecological support for rural land-use planning. Ecol. Appl. 2005, 15, 1906–1914. [Google Scholar] [CrossRef]
- Wang, S.W.; Gebru, B.M.; Lamchin, M.; Kayastha, R.B.; Lee, W.-K. Land Use and Land Cover Change Detection and Prediction in the Kathmandu District of Nepal Using Remote Sensing and GIS. Sustainability 2020, 12, 3925. [Google Scholar] [CrossRef]
- Gaur, S.; Singh, R. A Comprehensive Review on Land Use/Land Cover (LULC) Change Modeling for Urban Development: Current Status and Future Prospects. Sustainability 2023, 15, 903. [Google Scholar] [CrossRef]
- Huu, C.N.; Van, C.N.; My, T.N.N. Modeling land-use changes using logistic regression in Western Highlands of Vietnam: A case study of Lam Dong province. Agric. Nat. Resour. 2022, 56, 935–944. [Google Scholar] [CrossRef]
- Brown, D.G.; Goovaerts, P.; Burnicki, A.; Li, M.Y. Stochastic simulation of land-cover change using geostatistics and generalized additive models. Photogramm. Eng. Remote Sens. 2002, 68, 1051–1061. [Google Scholar]
- Kumar, S.; Radhakrishnan, N.; Mathew, S. Land use change modelling using a Markov model and remote sensing. Geomatics 2014, 5, 145–156. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, C.; Ma, S.; Yuan, H.; Gao, L.; Fan, W. Using Markov chains to analyze changes in wetland trends in arid Yinchuan Plain, China. Math. Comput. Model. 2011, 54, 924–930. [Google Scholar] [CrossRef]
- Singh, V.G.; Singh, S.K.; Kumar, N.; Singh, R.P. Simulation of land use/land cover change at a basin scale using satellite data and markov chain model. Geocarto Int. 2022, 37, 11339–11364. [Google Scholar] [CrossRef]
- Chasia, S.; Olang, L.O.; Sitoki, L. Modelling of land-use/cover change trajectories in a transboundary catchment of the Sio-Malaba-Malakisi Region in East Africa using the CLUE-s model. Ecol. Model. 2023, 476, 110256. [Google Scholar] [CrossRef]
- Islam, S.; Li, Y.; Ma, M.; Chen, A.; Ge, Z. Simulation and Prediction of the Spatial Dynamics of Land Use Changes Modelling Through CLUE-S in the Southeastern Region of Bangladesh. J. Indian Soc. Remote Sens. 2021, 49, 2755–2777. [Google Scholar] [CrossRef]
- Al-Darwish, Y.; Ayad, H.; Taha, D.; Saadallah, D. Predicting the future urban growth and it’s impacts on the surrounding environment using urban simulation models: Case study of Ibb city—Yemen. Alex. Eng. J. 2018, 57, 2887–2895. [Google Scholar] [CrossRef]
- Feng, Y.; Qi, Y. Modeling patterns of land use in Chinese cities using an integrated cellular automata model. ISPRS Int. J. Geo-Inf. 2018, 7, 403. [Google Scholar] [CrossRef]
- Kumar, V.; Agrawal, S. Urban modelling and forecasting of landuse using SLEUTH model. Int. J. Environ. Sci. Technol. 2022, 20, 6499–6518. [Google Scholar] [CrossRef]
- Saxena, A.; Jat, M.K. Land suitability and urban growth modeling: Development of SLEUTH-Suitability. Comput. Environ. Urban Syst. 2020, 81, 101475. [Google Scholar] [CrossRef]
- Dhanaraj, K.; Jain, G.V. Urban Growth Simulations in a Medium-Sized City of Mangaluru, India, Through CA-Based SLEUTH Urban Growth Model. J. Indian Soc. Remote Sens. 2022, 51, 497–517. [Google Scholar] [CrossRef]
- Sarica, G.M.; Zhu, T.; Jian, W.; Lo, E.Y.M.; Pan, T.C. Spatio-temporal dynamics of flood exposure in Shenzhen from present to future. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 1011–1024. [Google Scholar] [CrossRef]
- Clarke, K.C.; Johnson, J.M. Calibrating SLEUTH with big data: Projecting California’s land use to 2100. Comput. Environ. Urban Syst. 2020, 83, 101525. [Google Scholar] [CrossRef]
- Zhou, Y.; Varquez, A.C.; Kanda, M. High-resolution global urban growth projection based on multiple applications of the SLEUTH urban growth model. Sci. Data 2019, 6, 34. [Google Scholar] [CrossRef] [PubMed]
- Regmi, R.R.; Saha, S.K.; Subedi, D.S. Geospatial Analysis of Land Use Land Cover Change Modeling in Phewa Lake Watershed of Nepal by Using GEOMOD Model. Himal. Phys. 2017, 6, 65–72. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; de Noronha Vaz, E. Spatiotemporal simulation of urban growth patterns using agent-based modeling: The case of Tehran. Cities 2013, 32, 33–42. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, X.; Wang, L.; Zhou, Y.; Shu, B. Multi-agent based modeling of spatiotemporal dynamical urban growth in developing countries: Simulating future scenarios of Lianyungang city, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 63–78. [Google Scholar] [CrossRef]
- Li, F.; Li, Z.; Chen, H.; Chen, Z.; Li, M. An agent-based learning-embedded model (ABM-learning) for urban land use planning: A case study of residential land growth simulation in Shenzhen, China. Land Use Policy 2020, 95, 104620. [Google Scholar] [CrossRef]
- Maurya, N.K.; Rafi, S.; Shamoo, S. Land use/land cover dynamics study and prediction in jaipur city using CA markov model integrated with road network. GeoJournal 2023, 88, 137–160. [Google Scholar] [CrossRef]
- Beroho, M.; Briak, H.; Cherif, E.K.; Boulahfa, I.; Ouallali, A.; Mrabet, R.; Kebede, F.; Bernardino, A.; Aboumaria, K. Future Scenarios of Land Use/Land Cover (LULC) Based on a CA-Markov Simulation Model: Case of a Mediterranean Watershed in Morocco. Remote Sens. 2023, 15, 1162. [Google Scholar] [CrossRef]
- Hamad, R.; Balzter, H.; Kolo, K. Predicting Land Use/Land Cover Changes Using a CA-Markov Model under Two Different Scenarios. Sustainability 2018, 10, 3421. [Google Scholar] [CrossRef]
- Geoportale della Regione Calabria. Available online: http://geoportale.regione.calabria.it/ (accessed on 10 April 2023).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Frantz, D. FORCE—Landsat + Sentinel-2 Analysis Ready Data and Beyond. Remote Sens. 2019, 11, 1124. [Google Scholar] [CrossRef]
- Tassi, A.; Vizzari, M. Object-Oriented LULC Classification in Google Earth Engine Combining SNIC, GLCM, and Machine Learning Algorithms. Remote Sens. 2020, 12, 3776. [Google Scholar] [CrossRef]
- Liu, L.; Xiao, X.; Qin, Y.; Wang, J.; Xu, X.; Hu, Y.; Qiao, Z. Mapping Cropping Intensity in China Using Time Series Landsat and Sentinel-2 Images and Google Earth Engine. Remote Sens. Environ. 2020, 239, 111624. [Google Scholar] [CrossRef]
- Sentinel-2 Missions. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-2 (accessed on 14 April 2023).
- Database di Sintesi Nazionale. Available online: https://www.igmi.org/it/dbsn-database-di-sintesi-nazionale (accessed on 19 April 2023).
- Istituto Geografico Militare. Available online: https://www.igmi.org/it/descrizione-prodotti/cartografia-digitale/dtm-digital-terrain-model (accessed on 19 April 2023).
- OpenStreetMap. Available online: https://www.openstreetmap.org/#map=6/42.088/12.564 (accessed on 19 April 2023).
- 15° Censimento della Popolazione e delle Abitazioni. Available online: https://www.istat.it/it/censimenti-permanenti/censimenti-precedenti/popolazione-e-abitazioni/popolazione-2011 (accessed on 19 April 2023).
- PAI. Available online: https://www.distrettoappenninomeridionale.it/index.php/elaborati-di-piano-menu/ex-adb-calabria-menu (accessed on 19 April 2023).
- Francini, M.; Salvo, C.; Viscomi, A.; Vitale, A. A Deep Learning-Based Method for the Semi-Automatic Identification of Built-Up Areas within Risk Zones Using Aerial Imagery and Multi-Source GIS Data: An Application for Landslide Risk. Remote Sens. 2022, 14, 4279. [Google Scholar] [CrossRef]
- Francini, M.; Salvo, C.; Vitale, A. Combining Deep Learning and Multi-Source GIS Methods to Analyze Urban and Greening Changes. Sensors 2023, 23, 3805. [Google Scholar] [CrossRef]
- Semantic Segmentation Dataset. Available online: https://humansintheloop.org/semantic-segmentation-dataset/ (accessed on 10 April 2023).
- QGIS. 2023 QGIS User Guide. Available online: https://docs.qgis.org/3.22/it/docs/user_manual/ (accessed on 5 May 2023).
- Li, X.; Zhou, W.; Ouyang, Z. Forty years of urban expansion in Beijing: What is the relative importance of physical, socioeconomic, and neighborhood factors? Appl. Geogr. 2013, 38, 1–10. [Google Scholar] [CrossRef]
- Akdeniz, H.B.; Sag, N.S.; Inam, S. Analysis of land use/land cover changes and prediction of future changes with land change modeler: Case of Belek, Turkey. Environ. Monit. Assess. 2023, 195, 135. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, X.; Fu, Y.; Lu, Z.; Shen, X. Urban spatial growth modeling using logistic regression and cellular automata: A case study of Hangzhou. Ecol. Indic. 2020, 113, 106200. [Google Scholar] [CrossRef]
- Dadashpoor, H.; Azizi, P.; Moghadasi, M. Analyzing spatial patterns, driving forces and predicting future growth scenarios for supporting sustainable urban growth: Evidence from Tabriz metropolitan area, Iran. Sustain. Cities Soc. 2019, 47, 101502. [Google Scholar] [CrossRef]
- Ma, S.; Ai, B.; Jiang, H.; Cai, Y.; Xie, D. Exploring the growth pattern of urban agglomeration in the terminal urbanization stage by integrating inertial driving factors, spatial development strategy, and urbanization cycle. Ecol. Indic. 2023, 149, 110178. [Google Scholar] [CrossRef]
- Al-Shaar, W. Analyzing the effect size of urban growth driving factors: Application of multilayer-perceptron Markov-chain model for the Riyadh city. Model. Earth Syst. Environ. 2023, 1–10. [Google Scholar] [CrossRef]
- Kim, Y.; Newman, G.; Güneralp, B. A Review of Driving Factors, Scenarios, and Topics in Urban Land Change Models. Land 2020, 9, 246. [Google Scholar] [CrossRef]
- Seevarethnam, M.; Rusli, N.; Ling, G.H.T. Prediction of Urban Sprawl by Integrating Socioeconomic Factors in the Batticaloa Municipal Council, Sri Lanka. ISPRS Int. J. Geo-Inf. 2022, 11, 442. [Google Scholar] [CrossRef]
- Long, J.S. Regression Models for Categorical and Limited Dependent Variables; Sage: Thousand Oaks, CA, USA, 1997; Volume 7. [Google Scholar]
- MacCullagh, P.; Nelder, J.A. Generalized Linear Models; CRC Press: Boca Raton, FL, USA, 1989; Volume 37. [Google Scholar]
- Chang, X.; Zhang, F.; Cong, K.; Liu, X. Scenario simulation of land use and land cover change in mining area. Sci. Rep. 2021, 11, 12910. [Google Scholar] [CrossRef]
- SPSS Software. Available online: https://www.ibm.com/it-it/spss (accessed on 20 April 2023).
- Kohavi, R. A Study of Cross-validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI’95), Montreal, QC, Canada, 20–25 August 1995; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; Volume 2, pp. 1137–1143. [Google Scholar]
- García, S.; Herrera, F. An extension on “statistical comparisons of classifiers over multiple data sets” for all pairwise comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]
- Mahdianpari, M.; Salehi, B.; Rezaee, M.; Mohammadimanesh, F.; Zhang, Y. Very Deep Convolutional Neural Networks for Complex Land Cover Mapping Using Multispectral Remote Sensing Imagery. Remote Sens. 2018, 10, 1119. [Google Scholar] [CrossRef]
- Sharma, A.; Liu, X.; Yang, X.; Shi, D. A patch-based convolutional neural network for remote sensing image classification. Neural Netw. 2017, 95, 19–28. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Volume 1 (NIPS’12), Granada, Spain, 12–15 December 2011; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G. Rectified linear units improve Restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML 2010), Haifa, Israel, 21 June 2010; Fürnkranz, J., Joachims, T., Eds.; pp. 807–814. [Google Scholar]
- Boureau, Y.L.; Ponce, J.; Lecun, Y. A Theoretical Analysis of Feature Pooling in Visual Recognition. In Proceedings of the 27th International Conference on Machine Learning (ICML 2010), Haifa, Israel, 21 June 2010; Fürnkranz, J., Joachims, T., Eds.; pp. 111–118. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; Teh, Y.W., Titterington, M., Eds.; PMLR: Sardinia, Italy, 2010; Volume 9, pp. 249–256. [Google Scholar]
- Kim, J.H. Estimating classification error rate: Repeated cross-validation, repeated hold-out, and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. Available online: http://dblp.uni-trier.de/db/journals/csda/csda53.html#Kim09 (accessed on 24 July 2023). [CrossRef]
- Ghosh, D.; Yuan, Z. An improved model averaging scheme for logistic regression. J. Multivar. Anal. 2009, 100, 1670–1681. [Google Scholar] [CrossRef]
- Cascetta, E. Modelli di emissione e distribuzione degli spostamenti casa-lavoro nelle aree urbane di media dimensione: Aspetti metodologici e analisi sperimentali. In Proceedings of the III Convegno Nazionale del Progetto Finanziato Trasporti, Taormina, Italy, 1985. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Eyoh, A.; Olayinka, D.N.; Nwilo, P.; Okwuashi, O.; Isong, M.; Udoudo, D. Modelling and predicting future urban expansion of Lagos, Nigeria from remote sensing data using logistic regression and GIS. Int. J. Appl. 2012, 2, 58–71. [Google Scholar]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. Available online: https://pubmed.ncbi.nlm.nih.gov/843571/ (accessed on 24 July 2023). [CrossRef]
- Bajracharya, P.; Lippitt, C.D.; Sultana, S. Modeling urban growth and land cover change in Albuquerque using SLEUTH. Prof. Geogr. 2020, 72, 181–193. [Google Scholar] [CrossRef]
- Huang, K.; Li, X.; Liu, X.; Seto, K.C. Projecting global urban land expansion and heat island intensification through 2050. Environ. Res. Lett. 2019, 14, 114037. [Google Scholar] [CrossRef]
- Raduszynski, T.; Numada, M. Measure and spatial identification of social vulnerability, exposure and risk to natural hazards in Japan using open data. Sci. Rep. 2023, 13, 664. [Google Scholar] [CrossRef]
- Galderisi, A.; Limongi, G. A Comprehensive Assessment of Exposure and Vulnerabilities in Multi-Hazard Urban Environments: A Key Tool for Risk-Informed Planning Strategies. Sustainability 2021, 13, 9055. [Google Scholar] [CrossRef]
- Marin, G.; Modica, M. Socio-economic exposure to natural disasters. Environ. Impact Assess. Rev. 2017, 64, 57–66. [Google Scholar] [CrossRef]
- Li, K.; Feng, M.; Biswas, A.; Su, H.; Niu, Y.; Cao, J. Driving Factors and Future Prediction of Land Use and Cover Change Based on Satellite Remote Sensing Data by the LCM Model: A Case Study from Gansu Province, China. Sensors 2020, 20, 2757. [Google Scholar] [CrossRef]
- De Lotto, R.; Pietra, C.; Venco, E.M. Risk analysis: A focus on urban exposure estimation. In Proceedings of the Computational Science and Its Applications–ICCSA 2019: 19th International Conference, Saint Petersburg, Russia, 1–4 July 2019. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, W.; Xu, X. Changes of population, built-up land, and cropland exposure to natural hazards in China from 1995 to 2015. Int. J. Disaster Risk Sci. 2019, 10, 557–572. [Google Scholar] [CrossRef]
- Schumacher, I.; Strobl, E. Economic development and losses due to natural disasters: The role of hazard exposure. Ecol. Econ. 2011, 72, 97–105. [Google Scholar] [CrossRef]
- Freire, S.; Aubrecht, C. Integrating population dynamics into mapping human exposure to seismic hazard. Nat. Hazards Earth Syst. Sci. 2012, 12, 3533–3543. [Google Scholar] [CrossRef]
- Chen, Q.F.; Chen, Y.; Liu, J.I.E.; Chen, L. Quick and approximate estimation of earthquake loss based on macroscopic index of exposure and population distribution. Nat. Hazards 1997, 15, 215–229. [Google Scholar] [CrossRef]
- Ehrlich, D.; Kemper, T.; Pesaresi, M.; Corbane, C. Built-up area and population density: Two Essential Societal Variables to address climate hazard impact. Environ. Sci. Policy 2018, 90, 73–82. [Google Scholar] [CrossRef]
- Solórzano, J.V.; Mas, J.F.; Gao, Y.; Gallardo-Cruz, J.A. Land Use Land Cover Classification with U-Net: Advantages of Combining Sentinel-1 and Sentinel-2 Imagery. Remote Sens. 2021, 13, 3600. [Google Scholar] [CrossRef]
- Sarkar, A.; Chouhan, P. Modeling spatial determinants of urban expansion of Siliguri a metropolitan city of India using logistic regression. Model. Earth Syst. Environ. 2020, 6, 2317–2331. [Google Scholar] [CrossRef]
- Borzacchiello, M.T.; Nijkamp, P.; Scholten, H.J. A logistic regression model for explaining urban development on the basis of accessibility: A case study of Naples. Int. J. Environ. Sustain. Dev. 2009, 8, 300–313. [Google Scholar] [CrossRef]
- Hu, Z.; Lo, C.P. Modeling urban growth in Atlanta using logistic regression. Comput. Environ. Urban Syst. 2007, 31, 667–688. [Google Scholar] [CrossRef]
- Kucsicsa, G.; Grigorescu, I. Urban growth in the Bucharest metropolitan area: Spatial and temporal assessment using logistic regression. J. Urban Plan. Dev. 2018, 144, 05017013. [Google Scholar] [CrossRef]
- Achmad, A.; Hasyim, S.; Dahlan, B.; Aulia, D.N. Modeling of urban growth in tsunami-prone city using logistic regression: Analysis of Banda Aceh, Indonesia. Appl. Geogr. 2015, 62, 237–246. [Google Scholar] [CrossRef]
- Salem, M.; Bose, A.; Bashir, B.; Basak, D.; Roy, S.; Chowdhury, I.R.; Alsalman, A.; Tsurusaki, N. Urban Expansion Simulation Based on Various Driving Factors Using a Logistic Regression Model: Delhi as a Case Study. Sustainability 2021, 13, 10805. [Google Scholar] [CrossRef]
- Kim, Y.; Newman, G. Advancing scenario planning through integrating urban growth prediction with future flood risk models. Comput. Environ. Urban Syst. 2020, 82, 101498. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).