Abstract
In this work, Advanced SCATterometer (ASCAT) backscatter data are directly assimilated into the interactions between soil, biosphere, and atmosphere (ISBA) land surface model using Meteo-France’s global Land Data Assimilation System (LDAS-Monde) tool in order to jointly analyse soil moisture and leaf area index (LAI). For the first time, observation operators based on neural networks (NNs) are trained with ISBA simulations and LAI observations from the PROBA-V satellite to predict the ASCAT backscatter signal. The trained NN-based observation operators are implemented in LDAS-Monde, which allows the sequential assimilation of backscatter observations. The impact of the assimilation is evaluated over southwestern France. The simulated and analysed backscatter signal, surface soil moisture, and LAI are evaluated using satellite observations from ASCAT and PROBA-V as well as in situ soil moisture observations. An overall improvement in the variables is observed when comparing the analysis with the open-loop simulation. The impact of the assimilation is greater over agricultural areas.
1. Introduction
In the context of global warming, the frequency and intensity of extreme events such as agricultural droughts and heatwaves are increasing [1,2]. These events have significant environmental, economic, and social impacts, with droughts affecting more than 2 billion people and causing an estimated 11 million deaths in the 20th century [3]. Land surface variables (LSVs), such as soil moisture, soil temperature, and vegetation leaf area index (LAI) control terrestrial carbon, water, and energy fluxes at the interface with the atmosphere. Monitoring and prediction of LSVs is needed to better understand the impacts of extreme weather events [4,5].
A common method of monitoring LSVs is through Earth observation (EO). Observations from the fleet of Earth observation satellites allow LSVs to be tracked on a global scale. Satellite instruments provide measurements, such as radiance or reflectance, that must be processed to obtain retrievals such as surface soil moisture (SSM) [6] or leaf area index (LAI). The spatial and temporal resolution of these retrieval products is limited, and land surface models (LSMs) are often used operationally to produce continuous simulations [7]. LSMs were originally developed to provide boundary conditions for atmospheric models, but are now used for the monitoring and forecasting of LSVs [8,9,10]. They can be coupled with other components of Earth system models, such as atmospheric and oceanic models [9,11,12].
The integration of EOs into LSMs can be achieved by data assimilation (DA) using a land data assimilation system (LDAS). The DA methods allow to constrain the LSMs and to improve their performance [13,14]. LDAS-Monde [15,16,17,18] has been developed by the Centre National de Recherches Météorologiques (CNRM). LDAS-monde is an offline system (not coupled with the atmosphere) that allows the sequential joint assimilation of SSM and LAI at different spatial scales (from local to global). It uses a simplified extended Kalman filter (EKF) to constrain the LSVs of the ISBA (interactions between soil, biosphere, and atmosphere) LSM [19,20]. Several studies have shown the benefit of assimilating SSM products derived from either active or passive microwave sensors to improve the representation of soil moisture in LSMs [21,22,23,24]. More recently, there has been increased interest in the assimilation of vegetation-related variables such as LAI and microwave vegetation optical depth (VOD) [15,25,26,27].
The advantage of assimilating SSM and LAI retrievals is that these quantities are simulated by ISBA. For other observations, such as radar backscatter and microwave brightness temperatures, specific observation operators must be coupled with ISBA. The rationale for moving toward the assimilation of satellite radiance products is that (1) they may contain useful information that is lost in the production of retrievals and (2) the characterization of observational errors is easier. For example, the C-band radar backscatter coefficients from the Advanced SCATterometer (ASCAT) are used to produce SSM products [6]. During the SSM retrieval process, the vegetation information content of the backscatter signal can be retrieved, e.g., [28]. Direct assimilation of ASCAT backscatter observations instead of SSM retrievals could prove advantageous as it could provide information on (1) SSM, (2) vegetation stress related to drought soil conditions in the root zone, and (3) vegetation dynamics through the microwave vegetation optical depth [29,30]. Since ASCAT backscatter is not simulated by ISBA, an observation operator is needed to link the ISBA simulations to these observations. Typically, observation operators are based on physical equations using radiative transfer algorithms. Due to their computational cost, semi-empirical models can be used instead [31,32,33]. Several studies have shown that the use of neural networks (NNs) in retrieval algorithms is an efficient way to process radiance. SSM can be retrieved using microwave brightness temperatures using this method [11,34,35,36].
The main objectives of this study were to (1) develop a novel approach to simulate ASCAT backscatter observations using NNs as observation operators, (2) couple the observations operators with the ISBA LSM, (3) analyse soil moisture and LAI by assimilating ASCAT backscatter observations, and (4) evaluate the analysis. After a training phase of the NNs, the NN-based observation operator is implemented in LDAS-Monde and the impact of assimilating ASCAT backscatter observations in ISBA is evaluated over southwestern France.
The paper is organized as follows. Section 2 presents the different components of LDAS-Monde, starting with the interactive vegetation version of the ISBA LSM, as well as the data and methods used for NN training and assimilation. Details of the experimental setup and the specifics of the study area are also given in this section. Section 3 presents the results of the calibration of the NN hyperparameters and of the validation of the NN outputs. The impact of the assimilation on the ISBA simulations is shown. The results are discussed in Section 4. Section 5 summarizes the conclusions of this work.
2. Materials and Methods
2.1. The ISBA LSM
ISBA is an LSM that includes several options of varying complexity. It simulates the evolution of LSVs such as soil moisture, soil temperature or vegetation biomass within the SURFEX (SURface Externalisée) modelling platform [37] developed by the CNRM (http://www.umr-cnrm.fr/surfex, accessed on 2 August 2023). It calculates the transfer of water, carbon and energy between the land surface and the atmosphere. A simple version of ISBA is used for operational numerical weather prediction at Meteo-France [38,39]. For climate modelling, a more sophisticated version capable of representing the carbon cycle is used [40,41]. The version of the model that is used for this study is ISBA-A-gs, a CO2-responsive version of ISBA capable of representing photosynthesis, plant growth and senescence. Phenology is driven entirely by photosynthesis, using a simple allocation scheme. Net leaf CO2 assimilation is used to represent the incoming carbon flux for leaf biomass growth. A photosynthesis-dependent leaf mortality rate is calculated. The balance between the leaf carbon uptake and the leaf mortality rate results in an increase or a decrease in leaf biomass [15]. Leaf biomass is converted to LAI using a fixed value of specific leaf area (SLA) per plant functional type. The biochemical A-gs model described in [42] is used, together with advanced representations of the photosynthesis response to drought for low vegetation and for trees ([43] and [44], respectively). The evolution of the vertical soil moisture and soil temperature profiles is calculated using a multilayer diffusion scheme [45,46]. The soil is discretized in:
- 14 layers for soil temperature, down to 12 m (0–0.01 m, 0.01–0.04 m, 0.04–0.10 m, 0.1–0.2 m, 0.2–0.4 m), 0.4–0.6 m, 0.6–0.8 m, 0.8–1.0 m, 1.0–1.5 m, 1.5–2.0 m, 2–3 m, 3–5 m, 5–8 m and 8–12 m)
- 8 to 10 layers for soil moisture (same depths as for soil temperature), down to 1 m and 2 m depending on vegetation characteristics.
Surface soil evaporation is represented along with root water uptake related to leaf transpiration. A root density profile is used to calculate the water uptake and to calculate a weighted average soil water stress index. This index is then used to represent the effect of drought on photosynthesis. Agricultural practices such as irrigation and crop rotation are not represented in this version of the model
In ISBA, each grid cell is composed of four tiles (city, ocean, lake, and land). The diversity of land surfaces is represented by combining 12 generic surface patches: bare soil and deserts, rocks and urban areas, permanent snow and ice, broadleaf trees, coniferous trees, tropical broadleaf evergreen trees, C3 crops, C4 crops, irrigated crops, C3 grasslands, C4 grasslands, and wetlands. The global database ECOCLIMAP-II provides the information for each patch [47]. The grid cell LAI simulated by ISBA-A-gs is calculated by averaging the LAI of the different vegetation types weighted by the fractional area they cover. The model can be operated at different spatial scales, from local to global, and at different spatial resolutions.
2.2. LDAS-Monde
LDAS-Monde [15] is a sequential data assimilation system embedded in the SURFEX modelling platform in an offline configuration (without interaction with the atmosphere). It allows the joint assimilation of global satellite SSM and LAI products into ISBA-A-gs. The assimilation of satellite products with LDAS-Monde is performed using an EKF [48] and allows the direct update of eight control variables of the ISBA model, including soil moisture from 1 to 100 cm depth (corresponding to layers 2 to 8) and LAI, with a 24 h assimilation window [26]. Data assimilation is performed independently for each grid cell, and no spatial covariance is considered. A two-step sequential approach is used: a prior forecast step and an analysis step. The initial states are propagated using ISBA during the prior forecast step. The forecast is then corrected during the analysis step by assimilating the observations. The dynamic link between the observations and the prognostic variables is established by the observation operator. The Jacobian of the observation operator propagates the information from the observations to the control variables via finite difference calculations.
2.3. ASCAT Data
This paper focuses on the assimilation of ASCAT backscatter observations. ASCAT is a C-band (5.255 GHz) radar installed on the MetOp satellites. The ASCAT instruments use vertically polarized antennae for both transmitting and receiving signals. Backscatter measurements are gathered at three azimuth angles: 45°, 90°, and 135°. While the primary purpose of ASCAT is to measure wind speed and direction over oceans, these measurements can also be linked to other geophysical variables. In particular, over land, vegetation and surface soil moisture both affect the observed backscatter values. Retrieval methods have been developed to derive a soil moisture index, resulting in the creation of a surface soil moisture database [6]. While the assimilation of this SSM retrieval into the ISBA model has demonstrated benefits [15,18], the vegetation information contained in the backscatter observations remains untapped. A normalized ASCAT backscatter product at an angle of incidence of 40° with a spatial resolution of 25 km is available together with the SSM products disseminated by EUMETSAT. Since the original observations are at different angles of incidence, this product is obtained by interpolation using a linear regression between the measured backscatter values and the angle of incidence. The resulting interpolated product is called σ040.
An ASCAT SSM product is used in this study for model and data assimilation benchmarking purposes. The near-surface soil wetness index product SWI-001 is used as a proxy for the SSM. SWI-001 is a filtered version of the original SSM retrievals. A recursive exponential filter [49] with a time scale of 1 day is used. In order to assimilate this product without introducing biases, a seasonal rescaling to the model climatology is performed [21,24,50,51]. This product is available daily with a spatial resolution of 0.1°.
All data sets are interpolated from their respective native grids to a 0.25° resolution grid using a bilinear interpolation as per [52].
2.4. LAI Data
PROBA-V LAI retrievals from the Copernicus Global Land Service (CGLS) version 1 (GEOV1) with a spatial resolution of 1 km × 1 km are used. The LAI retrievals are derived from reflectance by using a machine learning algorithm [53]. This dataset is available at a 1 km resolution with observations every 10 days.
2.5. Observation Operator Based on Neural Networks
The observation operator serves as a link between the observations and the LSVs generated by the ISBA model. In this study, a novel observation operator based on NNs is developed. Previous research has shown that multi-layer feed-forward NNs, such as multi-layer perceptrons, are powerful tools for establishing statistical relationships between satellite observations and soil moisture [34,54]. The NNs used in this study are trained to simulate the σ040 observations using three predictors derived from ISBA outputs and satellite observations:
- Model soil moisture for the 0.01–0.04 m layer (WG2).
- Model soil temperature for the same layer.
- PROBA-V LAI provided by CGLS.
The inclusion of observed LAI as a predictor is crucial as it captures additional information related to agricultural practices that are not explicitly represented in the ISBA simulations. All the predictors are preprocessed using the common z-score normalization technique. First, the NNs are trained using σ040 data corresponding to a training period. Second, the trained NNs are implemented in LDAS-monde as observation operators and the assimilation is performed for a test period different from the training period. The assimilation of σ040 is performed for the test period. For the assimilation, the mean ASCAT σ040 observation error is set to 0.33 dB, based on [31].
Overall, this approach allows the assimilation of σ040 into ISBA, using the trained NN-based observation operators to effectively assimilate these data and improve the estimation of LSVs. The architecture of the neural network (NN) is chosen through a thorough analysis of the influence of the hyperparameters on the predictions. The influence of each hyperparameter is evaluated individually for all 247 grid cells within the study area.
2.6. In Situ Soil Moisture Observations
The Soil Moisture Observing System—Meteorological Automatic Network Integrated Application (SMOSMANIA) is a network of weather stations with frequency domain reflectometry soil moisture sensors installed along a 400 km Mediterranean–Atlantic transect in southern France that have been providing continuous measurements of soil moisture at different soil depths every 12 min from 2006 to the present [55]. The stations are equipped with soil moisture probes at four depths (0.05, 0.10, 0.20 and 0.30 m) and are separated by an average distance of 45 km. For this study, only the 14 stations located within the study area in southwestern France (SBR, URG, CRD, PRG, CDM, LHS, SVN, MNT, SFL, LZC, MTM, NBN, PZN, PRD) were considered, and are shown in Figure 1. The in situ SSM observations at 0.05 m depth are used to validate the SSM simulations.
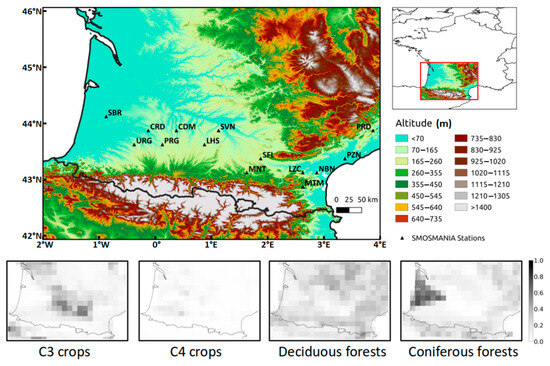
Figure 1.
Geographic altitude map of the domain of study from the SRTM 90 m digital elevation data (top). The black triangles indicate the locations of the SMOSMANIA stations. Fractional land occupation maps from the ECOCLIMAP II database (bottom).
2.7. Experimental Setup and Assessment
In this study, version 8.1 of SURFEX is used in the offline mode. The ISBA LSM is forced with the ERA5 atmospheric reanalysis [56,57], which is available globally from 1979 to the present with an hourly frequency and a horizontal resolution of 31 km. The ERA5 atmospheric variables are interpolated to the regular ISBA 0.25° × 0.25° grid using a bilinear interpolation. The study area (Figure 1) covers southwestern France and extends from 42.0°N to 46.0°N latitude and 2.0°W to 4.0°E longitude. This area was selected in part because of the wide variety of vegetation types present: grasslands, coniferous trees, deciduous broadleaf trees, C3 crops (mostly wheat and barley) and C4 crops (mostly maize). A period of 12 years, from 2007 to 2018, is considered. The period is divided in two parts. A training period, from 2007 to 2014 (8 years), is used to train the NN-based observation operator. Keras algorithms (https://keras.io/, accessed on 2 August 2023) with stochastic gradient descent using the Adam optimizer [58] are used to optimize the NN. The Relu activation function is used. The test period from 2015 to 2018 (4 years) is used to validate the NN and the analysis (Table 1). Masks for frozen soils, snow, complex topography, water bodies and urban areas are applied to both the model and the satellite data using information from ECOCLIMAP-II. As a result, 247 grid cells are considered.

Table 1.
Numerical experiments performed in this study.
Three configurations of LDAS-Monde are used for the comparison (Table 1):
- Open loop (OL), a 12-year ISBA run without assimilation performed after a 20-fold spin-up of the initial year—2007.
- A 4-year conventional simplified extended Kalman filter analysis based on the assimilation of the ASCAT SWI-001 product and LAI (EKF_SWI_LAI).
- A novel configuration based on the assimilation of σ040 (EKF).
The two 4-year data assimilation runs start from the same initial conditions on 1 January 2015, obtained from the OL simulation. They follow the same framework as described in Albergel et al. [15] and subsequent studies in terms of specified background error covariance matrix and run perturbations. The NN training is based on OL simulations, PROBA-V LAI observations, and ASCAT σ040 observations from 2007 to 2014.
NN performance is evaluated using the root-mean-square deviation (RMSD) of simulated vs. observed σ040 values and the Pearson correlation coefficient (R). The influence of each predictor is evaluated by imposing a constant mean value of each predictor, one at a time, on the simulations of the previously trained NN. The resulting RMSD maps indicate the geographic impact of the temporal variability of a given predictor on the simulated σ040.
3. Results
3.1. NN Training and Architecture Selection
We use a learning rate of 0.001 and 250 epochs to train the NN (Table 2). The choice of these values is based on the optimal result obtained after training while avoiding overfitting. The performance of the model does not improve for larger values of the number of epochs. Preliminary tests show that one NN per grid cell is necessary. A single NN for the whole domain or for specific vegetation types within the domain is not able to represent the spatial and temporal variability of σ040.

Table 2.
Hyper-parameters selected for all 247 individual neural networks.
Figure 2 shows the statistical distribution of the RMSD of the simulated σ040 after training the NNs. This figure shows that a single layer consisting of 40 neurons is sufficient to achieve a median RMSD value comparable to the observation error of ASCAT (0.33 dB). Further increasing the number of neurons only slightly decreases the RMSD, while adding hidden layers does not improve the σ040 predictions. The NNs with two or more hidden layers, especially those with 150 neurons per layer or more, show increased RMSD values, indicating potential overfitting during the training phase. Consequently, a single layer with 40 neurons is determined to be the optimal choice. The remaining hyperparameter values are selected using the same methodology, and their specific values can be found in Table 2.
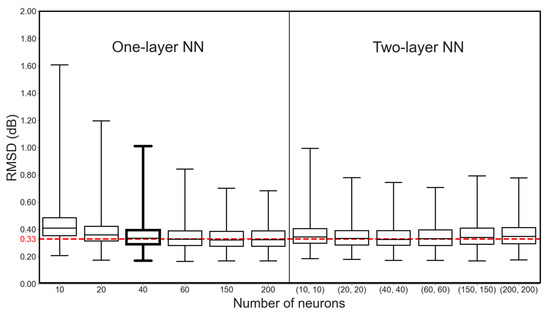
Figure 2.
Predicted σ040 RMSD values for 12 NN configurations (box plots) for the 2007–2014 training period for one-layer (left) and two-layer (right) NN configurations. The box plots show the RMSD computed for all the selected grid cells in the domain of study between the predicted σ040 values and the ASCAT observations. The chosen configuration (one-layer NN with 40 neurons) is in bold. Whiskers in box plots correspond to minimum, 25%, 50%, 75% percentiles, maximum values. The mean ASCAT σ040 observation error (0.33 dB) is indicated (red dashed line). The number of neurons per layer is indicated (x-axis).
3.2. NN Predictor Sensitivity
A sensitivity analysis was performed on the NNs to assess the influence of different predictors for each grid cell. By “neutralizing” individual predictors and examining their impact on the σ040 predictions (Section 2.7), the analysis provides insight into the LSVs that drive σ040 according to the land cover classes presented in Figure 1. The results shown in Figure 3 indicate that the predictions of σ040 are primarily influenced by the model’s SSM, with higher RMSD values observed in agricultural areas and over the Les Landes forest. In particular, the Les Landes forest, which is dominated by conifers, shows a particularly strong influence. In addition, the neutralization of the PROBA-V LAI has a noticeable impact on the σ040 predictions, especially over C3 agricultural areas. Although the surface soil temperature has a relatively smaller influence on the predictions, it still contributes to the predictions to some extent, especially over agricultural areas.
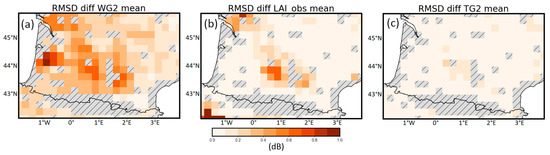
Figure 3.
Predictor sensitivity analysis of the 1 layer, 40 neuron NNs for the 2007–2014 training period. Three experiments are shown. For each experiment, one input variable is neutralized by using its mean value for the prediction of σ040. The maps show the difference between the σ040 RMSD calculated using all 3 predictors and the RMSD calculated with one neutralized predictor for the test period, in dB. The three experiments show the effects of neutralizing (a) SSM, (b) the interpolated PROBA-V LAI observations and (c) the surface soil temperature.
3.3. NN Validation
The validation of the NN observation operator is performed over the 2015–2018 test period, based on SSM and soil temperature simulations from the OL numerical experiment (Table 1) and from PROBA-V LAI observations. Figure 4 shows that the RMSD of the simulated σ040 is often in the range of 0.3 to 0.4 dB (for about 45% of the grid cells). This is in agreement with the mean ASCAT observational error of 0.33 dB. In the central region of the domain, specifically between the Condom (CDM) and Savenès (SVN) stations and around the Saint-Félix de Lauragais (SFL) station, some larger RMSD values in the range of 0.5 to 0.6 dB can be observed. RMSD values greater than 0.4 dB can be observed in about 15% of the grid cells, corresponding to agricultural areas consisting mainly of C3 crops (Figure 1).
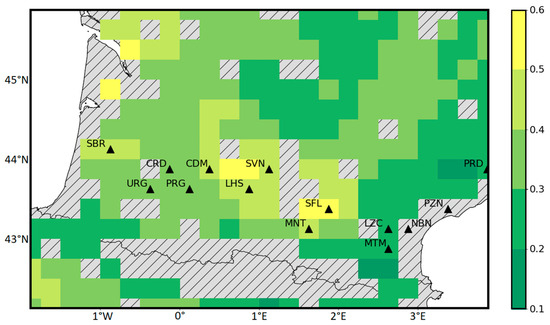
Figure 4.
Map of the RMSD of σ040 predictions (in dB) from the 1-layer, 40-neuron NNs using OL SSM and soil temperature as input together with PROBA-V LAI observations, for the 2015–2018 test period with respect to the ASCAT σ040 observations. Values are given for 247 grid cells. Hashed areas represent the zones that are masked. Triangles show the position of the SMOSMANIA stations.
3.4. Impact of Assimilating σ040 Observations
Once the trained NNs are coupled with the ISBA LSM, the ASCAT σ040 observations can be assimilated into the ISBA LSM (EKF experiment in Table 1) during the 2015–2018 test period. The σ040, LAI, and SSM simulations of the OL and EKF experiments are compared with the ASCAT σ040, PROBA-V LAI, and in situ SSM observations, respectively. The SWI-001 retrievals are also used to evaluate the analysed SSM. In both the OL and EKF experiments, the LAI values used as input to the NNs are simulated by the ISBA model.
3.4.1. Simulated σ040
The predicted OL and EKF σ040 values are compared with the ASCAT satellite observations to assess the impact of the assimilation. The EKF σ040 predictions (Figure 5a) show similar and sometimes even smaller RMSD values compared to the σ040 predictions based on the observed PROBA-V LAI (Figure 4). The previously largest RMSD values in the central region of the domain have decreased and are now closer to the observational error of ASCAT, with hardly any grid cells showing RMSD values above 0.4 dB.
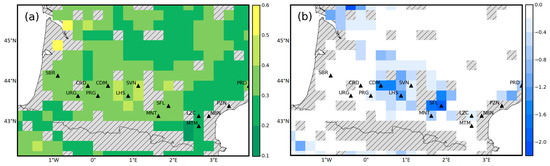
Figure 5.
RMSD (in dB) of the EKF σ040 predictions with respect to the ASCAT σ040 observations (a) and difference between the latter and the RMSD (in dB) of the OL σ040 predictions with respect to the ASCAT σ040 observations (b).
Figure 5b shows the difference in RMSD between the EKF and OL σ040 predictions, showing a reduction in RMSD across all grid cells in the study area. The most significant impact of the assimilation is observed in the central and northwestern regions of the domain. As mentioned in the previous section, these areas are characterized by C3 crops.
A closer examination of the grid cells corresponding to the 12 SMOSMANIA stations, which correspond to the grid cells where σ040 is assimilated (Table 3), shows that the assimilation has the greatest influence on the CDM, Lahas (LHS), Montaut (MNT), SFL and Prades-le-Lez (PRD) stations, with notable RMSD differences of −1.44, −1.29, −0.62, −1.96 and −0.67 dB, respectively. In addition, Table 3 highlights the positive impact of the assimilation on R, which is greater for all stations. In fact, the latter five stations have an R difference greater than 0.4, indicating a marked improvement in the simulated σ040 values resulting from the assimilation of σ040 observations. This shows that the assimilation is able to properly integrate σ040 observations into the ISBA LSM.

Table 3.
Statistics for EKF and OL σ040 predictions over grid cells covering SMOSMANIA stations, from west (top) to east (bottom). Scores are calculated with respect to the ASCAT σ040 observations. RMSD differences smaller than −0.5 dB and R differences larger or equal to 0.4 are in bold.
3.4.2. Simulated LAI
The EKF LAI RMSD, as shown in Figure 6a, is lower than 1 m2m−2 in the plains. Conversely, higher RMSD values are observed in the medium-altitude mountainous areas of the Massif Central and the Pyrenees (northeastern and southern parts of the domain, respectively). The map illustrating the difference in RMSD between the OL and the EKF LAI (Figure 6b) shows a reduction in RMSD over most of the domain. Similar to σ040, the LAI over agricultural areas is more affected by the assimilation. It can be noted that a slight increase in RMSD can be observed, especially in the southwestern part of the domain, in Spain.
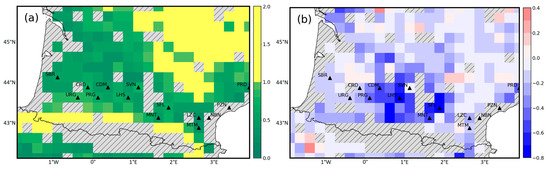
Figure 6.
RMSD (in m2m−2) of the EKF LAI predictions with respect to the PROBA-V LAI observations (a) and difference between the latter and the RMSD (in m2m−2) of the OL LAI predictions with respect to the PROBA-V LAI observations (b).
Table 4 shows that—similarly to the σ040 results in Table 3—the EKF vs. OL RMSD difference for LAI is negative for all stations considered. The agricultural areas experience the largest impact of the assimilation, with the MNT, CDM, LHS, and SFL stations showing a significant decrease in RMSD (<−0.5 m2m−2). Overall, there is an increase in R for all stations, except SBR, SVN, and SFL. However, despite the negative effect on R, assimilation still has a positive effect on the RMSD for these three stations. For SVN, the decrease in R is particularly strong (−0.23). SVN also shows the smallest decrease in RMSD (−0.08 m2m−2). A closer look at the LAI time series shows that in 2015, the annual cycle of the EKF LAI over SVN differs from the observations: the spring LAI peak is missed and the LAI is overestimated from October to December 2015. This difference is not observed for the other 3 years of the test period.

Table 4.
Statistics for EKF and OL LAI predictions over grid cells covering SMOSMANIA stations, from west (top) to east (bottom). Scores are calculated with respect to the PROBA-V LAI observations. RMSD differences smaller than −0.5 m2m−2 are in bold.
The LAI time series for the CDM station (Figure 7) shows that the annual cycle and the interannual variability of LAI are poorly captured by the OL. The OL shows a systematic positive bias in the summer, reaching 2 m2m−2 in the summer of 2018. This positive bias is also evident at the end of 2016, where a peak in LAI is predicted but not observed.
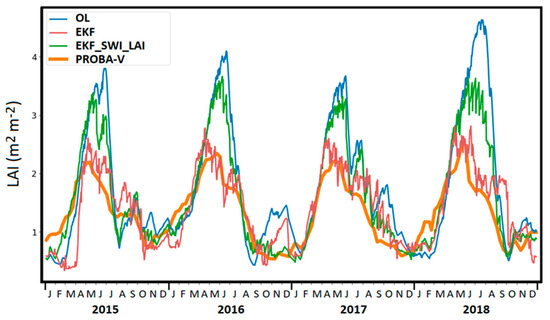
Figure 7.
LAI time series for the grid cell containing the station of CDM, from 2015 to 2018. The time series are shown for the PROBA-V LAI observations, the OL, EKF and EKF_SWI_LAI experiments (orange, blue, red and green lines, respectively).
The joint assimilation of LAI and SSM helps to correct the bias at the end of 2016 and brings the simulated results closer to the observed values during the summer. However, the positive bias is still present in summer. The assimilation of σ040 is more efficient in improving the modelled LAI, bringing it much closer to the observations compared to the OL and EKF_LAI_SWI experiments. The summer bias is almost completely reduced.
3.4.3. Simulated SSM
The difference map of the SSM temporal correlations between SWI-001 and the EKF SSM (Figure 8) shows that for most grid cells, larger R values are obtained after assimilation of σ040. The largest differences (>0.08) are observed in the agricultural area between the CDM and SVN stations and around SFL. However, small reductions in the correlations, smaller than −0.02, can be observed near the PRD station.
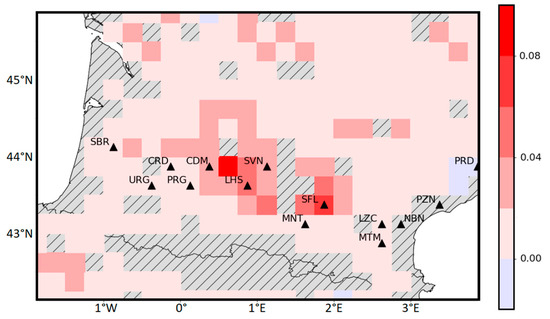
Figure 8.
Map of the difference in R values of SWI-001 vs. EKF SSM and SWI-001 vs. OL SSM.
The comparison of the OL, EKF, and EKF_SWI_LAI SSM values with the in situ SSM observations (Figure 9) shows that the assimilation of σ040 leads to a slight improvement in the 25th and 50th percentiles of the monthly R statistical distribution across stations and years. The median R value for EKF SSM consistently shows better results than OL and EKF_SWI_LAI in all months, except September and November, with the most significant effect observed in December, where all stations experience an improvement. The R 25% percentile is systematically better for EKF than for the other two experiments. For the three experiments, the lowest median values of R are observed in July, August and October. For these months, all stations except URG, LHS, SFL and PRD can present monthly R values smaller than −0.1.
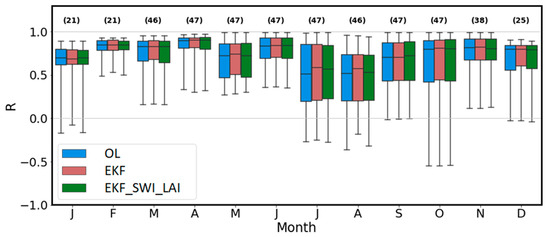
Figure 9.
Monthly statistical distribution of R values between in situ SSM and the simulated SSM for the OL, EKF, and EKF_SWI_LAI experiments (blue, brown, green bars, respectively), for the 12 SMOSMANIA stations listed in Table 3 and Table 4 and for the 4 years of the 2015–2018 test period (maximum of 48 R values), from January to December. Whiskers in box plots correspond to minimum, 25%, 50%, 75% percentiles, maximum values. The number of values is in parentheses.
4. Discussion
4.1. Assimilating Microwave Retrievals or Radiance?
The studies conducted by [11,34] demonstrate that a single NN with only one layer and five neurons can be used to retrieve SSM from multi-angular, dual-polarized SMOS L-band brightness temperatures (Tbs) as input. The single NN is trained to mimic the European Centre for Medium Range Weather Forecasts (ECMWF) SSM simulations using Tbs as input. The retrieved SSM can then be assimilated into the ECMWF land surface model without having to seasonally rescale the assimilated SSM observations to fit the physical range of the model SSM. In this study, we show that a more complex approach is required to assimilate ASCAT σ040, since we have to use a 40-neuron NN per grid cell. Assimilating microwave radiance (σ040 values in this study) instead of assimilating SSM retrievals is more complicated and at the same time more advantageous. The additional complexity is related to the difficulty of simulating a very complex microwave signal from the limited information content of LSMs [59]. Microwave radiance is influenced by factors that are not at all or not fully represented by LSMs, such as changes in the spatial extent of water bodies, subsurface scattering, surface roughness, or the presence of metal reflectors. This makes the prediction of radiance challenging. Using one NN per grid cell as a forward operator is one way to overcome this problem. Another difficulty is that the trained NN needs to be coupled with the LSM. This study shows that this is feasible and that σ040 can be sequentially assimilated in the ISBA LSM. The advantage of assimilating σ040 instead of SSM retrievals is that σ040 observations contain additional valuable vegetation information that would be missing in SSM retrievals. Our results show that using this methodology, LAI can be analysed together with SSM and root zone soil moisture (Figure 7).
4.2. What Are the Biophysical Drivers of ASCAT σ040?
Accurate prediction of radiance also requires the selection of appropriate predictors for the NNs. To aid in this selection process, we conducted a sensitivity analysis, which showed that σ040 predictions are mainly influenced by SSM, as well as LAI (Figure 3). The LAI influence on σ040 is more pronounced in agricultural areas and the assimilation of σ040 has the potential to improve the LAI simulations over these areas. The ISBA LSM is not a crop model, and agricultural practices such as crop rotation are not represented. Our results show that the assimilation of σ040 has the ability to improve LAI over agricultural areas (Figure 6). The analysis also shows that soil temperature has a smaller effect, but still shows a slight influence, especially over agricultural areas (Figure 3). The influence of soil temperature may be due to its influence on leaf water potential [60] and on below-ground hydraulic conductivity [61]. In addition to its effect on the root biological activity, soil temperature has a direct effect on water surface tension and on gas volume in soils [62]. Shan et al. [59] investigated a broader range of predictors, including interception water storage by vegetation. We evaluated the use of interception water storage and found that this variable has a rather neutral effect on the performance of the NNs, but tends to induce instabilities in the data assimilation process.
4.3. Assimilating Microwave Radiance or LAI?
Examining the results of the assimilation of ASCAT σ040 (Figure 6 and Figure 7), it is clear that the assimilation has a positive influence on the simulated LAI. This effect is particularly noticeable in the agricultural regions. The slight increases in RMSD that are sometimes observed in Figure 6, especially in Spain, can be explained by the fact that this area can be very dry in summer and is subject to subsurface scattering. Karst aquifers can also contribute to the degradation of the radar signal and the subsequent increase in RMSD [63]. Overall, Figure 6 shows a significant improvement in the LAI RMSD, which corresponds to the almost complete rectification of the systematic positive bias observed during summer in the LAI simulation of the OL run over these areas. This suggests that the σ040 product contains valuable information about agricultural activity that is missing from the OL ISBA simulations. This information is effectively captured by the NNs and used by LDAS-Monde to constrain the LSM. Furthermore, the EKF run shows superior performance compared to the EKF_SWI_LAI run in both LAI and SSM predictions. These improvements can be attributed, at least in part, to the higher frequency of σ040 observations compared to the PROBA-V LAI observations (daily vs. one observation every 10 days, respectively). This is shown in Figure 7 for the period June–July 2018. The abrupt changes in the LAI values analysed by EKF_SWI_LAI, observed every 10 days, are caused by the assimilation of LAI observations that are smaller than the modelled ones. The assimilation of daily σ040 values produces a smoother LAI. The ISBA version we used did not represent crop phenology or irrigation. Further work is needed to assess the impact of assimilating ASCAT σ040 over cropland when this functionality is enabled [64].
Finally, Figure 6 shows that the EKF LAI predictions are less accurate over mountainous areas (Massif Central and Pyrenees), with RMSD values exceeding 1 m2m−2. This could be due to (1) the mismatch between the ASCAT σ040 spatial resolution and the complex terrain and (2) the lower penetration depth within the vegetation canopy over the deciduous broadleaf forests present in these areas (Figure 1). In a data assimilation study over the continental United States, Seo et al. [65] found that topographic complexity can limit the usefulness of ASCAT data.
5. Conclusions
A new methodology for the assimilation of C-band ASCAT radar backscatter observations (σ040) into the ISBA land surface model is applied to a case study in southwestern France. This approach is made possible by the development of a new observation operator based on local neural networks (one per grid cell). First, the local NNs are trained to predict σ040 from PROBA-V LAI observations and model outputs of surface soil moisture (SSM) and soil temperature. The trained NNs are very efficient in predicting σ040, with RMSD values over the validation period close to the observation error of σ040 (0.33 dB). Once trained, the NNs are implemented as observation operators in the LDAS-Monde land data assimilation system. The assimilation of σ040 alone leads to an improvement in the simulated LAI and SSM. The most significant improvements occur over agricultural areas, some of which consist of C3 crops such as straw cereals. Using the PROBA-V LAI observations as a reference, the simulated LAI shows strong improvements in summer, with a correction of the positive bias caused by the lack of crop rotation representation. The comparison with a classical joint assimilation of PROBA-V LAI and SSM retrievals shows that better LAI predictions are obtained when assimilating σ040, possibly due to the more frequent ASCAT observations. Improvements in the SSM simulations are also observed when compared to ASCAT SSM retrievals. Correlations with in situ SSM observations also show an improvement with respect to the open loop and to the joint assimilation of PROBA-V LAI and SSM retrievals. The use of NN observation operators appears promising, and our results open the way for the assimilation of other radiance satellite products.
Author Contributions
Conceptualization, all authors; methodology, T.C., G.C., B.B., N.R.-F. and J.-C.C.; investigation, T.C., B.B., N.R.-F. and J.-C.C.; formal analysis, T.C.; supervision, J.-C.C. and N.R.-F.; writing—original draft preparation, T.C.; writing—review and editing, J.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
The PhD thesis of Timothée Corchia was funded by Météo-France and by CNES, France (Centre National d’Etudes Spatiales). This research received funding from the European Union Horizon 2020 Research and Innovation programme (grant agreement 958927 (CoCO2)) and Horizon Europe (grant agreement 101082194 (CORSO)).
Data Availability Statement
The PROBA-V LAI product is available from the CGLS portal (https://land.copernicus.eu/global/products/lai, accessed on 2 August 2023). The ASCAT σ040 is available from the EUMETSAT HSAF service (https://doi.org/10.15770/EUM_SAF_H_0009, accessed on 2 August 2023). The SMOSMANIA in situ soil moisture data are available from the International Soil Moisture Network (ISMN) portal (https://ismn.earth/, accessed on 2 August 2023).
Acknowledgments
The authors would like to thank the Copernicus Global Land Service for providing the satellite-derived LAI products and EUMETSAT HSAF for providing the ASCAT σ040.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the writing of the manuscript.
References
- Samaniego, L.; Thober, S.; Kumar, R.; Wanders, N.; Rakovec, O.; Pan, M.; Zink, M.; Sheffield, J.; Wood, E.F.; Marx, A. Anthropogenic Warming Exacerbates European Soil Moisture Droughts. Nat. Clim. Chang. 2018, 8, 421–426. [Google Scholar] [CrossRef]
- Grillakis, M.G. Increase in severe and extreme soil moisture droughts for Europe under climate change. Sci. Total Environ. 2019, 660, 1245–1255. [Google Scholar] [CrossRef] [PubMed]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Climatol. 2014, 34, 2792–2804. [Google Scholar] [CrossRef]
- Di Napoli, C.; Pappenberger, F.; Cloke, H.L. Verification of heat stress thresholds for a health-based heatwave definition. J. Appl. Meteorol. Climatol. 2019, 58, 1177–1194. [Google Scholar] [CrossRef]
- Beillouin, D.; Schauberger, B.; Bastos, A.; Ciais, P.; Makowski, D. Impact of extreme weather conditions on European crop production in 2018. Philos. Trans. R. Soc. B 2020, 375, 20190510. [Google Scholar] [CrossRef] [PubMed]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Balsamo, G.; Agustì-parareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Blyth, E.; Bousserez, N.; Boussetta, S.; Brown, A.; et al. Satellite and in situ observations for advancing global Earth surface modelling: A review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef]
- Mucia, A.; Bonan, B.; Zheng, Y.; Albergel, C.; Calvet, J.-C. From monitoring to forecasting land surface conditions using a land data assimilation system: Application over the Contiguous United States. Remote Sens. 2020, 12, 2020. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.; de Rosnay, P.; Albergel, C.; Richaume, P.; Aires, F.; Prigent, C.; Kerr, Y. SMOS neural network soil moisture data assimilation in a land surface model and atmospheric impact. Remote Sens. 2019, 11, 1334. [Google Scholar] [CrossRef]
- Séférian, R.; Nabat, P.; Michou, M.; Saint-Martin, D.; Voldoire, A.; Colin, J.; Decharme, B.; Delire, C.; Berthet, S.; Chevallier, M.; et al. Evaluation of CNRM Earth system model, CNRM-ESM2-1: Role of Earth system processes in present-day and future climate. J. Adv. Model. Earth Syst. 2019, 11, 4182–4227. [Google Scholar] [CrossRef]
- Kumar, S.; Kolassa, J.; Reichle, R.; Crow, W.; de Lannoy, G.; de Rosnay, P.; MacBean, N.; Girotto, M.; Fox, A.; Quaife, T.; et al. An agenda for land data assimilation priorities: Realizing the promise of terrestrial water, energy, and vegetation observations from space. J. Adv. Model. Earth Syst. 2022, 14, e2022MS003259. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Bechtold, M.; Albergel, C.; Brocca, L.; Calvet, J.-C.; Carrassi, A.; Crow, W.T.; de Rosnay, P.; Durand, M.; Forman, B.; et al. Perspective on satellite-based land data assimilation to estimate water cycle components in an era of advanced data availability and model sophistication. Front. Water 2022, 4, 981745. [Google Scholar] [CrossRef]
- Albergel, C.; Munier, S.; Jennifer Leroux, D.; Dewaele, H.; Fairbairn, D.; Lavinia Barbu, A.; Gelati, E.; Dorigo, W.; Faroux, S.; Meurey, C.; et al. Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX-v8.0: LDAS-Monde assessment over the Euro-Mediterranean area. Geosci. Model Dev. 2017, 10, 3889–3912. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Munier, S.; Calvet, J.C.; Munoz-Sabater, J.; De Rosnay, P.; Balsamo, G. ERA-5 and ERA-Interim driven ISBA land surface model simulations: Which one performs better? Hydrol. Earth Syst. Sci. 2018, 22, 3515–3532. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Bonan, B.; Zheng, Y.; Munier, S.; Balsamo, G.; de Rosnay, P.; Muñoz-Sabater, J.; Calvet, J.C. Monitoring and forecasting the impact of the 2018 summer heatwave on vegetation. Remote Sens. 2019, 11, 520. [Google Scholar] [CrossRef]
- Bonan, B.; Albergel, C.; Zheng, Y.; Lavinia Barbu, A.; Fairbairn, D.; Munier, S.; Calvet, J.C. An ensemble square root filter for the joint assimilation of surface soil moisture and leaf area index within the land data assimilation system LDAS-Monde: Application over the Euro-Mediterranean region. Hydrol. Earth Syst. Sci. 2020, 24, 325–347. [Google Scholar] [CrossRef]
- Noilhan, J.; Mahfouf, J.F. The ISBA land surface parameterisation scheme. Glob. Planet. Chang. 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Calvet, J.C.; Noilhan, J.; Roujean, J.L.; Bessemoulin, P.; Cabelguenne, M.; Olioso, A.; Wigneron, J.P. An interactive vegetation SVAT model tested against data from six contrasting sites. Agric. For. Meteorol. 1998, 92, 73–95. [Google Scholar] [CrossRef]
- Draper, C.S.; Mahfouf, J.F.; Walker, J.P. An EKF assimilation of AMSR-E soil moisture into the ISBA land surface scheme. J. Geophys. Res. Atmos. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Draper, C.; Mahfouf, J.F.; Calvet, J.C.; Martin, E.; Wagner, W. Assimilation of ASCAT near-surface soil moisture into the SIM hydrological model over France. Hydrol. Earth Syst. Sci. 2011, 15, 3829–3841. [Google Scholar] [CrossRef]
- Draper, C.S.; Reichle, R.H.; De Lannoy, G.J.M.; Liu, Q. Assimilation of passive and active microwave soil moisture retrievals. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Drusch, M.; Wood, E.F.; Gao, H. Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture. Geophys. Res. Lett. 2005, 32, 32–35. [Google Scholar] [CrossRef]
- Mucia, A.; Bonan, B.; Albergel, C.; Zheng, Y.; Calvet, J.C. Assimilation of passive microwave vegetation optical depth in LDAS-Monde: A case study over the continental USA. Biogeosciences 2022, 19, 2557–2581. [Google Scholar] [CrossRef]
- Barbu, A.L.; Calvet, J.C.; Mahfouf, J.F.; Lafont, S. Integrating ASCAT surface soil moisture and GEOV1 leaf area index into the SURFEX modelling platform: A land data assimilation application over France. Hydrol. Earth Syst. Sci. 2014, 18, 173–192. [Google Scholar] [CrossRef]
- Kumar, S.V.; Holmes, T.R.; Bindlish, R.; de Jeu, R.; Peters-Lidard, C. Assimilation of vegetation optical depth retrievals from passive microwave radiometry. Hydrol. Earth Syst. Sci. 2020, 24, 3431–3450. [Google Scholar] [CrossRef]
- Vreugdenhil, M.; Hahn, S.; Melzer, T.; Bauer-Marschallinger, B.; Reimer, C.; Dorigo, W.; Wagner, W. Characteristing vegetation dynamics over Australia with ASCAT. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2240–2248. [Google Scholar] [CrossRef]
- Pfeil, I.; Vreugdenhil, M.; Hahn, S.; Wagner, W.; Strauss, P.; Blöschl, G. Improving the seasonal representation of ASCAT soil moisture and vegetation dynamics in a temperate climate. Remote Sens. 2018, 10, 1788. [Google Scholar] [CrossRef]
- Liu, X.; Wigneron, J.-P.; Fan, L.; Frappart, F.; Ciais, P.; Baghdadi, N.; Moisy, C. ASCAT IB: A radar-based vegetation optical depth retrieved from the ASCAT scatterometer satellite. Remote Sens. Environ. 2021, 264, 112587. [Google Scholar] [CrossRef]
- Lievens, H.; Martens, B.; Verhoest, N.E.C.; Hahn, S.; Reichle, R.H.; Miralles, D.G. Assimilation of global radar backscatter and radiometer brightness temperature observations to improve soil moisture and land evaporation estimates. Remote Sens. Environ. 2017, 189, 194–210. [Google Scholar] [CrossRef]
- Rains, D.; Lievens, H.; De Lannoy, G.J.M.; McCabe, M.F.; de Jeu, R.A.M.; Miralles, D.G. Sentinel-1 backscatter assimilation using support vector regression or the water cloud model at European soil moisture sites. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Shamambo, D.C. Assimilation of Satellite Data for Water Resources Monitoring over the Euro-Mediterranean Area. Ph.D. Thesis, Université de Toulouse, Toulouse, France, 2020. Available online: http://thesesups.ups-tlse.fr/4766/1/2020TOU30143.pdf (accessed on 2 August 2023).
- Rodríguez-Fernández, N.J.; Aires, F.; Richaume, P.; Kerr, Y.H.; Prigent, C.; Kolassa, J.; Cabot, F.; Jiménez, C.; Mahmoodi, A.; Drusch, M. Soil moisture retrieval using neural networks: Application to SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5991–6007. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.J.; Kerr, Y.H.; van der Schalie, R.; Al-Yaari, A.; Wigneron, J.P.; de Jeu, R.; Richaume, P.; Dutra, E.; Mialon, A.; Drusch, M. Long term global surface soil moisture fields using an SMOS-trained neural network applied to AMSR-E data. Remote Sens. 2016, 8, 959. [Google Scholar] [CrossRef]
- Aires, F.; Weston, P.; de Rosnay, P.; Fairbairn, D. Statistical approaches to assimilate ASCAT soil moisture information—I. Methodologies and first assessment. Q. J. R. Meteorol. Soc. 2021, 147, 1823–1852. [Google Scholar] [CrossRef]
- Masson, V.; Le Moigne, P.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F.; et al. The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of Earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef]
- Seity, Y.; Brousseau, P.; Malardel, S.; Hello, G.; Bénard, P.; Bouttier, F.; Lac, C.; Masson, V. The AROME-France Convective-Scale Operational Model. Mon. Weather Rev. 2011, 139, 976–991. [Google Scholar] [CrossRef]
- Bouyssel, F.; Berre, L.; Bénichou, H.; Chambon, P.; Girardot, N.; Guidard, V.; Loo, C.; Mahfouf, J.-F.; Moll, P.; Payan, C.; et al. The 2020 Global Operational NWP Data Assimilation System at Météo-France. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. IV); Park, S.K., Xu, L., Eds.; Springer: Cham, Switzerland, 2022; pp. 645–664. [Google Scholar] [CrossRef]
- Decharme, B.; Delire, C.; Minvielle, M.; Colin, J.; Vergnes, J.P.; Alias, A.; Saint-Martin, D.; Séférian, R.; Sénési, S.; Voldoire, A. Recent changes in the ISBA-CTRIP land surface system for use in the CNRM-CM6 climate model and in global off-line hydrological applications. J. Adv. Model. Earth Syst. 2019, 11, 1207–1252. [Google Scholar] [CrossRef]
- Delire, C.; Séférian, R.; Decharme, B.; Alkama, R.; Calvet, J.C.; Carrer, D.; Gibelin, A.L.; Joetzjer, E.; Morel, X.; Rocher, M.; et al. The global land carbon cycle simulated with ISBA-CTRIP: Improvements over the last decade. J. Adv. Model. Earth Syst. 2020, 12, 1–31. [Google Scholar] [CrossRef]
- Jacobs, C.M.J.; Van Den Hurk, B.J.J.M.; De Bruin, H.A.R. Stomatal behaviour and photosynthetic rate of unstressed grapevines in semi-arid conditions. Agric. For. Meteorol. 1996, 80, 111–134. [Google Scholar] [CrossRef]
- Calvet, J.C.; Noilhan, J. From near-surface to root-zone soil moisture using year-round data. J. Hydrometeorol. 2000, 1, 393–411. [Google Scholar] [CrossRef]
- Calvet, J.C.; Rivalland, V.; Picon-Cochard, C.; Guehl, J.M. Modelling forest transpiration and CO2 fluxes—Response to soil moisture stress. Agric. For. Meteorol. 2004, 124, 143–156. [Google Scholar] [CrossRef]
- Boone, A.; Masson, V.; Meyers, T.; Noilhan, J. The influence of the inclusion of soil freezing on simulations by a soil-vegetation-atmosphere transfer scheme. J. Appl. Meteorol. 2000, 39, 1544–1569. [Google Scholar] [CrossRef]
- Decharme, B.; Boone, A.; Delire, C.; Noilhan, J. Local evaluation of the Interaction between Soil Biosphere Atmosphere soil multilayer diffusion scheme using four pedotransfer functions. J. Geophys. Res. 2011, 116, D20126. [Google Scholar] [CrossRef]
- Faroux, S.; Kaptué Tchuenté, A.T.; Roujean, J.-L.; Masson, V.; Martin, E.; Le Moigne, P. ECOCLIMAP-II/Europe: A twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models. Geosci. Model Dev. 2013, 6, 563–582. [Google Scholar] [CrossRef]
- Mahfouf, J.-F.; Bergaoui, K.; Draper, C.; Bouyssel, C.; Taillefer, F.; Taseva, L. A comparison of two offline soil analysis schemes for assimilation of screen-level observations. J. Geophys. Res. 2009, 114, D08105. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, 2–5. [Google Scholar] [CrossRef]
- Albergel, C.; Zheng, Y.; Bonan, B.; Dutra, E.; Rodríguez-Fernández, N.; Munier, S.; Draper, C.; De Rosnay, P.; Muñoz-Sabater, J.; Balsamo, G.; et al. Data assimilation for continuous global assessment of severe conditions over terrestrial surfaces. Hydrol. Earth Syst. Sci. 2020, 24, 4291–4316. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part1: Principles of development and droduction. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Calvet, J.; Roujean, J.; Zhang, S.; Maurel, W.; Piguet, B.; Barrié, J.; Bouhours, G.; Couzinier, J.; Garrouste, O.; Girres, S.; et al. METEOPOLE-FLUX: An observatory of terrestrial water, energy, and CO2 fluxes in Toulouse. Geophys. Res. Abstr. 2016, 18, 2264. [Google Scholar]
- Hersbach, H.; Rosnay, P.; Bell, B.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Alonso-Balmaseda, M.; Balsamo, G.; Bechtold, P.; et al. Operational global reanalysis: Progress, future directions and synergies with NWP. ERA Rep. Ser. 2018, 27, 1–63. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar] [CrossRef]
- Shan, X.; Steele-Dunne, S.; Huber, M.; Hahn, S.; Wagner, W.; Bonan, B.; Albergel, C.; Calvet, J.-C.; Ku, O.; Georgievska, S. Towards constraining soil and vegetation dynamics in land surface models: Modeling ASCAT backscatter incidence-angle dependence with a Deep Neural Network. Remote Sens. Environ. 2022, 279, 113116. [Google Scholar] [CrossRef]
- Ameglio, T.; Morizet, J.; Cruiziat, P.; Martignac, M.; Bodet, C.; Raynaud, H. The effects of root temperature on water flux, potential and root resistance in sunflower. Agronomie 1990, 10, 331–340. [Google Scholar] [CrossRef]
- Lintunen, A.; Paljakka, T.; Salmon, Y.; Dewar, R.; Riikonen, A.; Hölttä, T. The influence of soil temperature and water content on belowground hydraulic conductance and leaf gas exchange in mature trees of three boreal species. Plant Cell Environ. 2020, 43, 532–547. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, H.; Yu, Y.; Guo, L.; Zhao, W.; Yetemen, O. Revisiting soil water potential: Towards a better understanding of soil and plant interactions. Water 2022, 14, 3721. [Google Scholar] [CrossRef]
- Wagner, W.; Lindorfer, R.; Melzer, T.; Hahn, S.; Bauer-Marschallinger, B.; Morrison, K.; Calvet, J.C.; Hobbs, S.; Quast, R.; Greimeister-Pfeil, I.; et al. Widespread occurrence of anomalous C-band backscatter signals in arid environments caused by subsurface scattering. Remote Sens. Environ. 2022, 276, 113025. [Google Scholar] [CrossRef]
- Druel, A.; Munier, S.; Mucia, A.; Albergel, C.; Calvet, J.-C. Implementation of a new crop phenology and irrigation scheme in the ISBA land surface model using SURFEX_v8.1. Geosci. Model Dev. 2022, 15, 8453–8471. [Google Scholar] [CrossRef]
- Seo, E.; Lee, M.-I.; Reichle, R.H. Assimilation of SMAP and ASCAT soil moisture retrievals into the JULES land surface model using the Local Ensemble Transform Kalman Filter. Remote Sens. Environ. 2021, 253, 112222. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).