Comparison of Machine Learning Models to Predict Lake Area in an Arid Area
Abstract
:1. Introduction
2. Materials and Methods
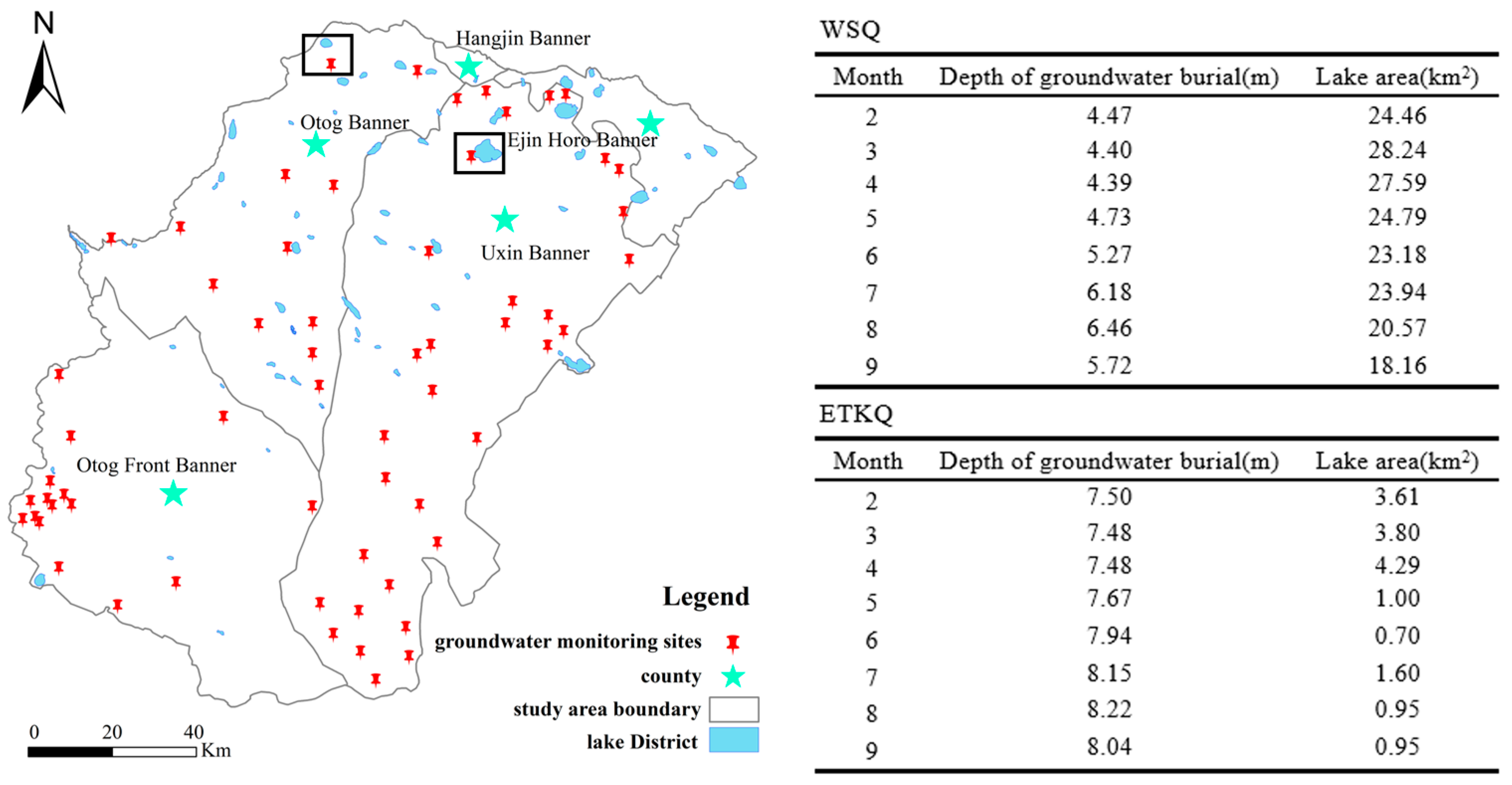
2.1. Study Area
2.2. Acquisition and Processing of Remote Sensing Data
2.2.1. Lake Extraction
2.2.2. NDVI Data
2.2.3. LUCC Data
2.3. Acquisition and Processing of Meteorological Data
2.4. SPEI Calculation
- (1)
- The calculation process of the SPEI involves four steps, as outlined by [35]. First, the climate level measure () is determined, representing the difference between precipitation () and potential evapotranspiration ().where is calculated using the Thornthwaite method in Section 2.3.
- (2)
- Next, a cumulative climate water balance series is established for different time scales (), typically in months, and n is the number of calculations, using Equation (7). This series considers the accumulated deviations from normal conditions over the specified time scale.
- (3)
- To create the data series, a log-logistic probability density function is fitted using Equation (8), with parameters α, β, and γ estimated through the L-moment parameter estimation method. The resulting cumulative probability (Equation (9)) represents the likelihood of exceeding the determined moisture gain or loss.
- (4)
- Finally, the cumulative probability densities are transformed to a standard normal distribution using Equation (10) to obtain the SPEI time series of change. The parameter W in the equation has a value of , while the other constant terms (, , , , , ) are assigned values of 2.515517.
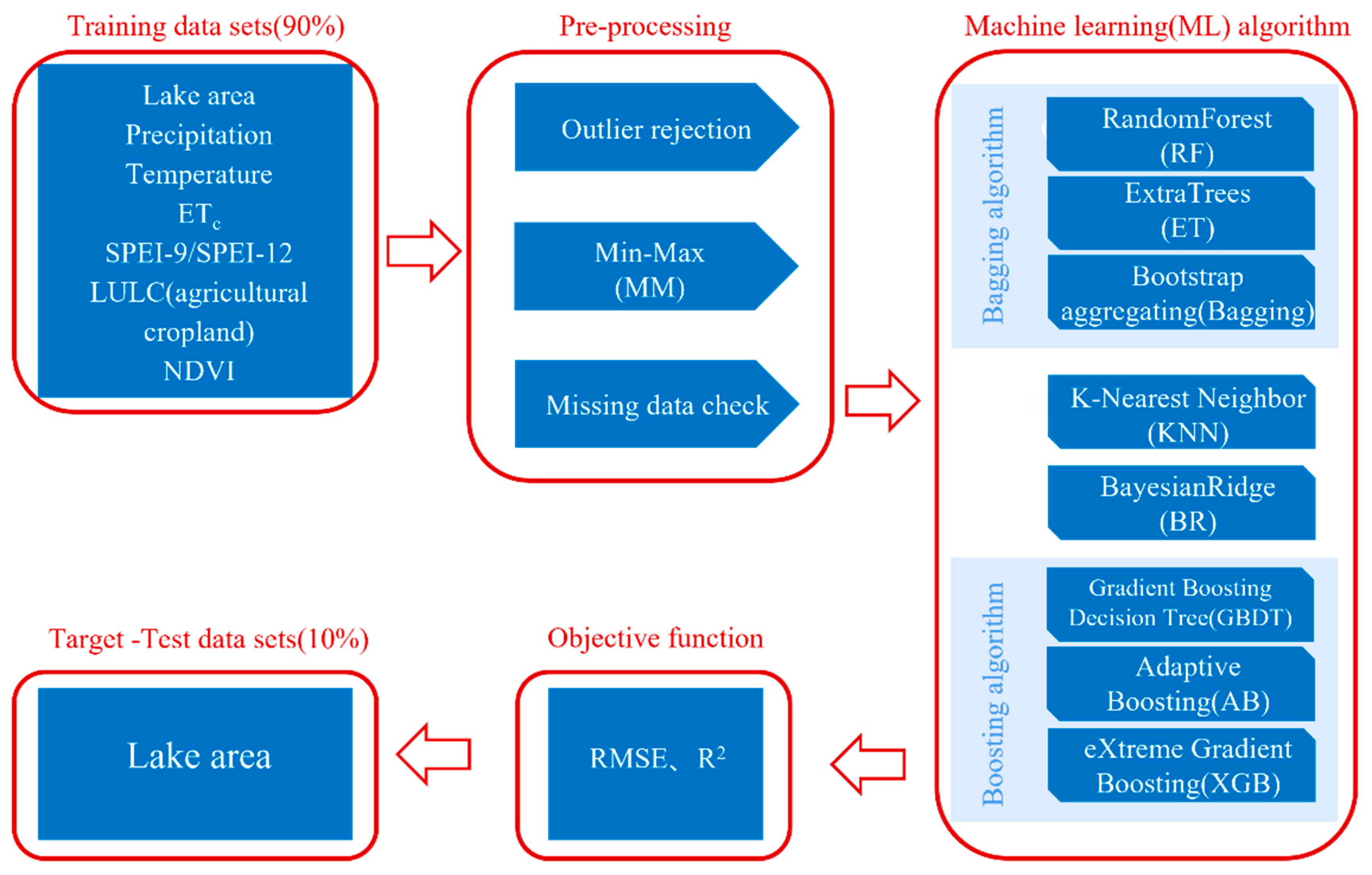
2.5. Development of ML Model to Predict Lake Area
2.5.1. Input Variables of ML Model
2.5.2. ML Algorithm
2.5.3. Training and Testing of ML Methods
2.5.4. Model Validation
- (1)
- Root mean square error or RMSE (km2):where in and are the actual and predicted areas of the ith lake, respectively, and is the total number of lakes. The greater the model prediction error, the greater the .
- (2)
- Coefficient of determination (R2):where is the average predicted lake area. R2 shows the degree of co-linearity between the observed and simulated time series and has a range of 0.0–1.0, with higher values indicating a higher degree of co-linearity.
- (3)
- weights averaging:Under weights averaging, the weight of the ith model () is estimated as [41]:where is the of the ith model and is the number of calibration samples.where and are the actual and predicted lake areas; and are the means for and ; and and are the corresponding variances and
- (4)
- Ratio of performance to deviation ():The formula of is as follows:where is the ratio of standard deviation and is the root mean square error.
3. Results
3.1. Lake Area Accuracy Assessment
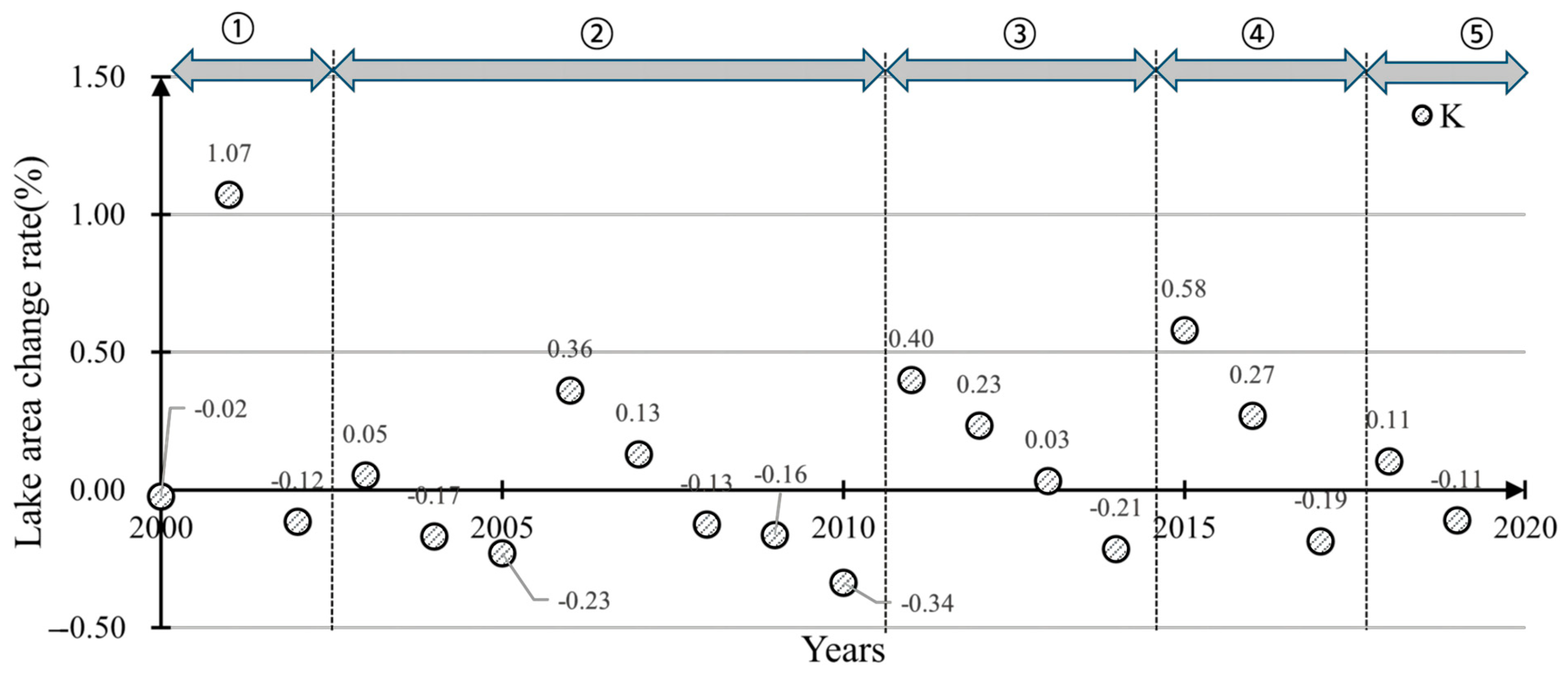
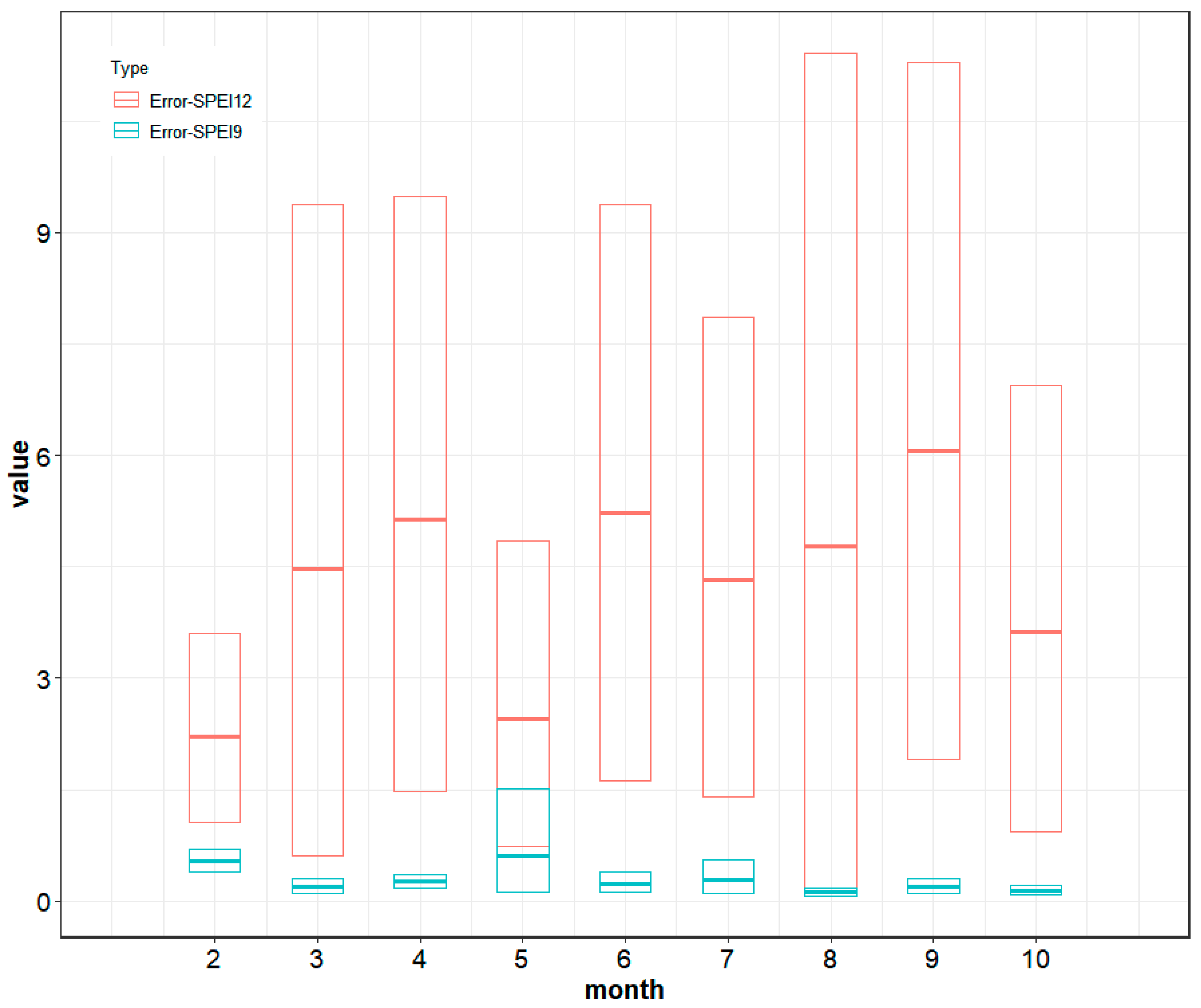
3.2. SPEI Time Scale Decisions
3.3. The Performance of the ML Algorithm
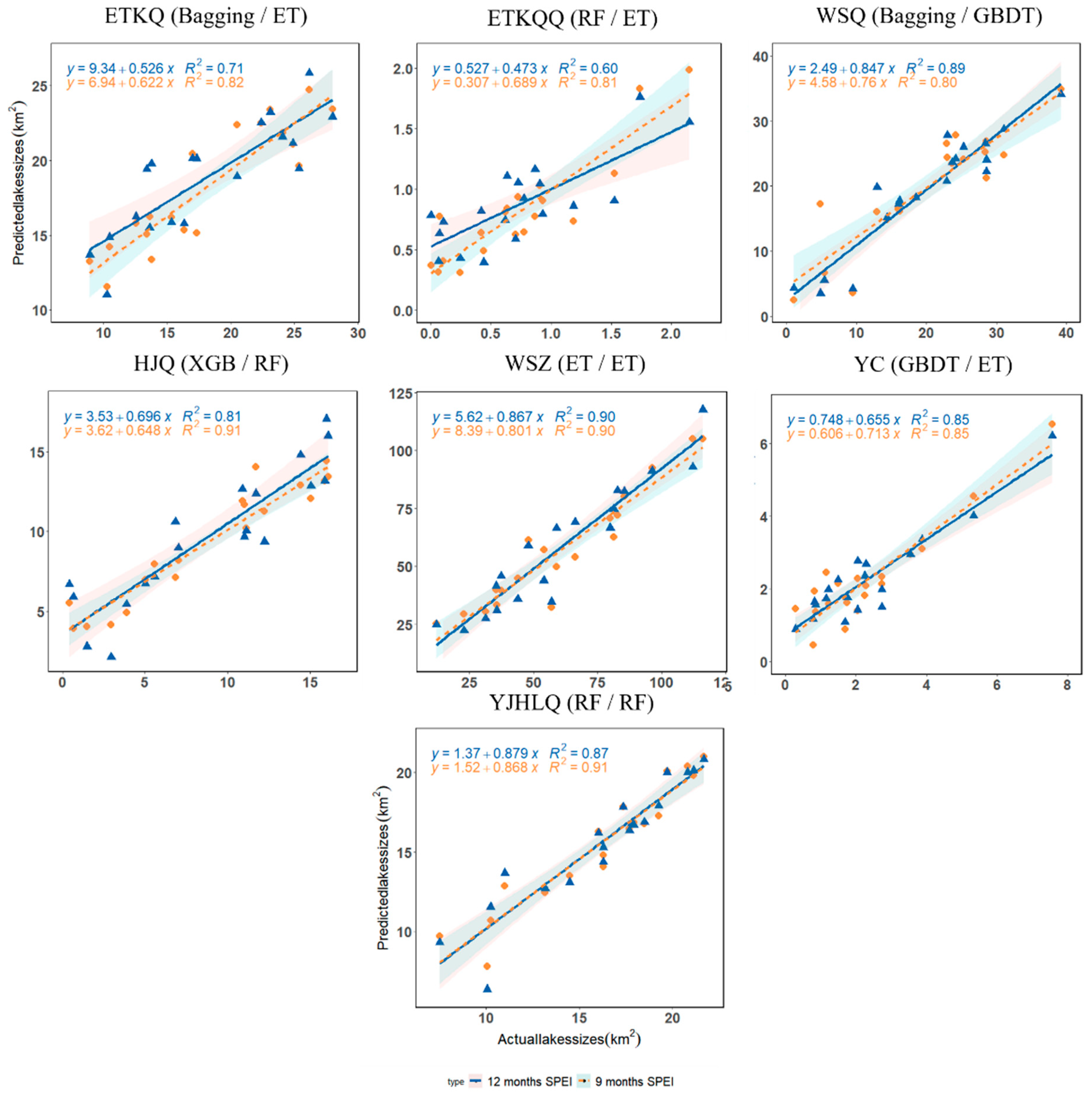
3.4. Performance of MLSPEI-9 and MLSPEI-12 Model to Estimate Lake Area
4. Discussion
4.1. Advantages of ML in Regression Analysis
4.2. Variation in the Performance of Different MLs in Different Regions
4.3. The Determination of Input Factors Is Key to the Accuracy of the Prediction Results
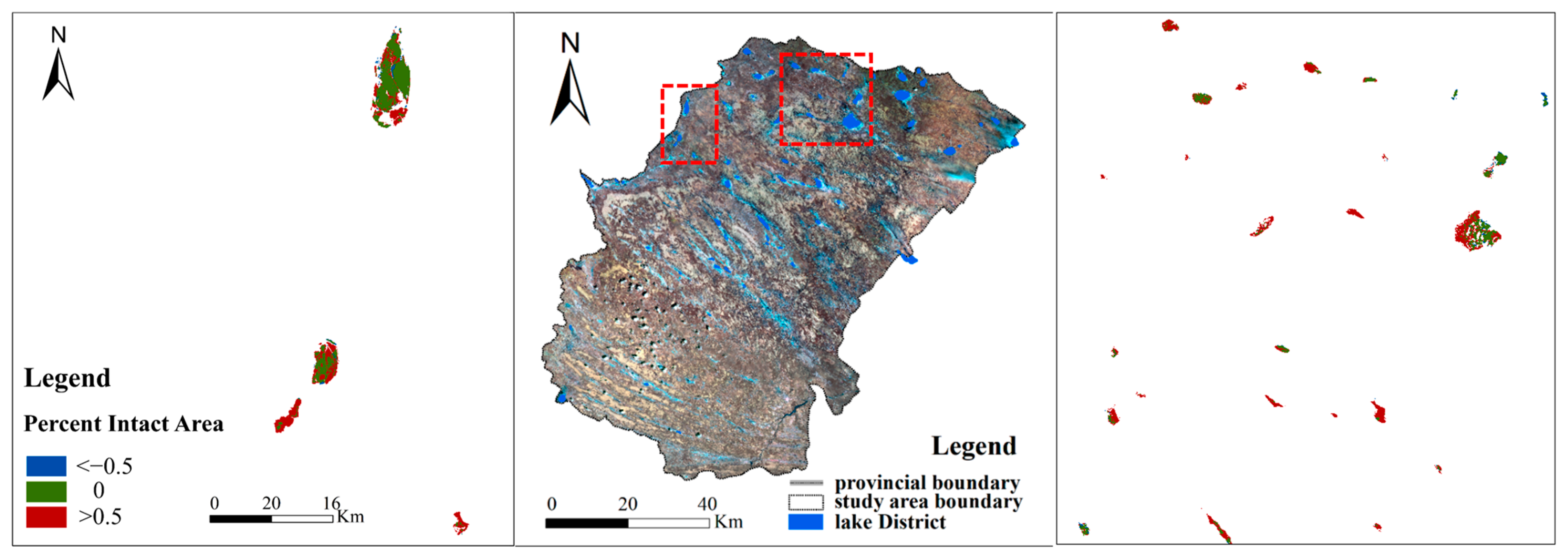
4.4. Accuracy and Limitations of JRC Dataset in Identifying Water Bodies at 30 m Resolution
4.5. Assessing the Use of Drought Indices and Potential of Lakes as Monitoring Wells in the Mu Us Sandy Land
5. Conclusions
- ML Models’ Performance: Eight different ML algorithms were utilised to predict the lake area based on the given input variables. The results indicate that all eight ML methods were able to effectively describe the relationship between lake area and both meteorological factors and human activities. This implies that ML models can be utilised to understand and predict the response of lake areas to various environmental and anthropogenic factors.
- Superiority of the RF Model: Among the various ML algorithms tested, the RF model emerged as the most robust performer. Its performance was quantified using the R2, and the RF model achieved an impressive R2 value of 0.88. This indicates that the RF model’s predictions closely matched the observed lake area data, making it a reliable tool for predicting lake area in the study area.
- Limited Performance of the BR and KNN Models: On the other hand, the study found that the BR and KNN models consistently provided poorer results compared to the other ML algorithms tested. These models may not capture the complex relationships between lake area and the predictor variables as effectively as the RF and other models.
- Importance of Meteorological Factors: The study also explored the impact of different meteorological factors on the lake area prediction. Specifically, the SPEI at various time scales was introduced as an input variable. The analysis revealed that SPEI-9, which represents a longer-term climate condition, had a positive effect on predicting lake area. This suggests that long-term meteorological patterns play a significant role in determining lake area variations in the arid area under investigation.
- Identifying Appropriate Predictor Variables: The success of applying ML algorithms to predict lake area largely depends on the selection of suitable predictor variables. This study emphasises the importance of including both meteorological and human activity factors in the inputs to achieve accurate predictions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| SPEI-9 | ||||||||||||||
| ETKQ | ETKQQ | HJQ | WSZ | WSQ | YC | YJHLQ | ||||||||
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| BayesianRidg | 5.896 (5.148) | 0.084 (0.231) | 0.678 (0.483) | 0.040 (0.286) | 4.676 (5.339) | 0.003 (−0.002) | 26.17 (26.291) | 0.208 (0.172) | 8.402 (7.576) | 0.233 (0.397) | 1.165 (1.281) | 0.417 (0.441) | 4.423 (3.849) | 0.075 (0.058) |
| KNN | 4.982 (5.268) | 0.346 (0.195) | 0.596 (0.504) | 0.258 (0.219) | 3.610 (3.601) | 0.406 (0.544) | 24.31 (26.297) | 0.317 (0.172) | 7.909 (10.447) | 0.320 (−0.146) | 1.201 (1.509) | 0.380 (0.225) | 3.632 (3.354) | 0.376 (0.285) |
| GBDT | 0.164 (3.805) | 0.999 (0.580) | 0.032 (0.349) | 0.998 (0.627) | 0.149 (2.537) | 0.999 (0.774) | 0.694 (14.511) | 0.999 (0.748) | 0.382 (4.351) | 0.998 (0.801) | 0.032 (0.813) | 0.999 (0.775) | 0.126 (2.231) | 0.999 (0.683) |
| ET | 2.745 (3.042) | 0.801 (0.731) | 0.378 (0.277) | 0.702 (0.765) | 2.535 (2.802) | 0.707 (0.724) | 11.12 (12.020) | 0.857 (0.827) | 4.530 (5.604) | 0.777 (0.670) | 0.629 (1.054) | 0.830 (0.622) | 1.841 (1.802) | 0.840 (0.793) |
| RF | 2.834 (3.549) | 0.788 (0.635) | 0.318 (0.307) | 0.788 (0.712) | 2.318 (2.315) | 0.755 (0.812) | 9.886 (13.735) | 0.887 (0.774) | 4.221 (4.195) | 0.809 (0.796) | 0.592 (0.951) | 0.849 (0.692) | 1.630 (1.382) | 0.874 (0.879) |
| AB | 3.760 (3.899) | 0.627 (0.559) | 0.464 (0.405) | 0.551 (0.498) | 2.901 (3.127) | 0.616 (0.656) | 14.023 (14.519) | 0.773 (0.748) | 5.303 (5.878) | 0.694 (0.637) | 0.807 (0.964) | 0.720 (0.684) | 2.365 (2.100) | 0.736 (0.719) |
| Bagging | 2.090 (3.481) | 0.885 (0.648) | 0.247 (0.315) | 0.872 (0.695) | 1.814 (2.392) | 0.850 (0.799) | 8.589 (12.395) | 0.915 (0.816) | 3.579 (4.693) | 0.861 (0.769) | 0.560 (1.036) | 0.865 (0.635) | 1.369 (2.138) | 0.911 (0.709) |
| XGB | 0.001 (3.680) | 0.999 (0.563) | 0.001 (0.402) | 0.999 (0.505) | 0.001 (2.484) | 0.999 (0.783) | 0.001 (13.577) | 0.999 (0.779) | 0.001 (4.632) | 0.999 (0.774) | 0.001 (1.006) | 0.999 (0.655) | 0.001 (2.058) | 0.999 (0.731) |
| grid search cross-validation | 1.529 (2.819) | 0.938 (0.769) | 0.223 (0.272) | 0.895 (0.773) | 1.835 (2.214) | 0.846 (0.828) | 6.366 (10.351) | 0.953 (0.872) | 0.653 (4.344) | 0.995 (0.802) | 8.403 (0.714) | 0.999 (0.826) | 1.477 (1.364) | 0.897 (0.882) |
| SPEI-9 | ||||||||||||||
| ETKQ | ETKQQ | HJQ | WSZ | WSQ | YC | YJHLQ | ||||||||
| LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | |
| BayesianRidg | 0.302 (0.658) | 113.1 (30.5) | 0.211 (0.860) | / (2224.5) | 0.094 (0.524) | / (259.8) | 0.461 (0.544) | 61.1 (43.0) | 0.487 (0.726) | / (103.8) | 0.646 (0.682) | / (67.1) | 0.278 (0.247) | / (23.6) |
| KNN | 0.594 (0.444) | 95.8 (29.0) | 0.509 (0.494) | / (875.7) | 0.644 (0.776) | / (136.9) | 0.567 (0.448) | 53.1 (47.2) | 0.569 (0.120) | / (1123.6) | 0.631 (0.506) | / (65.9) | 0.619 (0.634) | / (16.8) |
| GBDT | 0.999 (0.767) | 2.0 (17.4) | 0.999 (0.796) | / (965.6) | 0.999 (0.914) | / (79.068) | 0.999 (0.905) | 1.4 (16.3) | 0.999 (0.897) | / (31.8) | 0.999 (0.900) | / (60.2) | 0.999 (0.861) | / (12.6) |
| ET | 0.921 (0.907) | 47.9 (16.3) | 0.884 (0.923) | / (1314.4) | 0.881 (0.922) | / (115.1) | 0.938 (0.941) | 25.3 (21.3) | 0.914 (0.843) | / (70.4) | 0.929 (0.835) | / (60.7) | 0.930 (0.913) | / (9.1) |
| RF | 0.910 (0.802) | 58.1 (16.6) | 0.926 (0.864) | / (1331.4) | 0.899 (0.951) | / (120.1) | 0.949 (0.921) | 23.1 (23.0) | 0.923 (0.897) | / (37.8) | 0.946 (0.888) | / (53.9) | 0.946 (0.951) | / (8.3) |
| AB | 0.843 (0.826) | 44.0 (20.9) | 0.817 (0.830) | / (1657.6) | 0.840 (0.897) | / (138.5) | 0.892 (0.920) | 32.6 (26.2) | 0.874 (0.814) | / (60.3) | 0.886 (0.897) | / (57.2) | 0.896 (0.945) | / (11.4) |
| Bagging | 0.948 (0.818) | 41.5 (16.3) | 0.872 (0.845) | / (1030.9) | 0.932 (0.914) | / (110.8) | 0.962 (0.938) | 18.0 (21.7) | 0.940 (0.878) | / (34.8) | 0.938 (0.819) | / (64.9) | 0.959 (0.865) | / (13.3) |
| XGB | 0.999 (0.785) | 0.01 (16.9) | 0.999 (0.742) | / (2224.5) | 0.999 (0.913) | / (90.9) | 0.999 (0.913) | 0.002 (18.8) | 0.999 (0.883) | / (30.6) | 0.999 (0.819) | / (69.6) | 0.999 (0.900) | / (11.2) |
| grid search cross-validation | 0.976 (0.903) | 18.4 (14.8) | 0.963 (0.900) | / (1182.4) | 0.946 (0.956) | / (115.3) | 0.979 (0.948) | 13.1 (18.4) | 0.998 (0.897) | / (32.9) | 0.999 (0.922) | / (55.7) | 0.958 (0.952) | / (8.6) |
| SPEI-12 | ||||||||||||||
| ETKQ | ETKQQ | HJQ | WSZ | WSQ | YC | YJHLQ | ||||||||
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| BayesianRid | 5.903 (5.179) | 0.081 (0.222) | 0.678 (0.482) | 0.040 (0.286) | 4.676 (5.339) | 0.003 (−0.002) | 26.05 (26.345) | 0.215 (0.169) | 8.049 (5.974) | 0.296 (0.625) | 1.218 (1.294) | 0.362 (0.430) | 4.423 (3.849) | 0.075 (0.058) |
| KNN | 4.979 (5.268) | 0.347 (0.195) | 0.597 (0.504) | 0.256 (0.219) | 3.620 (3.601) | 0.402 (0.544) | 24.32 (26.954) | 0.316 (0.130) | 7.896 (10.211) | 0.323 (−0.095) | 1.199 (1.509) | 0.381 (0.225) | 3.641 (3.354) | 0.373 (0.285) |
| GBDT | 0.269 (4.565) | 0.998 (0.395) | 0.030 (0.451) | 0.998 (0.376) | 0.184 (3.194) | 0.998 (0.641) | 0.684 (14.171) | 0.999 (0.759) | 0.287 (3.694) | 0.999 (0.857) | 0.040 (0.789) | 0.999 (0.788) | 0.113 (2.288) | 0.999 (0.667) |
| ET | 2.989 (3.535) | 0.764 (0.637) | 0.388 (0.412) | 0.686 (0.479) | 2.506 (3.049) | 0.714 (0.673) | 9.604 (11.882) | 0.893 (0.831) | 4.152 (3.855) | 0.813 (0.844) | 0.645 (1.159) | 0.821 (0.542) | 1.868 (1.804) | 0.835 (0.793) |
| RF | 3.005 (3.507) | 0.762 (0.643) | 0.331 (0.398) | 0.771 (0.513) | 2.404 (3.136) | 0.736 (0.654) | 8.594 (13.938) | 0.915 (0.767) | 3.728 (3.472) | 0.849 (0.873) | 0.614 (1.095) | 0.838 (0.592) | 1.622 (1.526) | 0.876 (0.852) |
| AB | 3.961 (4.321) | 0.586 (0.458) | 0.446 (0.447) | 0.586 (0.388) | 2.927 (3.216) | 0.609 (0.637) | 13.52 (15.019) | 0.789 (0.730) | 5.394 (5.116) | 0.684 (0.725) | 0.781 (1.104) | 0.737 (0.585) | 2.487 (2.420) | 0.708 (0.628) |
| Bagging | 2.026 (3.135) | 0.892 (0.715) | 0.262 (0.423) | 0.857 (0.452) | 1.839 (3.368) | 0.846 (0.601) | 7.088 (13.392) | 0.942 (0.785) | 3.271 (3.392) | 0.884 (0.879) | 0.525 (1.049) | 0.881 (0.626) | 1.428 (1.772) | 0.904 (0.800) |
| XGB | 0.001 (3.793) | 0.99 9(0.582) | 0.001 (0.477) | 0.999 (0.303) | 0.001 (2.781) | 0.999 (0.728) | 0.001 (13.292) | 0.999 (0.788) | 0.001 (3.875) | 0.999 (0.842) | 0.001 (1.099) | 0.999 (0.589) | 0.001 (2.279) | 0.999 (0.670) |
| grid search cross-validation | 1.279 (2.290) | 0.913 (0.731) | 0.234 (0.396) | 0.886 (0.520) | 0.001 (2.544) | 0.999 (0.773) | 3.696 (9.703) | 0.984 (0.887) | 2.924 (3.369) | 0.907 (0.881) | 0.100 (0.755) | 0.996 (0.806) | 1.300 (1.519) | 0.920 (0.853) |
| SPEI−12 | ||||||||||||||
| ETKQ | ETKQQ | HJQ | WSZ | WSQ | YC | YJHLQ | ||||||||
| LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | LCCC | PRD | |
| BayesianRid | 0.299 (0.645) | 113.0 (30.7) | 0.211 (0.859) | / (2224.4) | 0.094 (0.524) | / (259.8) | 0.468 (0.530) | 60.9 (42.5) | 0.547 (0.871) | / (82.5) | 0.603 (0.705) | / (60.8) | 0.278 (0.248) | / (23.6) |
| KNN | 0.594 (0.444) | 95.8 (29.0) | 0.506 (0.494) | / (875.7) | 0.641 (0.776) | / (136.9) | 0.566 (0.399) | 53.1 (48.8) | 0.572 (0.192) | / (119.0) | 0.631 (0.505) | / (66.0) | 0.616 (0.634) | / (16.8) |
| GBDT | 0.999 (0.636) | 3.2 (23.6) | 0.999 (0.653) | / (2262.8) | 0.999 (0.835) | / (151.8) | 0.999 (0.887) | 1.283 (18.2) | 0.999 (0.930) | / (23.8) | 0.999 (0.910) | / (50.6) | 0.999 (0.845) | / (12.7) |
| ET | 0.897 (0.862) | 50.4 (20.5) | 0.887 (0.768) | / (2221.1) | 0.878 (0.879) | / (142.0) | 0.953 (0.924) | 22.8 (20.2) | 0.923 (0.930) | / (52.1) | 0.929 (0.798) | / (56.3) | 0.929 (0.913) | / (9.7) |
| RF | 0.904 (0.857) | 55.2 (19.8) | 0.92 (0.792) | / (2433.6) | 0.887 (0.858) | / (155.5) | 0.963 (0.892) | 19.9 (22.8) | 0.936 (0.938) | / (29.9) | 0.946 (0.832) | / (51.9) | 0.947 (0.935) | / (9.4) |
| AB | 0.818 (0.719) | 39.3 (23.9) | 0.81 (0.753) | / (2634.2) | 0.823 (0.860) | / (138.1) | 0.907 (0.913) | 31.9 (28.3) | 0.872 (0.876) | / (60.4) | 0.902 (0.850) | / (67.0) | 0.912 (0.893) | / (12.8) |
| Bagging | 0.954 (0.853) | 38.4 (17.1) | 0.942 (0.714) | / (2462.3) | 0.929 (0.815) | / (130.7) | 0.973 (0.888) | 15.8 (24.5) | 0.944 (0.941) | / (33.1) | 0.950 (0.841) | / (56.8) | 0.954 (0.909) | / (10.9) |
| XGB | 0.999 (0.773) | 0.01 (19.9) | 0.999 (0.655) | / (2651.2) | 0.999 (0.885) | / (150.6) | 1.000 (0.903) | 0.002 (20.9) | 0.999 (0.920) | / (23.9) | 0.999 (0.769) | / (60.8) | 0.999 (0.867) | / (11.9) |
| grid search cross-validation | 0.954 (0.866) | 47.8 (17.8) | 0.965 (0.848) | / (1958.0) | 0.999 (0.903) | / (142.9) | 0.993 (0.946) | 7.8 (18.0) | 0.964 (0.941) | / (29.5) | 0.998 (0.923) | / (46.1) | 0.969 (0.935) | / (9.6) |
References
- Wanders, N.; Wada, Y.; Van Lanen, H.A.J. Global hydrological droughts in the 21st century under a changing hydrological regime. Earth Syst. Dyn. 2015, 6, 1–15. [Google Scholar] [CrossRef]
- Gao, H. Satellite remote sensing of large lakes and reservoirs: From elevation and area to storage. WIREs Water 2015, 2, 147–157. [Google Scholar] [CrossRef]
- Venegas-Quiñones, H.L.; Thomasson, M.; Garcia-Chevesich, P.A. Water Scarcity or Drought? The cause and solution for the lack of water in laguna de aculeo. Water Conserv. Manag. 2020, 4, 42–50. [Google Scholar] [CrossRef]
- Fuentealba, M.; Latorre, C.; Frugone-Álvarez, M.; Sarricolea, P.; Giralt, S.; Contreras-Lopez, M.; Prego, R.; Bernárdez, P.; Valero-Garcés, B. A combined approach to establishing the timing and magnitude of anthropogenic nutrient alteration in a mediterranean coastal lake- watershed system. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Xu, F.; Bao, H.X.; Li, H.; Kwan, M.-P.; Huang, X. Land use policy and spatiotemporal changes in the water area of an arid region. Land Use Policy 2016, 54, 366–377. [Google Scholar] [CrossRef]
- Yan, D.; Xu, H.; Lan, J.; Zhou, K.; Ye, Y.; Zhang, J.; An, Z.; Yeager, K.M. Solar activity and the westerlies dominate decadal hydroclimatic changes over arid Central Asia. Glob. Planet. Chang. 2019, 173, 53–60. [Google Scholar] [CrossRef]
- Zhang, F.; Kung, H.-T.; Johnson, V.C. Assessment of Land-Cover/Land-Use Change and Landscape Patterns in the Two National Nature Reserves of Ebinur Lake Watershed, Xinjiang, China. Sustainability 2017, 9, 724. [Google Scholar] [CrossRef]
- Zhao, D.; Arshad, M.; Wang, J.; Triantafilis, J. Soil exchangeable cations estimation using Vis-NIR spectroscopy in different depths: Effects of multiple calibration models and spiking. Comput. Electron. Agric. 2021, 182, 105990. [Google Scholar] [CrossRef]
- Lu, S.; Ouyang, N.; Wu, B.; Wei, Y.; Tesemma, Z. Lake water volume calculation with time series remote-sensing images. Int. J. Remote. Sens. 2013, 34, 7962–7973. [Google Scholar] [CrossRef]
- Baup, F.; Frappart, F.; Maubant, J. Combining high-resolution satellite images and altimetry to estimate the volume of small lakes. Hydrol. Earth Syst. Sci. 2014, 18, 2007–2020. [Google Scholar] [CrossRef]
- Ovakoglou, G.; Alexandridis, T.K.; Crisman, T.L.; Skoulikaris, C.; Vergos, G.S. Use of MODIS satellite images for detailed lake morphometry: Application to basins with large water level fluctuations. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 37–46. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Wang, C.; Crétaux, J.-F. Constructing long-term high-frequency time series of global lake and reservoir areas using Landsat imagery. Remote. Sens. Environ. 2019, 232, 111210. [Google Scholar] [CrossRef]
- Guo, F.J.; Li, T.; Ji, M. Time series analysis and prediction of Qinghai Lake area from 2000 to 2019. Sci. Technol. Eng. 2022, 22, 740–748. [Google Scholar]
- Harris, A.R.; Mason, I.M. Lake area measurement using AVHRR A case study. Int. J. Remote Sens. 1989, 10, 885–895. [Google Scholar] [CrossRef]
- Zeng, Z.P.; Lu, X.H. Spatial-temporal evolution of urban lakes in Wuhan City based on remote sensing images. J. Lake Sci. 2008, 20, 648–654. [Google Scholar]
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine Learning for the Geosciences: Challenges and Opportunities. IEEE Trans. Knowl. Data Eng. 2018, 31, 1544–1554. [Google Scholar] [CrossRef]
- Chadalawada, J.; Herath, H.M.V.V.; Babovic, V. Hydrologically Informed Machine Learning for Rainfall-Runoff Modeling: A Genetic Programming-Based Toolkit for Automatic Model Induction. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Herath, H.M.V.V.; Chadalawada, J.; Babovic, V. Hydrologically informed machine learning for rainfall–runoff modelling: Towards distributed modelling. Hydrol. Earth Syst. Sci. 2021, 25, 4373–4401. [Google Scholar] [CrossRef]
- Cai, H.; Liu, S.; Shi, H.; Zhou, Z.; Jiang, S.; Babovic, V. Toward improved lumped groundwater level predictions at catchment scale: Mutual integration of water balance mechanism and deep learning method. J. Hydrol. 2022, 613, 128495. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Shrestha, N.; Mittelstet, A.R.; Gilmore, T.E.; Zlotnik, V.; Neale, C.M. Effects of drought on groundwater-fed lake areas in the Nebraska Sand Hills. J. Hydrol. Reg. Stud. 2021, 36, 100877. [Google Scholar] [CrossRef]
- Poul, A.K.; Shourian, M.; Ebrahimi, H. A Comparative Study of MLR, KNN, ANN and ANFIS Models with Wavelet Transform in Monthly Stream Flow Prediction. Water Resour. Manag. 2019, 33, 2907–2923. [Google Scholar] [CrossRef]
- Koranga, M.; Pant, P.; Kumar, T.; Pant, D.; Bhatt, A.K.; Pant, R. Efficient water quality prediction models based on machine learning algorithms for Nainital Lake, Uttarakhand. Mater. Today Proc. 2022, 57, 1706–1712. [Google Scholar] [CrossRef]
- Maier, P.M.; Keller, S. Estimating chlorophyll a concentrations of several inland waters with hyperspectral data and machine learning models. arXiv 2019, arXiv:1904.02052. [Google Scholar]
- Chen, H.; Yunus, A.P.; Nukapothula, S.; Avtar, R. Modelling Arctic coastal plain lake depths using machine learning and Google Earth Engine. Phys. Chem. Earth Parts A/B/C 2022, 126, 103138. [Google Scholar] [CrossRef]
- Ahirwal, J.; Nath, A.; Brahma, B.; Deb, S.; Sahoo, U.K.; Nath, A.J. Patterns and driving factors of biomass carbon and soil organic carbon stock in the Indian Himalayan region. Sci. Total Environ. 2021, 770, 145292. [Google Scholar] [CrossRef]
- Ngo, G.; Beard, R.; Chandra, R. Evolutionary bagging for ensemble learning. Neurocomputing 2022, 510, 1–14. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Dai, Z. Intensive agropastoralism: Dryland degradation, the Grain-to-Green Program and islands of sustainability in the Mu Us Sandy Land of China. Agric. Ecosyst. Environ. 2010, 138, 249–256. [Google Scholar] [CrossRef]
- Zhang, X. Principles and Optimal Models for Development of Maowusu Sandy Crassland. Chin. J. Plant Ecol. 1994, 18, 1–16. [Google Scholar]
- Xu, D.; Ding, J.; Wu, Y. Lake Area Change in the Mu Us Desert in 1989-2014. J. Desert Res. 2019, 39, 40–47. [Google Scholar]
- Fuentealba, M.; Bahamóndez, C.; Sarricolea, P.; Meseguer-Ruiz, O.; Latorre, C. The 2010–2020 ‘megadrought’ drives reduction in lake surface area in the Andes of central Chile (32°–36°S). J. Hydrol. Reg. Stud. 2021, 38, 100952. [Google Scholar] [CrossRef]
- Wright, J.L.; Jensen, M.E. Development and Evaluation of Evapotranspiration Models for Irrigation Scheduling. Trans. ASAE 1978, 21, 88–91. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Calamita, E.; Majone, B.; Gallice, A.; Siviglia, A.; Toffolon, M. Prediction of river water temperature: A comparison between a new family of hybrid models and statistical approaches. Hydrol. Process. 2016, 30, 3901–3917. [Google Scholar] [CrossRef]
- Toffolon, M.; Piccolroaz, S.; Calamita, E. On the use of averaged indicators to assess lakes’ thermal response to changes in climatic conditions. Environ. Res. Lett. 2020, 15, 034060. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1934–1965. [Google Scholar]
- Di Francescomarino, C.; Dumas, M.; Federici, M.; Ghidini, C.; Maggi, F.M.; Rizzi, W.; Simonetto, L. Genetic algorithms for hyperparameter optimization in predictive business process monitoring. Inf. Syst. 2018, 74, 67–83. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, J.; Zhao, X.; Triantafilis, J. Clay content mapping and uncertainty estimation using weighted model averaging. Catena 2022, 209, 105791. [Google Scholar] [CrossRef]
- Rossel, R.V.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Ji, W. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Karimi, S.; Shamshirband, S.; Motamedi, S.; Petković, D.; Hashim, R. A survey of water level fluctuation predicting in Urmia Lake using support vector machine with firefly algorithm. Appl. Math. Comput. 2015, 270, 731–743. [Google Scholar] [CrossRef]
- Li, C.; Bai, Y.; Zeng, B. Deep Feature Learning Architectures for Daily Reservoir Inflow Forecasting. Water Resour. Manag. 2016, 30, 5145–5161. [Google Scholar] [CrossRef]
- Shiri, J.; Shamshirband, S.; Kisi, O.; Karimi, S.; Bateni, S.M.; Nezhad, S.H.H.; Hashemi, A. Prediction of Water-Level in the Urmia Lake Using the Extreme Learning Machine Approach. Water Resour. Manag. 2016, 30, 5217–5229. [Google Scholar] [CrossRef]
- Afan, H.A.; El-Shafie, A.; Yaseen, Z.M.; Hameed, M.M.; Mohtar, W.H.M.W.; Hussain, A. ANN Based Sediment Prediction Model Utilizing Different Input Scenarios. Water Resour. Manag. 2015, 29, 1231–1245. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Hameed, M.; Sharqi, S.S.; Yaseen, Z.M.; Afan, H.A.; Hussain, A.; Elshafie, A. Application of artificial intelligence (AI) techniques in water quality index prediction: A case study in tropical region, Malaysia. Neural Comput. Appl. 2017, 28, 893–905. [Google Scholar] [CrossRef]
- Sulaiman, S.O.; Shiri, J.; Shiralizadeh, H.; Kisi, O.; Yaseen, Z.M. Precipitation pattern modeling using cross-station perception: Regional investigation. Environ. Earth Sci. 2018, 77, 1–11. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Khatibi, R.; Karimi, V.; Yaseen, Z.M.; Zounemat-Kermani, M. Learning from Multiple Models Using Artificial Intelligence to Improve Model Prediction Accuracies: Application to River Flows. Water Resour. Manag. 2018, 32, 4201–4215. [Google Scholar] [CrossRef]
- Zhu, S.; Heddam, S.; Nyarko, E.K.; Hadzima-Nyarko, M.; Piccolroaz, S.; Wu, S. Modeling daily water temperature for rivers: Comparison between adaptive neuro-fuzzy inference systems and artificial neural networks models. Environ. Sci. Pollut. Res. 2019, 26, 402–420. [Google Scholar] [CrossRef] [PubMed]
- Sanikhani, H.; Kisi, O.; Maroufpoor, E.; Yaseen, Z.M. Temperature-based modeling of reference evapotranspiration using several artificial intelligence models: Application of different modeling scenarios. Theor. Appl. Clim. 2019, 135, 449–462. [Google Scholar] [CrossRef]
- Zhang, B.; Schwartz, F.W.; Liu, G. Systematics in the size structure of prairie pothole lakes through drought and deluge. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Srivastava, G.; Kumar, P. Water quality index with missing parameters. Int. J. Res. Eng. Technol. 2013, 2, 609–614. [Google Scholar]
- Peters, E.; Bier, G.; van Lanen, H.; Torfs, P. Propagation and spatial distribution of drought in a groundwater catchment. J. Hydrol. 2006, 321, 257–275. [Google Scholar] [CrossRef]
- Pham, S.V.; Leavitt, P.R.; McGowan, S.; Peres-Neto, P. Spatial variability of climate and land-use effects on lakes of the northern Great Plains. Limnol. Oceanogr. 2008, 53, 728–742. [Google Scholar] [CrossRef]
- Tague, C.; Grant, G.; Farrell, M.; Choate, J.; Jefferson, A. Deep groundwater mediates streamflow response to climate warming in the Oregon Cascades. Clim. Chang. 2008, 86, 189–210. [Google Scholar] [CrossRef]
- Tweed, S.; Leblanc, M.; Cartwright, I. Groundwater–surface water interaction and the impact of a multi-year drought on lakes conditions in South-East Australia. J. Hydrol. 2009, 379, 41–53. [Google Scholar] [CrossRef]
- Adane, Z.; Zlotnik, V.A.; Rossman, N.R.; Wang, T.; Nasta, P. Sensitivity of Potential Groundwater Recharge to Projected Climate Change Scenarios: A Site-Specific Study in the Nebraska Sand Hills, USA. Water 2019, 11, 950. [Google Scholar] [CrossRef]
- Liao, J.; Shen, G.; Li, Y. Lake variations in response to climate change in the Tibetan Plateau in the past 40 years. Int. J. Digit. Earth 2013, 6, 534–549. [Google Scholar] [CrossRef]
- Tang, L.; Duan, X.; Kong, F.; Zhang, F.; Zheng, Y.; Li, Z.; Mei, Y.; Zhao, Y.; Hu, S. Influences of climate change on area variation of Qinghai Lake on Qinghai-Tibetan Plateau since 1980s. Sci. Rep. 2018, 8, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Zheng, M. The response of lake variations to climate change in the past forty years: A case study of the northeastern Tibetan Plateau and adjacent areas, China. Quat. Int. 2015, 371, 31–48. [Google Scholar] [CrossRef]
- Ozesmi, S.L.; Bauer, M.E. Satellite remote sensing of wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]



| Reference | Name | Description |
|---|---|---|
| Shrestha et al. (2021) [21] | NB | Default |
| Khazaee et al. (2019) [22] | KNN | Default |
| Koranga et al. (2022) [23] | GBDT | random_state = 2022, max_depth = 4, n_estimators = 200 |
| Maier et al. (2019) [24] | ExtraTrees | random_state = 2022, max_depth = 6, n_estimators = 100 |
| Chen et al. (2022) [25] | RF | random_state = 2022, max_depth = 6, n_estimators = 100 |
| Ahirwal et al. (2021) [26] | AB | random_state = 2022 |
| Ngo et al. (2022) [27] | Bagging | random_state = 2022 |
| Ma et al. (2021) [28] | XGB | random_state = 2022, max_depth = 6, n_estimators = 200, learning_rate = 0.3 |
| Lake Area (km2) | Percentage |
|---|---|
| 0.8–2 | 39.68 |
| 2–4 | 22.22 |
| 4–10 | 25.40 |
| >10 | 12.70 |
| %Change in Mu Us Desert | Study Area | ||||||
|---|---|---|---|---|---|---|---|
| ETKQQ | ETKQ | HJQ | WSQ | WSZ | YC | YJHLQ | |
| <20 | 25 | 60 | 45 | 50 | 50 | 25 | 90 |
| 20–40 | 20 | 20 | 10 | 15 | 25 | 30 | 5 |
| 40–60 | 15 | 15 | 15 | 20 | 5 | 30 | 5 |
| 60–100 | 10 | 5 | 25 | 5 | 5 | 5 | 0 |
| >100 | 30 | 0 | 5 | 10 | 15 | 10 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Huo, Z.; Miao, P.; Tian, X. Comparison of Machine Learning Models to Predict Lake Area in an Arid Area. Remote Sens. 2023, 15, 4153. https://doi.org/10.3390/rs15174153
Wang D, Huo Z, Miao P, Tian X. Comparison of Machine Learning Models to Predict Lake Area in an Arid Area. Remote Sensing. 2023; 15(17):4153. https://doi.org/10.3390/rs15174153
Chicago/Turabian StyleWang, Di, Zailin Huo, Ping Miao, and Xiaoqiang Tian. 2023. "Comparison of Machine Learning Models to Predict Lake Area in an Arid Area" Remote Sensing 15, no. 17: 4153. https://doi.org/10.3390/rs15174153
APA StyleWang, D., Huo, Z., Miao, P., & Tian, X. (2023). Comparison of Machine Learning Models to Predict Lake Area in an Arid Area. Remote Sensing, 15(17), 4153. https://doi.org/10.3390/rs15174153






