How Important Is Satellite-Retrieved Aerosol Optical Depth in Deriving Surface PM_2.5 Using Machine Learning?

Abstract

PM_2.5 refers to the total mass concentration of tiny particulates in the atmosphere near the surface, obtained by means of in situ observations and satellite remote sensing. Given the highly limited number of ground observation stations of inhomogeneous distribution and an ill-posed remote sensing approach, increasing efforts have been devoted to the application of machine-learning (ML) models to both ground and satellite data. A key satellite-derived parameter, aerosol optical thickness (AOD), has been most commonly used as a proxy of PM_2.5, although their correlation is fraught with large uncertainties. A critical question that has been overlooked concerns how much AOD helps to improve the retrieval of PM_2.5 relative to its uncertainty incurred concurrently. The question is addressed here by taking advantage of high-density PM_2.5 stations in eastern China to evaluate the contributions of AOD, determined as the difference in the accuracy of PM_2.5 retrievals with and without AOD for varying densities of PM_2.5 stations, using four popular ML models (i.e., Random Forest, Extra-trees, XGBoost, and LightGBM). Our results reveal that as the density of monitoring stations decreases, both the feature importance and permutation importance of satellite AOD demonstrate a consistent upward trend (p < 0.05). Furthermore, the ML models without AOD exhibit faster declines in overall accuracy and predictive ability compared with the models with AOD assessed using the sample-based and station-based (spatial) independent cross-validation approaches. Overall, a 10% reduction in the number of stations results in an increase of 0.7–1.2% and 0.6–1.2% in uncertainty in estimated and predicted accuracies, respectively. These findings attest to the indispensable role of satellite AOD in the PM_2.5 retrieval process through ML because it can significantly mitigate the negative impact of the sparse distribution of monitoring sites. This role becomes more important as the number of PM_2.5 stations decreases.

1. Introduction

PM_2.5 refers to the concentration of airborne particulate matter (PM) with an aerodynamic diameter of less than 2.5 microns. Although small, these particles are abundant and active, and attach easily to toxic and harmful substances. PM_2.5 can be suspended in the atmosphere for extended periods, ranging from months to even years, which has an important impact on air quality and visibility and also affects human health [1,2,3]. While PM_2.5 has been monitored in many parts of the world, observations are still highly limited and very inhomogeneous, with many regions not covered [4,5,6]. However, satellite remote sensing provides continuous spatial coverage and has been widely used in the estimation of surface PM_2.5 concentrations [7,8,9].

Previous studies have made great efforts to infer PM_2.5 from satellite retrievals of aerosol optical depth (AOD) by virtue of their positive correlation because AOD is much more monitored from both space and the ground. Many factors can influence their relationship, including aerosol vertical distribution, relative humidity, mixed-layer height, and topography, among others [10,11,12]. The relationship also varies with both location and time scale. Wang and Christopher (2003) [13] used the AOD product retrieved by the Moderate Resolution Imaging Spectroradiometer (MODIS) and in situ measurements of PM_2.5 at seven ground observation stations in Alabama, USA, finding a sound correlation between them on a monthly time scale. Natunen et al. (2010) [14] explored the relationship at four stations in Helsinki, Finland, on seasonal and monthly time scales and found that time averaging increased the correlation. Likewise, the correlation also varies with spatial resolution [15], indicating that different geographical locations, study area sizes, and spatial resolutions of MODIS AOD products can change the correlation between AOD and PM_2.5. In general, the relationship varies considerably with location and season [16,17]. Su et al. (2018) [18] studied the relationship extensively across China, one of the most polluted regions of the world, finding that the relationship differs considerably in different parts of China (better in northern than in southern China) and among the four seasons (better in winter than in summer). The relationship can be significantly improved by normalizing against the height of the planetary boundary layer.

Due to the complex relationships between AOD and PM_2.5, many statistical regression methods have been proposed for estimating PM_2.5 using satellite AOD retrievals [7,19,20,21], such as the multiple linear regression model [22], the geographically weighted regression model [23,24], the geographical spatiotemporal weighting regression model [25], and the linear mixed effects model [26]. To a certain extent, these models are capable of estimating surface PM_2.5 concentrations using satellite AOD data. However, they face challenges when it comes to studying the influences of various factors on PM_2.5, such as meteorological factors (boundary layer height, relative humidity, etc.) and surface factors (underlying surface types, etc.) [27,28]. Fortunately, machine-learning (ML) models have a strong data-mining capability and can establish robust nonlinear relationships. They allow for the extraction of pertinent information from very large numbers of auxiliary factors to improve the accuracy of PM_2.5 retrievals. Therefore, various types of ML models have been adopted in PM_2.5 inversion studies in recent years, e.g., the Random Forest model [29,30], the Extra-trees model [31,32], the XGBoost model [33], and the LightGBM model [34].

AOD has been regarded as an essential input variable in inferring PM_2.5 from satellites [7,19,27,35]. However, a handful of studies have presented contrasting results [36,37,38,39]. Chen et al. (2021) [38], for example, developed a Random Forest model for areas with and without AOD data, finding that the model or areas without AOD can result in better PM_2.5 retrievals. Yu et al. (2022) [39] developed a deep ensemble ML framework to estimate daily PM_2.5 concentrations in Italy from 2015 to 2019 and found similar accuracies (cross-validated R² = 0.853 and 0.857) in comparison with ground observations when including or not including satellite AOD in the model. These conflicting findings pose such critical questions as whether satellite-retrieved AOD plays any significant role in estimating surface PM_2.5 and what factor, if any, dictates its role in the ML application for estimating PM_2.5. We attempt to address these questions by taking advantage of rich satellite AOD data and in situ PM_2.5 measurements in eastern China, together with a large array of other ancillary data, introduced next.

2. Data and Methods

2.1. Study Area

The study area (approximately 1,830,000 km²) covers 14 provinces in China, including the North China Plain, the Yangtze River Delta, the Pearl River Delta, and parts of central China (Figure 1). As the most populated and advanced in economic development in China, these regions have experienced serious air pollution problems, thus garnering significant public attention. To monitor air pollution, relatively dense PM_2.5 ground observation stations have been uniformly distributed, enabling us to investigate the effects of satellite AOD on estimating PM_2.5 concentrations at different levels of ground observation station density.

2.2. Data Sources

The datasets used in this study consist of observed PM_2.5 concentrations, 1-km-resolution MODIS Multi-Angle Implementation of Atmospheric Correction (MAIAC) AOD products, and many auxiliary datasets related to PM_2.5, such as meteorological and land- and population-related information. The study period spans from 2018 to 2020, ensuring an adequate volume of data for conducting sensitivity analyses.

2.2.1. PM_2.5 Ground Measurements

The PM_2.5 observation station data used in this study are real-time ground-measured air quality data (including PM_2.5) in China from the China National Environment Monitoring Center. In this study, a total of 775 ground observation stations were chosen from the eastern region of China (Figure 1). Daily measurements recorded at each station were subsequently calculated and subjected to rigorous data quality control following Wei et al. (2019) [30]. These validated ground measurements were then utilized as ground truth for ML-modeling purposes.

2.2.2. MODIS AOD Products

The MODIS AOD product serves as the primary predictor for estimating surface PM_2.5 in this study. Specifically, Terra and Aqua MCD19A2 AOD products at a spatial resolution of 1 km are employed. This product is retrieved using the MAIAC inversion algorithm over land and incorporates various quality assurance (QA) measures [40,41]. For this study, to ensure the quality of the data, we only employed those MAIAC AOD retrievals passing the recommended QA measures, including cloud screening (QACloudMask = Clear) and adjacency (QAAdjacencyMask = Clear), following the methodology outlined in our previous study [30].

2.2.3. Auxiliary Data

Meteorological reanalysis data used in this paper are collected from the fifth-generation European Reanalysis Interim dataset (ERA5) released by the European Centre for Medium-Range Weather Forecasts. The global hourly dataset has characterized the states of the atmosphere, oceans, and surface since 1979 [42]. Specifically, seven meteorological parameters were employed: boundary layer height (BLH; unit: m), evaporation (ET; unit: mm), relative humidity (RH; unit: %), surface pressure (SP; unit: hPa), 2 m air temperature (TEM; unit: K), and 10 m U and V wind components (unit: m s⁻¹). Copernicus Atmospheric Monitoring Service (CAMS) emission inventories, including the four main precursors of PM_2.5, i.e., ammonia, nitrogen oxides, sulfur dioxide, and volatile organic compounds, were also considered [43,44]. In addition, parameters related to surface conditions and human activities, including the normalized vegetation index, a digital elevation model, and population density, were involved. In total, 15 predictor variables, including AOD, are utilized for PM_2.5 modeling through ML.

2.3. Methodology

2.3.1. Machine-Learning (ML) Models

ML applies complex statistical theories and algorithms to computer simulations in a somewhat human-learning behavior to acquire new knowledge. It can take advantage of any existing knowledge structure and ample information content to infer a piece of new knowledge. ML has been applied in various fields, including the remote sensing of PM_2.5 [45,46,47]. This study compares and analyzes four popular widely used ML algorithms, i.e., Random Forest, Extra-trees, XGBoost, and LightGBM models.

The Random Forest model constructs an ensemble of multiple decision trees, where each tree is generated by bootstrap sampling from the training dataset [48,49,50]. The Extremely Randomized Trees (Extra-trees) model is also a tree-based ensemble learning method, similar to Random Forest but introduces additional randomness in selecting features and splitting the points from all data samples in the tree-building process [31,32,51]. Both the Random Forest and Extra-trees models are ensemble-learning algorithms based on the bagging technique. In the bagging training process, the base classifiers (decision trees) are trained independently, and there is no strong dependence or correlation between them. This characteristic allows for parallel training of the base classifiers, which can significantly speed up the training process. By training the base classifiers in parallel, these integrated algorithms harness the power of parallel computing, making them efficient and scalable for large datasets.

In contrast, the XGBoost and LightGBM models are based on a boosting ensemble algorithm (Figure 2), where base classifiers are trained sequentially, and each classifier depends on the others. The main goal of boosting is to stack these classifiers on top of each other, with each layer assigning higher weights to samples that were incorrectly classified by the previous layers. However, these two models differ in several ways. XGBoost utilizes a pre-classification algorithm, meaning that all features of a sample are pre-sorted before iterated and repeated operations take place [33,52]. This sorting step significantly reduces the number of calculations required. LightGBM employs a histogram algorithm, which offers advantages such as reduced memory usage and a faster runtime [34,53]. In terms of growth strategy, XGBoost follows a level-wise approach. In this strategy, the child nodes of the same layer are split simultaneously. Conversely, LightGBM adopts a leaf-wise growth strategy, where each layer’s child node only needs to find the node with the largest gain (typically the one with the largest data volume) to perform the split.

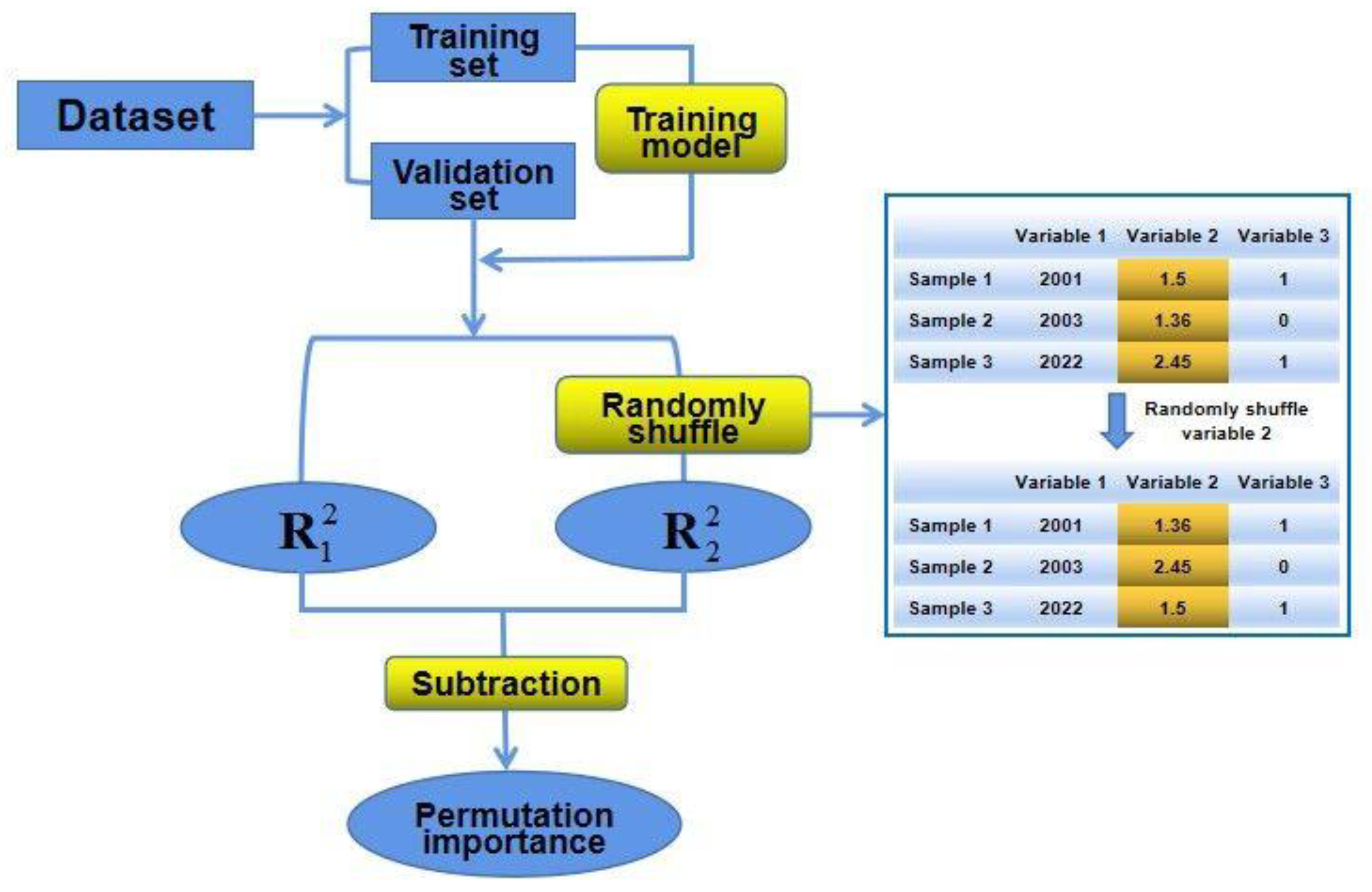
2.3.2. Importance Assessment Method

(1) Feature importance

The feature importance (FI) score is a common indicator reflecting the importance of input variables that comes with the tree-based ML models. The FI score is calculated via the Gini index based on the mean decrease impurity (MDI) and used to evaluate the importance of each feature by measuring its contribution to splitting in the decision tree [54]. Taking one decision tree as an example, VIM represents variable importance measures, and GI represents the Gini index. Assuming that there are m feature variables, the GI score of a feature (represented by X_i) is calculated (represented by ${\mathrm{VIM}}_{\mathrm{i}}^{\mathrm{Gini}}$), i.e., the average change in the node-splitting impurity of the ith feature in the tree model. The Gini index is calculated as

$${\mathrm{GI}}_{\mathrm{m}}={\displaystyle \sum _{\mathrm{k}=1}^{\left|\mathrm{K}\right|}{\displaystyle \sum _{{\mathrm{k}}^{\prime }\ne k}{p}_{mk}{p}_{mk\prime }=1-{\displaystyle \sum _{k=1}^{\left|K\right|}{p}_{mk}^2}}}$$

(1)

where K represents the total number of categories of a feature, and p_mk represents the proportion of a category k in node m. The importance of feature X_i in node m, i.e., the GI change before and after the node branch is expressed as

$${\mathrm{VIM}}_{\mathrm{im}}^{\left(\mathrm{Gini}\right)}={\mathrm{GI}}_{\mathrm{m}}-{\mathrm{GI}}_l-{\mathrm{GI}}_r$$

(2)

where GI_l and GI_r represent the Gini indices of the two new nodes after the branch. The node where feature X_i appears in the jth decision tree is set M. The importance of X_i in the jth tree then is

$${\mathrm{VIM}}_{\mathrm{ij}}^{\left(\mathrm{Gini}\right)}={\displaystyle \sum _{\mathrm{m}\in \mathrm{M}}{\mathrm{VIM}}_{\mathrm{im}}^{\left(\mathrm{Gini}\right)}}$$

(3)

(2) Permutation importance

Although the FI can reflect the characteristic importance of variables, it is more favorable when there are more variable categories. For characteristic variables with multiple correlations, FI may have a bias in describing correlation features, and its assessment could also be overfitted [55]. Therefore, the permutation importance (PI), another method for evaluating the contribution of each feature, is employed. The PI is a model-independent method applicable to almost all types of models, including deep-learning models. Its basic idea is to evaluate the importance of features on a test set by randomly shuffling a feature and then measuring the change in model performance to measure the importance of features. The PI of a feature is calculated as follows (Figure 3). First, the dataset is divided into a training set and a validation set. Second, a baseline metric, defined by scoring, is then evaluated on a (potentially different) dataset defined by the training set. Third, a feature column from the validation set is permutated randomly, and the metric is evaluated again. The PI can be obtained by calculating the difference between the baseline metric and the metric from permutating the feature column.

2.3.3. Model Validation Methods

In this study, two methods are used to evaluate the performance of ML models: sample-based and station-based ten-fold cross-validation (10-CV) [32,56]. In sample-based 10-CV, the sample dataset is randomly divided into ten groups. One group, comprising 10% of the samples, is set aside as the independent validation set, while the remaining nine groups (90%) form the training set. This process is repeated ten times, with each group serving as the validation set once, ensuring that all samples have been tested. The final accuracy is calculated as the average of the results obtained from the ten runs. This approach is commonly used to represent the overall accuracy of ML models in estimating PM_2.5 levels at locations where ground measurements are available.

The station-based 10-CV is another evaluation method used to assess the predictive ability of ML models in estimating PM_2.5 concentrations at locations where ground measurements are not available [57]. This method serves as a spatially independent validation technique. Similarly to the sample-based 10-CV, the station-based 10-CV involves dividing the ground observation stations in the study area into ten groups. One group, consisting of 10% of all stations, is designated as the validation set, while the dataset corresponding to the remaining nine groups of stations (90% of all stations) is used as the training set. This approach creates training and validation samples from different locations. This helps isolate spatial autocorrelations among the data samples, making it an effective spatially independent verification method.

2.3.4. Sensitivity Analysis Methods

This study starts by considering the study area as a whole, with 775 ground observation stations. The total number of stations in the study area is then randomly reduced by 10%. The remaining number of stations is again reduced by 10%. This process continues until the number of stations in a group is 31% of the original total number of stations. The end result is 12 groups of stations, each reflecting a certain station density in the study area. The smaller the proportion of remaining stations in a group, the smaller the density of stations in that group. This set of 12 groups of stations and their associated observations is used next to explore the influence of AOD on inversions of PM_2.5 from different ML models. To assess the importance and contribution of satellite AOD retrievals to ML modeling and quantitatively evaluate its impact on the performance of an ML model, this study incorporates an uncertainty analysis from three key aspects:

(1)

The importance scores of satellite AOD were first calculated employing two techniques (FI and PI) for four typical tree-based ML models as the density of ground-based stations in the study area gradually decreased. This analysis offers valuable insights into the role of satellite AOD in the modeling process. It allows for an understanding of the significance of satellite AOD under different station-density conditions.

(2)

The accuracies and differences in the estimation of PM_2.5, with and without satellite AOD as the primary predictor, were calculated using the sample-based 10-CV method. Four typical tree-based ML models were employed, each taking into consideration the decreasing density of ground-based stations in the study area. This analysis allows us to evaluate the importance of satellite AOD in enhancing the overall accuracy of PM_2.5 estimates for varying station densities.

(3)

Similarly, the accuracies and differences in the prediction of PM_2.5 in regions lacking PM_2.5 observations, with and without satellite AOD as the main predictor, were calculated using the station-based 10-CV method. Again, four typical tree-based ML models were employed, each taking into consideration the decreasing density of ground-based stations in the study area. This analysis enables us to assess the significance of satellite AOD in improving the predictive ability of PM_2.5 predictions for varying station densities.

3. Results

3.1. Variations of Satellite AOD Contributions

Figure 4 presents the FI and PI of satellite AOD retrievals in estimating PM_2.5 obtained by four ML models with the decrease in the density of ground-based monitoring stations. Also shown are the best-fit lines from linear regression and confidence intervals (CIs). CI is a statistical measure used to quantify the uncertainty of an estimate. Here, we used a 95% confidence level (pink-shaded areas in the figure). This indicates that there is a 95% probability that the true value will fall within the specified range, leaving a 5% probability of it falling outside this range. Figure 4a–c show that as the density of the monitoring station decreases, the FI score significantly increases, with regressed correlation of determination (R²) values of 0.84, 0.81, 0.77, and 0.43 for the Random Forest, Extra-trees, XGBoost, and LightGBM models, respectively. All pass the 99% or 95% confidence (p < 0.01 or 0.05) test. The spread of FI in the LightGBM case (Figure 4d) indicates a higher variance compared with other methods, which may be attributed to the use of the specific node-splitting method of the leaf-wise growth strategy. Similar conclusions can be made from the PI score analysis, i.e., the contribution of satellite AOD significantly increases as the density of monitoring stations decreases, with much higher regressed R² values (R² = 0.94–0.96) for the four ML models (Figure 4e–h). All regressed trends reach the 99% confidence (p < 0.01) level. Note that the values of FI and PI are different among the ML methods because these models employ distinct frameworks and operation methods, including sampling, feature selection, and node-splitting techniques. Additionally, the methods of computing FI and PI are also different, e.g., FI relies on the Gini index, which involves calculating the MDI, while PI assesses the change in model performance by randomly shuffling a feature. Results obtained by the two importance verification methods are consistent, suggesting that the two methods can complement and verify each other. These findings reveal that satellite AOD is crucial for PM_2.5 modeling using ML because it plays a dominant predictive role with the highest importance scores, particularly in regions with a small density of PM_2.5 ground observation stations.

3.2. Impacts of Satellite AOD on Overall Accuracy

Figure 5 shows the overall accuracies measured by the CV R² (CV-R²) of the daily estimates of PM_2.5 with and without AOD as model input as a function of decreasing station density using four ML models. Regarding model results where AOD was included as an input variable (Figure 5, red dots), it is clearly seen that as the station density decreases, the overall accuracy of the PM_2.5 estimates gradually decreases, showing an average significantly decreasing trend (i.e., change in sample-based CV-R² per 1% of discarded stations) of −0.16% (p < 0.01), −0.15% (p < 0.01), −0.19% (p < 0.01), and −0.11% (p < 0.01) for the Random Forest, Extra-trees, XGBoost, and LightGBM models, respectively. For model results where AOD was not included as an input variable (Figure 5, blue dots), when the station proportion is 100%, the CV-R² is 0.83 with AOD and 0.82 without AOD, a small difference of about 1.48%. However, as the station density decreases, the difference in accuracy between the models with and without AOD gradually increases (black diamonds in the figure). When the station density is 31%, the accuracy of the model with AOD is 0.72, while the accuracy of the model without AOD is 0.65. The relative difference in model accuracy with or without AOD significantly increases to 10.35%. Similarly, Figure 5b–d present comparable results: At 100% station density, the overall accuracies of the Extra-trees, XGBoost, and LightGBM models with AOD are 0.86, 0.84, and 0.85, respectively. Without AOD, the accuracies of these models are 0.86, 0.83, and 0.81, respectively, and the relative differences in model accuracy with or without AOD are 0.10%, 0.58%, and 4.80%, respectively. When the station density drops to 31%, the accuracies of the models with AOD become 0.76, 0.70, and 0.76, respectively, while the accuracies of the models without AOD are 0.71, 0.64, and 0.69, respectively. Consequently, the relative differences in overall accuracy between these three models with and without AOD increase to 6.48%, 9.41%, and 10.44%, respectively. In particular, when the number of monitoring stations decreases, the slopes of the decreased overall accuracy are much steeper for the Random Forest (−0.24%, p < 0.01), Extra-trees (−0.22%, p < 0.01), XGBoost (−0.27%, p < 0.01), and LightGBM (−0.16%, p < 0.01) models without using AOD compared to these models using AOD. This is because with the decrease in station density, the sample data volume gradually decreases, as do the accuracies of the models. In general, for every 10% reduction in station proportion, the four ML models without AOD experience a 1.2% (p < 0.01), 0.9% (p < 0.01), 1.1% (p < 0.01), and 0.7% (p < 0.01) increase in the uncertainty of the estimated results, respectively, compared with these models using AOD. These findings highlight the indispensable role of satellite AOD in improving the accuracy of estimating PM_2.5 through ML models, particularly in regions with limited observation stations.

3.3. Impacts of Satellite AOD on Predictive Ability

Here, the model performance in predicting the PM_2.5 level in areas without surface observations is examined based on results from the station-based 10-CV method. Figure 6 shows the predictive ability of four ML models in retrieving daily PM_2.5 with (red dots) and without (blue dots) AOD as inputs under different station density conditions. Overall, the trend observed in station-based 10-CV results aligns with those of sample-based 10-CV: When AOD is included as an input variable, with the decreasing number of monitoring stations, the predictive accuracies of the Random Forest, Extra-trees, XGBoost, and LightGBM models all show significantly decreasing trends (i.e., change in station-based CV-R² per 1% of discarded stations) of −0.14% (p < 0.01), −0.13% (p < 0.01), −0.18% (p < 0.01), and −0.10% (p < 0.01), respectively. However, the model’s predictive ability experiences a much faster decline, with larger slopes of −0.21%, −0.18%, −0.26%, and −0.13% for the four models without including satellite AOD, respectively. Specifically, when data from all PM_2.5 stations are used (100%), the Random Forest, Extra-trees, XGBoost, and LightGBM models that include AOD produce slightly better results, with higher station-based CV-R² values (0.81, 0.83, 0.80, and 0.79) than those without considering AOD (CV-R² = 0.77, 0.81, 0.76, and 0.71, respectively). However, when the proportion of monitoring stations drops to 31%, the predictive accuracies for the same four models decrease to 0.72, 0.75, 0.69, 0.73 (including AOD) and 0.64, 0.69, 0.61, 0.64 (not including AOD), respectively. More importantly, the average relative differences become 2.48, 2.68, 2.19, and 1.33 times larger than the results when all stations are considered. This is because station-based 10-CV uses known stations (regions) to predict unknown stations (regions), reflecting the spatial prediction ability of the model. However, it is difficult for an ML model to make predictions for regions without training samples, inevitably leading to lower prediction accuracies, consistent with existing cognitive rules of an ML model. In general, for every 10% reduction in the station density, the four ML models without and with AOD experience 1.0% (p < 0.01), 0.7% (p < 0.01), 1.2% (p < 0.01), and 0.6% (p < 0.01) increases in the uncertainty of the predicted results, respectively. These findings confirm the indispensable role of satellite AOD in predicting PM_2.5 concentration in areas without observations using ML models, particularly in low-station density situations.

The contrasting results with comparable superior accuracy in PM_2.5 estimation without incorporating AOD input can be attributed to the high density of ground observation stations in the specific study area. In areas with a sufficiently dense network of monitoring sites, excluding AOD can still lead to relatively accurate PM_2.5 estimations, which largely benefit from the presence of spatial autocorrelation in air pollution, e.g., PM_2.5 levels and auxiliary factors such as meteorological fields are highly similar in neighboring locations. As a result, PM_2.5 concentrations in nearby sites can be reasonably estimated based on the established relationships between PM_2.5 and non-AOD factors from nearby stations. Nevertheless, as the station density decreases, the spatial autocorrelation weakens, and the disparity between natural and human-influenced conditions grows, and consequently, the prediction error rapidly increases. This highlights the critical role of AOD in areas with limited ground monitoring because it significantly enhances the accuracy of PM_2.5 predictions by providing crucial background pollution information, compensating for the lack of ground observation data.

4. Conclusions

Machine learning (ML) has been used widely to infer ground-level PM_2.5 using satellite-retrieved aerosol optical depth (AOD) to fill large gaps between PM_2.5 stations without quantification of its contribution, which is the objective of this study. We rigorously and quantitatively assess the contribution of AOD to the ML-based estimation of PM_2.5 by applying four common ML models (the Random Forest model, the Extra-trees model, the XGBoost model, and the LightGBM model) to ample measurements from China’s high-density PM_2.5 observation network, the MODIS Multi-Angle Implementation of Atmospheric Correction satellite AOD retrieval product, and many other ancillary meteorological and environmental data from the eastern half of China. Two assessment methods are used, i.e., feature importance (FI) and permutation importance (PI). The contribution of AOD is also assessed by comparing the retrieval results obtained by including and not including AOD. All assessment tests are made for varying numbers of PM_2.5 stations whose data are sampled by station-based and sample-based 10-CV.

The major findings are summarized as follows: (1) As the station density decreases, the FI and PI of AOD in the four ML models have clear upward trends. This trend indicates the importance and contribution of AOD to improving the accuracy of estimating PM_2.5, becoming more pronounced in areas with sparse observation stations. (2) As the density of observation stations decreases, the ML models without AOD exhibit a more pronounced decline in overall accuracy compared to the models that incorporate AOD. Additionally, for every 10% reduction in the number of stations, the uncertainty in the estimated accuracy increases by approximately 0.7–1.2%. (3) As the station density decreases, the ML models without AOD exhibit a faster decline in predictive ability compared with these models with AOD. On average, for every 10% reduction in the number of stations, the uncertainty in the predicted accuracy increases by approximately 0.6–1.2%. These findings demonstrate the indispensable role of AOD in any ML model to effectively counteract the negative impact of no or sparse PM_2.5 stations, resulting in improved accuracy for both estimating and predicting PM_2.5 levels.

AOD represents the degree of light attenuation caused by the scattering and absorption of atmospheric aerosols in the vertical direction and has served as a crucial indicator in deriving surface particulate matter concentrations. The importance of AOD was confirmed through a sensitivity analysis showing that satellite AOD has the highest FI and PI values in PM_2.5 modeling using various ML models. As the number of ground stations decreases, the AOD contribution is more apparent, as is the faster drop in ML model performance without AOD. This further underlines how using satellite AOD is essential, providing key background pollution information in areas without ground stations, thereby improving the prediction capability of ground-based PM_2.5. On the contrary, in this case, relying solely on auxiliary factors such as meteorological fields is far from adequate.

Even though the chosen area in eastern China benefits from a dense and reasonably evenly distributed network of ground observation stations for PM_2.5, enhancing its representativeness, there still exists the question of the uniformity of the spatial distribution of stations. Further analysis incorporating spatial-block cross-validation is needed to effectively reduce the impact of this issue. This will be undertaken in our future study. Additionally, this approach could be applied to PM₁₀, considering its high similarities with PM_2.5, i.e., AOD retains its significance as a crucial input variable in PM₁₀ predictions [58]. However, additional sensitivity analyses are warranted to confirm this hypothesis. Regarding other pollutants, since they possess entirely different key input variables, further investigations are needed to accurately understand their behaviors [e.g., the importance of satellite tropospheric NO₂ in surface NO₂ modelling [59]].