Urban Treetop Detection and Tree-Height Estimation from Unmanned-Aerial-Vehicle Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Aerial Image Collection and Pre-Processing
2.3. Field Investigation
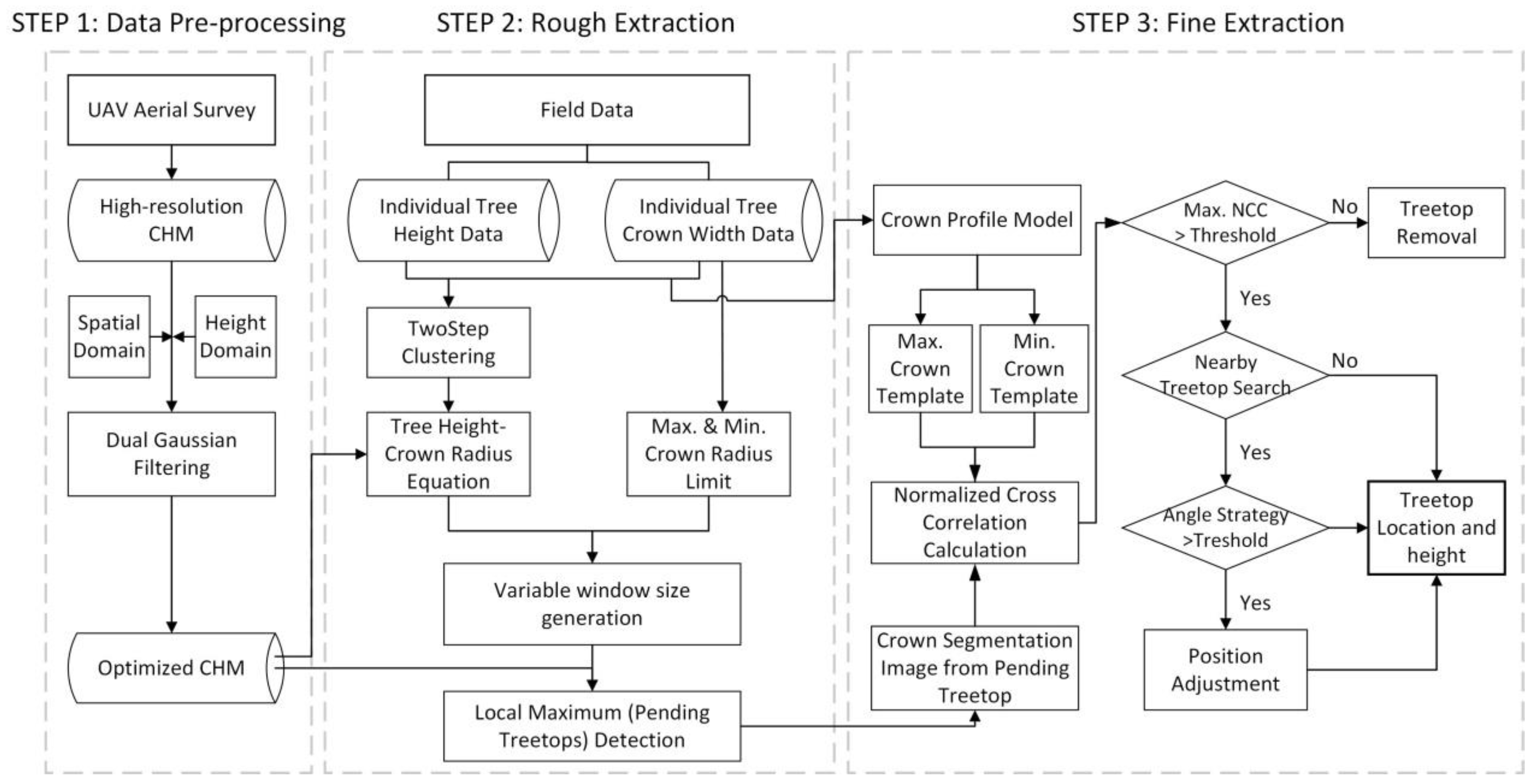
2.4. Improvement to Local-Maximum Algorithm
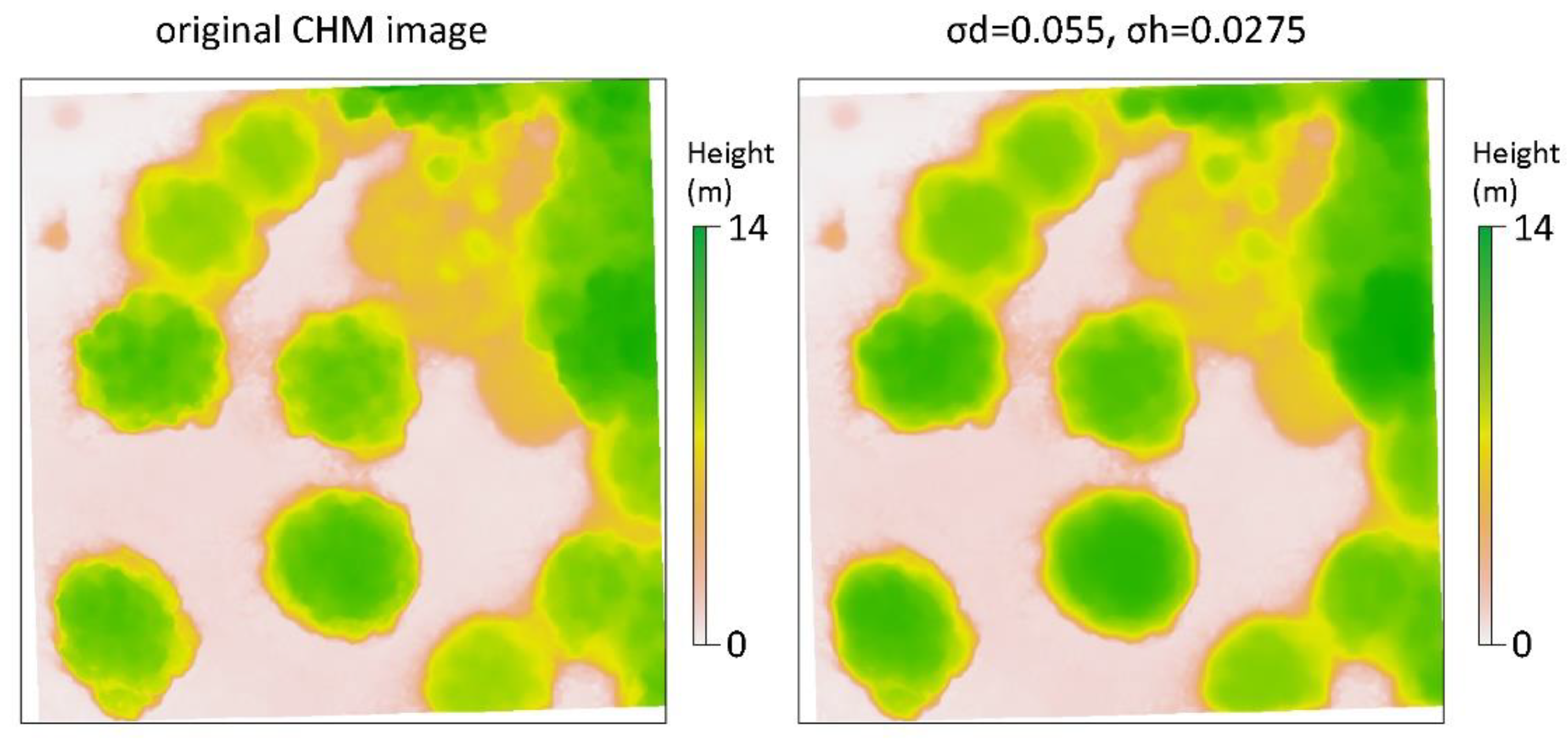
2.4.1. CHM Optimization Using Dual Gaussian Filtering
2.4.2. Selection of Suitable Window Size for Improved LM Algorithm
2.4.3. Fine Extraction
2.5. Accuracy Assessment
3. Results
3.1. Treetop Detection and Accuracy Assessment
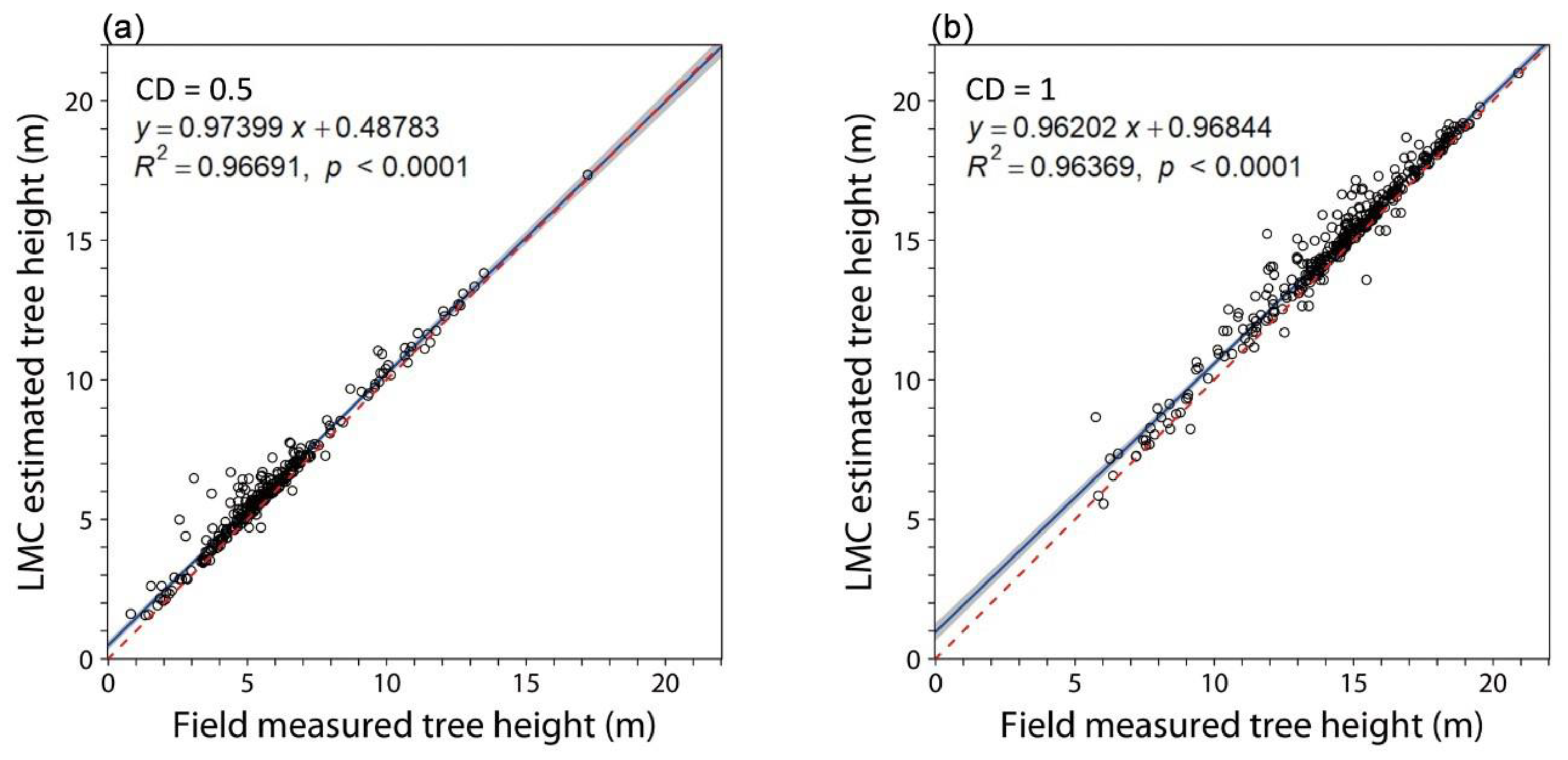
3.2. Tree-Height Estimation and Accuracy Evaluation
4. Discussion
4.1. The Influences of Parameter Settings in the LMC Algorithm
4.2. Error Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roy, S.; Byrne, J.; Pickering, C. A systematic quantitative review of urban tree benefits, costs, and assessment methods across cities in different climatic zones. Urban For. Urban Green. 2012, 11, 351–363. [Google Scholar] [CrossRef]
- Yao, J.; Liu, M.; Chen, N.; Wang, X.; He, X.; Hu, Y.; Wang, X.; Chen, W. Quantitative assessment of demand and supply of urban ecosystem services in different seasons: A case study on air purification in a temperate city. Landsc. Ecol. 2021, 36, 1971–1986. [Google Scholar] [CrossRef]
- Bhattacharjee, K.; Behera, B. Does forest cover help prevent flood damage? Empirical evidence from India. Glob. Environ. Chang. 2018, 53, 78–89. [Google Scholar] [CrossRef]
- Wehner, J.; Mittelbach, M.; Rillig, M.C.; Verbruggen, E. Specialist nectar-yeasts decline with urbanization in Berlin. Sci. Rep. 2017, 7, 45315. [Google Scholar] [CrossRef] [PubMed]
- Schwaab, J.; Meier, R.; Mussetti, G.; Seneviratne, S.; Bürgi, C.; Davin, E.L. The role of urban trees in reducing land surface temperatures in European cities. Nat. Commun. 2021, 12, 6763. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Huang, S.; Chen, Z.; Xing, Y.; Xing, F.; Leong, K.; Yang, Y.; Qiu, Y.; Qin, X. Species characteristics and cultural value of stone wall trees in the urban area of Macao. Sci. Rep. 2022, 12, 1562. [Google Scholar] [CrossRef]
- Fardusi, M.J.; Chianucci, F.; Barbati, A. Concept to Practice of Geospatial-Information Tools to Assist Forest Management and Planning under Precision Forestry Framework: A review. Ann. Silvic. Res. 2017, 41, 3–14. [Google Scholar] [CrossRef]
- Lin, J.; Wang, Q.; Li, X. Socioeconomic and spatial inequalities of street tree abundance, species diversity, and size structure in New York City. Landsc. Urban Plan. 2021, 206, 103992. [Google Scholar] [CrossRef]
- Davis, A.Y.; Jung, J.; Pijanowski, B.C.; Minor, E.S. Combined vegetation volume and “greenness” affect urban air temperature. Appl. Geogr. 2016, 71, 106–114. [Google Scholar] [CrossRef]
- Chen, S.; Liang, D.; Ying, B.; Zhu, W.; Zhou, G.; Wang, Y. Assessment of an improved individual tree detection method based on local-maximum algorithm from unmanned aerial vehicle RGB imagery in overlapping canopy mountain forests. Int. J. Remote Sens. 2021, 42, 106–125. [Google Scholar] [CrossRef]
- Hao, Y.; Widagdo, F.R.A.; Liu, X.; Quan, Y.; Dong, L.; Li, F. Individual Tree Diameter Estimation in Small-Scale Forest Inventory Using UAV Laser Scanning. Remote Sens. 2021, 13, 24. [Google Scholar] [CrossRef]
- Qiu, T.; Aravena, M.-C.; Andrus, R.; Ascoli, D.; Bergeron, Y.; Berretti, R.; Bogdziewicz, M.; Boivin, T.; Bonal, R.; Caignard, T.; et al. Is there tree senescence? The fecundity evidence. Proc. Natl. Acad. Sci. USA 2021, 118, e2106130118. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Chen, W.; Qian, T.; Shen, D.; Wang, J. The extraction of vegetation points from LiDAR using 3D fractal dimension analyses. Remote Sens. 2015, 7, 10815–10831. [Google Scholar] [CrossRef]
- Matese, A. Recent Advances in Unmanned Aerial Vehicles Forest Remote Sensing—A Systematic Review. Part II: Research Applications. Forests 2021, 12, 397. [Google Scholar] [CrossRef]
- Puliti, S.; Dash, J.P.; Watt, M.S.; Breidenbach, J.; Pearse, G.D. A comparison of UAV laser scanning, photogrammetry and airborne laser scanning for precision inventory of small-forest properties. For. Int. J. For. Res. 2020, 93, 150–162. [Google Scholar] [CrossRef]
- Gülci, S.; Akay, A.E.; Gülci, N.; Taş, İ. An assessment of conventional and drone-based measurements for tree attributes in timber volume estimation: A case study on stone pine plantation. Ecol. Inform. 2021, 63, 101303. [Google Scholar] [CrossRef]
- Zhao, Y.; Hao, Y.; Zhen, Z.; Quan, Y. A region-based hierarchical cross-section analysis for individual tree crown delineation using ALS data. Remote Sens. 2017, 9, 1084. [Google Scholar] [CrossRef]
- Hojjatoleslami, S.; Kittler, J. Region growing: A new approach. IEEE Trans. Image Process. 1998, 7, 1079–1084. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Wang, J.; Liu, W.; Wang, J. Weakly-supervised semantic segmentation network with deep seeded region growing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7014–7023. [Google Scholar]
- Huang, H.; Li, X.; Chen, C. Individual tree crown detection and delineation from very-high-resolution UAV images based on bias field and marker-controlled watershed segmentation algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2253–2262. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An individual tree segmentation method based on watershed algorithm and three-dimensional spatial distribution analysis from airborne LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Miraki, M.; Sohrabi, H.; Fatehi, P.; Kneubuehler, M. Individual tree crown delineation from high-resolution UAV images in broadleaf forest. Ecol. Inform. 2021, 61, 101207. [Google Scholar] [CrossRef]
- Haghshenas, N.; Shamsoddini, A.; Aghighi, H. Urban Tree Canopy Mapping Using Object Oriented Classification and Machine Learning Algorithms. Iran. J. Remote Sens. GIS 2021, 13, 17–32. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local maximum filtering for the extraction of tree locations and basal area from high spatial resolution imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest: Using lidar and multispectral data fusion with local filtering and variable window size for estimating tree height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A comparison of three methods for automatic tree crown detection and delineation from high spatial resolution imagery. Int. J. Remote Sens. 2011, 32, 3625–3647. [Google Scholar] [CrossRef]
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual Tree Detection from Unmanned Aerial Vehicle (UAV) Derived Canopy Height Model in an Open Canopy Mixed Conifer Forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Nelson, T.; Boots, B.; Wulder, M.A. Techniques for accuracy assessment of tree locations extracted from remotely sensed imagery. J. Environ. Manag. 2005, 74, 265–271. [Google Scholar] [CrossRef]
- Chen, W.; Xiang, H.; Moriya, K. Individual tree position extraction and structural parameter retrieval based on airborne LiDAR data: Performance evaluation and comparison of four algorithms. Remote Sens. 2020, 12, 571. [Google Scholar] [CrossRef]
- Ma, K.; Xiong, Y.; Jiang, F.; Chen, S.; Sun, H. A Novel Vegetation Point Cloud Density Tree-Segmentation Model for Overlapping Crowns Using UAV LiDAR. Remote Sens. 2021, 13, 1442. [Google Scholar] [CrossRef]
- Yi, H.; Xiaocheng, Z.; Hongyu, H.; Xueqin, X. Counting tree number in subtropical forest districts based on UAV remote sensing images. Remote Sens. Technol. Appl. 2018, 33, 168–176. [Google Scholar]
- Yun, T.; Jiang, K.; Li, G.; Eichhorn, M.P.; Fan, J.; Liu, F.; Chen, B.; An, F.; Cao, L. Individual tree crown segmentation from airborne LiDAR data using a novel Gaussian filter and energy function minimization-based approach. Remote Sens. Environ. 2021, 256, 112307. [Google Scholar] [CrossRef]
- Birdal, A.C.; Avdan, U.; Türk, T. Estimating tree heights with images from an unmanned aerial vehicle. Geomat. Nat. Hazards Risk 2017, 8, 1144–1156. [Google Scholar] [CrossRef]
- Franklin, S.; Wulder, M.; Lavigne, M. Automated derivation of geographic window sizes for use in remote sensing digital image texture analysis. Comput. Geosci. 1996, 22, 665–673. [Google Scholar] [CrossRef]
- Huang, H.; Gong, P.; Cheng, X.; Clinton, N.; Li, Z. Improving measurement of forest structural parameters by co-registering of high resolution aerial imagery and low density LiDAR data. Sensors 2009, 9, 1541–1558. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Li, J.; Kuang, S.; He, Y.; Chen, G.; Huang, Y.; Song, C.; Anderson, P.; Łowicki, D. Plant Diversity Along the Urban–Rural Gradient and Its Relationship with Urbanization Degree in Shanghai, China. Forests 2020, 11, 171. [Google Scholar] [CrossRef]
- Racurs. Digital Photogrammetric System Photomod, Version 6; User Manual; Racurs Company: Moscow, Russia, 2016. [Google Scholar]
- Su Mon, M.; Mizoue, N.; Htun, N.Z.; Kajisa, T.; Yoshida, S. Estimating forest canopy density of tropical mixed deciduous vegetation using Landsat data: A comparison of three classification approaches. Int. J. Remote Sens. 2012, 33, 1042–1057. [Google Scholar] [CrossRef]
- Ma, J.S. The Keys of Shanghai Vascular Plants; High Education Press: Beijing, China, 2014; 410p. (In Chinese) [Google Scholar]
- Plowright, A. ForestTools: Tools for Analyzing Remote Sensing Forest Data. R Package Version 1.0.0. 2023. Available online: https://github.com/andrew-plowright/ForestTools (accessed on 11 September 2021).
- Hijmans, R.J.; Van Etten, J.; Cheng, J.; Mattiuzzi, M.; Sumner, M.; Greenberg, J.A.; Lamigueiro, O.P.; Bevan, A.; Racine, E.B.; Shortridge, A. Package ‘raster’ 3.5-15. R Package 2022, 734. [Google Scholar]
- Paturkar, A.; Sen Gupta, G.; Bailey, D. Making Use of 3D Models for Plant Physiognomic Analysis: A Review. Remote Sens. 2021, 13, 2232. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation—Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Hirschmugl, M.; Ofner, M.; Raggam, J.; Schardt, M. Single tree detection in very high resolution remote sensing data. Remote Sens. Environ. 2007, 110, 533–544. [Google Scholar] [CrossRef]
- Apostol, B.; Petrila, M.; Lorenţ, A.; Ciceu, A.; Gancz, V.; Badea, O. Species discrimination and individual tree detection for predicting main dendrometric characteristics in mixed temperate forests by use of airborne laser scanning and ultra-high-resolution imagery. Sci. Total Environ. 2020, 698, 134074. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Deng, S.; Liang, D.; Cheng, X. A Crown Morphology-Based Approach to Individual Tree Detection in Subtropical Mixed Broadleaf Urban Forests Using UAV LiDAR Data. Remote Sens. 2021, 13, 1278. [Google Scholar] [CrossRef]
- Tkaczynski, A. Segmentation using two-step cluster analysis. In Segmentation in Social Marketing; Springer: Singapore, 2017; pp. 109–125. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E.; Masters, B.R. Digital Image Processing, Third Edition. J. Biomed. Opt. 2009, 14, 029901. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, H.; Luo, G.; Yang, L.; Wang, W.; Gui, D. Extraction and Counting of Populus Euphratica Crown Using UAV Images Integrated with U-Net Method. Remote Sens. Technol. Appl. 2019, 34, 939–949. [Google Scholar]
- Ma, K.; Chen, Z.; Fu, L.; Tian, W.; Jiang, F.; Yi, J.; Du, Z.; Sun, H. Performance and Sensitivity of Individual Tree Segmentation Methods for UAV-LiDAR in Multiple Forest Types. Remote Sens. 2022, 14, 298. [Google Scholar] [CrossRef]
- Liu, H.; Dong, P.; Wu, C.; Wang, P.; Fang, M. Individual tree identification using a new cluster-based approach with discrete-return airborne LiDAR data. Remote Sens. Environ. 2021, 258, 112382. [Google Scholar] [CrossRef]
- Ahmadi, S.A.; Ghorbanian, A.; Golparvar, F.; Mohammadzadeh, A.; Jamali, S. Individual tree detection from unmanned aerial vehicle (UAV) derived point cloud data in a mixed broadleaf forest using hierarchical graph approach. Eur. J. Remote Sens. 2022, 55, 520–539. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Cosenza, D.N.; Rodriguez, L.C.E.; Silva, M.; Tomé, M.; Díaz-Varela, R.A.; González-Ferreiro, E. Comparison of ALS- and UAV(SfM)-derived high-density point clouds for individual tree detection in Eucalyptus plantations. Int. J. Remote Sens. 2018, 39, 5211–5235. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. Comparison of UAV photograph-based and airborne lidar-based point clouds over forest from a forestry application perspective. Int. J. Remote Sens. 2017, 38, 2411–2426. [Google Scholar] [CrossRef]



| Group | Number | Indicator | Minimum (m) | Maximum (m) | Mean (m) | S.D. | Group |
|---|---|---|---|---|---|---|---|
| ≤12 m | 329 | Tree height | 3.00 | 12.00 | 7.95 | 2.35 | 3.00 |
| Canopy radius | 0.25 | 5.50 | 1.96 | 0.84 | 0.25 | ||
| >12 m | 225 | Tree height | 12.00 | 38.00 | 20.12 | 5.42 | 12.00 |
| Canopy radius | 0.88 | 5.75 | 2.57 | 0.95 | 0.88 |
| Group | Fitting Equation | R² | AIC |
|---|---|---|---|
| ≤12 m | y= −2.86598 × 10−4x5 + 8.27 × 10−3x4 − 0.08274 × x3 + 0.32921 × x2 − 0.29568 × x + 0.05897 | 0.8896 | − |
| 72.15 | |||
| >12 m | y= 1.86478 × 10−6x5 − 2.17364 × 10−4x4 + 9.4 × −3 × x3 − 0.18446 × x2 + 1.62422 × x − 3.87244 | 0.5207 | − |
| 53.35 |
| Sample Plot | Canopy Closure | Actual Tree Number | NDT | CE (%) | OE (%) | UA (%) | PA (%) | DET (%) | OA (%) |
|---|---|---|---|---|---|---|---|---|---|
| A | 0.5 | 84 | 93 | 13.98 | 23.66 | 86.02 | 76.34 | 84.52 | 90.32 |
| B | 0.5 | 28 | 28 | 17.86 | 17.86 | 82.14 | 82.14 | 82.14 | 100 |
| C | 0.5 | 34 | 37 | 13.51 | 13.51 | 86.49 | 86.49 | 85.29 | 91.89 |
| D | 0.5 | 153 | 168 | 5.36 | 13.69 | 94.64 | 86.31 | 94.12 | 91.07 |
| Mean (±SD) | 12.68 (±2.55) | 17.18 (±7.12) | 87.32 (±7.55) | 82.82 (±2.12) | 86.52 (±6.54) | 93.32 (±3.90) | |||
| E | 1 | 49 | 42 | 26.19 | 9.52 | 73.81 | 90.48 | 77.55 | 83.33 |
| F | 1 | 89 | 121 | 4.96 | 31.4 | 95.04 | 68.6 | 93.26 | 73.55 |
| G | 1 | 65 | 43 | 74.42 | 23.26 | 25.58 | 76.74 | 50.77 | 48.84 |
| H | 1 | 85 | 122 | 0.82 | 31.15 | 99.18 | 68.85 | 98.82 | 69.67 |
| I | 1 | 111 | 171 | 0.58 | 35.67 | 99.42 | 64.33 | 99.1 | 64.91 |
| Mean (±SD) | 21.39 (±31.47) | 26.2 (±10.34) | 78.61 (±31.47) | 73.8 (±10.34) | 83.9 (±20.49) | 68.06 (±12.70) | |||
| OM | 17.52 | 22.19 | 82.48 | 77.81 | 85.06 | 79.29 |
| Statistical Measure | NDT | Nv | UA | PA | DET | OA |
|---|---|---|---|---|---|---|
| F | 0.032 | 0.208 | 0.292 | 2.552 | 0.061 | 14.055 |
| p-value | 0.863 | 0.662 | 0.605 | 0.154 | 0.813 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhuang, M.; Chen, Y.; Meng, C.; Wu, C.; Ouyang, L.; Liu, Y.; Shu, Y.; Tao, Y.; Qiu, T.; et al. Urban Treetop Detection and Tree-Height Estimation from Unmanned-Aerial-Vehicle Images. Remote Sens. 2023, 15, 3779. https://doi.org/10.3390/rs15153779
Wu H, Zhuang M, Chen Y, Meng C, Wu C, Ouyang L, Liu Y, Shu Y, Tao Y, Qiu T, et al. Urban Treetop Detection and Tree-Height Estimation from Unmanned-Aerial-Vehicle Images. Remote Sensing. 2023; 15(15):3779. https://doi.org/10.3390/rs15153779
Chicago/Turabian StyleWu, Hui, Minghao Zhuang, Yuanchi Chen, Chen Meng, Caiyan Wu, Linke Ouyang, Yuhan Liu, Yi Shu, Yuzhong Tao, Tong Qiu, and et al. 2023. "Urban Treetop Detection and Tree-Height Estimation from Unmanned-Aerial-Vehicle Images" Remote Sensing 15, no. 15: 3779. https://doi.org/10.3390/rs15153779
APA StyleWu, H., Zhuang, M., Chen, Y., Meng, C., Wu, C., Ouyang, L., Liu, Y., Shu, Y., Tao, Y., Qiu, T., & Li, J. (2023). Urban Treetop Detection and Tree-Height Estimation from Unmanned-Aerial-Vehicle Images. Remote Sensing, 15(15), 3779. https://doi.org/10.3390/rs15153779






