Research on Dynamic Deformation Laws of Super High-Rise Buildings and Visualization Based on GB-RAR and LiDAR Technology
Abstract
1. Introduction
2. Research Methods
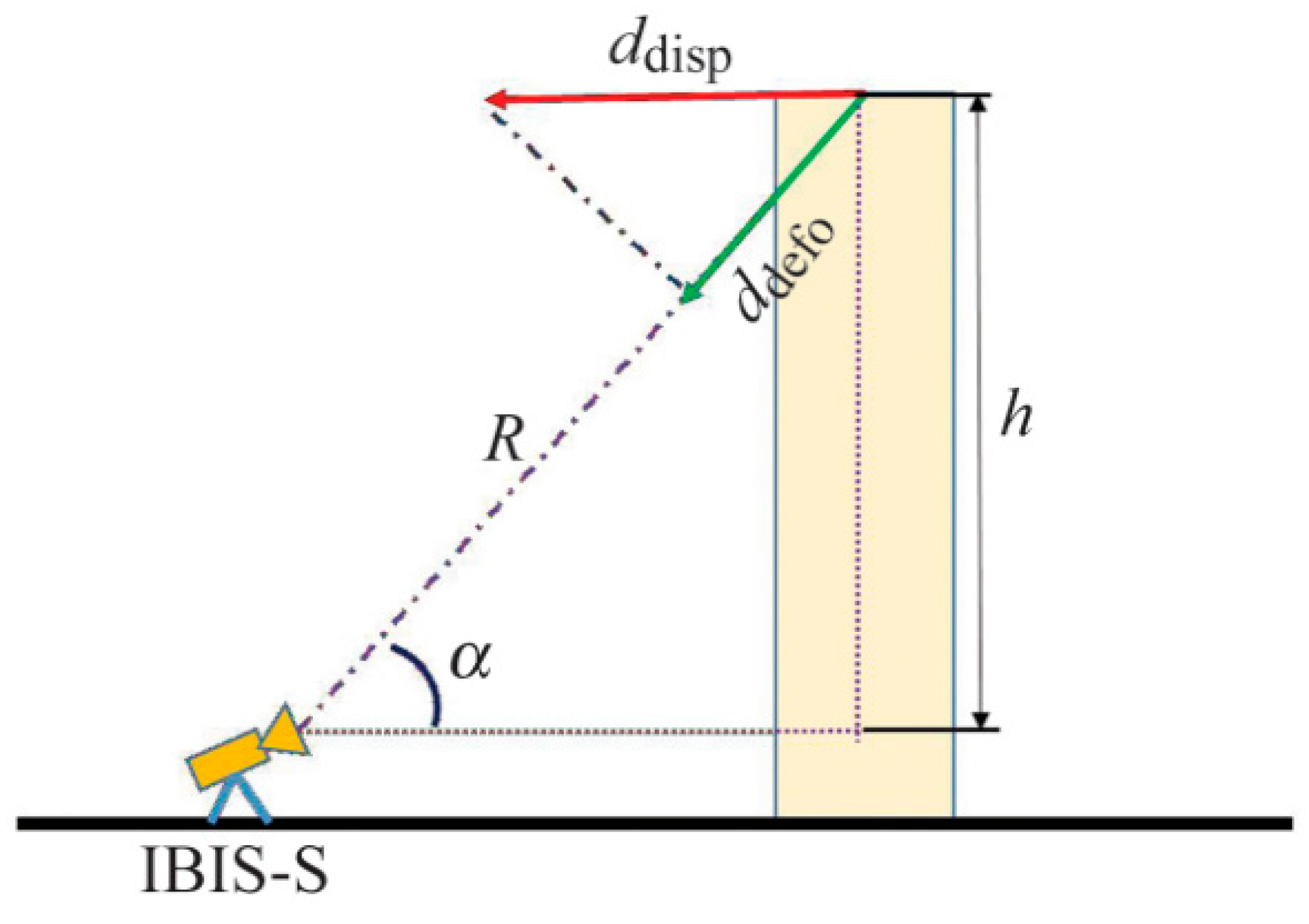
2.1. Differential Interference Processing
2.2. Wavelet Denoising
2.2.1. Wavelet Denoising Principle
2.2.2. Selection of Threshold
- (1)
- Fixed threshold (sqtwolog)
- (2)
- The unbiased risk estimation threshold (rigsure)
- (3)
- Heuristic threshold (heuresure)
2.2.3. Evaluation Standards
- (1)
- Root mean square error (RMSE)
- (2)
- SNR
- (3)
- Cross-correlation coefficient (R)
- (4)
- Smoothness index (r)
- (5)
- Sample Standard Deviation (SSD)
3. Accuracy Verification Experiment
4. Deformation Monitoring Test of Super High-Rise Buildings
4.1. Experimental Subjects
4.2. Experimental Scheme
- (1)
- 9:56~10:24: monitored the building with the IBIS-S system at the sampling frequency of 100 Hz;
- (2)
- 10:25~12:25: monitored the building with the IBIS-S system at the sampling frequency of 80 Hz;
- (3)
- 12:26~12:56: monitored the building with the IBIS-S system at the sampling frequency of 100 Hz.
- (1)
- 15:23~15:53: monitored the building with the IBIS-S system at the sampling frequency of 100 Hz;
- (2)
- 16:00~16:30: monitored the building with the IBIS-S system at the sampling frequency of 80 Hz;
- (3)
- 16:30~17:00: monitored the building with the IBIS-S system at the sampling frequency of 50 Hz;
- (4)
- 17:00~17:30: monitored the building with the IBIS-S system at the sampling frequency of 30 Hz.
5. Results and Discussion
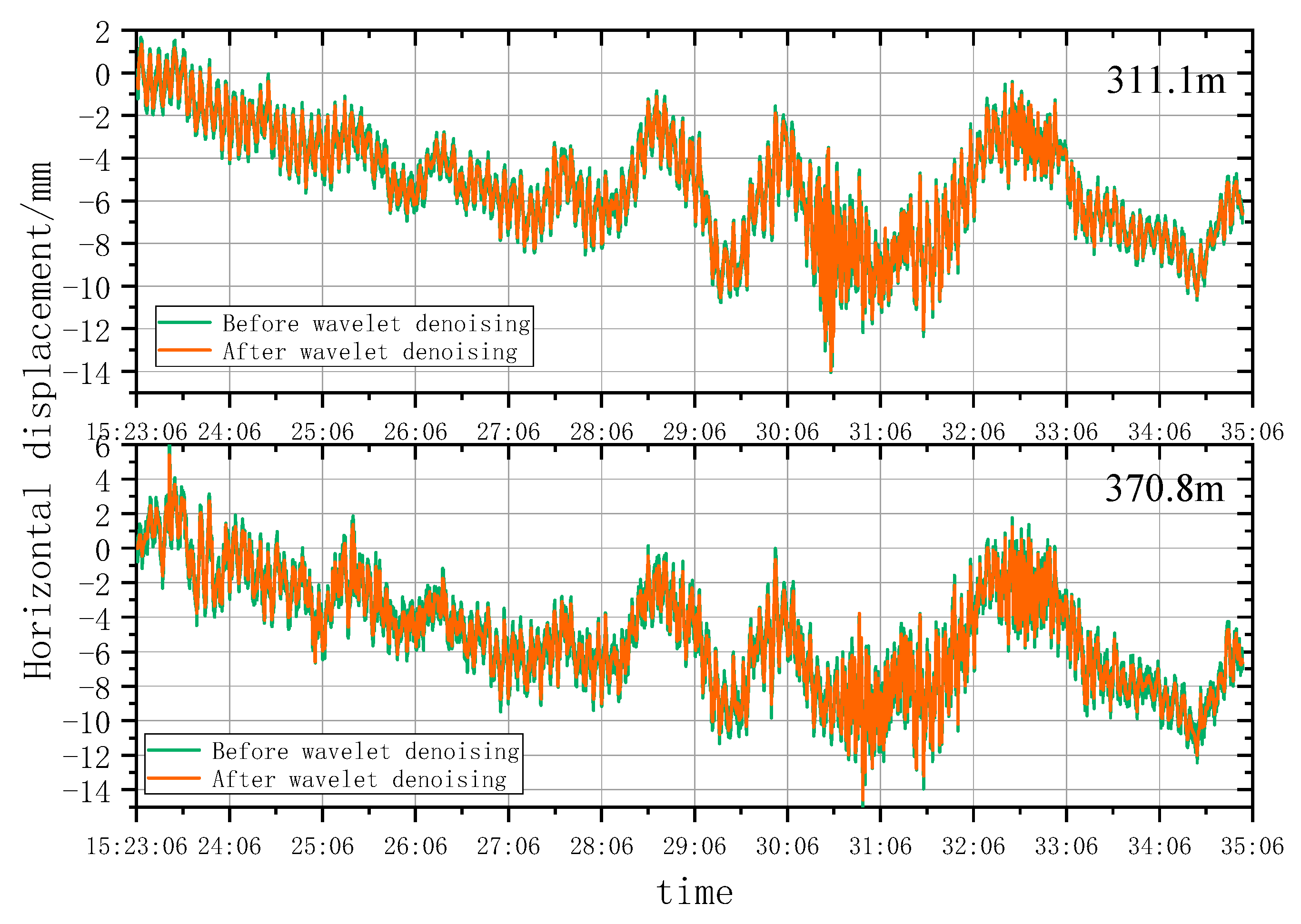
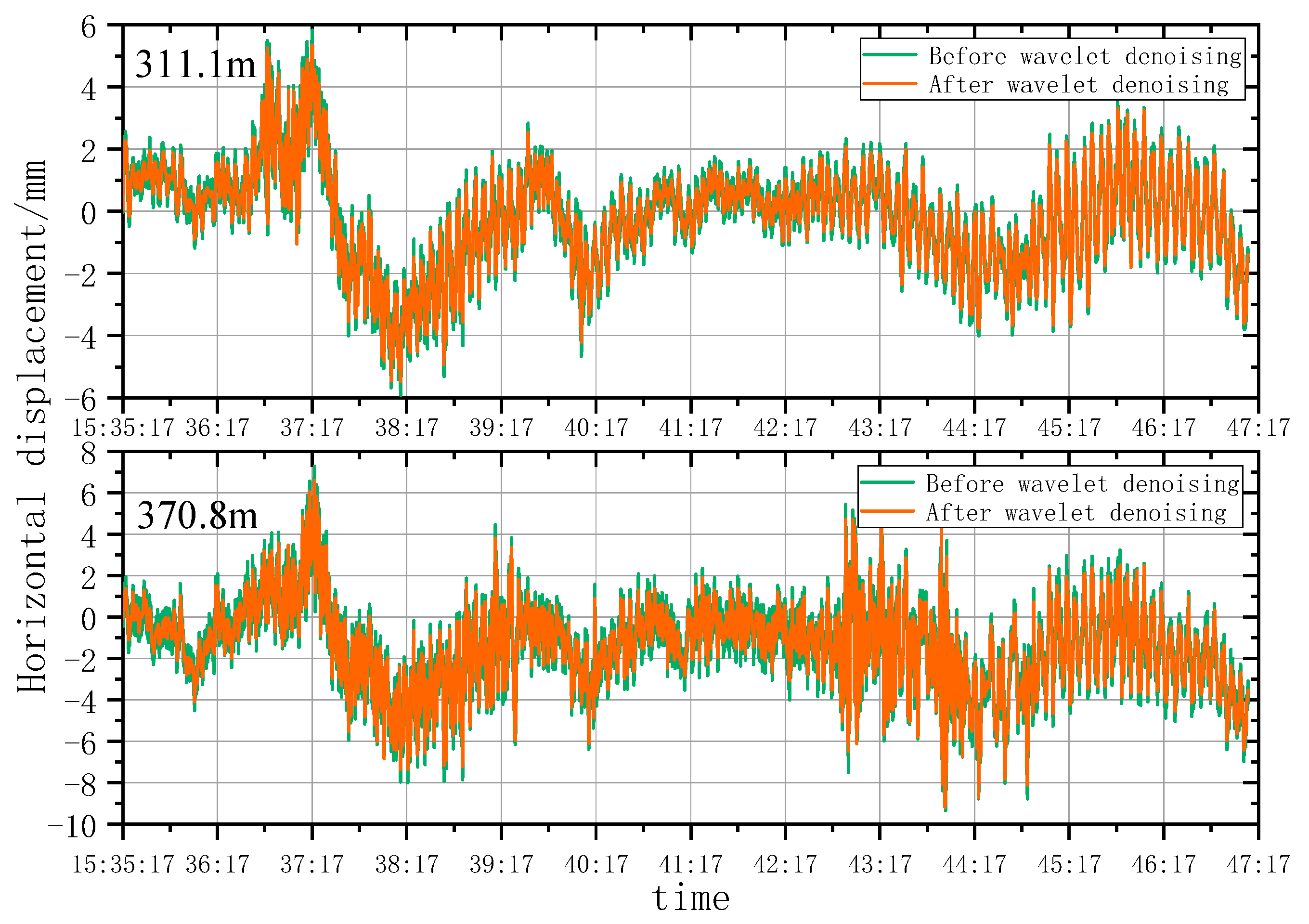
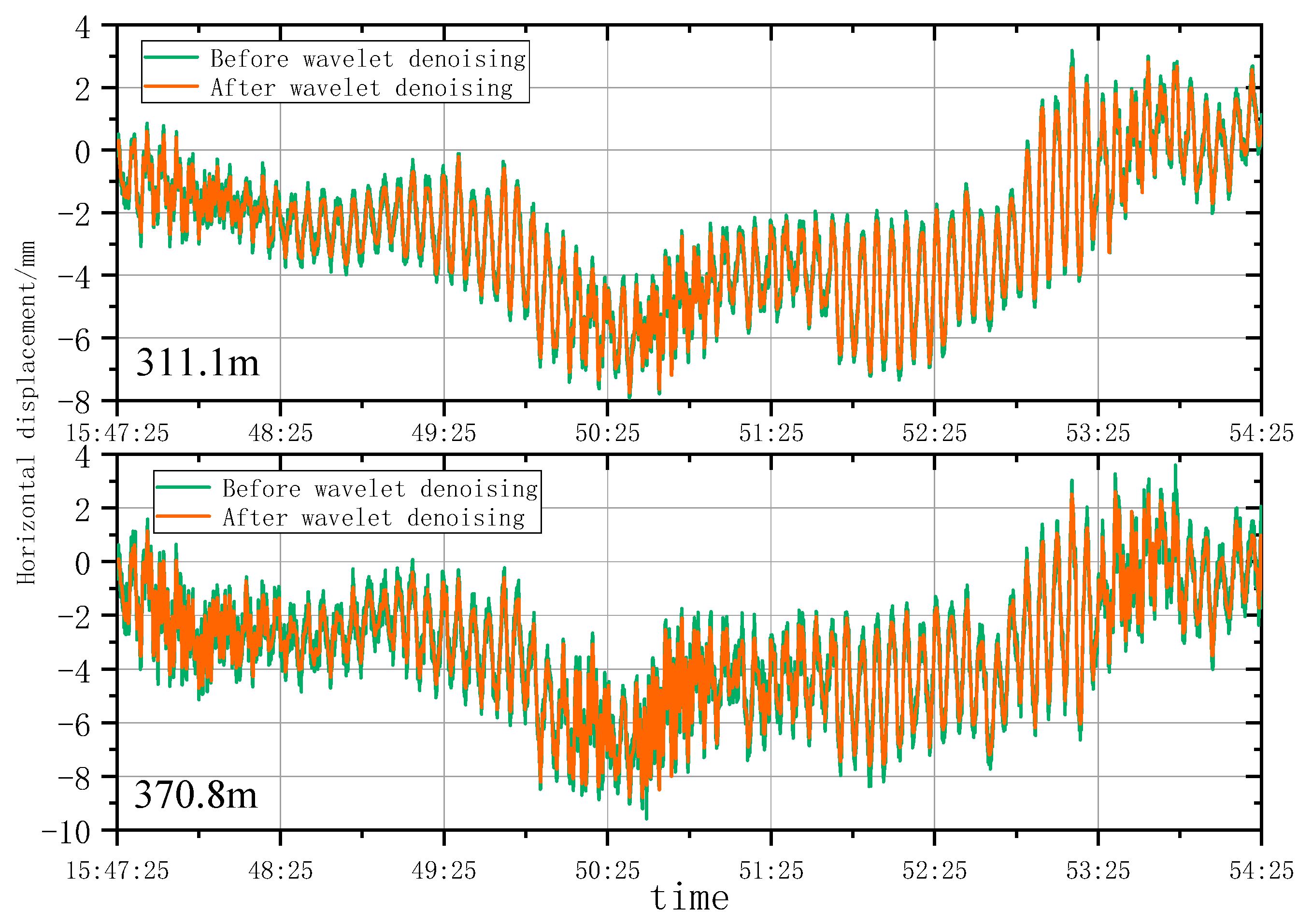
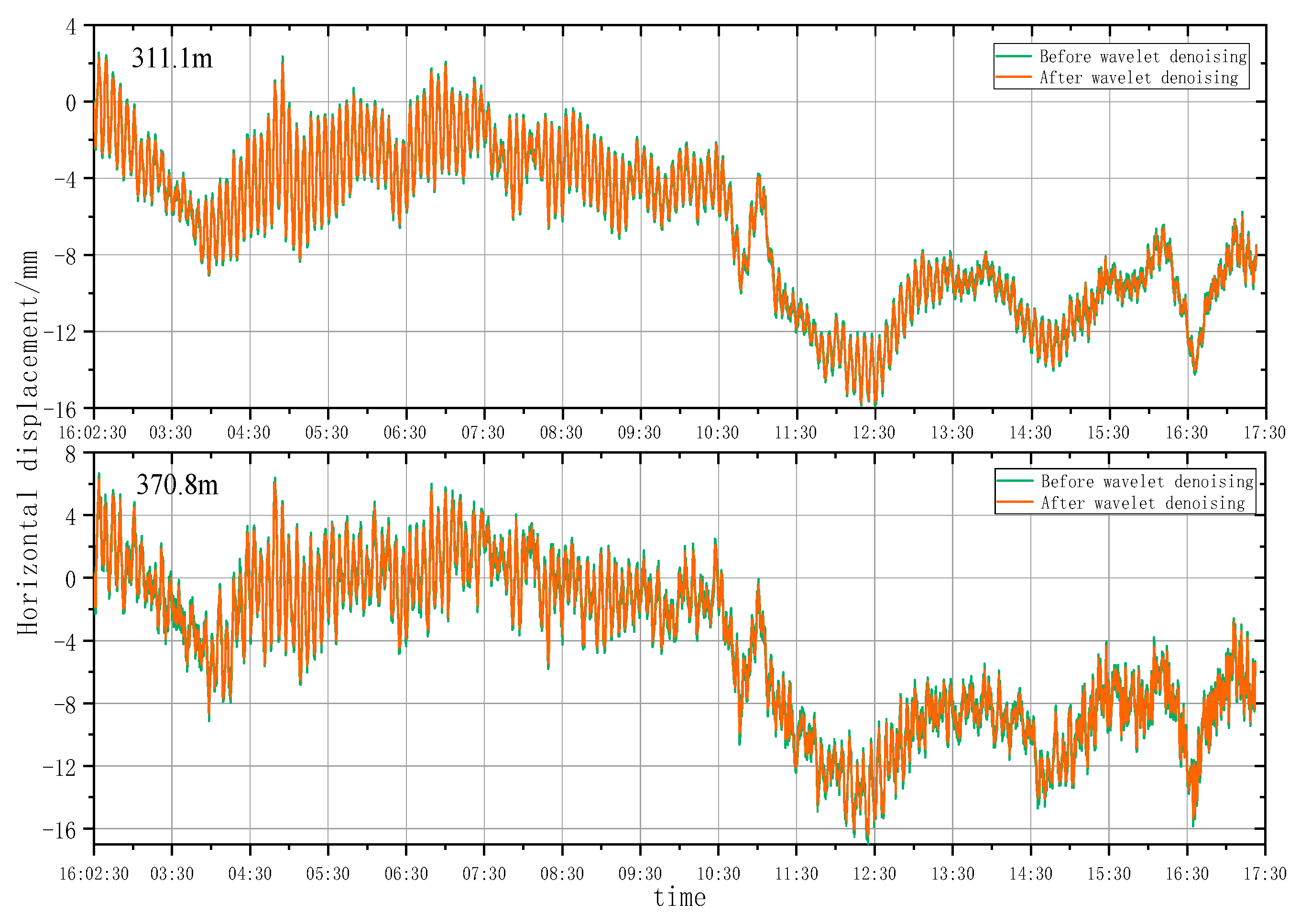
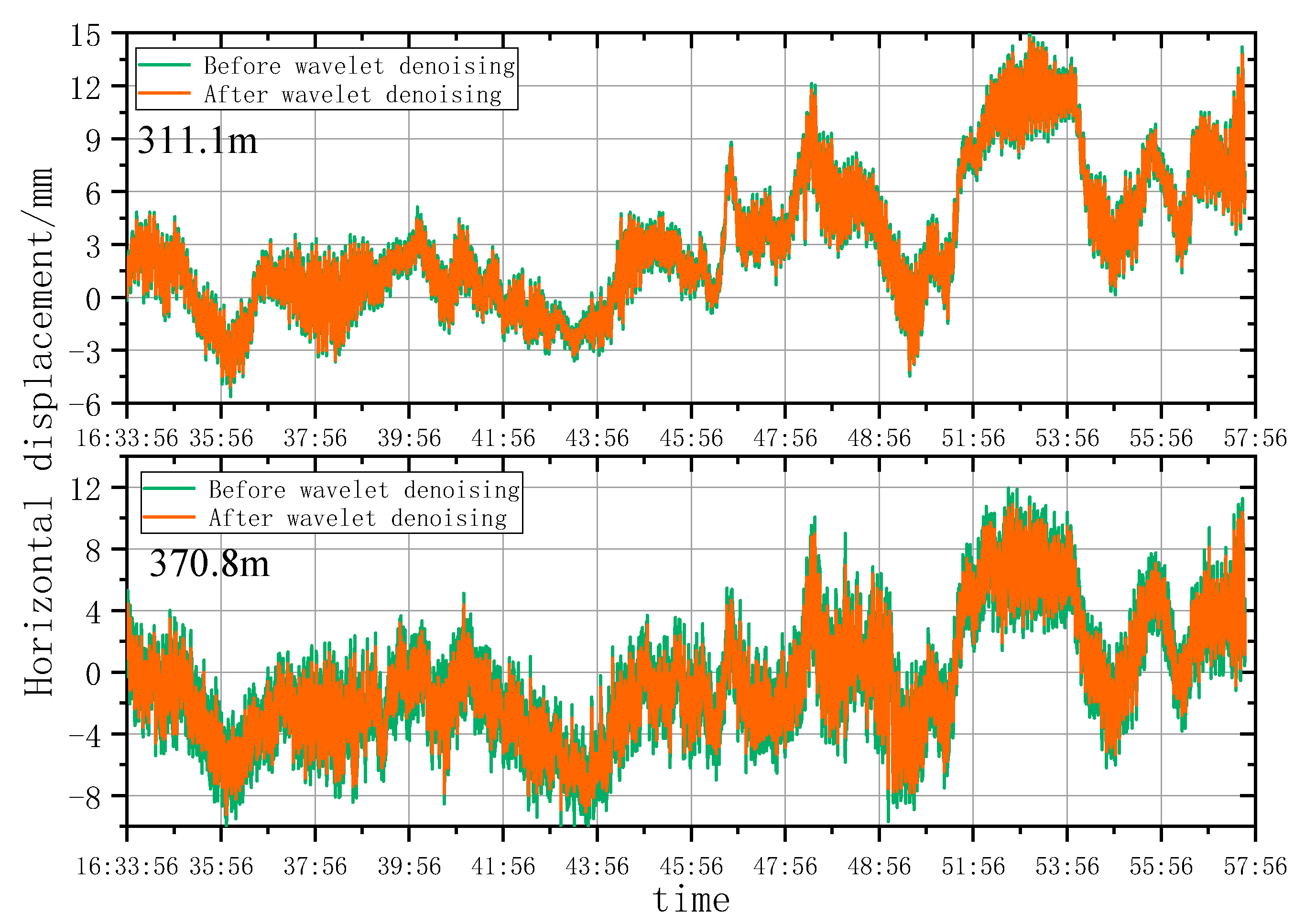
5.1. Wavelet Denoising Analysis
5.1.1. Wavelet Noise Reduction Rule Parameter Combination Debugging
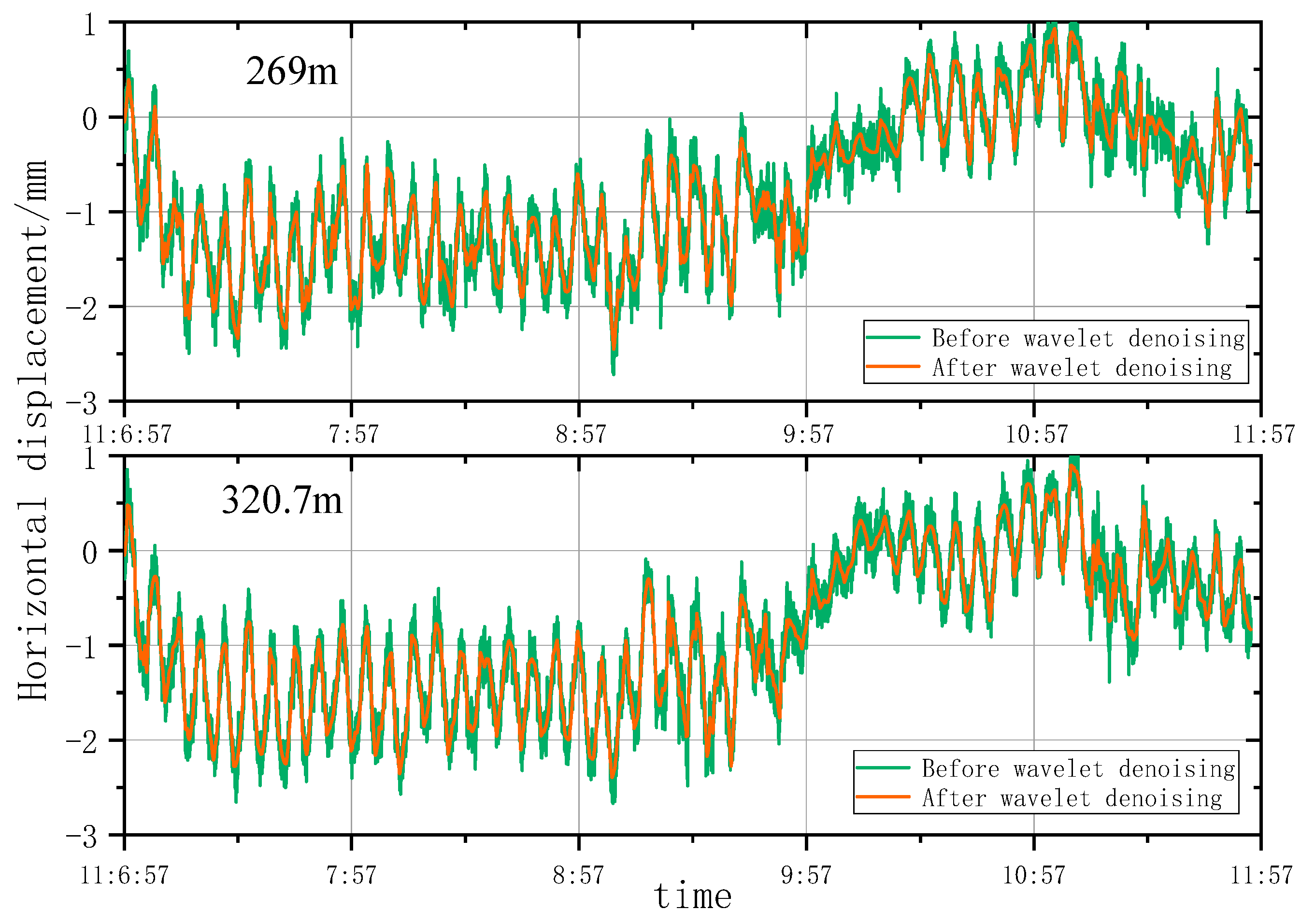
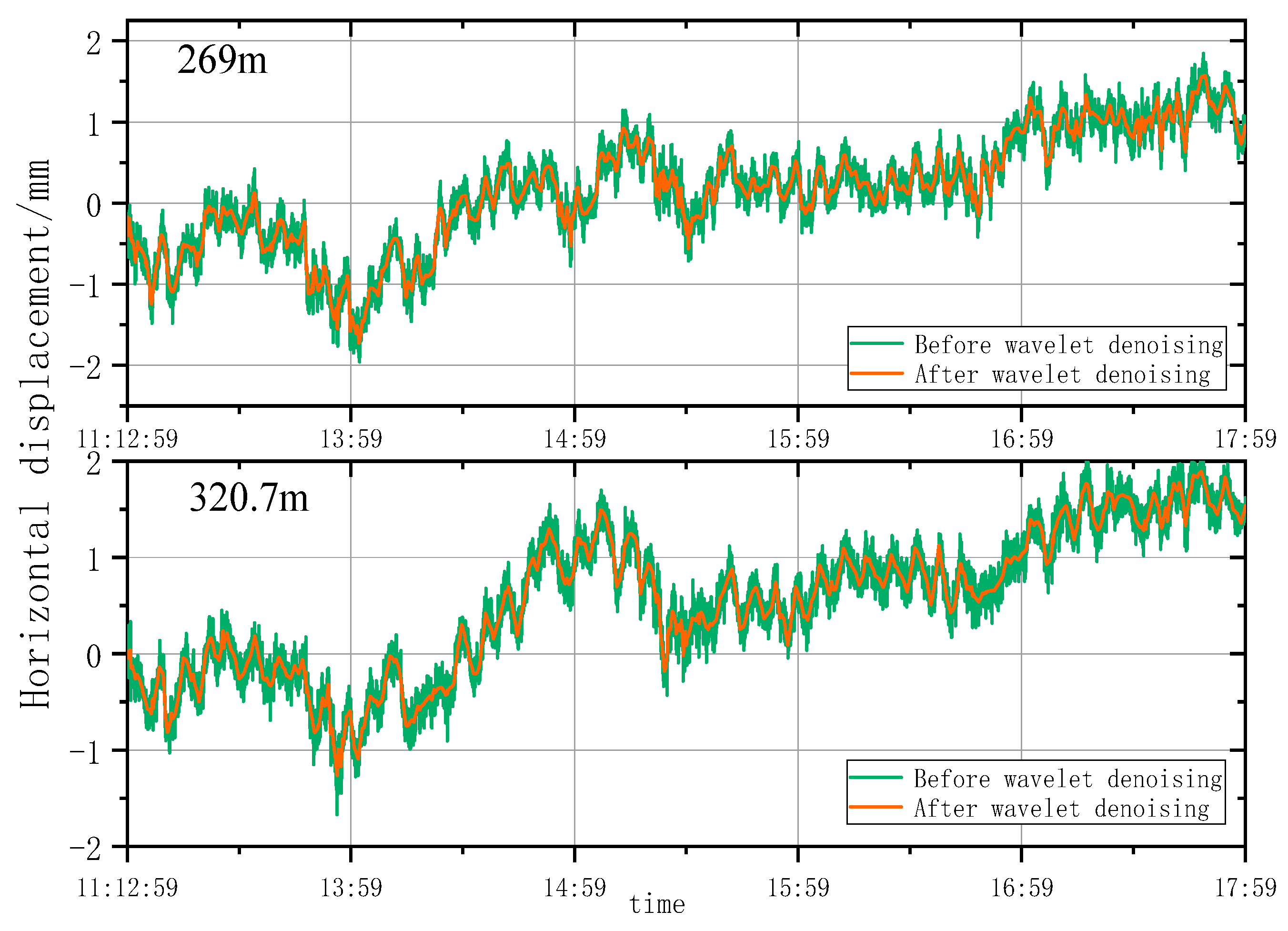
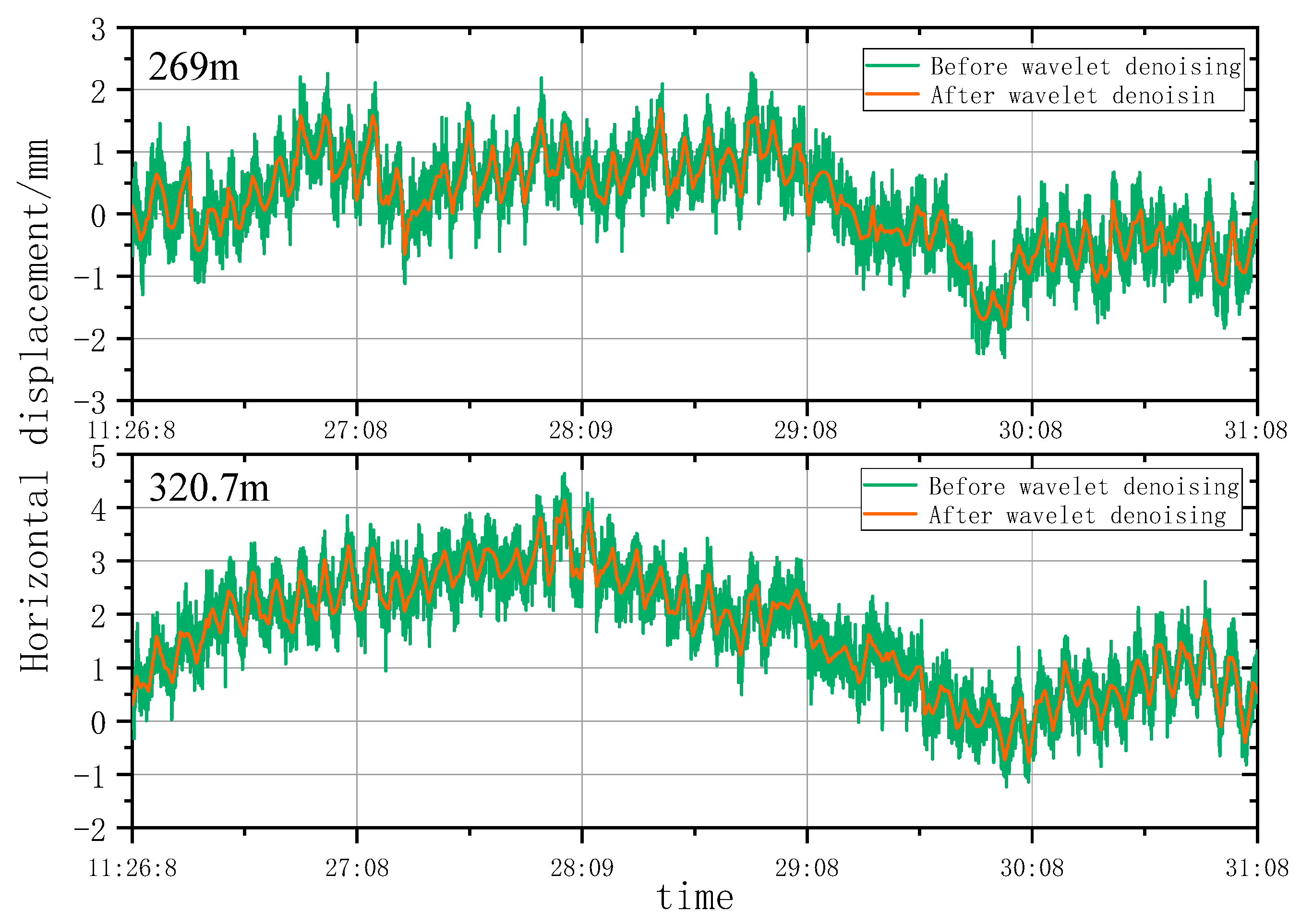
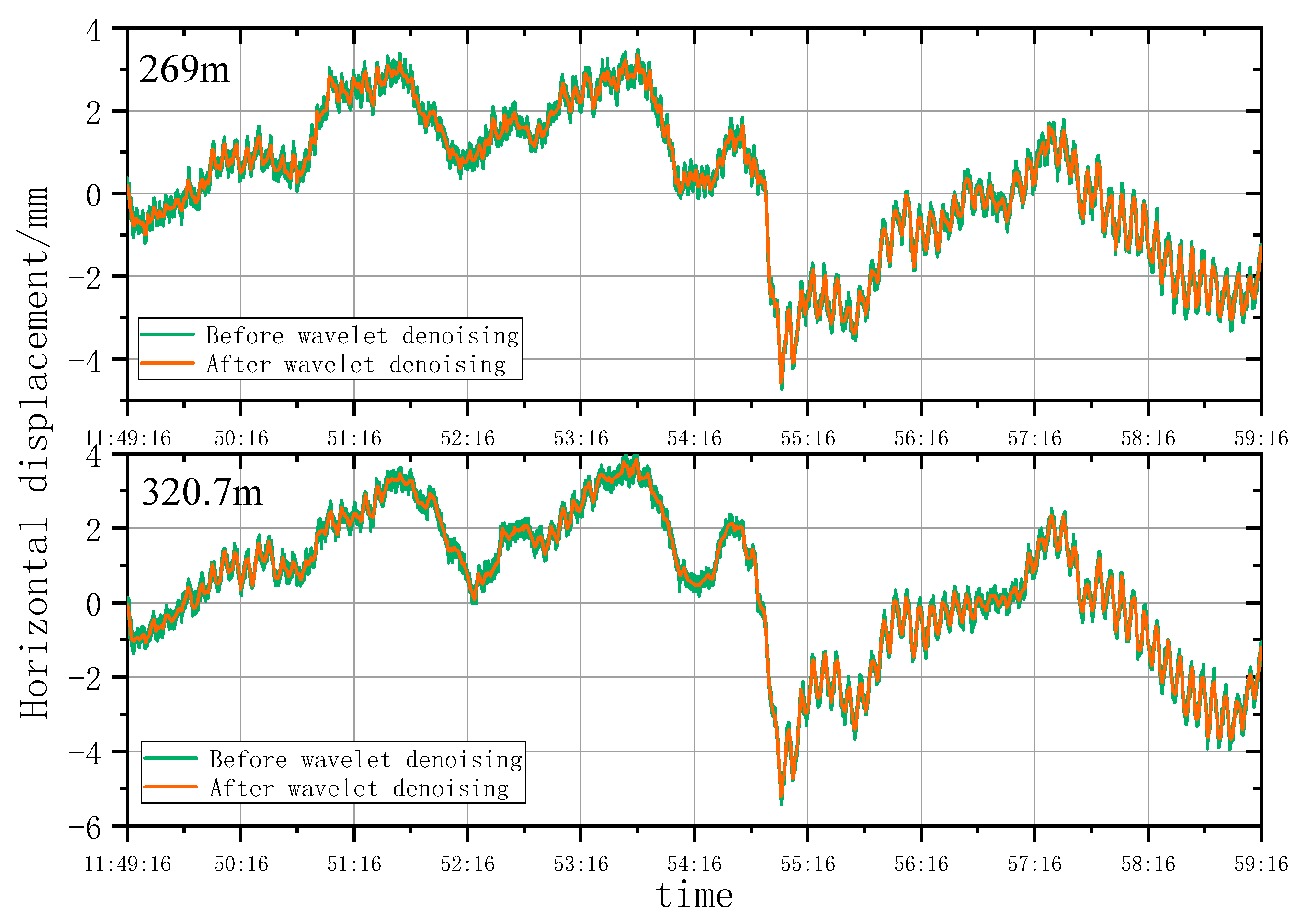
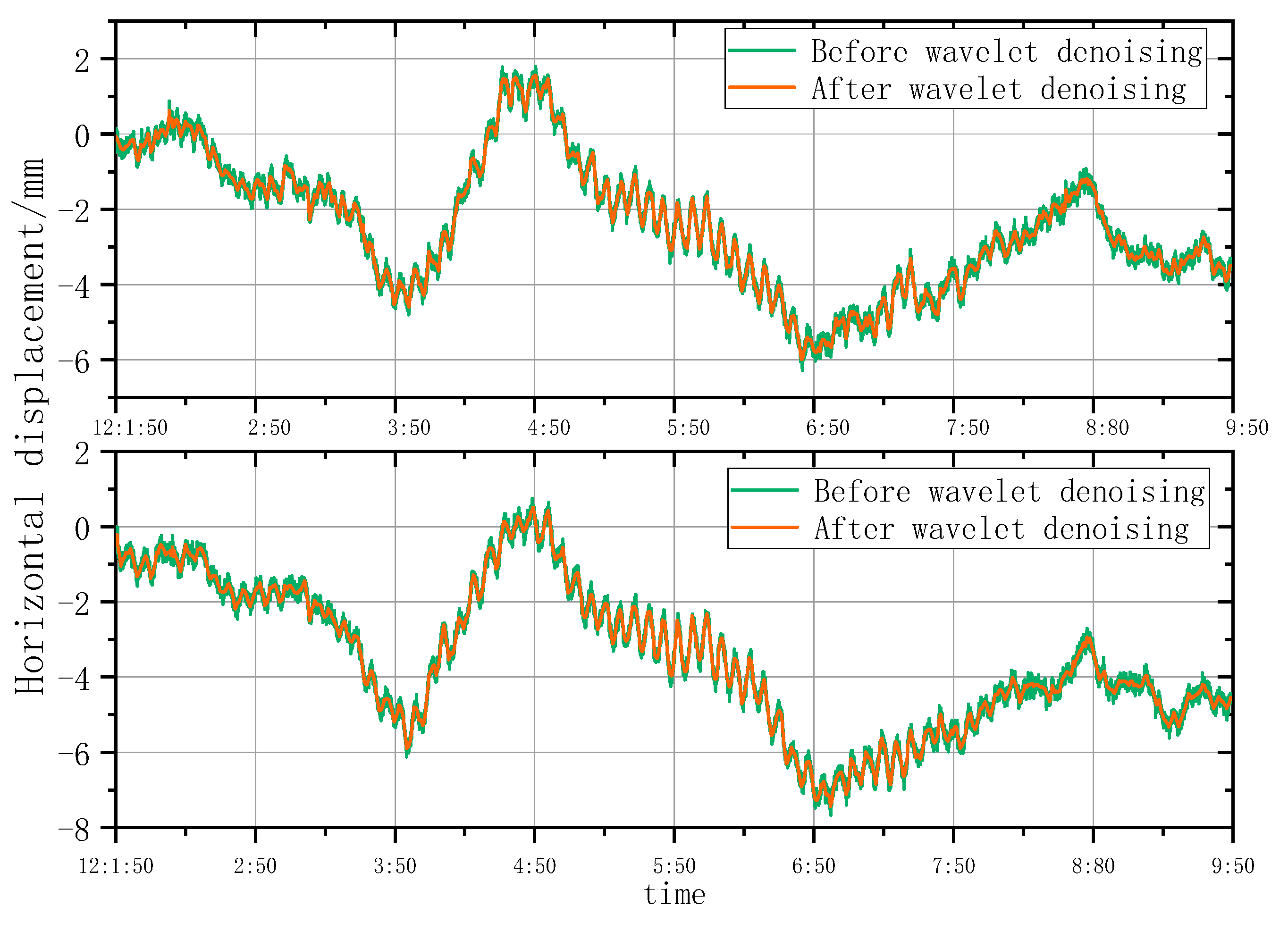
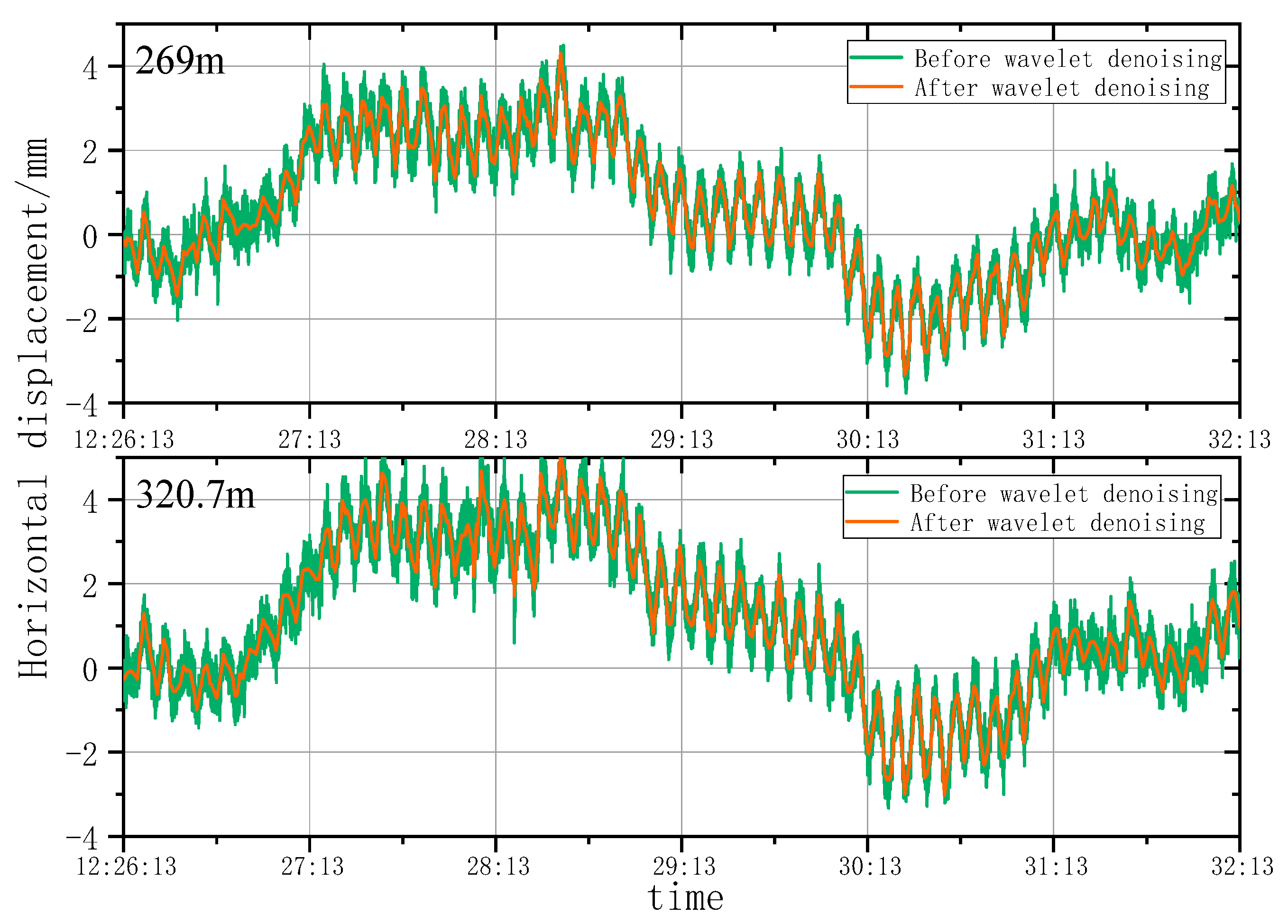
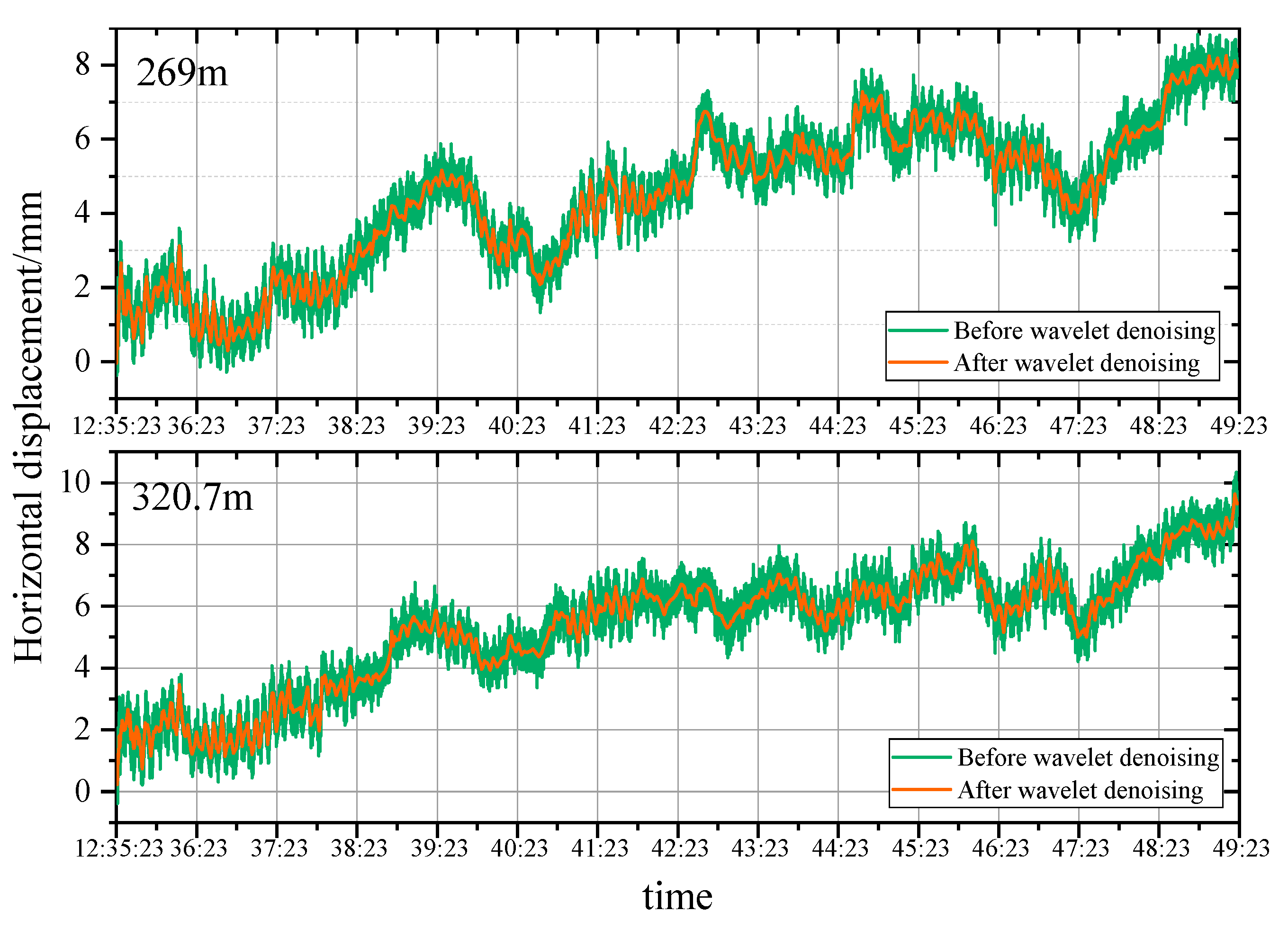
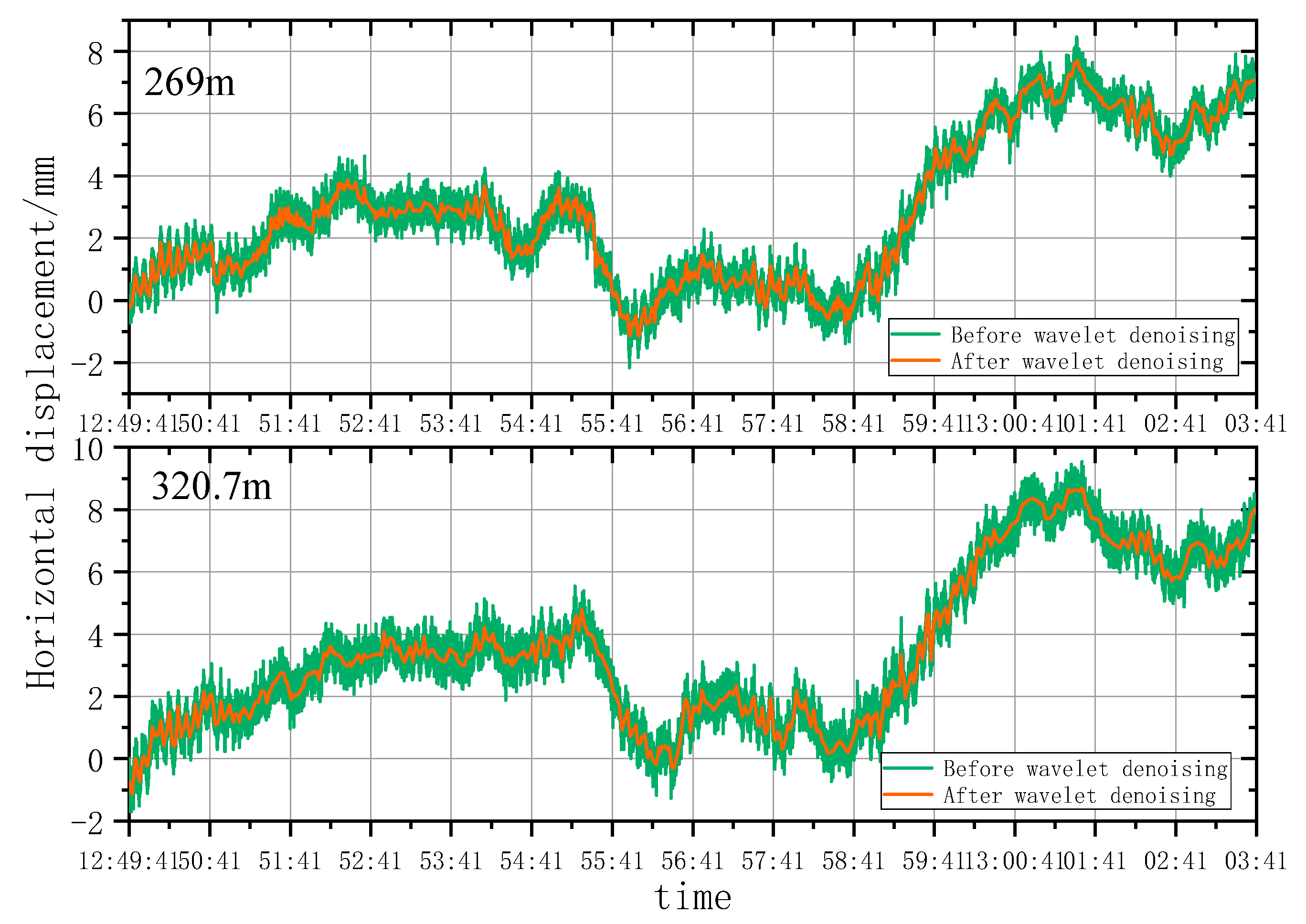
5.1.2. Analysis of Wavelet Denoising Results
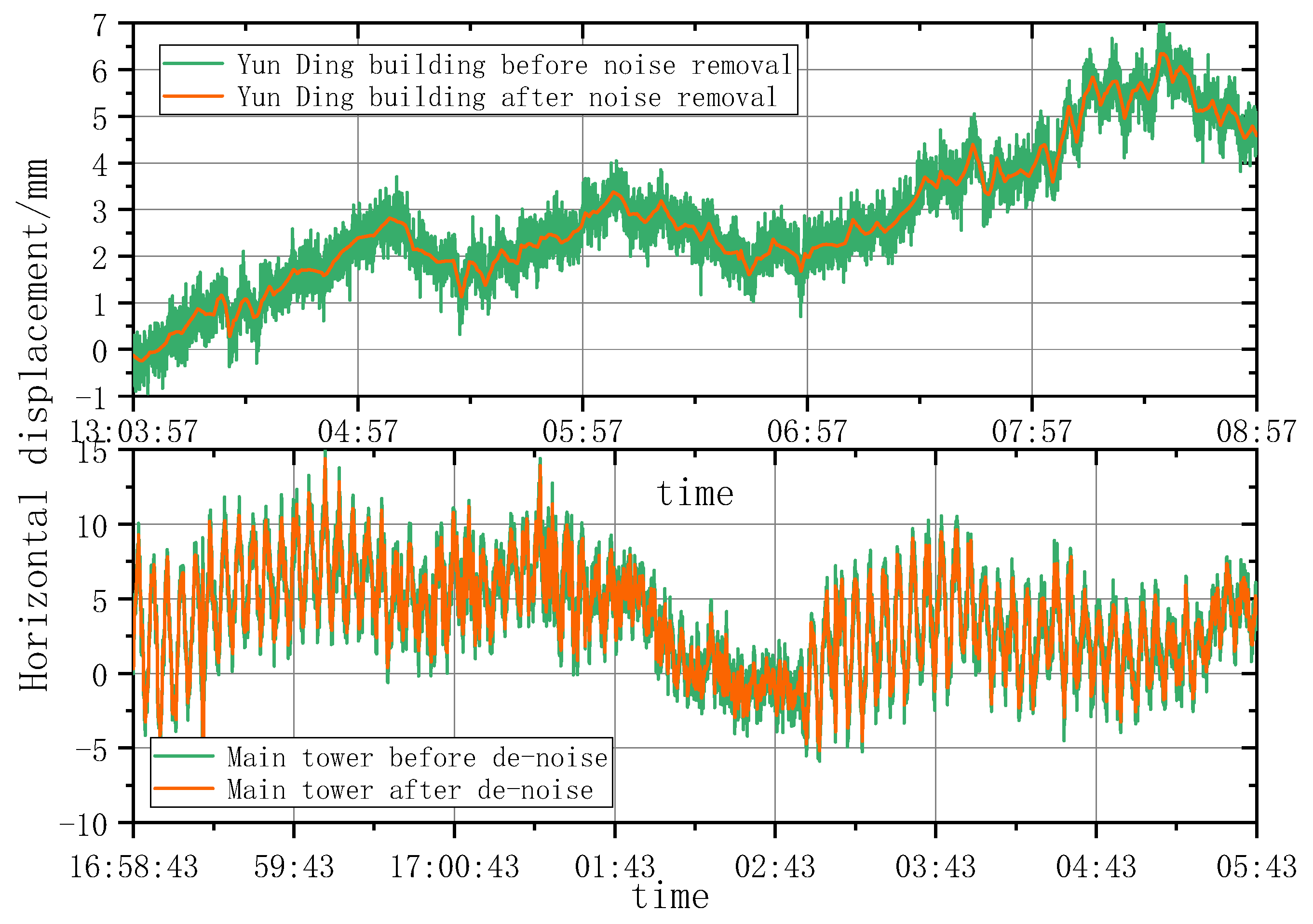
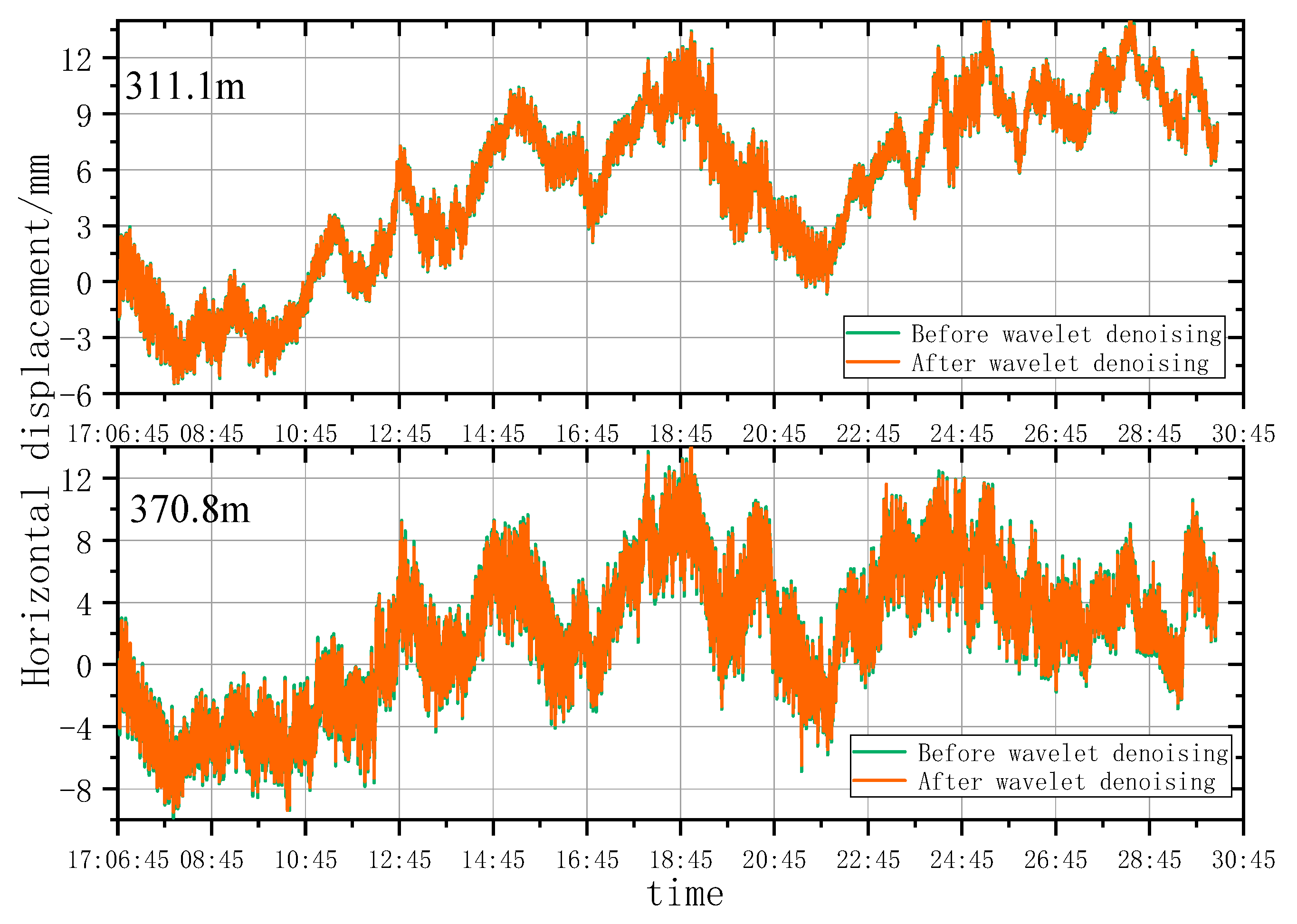
5.2. Motion State Analysis of the Yunding Building under Natural Conditions
5.3. Motion State Analysis of Main Tower under Natural Conditions
6. Dynamic Analysis of Super-Tall Buildings under Wind Load
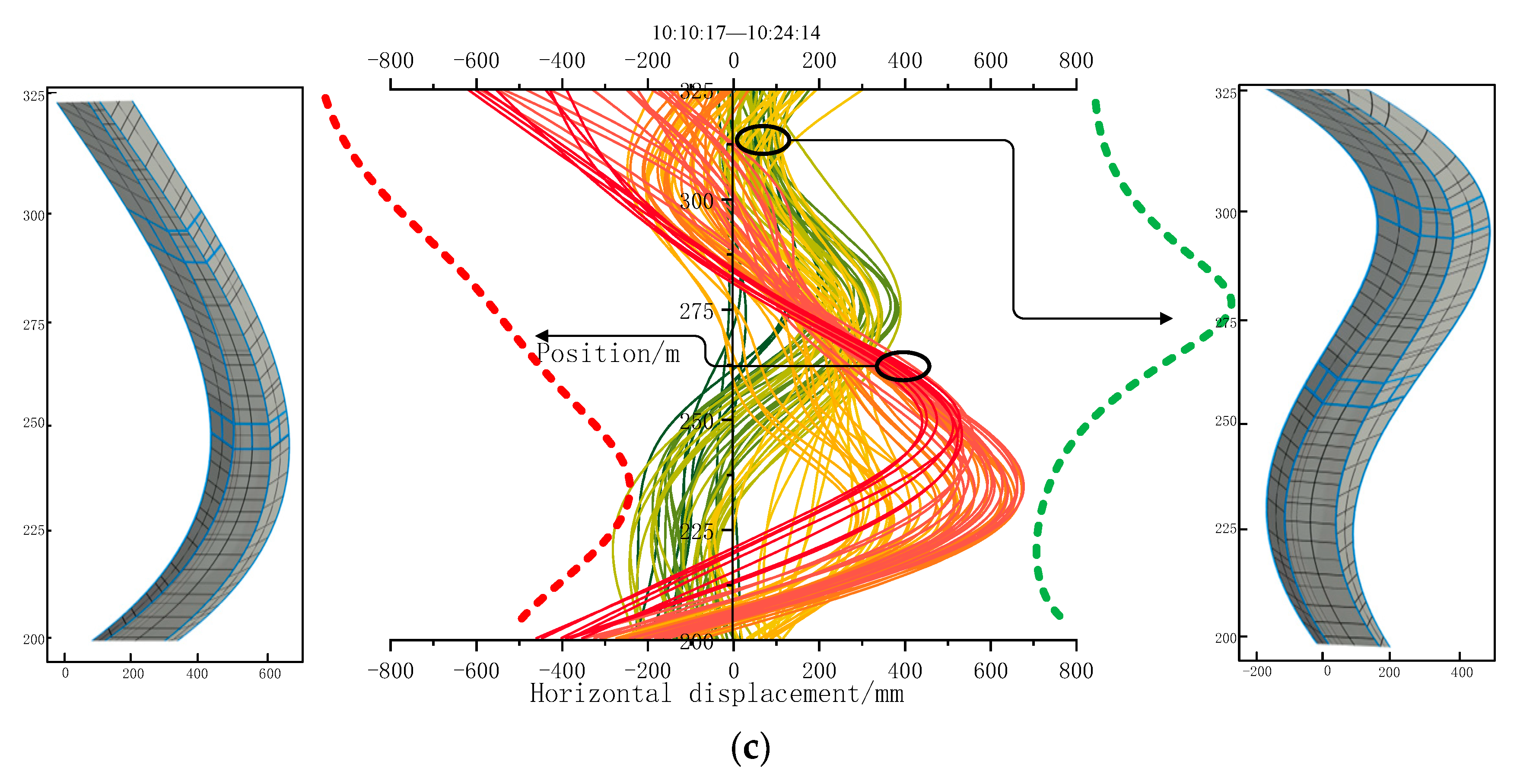
6.1. Motion State Analysis of the Yunding Building under Wind Loads
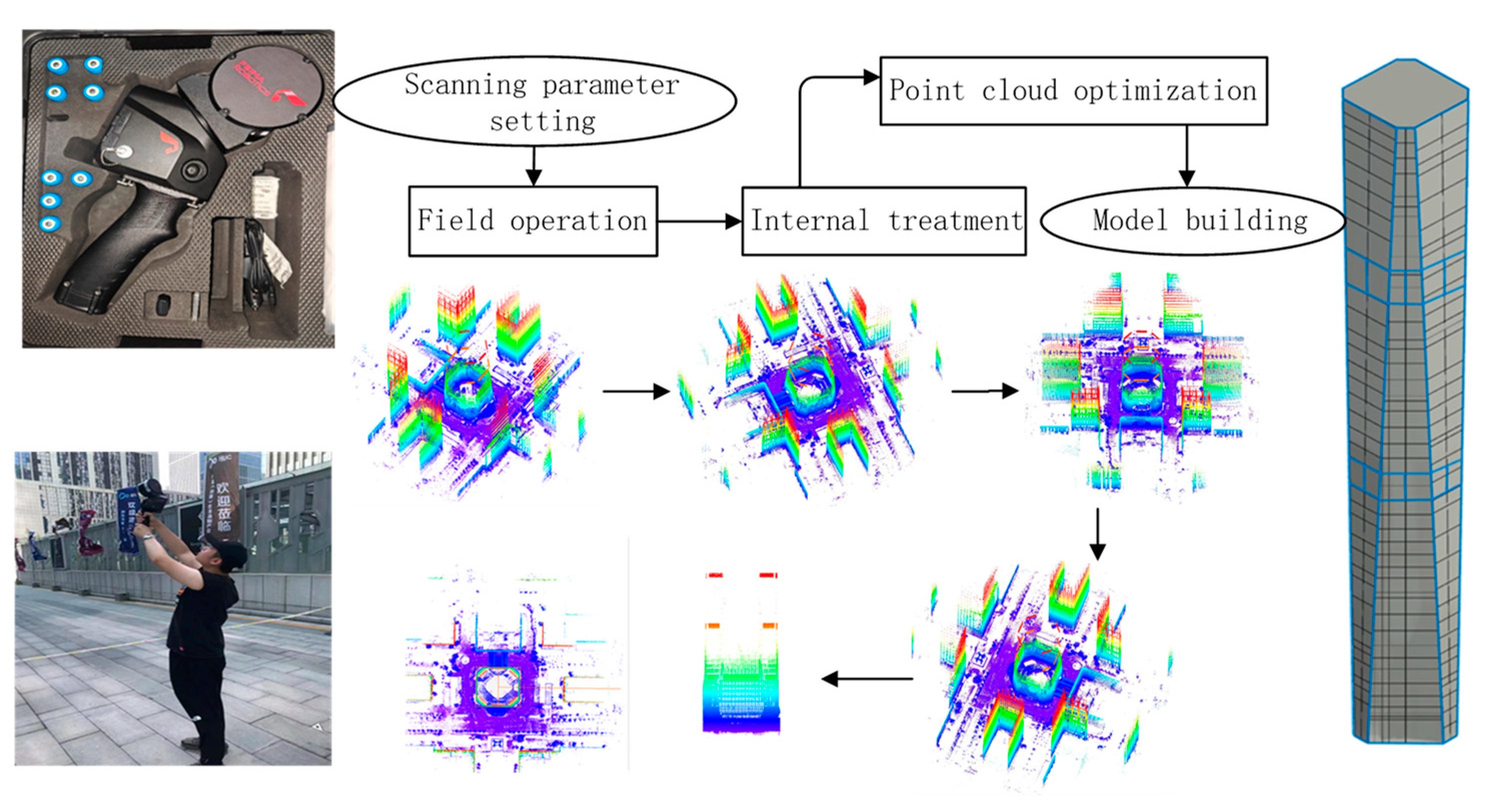
6.2. State Visualization of Genting Building under Wind Load Based on LiDAR Technology
- (1)
- Open the revit software, enter the interface, select a new volume in the panel, and click to enter.
- (2)
- After entering, according to the point cloud information of the Genting building, use the insertion cloud command and the line command to draw, paying special attention to the check of the 3D capture command.
- (3)
- Load the drawn model into the building template and modify the appearance of the volume. In this step, considering that the overall building structure of the Genting building tends to be integrated and similar, the modeling process can build the overall 339 m height building model through the principle of mirror symmetry according to the obtained point cloud information within 100 m of the height of the Genting building. Since the purpose of our modeling is to simulate the motion state of the building under wind load rather than the building itself, there are no special strict requirements for the width of the building during the modeling process.
- (4)
- Click volume and site, select wall, and add wall to volume model.
- (5)
- Click volume and site again. Select a curtain wall system and add a glass curtain wall to the volume model. The curtain wall network can be customized.
- (6)
- Use the type attribute to change the color of the window wall to silver gray in order to simulate the solid color of the Genting building and achieve a beautiful model. By combining the obtained model with Figure 24 in the previous section, it is found that the motion state of super-tall buildings under wind load mainly switches back and forth between the S-shape, hyperbolic line and oblique line, and has obvious elastic deformation characteristics.
7. Conclusions
- (1)
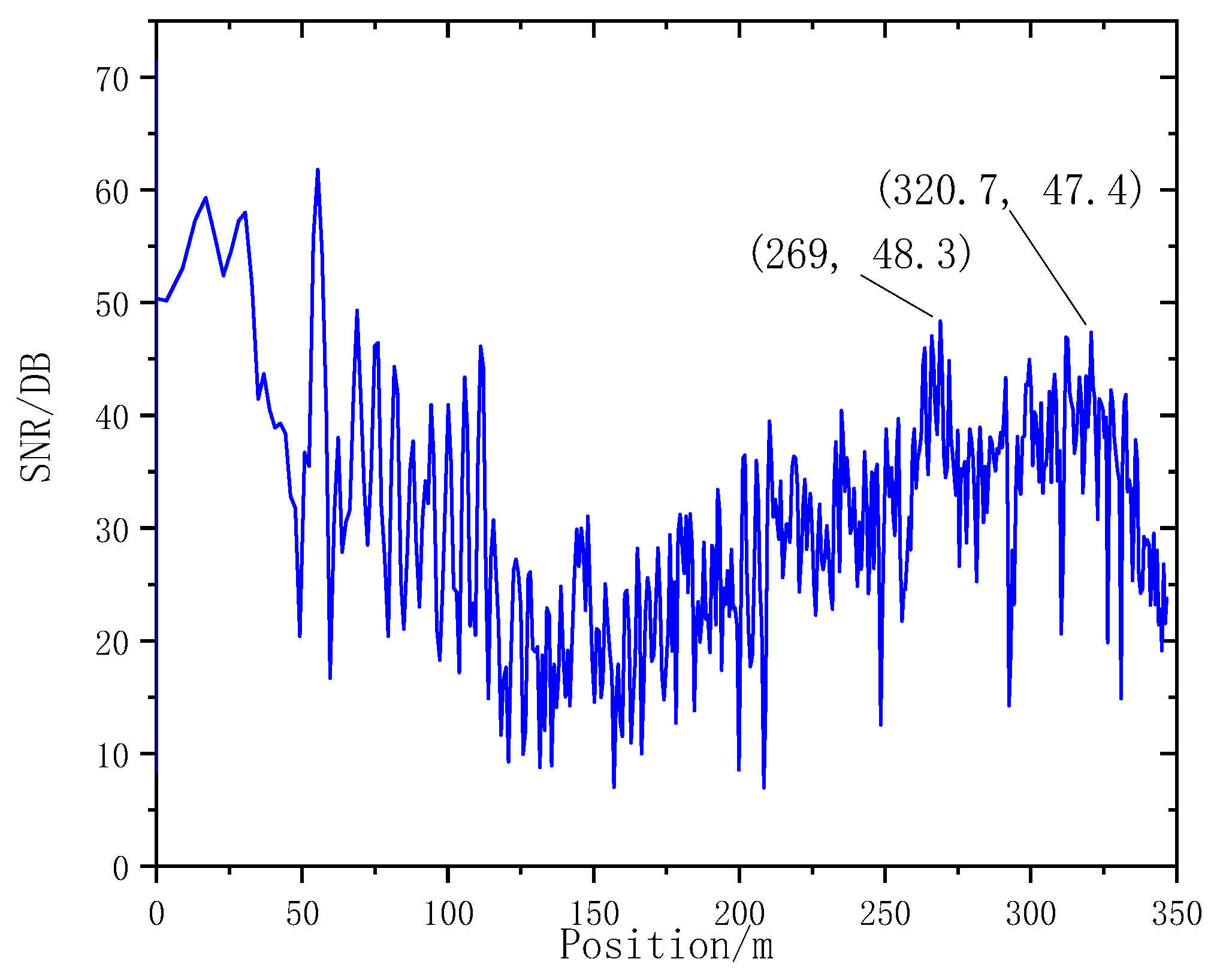
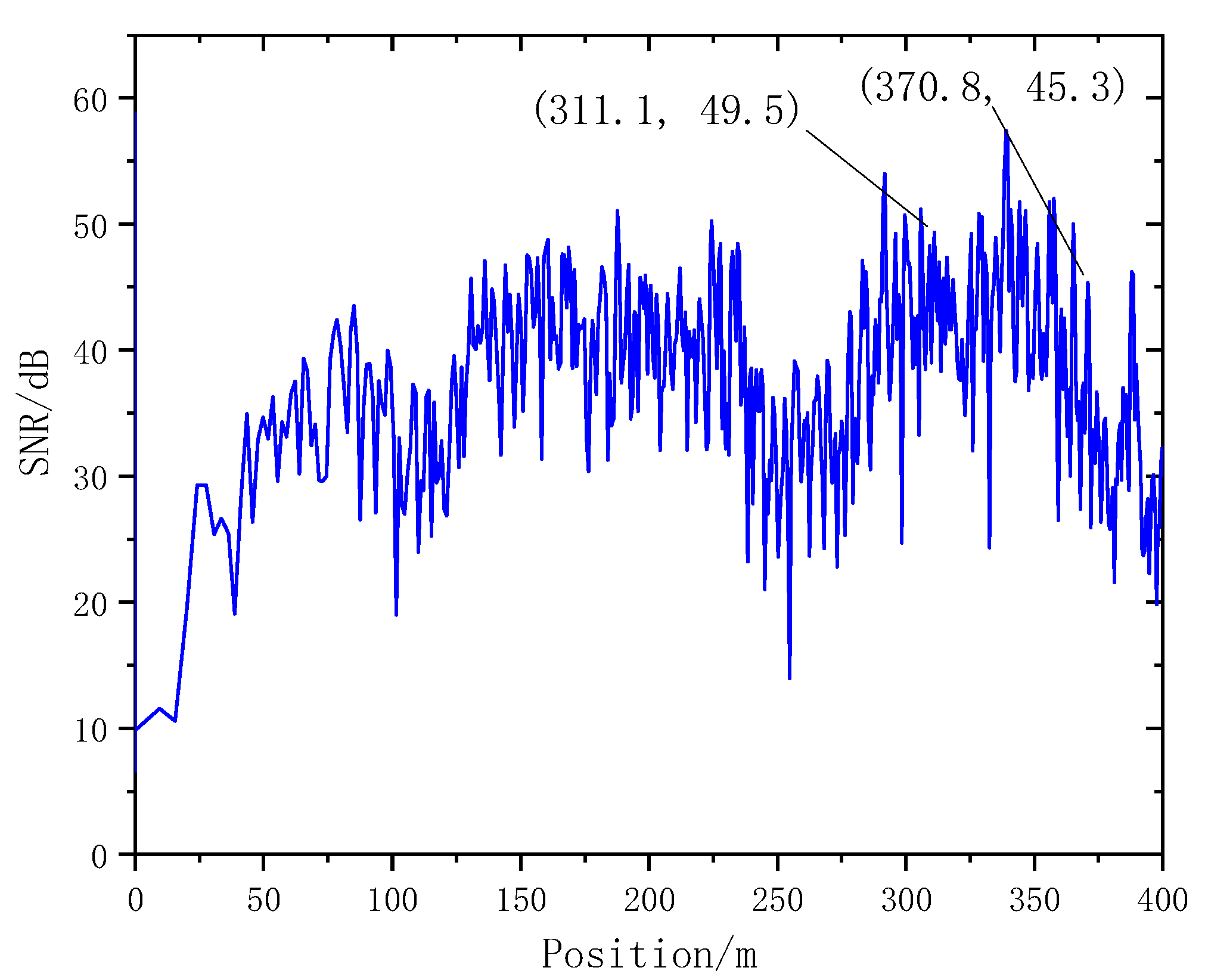
- Yunding Building is located in CBD, surrounded by high-rise buildings. The SNR of the radar in the height range of 200 m~350 m to the ground was higher than 30 db. The data collected by radar had good quality. The Main Tower of Shandong International Financial Center was surrounded by no high-rise buildings and had a small influence on radar signals. The SNR of radar above 50 m from the ground was higher than 30 db and the data collected by radar exhibited good quality.
- (2)
- According to the smoothness index and RMSE analysis, the wavelet analysis can effectively eliminate noises under natural conditions and remove burrs in the time series deformation curves of horizontal displacement significantly. However, the wavelet denoising effect is highly sensitive to construction factors when the architect is under construction. As a result, the time series deformation curves of horizontal displacement after denoising still had serious burrs.
- (3)
- The single-point motion state of super high-rise buildings presents an elastic motion state of nonlinear oscillation around the central axis. Motion states of the characteristic points at different heights generally had consistent trends at most moments, and obvious differences only occurred at specific moments. Under natural conditions, the maximum oscillation amplitude of the Yunding Building and the Main Tower was 9.63 mm and 16.55 mm, respectively.
- (4)
- The external wind loads suddenly increased from 9:56 to 10:30 on 25 September 2022. According to deformation monitoring data, the Yunding Building oscillated within −300.99 mm to 738.52 mm from 9:56:01 to 10:10:01. The Yunding Building oscillated within −633.09 mm to 854.21 mm from 10:10:17 to 10:24:14 and within −398.55 mm to 895.79 mm from 10:24:33 to 10:29:33.
- (5)
- The three-dimensional visualization model of the Genting Building was established based on handheld LiDAR technology, and the spatial state of the super tall building under wind load was obtained through simplified processing by revit, showing the characteristics of switching back and forth between an S-shape, hyperbolic line and oblique line and nonlinear elastic deformation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ji, S.; Liu, S.; Li, Y. Response characteristics of super high-rise building subjected to far-field long-period ground motion. J. Build. Struct. 2018, 11, 1–10. [Google Scholar]
- Fuyuki, A.; Kohei, F.; Masaaki, T.; Izuru, T. Importance of interstory velocity on optimal along-height allocation of viscous oil dampers in super high-rise buildings. Eng. Struct. 2013, 56, 489–500. [Google Scholar]
- Li, Q.; He, Y.; He, Y.; Zhou, K.; Han, X. Monitoring wind effects of a landfall typhoon on a 600 m high skyscraper. Struct. Infrastruct. Eng. 2019, 15, 54–71. [Google Scholar] [CrossRef]
- Silva, I.D.; Ibañez, W.; Poleszuk, G. Experience of Using Total Station and GNSS Technologies for Tall Building Construction Monitoring. In Proceedings of the International Congress and Exhibition Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology, Sharm El Sheikh, Egypt, 15–19 July 2017. [Google Scholar]
- Xu, J.; Jo, H. Development of High-Sensitivity and Low-Cost Electroluminescent Strain Sensor for Structural Health Monitoring. IEEE Sens. J. 2016, 16, 1962–1968. [Google Scholar]
- Li, Q.; Xiao, Y.; Wong, C. Full-scale monitoring of typhoon effects on super tall buildings. J. Fluids Struct. 2005, 20, 297–717. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, P.; Ni, Y.; Zhu, H. Deformation monitoring of a super-tall structure using real-time strain data. Eng. Struct. 2014, 67, 29–38. [Google Scholar] [CrossRef]
- Wang, T.; Xu, Y. Research on Dynamic Characteristic Monitoring Methods for Super High-rise Building. Bull. Surv. Mapp. 2017, 4, 89–92. [Google Scholar]
- Zhang, X.; Zhang, Y.; Li, B.; Qiu, G. GNSS-Based Verticality Monitoring of Super-Tall Buildings. Appl. Sci. 2018, 8, 991. [Google Scholar] [CrossRef]
- Li, Q.; Zhi, L.; Yi, J.; To, A.; Xie, J. Monitoring of typhoon effects on a super-tall building in Hong Kong. Struct. Control Health Monit. 2014, 21, 926–949. [Google Scholar] [CrossRef]
- Li, Q.; Yi, J. Monitoring of dynamic behaviour of super-tall buildings during typhoons. Struct. Infrastruct. Eng. 2016, 12, 289–311. [Google Scholar] [CrossRef]
- Hwang, J.; Yun, H.; Park, S.; Lee, S. Optimal methods of RTK-GPS/accelerometer integration to monitor the displacement of structures. Sensors 2012, 12, 1014–1034. [Google Scholar] [CrossRef]
- Fabio, C.; Clemente, F. Monitoring a steel building using GPS sensors. Smart Struct. Syst. 2011, 7, 349–363. [Google Scholar]
- Guo, Y.; Kareem, A.; Ni, Y.; Liao, W. Performance evaluation of Canton Tower under winds based on full-scale data. J. Wind Eng. Ind. Aerodyn. 2012, 104, 116–128. [Google Scholar]
- Xiong, C.; Niu, Y. Investigation of the Dynamic Behavior of a Super High-rise Structure using RTK-GNSS Technique. KSCE J. Civ. Eng. 2019, 23, 654–665. [Google Scholar]
- Gao, Y.; Dian, Z.; Zhang, S.; Zhang, Y.; Li, S. Adaptive local gradient estimation smoothing UKF phase unwrapping algorithm. J. China Univ. Min. Technol. 2022, 51, 1007–1015. [Google Scholar]
- Li, R.; Chang, L.; Qin, H. Application of InSAR Technology in Deformation Monitoring of Super High Rise Buildings. Constr. Qual. 2021, 39, 70–73. [Google Scholar]
- Wu, W.; Cui, H.; Hu, J.; Yao, L. Detection and 3D Visualization of Deformations for High-Rise Buildings in Shenzhen, China from High-Resolution TerraSAR-X Datasets. Appl. Sci. 2019, 9, 3818. [Google Scholar]
- Zhou, L. Monitoring and Analysis of Surface Subsidence and Building Deformation by Radar Interferometry. Ph.D. Thesis, Wuhan University, Wuhan, China, June 2018. [Google Scholar]
- Tapete, D.; Casagli, N.; Luzi, G.; Fanti, R.; Gigli, G.; Leva, D. Integrating radar and laser-based remote sensing techniques for monitoring structural deformation of archaeological monuments. J. Archaeol. Sci. 2013, 40, 176–189. [Google Scholar] [CrossRef]
- Marchisio, M.; Piroddi, L.; Ranieri, G.; Calcina, S.V.; Farina, P. Comparison of natural and artificial forcing to study the dynamic behaviour of bell towers in low wind context by means of ground-based radar interferometry: The case of the Leaning Tower in Pisa. J. Geophys. Eng. 2014, 11, 055004. [Google Scholar] [CrossRef]
- Luzi, G.; Monserrat, O.; Crosetto, M. The Potential of Coherent Radar to Support the Monitoring of the Health State of Buildings. Res. Nondestruct. Eval. 2012, 23, 125–145. [Google Scholar]
- Zhou, L.; Guo, J.; Wen, X.; Ma, J.; Yang, F.; Wang, C.; Zhang, D. Monitoring and Analysis of Dynamic Characteristics of Super High-rise Buildings using GB-RAR: A Case Study of the WGC under Construction, China. Appl. Sci. 2020, 10, 808. [Google Scholar] [CrossRef]
- Montuori, A.; Luzi, G.; Bignami, C.; Gaudiosi, I.; Stramondo, S.; Crosetto, M.; Buongiorno, M.F. The Interferometric Use of Radar Sensors for the Urban Monitoring of Structural Vibrations and Surface Displacements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3761–3776. [Google Scholar] [CrossRef]
- Cheng, Y.; Wu, Z.; Zhou, Y. Three-dimensional Reconstruction of Soviet-style Courtyard Based on Terrestrial LiDAR. Mod. Surv. Mapp. 2021, 5, 50–54. [Google Scholar]
- Zhou, J.; Tian, J.; Chen, Y.; Mao, Q.; Li, Q. Research on Data Fusion Method of Ground-Based SAR and 3D Lase Scanning. J. Geomat. 2015, 3, 26–30. [Google Scholar]







| Name | Number of Adjustments | IBIS Monitoring (mm) | TCA2003 Monitoring (mm) | Dial Meter Adjustment (mm) | IBIS Error (mm) | TCA2003 Error (mm) |
|---|---|---|---|---|---|---|
| Experiment 1 | 1 | 1.0274 | 1 | 1 | 0.0274 | 0 |
| 2 | 0.9786 | 1.02 | 1 | −0.0214 | 0.02 | |
| 3 | −0.9876 | −1.02 | −1 | −0.0124 | 0.02 | |
| 4 | −1.0502 | −0.98 | −1 | 0.0502 | −0.02 | |
| Experiment 2 | 1 | 0.4652 | 0.4 | 0.5 | −0.0348 | −0.1 |
| 2 | 0.5187 | 0.47 | 0.5 | 0.0187 | −0.03 | |
| 3 | 0.4634 | 0.58 | 0.5 | −0.0366 | 0.08 | |
| 4 | −0.4875 | −0.48 | −0.5 | −0.0125 | −0.02 | |
| 5 | −0.5248 | −0.5 | −0.5 | 0.0248 | 0 | |
| 6 | −0.5347 | −0.5 | −0.5 | 0.0347 | 0 | |
| Experiment 3 | 1 | 0.2157 | 0.17 | 0.2 | 0.0157 | −0.03 |
| 2 | 0.2034 | 0.18 | 0.2 | 0.0034 | −0.02 | |
| 3 | 0.0982 | 0.15 | 0.1 | 0.0022 | 0 | |
| 4 | 0.2048 | 0.25 | 0.2 | 0.0048 | 0.05 | |
| 5 | −0.1885 | −0.2 | −0.2 | −0.0115 | 0 | |
| 6 | −0.1918 | −0.18 | −0.2 | −0.0082 | −0.02 | |
| 7 | −0.209 | −0.22 | −0.2 | 0.009 | 0.02 | |
| 8 | −0.2234 | −0.18 | −0.2 | 0.0234 | −0.02 |
| Threshold Type | Threshold Function Type, Defined Threshold Rescaling Type, Wavelet Decomposition Layer Number, Wavelet Basis | R (Smoothness Index) | RMSE | SSD |
|---|---|---|---|---|
| heursure | s, sln, lev7, sym3 | 0.00925 | 0.14012 | 0.74264 |
| s, sln, lev7, sym8 | 0.00689 | 0.14083 | 0.74639 | |
| s, sln, lev7, sym10 | 0.00701 | 0.14061 | 0.74523 | |
| s, sln, lev1, sym3 | 0.25194 | 0.07988 | 0.42336 | |
| s, sln, lev5, sym3 | 0.01033 | 0.13421 | 0.71131 | |
| s, sln, lev6, sym7 | 0.00926 | 0.14012 | 0.74264 | |
| s, sln, lev7, sym1 | 0.09723 | 0.15029 | 0.79654 | |
| s, sln, lev7, sym2 | 0.01279 | 0.14495 | 0.76824 | |
| s, sln, lev7, sym4 | 0.00781 | 0.14098 | 0.74719 | |
| h, sln, lev7, sym3 | 0.02981 | 0.12421 | 0.65831 | |
| h, mln, lev7, sym3 | 0.00621 | 0.34994 | 1.85467 | |
| s, one, lev7, sym3 | 0.00605 | 0.22628 | 1.19928 | |
| s, mln, lev7, sym3 | 0.00069 | 0.35112 | 1.86094 | |
| s, one, lev7, sym3 | 0.00138 | 0.29108 | 1.54272 | |
| sqtwolog | s, sln, lev7, sym3 | 0.00712 | 0.15344 | 0.81323 |
| h, sln, lev7, sym3 | 0.02277 | 0.13012 | 0.68964 | |
| s, mln, lev7, sym3 | 0.00053 | 0.35137 | 1.86226 | |
| s, one, lev7, sym3 | 0.00066 | 0.32799 | 1.73835 | |
| Rigrsure | s, sln, lev7, sym3 | 0.05124 | 0.10059 | 0.53313 |
| h, sln, lev7, sym3 | 0.35572 | 0.08356 | 0.44287 | |
| s, mln, lev7, sym3 | 0.01666 | 0.34349 | 1.82049 | |
| s, one, lev7, sym3 | 0.00539 | 0.20022 | 1.06117 |
| Yunding Building | Main Tower | ||||||
|---|---|---|---|---|---|---|---|
| Segment of Survey | r (Smoothness Index) | RMSE | SSD | Segment of Survey | r (Smoothness Index) | RMSE | SSD |
| 1106571 | 0.00925 | 0.14012 | 0.75441 | 1547251 | 0.00782 | 0.14943 | 2.24509 |
| 1106572 | 0.00741 | 0.14121 | 0.77505 | 1547252 | 0.02069 | 0.25499 | 2.20841 |
| 1112591 | 0.00576 | 0.11541 | 0.67830 | 1535171 | 0.15125 | 0.17335 | 1.60989 |
| 1112592 | 0.00284 | 0.11416 | 0.72075 | 1535172 | 0.05515 | 0.29064 | 1.99589 |
| 1119581 | 0.00042 | 0.27306 | 0.39560 | 1523061 | 0.04298 | 0.16739 | 2.57050 |
| 1119582 | 0.00041 | 0.30948 | 0.47989 | 1523062 | 0.01066 | 0.26937 | 3.15948 |
| 1149161 | 0.0072 | 0.11138 | 1.72893 | 1706451 | 0.53105 | 0.05253 | 4.58172 |
| 1149162 | 0.00602 | 0.11251 | 1.89729 | 1706452 | 0.56674 | 0.15831 | 4.39969 |
| 1201501 | 0.00646 | 0.10794 | 1.71760 | 1633561 | 0.03586 | 0.16844 | 3.90771 |
| 1201502 | 0.00563 | 0.11081 | 1.89620 | 1633562 | 0.07 | 0.487 | 3.74168 |
| 1126081 | 0.00108 | 0.27459 | 0.72590 | 1617451 | 0.01061 | 0.11254 | 3.27263 |
| 1126082 | 0.00091 | 0.30371 | 1.05497 | 1617452 | 0.02368 | 0.18926 | 3.89401 |
| 1226131 | 0.00276 | 0.27737 | 1.49659 | 1602301 | 0.01812 | 0.11284 | 4.01258 |
| 1226132 | 0.00261 | 0.3204 | 1.71434 | 1602302 | 0.03153 | 0.19844 | 4.99208 |
| 1235231 | 0.00064 | 0.282 | 1.93375 | 1658431 | 0.05715 | 0.16601 | 2.60052 |
| 1235232 | 0.00052 | 0.31824 | 1.91998 | 1658432 | 0.14003 | 0.49929 | 3.24224 |
| average value | 0.00375 | 0.20702 | 1.24309 | average value | 0.11083 | 0.21561 | 3.27713 |
| Laser Field Angle | Camera Field Angle | Relative Accuracy/Precision | Number of Laser Channels | Maximum Ranging | Dot Frequency | Echo Intensity | Number of Cameras | Camera Resolution |
|---|---|---|---|---|---|---|---|---|
| 270° × 360° | 200° × 100° | 2 cm/5 cm | 16 | 100 m | 300 kpts/s | 8 bits | 3 | 500,000,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Wang, Z.; Sang, W.; Zhou, B.; Wang, Z.; Yao, G.; Bi, J. Research on Dynamic Deformation Laws of Super High-Rise Buildings and Visualization Based on GB-RAR and LiDAR Technology. Remote Sens. 2023, 15, 3651. https://doi.org/10.3390/rs15143651
Zhang G, Wang Z, Sang W, Zhou B, Wang Z, Yao G, Bi J. Research on Dynamic Deformation Laws of Super High-Rise Buildings and Visualization Based on GB-RAR and LiDAR Technology. Remote Sensing. 2023; 15(14):3651. https://doi.org/10.3390/rs15143651
Chicago/Turabian StyleZhang, Guojian, Zhiyang Wang, Wengang Sang, Baoxing Zhou, Zhiwei Wang, Guobiao Yao, and Jingxue Bi. 2023. "Research on Dynamic Deformation Laws of Super High-Rise Buildings and Visualization Based on GB-RAR and LiDAR Technology" Remote Sensing 15, no. 14: 3651. https://doi.org/10.3390/rs15143651
APA StyleZhang, G., Wang, Z., Sang, W., Zhou, B., Wang, Z., Yao, G., & Bi, J. (2023). Research on Dynamic Deformation Laws of Super High-Rise Buildings and Visualization Based on GB-RAR and LiDAR Technology. Remote Sensing, 15(14), 3651. https://doi.org/10.3390/rs15143651










