Greening and Browning Trends on the Pacific Slope of Peru and Northern Chile
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Remote Sensing Data
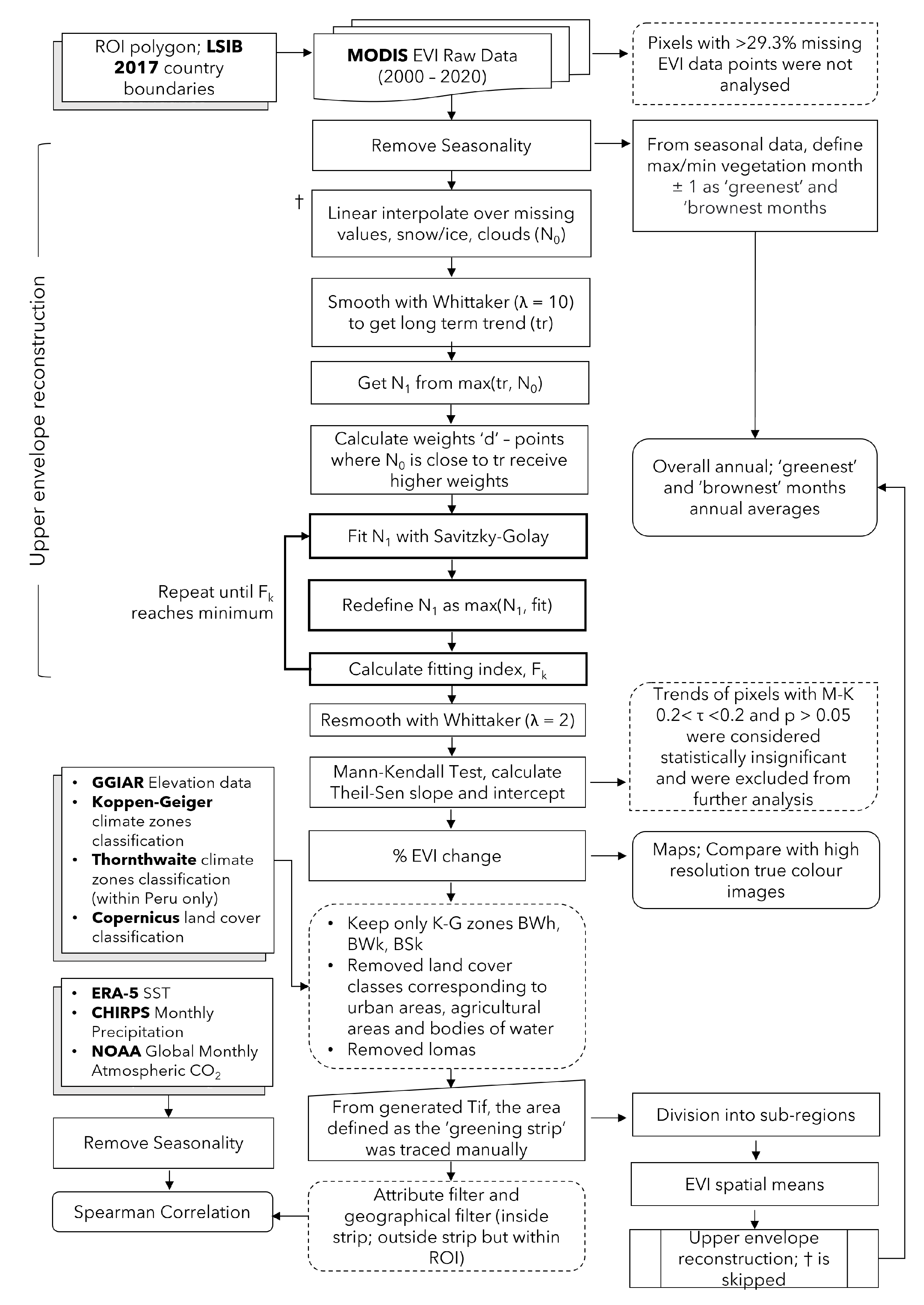
2.3. Data Analysis Workflow
2.4. Pixel Pre-Processing
2.5. Seasonal Decomposition
2.6. EVI Upper Envelope Calculation
- if , i.e., the iteration fit curve continually increased, the fit of the first iteration was taken,
- if, after 10 iterations, the condition was not met, i.e., iteration fit curve continually decreased, the fit of the last iteration was taken.
2.7. Assessment of Statistical Significance
2.8. Spatially Averaged Time Series
2.9. Statistical Correlations
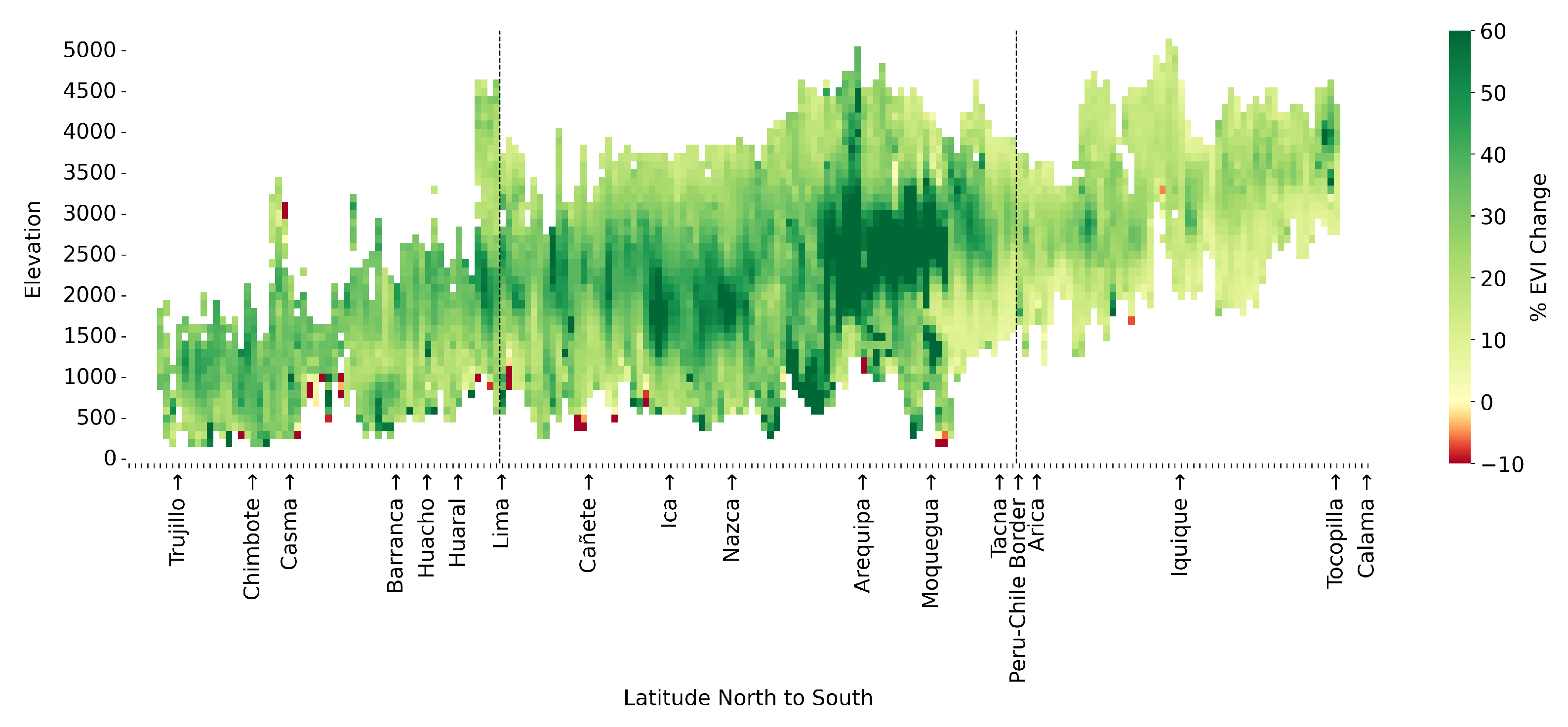
3. Results
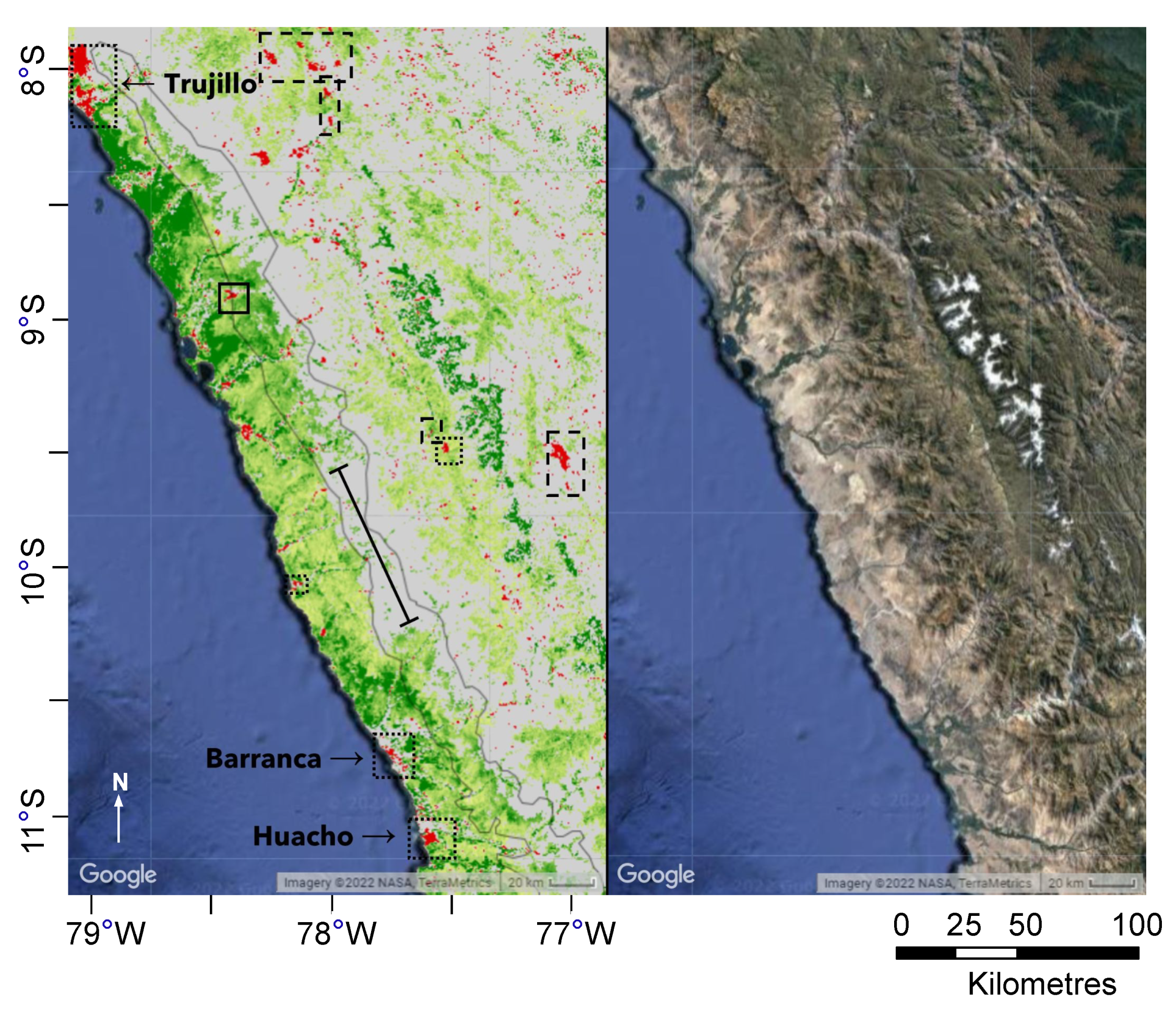
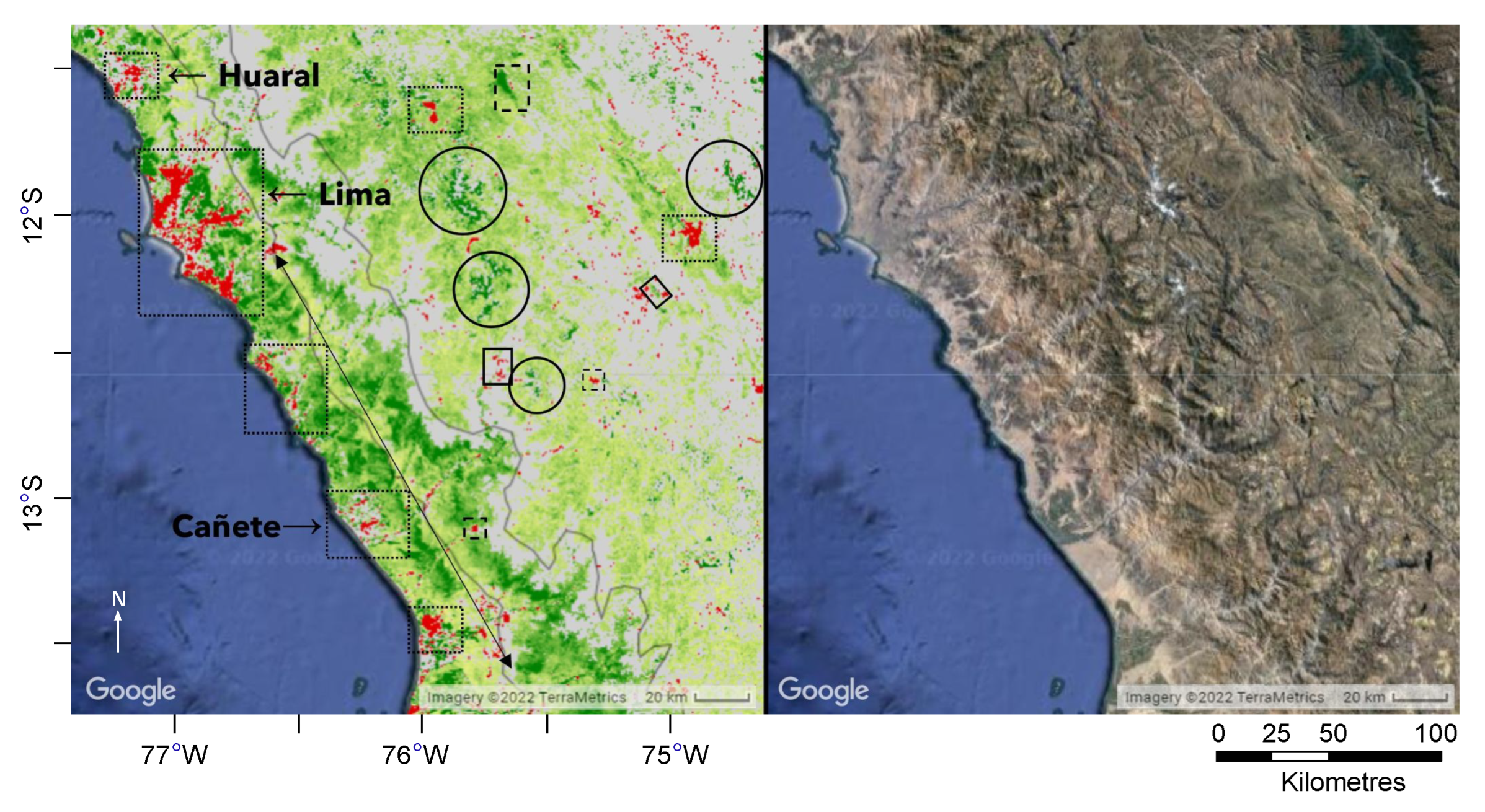
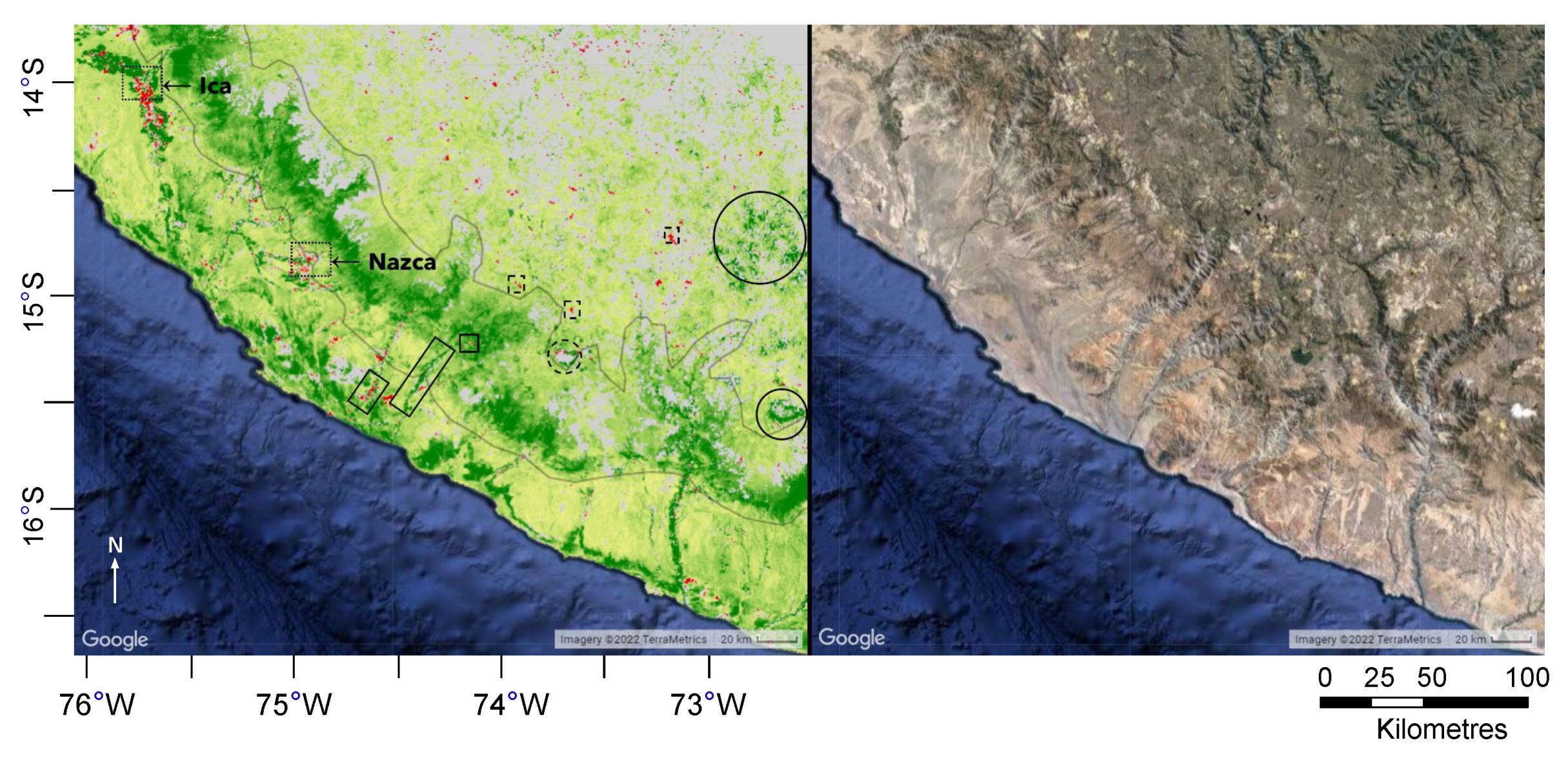
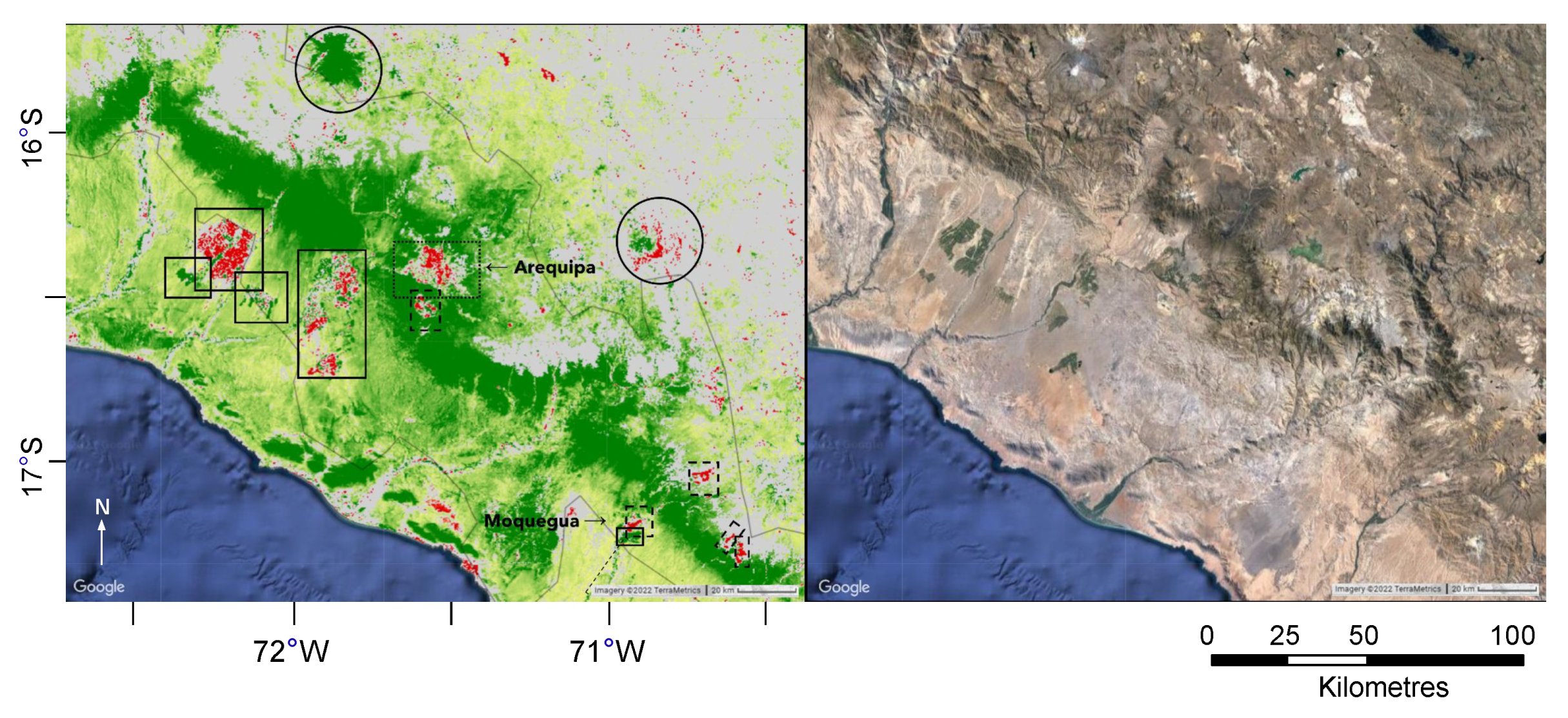
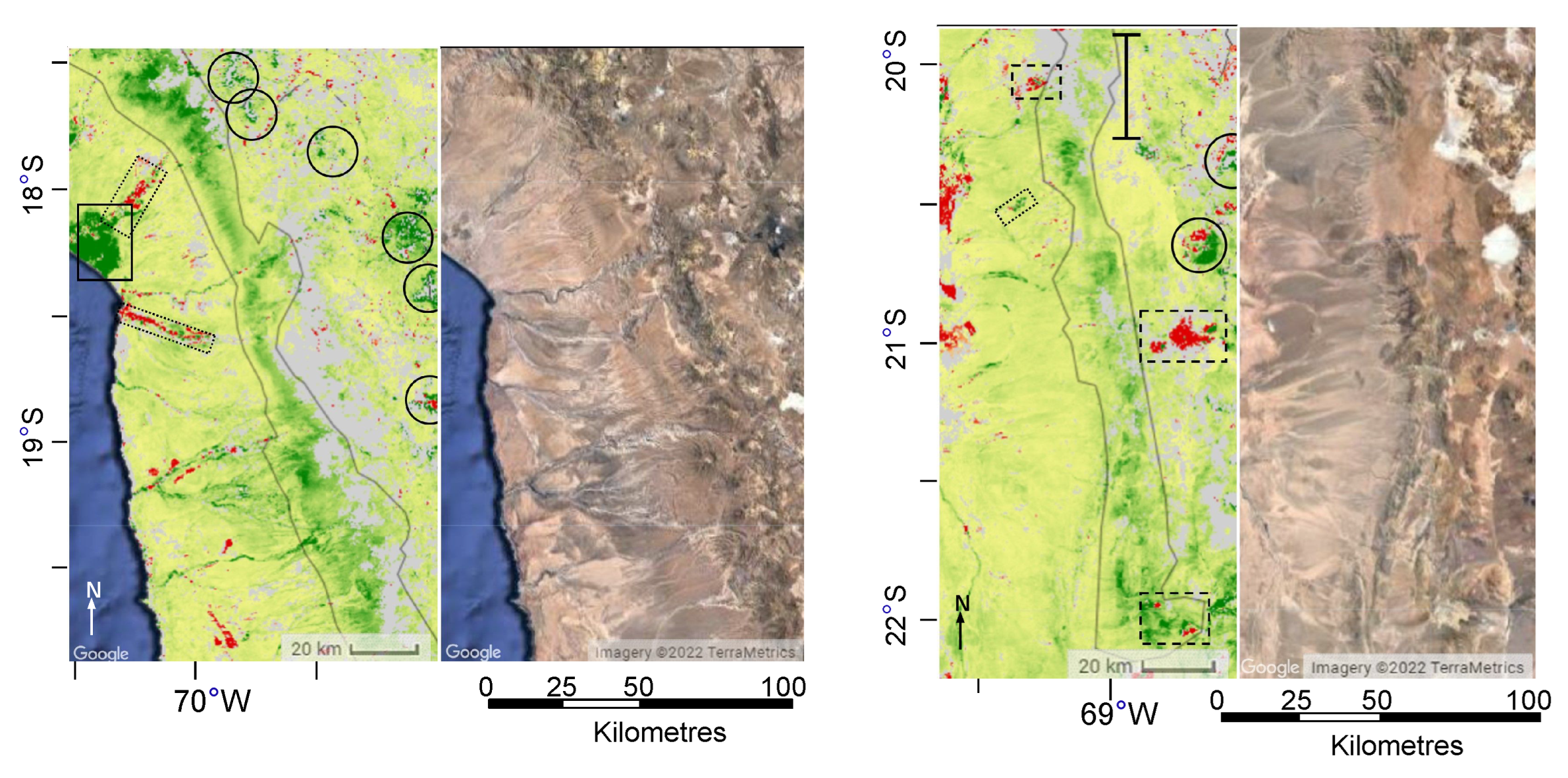
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| BWh | Hot arid desert |
| BWk | Cold arid desert |
| BSk | Cold arid steppe |
| BSh | Hot arid steppe |
| ET | Polar Tundra |
| GS | Greening Strip |
| NDVI | Normalized Difference Vegetation Index |
| EVI | Enhanced Vegetation Index |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| LSIB | Large Scale International Boundary |
| M–K | Mann–Kendall |
| ERA-5 | European Centre for Medium-Range Weather Forecasts reanalysis |
| CHIRPS | Climate Hazards Group InfraRed Precipitation with Station |
| NOAA | National Oceanic and Atmospheric Administration |
| CGIAR | Consultative Group for International Agricultural Research |
| LCCS | Land Cover Classification System |
| FAO | Food and Agriculture Organisation |
| SST | Sea Surface Temperature |
| LST | Land Surface Temperature |
| ROI | Region of Interest |
| ITCZ | Intertropical Convergence Zone |
| ENSO | El Niño Southern Oscillation |
References
- Holdridge, L.R. Determination of world plant formations from simple climatic data. Science 1947, 105, 367–368. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Köppen, W. Klassifikation der Klima nach Temperatur, Niederschlag und Jahreslauf. Pet. Mitt. 1918, 64, 243–248. [Google Scholar]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Drennan, P.M.; Nobel, P. Responses of CAM species to increasing atmospheric CO2 concentrations. Plant Cell Environ. 2000, 23, 767–781. [Google Scholar] [CrossRef]
- D’Odorico, P.; Laio, F.; Ridolfi, L. Vegetation patterns induced by random climate fluctuations. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Suc, J.P. Origin and evolution of the Mediterranean vegetation and climate in Europe. Nature 1984, 307, 429–432. [Google Scholar] [CrossRef]
- Magyari, E.; Jakab, G.; Bálint, M.; Kern, Z.; Buczkó, K.; Braun, M. Rapid vegetation response to Lateglacial and early Holocene climatic fluctuation in the South Carpathian Mountains (Romania). Quat. Sci. Rev. 2012, 35, 116–130. [Google Scholar] [CrossRef]
- Gitay, H.; Suárez, A.; Watson, R.T.; Dokken, D.J. Climate Change and Biodiversity; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2002. [Google Scholar]
- Mooney, H.; Larigauderie, A.; Cesario, M.; Elmquist, T.; Hoegh-Guldberg, O.; Lavorel, S.; Mace, G.M.; Palmer, M.; Scholes, R.; Yahara, T. Biodiversity, climate change, and ecosystem services. Curr. Opin. Environ. Sustain. 2009, 1, 46–54. [Google Scholar] [CrossRef]
- Scholes, R.J. Climate change and ecosystem services. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 537–550. [Google Scholar] [CrossRef]
- Song, X.P.; Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Tyukavina, A.; Vermote, E.F.; Townshend, J.R. Global land change from 1982 to 2016. Nature 2018, 560, 639–643. [Google Scholar] [CrossRef]
- NOAA. Global Monitoring Laboratory—Carbon Cycle Greenhouse Gases. 2022. Available online: https://gml.noaa.gov/ccgg/trends/global.html (accessed on 26 April 2023).
- Joos, F.; Spahni, R. Rates of change in natural and anthropogenic radiative forcing over the past 20,000 years. Proc. Natl. Acad. Sci. USA 2008, 105, 1425–1430. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Bakker, D.C.; Hauck, J.; Le Quéré, C.; Peters, G.P.; Peters, W.; Pongratz, J.; et al. Global carbon budget 2021. Earth Syst. Sci. Data 2022, 14, 1917–2005. [Google Scholar] [CrossRef]
- Ralph Keeling, R.; Tans, P. Trends in Atmospheric Carbon Dioxide, Mauna Loa CO2 Monthly Mean Data. Available online: https://gml.noaa.gov/ccgg/trends/ (accessed on 22 March 2022).
- Piao, S.; Wang, X.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tømmervik, H.; et al. Characteristics, drivers and feedbacks of global greening. Nat. Rev. Earth Environ. 2020, 1, 14–27. [Google Scholar] [CrossRef]
- Morison, J.; Lawlor, D. Interactions between increasing CO2 concentration and temperature on plant growth. Plant Cell Environ. 1999, 22, 659–682. [Google Scholar] [CrossRef]
- Mishra, N.B.; Mainali, K.P. Greening and browning of the Himalaya: Spatial patterns and the role of climatic change and human drivers. Sci. Total Environ. 2017, 587, 326–339. [Google Scholar] [CrossRef] [PubMed]
- Young, B.; Young, K.R.; Josse, C. Vulnerability of tropical Andean ecosystems to climate change. In Climate Change and Biodiversity in the Tropical Andes; SCOPE, IAI: Lod, Israel, 2011; pp. 170–181. [Google Scholar]
- Prieto-Torres, D.A.; Lira-Noriega, A.; Navarro-Sigüenza, A.G. Climate change promotes species loss and uneven modification of richness patterns in the avifauna associated to Neotropical seasonally dry forests. Perspect. Ecol. Conserv. 2020, 18, 19–30. [Google Scholar] [CrossRef]
- Ruhm, J.; Böhnert, T.; Weigend, M.; Merklinger, F.F.; Stoll, A.; Quandt, D.; Luebert, F. Plant life at the dry limit—Spatial patterns of floristic diversity and composition around the hyperarid core of the Atacama Desert. PLoS ONE 2020, 15, e0233729. [Google Scholar] [CrossRef] [PubMed]
- Romero, H.; Ordenes, F. Emerging urbanization in the Southern Andes. Mt. Res. Dev. 2004, 24, 197–201. [Google Scholar] [CrossRef]
- Nottingham, A.T.; Turner, B.L.; Whitaker, J.; Ostle, N.; Bardgett, R.D.; McNamara, N.P.; Salinas, N.; Meir, P. Temperature sensitivity of soil enzymes along an elevation gradient in the Peruvian Andes. Biogeochemistry 2016, 127, 217–230. [Google Scholar] [CrossRef]
- Horgan, F.G. Effects of deforestation on diversity, biomass and function of dung beetles on the eastern slopes of the Peruvian Andes. For. Ecol. Manag. 2005, 216, 117–133. [Google Scholar] [CrossRef]
- Bax, V.; Francesconi, W. Environmental predictors of forest change: An analysis of natural predisposition to deforestation in the tropical Andes region, Peru. Appl. Geogr. 2018, 91, 99–110. [Google Scholar] [CrossRef]
- Barnes, E.P.; Hunter, M.A.; Lepage, H.V.; Luján, H.E.V.; Jamanca, N.C. The avifauna of the río Fortaleza drainage basin, dptos. Lima and Ancash, Peru. Cotinga 2022, 44, 43–59. [Google Scholar]
- Best, B.; Kessler, M. Biodiversity and Conservation in Tumbesian Ecuador and Peru; BirdLife International: Cambridge, UK, 1995; Volume 218. [Google Scholar]
- Devenish, C.; Nuñez Cortez, E.; Buchanan, G.; Smith, G.R.; Marsden, S.J. Estimating ecological metrics for holistic conservation management in a biodiverse but information-poor tropical region. Conserv. Sci. Pract. 2020, 2, e153. [Google Scholar] [CrossRef]
- Stattersfield, A.J. Endemic Bird Areas of the World-Priorities for Biodiversity Conservation; Bird Life International: Cambridge, UK, 1998. [Google Scholar]
- Ioris, A.A. Water scarcity and the exclusionary city: The struggle for water justice in Lima, Peru. Water Int. 2016, 41, 125–139. [Google Scholar] [CrossRef]
- Salmoral, G.; Zegarra, E.; Vázquez-Rowe, I.; González, F.; Del Castillo, L.; Saravia, G.R.; Graves, A.; Rey, D.; Knox, J.W. Water-related challenges in nexus governance for sustainable development: Insights from the city of Arequipa, Peru. Sci. Total Environ. 2020, 747, 141114. [Google Scholar] [CrossRef]
- Fragkou, M.C.; McEvoy, J. Trust matters: Why augmenting water supplies via desalination may not overcome perceptual water scarcity. Desalination 2016, 397, 1–8. [Google Scholar] [CrossRef]
- Arp, W. Effects of source-sink relations on photosynthetic acclimation to elevated CO2. Plant Cell Environ. 1991, 14, 869–875. [Google Scholar] [CrossRef]
- Lawlor, D.; Mitchell, R. The effects of increasing CO2 on crop photosynthesis and productivity: A review of field studies. Plant Cell Environ. 1991, 14, 807–818. [Google Scholar] [CrossRef]
- Morison, J.I.; Morecroft, M.D. Plant Growth and Climate Change; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Smith, W.; Donahue, R. Simulated influence of altitude on photosynthetic CO2 uptake potential in plants. Plant Cell Environ. 1991, 14, 133–136. [Google Scholar] [CrossRef]
- Li, Y.; Deng, J.; Mu, C.; Xing, Z.; Du, K. Vertical distribution of CO2 in the atmospheric boundary layer: Characteristics and impact of meteorological variables. Atmos. Environ. 2014, 91, 110–117. [Google Scholar] [CrossRef]
- Rau, P.; Bourrel, L.; Labat, D.; Melo, P.; Dewitte, B.; Frappart, F.; Lavado, W.; Felipe, O. Regionalization of rainfall over the Peruvian Pacific slope and coast. Int. J. Climatol. 2017, 37, 143–158. [Google Scholar] [CrossRef]
- Sanabria, J.; Bourrel, L.; Dewitte, B.; Frappart, F.; Rau, P.; Solis, O.; Labat, D. Rainfall along the coast of Peru during strong El Niño events. Int. J. Climatol. 2018, 38, 1737–1747. [Google Scholar] [CrossRef]
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing; Guilford Press: New York City, NY, USA, 2011. [Google Scholar]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Cortés, J.; Mahecha, M.D.; Reichstein, M.; Myneni, R.B.; Chen, C.; Brenning, A. Where are global vegetation greening and browning trends significant? Geophys. Res. Lett. 2021, 48, e2020GL091496. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Egbert, S.L. A comparison of MODIS 250-m EVI and NDVI data for crop mapping: A case study for southwest Kansas. Int. J. Remote Sens. 2010, 31, 805–830. [Google Scholar] [CrossRef]
- Huete, A.R.; Didan, K.; Shimabukuro, Y.E.; Ratana, P.; Saleska, S.R.; Hutyra, L.R.; Yang, W.; Nemani, R.R.; Myneni, R. Amazon rainforests green-up with sunlight in dry season. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Verbyla, D. The greening and browning of Alaska based on 1982–2003 satellite data. Glob. Ecol. Biogeogr. 2008, 17, 547–555. [Google Scholar] [CrossRef]
- Parent, M.B.; Verbyla, D. The browning of Alaska’s boreal forest. Remote Sens. 2010, 2, 2729–2747. [Google Scholar] [CrossRef]
- Bhatt, U.S.; Walker, D.A.; Raynolds, M.K.; Comiso, J.C.; Epstein, H.E.; Jia, G.; Gens, R.; Pinzon, J.E.; Tucker, C.J.; Tweedie, C.E.; et al. Circumpolar Arctic tundra vegetation change is linked to sea ice decline. Earth Interact. 2010, 14, 1–20. [Google Scholar] [CrossRef]
- Aide, T.M.; Grau, H.R.; Graesser, J.; Andrade-Nuñez, M.J.; Aráoz, E.; Barros, A.P.; Campos-Cerqueira, M.; Chacon-Moreno, E.; Cuesta, F.; Espinoza, R.; et al. Woody vegetation dynamics in the tropical and subtropical Andes from 2001 to 2014: Satellite image interpretation and expert validation. Glob. Chang. Biol. 2019, 25, 2112–2126. [Google Scholar] [CrossRef]
- Carlson, B.Z.; Corona, M.C.; Dentant, C.; Bonet, R.; Thuiller, W.; Choler, P. Observed long-term greening of alpine vegetation—A case study in the French Alps. Environ. Res. Lett. 2017, 12, 114006. [Google Scholar] [CrossRef]
- Polk, M.H.; Mishra, N.B.; Young, K.R.; Mainali, K. Greening and Browning Trends across Peru’s Diverse Environments. Remote Sens. 2020, 12, 2418. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef]
- Saleska, S.R.; Wu, J.; Guan, K.; Araujo, A.C.; Huete, A.; Nobre, A.D.; Restrepo-Coupe, N. Dry-season greening of Amazon forests. Nature 2016, 531, E4–E5. [Google Scholar] [CrossRef] [PubMed]
- Morton, D.C.; Nagol, J.; Carabajal, C.C.; Rosette, J.; Palace, M.; Cook, B.D.; Vermote, E.F.; Harding, D.J.; North, P.R. Amazon forests maintain consistent canopy structure and greenness during the dry season. Nature 2014, 506, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Sylvester, S.P.; Sylvester, M.D.; Kessler, M. Inaccessible ledges as refuges for the natural vegetation of the high Andes. J. Veg. Sci. 2014, 25, 1225–1234. [Google Scholar] [CrossRef]
- Valencia, B.G.; Bush, M.B.; Coe, A.L.; Orren, E.; Gosling, W.D. Polylepis woodland dynamics during the last 20,000 years. J. Biogeogr. 2018, 45, 1019–1030. [Google Scholar] [CrossRef]
- Rundel, P.W.; Dillon, M.O.; Palma, B.; Mooney, H.A.; Gulmon, S.; Ehleringer, J. The phytogeography and ecology of the coastal Atacama and Peruvian deserts. Aliso J. Syst. Florist. Bot. 1991, 13, 1–49. [Google Scholar] [CrossRef]
- Sulca, J.; Takahashi, K.; Espinoza, J.C.; Vuille, M.; Lavado-Casimiro, W. Impacts of different ENSO flavors and tropical Pacific convection variability (ITCZ, SPCZ) on austral summer rainfall in South America, with a focus on Peru. Int. J. Climatol. 2018, 38, 420–435. [Google Scholar] [CrossRef]
- Fjeldså, J. The avifauna of the Polylepis woodlands of the Andean highlands: The efficiency of basing conservation priorities on patterns of endemism. Bird Conserv. Int. 1993, 3, 37–55. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250 m SIN Grid V006. 2015. Available online: https://lpdaac.usgs.gov/products/mod13q1v006/ (accessed on 26 April 2023).
- Validation at Stage 3 Has Been Achieved for the MODIS Vegetation Index (VI) Product Suite. Available online: https://modisland.gsfc.nasa.gov/ValStatus.php?ProductID=MOD13 (accessed on 26 April 2023).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Didan, K.; Munoz, A.B.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series) Version 3.00, June 2015 (Collection 6). 2015.
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Seabold, S.; Perktold, J. statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Whittaker, E.T. On a New Method of Graduation. Proc. Edinb. Math. Soc. 1922, 41, 63–75. [Google Scholar] [CrossRef]
- Eilers, P.H. A perfect smoother. Anal. Chem. 2003, 75, 3631–3636. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin Press: Salisbury, Australia, 1948. [Google Scholar]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. Indag. Math. 1950, 12, 173. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics; John Wiley & Sons: Hoboken, NJ, USA, 1999; Volume 350. [Google Scholar]
- Hussain, M.; Mahmud, I. pyMannKendall: A python package for non parametric Mann Kendall family of trend tests. J. Open Source Softw. 2019, 4, 1556. [Google Scholar] [CrossRef]
- Copernicus Global Land Operations “Vegetation and Energy”—MODERATE DYNAMIC LAND COVER 100M VERSION (COLLECTION) 3. Available online: https://land.copernicus.eu/global/sites/cgls.vito.be/files/products/CGLOPS1_PUM_LC100m-V3_I3.4.pdf (accessed on 26 April 2023).
- UC Santa Barbara, UCSB CHG. CHIRPS Daily: Climate Hazards Group InfraRed Precipitation with Station Data (Version 2.0 Final). Available online: https://developers.google.com/earth-engine/datasets/catalog/UCSB-CHG_CHIRPS_DAILY#bands (accessed on 26 April 2023).
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Monthly Averaged Data on Single Levels from 1979 to Present. 2019. Available online: https://doi.org/10.24381/cds.f17050d7 (accessed on 26 April 2023).
- Dlugokencky, E.; Tans, P. Trends in Atmospheric Carbon Dioxide, Globally Averaged Marine Surface Monthly Mean Data. Available online: https://gml.noaa.gov/ccgg/trends/ (accessed on 22 March 2022).
- Center, N.C.P. NOAA’s Climate Prediction Center. 2001. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 26 April 2023).
- Birkel, S. About Climate Reanalyzer. Available online: https://climatereanalyzer.org/about/ (accessed on 26 April 2023).
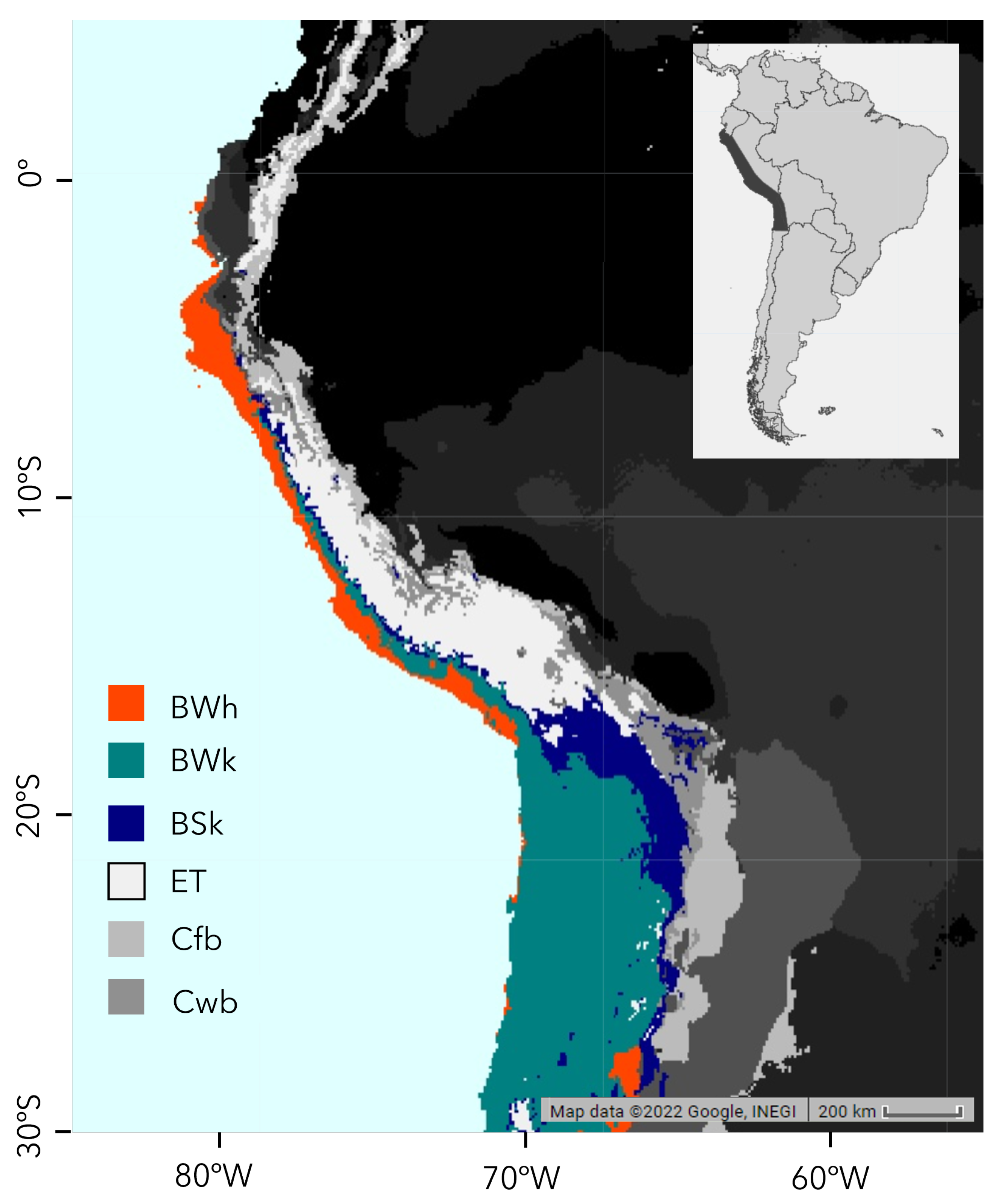


| Climate Zone | Code | Area Coverage |
|---|---|---|
| Arid, Desert, Cold | BWk | 30.0% |
| Polar, Tundra | ET | 29.2% |
| Arid, Desert, Hot | BWh | 16.7% |
| Arid, Steppe, Cold | BSk | 7.9% |
| Temperate, no dry season, warm summer | Cfb | 6.1% |
| Temperate, dry winter, warm summer | Cwb | 5.2% |
| Tropical, savannah | Aw | 2.0% |
| Arid, steppe, hot | BSh | 1.3% |
| Tropical, rainforest | Af | 0.9% |
| BWk | BSk | GS | GS_BWh | GS_BWk | GS_BSk | |
|---|---|---|---|---|---|---|
| BWh | 0.85 | 0.82 | 0.72 | 0.92 | 0.71 | 0.59 |
| BWk | 0.79 | 0.63 | 0.78 | 0.60 | 0.54 | |
| BSk | 0.69 | 0.79 | 0.67 | 0.64 | ||
| GS | 0.75 | 0.997 | 0.92 | |||
| GS_BWh | 0.72 | 0.60 | ||||
| GS_BWk | 0.91 |
| Region | Precipitation | SST | Global CO |
|---|---|---|---|
| BWh | 0.65 | 0.26 | 0.93 |
| BWk | 0.36 | 0.18 | 0.85 |
| BSk | 0.28 | 0.19 | 0.77 |
| GS | 0.53 | 0.38 | 0.60 |
| GS_BWh | 0.57 | 0.27 | 0.83 |
| GS_BWk | 0.52 | 0.39 | 0.58 |
| GS_BSk | 0.45 | 0.37 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lepage, H.V.; Barnes, E.; Kor, E.; Hunter, M.; Barnes, C.H.W. Greening and Browning Trends on the Pacific Slope of Peru and Northern Chile. Remote Sens. 2023, 15, 3628. https://doi.org/10.3390/rs15143628
Lepage HV, Barnes E, Kor E, Hunter M, Barnes CHW. Greening and Browning Trends on the Pacific Slope of Peru and Northern Chile. Remote Sensing. 2023; 15(14):3628. https://doi.org/10.3390/rs15143628
Chicago/Turabian StyleLepage, Hugo V., Eustace Barnes, Eleanor Kor, Morag Hunter, and Crispin H. W. Barnes. 2023. "Greening and Browning Trends on the Pacific Slope of Peru and Northern Chile" Remote Sensing 15, no. 14: 3628. https://doi.org/10.3390/rs15143628
APA StyleLepage, H. V., Barnes, E., Kor, E., Hunter, M., & Barnes, C. H. W. (2023). Greening and Browning Trends on the Pacific Slope of Peru and Northern Chile. Remote Sensing, 15(14), 3628. https://doi.org/10.3390/rs15143628






