A Critical Analysis of NeRF-Based 3D Reconstruction
Abstract
1. Introduction
Aims of This Research
2. The State of the Art
2.1. Photogrammetric-Based Methods
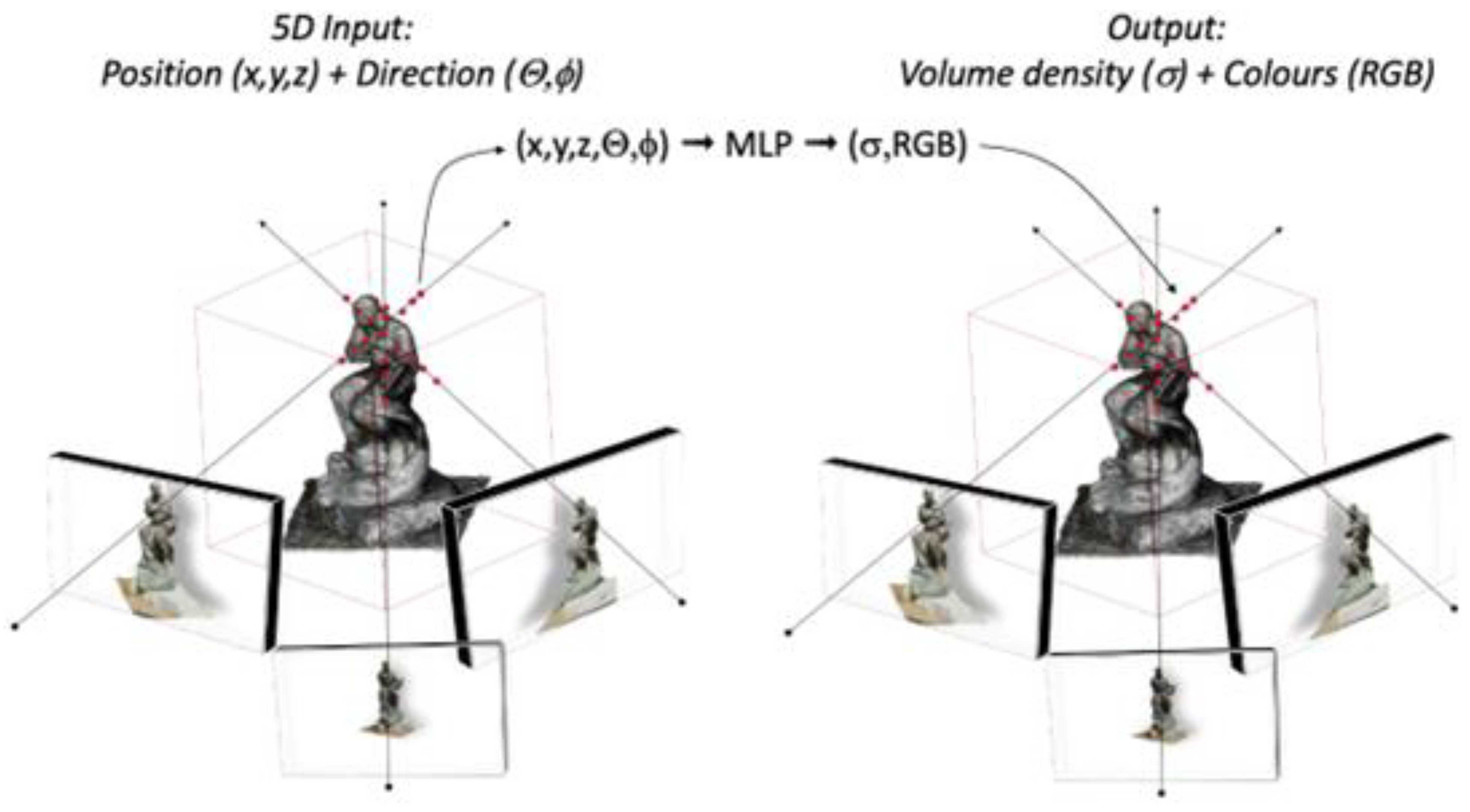
2.2. NeRF-Based Methods
- (1)
- The resolution of the generated neural renderings (afterward converted into a 3D mesh) can be limited by the quality and resolution of the input data. In general, higher-resolution input data will result in a higher-resolution 3D mesh, but the tradeoff is increased computational requirements.
- (2)
- Generating a neural rendering (and then a 3D mesh) using NeRF can be computationally intensive, requiring significant amounts of computing power and memory.
- (3)
- The general inability to accurately model the 3D shape of non-rigid objects.
- (4)
- The original NeRF model is optimized based on a per-pixel RGB reconstruction loss, which can result in a noisy reconstruction as an infinite number of photo-consistent explanations exist when using only RGB images as input.
- (5)
- NeRF generally requires a large number of input images with small baselines to generate an accurate 3D mesh, especially for scenes with complex geometry or occlusions. This can be a challenge in situations where images are difficult to acquire or when computational resources are limited.
3. Analysis and Evaluation Methodology
3.1. Proposed Methodology
3.2. Metrics
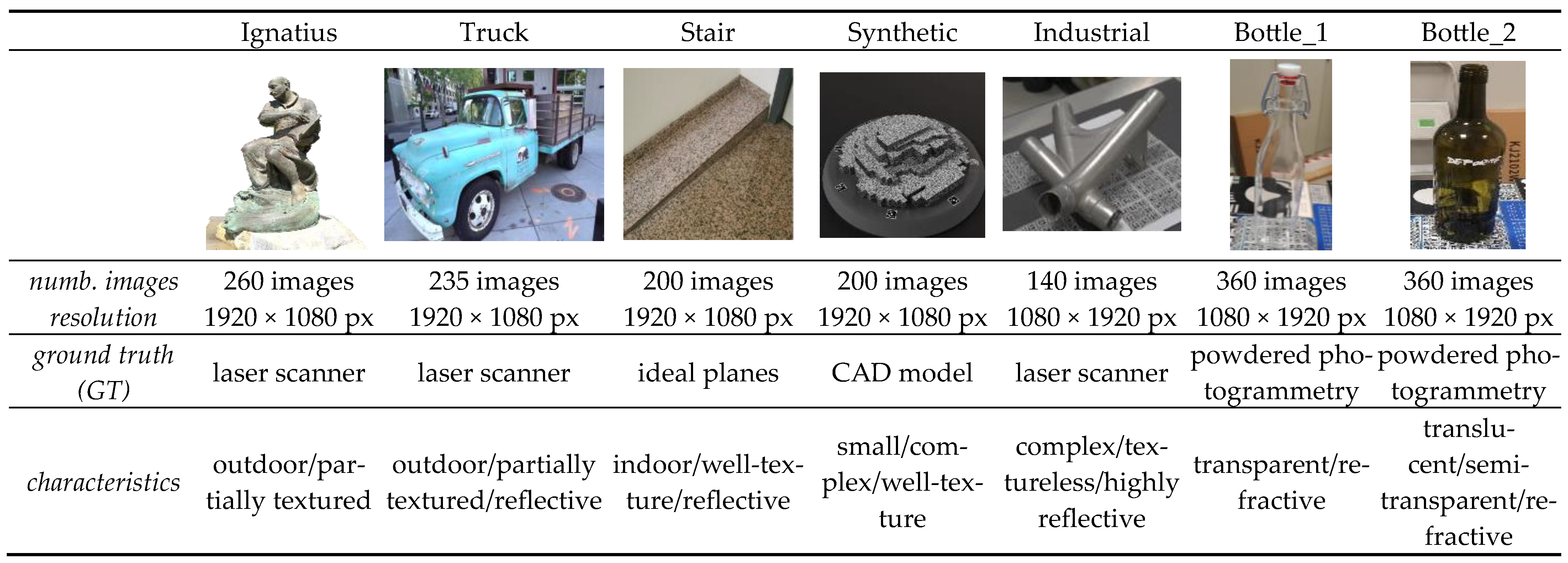
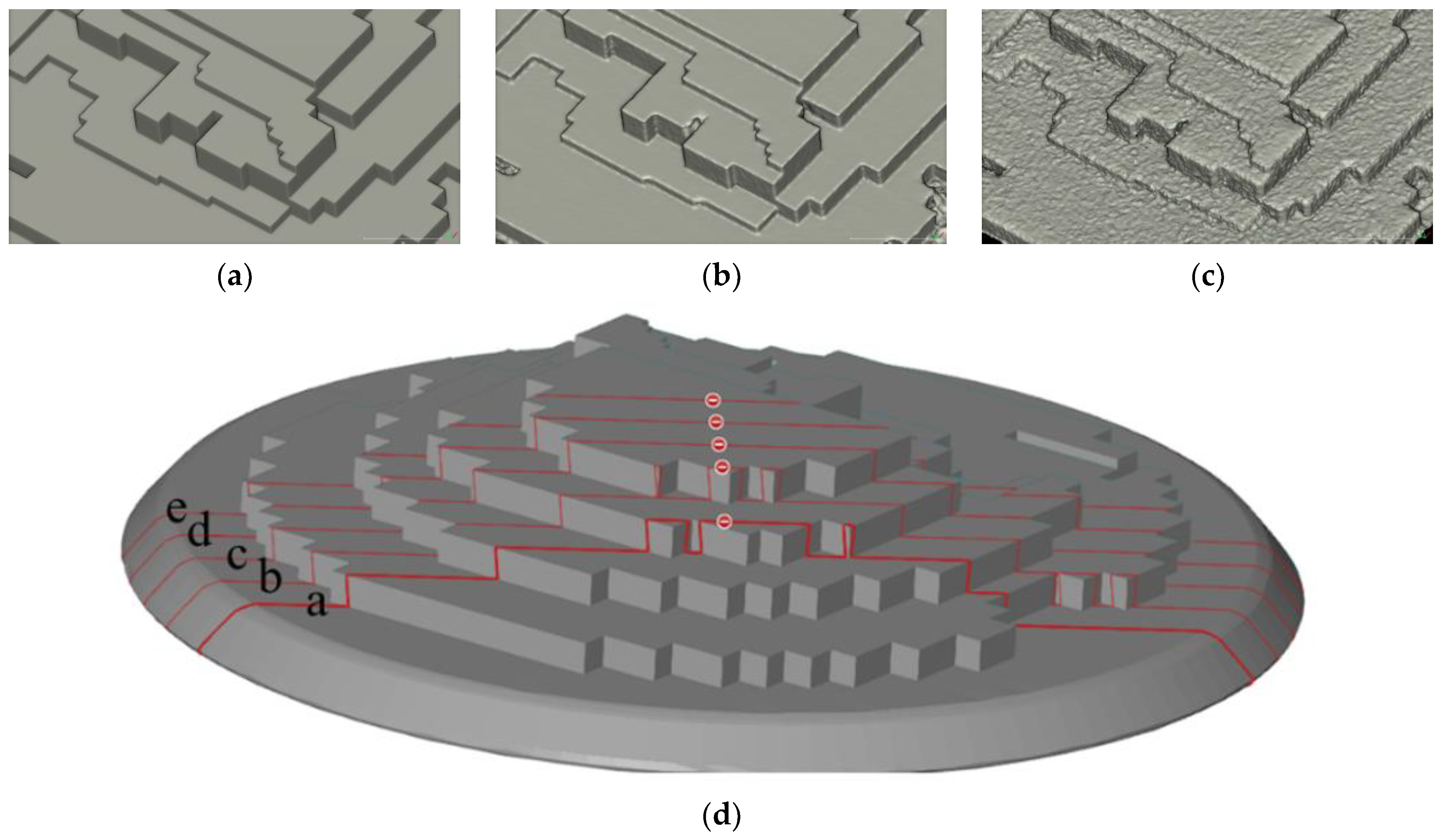
3.3. Testing Objects
4. Comparisons and Analyses
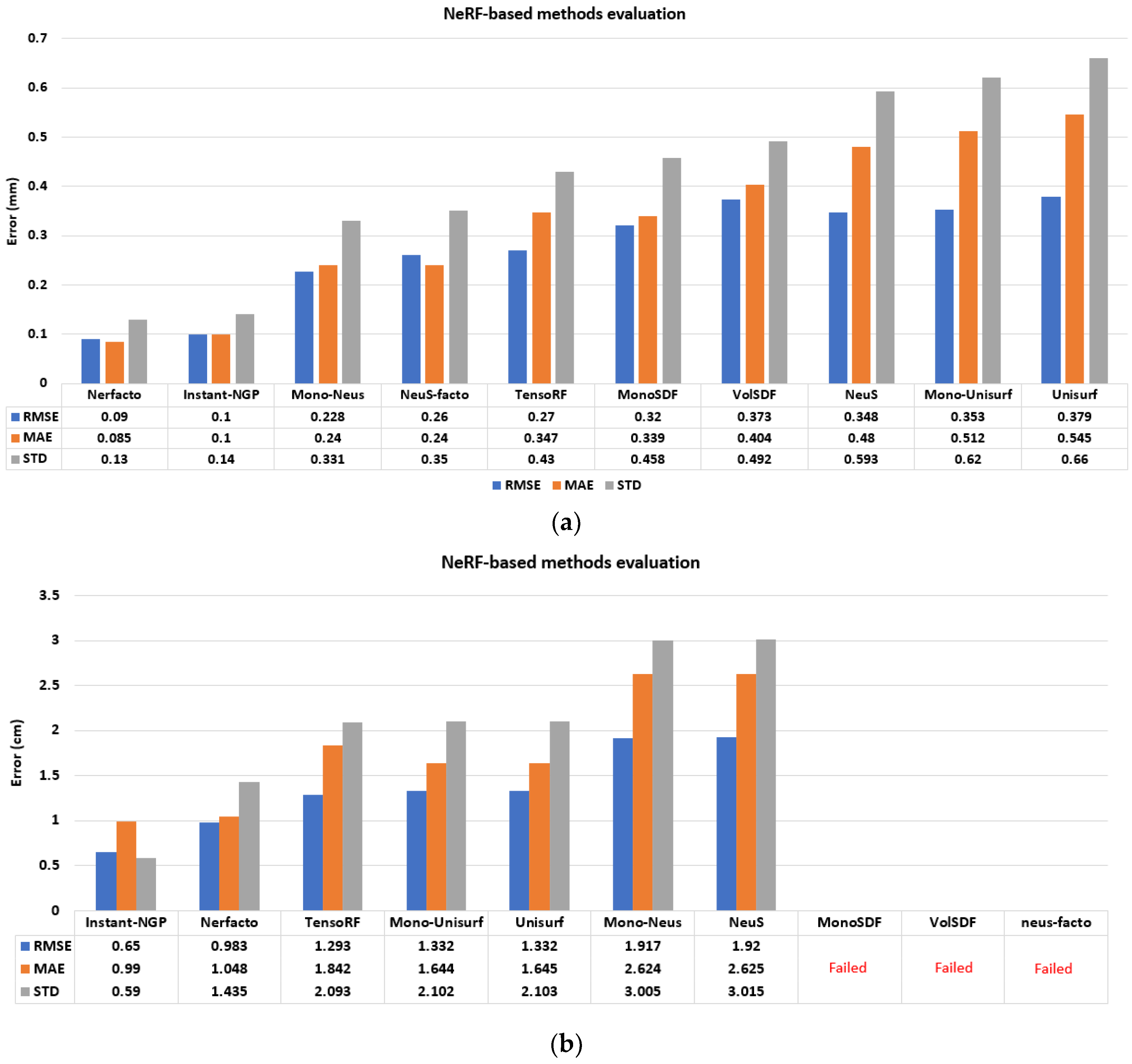
4.1. State-of-the-Art Comparison
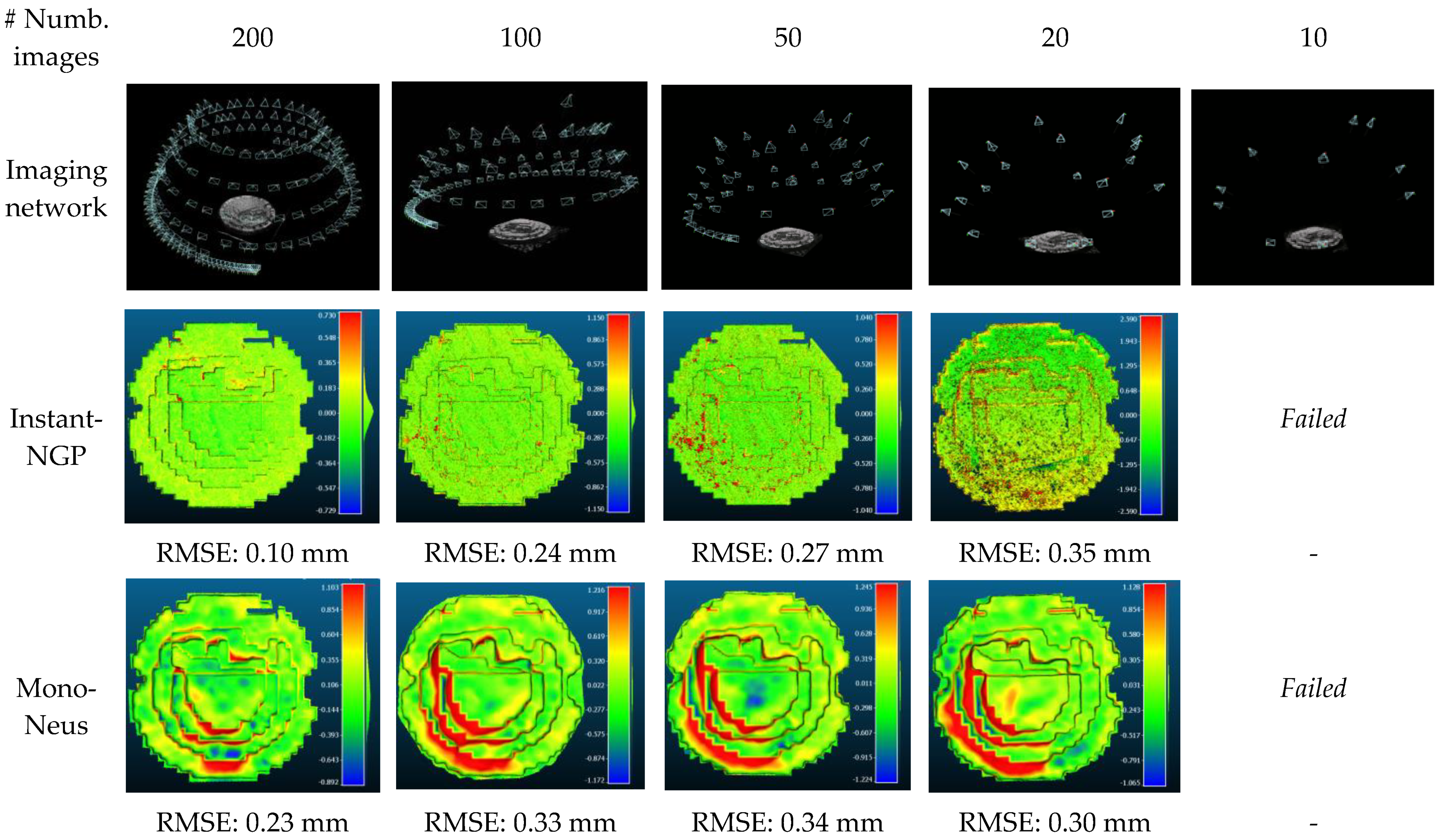
4.2. Image Baseline’s Evaluation
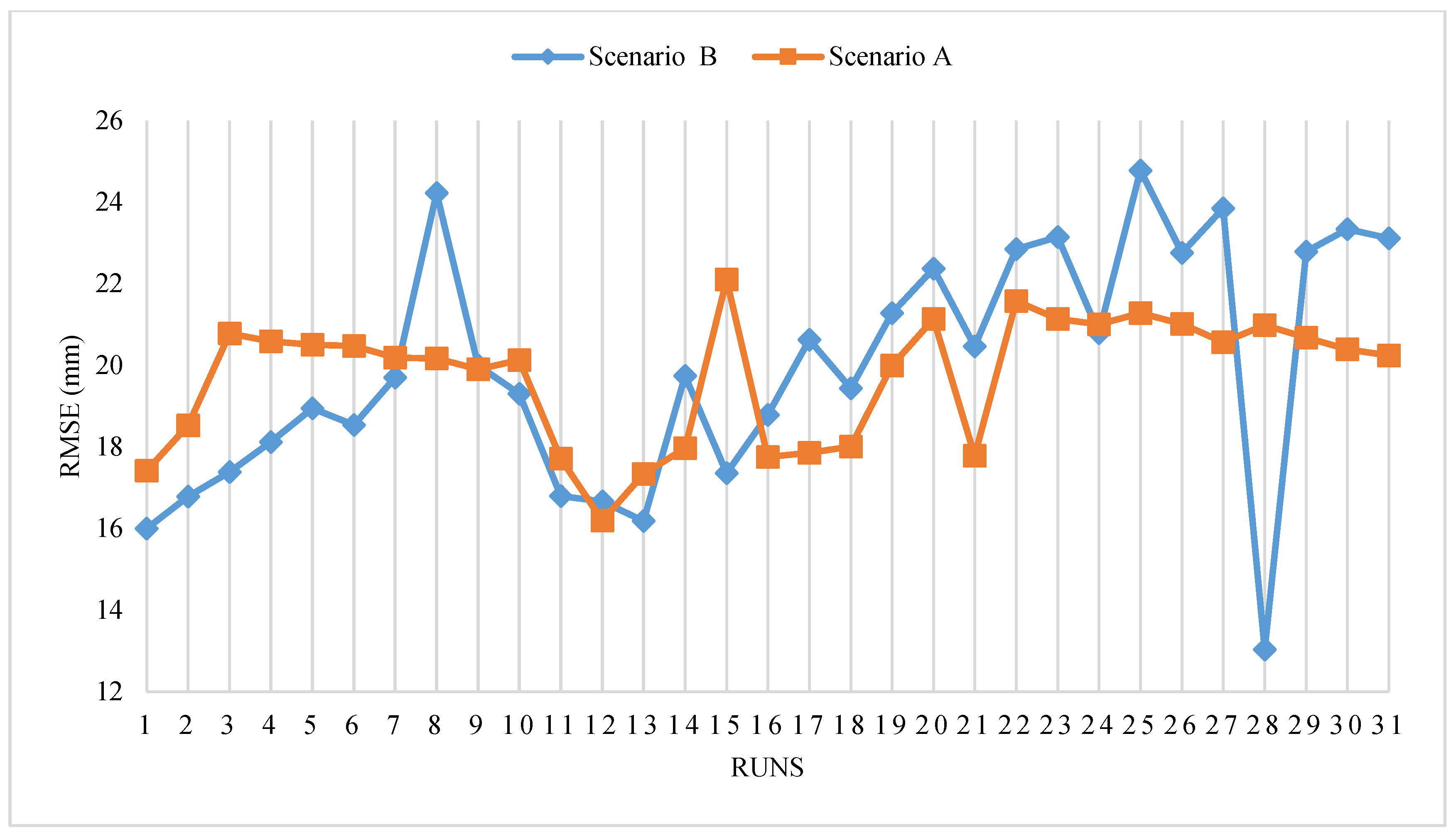
4.3. Monte Carlo Simulation
4.4. Plane Fitting
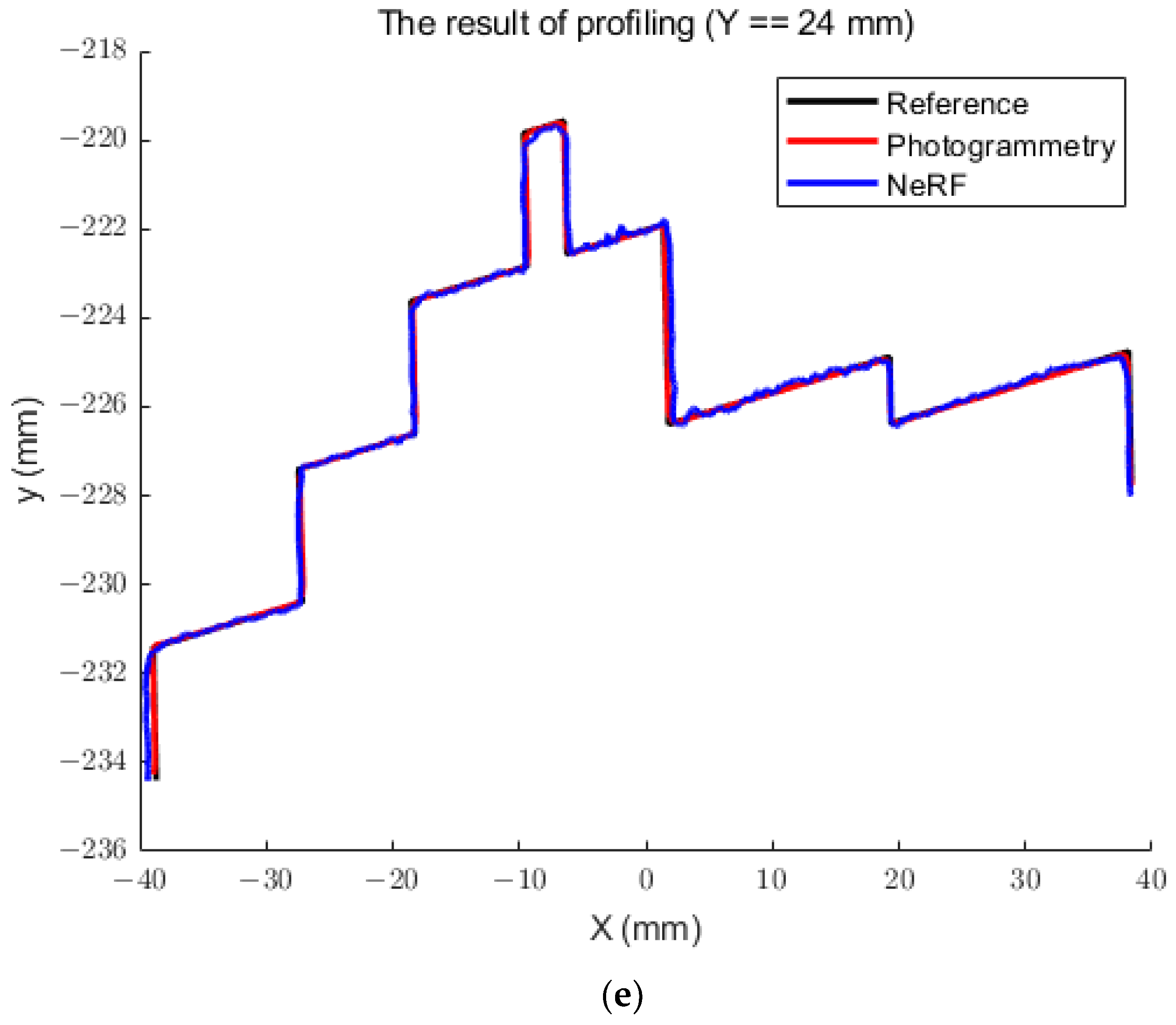
4.5. Profiling
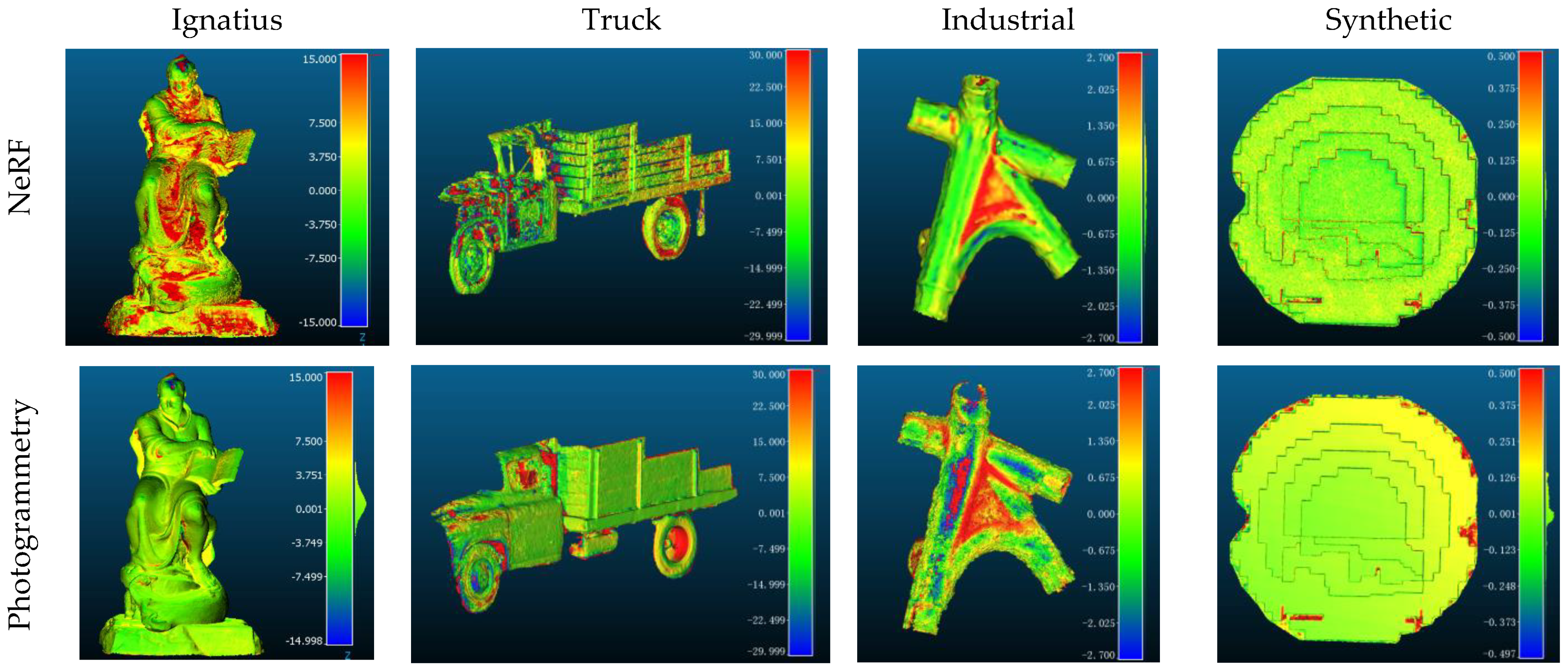
4.6. Cloud-to-Cloud Comparison
4.7. Accuracy and Completeness
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-range photogrammetry and 3D imaging. In Close-Range Photogrammetry and 3D Imaging; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Fraser, C.; Brow, D. Industrial photogrammetry: New developments and recent applications. Photogramm. Rec. 2006, 12, 197–217. [Google Scholar] [CrossRef]
- Sansoni, G.; Trebeschi, M.; Docchio, F. State-of-the-art and applications of 3D imaging sensors in industry, cultural heritage, medicine, and criminal investigation. Sensors 2009, 9, 568–601. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Martín, M.; Lagüela, S.; González-Aguilera, D.; Rodríguez-Gonzálvez, P. Procedure for quality inspection of welds based on macro-photogrammetric three-dimensional reconstruction. Opt. Laser Technol. 2015, 73, 54–62. [Google Scholar] [CrossRef]
- Karami, A.; Menna, F.; Remondino, F. Combining Photogrammetry and Photometric Stereo to Achieve Precise and Complete 3D Reconstruction. Sensors 2022, 22, 8172. [Google Scholar] [CrossRef] [PubMed]
- Remondino, F. Heritage recording and 3D modeling with photogrammetry and 3D scanning. Remote Sens. 2011, 3, 1104–1138. [Google Scholar] [CrossRef]
- Menna, F.; Nocerino, E.; Remondino, F.; Dellepiane, M.; Callieri, M.; Scopigno, R. 3D digitization of an heritage masterpiece-a critical analysis on quality assessment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 675–683. [Google Scholar] [CrossRef]
- Stylianidis, E.; Remondino, F. 3D Recording, Documentation and Management of Cultural Heritage; Whittles Publishing: Dunbeath, UK, 2016; 388p, ISBN 978-184995-168-5. [Google Scholar]
- Verhoeven, G.; Wild, B.; Schlegel, J.; Wieser, M.; Pfeifer, N.; Wogrin, S.; Eysn, L.; Carloni, M.; Koschiček-Krombholz, B.; Mola-da-Tebar, A.; et al. Project indigo—Document, disseminate & analyse a graffiti-scape. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 46, 513–520. [Google Scholar]
- Remondino, F.; El-Hakim, S. Image-based 3D modelling: A review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Remondino, F.; Menna, F.; Koutsoudis, A.; Chamzas, C.; El-Hakim, S. Design and implement a reality-based 3D igitization and modelling project. In Proceedings of the IEEE Conference “Digital Heritage 2013”, Marseille, France, 28 October–1 November 2013; Volume 1, pp. 137–144. [Google Scholar]
- Wu, B.; Zhou, Y.; Qian, Y.; Gong, M.; Huang, H. Full 3D reconstruction of transparent objects. arXiv 2018, arXiv:1805.03482. [Google Scholar] [CrossRef]
- Ahmadabadian, A.H.; Karami, A.; Yazdan, R. An automatic 3D reconstruction system for texture-less objects. Robot. Auton. Syst. 2019, 117, 29–39. [Google Scholar] [CrossRef]
- Santoši, Ž.; Budak, I.; Stojaković, V.; Šokac, M.; Vukelić, Đ. Evaluation of synthetically generated patterns for image-based 3D reconstruction of texture-less objects. Measurement 2019, 147, 106883. [Google Scholar] [CrossRef]
- Karami, A.; Battisti, R.; Menna, F.; Remondino, F. 3D digitization of transparent and glass surfaces: State of the art and analysis of some methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 695–702. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Tewari, A.; Fried, O.; Thies, J.; Sitzmann, V.; Lombardi, S.; Sunkavalli, K.; Martin-Brualla, R.; Simon, T.; Saragih, J.; Niessner, M.; et al. State of the Art on Neural Rendering. Comput. Graph. Forum 2020, 39, 701–727. [Google Scholar] [CrossRef]
- Martin-Brualla, R.; Radwan, N.; Sajjadi, M.S.; Barron, J.T.; Dosovitskiy, A.; Duckworth, D. Nerf in the wild: Neural radiance fields for unconstrained photo collections. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7210–7219. [Google Scholar]
- Wang, X.; Wang, C.; Liu, B.; Zhou, X.; Zhang, L.; Zheng, J.; Bai, X. Multi-view stereo in the deep learning era: A comprehensive review. Displays 2021, 70, 102102. [Google Scholar] [CrossRef]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. ToG 2022, 41, 1–15. [Google Scholar] [CrossRef]
- Li, Z.; Müller, T.; Evans, A.; Taylor, R.H.; Unberath, M.; Liu, M.Y.; Lin, C.H. Neuralangelo: High-Fidelity Neural Surface Recon-struction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 8456–8465. [Google Scholar]
- Tancik, M.; Weber, E.; Ng, E.; Li, R.; Yi, B.; Kerr, J.; Wang, T.; Kristoffersen, A.; Austin, J.; Salahi, K.; et al. Nerfstudio: A Modular Framework for Neural Radiance Field Development. arXiv 2023, arXiv:2302.04264. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3d surface construction algorithm. ACM Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Seitz, S.M.; Dyer, C.R. Photorealistic scene reconstruction by voxel coloring. In Proceedings of the IEEE Computer Society Con-ference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; IEEE: New York, NY, USA, 1997; pp. 1067–1073. [Google Scholar]
- Agrawal, M.; Davis, L.S. A probabilistic framework for surface reconstruction from multiple images. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, HI, USA, 8–14 December 2001; IEEE: New York, NY, USA, 2001; Volume 2, p. II. [Google Scholar]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; IEEE: New York, NY, USA, 2006; Volume 1, pp. 519–528. [Google Scholar]
- Bleyer, M.; Rhemann, C.; Rother, C. Patchmatch stereo-stereo matching with slanted support windows. In Proceedings of the BMVC 2011, Dundee, UK, 29 August–2 September 2011; Volume 11, pp. 1–11. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Frahm, J.M.; Pollefeys, M. Pixelwise view selection for unstructured multi-view stereo. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 501–518. [Google Scholar]
- Paschalidou, D.; Ulusoy, O.; Schmitt, C.; Van Gool, L.; Geiger, A. Raynet: Learning volumetric 3d reconstruction with ray po-tentials. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3897–3906. [Google Scholar]
- Morelli, L.; Bellavia, F.; Menna, F.; Remondino, F. PHOTOGRAMMETRY NOW AND THEN–FROM HAND-CRAFTED TO DEEP-LEARNING TIE POINTS–. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 48, 163–170. [Google Scholar] [CrossRef]
- Ulusoy, A.O.; Geiger, A.; Black, M.J. Towards probabilistic volumetric reconstruction using ray potentials. In Proceedings of the 2015 International Conference on 3D Vision, Lyon, France, 19–22 October 2015; IEEE: New York, NY, USA, 2015; pp. 10–18. [Google Scholar]
- Tulsiani, S.; Zhou, T.; Efros, A.A.; Malik, J. Multi-view supervision for single-view reconstruction via differentiable ray con-sistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2626–2634. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Learning to compare image patches via convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4353–4361. [Google Scholar]
- Luo, W.; Schwing, A.G.; Urtasun, R. Efficient deep learning for stereo matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5695–5703. [Google Scholar]
- Ummenhofer, B.; Zhou, H.; Uhrig, J.; Mayer, N.; Ilg, E.; Dosovitskiy, A.; Brox, T. Demon: Depth and motion network for learning monocular stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5038–5047. [Google Scholar]
- Leroy, V.; Franco, J.S.; Boyer, E. Shape reconstruction using volume sweeping and learned photoconsistency. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 781–796. [Google Scholar]
- Riegler, G.; Ulusoy, A.O.; Bischof, H.; Geiger, A. Octnetfusion: Learning depth fusion from data. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; IEEE: New York, NY, USA, 2017; pp. 57–66. [Google Scholar]
- Donne, S.; Geiger, A. Learning non-volumetric depth fusion using successive reprojections. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7634–7643. [Google Scholar]
- Huang, P.H.; Matzen, K.; Kopf, J.; Ahuja, N.; Huang, J.B. Deepmvs: Learning multi-view stereopsis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2821–2830. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Shen, T.; Fang, T.; Quan, L. Recurrent mvsnet for high-resolution multi-view stereo depth inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5525–5534. [Google Scholar]
- Yu, Z.; Gao, S. Fast-mvsnet: Sparse-to-dense multi-view stereo with learned propagation and gauss-newton refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1949–1958. [Google Scholar]
- Menna, F.; Nocerino, E.; Morabito, D.; Farella, E.M.; Perini, M.; Remondino, F. An open source low-cost automatic system for image-based 3D digitization. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 155. [Google Scholar] [CrossRef]
- Mousavi, V.; Khosravi, M.; Ahmadi, M.; Noori, N.; Haghshenas, S.; Hosseininaveh, A.; Varshosaz, M. The performance evalu-ation of multi-image 3D reconstruction software with different sensors. Measurement 2018, 120, 1–10. [Google Scholar] [CrossRef]
- Hafeez, J.; Lee, J.; Kwon, S.; Ha, S.; Hur, G.; Lee, S. Evaluating feature extraction methods with synthetic noise patterns for image-based modelling of texture-less objects. Remote Sens. 2020, 12, 3886. [Google Scholar] [CrossRef]
- Nicolae, C.; Nocerino, E.; Menna, F.; Remondino, F. Photogrammetry applied to problematic artefacts. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 451. [Google Scholar] [CrossRef]
- Wallis, R. An approach to the space variant restoration and enhancement of images. In Proceedings of the Symposium on Current Mathematical Problems in Image Science, Naval Postgraduate School, Monterey, CA, USA, 10-12 November 1976. [Google Scholar]
- Gaiani, M.; Remondino, F.; Apollonio, F.; Ballabeni, A. An advanced pre-processing pipeline to improve automated photo-grammetric reconstructions of architectural scenes. Remote Sens. 2016, 8, 178. [Google Scholar] [CrossRef]
- Karami, A.; Menna, F.; Remondino, F. Investigating 3D reconstruction of non-collaborative surfaces through photogrammetry and photometric stereo. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 519–526. [Google Scholar] [CrossRef]
- Karami, A.; Menna, F.; Remondino, F.; Varshosaz, M. Exploiting light directionality for image-based 3d reconstruction of non-collaborative surfaces. Photogramm. Rec. 2022, 37, 111–138. [Google Scholar] [CrossRef]
- Park, J.; Sinha, S.N.; Matsushita, Y.; Tai, Y.W.; Kweon, I.S. Robust igitizat photometric stereo using planar mesh parameterization. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1591–1604. [Google Scholar] [CrossRef]
- Logothetis, F.; Mecca, R.; Cipolla, R. A differential volumetric approach to multi-view photometric stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1052–1061. [Google Scholar]
- Li, M.; Zhou, Z.; Wu, Z.; Shi, B.; Diao, C.; Tan, P. Multi-view photometric stereo: A robust solution and benchmark dataset for spatially varying isotropic materials. IEEE Trans. Image Process. 2020, 29, 4159–4173. [Google Scholar] [CrossRef]
- Karami, A.; Varshosaz, M.; Menna, F.; Remondino, F.; Luhmann, T. FFT-based Filtering Approach to Fuse Photogrammetry and Photometric Stereo 3D Data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 14, 363–370. [Google Scholar] [CrossRef]
- Woodham, R.J. Photometric method for determining surface orientation from multiple images. Opt. Eng. 2021, 19, 191139. [Google Scholar] [CrossRef]
- Antensteiner, D.; Štolc, S.; Pock, T. A review of depth and normal fusion algorithms. Sensors 2018, 18, 431. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Han, K.; Wong, K.K. PS-FCN: A Flexible Learning Framework for Photometric Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Ju, Y.; Lam, K.M.; Chen, Y.; Qi, L.; Dong, J. Pay Attention to Devils: A Photometric Stereo Network for Better Details. In Proceedings of the 29th International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020. [Google Scholar]
- Logothetis, F.; Budvytis, I.; Mecca, R.; Cipolla, R. PX-NET: Simple and Efficient Pixel-Wise Training of Photometric Stereo Networks. arXiv 2021, arXiv:2008.04933v3. [Google Scholar]
- Tewari, A.; Thies, J.; Mildenhall, B.; Srinivasan, P.; Tretschk, E.; Yifan, W.; Lassner, C.; Sitzmann, V.; Martin-Brualla, R.; Lombardi, S.; et al. Advances in Neural Rendering. Comput. Graph. Forum 2022, 41, 703–735. [Google Scholar] [CrossRef]
- Niemeyer, M.; Barron, J.T.; Mildenhall, B.; Sajjadi, M.S.; Geiger, A.; Radwan, N. Regnerf: Regularizing neural radiance fields for view synthesis from sparse inputs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5480–5490. [Google Scholar]
- Deng, K.; Liu, A.; Zhu, J.Y.; Ramanan, D. Depth-supervised nerf: Fewer views and faster training for free. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12882–12891. [Google Scholar]
- Guo, Y.C.; Kang, D.; Bao, L.; He, Y.; Zhang, S.H. NeRFren: Neural radiance fields with reflections. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18409–18418. [Google Scholar]
- Zhang, X.; Srinivasan, P.P.; Deng, B.; Debevec, P.; Freeman, W.T.; Barron, J.T. Nerfactor: Neural factorization of shape and reflectance under an unknown illumination. ACM Trans. Graph. ToG 2021, 40, 1–18. [Google Scholar] [CrossRef]
- Barron, J.T.; Mildenhall, B.; Verbin, D.; Srinivasan, P.P.; Hedman, P. Mip-NeRF 360: Unbounded anti-aliased neural radiance fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5470–5479. [Google Scholar]
- Zhan, H.; Zheng, J.; Xu, Y.; Reid, I.; Rezatofighi, H. ActiveRMAP: Radiance Field for Active Mapping and Planning. arXiv 2022, arXiv:2211.12656. [Google Scholar]
- Gao, K.; Gao, Y.; He, H.; Lu, D.; Xu, L.; Li, J. NeRF: Neural radiance field in 3d vision, a comprehensive review. arXiv 2022, arXiv:2210.00379. [Google Scholar]
- Kolodiazhna, O.; Savin, V.; Uss, M.; Kussul, N. 3D Scene Reconstruction with Neural Radiance Fields (NeRF) Considering Dy-namic Illumination Conditions. In Proceedings of the International Conference on Applied Innovation in IT, Manchester, UK, 13–15 April 2023; Anhalt University of Applied Sciences: Köthen, Germany, 2023; Volume 11, pp. 233–238. [Google Scholar]
- Reiser, C.; Szeliski, R.; Verbin, D.; Srinivasan, P.P.; Mildenhall, B.; Geiger, A.; Barron, J.T.; Hedman, P. Merf: Memory-efficient radiance fields for real-time view synthesis in unbounded scenes. arXiv 2023, arXiv:2302.12249. [Google Scholar]
- Tancik, M.; Srinivasan, P.; Mildenhall, B.; Fridovich-Keil, S.; Raghavan, N.; Singhal, U.; Ramamoorthi, R.; Barron, J.; Ng, R. Fourier features let networks learn high frequency functions in low dimensional domains. Adv. Neural Inf. Process. Syst. 2020, 33, 7537–7547. [Google Scholar]
- Sitzmann, V.; Martel, J.; Bergman, A.; Lindell, D.; Wetzstein, G. Implicit neural representations with periodic activation functions. Adv. Neural Inf. Process. Syst. 2020, 33, 7462–7473. [Google Scholar]
- Sun, C.; Sun, M.; Chen, H.T. Direct voxel grid optimization: Super-fast convergence for radiance fields reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5459–5469. [Google Scholar]
- Chen, A.; Xu, Z.; Geiger, A.; Yu, J.; Su, H. Tensorf: Tensorial radiance fields. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part XXXII. Springer Nature: Cham, Switzerland, 2022; pp. 333–350. [Google Scholar]
- Rebain, D.; Jiang, W.; Yazdani, S.; Li, K.; Yi, K.M.; Tagliasacchi, A. Derf: Decomposed radiance fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19-25 June 2021; pp. 14153–14161. [Google Scholar]
- Takikawa, T.; Evans, A.; Tremblay, J.; Müller, T.; McGuire, M.; Jacobson, A.; Fidler, S. Variable bitrate neural fields. In Proceedings of the ACM SIGGRAPH 2022 Conference Proceedings, Vancouver, BC, Canada, 7–11 August 2022; pp. 1–9. [Google Scholar]
- Boss, M.; Braun, R.; Jampani, V.; Barron, J.T.; Liu, C.; Lensch, H. Nerd: Neural reflectance decomposition from image collections. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 20–25 June 2021; pp. 12684–12694. [Google Scholar]
- Srinivasan, P.P.; Deng, B.; Zhang, X.; Tancik, M.; Mildenhall, B.; Barron, J.T. Nerv: Neural reflectance and visibility fields for relighting and view synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, BC, Canada, 11–17 October 2021; pp. 7495–7504. [Google Scholar]
- Verbin, D.; Hedman, P.; Mildenhall, B.; Zickler, T.; Barron, J.T.; Srinivasan, P. Ref-NeRF: Structured view-dependent ap-pearance for neural radiance fields. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recog-nition (CVPR), New Orleans, LA, USA, 19–20 June 2022; IEEE: New York, NY, USA, 2022; pp. 5481–5490. [Google Scholar]
- Zhu, Z.; Peng, S.; Larsson, V.; Xu, W.; Bao, H.; Cui, Z.; Oswald, M.R.; Pollefeys, M. Nice-slam: Neural implicit scalable encoding for slam. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022. [Google Scholar]
- Barron, J.T.; Mildenhall, B.; Tancik, M.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P. Mip-NeRF: A multiscale representation for anti-aliasing neural radiance fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5855–5864. [Google Scholar]
- Yang, W.; Chen, G.; Chen, C.; Chen, Z.; Wong, K.Y.K. Ps-NeRF: Neural inverse rendering for multi-view photometric stereo. In Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part I; Springer Nature: Cham, Switzerland, 2022; pp. 266–284. [Google Scholar]
- Park, K.; Sinha, U.; Barron, J.T.; Bouaziz, S.; Goldman, D.B.; Seitz, S.M.; Martin-Brualla, R. Nerfies: Deformable neural radiance fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5865–5874. [Google Scholar]
- Pumarola, A.; Corona, E.; Pons-Moll, G.; Moreno-Noguer, F. D-NeRF: Neural Radiance Fields for Dynamic Scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Wu, T.; Zhong, F.; Tagliasacchi, A.; Cole, F.; Oztireli, C. D2 NeRF: Self-Supervised Decoupling of Dynamic and Static Objects from a Monocular Video. arXiv 2022, arXiv:2205.15838. [Google Scholar]
- Yan, Z.; Li, C.; Lee, G.H. NeRF-DS: Neural Radiance Fields for Dynamic Specular Objects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 8285–8295. [Google Scholar]
- Cao, A.; Johnson, J. Hexplane: A fast representation for dynamic scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 130–141. [Google Scholar]
- Jain, A.; Tancik, M.; Abbeel, P. Putting NeRF on a diet: Semantically consistent few-shot view synthesis. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 20–25 June 2021; pp. 5885–5894. [Google Scholar]
- Oechsle, M.; Peng, S.; Geiger, A. Unisurf: Unifying neural implicit surfaces and radiance fields for multi-view reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5589–5599. [Google Scholar]
- Zhang, K.; Riegler, G.; Snavely, N.; Koltun, V. NeRF++: Analyzing and improving neural radiance fields. arXiv 2020, arXiv:2010.07492. [Google Scholar]
- Guo, H.; Peng, S.; Lin, H.; Wang, Q.; Zhang, G.; Bao, H.; Zhou, X. Neural 3D scene reconstruction with the igitizat-world as-sumption. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5511–5520. [Google Scholar]
- Yu, Z.; Peng, S.; Niemeyer, M.; Sattler, T.; Geiger, A. MonoSDF: Exploring Monocular Geometric Cues for Neural Implicit Surface Reconstruction. Adv. Neural Inf. Process. Syst. 2022, 35, 25018–25032. [Google Scholar]
- Bian, W.; Wang, Z.; Li, K.; Bian, J.W.; Prisacariu, V.A. Nope-nerf: Optimising neural radiance field with no pose prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 4160–4169. [Google Scholar]
- Rakotosaona, M.J.; Manhardt, F.; Arroyo, D.M.; Niemeyer, M.; Kundu, A.; Tombari, F. NeRFMeshing: Distilling Neural Radiance Fields into Geometrically-Accurate 3D Meshes. arXiv 2023, arXiv:2303.09431. [Google Scholar]
- Elsner, T.; Czech, V.; Berger, J.; Selman, Z.; Lim, I.; Kobbelt, L. Adaptive Voronoi NeRFs. arXiv 2023, arXiv:2303.16001. [Google Scholar]
- Kulhanek, J.; Sattler, T. Tetra-NeRF: Representing Neural Radiance Fields Using Tetrahedra. arXiv 2023, arXiv:2304.09987. [Google Scholar]
- Yu, A.; Ye, V.; Tancik, M.; Kanazawa, A. pixelNeRF—Neural Radiance Fields from One or Few Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Croce, V.; Caroti, G.; De Luca, L.; Piemonte, A.; Véron, P. Neural Radiance Fields (NeRF): Review and potential applications to Digital Cultural Heritage. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 453–460. [Google Scholar]
- Mazzacca, G.; Karami, A.; Rigon, S.; Farella, E.M.; Trybala, P.; Remondino, F. NeRF for heritage 3D reconstruction. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 1051–1058. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, A.; Antic, B.; Peng, S.P.; Bhattacharyya, A.; Niemeyer, M.; Tang, S.; Sattler, T.; Geiger, A. SDFStudio: A Unified Framework for Surface Reconstruction. Available online: https://github.com/autonomousvision/sdfstudio (accessed on 1 July 2023).
- Besl, P.J.; McKay, N.D. A method for registration of 3D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rashidi, M.; Mousavi, V.; Karami, A.; Yu, Y.; Samali, B. Quality evaluation of digital twins generated based on UAV photogrammetry and TLS: Bridge case study. Remote Sens. 2021, 13, 3499. [Google Scholar] [CrossRef]
- Knapitsch, A.; Park, J.; Zhou, Q.Y.; Koltun, V. Tanks and temples: Benchmarking large-scale scene reconstruction. ACM Trans. Graph. ToG 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Nocerino, E.; Stathopoulou, E.K.; Rigon, S.; Remondino, F. Surface reconstruction assessment in photogrammetric applications. Sensors 2020, 20, 5863. [Google Scholar] [CrossRef] [PubMed]
- NeRFBK Dataset. Available online: https://github.com/3DOM-FBK/NeRFBK/ (accessed on 1 July 2023).
- Harrison, R.L. Introduction to monte carlo simulation. AIP Conf. Proc. 2021, 1204, 17–21. [Google Scholar]




| Scenario A | Scenario B | |
|---|---|---|
| Perturbing translation (mm) | ±20 | ±40 |
| Perturbing rotation (degree) | ±2 | ±4 |
| Average RMSE (mm) | 19.72 | 19.97 |
| Max RMSE (mm) | 22.10 | 24.78 |
| Min RMSE (mm) | 16.90 | 13.03 |
| Error range (mm) | 5.91 | 11.75 |
| Uncertainty (±mm) | 2.95 | 5.87 |
| Plane | Photogrammetry | NeRF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | STD | Mean Distance | Max Distance | RMSE | MAE | STD | Mean Distance | Max Distance | |
| H_plane_01 | 0.70 | 0.61 | 0.43 | 0.61 | 1.65 | 1.89 | 1.51 | 1.38 | 1.51 | 6.00 |
| H_plane_02 | 0.75 | 0.56 | 0.55 | 0.55 | 2.14 | 3.53 | 2.61 | 2.47 | 2.60 | 10.26 |
| V_plane_01 | 0.78 | 0.57 | 0.60 | 0.57 | 1.4 | 2.77 | 1.79 | 2.17 | 1.79 | 6.69 |
| V_plane_02 | 0.92 | 0.77 | 0.67 | 0.77 | 1.94 | 2.95 | 2.19 | 2.06 | 2.18 | 6.73 |
| V_plane_03 | 0.43 | 0.30 | 0.37 | 0.30 | 1.42 | 3.10 | 0.20 | 2.45 | 1.96 | 7.29 |
| Average | 0.72 | 0.56 | 0.52 | 0.56 | 1.65 | 2.84 | 1.66 | 4.74 | 2.10 | 7.39 |
| Plane | Photogrammetry | NeRF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | STD | Mean Error | Max Error | RMSE | MAE | STD | Mean Error | Max Error | |
| H_plane_01 | 0.015 | 0.020 | 0.017 | 0.012 | 0.150 | 0.070 | 0.100 | 0.086 | 0.070 | 0.600 |
| H_plane_02 | 0.014 | 0.014 | 0.016 | 0.010 | 0.190 | 0.110 | 0.120 | 0.130 | 0.090 | 0.600 |
| H_plane_03 | 0.015 | 0.011 | 0.013 | 0.014 | 0.200 | 0.040 | 0.040 | 0.060 | 0.020 | 0.300 |
| H_plane_04 | 0.012 | 0.012 | 0.013 | 0.010 | 0.070 | 0.040 | 0.050 | 0.050 | 0.040 | 0.290 |
| H_plane_05 | 0.080 | 0.025 | 0.080 | 0.020 | 0.170 | 0.070 | 0.080 | 0.080 | 0.070 | 0.450 |
| H_Average | 0.027 | 0.016 | 0.027 | 0.013 | 0.150 | 0.066 | 0.078 | 0.081 | 0.058 | 0.448 |
| V_plane_01 | 0.060 | 0.046 | 0.070 | 0.010 | 0.450 | 0.140 | 0.050 | 0.150 | 0.000 | 0.450 |
| V_plane_02 | 0.018 | 0.018 | 0.020 | 0.010 | 0.080 | 0.050 | 0.050 | 0.060 | 0.030 | 0.200 |
| V_plane_03 | 0.039 | 0.020 | 0.040 | 0.014 | 0.190 | 0.050 | 0.070 | 0.080 | 0.040 | 0.25 |
| V_plane_04 | 0.016 | 0.016 | 0.018 | 0.010 | 0.090 | 0.050 | 0.050 | 0.070 | 0.000 | 0.20 |
| V_plane_05 | 0.020 | 0.020 | 0.027 | 0.010 | 0.050 | 0.070 | 0.060 | 0.090 | 0.000 | 0.330 |
| V_Average | 0.030 | 0.024 | 0.035 | 0.010 | 0.170 | 0.072 | 0.056 | 0.090 | 0.014 | 0.286 |
| Cross-Section Profiles | Photogrammetry | NeRF | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | STD | Mean Error | Max Error | RMSE | STD | Mean Error | Max Error | |
| a | 0.09 | 0.14 | 0.07 | 0.20 | 0.12 | 0.11 | 0.04 | 0.80 |
| b | 0.11 | 0.13 | 0.08 | 0.22 | 0.18 | 0.15 | 0.18 | 1.20 |
| c | 0.09 | 0.05 | 0.05 | 0.22 | 0.16 | 0.13 | 0.12 | 1.40 |
| d | 0.08 | 0.05 | 0.06 | 0.21 | 0.15 | 0.09 | 0.09 | 1.50 |
| e | 0.09 | 0.05 | 0.07 | 0.17 | 0.12 | 0.21 | 0.11 | 1.60 |
| Average | 0.09 | 0.08 | 0.06 | 0.20 | 0.15 | 0.14 | 0.11 | 1.30 |
| Object | Method | Images | RMSE | MAE | STD |
|---|---|---|---|---|---|
| Industrial | Photogr | 140 | 0.85 | 1.10 | 1.50 |
| NeRF | 140 | 0.78 | 0.73 | 1.10 | |
| Synthetic | Photogr | 25 | 0.13 | 0.11 | 0.17 |
| NeRF | 200 | 0.19 | 0.13 | 0.23 | |
| Ignatius | Photogr | 130 | 2.50 | 0.90 | 2.00 |
| NeRF | 260 | 5.50 | 9.90 | 4.60 | |
| Truck | Photogr | 48 | 16.0 | 15.0 | 20.0 |
| NeRF | 235 | 38.0 | 55.0 | 49.0 |
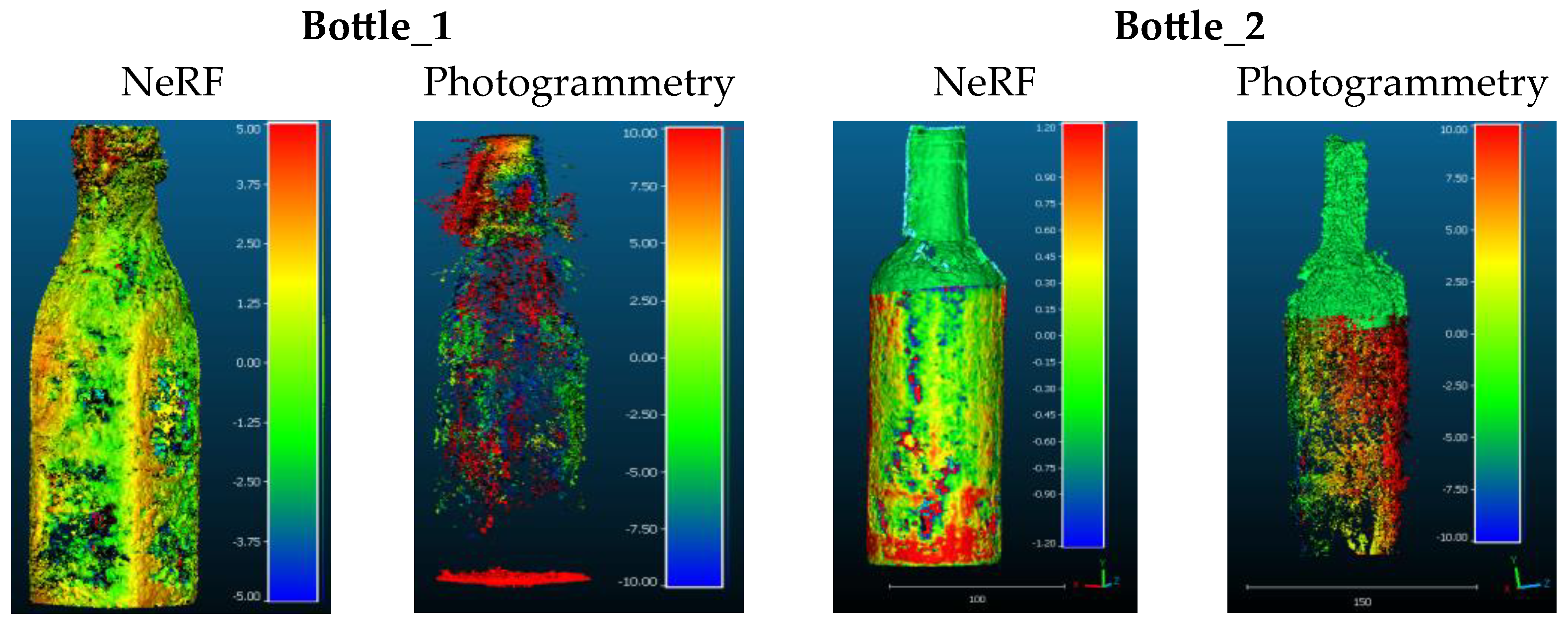
| Object | Method | Images | RMSE | MAE | STD |
|---|---|---|---|---|---|
| Bottle_1 | Pho | 360 | 6.50 | 7.10 | 7.50 |
| NeRF | 360 | 1.30 | 1.70 | 2.10 | |
| Bottle_2 | Pho | 360 | 4.50 | 5.20 | 5.10 |
| NeRF | 360 | 0.63 | 0.82 | 1.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Remondino, F.; Karami, A.; Yan, Z.; Mazzacca, G.; Rigon, S.; Qin, R. A Critical Analysis of NeRF-Based 3D Reconstruction. Remote Sens. 2023, 15, 3585. https://doi.org/10.3390/rs15143585
Remondino F, Karami A, Yan Z, Mazzacca G, Rigon S, Qin R. A Critical Analysis of NeRF-Based 3D Reconstruction. Remote Sensing. 2023; 15(14):3585. https://doi.org/10.3390/rs15143585
Chicago/Turabian StyleRemondino, Fabio, Ali Karami, Ziyang Yan, Gabriele Mazzacca, Simone Rigon, and Rongjun Qin. 2023. "A Critical Analysis of NeRF-Based 3D Reconstruction" Remote Sensing 15, no. 14: 3585. https://doi.org/10.3390/rs15143585
APA StyleRemondino, F., Karami, A., Yan, Z., Mazzacca, G., Rigon, S., & Qin, R. (2023). A Critical Analysis of NeRF-Based 3D Reconstruction. Remote Sensing, 15(14), 3585. https://doi.org/10.3390/rs15143585









