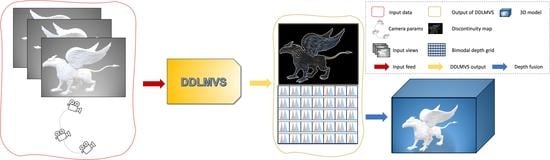
DDL-MVS: Depth Discontinuity Learning for Multi-View Stereo Networks
Abstract
1. Introduction
2. Related Work
2.1. Photogrammetry-Based MVS
2.2. Learning-Based Two-View Methods
2.3. Learning-Based MVS
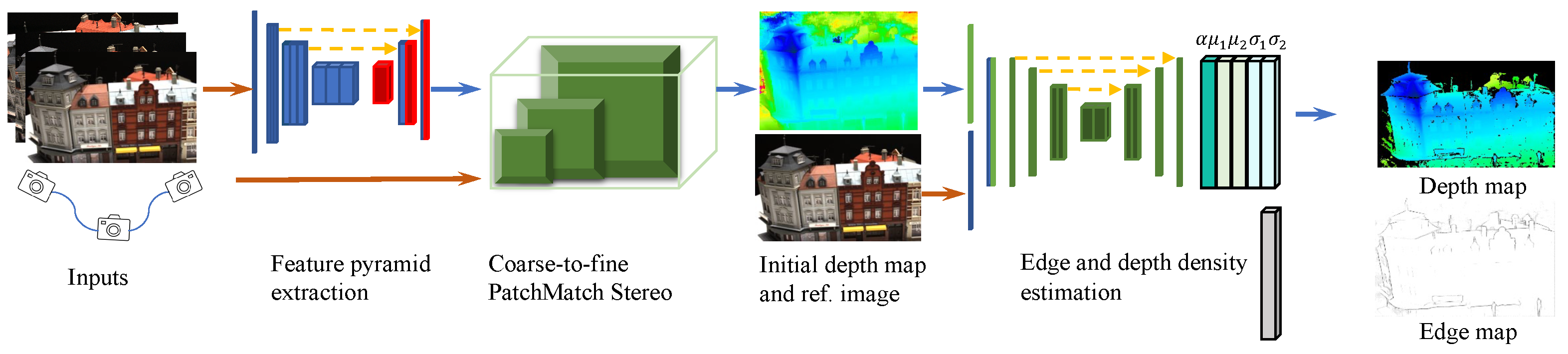
3. Method
3.1. Feature Extraction
3.2. Coarse-to-Fine PMS
3.3. Depth Discontinuity Learning
3.4. Loss Function
4. Experiments and Evaluation
4.1. Datasets
4.2. Evaluation on DTU Dataset
| Method | Accuracy (mm) ↓ | Completeness (mm) ↓ | Overall (mm) ↓ |
|---|---|---|---|
| Traditional photogrammetry-based | |||
| Camp [55] | 0.835 | 0.554 | 0.695 |
| Furu [4] | 0.613 | 0.941 | 0.777 |
| Tola [6] | 0.342 | 1.190 | 0.766 |
| Gipuma [5] | 0.283 | 0.873 | 0.578 |
| Learning-based | |||
| SurfaceNet [9] | 0.450 | 1.040 | 0.745 |
| MVSNet [7] | 0.396 | 0.527 | 0.462 |
| R-MVSNet [8] | 0.383 | 0.452 | 0.417 |
| CIDER [15] | 0.417 | 0.437 | 0.427 |
| P-MVSNet [14] | 0.406 | 0.434 | 0.420 |
| Point-MVSNet [10] | 0.342 | 0.411 | 0.376 |
| AttMVS [56] | 0.383 | 0.329 | 0.356 |
| Fast-MVSNet [11] | 0.336 | 0.403 | 0.370 |
| Vis-MVSNet [57] | 0.369 | 0.361 | 0.365 |
| CasMVSNet [13] | 0.325 | 0.385 | 0.355 |
| UCS-Net [12] | 0.338 | 0.349 | 0.344 |
| EPP-MVSNet [58] | 0.413 | 0.296 | 0.355 |
| CVP-MVSNet [16] | 0.296 | 0.406 | 0.351 |
| AA-RMVSNet [59] | 0.376 | 0.339 | 0.357 |
| DEF-MVSNET [38] | 0.402 | 0.375 | 0.388 |
| ElasticMVS [40] | 0.374 | 0.325 | 0.349 |
| MG-MVSNET [41] | 0.358 | 0.338 | 0.348 |
| BDE-MVSNet [39] | 0.338 | 0.302 | 0.320 |
| UniMVSNet [53] | 0.352 | 0.278 | 0.315 |
| TransMVSNet [54] | 0.321 | 0.289 | 0.305 |
| PatchmatchNet [17] | 0.427 | 0.277 | 0.352 |
| PatchmatchNet + Ours () | 0.405 | 0.267 | 0.336 |
| PatchmatchNet + Ours () | 0.399 | 0.280 | 0.339 |
4.3. Evaluation on “Tanks and Temples” Dataset
4.4. Evaluation on ETH3D Dataset
4.5. Ablation Study
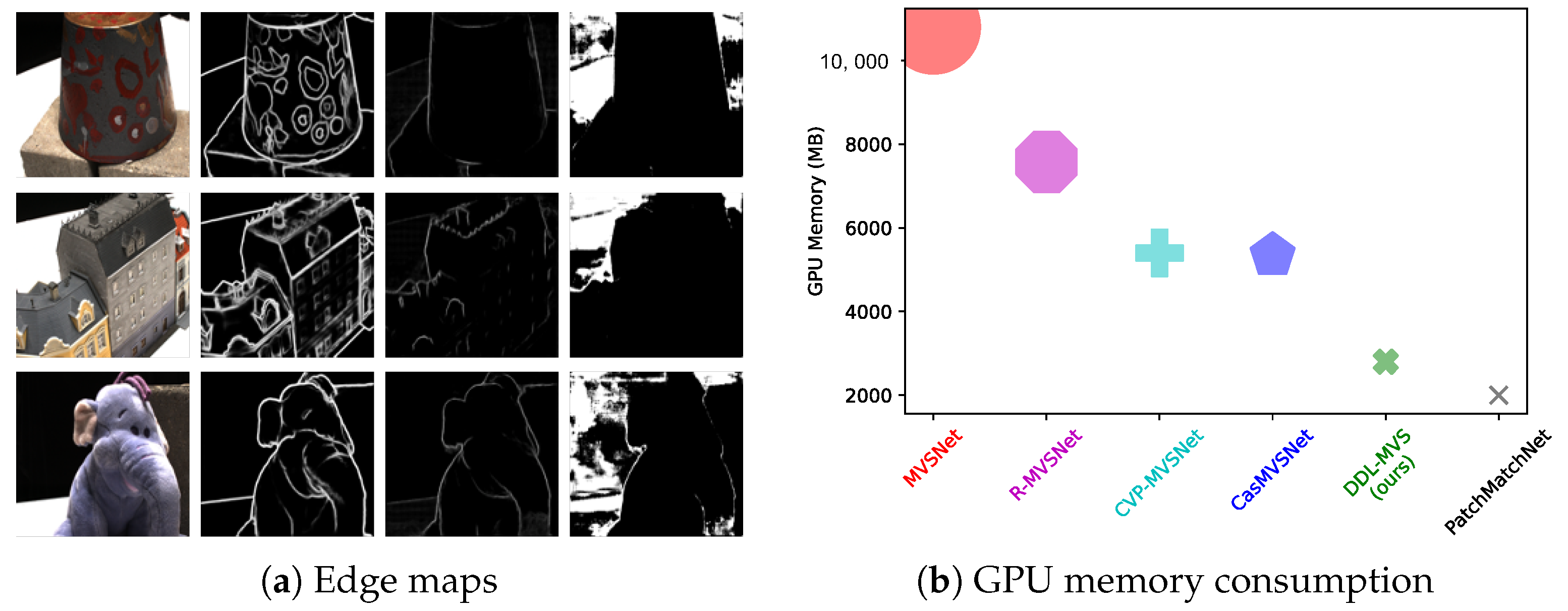
4.6. Effect of Depth Discontinuity Learning
4.7. Generalization to Aerial Images
4.8. Memory Consumption and Running Times
4.9. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lemaire, C. Aspects of the DSM production with high resolution images. ISPRS 2008, 37, 1143–1146. [Google Scholar]
- Peppa, M.V.; Mills, J.P.; Moore, P.; Miller, P.E.; Chambers, J.E. Automated co-registration and calibration in SfM photogrammetry for landslide change detection. Earth Surf. Process. Landf. 2019, 44, 287–303. [Google Scholar] [CrossRef]
- Nguatem, W.; Mayer, H. Modeling urban scenes from pointclouds. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3857–3866. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multi-view stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively parallel multiview stereopsis by surface normal diffusion. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 873–881. [Google Scholar]
- Tola, E.; Strecha, C.; Fua, P. Efficient large-scale multi-view stereo for ultra high-resolution image sets. Mach. Vis. Appl. 2012, 23, 903–920. [Google Scholar] [CrossRef]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. MVSNet: Depth inference for unstructured multi-view stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 767–783. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Shen, T.; Fang, T.; Quan, L. Recurrent MVSNet for high-resolution multi-view stereo depth inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5525–5534. [Google Scholar]
- Ji, M.; Gall, J.; Zheng, H.; Liu, Y.; Fang, L. SurfaceNet: An end-to-end 3D neural network for multiview stereopsis. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2307–2315. [Google Scholar]
- Chen, R.; Han, S.; Xu, J.; Su, H. Point-based multi-view stereo network. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1538–1547. [Google Scholar]
- Yu, Z.; Gao, S. Fast-MVSNet: Sparse-to-dense multi-view stereo with learned propagation and Gauss-Newton refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1949–1958. [Google Scholar]
- Cheng, S.; Xu, Z.; Zhu, S.; Li, Z.; Li, L.E.; Ramamoorthi, R.; Su, H. Deep stereo using adaptive thin volume representation with uncertainty awareness. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2524–2534. [Google Scholar]
- Gu, X.; Fan, Z.; Zhu, S.; Dai, Z.; Tan, F.; Tan, P. Cascade cost volume for high-resolution multi-view stereo and stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2495–2504. [Google Scholar]
- Luo, K.; Guan, T.; Ju, L.; Huang, H.; Luo, Y. P-MVSNet: Learning patch-wise matching confidence aggregation for multi-view stereo. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 10451–10460. [Google Scholar]
- Xu, Q.; Tao, W. Learning inverse depth regression for multi-view stereo with correlation cost volume. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence (AAAI-20), New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12508–12515. [Google Scholar]
- Yang, J.; Mao, W.; Alvarez, J.M.; Liu, M. Cost volume pyramid based depth inference for multi-view stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4877–4886. [Google Scholar]
- Wang, F.; Galliani, S.; Vogel, C.; Speciale, P.; Pollefeys, M. Patchmatchnet: Learned multi-view patchmatch stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 14194–14203. [Google Scholar]
- Duggal, S.; Wang, S.; Ma, W.C.; Hu, R.; Urtasun, R. DeepPruner: Learning efficient stereo matching via differentiable patchmatch. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4384–4393. [Google Scholar]
- Zhu, S.; Brazil, G.; Liu, X. The edge of depth: Explicit constraints between segmentation and depth. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 13116–13125. [Google Scholar]
- Tosi, F.; Liao, Y.; Schmitt, C.; Geiger, A. SMD-Nets: Stereo mixture density networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8942–8952. [Google Scholar]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Boykov, Y.; Veksler, O.; Zabih, R. Markov random fields with efficient approximations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Piscataway, NJ, USA, 1998; pp. 648–655. [Google Scholar]
- Garg, D.; Wang, Y.; Hariharan, B.; Campbell, M.; Weinberger, K.Q.; Chao, W.L. Wasserstein distances for stereo disparity estimation. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, BC, Canada, 11 December 2020; Volume 33, pp. 22517–22529. [Google Scholar]
- Janai, J.; Güney, F.; Behl, A.; Geiger, A. Computer vision for autonomous vehicles: Problems, datasets and state of the art. Found. Trends® Comput. Graph. Vis. 2020, 12, 1–308. [Google Scholar] [CrossRef]
- Kutulakos, K.N.; Seitz, S.M. A theory of shape by space carving. Int. J. Comput. Vis. 2000, 38, 199–218. [Google Scholar] [CrossRef]
- Faugeras, O.; Keriven, R. Variational Principles, Surface Evolution, PDE’s, Level Set Methods and the Stereo Problem; IEEE: Piscataway, NJ, USA, 2002. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 303–312. [Google Scholar]
- Zach, C.; Pock, T.; Bischof, H. A globally optimal algorithm for robust tv-l 1 range image integration. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Collins, R.T. A space-sweep approach to true multi-image matching. In Proceedings of the CVPR IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 358–363. [Google Scholar]
- Pollefeys, M.; Nistér, D.; Frahm, J.M.; Akbarzadeh, A.; Mordohai, P.; Clipp, B.; Engels, C.; Gallup, D.; Kim, S.J.; Merrell, P.; et al. Detailed real-time urban 3d reconstruction from video. Int. J. Comput. Vis. 2008, 78, 143–167. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Zheng, E.; Pollefeys, M.; Frahm, J.M. Pixelwise view selection for unstructured multi-view stereo. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Zbontar, J.; LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. J. Mach. Learn. Res. 2016, 17, 2287–2318. [Google Scholar]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-end learning of geometry and context for deep stereo regression. In Proceedings of the IEEE International Conference on Computer, Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 66–75. [Google Scholar]
- Chang, J.R.; Chen, Y.S. Pyramid stereo matching network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5410–5418. [Google Scholar]
- Yang, G.; Manela, J.; Happold, M.; Ramanan, D. Hierarchical deep stereo matching on high-resolution images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5515–5524. [Google Scholar]
- Song, X.; Zhao, X.; Hu, H.; Fang, L. Edgestereo: A context integrated residual pyramid network for stereo matching. In Proceedings of the Computer Vision—ACCV 2018: 14th Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Lin, K.; Li, L.; Zhang, J.; Zheng, X.; Wu, S. High-Resolution Multi-View Stereo with Dynamic Depth Edge Flow. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Ding, Y.; Li, Z.; Huang, D.; Zhang, K.; Li, Z.; Feng, W. Adaptive Range guided Multi-view Depth Estimation with Normal Ranking Loss. In Proceedings of the Asian Conference on Computer Vision, Macau, China, 4–8 December 2022; pp. 1892–1908. [Google Scholar]
- Zhang, J.; Tang, R.; Cao, Z.; Xiao, J.; Huang, R.; Fang, L. ElasticMVS: Learning elastic part representation for self-supervised multi-view stereopsis. NeurIPS 2022, 35, 23510–23523. [Google Scholar]
- Zhang, X.; Yang, F.; Chang, M.; Qin, X. MG-MVSNet: Multiple Granularities Feature Fusion Network for Multi-View Stereo. Neurocomputing 2023, 528, 35–47. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2117–2125. [Google Scholar]
- Hui, T.W.; Loy, C.C.; Tang, X. Depth map super-resolution by deep multi-scale guidance. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Yu, A.; Guo, W.; Liu, B.; Chen, X.; Wang, X.; Cao, X.; Jiang, B. Attention aware cost volume pyramid based multi-view stereo network for 3D reconstruction. ISPRS J. Photogramm. Remote Sens. 2021, 175, 448–460. [Google Scholar] [CrossRef]
- Huang, J.; Lee, A.; Mumford, D. Statistics of range images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2000, Hilton Head, SC, USA, 15–15 June 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 1, pp. 324–331. [Google Scholar]
- Laplace, P.S. Laplace distribution. Encyclopedia of Mathematics. 1801. Original Publication in 1801, Available in English Translation. Available online: https://encyclopediaofmath.org/wiki/Laplace_distribution (accessed on 6 June 2023).
- Aanæs, H.; Jensen, R.R.; Vogiatzis, G.; Tola, E.; Dahl, A.B. Large-scale data for multiple-view stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar] [CrossRef]
- Laplace, P.S. Laplace operator. Encyclopedia of Mathematics. 1820. Original Publication in 1820, Available in English Translation. Available online: https://encyclopediaofmath.org/wiki/Laplace_operator (accessed on 6 June 2023).
- Knapitsch, A.; Park, J.; Zhou, Q.Y.; Koltun, V. Tanks and Temples: Benchmarking large-scale scene reconstruction. ACM Trans. Graph. 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Schöps, T.; Schönberger, J.L.; Galliani, S.; Sattler, T.; Schindler, K.; Pollefeys, M.; Geiger, A. A Multi-View Stereo Benchmark with high-resolution images and multi-camera videos. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Zhang, J.; Ren, Y.; Zhou, L.; Fang, T.; Quan, L. Blendedmvs: A large-scale dataset for generalized multi-view stereo networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1790–1799. [Google Scholar]
- Peng, R.; Wang, R.; Wang, Z.; Lai, Y.; Wang, R. Rethinking depth estimation for multi-view stereo: A unified representation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19– 20 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 8645–8654. [Google Scholar]
- Wang, X.; Zhu, Z.; Huang, G.; Qin, F.; Ye, Y.; He, Y.; Chi, X.; Wang, X. MVSTER: Epipolar transformer for efficient multi-view stereo. In Proceedings of the Computer Vision—ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 573–591. [Google Scholar]
- Campbell, N.D.F.; Vogiatzis, G.; Hernández, C.; Cipolla, R. Using Multiple Hypotheses to Improve Depth-Maps for Multi-View Stereo. In Proceedings of the Computer Vision—ECCV 2008: 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Forsyth, D., Torr, P., Zisserman, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 766–779. [Google Scholar]
- Luo, K.; Guan, T.; Ju, L.; Wang, Y.; Chen, Z.; Luo, Y. Attention-aware multi-view stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Zhang, J.; Yao, Y.; Li, S.; Luo, Z.; Fang, T. Visibility-aware multi-view stereo network. In Proceedings of the 31st British Machine Vision Conference, Virtual Event, London, UK, 7–10 September 2020. [Google Scholar]
- Ma, X.; Gong, Y.; Wang, Q.; Huang, J.; Chen, L.; Yu, F. EPP-MVSNet: Epipolar-assembling based depth prediction for multi-view stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, New Orleans, LA, USA, 18–24 June 2022; IEEE: Piscataway, NJ, USA, 2021; pp. 5732–5740. [Google Scholar]
- Wei, Z.; Zhu, Q.; Min, C.; Chen, Y.; Wang, G. AA-RMVSNet: Adaptive aggregation recurrent multi-view stereo network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, New Orleans, LA, USA, 18–24 June 2022; IEEE: Piscataway, NJ, USA, 2021; pp. 6187–6196. [Google Scholar]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1395–1403. [Google Scholar]






| Intermediate Set | Advanced Set | |||||
|---|---|---|---|---|---|---|
| Methods | P (%) ↑ | R (%) ↑ | F-Score ↑ | P (%) ↑ | R (%) ↑ | F-Score ↑ |
| PatchmatchNet | 43.64 | 69.38 | 53.15 | 27.27 | 41.66 | 32.31 |
| Ours | 45.12 | 69.69 | 54.30 | 28.31 | 41.06 | 32.80 |
| Method | Accuracy (%) ↑ | Completeness (%) ↑ | F-Score ↑ |
|---|---|---|---|
| PatchmatchNet | 64.81 | 65.43 | 64.21 |
| Ours | 64.96 | 65.21 | 64.37 |
| Point Clouds (Testing) | Depth Maps (Validation) | ||||
|---|---|---|---|---|---|
| Methods | Acc. (mm)↓ | Comp. (mm)↓ | Overall (mm)↓ | Depth Map (mm)↓ | Error Ratio (%; error > 8 mm)↓ |
| PatchmatchNet [17] | 0.427 | 0.277 | 0.352 | 7.09 | 11.58 |
| Architecture + | 0.412 | 0.273 | 0.342 | 5.41 | 9.07 |
| Architecture + | 0.412 | 0.270 | 0.341 | 5.44 | 8.96 |
| Architecture + | 0.405 | 0.267 | 0.336 | 5.47 | 9.01 |
| Architecture + | 0.399 | 0.280 | 0.339 | 5.28 | 8.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahimli, N.; Ledoux, H.; Kooij, J.F.P.; Nan, L. DDL-MVS: Depth Discontinuity Learning for Multi-View Stereo Networks. Remote Sens. 2023, 15, 2970. https://doi.org/10.3390/rs15122970
Ibrahimli N, Ledoux H, Kooij JFP, Nan L. DDL-MVS: Depth Discontinuity Learning for Multi-View Stereo Networks. Remote Sensing. 2023; 15(12):2970. https://doi.org/10.3390/rs15122970
Chicago/Turabian StyleIbrahimli, Nail, Hugo Ledoux, Julian F. P. Kooij, and Liangliang Nan. 2023. "DDL-MVS: Depth Discontinuity Learning for Multi-View Stereo Networks" Remote Sensing 15, no. 12: 2970. https://doi.org/10.3390/rs15122970
APA StyleIbrahimli, N., Ledoux, H., Kooij, J. F. P., & Nan, L. (2023). DDL-MVS: Depth Discontinuity Learning for Multi-View Stereo Networks. Remote Sensing, 15(12), 2970. https://doi.org/10.3390/rs15122970