Multi-Source SAR-Based Surface Deformation Monitoring and Groundwater Relationship Analysis in the Yellow River Delta, China
Abstract
1. Introduction
2. Materials and Methods
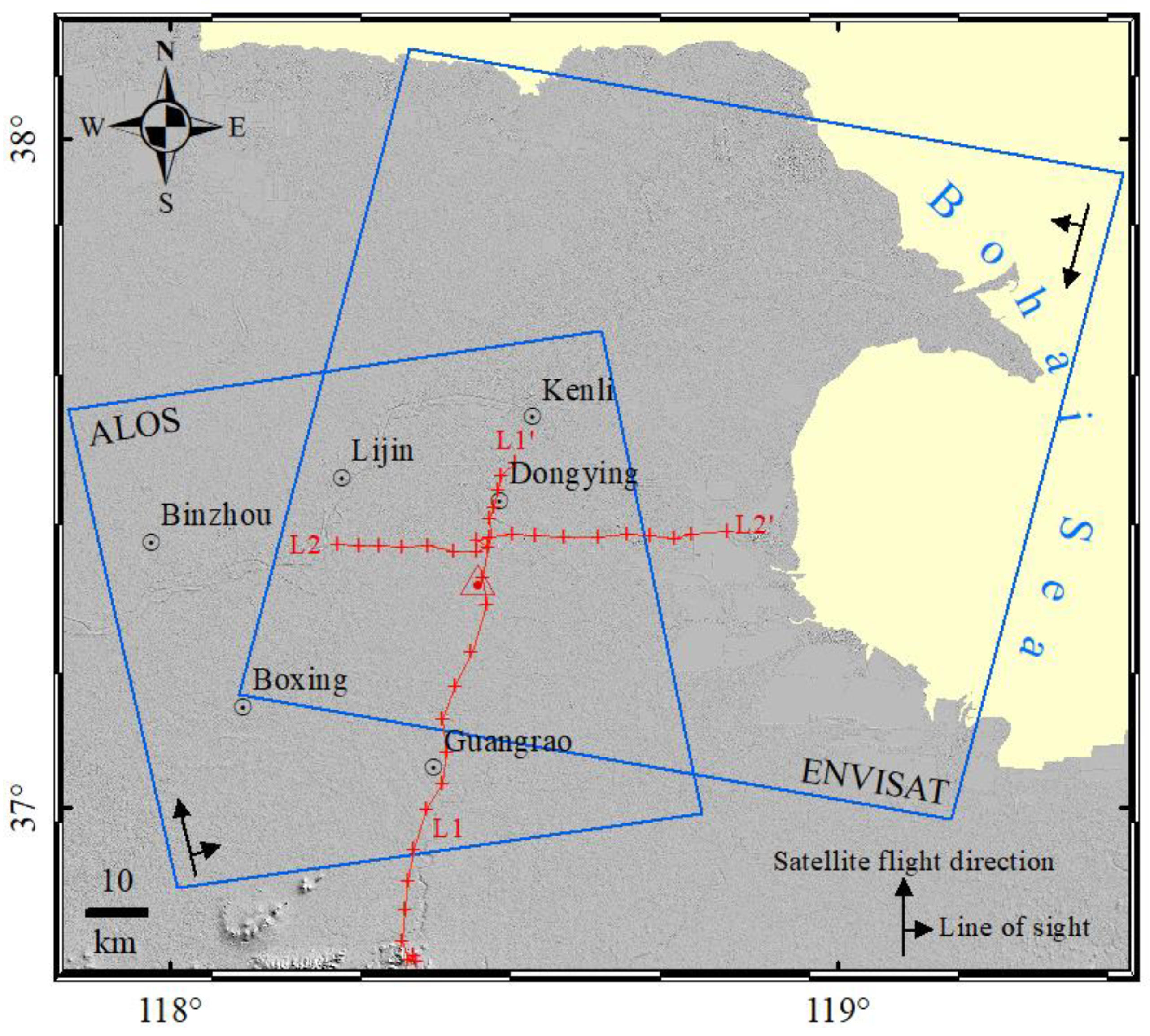
2.1. Study Area
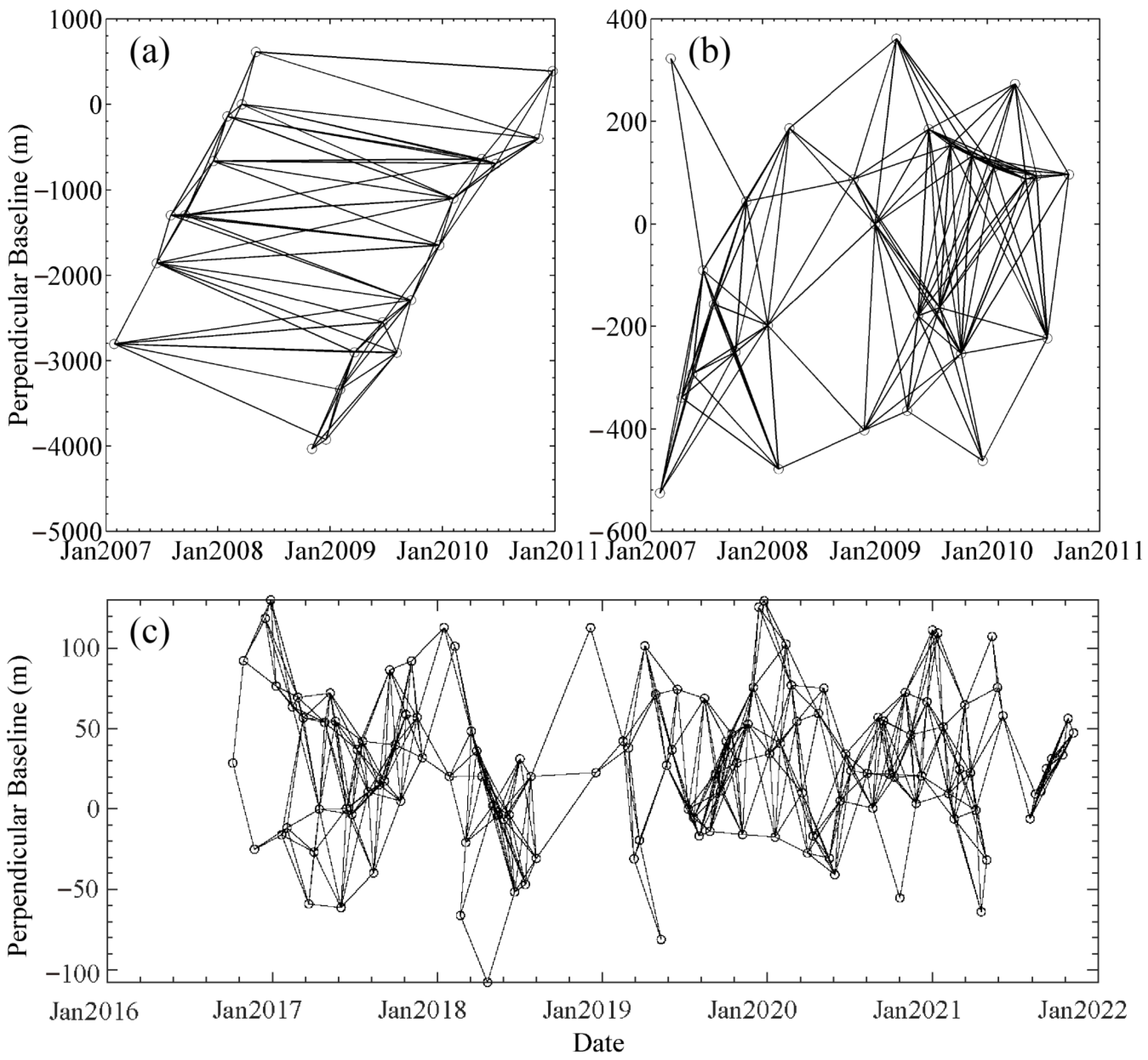
2.2. SAR Data
2.3. SBAS InSAR
2.4. Velocity Decomposition
2.5. Distributed Point-Source Model
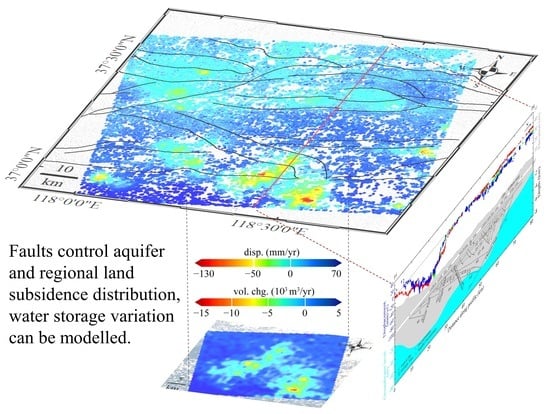
3. Results
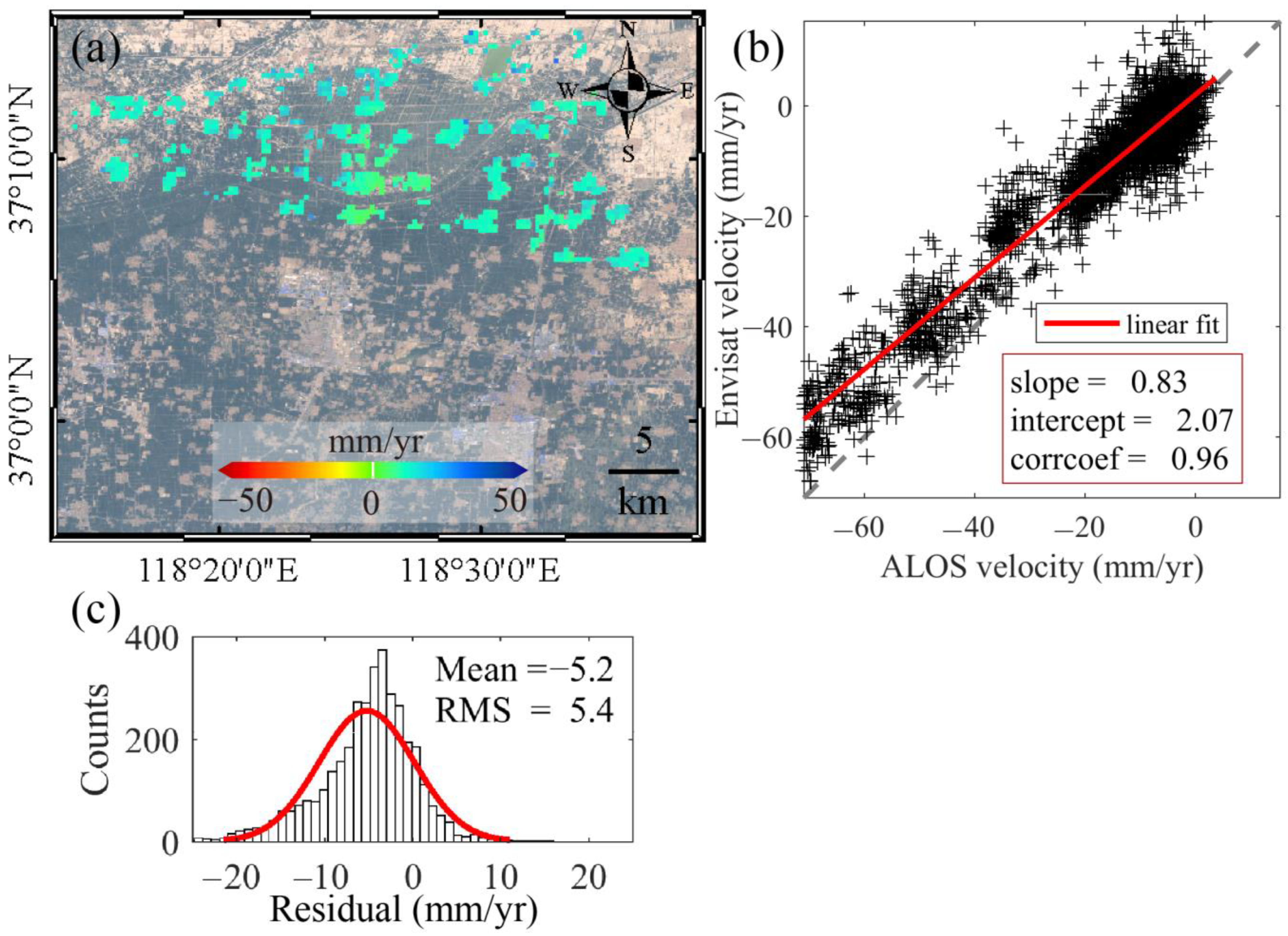
3.1. InSAR Results and Analysis
3.2. Modelling Results and Analysis
4. Discussion
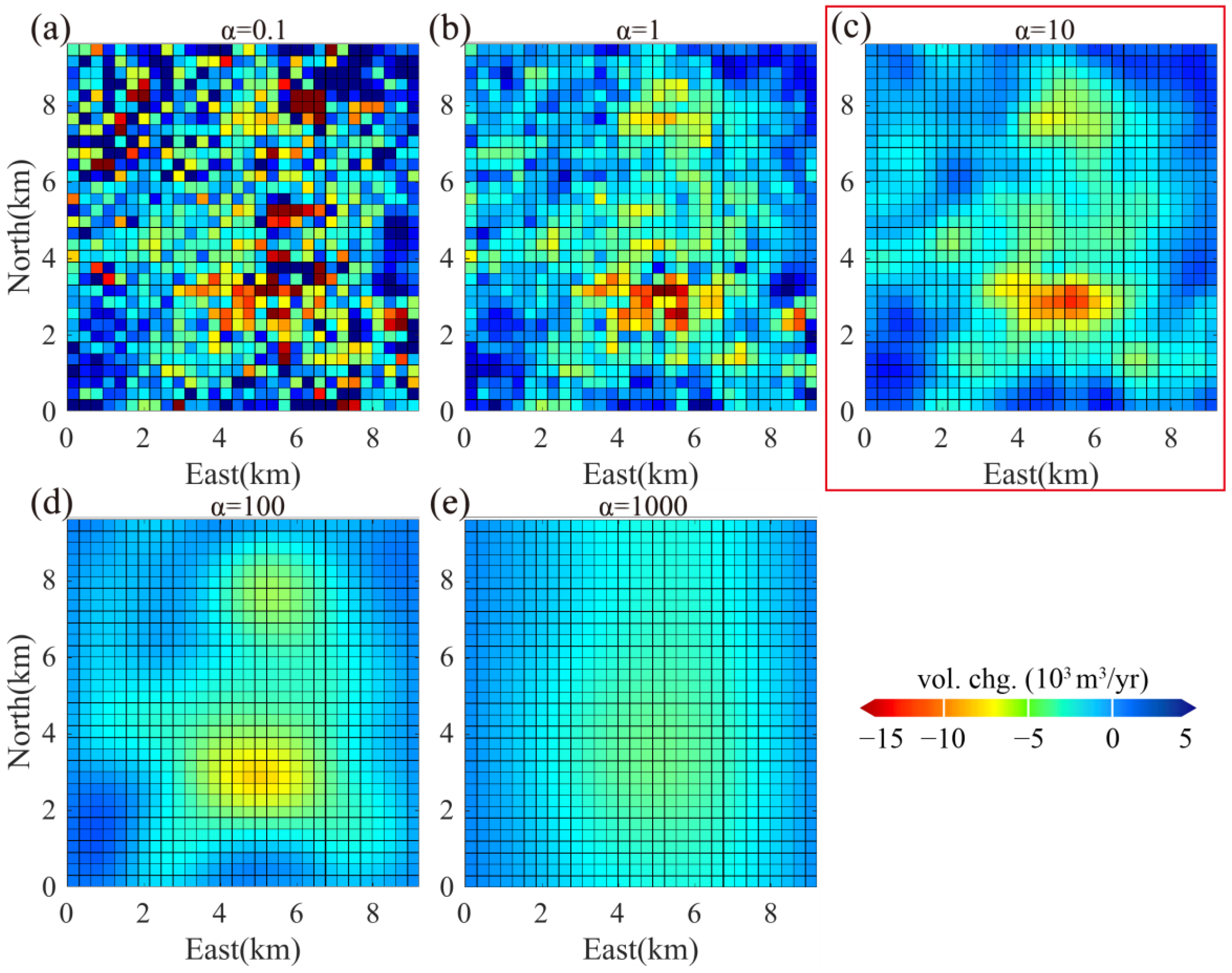
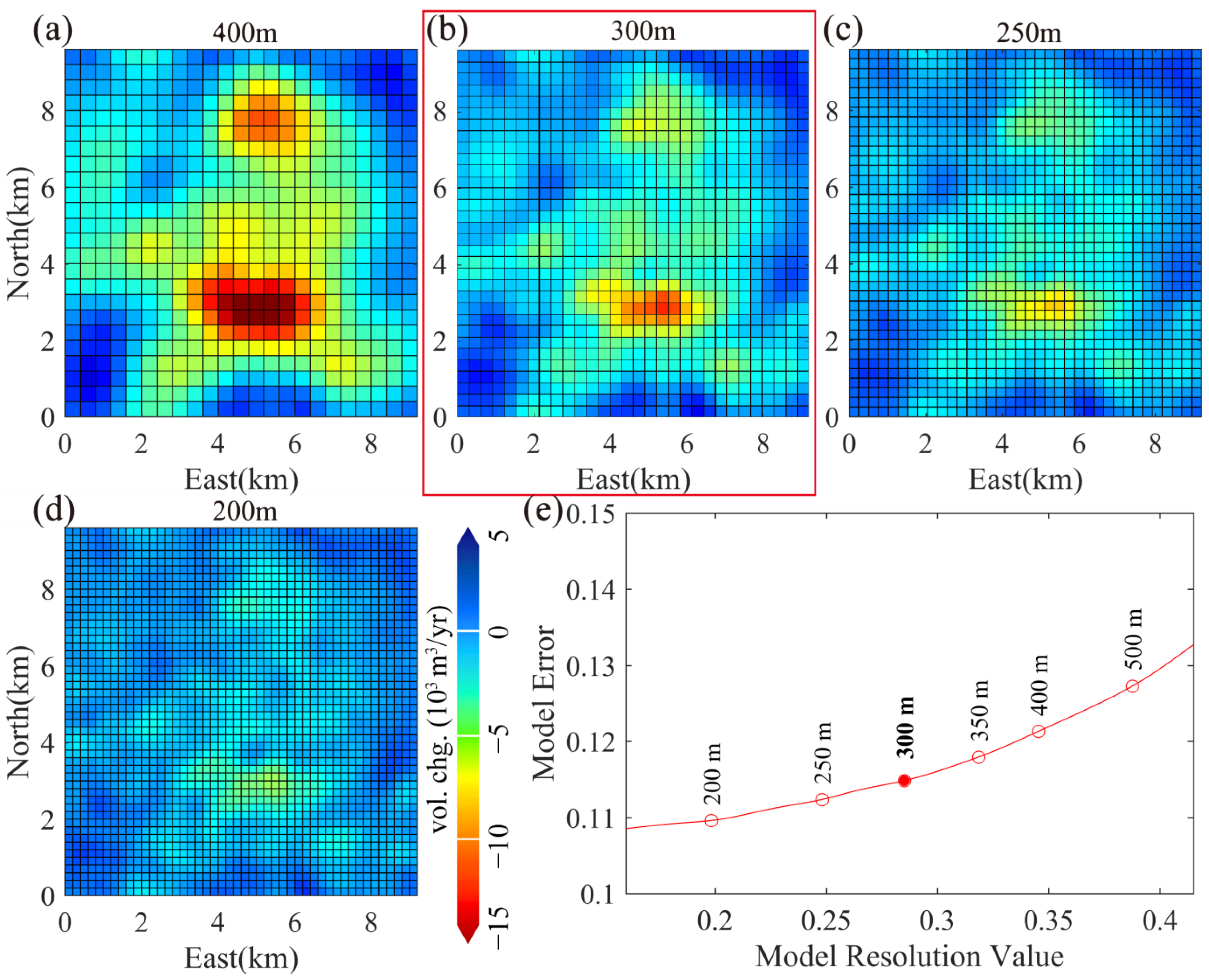
4.1. Impacts of Variable Model Parameters
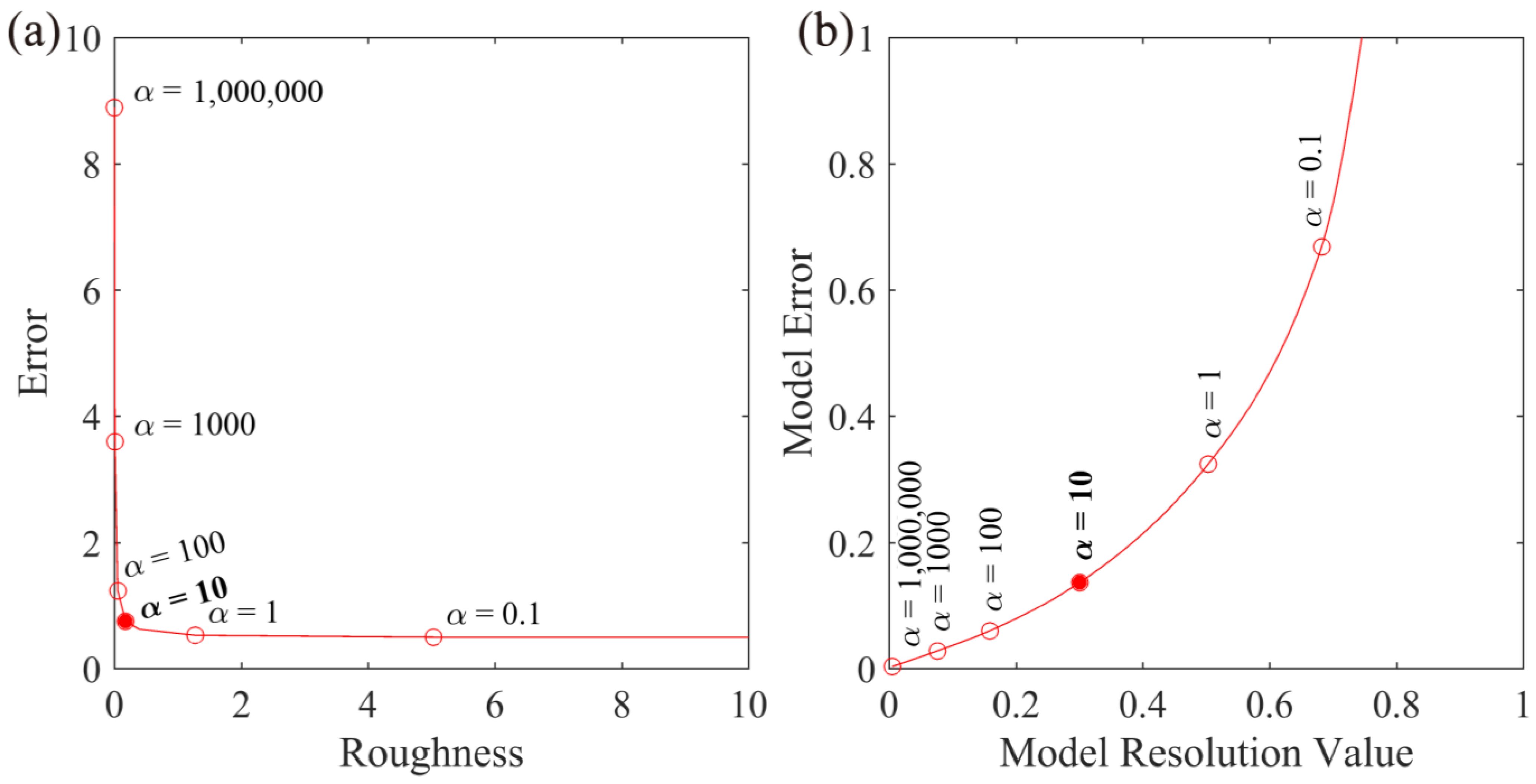
4.1.1. Smoothing Factor ()
4.1.2. Reservoir Grid Size
4.2. Impacts of Fault and Groundwater
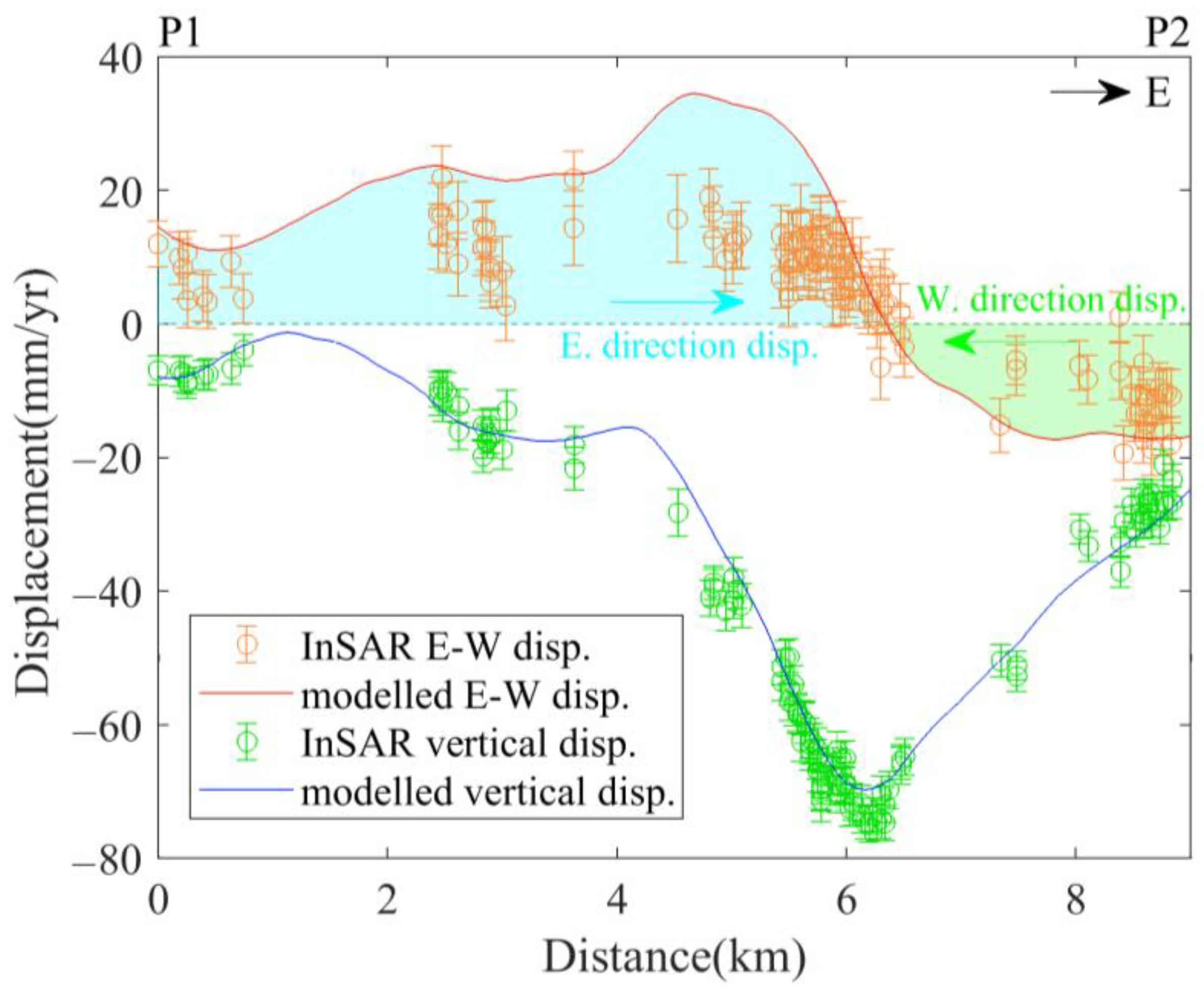
4.3. Impacts of Horizontal Displacement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Stratigraphic Age | Burial Depth of Floor (m) | Thickness (m) | Lithology |
|---|---|---|---|
| Holocene | |||
| Q43 | 1.1–2.0 | 1.1–2.0 | Silty clay, silt |
| 2.0–4.0 | 1.0–2.0 | ||
| Q42 | 7.0–9.0 | 4.0–6.0 | Silt, silty clay |
| 14.0–16.0 | 6.0–8.0 | ||
| 18.4–28.8 | 4.0–8.0 | ||
| Q41 | 25.2–31.8 | 2.0–10.3 | Fine sand |
| Late pleistocene | |||
| Q32 | 36.0–41.0 | 8.0–11.0 | Silty clay, silt |
| 45.0–50.0 | 8.0–10.0 | ||
| 60.0–70.8 | 10.0–13.0 | ||
| Q31 | 85.0–90.0 | 23.0–28.0 | Silty-fine sand, silty clay |
| 110–118 | 25.0–30.0 | ||
| Middle pleistocene | |||
| Q2 | 150–160 | 38.0–45.0 | Silty clay, sand layer |
| Early pleistocene | |||
| Q1 | 300–330 | 145–170 | |
| Pliocene | |||
| Nm3 | 400–460 | 105–150 | |
| Nm2 | 600–650 | 180–220 | Mid-fine sand, clay |
| Nm1 | 900–1000 | 280–380 | Clay, mid-fine sand |
Appendix B
Appendix C
References
- Giosan, L.; Syvitski, J.; Constantinescu, S.; Day, J. Climate change: Protect the world’s deltas. Nature 2014, 516, 31–33. [Google Scholar] [CrossRef]
- Syvitski, J.P.M. Deltas at risk. Sustain. Sci. 2008, 3, 23–32. [Google Scholar] [CrossRef]
- Minderhoud, P.S.J.; Middelkoop, H.; Erkens, G.; Stouthamer, E. Groundwater extraction may drown mega-delta: Projections of extraction-induced subsidence and elevation of the Mekong delta for the 21st century. Environ. Res. Commun. 2020, 2, 011005. [Google Scholar] [CrossRef]
- Erban, L.E.; Gorelick, S.M.; Zebker, H.A.; Fendorf, S. Release of arsenic to deep groundwater in the Mekong Delta, Vietnam, linked to pumping-induced land subsidence. Proc. Natl. Acad. Sci. USA 2013, 110, 13751–13756. [Google Scholar] [CrossRef] [PubMed]
- Syvitski, J.P.M.; Kettner, A.J.; Overeem, I.; Hutton, E.W.H.; Hannon, M.T.; Brakenridge, G.R.; Day, J.; Vorosmarty, C.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Pachauri, R.K., Meyer, L.A., Core Writing Team, Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Wong, P.P.; Losada, I.J.; Gattuso, J.-P.; Hinkel, J.; Khattabi, A.; McInnes, K.L.; Saito, Y.; Sallenger, A. Coastal systems and low-lying areas, in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 361–409. [Google Scholar]
- UNESCO/UN-Water. United Nations World Water Development Report 2020: Water and Climate Change; UNESCO: Paris, France, 2020. [Google Scholar]
- Zhang, Y.; Liu, Y.; Zhang, X.; Huang, H.; Qin, K.; Bai, Z.; Zhou, X. Correlation Analysis between Land-Use/Cover Change and Coastal Subsidence in the Yellow River Delta, China: Reviewing the Past and Prospecting the Future. Remote Sens. 2021, 13, 4563. [Google Scholar] [CrossRef]
- Lazos, I.; Papanikolaou, I.; Sboras, S.; Foumelis, M.; Pikridas, C. Geodetic Upper Crust Deformation Based on Primary GNSS and INSAR Data in the Strymon Basin, Northern Greece—Correlation with Active Faults. Appl. Sci. 2022, 12, 9391. [Google Scholar] [CrossRef]
- Shen, G.; Fu, W.; Guo, H.; Liao, J. Water Body Mapping Using Long Time Series Sentinel-1 SAR Data in Poyang Lake. Water 2022, 14, 1902. [Google Scholar] [CrossRef]
- Dixon, T.H.; Amelung, F.; Ferretti, A.; Novali, F.; Rocca, F.; Dokka, R.; Sella, G.; Kim, S.-W.; Wdowinski, S.; Whitman, D. Subsidence and flooding in New Orleans. Nature 2006, 441, 587–588. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T. Quantitative evidence that compaction of Holocene sediments drives the present land subsidence of the Po Delta, Italy. J. Geophys. Res. Solid Earth 2011, 116, B08407. [Google Scholar] [CrossRef]
- Higgins, S.A. Review: Advances in delta-subsidence research using satellite methods. Hydrogeol. J. 2016, 24, 587–600. [Google Scholar] [CrossRef]
- Qu, F.; Lu, Z.; Kim, J.; Turco, M.J. Mapping and characterizing land deformation during 2007–2011 over the Gulf Coast by L-band InSAR. Remote Sens. Environ. 2023, 284, 113342. [Google Scholar] [CrossRef]
- Qu, F.F.; Lu, Z.; Zhang, Q.; Bawden, G.W.; Kim, J.-W.; Zhao, C.Y.; Qu, W. Mapping ground deformation over Houston–Galveston, Texas using multi-temporal InSAR. Remote Sens. Environ. 2015, 169, 290–306. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Gebremichael, E.; Sultan, M.; Becker, R.; El Bastawesy, M.; Cherif, O.; Emil, M. Assessing Land Deformation and Sea Encroachment in the Nile Delta: A Radar Interferometric and Inundation Modeling Approach. J. Geophys. Res. Solid Earth 2018, 123, 3208–3224. [Google Scholar] [CrossRef]
- Liu, Y.L.; Huang, H.J.; Liu, Y.X.; Bi, H.B. Linking land subsidence over the Yellow River delta, China, to hydrocarbon exploitation using multi-temporal InSAR. Nat. Hazards 2016, 84, 271–291. [Google Scholar] [CrossRef]
- Fabris, M.; Battaglia, M.; Chen, X.; Menin, A.; Monego, M.; Floris, M. An Integrated InSAR and GNSS Approach to Monitor Land Subsidence in the Po River Delta (Italy). Remote Sens. 2022, 14, 5578. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F.; Massonet, D. InSAR Principles-Guidelines for SAR Interferometry Processing and Interpretation; Fletcher, K., Ed.; ESA Publications: Noordwijk, The Netherlands, 2007; Volume 19. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. Geosci. Remote Sens. IEEE Trans. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. Geosci. Remote Sens. IEEE Trans. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth (1978–2012) 2007, 112, B07407. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Canziani, O.F., Parry, M.L., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Richard, J., Eds.; Cambridge University Press: Cambridge, UK, 2007; p. 976. [Google Scholar]
- Liu, Y.L.; Huang, H.J.; Dong, J.F. Large-area land subsidence monitoring and mechanism research using the small baseline subset interferometric synthetic aperture radar technique over the Yellow River Delta, China. J. Appl. Remote Sens. 2015, 9, 096019. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; McGuire, V.L.; McMahon, P.B. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Müller Schmied, H.; van Beek, L.P.H.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef]
- Poland, J.F.; Davis, G.H. Land subsidence due to withdrawal of fluids. Rev. Eng. Geol. 1969, 2, 187–270. [Google Scholar] [CrossRef]
- Galloway, D.; Burbey, T. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Bawden, G.W.; Thatcher, W.; Stein, R.S.; Hudnut, K.W.; Peltzer, G. Tectonic contraction across Los Angeles after removal of groundwater pumping effects. Nature 2001, 412, 812–815. [Google Scholar] [CrossRef] [PubMed]
- Motagh, M.; Shamshiri, R.; Haghshenas Haghighi, M.; Wetzel, H.-U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Qu, F.F.; Zhang, Q.; Lu, Z.; Zhao, C.Y.; Yang, C.S.; Zhang, J. Land subsidence and ground fissures in Xi’an, China 2005–2012 revealed by multi-band InSAR time-series analysis. Remote Sens. Environ. 2014, 155, 366–376. [Google Scholar] [CrossRef]
- De Wit, K.; Lexmond, B.R.; Stouthamer, E.; Neussner, O.; Dörr, N.; Schenk, A.; Minderhoud, P.S.J. Identifying Causes of Urban Differential Subsidence in the Vietnamese Mekong Delta by Combining InSAR and Field Observations. Remote Sens. 2021, 13, 189. [Google Scholar] [CrossRef]
- Minderhoud, P.S.J.; Hlavacova, I.; Kolomaznik, J.; Neussner, O. Towards unraveling total subsidence of a mega-delta—The potential of new PS InSAR data for the Mekong delta. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 327–332. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Xia, X.; Bi, H.; Huang, H.; Ding, R.; Zhao, L. Land subsidence of the Yellow River Delta in China driven by river sediment compaction. Sci. Total Environ. 2021, 750, 142165. [Google Scholar] [CrossRef]
- Milliman, J.D.; Syvitski, J.P.M. Geomorphic/Tectonic Control of Sediment Discharge to the Ocean: The Importance of Small Mountainous Rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Ganti, V.; Chu, Z.; Lamb, M.P.; Nittrouer, J.A.; Parker, G. Testing morphodynamic controls on the location and frequency of river avulsions on fans versus deltas: Huanghe (Yellow River), China. Geophys. Res. Lett. 2014, 41, 7882–7890. [Google Scholar] [CrossRef]
- Fan, H.; Huang, H.J.; Zeng, T.Q.; Wang, K.R. River mouth bar formation, riverbed aggradation and channel migration in the modern Huanghe (Yellow) River delta, China. Geomorphology 2006, 74, 124–136. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Jia, Y.; Du, Q.; Sun, Y.; Yin, P.; Shan, H. Rapid consolidation characteristics of Yellow River-derived sediment: Geotechnical characterization and its implications for the deltaic geomorphic evolution. Eng. Geol. 2020, 270, 105578. [Google Scholar] [CrossRef]
- Zhang, S.W. The application of an integrated approach in exploration of lacustrine turbidites in Jiyang Sub-basin, Bohai Bay Basin, China. J. Pet. Sci. Eng. 2004, 41, 67–77. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Liu, Q.; Zhu, R.F.; Li, Z.; Lu, X.C. Source rocks in Mesozoic–Cenozoic continental rift basins, east China: A case from Dongying Depression, Bohai Bay Basin. Org. Geochem. 2009, 40, 229–242. [Google Scholar] [CrossRef]
- Li, S.N.; Wang, G.X.; Deng, W.; Lu, Y.X. Variations of Groundwater Depth in Yellow River Delta in Recent Two Decades. Prog. Geogr. 2008, 27, 49–56, (In Chinese with English Abstract). [Google Scholar]
- DBDMPG. Dongying Book, Dongying Municipal People’s Government. 2021. Available online: http://www.dongying.gov.cn/dynj/dynj2006-g1/index.html#p=50 (accessed on 20 May 2020). (In Chinese)
- DODMPG. Dongying Overview, Dongying Municipal People’s Government. 2021. Available online: http://www.dongying.gov.cn/col/col40583/index.html (accessed on 23 April 2021). (In Chinese)
- Hooper, A.; Zebker, H.A. Phase unwrapping in three dimensions with application to InSAR time series. J. Opt. Soc. Am. A 2007, 24, 2737–2747. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Garthwaite, M.C. Resolving Three-Dimensional Surface Motion with InSAR: Constraints from Multi-Geometry Data Fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef]
- Mogi, K. Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them. Bull. Earthq. Res. Inst. Univ. Tokyo 1958, 36, 99–134. [Google Scholar]
- Terzaghi, K.; Ralph, B.P.; Gholamreza, M. Soil Mechanics in Engineering Practice; JohnWiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Segall, P. Earthquake and Volcano Deformation; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Fokker, P.A.; Orlic, B. Semi-Analytic Modelling of Subsidence. Math. Geol. 2006, 38, 565–589. [Google Scholar] [CrossRef]
- Du, Y.; Aydin, A.; Segall, P. Comparison of various inversion techniques as applied to the determination of a geophysical deformation model for the 1983 Borah Peak earthquake. Bull. Seismol. Soc. Am. 1992, 82, 1840–1866. [Google Scholar] [CrossRef]
- Geertsma, J. Land subsidence above compacting oil and gas reservoirs. J. Pet. Technol. 1973, 25, 734–744. [Google Scholar] [CrossRef]
- Dusseault, M.; Rothenburg, L. Analysis of Deformation Measurements for Reservoir Managemen. Oil Gas Sci. Technol. 2002, 57, 539–554. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, H.; Liu, Y.; Liu, Y.; Bi, H. Spatial and temporal variations in subsidence due to the natural consolidation and compaction of sediment in the yellow river delta, china. Mar. Georesour. Geotechnol. 2018, 37, 152–163. [Google Scholar] [CrossRef]
- Liu, Y.; Du, T.; Huang, H.; Liu, Y.; Zhang, Y. Estimation of sediment compaction and its relationship with river channel distributions in the Yellow River delta, China. Catena 2019, 182, 104113. [Google Scholar] [CrossRef]
- Dijkstra, T.K. Latent Variables and Indices: Herman Wold’s Basic Design and Partial Least Squares. In Handbook of Partial Least Squares; Esposito, V.V., Chin, W., Henseler, J., Wang, H., Eds.; Springer Handbooks of Computational Statistics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 23–46. [Google Scholar] [CrossRef]
- SPGEMS. Report on the Investigation and Evaluation of Environmental Geological Issues in Key Groundwater Extraction Areas in Shandong Province; Shandong Provincial Geological Environment Monitoring Station: Jinan, China, 2013. (In Chinese) [Google Scholar]
- Zhang, S.W.; Wang, Y.S.; Shi, D.S.; Xu, H.M.; Pang, X.Q.; Li, M.W. Fault-fracture mesh petroleum plays in the Jiyang Superdepression of the Bohai Bay Basin, eastern China. Mar. Pet. Geol. 2004, 21, 651–668. [Google Scholar] [CrossRef]
- An, H.; Wang, B.; Changlong, Z. Study on Forming Mechanism of Structural Type Ground Fissures in Shandong Province. Shandong Land Resour. 2014, 32, 34–37, (In Chinese with English Abstract). [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, Y.; Zhao, F.; Ding, R.; Zhao, L.; Niu, Y.; Qu, F.; Ling, Z. Multi-Source SAR-Based Surface Deformation Monitoring and Groundwater Relationship Analysis in the Yellow River Delta, China. Remote Sens. 2023, 15, 3290. https://doi.org/10.3390/rs15133290
Liu Y, Zhang Y, Zhao F, Ding R, Zhao L, Niu Y, Qu F, Ling Z. Multi-Source SAR-Based Surface Deformation Monitoring and Groundwater Relationship Analysis in the Yellow River Delta, China. Remote Sensing. 2023; 15(13):3290. https://doi.org/10.3390/rs15133290
Chicago/Turabian StyleLiu, Yilin, Yi Zhang, Faqiang Zhao, Renwei Ding, Lihong Zhao, Yufen Niu, Feifei Qu, and Zilong Ling. 2023. "Multi-Source SAR-Based Surface Deformation Monitoring and Groundwater Relationship Analysis in the Yellow River Delta, China" Remote Sensing 15, no. 13: 3290. https://doi.org/10.3390/rs15133290
APA StyleLiu, Y., Zhang, Y., Zhao, F., Ding, R., Zhao, L., Niu, Y., Qu, F., & Ling, Z. (2023). Multi-Source SAR-Based Surface Deformation Monitoring and Groundwater Relationship Analysis in the Yellow River Delta, China. Remote Sensing, 15(13), 3290. https://doi.org/10.3390/rs15133290