Abstract
Filtering out vegetation from a point cloud based on color is only rarely used, largely due to the lack of knowledge of the suitability of input information (color, vegetation indices) and the thresholding methods. We have evaluated multiple vegetation indices (ExG, ExR, ExB, ExGr, GRVI, MGRVI, RGBVI, IKAW, VARI, CIVE, GLI, and VEG) and combined them with 10 methods of threshold determination based on training set selection (including machine learning methods) and the renowned Otsu’s method. All these combinations were applied to four clouds representing vegetated rocky terrain, and the results were compared. The ExG and GLI indices were generally the most suitable for this purpose, with the best F-scores of 97.7 and 95.4, respectively, and the best-balanced accuracies for the same combination of the method/vegetation index of 98.9 and 98.3%, respectively. Surprisingly, these best results were achieved using the simplest method of threshold determination, considering only a single class (vegetation) with a normal distribution. This algorithm outperformed all other methods, including those based on a support vector machine and a deep neural network. Thanks to its simplicity and ease of use (only several patches representing vegetation must be manually selected as a training set), this method can be recommended for vegetation removal from rocky and anthropogenic surfaces.
1. Introduction
Research on the complex morphology, genesis, and transformations of geological features cannot be conducted without accurate geodetic measurements that provide thorough surveys, maps, sections, and spatial models. Such objects can be studied using modern non-contact technologies such as digital photogrammetry [1] and laser scanning techniques [2], both ground-based [3] and airborne [4]. These methods usually produce a point cloud describing the measured surfaces in detail. Especially when mapping rock formations, landslides, etc., the presence of vegetation is one of the main obstacles [5,6,7] and, hence, must be filtered out before further processing. Various geometric and structural filters have been implemented in commercial or non-commercial software for use with LiDAR point clouds [8] or point clouds generated photogrammetrically [9]. New filtering algorithms or procedures have also been developed [10,11,12,13,14], some of which have been successfully applied to rock masses [15,16]. However, the successful use of algorithms with the geometric principle for rocky terrains is difficult due to the ruggedness of the formations.
To remove vegetation, color-based filtering (especially using green color) is a logical option. However, automated implementation of this solution in the RGB color space is complicated, although a human operator can distinguish between vegetation and ground under normal conditions without any problems. An alternative solution might lie in using vegetation indices.
A vegetation index is a numerical value that aims to express a characteristic of vegetation, such as its health. It can, therefore, be used to distinguish not only the quality of the vegetation but also whether it is vegetation or not. There are many vegetation indices calculated from different spectral bands of electromagnetic radiation. This approach is particularly used in conjunction with satellite imagery, where registered bands include invisible parts of electromagnetic radiation. However, for the application proposed here and in everyday practice, standard cameras are typically used due to the high costs of multispectral sensors and, in effect, only the visible bands captured by standard cameras (red, green, and blue) are usually available. This limits the range of usable indices, but a considerable number of such indices still remain available. Hereinafter, we will focus only on vegetation indices (VI) derived from the visible spectrum.
The use of vegetation indices to filter different vegetation types can be found in many studies. In a study by Meyer et al. [17], several vegetation indices were tested for the detection of soybean plants. Moorthy et al. in [18] detected sugar beet and corn using several established and one new vegetation indices. Kim et al. in [19] detected Chinese cabbage and white radish using multitemporal imagery and vegetation indices. Liu et al. in [20] worked with barley leaves and Ponti et al. in [21] used vegetation indices on images. All these studies show that the use of vegetation indices on image data is, to some extent, functional and useful. The use of color information in the cloud in conjunction with vegetation indices for vegetation filtering is addressed, e.g., by Anders et al. in [22]. Alba et al. in [23] very interestingly use first a near-infrared (NIR) camera cloud coloration from a laser scanner and only then apply an NDVI to filter the vegetation out. Cloud classification using vegetation indices for vine detection is addressed by Mesas-Carrascosa et al. in [24]. Núñez-Andrés in [25] compared vegetation filtering based on color information transformed into HSV (Hue, Saturation, and Value) and on ExG vegetation index on a rock massif, with both methods yielding good results. The use of colors for cloud processing can, therefore, greatly increase the efficiency of filtering or classification.
It is worth noting that although mass data collection methods are currently very popular in many fields of research involving complex terrain [26], such as coastal monitoring [27,28,29], volcano exploration [30], underground research [31,32], tree detection [33,34], the evolution of rock glaciers [35], monitoring of rock masses [36,37,38], or their geological analysis [39], vegetation filtering in such cases is typically handled by human operators as the performance of automated algorithms proposed for this purpose, so far, is generally poor as confirmed by Blanco et al. [6]. Specifically, they usually have problems when encountering highly rugged and/or sloped terrain [15]. Ignoring the vegetation and failing to remove it can greatly complicate the interpretation of the results [7], which further underlines the importance of introducing such an automated method.
One of the reasons why automatic vegetation filtering is problematic lies in the difficult determination of a threshold value for distinguishing green vegetation points from non-vegetation ones. Establishing any absolute and universally valid threshold is generally impossible because camera sensors are not identical and, in effect, such a threshold must necessarily differ among imagery acquisition systems. All the studies cited above use either Otsu’s method [40] or set a specific value for the threshold by estimation. Otsu’s method is an automated one, applicable to data where the representation of vegetation and ground classes are similar. It is, however, unsuitable for applications of general filtering of green vegetation from point clouds for the purpose of examining morphological formations, as the relative abundance of green vegetation in the cloud is highly variable (and in some cases very small), as stated in [41] or [42].
In view of the above, this paper aims to test different methods of threshold determination in conjunction with various visible vegetation indices and to find the most suitable method for filtering out green vegetation based on vegetation indices for rocky terrain. Our approach requires manual selection of sample areas (training data), which can overcome the problem with a variable amount of vegetation in the data. Testing will be performed on four real-world datasets capturing various types of rocks from different locations, providing a wide color range of rocks, vegetation, and surroundings. We employ multiple algorithms utilizing vegetation indices, from simple mathematical approaches, through the use of a support vector machine (SVM) approach, and up to a three-layer neural network (DNN). The latter two methods are used for individual vegetation indices as well as for their combinations. In addition, the results of these methods are compared with those acquired using the method devised by Otsu.
2. Materials and Methods
2.1. The Test Data
To evaluate whether green vegetation can be distinguished by the suggested approach, data on vegetated rock walls with varying color ranges were employed. Although the origin of the data plays no role in the evaluation, as we are looking for a universally applicable method of vegetation filtering, a brief description of the data collection process is provided below.
2.1.1. Data 1
The region of interest was in the town of Ledeč nad Sázavou (Central Bohemia, Czech Republic). The rock wall was approximately 55 m wide and 22 m high. The point cloud was acquired using the SfM-MVS method and the DJI Phantom 4 UAV camera. The flight was piloted manually, and imagery was acquired from a distance of 20 to 30 m from the terrain in a way that ascertains approximately 80% overlap. The original mean ground sampling distance (GSD) was 8 mm. For the purposes of this study, the cloud was diluted to an average point density of 1850 points/m2 (i.e., the points are roughly in a 0.02 m grid). In total, the diluted cloud contained 2,861,035 points. The representation of green vegetation in the dataset identified manually by the operator was 19.5%. The point cloud is shown in Figure 1a.

Figure 1.
Point clouds used in this study: (a) Data 1—Rock with brown clay and low grass (b) Data 2—Yellow-brown rock (c) Data 3—Light brown rock (d) Data 4—Gray rock with higher vegetation.
2.1.2. Data 2
The point cloud was acquired using the SfM-MVS method with the DJI Phantom 4 UAV’s internal camera in the area of Horní Počenice near the capital city of Prague (Czech Republic). The selected rock wall is approximately 15 m wide and 4 m high. The flight was piloted manually, and imagery was acquired from a distance of 20 to 30 m from the terrain in a way that ascertains approximately 80% overlap. The original mean ground sampling distance (GSD) was about 7 mm. For the purposes of this study, the cloud was diluted to an average point density of 11,900 points/m2 (i.e., the points are roughly in a 0.01 m grid). In total, the diluted cloud contained 1,973,242 points. The representation of green vegetation in the dataset identified manually by the operator was 38.5%. The point cloud is shown in Figure 1b.
2.1.3. Data 3
The point cloud was acquired using the SfM-MVS method and a DJI P1 camera carried by a DJI Matrice 300 UAV in the vicinity of the settlement of Dolní Kounice (approximately 10 km south-west of Brno, South Moravia, Czech Republic). The selected cliff is approximately 40 m in width and 16 m in height. The flight was piloted manually, and imagery was acquired from a distance of 20 to 30 m from the terrain in a way that ascertains approximately 80% overlap. The original mean ground sampling distance (GSD) was about 2 mm. For the purposes of this study, the cloud was diluted to an average point density of 1900 points/m2 (i.e., the points are roughly in a 0.02 m grid). In total, the diluted cloud contained 1,425,119 points. The representation of green vegetation in the dataset identified manually by the operator was 11.4%. The point cloud is shown in Figure 1c.
2.1.4. Data 4
The point cloud was acquired using the SfM-MVS method and the DJI Phantom 4 UAV’s internal camera in Porta Bohemica (on the banks of the Elbe River, between Malé Žernoseky and Litochovice nad Labem, Northern Bohemia, Czech Republic). The selected area is approximately 40 m in width and 30 m in height. The flight was piloted manually, and imagery was acquired from a distance of 20 to 30 m from the terrain in a way that ascertains approximately 80% overlap. The original mean ground sampling distance (GSD) was approximately 7 mm. For the purposes of this study, the cloud was diluted to an average point density of 900 points/m2 (i.e., the points are roughly in a 0.03 m grid). In total, the diluted cloud contained 1,504,239 points. The representation of green vegetation in the dataset identified manually by the operator was 29.6%. The point cloud is shown in Figure 1d.
2.2. Vegetation Indices Tested
The selected vegetation indices used for testing are listed in Table 1, along with the abbreviation, calculation formula, and literature reference detailing the original purpose for their creation or use. R, B, and G represent the digital number of red, green, and blue channels, respectively; the variables r, g, and b are defined as r = R/(R + G + B), g = G/(R + G + B), b = B/(R + G + B).

Table 1.
Vegetation indices used for testing.
2.3. Methods of the Threshold Determination
2.3.1. Data Distribution and Training Datasets
When designing the method, it is necessary to assume that camera sensors, vegetation, lighting, and other measurement circumstances vary from case to case, and, therefore, it is necessary to determine the threshold that distinguishes the points representing green vegetation from the other points individually for each point cloud.
To show that for typical real-world data, such as ours, it is practically impossible to perform automatic filtering, and that it is necessary to use operator-defined subsets, we show a histogram for the whole Data 1 cloud for ExG vegetation index (a typical representative) in Figure 2g (histograms for all indices and Data 1 are given in Appendix B).
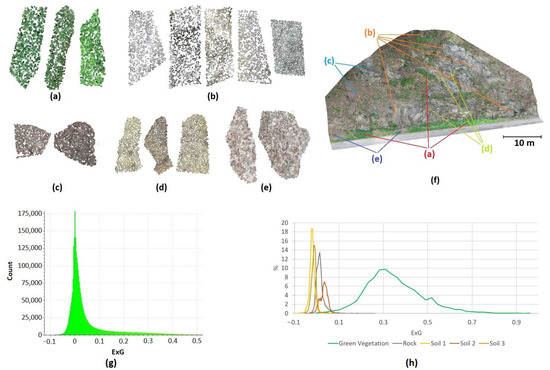
Figure 2.
Classes and their representation in the Data 1 dataset (a) green vegetation (b) rock (c–e) soil (different color shades) (f) positions of the samples within the Data 1 point cloud (g) histogram of frequencies of the ExG vegetation index for the whole cloud (h) Histograms of the ExG index for individual a-e subclasses.
The histogram is represented by a smooth curve with no obvious peaks indicating (at least) two different groups of data with different VI magnitudes.
The ExG histogram has a heavier tail on the right side, i.e., the statistical probability distribution is clearly not normal, nor is the neighborhood of the main peak symmetrical. This is due to the unequal representation of colors in the data, but this is to be expected.
It was, therefore, necessary to prepare training classes containing all color shades typical of individual classes as demonstrated in Figure 2, in which the Data 1 dataset is used to illustrate the selection of green vegetation intended to be filtered out (Figure 2a), rock (Figure 2b), and three different colors of clay surfaces (Figure 2c–e). The histograms of these subclasses are shown in Figure 2h, indicating that the values of vegetation indices differ even between groups of terrain points and highlighting the importance of the selection of multiple terrain colors for correct threshold determination. It should be noted that in this process, selecting terrain points representing various colors is more difficult than selecting vegetation. In our case, the training dataset for each data consisted of approximately 10,000 points per dataset.
Figure 2h also illustrates that the data are continuous, i.e., we cannot see any obvious gaps between the VI values for vegetation and non-vegetation. The distributions, however, differ, which makes the use of standard statistical methods feasible for distinguishing between them. Table 2 shows the overview of methods evaluated in this paper.

Table 2.
The overview of the methods for threshold determination evaluated in this paper, see Section 2.3 for a description of individual methods.
2.3.2. Single Class Method Based on Normal Distribution Assumption (SCND)
The single-class method assuming normal distribution (SCND) was the simplest method of threshold determination used in this paper. This method determines the threshold only from data representing the green vegetation class in the preselected training set (i.e., it ignores terrain data). The threshold determination is based on a simple assumption that 2.5% of the data at the margin of the distribution describing vegetation is already contaminated with terrain points. The threshold is then derived simply by calculating the mean and standard deviation (SD) of the distribution describing the vegetation and cutting off anything that lies further than 1.96·SD from the mean on the side adjacent to the histogram of terrain points (i.e., Figure 3a). The algorithm, therefore, works as follows:
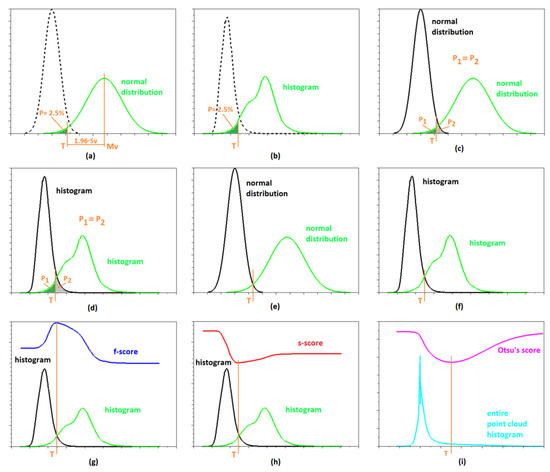
Figure 3.
A depiction of threshold determination using tested methods: (a) SCND, (b) SCHC, (c) TCNDp, (d) TCNDi, (e) TCHCp, (f) TCHCi, (g) TCSFf, (h) TCSFs, and (i) Otsu. Green color depicts the green vegetation, black the terrain/others, blue the f-score function for moving threshold, red the proposed s-score function, cyan shows the histogram of the entire cloud, and magenta Otsu’s score function.
- The mean (M) and standard deviation (SD) are determined from the VI values of the training set.
- The threshold T is calculated using the formula T = M + 1.96·SD or T = M − 1.96·SD; whether plus or minus is used depends on the orientation of the particular VI (if vegetation has higher values of VI than other points, the minus sign is applied, and vice versa).
- All points that exceed this threshold are removed from the cloud.
By observation, it was found that the histograms showing the distribution of the respective VIs for the vegetation class are very close to a normal distribution, and, therefore, the assumption of normality was met for our data. Another advantage is that, given the number of points in the point cloud, it is not a problem to select thousands to tens of thousands of points, and, thus, the statistical nature of the threshold is robust to small amounts of unwanted contamination (e.g., a few brown or black points remaining among the green points of a shrub).
2.3.3. Single Class Method Based on Histogram Calculation (SCHC)
The second simplest method, the single class method based on a histogram calculation (SCHC), is similar but does not assume a normal distribution (it is, therefore, universally applicable to any distribution). The threshold value is then determined as the value corresponding (in agreement with the previous method) to the 2.5-percentile from the histogram of the training vegetation class (see Figure 3b).
2.3.4. Two-Class Method Based on the Normal Distribution Assumption (TCND)
Classification methods based on the competition of two (or more) classes are generally considered more reliable. For this reason, the two-class method based on a normal distribution assumption (TCND) and the two-class method based on a histogram calculation (TCHC) were also tested. These methods do not determine the threshold using a fixed probability value, but attempt to separate two competing distributions.
The TCND method assumes that both the vegetation indices of the green vegetation and the rest of the cloud are normally distributed. It, therefore, uses both training classes as follows: the mean and standard deviation for the classes of green vegetation (MV, SV) and remaining points (MR, SR), respectively, are determined from the VI values of the training set.
Within this approach, two methods were employed for the threshold determination. In the percentile-based TCND method (TCNDp), the threshold was set to the points by removing identical percentiles from both vegetation and non-vegetation classes in the training set (see Figure 3c). The intersection-based methods (TCNDi) determine the threshold as the intersection of the two distributions (see Figure 3e).
The first method (TCNDp), therefore, calculates the threshold T using the formula:
This equation is based on the fact that at the threshold, the percentile cut off by the threshold is identical for both distributions and can be calculated as p-times the standard deviation (in SCND, p was set to 1.96). Therefore, the above equation is derived by equaling pv = pr from the equations pv = (Mv − T)/Sv for vegetation and pr = (T − MR)/SR for the remaining points; note that the signs in the brackets are inverse, since for one class, the cut-off percentile is to the right of the mean and for the other class, it is to the left. Nevertheless, whether the sign will be positive or negative in the individual equation depends on the vegetation index; see the explanation above in Section 2.3.1.
The second method (TCNDi) of two-class threshold determination is based on determining the intersection of the probability distribution functions of the two classes (i.e., green vegetation and remaining points). The calculation is based on solving the quadratic equation obtained by equaling two normal distribution functions:
The problem can be solved by logarithmization of the entire equation. The quadratic equation has generally two solutions—it is necessary to use the solution lying between MV and MR. It can be solved numerically as well.
2.3.5. Two-Class Method Based on Histogram Calculation (TCHC)
This method is basically a combination of the SCHC and TCND methods. The determination of the threshold is performed on the basis of shifting the provisional threshold until equal percentiles are cut off for both classes (TCHCp, see Figure 3e) or on the basis of the intersection of the histogram envelope curves (TCHCi, see Figure 3f).
We proposed numerical solutions by constructing a 1000-class histogram between the means of the vegetation (MV) and remaining points (MR), where the desired threshold must lie. The 1000 classes were used to create as fine a resolution as reasonably possible to improve the accuracy of the determined threshold. For the TCHCi method, it was necessary to smooth out the envelope curve of the histogram using a moving average as the representation within individual categories can vary; a window of 41 classes was used for this purpose.
2.3.6. Two-Class Methods Based on the Score Function Evaluation (TCSF)
The two-class method based on score function evaluation (TCSF) was another numerical method employed in this study. Two functions were used as the evaluation functions, namely f-score (TCSFf) and a custom function minimizing squares of the numbers of incorrect classifications (TCSFs).
TCSFf—the threshold is determined by maximizing the f-score. In practice, the score function is calculated for thresholds in regular steps (in our case, we used the step of a 1/10,000 of the interval between the means of the vegetation points and the remaining points); the point corresponding to the highest f-score was considered the threshold. The definition of the components for the equations below is given by the standard terminology of the binary classifiers (TP = true positive identification, FP = false positive, FN = false negative, TN = true negative) and is detailed in the next Section 2.4 since it is used for experimental results evaluation.
TCSFs = the threshold which is determined in a similar way based on the proposed s-score function describing the dependence of the percentage of unsuccessful classifications on the threshold (see Equation (1)). This approach supports a balanced minimization of the number of misclassified points in both classes (vegetation and remaining points).
2.3.7. Two-Class Method Based on the Support Vector Machine (SVM)
Automatic classification tools, such as support vector machines, can be used for distinguishing the training data classes without any additional assumptions. A support vector machine (SVM) is a supervised machine learning algorithm that can be used for both classification and regression. The goal of the SVM algorithm is to find a hyperplane in an N-dimensional space that distinctly classifies the data points. In our case, the freely available and easy-to-use LIBSVM toolbox (described in [53], downloadable at https://atoms.scilab.org/toolboxes/libsvm/1.5, accesses on 1 February 2023) for the Scilab universal computing system (version 6.1.1, www.scilab.org, accessed on 4 February 2023) was used. The input for training and classification can include virtually any number of parameters. The output of the classification is the value 0 or 1 (only two classes can be distinguished). In our case, only one input (vegetation index value) was used.
2.3.8. Two-Class Method Based on a Neural Network (DNN)
The use of machine learning in the form of a neural network is another option for data classification based on training sets. Classification using neural networks is a type of machine learning that involves training a model to recognize patterns in data and to make predictions about new data. Neural networks take inspiration from the learning process occurring in the human brain. Each element of the network (neuron) produces an output after receiving one or multiple inputs. Those outputs are then passed on to the next layer of neurons, which use them as inputs for their own function and produce further outputs. This continues until every layer of neurons has been considered and the terminal neurons have received their input. Those terminal neurons then output the final result for the model. The network used in our study was a three-layer network with one input neuron, 25 neurons of the hidden layer, and one output neuron. The number of neurons in the hidden layer may seem high; it was, however, determined through simple preliminary testing. We gradually increased their number to the point where the success rate of classifying the training data reached a plateau.
Similar to SVM, we used a toolbox for the Scilab system (ver. 6.1.1); this time, we employed the Neural Network Module (ver. 3.0, https://atoms.scilab.org/toolboxes/neuralnetwork/3.0/, accesses on 1 February 2023, created according to the book by Martin T. Hagan [54]). This toolbox supports several methods for learning the network. In our case, the Levenberg–Marquardt algorithm training function was clearly the best (based on preliminary testing, data not shown).
2.3.9. Two-Class Multi-VI Method Based on the Support Vector Machine (MSVM)
The SVM classification method can be easily used for a higher number of input parameters. We have, therefore, tested also the classification using a higher number of VIs, assuming a possible reduction in the uncertainty of the result. Based on the results of testing the previous methods, combinations of the 5, 3, and 2 most successful VIs were selected.
2.3.10. Two-Class Multi-VI Method Based on Neural Network (MDNN)
The reasoning is the same as in Section 2.3.8, as is the change in the number of input neurons to 5, 3, and 2, respectively.
2.3.11. Otsu’s Method (Otsu)
The method invented by Otsu [40] for automatic image thresholding was applied to the entire cloud as intended in their original paper. The algorithm returns a single threshold that separates values into two classes. The algorithm searches for the threshold that minimizes the intra-class variance, defined as a weighted sum of variances of the two classes. The class probability is computed from the bins of the histogram.
2.4. Testing of the Methods
For each test data, a reference dataset was manually created by classifying the whole point cloud into green vegetation and remaining (mostly terrain) data (all data shown in Appendix A). It should be noted that this is not only highly laborious but also partially subjective—especially in terms of assessing whether a particular point represents green vegetation or not. Here, the strategy used was that, if the assessment was uncertain, the point was not classified as a green vegetation point.
Due to the different percentages of points representing green vegetation in the whole cloud, it was necessary to manually prepare training classes containing an approximately equal representation of all color shades within the individual classes. These training sets were used to calculate the threshold for each VI and, based on the resulting thresholds, green vegetation was filtered out in the complete datasets and results were compared with the reference (manual) classification.
To determine the success of the filtering, established binary classification quality characteristics were calculated, namely the f-score (FS) and the balanced accuracy (BA which is clearly described, e.g., in the supplementary materials of [55]), the calculation is shown in Table 3. Because this classification is binary, the data is classified into two categories: vegetation was designated as positive (P) and remaining points as negative (N). Successful classification is denoted as true (T), while an unsuccessful classification as false (F). Thus, TP denotes true positives, i.e., points correctly classified as green vegetation, FP denotes false positives, i.e., points incorrectly identified as green vegetation points, TN denotes points correctly classified other points, and so on.

Table 3.
Overview of success rate characteristics used.
3. Results
The above-described procedures were used to compare the results to those determined manually by a human operator. F-scores and balanced accuracies for each index and method of threshold determination are summarized in Table 4 and Table 5, respectively (values shown are mean results from all four datasets). On the far right in each table, the average value for the particular index across all methods is always shown. The highest (best) value in each column is highlighted in bold, showing the index producing the best results when using the respective method. Full details for each VI, data, and method are given in Appendix C.

Table 4.
Results of the evaluation of the success of green vegetation filtering methods using individual VIs (F-score in %).

Table 5.
Results of the evaluation of the success of green vegetation filtering methods using individual VIs (Balanced accuracy in %).
In vegetation indices, the best average results were achieved when employing GLI and ExG. It is worth noting that the best results, namely an F-score of 97.7% and balanced accuracy of 98.9%, were acquired when using the simplest method, i.e., the SCND method, with the ExG vegetation index.
The ExG index generally performed best for SCND and SHC methods. When employing DND and DHC methods of filtering, the best results were achieved using GLI, followed by ExG.
From the machine learning methods, SVM and DNN yielded very similar results, with the best F-score and BA achieved in conjunction with GLI and ExG. Other VIs (in particular, IKAW, ExR, ExB, GRVI, MGRVI, and VARI with F-scores below 80%) were generally inferior.
Results of multi-VI methods are summarized in Table 6; in addition, the best results for several methods are illustrated in Figure 4. The most important observation here is that the results are very similar to the corresponding single VI method, suggesting that a well-chosen single VI, with a suitable method of threshold determination, which is significantly less computationally expensive, can be preferred to these relatively complicated methods.

Table 6.
Results of the evaluation of green vegetation filtering success methods using multiple VIs.

Figure 4.
Illustration of the performance of several methods of threshold determination for color-based vegetation removal, depicting the results always with the vegetation index performing best in the particular method according to the f-score. Correctly identified points are shown in grayscale, red points indicate terrain misclassified as vegetation, and green points vegetation misclassified as terrain. (a) SCND method + ExG vegetation index (b) Otsu + ExG (c) TCSFs + ExG (d) DNN + ExG. Note that the misclassified points are typically concentrated in shaded areas and on the margins of vegetation patches.
4. Discussion
In this paper, we aimed to evaluate various vegetation indices and methods of threshold determination allowing the identification of green vegetation and filtering it out from a dense colored point cloud. The combinations of the indices and algorithms for threshold determinations were tested on datasets of rocky terrain containing 11.4–38.5% of green vegetation.
Methods that can be used to automatically find the threshold in a histogram were published previously. One such algorithm has been published by Otsu et al. [40] and has been widely used since (e.g., Refs. [17,18,19,21,24]). Kittler et al. concluded that Otsu’s method performs well when the histogram has a bimodal distribution with a deep and sharp valley between the two peaks [41]. Similar to all other global thresholding methods, Otsu’s method performs badly in cases of heavy noise, small object sizes, inhomogeneous lighting, and larger intra-class than inter-class variance [42]. The successful use of this algorithm, therefore, requires both classified classes (here green vegetation and other points) to be similarly represented—if the representation of green vegetation in the point cloud is small, they are practically invisible in the histogram and cannot be successfully identified. This is also the case with our data (see Figure 2g for ExG, or Appendix B, Figure A5, for all VIs—Data 1). In our data, the Otsu’s method indeed performed generally worse than the other tested algorithms, especially where the F-score is concerned. Figure 4b confirms the numerical findings, showing that even with the best-performing combination of Otsu’s method and vegetation index, the results are poorer than those acquired using the remaining methods. However, considering the above-mentioned limitations of the method, the result was not as poor as expected, especially where the balanced accuracy criterion is concerned.
Other authors set the threshold as an estimated fixed value. Such arbitrarily set threshold, however, differs among individual studies. For example, if considering only the ExG index, Anders et al. use a threshold value of 0.1 [22], while Núnez et al. used a threshold of −0.02 [25]. As each sensor is slightly different in terms of color calibration and as lighting conditions are also variable, it is not possible to determine a universally valid threshold; for example, the thresholds determined by the SCND method for our Data 1–4 in our study were 0.085; 0.167; 0.093; and 0.068, respectively. Similar variability was observed for other VIs as well.
Therefore, we have devised several semiautomatic methods that could be almost universally applied to determine the threshold and tested the success of classifications using individual methods. All tested methods were designed to overcome the problem of unbalanced representation of individual classes—manual selection of representative patches containing individual classes (training data) is the crucial step in our algorithm.
The results for individual indices and threshold determination methods shown in Table 4 and Table 5 imply several important findings of our study. First of all, all proposed methods of threshold determination provide good results when combined with appropriate vegetation indices. Even the algorithm with the poorest performance (TCNDp) yielded an F-score of 92% and BA of 94% when paired with the GLI. Interestingly, even the simplest algorithm, SCND, performed very well with all datasets. In combination with ExG, it yielded even the absolute best result in our study, classifying with an average F-score of 97.7% and BA of 98.9%.
On the other hand, the selection of the appropriate vegetation index plays a major role in the successful identification of vegetation. IKAW was shown to be unsuitable for this application, yielding the poorest results of all indices (F-scores of less than 50%). ExR, ExB, GRVI, MGRVI, and VARI indices also produced relatively poor results, with F-scores of approximately 80%, compared to over 90% for ExG, ExGr, RGBVI, CIVE, GLI, and VEG (depending on the method).
The good performance of SCND is an extremely valuable result, especially considering that this method is based on vegetation only and, therefore, does not require the operator to manually select non-vegetation training classes (i.e., surfaces of various hues/colors). This makes the entire process much simpler, faster, and more user-friendly and, together with low computational demands, makes this method, especially in combination with ExG or GLI, the option of choice. This method (Figure 4a) performed equally well or even better than much more complicated algorithms, including those based on neural networks (Figure 4d). Of course, the prerequisite of normal distribution of the vegetation index employed together with this method must be met to be able to use it; ExG and GLI, however, appear to generally meet this requirement well.
Where machine learning methods combining multiple indices are concerned, their results were also very good. However, as with individual indices, these methods did not bring any improvement over the simplest SCND method and, hence, the increased computational costs of their use appear (even though the increase in computational costs is not major as the training is performed only on a subset of the data) to be unjustified.
Comparing the performance of the F-score and balanced accuracy as the parameters for the evaluation of the algorithms, F-score appears to be more suitable for this particular application. When intending to filter out green vegetation, it is more important to remove all vegetation points even at the cost of removing a certain portion of terrain points than leaving vegetation in the cloud and considering it to be terrain. Looking at the equations for F-score and BA (Table 2), F-score puts more emphasis on the correct identification of the desired class while BA provides rather an estimation of the overall accuracy.
It is necessary to point out that the method proposed in this paper is not intended to replace standard vegetation filtering. On a grassy terrain, this method would remove virtually all points, which is, of course, not a required result. The strength of this method, however, lies in its excellent performance in identifying relatively scarce vegetation on monomaterial surfaces, such as (even highly rugged) rock formations or various anthropogenic structures. Further, filtering is not as perfect as if performed by a human operator and additional filtering by geometrical filters might be necessary (for example, to remove brown branches that remain unfiltered based on the color). Still, employing this filter first greatly simplifies the use of geometrical filters, which would likely fail on such a rugged terrain with vegetation cover [27]. When dealing with terrain suitable for the proposed algorithm, we, therefore, suggest using first the method proposed in this paper to remove green points (which, outside of areas of human habitation, certainly capture vegetation), and subsequently, employing commonly used geometric or structural filtering, or even manually removing the relatively few remaining vegetation points.
In addition, one must consider the acquisition period when intending to remove green vegetation—some vegetation changes color over the growing season and deciduous species drop their leaves, which may render the method inapplicable in certain seasons.
We have strived to minimize any possible limitations in our study by using multiple indices, multiple methods, and two evaluation criteria. However, one limitation is inherent to any similar study—the reference data must be manually classified, which may always bring about a certain amount of error, especially on the edges of the vegetated areas where the gradual change of green to the terrain color may be problematic. However, the number of points that might be misclassified in this way in our areas is relatively low as the vegetated areas are rather continuous patches than dissipated small individual plants.
5. Conclusions
In this paper, a color-based method for filtering green vegetation out from point clouds with scarce vegetation was proposed, multiple algorithms for determining a threshold for vegetation removal were evaluated, and the results were compared. All evaluated methods of threshold determination performed relatively well when used together with appropriate vegetation indices. In general, ExG and GLI indices appear to be the most suitable for this purpose. Surprisingly, the simplest method (single-class normal distribution, SCND) required only a selection of the sample of the vegetated area as the training set performed best, outperforming even support vector machine or deep neural network approaches. This is all the more valuable that this method is fast, is not demanding complicated calculations, and is easy to use, i.e., not necessitating the selection of terrain samples as well. This rapid and simple method is, therefore, highly suitable for filtering out vegetation, for example, from rocky or anthropogenic terrain.
Author Contributions
Conceptualization, M.Š.; methodology, M.Š.; software, M.Š.; validation, R.U. and T.S.; formal analysis, M.Š. and R.U.; investigation, T.S.; writing—original draft preparation, M.Š.; writing—review and editing, R.U. and T.S.; visualization, M.Š.; funding acquisition, R.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Grant Agency of CTU in Prague—grant project “Optimization of acquisition and processing of 3D data for purpose of engineering surveying, geodesy in underground spaces and 3D scanning”, 2023; and by the Technology Agency of the Czech Republic—grant number CK03000168, “Intelligent methods of digital data acquisition and analysis for bridge inspections”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Reference Data Created by a Human Operator

Figure A1.
Reference Data 1 (a) Original point cloud (b) Point cloud with green vegetation highlighted in blue.


Figure A2.
Reference data 2 (a) Original point cloud (b) Point cloud with green vegetation highlighted in blue.

Figure A3.
Reference Data 3 (a) Original point cloud (b) Point cloud with green vegetation highlighted in blue.
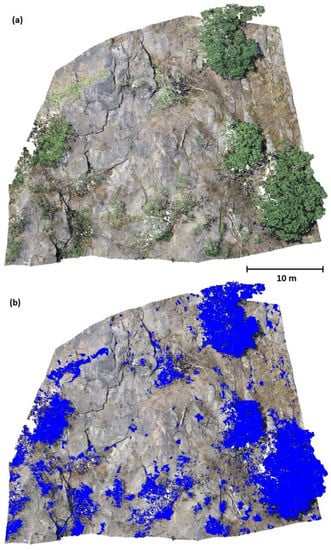
Figure A4.
Reference data 4 (a) Original point cloud (b) Point cloud with green vegetation highlighted in blue.
Appendix B. Histograms for Individual Vegetation Indices—Data 1
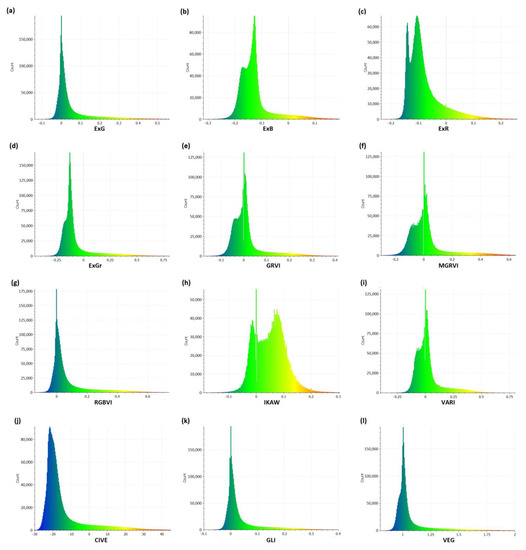
Figure A5.
Histograms of all vegetation indexes for Data 1 (a) ExG (b) ExB (c) ExR (d) ExGr (e) GRVI (f) MGRVI (g) RGBVI (h) IKAW (i) VARI (j) CIVE (k) GLI (l) VEG.
Appendix C. Detailed Evaluation Results

Table A1.
F-score in %—Data 1, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
Table A1.
F-score in %—Data 1, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 98.8 | 86.3 | 92.0 | 96.9 | 94.6 | 99.3 | 94.0 | 96.3 | 89.0 | 94.0 | 79.8 | 92.8 |
| ExR | 63.9 | 80.2 | 83.4 | 81.4 | 82.5 | 84.3 | 83.3 | 84.2 | 78.7 | 83.3 | 72.8 | 79.8 |
| ExB | 80.6 | 86.4 | 86.4 | 87.7 | 88.6 | 87.8 | 86.5 | 86.5 | 83.5 | 86.0 | 87.4 | 86.1 |
| ExGr | 95.0 | 88.5 | 93.7 | 92.0 | 94.0 | 94.6 | 91.8 | 92.4 | 88.8 | 91.5 | 76.7 | 90.8 |
| GRVI | 85.1 | 87.1 | 86.9 | 84.0 | 86.4 | 87.1 | 85.2 | 86.8 | 81.7 | 85.3 | 75.3 | 84.6 |
| MGRVI | 86.8 | 87.1 | 87.2 | 84.2 | 86.3 | 87.1 | 85.2 | 86.8 | 83.3 | 85.3 | 77.0 | 85.1 |
| RGBVI | 87.1 | 86.1 | 95.8 | 96.6 | 94.0 | 97.2 | 95.4 | 95.4 | 90.7 | 93.9 | 85.1 | 92.5 |
| IKAW | 32.4 | 32.4 | 33.3 | 33.6 | 33.1 | 33.4 | 33.5 | 33.0 | 32.6 | 32.6 | 33.6 | 33.1 |
| VARI | 83.8 | 84.2 | 84.7 | 82.6 | 84.2 | 84.8 | 82.9 | 84.2 | 81.6 | 83.4 | 75.6 | 82.9 |
| CIVE | 86.4 | 84.6 | 93.3 | 91.0 | 93.1 | 92.8 | 92.5 | 92.5 | 92.3 | 91.2 | 82.6 | 90.2 |
| GLI | 93.3 | 86.1 | 93.7 | 96.5 | 94.4 | 98.9 | 94.0 | 96.3 | 87.7 | 94.0 | 81.6 | 92.4 |
| VEG | 38.5 | 87.8 | 88.8 | 93.9 | 95.7 | 94.8 | 92.9 | 92.9 | 89.4 | 93.0 | 71.2 | 85.4 |

Table A2.
Balanced Accuracy in %—Data 1, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
Table A2.
Balanced Accuracy in %—Data 1, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 99.3 | 97.0 | 92.6 | 98.9 | 94.9 | 99.5 | 98.3 | 98.8 | 97.4 | 98.3 | 96.0 | 97.4 |
| ExR | 73.2 | 85.6 | 89.6 | 94.8 | 88.3 | 93.1 | 94.2 | 93.4 | 95.0 | 94.2 | 94.7 | 90.6 |
| ExB | 84.0 | 94.5 | 89.1 | 94.0 | 92.4 | 93.9 | 94.5 | 94.5 | 94.9 | 94.6 | 94.1 | 92.8 |
| ExGr | 97.0 | 97.1 | 94.7 | 97.6 | 95.1 | 97.4 | 97.5 | 97.6 | 97.2 | 97.5 | 95.5 | 96.8 |
| GRVI | 89.3 | 92.6 | 92.0 | 95.3 | 91.0 | 93.7 | 95.1 | 94.3 | 95.4 | 95.0 | 95.0 | 93.5 |
| MGRVI | 94.3 | 92.8 | 93.1 | 95.2 | 90.8 | 93.7 | 95.1 | 94.3 | 95.3 | 95.0 | 95.2 | 94.1 |
| RGBVI | 97.1 | 97.0 | 95.9 | 98.8 | 94.4 | 98.9 | 98.6 | 98.6 | 97.7 | 98.3 | 96.8 | 97.5 |
| IKAW | 21.9 | 23.3 | 53.6 | 53.7 | 53.5 | 53.6 | 53.7 | 53.5 | 9.7 | 9.7 | 53.7 | 40.0 |
| VARI | 88.9 | 89.5 | 90.7 | 94.1 | 89.6 | 92.5 | 94.0 | 93.3 | 94.3 | 93.8 | 94.5 | 92.3 |
| CIVE | 96.6 | 96.4 | 95.6 | 97.0 | 95.0 | 96.7 | 96.8 | 96.8 | 96.9 | 97.0 | 96.1 | 96.4 |
| GLI | 98.2 | 96.9 | 94.1 | 98.9 | 94.7 | 99.4 | 98.3 | 98.8 | 97.2 | 98.3 | 96.3 | 97.4 |
| VEG | 61.9 | 97.1 | 89.9 | 98.1 | 96.1 | 98.1 | 97.9 | 97.9 | 97.4 | 97.9 | 94.9 | 93.4 |

Table A3.
F-score and Balanced Accuracy—Data 1, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
Table A3.
F-score and Balanced Accuracy—Data 1, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
| MSVM | MDNN | Mean | ||||
|---|---|---|---|---|---|---|
| FS [%] | BA [%] | FS [%] | BA [%] | FS [%] | BA [%] | |
| ExG, ExGr, RBVI, CIVE, GLI | 91.7 | 97.0 | 91.7 | 97.1 | 91.7 | 97.0 |
| ExG, ExGr, RBVI, CIVE, VEG | 91.7 | 97.0 | 92.3 | 97.1 | 92.0 | 97.0 |
| ExG, RBVI, GLI | 89.6 | 97.5 | 92.7 | 97.6 | 91.1 | 97.5 |
| ExG, RBVI, CIVE | 91.9 | 96.9 | 90.4 | 96.7 | 91.2 | 96.8 |
| ExG, GLI, VEG | 89.0 | 97.4 | 93.5 | 98.3 | 91.3 | 97.9 |
| ExG, GLI | 88.5 | 97.3 | 93.9 | 98.3 | 91.2 | 97.8 |

Table A4.
F-score in %—Data 2, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
Table A4.
F-score in %—Data 2, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 99.7 | 95.4 | 90.0 | 90.3 | 94.8 | 96.0 | 95.4 | 94.8 | 97.3 | 95.1 | 90.0 | 94.4 |
| ExR | 81.3 | 88.3 | 81.7 | 83.7 | 88.5 | 87.5 | 88.1 | 88.5 | 88.5 | 88.2 | 85.2 | 86.3 |
| ExB | 87.7 | 90.1 | 92.0 | 92.5 | 88.6 | 90.0 | 88.9 | 87.5 | 88.9 | 88.6 | 91.0 | 89.6 |
| ExGr | 97.3 | 92.2 | 87.8 | 88.3 | 95.6 | 97.5 | 95.9 | 95.9 | 97.8 | 96.1 | 88.8 | 93.9 |
| GRVI | 93.1 | 90.7 | 85.5 | 86.7 | 93.0 | 92.4 | 93.0 | 93.2 | 92.4 | 92.8 | 88.0 | 91.0 |
| MGRVI | 93.1 | 90.7 | 85.9 | 87.0 | 93.0 | 92.4 | 93.0 | 93.2 | 92.6 | 92.8 | 88.7 | 91.1 |
| RGBVI | 97.0 | 97.1 | 94.7 | 95.0 | 93.1 | 94.2 | 93.2 | 93.0 | 93.9 | 93.3 | 94.9 | 94.5 |
| IKAW | 57.7 | 60.3 | 79.3 | 79.6 | 75.1 | 78.2 | 75.9 | 74.8 | 77.7 | 77.0 | 75.4 | 73.7 |
| VARI | 93.5 | 90.7 | 87.6 | 88.8 | 93.6 | 92.8 | 93.7 | 93.7 | 93.3 | 93.5 | 91.2 | 92.0 |
| CIVE | 93.5 | 93.5 | 90.8 | 91.0 | 95.1 | 95.7 | 95.2 | 95.2 | 95.3 | 95.2 | 91.3 | 93.8 |
| GLI | 98.1 | 95.4 | 91.5 | 91.8 | 94.9 | 96.0 | 95.4 | 94.8 | 97.4 | 95.1 | 91.8 | 94.7 |
| VEG | 55.3 | 97.1 | 80.8 | 83.3 | 94.2 | 96.2 | 94.5 | 93.7 | 96.6 | 94.4 | 74.3 | 87.3 |

Table A5.
Balanced Accuracy in %—Data 2, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
Table A5.
Balanced Accuracy in %—Data 2, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 99.7 | 97.4 | 94.8 | 95.0 | 95.1 | 96.2 | 95.6 | 95.1 | 97.3 | 95.4 | 94.9 | 96.0 |
| ExR | 83.5 | 91.7 | 91.8 | 92.4 | 93.1 | 93.4 | 93.4 | 93.1 | 93.0 | 93.3 | 92.9 | 92.0 |
| ExB | 89.1 | 91.0 | 94.8 | 94.9 | 89.8 | 90.9 | 90.0 | 88.9 | 90.0 | 89.7 | 94.5 | 91.2 |
| ExGr | 98.2 | 95.8 | 94.0 | 94.2 | 95.8 | 97.7 | 96.1 | 96.1 | 98.1 | 96.3 | 94.4 | 96.1 |
| GRVI | 94.9 | 95.1 | 93.1 | 93.6 | 95.7 | 95.6 | 95.7 | 95.7 | 95.6 | 95.7 | 94.0 | 95.0 |
| MGRVI | 95.6 | 95.1 | 93.2 | 93.7 | 95.6 | 95.6 | 95.7 | 95.7 | 95.7 | 95.7 | 94.3 | 95.1 |
| RGBVI | 97.6 | 97.6 | 96.8 | 96.9 | 93.5 | 94.5 | 93.6 | 93.5 | 94.2 | 93.8 | 96.8 | 95.3 |
| IKAW | 69.9 | 70.8 | 83.0 | 82.4 | 78.5 | 80.7 | 79.0 | 78.3 | 80.3 | 79.8 | 83.4 | 78.7 |
| VARI | 95.9 | 95.0 | 93.8 | 94.3 | 96.0 | 95.8 | 96.0 | 96.0 | 95.9 | 95.9 | 95.2 | 95.4 |
| CIVE | 96.3 | 96.3 | 95.2 | 95.3 | 95.6 | 96.3 | 95.6 | 95.6 | 95.8 | 95.7 | 95.4 | 95.7 |
| GLI | 98.8 | 97.4 | 95.5 | 95.6 | 95.1 | 96.1 | 95.6 | 95.1 | 97.5 | 95.4 | 95.6 | 96.1 |
| VEG | 19.4 | 98.2 | 91.6 | 92.4 | 94.5 | 96.4 | 94.8 | 94.1 | 96.8 | 94.8 | 89.8 | 87.5 |

Table A6.
F-score and Balanced Accuracy—Data 2, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
Table A6.
F-score and Balanced Accuracy—Data 2, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
| MSVM | MDNN | Mean | ||||
|---|---|---|---|---|---|---|
| FS [%] | BA [%] | FS [%] | BA [%] | FS [%] | BA [%] | |
| ExG, ExGr, RBVI, CIVE, GLI | 95.9 | 96.3 | 95.0 | 95.2 | 95.4 | 95.8 |
| ExG, ExGr, RBVI, CIVE, VEG | 96.1 | 96.4 | 94.1 | 94.5 | 95.1 | 95.5 |
| ExG, RBVI, GLI | 95.9 | 96.1 | 95.3 | 95.5 | 95.6 | 95.8 |
| ExG, RBVI, CIVE | 95.8 | 96.2 | 96.0 | 96.2 | 95.9 | 96.2 |
| ExG, GLI, VEG | 97.1 | 97.2 | 94.6 | 94.9 | 95.9 | 96.1 |
| ExG, GLI | 97.3 | 97.4 | 95.1 | 95.3 | 96.2 | 96.4 |

Table A7.
F-score in %—Data 3, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
Table A7.
F-score in %—Data 3, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 98.1 | 91.5 | 82.2 | 86.6 | 95.1 | 93.4 | 96.9 | 97.3 | 95.2 | 96.1 | 96.5 | 93.5 |
| ExR | 53.7 | 50.9 | 52.0 | 53.7 | 52.9 | 53.8 | 50.8 | 49.9 | 51.2 | 49.6 | 28.9 | 49.8 |
| ExB | 38.3 | 51.4 | 58.0 | 63.4 | 59.4 | 57.4 | 59.9 | 63.1 | 63.8 | 61.3 | 64.8 | 58.3 |
| ExGr | 82.0 | 79.9 | 86.3 | 86.0 | 85.6 | 85.9 | 84.6 | 83.8 | 84.5 | 84.5 | 80.7 | 84.0 |
| GRVI | 62.6 | 63.9 | 61.7 | 63.2 | 63.2 | 63.8 | 60.2 | 60.2 | 60.4 | 59.6 | 38.6 | 59.8 |
| MGRVI | 62.6 | 63.9 | 61.9 | 63.2 | 63.2 | 63.8 | 60.2 | 60.2 | 60.7 | 59.9 | 43.7 | 60.3 |
| RGBVI | 83.7 | 88.2 | 75.6 | 80.2 | 85.9 | 84.2 | 85.0 | 86.2 | 84.9 | 85.1 | 86.7 | 84.2 |
| IKAW | 21.6 | 22.9 | 30.3 | 28.9 | 29.5 | 31.0 | 27.7 | 32.5 | 7.5 | 34.2 | 33.5 | 27.2 |
| VARI | 64.8 | 68.3 | 65.6 | 67.1 | 66.8 | 68.8 | 64.0 | 64.0 | 64.6 | 64.8 | 63.4 | 65.7 |
| CIVE | 86.0 | 85.0 | 88.9 | 89.8 | 85.8 | 86.5 | 88.1 | 88.1 | 88.5 | 88.1 | 88.3 | 87.6 |
| GLI | 97.1 | 91.4 | 83.1 | 87.0 | 95.2 | 93.4 | 96.9 | 97.3 | 95.2 | 96.0 | 91.4 | 93.1 |
| VEG | 94.5 | 89.9 | 82.7 | 89.3 | 96.4 | 96.1 | 96.0 | 96.0 | 96.6 | 96.5 | 96.3 | 93.7 |

Table A8.
Balanced Accuracy in %—Data 3, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
Table A8.
Balanced Accuracy in %—Data 3, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 99.0 | 98.4 | 84.9 | 88.2 | 95.6 | 94.0 | 97.4 | 97.8 | 95.7 | 96.6 | 97.0 | 95.0 |
| ExR | 72.0 | 67.7 | 74.7 | 72.2 | 73.7 | 72.1 | 75.8 | 76.5 | 75.5 | 76.6 | 57.5 | 72.2 |
| ExB | 61.8 | 67.2 | 70.5 | 73.6 | 71.3 | 70.2 | 71.5 | 73.4 | 73.8 | 72.3 | 74.5 | 70.9 |
| ExGr | 95.9 | 96.2 | 94.0 | 94.5 | 94.7 | 94.5 | 95.3 | 95.5 | 95.3 | 95.3 | 84.7 | 94.2 |
| GRVI | 81.1 | 77.6 | 82.0 | 80.2 | 80.2 | 78.7 | 83.6 | 83.6 | 83.1 | 84.0 | 61.6 | 79.6 |
| MGRVI | 81.1 | 77.5 | 81.9 | 80.2 | 80.2 | 78.7 | 83.6 | 83.6 | 82.9 | 83.8 | 63.6 | 79.7 |
| RGBVI | 86.2 | 90.9 | 80.4 | 83.5 | 88.1 | 86.6 | 87.3 | 88.4 | 87.2 | 87.4 | 88.9 | 86.8 |
| IKAW | 55.3 | 55.6 | 57.2 | 56.9 | 57.0 | 57.3 | 56.6 | 57.8 | 57.8 | 59.0 | 58.3 | 57.2 |
| VARI | 84.5 | 81.8 | 84.0 | 82.9 | 83.0 | 81.1 | 85.0 | 85.0 | 84.5 | 84.4 | 73.8 | 82.7 |
| CIVE | 98.5 | 98.4 | 91.0 | 92.1 | 87.9 | 88.5 | 90.1 | 90.1 | 90.5 | 90.1 | 90.3 | 91.6 |
| GLI | 98.9 | 98.4 | 85.5 | 88.5 | 95.7 | 94.0 | 97.4 | 97.8 | 95.7 | 96.5 | 92.2 | 94.6 |
| VEG | 95.0 | 97.8 | 85.3 | 90.3 | 97.6 | 96.7 | 97.7 | 97.7 | 97.3 | 97.5 | 96.9 | 95.4 |

Table A9.
F-score and Balanced Accuracy—Data 3, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
Table A9.
F-score and Balanced Accuracy—Data 3, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
| MSVM | MDNN | Mean | ||||
|---|---|---|---|---|---|---|
| FS [%] | BA [%] | FS [%] | BA [%] | FS [%] | BA [%] | |
| ExG, ExGr, RBVI, CIVE, GLI | 89.6 | 91.4 | 91.4 | 95.6 | 90.5 | 93.5 |
| ExG, ExGr, RBVI, CIVE, VEG | 90.0 | 91.7 | 90.5 | 95.2 | 90.3 | 93.5 |
| ExG, RBVI, GLI | 92.7 | 93.4 | 94.0 | 97.2 | 93.4 | 95.3 |
| ExG, RBVI, CIVE | 89.1 | 90.9 | 94.0 | 95.7 | 91.6 | 93.3 |
| ExG, GLI, VEG | 96.0 | 96.6 | 96.5 | 97.1 | 96.3 | 96.8 |
| ExG, GLI | 95.2 | 95.7 | 96.4 | 96.9 | 95.8 | 96.3 |

Table A10.
F-score in %—Data 4, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
Table A10.
F-score in %—Data 4, single VI methods—results of the evaluation of green vegetation filtering success using the manually prepared reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 94.2 | 97.4 | 99.2 | 92.9 | 89.5 | 91.7 | 91.4 | 90.4 | 94.4 | 91.2 | 75.6 | 91.6 |
| ExR | 77.3 | 78.7 | 72.9 | 69.8 | 70.6 | 78.2 | 78.7 | 78.1 | 74.5 | 78.6 | 71.5 | 75.4 |
| ExB | 67.8 | 63.0 | 80.2 | 81.1 | 71.6 | 76.6 | 76.3 | 74.0 | 79.0 | 76.8 | 82.1 | 75.3 |
| ExGr | 89.8 | 90.2 | 88.0 | 84.0 | 88.0 | 83.6 | 86.0 | 86.6 | 87.1 | 85.4 | 73.8 | 85.7 |
| GRVI | 81.5 | 82.0 | 75.2 | 71.9 | 72.4 | 81.1 | 81.9 | 78.6 | 77.0 | 81.8 | 73.7 | 77.9 |
| MGRVI | 82.0 | 82.0 | 75.1 | 72.7 | 72.4 | 80.0 | 81.9 | 78.6 | 77.9 | 81.8 | 74.5 | 78.1 |
| RGBVI | 92.6 | 97.4 | 98.2 | 95.2 | 91.3 | 94.1 | 90.7 | 90.7 | 94.4 | 92.5 | 80.3 | 92.5 |
| IKAW | 45.3 | 45.4 | 42.5 | 42.6 | 43.1 | 42.8 | 43.0 | 42.6 | 43.1 | 36.1 | 42.1 | 42.6 |
| VARI | 47.5 | 80.1 | 72.8 | 62.9 | 68.1 | 76.1 | 80.3 | 79.1 | 78.0 | 45.7 | 68.5 | 69.0 |
| CIVE | 85.6 | 86.5 | 88.7 | 89.4 | 82.6 | 84.5 | 82.8 | 82.7 | 83.6 | 83.6 | 77.0 | 84.3 |
| GLI | 93.0 | 97.4 | 99.6 | 94.1 | 89.5 | 91.4 | 91.4 | 90.4 | 95.9 | 91.6 | 79.3 | 92.1 |
| VEG | 93.4 | 91.7 | 88.9 | 82.8 | 89.5 | 83.6 | 87.5 | 88.9 | 88.6 | 87.3 | 67.1 | 86.3 |

Table A11.
Balanced Accuracy in %—Data 4, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
Table A11.
Balanced Accuracy in %—Data 4, single VI methods—Results of the evaluation of green vegetation filtering success using the manually created reference data.
| VVI | SCND | SCHC | TCND p | TCND i | TCHCp | TCHC i | TCSF f | TCSF s | SVM | DNN | Otsu | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ExG | 97.7 | 98.8 | 99.5 | 97.2 | 90.5 | 92.3 | 92.1 | 91.2 | 94.7 | 91.9 | 92.9 | 94.4 |
| ExR | 81.8 | 83.3 | 86.0 | 86.1 | 86.1 | 85.7 | 85.6 | 85.8 | 86.0 | 85.6 | 86.1 | 85.3 |
| ExB | 74.8 | 72.1 | 83.8 | 84.8 | 77.2 | 80.8 | 80.6 | 78.9 | 82.8 | 80.9 | 88.1 | 80.4 |
| ExGr | 94.1 | 94.1 | 94.1 | 93.8 | 94.1 | 93.7 | 94.0 | 94.0 | 94.0 | 93.9 | 92.3 | 93.8 |
| GRVI | 85.3 | 86.4 | 87.4 | 87.3 | 87.3 | 87.3 | 86.8 | 87.4 | 87.3 | 86.8 | 87.3 | 87.0 |
| MGRVI | 86.5 | 86.4 | 87.4 | 87.3 | 87.3 | 87.3 | 86.8 | 87.4 | 87.3 | 86.8 | 87.3 | 87.1 |
| RGBVI | 97.1 | 98.5 | 98.3 | 97.9 | 92.0 | 94.4 | 91.5 | 91.5 | 94.7 | 93.0 | 93.8 | 94.8 |
| IKAW | 49.6 | 49.8 | 50.1 | 47.5 | 52.7 | 51.3 | 49.4 | 50.5 | 45.8 | 52.9 | 48.7 | 49.9 |
| VARI | 65.0 | 83.9 | 85.5 | 83.9 | 84.8 | 85.9 | 86.2 | 86.2 | 86.2 | 49.9 | 84.9 | 80.2 |
| CIVE | 87.6 | 88.4 | 91.0 | 94.6 | 85.2 | 86.6 | 85.3 | 85.2 | 86.0 | 86.0 | 93.2 | 88.1 |
| GLI | 97.2 | 98.8 | 99.6 | 97.6 | 90.5 | 92.1 | 92.1 | 91.3 | 96.0 | 92.2 | 93.6 | 94.7 |
| VEG | 94.6 | 95.0 | 94.7 | 93.7 | 94.7 | 93.8 | 94.4 | 94.7 | 94.6 | 94.4 | 91.1 | 94.2 |

Table A12.
F-score and Balanced Accuracy—Data 4, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
Table A12.
F-score and Balanced Accuracy—Data 4, multi VI methods—results of the evaluation of green vegetation filtration success using the etalon.
| MSVM | MDNN | Mean | ||||
|---|---|---|---|---|---|---|
| FS [%] | BA [%] | FS [%] | BA [%] | FS [%] | BA [%] | |
| ExG, ExGr, RBVI, CIVE, GLI | 84.7 | 86.8 | 83.5 | 85.8 | 84.1 | 86.3 |
| ExG, ExGr, RBVI, CIVE, VEG | 84.6 | 86.7 | 81.5 | 84.4 | 83.1 | 85.6 |
| ExG, RBVI, GLI | 94.6 | 94.9 | 84.8 | 86.8 | 89.7 | 90.9 |
| ExG, RBVI, CIVE | 85.2 | 87.1 | 83.4 | 85.8 | 84.3 | 86.5 |
| ExG, GLI, VEG | 96.0 | 96.2 | 82.3 | 85.0 | 89.2 | 90.6 |
| ExG, GLI | 95.0 | 95.3 | 91.8 | 92.4 | 93.4 | 93.8 |
References
- Kršák, B.; Blišťan, P.; Pauliková, A.; Puškárová, P.; Kovanič, Ľ.; Palková, J.; Zelizňaková, V. Use of Low-Cost UAV Photogrammetry to Analyze the Accuracy of a Digital Elevation Model in a Case Study. Measurement 2016, 91, 276–287. [Google Scholar] [CrossRef]
- Szostak, M.; Pająk, M. LiDAR Point Clouds Usage for Mapping the Vegetation Cover of the “Fryderyk” Mine Repository. Remote Sens. 2023, 15, 201. [Google Scholar] [CrossRef]
- Koska, B.; Křemen, T. The Combination of Laser Scanning and Structure from Motion Technology for Creation of Accurate Exterior and Interior Orthophotos of St. Nicholas Baroque Church. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W1, 133–138. [Google Scholar] [CrossRef]
- Jon, J.; Koska, B.; Pospíšil, J. Autonomous Airship Equipped by Multi-Sensor Mapping Platform. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W1, 119–124. [Google Scholar] [CrossRef]
- Urban, R.; Štroner, M.; Blistan, P.; Kovanič, Ľ.; Patera, M.; Jacko, S.; Ďuriška, I.; Kelemen, M.; Szabo, S. The Suitability of UAS for Mass Movement Monitoring Caused by Torrential Rainfall—A Study on the Talus Cones in the Alpine Terrain in High Tatras, Slovakia. ISPRS Int. J. Geo-Inf. 2019, 8, 317. [Google Scholar] [CrossRef]
- Blanco, L.; García-Sellés, D.; Guinau, M.; Zoumpekas, T.; Puig, A.; Salamó, M.; Gratacós, O.; Muñoz, J.A.; Janeras, M.; Pedraza, O. Machine Learning-Based Rockfalls Detection with 3D Point Clouds, Example in the Montserrat Massif (Spain). Remote Sens. 2022, 14, 4306. [Google Scholar] [CrossRef]
- Loiotine, L.; Andriani, G.F.; Jaboyedoff, M.; Parise, M.; Derron, M.-H. Compari-son of Remote Sensing Techniques for Geostructural Analysis and Cliff Monitoring in Coastal Areas of High Tourist Attraction: The Case Study of Polignano a Mare (Southern Italy). Remote Sens. 2021, 13, 5045. [Google Scholar] [CrossRef]
- Moudrý, V.; Klápště, P.; Fogl, M.; Gdulová, K.; Barták, V.; Urban, R. Assessment of LiDAR Ground Filtering Algorithms for Determining Ground Surface of Non-Natural Terrain Overgrown with Forest and Steppe Vegetation. Measurement 2020, 150, 107047. [Google Scholar] [CrossRef]
- Klápště, P.; Fogl, M.; Barták, V.; Gdulová, K.; Urban, R.; Moudrý, V. Sensitivity Analysis of Parameters and Contrasting Performance of Ground Filtering Algorithms with UAV Photogrammetry-Based and LiDAR Point Clouds. Int. J. Digit. Earth 2020, 13, 1672–1694. [Google Scholar] [CrossRef]
- Tomková, M.; Potůčková, M.; Lysák, J.; Jančovič, M.; Holman, L.; Vilímek, V. Improvements to Airborne Laser Scanning Data Filtering in Sandstone Landscapes. Geomorphology 2022, 414, 108377. [Google Scholar] [CrossRef]
- Wang, Y.; Koo, K.-Y. Vegetation Removal on 3D Point Cloud Reconstruction of Cut-Slopes Using U-Net. Appl. Sci. 2021, 12, 395. [Google Scholar] [CrossRef]
- Braun, J.; Braunova, H.; Suk, T.; Michal, O.; Petovsky, P.; Kuric, I. Structural and Geometrical Vegetation Filtering—Case Study on Mining Area Point Cloud Acquired by UAV Lidar. Acta Montan. Slovaca 2022, 26, 661–674. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Línková, L. Multidirectional Shift Rasterization (MDSR) Algorithm for Effective Identification of Ground in Dense Point Clouds. Remote Sens. 2022, 14, 4916. [Google Scholar] [CrossRef]
- Wu, Y.; Sang, M.; Wang, W. A Novel Ground Filtering Method for Point Clouds in a Forestry Area Based on Local Minimum Value and Machine Learning. Appl. Sci. 2022, 12, 9113. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Lidmila, M.; Kolář, V.; Křemen, T. Vegetation Filtering of a Steep Rugged Terrain: The Performance of Standard Algorithms and a Newly Proposed Workflow on an Example of a Railway Ledge. Remote Sens. 2021, 13, 3050. [Google Scholar] [CrossRef]
- Bulatov, D.; Stütz, D.; Hacker, J.; Weinmann, M. Classification of Airborne 3D Point Clouds Regarding Separation of Vegetation in Complex Environments. Appl. Opt. 2021, 60, F6. [Google Scholar] [CrossRef]
- Meyer, G.E.; Neto, J.C. Verification of Color Vegetation Indices for Automated Crop Imaging Applications. Comput. Electron. Agric. 2008, 63, 282–293. [Google Scholar] [CrossRef]
- Moorthy, S.; Boigelot, B.; Mercatoris, B.C.N. Effective Segmentation of Green Vegetation for Resource-Constrained Real-Time Applications. Precis. Agric. 2015, 15, 257–266. [Google Scholar] [CrossRef]
- Kim, D.-W.; Yun, H.; Jeong, S.-J.; Kwon, Y.-S.; Kim, S.-G.; Lee, W.; Kim, H.-J. Modeling and Testing of Growth Status for Chinese Cabbage and White Radish with UAV-Based RGB Imagery. Remote Sens. 2018, 10, 563. [Google Scholar] [CrossRef]
- Liu, Y.; Hatou, K.; Aihara, T.; Kurose, S.; Akiyama, T.; Kohno, Y.; Lu, S.; Omasa, K. A Robust Vegetation Index Based on Different UAV RGB Images to Estimate SPAD Values of Naked Barley Leaves. Remote Sens. 2021, 13, 686. [Google Scholar] [CrossRef]
- Ponti, M.P. Segmentation of Low-Cost Remote Sensing Images Combining Vegetation Indices and Mean Shift. IEEE Geosci. Remote Sens. Lett. 2013, 10, 67–70. [Google Scholar] [CrossRef]
- Anders, N.; Valente, J.; Masselink, R.; Keesstra, S. Comparing Filtering Techniques for Removing Vegetation from UAV-Based Photogrammetric Point Clouds. Drones 2019, 3, 61. [Google Scholar] [CrossRef]
- Alba, M.; Barazzetti, L.; Fabio, F.; Scaioni, M. Filtering Vegetation from Terrestrial Point Clouds with Low-Cost near Infrared Cameras. Ital. J. Remote Sens. 2011, 43, 55–75. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.-J.; de Castro, A.I.; Torres-Sánchez, J.; Triviño-Tarradas, P.; Jiménez-Brenes, F.M.; García-Ferrer, A.; López-Granados, F. Classification of 3D Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications. Remote Sens. 2020, 12, 317. [Google Scholar] [CrossRef]
- Núñez-Andrés, M.; Prades, A.; Buill, F. Vegetation Filtering Using Colour for Monitoring Applications from Photogrammetric Data. In Proceedings of the 7th International Conference on Geographical Information Systems Theory, Applications and Management, Prague, Czech Republic, 23–25 April 2021. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Ferrer-González, E.; Carvajal-Ramírez, F.; Martínez-Carricondo, P.; Rossi, P.; Mancini, F. Influence of AGL Flight and Off-Nadir Images on UAV-SfM Accuracy in Complex Morphology Terrains. Geocarto Int. 2022, 37, 12892–12912. [Google Scholar] [CrossRef]
- Bertin, S.; Stéphan, P.; Ammann, J. Assessment of RTK Quadcopter and Structure-from-Motion Photogrammetry for Fine-Scale Monitoring of Coastal Topographic Complexity. Remote Sens. 2022, 14, 1679. [Google Scholar] [CrossRef]
- Gonçalves, D.; Gonçalves, G.; Pérez-Alvávez, J.A.; Andriolo, U. On the 3D Reconstruction of Coastal Structures by Unmanned Aerial Systems with Onboard Global Navigation Satellite System and Real-Time Kinematics and Terrestrial Laser Scanning. Remote Sens. 2022, 14, 1485. [Google Scholar] [CrossRef]
- Brunier, G.; Oiry, S.; Gruet, Y.; Dubois, S.F.; Barillé, L. Topographic Analysis of Intertidal Polychaete Reefs (Sabellaria Alveolata) at a Very High Spatial Resolution. Remote Sens. 2022, 14, 307. [Google Scholar] [CrossRef]
- Gracchi, T.; Tacconi Stefanelli, C.; Rossi, G.; Di Traglia, F.; Nolesini, T.; Tanteri, L.; Casagli, N. UAV-Based Multitemporal Remote Sensing Surveys of Volcano Unstable Flanks: A Case Study from Stromboli. Remote Sens. 2022, 14, 2489. [Google Scholar] [CrossRef]
- Park, S.; Choi, Y. Applications of Unmanned Aerial Vehicles in Mining from Exploration to Reclamation: A Review. Minerals 2020, 10, 663. [Google Scholar] [CrossRef]
- Pukanská, K.; Bartoš, K.; Bella, P.; Rákay ml., Š.; Sabová, J. Comparison of non-contact surveying technologies for modelling underground morphological structures. Acta Montan. Slovaca 2017, 22, 246–256. [Google Scholar]
- Komárek, J.; Klápště, P.; Hrach, K.; Klouček, T. The Potential of Widespread UAV Cameras in the Identification of Conifers and the Delineation of Their Crowns. Forests 2022, 13, 710. [Google Scholar] [CrossRef]
- Kuželka, K.; Surový, P. Automatic Detection and Quantification of Wild Game Crop Damage Using an Unmanned Aerial Vehicle (UAV) Equipped with an Optical Sensor Payload: A Case Study in Wheat. Eur. J. Remote Sens. 2018, 51, 241–250. [Google Scholar] [CrossRef]
- Santos-González, J.; González-Gutiérrez, R.B.; Redondo-Vega, J.M.; Gómez-Villar, A.; Jomelli, V.; Fernández-Fernández, J.M.; Andrés, N.; García-Ruiz, J.M.; Peña-Pérez, S.A.; Melón-Nava, A.; et al. The Origin and Collapse of Rock Glaciers during the Bølling-Allerød Interstadial: A New Study Case from the Cantabrian Mountains (Spain). Geomorphology 2022, 401, 108112. [Google Scholar] [CrossRef]
- Menegoni, N.; Inama, R.; Crozi, M.; Perotti, C. Early Deformation Structures Connected to the Progradation of a Carbonate Platform: The Case of the Nuvolau Cassian Platform (Dolomites-Italy). Mar. Pet. Geol. 2022, 138, 105574. [Google Scholar] [CrossRef]
- Nesbit, P.R.; Hubbard, S.M.; Hugenholtz, C.H. Direct Georeferencing UAV-SfM in High-Relief Topography: Accuracy Assessment and Alternative Ground Control Strategies along Steep Inaccessible Rock Slopes. Remote Sens. 2022, 14, 490. [Google Scholar] [CrossRef]
- Fraštia, M.; Liščák, P.; Žilka, A.; Pauditš, P.; Bobáľ, P.; Hronček, S.; Sipina, S.; Ihring, P.; Marčiš, M. Mapping of Debris Flows by the Morphometric Analysis of DTM: A Case Study of the Vrátna Dolina Valley, Slovakia. Geogr. Časopis Geogr. J. 2019, 71, 101–120. [Google Scholar] [CrossRef]
- Cirillo, D.; Cerritelli, F.; Agostini, S.; Bello, S.; Lavecchia, G.; Brozzetti, F. Integrating Post-Processing Kinematic (PPK)–Structure-from-Motion (SfM) with Unmanned Aerial Vehicle (UAV) Photogrammetry and Digital Field Mapping for Structural Geological Analysis. ISPRS Int. J. Geo-Inf. 2022, 11, 437. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Kittler, J.; Illingworth, J. On Threshold Selection Using Clustering Criteria. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 652–655. [Google Scholar] [CrossRef]
- Lee, S.U.; Yoon Chung, S.; Park, R.H. A Comparative Performance Study of Several Global Thresholding Techniques for Segmentation. Comput. Vis. Graph. Image Process. 1990, 52, 171–190. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color Indices for Weed Identification Under Various Soil, Residue, and Lighting Conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Mao, W.; Wang, Y.; Wang, Y. Real-time detection of between-row weeds using machine vision. In Proceedings of the 2003 ASAE Annual Meeting, Las Vegas, NV, USA, 27–30 July 2003; p. 1. [Google Scholar] [CrossRef]
- Neto, J.C. A Combined Statistical-Soft Computing Approach for Classification and Mapping Weed Species in Minimum-Tillage Systems. Ph.D. thesis, University of Nebraska, Lincoln, NE, USA, 2004. Available online: http://digitalcommons.unl.edu/dissertations/AAI3147135 (accessed on 1 February 2023).
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-Based Plant Height from Crop Surface Models, Visible, and near Infrared Vegetation Indices for Biomass Monitoring in Barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Kawashima, S. An Algorithm for Estimating Chlorophyll Content in Leaves Using a Video Camera. Ann. Bot. 1998, 81, 49–54. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel Algorithms for Remote Estimation of Vegetation Fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Kataoka, T.; Kaneko, T.; Okamoto, H.; Hata, S. Crop Growth Estimation System Using Machine Vision. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 2, pp. b1079–b1083. [Google Scholar] [CrossRef]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially Located Platform and Aerial Photography for Documentation of Grazing Impacts on Wheat. Geocarto Int. 2001, 16, 65–70. [Google Scholar] [CrossRef]
- Marchant, J.A.; Onyango, C.M. Shadow-Invariant Classification for Scenes Illuminated by Daylight. J. Opt. Soc. Am. A 2000, 17, 1952. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Hagan, M.; Demuth, H.; Beale, M.; Jesus, O.D. Neural Network Design, 2nd ed.; Oklahoma State University: Stillwater, OK, USA, 2014; ISBN 978-0-9717321-1-7. [Google Scholar]
- You, S.-H.; Jang, E.J.; Kim, M.-S.; Lee, M.-T.; Kang, Y.-J.; Lee, J.-E.; Eom, J.-H.; Jung, S.-Y. Change Point Analysis for Detecting Vaccine Safety Signals. Vaccines 2021, 9, 206. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).