The Mean Moment of Inertia for Irregularly Shaped Phobos and Its Application to the Constraint for the Two-Layer Interior Structure for the Martian Moon
Abstract
1. Introduction
2. Shape of Phobos and Its Two-Layer Model
3. Theory and Method
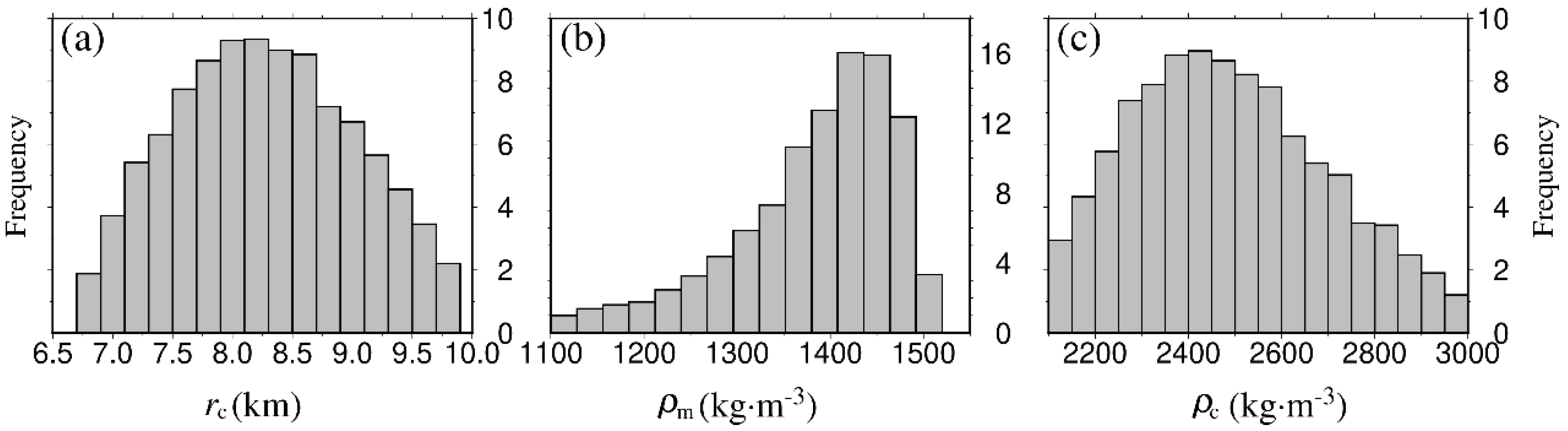
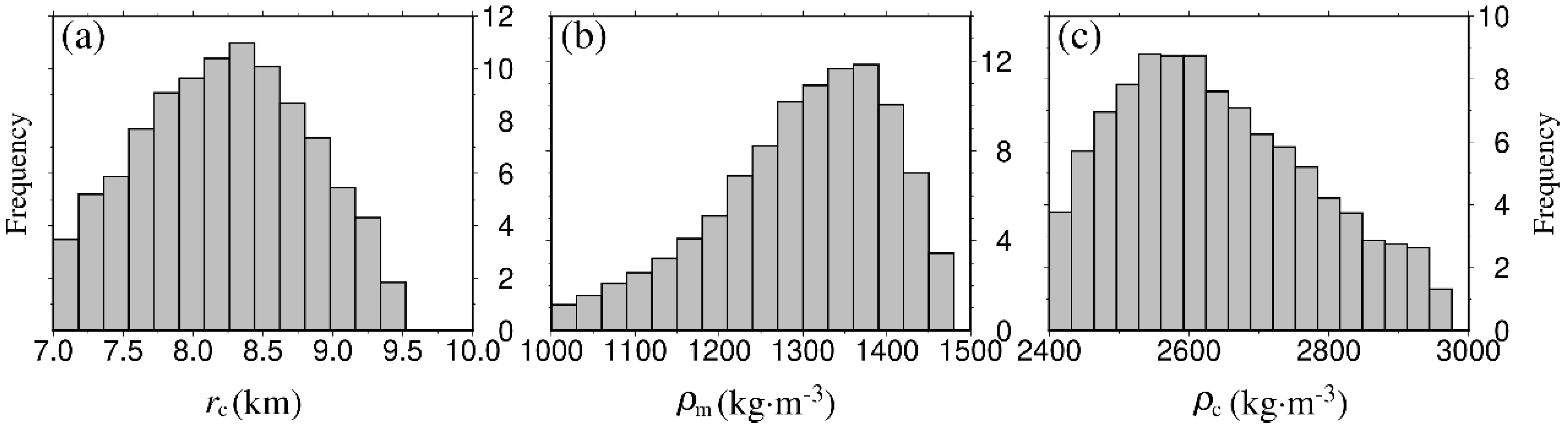
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Willner, K.; Shi, X.; Oberst, J. Phobos’ shape and topography models. Planet. Space Sci. 2014, 102, 51–59. [Google Scholar] [CrossRef]
- Schmedemann, N.; Kneisslm, T.; Ivanov, B.A.; Michael, G.G.; Wagner, R.J.; Neukum, G.; Ruesch, O.; Hiesinger, H.; Krohn, K.; Roatsch, T.; et al. The cratering record, chronology and surface ages of (4) Vesta in comparison to smaller asteroids and the ages of HED meteorites. Planet. Space Sci. 2014, 103, 104–130. [Google Scholar] [CrossRef]
- Syal, M.B.; Rovny, J.; Owen, J.M.; Miller, P. Excavating Stickney crater at Phobos. Geophys. Res. Lett. 2016, 43, 595–601. [Google Scholar]
- Matsumoto, K.; Hirata, N.; Ikeda, H.; Kouyama, T.; Senshu, H.; Yamamoto, K.; Noda, H.; Miyamoto, H.; Araya, A.; Araki, H.; et al. MMX geodesy investigations: Science requirements and observation strategy. Earth Planets Space 2021, 73, 226. [Google Scholar] [CrossRef]
- Poggiali, G.; Matsuoka, M.; Barucci, M.A.; Brucato, J.R.; Beck, P.; Fornasier, S.; Doressoundiram, A.; Merlin, F.; Alberini, A. Phobos and Deimos surface composition: Search for spectroscopic analogues Get access Arrow. Mon. Not. R. astron. Soc. 2022, 516, 465–476. [Google Scholar] [CrossRef]
- Hesselbrock, A.J.; Minton, D.A. An ongoing satellite–ring cycle of Mars and the origins of Phobos and Deimos. Nat. Geosci. 2017, 10, 266–269. [Google Scholar] [CrossRef]
- Usui, T.; Bajo, K.; Fujiya, W.; Furukawa, Y.; Koike, M.; Miura, Y.N.; Sugahara, H.; Tachibana, S.; Takano, Y.; Kuramoto, K. The Importance of Phobos Sample Return for Understanding the Mars-Moon System. Space Sci. Rev. 2020, 216, 49. [Google Scholar] [CrossRef]
- Kuramoto, K.; Kawakatsu, Y.; Fujimoto, M.; Araya, A.; Barucci, M.A.; Genda, H.; Hirata, N.; Ikeda, H.; Imamura, T.; Helbert, J.; et al. Martian moons exploration MMX: Sample return mission to Phobos elucidating formation processes of habitable planets. Earth Planets Space 2022, 74, 12. [Google Scholar] [CrossRef]
- Duxbury, T.C. The figure of Phobos. Icarus 1989, 78, 169–180. [Google Scholar] [CrossRef]
- Willner, K.; Oberst, J.; Hussmann, H.; Giese, B.; Hoffmann, H.; Matz, K.D.; Roatsch, T.; Duxbury, T. Phobos control point network, rotation, and shape. Earth Planet. Sc. Lett. 2010, 294, 541–546. [Google Scholar] [CrossRef]
- Lainey, V.; Pasewaldt, A.; Robert, V.; Rosenblatt, P.; Jaumann, R.; Oberst, J.; Roatsch, T.; Willner, K.; Ziese, R.; Thuillot, W. Mars moon ephemerides after 14 years of Mars Express data. Astron. Astrophys. 2021, 650, A64. [Google Scholar] [CrossRef]
- Burmeister, S.; Willner, K.; Schmidt, V.; Oberst, J. Determination of Phobos’ rotational parameters by an inertial frame bundle block adjustment. J. Geodesy. 2018, 92, 963–973. [Google Scholar] [CrossRef]
- Le Maistre, S.; Rivoldini, A.; Rosenblatt, P. Signature of Phobos’ interior structure in its gravity field and libration. Icarus 2019, 321, 272–290. [Google Scholar] [CrossRef]
- Dmitrovskii, A.A.; Khan, A.; Boehm, C.; Bagheri, A.; Driel, M.V.C. Constraints on the interior structure of Phobos from tidal deformation modeling. Icarus 2022, 372, 114714. [Google Scholar] [CrossRef]
- Sohl, F.; Schubert, G.; Spohn, T. Geophysical constraints on the composition and structure of the Martian interior. J. Geophys. Res. Planet. 2005, 110, E12008. [Google Scholar] [CrossRef]
- Yan, J.; Xu, L.; Li, F.; Matsumoto, K.; Rodriguez, J.A.P.; Miyamoto, H.; Dohm, J.M. Lunar core structure investigation: Implication of GRAIL gravity field model. Adv. Space Res. 2015, 55, 1721–1727. [Google Scholar] [CrossRef]
- Kahan, D.S.; Folkner, W.M.; Buccino, D.R.; Dehant, V.; Le Maistre, S.; Rivoldini, A.; Van Hoolst, T.; Yseboodt, M.; Marty, J.C. Mars precession rate determined from radiometric tracking of the Insight Lander. Planet. Space Sci. 2021, 199, 105208. [Google Scholar] [CrossRef]
- Zhong, Z.; Wen, Q.; Liang, J. Constraining the size and density composition of the Martian core by using second-order potential coefficient and recent precession rate of gravity field model. Acta Phys. Sin. 2023, 72, 029601. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.G.; Andert, T.; Ye, M.; Pätzold, M.; Hahn, M.; Jin, W.T.; Li, F.; Barriot, J.P. The second-degree gravity coefficients of Phobos from two Mars Express flybys. Mon. Not. R. Astron. Soc. 2019, 490, 2007–2012. [Google Scholar] [CrossRef]
- Beitz, E.; Blum, J.; Parisi, M.G.; Trigo-Rodríguez, J. The collisional evolution of undifferentiated asteroids and the formation of chondritic meteroroids. Astrophys. J. 2016, 824, 12. [Google Scholar] [CrossRef]
- Guo, X.; Yan, J.; Andert, T.; Yang, X.; Pätzold, M.; Hahn, M.; Ye, M.; Liu, S.; Li, F.; Barriot, J.P. A lighter core for Phobos? Astron. Astrophys. 2021, 651, A110. [Google Scholar] [CrossRef]
- Thomas, P.C. The shapes of small satellites. Icarus 1989, 77, 248–274. [Google Scholar] [CrossRef]
- Simonelli, D.P.; Thomas, P.C.; Carcich, B.T.; Veverka, J. The generation and use of numerical shape models for irregular solar system objects. Icarus 1993, 103, 49–61. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X. Analysis of Phobos’ dynamical environment considering effects of ephemerides and physical libration. Mon. Not. R. Astron. Soc. 2020, 497, 416–434. [Google Scholar] [CrossRef]
- Mueller, N.; Piqueux, S.; Lemmon, M.; Maki, J.; Lorenz, R.D.; Grott, M.; Spohn, T.; Smrekar, S.E.; Knollenberg, J.; Hudson, T.L.; et al. Near Surface Properties of Martian Regolith Derived From InSight HP3-RAD Temperature Observations During Phobos Transits. Geophys. Res. Lett. 2021, 48, e2021GL093542. [Google Scholar] [CrossRef]
- Available online: https://pds-geosciences.wustl.edu/mex/mex-msa-hrsc-5-refdr-phobos-maps-v1/mexhrs_5001/data/dtm/ (accessed on 19 April 2023).
- Bagheri, A.; Khan, A.; Efroimsky, M.; Kruglyakov, M.; Giardini, D. Dynamical evidence for Phobos and Deimos as remnants of a disrupted common progenitor. Nat. Astron. 2021, 5, 539–543. [Google Scholar] [CrossRef]
- Guo, X.; Yan, J.G.; Yang, X.; Liu, L.; Chen, Y.H.; Barriot, J.P. Simulation of Phobos gravity field estimation from Tianwen-1 flybys and implications for the modelling of Phobos’ internal structure. Mon. Not. R. Astron. Soc. 2023, 520, 925–934. [Google Scholar] [CrossRef]
- Rambaux, N.; Castillo-Rogez, J.C.; Le Maistre, S.; Rosenblatt, P. Rotational motion of Phobos. Astron. Astrophys. 2012, 548, A14. [Google Scholar] [CrossRef]
- Jacobson, R.A. The orbits and masses of the Martian satellites and the libration of Phobos. Astron. J. 2010, 139, 668. [Google Scholar] [CrossRef]
- Oberst, J.; Zubarev, A.; Nadezhdina, I.; Shishkina, L.; Rambaux, N. The Phobos geodetic control point network and rotation model. Planet. Space Sci. 2014, 102, 45–50. [Google Scholar] [CrossRef]
- Zhong, Z.; Yan, J.; Jin, S.; Zhu, M.; Rodriguez, J.A.P.; Zhu, H.; Li, Y. Selenophysical parameter inversion in the Lunar Southern Hemisphere Highland based on mutant particle swarm optimization. Phys. Earth Planet. In. 2019, 292, 55–66. [Google Scholar] [CrossRef]
- Rosenblatt, P.; Charnoz, S.; Dunseath, K.M.; Terao-Dunseath, M.; Trinh, A.; Hyodo, R.; Genda, H.; Toupin, S. Accretion of Phobos and Deimos in an extended debris disc stirred by transient moons. Nat. Geosci. 2016, 9, 581–583. [Google Scholar] [CrossRef]
- Canup, R.; Salmon, J. Origin of Phobos and Deimos by the impact of a Vesta-to-Ceres sized body with Mars. Sci. Adv. 2018, 4, eaar6887. [Google Scholar] [CrossRef] [PubMed]
- Ćuk, M.; Minton, D.A.; Pouplin, J.L.L.; Wishard, C. Evidence for a Past Martian Ring from the Orbital Inclination of Deimos. Astrophys. J. Lett. 2020, 896, L28. [Google Scholar] [CrossRef]
- Busch, M.W.; Ostro, S.J.; Benner, L.A.M.; Giorgini, J.D.; Magri, C.; Howell, E.S.; Nolan, M.C.; Hine, A.A.; Campbell, D.B.; Shapiro, I.I.; et al. Arecibo radar observations of Phobos and Deimos. Icarus 2007, 186, 581–584. [Google Scholar] [CrossRef]
- Pätzold, M.; Andert, T.P.; Tyler, G.L.; Asmar, S.W.; Häusler, B.; Tellmann, S. Phobos mass determination from the very close flyby of Mars Express in 2010. Icarus 2014, 229, 92–98. [Google Scholar] [CrossRef]
- Macke, R.J.; Consolmagno, G.J.; Britt, D.T. Density, porosity, and magnetic susceptibility of carbonaceous chondrites. Meteorit. Planet. Sci. 2011, 46, 1842–1862. [Google Scholar] [CrossRef]
- Trigo-Rodríguez, J.M.; Rimola, A.; Tanbakouei, S.; Soto, V.C.; Lee, M. Accretion of water in carbonaceous chondrites: Current evidence and implications for the delivery of water to early Earth. Space Sci. Rev. 2019, 215, 18. [Google Scholar] [CrossRef]
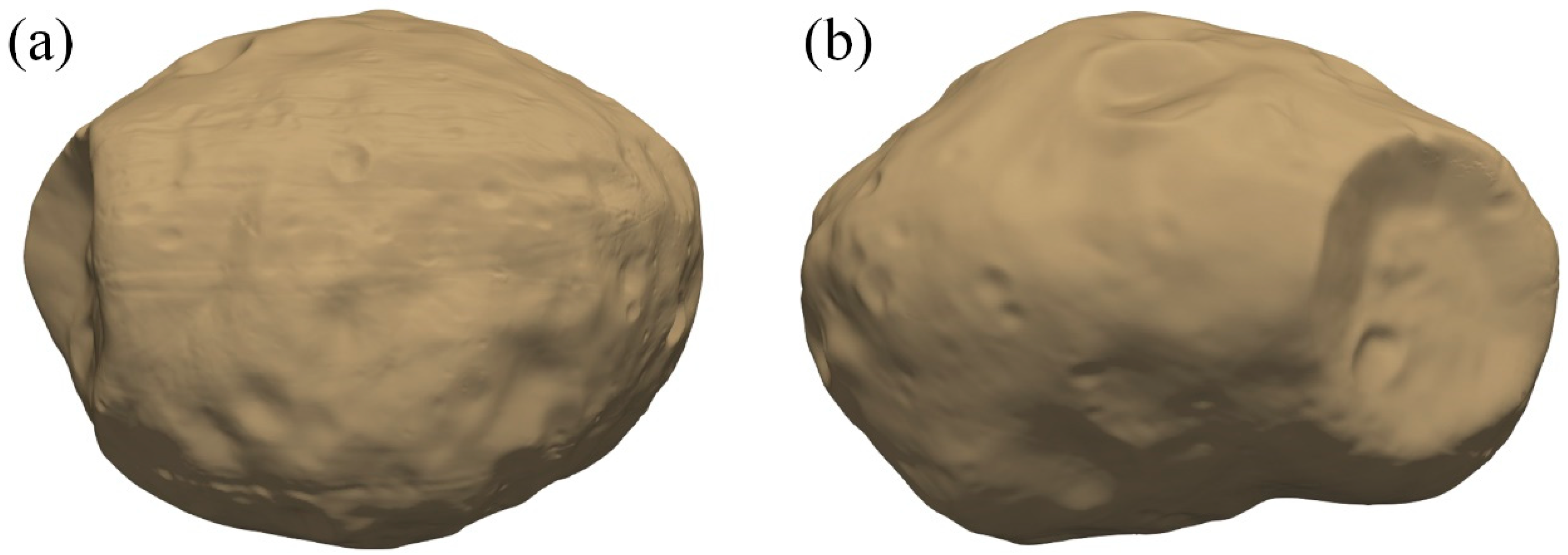
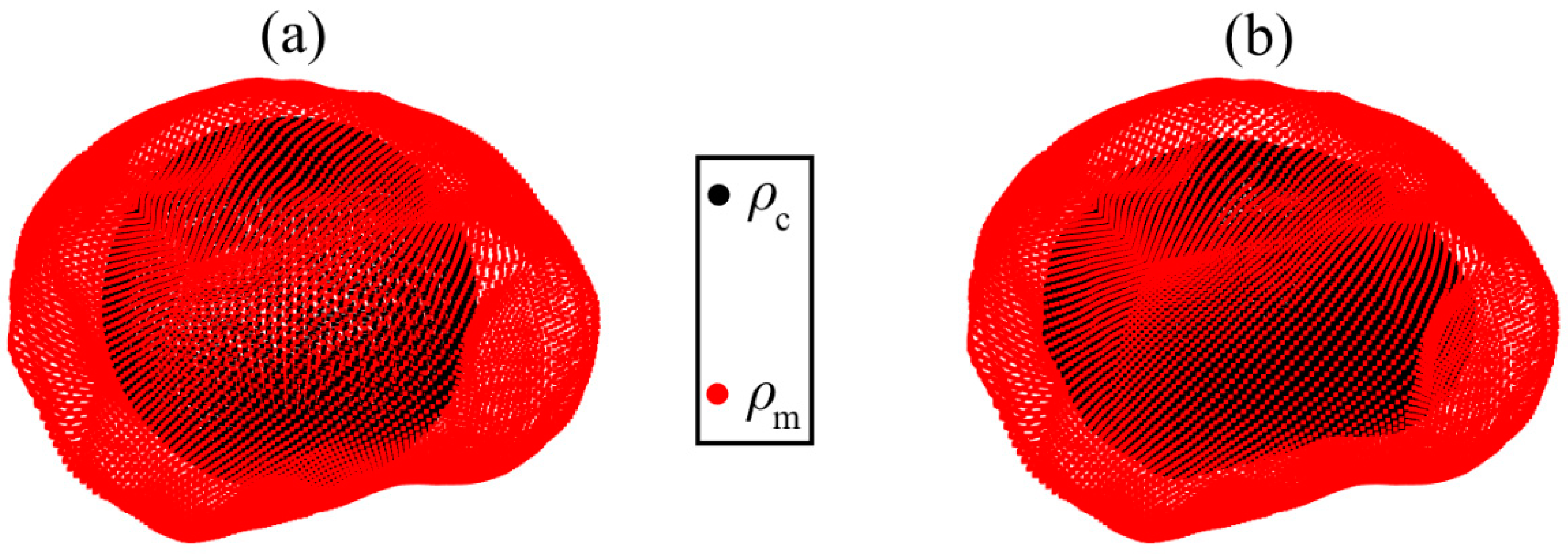
| Number | Parameters | Values |
|---|---|---|
| 1 | Mass M [19] | (1.060261 ± 0.001124) × 1016 kg |
| 2 | Volume V [1] | 5742 ± 35 km3 |
| 3 | Mean radius R [1] | ~11.1 km |
| 4 | Mean density [19] | 1846 ± 11 kg·m−3 |
| 5 | Orbital eccentricity e [30] | 0.01511° |
| 6 | Libration amplitude θA | −1.09° ± 0.10° observed by Oberst et al. [31] −1.143° ± 0.025° observed by Burmeister et al. [12] −1.09° ± 0.01° from Phobos ephemeris [11] |
| 7 | Unnormalized gravity coefficients of degree-2 [19] | C2,0 = −0.1378 ± 0.0348, C2,2 = 0.0166 ± 0.0153 |
| 8 | Core radius rc | 0–10 km |
| 9 | Core density ρc | 1000–3000 kg·m−3 |
| 10 | The outer layer density ρm | 1000–3000 kg·m−3 |
| Target | rc (km) | ρm (kg·m−3) | ρc (kg·m−3) |
|---|---|---|---|
| Estimated parameters for Model-I | |||
| Estimated parameters for Model-II | |||
| Sensitivities S1(f, x) of various optimized parameters for Model-I | −4.6 | −6.2 | −2.3 |
| Sensitivities S2(f, x) of various optimized parameters for Model-II | −5.8 | −4.5 | −2.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Z.; Wen, Q.; Yan, J.; Pang, L. The Mean Moment of Inertia for Irregularly Shaped Phobos and Its Application to the Constraint for the Two-Layer Interior Structure for the Martian Moon. Remote Sens. 2023, 15, 3162. https://doi.org/10.3390/rs15123162
Zhong Z, Wen Q, Yan J, Pang L. The Mean Moment of Inertia for Irregularly Shaped Phobos and Its Application to the Constraint for the Two-Layer Interior Structure for the Martian Moon. Remote Sensing. 2023; 15(12):3162. https://doi.org/10.3390/rs15123162
Chicago/Turabian StyleZhong, Zhen, Qilin Wen, Jianguo Yan, and Lijun Pang. 2023. "The Mean Moment of Inertia for Irregularly Shaped Phobos and Its Application to the Constraint for the Two-Layer Interior Structure for the Martian Moon" Remote Sensing 15, no. 12: 3162. https://doi.org/10.3390/rs15123162
APA StyleZhong, Z., Wen, Q., Yan, J., & Pang, L. (2023). The Mean Moment of Inertia for Irregularly Shaped Phobos and Its Application to the Constraint for the Two-Layer Interior Structure for the Martian Moon. Remote Sensing, 15(12), 3162. https://doi.org/10.3390/rs15123162






