Refocusing Swing Ships in SAR Imagery Based on Spatial-Variant Defocusing Property

Abstract

Synthetic aperture radar (SAR) is an essential tool for maritime surveillance in all weather conditions and at night. Ships are often affected by sea breezes and waves, generating a three-dimensional (3D) swinging motion. The 3D swing ship can thereby become severely defocused in SAR images, making it extremely difficult to recognize them. However, refocusing 3D swing ships in SAR imagery is challenging with traditional approaches due to different phase errors at each scattering point on the ship. In order to solve this problem, a novel method for refocusing swing ships in SAR imagery based on the spatial-variant defocusing property is proposed in this paper. Firstly, the spatial-variant defocusing property of a 3D swing ship is derived according to the SAR imaging mechanism. Secondly, considering the spatial-variant defocusing property, each azimuth line of the SAR 3D swing ship image is modeled as a multi-component linear frequency modulation (MC-LFM) signal. Thirdly, Fractional Autocorrelation (FrAc) is implemented in order to quickly calculate the optimal rotation order set for each azimuth line. Thereafter, Fractional Fourier Transform (FrFT) is performed on the azimuth lines to refocus their linear frequency modulation (LFM) components one by one. Finally, the original azimuth lines are replaced in the SAR image with their focused signals to generate the refocused SAR image. The experimental results from a large amount of simulated data and real Gaofen-3 data show that the proposed algorithm can overcome the spatial-variant defocusing of 3D swing ships. Compared with state-of-the-art algorithms, our approach reduces the image entropy by an order of magnitude, leading to a visible improvement in image quality, which makes it possible to recognize swing ships in SAR images.

1. Introduction

Synthetic aperture radar (SAR) is capable of obtaining high-resolution images of the sea surface, even in adverse weather conditions or at night, which is not possible with passive sensors, such as optical cameras [1,2,3]. Ships are critical targets for maritime surveillance and their detection and identification in SAR images hold significant value for economic and military interests [4,5,6]. Researchers have proposed numerous algorithms for ship detection in SAR images, with satisfactory results [7,8,9,10,11,12,13,14,15,16,17,18,19]. However, it is very difficult to further recognize ships, because ships in motion at sea exhibit azimuthal defocusing in SAR imagery [20,21,22,23,24,25,26,27,28,29].

In ideal conditions, SAR emits electromagnetic waves in a uniform linear motion to illuminate a stationary target on the ground. The reflected signal from the target is then collected and compressed in the range and azimuth direction to generate a two-dimensional image. In practice, the trajectory of the SAR platform is non-ideal, due to the effects of turbulence and wind. In order to achieve high resolution imaging, researchers have proposed numerous autofocus algorithms [30]. However, these autofocus algorithms only compensate for phase errors caused by the non-ideal motion of the SAR platform, and not those caused by the ship’s motion. As a result, the moving ship remains defocused in the SAR image.

In order to improve the recognition performance, we need to refocus SAR for moving ships to accurately obtain the structure of the ship. Since the motion of ships can be equated to the non-ideal motion of the SAR platform, SAR autofocus methods are also applicable to SAR moving ship refocusing. Classical SAR autofocus methods assume that each scattering point has the same phase error. There are two main types of autofocus algorithms. One class of methods for autofocusing is based on phase error function, such as map drift (MD) [31,32] and phase gradient autofocus algorithms (PGAs) [33,34]. Another class of methods is based on SAR image quality, such as fast minimum entropy phase compensation (FMEPC) algorithms [35,36,37,38] and maximum contrast algorithms [39,40,41]. In calm sea conditions, ships primarily move in linear motion through their own propulsion, and the phase error of each scattering point on the translational ship is the same. Therefore, the above methods can improve the image quality of SAR-translated ships. However, ships can swing as they are affected by wind and waves in rough seas [42,43,44]. When this occurs, the velocity of each scattering point on the ship is different, resulting in varying phase error for each part of the ship. Therefore, the above traditional methods cannot achieve well-focused performance on the SAR images of swing ships.

There are currently four types of methods with which to refocus 3D swing ships in SAR images. The first class of methods is based on the idea of splitting the image into subimages. Aron Sommer et al. [45] first split an SAR ship image into subimages and used a maximum contrast algorithm to estimate the phase error of each subimage. A second-order fit was then performed with the Levenberg–Marquardt algorithm in order to obtain the phase error of the entire SAR image, thus refocusing the SAR 3D swing ship image. Based on this, Li et al. [46] proposed a hybrid coordinate system and improved the calculation of the phase error for the subimages, which ultimately improved the speed of the algorithm. Yu et al. [47] divided the ship image into subimages with different sizes, according to the difference in the image entropy of a ship’s different parts, and then used the PGA algorithm to compensate for each subimage. However, this type of approach must ensure that each subblock is small enough that the phase error within the subimage can be considered spatial-invariant phase error. Moreover, reducing the size of the subimage can lead to a decrease in the accuracy of the phase error estimation. In contrast, if the subimage is large, the phase error may still contain spatial-variant phase error.

The second class of methods aims to establish a fine spatial-variant phase error model. Brian et al. [48] constructed a range-variant phase error model that solved phase error through image quality optimization and used it to refocus the SAR images of rotating targets. Huang et al. [49] considered the azimuth-variant phase error and proposed a two-dimensional spatial-variant phase error compensation method based on maximum image contrast for refocusing ISAR images. However, the phase error model constructed using these methods may not represent the true phase error of swing ships.

The third class of methods uses ISAR techniques to select the time period when the ship’s motion is stable. Based on this idea, Jia et al. [50] mapped the SAR defocused ship images into the ISAR equivalent echo domain. The phase error caused by the ship translation is first compensated. Thereafter, the optimal imaging time was selected using a maximum image contrast search method. Finally, a high-resolution image was obtained using an iterative adaptive method. Cao et al. [51] used the range-instantaneous Doppler (RID) algorithm in the equivalent ISAR echo domain to obtain a clear SAR ship image. However, this type of approach reduces the resolution of the SAR image, as it selects only a part of the time.

The final class of methods uses deep learning techniques to learn complex mapping relationships between defocused and focused SAR ship images. Lu et al. [52] improved the original Unet network based on SAR imaging characteristics. The trained network was able to refocus simulated moving targets, demonstrating the effectiveness of deep learning techniques in SAR moving target refocusing. Liu et al. [53] proposed an autofocus method based on ensemble learning, constructing a convolutional extreme learning machine (CELM) with which to estimate phase errors. This method achieved a good balance between focusing quality and processing speed. Hua et al. [54] considered this problem as a regression problem in the field of deep learning. A complex-valued neural network was then constructed and trained using simulated data to refocus SAR 3D swing ship images. However, deep learning techniques require a large dataset, and obtaining real samples can be difficult.

In fact, the main reason for SAR moving ship defocusing is the erroneous matched filtering in the azimuth direction, which results in residual linear frequency-modulated (LFM) signals in this direction of the SAR image. The LFM signal exhibits excellent energy aggregation after Fractional Fourier Transform (FrFT) at its optimal rotation order [55]. The application of FrFT to SAR moving targets has been extensively studied in recent years [56,57,58,59,60,61,62,63]. These methods are all specific to SAR echo data, while Pelich et al. [64] used this property to perform FrFT on each azimuth line of the single-look complex (SLC) SAR image, which can refocus the SAR translational ship very well. However, each azimuth line of the 3D swing ship is not a single LFM signal, as there are multiple scattering points with different velocities at each range cell. In this paper, the phenomenon that scattering points at different locations on a 3D swing ship exhibit different degrees of defocusing is defined as the spatial-variant defocusing property. Based on the spatial-variant defocusing property, a new SAR 3D swing ship image refocusing algorithm is proposed in this paper. The contribution of this paper mainly includes the following aspects:

• By investigating the SAR imaging characteristics of 3D swing ships, this paper constructs a SAR imaging model for such ships and further reveals the spatial-variant defocusing property of 3D swing ships in SAR imaging.
• The authors of this paper propose to model each azimuth line of the SAR 3D swing ship image as an MC-LFM signal to address the spatial-variant defocusing problem. This approach simplifies the task of refocusing the 3D swing ship by converting it into the task of refocusing the MC-LFM signal.
• In order to refocus each azimuth line, the authors of this paper first use Fractional Autocorrelation (FrAc) to accelerate the precise estimate for the optimal rotation order set of the MC-LFM signal [65]. The azimuth line is then refocused by performing FrFT on each LFM component at its optimal rotation order. This achieves a good balance between focusing quality and processing speed.
• We conduct sufficient experiments using simulated data and Gaofen-3 SAR images. The experimental results show that the proposed algorithm can overcome the spatial-variant defocusing property of 3D swing ships. Compared with state-of-the-art algorithms, our method reduces image entropy by an order of magnitude, which can improve the recognition of SAR ships. These experimental data are published at https://github.com/RefocusWang/SAR_Swing_Ship (accessed on 1 June 2023). Scholars interested in this issue can further study this data.

The remainder of this paper is organized as follows. Section 2 establishes the SAR imaging signal model for a 3D swing ship and analyzes its spatial-variant defocusing property. Section 3 introduces the method that the authors of this paper propose. Section 4 validates the performance of the proposed method using simulated SAR images and real high-resolution SAR images from Gaofen-3.

2. Geometry and Signal Model

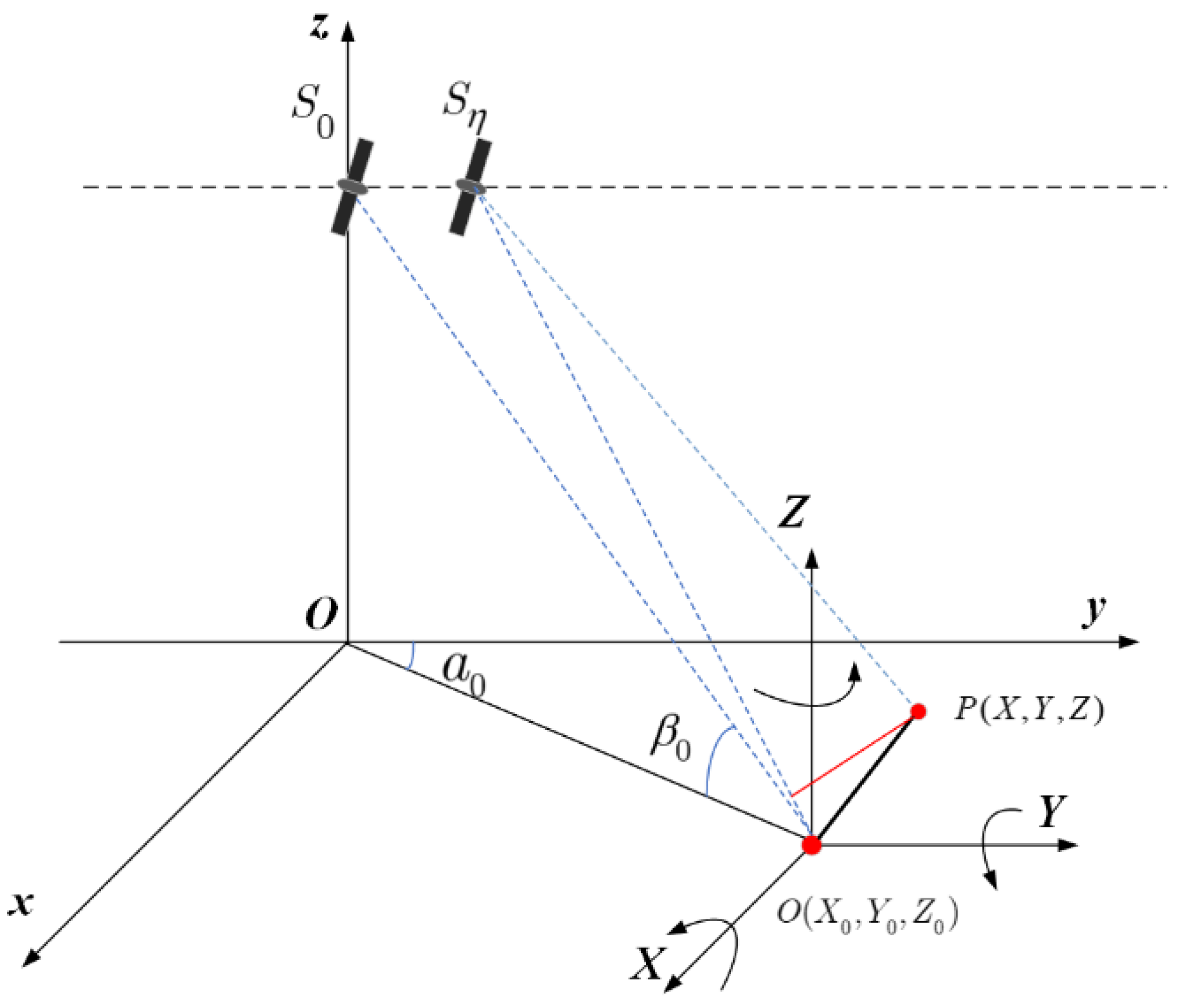
The 3D swing of a ship is the pendulum motion of the ship around its own longitudinal, lateral, and vertical axes [27], which are referred to as roll, pitch, and yaw, respectively, as shown in Figure 1. The geometric relationship between the 3D swing ship and the SAR platform is shown in Figure 2. Firstly, a fixed space coordinate system $o-xyz$ is established to describe the absolute motion of the ship. Assume that the coordinate of the ship’s center of gravity $O$ in the fixed-space coordinate system is represented by $(x_{0,}{y}_{0,}0)$. Taking the ship’s center of gravity $O$ as the origin, the bow direction as the axis $X$, a direction perpendicular to the bow direction and parallel to the plane of the ship’s body as the axis $Y$, and a direction perpendicular to the plane of the ship’s body as the axis $Z$, a ship-fixed coordinate system $O-XYZ$, which describes the positions of a ship’s scattering points relative to the ship’s center of gravity $O$, is established.

Assume that at the initial moment, the ship-fixed coordinate system is parallel to the fixed-space coordinate system. At time $\eta$, the roll, pitch, and yaw angles of a certain scattering point P$(X_p,Y_p,Z_p)$ on the ship-fixed coordinate system are represented by ${\theta }_x,{\theta }_y,$ and ${\theta }_z$ respectively.

$$\{\begin{array}{c}{\theta }_x=A_x\sin (w_x\eta +{\phi }_x)\\ {\theta }_y=A_y\sin (w_y\eta +{\phi }_y)\\ {\theta }_z=A_z\sin (w_z\eta +{\phi }_z)\end{array}$$

(1)

where $A_x,A_y,A_z$ represent the maximum swing amplitude of roll, pitch, and yaw motions, $w_x,w_y,w_z$ represent the angular frequencies of swing motions, and ${\phi }_x,{\phi }_y,{\phi }_z$ represent the values at the initial phase. Thereafter, the coordinates of point P in the fixed-space coordinate system can be expressed through the coordinate rotation matrix $\mathrm{Rot}\left({\theta }_x,{\theta }_y,{\theta }_z\right)$ as

$$\left[\begin{array}{l}{x}_p(\eta )\hfill \\ y_p(\eta )\hfill \\ z_p(\eta )\hfill \end{array}\right]=\mathrm{Rot}\left({\theta }_x,{\theta }_y,{\theta }_z\right)\left[\begin{array}{c}{X}_p\\ Y_p\\ Z_p\end{array}\right]+\left[\begin{array}{c}{x}_0\\ y_0\\ 0\end{array}\right]$$

(2)

$$\mathrm{Rot}\left({\theta }_x,{\theta }_y,{\theta }_z\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos {\theta }_x& -\sin {\theta }_x\\ 0& \sin {\theta }_x& \cos {\theta }_x\end{array}\right]\left[\begin{array}{ccc}\cos {\theta }_y& 0& \sin {\theta }_y\\ 0& 1& 0\\ -\sin {\theta }_y& 0& \cos {\theta }_y\end{array}\right]\left[\begin{array}{ccc}\cos {\theta }_z& -\sin {\theta }_z& 0\\ \sin {\theta }_z& \cos {\theta }_z& 0\\ 0& 0& 1\end{array}\right]$$

(3)

The distance from the SAR platform to point P can be approximately expressed as

$$\begin{array}{l}R(\eta )\approx \left|O{S}_{\eta }\right|-\left|OP\right|\cos \langle O{S}_{\eta },OP\rangle \approx \left|O{S}_{\eta }\right|-\left|OP\right|\cos \langle O{S}_0,OP\rangle \\ =\sqrt{x_0{}^2+{(v_{sar}\eta -y_0)}^2+H^2}-\\ \hspace{1em}(-\sin a_0\cos {\beta }_0,-\cos a_0\cos {\beta }_0,\sin {\beta }_0)\ast Rot({\theta }_x,{\theta }_y,{\theta }_z){(X_p,Y_p,Z_p)}^T\end{array}$$

(4)

From the above equation, it can be seen that an additional phase is created when the ship swings, compared with a stationary target. To simplify the analysis, when the ship is only yawing (i.e., ${\theta }_x={\theta }_y=0$), the additional phase error can be expressed as follows:

$$\begin{array}{l}{\phi }_{m-yaw}=-\frac{4\pi }{\lambda }(\cos {\beta }_0\sqrt{X_p^2+Y_p^2}\ast \sin ({\theta }_z+a_0+\arg (X_p+j{Y}_p))-Z_p\sin {\beta }_0)\\ \hspace{1em}\hspace{1em} =-\frac{4\pi }{\lambda }(L_{zeff}\ast \sin (\sin (w_{z}t+{\theta }_z)+{\theta }_{z0rff})-Z_p\sin {\beta }_0)\end{array}$$

(5)

where $L_{zeff}=\cos {\beta }_0\sqrt{X_p^2+Y_p^2}$ and ${\theta }_{z0eff}=a_0+\arg (X_p+jY)$.

The above equation shows that the phase error caused by yaw is a sinusoidal function. As the ship swings slowly, over a period of more than ten seconds, the phase error can be approximated as a polynomial of no higher than third order using Taylor expansion within the synthetic aperture time (one second) of the space-borne SAR.

However, compared with the ship’s translational motion, the ship’s 3D swing is not a homogeneous motion, resulting in spatial-variant phase error. In the above equation, $\sqrt{X_p{}^2+Y_p{}^2}$ represents the distance from the scattering point to the swing axis $Z$. This shows that the phase error of each scattering point is related to its distance from the swing axis when the ship yaws. Therefore, the 3D swing of the ship causes the phase error of each scattering point to be closely related to its spatial position, resulting in spatial-variant phase error. The spatial-variant phase error caused by the ship’s 3D swing renders traditional autofocus algorithms ineffective. Consequently, refocusing 3D swing ship images is a very challenging problem.

3. Proposed Method

In this section, the proposed method for refocusing swing ships in SAR imagery based on the spatial-variant defocusing property is described. The flowchart of the proposed method is shown in Figure 3.

3.1. Selecting a Ship’s Azimuth Lines

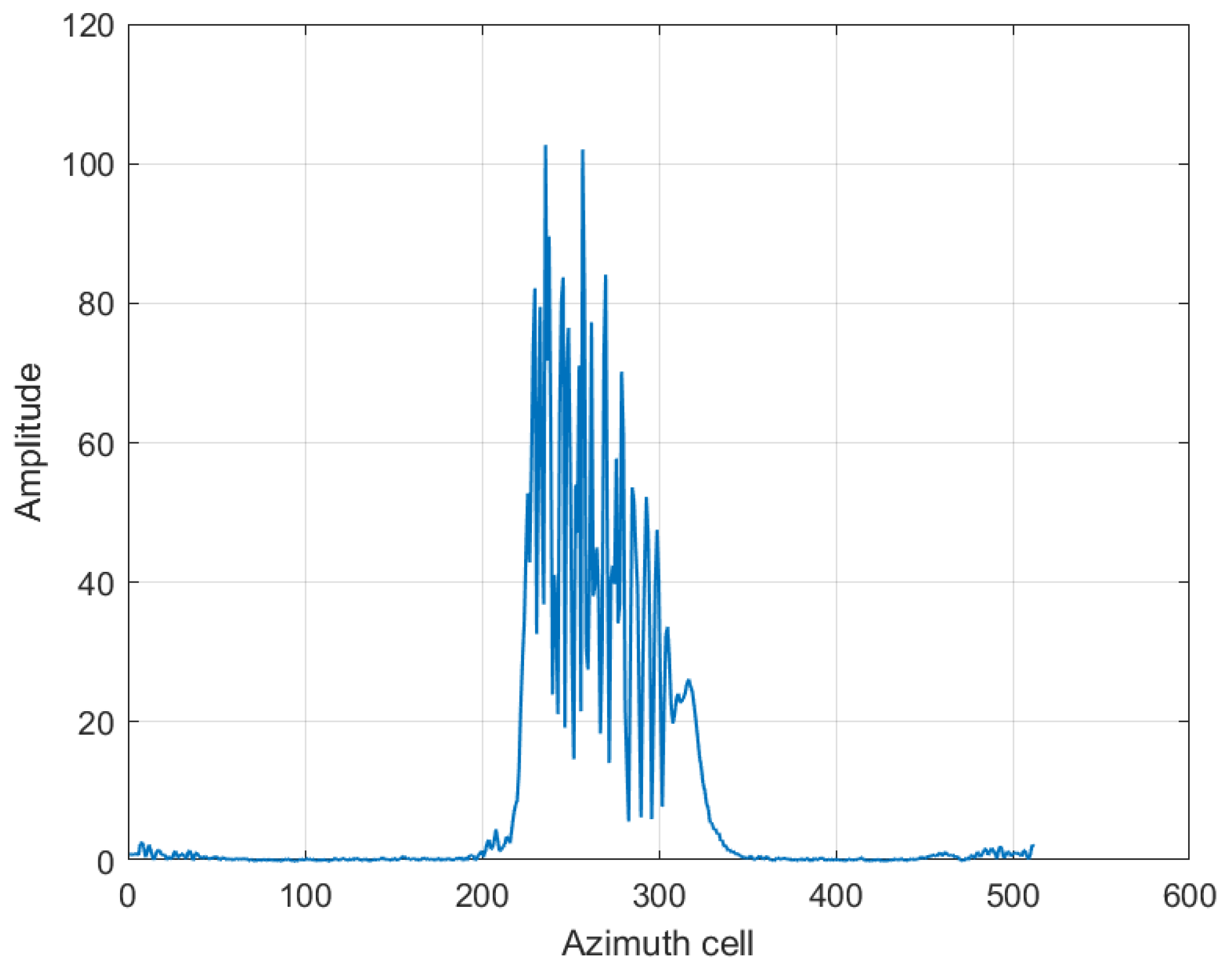
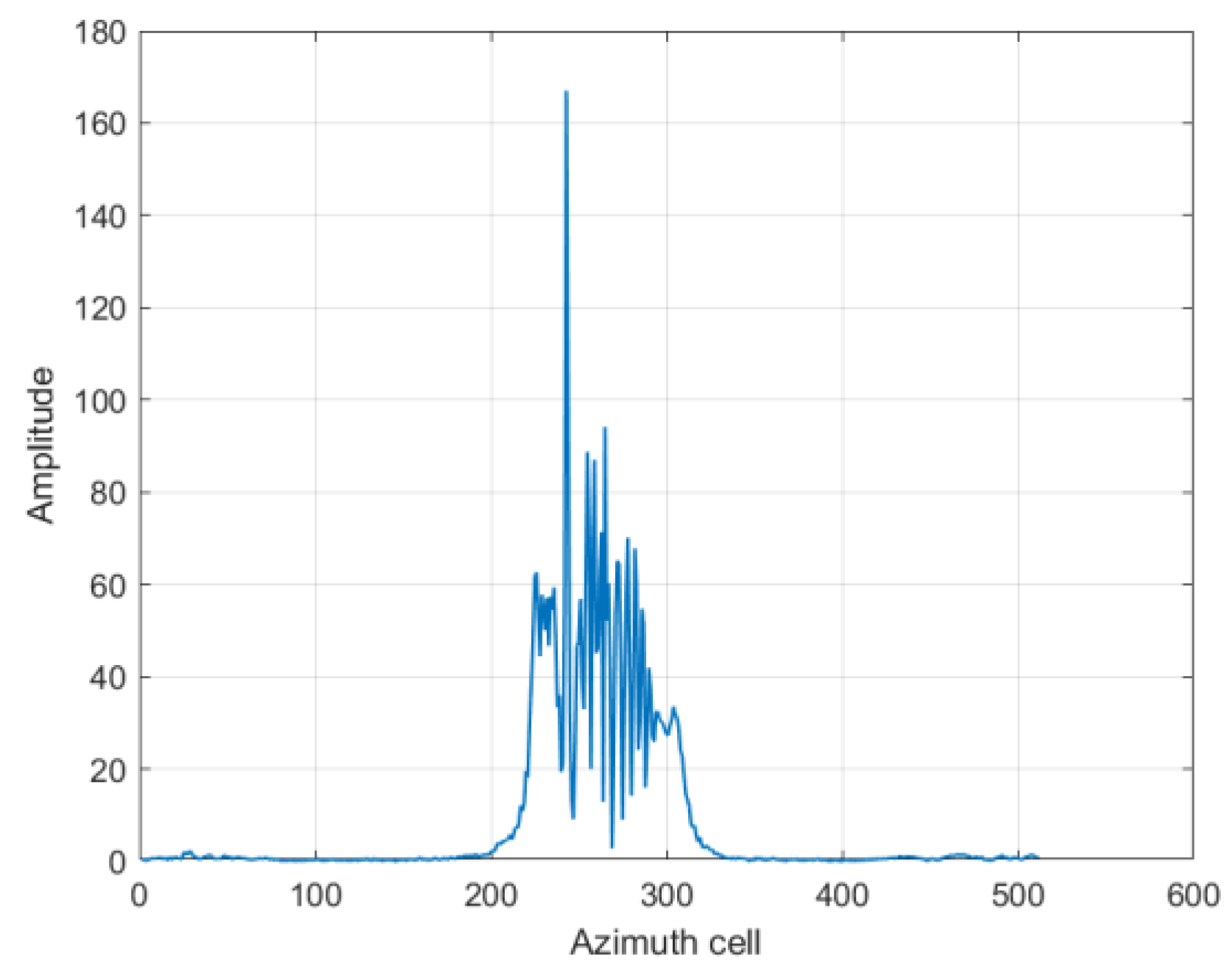
SAR usually obtains large-area images of the sea, and in order to refocus SAR moving ships, it is first necessary to obtain a subimage of the ship through ship detection algorithms. However, there are still sea surface backgrounds in the subimage, which need to be further removed in order to obtain the azimuth line set of the ship target. Only the signals in the azimuth line set need to be processed, which can effectively reduce the computational load. Ships are typically made of metal, and their backscattering coefficients are strong, so a ship’s azimuth lines can be selected based on the energy difference between the ship target and the sea surface background.

For a SAR ship image $\mathrm{g}(m,n)$ with a size of $M\times N$, the energy of the azimuth line at the n’th range cell $E(n)$ and the mean energy of all azimuth lines $\overline{E}$ can be defined as

$$E(n)={\displaystyle \sum _{m=1}^M|\mathrm{g}(m,n){|}^2}$$

(6)

$$\overline{E}=\frac{1}{N}{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N|\mathrm{g}(m,n){|}^2}}$$

(7)

where $M$ represents the number of azimuth cells, $N$ represents the number of range cells, and $\mathrm{g}(m,n)$ is a two-dimensional complex matrix representing a single-look complex (SLC) SAR image.

As the energy of a ship’s azimuth lines on the SAR image is much greater than the energy of the azimuth lines on the sea surface, the azimuth lines with energy greater than the average energy $\overline{E}$ are selected as the ship’s azimuth line set $\mathrm{S}$.

$$\mathrm{S}=[\mathrm{g}(:,n_1),\mathrm{g}(:,n_2),\cdots ,\mathrm{g}(:,n_k)]$$

(8)

3.2. Modeling Each Azimuth Line as an MC-LFM Signal

From the analysis in Section 2, it is clear that the phase error of scattering points at different positions on the 3D swing ship in SAR imaging is not the same. The Equation (5) can be further derived as

$$\begin{array}{l}{\phi }_{m-yaw}=-\frac{4\pi }{\lambda }(L_{zeff}\ast \sin (\sin (w_{z}t+{\theta }_z)+{\theta }_{z0rff})-Z_p\sin {\beta }_0)\\ =-\frac{4\pi }{\lambda }(L_{zeff}\ast (\sin (\sin (w_{z}t+{\theta }_z))\cos {\theta }_{z0rff})+\cos (\sin (w_{z}t+{\theta }_z))\sin {\theta }_{z0rff}-Z_p\sin {\beta }_0)\end{array}$$

(9)

Since the swing period of the ship is much longer than the synthetic aperture time of space-borne SAR, the above equation can be approximated using the Taylor expansion as

$$\sin (A_z\sin (w_{z}t+{\theta }_z))\approx A_z{w}_{z}t$$

(10)

$$\cos (A_z\sin (w_{z}t+{\theta }_z))=1-\frac{A_z^2}{2}{w}^2{t}^2$$

(11)

$${\phi }_{m-yaw}=-\frac{4\pi }{\lambda }{L}_{zeff}(A_z\cos {\theta }_{z0rff}{w}_{z}t-\frac{A_z^2}{2}\sin {\theta }_{z0rff}{w}^2{t}^2+\sin {\theta }_{z0rff}-Z_p\sin {\beta }_0)$$

(12)

As shown in Equation (12), the phase error of a scattering point on the 3D swing ship is an LFM signal, where $L_{zeff}$ is the distance between the scattering point and the swing axis. Therefore, the phase error of each scattering point on the 3D swing ship is the LFM signal with different modulation frequencies. After azimuth compression, each scattering point on the ship corresponds to a residual LFM signal in the SAR image due to the erroneous matched filtering. Based on the spatial-variant defocusing property of the SAR 3D swing ship image, each range cell in the SAR image can be modeled as an MC-LFM signal. Thus, the azimuth line $\mathrm{g}(:,n_j)$ in the ship’s azimuth line set $\mathrm{S}$ can be represented as

$$\mathrm{g}(:,n_j)={\displaystyle \sum _{i=1}^N{l}_i}(m)={\displaystyle \sum _{i=1}^N{e}^{j2\pi \left(\frac{1}{2}{a}_i{m}^2+b_{i}m\right)}}$$

(13)

where $l_i(m)$ is the i’th component of $\mathrm{g}(:,n_j)$, with a modulation frequency of $a_i$ and a center frequency of $b_i$.

3.3. Calculating the Optimal Rotation Order Set

FrFT decomposes a signal into the space of orthogonal basis functions consisting of LFM functions and is a generalized form of the Fourier Transform. The FrFT of a signal $x(t)$ can be expressed as

$$X_a(u)={\displaystyle {\int }_{-\infty }^{+\infty }x(t)K_a(t,u)dt}$$

(14)

where the kernel function $K_a(t,u)$ is defined as

$$K_a(t,u)=\{\begin{array}{c}\sqrt{\frac{1-j\cot a}{2\pi }}{\mathrm{e}}^{j(\frac{1}{2}{t}^2\cot a-ut\csc a+\frac{1}{2}{u}^2\cot a)},a\ne n\pi \\ \delta (t+u),a=2n\pi \\ \delta (t-u),a=(2n+1)\pi \end{array}$$

(15)

where $n$ is an integer, $a=p\pi /2$ is the rotation angle, and $p$ is the rotation order of the FrFT.

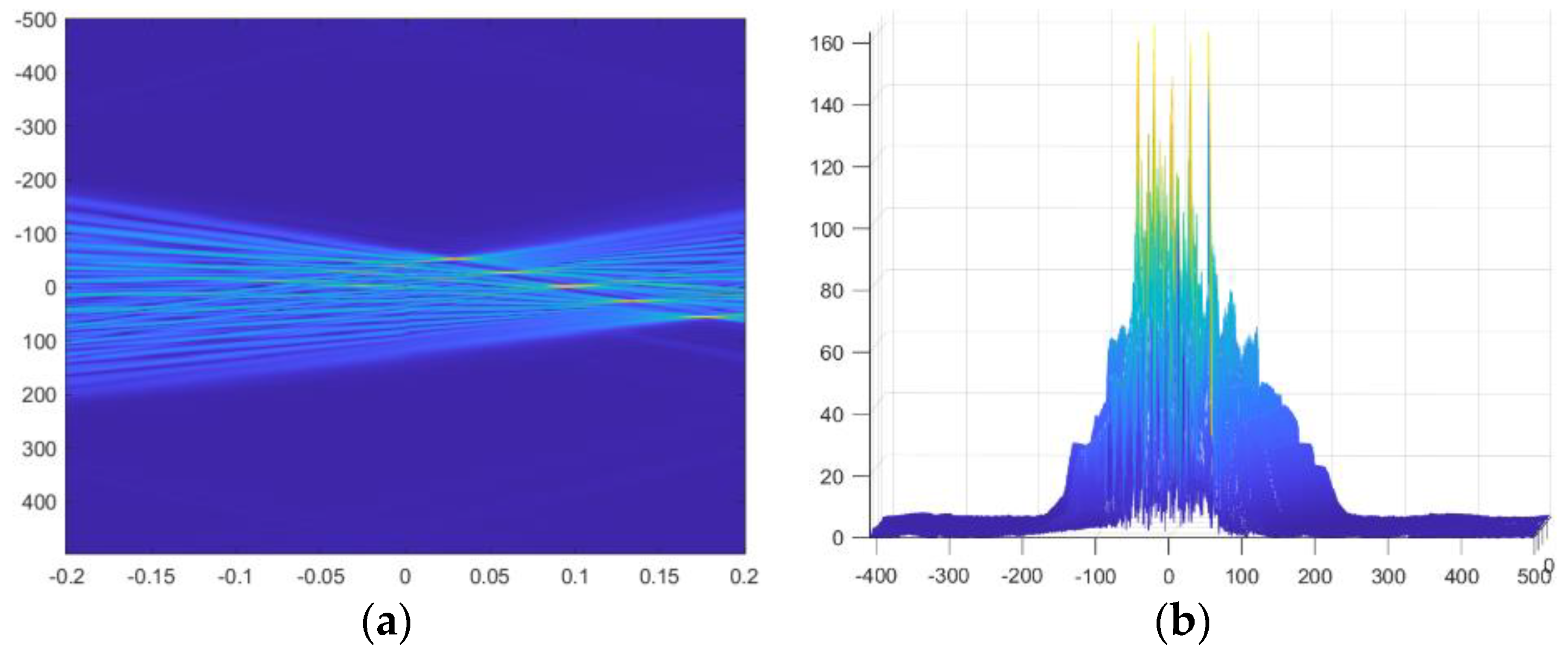
In FrFT, the modulation frequency $\cot (-a)$ and initial frequency $u\csc a$ of the LFM basis function change as the rotation angle $a$ changes from $0$ to $2\pi$. As a result, the signal is projected on different LFM basis functions as the rotation angle changes, and the magnitude of the projection value reflects the similarity of the signal to the different LFM basis functions. Therefore, by selecting the optimal rotation order in which to perform FrFT on the LFM signal, the LFM signal after FrFT will exhibit energy aggregation and become an impulse signal. In order to obtain the optimal rotation order in practical calculation, it is necessary to perform FrFT on the LFM signal at different rotation orders. The maximum value of the transformed signal energy in the two-dimensional parameter space $\left(a,u\right)$ corresponds to the optimal rotation order of the LFM signal.

$$(a_{opt},u_{opt})=\underset{a,u}{\arg \max }{|X_a(u)|}^2$$

(16)

Based on the excellent aggregation capability of FrFT on the LFM signal, Pelich performed FrFT for each azimuth line on the SAR image at its optimal rotation order to obtain a clear SAR image of the moving ship. However, the azimuth line of a 3D swing ship is an MC-LFM signal. At the optimal rotation order, only one LFM component of the azimuth line can be refocused using FrFT, but the rest of the LFM components cannot be refocused. In order to refocus the MC-LFM signal, the optimal rotation order of each LFM component must be obtained. The optimal rotational order for each component of the MC-LFM signal is combined as its optimal rotation order set in this paper. Fractional autocorrelation (FrAc) can effectively distinguish LFM signals with different modulation frequencies. Therefore, the authors of this paper use FrAc to calculate the optimal rotation order set of the MC-LFM signal.

The FrAc of the signal $x(t)$ can be expressed as

$$R_{\beta }(\rho )=e^{j\pi {\rho }^2\cos \beta \sin \beta }\int x(t)\overline{x}(t-\rho \cos \beta )e^{-j2\pi t\rho \sin \beta }dt$$

(17)

where $\overline{x}$ represents the complex conjugate, $\rho$ represents the delay factor, and $\beta$ represents the rotation angle. The FrAc of the signal can be calculated using FrFT and inverse Fourier Transform.

$$R_{\beta }(\rho )=F_{u\to r}^{-1}\left\{{\left|X^{\beta +\frac{\pi }{2}}(u)\right|}^2\right\}$$

(18)

where $F^{-1}$ represents the inverse Fourier Transform and $X^{\beta +\frac{\pi }{2}}(u)$ represents the signal $x(t)$ after FrFT at the rotation angle $\beta +0.5\pi$.

The FrAc for one azimuth line $\mathrm{g}(:,n_j)$ of the SAR 3D swing ship image $\mathrm{g}(m,n)$ can be expressed as

$$R_{\beta }(\rho )=e^{j\pi {\rho }^2\cos \beta \sin \beta }{\displaystyle \sum _{i,i^{\prime }=1}^N{F}_{t\to \rho \sin \beta }}\left\{l_i(t)l_{i^{\prime }}^{*}(m-\rho \cos \beta )\right\}$$

(19)

For $i=i^{\prime }$, the auto-term of $R_{\beta }(\rho )$ can be expressed as

$$R_{\beta }{(\rho )}_{auto}={\displaystyle \sum _{i=1}^N{e}^{j2\pi b_i\rho \cos \beta }\delta (\rho \sin \beta -a_i}\rho \cos \beta )$$

(20)

For $i\ne i^{\prime }$, the cross-term of $R_{\beta }(\rho )$ can be expressed as

$$\begin{array}{l}{R}_{\beta }{(\rho )}_{\mathrm{cross}}={\displaystyle \sum _{\begin{array}{c}i,i^{\prime }=1,i<i^{\prime }\\ a_i=a_{i^{\prime }}\end{array}}{e}^{j\pi \left(b_i+b_{i^{\prime }}\right)\rho \cos \beta }}\times \left[\delta \left(\rho \sin \beta -a_i\rho \cos \beta -b_{i{i}^{\prime }}\right)+\delta \left(\rho \sin \beta -a_i\rho \cos \beta +b_{i{i}^{\prime }}\right)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \sum _{\begin{array}{c}i,i^{\prime }=1:1i<i^{\prime }\\ a_i\ne a_{i^{\prime }}\end{array}}^N\frac{2}{\sqrt{a_{i{i}^{\prime }}}}}{e}^{j\frac{2\pi \rho }{a_{i{i}^{\prime }}}\left[b_i\left(\sin \beta -a_{i^{\prime }}\cos \beta \right)-b_{i^{\prime }}\left(\sin \beta -a_i\cos \beta \right)\right]}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \times \cos \left(\frac{\pi }{a_{i{i}^{\prime }}}\left[{\rho }^2\left(\sin \beta -a_i\cos \beta \right)\left(\sin \beta -a_{i^{\prime }}\cos \beta \right)+b_{i{i}^{\prime }}^2-\frac{a_{i{i}^{\prime }}}{4}\right]\right)\end{array}$$

(21)

From the expressions of the auto-term and cross-term, it can be seen that the energy of the auto-term is concentrated on the straight lines passing through the origin, where the slopes of these lines represent the different modulation frequencies of the LFM component $l_i(m)$. On the other hand, most of the cross-term energy is concentrated on straight lines that do not pass through the origin, and cross-term energy with different modulation frequencies can be ignored, compared with the auto-term. The energy of the signal after FrAc is defined as

$$E_{\rho }(\beta )={\displaystyle {\int }_{-\infty }^{+\infty }{\left|R(\beta )(\rho )\right|}^2}d\rho$$

(22)

When the rotation order $\beta$ matches the modulation frequency of one LFM component, the energy of the signal after FrAc has a peak, and the optimal rotation order corresponding to this component in FrFT is $\alpha =\beta +0.5\pi$. Therefore, the energy distribution of the signal after FrAc at different rotation angles can be used to calculate the parameters of each component for the MC-LFM signal.

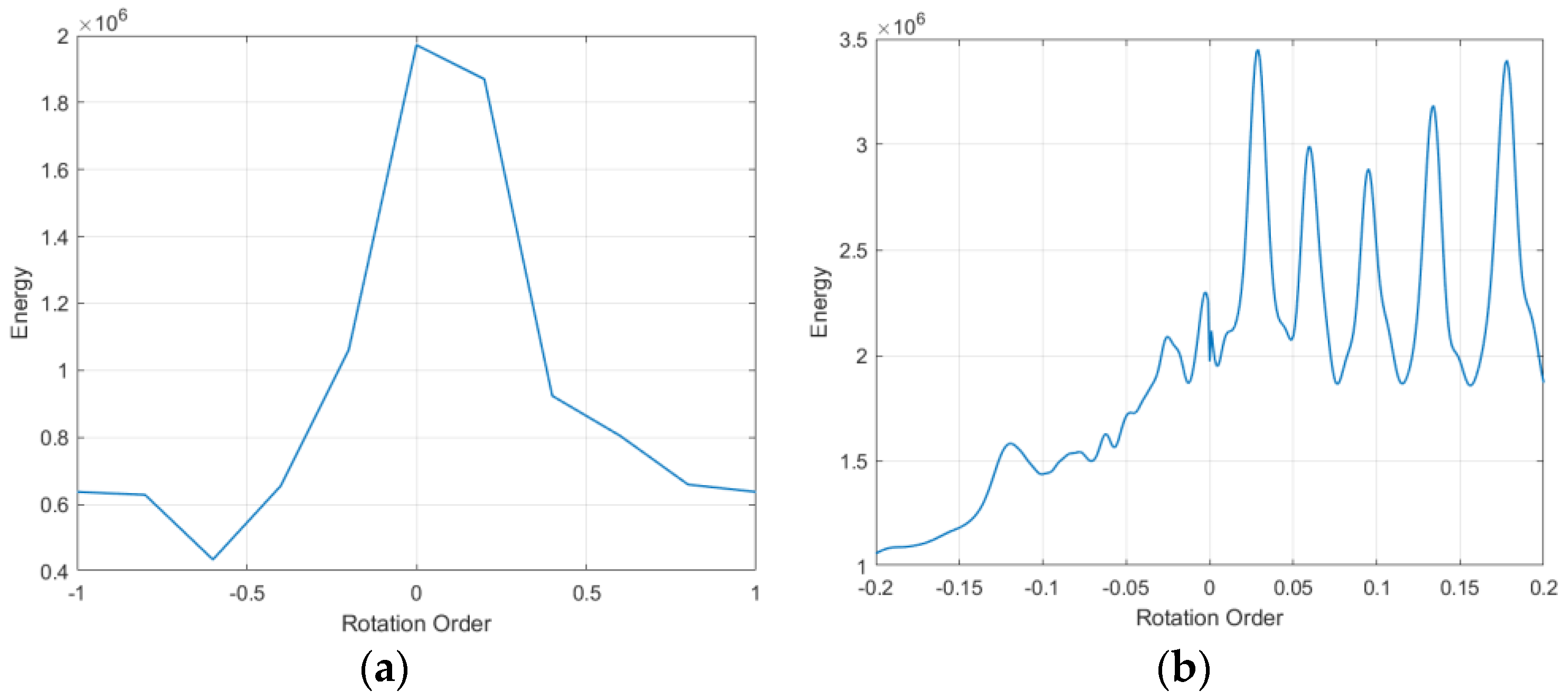
The scattering points on the 3D swing ship have different velocities, but the velocities are relatively close in magnitude, which places the optimal rotation order of each LFM component within a certain range. Therefore, the optimal rotation order set is calculated using a two-step method and Algorithm 1 illustrates the specific implementation. First, the energy $E_{\rho }(\beta )$ of the MC-LFM signal after FrAc with a greater step size $\Delta$ in the interval ${\beta }_1=linspace(-\frac{\pi }{2},\frac{\pi }{2},\Delta )$ is calculated, and the rotation order ${\beta }_{coarse}$ in which the position of the maximum value of $E_{\rho }(\beta )$ is obtained. Since there are multiple optimal rotational orders of the MC-LFM signal near the rotation order ${\beta }_{coarse}$, the energy $E_{\rho }(\beta )$ of the MC-LFM signal after FrAc is further calculated using a smaller step ${\Delta }^{\prime }$ in the subinterval ${\beta }_2=linspace({\beta }_{coarse}-\Delta ,{\beta }_{coarse}+\Delta ,{\Delta }^{\prime })$. As a result, the peaks of the energy $E_{\rho }(\beta )$ correspond to the precise optimal rotation order of each LFM component. Finally, the corresponding rotation orders are sorted according to the magnitude of the peak to obtain the optimal rotation order set ${\alpha }_{fine}$ of the MC-LFM signal.

$${\beta }_{coarse}=\underset{\beta }{\arg \max }(E_{\rho }(\beta ))$$

(23)

$${\alpha }_{fine}=[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_q]$$

(24)

Algorithm 1 The algorithm of calculating the optimal rotation order set

Input: A ship’s azimuth line $\mathrm{g}(:,n_j)$

Output: The optimal rotation order set ${\alpha }_{fine}=[{\alpha }_1,{\alpha }_2,\cdots {\alpha }_q]$

${\beta }_1=linspace(-0.5\pi ,0.5\pi ,\Delta )$

for $\beta$ in ${\beta }_1$

$E_{\rho }(\beta )={\displaystyle {\int }_{-\infty }^{+\infty }abs(FrAc(\mathrm{g}(:,n_j),\beta )}{)}^{2}d\rho$

end for

${\beta }_{coarse}=\underset{\beta }{\arg \max }(E_{\rho }(\beta ))$

${\beta }_2=linspace({\beta }_{coarse}-\Delta ,{\beta }_{coarse}+\Delta ,{\Delta }^{\prime })$

for $\beta$ in ${\beta }_2$

$E_{\rho }(\beta )={\displaystyle {\int }_{-\infty }^{+\infty }abs(FrAc(\mathrm{g}(:,n_j),\beta )}{)}^{2}d\rho$

end for

$[{\beta }_1,{\beta }_2,\cdots {\beta }_q]=Sort(Findpeaks(E_p(\beta )))$

${\alpha }_{fine}=[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_q]=[{\beta }_1+0.5\pi ,{\beta }_2+0.5\pi ,\cdots ,{\beta }_q+0.5\pi ]$

3.4. Refocusing Each Azimuth Line

The components of the MC-LFM signal are difficult to distinguish in the time domain, but after performing FrFT at each component’s optimal rotation order, each component will become an impulse signal. Therefore, after obtaining the optimal rotation order set for the azimuth line, the azimuth line can be refocused using FrFT and Algorithm 2 illustrates the specific implementation.

First, FrFT is performed at the optimal rotation order ${\alpha }_1$ on the azimuth line $\mathrm{g}(:,n_j)$, and the LFM component corresponding to this optimal rotation order ${\alpha }_1$ will be refocused. All peaks of the signal $\mathrm{g}{(:,n_j)}_{FrFT}$ are detected, and if the peak magnitude of the signal $\mathrm{g}{(:,n_j)}_{FrFT}$ is close to its maximum value, the peak is the refocused signal of the corresponding LFM component. In the fractional-order domain, each refocused signal is filtered out with a narrowband filter and accumulated to obtain the refocused signal $\mathrm{g}{(:,n_j)}_{refocus\_1}$ of the corresponding LFM component at optimal rotational order ${\alpha }_1$. The residual signal $\mathrm{g}{(:,n_j)}_{left}$ is further transformed to the time domain using inverse FrFT.

$$\mathrm{g}{(:,n_j)}_{FrFT}=FrFT(\mathrm{g}(:,n_j),{\alpha }_i)$$

(25)

$$[p_1,p_2,\cdots p_K]=FindPeak(abs(\mathrm{g}{(:,n_j)}_{FrFT})>0.7\ast \max (abs(\mathrm{g}{(:,n_j)}_{FrFT})))$$

(26)

$$Win(p_k)=\{\begin{array}{c}1,\hspace{1em}\hspace{1em}\hspace{1em}{p}_k-l/2<p_k<p_k+l/2\hfill \\ 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \end{array}$$

(27)

$$\mathrm{g}{(:,n_j)}_{refocus\_i}={\displaystyle \sum _{k=1}^K\mathrm{g}{(:,n_j)}_{FrFT}\ast Win(p_k)}$$

(28)

$$\mathrm{g}{(:,n_j)}_{left}=FrFT(\mathrm{g}{(:,n_j)}_{FrFT}-\mathrm{g}{(:,n_j)}_{refocus\_i},-{\alpha }_i)$$

(29)

Thereafter, FrFT is performed on the residual signal $\mathrm{g}{(:,n_j)}_{left}$ at the second optimal rotation order ${\alpha }_2$. If the maximum value of the refocused signal after the second transformation is much less than that of the first transformation, the loop is terminated. Otherwise, the refocused signal $\mathrm{g}{(:,n_j)}_{refocus\_2}$ is continually filtered. By repeating this operation, each refocused signal obtained is accumulated to obtain the entire refocused signal $\mathrm{g}{(:,n_j)}_{refocus}$ from the MC-LFM signal.

$$\mathrm{g}{(:,n_j)}_{refocus}=\mathrm{g}{(:,n_j)}_{refocus\_1}+\mathrm{g}{(:,n_j)}_{refocus\_2}+\cdots +\mathrm{g}{(:,n_j)}_{i-1}$$

(30)

If the energy of the refocused signal $\mathrm{g}{(:,n_j)}_{refocus}$ is less than a certain proportion of the energy of the original signal $\mathrm{g}(:,n_j)$, this indicates that there are still LFM components outside of the current subinterval. In this case, the subinterval is further expanded, the optimal rotation order set is recalculated, and the refocusing process is repeated as described above until the energy of the refocused signal meets the predetermined threshold. Finally, by replacing the corresponding original azimuth lines in the SAR image with the refocused azimuth lines, a clear SAR image of the 3D swing ship can be obtained.

Algorithm 2 The specific implementation of refocusing one azimuth line

Input: Optimal rotation order set ${\alpha }_{fine}=[{\alpha }_1,{\alpha }_2,\cdots {\alpha }_q]$ and azimuth line $\mathrm{g}(:,n_j)$

Output: Refocused azimuth line $\mathrm{g}{(:,n_j)}_{refocuse}$

for $i=1,2,\cdots ,q$

$\mathrm{g}{(:,n_j)}_{FrFT}=FrFT(\mathrm{g}(:,n_j),{\alpha }_i)$

$[p_1,p_2,\cdots p_K]=FindPeak(abs(\mathrm{g}{(:,n_j)}_{FrFT})>0.7\ast \max (abs(\mathrm{g}{(:,n_j)}_{FrFT})))$

$\mathrm{g}{(:,n_j)}_{refocus\_i}={\displaystyle \sum _{k=1}^K\mathrm{g}{(:,n_j)}_{FrFT}\ast Win(p_k)}$

if  $\max (abs(\mathrm{g}{(:,n_j)}_{refocus\_i}))<0.7\ast \max (abs(\mathrm{g}{(:,n_j)}_{refocus\_1}))$

break

else

$\mathrm{g}{(:,n_j)}_{left}=FrFT(\mathrm{g}{(:,n_j)}_{FrFT}-\mathrm{g}{(:,n_j)}_{refocus\_i},-{\alpha }_i)$

$\mathrm{g}(:,n_j)=\mathrm{g}{(:,n_j)}_{left}$

end if

end for

$\mathrm{g}{(:,n_j)}_{refocus}=\mathrm{g}{(:,n_j)}_{refocus\_1}+\mathrm{g}{(:,n_j)}_{refocus\_2}+\cdots +\mathrm{g}{(:,n_j)}_{i-1}$

3.5. Numerical Analysis of Computional Burden

Suppose the size of a SAR 3D swing ship image is $M\times N$, where $M$ is the number of range cells and $N$ is the number of azimuth cells. The time complexity, for both the inverse FFT and the Discrete FrFT, for a signal of length $N$ is $O(N{\log }_{2}N)$. Therefore, the time complexity required to calculate the energy of an azimuth line after FrAc at each rotation order is $2O(N{\log }_{2}N)$. If the coarse step is $a_1$ and the fine step is $a_2$, then the time complexity required to compute the optimal rotation order set for the azimuth line of the i’th range cell is $C_1$.

$$C_1=2\ast (\frac{2}{a_1}+\frac{2a_1}{a_2})O(N{\log }_{2}N)$$

(31)

If the azimuth line consists of $K_i$ LFM signals with different tuning frequencies, the time complexity required to refocus the azimuth line is $C_2$.

$$C_2=C_1+K_{i}O(N{\log }_{2}N)=(K_i+4\frac{a_2+a_1^2}{a_1{a}_2})O(N{\log }_{2}N)$$

(32)

Thus, the time complexity $C_3$ required to refocus the entire SAR image can be expressed as

$$C_3=M\ast C_2=({\displaystyle \sum _{i=1}^M{K}_i}+4M\frac{a_2+a_1^2}{a_1{a}_2})O(N{\log }_{2}N)$$

(33)

If the optimal rotation order set of the azimuth line is calculated using the method in [56], the required time complexity $C_4$ can be expressed as

$$C_4=K_i\ast (\frac{2}{a_1}+\frac{2a_1}{a_2})O(N{\log }_{2}N)$$

(34)

For a 3D swing ship, there are multiple scattering points at each range cell, and $K_i$ is much greater than 2. Therefore, the proposed algorithm can reduce the time complexity.

4. Experiments

4.1. Refocusing the MC-LFM Signal of One Azimuth Line

For SAR 3D swing ship images, there are several different LFM signals in each range cell. Therefore, in order to refocus a SAR 3D swing ship image, it is first necessary to refocus the MC-LFM signal of each range cell. The authors of this paper conduct a simulation experiment in order to validate the refocusing performance of the algorithm for MC-LFM signals.

Table 1. The SAR system parameters of the simulation experiment.

Parameter	Value
Carrier Frequency	3 GHZ
Pulse Repetition Frequency	188 HZ
Band Width	150 MHZ
Platform Height	3000 m
Antenna Length	2 m
Platform Velocity	150 m/s
Pulse Width	1.5 μs

shows the simulation parameters for the radar system, and

Table 2. The azimuth velocity value of each scattering point.

Scattering Point	P1	P2	P3	P4	P5
Azimuth Velocity	5 m/s	10 m/s	15 m/s	20 m/s	25 m/s

shows the azimuth velocity value of each scattering point in the same range cell.

The SAR images of these five scattering points, as they move individually, are shown in Figure 4. It can be observed that, due to the various azimuth velocities, each scattering point exhibits a different degree of defocusing. Specifically, the greater the velocity of the scattering point, the more severe the defocus. The SAR image of these five scattering points when stationary is shown in Figure 5a, and the SAR image of these five scattering points as they move together is shown in Figure 5b. The azimuthal profile of the range cell where these five scattering points are located is shown in Figure 6. It can be seen that the signals of the five scattering points are gathered together, so it is difficult to distinguish the signal of each scattering point. As a result, the problem of azimuth-variant defocusing is difficult to overcome using the split-block method.

The two-dimensional distribution of the time–frequency spectrum obtained using FrFT on the azimuth line where these five scattering points are located is shown in Figure 7a, and its three-dimensional distribution is shown in Figure 7b. It can be observed that there are five energy concentration points in this figure, and the scattering points, each with a different velocity, are well distinguished from one another after FrFT. Moreover, the defocused signal of each scattering point becomes the impulse signal at its respective optimal rotation order, which is equivalent to being re-matched. The correlation between the signal energy after FrAc and the rotation order when a coarse step is used is illustrated in Figure 8a. Similarly, this relationship is shown in Figure 8b when a fine step is used. Five distinct peaks can be seen in Figure 8b, and the positions of these peaks correspond to the optimal rotation order set. The result of performing FrFT at one of the optimal rotation orders on the azimuth line is shown in Figure 9, where a focused impulse signal appears. Thus, by performing FrFT on the MC-LFM signal in its optimal rotational order set, and then accumulating the refocused signal of each LFM component, the original azimuth line can be refocused. This is the main idea of the algorithm proposed in this paper, and the specific details were explained in the previous section. The results of the defocused SAR image in Figure 5b after processing with PGA, FMEPC, and Pelich’s method, and the proposed algorithm are shown in Figure 10. It can be seen that only one scattering point is refocused when using PGA, FMEPC, and Pelich’s method, while the proposed algorithm can refocus all five scattering points. This demonstrates the effectiveness of the proposed algorithm in refocusing the MC-LFM signal. For a SAR image of a 3D swing ship, a clear image can be obtained by refocusing each of its azimuth lines. The following experiments show the performance of the proposed algorithm in refocusing SAR 3D swing ship images.

4.2. Refocusing Simulated SAR Images of 3D Swing Ship

In order to simulate the SAR image of a 3D swing ship, the 3D swing parameters of the ship in this experiment are shown in

Table 3. The 3D swing parameters of a simulated ship.

	Roll	Pitch	Yaw
Double Amplitude (deg)	17.2	3.4	38
Average Period (s)	12.2	6.7	14.2

, with an initial phase of $0.5\pi$. Simulated SAR images of the rolling, pitching and yawing ship, as well as the corresponding SAR images when the ship is stationary, are shown in Figure 11. It can be seen that, compared with those of a stationary ship, SAR 3D swing ship images are severely defocused, making it difficult to distinguish its scattering points. Although each scattering point on the ship has the same amplitude and frequency of swing, the velocity of each scattering point is also related to its distance from the swing axis, due to the particular nature of the swing motion. As a result, the velocity of each scattering point on the ship is no longer the same, resulting in spatial-variant defocusing. As can be seen from Figure 11, the further the point on the ship is from the swing axis, the more severe the defocus appears, and the final SAR imaging results form an ‘X’ shape.

The results of refocusing simulated SAR images using the PGA, FMEPC, and Pelich’s methods, and the algorithm proposed in this paper are shown in Figure 12, Figure 13 and Figure 14. It can be seen that the PGA and FMEPC methods cannot refocus the SAR image of a 3D swing ship. This is because the phase error of each part of the 3D swing ship is different, while the PGA and FMEPC methods use a unified phase error to compensate. Pelich’s method can overcome range-variant defocusing because it processes each azimuth line of the ship separately. When the ship pitches, the phase error of each scattering point on the ship is related to its proximity to the transverse axis, exhibiting only range-variant defocusing. Thus, Pelich’s method is able to refocus the SAR image of a pitching ship. However, when the ship experiences yaw or roll, both azimuth-variant and range-variant defocusing exist. In such situations, Pelich’s method is only capable of refocusing certain scattering points, while others remain defocused.The proposed method in this paper models each azimuth line as an MC-LFM signal and processes each azimuth line of the ship separately. As a result, it can overcome both azimuth-variant and range-variant defocusing. The severely defocused SAR images of the 3D swing ship are successfully refocused to 57 scattering points, as shown in Figure 12, Figure 13 and Figure 14. The experimental results from simulated images show that the proposed method effectively refocuses SAR 3D swing ship imagery with high accuracy. It is worth noting that the refocused SAR ship images obtained using the proposed method still exhibit some deformation compared with the corresponding stationary ship. This is due to the fact that, in SAR imaging, velocity along the range direction causes targets to shift additionally in the azimuth direction. When the ship undergoes 3D swing, different velocities along the range direction of each scattering point result in different azimuth shifts, leading to distortions in the final SAR imaging of the ship.

Table 4. The image entropies of different algorithms on simulated SAR swing ship images.

Simulated Image	Rolling Ship	Pitching Ship	Yawing Ship	Average
Original Image	7.05	6.57	7.67	7.10
PGA	7.03	6.63	7.45	7.04
FMEPC	6.90	6.49	7.32	6.90
Pelich’s Method	6.40	6.04	6.62	6.35
Proposed Method	5.50	5.95	5.57	5.67

shows the image entropy of simulated 3D swing ships after refocusing with different algorithms. From the average entropies presented in the table, it can be seen that the average entropy of the proposed algorithm is much lower than those of other algorithms.

4.3. Refocusing Gaofen-3 SAR Images of a 3D Swing Ship

Gaofen-3 is a Chinese C-band polarimetric synthetic aperture radar satellite launched in August 2016. It includes multiple imaging modes, with a resolution of one meter in sliding spotlight mode. However, severe defocusing occurs when imaging moving ships in this mode. In order to further validate the performance of the proposed algorithm, the authors of this paper also conduct experiments on seven defocused SAR swing ship images taken using Gaofen-3 in sliding spotlight mode. Each SAR image is processed separately using the PGA, FMEPC, and Pelich’s methods, and the proposed algorithm.

Table 5. The system parameters of Gaofen-3, SL mode.

Parameter	Value
Carrier frequency (GHZ)	5.4
Platform velocity (m/s)	7567
Band width(MHZ)	240
Pulse Width (μs)	45
Pulse repetition frequency (Hz)	3738

shows the system parameters of Gaofen-3 in sliding spotlight (SL) mode. The experimental results are shown in Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. It can be seen that each ship has a different degree of defocus at different parts, exhibiting severe spatial-variant defocusing and making it impossible to determine the true shape of the ship. After being processed using the PGA and FMEPC methods, some parts of the defocused ships are refocused, while the rest are still defocused. When using Pelich’s method, the range-variant defocusing is alleviated, but there are still many defocused scattering points. After applying the algorithm proposed in this paper, it can be observed that all seven ships show clear structural characteristics, making it easier to recognize them.

In order to quantitatively evaluate focusing quality with different algorithms, the authors of this paper use image entropy as a metric. Image entropy can be used to characterize the aggregation of strong scattering points in an image. The greater the image entropy, the more severe the defocusing of ships, while a lower image entropy indicates a better focusing quality of ships. The definition of image entropy is as follows

$$E(I)={\displaystyle \sum _{m=0}^{M-1}{\displaystyle \sum _{n=0}^{N-1}\frac{|I(m,n){|}^2}{S}}}\ln \frac{S}{|I(m,n){|}^2}$$

(35)

where $I(m,n)$ represents the complex scattering intensity of a SAR complex image, $m$ represents the azimuth position, $n$ represents the range position, and $S$ represents the total energy of the image.

$$S={\displaystyle \sum _{m=0}^{M-1}{\displaystyle \sum _{n=0}^{N-1}|}}I(m,n){|}^2$$

(36)

Table 6. The image entropy of different algorithms.

Real SAR Image	Ship1	Ship2	Ship3	Ship4	Ship5	Ship6	Ship7	Average
Original Image	7.94	6.94	9.22	7.19	8.03	7.27	7.98	7.80
PGA	7.24	6.35	8.75	6.97	7.40	7.24	7.36	7.33
FMEPC	6.51	5.82	8.30	6.52	6.95	7.22	7.23	6.94
Pelich’s Method	6.53	6.22	8.00	5.99	6.80	7.14	6.81	6.78
Proposed Method	5.71	5.42	7.12	5.16	5.80	6.40	6.0	5.94

shows the original image entropy of the seven SAR ship images and their image entropies after being processed using different algorithms. The average image entropy of the proposed algorithm is 5.94, which is an order of magnitude lower than the average image entropies obtained using other algorithms, indicating its superior focusing quality over other methods.

5. Conclusions

This research proposed a new method for refocusing swing ships in SAR imagery. We first derived the spatial-variant defocusing property of SAR swing ship images from SAR imaging principles. Based on the spatial-variant defocusing property, each azimuth line of a SAR swing ship image was modeled as an MC-LFM signal. The optimal rotation order for each MC-LFM signal was quickly calculated using FrAC, and then FrFT was performed on each LFM component individually in order to obtain the refocused azimuth lines. Finally, the refocused signal was used to replace the original azimuth lines of the SAR image. Experiments on both simulated and Gaofen-3 SAR images demonstrated that the proposed algorithm can effectively refocus the SAR images of 3D swing ships. It should be noted that, as the synthetic aperture time becomes longer, scattering points on the ship will become a nonlinear frequency modulation signal in the SAR image. Therefore, refocusing SAR images of swing ships with long synthetic aperture times needs to be studied in the future. In addition, the algorithm proposed in this paper can further improve the processing speed with parallel processing.