Robust LiDAR-Based Vehicle Detection for On-Road Autonomous Driving
Abstract
1. Introduction
1.1. Background
1.2. Related Research
1.3. Main Work
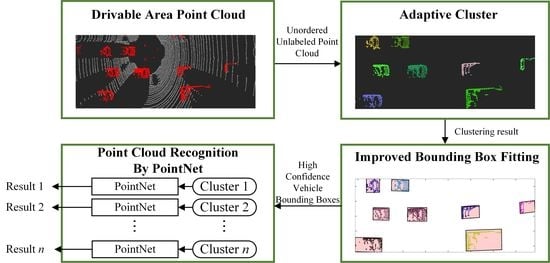
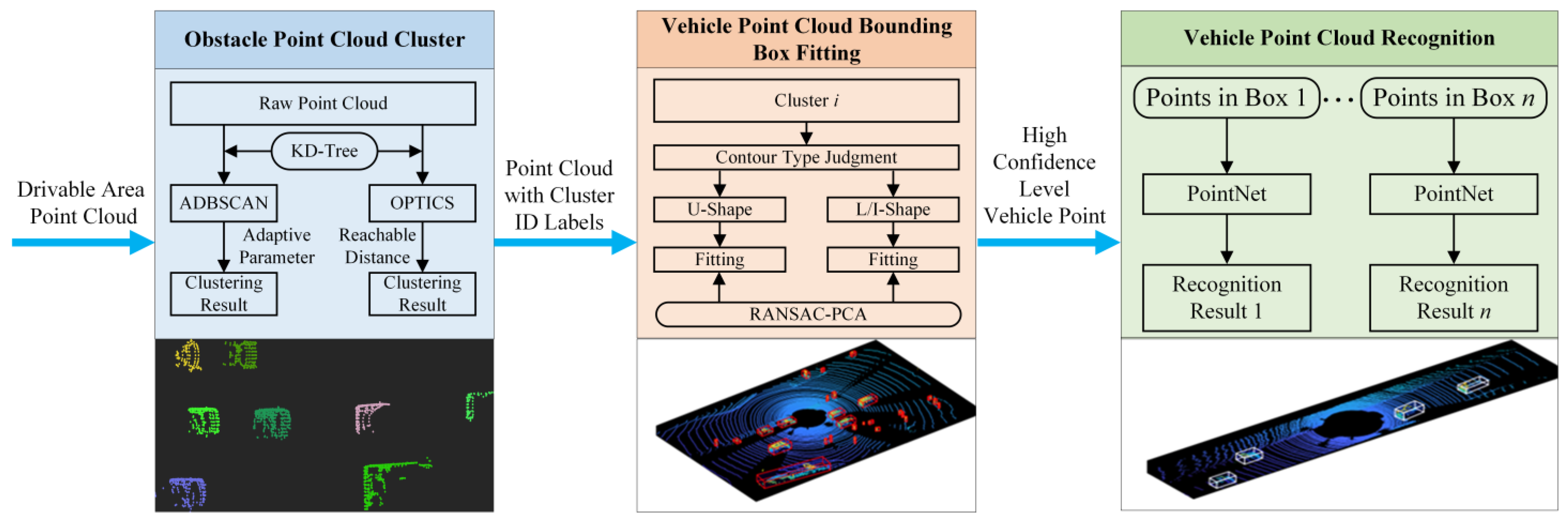
2. Point Cloud Clustering and Vehicle Bounding Box Fitting Algorithm
2.1. ADBSCAN Algorithm for Point Cloud Clustering
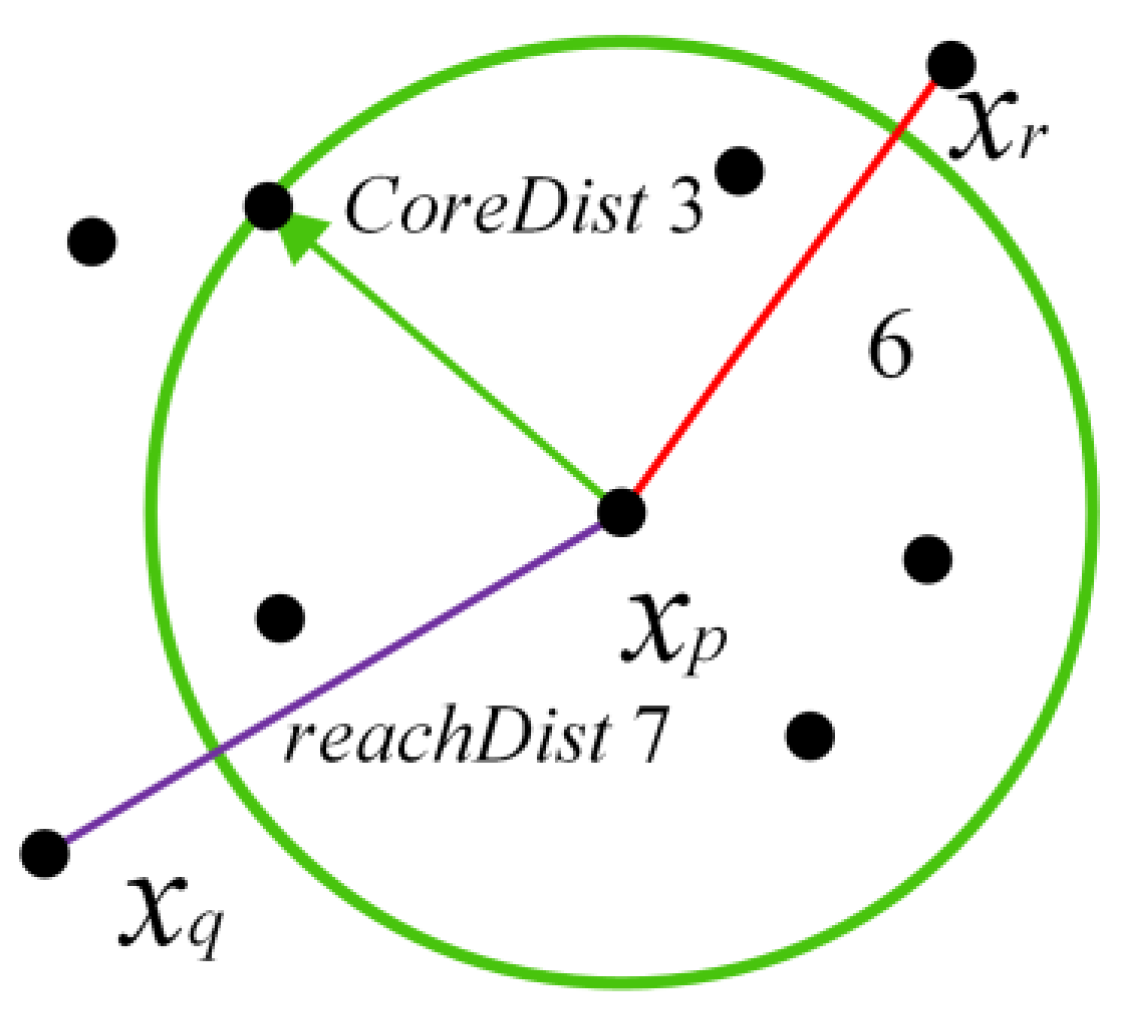
2.2. Ordering Points to Identify the Clustering Structure
| Algorithm 1 OPTICS clustering algorithm |
| Input: X, eps, minPts Output: orderList 01: corepoints = getcoreDist (X, eps, minPts)//Calculate reachable distance 02: coreDist = computecoreDist (X, eps, minPts)//Compute Kernel Distance 03: for unprocessed point p in corepoints 04: Np = getneighbors (p, eps) 05: mark p as processed and output p to the ordered list 06: if Np > minPts 07: Seeds = empty priority queue 08: update (Np, p, Seeds, coreDist)//update sequence 09: for q in Seeds 10: Nq = getneighbors (q, eps)//Number of points to calculate, defaults to all points 11: if Nq > minPts 12: update (Nq, q, Seeds, coreDist)//update sequence 13: return orderList |
2.3. Improved L-Shape Vehicle Bounding Box Fitting
3. Vehicle Point Cloud Recognition with PointNet
3.1. PointNet Point Cloud Classification Network
3.2. PointNet Training Process
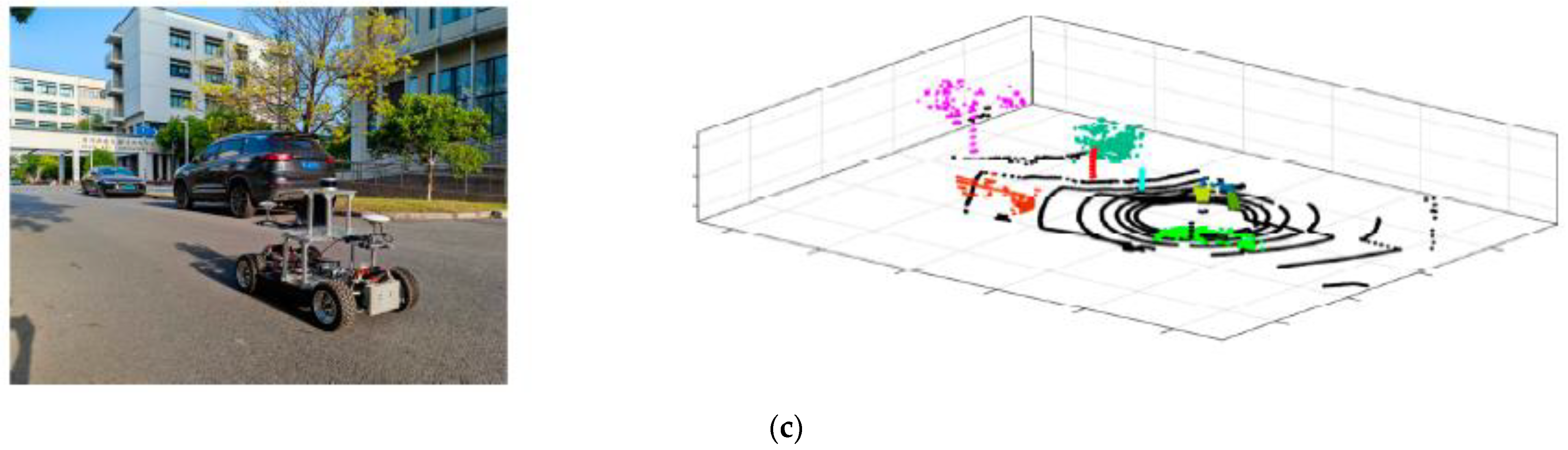
4. Experiment Results and Analysis
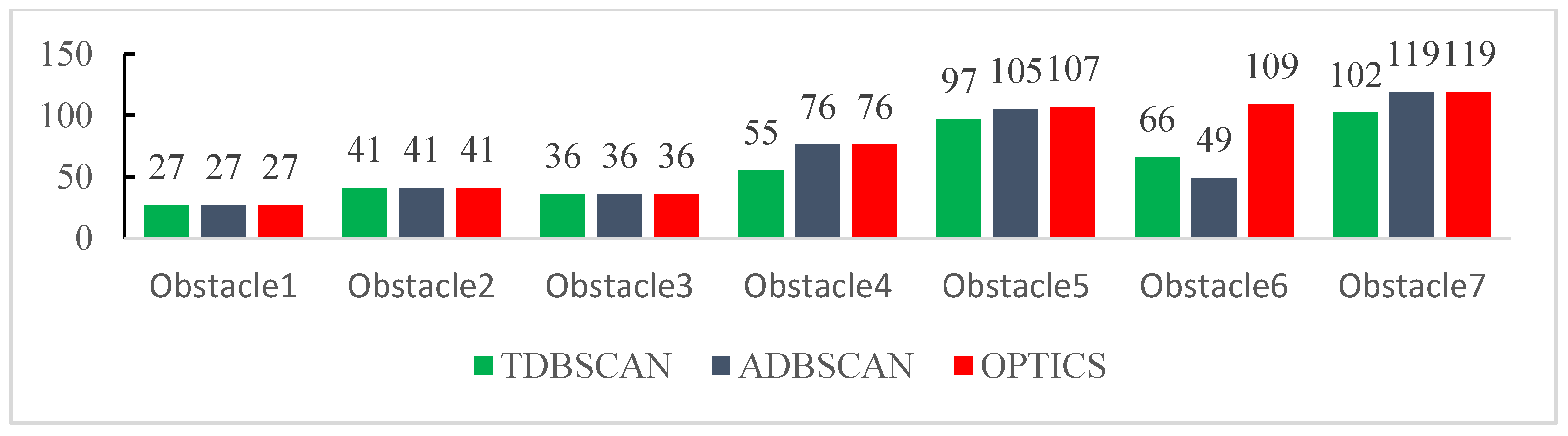
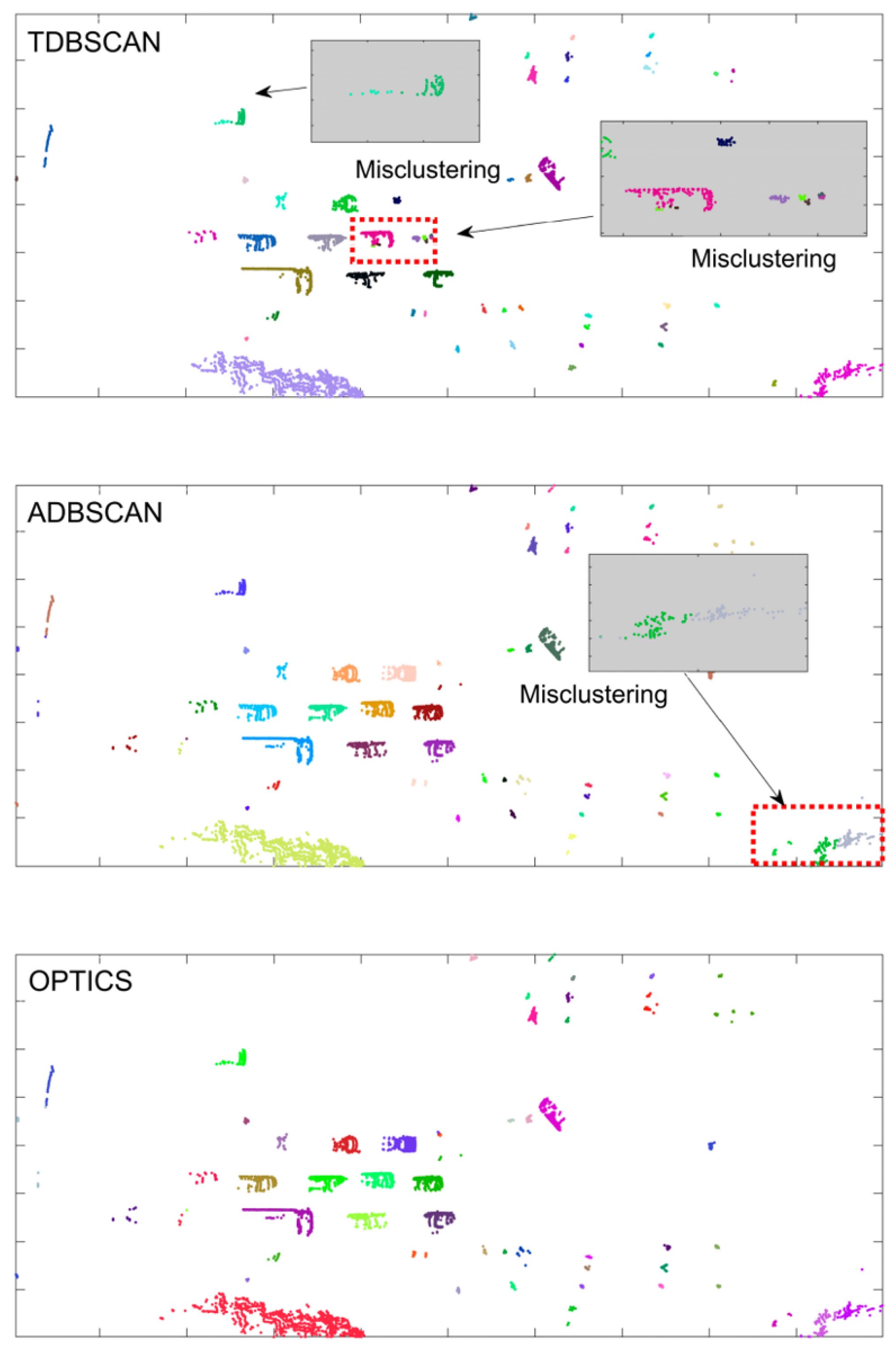
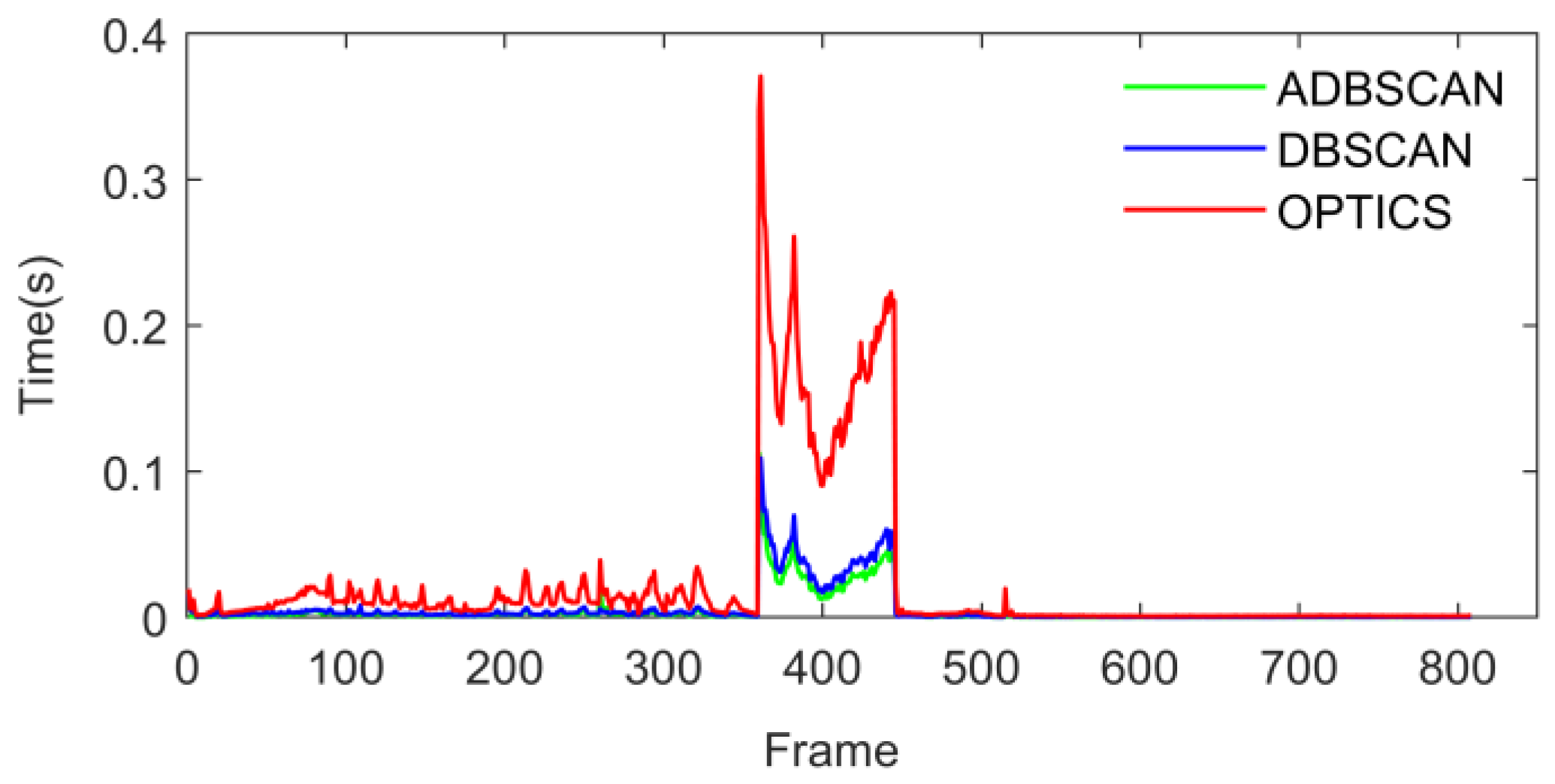
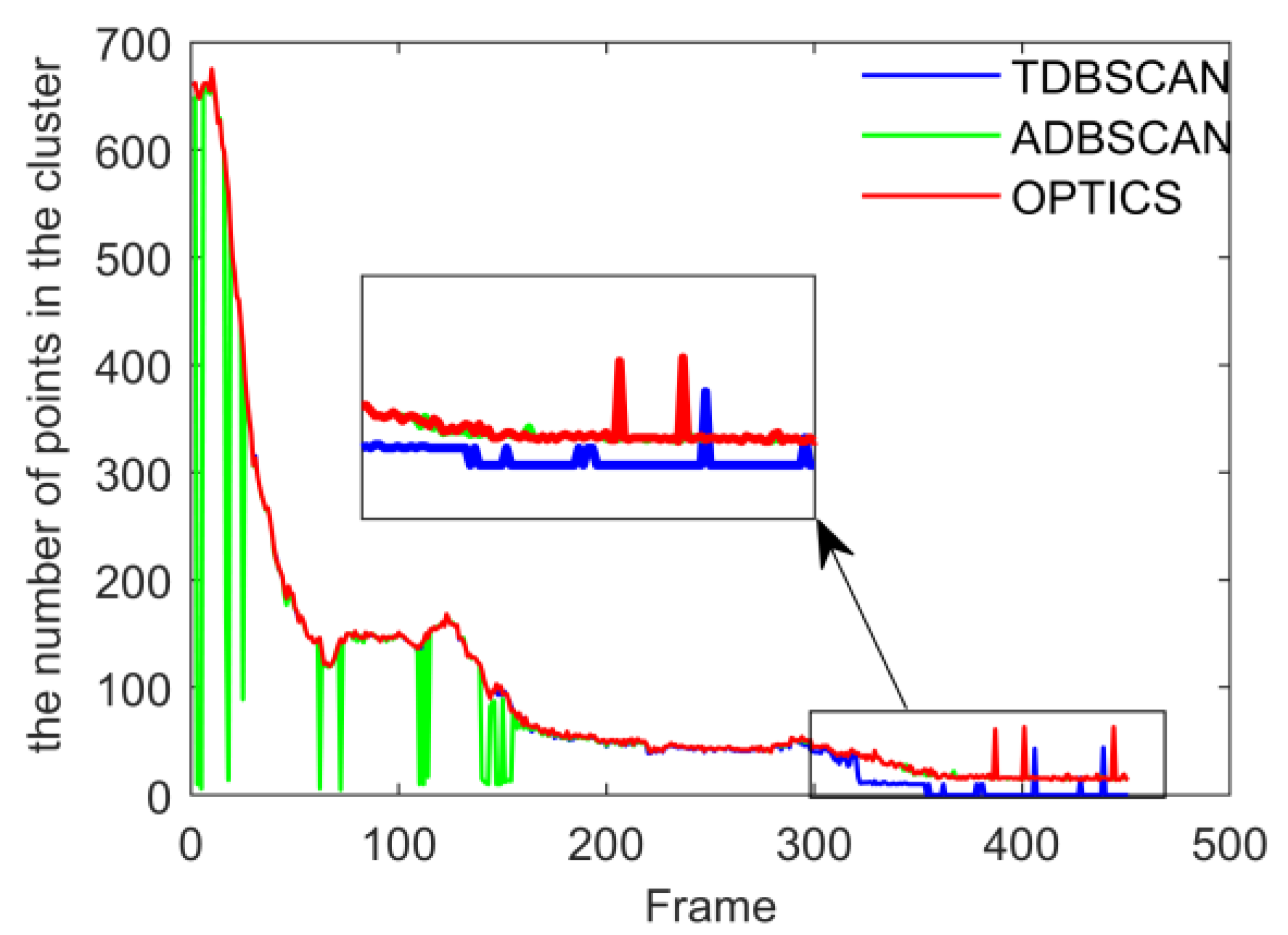
4.1. Validation of Clustering Algorithms
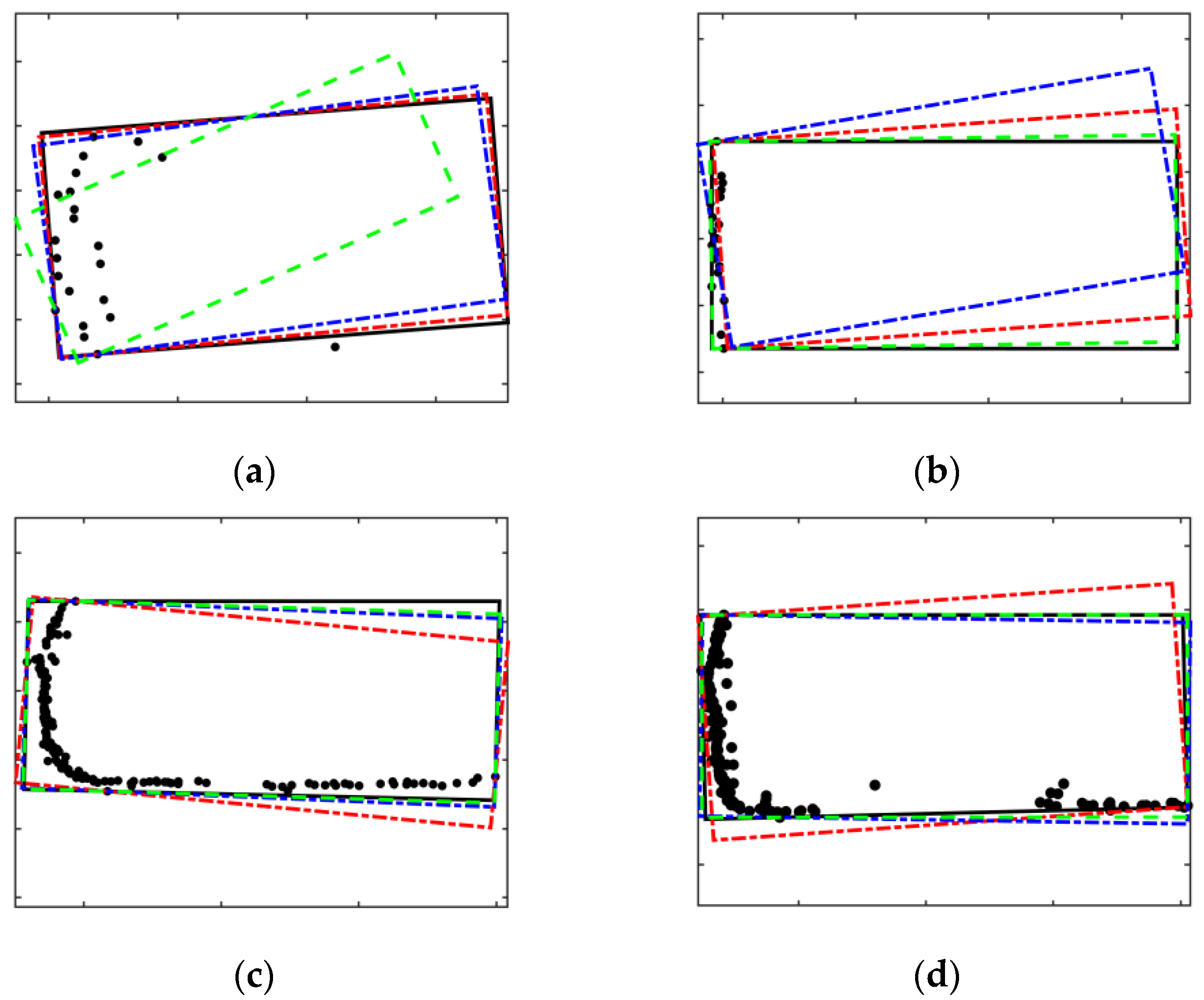
4.2. Validation of Bounding Box Fitting Algorithm
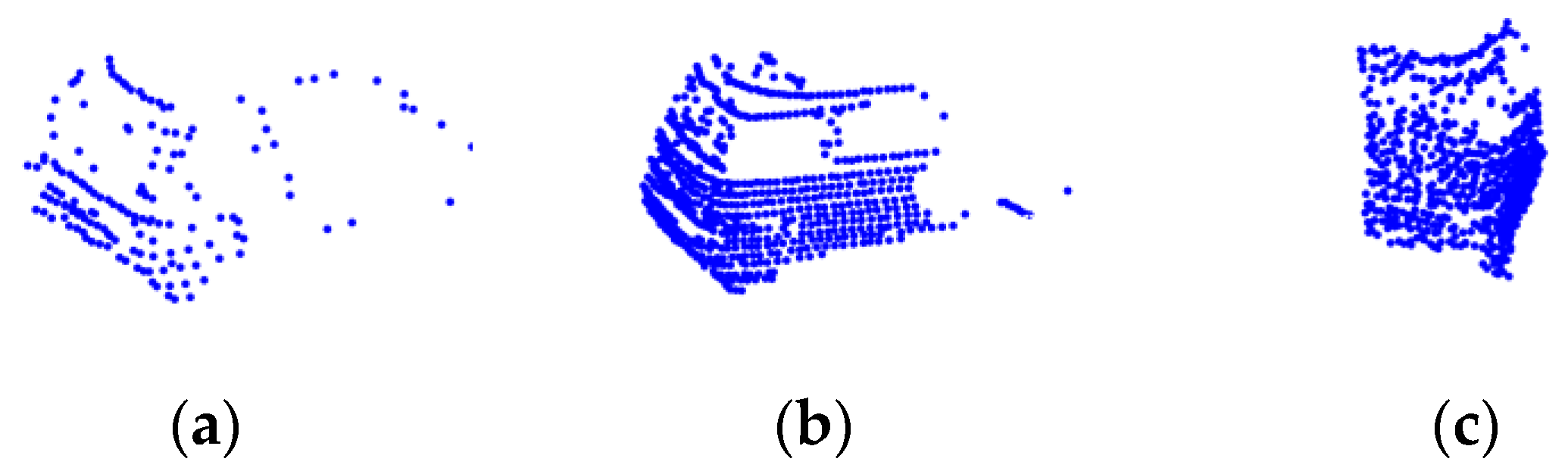
4.3. Verification of Comprehensive Detection and Identification Results
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Zhan, J.; Duan, C.; Guan, X.; Lu, P.; Yang, K. A review of vehicle detection techniques for intelligent vehicles. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Wang, J.; He, X.; Yan, Z.; Xu, L.; Wei, C.; Yin, G. Improving Vibration Performance of Electric Vehicles Based on In-Wheel Motor-Active Suspension System via Robust Finite Frequency Control. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1631–1643. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Q.; Yan, Z.; Yang, H. Nonlinear robust control of trajectory-following for autonomous ground electric vehicles with active front steering system. AIMS Math. 2023, 8, 11151–11179. [Google Scholar] [CrossRef]
- Jin, X.; Wang, J.; Yan, Z.; Xu, L.; Yin, G.; Chen, N. Robust vibration control for active suspension system of in-wheel-motor-driven electric vehicle via μ-synthesis methodology. ASME Trans. J. Dyn. Syst. Meas. Control. 2022, 144, 051007. [Google Scholar] [CrossRef]
- Xia, X.; Meng, Z.; Han, X.; Li, H.; Tsukiji, T.; Xu, R.; Zheng, Z.; Ma, J. An automated driving systems data acquisition and analytics platform. Transp. Res. Part C Emerg. Technol. 2023, 151, 104120. [Google Scholar] [CrossRef]
- Liu, W.; Quijano, K.; Crawford, M.M. YOLOv5-Tassel: Detecting tassels in RGB UAV imagery with improved YOLOv5 based on transfer learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8085–8094. [Google Scholar] [CrossRef]
- Monisha, A.A.; Reshmi, T.; Murugan, K. ERNSS-MCC: Efficient relay node selection scheme for mission critical communication using machine learning in VANET. Peer-to-Peer Netw. Appl. 2023, 1–24. [Google Scholar] [CrossRef]
- Kingston Roberts, M.; Thangavel, J. An improved optimal energy aware data availability approach for secure clustering and routing in wireless sensor networks. Trans. Emerg. Telecommun. Technol. 2023, 34, e4711. [Google Scholar] [CrossRef]
- So, J.; Hwangbo, J.; Kim, S.H.; Yun, I. Analysis on autonomous vehicle detection performance according to various road geometry settings. J. Intell. Transp. Syst. 2022, 27, 384–395. [Google Scholar] [CrossRef]
- Ali, W.; Abdelkarim, S.; Zidan, M.; Zahran, M.; El Sallab, A. Yolo3d: End-to-end real-time 3d oriented object bounding box detection from lidar point cloud. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018; pp. 716–728. [Google Scholar]
- Yang, B.; Luo, W.; Urtasun, R. Pixor: Real-time 3d object detection from point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Salt Lake, UT, USA, 18–22 June 2018; pp. 7652–7660. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Honolulu, HS, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; Li, H. Pv-rcnn: Point-voxel feature set abstraction for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition(CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 10529–10538. [Google Scholar]
- Li, Z.; Wang, F.; Wang, N. Lidar r-cnn: An efficient and universal 3d object detector. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition(CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 7546–7555. [Google Scholar]
- Zhou, Y.; Tuzel, O. Voxelnet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Salt Lake, UT, USA, 18–22 June 2018; pp. 4490–4499. [Google Scholar]
- Yan, Y.; Mao, Y.; Li, B. Second: Sparsely embedded convolutional detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef]
- Deng, J.; Shi, S.; Li, P.; Zhou, W.; Zhang, Y.; Li, H. Voxel r-cnn: Towards high performance voxel-based 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence(AAAI), Vancouver, BC, Canada, 2–9 February 2021; pp. 1201–1209. [Google Scholar]
- Chen, H.; Liang, M.; Liu, W.; Wang, W.; Liu, P.X. An approach to boundary detection for 3D point clouds based on DBSCAN clustering. Pattern Recognit. 2022, 124, 108431. [Google Scholar] [CrossRef]
- Wang, C.; Ji, M.; Wang, J.; Wen, W.; Li, T.; Sun, Y. An improved DBSCAN method for LiDAR data segmentation with automatic Eps estimation. Sensors 2019, 19, 172. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Chen, Y.; Junior, J.M.; Wang, C.; Li, J. Rapid extraction of urban road guardrails from mobile LiDAR point clouds. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1572–1577. [Google Scholar] [CrossRef]
- Miao, Y.; Tang, Y.; Alzahrani, B.A.; Barnawi, A.; Alafif, T.; Hu, L. Airborne LiDAR assisted obstacle recognition and intrusion detection towards unmanned aerial vehicle: Architecture, modeling and evaluation. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4531–4540. [Google Scholar] [CrossRef]
- El Yabroudi, M.; Awedat, K.; Chabaan, R.C.; Abudayyeh, O.; Abdel-Qader, I. Adaptive DBSCAN LiDAR Point Cloud Clustering For Autonomous Driving Applications. In Proceedings of the 2022 IEEE International Conference on Electro Information Technology (eIT), Mankato, MN, USA, 19–21 May 2022; pp. 221–224. [Google Scholar]
- Wen, L.; He, L.; Gao, Z. Research on 3D Point Cloud De-Distortion Algorithm and Its Application on Euclidean Clustering. IEEE Access 2019, 7, 86041–86053. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, W.; Dong, C.; Dolan, J.M. Efficient L-shape fitting for vehicle detection using laser scanners. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Redondo Beach, CA, USA, 11–14 June 2017; pp. 54–59. [Google Scholar]
- Zhao, C.; Fu, C.; Dolan, J.M.; Wang, J. L-shape fitting-based vehicle pose estimation and tracking using 3D-LiDAR. IEEE Trans. Intell. Veh. 2021, 6, 787–798. [Google Scholar] [CrossRef]
- Kim, D.; Jo, K.; Lee, M.; Sunwoo, M. L-shape model switching-based precise motion tracking of moving vehicles using laser scanners. IEEE Trans. Intell. Transp. Syst. 2017, 19, 598–612. [Google Scholar] [CrossRef]
- Sun, P.; Zhao, X.; Xu, Z.; Wang, R.; Min, H. A 3D LiDAR data-based dedicated road boundary detection algorithm for autonomous vehicles. IEEE Access 2019, 7, 29623–29638. [Google Scholar] [CrossRef]
- Guo, G.; Zhao, S. 3D multi-object tracking with adaptive cubature Kalman filter for autonomous driving. IEEE Trans. Intell. Veh. 2022, 8, 512–519. [Google Scholar] [CrossRef]
- Liu, K.; Wang, W.; Tharmarasa, R.; Wang, J. Dynamic vehicle detection with sparse point clouds based on PE-CPD. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1964–1977. [Google Scholar] [CrossRef]
- Kim, T.; Park, T.-H. Extended Kalman filter (EKF) design for vehicle position tracking using reliability function of radar and lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef]
- Golovinskiy, A.; Kim, V.G.; Funkhouser, T. Shape-based recognition of 3D point clouds in urban environments. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision(ICCV), Kyoto, Japan, 1–2 October 2009; pp. 2154–2161. [Google Scholar]
- Chen, T.; Dai, B.; Wang, R.; Liu, D. Gaussian-process-based real-time ground segmentation for autonomous land vehicles. J. Intell. Robot. Syst. 2014, 76, 563–582. [Google Scholar] [CrossRef]
- Eum, J.; Bae, M.; Jeon, J.; Lee, H.; Oh, S.; Lee, M. Vehicle detection from airborne LiDAR point clouds based on a decision tree algorithm with horizontal and vertical features. Remote Sens. 2017, 8, 409–418. [Google Scholar] [CrossRef]
- Jin, X.; Yang, H.; Liao, X.; Yan, Z.; Wang, Q.; Li, Z.; Wang, Z. A Robust Gaussian Process-Based LiDAR Ground Segmentation Algorithm for Autonomous Driving. Machines 2022, 10, 507. [Google Scholar] [CrossRef]

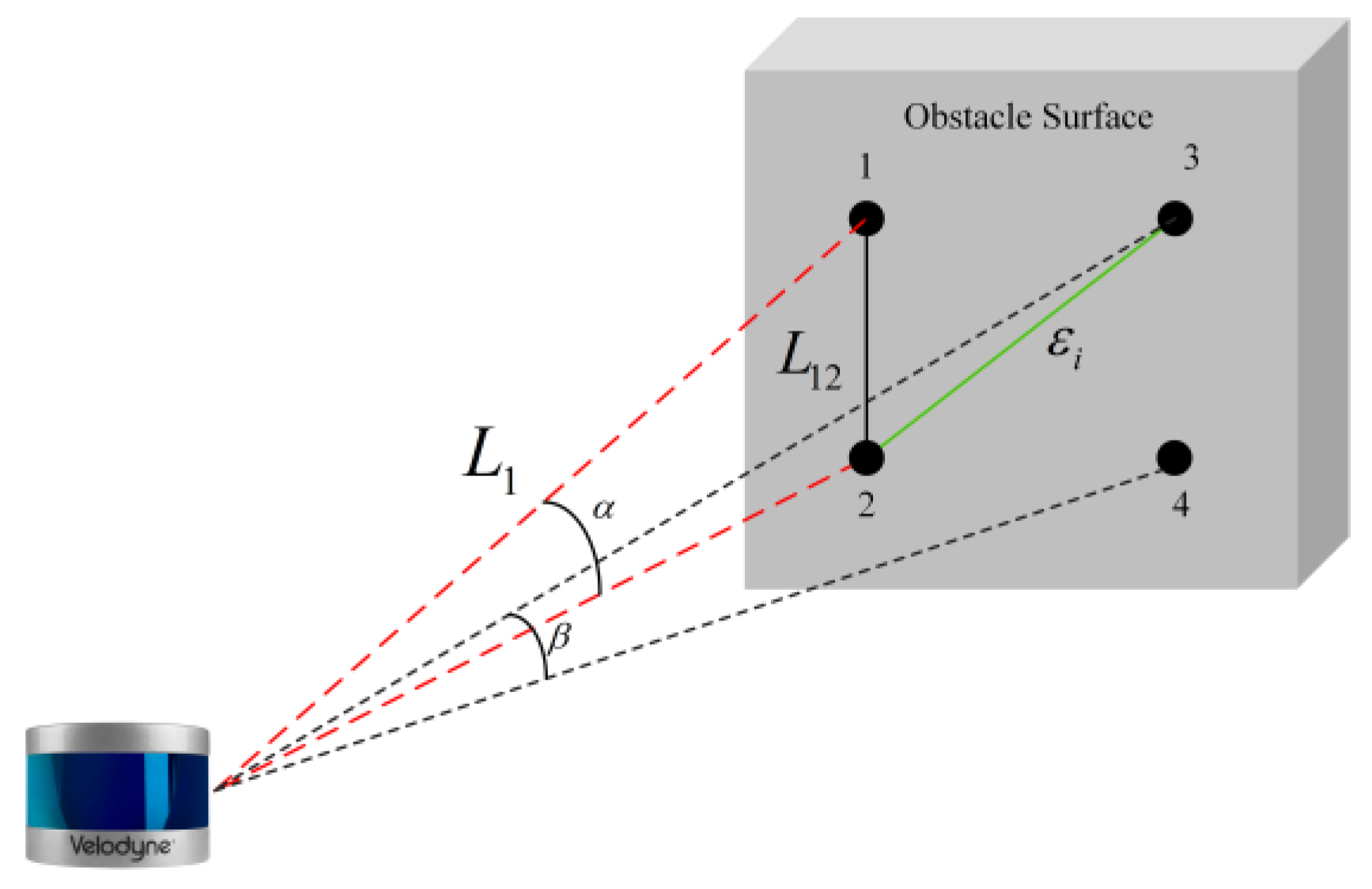


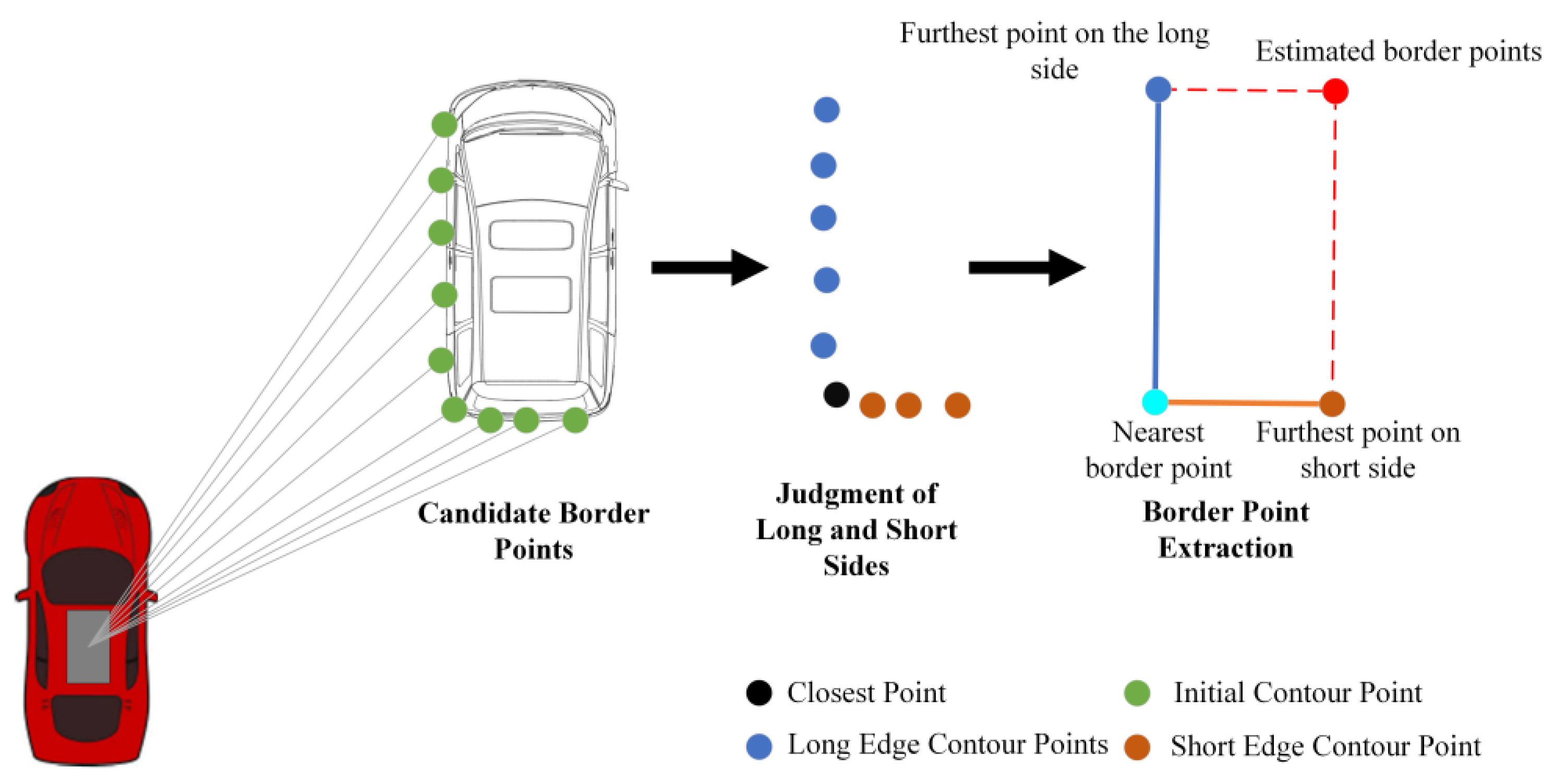
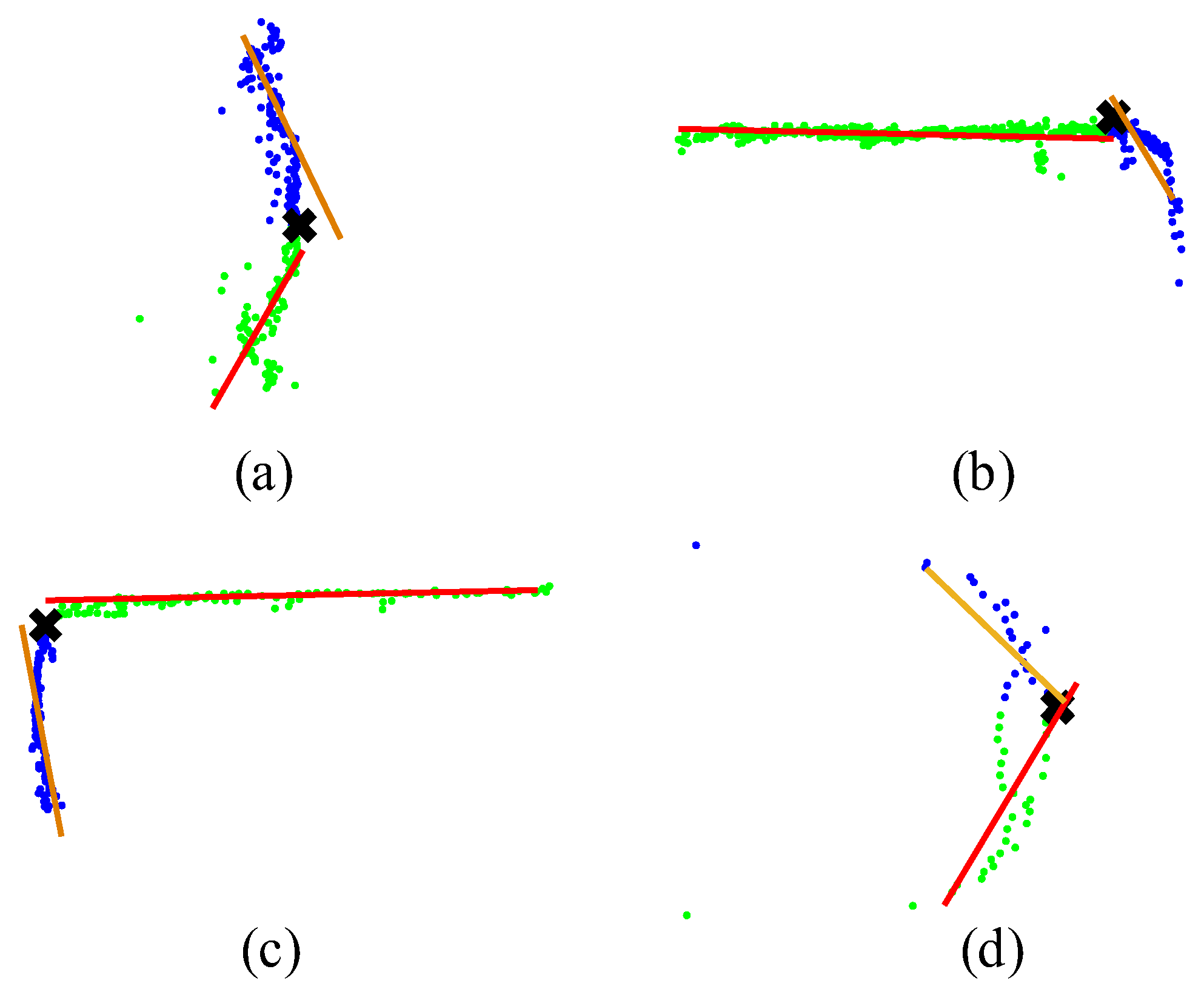
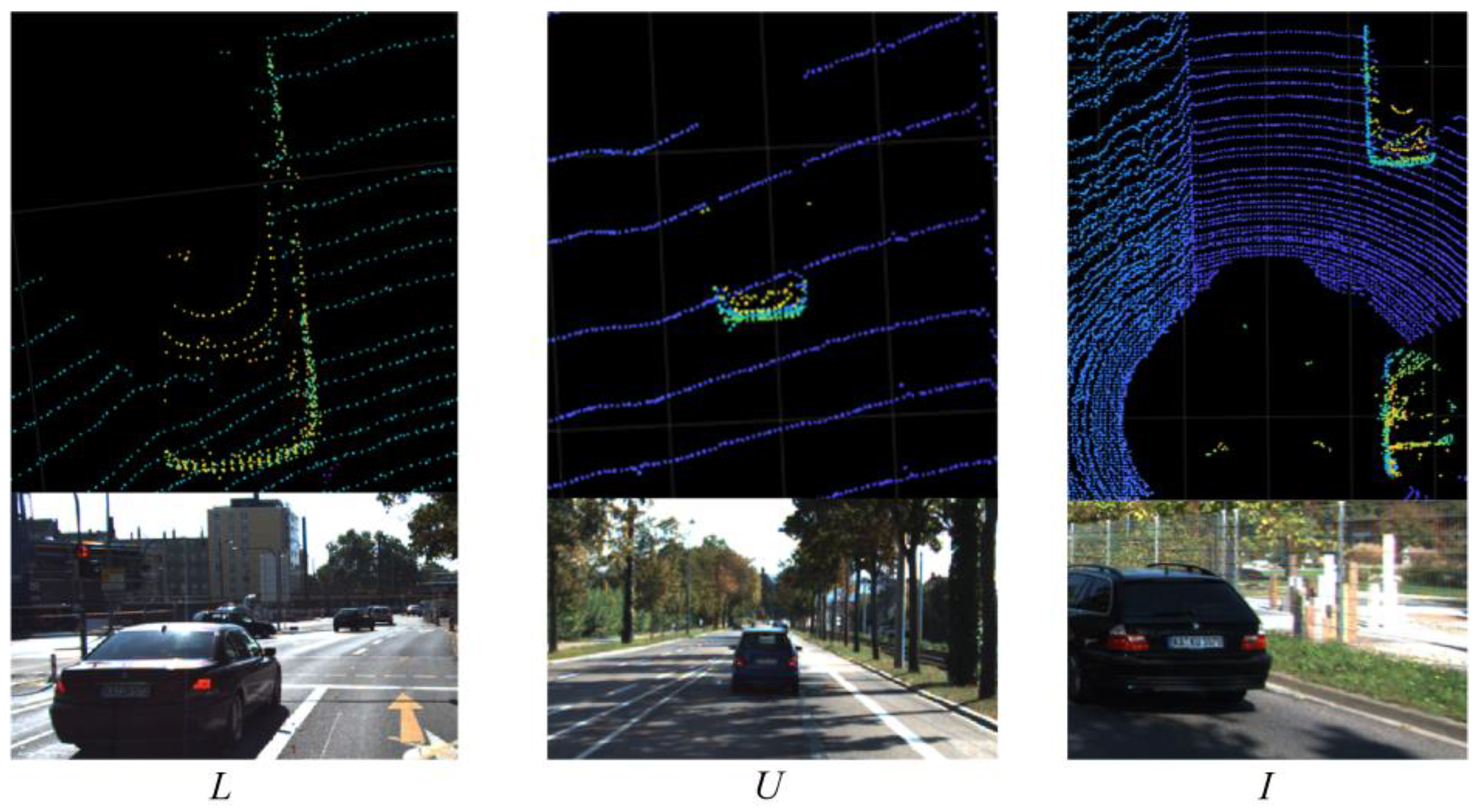

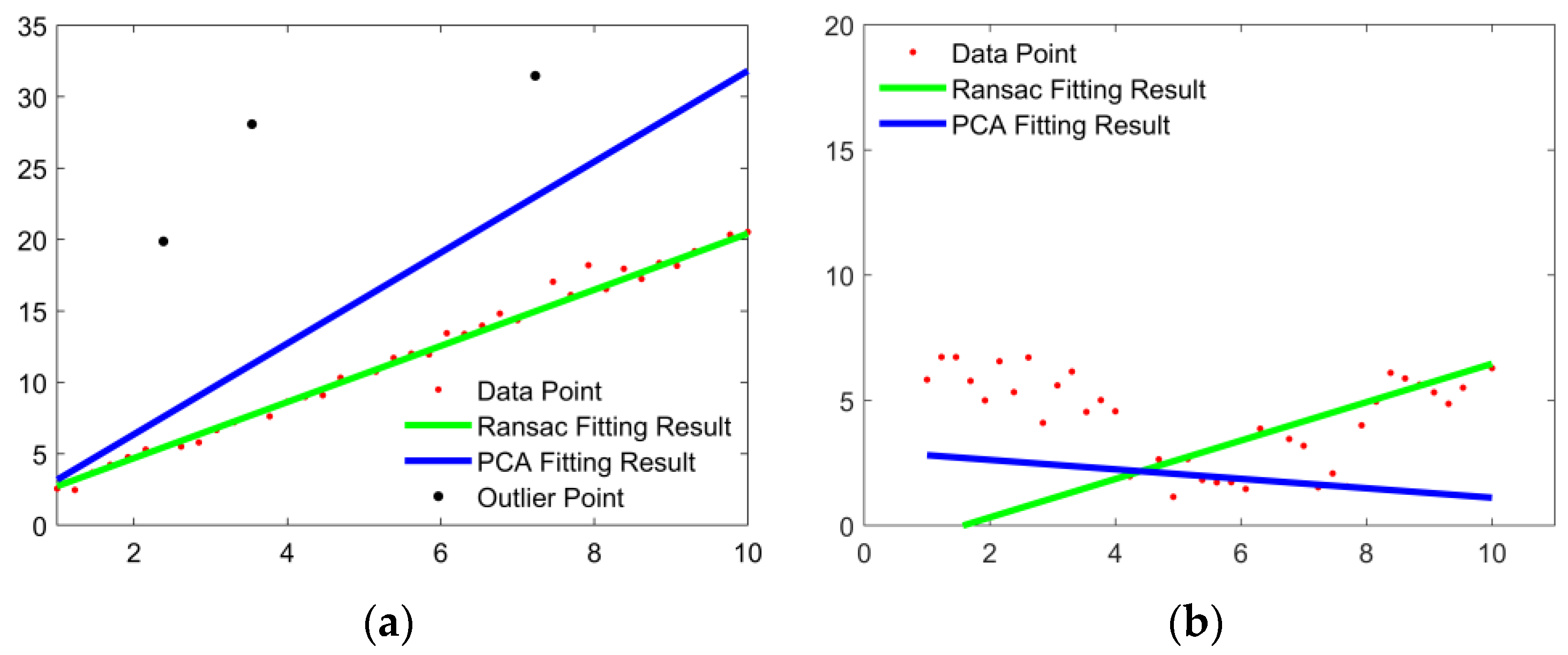
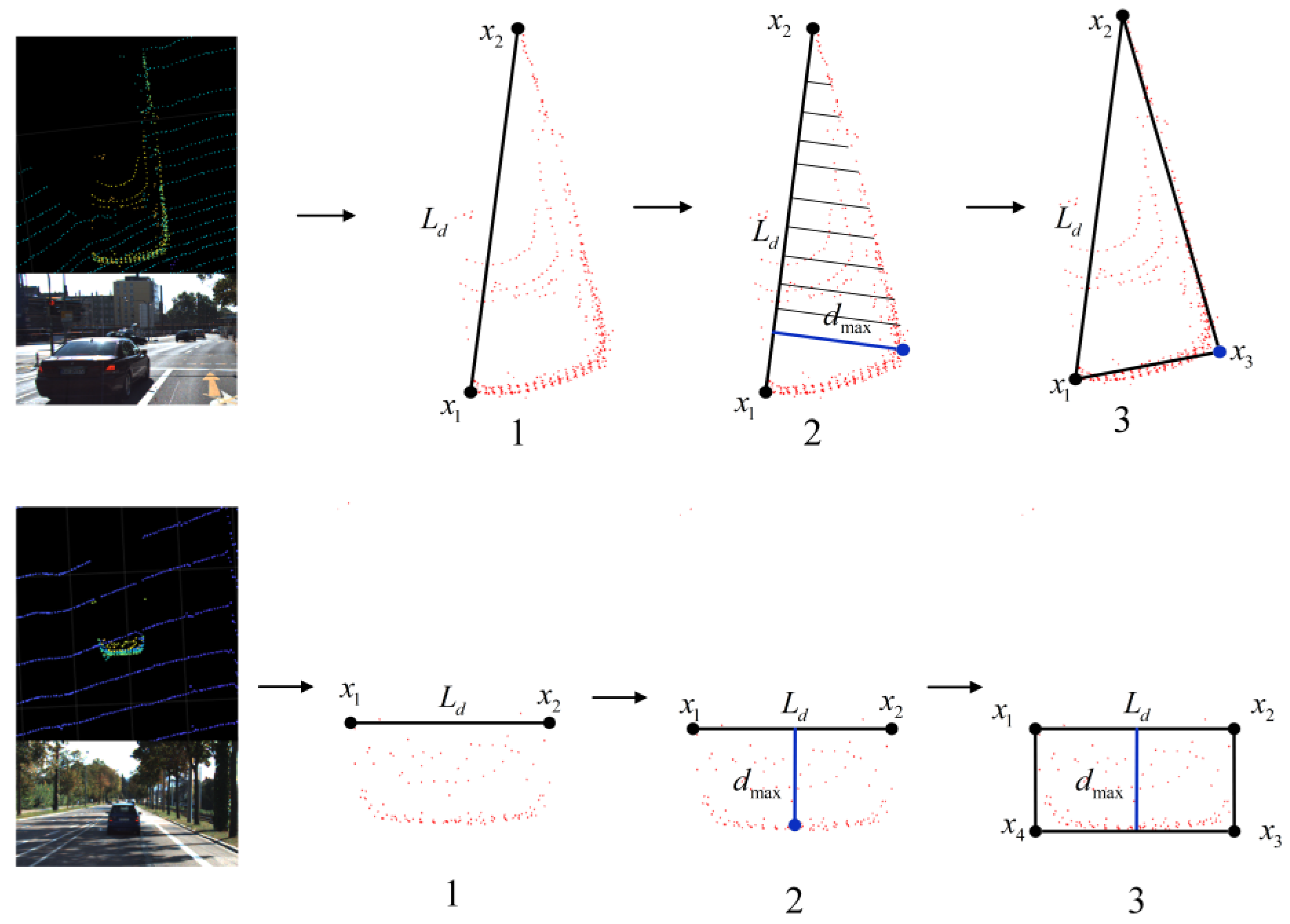



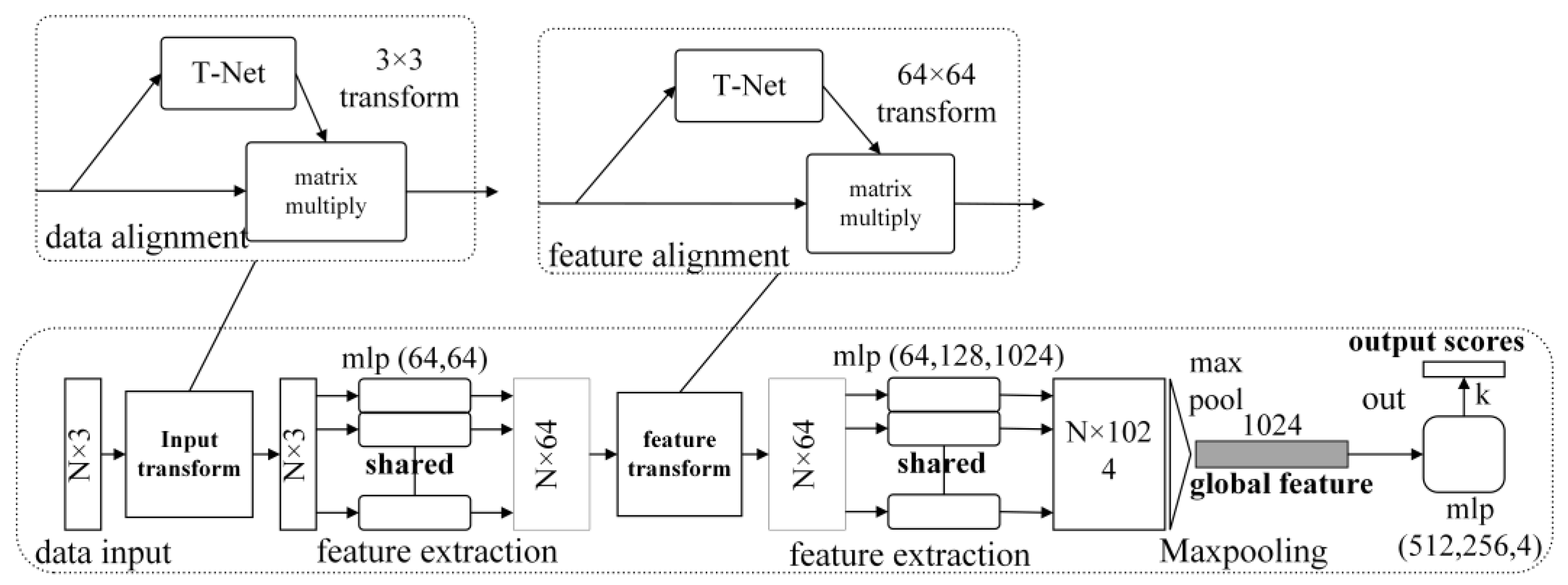
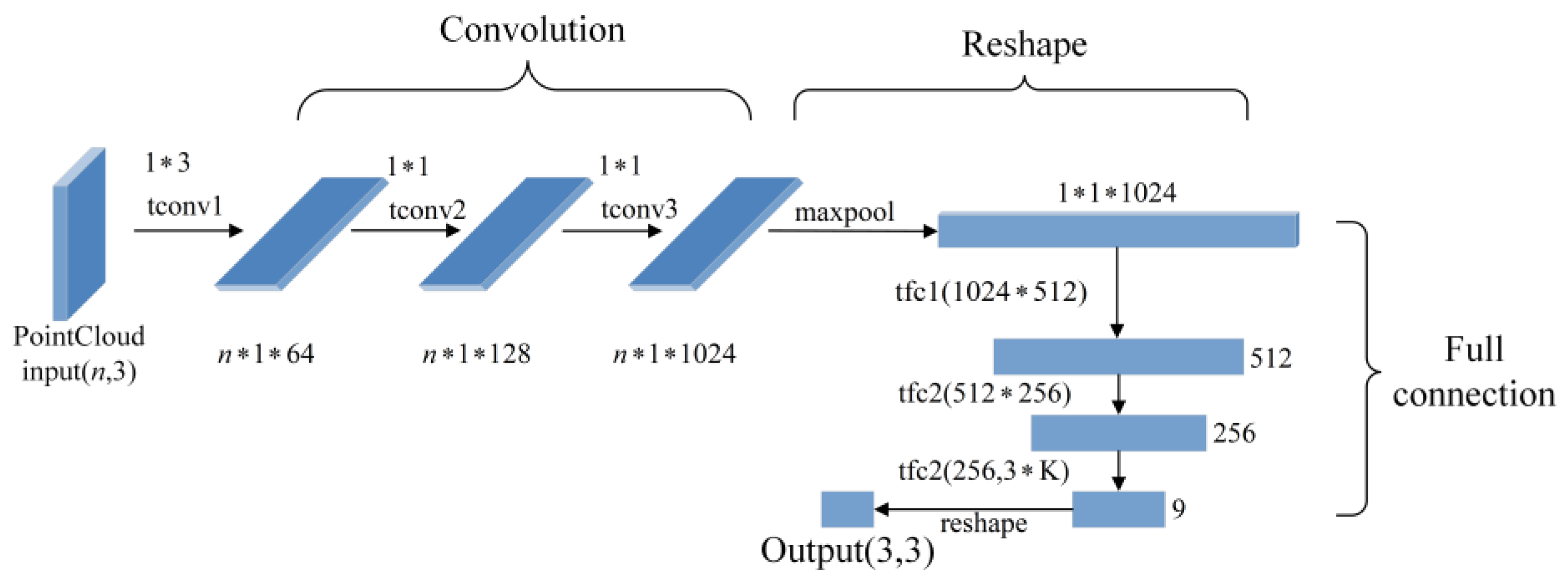









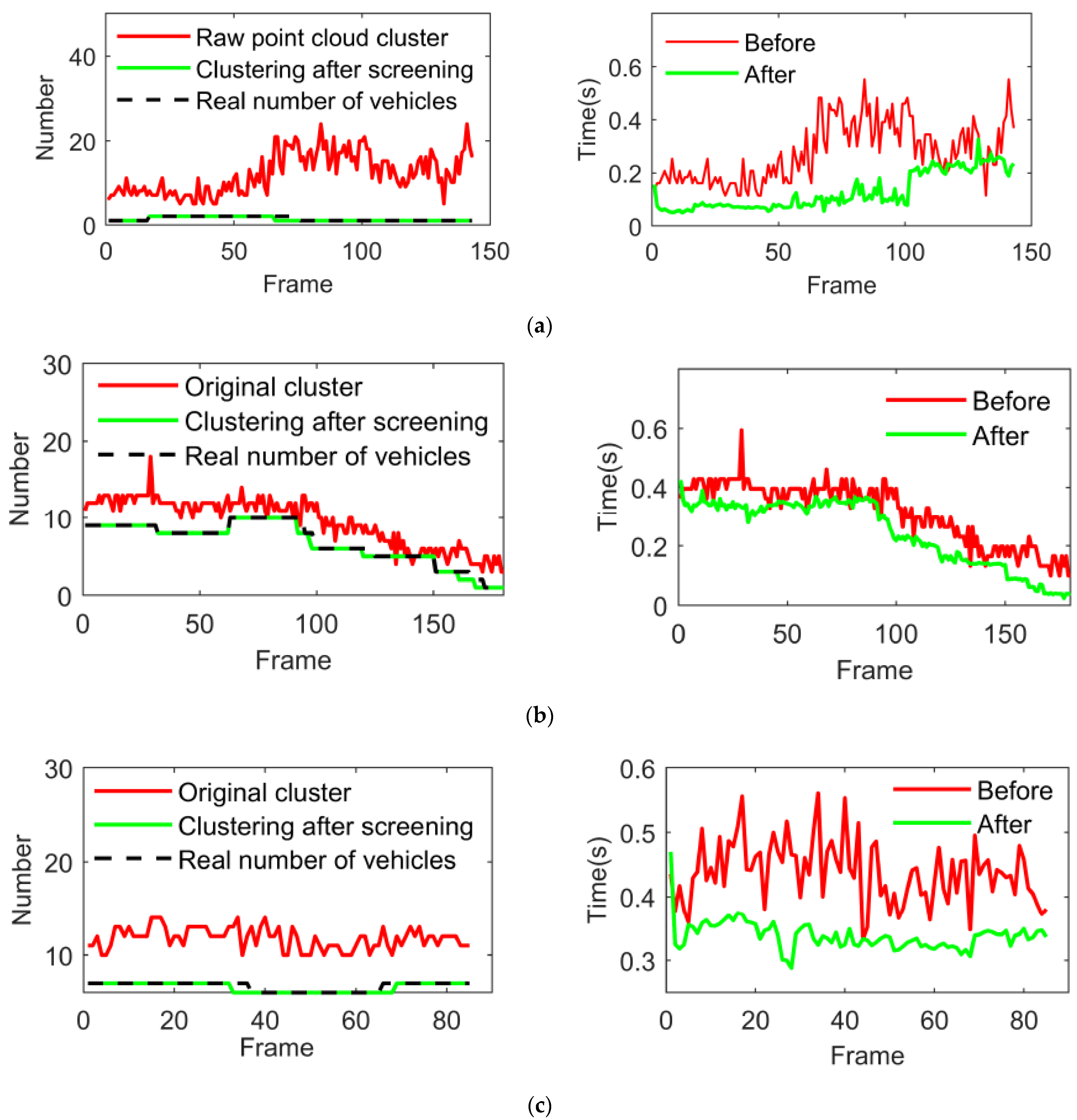
| Number | Threshold | Definition |
|---|---|---|
| 1 | Maximum and minimum height of obstacles | |
| 2 | Maximum and minimum width of obstacles | |
| 3 | Maximum and minimum length of obstacles | |
| 4 | Top View Area of Obstacles | |
| 5 | The aspect ratio of the obstacle | |
| 6 | Aspect ratio threshold for obstacles | |
| 7 | The number of points contained within the obstacle |
| Class | Index | Car | Cyclist | Pedestrian | Other |
|---|---|---|---|---|---|
| Before | Number | 10,341 | 1595 | 4767 | 1863 |
| Ratio | 55.69% | 8.59% | 25.67% | 10.03% | |
| After | Number | 8632 | 5403 | 6093 | 5023 |
| Ratio | 34.3% | 21.48% | 24.23% | 19.97% |
| Serial Number | Algorithm | Correct Frame | Wrong Frame | Right Ratio |
|---|---|---|---|---|
| 0004 | DBSCAN | 173 | 86 | 66.8% |
| ADBSCAN | 248 | 11 | 96.50% | |
| OPTICS | 257 | 2 | 99.22% | |
| 0018 | DBSCAN | 66 | 34 | 66% |
| ADBSCAN | 89 | 11 | 89% | |
| OPTICS | 82 | 18 | 82% | |
| 0020 | DBSCAN | 55 | 31 | 63.95% |
| ADBSCAN | 61 | 25 | 70.93% | |
| OPTICS | 80 | 6 | 93.02% | |
| 0026 | DBSCAN | 50 | 17 | 74.63% |
| ADBSCAN | 62 | 5 | 92.54% | |
| OPTICS | 67 | 2 | 97.1% | |
| 0056 | DBSCAN | 258 | 36 | 87.76% |
| ADBSCAN | 284 | 10 | 96.6% | |
| OPTICS | 294 | 0 | 100% |
| Serial Number | Algorithm | Horizontal | Vertical | ||
|---|---|---|---|---|---|
| Mean | Variance | Mean | Variance | ||
| 0001 | Regular | 0.0986 | 0.056 | 0.1435 | 0.1368 |
| Proposed | 0.0688 | 0.0458 | 0.1143 | 0.1415 | |
| 0015 | Regular | 0.1191 | 0.0935 | 0.515 | 0.135 |
| Proposed | 0.0912 | 0.0721 | 0.265 | 0.126 | |
| 0020 | Regular | 0.0742 | 0.0749 | 0.3979 | 0.1288 |
| Proposed | 0.0652 | 0.0689 | 0.2950 | 0.132 | |
| 0032 | Regular | 0.1065 | 0.0912 | 0.3998 | 0.251 |
| Proposed | 0.0842 | 0.0688 | 0.2829 | 0.299 | |
| Algorithm | Dataset | Precision P | Recall R | F |
|---|---|---|---|---|
| Regular | 0013 | 0.926 | 0.846 | 0.884 |
| 0018 | 0.903 | 0.861 | 0.882 | |
| 0026 | 0.891 | 0.847 | 0.868 | |
| Proposed | 0013 | 0.982 | 0.864 | 0.919 |
| 0018 | 0.965 | 0.904 | 0.934 | |
| 0026 | 0.943 | 0.901 | 0.922 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Yang, H.; He, X.; Liu, G.; Yan, Z.; Wang, Q. Robust LiDAR-Based Vehicle Detection for On-Road Autonomous Driving. Remote Sens. 2023, 15, 3160. https://doi.org/10.3390/rs15123160
Jin X, Yang H, He X, Liu G, Yan Z, Wang Q. Robust LiDAR-Based Vehicle Detection for On-Road Autonomous Driving. Remote Sensing. 2023; 15(12):3160. https://doi.org/10.3390/rs15123160
Chicago/Turabian StyleJin, Xianjian, Hang Yang, Xiongkui He, Guohua Liu, Zeyuan Yan, and Qikang Wang. 2023. "Robust LiDAR-Based Vehicle Detection for On-Road Autonomous Driving" Remote Sensing 15, no. 12: 3160. https://doi.org/10.3390/rs15123160
APA StyleJin, X., Yang, H., He, X., Liu, G., Yan, Z., & Wang, Q. (2023). Robust LiDAR-Based Vehicle Detection for On-Road Autonomous Driving. Remote Sensing, 15(12), 3160. https://doi.org/10.3390/rs15123160