Eddy Covariance CO2 Flux Gap Filling for Long Data Gaps: A Novel Framework Based on Machine Learning and Time Series Decomposition
Abstract
1. Introduction
2. Data Sets and Study Sites
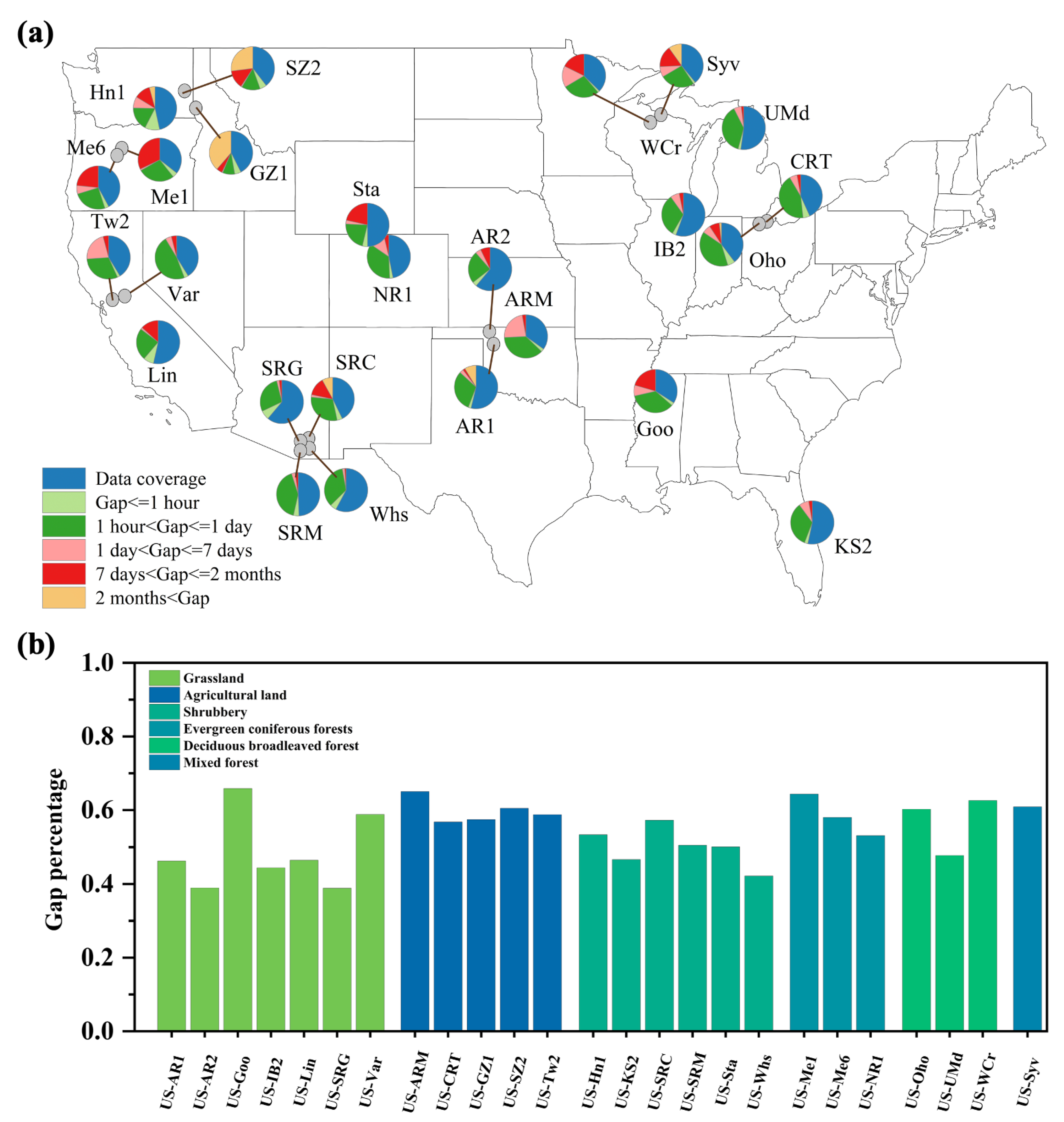
2.1. Eddy Covariance CO2 Fluxes
2.2. Ancillary Data for Gap-Filling Algorithms
2.3. Study Sites
3. Methodology
3.1. Time Series Decomposition Approaches
3.1.1. Moving Average (MA)
3.1.2. Empirical Mode Decomposition (EMD)
3.2. Machine Learning Approaches
3.2.1. Random Forest (RF)
3.2.2. EXtreme Gradient Boosting (XGboost)
3.2.3. Support Vector Regression (SVR)
3.2.4. Back Propagation (BP) Neural Network
3.3. The Novel Framework Based on ML and Time Series Decomposition
3.4. Model Evaluation
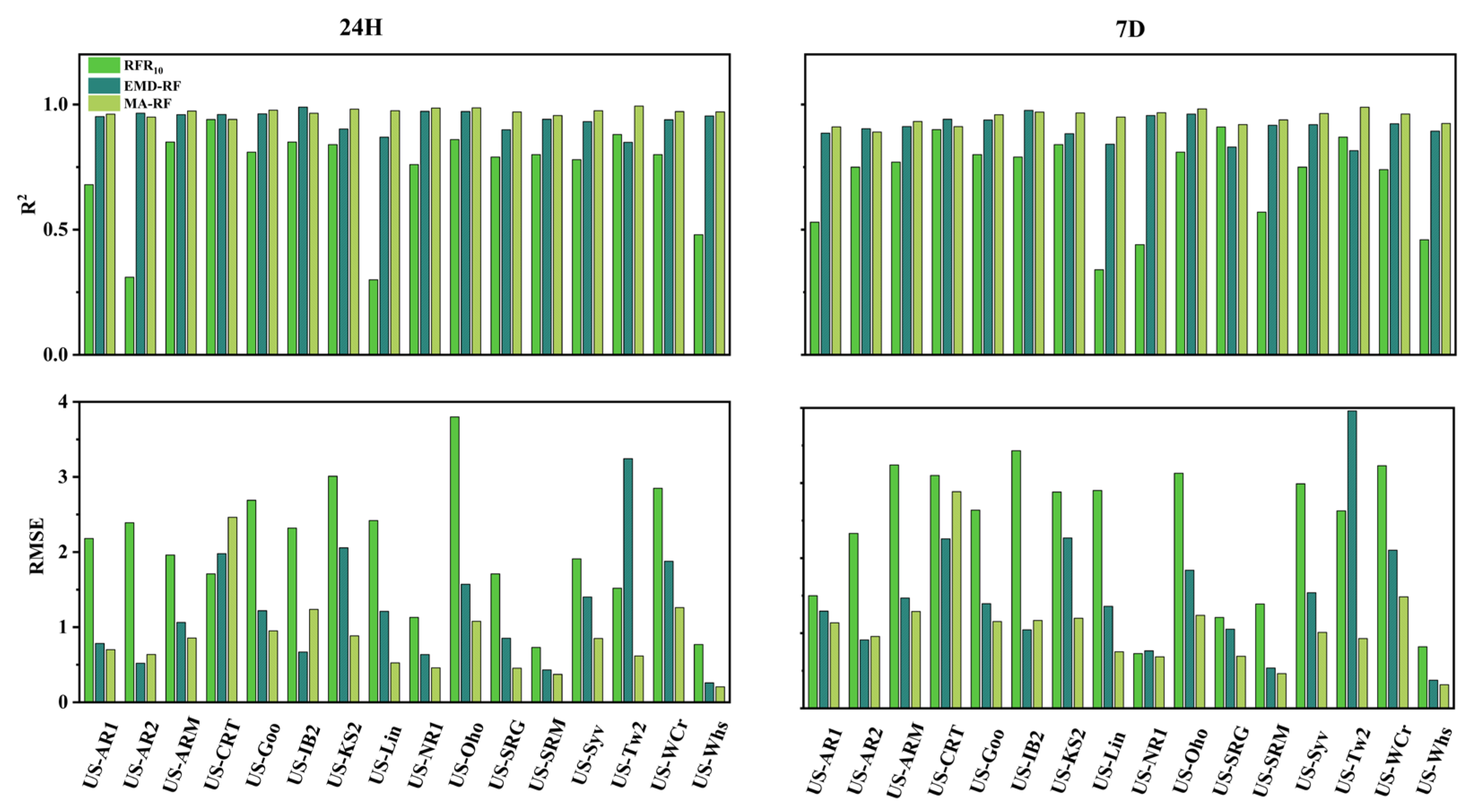
4. Results
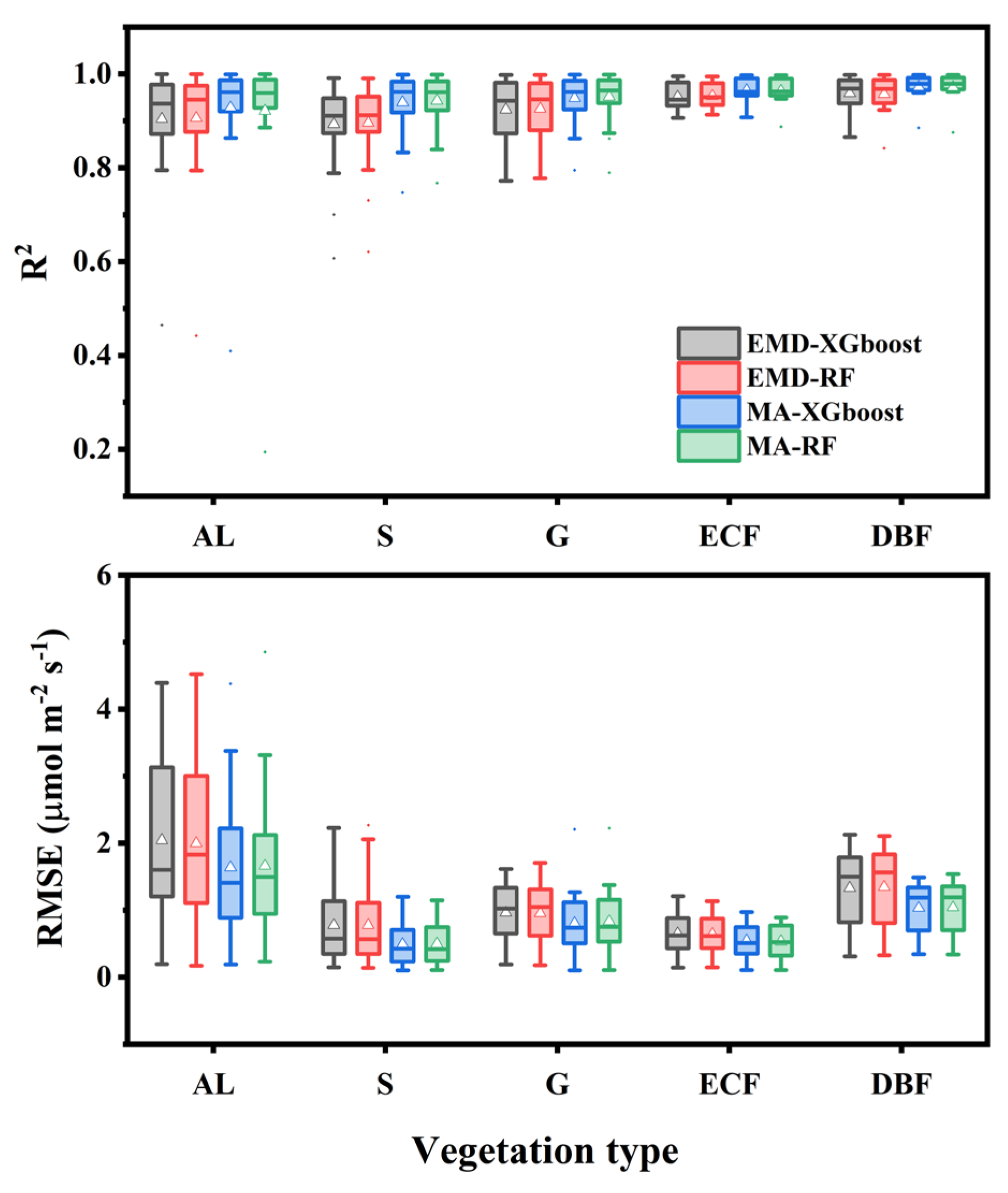
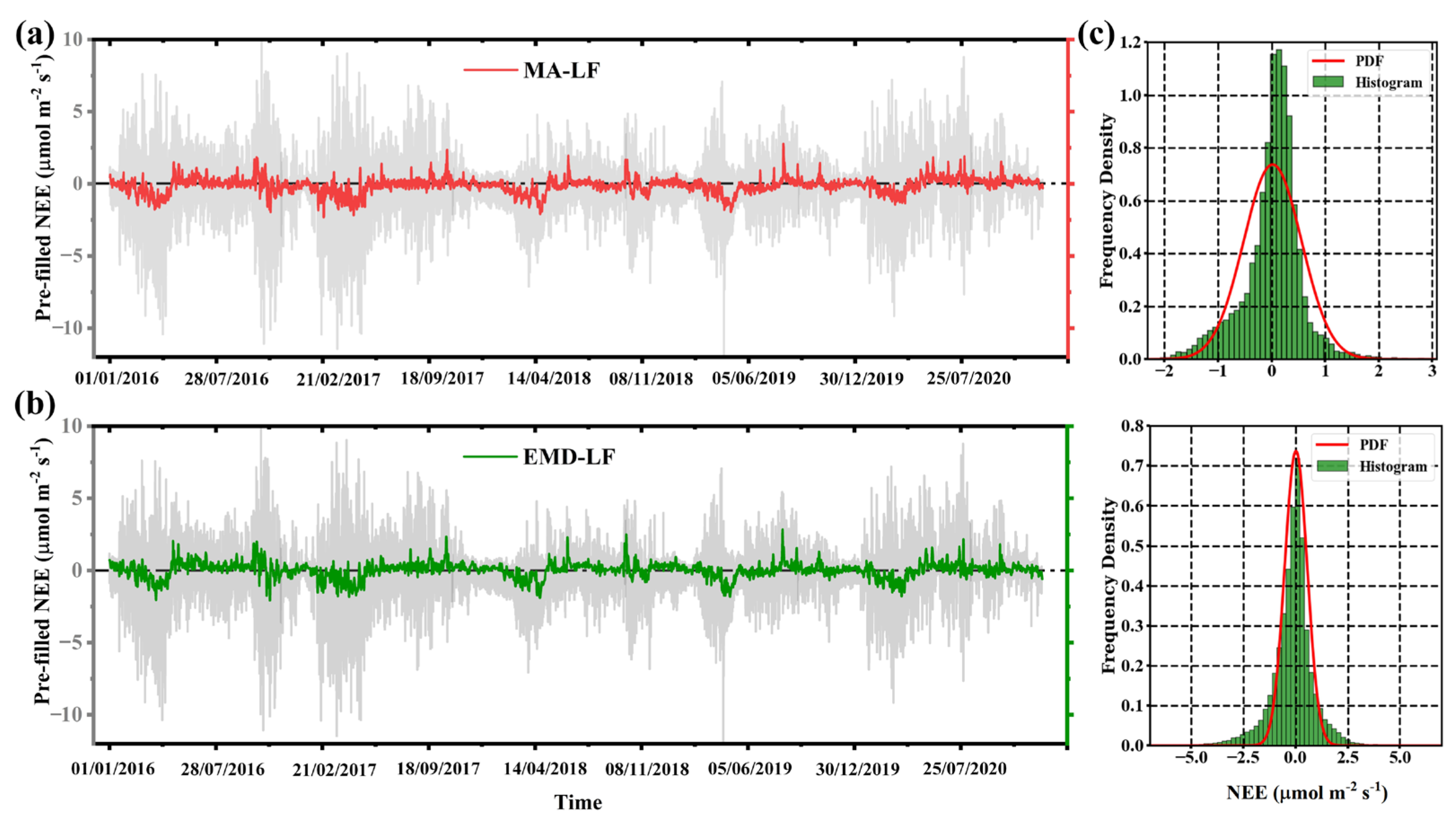
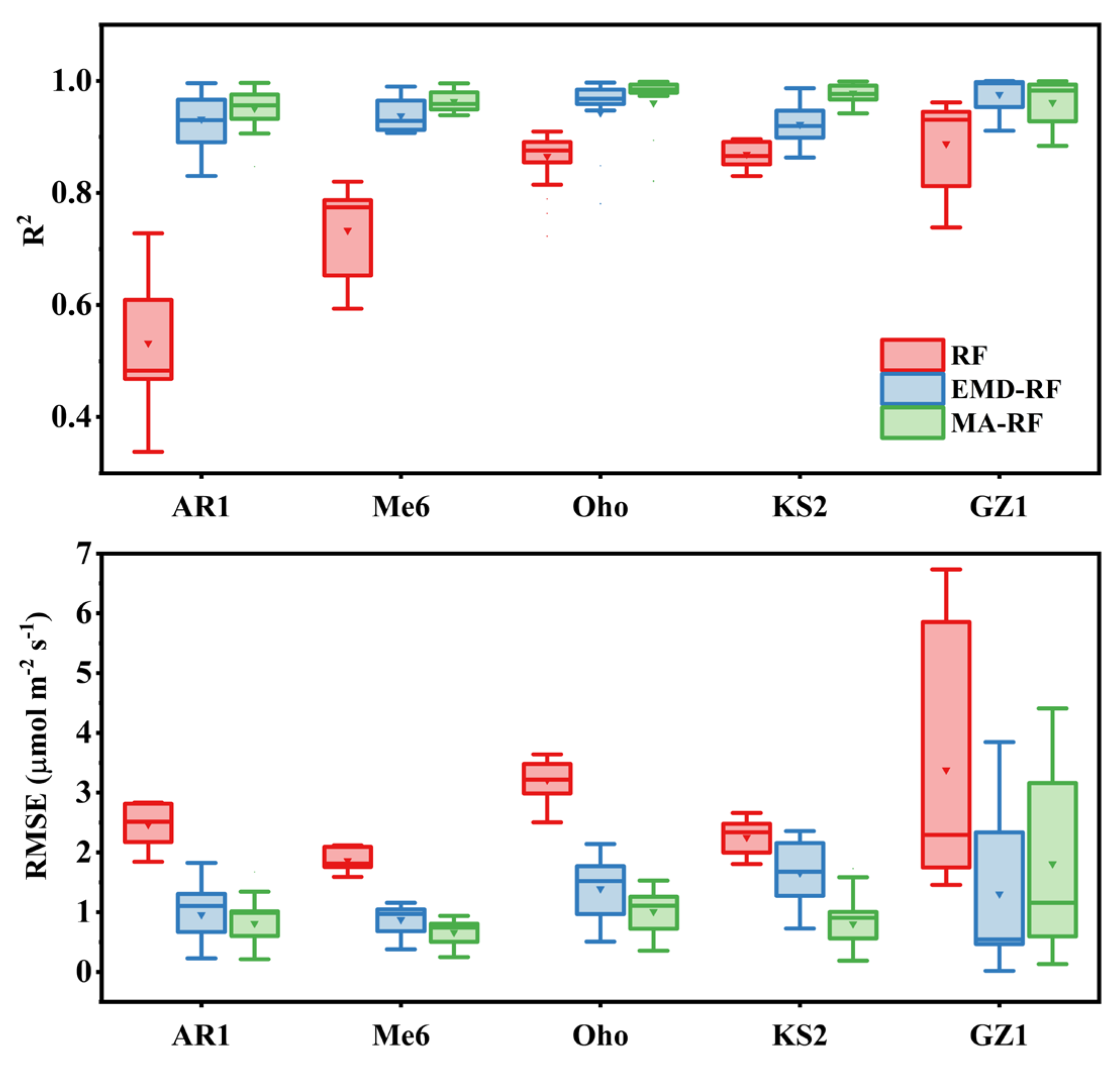
4.1. Comparison of Model Performance between the Traditional and Proposed Gap-Filling Frameworks
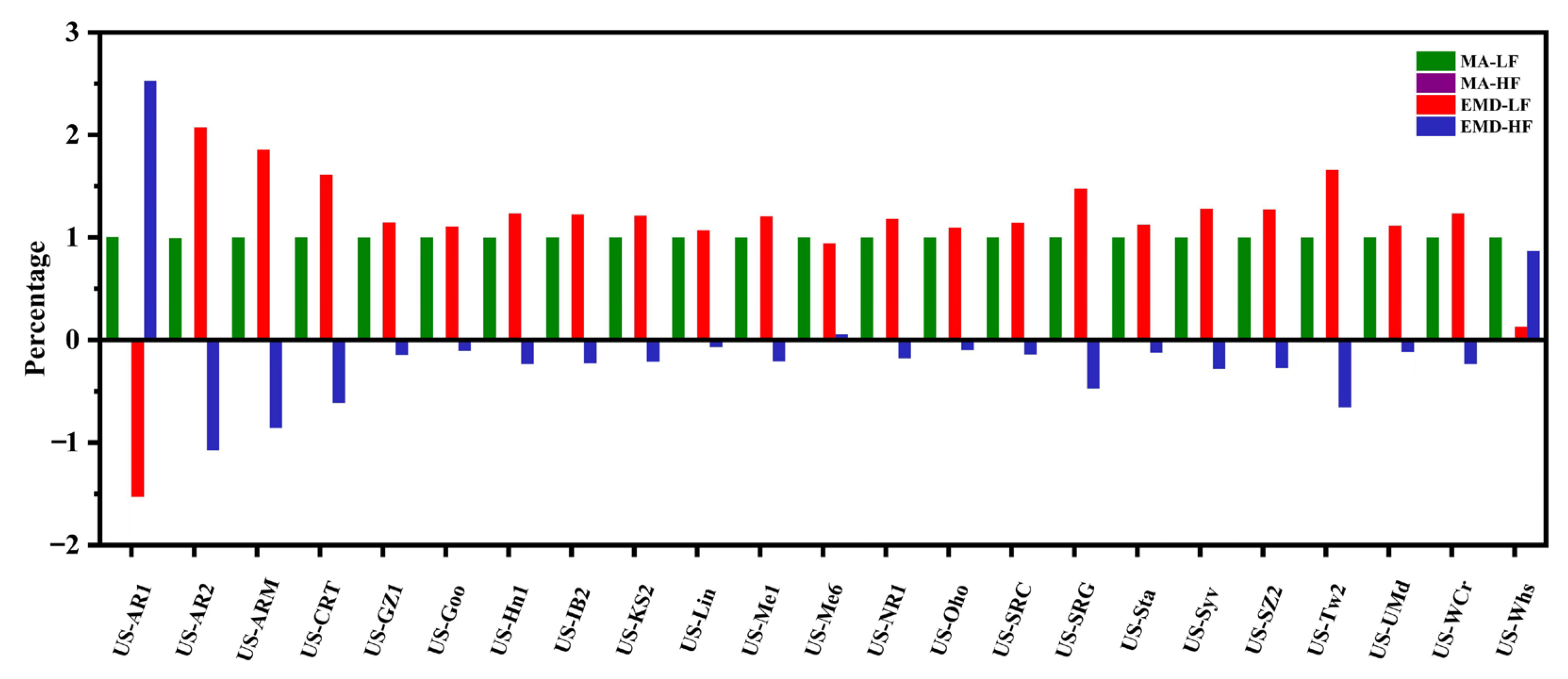
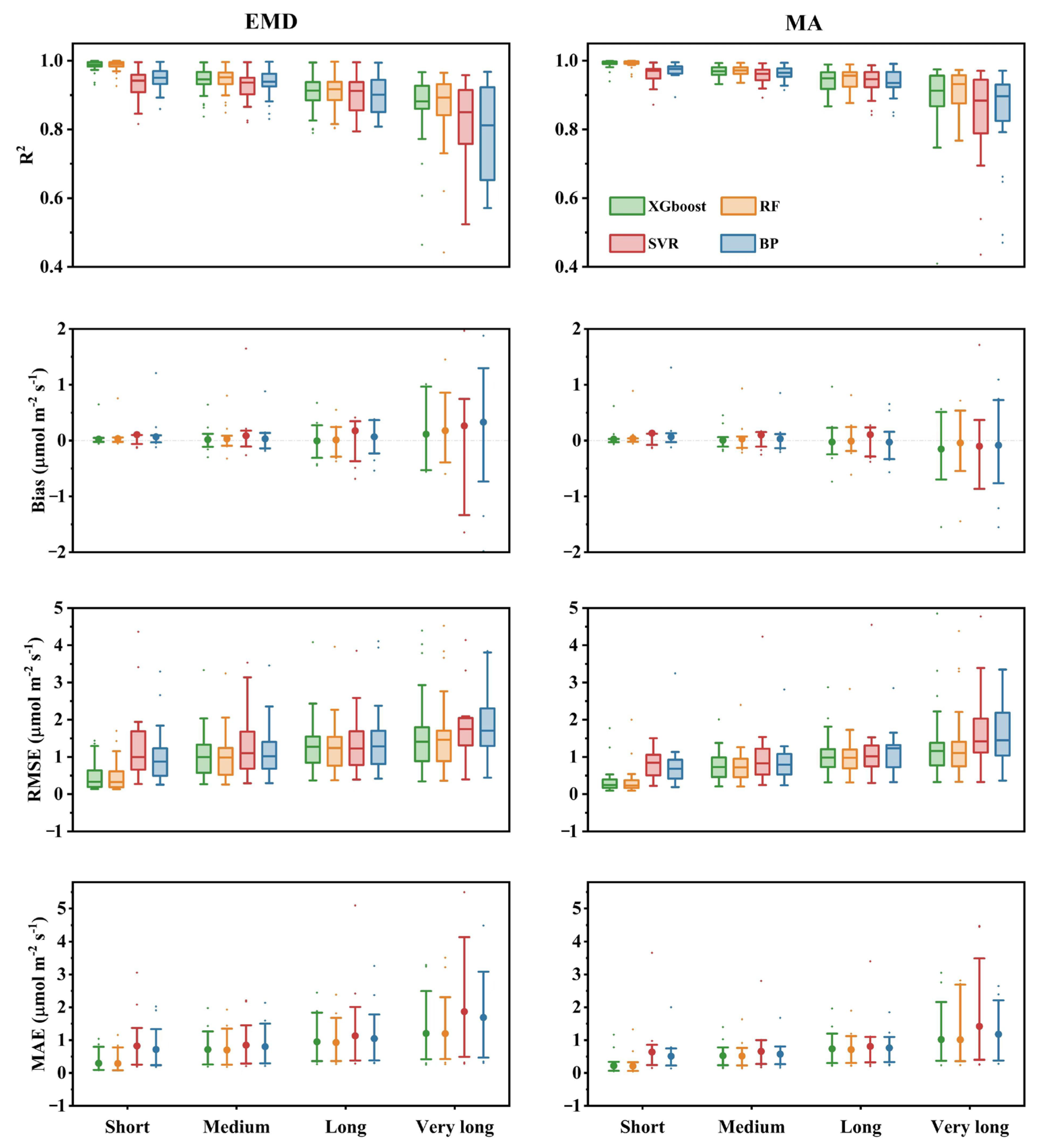
4.2. Comparison of the Model Performance of the Proposed Framework in Combination with Different ML Algorithms
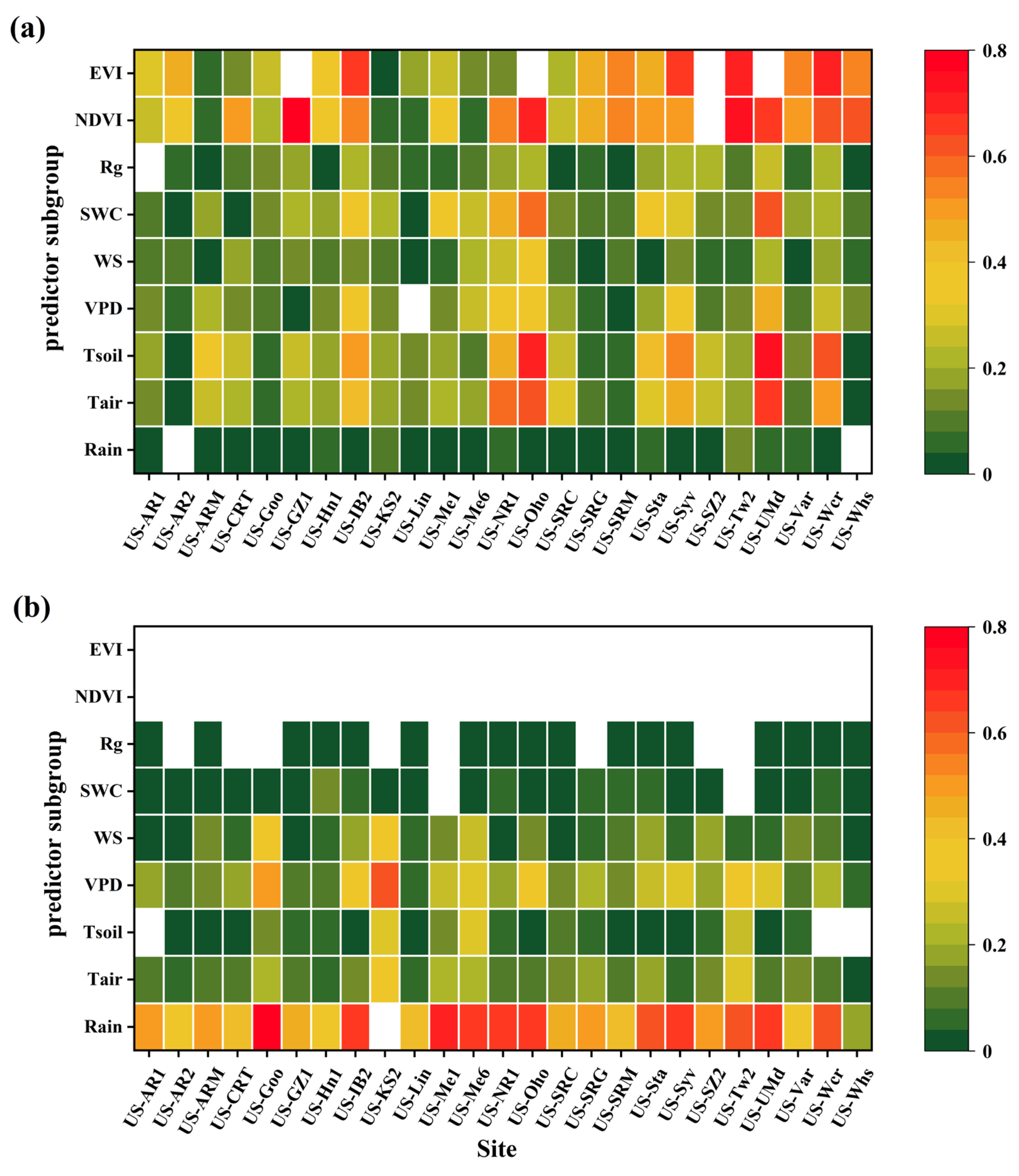
4.3. Relative Importance of the Input Variables
4.4. Comparison with Results in a Peer’s Study
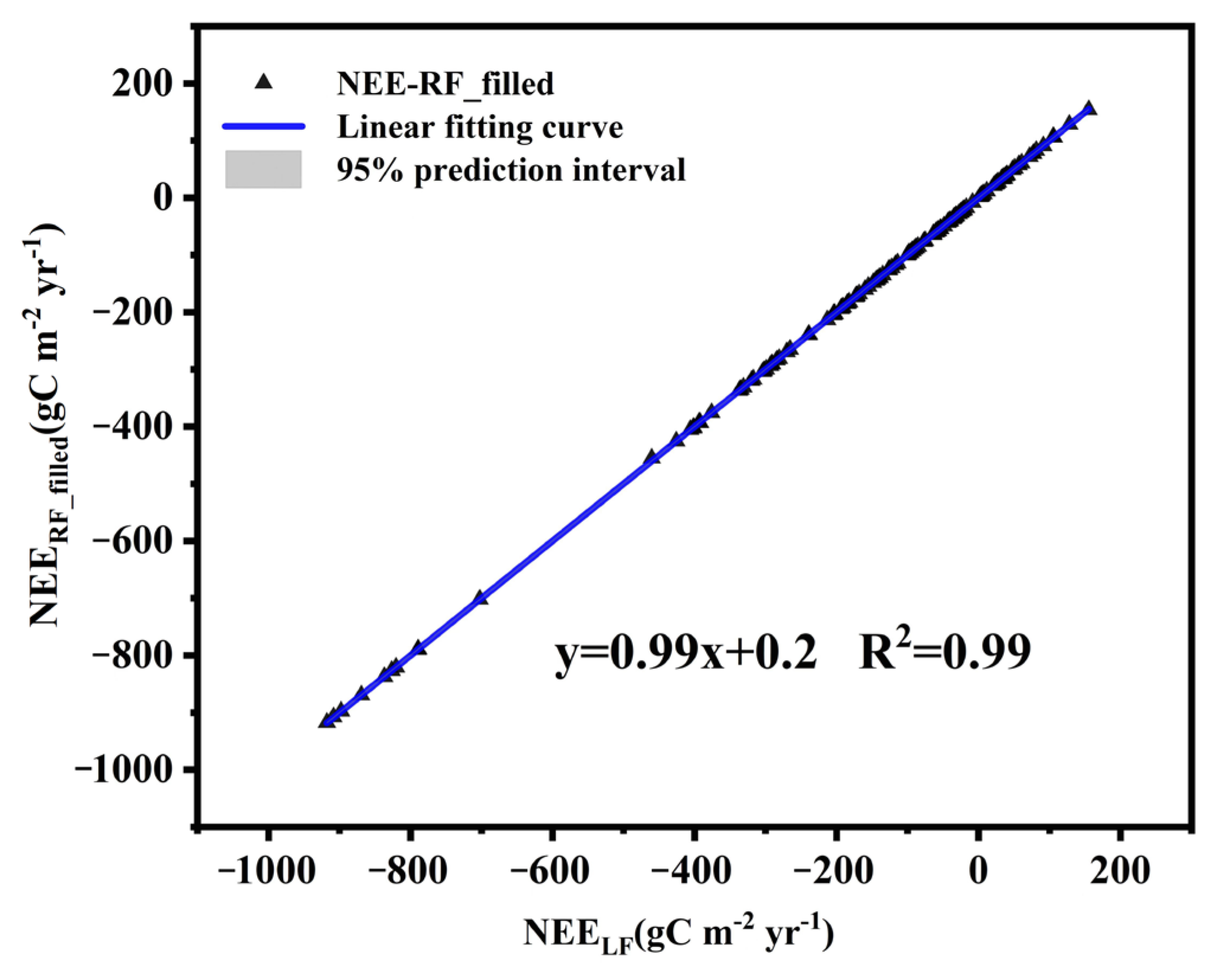
4.5. Consistency of the Annual Total NEE Filled Using Different Methods
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| ML Algorithms | Best Parameters |
|---|---|
| RF | n_estimators = 1636, min_samples_split = 5, min_saples_leaf = 2, max_features = 0.5, max_depth = None, bootstrap = False, random_state = 0 |
| XGboost | Subsample = 0.8, seed = 0, reg_lambda = 1, reg_alpha = 0, n_jobs = −1, n_estimtors = 3333, min_child_weight = 5, max_depth = 298, learning_rate = 0.01, gamma = 0.0, colsample_bytree = 0.7 |
| SVR | kernel = ‘rbf’, gamma = 0.1, C = 100 |
| BP neural network | input layer-intermediate layer-output layer = 120-10-1, activation function: sigmoid, trained 200 times |

References
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Loescher, H.W.; Oberbauer, S.F.; Gholz, H.L.; Clark, D.B. Environmental controls on net ecosystem-level carbon exchange and productivity in a Central American tropical wet forest. Glob. Chang. Biol. 2003, 9, 396–412. [Google Scholar] [CrossRef]
- Baldocchi, D.D. How eddy covariance flux measurements have contributed to our understanding of Global Change Biology. Glob. Chang. Biol. 2020, 26, 242–260. [Google Scholar] [CrossRef] [PubMed]
- Goulden, M.L.; Munger, J.W.; Fan, S.-M.; Daube, B.C.; Wofsy, S.C. Exchange of Carbon Dioxide by a Deciduous Forest: Response to Interannual Climate Variability. Science 1996, 271, 1576–1578. [Google Scholar] [CrossRef]
- Schimel, D.; Melillo, J.; Tian, H.; McGuire, A.D.; Kicklighter, D.; Kittel, T.; Rosenbloom, N.; Running, S.; Thornton, P.; Ojima, D.; et al. Contribution of increasing CO2 and climate to carbon storage by ecosystems in the United States. Science 2000, 287, 2004–2006. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem–Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Dragoni, D.; Schmid, H.P.; Grimmond, C.S.B.; Loescher, H.W. Uncertainty of annual net ecosystem productivity estimated using eddy covariance flux measurements. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Lee, S.-C.; Christen, A.; Black, T.A.; Jassal, R.S.; Briegel, F.; Nesic, Z. Combining flux variance similarity partitioning with artificial neural networks to gap-fill measurements of net ecosystem production of a Pacific Northwest Douglas-fir stand. Agric. For. Meteorol. 2021, 303, 108382. [Google Scholar] [CrossRef]
- Missik, J.E.C.; Liu, H.; Gao, Z.; Huang, M.; Chen, X.; Arntzen, E.; McFarland, D.P.; Ren, H.; Titzler, P.S.; Thomle, J.N.; et al. Groundwater—River Water Exchange Enhances Growing Season Evapotranspiration and Carbon Uptake in a Semiarid Riparian Ecosystem. J. Geophys. Res. Biogeosci. 2019, 124, 99–114. [Google Scholar] [CrossRef]
- Moffat, A.M.; Papale, D.; Reichstein, M.; Hollinger, D.Y.; Richardson, A.D.; Barr, A.G.; Beckstein, C.; Braswell, B.H.; Churkina, G.; Desai, A.R.; et al. Comprehensive comparison of gap-filling techniques for eddy covariance net carbon fluxes. Agric. For. Meteorol. 2007, 147, 209–232. [Google Scholar] [CrossRef]
- Soloway, A.D.; Amiro, B.D.; Dunn, A.L.; Wofsy, S.C. Carbon neutral or a sink? Uncertainty caused by gap-filling long-term flux measurements for an old-growth boreal black spruce forest. Agric. For. Meteorol. 2017, 233, 110–121. [Google Scholar] [CrossRef]
- Wutzler, T.; Lucas-Moffat, A.; Migliavacca, M.; Knauer, J.; Sickel, K.; Šigut, L.; Menzer, O.; Reichstein, M. Basic and extensible post-processing of eddy covariance flux data with REddyProc. Biogeosciences 2018, 15, 5015–5030. [Google Scholar] [CrossRef]
- Whelan, A.; Mitchell, R.; Staudhammer, C.; Starr, G. Cyclic occurrence of fire and its role in carbon dynamics along an edaphic moisture gradient in longleaf pine ecosystems. PLoS ONE 2013, 8, e54045. [Google Scholar] [CrossRef]
- Irvin, J.; Zhou, S.; McNicol, G.; Lu, F.; Liu, V.; Fluet-Chouinard, E.; Ouyang, Z.; Knox, S.H.; Lucas-Moffat, A.; Trotta, C.; et al. Gap-filling eddy covariance methane fluxes: Comparison of machine learning model predictions and uncertainties at FLUXNET-CH4 wetlands. Agric. For. Meteorol. 2021, 308–309, 108528. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Boudhina, N.; Zitouna-Chebbi, R.; Mekki, I.; Jacob, F.; Ben Mechlia, N.; Masmoudi, M.; Prévot, L. Evaluating four gap-filling methods for eddy covariance measurements of evapotranspiration over hilly crop fields. Geosci. Instrum. Methods Data Syst. 2018, 7, 151–167. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for long term energy flux data sets. Agric. For. Meteorol. 2001, 107, 71–77. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Wang, E.; Smith, C.J.; Macdonald, B.C.T.; Hunt, J.R.; Xing, H.; Denmead, O.T.; Zeglin, S.; Zhao, Z.; Isaac, P. Making sense of cosmic-ray soil moisture measurements and eddy covariance data with regard to crop water use and field water balance. Agric. Water Manag. 2018, 204, 271–280. [Google Scholar] [CrossRef]
- Hui, D.; Wan, S.; Su, B.; Katul, G.; Monson, R.; Luo, Y. Gap-filling missing data in eddy covariance measurements using multiple imputation (MI) for annual estimations. Agric. For. Meteorol. 2004, 121, 93–111. [Google Scholar] [CrossRef]
- Kim, Y.; Johnson, M.S.; Knox, S.H.; Black, T.A.; Dalmagro, H.J.; Kang, M.; Kim, J.; Baldocchi, D. Gap-filling approaches for eddy covariance methane fluxes: A comparison of three machine learning algorithms and a traditional method with principal component analysis. Glob. Chang. Biol. 2020, 26, 1499–1518. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Hollinger, D.Y. A method to estimate the additional uncertainty in gap-filled NEE resulting from long gaps in the CO2 flux record. Agric. For. Meteorol. 2007, 147, 199–208. [Google Scholar] [CrossRef]
- Yao, J.; Gao, Z.; Huang, J.; Liu, H.; Wang, G. Technical note: Uncertainties in eddy covariance CO2 fluxes in a semiarid sagebrush ecosystem caused by gap-filling approaches. Atmos. Chem. Phys. 2021, 21, 15589–15603. [Google Scholar] [CrossRef]
- Huang, H.; Hsieh, C. Gap-Filling of Surface Fluxes Using Machine Learning Algorithms in Various Ecosystems. Water 2020, 12, 3415. [Google Scholar] [CrossRef]
- Mahabbati, A.; Beringer, J.; Leopold, M.; McHugh, I.; Cleverly, J.; Isaac, P.; Izady, A. A comparison of gap-filling algorithms for eddy covariance fluxes and their drivers. Geosci. Instrum. Methods Data Syst. 2021, 10, 123–140. [Google Scholar] [CrossRef]
- Zhu, S.; Clement, R.; McCalmont, J.; Davies, C.A.; Hill, T. Stable gap-filling for longer eddy covariance data gaps: A globally validated machine-learning approach for carbon dioxide, water, and energy fluxes. Agric. For. Meteorol. 2022, 314, 108777. [Google Scholar] [CrossRef]
- Cui, X.; Goff, T.; Cui, S.; Menefee, D.; Wu, Q.; Rajan, N.; Nair, S.; Phillips, N.; Walker, F. Predicting carbon and water vapor fluxes using machine learning and novel feature ranking algorithms. Sci. Total Environ. 2021, 775, 145130. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Yang, S.; Zhang, J. Rice evapotranspiration at the field and canopy scales under water-saving irrigation. Meteorol. Atmos. Phys. 2017, 130, 227–240. [Google Scholar] [CrossRef]
- Ouyang, Z.; Chen, J.; Becker, R.; Chu, H.; Xie, J.; Shao, C.; John, R. Disentangling the confounding effects of PAR and air temperature on net ecosystem exchange at multiple time scales. Ecol. Complex. 2014, 19, 46–58. [Google Scholar] [CrossRef]
- Pahari, R.; Leclerc, M.Y.; Zhang, G.; Nahrawi, H.; Raymer, P. Carbon dynamics of a warm season turfgrass using the eddy-covariance technique. Agric. Ecosyst. Environ. 2018, 251, 11–25. [Google Scholar] [CrossRef]
- Li, C.; Li, Z.; Zhang, F.; Lu, Y.; Duan, C.; Xu, Y. Seasonal dynamics of carbon dioxide and water fluxes in a rice-wheat rotation system in the Yangtze-Huaihe region of China. Agric. Water Manag. 2023, 275, 107992. [Google Scholar] [CrossRef]
- Eckhardt, T.; Knoblauch, C.; Kutzbach, L.; Holl, D.; Simpson, G.; Abakumov, E.; Pfeiffer, E.-M. Partitioning net ecosystem exchange of CO2 on the pedon scale in the Lena River Delta, Siberia. Biogeosciences 2019, 16, 1543–1562. [Google Scholar] [CrossRef]
- Natali, S.M.; Watts, J.D.; Rogers, B.M.; Potter, S.; Ludwig, S.M.; Selbmann, A.-K.; Sullivan, P.F.; Abbott, B.W.; Arndt, K.A.; Birch, L.; et al. Large loss of CO2 in winter observed across the northern permafrost region. Nat. Clim. Chang. 2019, 9, 852–857. [Google Scholar] [CrossRef]
- Whelan, A.; Starr, G.; Staudhammer, C.L.; Loescher, H.W.; Mitchell, R.J. Effects of drought and prescribed fire on energy exchange in longleaf pine ecosystems. Ecosphere 2015, 6, art128. [Google Scholar] [CrossRef]
- Gao, Z.M.; Liu, H.P.; Missik, J.E.C.; Yao, J.Y.; Huang, M.Y.; Chen, X.Y.; Arntzen, E.; Mcfarland, D.P. Mechanistic links between underestimated CO2 fluxes and non-closure of the surface energy balance in a semi-arid sagebrush ecosystem. Environ. Res. Lett. 2019, 14, 044016. [Google Scholar] [CrossRef]
- Chu, D.; Shen, H.; Guan, X.; Chen, J.M.; Li, X.; Li, J.; Zhang, L. Long time-series NDVI reconstruction in cloud-prone regions via spatio-temporal tensor completion. Remote Sens. Environ. 2021, 264, 112632. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Barnhart, B.L.; Nandage, H.K.W.; Eichinger, W. Assessing Discontinuous Data Using Ensemble Empirical Mode Decomposition. Adv. Adapt. Data Anal. 2012, 3, 483–491. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C.J.A. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Chu, H.; Luo, X.; Ouyang, Z.; Chan, W.S.; Dengel, S.; Biraud, S.C.; Torn, M.S.; Metzger, S.; Kumar, J.; Arain, M.A.; et al. Representativeness of Eddy-Covariance flux footprints for areas surrounding AmeriFlux sites. Agric. For. Meteorol. 2021, 301-302, 108350. [Google Scholar] [CrossRef]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C.; et al. A data-driven analysis of energy balance closure across FLUXNET research sites: The role of landscape scale heterogeneity. Agric. For. Meteorol. 2013, 171–172, 137–152. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, D.; Yao, J.; Yu, S.; Ma, Y.; Li, L.; Gao, Z. Eddy Covariance CO2 Flux Gap Filling for Long Data Gaps: A Novel Framework Based on Machine Learning and Time Series Decomposition. Remote Sens. 2023, 15, 2695. https://doi.org/10.3390/rs15102695
Gao D, Yao J, Yu S, Ma Y, Li L, Gao Z. Eddy Covariance CO2 Flux Gap Filling for Long Data Gaps: A Novel Framework Based on Machine Learning and Time Series Decomposition. Remote Sensing. 2023; 15(10):2695. https://doi.org/10.3390/rs15102695
Chicago/Turabian StyleGao, Dexiang, Jingyu Yao, Shuting Yu, Yulong Ma, Lei Li, and Zhongming Gao. 2023. "Eddy Covariance CO2 Flux Gap Filling for Long Data Gaps: A Novel Framework Based on Machine Learning and Time Series Decomposition" Remote Sensing 15, no. 10: 2695. https://doi.org/10.3390/rs15102695
APA StyleGao, D., Yao, J., Yu, S., Ma, Y., Li, L., & Gao, Z. (2023). Eddy Covariance CO2 Flux Gap Filling for Long Data Gaps: A Novel Framework Based on Machine Learning and Time Series Decomposition. Remote Sensing, 15(10), 2695. https://doi.org/10.3390/rs15102695










