A Novel Multistage Back Projection Fast Imaging Algorithm for Terahertz Video Synthetic Aperture Radar
Abstract
1. Introduction
- (1)
- FFBP uses inefficient BP integration to obtain the sub-images in the initial stage. The calculation amount increases with the sub-aperture length and is close to BPA. Differently, the proposed algorithm uses more efficient PFA to process the sub-aperture data, reducing the number of interpolations in this stage.
- (2)
- FFBP is based on local polar coordinates, and the fusion stage requires many 2D interpolations. Differently, the proposed algorithm is based on the global Cartesian coordinate with a simpler geometric configuration, and the fusion stage can be realized by wavenumber domain splicing, preventing the introduction and accumulation of interpolation errors in FFBP. Through the above improvements, the efficiency is significantly improved.
- (3)
- Aiming at the geometric distortion caused by linear phase error (LPE) and considering the image rotation caused by different flight trajectories, the proposed algorithm carries out 2D resampling to correct the geometric distortion and rotate the images into the same ground Cartesian coordinate.
2. Materials
2.1. Radar Echo Model
2.2. Review of FFBP
3. Methods
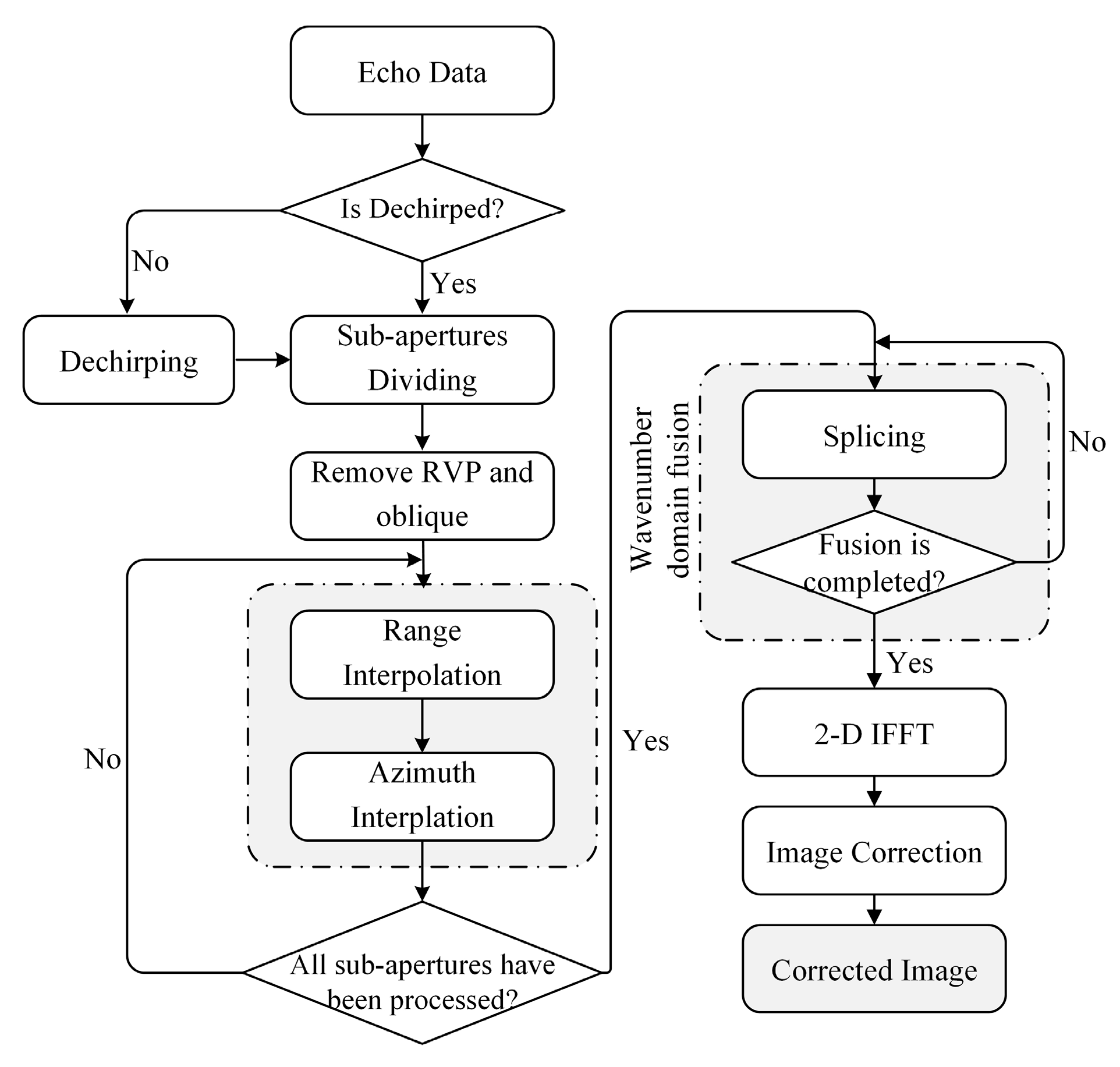
3.1. Principle of the Proposed Algorithm
3.2. Geometric Distortion Analysis and Correction
3.3. Algorithm Processing Flow
3.4. Computing Load Analysis
4. Results
4.1. Point Targets Simulation Results
4.2. Surface Target Simulation Results
5. Conclusions
- (1)
- By analyzing the number of complex multiplications, it is shown that the computational effort of the proposed algorithm is significantly lower than that of FFBP.
- (2)
- The point target simulation experiment analyses the IRW, PSLR, and ISLR at each stage, confirming that the proposed algorithm and the FFBP focusing effect is comparable. Analyzing the positions of point targets before and after image correction confirms that the proposed algorithm can effectively complete the correction of geometric distortion and rotation.
- (3)
- The surface target simulation experiment analyses the entropy, NRMSE, PSNR, and the running time of different algorithms, indicating that the proposed algorithm is more efficient and ensures the quality and uniformity of images.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, X.; Yu, W. Processing video-SAR data with the fast backprojection method. IEEE Trans. Aerosp. Electron. Syst. 2017, 52, 2838–2848. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Yu, H.; Chen, J.; Xing, M.; Hong, W. Sparse synthetic aperture radar imaging from compressed sensing and machine learning: Theories, applications, and trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–69. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, G.; Zhou, R.; Zhang, H.; Hong, W. Multi-channel back-projection algorithm for mmwave automotive MIMO SAR imaging with Doppler-division multiplexing. IEEE J. Sel. Top. Signal Process. 2022, 1–13. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, Y.; Xie, Z.; Yang, X.; Guo, W.; Wu, F.; Li, C.; Zhang, X. Joint autofocus and registration for video-SAR by using sub-aperture point cloud. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103295. [Google Scholar] [CrossRef]
- Defense Advanced Research Projects Agency. Broad Agency Announcement: Video Synthetic Aperture Radar (Visar) System Design and Development. 2012. Available online: https://govtribe.com/project/videosynthetic-aperture-radarvisar-system-design-and-development (accessed on 2 March 2022).
- Zuo, F.; Li, J.; Hu, R.; Pi, Y. Unified Coordinate System Algorithm for Terahertz Video-SAR Image Formation. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 725–735. [Google Scholar] [CrossRef]
- Zhao, B.; Han, Y.; Wang, H.; Tang, L.; Liu, X.; Wang, T. Robust shadow tracking for video SAR. IEEE Geosci. Remote Sens. Lett. 2021, 18, 821–825. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, W.; Xia, L.; Lin, Y.; Shang, S.; Hong, W. Video SAR Moving Target Shadow Detection Based on Intensity Information and Neighborhood Similarity. Remote Sens. 2023, 15, 1859. [Google Scholar] [CrossRef]
- Yang, C.; Chen, Z.; Deng, Y.; Wang, W.; Wang, P.; Zhao, F. Generation of Multiple Frames for High Resolution Video SAR Based on Time Frequency Sub-Aperture Technique. Remote Sens. 2023, 15, 264. [Google Scholar] [CrossRef]
- Miller, J.; Bishop, E.; Doerry, A. An application of backprojection for video SAR image formation exploiting a subaperature circular shift register. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XX, Baltimore, MD, USA, 23 May 2013; pp. 874609.1–874609.14. [Google Scholar]
- Wallace, H.B. Development of a video SAR for FMV through clouds. In Proceedings of the Open Architecture/Open Business Model Net-Centric Systems and Defense Transformation, Baltimore, MD, USA, 21 May 2015; pp. 64–65. [Google Scholar]
- Langdon, R.M.; Handerek, V.; Harrison, P.; Eisele, H.; Stringer, M.; Tae, C.F.; Dunn, M.H. Military applications of terahertz imaging. In Proceedings of the 1st EMRS DTC Technical Conference, Edinburgh, UK, 20–21 May 2004. [Google Scholar]
- Li, Y.; Wu, Q.; Jiang, J.; Ding, X.; Zheng, Q.; Zhu, Y. A High-Frequency Vibration Error Compensation Method for Terahertz SAR Imaging Based on Short-Time Fourier Transform. Appl. Sci. 2021, 11, 10862. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Li, Y.; Ding, L.; Zheng, Q.; Zhu, Y.; Sheng, J. A Novel High-Frequency Vibration Error Estimation and Compensation Algorithm for THz-SAR Imaging Based on Local FrFT. Sensors 2020, 20, 2669. [Google Scholar] [CrossRef] [PubMed]
- Appleby, R.; Anderton, R.N. Millimeter-Wave and Submillimeter-Wave Imaging for Security and Surveillance. Proc. IEEE 2007, 95, 1683–1690. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Q.; Wu, J.; Li, P.; Ding, L. Estimation of High-Frequency Vibration Parameters for Terahertz SAR Imaging Based on FrFT with Combination of QML and RANSAC. IEEE Access 2021, 9, 5485–5496. [Google Scholar] [CrossRef]
- Jiang, J.; Li, Y.; Zheng, Q. A THz Video SAR Imaging Algorithm Based on Chirp Scaling. In Proceedings of the 2021 CIE International Conference on Radar, Haikou, China, 15–19 December 2021; pp. 656–660. [Google Scholar]
- Pu, W.; Wang, X.; Wu, J.; Huang, Y.; Yang, J. Video SAR Imaging Based on Low-Rank Tensor Recovery. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 188–202. [Google Scholar] [CrossRef] [PubMed]
- An, H.; Wu, J.; Teh, K.C.; Sun, Z.; Li, Z.; Yang, J. Joint Low-Rank and Sparse Tensors Recovery for Video Synthetic Aperture Radar Imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5214913. [Google Scholar] [CrossRef]
- Moradikia, M.; Samadi, S.; Hashempour, H.R.; Cetin, M. Video-SAR Imaging of Dynamic Scenes Using Low-Rank and Sparse Decomposition. IEEE Trans. Comput. Imaging 2021, 7, 384–398. [Google Scholar] [CrossRef]
- Gorham, L.; Moore, R.J. SAR image formation toolbox for MATLAB. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XVII, Orlando, FL, USA, 8–9 April 2010; Volume 7699, pp. 223–263. [Google Scholar]
- Musgrove, C. Polar Format Algorithm: Survey of Assumptions and Approximations; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2012.
- Yegulalp, A.F. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium (Cat. No. 99CH36249), Waltham, MA, USA, 22–22 April 1999. [Google Scholar]
- Basu, S.K.; Bresler, Y. O(N2log2N) filtered backprojection reconstruction algorithm for tomography. IEEE Trans. Image Process. 2000, 9, 1760–1773. [Google Scholar] [CrossRef]
- Ulander, L.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Wahl, D.E.; Yocky, D.A.; Jakowatz, C.V., Jr.; Zelnio, E.G.; Garber, F.D. An implementation of a fast backprojection image formation algorithm for spotlight-mode SAR. Proc. Spie 2008, 6970, 8. [Google Scholar]
- Yang, Z.M.; Sun, G.C.; Xing, M. A new fast Back-Projection Algorithm using Polar Format Algorithm. In Proceedings of the Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013; pp. 373–376. [Google Scholar]
- Lei, Z.; Li, H.L.; Qiao, Z.J.; Xu, Z.W. A Fast BP Algorithm With Wavenumber Spectrum Fusion for High-Resolution Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1460–1464. [Google Scholar]
- Yang, Z.; Xing, M.; Zhang, L.; Bao, Z. A coordinate-transform based FFBP algorithm for high-resolution spotlight SAR imaging. Sci. China Inf. Sci. 2015, 2, 11. [Google Scholar] [CrossRef]
- Gorham, L.; Majumder, U.K.; Buxa, P.; Backues, M.J.; Lindgren, A.C. Implementation and analysis of a fast backprojection algorithm. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XIII, Orlando, FL, USA, 17–21 April 2006; Volume 6237. [Google Scholar]
- Rodriguez-Cassola, M.; Prats, P.; Krieger, G.; Moreira, A. Efficient Time-Domain Image Formation with Precise Topography Accommodation for General Bistatic SAR Configurations. Aerosp. Electron. Syst. IEEE Trans. 2011, 47, 2949–2966. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, L.; Zhou, S.; Bi, G.; Yang, H. Spectrum-Oriented FFBP Algorithm in Quasi-Polar Grid for SAR Imaging on Maneuvering Platform. IEEE Geosci. Remote Sens. Lett. 2017, 14, 724–728. [Google Scholar] [CrossRef]
- Xie, H.; Shi, S.; An, D.; Wang, G.; Wang, G.; Hui, X.; Huang, X.; Zhou, Z.; Chao, X.; Feng, W. Fast Factorized Backprojection Algorithm for One-Stationary Bistatic Spotlight Circular SAR Image Formation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1494–1510. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Xu, Z.; Wang, H.; Yang, L.; Bao, Z. Application of fast factorized back-projection algorithm for high-resolution highly squinted airborne SAR imaging. Sci. China Inf. Sci. 2017, 60, 1–17. [Google Scholar] [CrossRef]
- Frölind, P.O.; Ulander, L. Evaluation of angular interpolation kernels in fast back-projection SAR processing. IEE Proc.-Radar Sonar Navig. 2006, 153, 243–249. [Google Scholar] [CrossRef]
- Hanssen, R.; Bamler, R. Evaluation of Interpolation Kernels for SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 1999, 37, 318–321. [Google Scholar] [CrossRef]
- Selva, J.; Lopez-Sanchez, J.M. Efficient Interpolation of SAR Images for Coregistration in SAR Interferometry. IEEE Geosci. Remote Sens. Lett. 2007, 4, 411–415. [Google Scholar] [CrossRef]
- Garber, W.L.; Hawley, R.W. Extensions to polar formatting with spatially variant post-filtering. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XVIII, Orlando, FL, USA, 25–29 April 2011; p. 8051. [Google Scholar]
- Mao, D.; Rigling, B.D. Distortion correction and scene size limits for SAR bistatic polar format algorithm. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1103–1108. [Google Scholar]
- Rigling, B.D.; Moses, R.L. Taylor expansion of the differential range for monostatic SAR. IEEE Trans. Aerosp. Electron. Syst. 2008, 41, 60–64. [Google Scholar] [CrossRef]
- Jakowatz, C.V.; Wahl, D.E.; Thompson, P.A.; Doren, N.E. Space-variant filtering for correction of wavefront curvature effects in spotlight-mode SAR imagery formed via polar formatting. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery IV, Orlando, FL, USA, 21–25 April 1997; pp. 33–42. [Google Scholar]
- Doerry, A.W. Wavefront Curvature Limitations and Compensation to Polar Format Processing for Synthetic Aperture Radar Images; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2007.
- Zhu, D.; Zhu, Z. Range resampling in the polar format algorithm for spotlight SAR image formation using the chirp z-transform. IEEE Trans. Signal Process. 2007, 55, 1011–1023. [Google Scholar] [CrossRef]
- Yu, T.; Xing, M.; Zheng, B. The Polar Format Imaging Algorithm Based on Double Chirp-Z Transforms. IEEE Geosci. Remote Sens. Lett. 2008, 5, 610–614. [Google Scholar]
- Zuo, F.; Li, J. A ViSAR Imaging Method for Terahertz Band Using Chirp Z-Transform. In Proceedings of the Communications, Signal Processing, and Systems: Proceedings of the 2018 CSPS Volume II: Signal Processing 7th, Dalian, China, 14–16 July 2018; pp. 796–804. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Mao, Y.; Wang, X.; Xiang, M. Joint Three-dimensional Location Algorithm for Airborne Interferometric SAR System. J. Radars 2013, 2, 60–67. [Google Scholar] [CrossRef]
- Franceschetti, G.; Migliaccio, M.; Riccio, D.; Schirinzi, G. SARAS: A synthetic aperture radar(SAR) raw signal simulator. IEEE Trans. Geosci. Remote Sens. 1992, 30, 110–123. [Google Scholar] [CrossRef]
- Shoalehvar, A. Synthetic Aperture Radar (SAR) Raw Signal Simulation. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2012. [Google Scholar]
- Zhang, S.-S.; Zeng, T.; Long, T.; Chen, J. Research on echo simulation of space-borne bistatic SAR. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]

















| Parameters | Explain | Value |
|---|---|---|
| center frequency | 220 GHz | |
| bandwidth | 1.2 GHz | |
| pulse width | 50 μs | |
| elevation angle | 45° | |
| slant range of scene center | 1 km | |
| flight speed | 50 m/s | |
| radius of the imaging area | 60 m | |
| range resolution | 0.12 m | |
| azimuth resolution | 0.12 m |
| Sub-Image 1 of the Proposed Algorithm (A/B/C) | Sub-Image 2 of the Proposed Algorithm (A/B/C) | Sub-Image 1 of FFBP (A/B/C) | ||
|---|---|---|---|---|
| IRW (m) | Range | 0.16/0.15/0.16 | 0.16/0.16/0.15 | 0.16/0.15/0.15 |
| Azimuth | 1.03/0.99/1.04 | 1.01/0.97/1.02 | 0.93/0.97/0.98 | |
| PSLR (dB) | Range | −12.90/−13.31/−13.16 | −12.95/−13.22/−13.04 | −13.30/−13.43/−13.26 |
| Azimuth | −12.38/−12.97/−12.88 | −12.33/−11.69/−12.53 | −17.80/−11.79/−12.70 | |
| ISLR (dB) | Azimuth | −28.49/−29.21/−31.64 | −28.43/−30.35/−28.63 | −26.70/−27.91/−25.82 |
| Range | −26.81/−25.75/−29.48 | −27.66/−23.92/−22.39 | −45.21/−26.27/−29.89 |
| The Proposed Algorithm (A/B/C) | FFBP (A/B/C) | ||
|---|---|---|---|
| IRW (m) | Range | 0.15/0.15/0.15 | 0.16/0.16/0.15 |
| Azimuth | 0.14/0.12/0.15 | 0.11/0.12/0.12 | |
| PSLR (dB) | Range | −11.89/−11.69/−12.23 | −11.18/−10.88/−13.10 |
| Azimuth | −18.35/−13.42/−14.17 | −3.95/−14.03/−10.20 | |
| ISLR (dB) | Range | −Inf/-Inf/-Inf | −22.53/−23.51/−25.57 |
| Azimuth | −Inf/−25.08/-Inf | −15.85/−25.90/−19.91 |
| Point A | Point B | Point C | |
|---|---|---|---|
| Real Position | (−50, 50) | (0, 0) | (10, −40) |
| Before Correction | (−48.9, 52.6) | (0.1, 0.1) | (10.6, −39.4) |
| After Correction | (−50.4, 50.2) | (0.1, 0.1) | (10.3, −39.8) |
| The Proposed Algorithm (A/B/C) | FFBP (A/B/C) | ||
|---|---|---|---|
| IRW (m) | Range | 0.15/0.15/0.16 | 0.17/0.16/0.15 |
| Azimuth | 0.16/0.12/0.14 | 0.11/0.12/0.12 | |
| PSLR (dB) | Range | −12.65/−11.77/−14.61 | −13.02/−10.79/−13.03 |
| Azimuth | −12.36/−13.30/−16.68 | −9.43/−13.73/−9.77 | |
| ISLR (dB) | Range | −34.70/-Inf/−34.38 | −27.51/−23.52/−25.92 |
| Azimuth | -Inf/−24.84/-Inf | −27.57/−25.75/−25.63 |
| Point A | Point B | Point C | |
|---|---|---|---|
| Real Position | (−50, 50) | (0, 0) | (10, −40) |
| Before Correction | (−17.6, 70.1) | (0.1, −0.1) | (−11.81, −39.1) |
| After Correction | (−50.5, 50) | (−0.1, 0) | (9.6, −40) |
| Entropy | NRMSE | PSNR (dB) | Running Time (min) | |
|---|---|---|---|---|
| Input image | 12.88 | 0 | ∞ | / |
| Imaging of the proposed algorithm | 13.74 | 0.18 | 31.05 | 2.12 |
| Imaging of FFBP | 13.52 | 0.22 | 30.14 | 35.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Q.; Shang, S.; Li, Y.; Zhu, Y. A Novel Multistage Back Projection Fast Imaging Algorithm for Terahertz Video Synthetic Aperture Radar. Remote Sens. 2023, 15, 2602. https://doi.org/10.3390/rs15102602
Zheng Q, Shang S, Li Y, Zhu Y. A Novel Multistage Back Projection Fast Imaging Algorithm for Terahertz Video Synthetic Aperture Radar. Remote Sensing. 2023; 15(10):2602. https://doi.org/10.3390/rs15102602
Chicago/Turabian StyleZheng, Qibin, Shuangli Shang, Yinwei Li, and Yiming Zhu. 2023. "A Novel Multistage Back Projection Fast Imaging Algorithm for Terahertz Video Synthetic Aperture Radar" Remote Sensing 15, no. 10: 2602. https://doi.org/10.3390/rs15102602
APA StyleZheng, Q., Shang, S., Li, Y., & Zhu, Y. (2023). A Novel Multistage Back Projection Fast Imaging Algorithm for Terahertz Video Synthetic Aperture Radar. Remote Sensing, 15(10), 2602. https://doi.org/10.3390/rs15102602








