Distillation Sparsity Training Algorithm for Accelerating Convolutional Neural Networks in Embedded Systems
Abstract
1. Introduction
- We design a unified training framework based on KD and network sparsity for model compression techniques.
- Combined with general-purpose hardware, a uniform compression format is designed, to implement this pruning matrix for efficient storage and memory indexing.
- The sparse model can be used for any general-purpose hardware acceleration. We tested the DST algorithm on an embedded system, and the acceleration result was significant.
- The proposed algorithm was tested on the CIFAR-100, MSTAR, and FUSAR-Ship data sets. Its performance was significant on both SAR and optical data sets.
2. Related Work
2.1. KD
2.2. Pruning
2.2.1. Unstructured Pruning
2.2.2. Structured Pruning
2.2.3. KD and Pruning
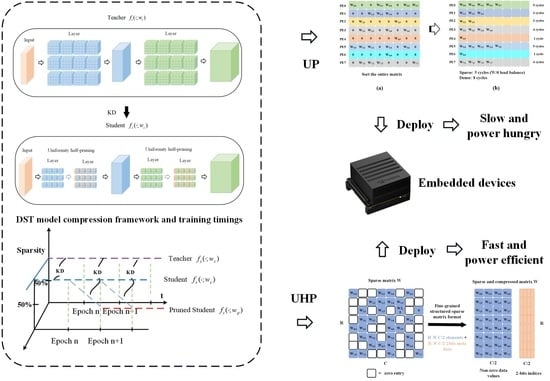
3. Motivation
3.1. Redundancy in the Student Network
3.2. Acceleration and Storage of Unstructured Pruning
4. Methodology
4.1. Overview
- (1)
- Train a teacher network and obtain .
- (2)
- Apply the UHP algorithm to prune and obtain the pruned student network .
- (3)
- Distill the teacher network to the student network .
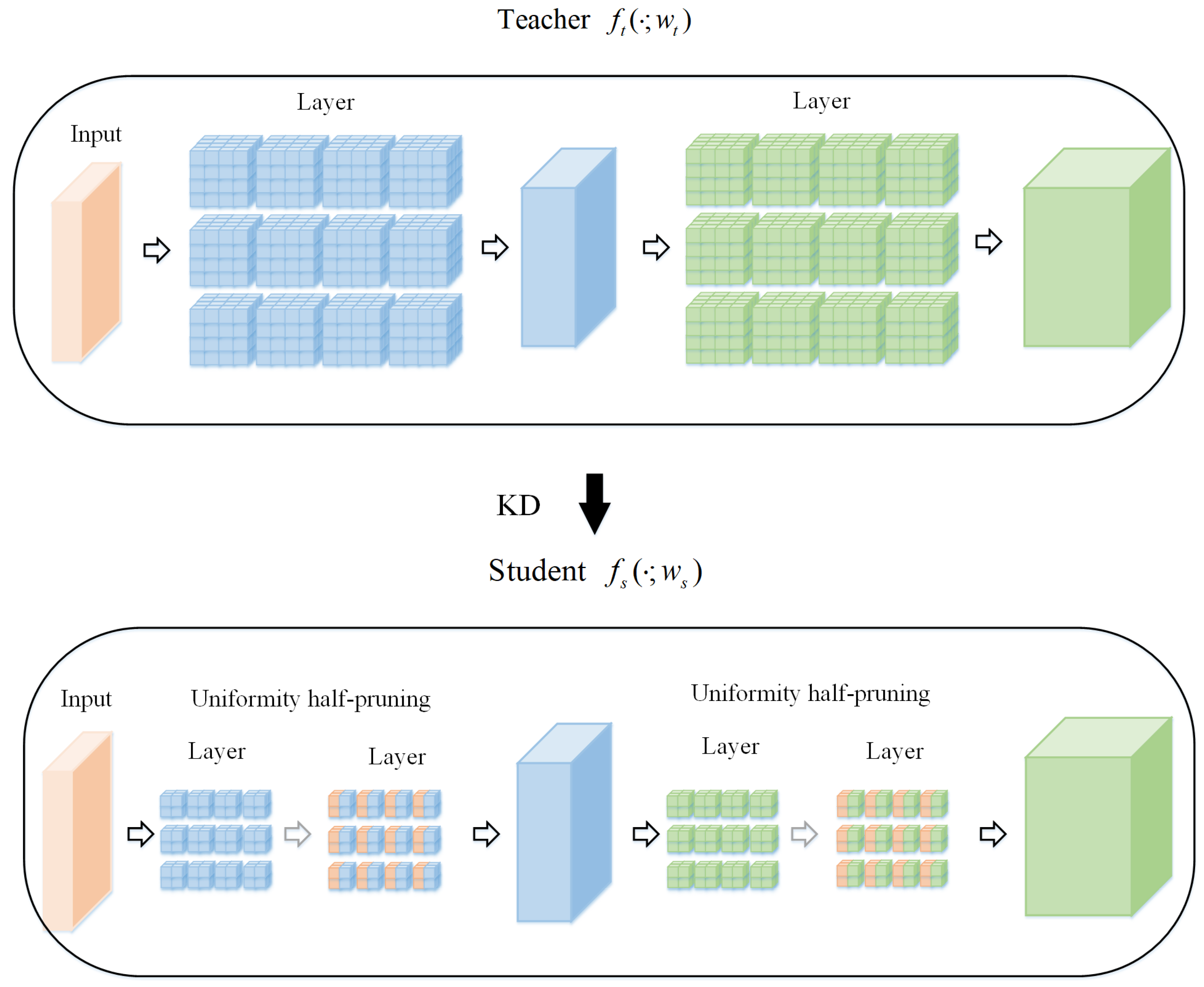
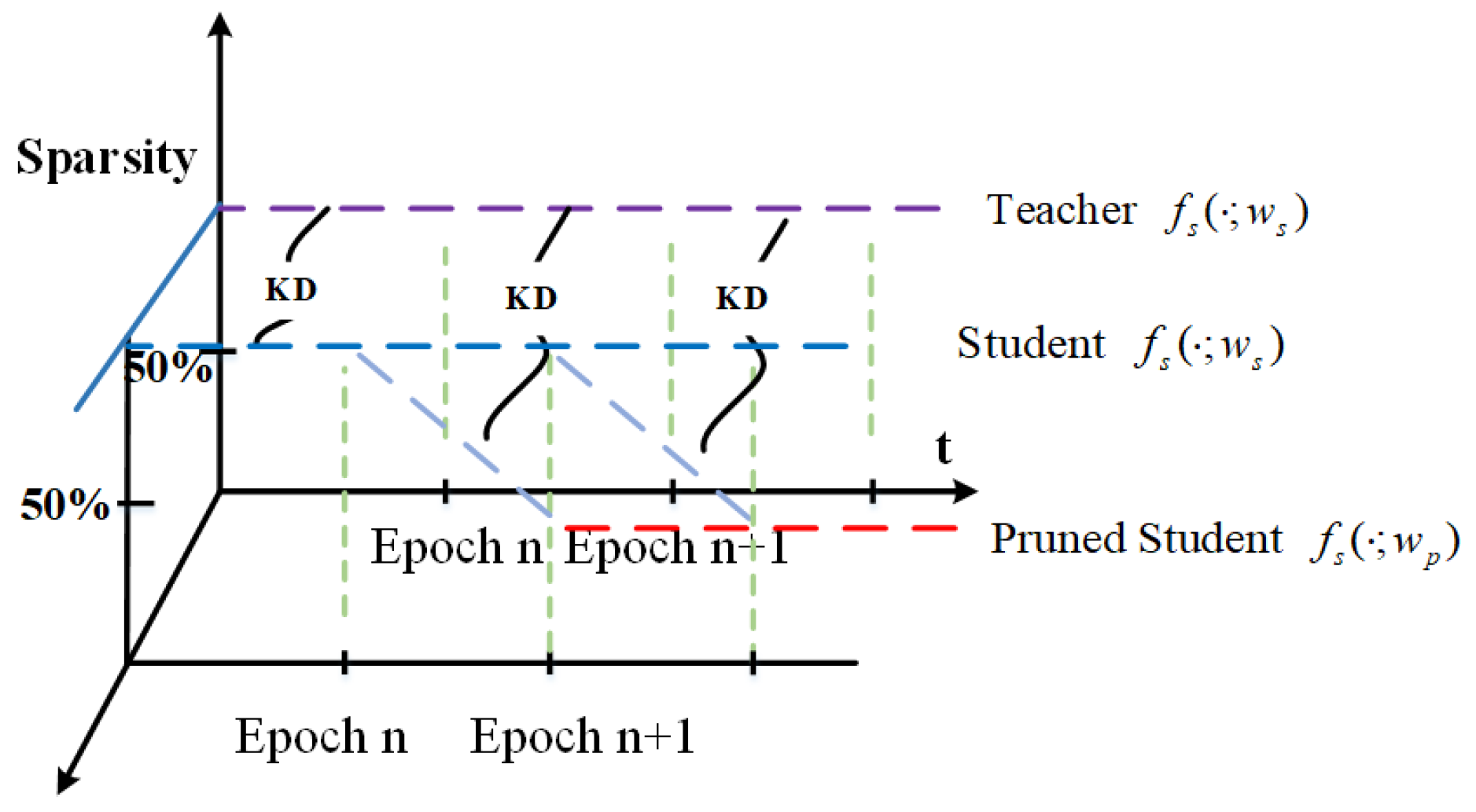
4.2. Distillation Formulation
4.3. Pruned Student Distillation
4.4. Pruning Formulation
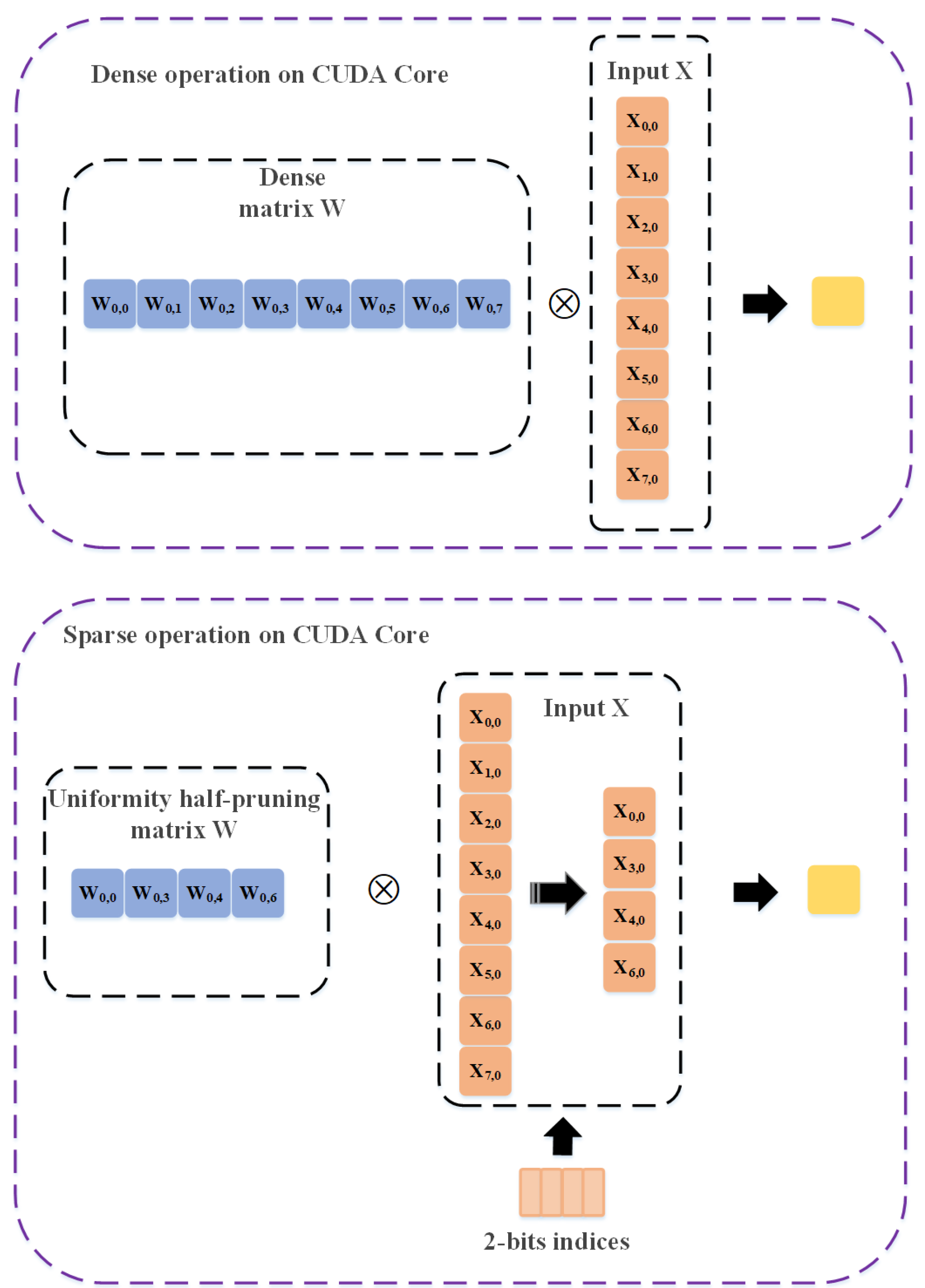
4.5. Uniformity Half-Pruning
4.5.1. Pruning Structure
4.5.2. Efficient Storage and Accelerating Computation
4.5.3. UHP Computation Overhead
4.6. DST Workflow
| Algorithm 1: Distillation Sparsity Training (DST) |
| input: teacher network pretrained student network Initialize: KD , if ← then ← by UHP end Initialize: KD , if ← then output: end |
5. Experiment
5.1. Data Sets
5.2. Experiment Setup and Implementation Details
5.3. Pruning Analysis
5.4. Computational Performance Evaluation
5.5. Accuracy Evaluation
5.5.1. Results on CIFAR-100
5.5.2. MSTAR Results
5.5.3. FUSAR-Ship Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ATR | Automatic Target Recognition |
| KD | Knowledge Distillation |
| DST | Distillation Sparsity Training |
| CNNs | Convolutional Neural Networks |
| PKT | Probabilistic Knowledge Transfer |
| AT | Attention Transfer |
| HSAKD | Hierarchical Self-supervised Augmented Knowledge Distillation |
| IMP | Iterative Magnitude Pruning |
| LTR | Lottery Ticket Rewinding |
| LR | Learning Rate |
| BN | Batch Normalization |
| PEs | multiple Processing units |
| ALUs | Arithmetic Logic Units |
| FPS | Frames Per Second |
| UHP | Uniformity Half-Pruning |
| UP | Unstructured Pruning |
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep Ordinal Regression Network for Monocular Depth Estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2002–2011. [Google Scholar] [CrossRef]
- Godard, C.; Aodha, O.M.; Brostow, G.J. Unsupervised Monocular Depth Estimation with Left-Right Consistency. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6602–6611. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. arXiv 2017, arXiv:1708.02002. [Google Scholar]
- Hestness, J.; Narang, S.; Ardalani, N.; Diamos, G.; Jun, H.; Kianinejad, H.; Patwary, M.M.A.; Yang, Y.; Zhou, Y. Deep Learning Scaling Is Predictable, Empirically. arXiv 2017, arXiv:1712.00409. [Google Scholar]
- Hestness, J.; Ardalani, N.; Diamos, G. Beyond Human-Level Accuracy: Computational Challenges in Deep Learning. arXiv 2019, arXiv:1909.01736. [Google Scholar]
- Patwary, M.; Chabbi, M.; Jun, H.; Huang, J.; Diamos, G.; Church, K. Language Modeling at Scale. arXiv 2018, arXiv:1810.10045. [Google Scholar]
- Shazeer, N.; Cheng, Y.; Parmar, N.; Tran, D.; Vaswani, A.; Koanantakool, P.; Hawkins, P.; Lee, H.; Hong, M.; Young, C.; et al. Mesh-TensorFlow: Deep Learning for Supercomputers. Adv. Neural Inf. Process. Syst. 2018, 31, 1–10. [Google Scholar]
- Choudhary, T.; Mishra, V.; Goswami, A.; Sarangapani, J. A Comprehensive Survey on Model Compression and Acceleration. Artif. Intell. Rev. 2020, 53, 5113–5155. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. Model Compression and Acceleration for Deep Neural Networks: The Principles, Progress, and Challenges. IEEE Signal Process. Mag. 2018, 35, 126–136. [Google Scholar] [CrossRef]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge Distillation: A Survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Mirzadeh, S.I.; Farajtabar, M.; Li, A.; Levine, N.; Matsukawa, A.; Ghasemzadeh, H. Improved Knowledge Distillation via Teacher Assistant. AAAI 2020, 34, 5191–5198. [Google Scholar] [CrossRef]
- Park, D.Y.; Cha, M.H.; Jeong, C.; Kim, D.S.; Han, B. Learning Student-Friendly Teacher Networks for Knowledge Distillation. Adv. Neural Inf. Process. Syst. 2021, 34, 13292–13303. [Google Scholar]
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal Brain Damage. Adv. Neural Inf. Process. Syst. 1990, 2, 598–605. [Google Scholar]
- Walsh, C.A. Peter huttenlocher (1931–2013). Nature 2013, 502, 172. [Google Scholar] [CrossRef]
- Ström, N. Sparse Connection and Pruning in Large Dynamic Artificial Neural Networks. In Proceedings of the 5th European Conference on Speech Communication and Technology (Eurospeech 1997), Rhodes, Greece, 22–25 September 1997; pp. 2807–2810. [Google Scholar] [CrossRef]
- Frankle, J.; Carbin, M. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. arXiv 2019, arXiv:1803.03635. [Google Scholar]
- NVIDIA. NVIDIA Turing GPU Architecture Whitepaper; NVIDIA: Santa Clara, CA, USA, 2018. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Gordon, A.; Eban, E.; Nachum, O.; Chen, B.; Wu, H.; Yang, T.J.; Choi, E. MorphNet: Fast & Simple Resource-Constrained Structure Learning of Deep Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1586–1595. [Google Scholar] [CrossRef]
- Passalis, N.; Tefas, A. Learning Deep Representations with Probabilistic Knowledge Transfer. In Computer Vision–ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11215, pp. 283–299. [Google Scholar] [CrossRef]
- Zagoruyko, S.; Komodakis, N. Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer. arXiv 2017, arXiv:1612.03928. [Google Scholar]
- Tian, Y.; Krishnan, D.; Isola, P. Contrastive Representation Distillation. arXiv 2022, arXiv:1910.10699. [Google Scholar]
- Kim, J.; Park, S.; Kwak, N. Paraphrasing Complex Network: Network Compression via Factor Transfer. Adv. Neural Inf. Process. Syst. 2018, 31, 1–13. [Google Scholar]
- Denil, M.; Shakibi, B.; Dinh, L.; Ranzato, M. Predicting Parameters in Deep Learning. Adv. Neural Inf. Process. Syst. 2013, 26, 1–9. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network In Network. arXiv 2014, arXiv:1312.4400. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Hanson, S.J.; Pratt, L.Y. Comparing Biases for Minimal Network Construction with Back-Propagation. Adv. Neural Inf. Process. Syst. 1988, 1, 177–185. [Google Scholar]
- Hassibi, B.; Stork, D.G. Second Order Derivatives for Network Pruning: Optimal Brain Surgeon. Adv. Neural Inf. Process. Syst. 1992, 5, 164–171. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2016, arXiv:1510.00149. [Google Scholar]
- Liu, Z.; Sun, M.; Zhou, T.; Huang, G.; Darrell, T. Rethinking the Value of Network Pruning. arXiv 2019, arXiv:1810.05270. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Han, S.; Liu, X.; Mao, H.; Pu, J.; Pedram, A.; Horowitz, M.A.; Dally, W.J. EIE: Efficient Inference Engine on Compressed Deep Neural Network. arXiv 2016, arXiv:1602.01528. [Google Scholar] [CrossRef]
- Anwar, S.; Hwang, K.; Sung, W. Structured Pruning of Deep Convolutional Neural Networks. J. Emerg. Technol. Comput. Syst. 2017, 13, 1–18. [Google Scholar] [CrossRef]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. arXiv 2017, arXiv:1608.08710. [Google Scholar]
- Liu, Z.; Mu, H.; Zhang, X.; Guo, Z.; Yang, X.; Cheng, K.T.; Sun, J. MetaPruning: Meta Learning for Automatic Neural Network Channel Pruning. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3295–3304. [Google Scholar] [CrossRef]
- Su, X.; You, S.; Wang, F.; Qian, C.; Zhang, C.; Xu, C. BCNet: Searching for Network Width with Bilaterally Coupled Network. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 2175–2184. [Google Scholar] [CrossRef]
- He, Y.; Kang, G.; Dong, X.; Fu, Y.; Yang, Y. Soft Filter Pruning for Accelerating Deep Convolutional Neural Networks. arXiv 2018, arXiv:1808.06866. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1398–1406. [Google Scholar] [CrossRef]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning Structured Sparsity in Deep Neural Networks. Adv. Neural Inf. Process. Syst. 2016, 29, 1–9. [Google Scholar]
- Zhou, H.; Alvarez, J.M.; Porikli, F. Less Is More: Towards Compact CNNs. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Volume 9908, pp. 662–677. [Google Scholar] [CrossRef]
- Ye, J.; Lu, X.; Lin, Z.; Wang, J.Z. Rethinking the Smaller-Norm-Less-Informative Assumption in Channel Pruning of Convolution Layers. arXiv 2018, arXiv:1802.00124. [Google Scholar]
- Zhuang, T.; Zhang, Z.; Huang, Y.; Zeng, X.; Shuang, K.; Li, X. Neuron-Level Structured Pruning Using Polarization Regularizer. Adv. Neural Inf. Process. Syst. 2020, 33, 9865–9877. [Google Scholar]
- Aghli, N.; Ribeiro, E. Combining Weight Pruning and Knowledge Distillation For CNN Compression. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 20–25 June 2021; pp. 3185–3192. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Q. Shallowing Deep Networks: Layer-Wise Pruning Based on Feature Representations. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 3048–3056. [Google Scholar] [CrossRef] [PubMed]
- Sarridis, I.; Koutlis, C.; Kordopatis-Zilos, G.; Kompatsiaris, I.; Papadopoulos, S. InDistill: Information Flow-Preserving Knowledge Distillation for Model Compression. arXiv 2022, arXiv:2205.10003. [Google Scholar]
- Park, J.; No, A. Prune Your Model Before Distill It. arXiv 2022, arXiv:2109.14960. [Google Scholar]
- Romero, A.; Ballas, N.; Kahou, S.E.; Chassang, A.; Gatta, C.; Bengio, Y. FitNets: Hints for Thin Deep Nets. arXiv 2015, arXiv:1412.6550. [Google Scholar]
- Yang, Y.; Qiu, J.; Song, M.; Tao, D.; Wang, X. Distilling Knowledge From Graph Convolutional Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7072–7081. [Google Scholar] [CrossRef]
- Yuan, L.; Tay, F.E.; Li, G.; Wang, T.; Feng, J. Revisiting Knowledge Distillation via Label Smoothing Regularization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3902–3910. [Google Scholar] [CrossRef]
- NVIDIA. Sparse Matrix Storage Formats. 2020. Available online: https://www.gnu.org/software/gsl/doc/html/spmatrix.html (accessed on 1 September 2022).
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Keydel, E.R.; Lee, S.W.; Moore, J.T. MSTAR Extended Operating Conditions: A Tutorial. In Aerospace/Defense Sensing and Controls; Zelnio, E.G., Douglass, R.J., Eds.; Sandia National Laboratory: Albuquerque, NM, USA, 1996; pp. 228–242. [Google Scholar] [CrossRef]
- Hou, X.; Ao, W.; Song, Q.; Lai, J.; Wang, H.; Xu, F. FUSAR-Ship: Building a High-Resolution SAR-AIS Matchup Dataset of Gaofen-3 for Ship Detection and Recognition. Sci. China Inf. Sci. 2020, 63, 140303. [Google Scholar] [CrossRef]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning Both Weights and Connections for Efficient Neural Network. Adv. Neural Inf. Process. Syst. 2018, 28, 1–9. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chen, B.; Wang, W.; Chen, L.C.; Tan, M.; Chu, G.; Vasudevan, V.; Zhu, Y.; Pang, R.; et al. Searching for MobileNetV3. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar] [CrossRef]


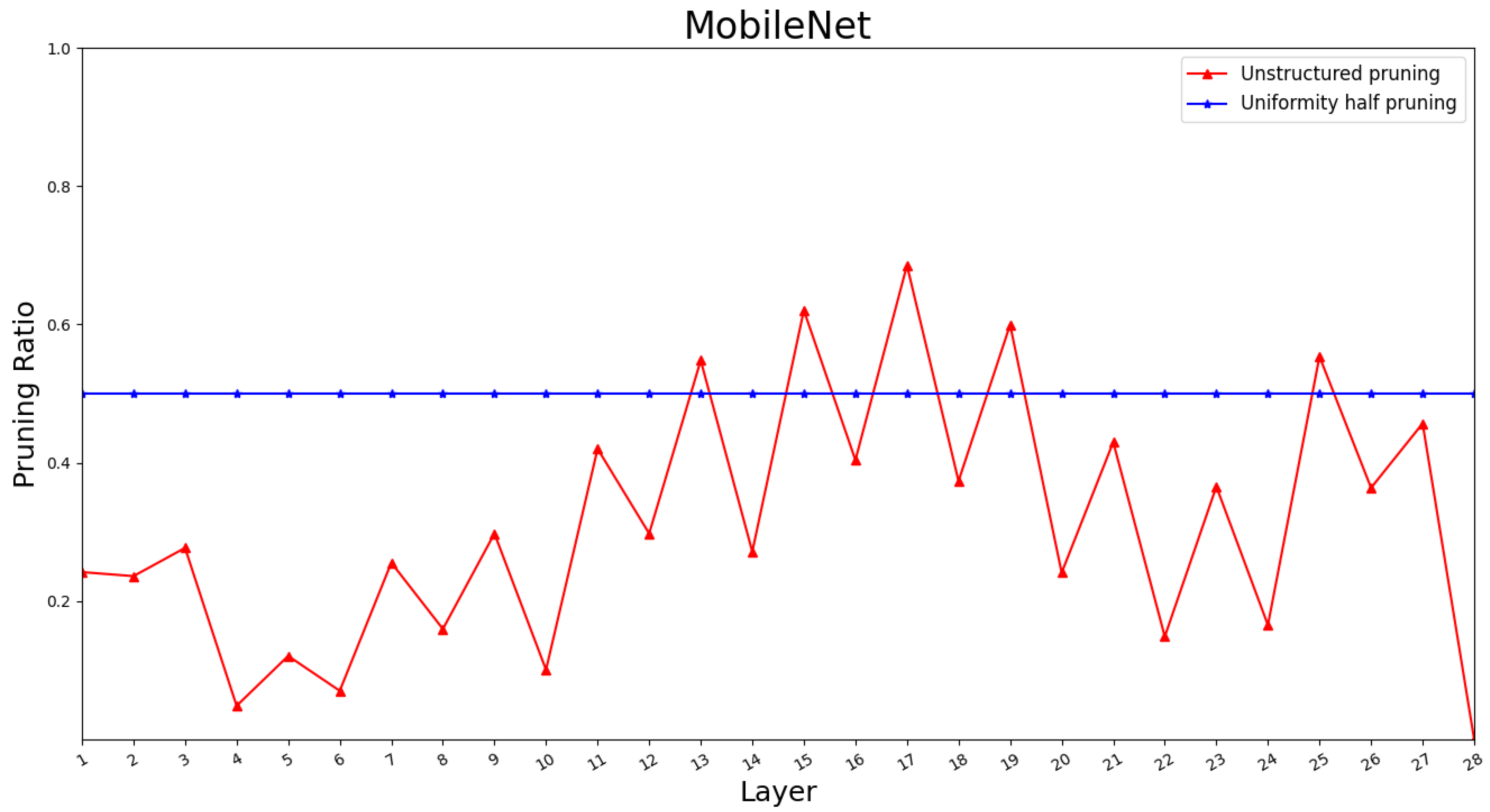
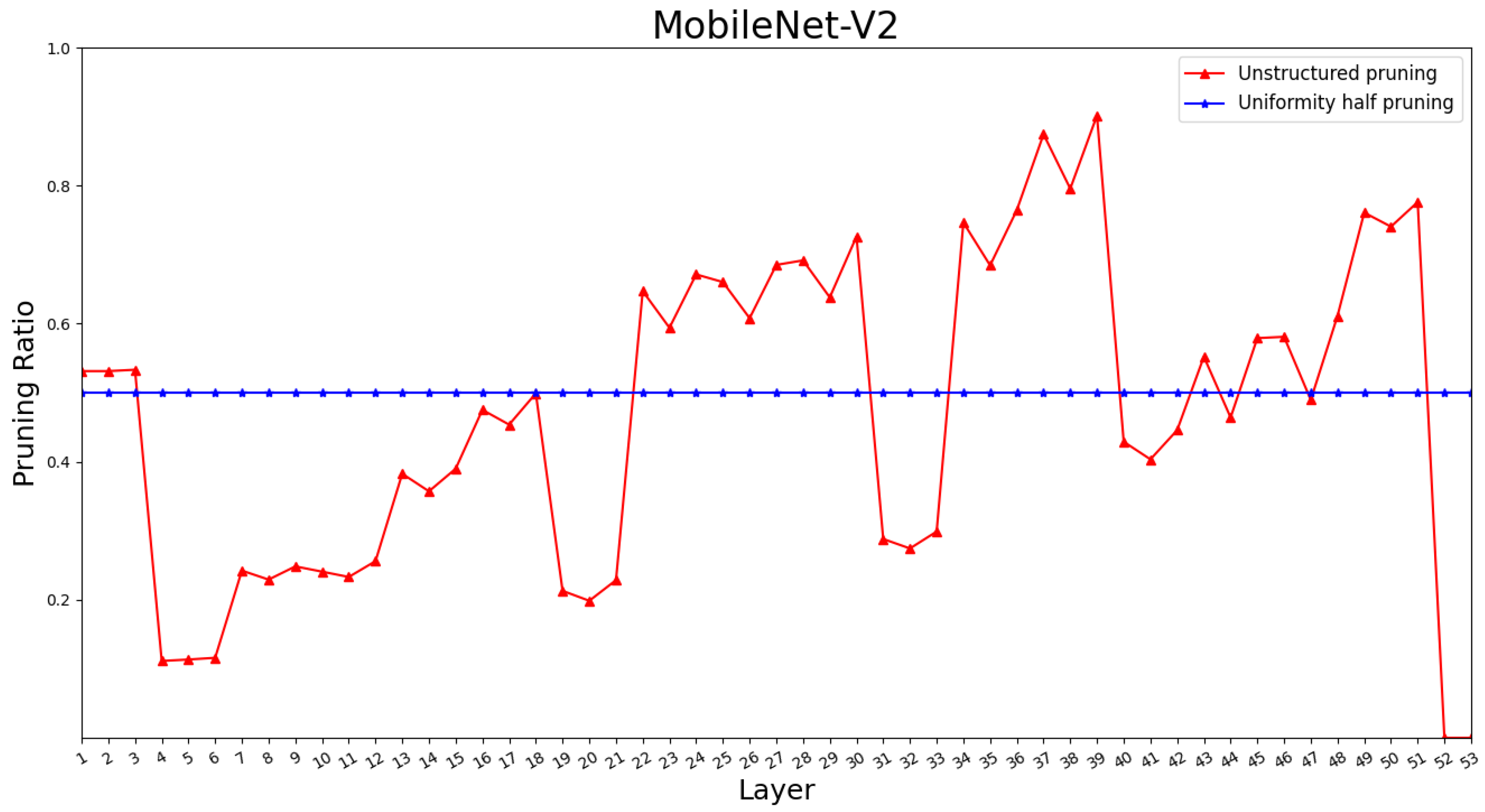


| MobileNet | MobileNetV2 | MobileNetV3 | Baseline | |||
|---|---|---|---|---|---|---|
| Model Size (MB) | Pretrained | 12.70 | 9.69 | 16.70 | ✔ | |
| DST-UP [48] | 12.90 | 9.16 | 16.20 | - | ||
| DST-UHP (Ours) | 9.84 | 5.78 | 10.40 | - | ||
| Relative | +1.57%/ | 5.47%/ | −2.99%/ | - | ||
| Parameters (M) | Pretrained | 4.20 | 3.40 | 5.40 | ✔ | |
| DST-UP [48] | 2.10 | 1.70 | 2.70 | - | ||
| DST-UHP (Ours) | 2.10 | 1.70 | 2.70 | - | ||
| Relative | −50.00%/ | −50.00%/ | −50.00%/ | - | ||
| FPS | Pretrained | 1160 | 675 | 622 | ✔ | |
| Input | DST-UP [48] | 1230 | 693 | 682 | - | |
| 32 × 32 | DST-UHP (Ours) | 2668 | 1418 | 1386 | - | |
| Relative | +6.03%/+130.00% | +2.67%/+110.70% | +3.22%/+122.83% | - | ||
| Pretrained | 748 | 422 | 510 | ✔ | ||
| Input | DST-UP [48] | 769 | 431 | 538 | - | |
| 224 × 224 | DST-UHP (Ours) | 1720 | 886 | 1078 | - | |
| Relative | +2.81%/+129.90% | +2.13%/+110.00% | +5.49%/+111.37% | - |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNet | * | * | * | 67.58% [59] | Baseline |
| * | ✔ | * | 68.26% [58] | +0.68% | |||
| * | * | ✔ | 67.62% | −0.32% | |||
| ResNet18 | 76.41% | MobileNet | ✔ | * | * | 71.62% [14] | +4.04% |
| ✔ | ✔ | * | 70.75% [48] | +3.17% | |||
| ✔ | * | ✔ | 71.48% | +4.00% | |||
| ResNet34 | 78.05% | ✔ | * | * | 70.17% [14] | +2.59% | |
| ✔ | ✔ | * | 69.88% [48] | +2.30% | |||
| ✔ | * | ✔ | 70.79% | +3.21% | |||
| ResNet50 | 78.87% | ✔ | * | * | 71.25% [14] | +3.67% | |
| ✔ | ✔ | * | 70.16% [48] | +2.58% | |||
| ✔ | * | ✔ | 71.30% | +3.72% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNetV2 | * | * | * | 68.90% [60] | Baseline |
| * | ✔ | * | 69.10% [58] | +0.20% | |||
| * | * | ✔ | 68.33% | −0.57% | |||
| ResNet18 | 76.41% | MobileNetV2 | ✔ | * | * | 70.17% [14] | +1.27% |
| ✔ | ✔ | * | 68.93% [48] | +0.03% | |||
| ✔ | * | ✔ | 69.72% | +0.82% | |||
| ResNet34 | 78.05% | ✔ | * | * | 69.89% [14] | +0.99% | |
| ✔ | ✔ | * | 68.00% [48] | −0.90% | |||
| ✔ | * | ✔ | 69.17% | +0.27% | |||
| ResNet50 | 78.87% | ✔ | * | * | 69.75% [14] | +0.85% | |
| ✔ | ✔ | * | 69.13% [48] | +0.23% | |||
| ✔ | * | ✔ | 69.45% | +0.55% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNetV3 | * | * | * | 71.79% [61] | Baseline |
| * | ✔ | * | 72.03% [58] | +0.24% | |||
| * | * | ✔ | 71.75% | −0.04% | |||
| ResNet18 | 76.41% | MobileNetV3 | ✔ | * | * | 73.41% [14] | +1.62% |
| ✔ | ✔ | * | 72.69% [48] | +0.90% | |||
| ✔ | * | ✔ | 73.37% | +1.58% | |||
| ResNet34 | 78.05% | ✔ | * | * | 73.54% [14] | +1.75% | |
| ✔ | ✔ | * | 72.15% [48] | +0.36% | |||
| ✔ | * | ✔ | 73.47% | +1.68% | |||
| ResNet50 | 78.87% | ✔ | * | * | 74.52% [14] | +2.73% | |
| ✔ | ✔ | * | 73.96% [48] | +2.17% | |||
| ✔ | * | ✔ | 74.49% | +2.70% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNet | * | * | * | 98.56% [59] | Baseline |
| * | ✔ | * | 98.34% [58] | −0.22% | |||
| * | * | ✔ | 98.21% | −0.35% | |||
| ResNet18 | 99.78% | MobileNet | ✔ | * | * | 99.32% [14] | +0.76% |
| ✔ | ✔ | * | 99.24% [48] | +0.68% | |||
| ✔ | * | ✔ | 99.31% | +0.75% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNetV2 | * | * | * | 96.54% [60] | Baseline |
| * | ✔ | * | 96.55% [58] | +0.01% | |||
| * | * | ✔ | 96.48% | −0.06% | |||
| ResNet18 | 99.78% | MobileNetV2 | ✔ | * | * | 99.40% [14] | +2.86% |
| ✔ | ✔ | * | 99.36% [48] | +2.82% | |||
| ✔ | * | ✔ | 99.39% | +2.85% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNetV3 | * | * | * | 99.13% [61] | Baseline |
| * | ✔ | * | 99.06% [58] | +0.07% | |||
| * | * | ✔ | 99.05% | −0.08% | |||
| ResNet18 | 99.78% | MobileNetV3 | ✔ | * | * | 99.59% [14] | +0.46% |
| ✔ | ✔ | * | 99.55% [48] | +0.42% | |||
| ✔ | * | ✔ | 99.58% | +0.45% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNet | * | * | * | 70.42% [59] | Baseline |
| * | ✔ | * | 70.35% [58] | −0.07% | |||
| * | * | ✔ | 70.67% | +0.25% | |||
| ResNet18 | 74.38% | MobileNet | ✔ | * | * | 74.82% [14] | +4.40% |
| ✔ | ✔ | * | 73.59% [48] | +3.17% | |||
| ✔ | * | ✔ | 74.31% | +3.89% | |||
| ResNet34 | 75.31% | ✔ | * | * | 75.35% [14] | +4.93% | |
| ✔ | ✔ | * | 73.82% [48] | +3.40% | |||
| ✔ | * | ✔ | 74.92% | +4.50% | |||
| ResNet50 | 75.87% | ✔ | * | * | 75.62% [14] | +5.20% | |
| ✔ | ✔ | * | 74.01% [48] | +3.59% | |||
| ✔ | * | ✔ | 74.62% | +4.20% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNetV2 | * | * | * | 71.37% [60] | Baseline |
| * | ✔ | * | 70.16% [58] | −1.21% | |||
| * | * | ✔ | 69.27% | −2.10% | |||
| ResNet18 | 74.38% | MobileNetV2 | ✔ | * | * | 74.16% [14] | +2.79% |
| ✔ | ✔ | * | 73.29% [48] | +1.92% | |||
| ✔ | * | ✔ | 74.25% | +2.88% | |||
| ResNet34 | 75.31% | ✔ | * | * | 74.87% [14] | +3.50% | |
| ✔ | ✔ | * | 73.74% [48] | +2.37% | |||
| ✔ | * | ✔ | 74.68% | +3.31% | |||
| ResNet50 | 75.87% | ✔ | * | * | 74.98% [14] | +3.61% | |
| ✔ | ✔ | * | 73.85% [48] | +2.48% | |||
| ✔ | * | ✔ | 74.96% | +3.59% |
| Teacher | Teacher Acc (Top-1) | Student | KD | UP [58] | UHP (Ours) | Student Acc (Top-1) | Relative |
|---|---|---|---|---|---|---|---|
| * | * | MobileNetV3 | * | * | * | 71.12% [61] | Baseline |
| * | ✔ | * | 70.19% [58] | −0.93% | |||
| * | * | ✔ | 71.44% | +0.12% | |||
| ResNet18 | 74.38% | MobileNetV3 | ✔ | * | * | 74.57% [14] | +3.45% |
| ✔ | ✔ | * | 73.18% [48] | +2.06% | |||
| ✔ | * | ✔ | 74.58% | +3.46% | |||
| ResNet34 | 75.31% | ✔ | * | * | 74.98% [14] | +3.86% | |
| ✔ | ✔ | * | 74.15% [48] | +3.03% | |||
| ✔ | * | ✔ | 74.92% | +3.80% | |||
| ResNet50 | 75.87% | ✔ | * | * | 75.92% [14] | +4.80% | |
| ✔ | ✔ | * | 74.13% [48] | +3.01% | |||
| ✔ | * | ✔ | 75.64% | +4.52% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, P.; Xu, T.; Xiao, X.; Li, W.; Wang, H. Distillation Sparsity Training Algorithm for Accelerating Convolutional Neural Networks in Embedded Systems. Remote Sens. 2023, 15, 2609. https://doi.org/10.3390/rs15102609
Xiao P, Xu T, Xiao X, Li W, Wang H. Distillation Sparsity Training Algorithm for Accelerating Convolutional Neural Networks in Embedded Systems. Remote Sensing. 2023; 15(10):2609. https://doi.org/10.3390/rs15102609
Chicago/Turabian StyleXiao, Penghao, Teng Xu, Xiayang Xiao, Weisong Li, and Haipeng Wang. 2023. "Distillation Sparsity Training Algorithm for Accelerating Convolutional Neural Networks in Embedded Systems" Remote Sensing 15, no. 10: 2609. https://doi.org/10.3390/rs15102609
APA StyleXiao, P., Xu, T., Xiao, X., Li, W., & Wang, H. (2023). Distillation Sparsity Training Algorithm for Accelerating Convolutional Neural Networks in Embedded Systems. Remote Sensing, 15(10), 2609. https://doi.org/10.3390/rs15102609