Abstract
Leaf Area Index (LAI) is an important parameter which can be used for crop growth monitoring and yield estimation. Many studies have been carried out to estimate LAI with remote sensing data obtained by sensors mounted on Unmanned Aerial Vehicles (UAVs) in major crops; however, most of the studies used only a single type of sensor, and the comparative study of different sensors and sensor combinations in the model construction of LAI was rarely reported, especially in soybean. In this study, three types of sensors, i.e., hyperspectral, multispectral, and LiDAR, were used to collect remote sensing data at three growth stages in soybean. Six typical machine learning algorithms, including Unary Linear Regression (ULR), Multiple Linear Regression (MLR), Random Forest (RF), eXtreme Gradient Boosting (XGBoost), Support Vector Machine (SVM) and Back Propagation (BP), were used to construct prediction models of LAI. The results indicated that the hyperspectral and LiDAR data did not significantly improve the prediction accuracy of LAI. Comparison of different sensors and sensor combinations showed that the fusion of the hyperspectral and multispectral data could significantly improve the predictive ability of the models, and among all the prediction models constructed by different algorithms, the prediction model built by XGBoost based on multimodal data showed the best performance. Comparison of the models for different growth stages showed that the XGBoost-LAI model for the flowering stage and the universal models of the XGBoost-LAI and RF-LAI for three growth stages showed the best performances. The results of this study might provide some ideas for the accurate estimation of LAI, and also provide novel insights toward high-throughput phenotyping of soybean with multi-modal remote sensing data.
1. Introduction
Soybean is one of the most important crops in China and around the world [1]. High-throughput phenotyping enables efficient and accurate characterization of soybean plants at different growing stages, and the quantitative information is of great value for the yield estimation and assessment of varieties in soybean breeding. Leaf Area Index (LAI) is the total one-sided area of leaf tissue per unit ground surface area [2], and it is considered as an important indicator to reflect the change of vegetation leaf coverage and leaf area size, and being used to monitor the change of canopy structure and assess its adaptive ability to environment [3,4]. In crop breeding and production, LAI is also used for crop growth monitoring and yield estimation [5]. Therefore, it is of great importance to estimate LAI and obtain its dynamic changes during different growth stages.
Traditional methods for crop phenotype acquisition generally require on-site measurements and destructive sampling, which are labor-intensive, time-consuming, and difficult to apply to large-scale phenotyping due to their low efficiencies [6,7]. With the rapid development of remote sensing sensors and Unmanned Aerial Vehicle (UAV) technology, UAV-based phenotyping is widely applied in crop nutrient diagnosis [8], plant density estimation [9], pest and disease monitoring [10], and crop growth evaluation [11,12], etc., for the advantages of easy operation, low cost, fast acquisition, and high spatial and temporal resolution [13,14]. Specific traits such as Above-Ground Biomass (AGB) [15], LAI [16], and chlorophyll contents [17] in plants have also been estimated using UAV-based remote sensing data. In particular for LAI estimation, significant progresses have been achieved in various crops by different types of sensors, such as digital cameras [18], multispectral sensors [19], hyperspectral sensors [20], and LiDAR [21].
In addition to the choice of sensors, algorithms are also very important for the accurate prediction of phenotypes. Unary Linear Regression (ULR) and Multiple Linear Regression (MLR) are two traditional machine learning algorithms, which could perform efficiently upon large amounts of data without long running calculations [22]. Random Forest (RF) algorithm generates multiple decision trees by randomly selecting samples and features and obtains prediction results in a parallel manner [23]. Previous studies showed that RF performed better than linear regression in model construction [24,25]. Additionally, eXtreme Gradient Boosting (XGBoost) has been widely used in model construction in recent years [26]. XGBoost also adopts a sampling method that is similar to RF algorithm, which improves the operation speed and the prediction accuracy of the models [27]. Support Vector Machine (SVM) has excellent generalization capabilities and is robust to high-input space dimension. In recent years, SVM has become increasingly popular for solving regression and various classification problems with small samples, nonlinearity and high dimensionality [28]. Back Propagation (BP) neural network is the most widely used Artificial Neural Network (ANN) which is applicable for solving complex nonlinear problems with a higher accuracy and better generalization ability [29,30]. To data, different categories of algorithms, from traditional machine learning to deep learning, have been applied to construct phenotype estimation models in crops [31]. Siegmann and Jarmer [32] compared different algorithms, i.e., Support Vector Regression (SVR), RF, and Partial Least Squares Regression (PLSR), for the construction of estimation models of LAI in wheat, and found that SVR showed the best results in the case of cross-validation. Yuan et al. [33] compared the prediction models of LAI constructed by RF, ANN, SVM and PLSR in soybean. The results showed that RF performed the best for LAI estimation if the sample plots had large variances, while ANN performed the best if the sample plots had small variances. Wang et al. [29] used BP algorithm to construct models for growth monitoring in maize, and found that BP neural network algorithm could integrate multiple growth-related factors at each growth stage and the prediction models performed well in monitoring the growth conditions.
Many studies have been carried out to construct prediction models of LAI by remote sensing in crops with a simple or tall canopy structure, such as rice, maize, wheat and cotton [21,34]; however, most of the studies used one single type of sensor and only a few types of algorithms, while a systematic performance comparison of different sensors and sensor combinations, as well as different types of machine learning algorithms, in the model construction of LAI has been rarely reported, especially in soybean [35,36]. In this study, three different types of UAV-equipped sensors, i.e., hyperspectral, multispectral and LiDAR, and six typical machine learning algorithms, including ULR, MLR, RF, XGBoost, SVM and BP, were used to construct prediction models of LAI at three important growth stages in soybean. A systematical comparison of the models was performed. The objectives of this study were: (1) to compare the capability of different sensors and sensor combinations in characterizing soybean LAI, (2) to compare the ability of different machine learning algorithms in the construction of prediction models for LAI estimation, and (3) to explore the accurate prediction models for LAI at different development stages in soybean.
2. Materials and Methods
2.1. Field Experiment
The field experiment was conducted in the summer of 2021 at the agriculture station of Yunnan University in Chengjiang, Yunnan, China (24°40N, 102°56E). In order to increase the variations of LAI and improve the universality of the prediction models, 20 soybean lines including landraces and elite cultivars were planted with three replicates in a randomized complete block design (Figure 1). The plots were planted in rows 6.0 m long and 0.6 m row spacing, with a plot area of 30 m2.

Figure 1.
Field location and experimental design. The field trial was conducted in Chengjiang, Yunnan, China in 2021. The soybean lines were planted with three replicates in a randomized complete block design. 1–20 represent the entry number of each soybean line, and the color boxes indicate different replicates.
2.2. Data Collection
The hyperspectral data were acquired by a Gaiasky-mini2-VN mounted on the DJI M600 six-axis spacecraft, which has a spectral range of 400–1000 nm, a spatial resolution of 0.04 m, and a spectral resolution of 3 nm. The multispectral data were acquired by a DJI P4M multispectral sensor with a ground resolution of 5.3 cm at the flight height of 100 m. The LiDAR data were acquired by a DJI L1 mounted on the M300RTK aircraft (Figure 2a,c). The hyperspectral data were collected on August 4, August 21 and September 17, which was during the flowering, podding and mature stages, respectively, of the majority of the soybean plants. The multispectral and LiDAR data were only collected at the flowering and mature stage.

Figure 2.
Remote sensing data and ground data collection. (a) Gaiasky mini2-VN mounted on a DJI M600 was used for the hyperspectral data collection; (b) a DJI P4M was used for the multispectral data collection; (c) a DJI L1 on a M300RTK was used for the LiDAR data collection; (d) LAI measurement from the ground using a CI-110 plant canopy analyzer.
Ground LAI of each plot was determined by a CI-110 Plant Canopy Analyzer right after remote sensing data were obtained on the same day (Figure 2d). A five-point sampling method was adopted, and at each sampling point, LAI was measured six times. The average of the 30 readings was used as the LAI value for each plot. At each growth stage, 60 LAI values (one for each of the 60 plots) were obtained and were used to construct the prediction models.
2.3. Data Processing
PhotoScan and HiRegistrator were used to mosaic and correct the hyperspectral images, and SpecView was used to preprocess the hyperspectral data. ENVI 5.3 was used to establish the Region of Interest (ROI) and extract various reflectance metrics, including the Raw Reflectance (RR), the First Derivative Reflectance (FDR), the Red Edge Position (REP) [37], the maximum red-edge amplitude (Drmax) and minimum red-edge amplitude (Drmin) [38]. The RR-sensitive band, FDR-sensitive band, Red Edge Amplitude (Dr) and Red Edge Area (SDr) were obtained according to the Pearson correlation coefficient (Table 1).
DJI Terra was used to process the multispectral data, including the multispectral image mosaicing, geometric correction, de-noising and other basic operations, then subsequently to extract the different Vegetation Indices (VIs). A total of five VIs were analyzed, including the Normalized Difference Vegetation Index (NDVI), Green Normalized Difference Vegetative Index (GNDVI), Optimized Soil Adjusted Vegetation Index (OSAVI), Normalized Difference Red Edge Index (NDRE), and Land Cover Index (LCI) (Table 1).
The LiDAR point cloud data were preprocessed by DJI Terra to generate a LAS data set. In cloud compare, the ground points and vegetation points were roughly distinguished by Cloth Simulation Filter (CSF), and then were manually re-discriminated (Figure 3). Triangulated Irregular Network (TIN) algorithm was used to process the separated ground points in ArcGIS 10.3, and new ground points were generated by continuous encryption and iteration of the separated ground point cloud, so as to establish the TIN ground data. A Digital Elevation Model (DEM) of 0.1 m × 0.1 m was generated from the TIN ground data, and then a Digital Surface Model (DSM) was established. Finally, the DEM and DSM were used to generate a Canopy Height Model (CHM) [39,40]. Five LiDAR indices, including the Mean Plant Height (Hmean), 50 Percentile Plant Height (H50), 75 Percentile Plant Height (H75), Laser Penetration Index (LPI), and Three-Dimensional Volumetric Parameters (BIOVP) were extracted (Table 1).

Figure 3.
Ground point separation using the CHF algorithm. (a) Before separation; (b) after separation.
In order to fully explore useful parameters, processing methods of extracting data directly from the point cloud without destroying the original 3D structure were adopted, and the point cloud data were extracted using the software Agisoft. The point cloud data of the 60 plots were obtained and stratified separately. The overall point cloud was divided into four parts according to the point cloud height, and each part accounted for a quarter of the overall height from high to low. Six parameters, including P0–25, P25–50, P50–75, P25–100, P50–100, and P75–100, were obtained. Meanwhile, the Pmax, PCHmean and PAPCH were also calculated (Table 1).

Table 1.
Description/formula of modeling parameters used in this study.
Table 1.
Description/formula of modeling parameters used in this study.
| Type of Sensor | Modeling Parameters | Description/Formula | References |
|---|---|---|---|
| Hyperspectral | RR sensitive band | The RR band with the highest correlation with LAI | [41] |
| FDR sensitive band | The FDR band with the highest correlation with LAI | [42] | |
| Dr | The value of the first derivative corresponding to the position of the red edge | [38] | |
| SDr | Area enclosed by first derivative spectra in the red-edge range (680nm~760nm) | [38] | |
| Multispectral | LCI | (NIR − RE)/(NIR + R) 1 | [43] |
| NDRE | (NIR − RE)/(NIR + RE) 1 | [44] | |
| NDVI | (NIR − R)/(NIR + R) 1 | [45] | |
| GNDVI | (NIR − G)/(NIR + G) 1 | [46] | |
| OSAVI | (1 + 0.16)(NIR − R)/(NIR + R + 0.16) 1 | [47] | |
| LiDAR | Hmean | 2 | [48] |
| H50 | 2 | [48] | |
| H75 | 2 | [48] | |
| LPI | 3 | [49] | |
| BIOVP | 4 | [50] | |
| PAPCH | The percentage of point clouds above the average point cloud height in the total number of point clouds | - | |
| Pmax | The height with the largest number of point clouds was extracted and the percentage of the number of point clouds at this height | - | |
| P25–100 | The percentage of 25%~100% Height Point Cloud | - | |
| P50–100 | The percentage of 50%~100% Height Point Cloud | - | |
| P75–100 | The percentage of 75%~100% Height Point Cloud | - | |
| PCHmean | The percentage of the average Point Cloud Height | - | |
| P0–25 | The percentage of 0%~25% Height Point Cloud | - | |
| P25–50 | The percentage of 25%~50% Height Point Cloud | - | |
| P50–75 | The percentage of 50%~75% Height Point Cloud | - |
Notes: 1: R, G, NIR, and RE represent the reflectance values of red, green, near-infrared, and red-edge bands, respectively. 2: is the height of the ith height value, is the total number of height values in the plot, is the value from the standard normal distribution for the desired percentile and is the standard deviation of the variable. 3: is the total number of ground returns, and is the total number of returns. 4: represents the area covered by plants after resampling and image segmentation, indicates the plant height represented by the ith pixel, and is the number of pixels within .
2.4. Machine Learning Methods
A total of 60 LAI readings from all plots were obtained at each sampling stage. Among which, 2/3 of the data of each growth stage served as the training set, and the remaining 1/3 of the data as the validation set [11,51]. The ULR, MLR, RF, XGBoost, SVM and BP were adopted to construct the prediction models at each growth stage. All the prediction models were implemented in python.
In RF modeling, n estimators were set in the range of 1–200, and the max_depth was set in the range of 1–10. In XGBoost modeling, the n_estimators, learning_rate and max_depth were set in the ranges of 1–500, 0–1, and 1–10, respectively. In SVM modeling, the Radial Basis Function (RBF) was selected as the kernel function, and the best regularization parameter (C), parameter epsilon (epsilon) and model parameter gamma (gamma) were selected using the grid search method with a five-fold cross-validation. In BP modeling, the hidden layer was set to 1 or 2, the number of nodes in the hidden layer ranged from 3 to 40, and the number of nodes in the output layer was set to 1. The implicit layer used the Rectified Linear Unit (ReLU) activation function as the transfer function, while the output layer used the linear transfer function.
2.5. Model Accuracy Assessment
The predictive abilities of the univariate and multivariate models were evaluated by the R2 value, the accuracy of the model was evaluated by the RMSE, and the stabilities of the models were evaluated by the difference of the R2 values between the training set and the validation set.
An overview figure of the whole proposed framework is shown in Figure 4.
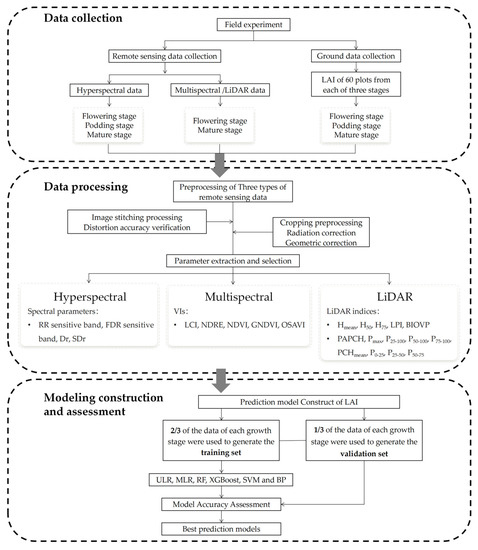
Figure 4.
An overview figure of the whole proposed framework of LAI prediction model construction in soybean.
3. Results
3.1. Prediction Models of LAI Based on Hyperspectral Data
3.1.1. Modeling Parameter Selection
The position and area of the red edge are two indicators which reflect the growth vigor of the plant [52]. The first-order derivative of the raw reflectance bands was calculated to extract the Dr and SDr at each growth stage. The results showed that the Dr values at the flowering and podding stages were both located at 728 nm, indicating that the soybean plants in these two stages had high growth vigor (Figure 5). However, at the mature stage, there was a “blue shift” of the REP to 718 nm, indicating that growth of soybean plants receded at the mature stage. The SDr value at the flowering stage was 0.510, which was the largest among the three growth stages, indicating that the flowering stage might be the most vigorous growth stage. The SDr value at the podding stage was 0.475, indicating that the growth of the soybean plants in this stage was still relatively vigorous. Similar to the trend of the Dr values, the SDr value at the mature stage dropped dramatically to 0.377 (Figure 5).
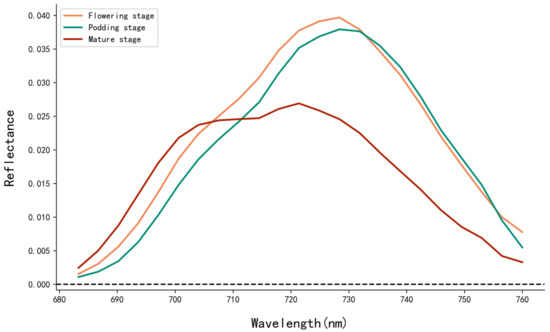
Figure 5.
First derivative reflectance of soybean at different growth stages: (680–760 nm).
Pearson correlation coefficient analysis was carried out between LAI and RR at the three growth stages, and the band with the highest correlation coefficient to LAI was selected as the raw reflectance-sensitive band to participate in the model construction (Figure 6a). Similarly, Pearson correlation coefficient analysis was carried out between LAI and the FDR, and the band with the highest correlation coefficient to LAI was selected as the FDR-sensitive band (Figure 6b).
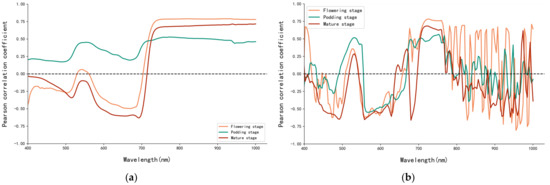
Figure 6.
Pearson correlation coefficient between LAI and spectral reflectance at different growth stages. (a) Raw reflectance and LAI; (b) first derivative reflectance and LAI.
The highest Pearson correlation coefficient between LAI and RR was 0.791 and the corresponding wavelength was 933 nm at the flowering stage (Table 2 and Figure 5a). The highest Pearson correlation coefficients between LAI and FDR was −0.806 and the corresponding wavelength was 955 nm also at the flowering stage (Table 2 and Figure 5b). The Pearson correlation coefficient between LAI and extracted Dr values at the three stages were 0.781, 0.487 and 0.672, respectively, and the Pearson correlation coefficients between LAI and the extracted SDr values at the three stages were 0.788, 0.536 and 0.673, respectively (Table 2).

Table 2.
Correlation coefficient between spectral indices and LAI at different growth stages.
3.1.2. Prediction Models of LAI Constructed by Different Algorithms
Four hyperspectral indices, i.e., the best RR-sensitive band, the FDR-sensitive band, the Dr and SDr, were used to construct univariate regression models.
At the flowering stage, the model built by the RR-sensitive band and LAI showed the highest R2 in the training set, but a relatively low R2 in the validation set. The prediction model constructed by the SDr and LAI showed the closest R2 in both the training and validation sets, indicating the highest stability among all models. In terms of the predictive ability and stability, the prediction model constructed by the FDR-sensitive band and LAI performed well on both the training and the validation sets, indicating that this model should be the optimal prediction model for the flowering stage.
At the podding stage, the prediction model constructed by the FDR-sensitive band and LAI showed the highest R2 for both the training and validation sets, and the R2 difference between the training and validation sets was the smallest, indicating that this prediction model should be the best model for the podding stage.
At the mature stage, the prediction model constructed from the raw spectrally-sensitive band and LAI showed the highest R2 and the lowest RMSE in both the training and validation sets. In comparison, the SDr performed the worst in both the training and validation sets; therefore, the model based on the raw spectral-sensitive band and LAI should be the optimal model for the mature stage.
In summary, the predictive abilities and stabilities of the tested models differed significantly with regards to the VIs and growth stages. Among the four spectral parameters, the FDR-sensitive band performed the best at the flowering and podding stages, whereas the raw spectral-sensitive band performed the best at the mature stages. In terms of the overall performance at all growth stages, the prediction models constructed by the raw spectral-sensitive band and the FDR-sensitive band were better than those constructed by the Dr and SDr (Table 3).

Table 3.
Univariate prediction models of LAI constructed by hyperspectral data at different development stages in soybean.
To compare the different modeling strategies, five modeling methods, including MLR, RF, XGBoost, SVM and BP, were also used to construct multivariate regression models of LAI (Table 4).

Table 4.
Multivariate prediction models of LAI constructed by hyperspectral data at different development stages in soybean.
At the flowering stage, the BP-LAI model and SVM-LAI model showed the lowest R2 in both the training and validation sets, while the XGBoost-LAI model showed the best accuracy and stability in both the training and validation sets, indicating this model should be the best model for the flowering stage.
At the podding stage, the XGBoost-LAI prediction model showed the highest R2 in the training set, while both the MLR-LAI and RF-LAI models showed the highest R2 in the validation set. In terms of the predictive ability and stability, the model constructed by the RF algorithm should be the optimal prediction model for this stage.
At the mature stage, the RF-LAI model showed the best accuracy and fitting degrees in both the training and validation sets. Meanwhile, the model also showed the highest stability; therefore, this model should be the best prediction model for the mature stage.
In summary, the prediction models constructed by the XGBoost and RF algorithms generally showed better performances for soybean LAI prediction at the different growth stages. Comparing the prediction models built at the different growth stages, the models built at the flowering and mature stages were better than those at the podding stage.
3.1.3. Comparison of Prediction Models Constructed by Different Algorithms
In order to select the best prediction models of LAI for different development stages, the predictive abilities and stabilities of the univariate and multivariate models were compared. The results showed that the multivariate models showed better predictive abilities and stabilities than the univariate models, and the best models for the flowering, podding and mature stages were the XGBoost-LAI, RF-LAI and RF-LAI, with a R2 of 0.767, 0.508 and 0.614 in the training set, respectively, and with a R2 of 0.762, 0.495 and 0.618 in the validation set, respectively (Figure 7).
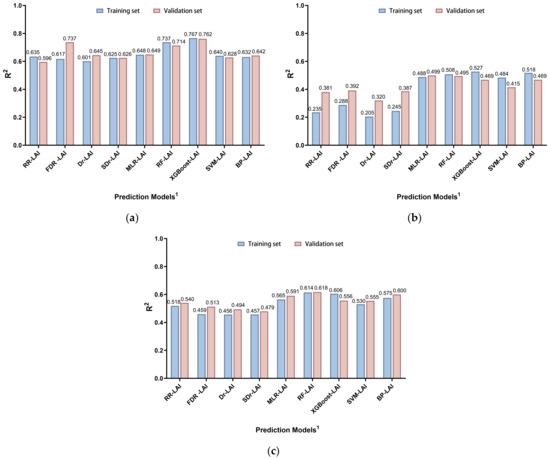
Figure 7.
Comparison of predictive ability and stability of univariate and multivariate models at different development stages. (a) Flowering stage; (b) podding stage; (c) mature stage. 1 Note: the prediction model constructed by the LAI and raw reflectance-sensitive band, first derivative reflectance-sensitive band, red edge amplitude, red edge area, MLR, RF, XGBoost, SVM and BP were abbreviated as RR-LAI, FDR-LAI, Dr-LAI, SDr-LAI, MLR-LAI, RF-LAI, XGBoost-LAI, SVM-LAI, and BP-LAI, respectively.
3.1.4. Universal Model of LAI for Multiple Growth Stages
To construct a universal model which can be applied to estimate soybean LAI at all growth stages, multivariate models were built with five modeling methods using the LAI and hyperspectral data from all plots at the three growth stages.
Among all the models, the RF-LAI and XGBoost-LAI models showed the highest R2 and the best accuracy in both the training and validation sets. Compared to the models for the single growth stages, the model for multiple growth stages performed better than most of the single stage models except for the model at the flowering stage (Table 5).

Table 5.
Universal models of LAI for multiple growth stages based on hyperspectral data.
3.2. Prediction Models of LAI Based on Multispectral Data
Five VIs, i.e., LCI, NDRE, NDVI, GNDVI and OSAVI, were extracted to develop univariate regression models of LAI using multispectral remote sensing data collected at the flowering and mature stages. Correlation analysis between the five VIs and LAI was carried out, and the results showed that the correlation coefficient between the OSAVI and LAI was the highest among all five VIs at both the flowering and mature stages (Table 6).

Table 6.
Correlation coefficient between vegetation indices and LAI at two growth stages.
At the flowering stage, the prediction model established by the vegetation index OSAVI exhibited a relatively higher R2 and a lower RMSE in both the training and validation sets, while the prediction model established by the vegetation index GNDVI exhibited a higher R2 in the validation set, but a lower R2 in the training set. According to the R2 difference between the two sets, the prediction model constructed by the vegetation index OSAVI showed the best stability and should be the best prediction model for the flowering stage. At the mature stage, the model established by the OSAVI showed the best R2 in both the training and validation sets and the best stability, indicating that this model had the best predictive ability and stability among all the models (Table 7).

Table 7.
Univariate prediction models of LAI constructed by multispectral data at the flowering and mature stages in soybean.
The five VIs from the multispectral data were modeled together to construct multivariate prediction models of LAI (Table 8). At the flowering stage, the XGBoost-LAI model showed the best R2 in both the training and validation sets, demonstrating the highest predictive ability; therefore, the XGBoost-LAI model should be the optimal prediction model for the flowering stage. At the mature stage, the SVM-LAI model performed best in the training set, whereas in the validation set, the BP-LAI model performed the best, followed by the SVM-LAI model. Taking the predictive ability and stability together, the SVM-LAI model should be the best prediction model for the mature stage.

Table 8.
Multivariate prediction models of LAI constructed by multispectral data at the flowering and mature stages in soybean.
3.3. Prediction Models of LAI Based on LiDAR Data
Correlation analysis was conducted among the point cloud data and LAI at the flowering and mature stages (Figure 8). At the flowering stage, the correlations between LAI and the point cloud parameters extracted by the direct method were significantly stronger than those of the parameters extracted by the CHM method. Among all the point cloud parameters, the P75–100 showed the highest correlation with LAI with a correlation coefficient of 0.68 (Figure 8a). At the mature stage, the parameters extracted by the two methods showed relatively lower correlations with LAI (Figure 8b). To ensure the effectiveness of the inverse model, the five parameters with the top correlation coefficients were selected for the model construction at each of the growth stages.
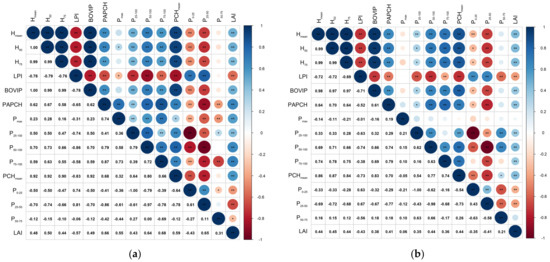
Figure 8.
Correlation coefficients among all LiDAR parameters and LAI at different development stages. (a) Flowering stage; (b) mature stage.
At the flowering stage, the LiDAR parameters of P75–100, PAPCH, P25–50, P50–100 and PCHmean showed the highest correlation coefficients with LAI and were chosen to construct unary linear regression prediction models. All the models showed a low R2 and low stability between the training and validation sets. The model constructed by the P75–100 performed relatively well in terms of its prediction ability and stability, and thus it should be considered as the best prediction model for the flowering stage. At the mature stage, the LiDAR parameters of H50, Hmean, H75, P50–100, and PCHmean were chosen to construct prediction models. The results showed that the prediction model constructed by the H75 showed the highest R2 in the training set, while the prediction model constructed by the P50–100 showed the highest R2 in the validation set. Taken together, the model constructed by the H75 should be the best prediction model for the mature stage (Table 9).

Table 9.
Univariate prediction models of LAI constructed by LiDAR data at the flowering and mature stages in soybean.
At the flowering stage, the prediction model established by RF algorithm performed the highest R2 in both the training and validation sets, while the prediction model established by the BP algorithm performed the best stability. Considering both the predictive ability and stability, the model constructed by the RF algorithm should be the best prediction model for the flowering stage. At the mature stage, all models showed a relatively poor performance compared with those of the flowering stage. Among them, the RF-LAI model had a better performance in the training set, while the XGBoost-LAI model had a better performance in the validation set. However, the stability of the XGBoost-LAI model was relatively better; therefore, the XGBoost-LAI model should be the best prediction model for the mature stage (Table 10).

Table 10.
Multivariate prediction models of LAI constructed by LiDAR data at the flowering and mature stages in soybean.
3.4. Prediction Models of LAI Based on Multimodal Data
3.4.1. Prediction Models of LAI by Integrating Three Types of Remote Sensing Data
In order to improve the predictive ability and accuracy of the models, the three types of remote sensing data, i.e., the hyperspectral, multispectral and LiDAR data, were used to build multivariate prediction models for the flowering and mature stages. The results showed that at the flowering stage, the RF-LAI and XGBoost-LAI models exhibited a relatively high R2 in both the training and validation sets; therefore, these two models demonstrating a high predictive ability could be used for LAI prediction for the flowering stage. At the mature stage, the RF-LAI model performed better in both the training and validation sets, indicating that this model could be used for LAI prediction for the mature stage (Table 11).

Table 11.
Multivariate prediction models established based on three types of remote sensing data for the flowering and mature stages.
3.4.2. Prediction Models of LAI by Integrating Hyperspectral and Multispectral Data
As shown in Table 11, the multivariate prediction models integrating three types of remote sensing data demonstrated no significant improvement over the models based on a single remote sensing data. Correlation analysis between the parameters and LAI at the flowering and mature stages revealed that the LiDAR parameters were poorly correlated with LAI. To exclude the negative interference of the LiDAR data, the prediction models of LAI based on the hyperspectral and multispectral parameters were established.
As shown in Figure 9, the XGBoost-LAI model showed the best overall performance in the training and validation sets, indicating that the XGBoost-LAI model based on hyperspectral and multispectral data should be the best prediction model for the flowering stage.
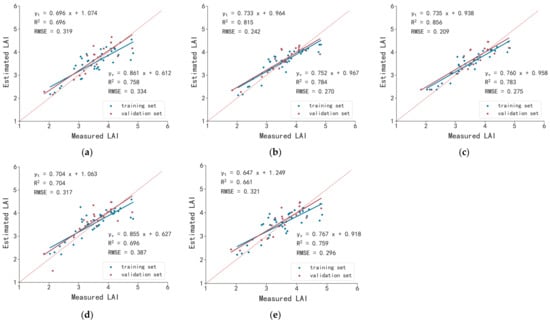
Figure 9.
Prediction models of LAI based on the fusion of hyperspectral and multispectral parameters by different modeling methods at the flowering stage. (a) MLR-LAI; (b) RF-LAI; (c) XGBoost-LAI; (d) SVM-LAI; (e) BP-LAI. Note: yt indicates the training set; yv indicates the validation set.
At the mature stage, the XGBoost-LAI model performed the best in the training set with the highest R2, and performed relatively well in the validation set. In addition, the RF-LAI model also performed quite well in both the training and validation sets. Therefore, both the XGBoost-LAI and RF-LAI prediction models could be an option for evaluating LAI for the mature stage (Figure 10).
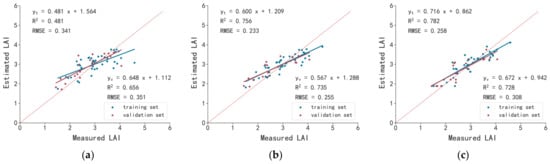
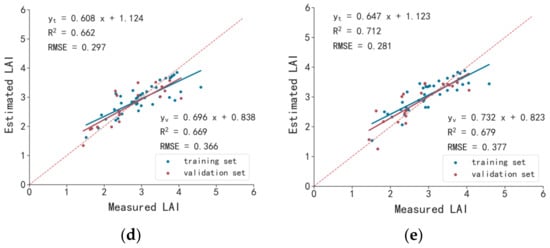
Figure 10.
Prediction models of LAI based on the fusion of hyperspectral and multispectral parameters by different modeling methods at the mature stage. (a) MLR-LAI; (b) RF-LAI; (c) XGBoost-LAI; (d) SVM-LAI; (e) BP-LAI. Note: yt indicates the training set; yv indicates the validation set.
4. Discussion
4.1. Parameter Selection for Model Construction of LAI with Different Types of Remote Sensing Data
Spectral VIs from remote sensing data are regarded as effective parameters for monitoring plant phenology [53]. Different types of remote sensing data have different characteristics, from which the most suitable parameters can be extracted to construct prediction models. For hyperspectral remote sensing data, band features, spectral location features, and VIs were used as the effective parameters for the prediction model construction of LAI [54]. In order to select the suitable spectral features for LAI estimation, Li et al. [55] evaluated different features such as the spectral band, spectral position and VIs, and found that the first derivative spectral band at a wavelength of 750 nm exhibited the highest correlation with LAI among all the features. Gong et al. [56] studied the LAI of ponderosa pine forests using three spectral parameters, i.e., individual spectral band, first-order derivative spectrum and second-order derivative spectrum, and found that the accuracy of LAI estimation using first- and second-order derivatives was significantly higher than that using the individual spectral band. In this study, four spectral parameters were extracted and were used to construct prediction models of LAI. The results showed that the models constructed with different spectral parameters exhibited different predictive abilities, and the model constructed with the RR-sensitive band and the FDR-sensitive band performed better than the models constructed with other spectral parameters, which was in accordance with the results of previous studies [57,58]. Therefore, we speculated that the RR-sensitive band and the FDR-sensitive band might be the optimal parameters for the construction of prediction models of LAI with hyperspectral data in soybean.
For multispectral remote sensing data, OSAVI has been widely used to construct prediction models for LAI. Das et al. [59] concluded that the OSAVI was the best VI from multispectral data. Liang et al. [60] found that OSVAI and MTVI2 were the most sensitive indices to LAI among 43 VIs. In this study, the prediction models constructed with OSAVI also outperformed the other models at both the flowering and mature stages, which was highly consistent with previous studies [61,62]. The possible reason for this may be that OSAVI can exclude soil effects better than other VIs at the development stages during which the soil is more exposed due to less soybean leaf coverage [47,53].
For LiDAR remote sensing data, height percentile metrics have been widely used to study LAI in plants [63]. Qu et al. [64] used height percentile metrics derived from LiDAR data to estimate LAI of dense forests, and their results showed that the prediction ability of LAI based on LiDAR data was better than that based on MODIS. Pearse et al. [65] estimated LAI of a forest using LiDAR data and found that height proportional-based correlation metrics were more suitable for LAI prediction. In this study, 14 parameters were extracted from LiDAR remote sending data, and were correlated with LAI. The results showed that the height proportional-related correlation parameters had higher correlation coefficients with LAI than the other parameters, which was similar to the results of previous studies [66,67]. The results also indicated that the height proportional-related parameters extracted from the LiDAR remote sensing data could be used for the prediction of LAI in soybean.
A previous study also found that the height metrics extracted from the upper part of plants were more suitable for the prediction of LAI than those extracted from the low parts [68]. Qu et al. [64] estimated the LAI of a tropical forest using LiDAR data, and found that the point cloud data from the middle and upper parts of trees contributed more to LAI prediction than those from the middle and lower parts. Similar results were also found in the study of LAI in maize [69]. In this study, the height parameters from the upper to middle parts of the plants, such as H75 and Hmean, showed high correlations with LAI (Figure 7), which was also consistent with the results in previous studies.
4.2. Performance Comparison of Three Types of Remote Sensing Data on LAI Prediction
Hyperspectral and multispectral remote sensing data have been widely used to study LAI [70]. Compared with multispectral sensor, hyperspectral sensor has the advantage of acquiring more bands, but the difficulties or inconveniences in its data processing are also well-known. Currently, it is still controversial which one is better for LAI study [71]. Mananze et al. [72] used hyperspectral and multispectral sensors to study LAI in maize, and found that there was no significant improvement in the accuracy between the prediction models constructed with hyperspectral data and multispectral data. De Castro et al. [73] found that hyperspectral dataset showed almost no advantage over multispectral dataset in weed identification, and that multispectral sensor might be a better choice for its low price and fast data processing. In this study, the R2 values of the best models constructed with hyperspectral data in the training and validation sets were 0.767 and 0.762, respectively, while the R2 values of the best models constructed with multispectral data in the training and validation sets were 0.749 and 0.662, respectively. The results indicated that the hyperspectral remote sensing data showed no significant advantage over the multispectral remote sensing data for LAI prediction in soybean, which was similar to the results of the previous studies in trees and in maize [71,72]. Based on the above-mentioned results, we would suggest using multispectral data instead of hyperspectral data for the study of LAI in crops considering the economy and data processing efficiency.
LiDAR remote sensing has been widely used to study LAI in tall forest trees, while few studies have been carried out in crops with a small architecture such as soybean [74]. Sheng et al. [21] used LiDAR remote sensing data to predict LAI in corn, and constructed a prediction model with a R2 value of 0.724, which was similar to the prediction effect of our LiDAR-based model at the flowering stage (i.e., R2 = 0.710, Table 10). The complexity of a plant’s morphological structure directly affects the accuracy of LAI prediction, which has been proved in many studies in trees [75,76]. A previous study indicated that the prediction of LAI in tropical forests with dense foliage and high tree density was significantly more difficult than in temperate forests and plantation forests [64]. In crops, Lei et al. [69] found that the correlation between LiDAR data and LAI was affected by the plant density, flight angle, and point cloud height division. Similar results were also found at the mature stage in this study. The possible reason for this might be that the complexity of the soybean canopy structure at maturity increased the difficulty of the branch and leaf structure identification from the point cloud data and decreased the predictive ability of the models. Therefore, we conclude that the density of the canopy structure and the complexity of branch and leaf may significantly affect the prediction abilities of models constructed with LiDAR data.
LiDAR remote sensing data have been proved to be suitable for the prediction of plant height in trees [77], and also in crops such as wheat [78], triticale [79], maize [80] and rice [81]. In this study, plant height data were also collected at the flowering stage in soybean. Two height-related parameters, i.e., the Hmean and PCHmean, were calculated and used to construct multivariate prediction models of the plant height. The results showed that all the models displayed an acceptable performance in both the training and validation sets, with a R2 > 0.82 in the training set and R2 > 0.75 in the validation set, respectively (Figure 11). Compared with the LAI models, the prediction models of plant height performed much better; therefore, we speculate that LiDAR sensor might be more suitable for the study of 3D-related traits, such as plant height.
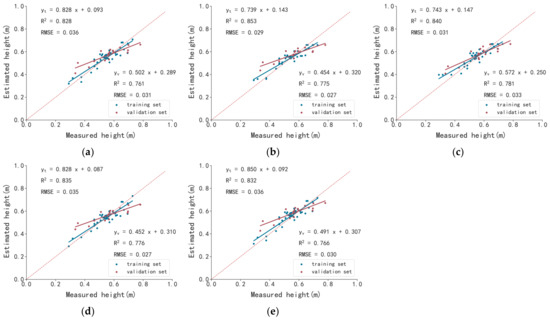
Figure 11.
Prediction models of plant height constructed with LiDAR data by different modeling methods at the flowering stage. (a) MLR-LAI; (b) RF-LAI; (c) XGBoost-LAI; (d) SVM-LAI; (e) BP-LAI. Note: yt indicates the training set; yv indicates the validation set.
4.3. Models of LAI Constructed with Multimodal Data
At present, most of the prediction models of LAI in crops have been constructed with a single type of remote sensing data, and only a few models have been built using multi-source remote sensing data [36,82]. Some researchers have tried to improve the prediction ability of the models of LAI by fusing LiDAR data with spectral data [83]. In addition, Bahrami et al. [84] constructed prediction models of LAI and biomass by combining LiDAR and optical earth observations. Luo et al. [85] estimated the biomass of short, wetland reed using a combination of LiDAR and hyperspectral data, and found that combining the LiDAR with hyperspectral data could improve the estimation accuracy of reed biomass. Lou et al. [86] also found that the fusion of hyperspectral and LiDAR data could improve the accuracy of the prediction model of LAI in maize. In this study, we aimed to construct a high-performance prediction model of LAI by combining three types of remote sensing data; however, the performance of the prediction model was not improved as expected. The possible reason for this might be due to the short plant height and complicated plant structure of soybean, which caused the point cloud data to fail to reflect the real shape of soybean, limiting the full utilization of the point cloud data. Nevertheless, the prediction ability of the prediction model based on multispectral and hyperspectral data was indeed improved in this study, which was similar to the results of a previous study [82].
4.4. Comparison of Prediction Models of LAI Based on Different Algorithms
Algorithm is also very critical for the construction of prediction models. In most cases, multivariate prediction models of LAI outperformed univariate models in terms of their accuracy and stability [87]. Yu et al. [88] used both multivariate and univariate algorithms to construct prediction models of LAI, and found that the multivariate models outperformed the univariate models in estimating LAI in a forest. Similar results were also found in the studies of LAI in wheat [75,76], kiwifruit orchard [89] and soybean in this study. The possible reason for this might be that multivariate algorithms can include more variables with explanatory power and can reduce the possibility of omitting variable bias.
Afrasiabian et al. [90] used simple linear regression, SVM and RF algorithms to construct prediction models for LAI, and found that RF was the best algorithm for the model construction of LAI. Zhang et al. [27] used PLSR, SVR, and XGBoost algorithms to construct estimation models of LAI in winter wheat, and found that the XGBoost algorithm showed the best performance. In this study, six machine learning algorithms were used to construct prediction models of LAI in soybean. The results showed that the XGBoost and RF algorithms performed the best among all the machine learning algorithms, which was quite similar to previous results [25]. The possible reason for this might be that both the XGBoost and RF algorithms belong to integrated learning, which aims to improve a single learner’s generalization ability and robustness by combining the prediction results of multiple base learners [26,91]. The model constructed by the RF algorithm had a better generalization ability and could solve the problem of multiple collinearities for unbalanced data sets and reduce the data errors [33]. In comparison, the XGBoost algorithm added a regularization term that prevented data overfitting and defined a loss function that made the loss more accurate [92]. Therefore, the RF and XGBoost algorithms should be the optimal algorithms for the construction of prediction models of LAI in soybean.
4.5. Prediction Models of LAI at Different Growth Stages Based on Hyperspectral Data
In this study, the prediction models of LAI at three growth stages, i.e., the flowering, podding and mature stages, were established based on hyperspectral remote sensing data in soybean. The results showed that the preferable models for the flowering, podding and mature stages was the XGBoost-LAI, RF-LAI and RF-LAI, respectively (Table 4). Furthermore, the prediction model of LAI at the flowering stage performed the best, followed by the ones at the mature and podding stages. This result was similar to that of a previous study in wheat, in which the flowering stage was the best growth stage for the estimation of LAI and AGB [11,93].
To construct a universal model that can be applied for multiple growth stages, the multivariate models were built with the data collected from all three growth stages (Table 5). The results showed that the XGBoost-LAI and RF-LAI models were the best universal models among all the models for the multiple growth stages in soybean. Kamenova et al. [94] constructed a universal prediction model of LAI based on the whole growth stage data in winter wheat, and found that the performance of the universal model was worse than those of the models constructed with a single growth stage, i.e., the tillering or the stem elongation stages. The morphology of a plant varies in the different growth stages and, therefore, the best-fit predictors might change with different developmental stages. This might lead to difficulties in constructing a universal model suitable for multiple growth stages.
5. Conclusions
In this study, three types of UAV-mounted sensors and six machine learning algorithms were used to construct prediction models of LAI at three growth stages in soybean. Performance comparison of different remote sensing sensors showed that multispectral sensor might be better than hyperspectral sensor for LAI prediction in soybean for its considerable low cost yet comparable accuracy, and that LiDAR sensor could be suitable for the study of 3D-related traits such as plant height. The fusion of three types of remote sensing data failed to significantly improve the prediction abilities of the models; however, the fusion of hyperspectral and multispectral remote sensing data could significantly improve the prediction ability of the models. Among all the prediction models, the model built by the XGBoost algorithm at the flowering stage showed the best performance, with a R2 value of 0.856 and 0.783 in the training and validation sets, respectively. Among the models constructed with a single type of sensor data for the different growth stages, the XGBoost-LAI model at the flowering stage showed the best performance. Among the universal models based on the multiple growth stages, the XGBoost-LAI and RF-LAI models showed the best performances. This study not only offers useful models for the prediction of LAI at multiple growth stages in soybean, but also provides some new insights towards the high-throughput phenotyping of soybean with multi-modal UAV remote sensing data.
Author Contributions
Conceptualization, Y.Z., Y.Y., Y.Q. and X.W.; formal analysis, Y.Z. and Y.Y.; funding acquisition, X.W.; investigation, Y.Z., Y.Y., Q.Z., R.D. and J.L.; methodology, Y.Z. Y.Y. and Y.Q.; supervision, X.W.; writing—original draft preparation, Y.Z. and Y.Y.; writing—review and editing, Y.Q. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (No. 31860385), Natural Science Foundation of Yunnan (No. 2018FB061) and Key Science and Technology Project of Yunnan (No. 202202AE090014).
Data Availability Statement
Not applicable.
Acknowledgments
We thank Kailei Tang, Yunnan University, for providing constructive suggestions to this project; Zheng Li, Yunnan University, for revising this manuscript; Da-Jiang Innovations Co., Yunnan New Coordinate Mapping Instrument Co., and Yunnan Here Information Technology Co., for their assistance in data collection.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| LAI | Leaf Area Index |
| AGB | Above-Ground Biomass |
| RR | Raw Reflectance |
| FDR | First Derivative Reflectance |
| REP | Red Edge Position |
| Dr | Red Edge Amplitude |
| SDr | Red Edge Area |
| Drmax | Maximum Red-edge Amplitude |
| Drmin | Minimum Red-edge Amplitude |
| LCI | Land Cover Index |
| OSAVI | Optimized Soil Adjusted Vegetation Index |
| NDVI | Normalized Difference Vegetation Index |
| GNDVI | Green Normalized Difference Vegetative Index |
| NDRE | Normalized Difference Red Edge |
| ROI | Region of Interest |
| CSF | Cloth Simulation Filter |
| TIN | Triangulated Irregular Network |
| DEM | Digital Elevation Model |
| DSM | Digital Surface Model |
| CHM | Canopy Height Model |
| Hmean | Mean Plant Height |
| H50 | 50 Percentile Plant Height |
| H75 | 75 Percentile Plant Height |
| LPI | Laser Penetration Index |
| BIOVP | Three-Dimensional Volumetric Parameters |
| P0–25 | The percentage of 0%~25% height point cloud |
| P25–50 | The percentage of 25%~50% height point cloud |
| P50–75 | The percentage of 50%~75% height point cloud |
| P25–100 | The percentage of 25%~100% height point cloud |
| P50–100 | The percentage of 50%~100% height point cloud |
| P75–100 | The percentage of 75%~100% height point cloud. |
| Pmax | The percentage of the number of point clouds at the height with the largest number of point clouds |
| PCHmean | The percentage of the average point cloud height |
| PAPCH | The percentage of point clouds above the average point cloud height in the total number of point clouds |
| ULR | Unary Linear Regression |
| PLSR | Partial Least Squares Regression |
| MLR | Multivariable Linear Regression |
| RF | Random Forest |
| XGBoost | eXtreme Gradient Boosting |
| SVR | Support Vector Regression |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| BP | Back Propagation |
| RBF | Radial Basis Function |
| ReLU | Rectified Linear Unit |
References
- Singh, G. The Soybean: Botany, Production and Uses; CABI: Wallingford, UK, 2010. [Google Scholar]
- Bréda, N.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef]
- Haboudane, D. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Alexandridis, T.K.; Ovakoglou, G.; Clevers, J.G. Relationship between MODIS EVI and LAI across time and space. Geocarto Int. 2020, 35, 1385–1399. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X. Unmanned aerial vehicle remote sensing for field-based crop phenotyping: Current status and perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef]
- Underwood, J.; Wendel, A.; Schofield, B.; McMurray, L.; Kimber, R. Efficient in-field plant phenomics for row-crops with an autonomous ground vehicle. J. Field Robot. 2017, 34, 1061–1083. [Google Scholar] [CrossRef]
- Pratap, A.; Gupta, S.; Nair, R.M.; Gupta, S.; Schafleitner, R.; Basu, P.; Singh, C.M.; Prajapati, U.; Gupta, A.K.; Nayyar, H. Using plant phenomics to exploit the gains of genomics. Agronomy 2019, 9, 126. [Google Scholar] [CrossRef]
- Feng, D.; Xu, W.; He, Z.; Zhao, W.; Yang, M. Advances in plant nutrition diagnosis based on remote sensing and computer application. Neural Comput. Appl. 2020, 32, 16833–16842. [Google Scholar] [CrossRef]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Y.; Pu, R.; Gonzalez-Moreno, P.; Yuan, L.; Wu, K.; Huang, W. Monitoring plant diseases and pests through remote sensing technology: A review. Comput. Electron. Agric. 2019, 165, 104943. [Google Scholar] [CrossRef]
- Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of crop growth parameters using UAV-based hyperspectral remote sensing data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Perspectives for remote sensing with unmanned aerial vehicles in precision agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Berni, J.A.; Zarco-Tejada, P.J.; Suárez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Yue, J.; Lei, T.; Li, C.; Zhu, J. The application of unmanned aerial vehicle remote sensing in quickly monitoring crop pests. Intell. Autom. Soft Comput. 2012, 18, 1043–1052. [Google Scholar] [CrossRef]
- Hunt, E.R.; Cavigelli, M.; Daughtry, C.S.; Mcmurtrey, J.E.; Walthall, C.L. Evaluation of digital photography from model aircraft for remote sensing of crop biomass and nitrogen status. Precis. Agric. 2005, 6, 359–378. [Google Scholar] [CrossRef]
- Córcoles, J.I.; Ortega, J.F.; Hernández, D.; Moreno, M.A. Estimation of leaf area index in onion (Allium cepa L.) using an unmanned aerial vehicle. Biosyst. Eng. 2013, 115, 31–42. [Google Scholar] [CrossRef]
- Kanning, M.; Kühling, I.; Trautz, D.; Jarmer, T. High-resolution UAV-based hyperspectral imagery for LAI and chlorophyll estimations from wheat for yield prediction. Remote Sens. 2018, 10, 2000. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating biomass of barley using crop surface models (CSMs) derived from UAV-based RGB imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Broge, N.; Hasager, C.; Jensen, N.; Schelde, K.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Xi, X. Estimating leaf area index of maize using airborne full-waveform lidar data. Remote Sens. Lett. 2016, 7, 111–120. [Google Scholar] [CrossRef]
- Ta, N.; Chang, Q.; Zhang, Y. Estimation of apple tree leaf chlorophyll content based on machine learning methods. Remote Sens. 2021, 13, 3902. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, H.; Yan, X.; Liu, X. MapReduce-based adaptive random forest algorithm for multi-label classification. Neural Comput. Appl. 2019, 31, 8239–8252. [Google Scholar] [CrossRef]
- Luo, S.; Chen, J.M.; Wang, C.; Gonsamo, A.; Xi, X.; Lin, Y.; Qian, M.; Peng, D.; Nie, S.; Qin, H. Comparative performances of airborne LiDAR height and intensity data for leaf area index estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 300–310. [Google Scholar] [CrossRef]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A random forest machine learning approach for the retrieval of leaf chlorophyll content in wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar] [CrossRef]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Wang, L.; Wang, P.; Liang, S.; Qi, X.; Li, L.; Xu, L. Monitoring maize growth conditions by training a BP neural network with remotely sensed vegetation temperature condition index and leaf area index. Comput. Electron. Agric. 2019, 160, 82–90. [Google Scholar] [CrossRef]
- Abraham, A. Artificial neural networks. In Handbook of Measuring System Design; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chandra, A.L.; Desai, S.V.; Guo, W.; Balasubramanian, V.N. Computer vision with deep learning for plant phenotyping in agriculture: A survey. arXiv 2020, arXiv:2006.11391. [Google Scholar]
- Siegmann, B.; Jarmer, T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Remote Sens. 2015, 36, 4519–4534. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving soybean leaf area index from unmanned aerial vehicle hyperspectral remote sensing: Analysis of RF, ANN, and SVM regression models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Q.; Yi, X.; Ma, L.; Zhang, L.; Huang, C.; Zhang, Z.; Lv, X. Estimation of Cotton Leaf Area Index (LAI) Based on Spectral Transformation and Vegetation Index. Remote Sens. 2022, 14, 136. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Zhang, J. Multi-source remote sensing data fusion: Status and trends. Int. J. Image Data Fusion. 2010, 1, 5–24. [Google Scholar] [CrossRef]
- Dawson, T.; Curran, P. Technical note A new technique for interpolating the reflectance red edge position. Int. J. Remote Sens. 1998, 19, 2133–2139. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Heald, R. Analysis of in situ hyperspectral data for nutrient estimation of giant sequoia. Int. J. Remote Sens. 2002, 23, 1827–1850. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D.; Wu, M.; Zhao, W. Remote estimation of canopy height and aboveground biomass of maize using high-resolution stereo images from a low-cost unmanned aerial vehicle system. Ecol. Indic. 2016, 67, 637–648. [Google Scholar] [CrossRef]
- Luo, S.; Liu, W.; Zhang, Y.; Wang, C.; Xi, X.; Nie, S.; Ma, D.; Lin, Y.; Zhou, G. Maize and soybean heights estimation from unmanned aerial vehicle (UAV) LiDAR data. Comput. Electron. Agric. 2021, 182, 106005. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, H.; Zhang, X.-B.; Zhu, L.-F.; Zheng, K.-F.; Jin, Q.-Y.; Zeng, F.-P. Estimation of rice neck blasts severity using spectral reflectance based on BP-neural network. Acta Physiol. Plant. 2011, 33, 2461–2466. [Google Scholar] [CrossRef]
- Datt, B. Visible/near infrared reflectance and chlorophyll content in Eucalyptus leaves. Int. J. Remote Sens. 1999, 20, 2741–2759. [Google Scholar] [CrossRef]
- Datt, B.; McVicar, T.R.; Van Niel, T.G.; Jupp, D.L.; Pearlman, J.S. Preprocessing EO-1 Hyperion hyperspectral data to support the application of agricultural indexes. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1246–1259. [Google Scholar] [CrossRef]
- Fitzgerald, G.; Rodriguez, D.; Christensen, L.; Belford, R.; Sadras, V.; Clarke, T. Spectral and thermal sensing for nitrogen and water status in rainfed and irrigated wheat environments. Precis. Agric. 2006, 7, 233–248. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Combining unmanned aerial vehicle (UAV)-based multispectral imagery and ground-based hyperspectral data for plant nitrogen concentration estimation in rice. Front. Plant Sci. 2018, 9, 936. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Viljanen, N.; Honkavaara, E.; Näsi, R.; Hakala, T.; Niemeläinen, O.; Kaivosoja, J. A novel machine learning method for estimating biomass of grass swards using a photogrammetric canopy height model, images and vegetation indices captured by a drone. Agriculture 2018, 8, 70. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Pan, F.; Xi, X.; Li, G.; Nie, S.; Xia, S. Estimation of wetland vegetation height and leaf area index using airborne laser scanning data. Ecol. Indic. 2015, 48, 550–559. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling maize above-ground biomass based on machine learning approaches using UAV remote-sensing data. Plant Methods 2019, 15, 10. [Google Scholar] [CrossRef]
- Wang, F.-m.; Huang, J.-f.; Lou, Z.-h. A comparison of three methods for estimating leaf area index of paddy rice from optimal hyperspectral bands. Precis. Agric. 2011, 12, 439–447. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G. Estimation of vegetation water content using hyperspectral vegetation indices: A comparison of crop water indicators in response to water stress treatments for summer maize. BMC Ecol. 2019, 19, 18. [Google Scholar]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens. Environ. 2000, 71, 1353691. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Bao, Y.; Luo, J.; Jin, X.; Xu, X.; Song, X.; Yang, G. Exploring the best hyperspectral features for LAI estimation using partial least squares regression. Remote Sens. 2014, 6, 6221–6241. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Miller, J.R. Correlating leaf area index of ponderosa pine with hyperspectral CASI data. Can. J. Remote Sens. 1992, 18, 275–282. [Google Scholar] [CrossRef]
- Sun, Q.; Gu, X.; Sun, L.; Yang, G.; Zhou, L.; Guo, W. Dynamic change in rice leaf area index and spectral response under flooding stress. Paddy Water Environ. 2020, 18, 223–233. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J.; Li, Y.; Wang, R. Rice leaf area index (LAI) estimates from hyperspectral data. In Proceedings of the Ecosystems Dynamics, Ecosystem-Society Interactions, and Remote Sensing Applications for Semi-Arid and Arid Land, Hangzhou, China, 23–27 October 2002; pp. 758–768. [Google Scholar]
- Das, B.; Sahoo, R.N.; Pargal, S.; Krishna, G.; Verma, R.; Chinnusamy, V.; Sehgal, V.K.; Gupta, V.K. Comparative analysis of index and chemometric techniques-based assessment of leaf area index (LAI) in wheat through field spectroradiometer, Landsat-8, Sentinel-2 and Hyperion bands. Geocarto Int. 2020, 35, 1415–1432. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Bandaru, V.; Daughtry, C.S.; Codling, E.E.; Hansen, D.J.; White-Hansen, S.; Green, C.E. Evaluating Leaf and Canopy Reflectance of Stressed Rice Plants to Monitor Arsenic Contamination. Int. J. Environ. Res. Public Health. 2016, 13, 606. [Google Scholar] [CrossRef]
- Xing, N.; Huang, W.; Xie, Q.; Shi, Y.; Ye, H.; Dong, Y.; Wu, M.; Sun, G.; Jiao, Q. A Transformed Triangular Vegetation Index for Estimating Winter Wheat Leaf Area Index. Remote Sens. 2020, 12, 16. [Google Scholar] [CrossRef]
- Peduzzi, A.; Wynne, R.H.; Fox, T.R.; Nelson, R.F.; Thomas, V.A. Estimating leaf area index in intensively managed pine plantations using airborne laser scanner data. For. Ecol. Manag. 2012, 270, 54–65. [Google Scholar] [CrossRef]
- Qu, Y.; Shaker, A.; Silva, C.A.; Klauberg, C.; Pinagé, E.R. Remote Sensing of Leaf Area Index from LiDAR Height Percentile Metrics and Comparison with MODIS Product in a Selectively Logged Tropical Forest Area in Eastern Amazonia. Remote Sens. 2018, 10, 970. [Google Scholar] [CrossRef]
- Pearse, G.D.; Morgenroth, J.; Watt, M.S.; Dash, J.P. Optimising prediction of forest leaf area index from discrete airborne lidar. Remote Sens. Environ. 2017, 200, 220–239. [Google Scholar] [CrossRef]
- Jensen, J.L.; Humes, K.S.; Vierling, L.A.; Hudak, A.T. Discrete return lidar-based prediction of leaf area index in two conifer forests. Remote Sens. Environ. 2008, 112, 3947–3957. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Romero Ramírez, F.J.; Hornero, A.; Zarco-Tejada, P.J. A novel methodology to estimate single-tree biophysical parameters from 3D digital imagery compared to aerial laser scanner data. Remote Sens. 2014, 6, 11627–11648. [Google Scholar] [CrossRef]
- Hirigoyen, A.; Acosta-Muñoz, C.; Salamanca, A.J.A.; Varo-Martinez, M.Á.; Rachid-Casnati, C.; Franco, J.; Navarro-Cerrillo, R. A machine learning approach to model leaf area index in Eucalyptus plantations using high-resolution satellite imagery and airborne laser scanner data. Ann. For. Res. 2021, 64, 165–183. [Google Scholar] [CrossRef]
- Lei, L.; Qiu, C.; Li, Z.; Han, D.; Han, L.; Zhu, Y.; Wu, J.; Xu, B.; Feng, H.; Yang, H.; et al. Effect of Leaf Occlusion on Leaf Area Index Inversion of Maize Using UAV–LiDAR Data. Remote Sens. 2019, 11, 1067. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving leaf area index (LAI) using remote sensing: Theories, methods and sensors. Sensors. 2009, 9, 2719–2745. [Google Scholar] [CrossRef]
- Ke, L.; Zhou, Q.-B.; WU, W.-B.; Tian, X.; Tang, H.-J. Estimating the crop leaf area index using hyperspectral remote sensing. J. Integr. Agric. 2016, 15, 475–491. [Google Scholar]
- Mananze, S.; Pôças, I.; Cunha, M. Retrieval of maize leaf area index using hyperspectral and multispectral data. Remote Sens. 2018, 10, 1942. [Google Scholar] [CrossRef]
- De Castro, A.-I.; Jurado-Expósito, M.; Gómez-Casero, M.-T.; López-Granados, F. Applying neural networks to hyperspectral and multispectral field data for discrimination of cruciferous weeds in winter crops. Sci. World J. 2012, 2012, 630390. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H. Estimation of LAI with the LiDAR technology: A review. Remote Sens. 2020, 12, 3457. [Google Scholar] [CrossRef]
- Holmgren, J.; Nilsson, M.; Olsson, H. Simulating the effects of lidar scanning angle for estimation of mean tree height and canopy closure. Can. J. Remote Sens. 2003, 29, 623–632. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Forest understory trees can be segmented accurately within sufficiently dense airborne laser scanning point clouds. Sci. Rep. 2017, 7, 6770. [Google Scholar] [CrossRef] [PubMed]
- Popescu, S.C.; Zhao, K. A voxel-based lidar method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Jimenez-Berni, J.A.; Deery, D.M.; Rozas-Larraondo, P.; Condon, A.G.; Rebetzke, G.J.; James, R.A.; Bovill, W.D.; Furbank, R.T.; Sirault, X.R. High throughput determination of plant height, ground cover, and above-ground biomass in wheat with LiDAR. Front. Plant Sci. 2018, 9, 237. [Google Scholar] [CrossRef]
- Busemeyer, L.; Mentrup, D.; Möller, K.; Wunder, E.; Alheit, K.; Hahn, V.; Maurer, H.P.; Reif, J.C.; Würschum, T.; Müller, J. BreedVision—A multi-sensor platform for non-destructive field-based phenotyping in plant breeding. Sensors 2013, 13, 2830–2847. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Gu, X.; Cheng, S.; Yang, G.; Shu, M.; Sun, Q. Analysis of plant height changes of lodged maize using UAV-LiDAR data. Agriculture 2020, 10, 146. [Google Scholar] [CrossRef]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 083671. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of spectral–temporal response surfaces by combining multispectral satellite and hyperspectral UAV imagery for precision agriculture applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Ma, H.; Song, J.; Wang, J.; Xiao, Z.; Fu, Z. Improvement of spatially continuous forest LAI retrieval by integration of discrete airborne LiDAR and remote sensing multi-angle optical data. Agric. For. Meteorol. 2014, 189, 60–70. [Google Scholar] [CrossRef]
- Bahrami, H.; Homayouni, S.; Safari, A.; Mirzaei, S.; Mahdianpari, M.; Reisi-Gahrouei, O. Deep learning-based estimation of crop biophysical parameters using multi-source and multi-temporal remote sensing observations. Agronomy 2021, 11, 1363. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Qian, M.; Peng, D.; Nie, S.; Qin, H.; Lin, Y. Retrieving aboveground biomass of wetland Phragmites australis (common reed) using a combination of airborne discrete-return LiDAR and hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 107–117. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Nie, S.; Fan, X.; Chen, H.; Yang, X.; Peng, D.; Lin, Y.; Zhou, G. Combining hyperspectral imagery and LiDAR pseudo-waveform for predicting crop LAI, canopy height and above-ground biomass. Ecol. Indic. 2019, 102, 801–812. [Google Scholar] [CrossRef]
- Wang, L.; Chang, Q.; Li, F.; Yan, L.; Huang, Y.; Wang, Q.; Luo, L. Effects of growth stage development on paddy rice leaf area index prediction models. Remote Sens. 2019, 11, 361. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J.; Liu, G.; Cheng, F. Forest leaf area index inversion based on landsat OLI data in the Shangri-La City. J. Indian Soc. Remote Sens. 2019, 47, 967–976. [Google Scholar] [CrossRef]
- Zhang, Y.; Ta, N.; Guo, S.; Chen, Q.; Zhao, L.; Li, F.; Chang, Q. Combining Spectral and Textural Information from UAV RGB Images for Leaf Area Index Monitoring in Kiwifruit Orchard. Remote Sens. 2022, 14, 1063. [Google Scholar] [CrossRef]
- Afrasiabian, Y.; Mokhtari, A.; Yu, K. Machine Learning on the estimation of Leaf Area Index. In Proceedings of the 42. GIL-Jahrestagung, Künstliche Intelligenz in der Agrar-und Ernährungswirtschaft, Ettenhausen, Schweiz, 21–22 February 2022; pp. 21–26. [Google Scholar]
- Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Ma, C.; Ding, F.; Li, Y.; Chen, W.; Li, J.; Xiao, Z. Hyperspectral estimation of winter wheat leaf area index based on continuous wavelet transform and fractional order differentiation. Sensors 2021, 21, 8497. [Google Scholar] [CrossRef]
- Kamenova, I.; Dimitrov, P. Evaluation of Sentinel-2 vegetation indices for prediction of LAI, fAPAR and fCover of winter wheat in Bulgaria. Eur. J. Remote Sens. 2021, 54, 89–108. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).