Comparison of GRACE/GRACE-FO Spherical Harmonic and Mascon Products in Interpreting GNSS Vertical Loading Deformations over the Amazon Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. GNSS Data
2.2. GRACE and GRACE-FO Data
2.3. Methods
2.3.1. GRACE/GRACE-FO SH and Mascon Derived Loading Deformation
2.3.2. Agreement Assessments between GNSS and GRACE/GRACE-FO
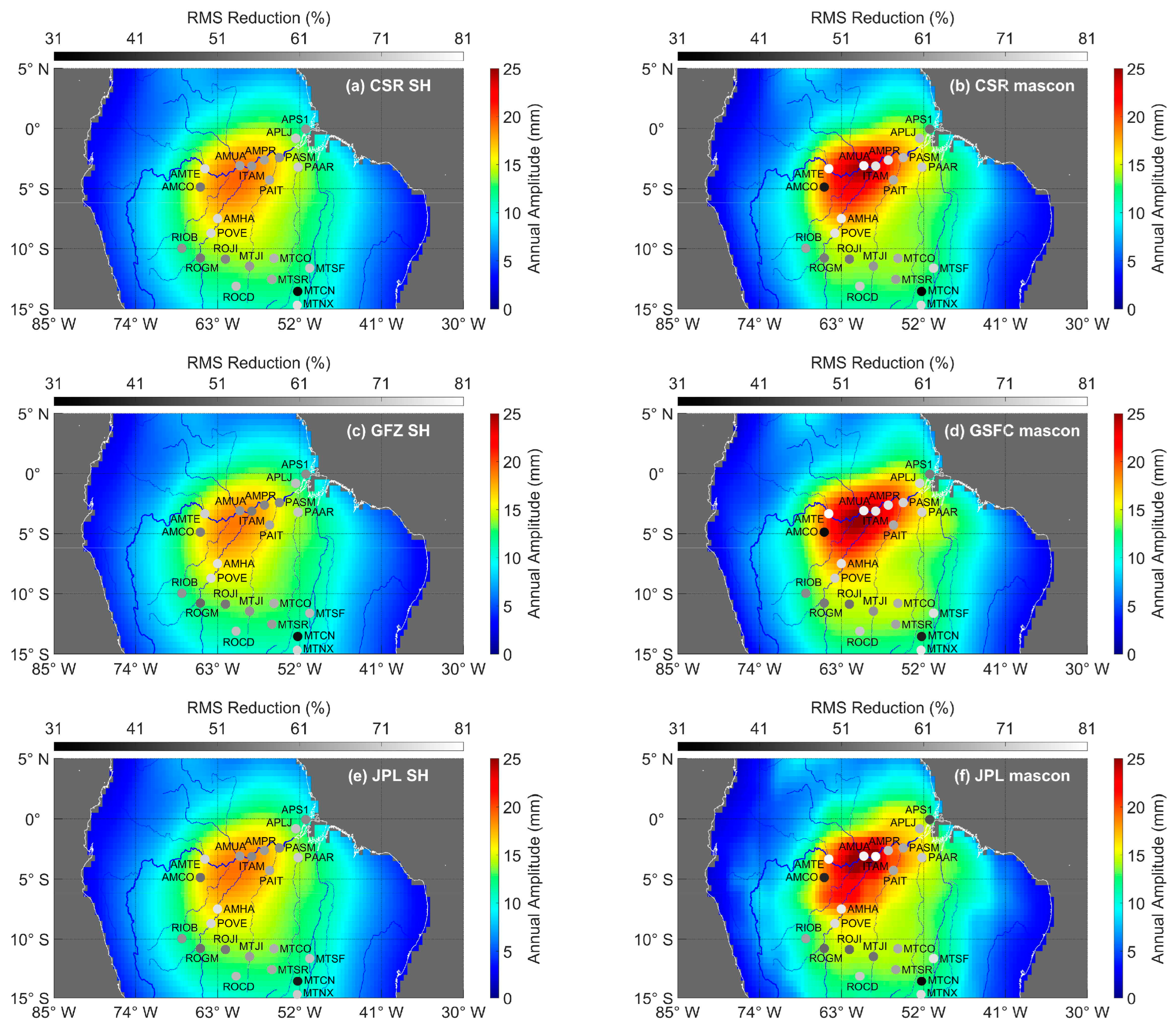
3. Results
3.1. Comparison of Loading Deformations between GNSS and GRACE/GRACE-FO
3.1.1. Annual Variations Estimated from GNSS and GRACE/GRACE-FO
3.1.2. Agreement Evaluation of GNSS and GRACE/GRACE-FO Loading Deformations
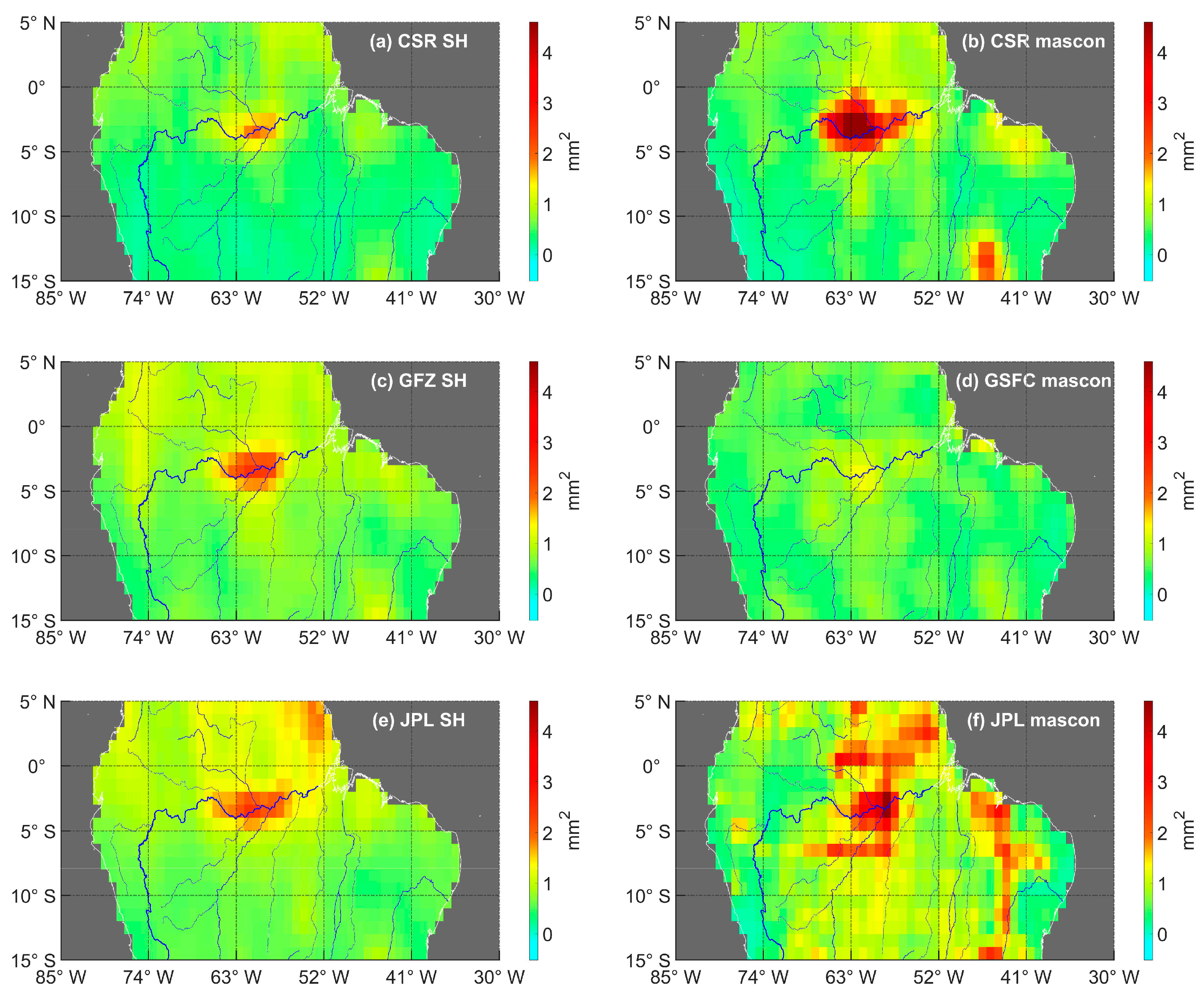
3.2. Uncertainty Assessment of Loading Deformations from Different GRACE Products
4. Discussion
4.1. Possible Reasons for the Agreement Differences over Different Regions and Using Different GRACE/GRACE-FO Solutions
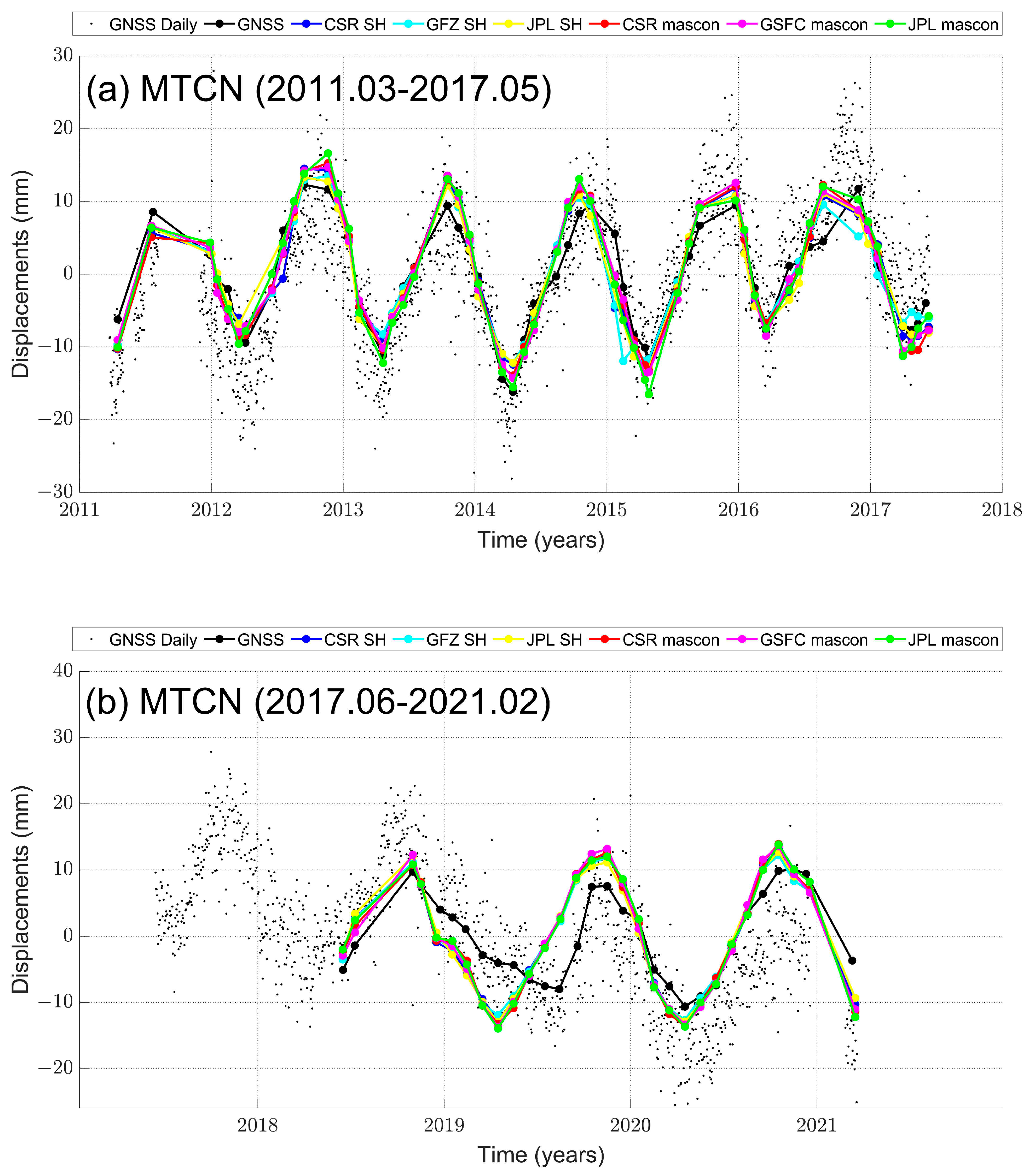
4.2. Explanations for the Disagreements at Specific GNSS Stations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Longman, I.M. A Green’s Function for Determining the Deformation of the Earth under Surface Mass Loads: 2. Computations and Numerical Results. J. Geophys. Res. 1963, 68, 485–496. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by Surface Loads. Rev. Geophys. 1972, 10, 761. [Google Scholar] [CrossRef]
- Abdrakhmatov, K.Y.; Aldazhanov, S.A.; Hager, B.H.; Hamburger, M.W.; Herring, T.A.; Kalabaev, K.B.; Makarov, V.I.; Molnar, P.; Panasyuk, S.V.; Prilepin, M.T.; et al. Relatively Recent Construction of the Tien Shan Inferred from GPS Measurements of Present-Day Crustal Deformation Rates. Nature 1996, 384, 450–453. [Google Scholar] [CrossRef]
- Segall, P.; Davis, J.L. GPS Applications for geodynamics and earthquake studies. Annu. Rev. Earth Planet. Sci. 1997, 25, 301–336. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of Apparent Seasonal Variations from GPS-Derived Site Position Time Series: Seasonal variations from GPS site time series. J. Geophys. Res. Solid Earth 2002, 107, 2075. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A New Global Mode of Earth Deformation: Seasonal Cycle Detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef]
- Dam, T.M.; Wahr, J.; Chao, Y.; Leuliette, E. Predictions of Crustal Deformation and of Geoid and Sea-Level Variability Caused by Oceanic and Atmospheric Loading. Geophys. J. Int. 1997, 129, 507–517. [Google Scholar] [CrossRef]
- Khan, S.A.; Wahr, J.; Stearns, L.A.; Hamilton, G.S.; van Dam, T.; Larson, K.M.; Francis, O. Elastic Uplift in Southeast Greenland Due to Rapid Ice Mass Loss. Geophys. Res. Lett. 2007, 34, L21701. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-Variable Gravity from GRACE: First Results: Time-variable gravity from grace. Geophys. Res. Lett. 2004, 31, L11501. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of Scaled GRACE Terrestrial Water Storage Estimates: Accuracy of grace-tws. Water Resour. Res. 2012, 48, 4531. [Google Scholar] [CrossRef]
- Chambers, D.P. Observing Seasonal Steric Sea Level Variations with GRACE and Satellite Altimetry. J. Geophys. Res. 2006, 111, C03010. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Satellite Gravity Measurements Confirm Accelerated Melting of Greenland Ice Sheet. Science 2006, 313, 1958–1960. [Google Scholar] [CrossRef] [PubMed]
- van Dam, T.; Wahr, J.; Lavallée, D. A Comparison of Annual Vertical Crustal Displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. 2007, 112, B03404. [Google Scholar] [CrossRef]
- Fu, Y.; Freymueller, J.T. Seasonal and Long-Term Vertical Deformation in the Nepal Himalaya Constrained by GPS and GRACE Measurements: GPS/GRACE vertical deformation in nepal. J. Geophys. Res. Solid Earth 2012, 117, 409–421. [Google Scholar] [CrossRef]
- Chanard, K.; Fleitout, L.; Calais, E.; Rebischung, P.; Avouac, J. Toward a Global Horizontal and Vertical Elastic Load Deformation Model Derived from GRACE and GNSS Station Position Time Series. J. Geophys. Res. Solid Earth 2018, 123, 3225–3237. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Freymueller, J.T.; Heflin, M.B. Horizontal Motion in Elastic Response to Seasonal Loading of Rain Water in the Amazon Basin and Monsoon Water in Southeast Asia Observed by GPS and Inferred from GRACE: Horizontal seasonal motions by GPS/GRACE. Geophys. Res. Lett. 2013, 40, 6048–6053. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global Evaluation of New GRACE Mascon Products for Hydrologic Applications: Global analysis of grace mascon products. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Zhang, L.; Yi, S.; Wang, Q.; Chang, L.; Tang, H.; Sun, W. Evaluation of GRACE Mascon Solutions for Small Spatial Scales and Localized Mass Sources. Geophys. J. Int. 2019, 218, 1307–1321. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, H.; Chang, L.; Sun, W. Performance of GRACE Mascon Solutions in Studying Seismic Deformations. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019510. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Wilson, C.; Cazenave, A.; Seo, K.; Kim, J. Global Ocean Mass Change From GRACE and GRACE Follow-On and Altimeter and Argo Measurements. Geophys. Res. Lett. 2020, 47, e2020GL090656. [Google Scholar] [CrossRef]
- Wang, L.; Chen, C.; Ma, X.; Fu, Z.; Zheng, Y.; Peng, Z. Evaluation of GRACE Mascon Solutions Using In-Situ Geodetic Data: The Case of Hydrologic-Induced Crust Displacement in the Yangtze River Basin. Sci. Total Environ. 2020, 707, 135606. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Fan, D.; You, W. Comparison of Observed and Modeled Seasonal Crustal Vertical Displacements Derived from Multi-Institution GPS and GRACE Solutions: GPS-Observed and GRACE-Modeled CVD Data. Geophys. Res. Lett. 2017, 44, 7219–7227. [Google Scholar] [CrossRef]
- Blewitt, G. Harnessing the GPS Data Explosion for Interdisciplinary Science. Available online: http://eos.org/science-updates/harnessing-the-gps-data-explosion-for-interdisciplinary-science (accessed on 20 October 2022).
- Save, H. CSR GRACE and GRACE-FO RL06 Mascon Solutions v02. 2020. Available online: https://doi.org/10.15781/cgq9-nh24 (accessed on 5 July 2022).
- Loomis, B.D.; Felikson, D.; Sabaka, T.J.; Medley, B. High-Spatial-Resolution Mass Rates From GRACE and GRACE-FO: Global and Ice Sheet Analyses. J. Geophys. Res. Solid Earth 2021, 126, e2021JB023024. [Google Scholar] [CrossRef]
- Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W.; Watkins, M.M. JPL GRACE Mascon Ocean, Ice, and Hydrology Equivalent Water Height Release 06 Coastal Resolution Improvement (CRI) Filtered Version 1.0. Ver. 1.0. PO.DAAC, CA, USA. 2018. Available online: http://doi.org/10.5067/TEMSC-3MJC6 (accessed on 1 March 2022).
- Loomis, B.D.; Rachlin, K.E.; Wiese, D.N.; Landerer, F.W.; Luthcke, S.B. Replacing GRACE/GRACE-FO With Satellite Laser Ranging: Impacts on Antarctic Ice Sheet Mass Change. Geophys. Res. Lett. 2020, 47, e2019GL085488. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Comment on “An Assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment Model” by Purcell et al. Available online: https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1002/2016JB013844 (accessed on 7 July 2022).
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Blankenship, D.; Young, D. Antarctic Regional Ice Loss Rates from GRACE. Earth Planet. Sci. Lett. 2008, 266, 140–148. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-Processing Removal of Correlated Errors in GRACE Data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Jekeli, C. Alternative Methods to Smooth the Earth’s Gravity Field; Report No. 327, Reports of the Department of Geodetic Science and Surveying; Ohio State University: Columbus, OH, USA, 1981. [Google Scholar]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing Estimates of Annual Variations and Trends in Geocenter Motion and J 2 from a Combination of GRACE Data and Geophysical Models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output: Estimating geocenter variations. J. Geophys. Res. Solid Earth 2008, 113, B08410. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B. Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise. Geophys. Res. Lett. 2019, 46, 6910–6917. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s Figure Axis from Satellite Laser Ranging and GRACE. J. Geophys. Res. 2011, 116, B01409. [Google Scholar] [CrossRef]
- Kusche, J.; Schrama, E.J.O. Surface Mass Redistribution Inversion from Global GPS Deformation and Gravity Recovery and Climate Experiment (GRACE) Gravity Data: Surface mass redistribution from GPS and GRACE. J. Geophys. Res. Solid Earth 2005, 110, B09409. [Google Scholar] [CrossRef]
- Premoli, A.; Tavella, P. A Revisited Three-Cornered Hat Method for Estimating Frequency Standard Instability. IEEE Trans. Instrum. Meas. 1993, 42, 7–13. [Google Scholar] [CrossRef]
- Ditmar, P. Conversion of Time-Varying Stokes Coefficients into Mass Anomalies at the Earth’s Surface Considering the Earth’s Oblateness. J. Geod. 2018, 92, 1401–1412. [Google Scholar] [CrossRef] [PubMed]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved Methods for Observing Earth’s Time Variable Mass Distribution with GRACE Using Spherical Cap Mascons: Improved Gravity Observations from GRACE. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Niu, Y.; Wei, N.; Li, M.; Rebischung, P.; Shi, C.; Chen, G. Quantifying Discrepancies in the Three-Dimensional Seasonal Variations between IGS Station Positions and Load Models. J. Geod. 2022, 96, 31. [Google Scholar] [CrossRef]
- Youm, K.; Eom, J.; Seo, K.-W.; Chen, J.; Wilson, C.R.; Oh, S. High-Resolution Surface Mass Loads in the Amazon Basin Combining GRACE and River Routing Model. Geophys. J. Int. 2022, 232, ggac439. [Google Scholar] [CrossRef]

| Station | Latitude | Longitude | Time Span (Decimal Year) |
|---|---|---|---|
| AMCO | −4.9 | 294.7 | 2012.7–2021.1 |
| AMHA | −7.5 | 297.0 | 2015.1–2020.5 |
| AMPR | −2.6 | 303.3 | 2015.1–2018.8 |
| AMTE | −3.3 | 295.3 | 2013.9–2021.2 |
| AMUA | −3.1 | 300.0 | 2015.2–2021.1 |
| APLJ | −0.8 | 307.5 | 2014.9–2021.2 |
| APS1 | −0.1 | 308.8 | 2016.1–2021.2 |
| ITAM | −3.1 | 301.6 | 2015.1–2018.5 |
| MTCN | −13.6 | 307.7 | 2011.3–2021.2 |
| MTCO | −10.8 | 304.5 | 2009.5–2019.5 |
| MTJI | −11.4 | 301.3 | 2014.8–2021.2 |
| MTNX | −14.7 | 307.7 | 2016.2–2019.9 |
| MTSF | −11.6 | 309.3 | 2008.3–2018.5 |
| MTSR | −12.5 | 304.3 | 2011.1–2021.2 |
| PAAR | −3.2 | 307.8 | 2017.5–2021.2 |
| PAIT | −4.3 | 304.0 | 2014.6–2021.1 |
| PASM | −2.4 | 305.3 | 2015.6–2021.2 |
| POVE | −8.7 | 296.1 | 2006.0–2021.2 |
| RIOB | −10.0 | 292.2 | 2007.7–2021.2 |
| ROCD | −13.1 | 299.5 | 2010.3–2019.4 |
| ROGM | −10.8 | 294.7 | 2008.0–2020.5 |
| ROJI | −10.9 | 298.0 | 2008.3–2021.2 |
| Station | Annual Amplitudes (mm) | Annual Phases (Degree) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GNSS | CSR SH | GFZ SH | JPL SH | CSR Mascon | GSFC Mascon | JPL Mascon | GNSS | CSR SH | GFZ SH | JPL SH | CSR Mascon | GSFC Mascon | JPL Mascon | |
| AMCO | 12.7 | 16.7 | 16.2 | 16.3 | 19.7 | 20.2 | 19.3 | 314.7 | 304.9 | 303.5 | 303.8 | 301.3 | 301.7 | 301.0 |
| AMHA | 18.1 | 16.4 | 16.0 | 16.7 | 17.5 | 18.0 | 17.7 | 291.4 | 292.8 | 291.4 | 292.6 | 285.1 | 283.0 | 286.2 |
| AMPR | 25.2 | 18.4 | 16.5 | 18.3 | 21.8 | 22.3 | 19.3 | 336.9 | 326.8 | 325.8 | 326.6 | 329.7 | 328.4 | 326.8 |
| AMTE | 19.8 | 16.4 | 15.8 | 16.2 | 20.3 | 20.6 | 19.4 | 317.0 | 314.6 | 313.6 | 313.7 | 314.4 | 315.0 | 313.5 |
| AMUA | 29.4 | 20.0 | 19.3 | 20 | 25.3 | 25.6 | 26.0 | 326.8 | 317.9 | 317.7 | 316.8 | 321.8 | 321.7 | 321.8 |
| APLJ | 14.2 | 13.1 | 12.5 | 13.0 | 14.9 | 14.7 | 15.3 | 335.0 | 321.4 | 320.9 | 319.7 | 321.0 | 322.8 | 319.3 |
| APS1 | 9.5 | 11.6 | 10.9 | 11.9 | 12.8 | 12.3 | 13.6 | 333.5 | 317.1 | 315.5 | 316.1 | 316.7 | 316.1 | 315.3 |
| ITAM | 28.1 | 19.1 | 17.1 | 17.2 | 23.0 | 23.3 | 23.7 | 338.2 | 326 | 326.1 | 332.2 | 332.5 | 330.7 | 334.5 |
| MTCN | 7.8 | 11.0 | 10.5 | 10.8 | 11.6 | 11.6 | 11.8 | 291.8 | 284.1 | 281.2 | 281.9 | 284.8 | 284.0 | 284.4 |
| MTCO | 12.9 | 13.5 | 12.9 | 13.4 | 13.9 | 14.6 | 14.1 | 288.5 | 283 | 281.4 | 281.9 | 281.2 | 284.1 | 280.3 |
| MTJI | 12.8 | 13.2 | 12.7 | 13.3 | 13.3 | 14.1 | 14.0 | 292.6 | 286 | 283.2 | 284.9 | 285.9 | 287.0 | 285.5 |
| MTNX | 10.2 | 10.1 | 9.2 | 10.2 | 10.6 | 10.8 | 10.6 | 275.7 | 280.8 | 278.5 | 280 | 281.7 | 279.7 | 281.8 |
| MTSF | 13.5 | 11.5 | 11.1 | 11.3 | 12.6 | 12.8 | 12.9 | 278.7 | 282.2 | 280 | 279.7 | 279.7 | 280.4 | 278.2 |
| MTSR | 11.9 | 12.2 | 11.7 | 12.2 | 13.0 | 13.0 | 13.2 | 294.9 | 285.9 | 283.8 | 283.6 | 285.8 | 286.6 | 285.2 |
| PAAR | 14.3 | 14.3 | 14.3 | 14.7 | 15.8 | 16.3 | 16.5 | 316.8 | 307.2 | 307.3 | 306.6 | 308.8 | 311.3 | 307.9 |
| PAIT | 15.8 | 16.7 | 15.9 | 16.9 | 17.7 | 18.9 | 18.2 | 323.7 | 314.5 | 313.1 | 313.9 | 314.2 | 316.0 | 313.5 |
| PASM | 24.5 | 15.7 | 15.1 | 15.8 | 17.7 | 19.0 | 17.4 | 332.5 | 323.0 | 323.0 | 321.0 | 323.6 | 324.8 | 319.5 |
| POVE | 14.8 | 15.6 | 15.3 | 15.6 | 16.0 | 16.6 | 16.1 | 285.4 | 287.0 | 286.2 | 285.8 | 281.3 | 281.4 | 281.0 |
| RIOB | 10.4 | 12.4 | 12.1 | 12.2 | 11.8 | 12.7 | 12.0 | 283.6 | 284.3 | 283.6 | 282.4 | 282.9 | 285.1 | 280.4 |
| ROCD | 13.4 | 11.9 | 11.7 | 11.9 | 12.6 | 13.3 | 12.5 | 287.0 | 284.9 | 282.8 | 281.9 | 286.8 | 285.5 | 286.6 |
| ROGM | 14.1 | 13.1 | 12.8 | 13.1 | 13.7 | 14.1 | 13.9 | 290.7 | 284.1 | 284.1 | 282.1 | 282.9 | 284.5 | 281.7 |
| ROJI | 12.1 | 14.0 | 13.6 | 13.9 | 14.5 | 14.8 | 14.9 | 292.2 | 285.3 | 284.4 | 283.9 | 283.3 | 284.5 | 283.2 |
| Average | 15.7 | 14.4 | 13.8 | 14.3 | 15.9 | 16.3 | 16.0 | 305.8 | 299.7 | 298.5 | 298.7 | 299.3 | 299.7 | 298.5 |
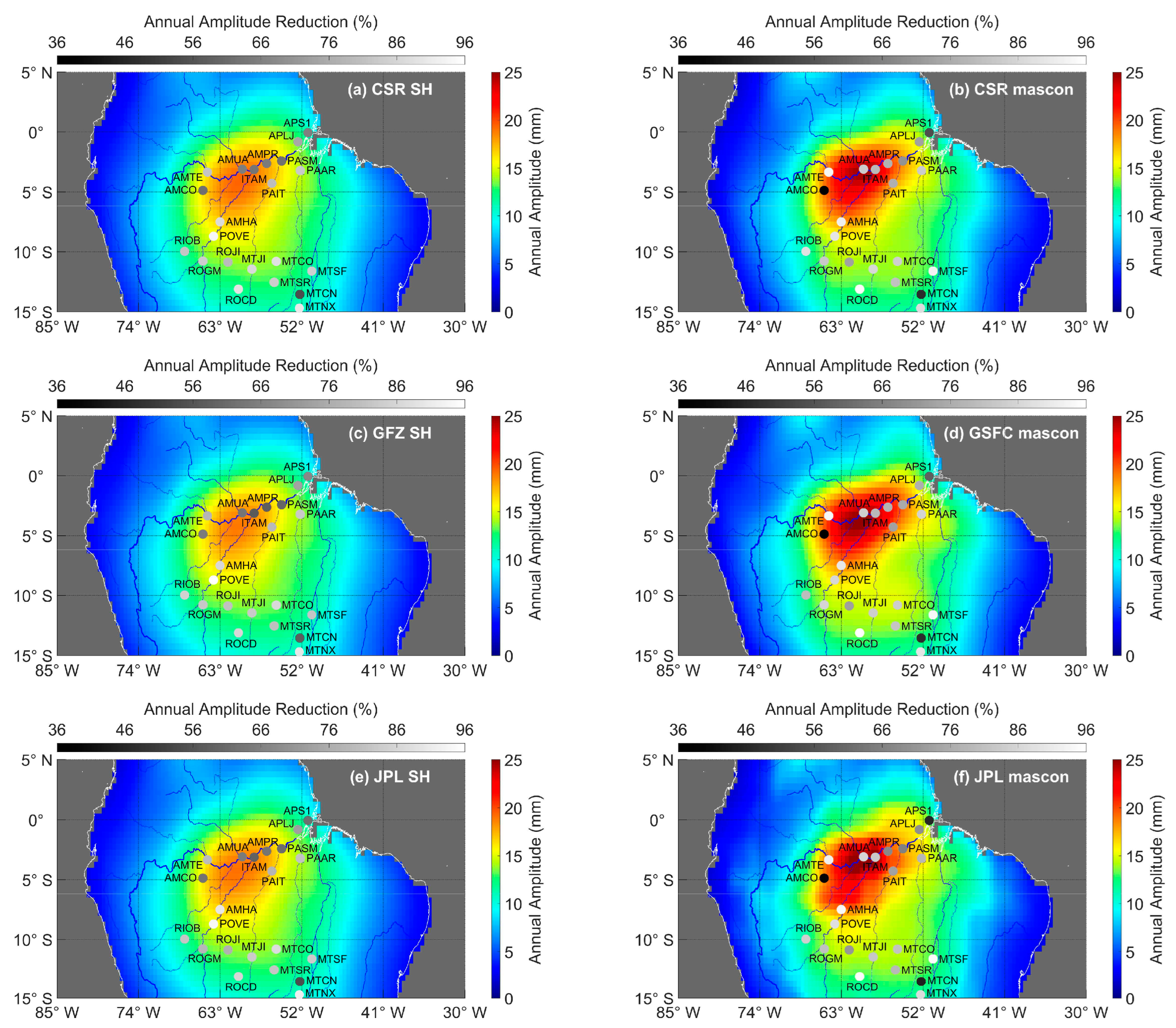
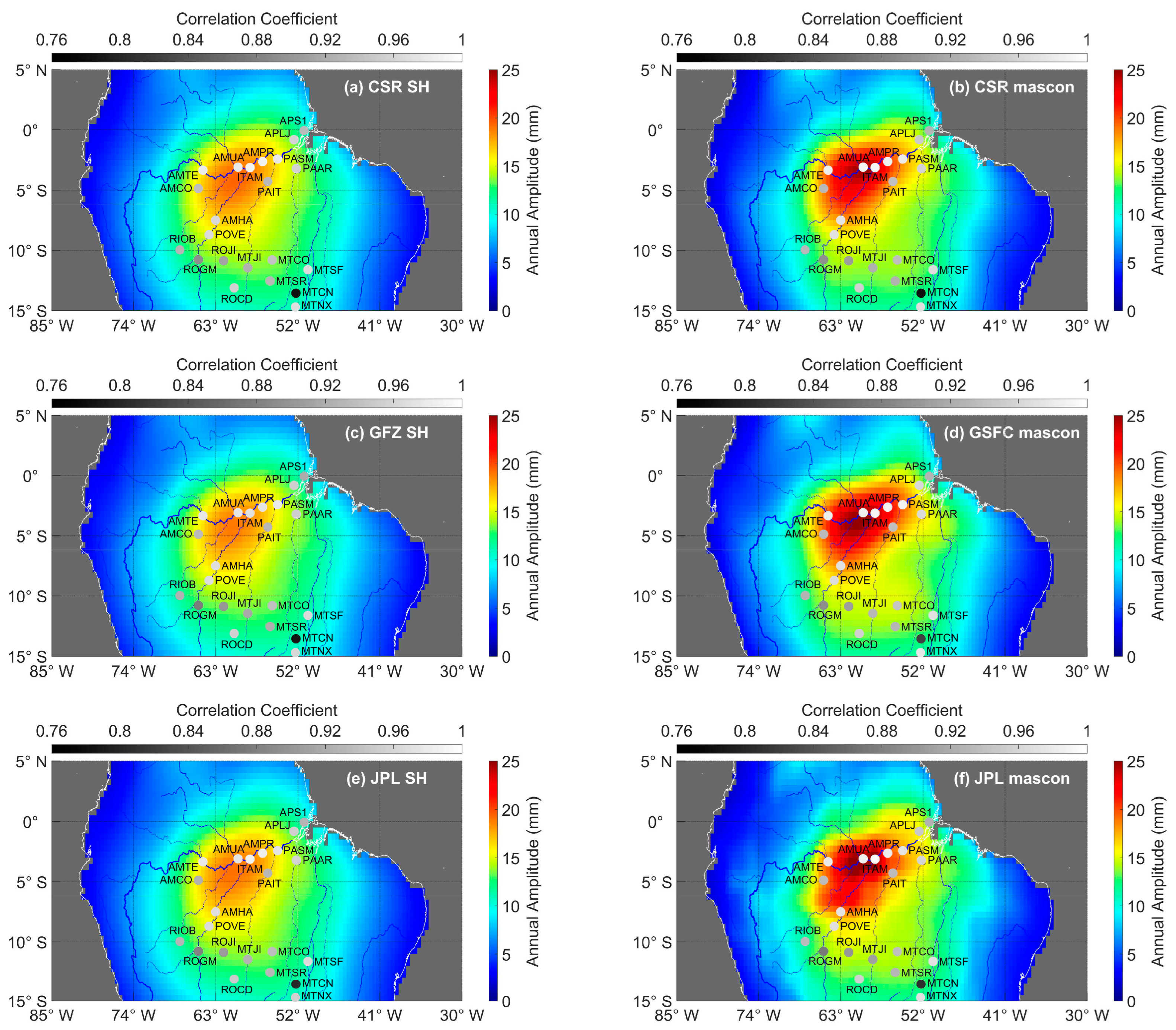
| Annual Amplitude Reduction (%) | Correlation Coefficient | RMS Reduction (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Whole Basin | Center | South | Whole Basin | Center | South | Whole Basin | Center | South | |
| CSR SH | 77.6 | 70.4 | 83.6 | 0.944 | 0.963 | 0.928 | 63.2 | 63.8 | 62.7 |
| GFZ SH | 76.4 | 68.5 | 83.1 | 0.938 | 0.956 | 0.923 | 61.7 | 61.5 | 61.8 |
| JPL SH | 76.3 | 68.7 | 82.6 | 0.941 | 0.959 | 0.926 | 62.3 | 62.4 | 62.2 |
| CSR Mascon | 78.6 | 72.8 | 83.4 | 0.944 | 0.963 | 0.928 | 64.9 | 67.3 | 63.0 |
| GSFC mascon | 78.5 | 73.7 | 82.6 | 0.947 | 0.966 | 0.932 | 65.3 | 68.1 | 63.0 |
| JPL Mascon | 76.6 | 70.1 | 82.0 | 0.943 | 0.961 | 0.928 | 63.8 | 65.7 | 62.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Wang, S.-Y.; Li, J.; Chen, J.; Qi, Z. Comparison of GRACE/GRACE-FO Spherical Harmonic and Mascon Products in Interpreting GNSS Vertical Loading Deformations over the Amazon Basin. Remote Sens. 2023, 15, 252. https://doi.org/10.3390/rs15010252
Wang P, Wang S-Y, Li J, Chen J, Qi Z. Comparison of GRACE/GRACE-FO Spherical Harmonic and Mascon Products in Interpreting GNSS Vertical Loading Deformations over the Amazon Basin. Remote Sensing. 2023; 15(1):252. https://doi.org/10.3390/rs15010252
Chicago/Turabian StyleWang, Pengfei, Song-Yun Wang, Jin Li, Jianli Chen, and Zhaoxiang Qi. 2023. "Comparison of GRACE/GRACE-FO Spherical Harmonic and Mascon Products in Interpreting GNSS Vertical Loading Deformations over the Amazon Basin" Remote Sensing 15, no. 1: 252. https://doi.org/10.3390/rs15010252
APA StyleWang, P., Wang, S.-Y., Li, J., Chen, J., & Qi, Z. (2023). Comparison of GRACE/GRACE-FO Spherical Harmonic and Mascon Products in Interpreting GNSS Vertical Loading Deformations over the Amazon Basin. Remote Sensing, 15(1), 252. https://doi.org/10.3390/rs15010252






