A New Spatial–Temporal Depthwise Separable Convolutional Fusion Network for Generating Landsat 8-Day Surface Reflectance Time Series over Forest Regions
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
2.2. Landsat 5 TM data
2.3. MODIS Data
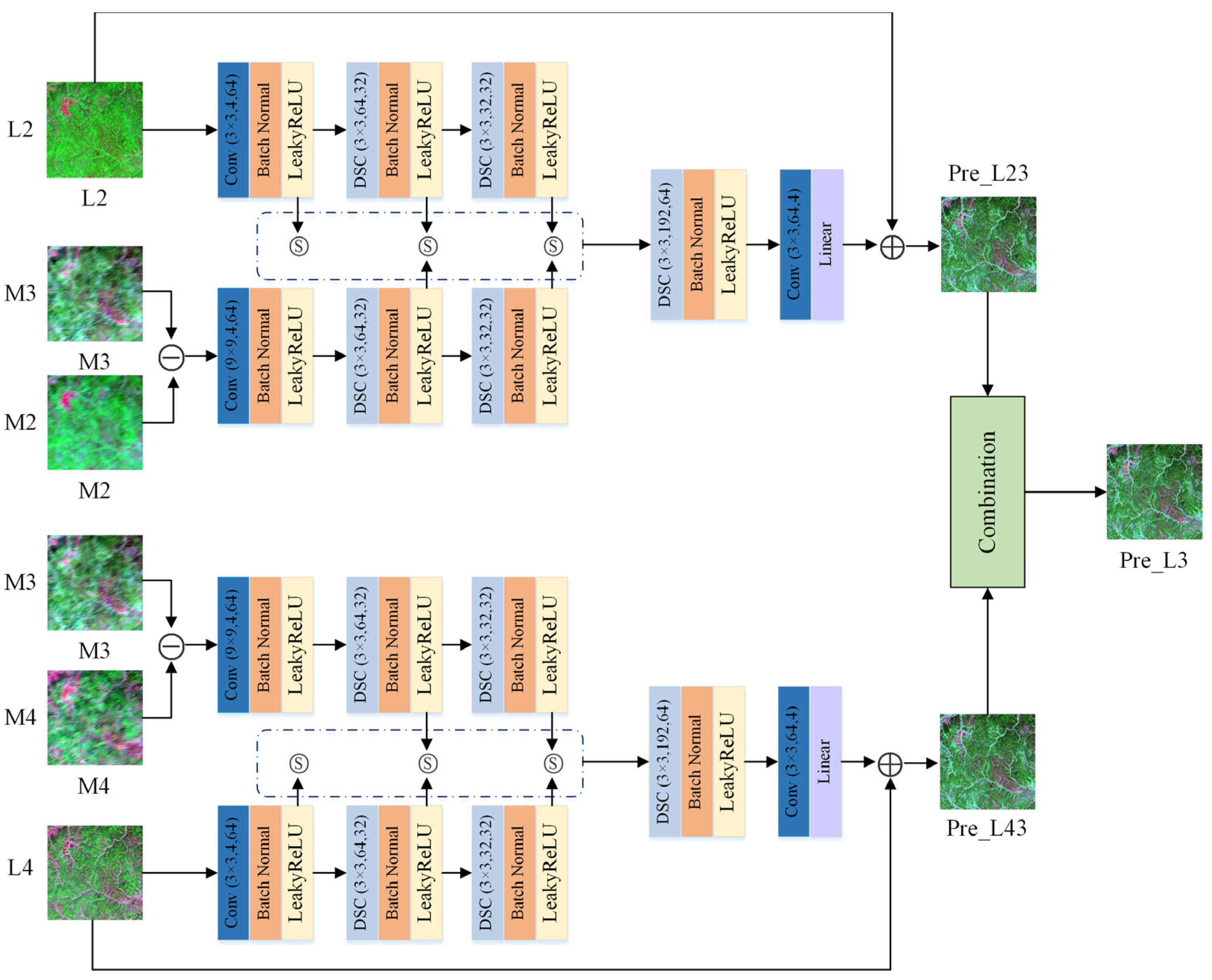
2.4. STFDSC Fusion Method
2.4.1. Architecture of STFDSC
2.4.2. Training
2.5. Comparison of Experiments
2.6. Generating Landsat Surface Reflectance Time Series
2.7. Accuracy Assessment
3. Results
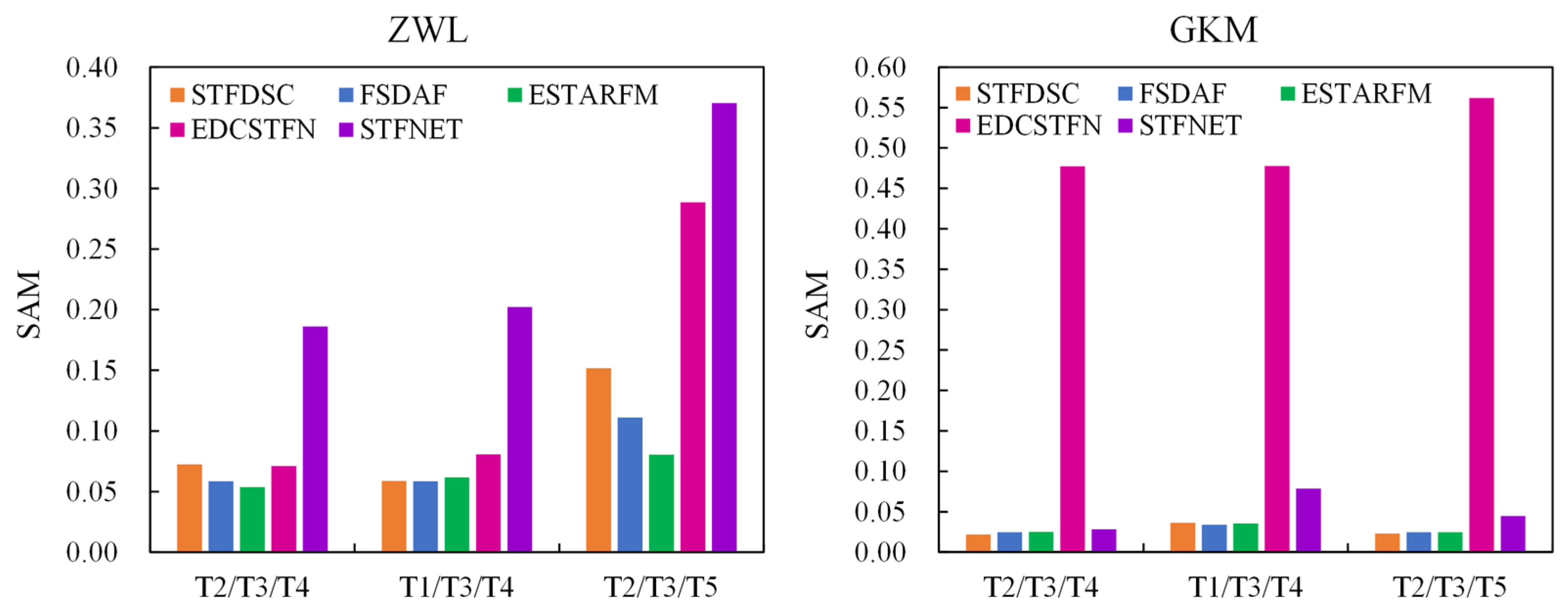
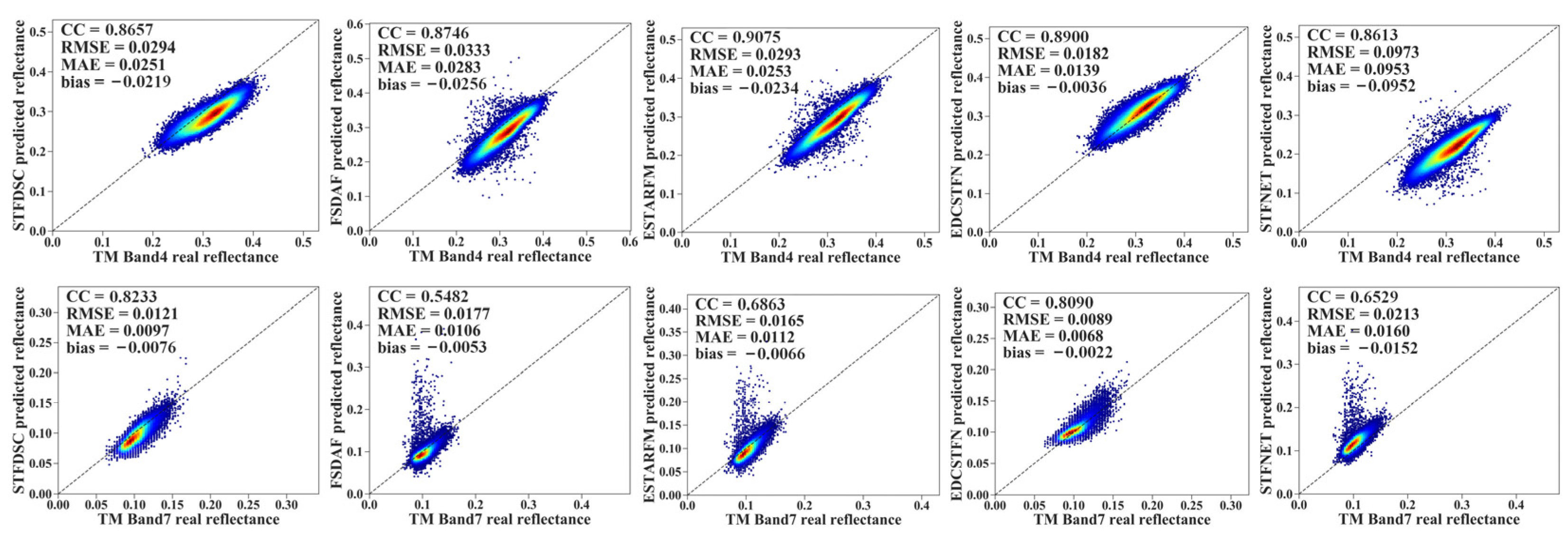
3.1. Performance of STF Methods in the Three Experiments
3.2. Performance of STF Methods in Deriving the NDVI and NBR
3.3. Visual Assessment of the Five STF Fusion Methods
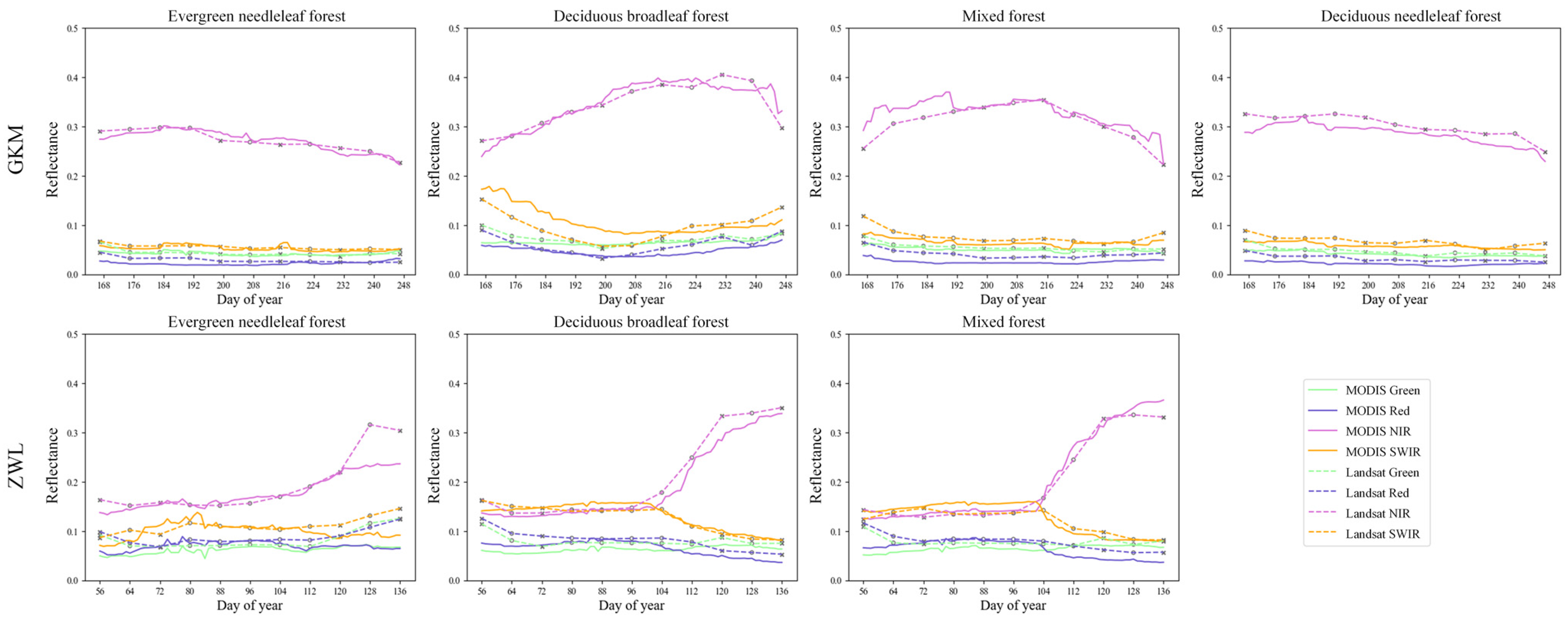
3.4. Landsat Surface Reflectance Time Series Generated Using STFDSC
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free Access to Landsat Imagery. Science 2008, 320, 11011. [Google Scholar] [CrossRef] [PubMed]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Jones, S.; Soto-Berelov, M.; Haywood, A.; Hislop, S. Landsat Time-Series for Estimating Forest Aboveground Biomass and Its Dynamics across Space and Time: A Review. Remote Sens. 2020, 12, 98. [Google Scholar] [CrossRef] [Green Version]
- Bolton, D.K.; Gray, J.M.; Melaas, E.K.; Moon, M.; Eklundh, L.; Friedl, M.A. Continental-scale land surface phenology from harmonized Landsat 8 and Sentinel-2 imagery. Remote Sens. Environ. 2020, 240, 111685. [Google Scholar] [CrossRef]
- Huang, H.; Chen, Y.; Clinton, N.; Wang, J.; Wang, X.; Liu, C.; Gong, P.; Yang, J.; Bai, Y.; Zheng, Y.; et al. Mapping major land cover dynamics in Beijing using all Landsat images in Google Earth Engine. Remote Sens. Environ. 2017, 202, 166–176. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Xiao, X.; Li, X.; Pan, L.; Doughty, R.; Ma, J.; Dong, J.; Qin, Y.; Zhao, B.; Wu, Z.; et al. A mangrove forest map of China in 2015: Analysis of time series Landsat 7/8 and Sentinel-1A imagery in Google Earth Engine cloud computing platform. ISPRS J. Photogramm. Remote Sens. 2017, 131, 104–120. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Hermosilla, T.; Coops, N.C.; Hobart, G.W. A nationwide annual characterization of 25 years of forest disturbance and recovery for Canada using Landsat time series. Remote Sens. Environ. 2017, 194, 303–321. [Google Scholar] [CrossRef]
- Griffiths, P.; Kuemmerle, T.; Baumann, M.; Radeloff, V.C.; Abrudan, I.V.; Lieskovsky, J.; Munteanu, C.; Ostapowicz, K.; Hostert, P. Forest disturbances, forest recovery, and changes in forest types across the Carpathian ecoregion from 1985 to 2010 based on Landsat image composites. Remote Sens. Environ. 2014, 151, 72–88. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D.P. Large-Area Gap Filling of Landsat Reflectance Time Series by Spectral-Angle-Mapper Based Spatio-Temporal Similarity (SAMSTS). Remote Sens. 2018, 10, 609. [Google Scholar] [CrossRef] [Green Version]
- Meng, Q.; Cooke, W.H.; Rodgers, J. Derivation of 16-day time-series NDVI data for environmental studies using a data assimilation approach. GIScience Remote Sens. 2013, 50, 500–514. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, J.; Chen, X.; Zhu, X.; Qiu, Y.; Song, H.; Rao, Y.; Zhang, C.; Cao, X.; Cui, X. Sensitivity of six typical spatiotemporal fusion methods to different influential factors: A comparative study for a normalized difference vegetation index time series reconstruction. Remote Sens. Environ. 2021, 252, 112130. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Seitz, N.; White, J.C.; Gao, F.; Masek, J.G.; Stenhouse, G. Generation of dense time series synthetic Landsat data through data blending with MODIS using a spatial and temporal adaptive reflectance fusion model. Remote Sens. Environ. 2009, 113, 1988–1999. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Dao, P.D.; Mong, N.T.; Chan, H.-P. Landsat-MODIS image fusion and object-based image analysis for observing flood inundation in a heterogeneous vegetated scene. GISci. Remote Sens. 2019, 56, 1148–1169. [Google Scholar] [CrossRef]
- Wu, M.; Niu, Z.; Wang, C.; Wu, C.; Wang, L. Use of MODIS and Landsat time series data to generate high-resolution temporal synthetic Landsat data using a spatial and temporal reflectance fusion model. J. Appl. Remote Sens. 2012, 6, 063507. [Google Scholar]
- Huang, B.; Zhang, H. Spatio-temporal reflectance fusion via unmixing: Accounting for both phenological and land-cover changes. Int. J. Remote Sens. 2014, 35, 6213–6233. [Google Scholar] [CrossRef]
- Gevaert, C.M.; García-Haro, F.J. A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion. Remote Sens. Environ. 2015, 156, 34–44. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. An Augmented Linear Mixing Model to Address Spectral Variability for Hyperspectral Unmixing. IEEE Trans. Image Processing 2019, 28, 1923–1938. [Google Scholar] [CrossRef] [Green Version]
- Tan, Z.; Di, L.; Zhang, M.; Guo, L.; Gao, M. An Enhanced Deep Convolutional Model for Spatiotemporal Image Fusion. Remote Sens. 2019, 11, 2898. [Google Scholar] [CrossRef] [Green Version]
- Huang, B.; Song, H. Spatiotemporal Reflectance Fusion via Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Song, H.; Huang, B. Spatiotemporal Satellite Image Fusion Through One-Pair Image Learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1883–1896. [Google Scholar] [CrossRef]
- Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal Satellite Image Fusion Using Deep Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Liu, X.; Deng, C.; Chanussot, J.; Hong, D.; Zhao, B. StfNet: A Two-Stream Convolutional Neural Network for Spatiotemporal Image Fusion. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6552–6564. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Peng, Y.; Dong, M. Spatiotemporal Fusion of Remote Sensing Images using a Convolutional Neural Network with Attention and Multiscale Mechanisms. Int. J. Remote Sens. 2021, 42, 1973–1993. [Google Scholar] [CrossRef]
- Chen, B.; Li, J.; Jin, Y.F. Deep Learning for Feature-Level Data Fusion: Higher Resolution Reconstruction of Historical Landsat Archive. Remote Sens. 2021, 13, 167. [Google Scholar] [CrossRef]
- Gao, J.; Yuan, Q.; Li, J.; Zhang, H.; Su, X. Cloud Removal with Fusion of High Resolution Optical and SAR Images Using Generative Adversarial Networks. Remote Sens. 2020, 12, 191. [Google Scholar] [CrossRef] [Green Version]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar]
- Lin, T.Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Fu, Y.; He, H.S.; Zhao, J.; Larsen, D.R.; Zhang, H.; Sunde, M.G.; Duan, S. Climate and Spring Phenology Effects on Autumn Phenology in the Greater Khingan Mountains, Northeastern China. Remote Sens. 2018, 10, 449. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.-y.; Zhang, H.-y.; Wang, Y.-q.; Zhao, J.-j.; Zhang, Z.-x. The driving factors and their interactions of fire occurrence in Greater Khingan Mountains, China. J. Mt. Sci. 2020, 17, 2674–2690. [Google Scholar] [CrossRef]
- Kang, D.; Guo, Y.; Ren, C.; Zhao, F.; Feng, Y.; Han, X.; Yang, G. Population Structure and Spatial Pattern of Main Tree Species in Secondary Betula platyphylla Forest in Ziwuling Mountains, China. Sci. Rep. 2014, 4, 6873. [Google Scholar] [CrossRef] [Green Version]
- Zheng, F.; He, X.; Gao, X.; Zhang, C.-e.; Tang, K. Effects of erosion patterns on nutrient loss following deforestation on the Loess Plateau of China. Agric. Ecosyst. Environ. 2005, 108, 85–97. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Hu, L.; Yu, L.; Clinton, N.; Huang, H.; Yang, J.; Gong, P. A Circa 2010 Thirty Meter Resolution Forest Map for China. Remote Sens. 2014, 6, 5325–5343. [Google Scholar] [CrossRef] [Green Version]
- USGS. Landsat Collection 1 Level 1 Product Definition; United State Geological Survey: Reston, VA, USA, 2019.
- Hislop, S.; Jones, S.; Soto-Berelov, M.; Skidmore, A.; Haywood, A.; Nguyen, T.H. Using Landsat Spectral Indices in Time-Series to Assess Wildfire Disturbance and Recovery. Remote Sens. 2018, 10, 460. [Google Scholar] [CrossRef] [Green Version]
- Walker, J.J.; de Beurs, K.M.; Wynne, R.H.; Gao, F. Evaluation of Landsat and MODIS data fusion products for analysis of dryland forest phenology. Remote Sens. Environ. 2012, 117, 381–393. [Google Scholar] [CrossRef]
- Walker, J.J.; de Beurs, K.M.; Wynne, R.H. Dryland vegetation phenology across an elevation gradient in Arizona, USA, investigated with fused MODIS and Landsat data. Remote Sens. Environ. 2014, 144, 85–97. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Yin, Z.X.; Wu, P.H.; Foody, G.M.; Wu, Y.L.; Liu, Z.H.; Du, Y.; Ling, F. Spatiotemporal Fusion of Land Surface Temperature Based on a Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1808–1822. [Google Scholar] [CrossRef]
- Ju, J.; Roy, D.P.; Shuai, Y.; Schaaf, C. Development of an approach for generation of temporally complete daily nadir MODIS reflectance time series. Remote Sens. Environ. 2010, 114, 1–20. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; He, L.; Chen, J.; Plaza, A. A new sensor bias-driven spatio-temporal fusion model based on convolutional neural networks. Sci. China Inf. Sci. 2020, 63, 140302. [Google Scholar] [CrossRef] [Green Version]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Hirschmugl, M.; Deutscher, J.; Sobe, C.; Bouvet, A.; Mermoz, S.; Schardt, M. Use of SAR and Optical Time Series for Tropical Forest Disturbance Mapping. Remote Sens. 2020, 12, 727. [Google Scholar] [CrossRef] [Green Version]
- Nikolakopoulos, K.; Oikonomidis, D. Quality assessment of ten fusion techniques applied on Worldview-2. Eur. J. Remote Sens. 2015, 48, 141–167. [Google Scholar] [CrossRef]
- Ao, Z.; Sun, Y.; Xin, Q. Constructing 10-m NDVI Time Series From Landsat 8 and Sentinel 2 Images Using Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1461–1465. [Google Scholar] [CrossRef]
- Sadeh, Y.; Zhu, X.; Dunkerley, D.; Walker, J.P.; Zhang, Y.; Rozenstein, O.; Manivasagam, V.S.; Chenu, K. Fusion of Sentinel-2 and PlanetScope time-series data into daily 3 m surface reflectance and wheat LAI monitoring. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102260. [Google Scholar] [CrossRef]
- Hernández, C.; Nunes, L.; Lopes, D.; Graña, M. Data fusion for high spatial resolution LAI estimation. Inf. Fusion 2014, 16, 59–67. [Google Scholar] [CrossRef]







| Study Area | Landsat Path/Row | MODIS Tile | Acquisition Dates of Good Quality Landsat and MODIS Data | ||||
|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | T5 | |||
| ZWL | 127/035 | h26v05 | 25 February | 12 March | 29 April | 15 May | 6 October |
| GKM | 120/024 | h25v03 | 15 June | 17 July | 2 August | 18 August | 3 September |
| Study Area | Experiment | Time Intervals (Days) between the Left/Right Reference Image and Target Image |
|---|---|---|
| ZWL | T2/T3/T4 | 48/16 |
| T1/T3/T4 | 64/16 | |
| T2/T3/T5 | 48/160 | |
| GKM | T2/T3/T4 | 16/16 |
| T1/T3/T4 | 48/16 | |
| T2/T3/T5 | 16/32 |
| Method | ZWL | GKM | ||||||
|---|---|---|---|---|---|---|---|---|
| NDVI RMSE | NDVI CC | NBR RMSE | NBR CC | NDVI RMSE | NDVI CC | NBR RMSE | NBR CC | |
| STFDSC | 0.0677 | 0.8825 | 0.0526 | 0.9268 | 0.0226 | 0.9114 | 0.0281 | 0.8891 |
| FSDAF | 0.0726 | 0.8455 | 0.0543 | 0.9361 | 0.0288 | 0.8509 | 0.0339 | 0.8433 |
| ESTARFM | 0.0696 | 0.8669 | 0.0482 | 0.9444 | 0.0262 | 0.8685 | 0.0354 | 0.8338 |
| EDCSTFN | 0.0800 | 0.9005 | 0.0457 | 0.9467 | 4.6585 | −0.0406 | 0.0353 | 0.8202 |
| STFNET | 0.1386 | 0.8656 | 0.2198 | 0.9287 | 0.0345 | 0.8682 | 0.0342 | 0.8649 |
| Method | Trainable Parameters | Million FLOPs |
|---|---|---|
| STFNET | 70,376 | 1583.5 |
| STFDSC | 97,288 | 2220.7 |
| EDCSTFN | 281,764 | 10,600.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, J.; Liang, S.; Li, M. A New Spatial–Temporal Depthwise Separable Convolutional Fusion Network for Generating Landsat 8-Day Surface Reflectance Time Series over Forest Regions. Remote Sens. 2022, 14, 2199. https://doi.org/10.3390/rs14092199
Zhang Y, Liu J, Liang S, Li M. A New Spatial–Temporal Depthwise Separable Convolutional Fusion Network for Generating Landsat 8-Day Surface Reflectance Time Series over Forest Regions. Remote Sensing. 2022; 14(9):2199. https://doi.org/10.3390/rs14092199
Chicago/Turabian StyleZhang, Yuzhen, Jindong Liu, Shunlin Liang, and Manyao Li. 2022. "A New Spatial–Temporal Depthwise Separable Convolutional Fusion Network for Generating Landsat 8-Day Surface Reflectance Time Series over Forest Regions" Remote Sensing 14, no. 9: 2199. https://doi.org/10.3390/rs14092199
APA StyleZhang, Y., Liu, J., Liang, S., & Li, M. (2022). A New Spatial–Temporal Depthwise Separable Convolutional Fusion Network for Generating Landsat 8-Day Surface Reflectance Time Series over Forest Regions. Remote Sensing, 14(9), 2199. https://doi.org/10.3390/rs14092199







