Fusion of a Static and Dynamic Convolutional Neural Network for Multiview 3D Point Cloud Classification
Abstract
:1. Introduction
1.1. Voxel-Based
1.2. Point Cloud-Based
1.3. Multiview-Based
- (1)
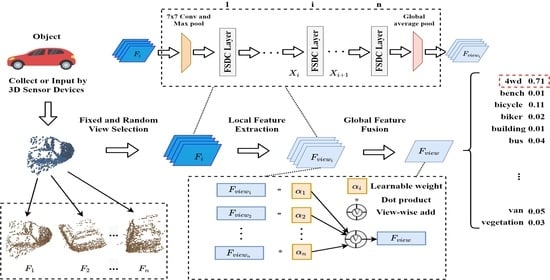
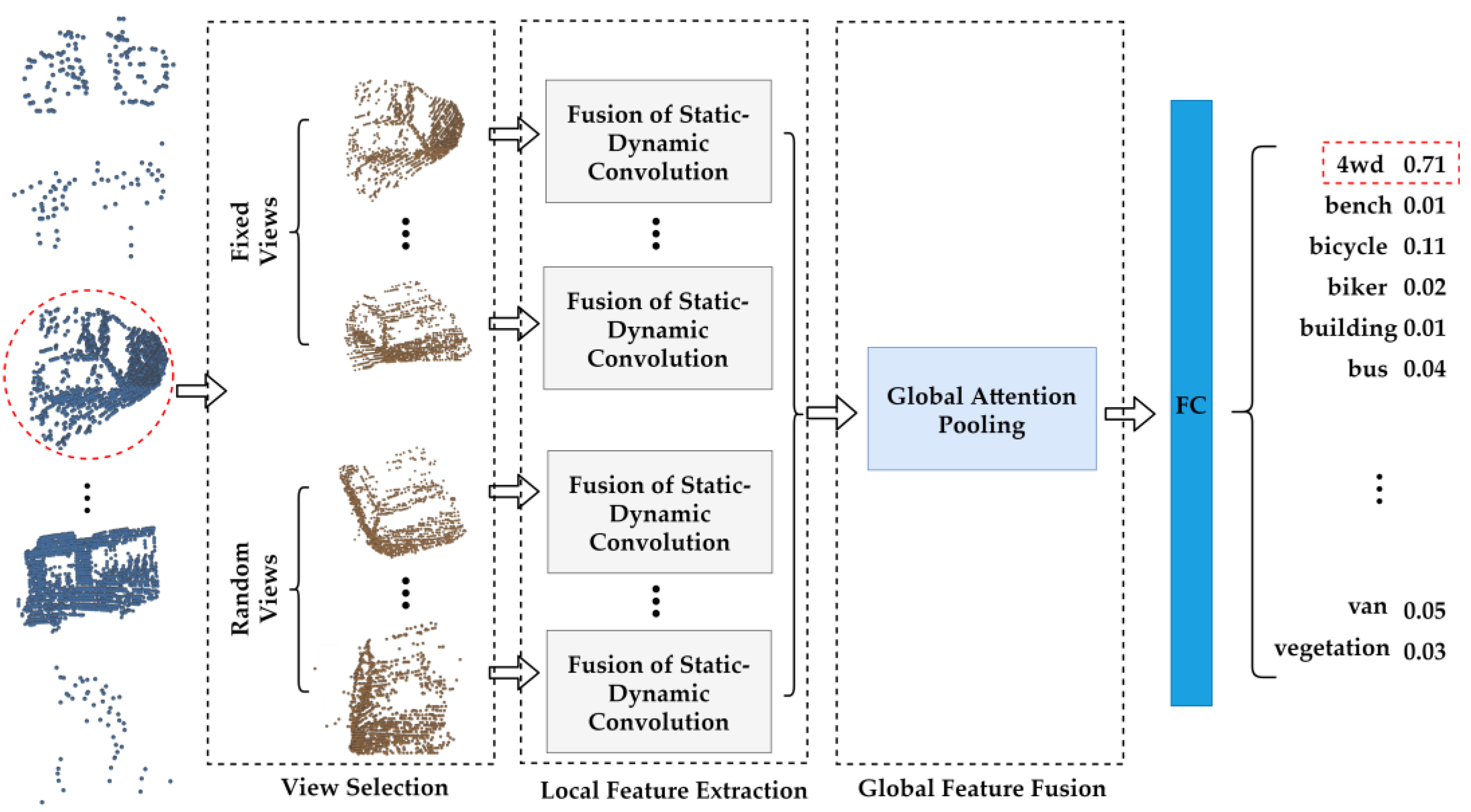
- FSDCNet, a fusion static and dynamic convolution neural network, is proposed and applied to the classification of a 3D point cloud. The network adopts fixed and random viewpoint selection method for multiview generation. Meanwhile, it carries out local feature extraction by combining lightweight dynamic convolution with traditional static convolution in parallel. In addition, adaptive global attention pooling is used for global feature fusion. The network model is applicable not only to dense point clouds (ModelNet40), but also to sparse point clouds (Sydney Urban Objects). Our experiments demonstrate that it can achieve state-of-the-art classification accuracy on two datasets. Our algorithm framework, FSDCNet, is evidently different from other advanced algorithm frameworks.
- (2)
- FSDCNet devises a view selection method of fixed and random viewpoints in the process of converting a point cloud into a multiview representation. The combination of random viewpoints avoids the problem of high similarity among views obtained by the traditional fixed viewpoint and improves the generalization of the model.
- (3)
- FSDCNet constructs a lightweight dynamic convolution operator. The operator solves the problems of large parameters and expensive computational complexity in dynamic convolution, while maintaining the advantages of dynamic convolution; the complexity is only equivalent to that of traditional static convolution. Meanwhile, it can obtain abundant feature information in different receptive fields.
- (4)
- FSDCNet proposes an adaptive fusion method of static and dynamic convolution. It can solve the problem of weak adaptability associated with traditional static convolution and extract more fine-grained feature information, which significantly improves the performance of the network model.
- (5)
- FSDCNet designs adaptive global attention pooling to avert the low efficiency of global feature fusion with maximum and average pooling. It can integrate the most crucial details on multiple local views and improve the fusion efficiency of multiview features.
2. Methods
2.1. Multiview Selection of Fixed and Random Viewpoints
- (1)
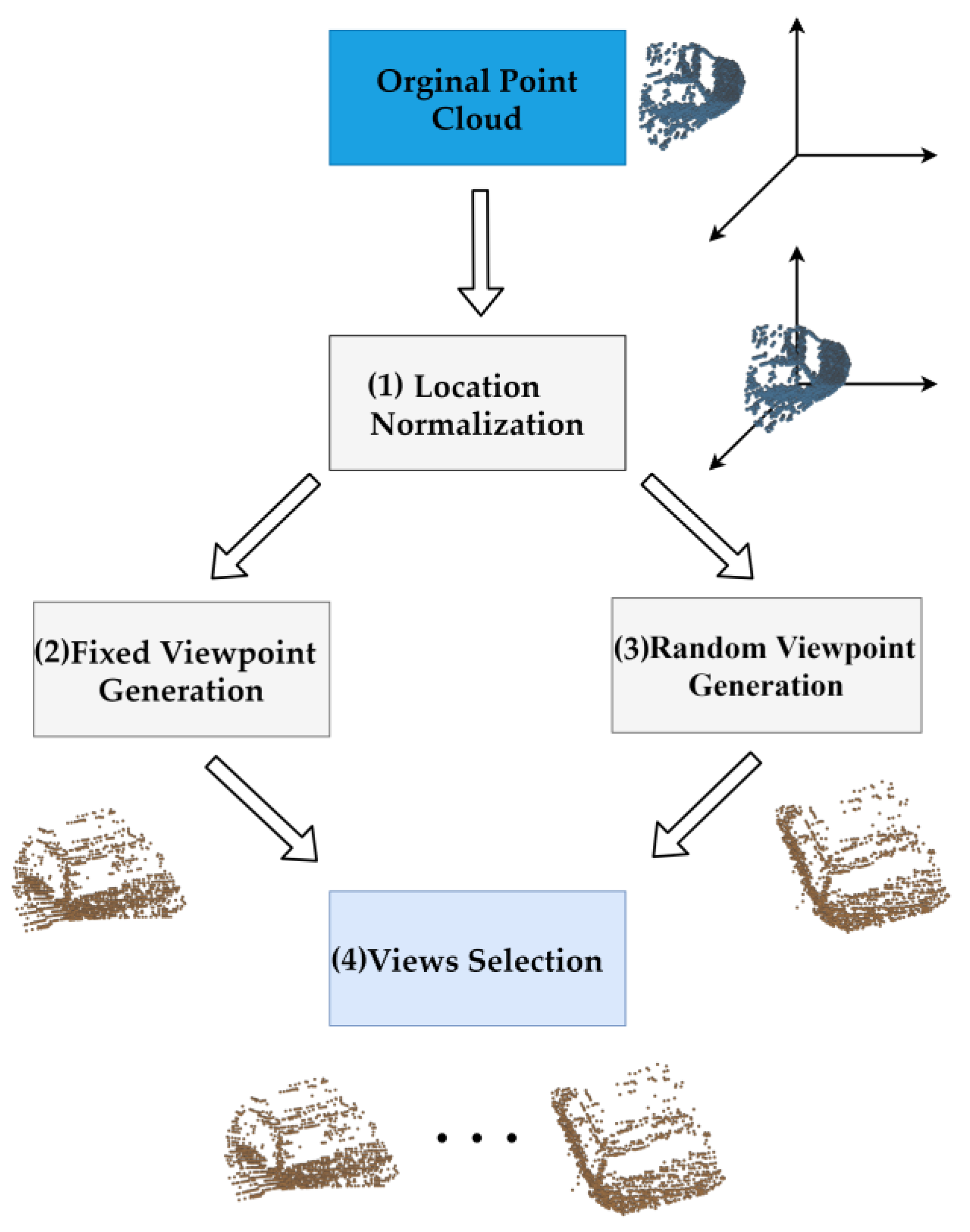
- Normalization of point cloud spatial location: Because the location distribution of the original point cloud group may be inconsistent, the virtual camera must move the viewpoint to the center of different objects. Therefore, we normalize the position information of each point of all the point clouds to build its position distribution around the origin of the 3D coordinate system. Normalization is represented by Equation (1) as follows:where is any point in the point cloud, and and represent the points obtained by taking the minimum and maximum values, respectively, of the X, Y, and Z coordinate axes in the point cloud.
- (2)
- Fixed viewpoint generation: Next, viewpoint selection is required. Since it is more complex to fix the original point cloud and then move the virtual camera frequently in space, we use an equivalent method, which is to rotate the object around a stationary virtual camera. We define a set of rotation angles, , where represent the rotation angles of the original point cloud in , , and coordinates, respectively. We rotate the object at equal intervals on the remaining coordinate axis, use the virtual camera for 2D projection, and choose the required view on the fixed viewpoint. Then, we place the virtual camera in a fixed position, keep the positions of two coordinate axes unchanged, rotate at equal intervals on the third coordinate axis, employ the virtual camera for 2D projection, and select the required view on the fixed viewpoint.
- (3)
- Random viewpoint generation: Then, we randomly generate on the rotation angle set of the original point cloud and rotate the center point of the object to this angle. The virtual camera is used for projection to obtain the required view on the random viewpoint.
- (4)
- Multiview selection of fixed and random views: After many views are selected from fixed and random viewpoints, they must be combined in a certain proportion to generate the ultimate multiview representation in the initial stage. It is assumed that the fixed view set and the random view set have been obtained by the fixed and random projection methods, respectively. represents the number of views and is the number of random views. Defining as the i-th view, indicates the final multiview combination, as shown in Equation (2):In practice, when , we take the view obtained from the fixed viewpoint; thus, . Otherwise, we add one random view for every five fixed views, i.e., . The original multiview combination in different conditions is represented by Equation (3) as follows:
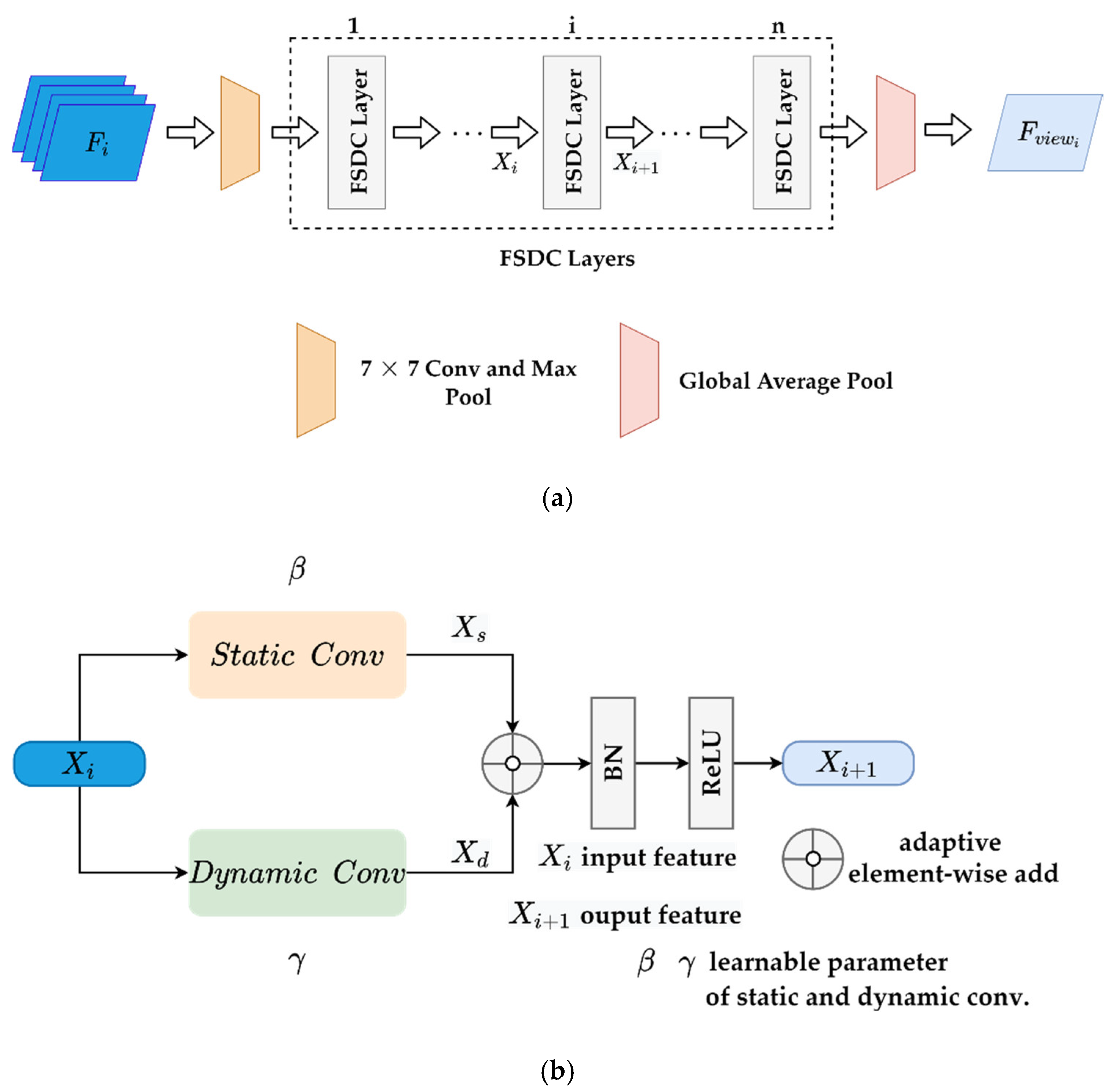
2.2. FSDC Local Feature Processing Operator
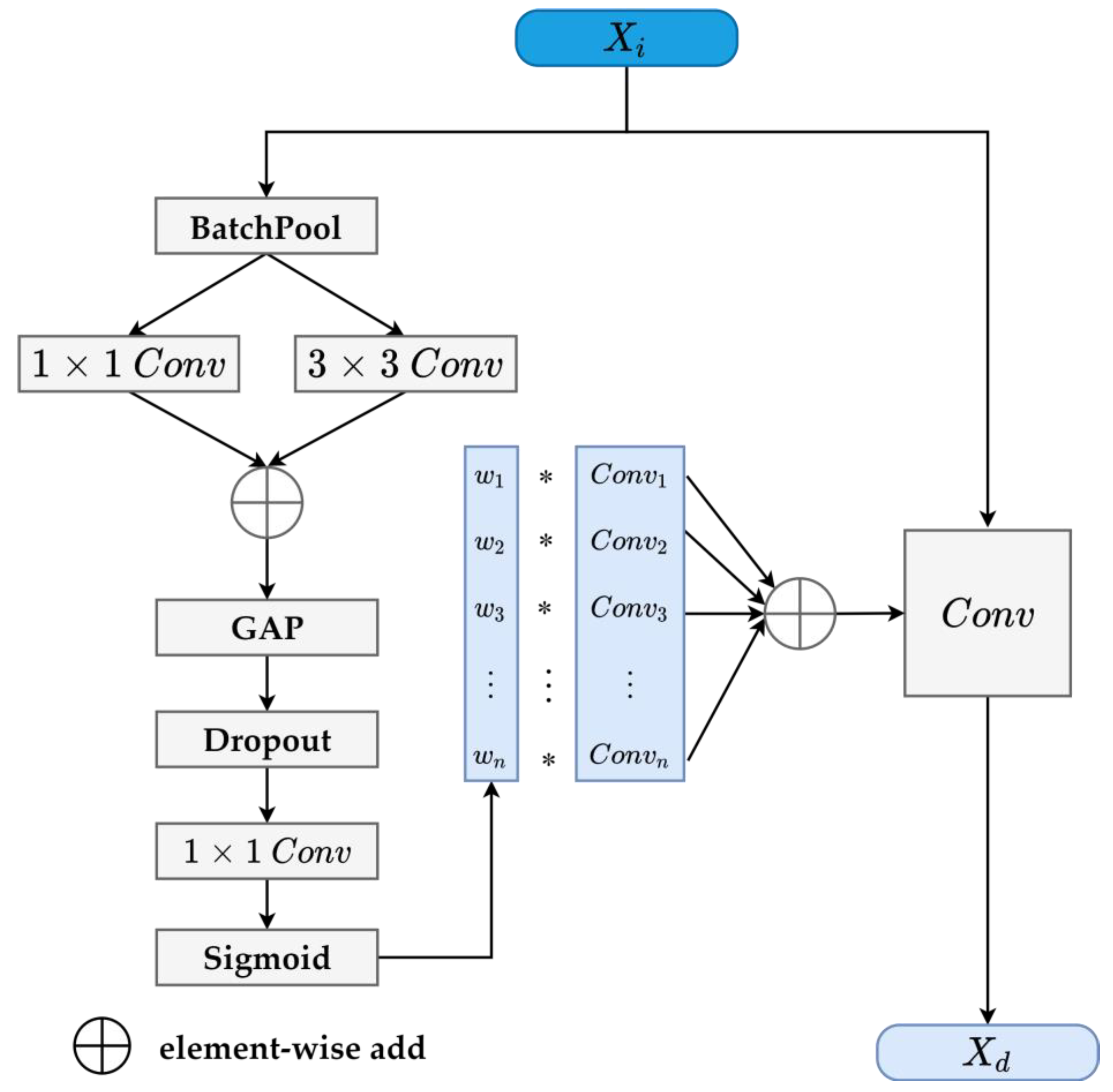
2.2.1. Lightweight Dynamic Convolution Generator
- (1)
- Pooling of batch size dimension: First, we define a batch pool function, which fuses the original input feature map in the batch dimension to achieve a lightweight effect and ensure that the most critical feature information is obtained; the function is defined in Equation (4) as follows:
- (2)
- Convolution operation on different receptive fields: The original input features are convoluted from different receptive fields using 1 × 1 and 3 × 3 convolution, shown in Equations (5) and (6) as follows:
- (3)
- Fusion of information from different receptive fields: We add the output features and element by element and shrink them to , whose dimensions are , using spatial average pooling, as shown in Equation (7):
- (4)
- Dropout to avoiding overfitting: The dropout layer causes the neurons to randomly inactivate in a certain proportion, which can avoid overfitting while dynamically generating convolution, as shown in Equation (8) below:
- (5)
- Generation of dynamic weight: Here, we change the original dynamic weight to the appropriate number of channels through the convolution of W3 and employ sigmoid activation to obtain a probability between 0 and 1 as the dynamic weight to generate the final convolution layer, as shown in Equation (9) below:
- (6)
- Generation of dynamic convolution kernel: Next, we multiply the original groups of convolution kernels by the dynamically generated weights to generate the final dynamic convolution kernels, as shown in Equation (10):
- (1)
- Parameters
- (2)
- FLOPs
2.2.2. Adaptive Process Combining Static and Dynamic Convolution
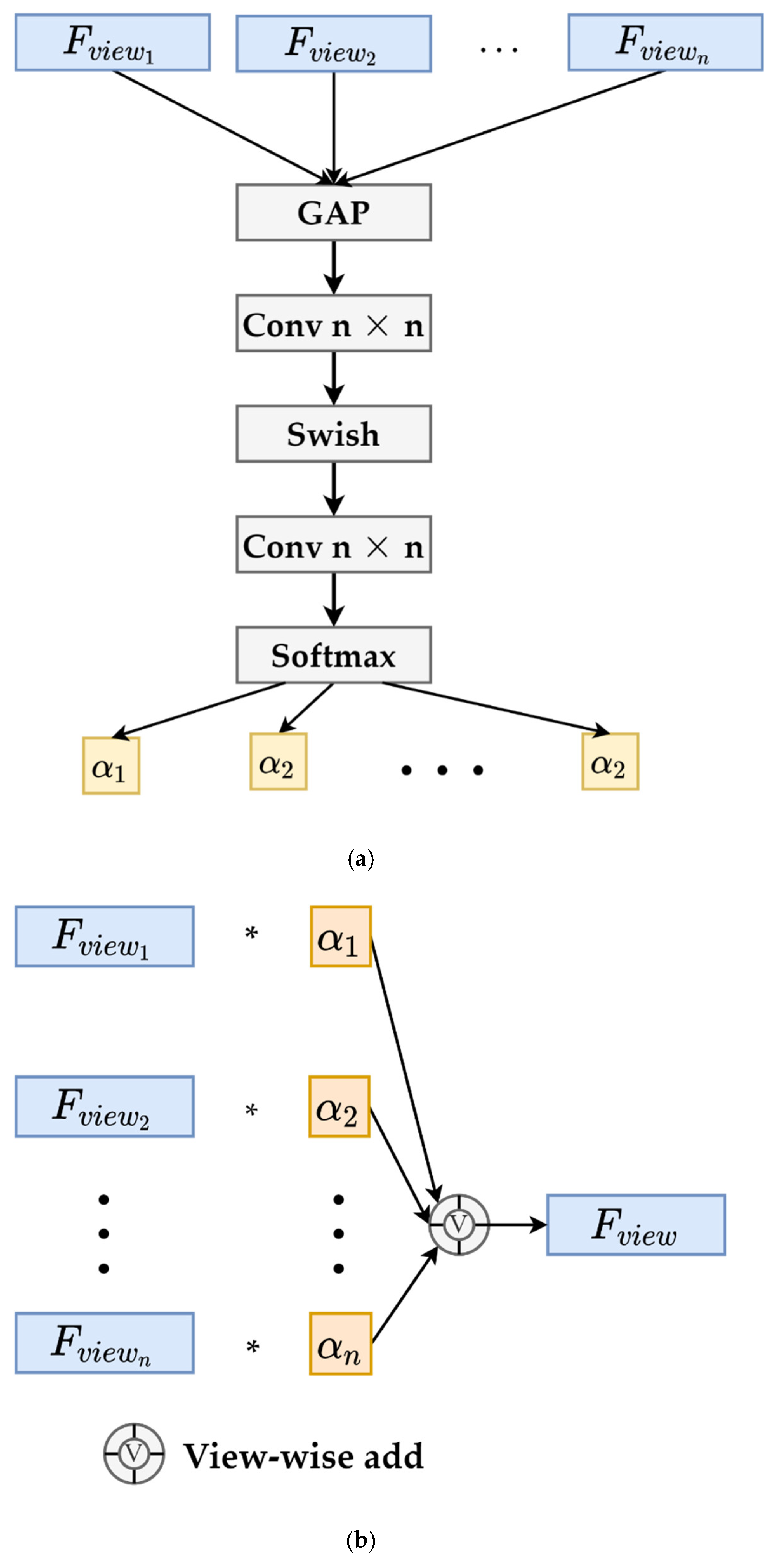
2.3. Adaptive Global Attention Pooling
- (1)
- Global average pooling (GAP) of local features: Global average pooling is applied to local features , and an n-dimensional vector is obtained as the initial value set of all dynamic weights, as shown in Equation (13) below:where , and and are the height and width, respectively, of the local features. In general, either or is 1, and is the value of a feature at the subscript position.
- (2)
- Dynamic weight generation of local features: Next, we apply two convolutions to the n-dimensional vector and add a nonlinear activation function, Swish [45], between them. This is similar to the attention mechanism of SENet [46]; however, we do not squeeze and excite the channel, and the activation function is Swish. Then, the feature weight of each view can be acquired through the softmax activation function. The generation process is shown in Figure 5a. The dynamically generated weight is shown in Equation (14) below:where and are the softmax and Swish activation functions, respectively, and Conv1×1 is a convolution with input and output channels.
- (3)
- Global feature fusion: Finally, we multiply each view by its learned weight and add them in the view dimension. The ultimate global representation contains the feature information of all local views. The global representation fusion process is shown in Figure 5b and Equation (15):
3. Experiment
3.1. Dataset
3.2. Implementation
3.3. Metrics
3.4. Experimental Results and Analysis
3.4.1. Comparison with State-of-the-Art Methods
| (a) ModelNet40 | ||||
| Method | Views | Modality | OA | AA |
| VoxelNet [50] | - | Voxel | - | 83.0 |
| VRN [51] | - | Voxel | - | 91.3 |
| 3D Capsule [52] | - | Point | 89.3 | - |
| PointNet [10] | - | Point | 89.2 | 86.2 |
| PointNet++ [11] | - | Point | 91.9 | - |
| PointGrid [53] | - | Point | 92.0 | 88.9 |
| PointASNL [31] | - | Point | 93.2 | - |
| SimpleView [54] | - | Point | 93.9 | 91.8 |
| MVCNN [9] | 12 | Views | 92.1 | 89.9 |
| GVCNN [12] | 12 | Views | 92.6 | - |
| MVTN [55] | 12 | Views | 93.8 | 92.0 |
| MHBN [13] | 6 | Views | 94.1 | 92.2 |
| FSDCNet (ours) | 1 | Views | 93.8 | 91.2 |
| FSDCNet (ours) | 6 | Views | 94.6 | 93.3 |
| FSDCNet (ours) | 12 | Views | 95.3 | 93.6 |
| (b) Sydney Urban Objects | ||||
| Method | Views | Modality | OA | F1 |
| VoxelNet [50] | - | Voxel | - | 73.0 |
| ORION [56] | -- | Voxel | - | 77.8 |
| ECC [57] | - | Point | - | 78.4 |
| LightNet [58] | - | Voxel | - | 79.8 |
| MVCNN [9] | 6 | Views | 81.4 | 80.2 |
| GVCNN [12] | 6 | Views | 83.9 | 82.5 |
| FSDCNet (ours) | 1 | Views | 81.2 | 80.1 |
| FSDCNet (ours) | 6 | Views | 85.3 | 83.6 |
| FSDCNet (ours) | 12 | Views | 85.5 | 83.7 |
3.4.2. Influence of the Multi-Perspective Selection Method
3.4.3. Influence of the Number of Views
3.4.4. Influence of Static Convolution and Dynamic Convolution
| CNN Model | ModelNet40 | Sydney Urban Objects | ||
|---|---|---|---|---|
| OA | AA | OA | F1 | |
| ResNet50 [59] | 93.0 | 92.0 | 83.1 | 81.7 |
| FSDCNet-ResNet50 | 93.8 | 92.6 | 84.5 | 82.3 |
| ResNext50 [60] | 92.9 | 92.2 | 83.8 | 81.7 |
| FSDCNet-ResNext50 | 94.1 | 92.7 | 84.8 | 82.5 |
| SENet50 [46] | 93.5 | 92.3 | 84.0 | 82.2 |
| FSDCNet-SENet50 | 94.6 | 93.3 | 85.3 | 83.6 |
3.4.5. Influence of Fusion Strategy
3.4.6. Influence of Pooling
| Method | ModelNet40 | Sydney Urban Object | ||
|---|---|---|---|---|
| OA | AA | OA | F1 | |
| MaxPooling | 94.2 | 92.5 | 84.9 | 83.1 |
| MeanPooling | 93.7 | 92.1 | 84.1 | 82.3 |
| Max+Mean | 94.2 | 92.8 | 85.2 | 83.1 |
| SoftPool [61] | 93.7 | 91.9 | 84.5 | 83.0 |
| FSDCNet (ours) | 94.6 | 93.3 | 85.3 | 83.6 |
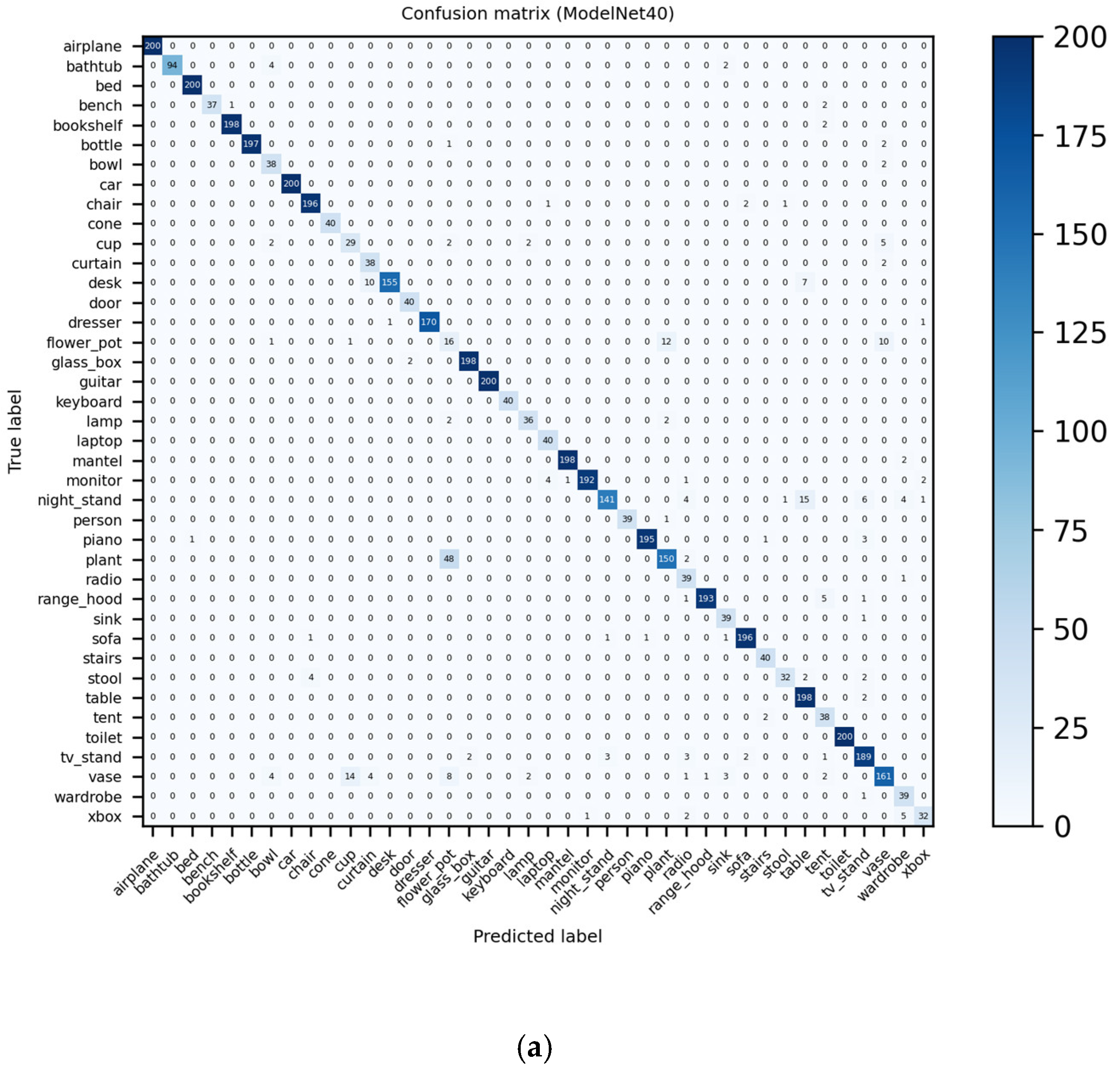
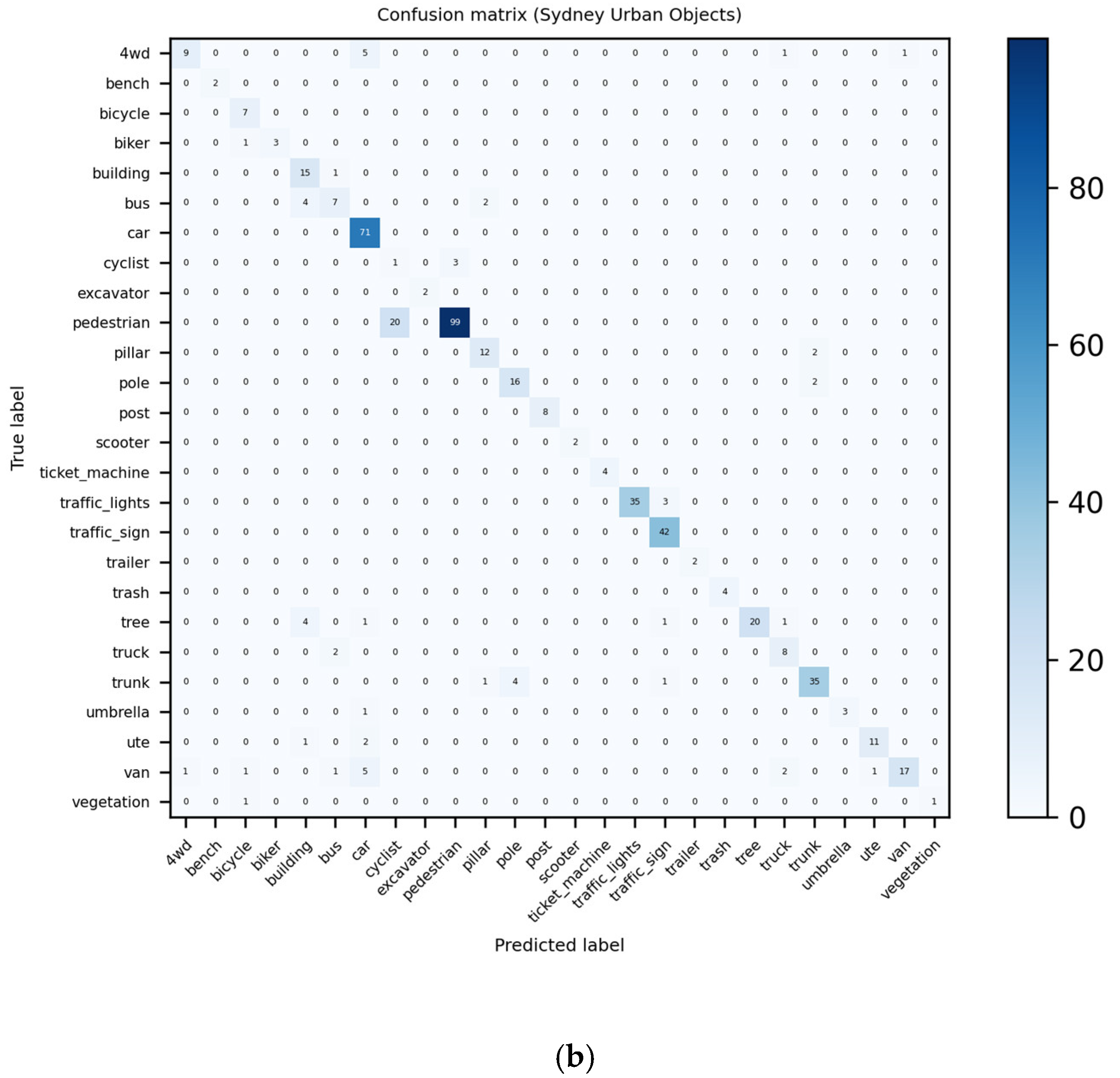
3.4.7. Visualization and Analysis of Confusion Matrices and ROC Curves
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| FSDCNet | Fusion static and dynamic convolutional neural network |
| OA | Overall accuracy |
| AA | Average accuracy |
| LiDAR | Light detection and ranging |
| RGB-D | Red, green, blue, and depth |
| MLP | Multilayer perceptron |
| CNN | Convolutional neural network |
| VB-Net | Voxel-based broad learning network |
| TVS | Tri-projection voxel splatting |
| RCC | Reflection convolution concatenation |
| GPU | Graphics processing unit |
| GSA | Group shuffle attention |
| GSS | Gumble subset sampling |
| MCMC | Markov chain Monte Carlo |
| PointASNL | Point adaptive sampling and local and nonlocal module |
| FPS | Farthest point sampling |
| FLOPs | Floating point operations |
| GVCNN | Group view convolution neural network |
| MVHFN | Multiview hierarchical fusion network |
| EM | Expectation maximization |
| GPVLM | Gaussian process latent variable model |
| RBF | Radial basis function |
| LMVCNN | Latent multiview CNN |
| MHBN | Multiview harmonized bilinear network |
| GAP | Global average pooling/global attention pooling |
| RAM | Random access memory |
| CUDA | Compute unified device architecture |
| GB | Gigabyte (1024 megabytes) |
| ROC | Receiver operating characteristic curve |
| AUC | Area under curve |
| FPR | False positive rate |
| TPR | True positive rate |
References
- Zhang, J.X.; Lin, X.G. Advances in fusion of optical imagery and LiDAR point cloud applied to photogrammetry and remote sensing. Int. J. Image Data Fusion 2017, 8, 1–31. [Google Scholar] [CrossRef]
- Wentz, E.A.; York, A.M.; Alberti, M.; Conrow, L.; Fischer, H.; Inostroza, L.; Jantz, C.; Pickett, S.T.A.; Seto, K.C.; Taubenbock, H. Six fundamental aspects for conceptualizing multidimensional urban form: A spatial mapping perspective. Landsc. Urban Plan. 2018, 179, 55–62. [Google Scholar] [CrossRef]
- Yue, X.Y.; Wu, B.C.; Seshia, S.A.; Keutzer, K.; Sangiovanni-Vincentelli, A.L.; Assoc Comp, M. A LiDAR Point Cloud Generator: From a Virtual World to Autonomous Driving. In Proceedings of the 8th ACM International Conference on Multimedia Retrieval (ACM ICMR), Yokohama, Japan, 11–14 June 2018; pp. 458–464. [Google Scholar]
- Chen, X.Z.; Ma, H.M.; Wan, J.; Li, B.; Xia, T. Multi-View 3D Object Detection Network for Autonomous Driving. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6526–6534. [Google Scholar]
- Braun, A.; Tuttas, S.; Borrmann, A.; Stilla, U. Improving progress monitoring by fusing point clouds, semantic data and computer vision. Autom. Constr. 2020, 116, 103210. [Google Scholar] [CrossRef]
- Jaritz, M.; Gu, J.Y.; Su, H. Multi-view PointNet for 3D Scene Understanding. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 3995–4003. [Google Scholar]
- Duan, H.; Wang, P.; Huang, Y.; Xu, G.; Wei, W.; Shen, X. Robotics Dexterous Grasping: The Methods Based on Point Cloud and Deep Learning. Front. Neurorobot. 2021, 15, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Fang, H.R.; Fang, Y.F.; Shi, S.J. Three-dimensional point cloud data subtle feature extraction algorithm for laser scanning measurement of large-scale irregular surface in reverse engineering. Measurement 2020, 151, 107220. [Google Scholar] [CrossRef]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view Convolutional Neural Networks for 3D Shape Recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 945–953. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.C.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet plus plus: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 4–9. [Google Scholar]
- Feng, Y.F.; Zhang, Z.Z.; Zhao, X.B.; Ji, R.R.; Gao, Y. GVCNN: Group-View Convolutional Neural Networks for 3D Shape Recognition. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 264–272. [Google Scholar]
- Yu, T.; Meng, J.J.; Yuan, J.S. Multi-view Harmonized Bilinear Network for 3D Object Recognition. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 186–194. [Google Scholar]
- Wei, X.; Yu, R.X.; Sun, J. View-GCN: View-based Graph Convolutional Network for 3D Shape Analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 1847–1856. [Google Scholar]
- Li, L.; Zhu, S.Y.; Fu, H.B.; Tan, P.; Tai, C.L. End-to-End Learning Local Multi-View Descriptors for 3D Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 1916–1925. [Google Scholar]
- Xiong, B.A.; Jiang, W.Z.; Li, D.K.; Qi, M. Voxel Grid-Based Fast Registration of Terrestrial Point Cloud. Remote Sens. 2021, 13, 1905. [Google Scholar] [CrossRef]
- Plaza, V.; Gomez-Ruiz, J.A.; Mandow, A.; Garcia-Cerezo, A.J. Multi-layer Perceptrons for Voxel-Based Classification of Point Clouds from Natural Environments. In Proceedings of the 13th International Work-Conference on Artificial Neural Networks (IWANN), Palma de Mallorca, Spain, 10–12 June 2015; pp. 250–261. [Google Scholar]
- Liu, Z.J.; Tang, H.T.; Lin, Y.J.; Han, S. Point-Voxel CNN for Efficient 3D Deep Learning. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; pp. 965–975. [Google Scholar]
- Plaza-Leiva, V.; Gomez-Ruiz, J.A.; Mandow, A.; Garcia-Cerezo, A. Voxel-Based Neighborhood for Spatial Shape Pattern Classification of Lidar Point Clouds with Supervised Learning. Sensors 2017, 17, 594. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.S.; Song, W.; Tian, Y.F.; Ji, S.M.; Sung, Y.S.; Wen, L.; Zhang, T.; Song, L.L.; Gozho, A. VB-Net: Voxel-Based Broad Learning Network for 3D Object Classification. Appl. Sci. 2020, 10, 6735. [Google Scholar] [CrossRef]
- Hamada, K.; Aono, M. 3D Indoor Scene Classification using Tri-projection Voxel Splatting. In Proceedings of the 10th Asia-Pacific-Signal-and-Information-Processing-Association Annual Summit and Conference (APSIPA ASC), Honolulu, HI, USA, 12–15 November 2018; pp. 317–323. [Google Scholar]
- Wang, C.; Cheng, M.; Sohel, F.; Bennamoun, M.; Li, J. NormalNet: A voxel-based CNN for 3D object classification and retrieval. Neurocomputing 2019, 323, 139–147. [Google Scholar] [CrossRef]
- Hui, C.; Jie, W.; Yuqi, L.; Siyu, Z.; Shen, C. Fast Hybrid Cascade for Voxel-based 3D Object Classification. arXiv 2020, arXiv:2011.04522. [Google Scholar]
- Zhao, Z.; Cheng, Y.; Shi, X.; Qin, X.; Sun, L. Classification of LiDAR Point Cloud based on Multiscale Features and PointNet. In Proceedings of the Eighth International Conference on Image Processing Theory, Tools and Applications (IPTA), Xi’an, China, 7–10 November 2018; p. 7. [Google Scholar] [CrossRef]
- Li, Z.Z.; Li, W.M.; Liu, H.Y.; Wang, Y.; Gui, G. Optimized PointNet for 3D Object Classification. In Proceedings of the 3rd European-Alliance-for-Innovation (EAI) International Conference on Advanced Hybrid Information Processing (ADHIP), Nanjing, China, 21–22 September 2019; pp. 271–278. [Google Scholar]
- Kuangen, Z.; Jing, W.; Chenglong, F. Directional PointNet: 3D Environmental Classification for Wearable Robotics. arXiv 2019, arXiv:1903.06846. [Google Scholar]
- Joseph-Rivlin, M.; Zvirin, A.; Kimmel, R. Momenet: Flavor the Moments in Learning to Classify Shapes. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 4085–4094. [Google Scholar]
- Yang, J.C.; Zhang, Q.; Ni, B.B.; Li, L.G.; Liu, J.X.; Zhou, M.D.; Tian, Q.; Soc, I.C. Modeling Point Clouds with Self-Attention and Gumbel Subset Sampling. In Proceedings of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 3318–3327. [Google Scholar]
- Hengshuang, Z.; Li, J.; Chi-Wing, F.; Jiaya, J. PointWeb: Enhancing Local Neighborhood Features for Point Cloud Processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5560–5568. [Google Scholar] [CrossRef]
- Xie, J.; Xu, Y.; Zheng, Z.; Zhu, S.-C.; Wu, Y.N. Generative PointNet: Deep Energy-Based Learning on Unordered Point Sets for 3D Generation, Reconstruction and Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14976–14985. [Google Scholar]
- Yan, X.; Zheng, C.D.; Li, Z.; Wang, S.; Cui, S.G. PointASNL: Robust Point Clouds Processing using Nonlocal Neural Networks with Adaptive Sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 5588–5597. [Google Scholar]
- Jing, W.; Zhang, W.; Li, L.; Di, D.; Chen, G.; Wang, J. AGNet: An Attention-Based Graph Network for Point Cloud Classification and Segmentation. Remote Sens. 2022, 14, 1036. [Google Scholar] [CrossRef]
- Papadakis, P. A Use-Case Study on Multi-View Hypothesis Fusion for 3D Object Classification. In Proceedings of the 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2446–2452. [Google Scholar]
- Cheng, X.H.; Zhu, Y.H.; Song, J.K.; Wen, G.Q.; He, W. A novel low-rank hypergraph feature selection for multi-view classification. Neurocomputing 2017, 253, 115–121. [Google Scholar] [CrossRef]
- Pramerdorfer, C.; Kampel, M.; Van Loock, M. Multi-View Classification and 3D Bounding Box Regression Networks. In Proceedings of the 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 734–739. [Google Scholar]
- Liu, A.A.; Hu, N.; Song, D.; Guo, F.B.; Zhou, H.Y.; Hao, T. Multi-View Hierarchical Fusion Network for 3D Object Retrieval and Classification. IEEE Access 2019, 7, 153021–153030. [Google Scholar] [CrossRef]
- Li, J.X.; Yong, H.W.; Zhang, B.; Li, M.; Zhang, L.; Zhang, D. A Probabilistic Hierarchical Model for Multi-View and Multi-Feature Classification. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence/30th Innovative Applications of Artificial Intelligence Conference/8th AAAI Symposium on Educational Advances in Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 3498–3505. [Google Scholar]
- He, J.; Du, C.Y.; Zhuang, F.Z.; Yin, X.; He, Q.; Long, G.P. Online Bayesian max-margin subspace learning for multi-view classification and regression. Mach. Learn. 2020, 109, 219–249. [Google Scholar] [CrossRef]
- Li, J.X.; Li, Z.Q.; Lu, G.M.; Xu, Y.; Zhang, B.; Zhang, D. Asymmetric Gaussian Process multi-view learning for visual classification. Inf. Fusion 2021, 65, 108–118. [Google Scholar] [CrossRef]
- Yu, Q.; Yang, C.Z.; Fan, H.H.; Wei, H. Latent-MVCNN: 3D Shape Recognition Using Multiple Views from Pre-defined or Random Viewpoints. Neural Processing Lett. 2020, 52, 581–602. [Google Scholar] [CrossRef]
- Yang, B.; Bender, G.; Le, Q.V.; Ngiam, J. CondConv: Conditionally Parameterized Convolutions for Efficient Inference. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Zhou, J.; Jampani, V.; Pi, Z.; Liu, Q.; Yang, M.-H. Decoupled Dynamic Filter Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6647–6656. [Google Scholar]
- He, F.X.; Liu, T.L.; Tao, D.C. Control Batch Size and Learning Rate to Generalize Well: Theoretical and Empirical Evidence. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; pp. 1143–1152. [Google Scholar]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv:1710.05941. preprint. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wu, Z.R.; Song, S.R.; Khosla, A.; Yu, F.; Zhang, L.G.; Tang, X.O.; Xiao, J.X. 3D ShapeNets: A Deep Representation for Volumetric Shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- De Deuge, M.; Quadros, A.; Hung, C.; Douillard, B. Unsupervised Feature Learning for Classification of Outdoor 3D Scans. In Proceedings of the Australasian Conference on Robitics and Automation, Sydney, Australia, 2–4 December 2013; p. 1. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4490–4499. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Generative and Discriminative Voxel Modeling with Convolutional Neural Networks. arXiv 2016, arXiv:1608.04236. [Google Scholar]
- Zhao, Y.H.; Birdal, T.; Deng, H.W.; Tombari, F.; Soc, I.C. 3D Point Capsule Networks. In Proceedings of the 32nd IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1009–1018. [Google Scholar]
- Le, T.; Duan, Y. PointGrid: A Deep Network for 3D Shape Understanding. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9204–9214. [Google Scholar]
- Goyal, A.; Law, H.; Liu, B.W.; Newel, A.; Deng, J. Revisiting Point Cloud Shape Classification with a Simple and Effective Baseline. In Proceedings of the International Conference on Machine Learning (ICML), Online, 18–24 July 2021. [Google Scholar]
- Hamdi, A.; Giancola, S.; Ghanem, B. MVTN: Multi-view transformation network for 3D shape recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2021; pp. 1–11. [Google Scholar]
- Sedaghat, N.; Zolfaghari, M.; Brox, T. Orientation-boosted Voxel Nets for 3D Object Recognition. arXiv 2016, arXiv:1604.03351v2. [Google Scholar]
- Simonovsky, M.; Komodakis, N. Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 29–38. [Google Scholar]
- Zhi, S.F.; Liu, Y.X.; Li, X.; Guo, Y.L. Toward real-time 3D object recognition: A lightweight volumetric CNN framework using multitask learning. Comput. Graph. 2018, 71, 199–207. [Google Scholar] [CrossRef]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Xie, S.N.; Girshick, R.; Dollar, P.; Tu, Z.W.; He, K.M. IEEE Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5987–5995. [Google Scholar]
- Stergiou, A.; Poppe, R.; Kalliatakis, G. Refining activation downsampling with SoftPool. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 10357–10366. [Google Scholar]


| Conv. Type | Static Conv. | Dynamic Conv. | FSDC |
|---|---|---|---|
| Parameters | |||
| FLOPs |
| (a) ModelNet40 | ||
| Preprocessing | Views | OA |
| Fixed | 6 | 94.1 |
| Fixed and random | 6 | 94.6 |
| Fixed | 12 | 94.7 |
| Fixed and random | 12 | 95.3 |
| (b) Sydney Urban Objects | ||
| Preprocessing | Views | OA |
| Fixed | 6 | 84.1 |
| Fixed and random | 6 | 85.3 |
| Fixed | 12 | 84.9 |
| Fixed and random | 12 | 85.5 |
| (a) ModelNet40 | |||
| Method | Views | OA | AA |
| MVCNN [9] | 6 | 92.0 | - |
| MVCNN [9] | 12 | 91.5 | - |
| GVCNN [12] | 12 | 92.6 | - |
| MVTN [55] | 12 | 93.8 | 92.0 |
| MHBN [13] | 6 | 94.1 | 92.2 |
| MHBN [13] | 12 | 93.4 | - |
| FSDCNet (ours) | 1 | 93.8 | 91.2 |
| FSDCNet (ours) | 6 | 94.6 | 93.3 |
| FSDCNet (ours) | 12 | 95.3 | 93.6 |
| (b) Sydney Urban Objects | |||
| Method | Views | OA | F1 |
| VoxelNet [50] | - | - | 73.0 |
| ORION [56] | - | - | 77.8 |
| ECC [57] | - | - | 78.4 |
| LightNet [58] | - | - | 79.8 |
| MVCNN [9] | 6 | 81.4 | 80.2 |
| GVCNN [12] | 6 | 83.9 | 82.5 |
| FSDCNet | 1 | 81.2 | 80.1 |
| FSDCNet | 6 | 85.3 | 83.6 |
| FSDCNet | 12 | 85.5 | 83.7 |
| (a) ModelNet40 | ||||
| Learnable Parameters | 6 views | 12 views | ||
| OA | AA | OA | AA | |
| With and | 94.6 | 93.3 | 95.3 | 93.6 |
| Without and | 94.2 | 92.0 | 94.9 | 93.1 |
| (b) Sydney Urban Objects | ||||
| Learnable Parameters | 6 views | 12 views | ||
| OA | F1 | OA | F1 | |
| With and | 85.3 | 83.6 | 85.5 | 83.7 |
| Without and | 84.5 | 82.5 | 84.9 | 82.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhou, H.; Chen, G.; Wang, X. Fusion of a Static and Dynamic Convolutional Neural Network for Multiview 3D Point Cloud Classification. Remote Sens. 2022, 14, 1996. https://doi.org/10.3390/rs14091996
Wang W, Zhou H, Chen G, Wang X. Fusion of a Static and Dynamic Convolutional Neural Network for Multiview 3D Point Cloud Classification. Remote Sensing. 2022; 14(9):1996. https://doi.org/10.3390/rs14091996
Chicago/Turabian StyleWang, Wenju, Haoran Zhou, Gang Chen, and Xiaolin Wang. 2022. "Fusion of a Static and Dynamic Convolutional Neural Network for Multiview 3D Point Cloud Classification" Remote Sensing 14, no. 9: 1996. https://doi.org/10.3390/rs14091996
APA StyleWang, W., Zhou, H., Chen, G., & Wang, X. (2022). Fusion of a Static and Dynamic Convolutional Neural Network for Multiview 3D Point Cloud Classification. Remote Sensing, 14(9), 1996. https://doi.org/10.3390/rs14091996