Tensor-Based Target Parameter Estimation Algorithm for FDA-MIMO Radar with Array Gain-Phase Error

Abstract

As a new radar system, FDA-MIMO radar has recently developed rapidly, as it has broad prospects in angle-range estimation. Unfortunately, the performance of existing algorithms for FDA-MIMO radar is greatly degrading or even failing under the condition of array gain-phase error. This paper proposes an innovative solution to the joint angle and range estimation of FDA-MIMO radar under the condition of array gain-phase error and an estimation algorithm is developed. Moreover, the corresponding Cramér-Rao bound (CRB) is derived to evaluate the algorithm. The parallel factor (PARAFAC) decomposition technique can be utilized to calculate transmitter and receiver direction matrices. Taking advantage of receiver direction matrix, the angle estimation can be obtained. The range estimation can be estimated by transmitter direction matrix and angle estimation. To eliminate the error accumulation effect of array gain-phase error, the gain error and phase error are obtained separately. In this algorithm, the impact of gain-phase error on parameter estimation is removed and so is the error accumulation effect. Therefore, the proposed algorithm can provide excellent performance of angle-range and gain-phase error estimation. Numerical experiments prove the validity and advantages of the proposed method.

1. Introduction

In 2004, Fishler and others proposed the concept of Multiple input Multiple output (MIMO) radar based on the idea of spatial diversity [1,2,3,4]. Owing to the use of waveform diversity technology, MIMO radar has lots of advantages including flexible operation mode, high angle measurement accuracy, low probability of interception and strong multi-target tracking ability. The research contents in this field mainly include waveform design, beamforming, and parameter estimation [5,6]. In view of the defects in beam pointing of phased array radar and the contradiction between doppler ambiguity and range ambiguity, a new concept of frequency diversity array (FDA) is proposed [7]. In recent years, the FDA system was introduced into MIMO radar, which is how the FDA-MIMO radar came into being [8]. As a new radar system recently proposed, the FDA-MIMO radar has great advantages in parameter estimation, especially in target angle and range estimation [9]. According to the spatial distribution of radar antennas, there are two main types of the MIMO radar: statistical MIMO radar with widely separated antennas [10,11] and collocated MIMO radar with close spacing antennas [12,13]. The research object of this paper is monostatic MIMO radar, which belongs to collocated MIMO radar.

The FDA-MIMO radar is different from the traditional array radar, and the carrier frequency of its transmitted signal is slightly different [14]. Therefore, the phase difference of electromagnetic wave propagation of FDA-MIMO radar is related not only to the spatial angle, but also to the propagation range. In other words, the steering vector of FDA-MIMO radar signal has a two-dimensional dependence on range and angle, so it can effectively estimate the angle and range information of the target. The controllable degree of freedom (DOF) of range dimension of FDA-MIMO radar increases the flexibility of radar signal processing [15]. It can meet the tasks of moving target detection and high-resolution radar imaging at the same time. In addition, FDA-MIMO radar can introduce more system controllable DOFs to solve the key problems faced by moving target detection of high-speed radar platform, such as range ambiguity, clutter suppression, and so on [9]. Therefore, it is of great significance to study the target parameter estimation algorithm of FDA-MIMO radar.

The FDA-MIMO radar introduces the concept of frequency diversity on the basis of the MIMO radar. This kind of radar can make use of angle and range information of a target contained in a transmitting steering vector to solve the doppler ambiguity and range ambiguity in the traditional radar parameter estimation. Xu et al. realized the unambiguous estimation of angle and range by MLE algorithm [16], while Chen et al. used sparse reconstruction method to estimate parameters [17]. For the angle-range coupling problem, Wang et al. turned the transmitting array into sub-arrays, and the frequency increment between each sub-array was different [18]. Wang et al. proposed to transmit two pulses with zero and non-zero frequency increments, respectively [19]. There are many algorithms in MIMO radar applied to FDA-MIMO radar. In [20,21], the angle and range estimation of the target is achieved by the multiple signal classification (MUSIC) scheme. Owning to the spatial spectrum search process, the algorithm has large computational redundancy. To reduce the large computational redundancy caused by spatial spectrum search, many improved algorithms have been proposed. In [22], Yan et al. proposed a two-stage estimating signal parameters via rotation invariance technique (ESPRIT) scheme for FDA-MIMO radar to achieve both range and angle estimations. To further reduce the computational redundancy, Liu et al. developed a real-valued ESPRIT scheme in [23]. This algorithm utilizes the extended real-valued data constructed by the Centro-Hermitian property to cut down the computational redundancy.

All the above algorithms are based on well calibrated array. In other words, the above algorithms do not consider the influence of array gain-phase error [24,25]. Owning to the existence of gain-phase errors, the performance of many algorithms will be greatly reduced or even become invalid [26,27]. Unfortunately, for FDA-MIMO radar, few research work takes the impact of gain-phase error into account. For MIMO radar, many scholars have been using different methods to overcome the effect of array gain-phase error. A original ESPRIT-like method is developed in [28], which utilizes the instrumental sensors method (ISM) to achieve the angle estimation. In [29], an ESPRIT-based method is developed to obtain angle and gain-phase errors estimation. The ESPRIT-based algorithm first achieves the angle estimation. Then the gain-phase error is estimated subsequently. Besides subspace algorithms, the tensor-based algorithms also perform well in gain-phase error estimation. In [30], a joint method for angle and gain-phase error estimation according to trilinear decomposition is proposed. This algorithm takes advantage of the parallel factor (PARAFAC) decomposition technique to obtain direction matrix estimation, and then estimates the angle and gain-phase error. In this work, there is no need for spatial spectrum search to realize automatically paired angle estimation. Moreover, this tensor based algorithm makes use of the multidimensional characteristics of multidimensional data and improves the performance of angle estimation. Therefore, this algorithm outperforms other subspace algorithms mentioned before. Unfortunately, there exists an error accumulation effect in the algorithm, which affects the accuracy of array gain-phase error estimation.

In this paper, aiming at the angle-range estimation problem of FDA-MIMO radar under the condition of gain-phase error, a high performance estimation algorithm is developed. The algorithm is on the basis of tensor and utilizes the multidimensional characteristics of multidimensional data. Firstly, the received data can be rewritten as a three-dimensional(3D) tensor. Then, the PARAFAC decomposition is utilized to decompose the 3D tensor to obtain the direction matrix containing the target information. After that, the direction matrix and auxiliary elements are used to track the angle of the target. Finally, the proposed algorithm takes advantage of the special properties of FDA-MIMO radar transmitting array and the angle estimation to achieve the range estimation. To remove the error accumulation influence in parameter estimation, the estimations of phase error and gain error are obtained separately. The gain error estimation is firstly achieved by the relationship between any two steering vectors and then the phase error estimation is obtained by the phase of all elements and the angle-range estimation. Since the estimation of phase error and gain error are achieved separately, the effect of each other is removed in the process of estimation. In brief, the algorithm removes the influence of error accumulation. Hence, this scheme can provide more outstanding angle-range and gain-phase error estimation performance than other algorithms.

To summarize, our contributions are as follows:

(1)

The proposed algorithm solves the joint angle-range estimation problem of FDA-MIMO radar with array gain-phase error. A tensor-based estimation scheme that can provide superior estimation performance is developed;

(2)

In this paper, an gain-phase error estimation method that can eliminate the influence of error accumulation is presented. The proposed algorithm can obtain more accurate gain-phase error estimation;

(3)

In this paper, the Cramer-Rao bound (CRB) is derived for angle and range estimation and gain-phase error estimation in FDA-MIMO radar with array gain-phase error (see Appendix A for details).

This paper can be divided into the following parts. Section 2 expounds the signal model. Section 3 is the target parameter estimation scheme of FDA-MIMO radar. Numerical experiments are presented in Section 4. Section 5 is the conclusion, and the Appendix A is at the end of the paper.

The notations related to this paper are shown in the following

Table 1. Related notation.

Notation	Definition
${(·)}^{*}$	conjugate
${(·)}^T$	transpose
${(·)}^H$	conjugate-transpose
${(·)}^{-1}$	inverse
${(·)}^{†}$	pseudo-inverse
⊗	Kronecker product
⊙	Khatri-Rao product
∘	outer product
⋆	Hadamard product
⊘	point division
${\mathrm{\Delta }}_n$(A)	a diagonal matrix with the nth row of A
$angle(·)$	the phase of array elements
$Re(·)$	the real part for each element of the array
${\parallel ·\parallel }_F$	Frobenius norm

.

2. Tensor-Based Data Model

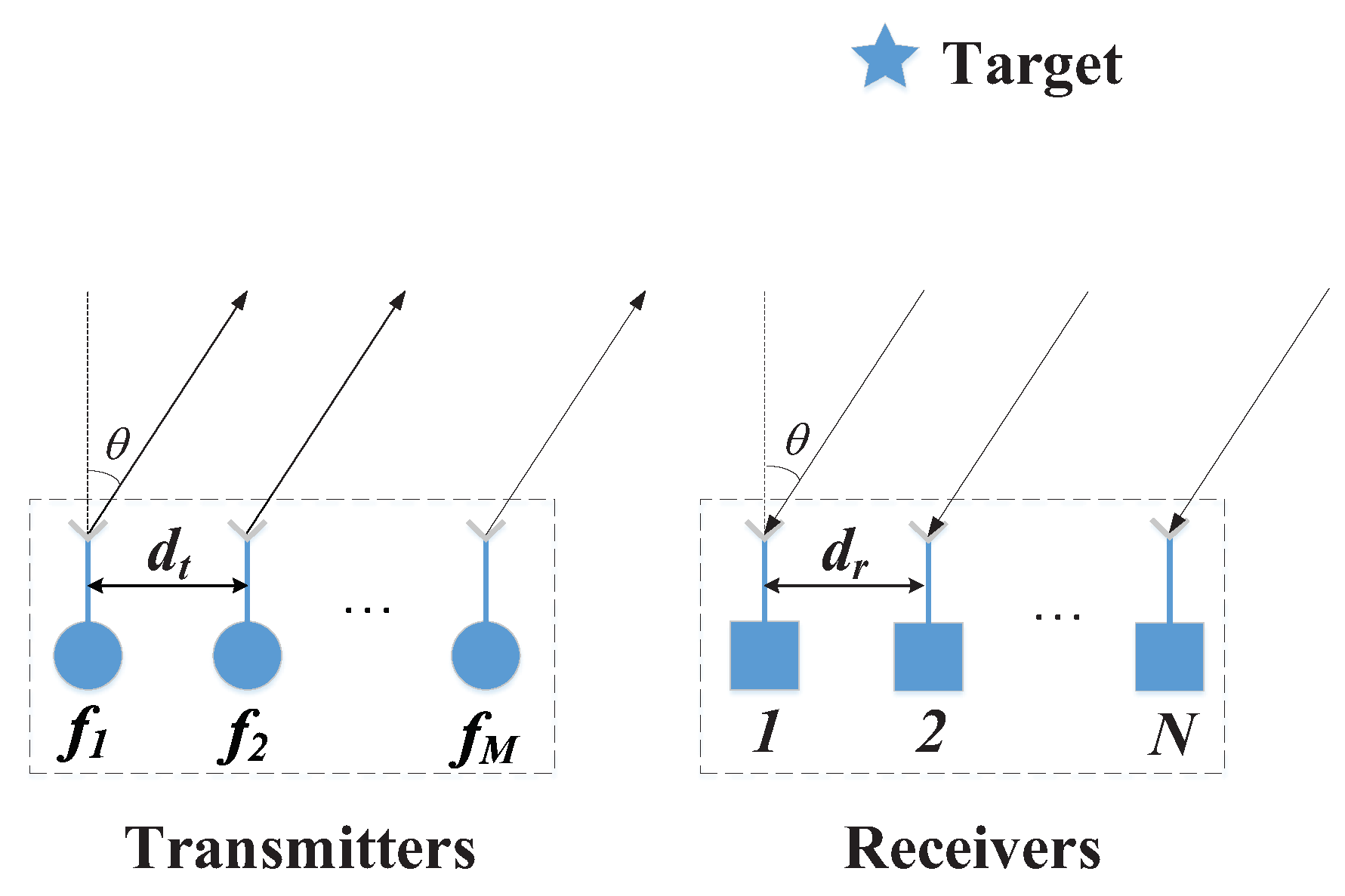
In this paper, a narrowband monostatic FDA-MIMO radar is considered. The radar array configuration is depicted in Figure 1. The number of receiving and transmitting antennas is N and M, respectively. Both transmitting and receiving arrays are uniform linear arrays (ULA) with half wavelength spacing. The spacing of transmitting and receiving arrays is defined as $d_t$ and $d_r$, respectively. According to the characteristics of frequency diversity, there is a small frequency increment between adjacent transmitting elements. If the first transmitting antenna is taken as the reference element, the signal carrier frequency on m-th element can be given by [31].

$$f_m=f_0+(m-1)\mathrm{\Delta }f,\hspace{1em}m=1,2,\cdots ,M$$

(1)

where $f_0$ is the original carrier frequency of a radar. $\mathrm{\Delta }f$ is a well small frequency increment. Therefore, the transmitting signal on m-th element is given by

$$\begin{array}{c}\hfill s_m\left(t\right)=\sqrt{\frac{E}{M}}{\psi }_m\left(t\right)e^{j2\pi f_{m}t},\\ \hfill 0\le t\le T,\hspace{1em}m=1,2,\cdots ,M\end{array}$$

(2)

where E is total emission energy, ${\psi }_m\left(t\right)$ is the transmission waveform, and T is pulse delay. Assume that the transmitting waveform satisfies orthogonality. In other words, $\psi \left(t\right)$ satisfies the following equation

$${\int }_T{\psi }_m\left(t\right){\psi }_n^{*}(t-\tau )e^{j2\pi (m-n)\mathrm{\Delta }ft}\mathrm{d}t=\left\{\begin{array}{cc}0,\hfill & m\ne n,\forall \tau \hfill \\ 1,\hfill & m=n,\forall \tau \hfill \end{array}\right.$$

(3)

Assuming that there are K independent targets in the far field. The direction of arrival (DOA) of k-th target is defined as ${\theta }_k$. Similarly, the range of k-th target is given by $r_k$. The received data from the m-th antenna is given by [16,32]

$$y_m\left(t\right)={\rho }_k\sum _{n=1}^N{\psi }_n\left(t-{\tau }_{m,n}^{\prime }\right)e^{j2\pi f_n(t-{\tau }_{m,n}^{\prime })}$$

(4)

where ${\rho }_k$ is the complex-valued reflection coefficient of k-th target, ${\tau }_{m,n}^{\prime }$ is the time delay.

After matched filtering, the received snapshot can be written as [33]

$${\mathit{X}}_0=\sum _{k=1}^K{\xi }_k{\mathit{a}}_R\left({\theta }_k\right){\mathit{a}}_T^T\left(r_k,{\theta }_k\right)+\mathit{N}$$

(5)

$${\xi }_k={\rho }_k{e}^{j2\pi f_0{r}_k/c}$$

(6)

where $N$ is the noise vector.

Therefore, the transmitting steering vector ${\mathit{a}}_T(r_k,{\theta }_k)$ can be expressed by the following formula [34]

$${\mathit{a}}_T(r_k,{\theta }_k)=\mathit{r}\left(r_k\right)\odot \mathit{d}\left({\theta }_k\right)\in {\mathbb{C}}^{M\times 1}$$

(7)

$$\begin{array}{c}\hfill \mathit{r}\left(r_k\right)={\left[1,e^{-j4\pi \mathrm{\Delta }f{r}_k/c},\dots ,e^{-j4\pi \mathrm{\Delta }f(M-1)r_k/c}\right]}^{\mathrm{T}}\end{array}$$

(8)

$$\begin{array}{c}\hfill \mathit{d}\left({\theta }_k\right)={\left[1,e^{j2\pi d_{t}sin{\theta }_k/\lambda },\dots ,e^{j2\pi d_t(M-1)sin{\theta }_k/\lambda }\right]}^{\mathrm{T}}\end{array}$$

(9)

where $\mathit{r}\left(r_k\right)\in {\mathbb{C}}^{M\times 1}$, $\mathit{d}\left({\theta }_k\right)\in {\mathbb{C}}^{M\times 1}$. The propagation velocity and wavelength of the transmitted signal are represented by c and $\lambda$, respectively. It is not difficult to find that the range and angle information are contained in transmitting steering vector. However, there exists a coupling phenomenon in the range and angle field. According to the characteristics of FDA-MIMO radar, there are differences between transmitting array and receiving array. The receiving steering vector ${\mathit{a}}_R\left({\theta }_k\right)$ can be expressed as

$$\begin{array}{c}\hfill {\mathit{a}}_R\left({\theta }_k\right)={\left[1,e^{j2\pi d_{r}sin{\theta }_k/\lambda },\dots ,e^{j2\pi d_r(N-1)sin{\theta }_k/\lambda }\right]}^{\mathrm{T}}\in {\mathbb{C}}^{N\times 1}\end{array}$$

(10)

The formula in Equation (5) is expressed in ideal condition. The array elements are not impacted by gain-phase errors. In practice, it is impossible to calibrate all the elements accurately. Therefore, there will be gain-phase errors between array elements. Thus, the signal model with gain-phase errors is given by

$$\mathit{X}=\sum _{k=1}^K{\xi }_k{\widehat{\mathit{a}}}_R\left({\theta }_k\right){\widehat{\mathit{a}}}_T^T\left(r_k,{\theta }_k\right)+\mathit{N}$$

(11)

where ${\widehat{\mathit{a}}}_T(r_k,{\theta }_k)={\mathit{C}}_t{\mathit{a}}_T(r_k,{\theta }_k)$, ${\widehat{\mathit{a}}}_R\left({\theta }_k\right)={\mathit{C}}_r{\mathit{a}}_T\left({\theta }_k\right)$. ${\mathit{C}}_t$ and ${\mathit{C}}_r$ are array gain-phase error matrices of transmit array and receive array, respectively, and they are both diagonal matrices. To eliminate the gain-phase error, the well-calibrated array element needs to be used. Given m and n well-calibrated array elements at transmitter and receiver, the first element of transmitter and receiver is set as the reference of transmitter and receiver, respectively. Therefore, the steering vector with gain-phase error is expressed as

$$\begin{array}{cc}\hfill & {\widehat{\mathit{a}}}_T(r_k,{\theta }_k)={\mathit{C}}_t{\mathit{a}}_T(r_k,{\theta }_k)=\hfill \\ \hfill & \left[\begin{array}{c}1\\ e^{-j4\pi \mathrm{\Delta }{f}_2^M{r}_k/c+j2\pi d_2^{M}sin{\theta }_k/\lambda }\\ ⋮\\ e^{-j4\pi \mathrm{\Delta }{f}_m^M{r}_k/c+j2\pi d_m^{M}sin{\theta }_k/\lambda }\\ g_{t1}{e}^{-j4\pi \mathrm{\Delta }{f}_{m+1}^M{r}_k/c+j2\pi d_{m+1}^{M}sin{\theta }_k/\lambda +j{\varphi }_{t1}}\\ ⋮\\ g_{t(M-m)}{e}^{-j4\pi \mathrm{\Delta }{f}_M^M{r}_k/c+j2\pi d_M^{M}sin{\theta }_k/\lambda +j{\varphi }_{t(M-m)}}\end{array}\right]\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\widehat{\mathit{a}}}_R\left({\theta }_k\right)& ={\mathit{C}}_r{\mathit{a}}_R\left({\theta }_k\right)\hfill \\ \hfill & =\left[\begin{array}{c}1\\ e^{j2\pi d_2^{N}sin{\theta }_k/\lambda }\\ ⋮\\ e^{j2\pi d_n^{N}sin{\theta }_k/\lambda }\\ g_{r1}{e}^{j2\pi d_{n+1}^{N}sin{\theta }_k/\lambda +j{\varphi }_{r1}}\\ ⋮\\ g_{r(N-n)}{e}^{j2\pi d_N^{N}sin{\theta }_k/\lambda +j{\varphi }_{r(N-n)}}\end{array}\right]\hfill \end{array}$$

(13)

where the space between n-th receive array and reference array can be expressed by $d_n^N$. Similarly, the distance between m-th transmit array and reference array is given by $d_m^M$. The definition of ${\mathit{C}}_r$ and ${\mathit{C}}_t$ is given by

$${\mathit{C}}_t=diag[\underset{m}{\underbrace{1,\dots ,1}},g_{t1}{e}^{j{\varphi }_{t1}},\dots ,g_{t(M-m)}{e}^{j{\varphi }_{t(M-m)}}]$$

(14)

$${\mathit{C}}_r=diag[\underset{n}{\underbrace{1,\dots ,1}},g_{r1}{e}^{j{\varphi }_{r1}},\dots ,g_{r(N-n)}{e}^{j{\varphi }_{r(N-n)}}]$$

(15)

Since the signal model is three-dimensional, the signal model can be constructed in tensor form, which is written as

$$\begin{array}{cc}\hfill & \mathcal{X}(n,m,l)=\sum _{k=1}^K{\widehat{\mathit{A}}}_R(n,k)\circ {\widehat{\mathit{A}}}_T(m,k)\circ \mathit{S}(l,k)+{\mathit{N}}_{n,m,l}\hfill \\ \hfill & n=1,2,\dots ,Nm=1,2,\dots ,Ml=1,2,\dots ,L\hfill \end{array}$$

(16)

where L stand for the number of snapshots, the $(m,k)$-th element of the transmit direction matrix ${\widehat{\mathit{A}}}_T$ is represented by ${\widehat{\mathit{A}}}_T(m,k)$, $(n,k)$-th element of ${\widehat{\mathit{A}}}_R$ can be expressed as ${\widehat{\mathit{A}}}_R(n,k)$, $\mathit{S}(l,k)$ is the $(l,k)$-th element of $\mathit{S}$, while $\mathit{S}={[{\xi }_1,{\xi }_2,\dots ,{\xi }_k]}^T$. ${\mathit{N}}_{n,m,l}$ is the noise matrix.

By definition, the third-order signal $\mathcal{X}\in {\mathbb{C}}^{N\times M\times L}$ is decomposed into three parts in three directions. In order to simplify the expression, the mode-3 matrix unfolding of the third-order signal $\mathcal{X}\in {\mathbb{C}}^{N\times M\times L}$ is represented by $\mathit{X}={\left[\mathcal{X}\right]}_{\left(3\right)}$, where ${\left[\mathcal{X}\right]}_{\left(3\right)}$ can be expressed as [35]

$$\begin{array}{cc}\hfill {\mathcal{X}t}_{\left(3\right)}& =\left[\begin{array}{c}{\mathit{X}}_1\\ {\mathit{X}}_2\\ ⋮\\ {\mathit{X}}_N\end{array}\right]=\left[\begin{array}{c}{\widehat{\mathit{A}}}_T{\mathrm{\Delta }}_1\left({\widehat{\mathit{A}}}_R\right)\\ {\widehat{\mathit{A}}}_T{\mathrm{\Delta }}_2\left({\widehat{\mathit{A}}}_R\right)\\ ⋮\\ {\widehat{\mathit{A}}}_T{\mathrm{\Delta }}_N\left({\widehat{\mathit{A}}}_R\right)\end{array}\right]{\mathit{S}}^{\mathrm{T}}+\left[\begin{array}{c}{\mathit{N}}_{x1}\\ {\mathit{N}}_{x2}\\ ⋮\\ {\mathit{N}}_{xN}\end{array}\right]\hfill \\ \hfill & =[{\widehat{\mathit{A}}}_R\odot {\widehat{\mathit{A}}}_T]{\mathit{S}}^{\mathrm{T}}+{\mathit{N}}_x\hfill \end{array}$$

(17)

where ${\mathit{X}}_n$ can be given by

$${\mathit{X}}_n={\widehat{\mathit{A}}}_T{\mathrm{\Delta }}_n\left({\widehat{\mathit{A}}}_R\right){\mathit{S}}^{\mathrm{T}}+{\mathit{N}}_{xn},\hspace{1em}n=1,2,\dots ,N.$$

(18)

Similarly, in order to simplify the expression, the other two directions of the third-order signal $\mathcal{X}\in {\mathbb{C}}^{N\times M\times L}$ can be represented by $\mathit{Y}={\left[\mathcal{X}\right]}_{\left(2\right)}$ and $\mathit{Z}={\left[\mathcal{X}\right]}_{\left(1\right)}$, where ${\left[\mathcal{X}\right]}_{\left(2\right)}$ and ${\left[\mathcal{X}\right]}_{\left(1\right)}$ can be expressed as [35]

$$\begin{array}{cc}\hfill {\mathcal{X}t}_{\left(2\right)}& =\left[\begin{array}{c}{\mathit{Y}}_1\\ {\mathit{Y}}_2\\ ⋮\\ {\mathit{Y}}_M\end{array}\right]=\left[\begin{array}{c}\mathit{S}{\mathrm{\Delta }}_1\left({\widehat{\mathit{A}}}_T\right)\\ \mathit{S}{\mathrm{\Delta }}_2\left({\widehat{\mathit{A}}}_T\right)\\ ⋮\\ \mathit{S}{\mathrm{\Delta }}_M\left({\widehat{\mathit{A}}}_T\right)\end{array}\right]{\widehat{\mathit{A}}}_R^{\mathrm{T}}+\left[\begin{array}{c}{\mathit{N}}_{y1}\\ {\mathit{N}}_{y2}\\ ⋮\\ {\mathit{N}}_{yM}\end{array}\right]\hfill \\ \hfill & =[{\widehat{\mathit{A}}}_T\odot \mathit{S}]{\widehat{\mathit{A}}}_R^{\mathrm{T}}+{\mathit{N}}_y\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\mathcal{X}t}_{\left(1\right)}& =\left[\begin{array}{c}{\mathit{Z}}_1\\ {\mathit{Z}}_2\\ ⋮\\ {\mathit{Z}}_L\end{array}\right]=\left[\begin{array}{c}{\widehat{\mathit{A}}}_R{\mathrm{\Delta }}_1\left(\mathit{S}\right)\\ {\widehat{\mathit{A}}}_R{\mathrm{\Delta }}_2\left(\mathit{S}\right)\\ ⋮\\ {\widehat{\mathit{A}}}_R{\mathrm{\Delta }}_L\left(\mathit{S}\right)\end{array}\right]{\widehat{\mathit{A}}}_T^{\mathrm{T}}+\left[\begin{array}{c}{\mathit{N}}_{z1}\\ {\mathit{N}}_{z2}\\ ⋮\\ {\mathit{N}}_{zL}\end{array}\right]\hfill \\ \hfill & =[\mathit{S}\odot {\widehat{\mathit{A}}}_R]{\widehat{\mathit{A}}}_T^{\mathrm{T}}+{\mathit{N}}_z\hfill \end{array}$$

(20)

where ${\mathit{N}}_y$ and ${\mathit{N}}_z$ represent the noise matrices of the corresponding direction, respectively.

3. The Proposed Algorithm

3.1. Direction Matrix Estimation

To estimate the direction matrix, the trilinear alternating LS (TALS) algorithm is employed in the first step.

Utilizing the algorithm in [36], the third-order received data is decomposed by the trilinear decomposition method firstly. Then the least squares (LS) fitting of Equation (17) is given by [37]

$$\underset{{\widehat{\mathit{A}}}_R,{\widehat{\mathit{A}}}_T,\mathit{S}}{min}{\parallel \mathit{X}-[{\widehat{\mathit{A}}}_R\odot {\widehat{\mathit{A}}}_T]{\mathit{S}}^{\mathrm{T}}\parallel }_F.$$

(21)

where $\mathit{X}={\left[\mathcal{X}\right]}_{\left(1\right)}$. The update of $\mathit{S}$ based on LS is given by

$${\tilde{\mathit{S}}}^{\mathrm{T}}={[{\widetilde{\widehat{\mathit{A}}}}_R\odot {\widetilde{\widehat{\mathit{A}}}}_T]}^{†}\mathit{X}$$

(22)

where the estimations of ${\widehat{\mathit{A}}}_R$ and ${\widehat{\mathit{A}}}_T$ can be expressed as ${\widetilde{\widehat{\mathit{A}}}}_R$ and ${\widetilde{\widehat{\mathit{A}}}}_T$, respectively.

The LS fitting of Equation (19) can be given by

$$\underset{{\widehat{\mathit{A}}}_R,{\widehat{\mathit{A}}}_T,\mathit{S}}{min}{\parallel \mathit{Y}-[{\widehat{\mathit{A}}}_T\odot \mathit{S}]{\widehat{\mathit{A}}}_R^{\mathrm{T}}\parallel }_F.$$

(23)

where $\mathit{Y}={\left[\mathcal{X}\right]}_{\left(2\right)}$. The update of ${\widehat{\mathit{A}}}_R$ based on LS is given by

$${\widetilde{\widehat{\mathit{A}}}}_R^{\mathrm{T}}={[{\widetilde{\widehat{\mathit{A}}}}_T\odot \tilde{\mathit{S}}]}^{†}\mathit{Y}$$

(24)

where the estimations of ${\widehat{\mathit{A}}}_T$ and $\mathit{S}$ can be expressed as ${\widetilde{\widehat{\mathit{A}}}}_T$ and $\tilde{\mathit{S}}$, respectively.

The LS fitting of Equation (20) can be given by

$$\underset{{\widehat{\mathit{A}}}_R,{\widehat{\mathit{A}}}_T,\mathit{S}}{min}{\parallel \mathit{Z}-[\mathit{S}\odot {\widehat{\mathit{A}}}_R]{\widehat{\mathit{A}}}_T^{\mathrm{T}}\parallel }_F.$$

(25)

where $\mathit{Z}={\left[\mathcal{X}\right]}_{\left(3\right)}$. The update of matrix ${\widehat{\mathit{A}}}_T$ based on LS is given by

$${\widetilde{\widehat{\mathit{A}}}}_T^{\mathrm{T}}={[\tilde{\mathit{S}}\odot {\widetilde{\widehat{\mathit{A}}}}_R]}^{†}\mathit{Z}$$

(26)

where the estimations of $\mathit{S}$ and ${\widehat{\mathit{A}}}_R$ is written as $\tilde{\mathit{S}}$ and ${\widetilde{\widehat{\mathit{A}}}}_R$, respectively.

According to [37], the inputs of the alternating iteration are $\mathit{X}$ and $F=3$, where $\mathit{X}$ is the input signal and $F=3$ is the dimension of the signal. Thus, the estimations of $\mathit{S}$, ${\widehat{\mathit{A}}}_R$ and ${\widehat{\mathit{A}}}_T$ can be obtained, and these estimations can be updated based on LS. When LS update converges, the iteration will stop. The termination threshold is $\parallel \mathit{X}-[{\widetilde{\widehat{\mathit{A}}}}_R\odot {\widetilde{\widehat{\mathit{A}}}}_T]{\tilde{\mathit{S}}}^{\mathrm{T}}{\parallel }_F^2\le {10}^{-10}$.

Consider the noise in received data, ${\widetilde{\widehat{\mathit{A}}}}_R$, ${\widetilde{\widehat{\mathit{A}}}}_T$, and $\tilde{\mathit{S}}$ obtained through trilinear decomposition have the following forms respectively: ${\widetilde{\widehat{\mathit{A}}}}_R={\widehat{\mathit{A}}}_R\psi {\xi }_1+{\delta }_1$, ${\widetilde{\widehat{\mathit{A}}}}_T={\widehat{\mathit{A}}}_T\psi {\xi }_2+{\delta }_2$, and $\tilde{\mathit{S}}=\mathit{S}\psi {\xi }_3+{\delta }_3$, where $\psi$ is the permutation matrix. ${\xi }_1$, ${\xi }_2$, and ${\xi }_3$ represent the diagonal scaling matrices, satisfying ${\xi }_1{\xi }_2{\xi }_3={\mathit{I}}_K$. In addition, ${\delta }_1$, ${\delta }_2$, and ${\delta }_3$ denote the estimation errors. The direction matrix estimation by trilinear permutation ambiguity and scale ambiguity can be proved. To remove the influence of scale ambiguity, the normalization process is required.

3.2. The Angle Estimation

By employing the well-calibrated auxiliary sensors, the received steering vector is without gain-phase error. Therefore, the correct angle estimation can be obtained through the received steering vector. The received steering vector of auxiliary elements can be denoted as

$${\overline{\mathit{a}}}_R\left({\theta }_k\right)={[1,e^{j2\pi d_2^{N}sin{\theta }_k/\lambda },\dots ,e^{j2\pi d_n^{N}sin{\theta }_k/\lambda }]}^{\mathrm{T}}.$$

(27)

where $\omega$ is defined as a vector including the angles of the elements in ${\overline{\mathit{a}}}_R\left({\theta }_k\right)$, where

$$\begin{array}{cc}\hfill \omega & =angle\left({\overline{\mathit{a}}}_R\left({\theta }_k\right)\right)\hfill \\ \hfill & ={[0,2\pi d_2^{N}sin{\theta }_k/\lambda ,\dots ,2\pi d_n^{N}sin{\theta }_k/\lambda ]}^{\mathrm{T}}.\hfill \end{array}$$

(28)

where ${\widetilde{\overline{\mathit{a}}}}_R\left({\theta }_k\right)$ is the steering vector estimation derived from the additional well-calibrated elements. Firstly, ${\widetilde{\overline{\mathit{a}}}}_R\left({\theta }_k\right)$ is normalized to eliminate the influence of scale ambiguity. Through Equation (28), we can get $\tilde{\omega }$ containing ${\widetilde{\overline{\mathit{a}}}}_R\left({\theta }_k\right)$ information. Through the LS fitting, $\mathrm{\Pi }\mathit{c}=\tilde{\omega }$ can be constructed, where $\mathit{c}\in {\mathbb{C}}^{2\times 1}$ is the estimated vector. The definition of $\mathrm{\Pi }$ is given by

$$\mathrm{\Pi }=\left[\begin{array}{cc}1& 0\\ 1& 2\pi d_2^N/\lambda \\ ⋮& ⋮\\ 1& 2\pi d_n^N/\lambda \end{array}\right]\in {\mathbb{C}}^{n\times 2}.$$

(29)

where $\tilde{\mathit{c}}$ is the estimation of $\mathit{c}$, which is expressed as

$$\tilde{\mathit{c}}={\left({\mathrm{\Pi }}^{\mathrm{T}}\mathrm{\Pi }\right)}^{-1}{\mathrm{\Pi }}^{\mathrm{T}}\tilde{\omega }.$$

(30)

Then the angle estimation of the target can be obtained, which can be expressed as

$${\tilde{\theta }}_k={sin}^{-1}\left(\tilde{\mathit{c}}\left(2\right)\right)\hspace{1em}k=1,2,\dots ,K$$

(31)

where $\tilde{\mathit{c}}\left(2\right)$ is the second element of $\tilde{\mathit{c}}$.

3.3. The Range Estimation

Since the angle estimation of a target has been achieved, the auxiliary elements of transmitter are used to estimate the range of target.

Since the auxiliary array element is composed of well-calibrated sensors, the transmitting steering vector obtained by the auxiliary array element can be expressed as

$$\begin{array}{cc}\hfill {\overline{\mathit{a}}}_T(r_k,{\theta }_k)=& {[1,e^{-j4\pi \mathrm{\Delta }{f}_2^M{r}_k/c+j2\pi d_2^{M}sin{\theta }_k/\lambda },\dots ,e^{-j4\pi \mathrm{\Delta }{f}_m^M{r}_k/c+j2\pi d_m^{M}sin{\theta }_k/\lambda }]}^{\mathrm{T}}.\hfill \end{array}$$

(32)

${\omega }_2$ can be given by

$$\begin{array}{cc}\hfill {\omega }_2=& angle\left({\overline{\mathit{a}}}_T(r_k,{\theta }_k)\right)\hfill \\ \hfill =& {[0,-4\pi \mathrm{\Delta }{f}_2^M{r}_k/c+2\pi d_2^{M}sin{\theta }_k/\lambda ,\dots ,-4\pi \mathrm{\Delta }{f}_m^M{r}_k/c+2\pi d_m^{M}sin{\theta }_k/\lambda ]}^{\mathrm{T}}.\hfill \end{array}$$

(33)

The transmitting steering vector estimation obtained from the additional well-calibrated elements is ${\widetilde{\overline{\mathit{a}}}}_T(r_k,{\theta }_k)$. After obtaining ${\widetilde{\overline{\mathit{a}}}}_T(r_k,{\theta }_k)$, it needs to be normalized to remove the effect of scale ambiguity. The phase of ${\widetilde{\overline{\mathit{a}}}}_T(r_k,{\theta }_k)$ can be obtained by Equation (33), which is expressed as ${\tilde{\omega }}_2$. In order to get the estimated vector $\mathit{z}\in {\mathbb{C}}^{2\times 1}$ which contains the target range information, the LS fitting can be constructed and expressed as ${\mathrm{\Pi }}_2\mathit{z}={\tilde{\omega }}_2$. The definition of ${\mathrm{\Pi }}_2$ can be expressed as

$${\mathrm{\Pi }}_2=\left[\begin{array}{cc}1& 0\\ 1& 2\pi d_2^M\\ ⋮& ⋮\\ 1& 2\pi d_m^M\end{array}\right]\in {\mathbb{C}}^{m\times 2}.$$

(34)

$\tilde{\mathit{z}}$ is the LS solution for $\mathit{z}$, which is given by

$$\tilde{\mathit{z}}={\left({\mathrm{\Pi }}_2^{\mathrm{T}}{\mathrm{\Pi }}_2\right)}^{-1}{\mathrm{\Pi }}_2^{\mathrm{T}}{\tilde{\omega }}_2.$$

(35)

where $\tilde{\mathit{z}}$ contains angle and range information. The range estimation is obtained by the following formula, which can be given by

$${\tilde{\mathit{r}}}_k=\frac{\left(sin\left({\tilde{\theta }}_k\right)-\tilde{\mathit{z}}\left(2\right)\right)·c}{4\mathrm{\Delta }f}\hspace{1em}k=1,2,\dots ,K$$

(36)

where $\tilde{\mathit{z}}\left(2\right)$ is the second element of $\tilde{\mathit{z}}$.

3.4. The Gain Error Estimation

The gain error estimation can be obtained by removing the influence of phase error.

According to the fact that the steering vectors of any target own the same gain-phase error, the gain error can be estimated with any two steering vectors. Using this property, we construct the following equation, which is expressed as

$$\begin{array}{cc}\hfill & {\mathit{G}}_1={\widehat{\mathit{a}}}_R\left({\theta }_i\right)\oslash {\widehat{\mathit{a}}}_R\left({\theta }_j\right)\hfill \\ \hfill & =[1,e^{j2\pi d_2^N(sin{\theta }_i-sin{\theta }_j)/\lambda },\dots ,e^{j2\pi d_n^N(sin{\theta }_i-sin{\theta }_j)/\lambda },\hfill \\ \hfill & \frac{g_{ri1}}{g_{rj1}}{e}^{j[2\pi d_{n+1}^N(sin{\theta }_i-sin{\theta }_j)/\lambda +{\varphi }_{ri1}-{\varphi }_{rj1}]},\dots ,\hfill \\ \hfill & \frac{g_{ri(N-n)}}{g_{rj(N-n)}}{e}^{j[2\pi d_N^N(sin{\theta }_i-sin{\theta }_j)/\lambda +{\varphi }_{ri(N-n)}-{\varphi }_{rj(N-n)}]}{]}^{\mathrm{T}}\hfill \end{array}$$

(37)

where ${\widehat{\mathit{a}}}_R\left({\theta }_i\right)$ and ${\widehat{\mathit{a}}}_R\left({\theta }_j\right)$ represent the steering vectors of the ith and jth targets, respectively. Moreover, i can equal to j. For removing the effect of the scale ambiguity, both ${\widehat{\mathit{a}}}_R\left({\theta }_i\right)$ and ${\widehat{\mathit{a}}}_R\left({\theta }_j\right)$ need the process of normalization. Then the following equation can be constructed and expressed as

$$\begin{array}{cc}\hfill & {\mathit{G}}_2={\widehat{\mathit{a}}}_R\left({\theta }_i\right)\star {\widehat{\mathit{a}}}_R^{*}\left({\theta }_j\right)\hfill \\ \hfill & =[1,e^{j2\pi d_2^N(sin{\theta }_i-sin{\theta }_j)/\lambda },\dots ,e^{j2\pi d_n^N(sin{\theta }_i-sin{\theta }_j)/\lambda },\hfill \\ \hfill & g_{ri1}{g}_{rj1}{e}^{j[2\pi d_{n+1}^N(sin{\theta }_i-sin{\theta }_j)/\lambda +{\varphi }_{ri1}-{\varphi }_{rj1}]},\dots ,\hfill \\ \hfill & g_{ri(N-n)}{g}_{rj(N-n)}{e}^{j[2\pi d_N^N(sin{\theta }_i-sin{\theta }_j)/\lambda +{\varphi }_{ri(N-n)}-{\varphi }_{rj(N-n)}]}{]}^{\mathrm{T}}\hfill \end{array}$$

(38)

As can be seen from Equations (37) and (38), ${\mathit{G}}_1$ and ${\mathit{G}}_2$ have the same argument, but the value of the modules are not the same. According to the characteristic, we can estimate the gain error without being affected by the phase error. Then we can get that

$$\begin{array}{cc}\hfill g_r& =\sqrt{Re\left({\mathit{G}}_2\right)\oslash Re\left({\mathit{G}}_1\right)}\hfill \\ \hfill & ={[\underset{n}{\underbrace{1,\dots ,1}},g_{rj1},\dots ,g_{rj(N-n)}]}^{\mathrm{T}}.\hfill \end{array}$$

(39)

It is obvious that the gain error estimation is not impacted by phase error. The error accumulation influence is eliminated, so better estimation performance can be obtained.

According to the scheme, the gain error estimation of transmitter ${\mathit{g}}_t$ can be obtained. So the following two equations can be derived.

$$\begin{array}{cc}\hfill {\mathit{G}}_3& ={\widehat{\mathit{a}}}_T(r_i,{\theta }_i)\oslash {\widehat{\mathit{a}}}_T(r_j,{\theta }_j)\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\mathit{G}}_4& ={\widehat{\mathit{a}}}_T(r_i,{\theta }_i)\star {\widehat{\mathit{a}}}_T^{*}(r_j,{\theta }_j)\hfill \end{array}$$

(41)

Therefore, the gain error estimation of transmitting array is expressed as

$$\begin{array}{cc}\hfill {\mathit{g}}_t& =\sqrt{Re\left({\mathit{G}}_4\right)\oslash Re\left({\mathit{G}}_3\right)}\hfill \\ \hfill & ={[\underset{m}{\underbrace{1,\dots ,1}},g_{tj1},\dots ,g_{tj(M-m)}]}^{\mathrm{T}}.\hfill \end{array}$$

(42)

3.5. The Phase Error Estimation

The phase error estimation is obtained by the relationship between the steering vector achieved by the additional well-calibrated elements and the steering vector obtained by other elements.

For getting the argument of the received steering vector with array gain-phase errors, the following formula can be constructed

$$\begin{array}{cc}\hfill & {\mathrm{\Phi }}_1=angle\left({\widehat{\mathit{a}}}_R\left({\theta }_k\right)\right)\hfill \\ \hfill & =[0,2\pi d_2^{N}sin{\theta }_k/\lambda ,\dots ,2\pi d_n^{N}sin{\theta }_k/\lambda ,2\pi d_{n+1}^{N}sin{\theta }_k/\lambda +{\varphi }_{r1},\dots ,\hfill \\ \hfill & 2\pi d_N^{N}sin{\theta }_k/\lambda +{\varphi }_{r(N-n)}{]}^{\mathrm{T}}\hfill \end{array}$$

(43)

where ${\widehat{\mathit{a}}}_R\left({\theta }_k\right)$ is the received steering vector of the kth target with gain-phase errors.

In order to obtain the argument of the received steering vector achieved by the additional well-calibrated elements, the following formula can be defined

$${\mathrm{\Pi }}_3=\left[\begin{array}{cc}1& 0\\ 1& 2\pi d_2^N\\ ⋮& ⋮\\ 1& 2\pi d_N^N\end{array}\right]\in {\mathbb{C}}^{N\times 2}.$$

(44)

By the LS fitting, the following formula is defined as

$${\tilde{\omega }}_3={\mathrm{\Pi }}_3\tilde{\mathit{c}}.$$

(45)

where $\tilde{\mathit{c}}$ is the estimated vector, which is obtained by Equation (30).

The argument of the received steering vector without gain-phase errors can be expressed as

$$\begin{array}{cc}\hfill & {\mathrm{\Phi }}_2={\tilde{\omega }}_3=angle\left({\mathit{a}}_R\left({\theta }_k\right)\right)\hfill \\ \hfill & ={[0,2\pi d_2^{N}sin{\theta }_k/\lambda ,\dots ,2\pi d_n^{N}sin{\theta }_k/\lambda ,2\pi d_{n+1}^{N}sin{\theta }_k/\lambda ,\dots ,2\pi d_N^{N}sin{\theta }_k/\lambda ]}^{\mathrm{T}}\hfill \end{array}$$

(46)

where ${\mathit{a}}_R\left({\theta }_k\right)$ is the received steering vector of the kth target obtained by the additional well-calibrated elements.

The array gain-phase error estimation of the received array is achieved, which can be expressed as

$$\begin{array}{cc}\hfill {\mathit{p}}_r& ={\mathrm{\Phi }}_1-{\mathrm{\Phi }}_2\hfill \\ \hfill & ={[\underset{n}{\underbrace{0,\dots ,0}},{\varphi }_{r1},\dots ,{\varphi }_{r(N-n)}]}^{\mathrm{T}}.\hfill \end{array}$$

(47)

We can see that the impact of gain error is removed in the obtained phase error estimation, which is the key reason to improve the estimation accuracy.

To achieve the phase error estimation of the transmitting array, the same method can be employed. Similarly, the phase of the transmitting array can be represented by ${\mathrm{\Phi }}_3$, which can be expressed as

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}_3& =angle\left({\widehat{\mathit{a}}}_T(r_k,{\theta }_k)\right)=\hfill \\ \hfill & \left[\begin{array}{c}0\\ -j4\pi \mathrm{\Delta }{f}_2^M{r}_k/c+j2\pi d_2^{M}sin{\theta }_k/\lambda \\ ⋮\\ -j4\pi \mathrm{\Delta }{f}_m^M{r}_k/c+j2\pi d_m^{M}sin{\theta }_k/\lambda \\ -j4\pi \mathrm{\Delta }{f}_{m+1}^M{r}_k/c+j2\pi d_{m+1}^{M}sin{\theta }_k/\lambda +j{\varphi }_{t1}\\ ⋮\\ -j4\pi \mathrm{\Delta }{f}_M^M{r}_k/c+j2\pi d_M^{M}sin{\theta }_k/\lambda +j{\varphi }_{t(M-m)}\end{array}\right]\hfill \end{array}$$

(48)

In order to obtain the transmitting element phase without gain-phase error, ${\mathrm{\Pi }}_4$ is constructed as

$${\mathrm{\Pi }}_4=\left[\begin{array}{cc}1& 0\\ 1& 2\pi d_2^M\\ ⋮& ⋮\\ 1& 2\pi d_M^M\end{array}\right]\in {\mathbb{C}}^{M\times 2}.$$

(49)

According to Equation (35), we can get

$${\tilde{\omega }}_4={\mathrm{\Pi }}_4\tilde{\mathit{z}}.$$

(50)

where $\tilde{\mathit{z}}$ contains angle and range information. Therefore, the phase of the transmitter without the array gain-phase error is given by

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}_4& ={\tilde{\omega }}_4=angle\left({\mathit{a}}_T(r_k,{\theta }_k)\right)=\hfill \\ \hfill & \left[\begin{array}{c}0\\ -j4\pi \mathrm{\Delta }{f}_2^M{r}_k/c+j2\pi d_2^{M}sin{\theta }_k/\lambda \\ ⋮\\ -j4\pi \mathrm{\Delta }{f}_m^M{r}_k/c+j2\pi d_m^{M}sin{\theta }_k/\lambda \\ -j4\pi \mathrm{\Delta }{f}_{m+1}^M{r}_k/c+j2\pi d_{m+1}^{M}sin{\theta }_k/\lambda \\ ⋮\\ -j4\pi \mathrm{\Delta }{f}_M^M{r}_k/c+j2\pi d_M^{M}sin{\theta }_k/\lambda \end{array}\right]\hfill \end{array}.$$

(51)

Utilizing the obtained ${\mathrm{\Phi }}_3$ and ${\mathrm{\Phi }}_4$, the phase error estimation of the transmitter can be obtained by the following equation.

$$\begin{array}{cc}\hfill {\mathit{p}}_t& ={\mathrm{\Phi }}_3-{\mathrm{\Phi }}_4\hfill \\ \hfill & ={[\underset{m}{\underbrace{0,\dots ,0}},{\varphi }_{t1},\dots ,{\varphi }_{t(M-m)}]}^{\mathrm{T}}.\hfill \end{array}$$

(52)

The proposed target parameter estimation algorithm for FDA-MIMO radar under the circumstance of array gain-phase errors can be summarized in Algorithm 1.

Algorithm 1 Tensor-based target parameter estimation algorithm for FDA-MIMO radar.

1: FDA-MIMO radar receives signal $\mathit{X}$; 2: Calculate ${\widetilde{\widehat{\mathit{A}}}}_R$ and ${\widetilde{\widehat{\mathit{A}}}}_T$ by Equations (24) and (26), 3: Calculate $\mathit{c}$ by Equation (30), 4: ${\tilde{\theta }}_k$ can be obtained by Equation (31), 5: Calculate $\tilde{\mathit{z}}$ by Equation (35), 6: ${\tilde{\mathit{r}}}_k$ can be obtained by Equation (36), 7: Calculate ${\mathit{G}}_1$ and ${\mathit{G}}_2$ by Equations (37) and (38), calculate ${\mathit{G}}_3$ and ${\mathit{G}}_4$ by Equations (40) and (41) 8: ${\mathit{g}}_r$ can be obtained through Equation (39). ${\mathit{g}}_t$ is estimated by Equation (42), 9: Calculate ${\tilde{\omega }}_3$ and ${\tilde{\omega }}_4$ by Equations (45) and (50), 10: ${\mathit{p}}_r$ and ${\mathit{p}}_t$ can be estimated by Equations (47) and (52), respectively.

4. Simulation Results

To verify the effectiveness of the proposed method and highlight its advantages, several groups of numerical experiments are presented in this part. MUSIC method [21], Unitary ESPRIT algorithm [23], ESPRIT-based algorithm [29], Li’s method [30], and Cramer-Rao bound (CRB) (see Appendix A for details) are used to compare with the proposed method. It is worth mentioning that the ESPRIT-based algorithm and Li’s method are for MIMO radar. In this paper, we combine the ESPRIT-based method and Li’s method with the proposed method, respectively. Then ESPRIT-based method and Li’s method are introduced into FDA-MIMO radar.

In this part, the monostatic FDA-MIMO is composed of $M=8$ transmit elements and $N=6$ received elements. In the simulation experiment, suppose there are $K=3$ uncorrelated targets. Specifically, the positions of the three targets are $({\theta }_1,r_1)=(-{15}^{\circ },500)$ m, $({\theta }_2,r_2)=(0^{\circ },6000)$ m, and $({\theta }_3,r_3)=({20}^{\circ },80,000)$ m. Since the proposed algorithm is under the condition of gain-phase error, the array gain-phase error is added to the receiving and transmitting elements in the simulation. The coefficients of gain-phase error are stochastically written as: ${\mathit{c}}_t=[1,1,1,1.21e^{j0.12},1.1e^{j1.35},0.89e^{j0.98},1.35e^{j2.65},0.92e^{j1.97}]$ and ${\mathit{c}}_r=[1,1,0.94e^{j1.12},1.23e^{j2.35},1.49e^{j0.58},0.75e^{j0.65}]$. The root mean square error (RMSE) is used to evaluate the developed algorithm’s performance. The RMSEs of the angle estimation and range estimation are given by

$${\mathrm{RMSE}}_{\theta }=\frac{1}{K}\sum _{k=1}^K\sqrt{\frac{1}{\zeta }\sum _{i=1}^{\zeta }{\left({\tilde{\theta }}_{k,i}-{\theta }_k\right)}^2}$$

(53)

$${\mathrm{RMSE}}_r=\frac{1}{K}\sum _{k=1}^K\sqrt{\frac{1}{\zeta }\sum _{i=1}^{\zeta }{\left({\tilde{r}}_{k,i}-r_k\right)}^2}$$

(54)

where the ith Monte Carlo tests of ${\theta }_k$ and $r_k$ can be represented by ${\tilde{\theta }}_{k,i}$ and ${\tilde{r}}_{k,i}$, respectively. In addition, the total number of Monte Carlo tests is given by $\zeta =500$.

For the gain-phase error estimation, the RMSE is given by

$$\mathrm{RMSE}=\sqrt{\frac{1}{\zeta }\sum _{i=1}^{\zeta }\left\{{∥{\tilde{\mathit{c}}}_{t,i}-{\mathit{c}}_t∥}_F^2+{∥{\tilde{\mathit{c}}}_{r,i}-{\mathit{c}}_r∥}_F^2\right\}}$$

(55)

where the ith Monte Carlo tests of ${\mathit{c}}_t$ and ${\mathit{c}}_r$ are written as ${\tilde{\mathit{c}}}_{t,i}$ and ${\tilde{\mathit{c}}}_{r,i}$, respectively.

The probability of the successful detection (PSD) is another standard to evaluate the performance of the proposed algorithm, where PSD can be defined as

$$\mathrm{PSD}=\frac{D}{\zeta }\times 100\%$$

(56)

where D is the total number of correct results. When the absolute error of a simulation result is less than $min\left[{({\tilde{\theta }}_k-{\theta }_k)}_{k=1}^K\right]$, we define it as a successful experiment.

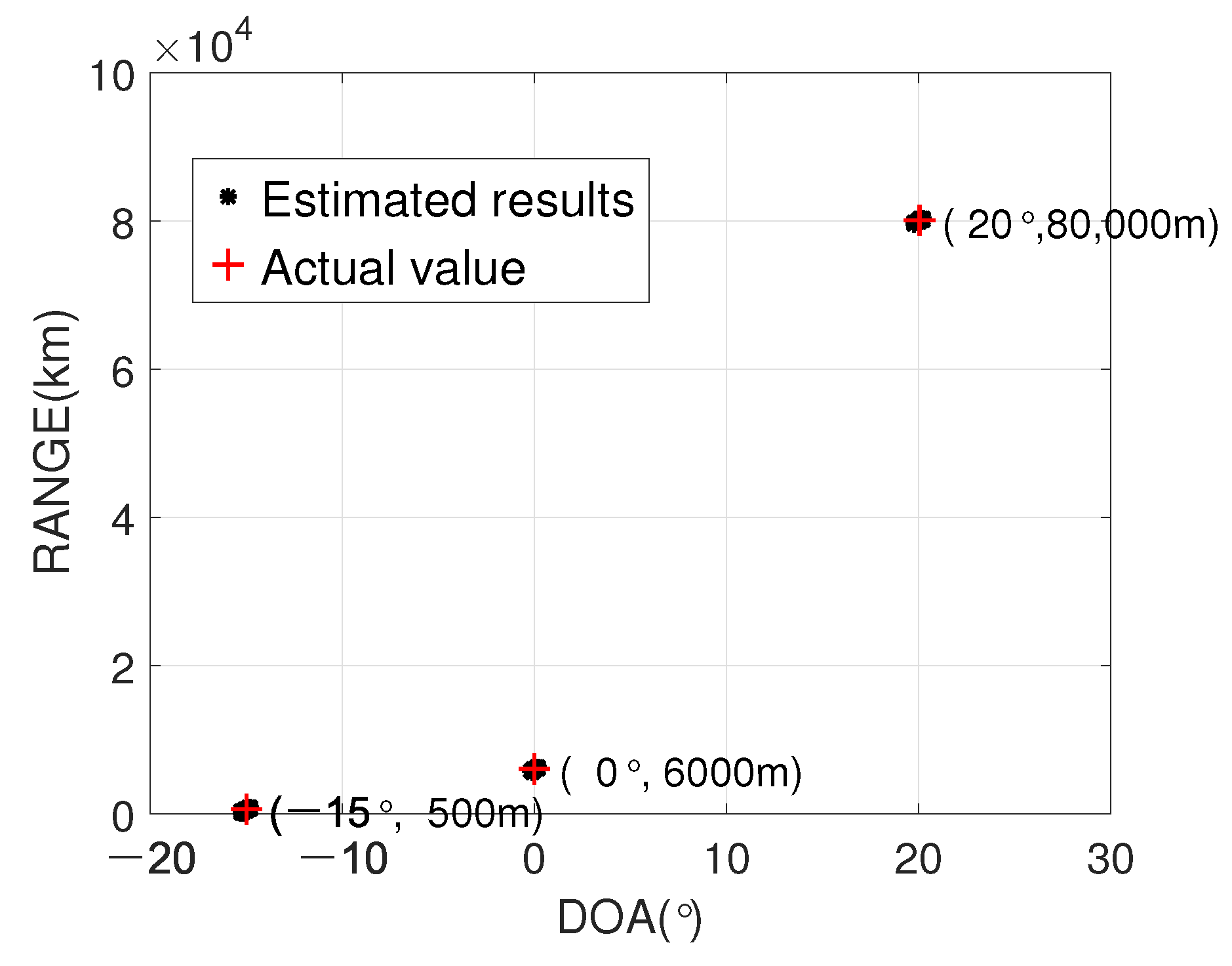
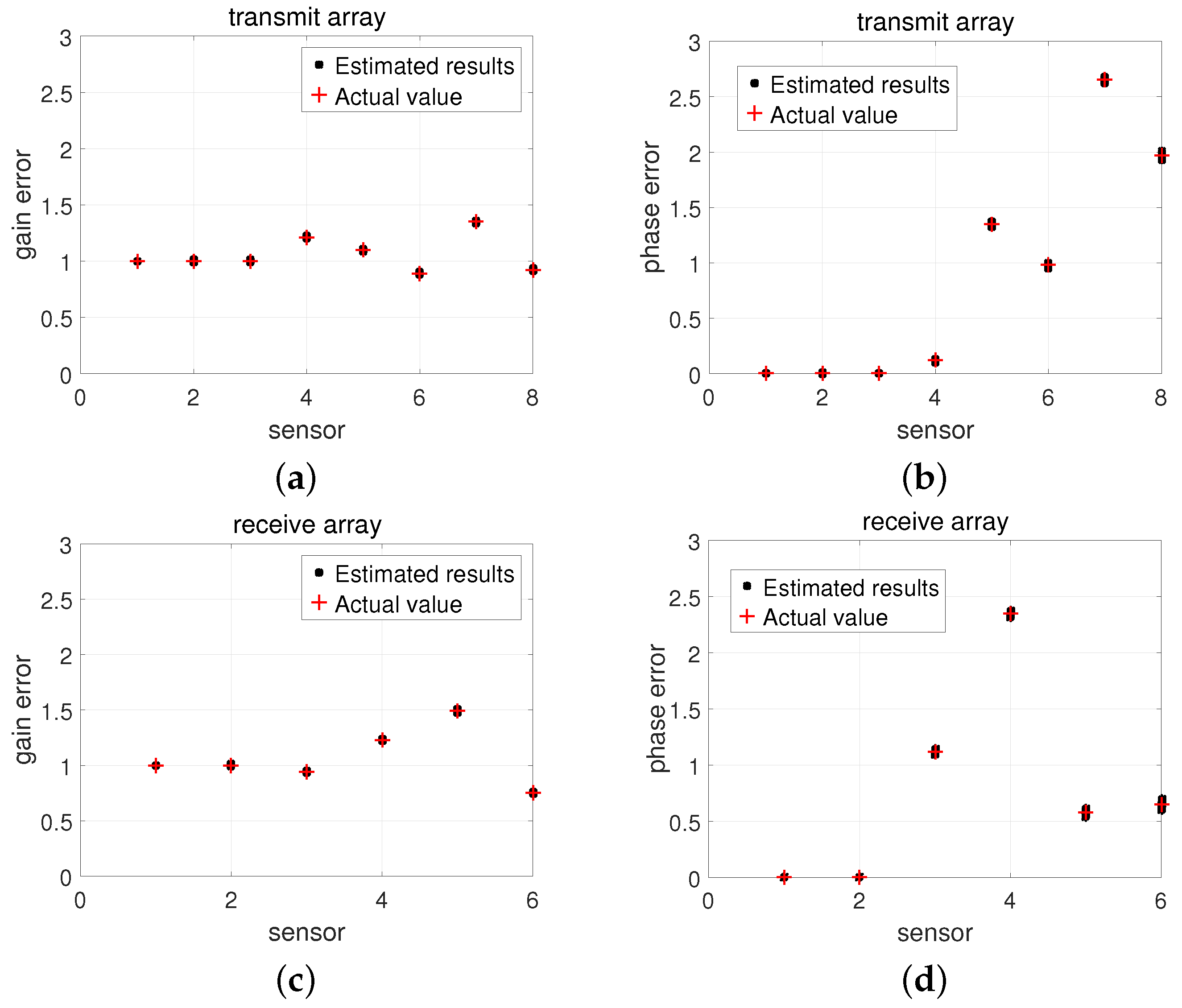
Figure 2 and Figure 3 show the joint estimation results of angle-range and the estimation results of gain-phase error, respectively. In this experiment, the number of snapshots $L=200$, while $\mathrm{SNR}=20\mathrm{dB}$. It is obvious from Figure 2 that the developed scheme can accurately obtain the joint angle and range estimation. In addition, we can see from Figure 3 that the gain-phase error estimation is also correct. Therefore, the two graphs testify the availability of the proposed method.

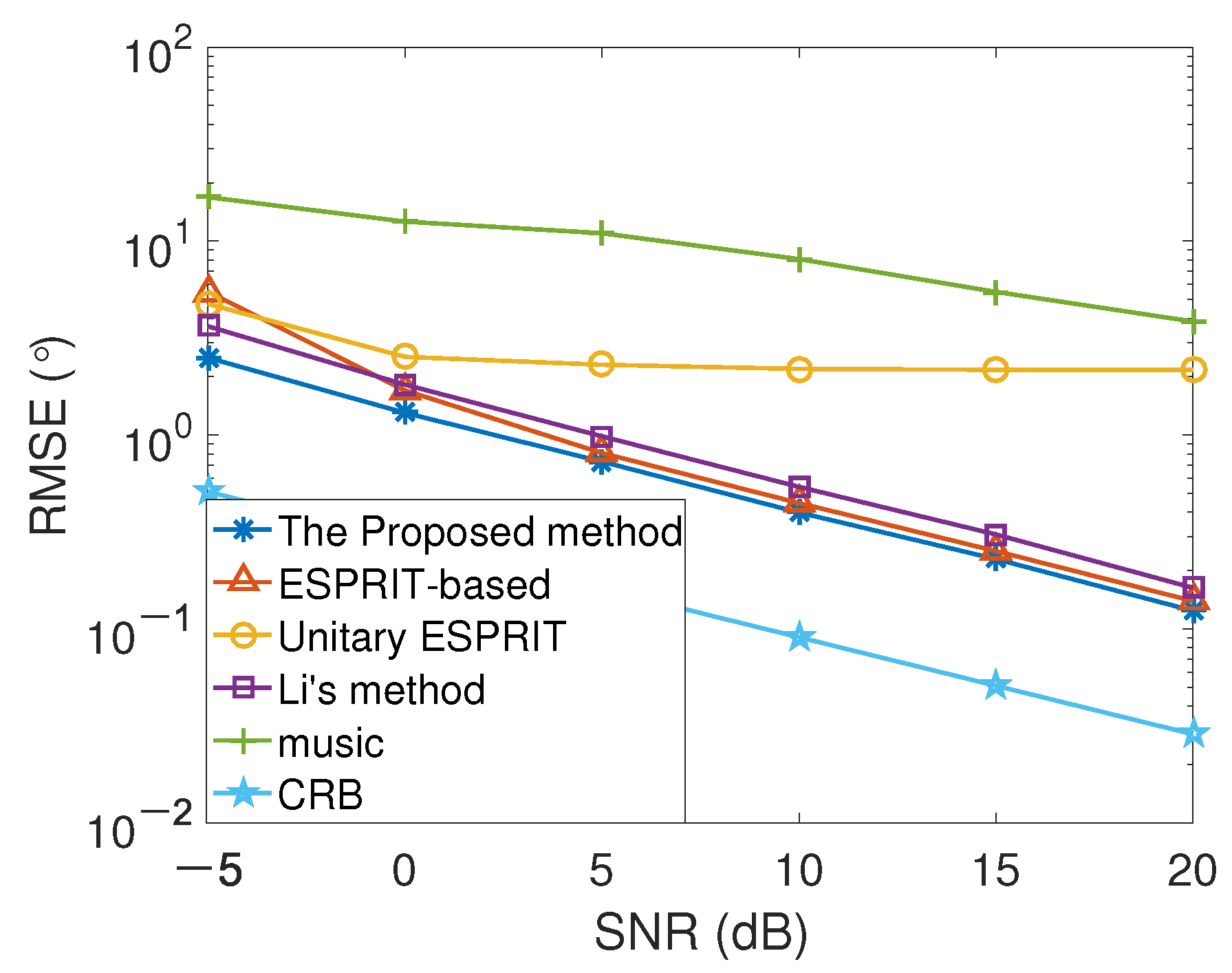
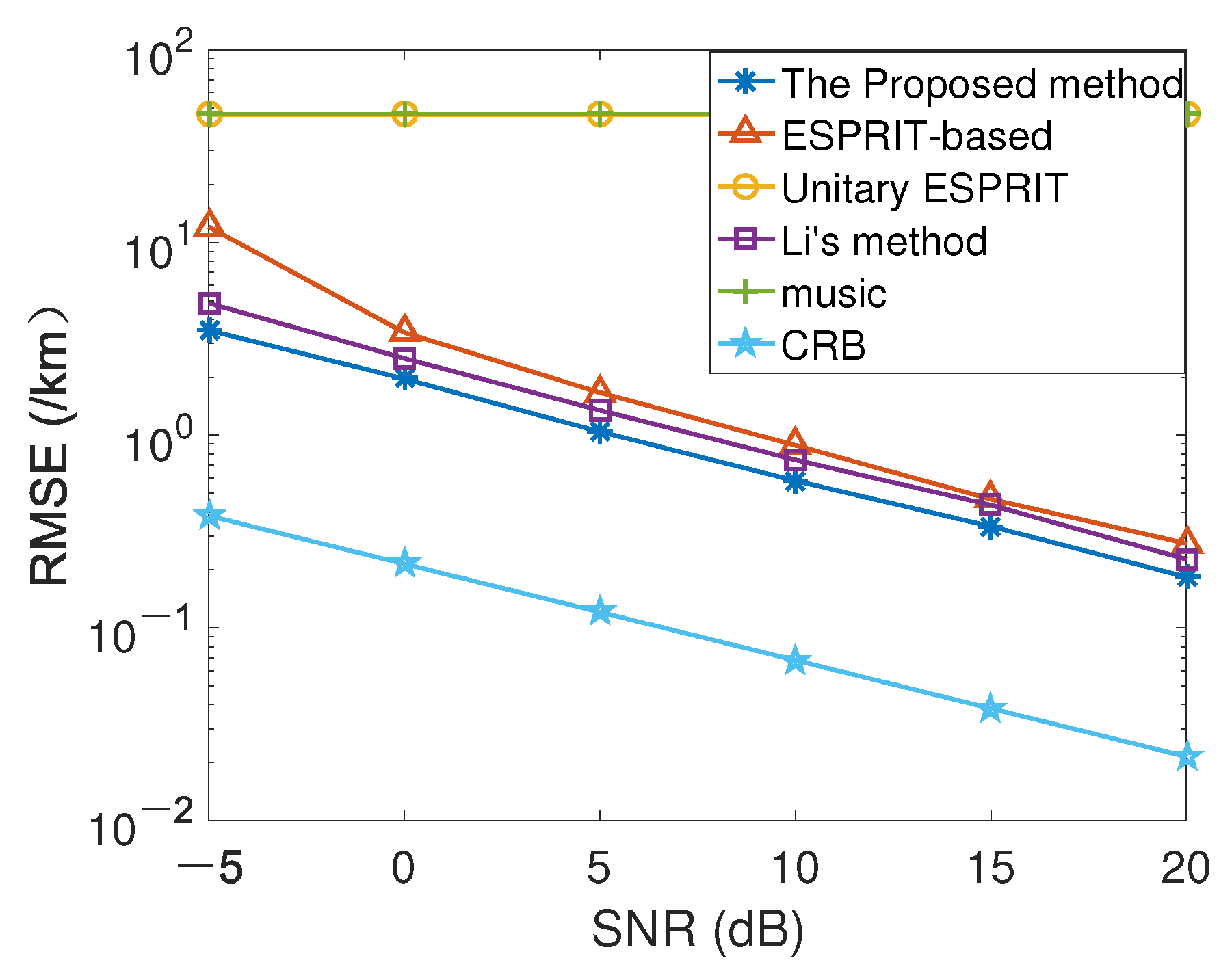
For testifying the advantages of the proposed method, several groups of numerical experiments are presented. The first set of numerical experiments shows the connection between RMSE and $\mathrm{SNR}$ in angle and range estimation. The experimental consequence are shown in Figure 4 and Figure 5. The number of snapshots $L=50$. The MUSIC method, the unitary ESPRIT algorithm, the ESPRIT-based algorithm, Li’s method, and CRB are used to contrast the performance with the method in this paper. From Figure 4 and Figure 5, we can know that the performance of the proposed algorithm is more outstanding than that of the others. It is worth mentioning that the MUSIC method and the unitary ESPRIT algorithm directly fail in the presence of gain-phase errors. It fails to obtain the correct estimations of angle and range. Most of the existing joint angle and range estimation algorithms for FDA-MIMO radar will fail in the presence of gain-phase error. In brief, the method in this paper is very meaningful. The angle and range estimation performance of this algorithm with gain-phase error is not only more outstanding than that of the others, but also closer to CRB curve, which is verified by Figure 4 and Figure 5. The reason why the angle and range estimation performance of the developed scheme is superior than that of the others is that the developed scheme takes advantage of multi-dimensional characteristics and retains the original structure of multidimensional data. In the data processing stage, the proposed algorithm uses more effective information.

To verify the superiority of the proposed algorithm in gain-phase error estimation, the second numerical simulations can be presented. Figure 6 shows the performance of different algorithms for gain-phase error estimation under different $\mathrm{SNR}$. The number of snapshots $L=50$. From the last experiment, it can be known that the MUSIC method and the unitary ESPRIT algorithm have been invalid under the condition of gain-phase error. Therefore, in this numerical experiment, the MUSIC method and the unitary ESPRIT algorithm will not be added to the comparison. From Figure 6 we can know that the gain-phase error estimation performance of the three algorithms advances with the increase of $\mathrm{SNR}$. However, the performance of the proposed method is obviously superior than that of Li’s method and the ESPRIT-based method. The multi-dimensional structure of data is considered in the proposed algorithm. Moreover, the gain error and the phase error are estimated separately. Thus the error accumulation effect is eliminated, which is the reason why the performance of the method in this paper is more outstanding.

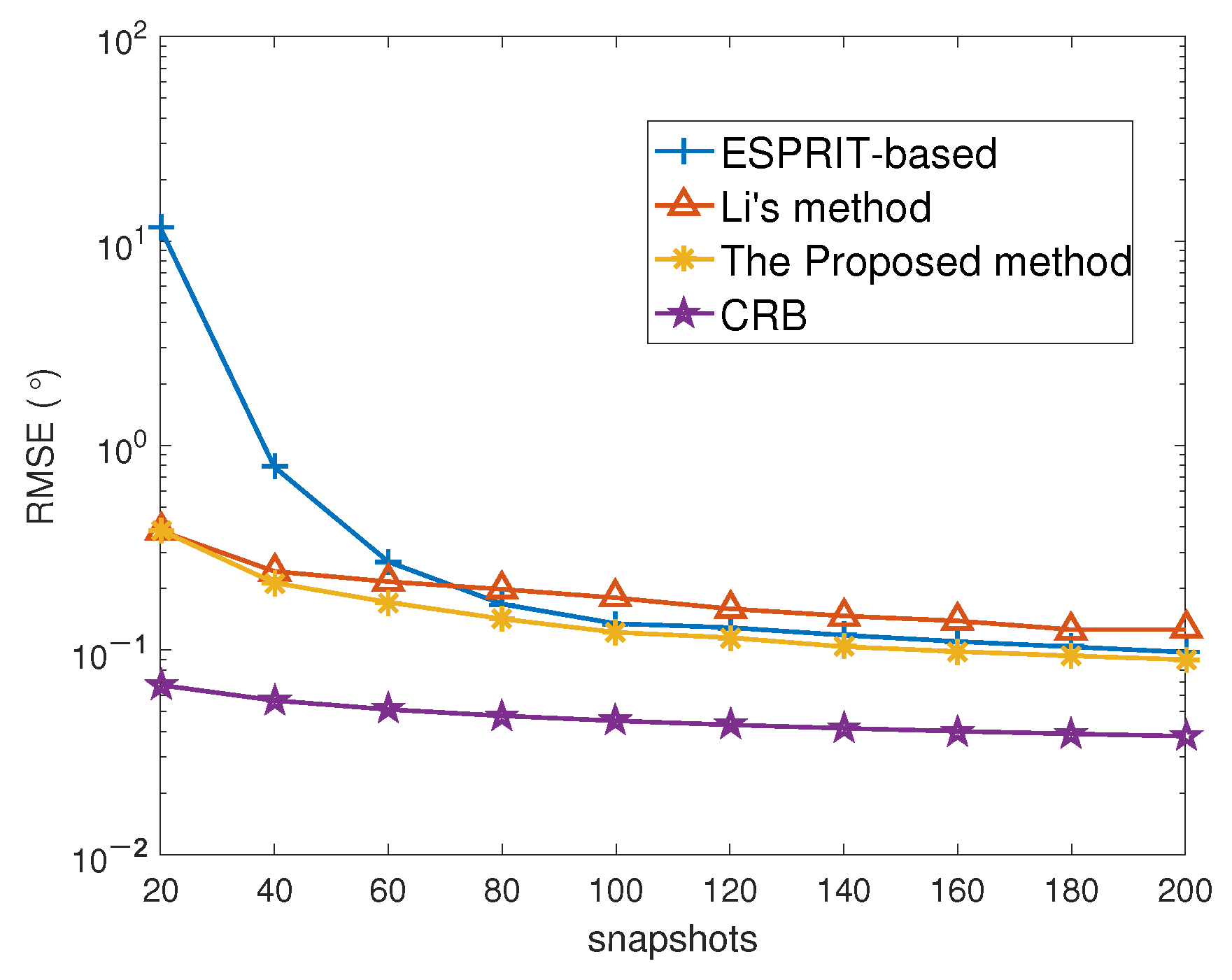
The following numerical simulations can be designed to find out the effect of snapshot number on the performance of angle and range estimation with $\mathrm{SNR}=20\mathrm{dB}$. Figure 7 and Figure 8 show the influence of different snapshot numbers on angle estimation performance and range estimation performance of different methods, respectively. From Figure 7, we can see that the angle estimation performance of the proposed method is obviously superior than that of the ESPRIT-based method when the number of snapshots is lower than 100. With the increase of the number of snapshots, the angle estimation performance of the two methods has been advanced to varying degrees. When the number of snapshots is more than 100, the angle estimation performance gap between the two algorithms is very small. However, the angle estimation performance of method in this paper is still superior to that of the ESPRIT-based algorithm, and closer to the CRB curve. In addition, the performance of the proposed algorithm is always superior to that of Li’s algorithm. 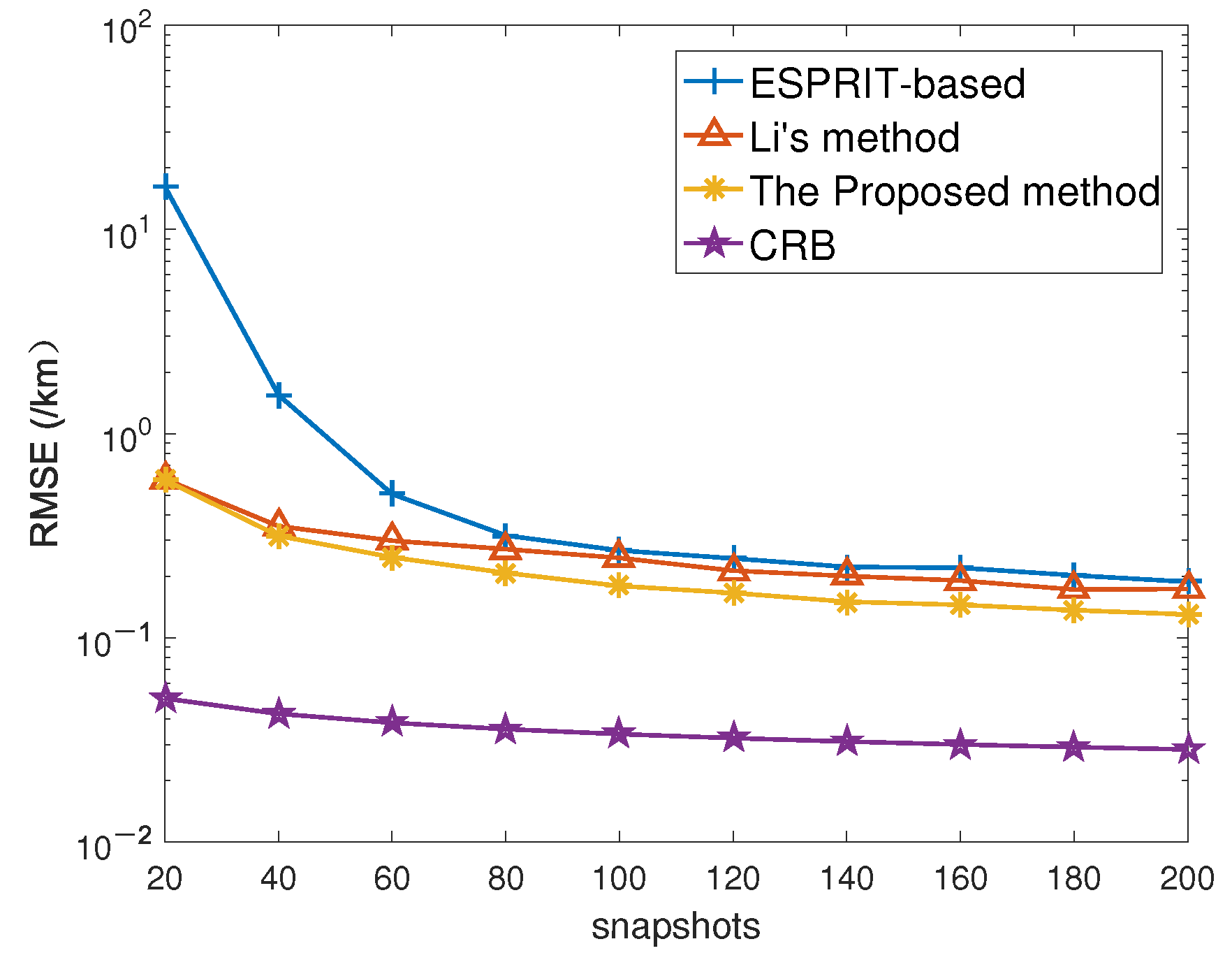Figure 8 shows the influence of the number of snapshots on range estimation performance. According to Figure 8, as the number of snapshots increases, the range estimation performance of both algorithms has been improved. When the number of snapshots is lower than 80, the range estimation accuracy of the proposed method is obviously superior to that of the ESPRIT-based method. When the number of snapshots is more than 80, the performance gap between the two algorithms tends to be stable, but the range estimation accuracy of the method in this paper is still significantly superior to that of the ESPRIT-based method. The performance of Li’s algorithm is at the average level of the other two algorithms. Since the proposed algorithm utilizes the multi-dimensional structure of data, its performance is obviously more outstanding than that of Li’s algorithm and the ESPRIT-based method.

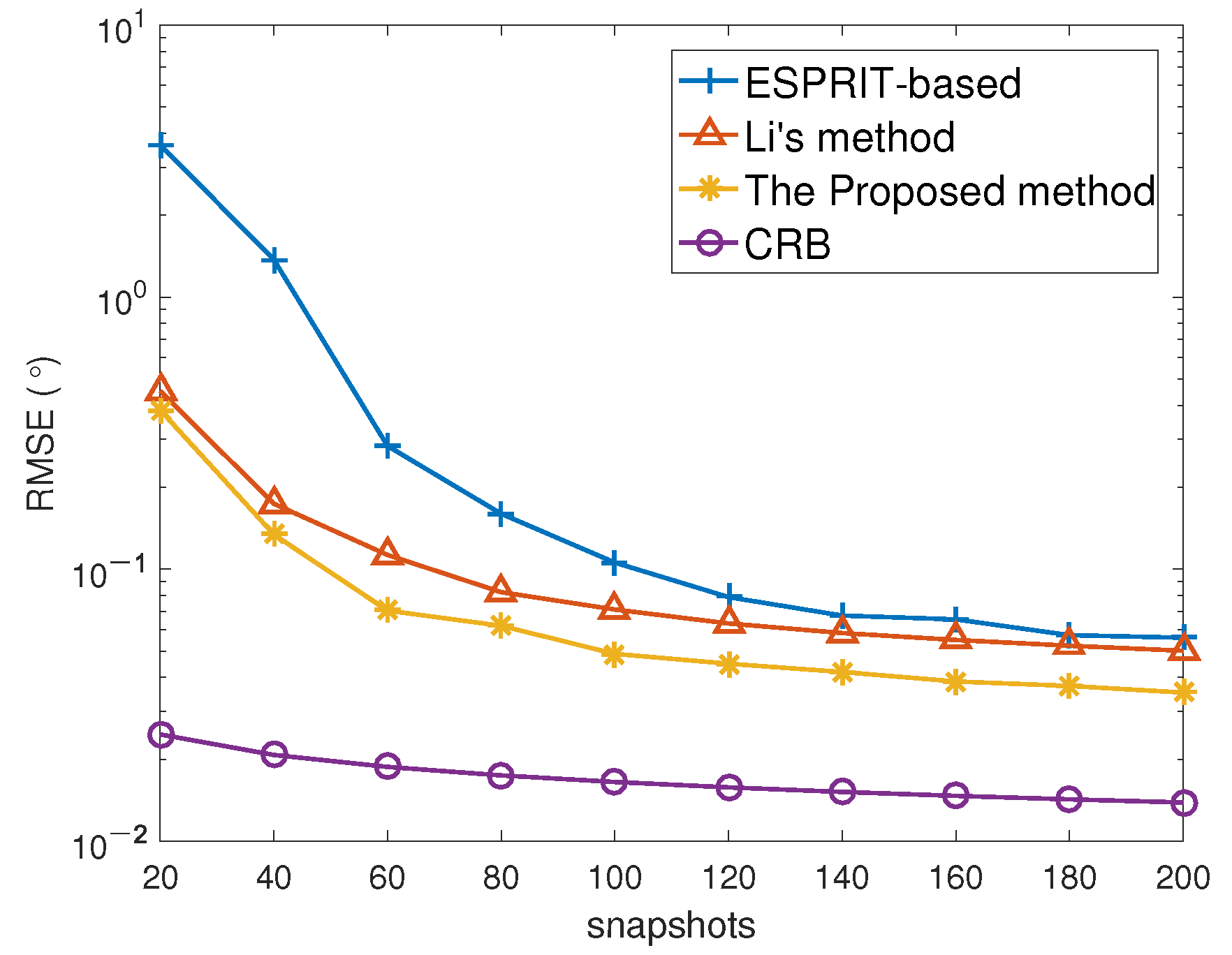
The following numerical experiment is designed to demonstrate the superiority of the method in this paper for gain-phase error estimation. In this experiment, $\mathrm{SNR}$ is 20 dB. According to Figure 9, we can see that the gain-phase error estimation accuracy of the three algorithms is improved with the increase of the number of snapshots. It is worth mentioning that the gain-phase error estimation accuracy of the method in this paper is always superior to that of the other two algorithms. The performance of the method in this paper is more stable. There are two main reasons for this. On the one hand, the proposed method takes advantage of the multi-dimensional structure and improves the gain-phase error estimation performance of the algorithm. On the other hand, the proposed algorithm eliminates the error accumulation effect in the gain-phase error estimation, so the estimation performance is not only superior but also more stable.

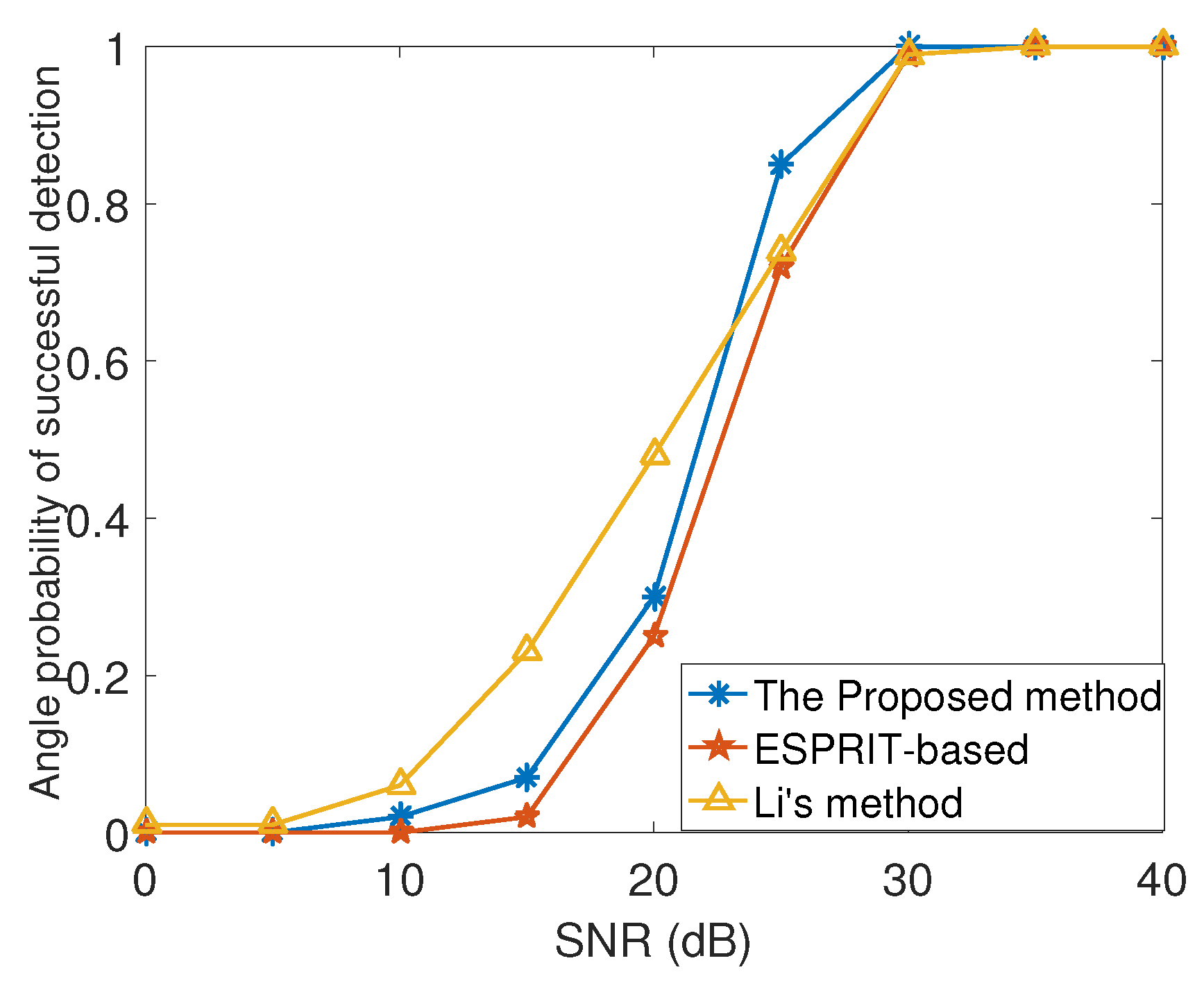
In this experiment, the advantage of the proposed algorithm in probability of the successful detection in angle and range estimation is demonstrated. It should be noted that the number of snapshots $L=200$. Figure 10 and Figure 11 represent PSD of angle estimation and range estimation of different algorithms, respectively. From the curve shown in Figure 10, the PSD of both algorithms can reach $100\%$ when $\mathrm{SNR}$ reaches 35 $\mathrm{dB}$. The PSD of the proposed method is lower than that of Li’s algorithm when the $\mathrm{SNR}$ is less than 25 $\mathrm{dB}$. However, the PSD of the proposed method is significantly greater than that of the other two methods when the $\mathrm{SNR}$ is more than 25 $\mathrm{dB}$. 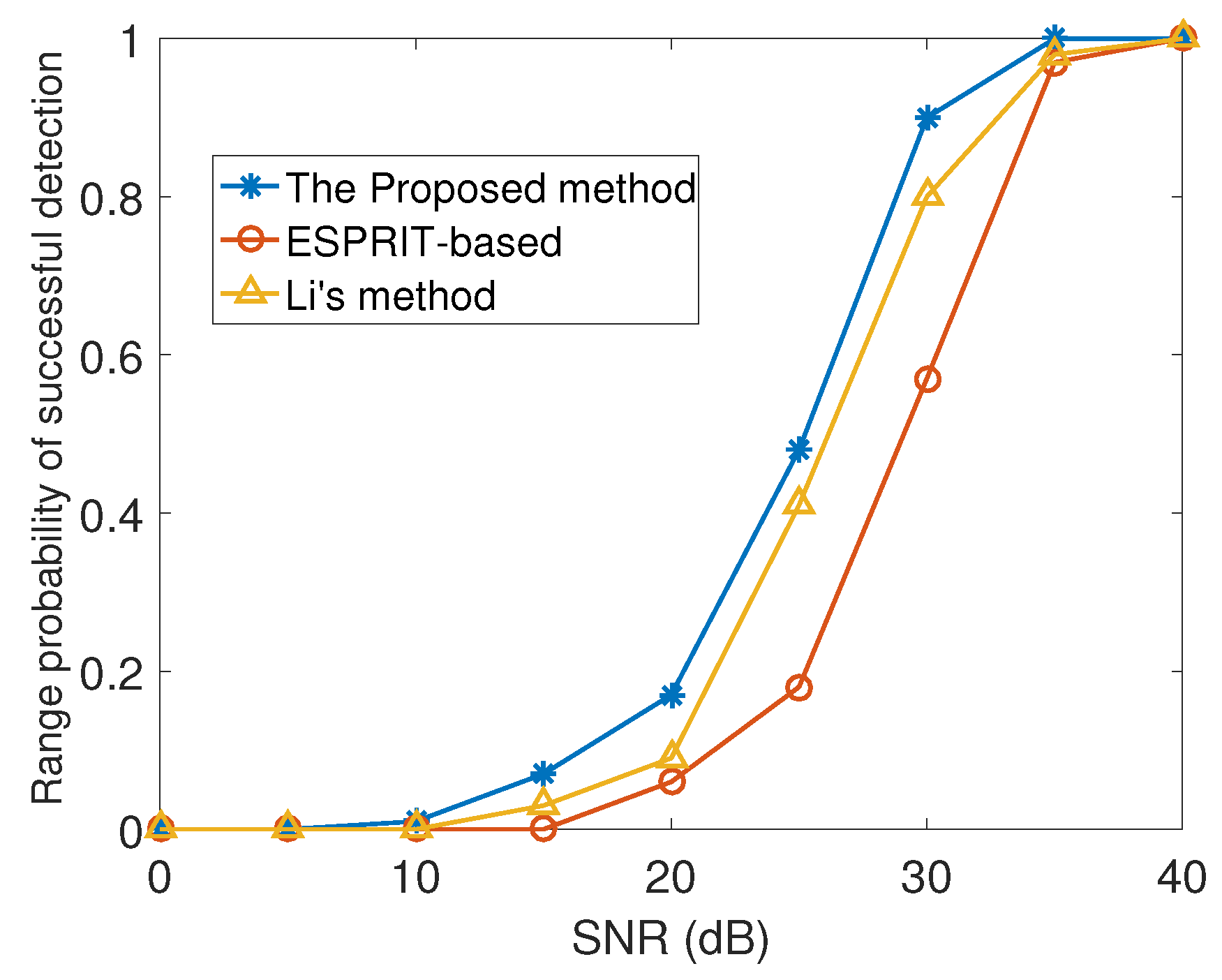Figure 11 shows the advantages of the proposed method in range estimation. According to Figure 11, we can see that the method in this paper has more significant advantages in range estimation. Under the same $\mathrm{SNR}$, the proposed method always has more excellent PSD than the other two methods. Moreover, when the PSD of the proposed algorithm reaches $100\%$, the $\mathrm{SNR}$ is lower than that of the other two algorithms. This means that the method in this paper can perform more outstanding range estimation performance in poor environment.

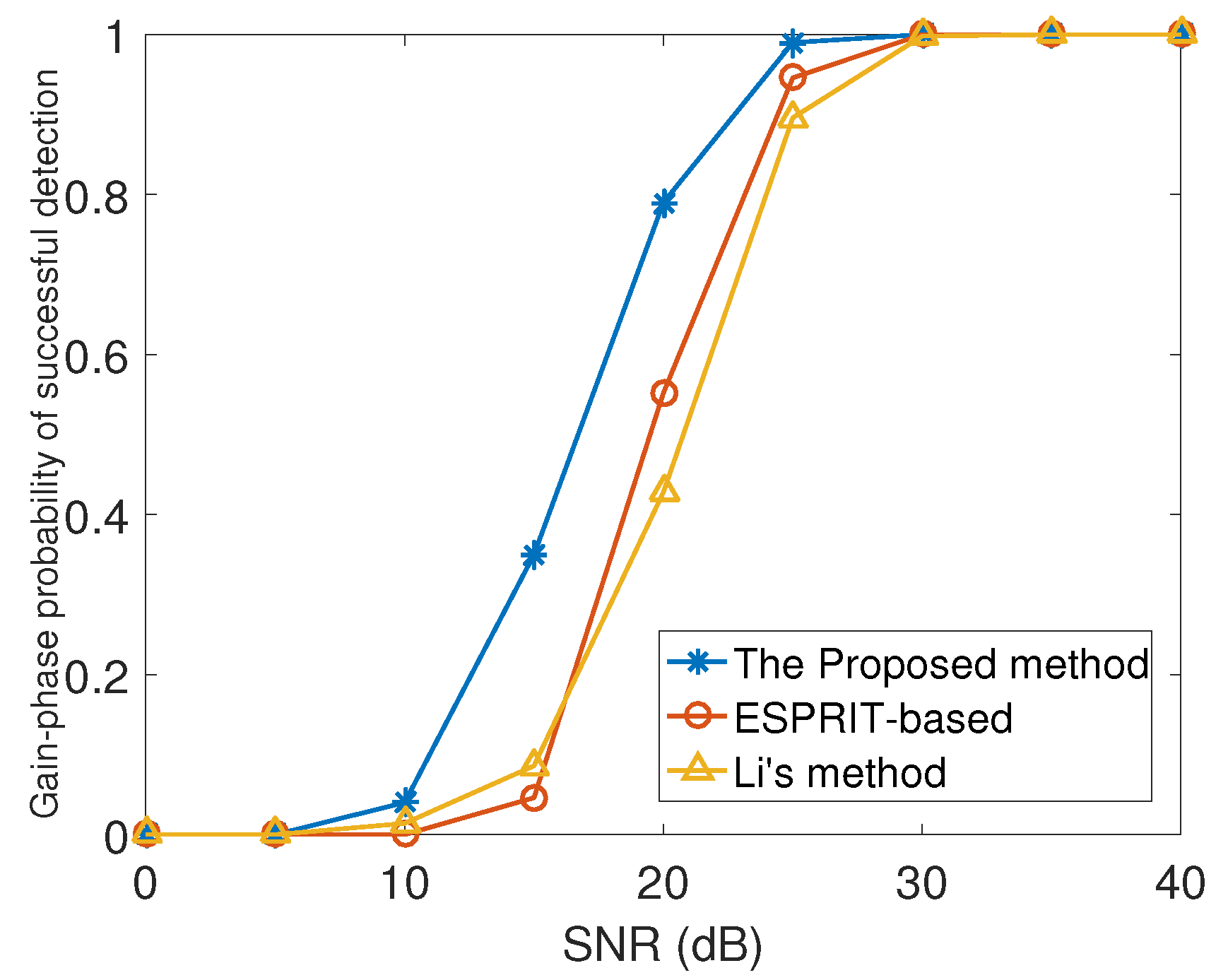
The proposed algorithm also has significant advantages in gain-phase error estimation, which can be verified by following numerical experiments. In this experiment, the number of snapshots $L=200$. According to Figure 12, we can see that the PSD of both methods augments with the rise of $\mathrm{SNR}$, and eventually reaches $100\%$. In addition, the PSD of the proposed method can achieve $100\%$ faster and the $\mathrm{SNR}$ threshold is lower. The reason why the PSD of the method in this paper is higher at the same $\mathrm{SNR}$ is that it eliminates the error accumulation effect in the gain-phase error estimation, so it can obtain more accurate gain-phase error estimation.

5. Conclusions

In this paper, a tensor-based joint angle-range estimation scheme is proposed for FDA-MIMO radar under the condition of gain-phase error. Moreover, the CRB is derived for angle-range estimation and gain-phase error estimation in FDA-MIMO radar. According to the idea of tensor analysis, the direction matrix containing target information is obtained by PARAFAC decomposition. Based on the direction matrix, the angle and range estimations of the target can be achieved. To remove the error accumulation influence in parameter estimation, the estimations of phase error and gain error are obtained separately. The array gain error can be calculated by using the characteristics of steering vectors among different targets. By calculating the estimated vector at the transmitter or receiver, the phase error estimation can be obtained. The proposed algorithm can eliminate the error accumulation effect in gain-phase error estimation. In addition, the proposed scheme can obtain superior estimation performance than the subspace algorithms by using the multidimensional characteristics of the data. The superiority of the proposed method for target parameter estimation in FDA-MIMO radar is proved by numerical experiments.