Abstract
The Earth’s ionosphere is a highly variable medium on a wide range of spatio-temporal scales. The responsiveness of plasma to the geomagnetic field and its changes gives rise to anisotropy, which may introduce wave-like characteristics while scanning the ionosphere with a line-of-sight towards a radio source. Previous studies of LOw Frequency ARray (LOFAR) calibration phase solutions report that the estimated beta parameter of a structure function calculated over 6–8 h of astronomical observation timespan has a range of values from 1.6 to 2.0, with an average of 1.89. Such difference between the observations could result from transient wave-like disturbances within the data. This study aims to present a method of signal processing of ionospheric calibration datasets that allows the extraction of a transient wave-like signal and discuss its possible origin. We use complex Morlet wavelet analysis applied to two 8 h observations corresponding to very quiet geomagnetic conditions. We find a wave-like signal in the interferometric Total Electron Content data even during periods of no geomagnetic activity. We suggest it results from the relative velocity changes between the LOFAR line-of-sight and a convection pattern in the ionospheric F layer. Establishing the relationship between quiet time ionosphere, geomagnetic field changes and LOFAR’s calibration solutions may prove beneficial to determination of the dominant signals in the more disturbed conditions, which we leave for future study.
1. Introduction
The influence of the ionosphere is recognized as a limiting factor on the quality of astronomical observations carried out with radio interferometers operating at low frequencies [1]. To this group of instruments belong the LOw Frequency ARray (LOFAR) with the center in the Netherlands, the Murchison Widefield Array (MWA) located in Australia, and the Very Large Array (VLA) in the United States. Studying the phase offsets introduced by the propagation of a signal through the ionospheric plasma may improve our understanding of processes taking place within this medium (e.g., [2,3,4]), and each of these radio interferometers contributes to this understanding in its own way due to differences in antenna setup, operating frequencies, and location. The MWA consists of densely populated antennas with baselines lengths up to 5 km (after upgrade into phase II) and operating at frequencies 75–300 MHz; the VLA interferometer has its antennas aligned with the Y letter, with a changeable distance between them. The VLA baselines are up to ca. 40 km, operating at frequencies between 75 MHz and 50 GHz. The LOFAR interferometer combines advantages of both network layouts, having a dense core with baselines up to 3 km and fewer remote stations of up to 100 km and international stations, yielding baselines of from hundreds of meters to thousands of kilometers. The operating frequency spans 30–250 MHz and is divided into two bands: low band (LBA, between 30 and 110 MHz) and high band (HBA, 120–250 MHz). The lower operating frequencies and higher number of baselines that cover different spatial scales allow LOFAR to uniquely contribute to the description of the state of the ionosphere at mid-latitudes.
Calibration solutions from LOFAR have been used before to characterize the state of the ionosphere throughout the observation duration (6–8 h) by providing a quantitative index which would indicate the expected quality of radio images [5]. It was achieved by analysis of the structure function over all possible LOFAR baselines, defined as:
where measures calibration phase as a function of spatial coordinates, and are the endpoints of a baseline, and denotes time average taken over the entire observation’s timespan. For turbulent medium this function exhibits a power-law behavior, with the slope described by parameter. The authors reported the estimated values of are higher than in the case of pure Kolmogorov turbulence, ranging from 1.6 to 2.0. Since the value of 2.0 is characteristic for waves, we suggest that these lower values may be the effect of transient wave-like disturbance signals within the data.
In this paper, we present a method to detect the wave-like transient signals. Since an interferometer measures phase differences, it is only sensitive to the differential TEC signal (dTEC) between the two endpoints of a baseline. The dTEC of unprecedented sensitivity (less than 0.001 TECU) is our input to a Continuous Wavelet Transform analysis. We expect this approach to better estimate disturbance parameters at different scales and provide a distinction between random small-scale noise and wave-like disturbances in the Earth’s ionosphere. We establish a relationship between the LOFAR solutions, geomagnetic field and ionospheric F region plasma drift data for the quiet geomagnetic conditions (Kp 0). This may serve as a reference for future investigations of dynamical changes occurring in the ionosphere and originating from space weather events with LOFAR.
2. Materials and Methods
We use two calibration datasets of the Epoch of Reionization (EoR) LOFAR key scientific project. They are nighttime observations of the bright radio source 3C196 (J2000:RA08h13m36s, Dec +48d13m03) starting on 6.12.2012 at 22:41:05 UT (L79324) and 1.01.2013 at 20:58:51 UT (L82655), each having a duration of 8 h. The calibration solutions have a time resolution of 10 seconds and cover frequencies between 115 and 189 MHz with 380 subbands, each with a 195.3 kHz width. The calibration procedure consists of finding the time and frequency dependent station amplitudes and phases that minimise the difference between a model of the instrument response to the bright radio source and the data. The resulting station calibration phases can then be separated into instrumental and ionospheric effects, converting the latter to differential TEC, by making use of the large bandwidth and the known frequency dependence:
where is a phase difference between baseline’s endpoints, is an observing frequency, is a difference in the TEC value integrated along the line-of-sight to the source between stations i and j expressed in TEC units (1 TECU equals m). A detailed description of the applied procedure to extract the ionospheric phase solutions can be found in [5].
The dTEC values for baselines referenced to the same station in the center of the LOFAR field are shown in Figure 1 for both observations.
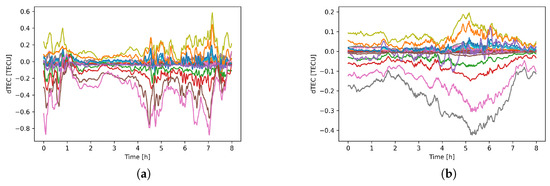
Figure 1.
Differential Total Electron Content (dTEC) variations with time for LOFAR baselines; (a) observation L79324, (b) observation L82655.
These two datasets differ in the number of the available stations, with L82655 having one extra station with respect to the L79324 network. This is due to the exclusion of baselines during the calibration step of astronomical observation processing. Stations’ flagging means that not the whole network is used for the analysis, affecting the distance/azimuth coverage of the baselines. LOFAR network layout is shown in Figure 2. Stations used in observation L79324 are marked with red stars (core stations with a blue star denoting the reference station) and black stars (remote stations). The additional remote station of L82655 is shown as a green star.
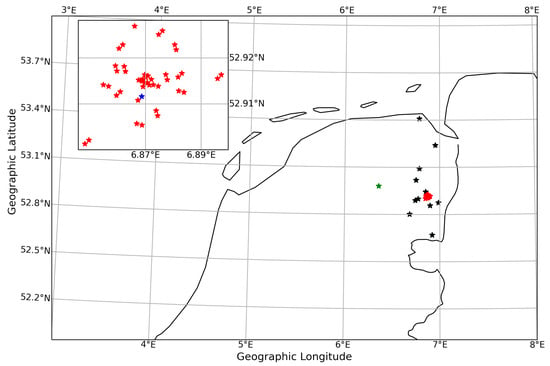
Figure 2.
LOFAR stations’ location; black stars denote remote stations, red stars: core stations, green star: additional station of L82655 observation (see text). Blue star in the inset map shows the reference station.
Wavelet Analysis
The Earth’s ionosphere is a highly variable medium in a wide range of spatial and temporal scales. Many transient signals may occur within 8 h, which is a typical duration of calibration observation for EoR data. Non-stationary signals can be successfully analyzed employing a Wavelet Transform. By definition, wavelet coefficients (W) are a convolution of the basis functions with the input signal, given by the following equation:
where a is a scale and b is translation. The resulting coefficients’ values measure the correlation between the wavelet and the input signal as a function of translation and scale.
Choosing an appropriate mother wavelet to create a family of scaled and translated wavelets plays a crucial role in the analysis. Assuming that a wave-like disturbance propagates within the LOFAR field of view, an interferometric signal of such disturbance would be a difference of the same wave at the endpoints of baselines, resulting in the original wave having sinusoidal amplitude modulation. We use the complex Morlet wavelet, which describes a sine wave with its amplitude modulated by a Gaussian window for a central frequency , bandwidth B and time t, given by the equation:
The bandwidth parameter, in our case, equals 1. Amplitudes of the complex W are calculated directly as , while the power of the signal P is calculated as .
For the subsequent analysis, we choose points based on the measure of intermittency, defined as:
where denotes a mean value taken over translation b. The strongest signal appears where there is a sudden jump in dTEC data, which may be caused by a change of the direction of the governing process (and thus the sensitivity of the baselines), or a change of the process itself. A wave-like field sensed by the LOFAR network for some period of time will also increase intermittency value, under a condition that this wave field is not present throughout the observation time span.
We calculate the mean value of the intermittency over all baselines. Figure 3 shows the mean intermittency for both observations. Next, we take a horizontal slice of the Figure 3 at 30 min central period, shown in Figure 4. For each observation, we identify the dominant peaks (numbers 1, 3 and 5) based on a condition that the minimum prominence of a peak equals 0.2. We then add two other time instances (numbers 2 and 4) for comparison, selected based on a width parameter of peak 3 and denoting its start and end time. We will also call these additional extrema points peaks in the following text. Table 1 shows the UT time of the selected peaks.
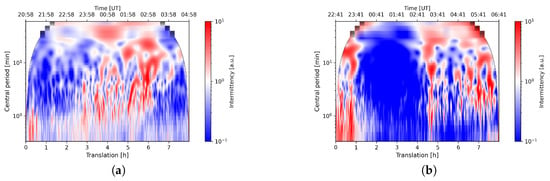
Figure 3.
Intermittency for observations (a) L82655, (b) L79324.
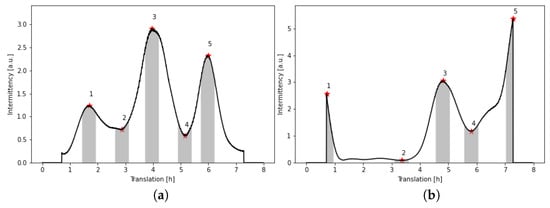
Figure 4.
Selection of time instances for analysis for observation (a) L82655, (b) L79324.

Table 1.
UT time of the peaks for the selected intervals.
For the analysis of spatial scales we convert the geodetic coordinates of the ionospheric pierce points into the local NED reference frame at an arbitrarily chosen height of 400 km, with spatial origin at the LOFAR reference station and temporal origin in the middle of the observation.
3. Results
We start by analyzing the L82655 observation. It can be seen in Figure 4 that this observation has more uniformly distributed peaks as compared to L79324. We also notice in Figure 3 an increase in the intermittency after 3 h from the beginning of the observation and propagation of the signal’s power towards longer periods with time. Figure 5 shows the spatial distribution of amplitudes for this observation, calculated for four different central periods: 3, 4, 12, and 27 min. Positions of the fields are centered at the local NED coordinate of the reference station for the time instances of the peaks shown in Figure 4, while each field is a combination of all available remote stations, with coordinates being a difference of baselines’ endpoints in the local NED coordinates. As the radio source is tracked, its pierce points move from east to west, so the easternmost position corresponds to the first instance.
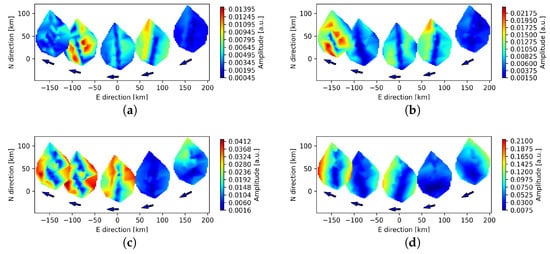
Figure 5.
Spatial distribution of amplitudes for remote stations of L82655 at 3, 4, 12 and 27 min central periods (panels (a–d), respectively). Arrows indicate the direction of LOS propagation.
We compare these results with observation L79324. Figure 6 shows the spatial distribution of amplitudes for the detected peaks. The missing station affects the number of possible baseline combinations, decreasing spatial scales in the E-W direction, making the network more elongated in the N-S direction. Comparison of baselines’ azimuth/length coverage for both observations is shown in Figure 7. As in L82655, most of the signal is concentrated in the second half of observation. However, stronger signals are recorded at the edges of the observation. Since this observation ends at 06:41 UT, it also spans the time of terminator propagation. Astronomical twilight starts around 05:30 UT for our pierce points field, and it can be seen as a sudden increase in the intermittency towards the end of observation (see Figure 4b).
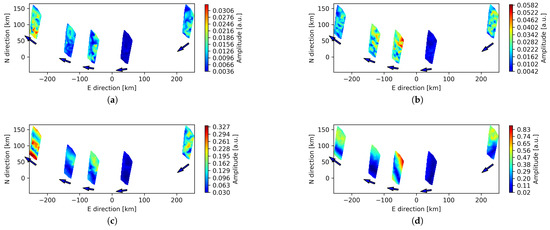
Figure 6.
Spatial distribution of amplitudes for remote stations of L79324 at 3, 4, 12 and 27 min central periods (panels (a–d), respectively). Arrows indicate the direction of LOS propagation.
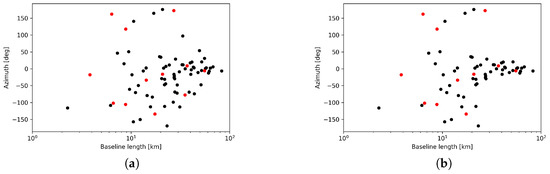
Figure 7.
Baselines’ azimuths and lengths distribution for all combinations of remote stations for (a) L82655 and (b) L79324. Red dots denote original baselines, black dots denote additional combinations.
LOS Geometry
We notice that the pattern of amplitudes visible in Figure 5 changes its direction almost with a constant speed of LOS propagation for the detected peaks. This change can be seen especially for the shorter filter lengths. The amplitude minima show N-S alignment for peak 3, which is approximately in the middle of the observation. At the same time, amplitude maxima do not have such a good alignment, exhibiting a perpendicular component. Comparing this peak at different central periods of the filter shows a change in the dominant direction across the scales, which may be caused either by a signal concentrated non-uniformly with respect to the peak time instance, by different sensitivity to spatial scales for different filter lengths, or by plotting artifacts due to interpolation. We investigate the interpolation effect by comparing the amplitudes of remote stations to the core stations, which are more densely and uniformly populated. The spatial distribution of the core stations amplitudes for peak 4 is shown in Figure 8. The rotation of the dominant direction is visible, thus excluding the interpolation effect.
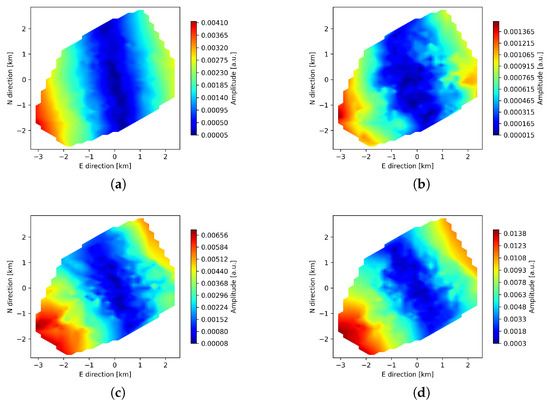
Figure 8.
Amplitudes of core stations for the peak 4 of L82655; panels (a–d) correspond to 3, 4, 12 and 27 min central periods, respectively.
We also note that due to the disturbances connected to the terminator, the effect of dominant direction propagation visible for L82655 (Figure 5) is not so readily detectable for L79324 (Figure 6). Observation L82655, however, is unique since the highest peak corresponds to the middle of observation time. If the observed effect originates from purely geometrical phenomena, the same directions should be visible for both observations at specific translation instances, as the radio source is at zenith in the middle of the observations. For this reason, we take translational values of L82655 peaks and apply them to L79324. Figure 9 and Figure 10 show the results at 4 min central period, with the color scale now normalized to the maximum value of amplitude in the field for each peak. It is then visible that the N-S alignment of amplitude minima can be detected in both observations, centered around peak 2 for L82655 and peak 3 for L79324. Such difference in time may indicate that the amplitude pattern depends on the relative movement of ionospheric plasma and LOFAR pierce points.
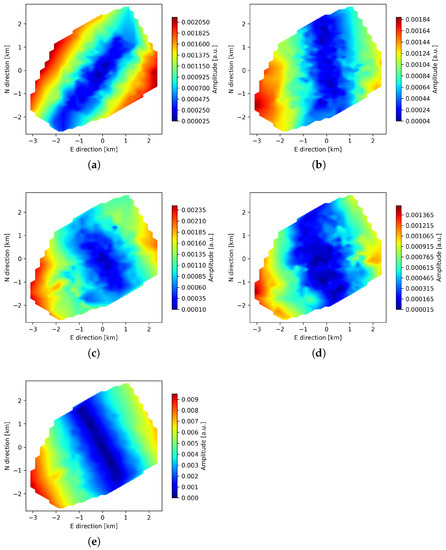
Figure 9.
Amplitudes of core stations for observation L82655 for peaks 1–5 of L82655 peaks set (panels (a–e)) at 4 min central period (see text).
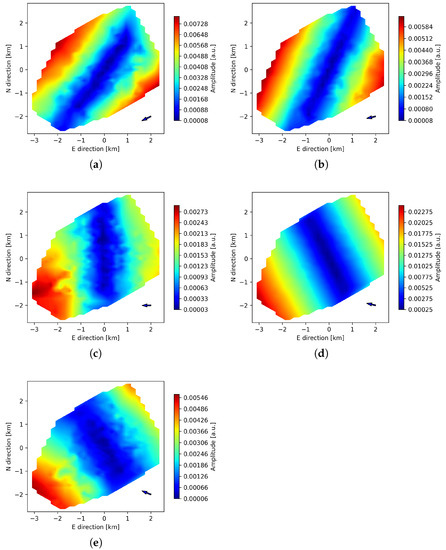
Figure 10.
Amplitudes of core stations for observation L79324 for peaks 1–5 of L82655 peaks set (panels (a–e)) at 4 min central period (see text).
4. Ionospheric Convection
The main, large scale drift of the quiet ionosphere is connected to the plasma convection pattern due to drift. It depends on the local time and the spatio-temporal structure of the geomagnetic field, the latter being affected by the geomagnetic activity. In the following subsections, we describe the overall conditions in the ionosphere based on geomagnetic data from Dourbes (DOU) and Wingst (WNG) observatories, auroral electrojet (AE) index, as well as plasma drift data from four digisondes of the GIRO network: Dourbes (DB), Juliusruhe (JR), Pruhonice (PQ) and Fairford (FF) [6]. Positions of the observatories used in the study and LOFAR pierce points of the reference station are shown in Figure 11. We compare it to the spatio-temporal changes detected with LOFAR solutions to establish the source of wave-like patterns in the dTEC.
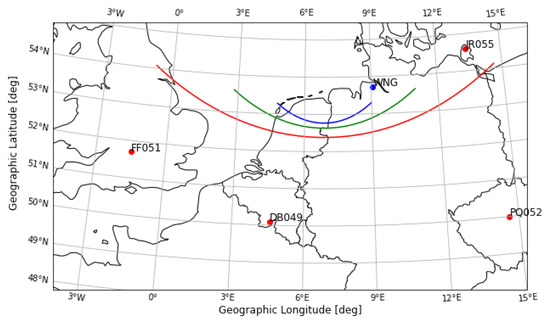
Figure 11.
Location of LOFAR pierce points (at 200, 400 and 800 km altitude marked with blue, green and red line, respectively) relative to the observatories used in the analysis. Red dots: stations that serve as a source of ionospheric plasma drift data; geomagnetic field data were obtained from the stations WNG and DOU (marked as DB049).
4.1. Geomagnetic Field
First, we characterize the overall geomagnetic field structure during the time of observations. Comparison of geomagnetic field values and geomagnetic activity expressed by auroral electrojet index (AE) between the two observations is shown in Figure 12. The third panel from the top shows the sum of input dTEC values for a set of the same LOFAR baselines for L82655 and L79324.
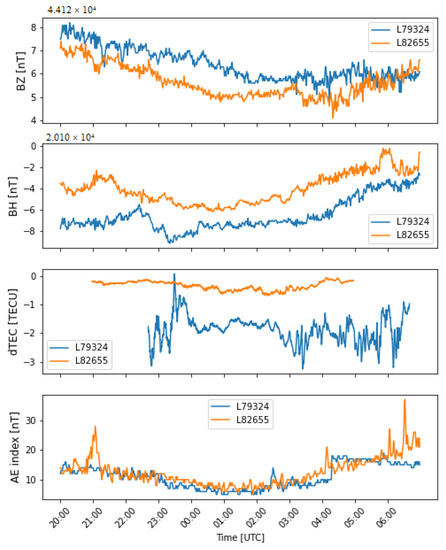
Figure 12.
Geomagnetic field for DOU station and LOFAR dTEC signal for both observations. From top to bottom: vertical component of geomagnetic field (BZ), horizontal component of geomagnetic field (BH), sum of dTEC values of LOFAR baselines, auroral electrojet index value (AE).
As seen in Figure 12, there are slightly different values of geomagnetic field vector during the two observations. The gradients detected in LOFAR baselines are higher for L79324, in correlation with lower value of horizontal component of the geomagnetic field vector. We note the increased variability in the L79324 observation till UT midnight, visible also in the horizontal magnetic component. Both observations have increased noise level in the magnetic field vector in the dawn hours due to terminator propagation, but only a part of this effect will be visible in L82655, spanning different UT hours than L79324.
In the Figure 12 the geomagnetic field vector is taken from DOU observatory. We see that even small changes in the field value correspond to changes in the LOFAR signal. The LOFAR LOS propagates with time, so the pierce points change their geomagnetic coordinates and the main field value. We then include the WNG observatory, which provides spatial information on the geomagnetic field.
In Figure 13 we present geomagnetic field component changes throughout the observation period for both observations with respect to their mean values: upper row corresponds to L82655 and lower row to L79324, while left and right columns show DOU and WNG data, respectively. Azimuth values given in each panel are calculated based on Principal Component Analysis (PCA) and correspond to the direction of the highest variance.
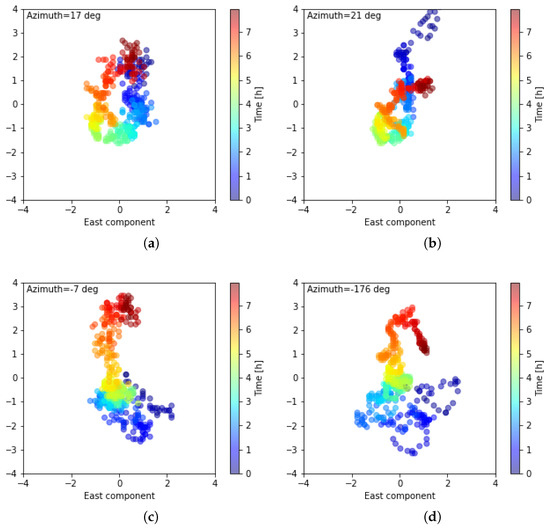
Figure 13.
Changes of the geomagnetic field with respect to the mean value of the observation timespan; (a) L82655, DOU observatory; (b) L82655, WNG observatory; (c) L79324, DOU observatory; (d) L79324, WNG observatory. Color scale shows time from the start of the observations.
It can be seen that in both observations, the low-frequency signal follows the rotational movement (more prominent for L82655). These two observations do not differ in geomagnetic coordinates (the pierce points locations are the same for L82655 and L79324), but there is a difference in Magnetic Local Time (MLT) coverage: L82655 reaches magnetic midnight after around 3 h and 15 min. In the case of ionospheric convection, around magnetic midnight, we would expect predominantly N-S plasma drift, which agrees with visible E-W change in the geomagnetic field. On the other hand, observation L79324 starts around one hour before magnetic midnight. We can see a hint of this E-W change at the beginning of the signal from the magnetometers. However, for the LOFAR amplitudes, this signal is hidden underneath the higher variance connected to the terminator propagation.
We determine the dominant azimuth of the observed LOFAR signals with PCA applied to the real part of LOFAR amplitudes. We project these real amplitudes of each baseline into North and East components for all time instances and solve for 2 dominant directions, which corresponds to fitting an ellipse into these data points. Results are presented in Figure 14. Panel (a), corresponding to L82655, shows a change of dominant direction with time in an organized manner. We can notice that the variance at the end of observation (red colors) is perpendicular to the slow variation of geomagnetic field. Panel (b), which shows the real part of the L79324 signal, is more chaotic, and the fitted directions are governed mainly by the signals at the beginning and end of the observation.
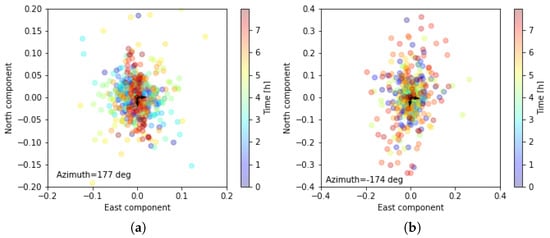
Figure 14.
LOFAR amplitudes for 3 min central period for (a) L82655 and (b) L79324. Color scale shows time from the start of observation. Black arrows indicate the dominant directions calculated from Principal Components Analysis (PCA), with the azimuth value provided for the direction explaining majority of variance.
4.2. Plasma Drift
As the last step, we analyze the plasma drift data. Since the wavelet coefficients result from time integration, they are affected not only by density gradients, but also their evolution in time. If temporal changes in the F layer cause their time evolution, we should see a correlation with the changes in the behavior of plasma drift velocity data.
Figure 15 and Figure 16 show the plasma velocity of F region as detected with four digisondes of the GIRO network (see Figure 11) for L82655 and L79324, respectively.
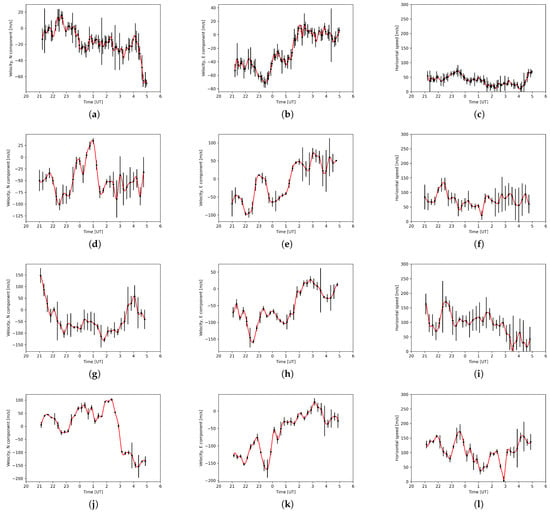
Figure 15.
F layer plasma drift velocity data for L82655 with interpolated values (red line) for the North component, East component and horizontal speed of (a–c) DB, (d–f) JR, (g–i) PQ and (j–l) FF stations, respectively.
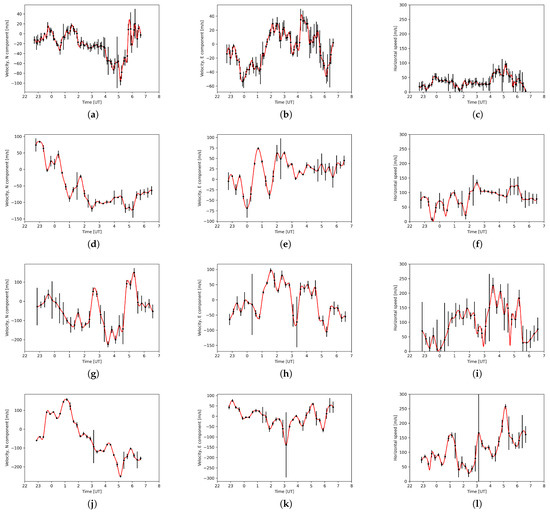
Figure 16.
F layer plasma drift velocity data for L79324 with interpolated values (red line) for the North component, East component and horizontal speed of (a–c) DB, (d–f) JR, (g–i) PQ and (j–l) FF stations, respectively.
We interpolate the datasets onto 1 min intervals using cubic spline interpolation. The time series show temporal variations of plasma drift velocity with interpolated values indicated by a red line.
Taking real parts of LOFAR wavelets coefficients at 3 and 12 min central periods for half-hour intervals, sliding every one minute, and solving for dominant directions with PCA, we obtain a temporal change of dominant disturbances directions. The calculated azimuths for L82655 are presented in Figure 17, with panel (a) being a principal component for 3 min central period, panel (b): principal component of 12 min central period. Color scale indicates the ratio of explained variance to the total variance of the signal. Figure 18 shows the same for observation L79324.
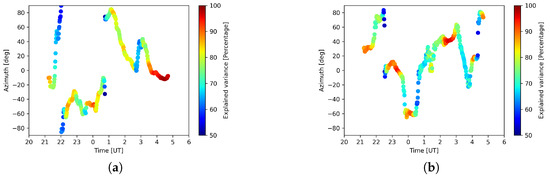
Figure 17.
L82655 PCA azimuths for principal components (a) at 3 min central period and (b) at 12 min central period. Color scale shows percentage of signal’s variance explained by the components.
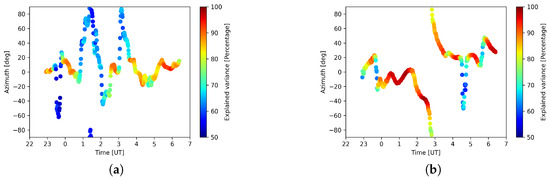
Figure 18.
L79324 PCA azimuths for principal components (a) at 3 min central period and (b) at 12 min central period. Color scale shows percentage of signal’s variance explained by the components.
Figure 19 and Figure 20 show the spatial distribution of plasma drift velocities vectors (colored lines), isolines of horizontal drift velocity as blue dashed lines, PCA directions at 4 min central period as red arrows (scaled with explained variance), and LOFAR LOS propagation direction as a blue arrow, for the chosen peaks of L82655 and L79324, respectively.
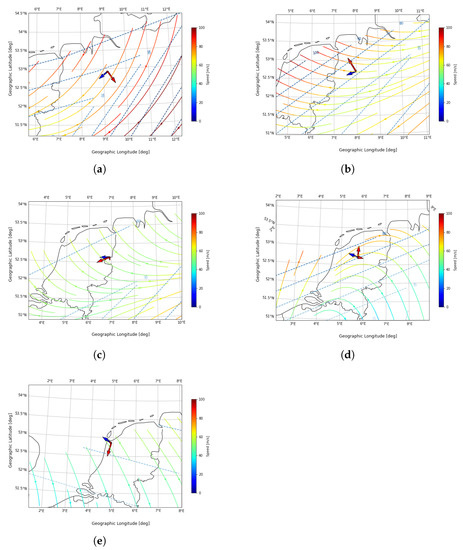
Figure 19.
Spatial distribution of plasma drift velocity for the peaks 1-5 (panels (a–e), respectively) of L82655. Streamlines show plasma velocity vectors based on four digisondes (outside the map’s scope), blue lines: isolines of horizontal speed. Blue arrow: LOS propagation direction, red arrows: fitted directions of the disturbances based on 4 min central period wavelet coefficients, scaled by the percentage of explained variance.
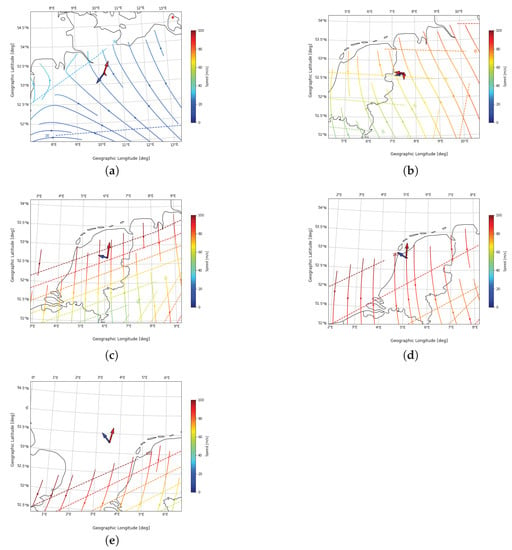
Figure 20.
Spatial distribution of plasma drift velocity for the peaks 1-5 (panels (a–e), respectively) of L79324. Streamlines show plasma velocity vectors based on four digisondes (outside the map’s scope), blue lines: isolines of horizontal speed. Blue arrow: LOS propagation direction, red arrows: fitted directions of the disturbances based on 4 minutes central period wavelet coefficients, scaled by the percentage of explained variance.
In Figure 19, showing results for L82655, we can see that for panels (a), (b) and (e), corresponding to peak 1, 2 and 5, there is an agreement between the dominant direction of LOFAR disturbances and the plasma drift velocity gradients. Panels (c) and (d) do not show this alignment. Instead, peak 3 presented in panel (c) shows direction aligned with the velocity isoline, while peak 4 in panel (d) has dominant directions aligned with and perpendicular to the LOS velocity. This peak also shows that the dominant component explains just slightly more observed variance than the secondary component, indicated by the similar lengths of the red arrows. Different behavior of peaks 3, corresponding to 00:56 UT, may be connected to rapid changes in the disturbance’s azimuth (and primary components capturing some average values) or to change in the dominant effect: detecting the small-scale density structures drifting in the plasma drift direction. Comparing this with station JR in Figure 15, we see the sudden direction change due to change in the north component of the velocity vector, indicating the influence of temporal plasma flow changes.
Peak 4, on the other hand, corresponding to 2:07 UT, due to high gradients in the plasma speed and temporal changes of the plasma flow field, may exhibit more complicated behavior, indicated by two directions explaining a similar percentage of variance. It is worth noting that this peak, as well as peak 2, were added for the comparison. They would not be considered if we chose peaks based on the requirement of the intermittency value higher than 1.
Results for observation L79324 are shown in Figure 20. Peak 1 in panel (a) corresponds to 23:23 UT. This peak is on the border of the cone of influence for a central period of 30 min, used for choosing the peaks. We suggest that the real peak for the disturbance, which would allow for spatial analysis, occurred earlier. This would agree with changes in the horizontal component of the geomagnetic field, presented in Figure 12.
Peak 2 does not show any arrows. The intermittency value for this peak was very low, and it was added just for comparison. It corresponds to 02:02 UT and includes low plasma speeds from ionosonde data in its interval. Combined with LOS propagation almost along the speed isoline, it can yield results much below the intermittency of 1.
Peaks 3, 4 and 5 in panels (c)–(e) show more pronounced agreement with the plasma velocity streamlines. Peak 3 at 3:29 UT marks the beginning of this behavior, achieving the best alignment at peaks 4 and 5. For this part of the L79324 observation, we notice high values of the N-S plasma velocity. In this case, the detected dominant direction can be caused by drifting small-scale density structures created at the terminator, and the propagation of LOS along the velocity gradient would be a secondary effect.
5. Discussion
LOFAR calibration solutions were investigated in [5] to establish a single parameter that would characterize the effect of the ionosphere on noise levels in astronomical observations, based on 2D structure function investigations of the whole observation duration. The authors report for L79324 a diffractive scale of 4.3 km, with the major axis having 5.8 ± 0.2 km and direction 158.9 ± 1.9 degrees (azimuth of ca. −70 degrees). The ratio of structures aligned with the main geomagnetic field direction to the perpendicular direction (fa) is reported to be 3.2. Since in this analysis it is the minor axis that corresponds to the highest variability in dTEC, the direction that should be compared to our results corresponds to the azimuth of around 20 degrees. Similar values can be seen in the Figure 18 for the central period of 12 min. In the case of L82655, the major axis has a length of 18.0 ± 0.4 km, minor axis equals 9.5 ± 0.3 km, giving a diffraction scale of 12.4 km. The direction of the major axis is 122.5 ± 1.9 degrees (azimuth ca. −33 degrees), and fa equals 1.5. This would indicate the azimuth of the highest variability to equal 57 degrees. Comparing it with Figure 17 and Figure 19, where we can see a range of dominant directions that change with time, we suggest that this value is a result of averaging over low-frequency temporal changes of the ionospheric convection pattern. Different magnetic local time coverage between the observations would also explain the difference in reported directionality, including the fa ratio. We show that the average direction of L79324 is governed by a higher power signal at the edges of the observation, with the influence of terminator propagation in the dawn hours. Small-scale density structures drift is also reflected in the smaller diffractive scale for this observation, compared to L82655.
Worth noting is also the behavior of the velocity field and disturbance direction from LOFAR at around ca. 2:30–3:00 UT for L82655 and L79324. The dominant directions of LOFAR show alignment with the main geomagnetic field direction. While there may be different possible explanations for this effect, including interaction with upward propagating gravity waves, we note its time coincidence with statistical times of inter-hemispheric field-aligned currents (IHFACs). The existence of such currents has been studied f.e. in ([7,8]). Combining more LOFAR observations would allow us to determine if these currents could be detectable in the calibration solutions.
6. Conclusions
In this study we presented a method for dynamical investigations of the ionospheric conditions based on calibration phase solutions. We applied it to two very quiet geomagnetically datasets in order to detect dominant signals during periods of no activity. Our analysis of LOFAR datasets shows that even for the quietest geomagnetic conditions, the Earth’s ionosphere is a source of apparent wave-like disturbances detected within the phase solutions. They arise from an interplay between spatio-temporal changes in the ionospheric plasma drift velocity, line-of-sight propagation across the ionosphere, and small-scale density structures that drift within the ionospheric F layer or possibly even radially out of the F layer along the geomagnetic field lines. The general agreement of LOFAR calibration solutions with data from ionosondes and magnetometers shows that the calibration solutions could complement other datasets with the medium and small scales of disturbances. Establishing a relationship between changes in the ionosphere and LOFAR’s response for different geomagnetic conditions could support the existing calibration routine of astronomical observations while yielding sensitive measurements for the purpose of space weather studies.
Author Contributions
Conceptualization, K.B., M.M.; methodology, K.B.; software, K.B.; validation, M.M., M.G. and H.R.; formal analysis, K.B.; investigation, K.B.; resources, M.M., K.B., M.G.; data curation, M.M.; writing—original draft preparation, K.B.; writing—review and editing, M.M.; visualization, K.B.; supervision, H.R., M.G.; funding acquisition, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded in the frame of the 6/E-73/SPUB/SP/2019. We thank the Ministry of Science and Higher Education (MSHE), Poland for granting funds for the Polish contribution to the International LOFAR Telescope (MSHE decision no. DIR/WK/2016/2017/05-1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
LOFAR data presented in the article are made available upon request by the corresponding author.
Acknowledgments
We would like to thank the EoR team for making the LOFAR data available. We acknowledge using data of the Global Ionosphere Radio Observatory (GIRO), http://giro.uml.edu/ (accessed on 4 February 2022). The plasma drift velocity data used for this research can be obtained from the corresponding GIRO databases.We would like to thank the INTERMAGNET network for the free access to Wingst and Dourbes geomagnetic observatory data (www.intermagnet.org, accessed on 29 January 2022) and WDC for geomagnetism, Kyoto, for the provisional AE index data (https://wdc.kugi.kyoto-u.ac.jp/, accessed on 9 December 2021).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| LOFAR | Low Frequency Array |
| TEC | Total Electron Content |
| dTEC | differential Total Electron Content |
| LOS | Line-of-sight |
| PCA | Principal components analysis |
References
- Intema, H.; Tol, S.; Cotton, W.; Cohen, A.; Bemmel, I.; Rottgering, H. Ionospheric Calibration of Low Frequency Radio Interferometric Observations using the Peeling Scheme: I. Method Description and First Results. Astron. Astrophys. 2009, 501, 1185–1205. [Google Scholar] [CrossRef]
- Jacobson, A.R.; Erickson, W.C. Wavenumber-resolved observations of ionospheric waves using the very large array radiotelescope. Plant. Space Sci. 1992, 40, 447–455. [Google Scholar] [CrossRef]
- Jordan, C.; Murray, S.; Trott, C.; Wayth, R.; Mitchell, D.; Rahimi, M.; Pindor, B.; Procopio, P.; Morgan, J. Characterisation of the ionosphere above the Murchison Radio Observatory using the Murchison Widefield Array. Mon. Notices R. Astron. Soc. 2017, 471, 3974–3987. [Google Scholar] [CrossRef] [Green Version]
- Loi, S.T.; Trott, C.M.; Murphy, T.; Cairns, I.H.; Bell, M.; Hurley-Walker, N.; Morgan, J.; Lenc, E.; Offringa, A.R.; Feng, L.; et al. Power spectrum analysis of ionospheric fluctuations with the Murchison Widefield Array. Radio Sci. 2015, 50, 574–597. [Google Scholar] [CrossRef]
- Mevius, M.; van der Tol, S.; Pandey, V.N.; Vedantham, H.K.; Brentjens, M.A.; de Bruyn, A.G.; Abdalla, F.B.; Asad, K.M.B.; Bregman, J.D.; Brouw, W.N.; et al. Probing ionospheric structures using the LOFAR radio telescope. Radio Sci. 2016, 51, 927–941. [Google Scholar] [CrossRef] [Green Version]
- Reinisch, B.; Galkin, I.; Belehaki, A.; Paznukhov, V.; Huang, X.; Altadill, D.; Buresova, D.; Mielich, J.; Verhulst, T.; Stankov, S.; et al. Pilot Ionosonde Network for Identification of Traveling Ionospheric Disturbances. Radio Sci. 2018, 53, 365–378. [Google Scholar] [CrossRef]
- Park, J.; Stolle, C.; Yamazaki, Y.; Rauberg, J.; Michaelis, I.; Olsen, N. Diagnosing low-/mid-latitude ionospheric currents using platform magnetometers: CryoSat-2 and GRACE-FO. Earth Planets Space 2020, 72, 1–18. [Google Scholar] [CrossRef]
- Park, J.; Yamazaki, Y.; Lühr, H. Latitude Dependence of Interhemispheric Field-Aligned Currents (IHFACs) as Observed by the Swarm Constellation. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027694. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).