Three-Dimensional Surface Displacements of the 8 January 2022 Mw6.7 Menyuan Earthquake, China from Sentinel-1 and ALOS-2 SAR Observations
Abstract
:1. Introduction
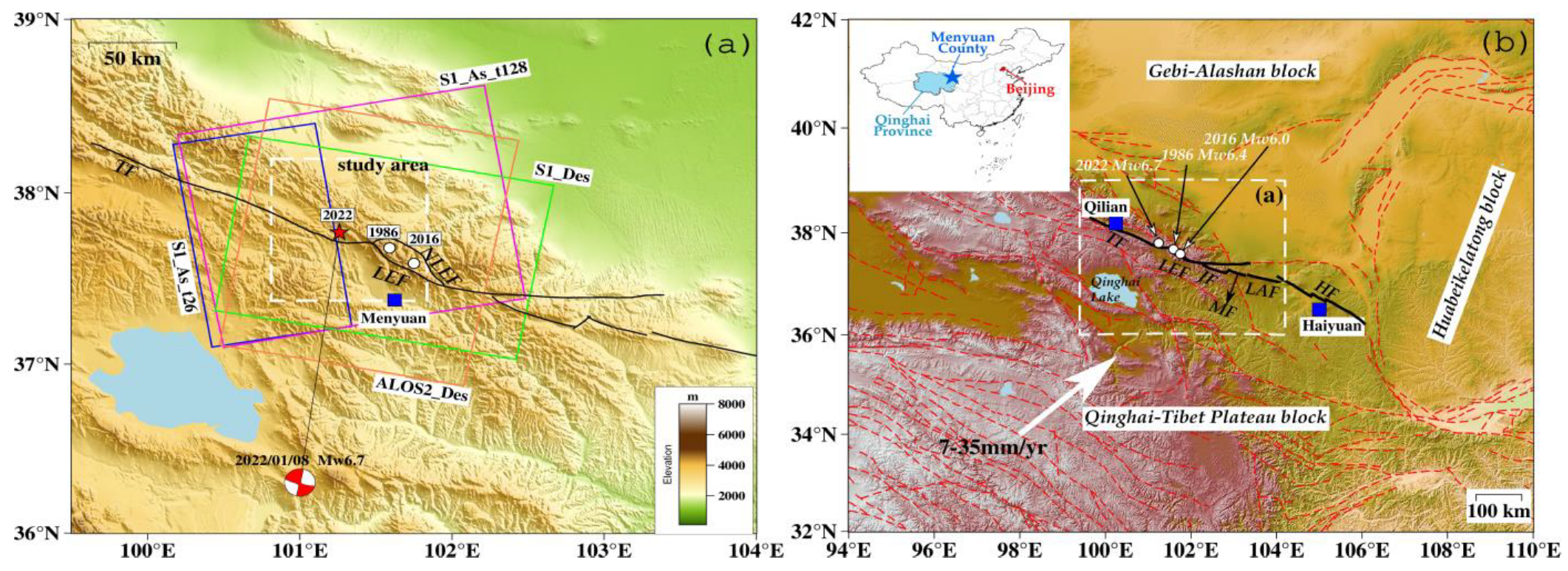
2. Data and Methods
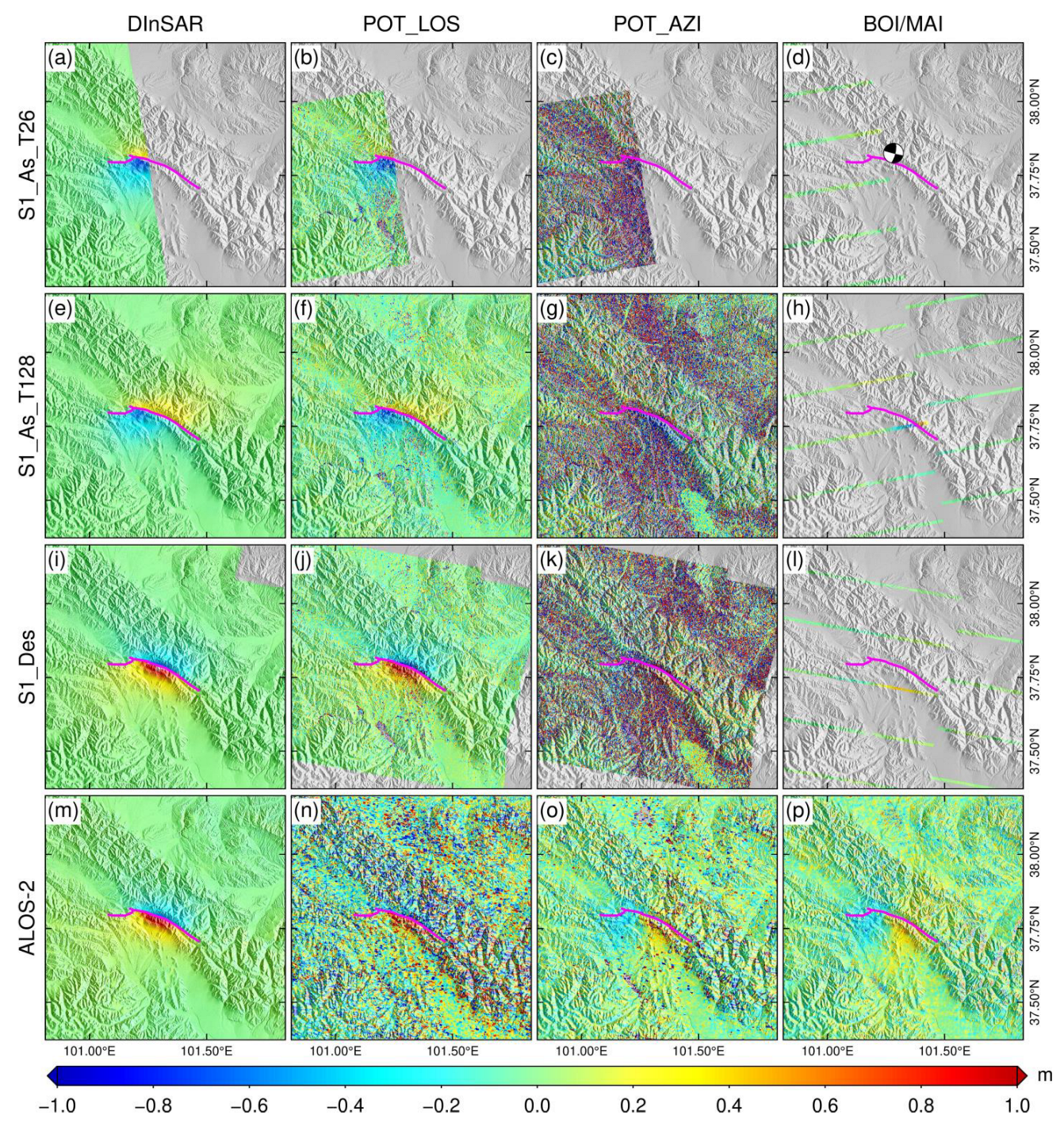
2.1. The Used SAR Data
2.2. The SM-VCE Method
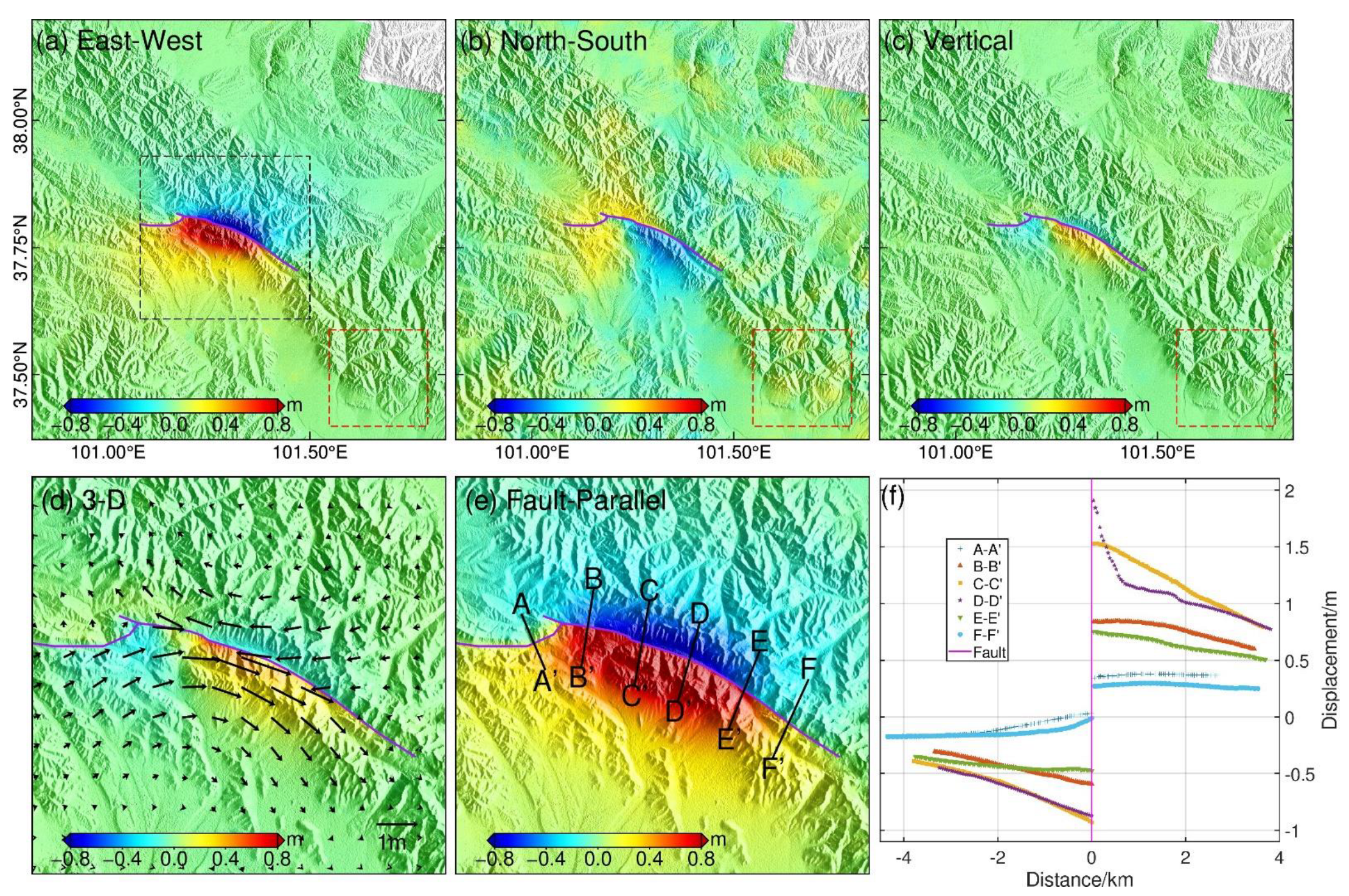
3. Results
4. Discussion
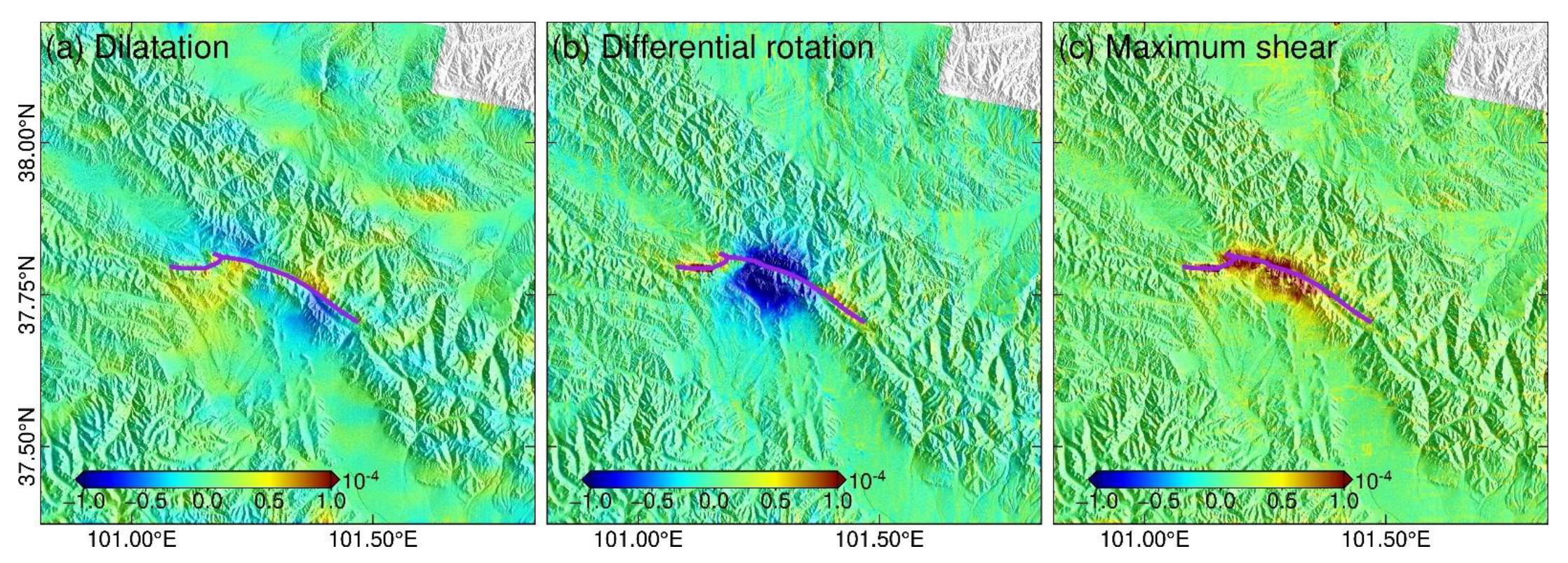
4.1. Three Strain Invariants of the 2022 Menyuan Earthquake
4.2. The Contributions of Different SAR Observations to the 3D Displacements
4.3. Calculating the Displacements/Strains near the Ruptured Fault Zone
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y.; Guo, X.; Feng, L. Relocation and focal mechanism solutions of the Ms6.9 Menyuan earthquake sequence on January 8, 2022 in Qinghai Province. Acta Seismol. Sin. 2022, 44, 1–16. [Google Scholar] [CrossRef]
- Li, Z.; Han, B.; Liu, Z.; Zhang, M.; Yu, C.; Chen, B.; Liu, H.; Du, J.; Zhang, S.; Zhu, W.; et al. Source Parameters and Slip Distributions of the 2016 and 2022 Menyuan, Qinghai Earthquakes Constrained by InSAR Observations. Geomat. Inf. Sci. Wuhan Univ. 2022. [Google Scholar] [CrossRef]
- Zheng, W.-J.; Zhang, P.-Z.; He, W.-G.; Yuan, D.-Y.; Shao, Y.-X.; Zheng, D.-W.; Ge, W.-P.; Min, W. Transformation of displacement between strike-slip and crustal shortening in the northern margin of the Tibetan Plateau: Evidence from decadal GPS measurements and late Quaternary slip rates on faults. Tectonophysics 2013, 584, 267–280. [Google Scholar] [CrossRef]
- Guo, P.; Han, Z.; An, Y.; Jiang, W.; Mao, Z.; Feng, W. Activity of the Lenglongling fault system and seismotectonics of the 2016 MS6.4 Menyuan earthquake. Sci. China Earth Sci. 2017, 60, 929–942. [Google Scholar] [CrossRef]
- Jiang, W.-L.; Li, Y.-S.; Tian, Y.-F.; Han, Z.-J.; Zhang, J.-F. Research of seismogenic structure of the Menyuan MS6.4 earthquake on January 21, 2016 in Lenglongling area of NE Tibetan plateau. Seismol. Egology 2017, 39, 536. [Google Scholar] [CrossRef]
- Qu, W.; Gao, Y.; Chen, H.-L.; Liang, S.-C.; Han, Y.-X.; Zhang, Q.; Wang, Q.-L.; Hao, M. Review on Characteristics of Present Crustal Tectonic Movement and Deformation in Qinghai-Tibet Plateau, China Using GPS High Precision Monitoring Data. J. Earth Sci. Environ. 2021, 43, 182–204. [Google Scholar] [CrossRef]
- Hao, M.; Li, Y.; Zhuang, W. Crustal movement and strain distribution in East Asia revealed by GPS observations. Sci. Rep. 2019, 9, 16797. [Google Scholar] [CrossRef] [PubMed]
- Gaudemer, Y.; Tapponnier, P.; Meyer, B.; Peltzer, G.; Shunmin, G.; Zhitai, C.; Huagung, D.; Cifuentes, I. Partitioning of crustal slip between linked, active faults in the eastern Qilian Shan, and evidence for a major seismic gap, the ‘Tianzhu gap’, on the western Haiyuan Fault, Gansu (China). Geophys. J. Int. 1995, 120, 599–645. [Google Scholar] [CrossRef] [Green Version]
- Lasserre, C.; Gaudemer, Y.; Tapponnier, P.; Mériaux, A.S.; Van der Woerd, J.; Daoyang, Y.; Ryerson, F.; Finkel, R.; Caffee, M. Fast late Pleistocene slip rate on the Leng Long Ling segment of the Haiyuan fault, Qinghai, China. J. Geophys. Res. Solid Earth 2002, 107, ETG 4-1–ETG 4-15. [Google Scholar] [CrossRef]
- Li, Y.; Gan, W.; Wang, Y.; Chen, W.; Zhang, K.; Liang, S.; Zhang, Y. Seismogenic Structure of the 2016 Ms6.4 Menyuan Earthquake and its Effect on the Tianzhu Seismic Gap. J. Geod. Geodyn. 2017, 37, 792. [Google Scholar] [CrossRef]
- Yang, H.; Wang, D.; Guo, R.; Xie, M.; Zang, Y.; Wang, Y.; Yao, Q.; Cheng, C.; An, Y.; Zhang, Y. Rapid report of the 8 January 2022 Ms 6.9 Menyuan earthquake, Qinghai, China. Earthq. Res. Adv. 2022, 100113. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the Landers Earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef] [Green Version]
- Bechor, N.B.D.; Zebker, H.A. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006, 33, 275–303. [Google Scholar] [CrossRef] [Green Version]
- Grandin, R.; Klein, E.; Métois, M.; Vigny, C. 3D displacement field of the 2015 MW8.3 Illapel earthquake (Chile) from across- and along-track Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2016, 43, 2552–2561. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.S.; Lu, Z.; Won, J.S.; Poland, M.P.; Miklius, A. Mapping Three-Dimensional Surface Deformation by Combining Multiple-Aperture Interferometry and Conventional Interferometry: Application to the June 2007 Eruption of Kilauea Volcano, Hawaii. IEEE Geosci. Remote Sens. Lett. 2011, 8, 34–38. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31, 169–178. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Hu, J.; Li, Z.; Zhu, J.J.; Sun, Q.; Gan, J. A Method for Measuring 3-D Surface Deformations With InSAR Based on Strain Model and Variance Component Estimation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 239–250. [Google Scholar] [CrossRef]
- Liu, J.; Hu, J.; Xu, W.; Li, Z.; Zhu, J.; Ding, X.; Zhang, L. Complete three-dimensional co-seismic deformation fields of the 2016 Central Tottori earthquake by integrating left- and right-looking InSAR with the improved SM-VCE method. J. Geophys. Res. Solid Earth 2019, 124, 12099–12115. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Liu, J.; Li, Z.; Zhu, J.; Wu, L.; Sun, Q.; Wu, W. Estimating three-dimensional coseismic deformations with the SM-VCE method based on heterogeneous SAR observations: Selection of homogeneous points and analysis of observation combinations. Remote Sens. Environ. 2021, 255, 112298. [Google Scholar] [CrossRef]
- Liu, J.; Hu, J.; Li, Z.; Ma, Z.; Wu, L.; Jiang, W.; Feng, G.; Zhu, J. Complete three-dimensional coseismic displacements due to the 2021 Maduo earthquake in Qinghai Province, China from Sentinel-1 and ALOS-2 SAR images. Sci. China Earth Sci. 2022, 65, 1–11. [Google Scholar] [CrossRef]
- Fialko, Y. Evidence of fluid-filled upper crust from observations of postseismic deformation due to the 1992 MW7.3 Landers earthquake. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, A.; Sandwell, D.; Fialko, Y.; Sichoix, L. The 1999 (MW7.1) Hector Mine, California, earthquake: Near-field postseismic deformation from ERS interferometry. Bull. Seismol. Soc. Am. 2002, 92, 1433–1442. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.; Zhu, J.; Zhang, L.; Sun, Q. 3D coseismic Displacement of 2010 Darfield, New Zealand earthquake estimated from multi-aperture InSAR and D-InSAR measurements. J. Geod. 2012, 86, 1029–1041. [Google Scholar] [CrossRef]
- Vaníček, P.; Grafarend, E.W.; Berber, M. Short Note: Strain invariants. J. Geod. 2008, 82, 263–268. [Google Scholar] [CrossRef]
- Guglielmino, F.; Nunnari, G.; Puglisi, G.; Spata, A. Simultaneous and Integrated Strain Tensor Estimation From Geodetic and Satellite Deformation Measurements to Obtain Three-Dimensional Displacement Maps. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1815–1826. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.; Sun, Q.; Zhu, J.J.; Ding, X.L. Three-Dimensional Surface Displacements From InSAR and GPS Measurements With Variance Component Estimation. IEEE Geosci. Remote Sens. Lett. 2012, 9, 754–758. [Google Scholar] [CrossRef]
- Hu, S.W.; Xiao, B.L. Modern Theory and Application of Surveying Data Processing; Surveying and Mapping Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Yuan, D.; Zhang, P.; Liu, B.; Gan, W.; Mao, F.; Wang, Z.; Zheng, W.; Guo, H. Geometrical Imagery and Tectonic Transformation of Late Quaternary Active Tectonics in Northeastern Margin of Qinghai-Xizang Platean. Acta Geol. Sin. 2004, 78, 270. (In Chinese) [Google Scholar]
- Liu, J.; Hu, J.; Li, Z.; Sun, Q.; Ma, Z.; Zhu, J.; Wen, Y. Dynamic Estimation of Multi-Dimensional Deformation Time Series from InSAR Based on Kalman Filter and Strain Model. IEEE Trans. Geosci. Remote Sens. 2022, 60. [Google Scholar] [CrossRef]
- Clarke, P.J.; Davies, R.R.; England, P.C.; Parsons, B.; Billiris, H.; Paradissis, D.; Veis, G.; Cross, P.A.; Denys, P.H.; Ashkenazi, V.; et al. Crustal strain in central Greece from repeated GPS measurements in the interval 1989–1997. Geophys. J. Int. 1998, 135, 195–214. [Google Scholar] [CrossRef] [Green Version]
- Lin, K.C.; Hu, J.C.; Ching, K.E.; Angelier, J.; Rau, R.J.; Yu, S.B.; Tsai, C.H.; Shin, T.C.; Huang, M.H. GPS crustal deformation, strain rate and seismic activity after the 1999 Chi-Chi earthquake in Taiwan. J. Geophys. Res. Solid Earth 2010, 115, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.-K.; Jackson, D.D.; Ge, B.X. Crustal deformation across and beyond the Los Angeles basin from geodetic measurements. J. Geophys. Res. Solid Earth 1996, 101, 27957–27980. [Google Scholar] [CrossRef]
- Mehrabi, H. Three-dimensional strain descriptors at the Earth’s surface through 3D retrieved co-event displacement fields of differential interferometric synthetic aperture radar. J. Geod. 2021, 95, 39. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Q.J.; Li, Z.W.; Xie, R.A.; Zhang, X.Q.; Sun, Q. Retrieving three-dimensional coseismic displacements of the 2008 Gaize, Tibet earthquake from multi-path interferometric phase analysis. Nat. Hazards 2014, 73, 1311–1322. [Google Scholar] [CrossRef]
- Gan, J.; Hu, J.; Li, Z.; Yang, C.; Liu, J.; Sun, Q.; Zheng, W. Mapping three-dimensional co-seismic surface deformations associated with the 2015 Mw7.2 Murghab earthquake based on InSAR and characteristics of crustal strain. Sci. China Earth Sci. 2018, 61, 1451–1466. [Google Scholar] [CrossRef]
- Zhao, D.; Qu, C.; Chen, H.; Shan, X.; Song, X.; Gong, W. Tectonic and Geometric Control on Fault Kinematics of the 2021 Mw7. 3 Maduo (China) Earthquake Inferred From Interseismic, Coseismic, and Postseismic InSAR Observations. Geophys. Res. Lett. 2021, 48, e2021GL095417. [Google Scholar] [CrossRef]
- Samsonov, S.; D’Oreye, N. Multidimensional time-series analysis of ground deformation from multiple InSAR data sets applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Ding, X.L.; Li, Z.W.; Zhu, J.J.; Sun, Q.; Zhang, L. Kalman-Filter-Based Approach for Multisensor, Multitrack, and Multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4226–4239. [Google Scholar] [CrossRef]
- Liu, J.; Hu, J.; Burgmann, R.; Li, Z.; Sun, Q.; Ma, Z. A Strain-Model Based InSAR Time Series Method and its Application to The Geysers Geothermal Field, California. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021939. [Google Scholar] [CrossRef]
- Pepe, A.; Solaro, G.; Calo, F.; Dema, C. A Minimum Acceleration Approach for the Retrieval of Multiplatform InSAR Deformation Time Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3883–3898. [Google Scholar] [CrossRef]
- Samsonov, S.; D’Oreye, N. Multidimensional Small Baseline Subset (MSBAS) for Two-Dimensional Deformation Analysis: Case Study Mexico City. J. Geod. 2017, 43, 318–329. [Google Scholar] [CrossRef]
- Morishita, Y.; Kobayashi, T.; Yarai, H. Three-dimensional deformation mapping of a dike intrusion event in Sakurajima in 2015 by exploiting the right- and left-looking ALOS-2 InSAR. Geophys. Res. Lett. 2016, 43, 4197–4204. [Google Scholar] [CrossRef] [Green Version]
- Fialko, Y.; Sandwell, D.; Simons, M.; Rosen, P. Three-dimensional deformation caused by the Bam, Iran, earthquake and the origin of shallow slip deficit. Nature 2005, 435, 295–299. [Google Scholar] [CrossRef]
- Funning, G.J.; Parsons, B.; Wright, T.J.; Jackson, J.A.; Fielding, E.J. Surface displacements and source parameters of the 2003 Bam (Iran) earthquake from Envisat advanced synthetic aperture radar imagery. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Jo, M.J.; Jung, H.S.; Won, J.S. Measurement of precise three-dimensional volcanic deformations via TerraSAR-X synthetic aperture radar interferometry. Remote Sens. Environ. 2017, 192, 228–237. [Google Scholar] [CrossRef]
- Jo, M.J.; Jung, H.S.; Won, J.S.; Poland, M.P.; Miklius, A.; Lu, Z. Measurement of slow-moving along-track displacement from an efficient multiple-aperture SAR interferometry (MAI) stacking. J. Geod. 2015, 89, 411–425. [Google Scholar] [CrossRef]
- He, P.; Wen, Y.; Xu, C.; Chen, Y. High-quality three-dimensional displacement fields from new-generation SAR imagery: Application to the 2017 Ezgeleh, Iran, earthquake. J. Geod. 2018, 93, 573–591. [Google Scholar] [CrossRef]
- He, P.; Wen, Y.; Xu, C.; Chen, Y. Complete three-dimensional near-field surface displacements from imaging geodesy techniques applied to the 2016 Kumamoto earthquake. Remote Sens. Environ. 2019, 232, 111321. [Google Scholar] [CrossRef]
- Wang, X.; Liu, G.; Yu, B.; Dai, K.; Zhang, R.; Ma, D.; Li, Z. An integrated method based on DInSAR, MAI and displacement gradient tensor for mapping the 3D coseismic deformation field related to the 2011 Tarlay earthquake (Myanmar). Remote Sens. Environ. 2015, 170, 388–404. [Google Scholar] [CrossRef]
- Han, L. Focal mechanism of 2022 Menyuan MS6.9 earthquake in Qinghai Province. Prog. Earthq. Sci. 2022, 52, 49–54. [Google Scholar] [CrossRef]

| Sensor | Orbit Direction | Master-Slave Date | Track | Spatial Perpendicular Baseline (m) | Wavelength (cm) | Incident Angle (°) | Azimuth Angle (°) | Pixel Resolution (m) (Range × Azimuth) | Imaging Mode |
|---|---|---|---|---|---|---|---|---|---|
| Sentinel-1 | Ascending | 20211229–20220110 | T26 | −104 | 5.6 | 44 | −13 | 2.3 × 14.0 | TOPS |
| Sentinel-1 | Ascending | 20220105–20220117 | T128 | 39 | 5.6 | 37 | −13 | 2.3 × 14.0 | TOPS |
| Sentinel-1 | Descending | 20211229–20220110 | T33 | 56 | 5.6 | 37 | −167 | 2.3 × 14.0 | TOPS |
| ALOS-2 | Descending | 20201212–20220123 | T41 | 296 | 23.6 | 34 | −167 | 8.6 × 2.1 | ScanSAR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Hu, J.; Li, Z.; Ma, Z.; Shi, J.; Xu, W.; Sun, Q. Three-Dimensional Surface Displacements of the 8 January 2022 Mw6.7 Menyuan Earthquake, China from Sentinel-1 and ALOS-2 SAR Observations. Remote Sens. 2022, 14, 1404. https://doi.org/10.3390/rs14061404
Liu J, Hu J, Li Z, Ma Z, Shi J, Xu W, Sun Q. Three-Dimensional Surface Displacements of the 8 January 2022 Mw6.7 Menyuan Earthquake, China from Sentinel-1 and ALOS-2 SAR Observations. Remote Sensing. 2022; 14(6):1404. https://doi.org/10.3390/rs14061404
Chicago/Turabian StyleLiu, Jihong, Jun Hu, Zhiwei Li, Zhangfeng Ma, Jianwen Shi, Wenbin Xu, and Qian Sun. 2022. "Three-Dimensional Surface Displacements of the 8 January 2022 Mw6.7 Menyuan Earthquake, China from Sentinel-1 and ALOS-2 SAR Observations" Remote Sensing 14, no. 6: 1404. https://doi.org/10.3390/rs14061404
APA StyleLiu, J., Hu, J., Li, Z., Ma, Z., Shi, J., Xu, W., & Sun, Q. (2022). Three-Dimensional Surface Displacements of the 8 January 2022 Mw6.7 Menyuan Earthquake, China from Sentinel-1 and ALOS-2 SAR Observations. Remote Sensing, 14(6), 1404. https://doi.org/10.3390/rs14061404






