Soil Moisture Estimation for Winter-Wheat Waterlogging Monitoring by Assimilating Remote Sensing Inversion Data into the Distributed Hydrology Soil Vegetation Model
Abstract
:1. Introduction
2. Study Area and Data Acquisition
2.1. Study Area
2.2. Data Acquisition
2.2.1. Data for the DHSVM
2.2.2. Satellite Data
2.2.3. Field Measured Data of Soil Moisture
3. Methods
3.1. The Profile of DHSVM
3.2. Parameter Optimization for the DHSVM
3.2.1. The Parameter Sensitivity Analysis
3.2.2. The Parameter Calibration
- The particle swarm settings are input to the DHSVM to calculate the fitness of these settings.
- Each particle’s best fitness setting Pbest is compared to update the group particle best fitness Gbest.
- The positions and velocities are updated, and the value beyond the boundary needs to be adjusted. It can be expressed as:where ω is the inertia weight, which is the number of [0, 1]; c1 and c2 are acceleration coefficients, which are usually fixed at 2.0; and r1 and r2 are random numbers in [0, 1].
- Iterating to the maximum number or NSE coefficient meets the requirements.
3.3. Remote Sensing Inversion Method of Soil Moisture Data
3.4. The Agro-Hydrological Assimilation Model for Winter-Wheat Waterlogging Monitoring
3.5. The Identification Criterion of Waterlogging Damage Distribution
4. Results
4.1. The Parameter Optimization Results of the DHSVM Model
4.1.1. Results of Parameter Sensitivity Analysis
4.1.2. Results of Parameter Calibration
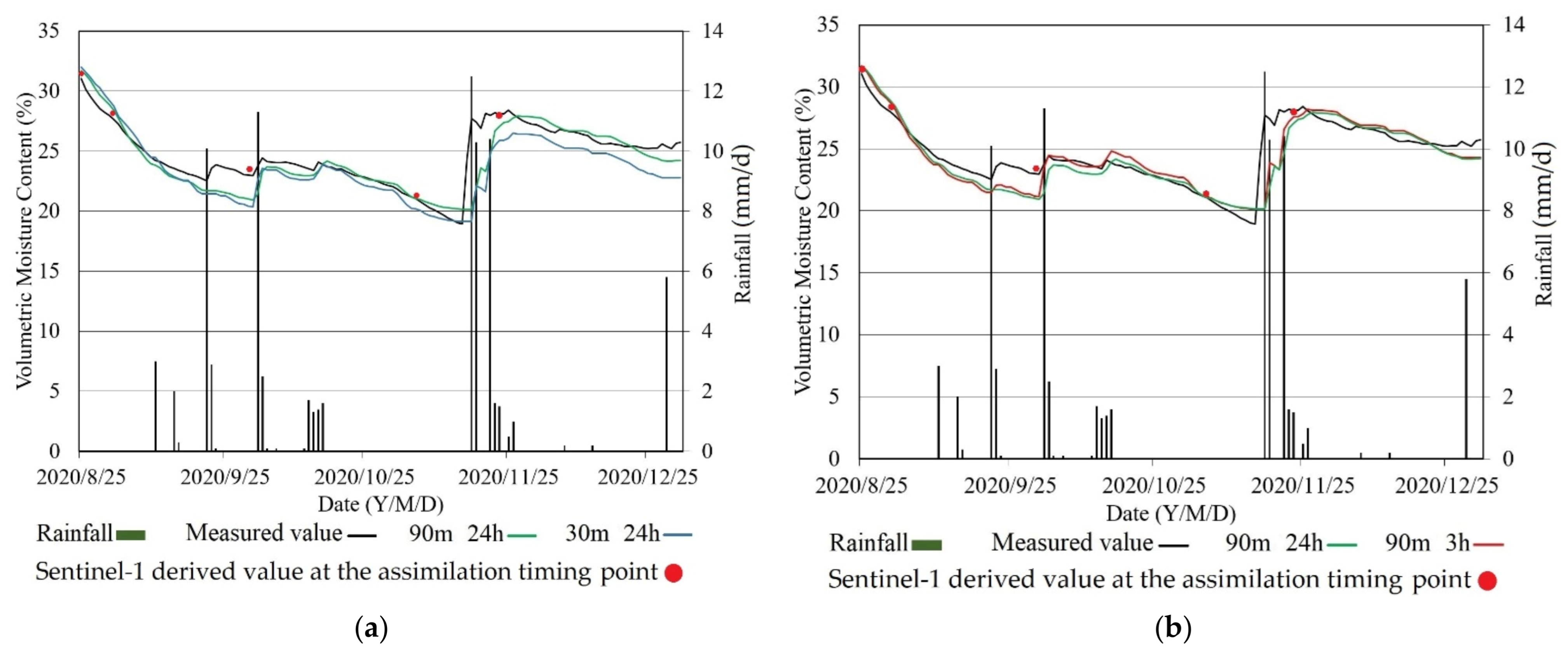
4.1.3. Results of Spatiotemporal Resolution Selection
4.2. The Improvement Effect of the Agro-Hydrological Assimilation Model for Winter-Wheat Waterlogging Monitoring
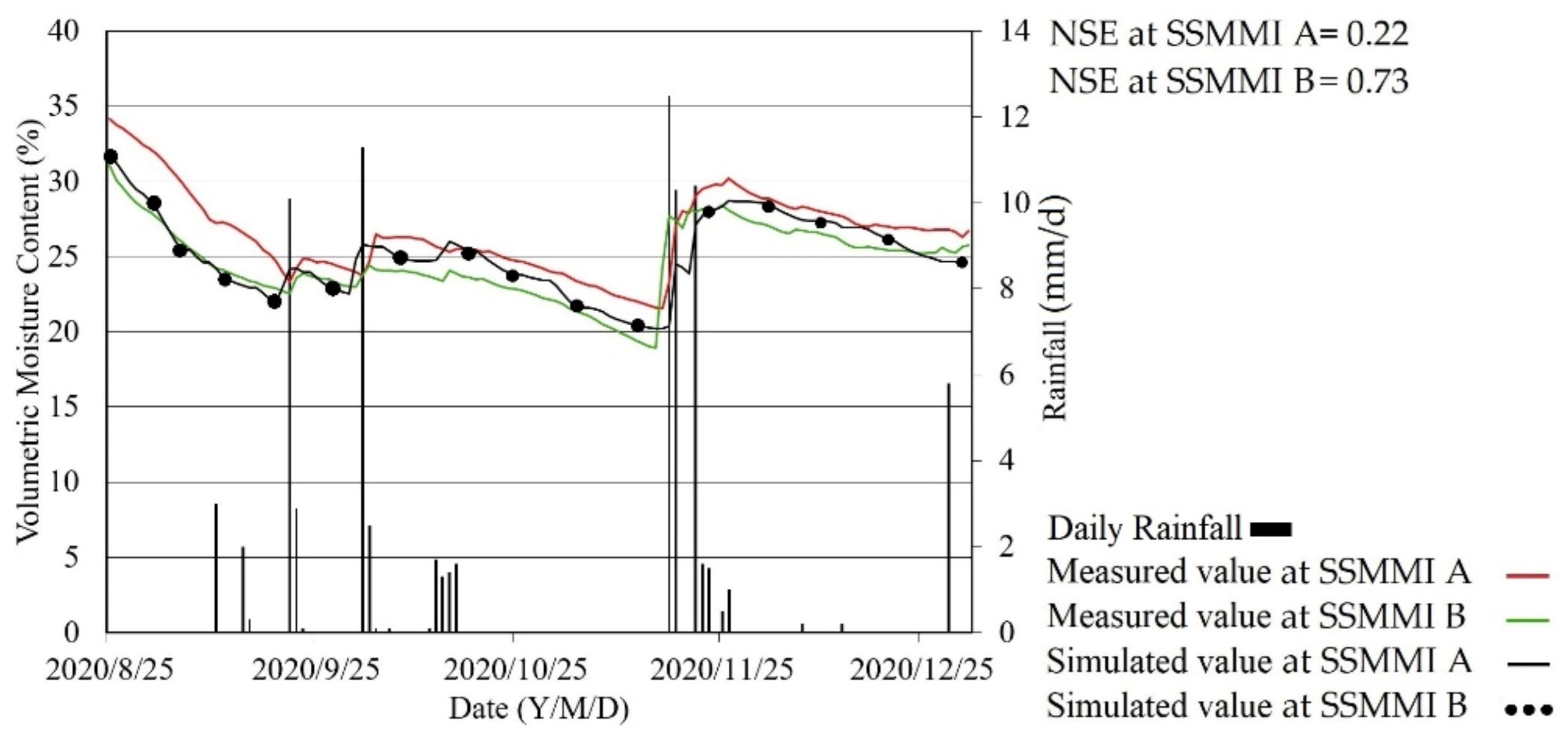
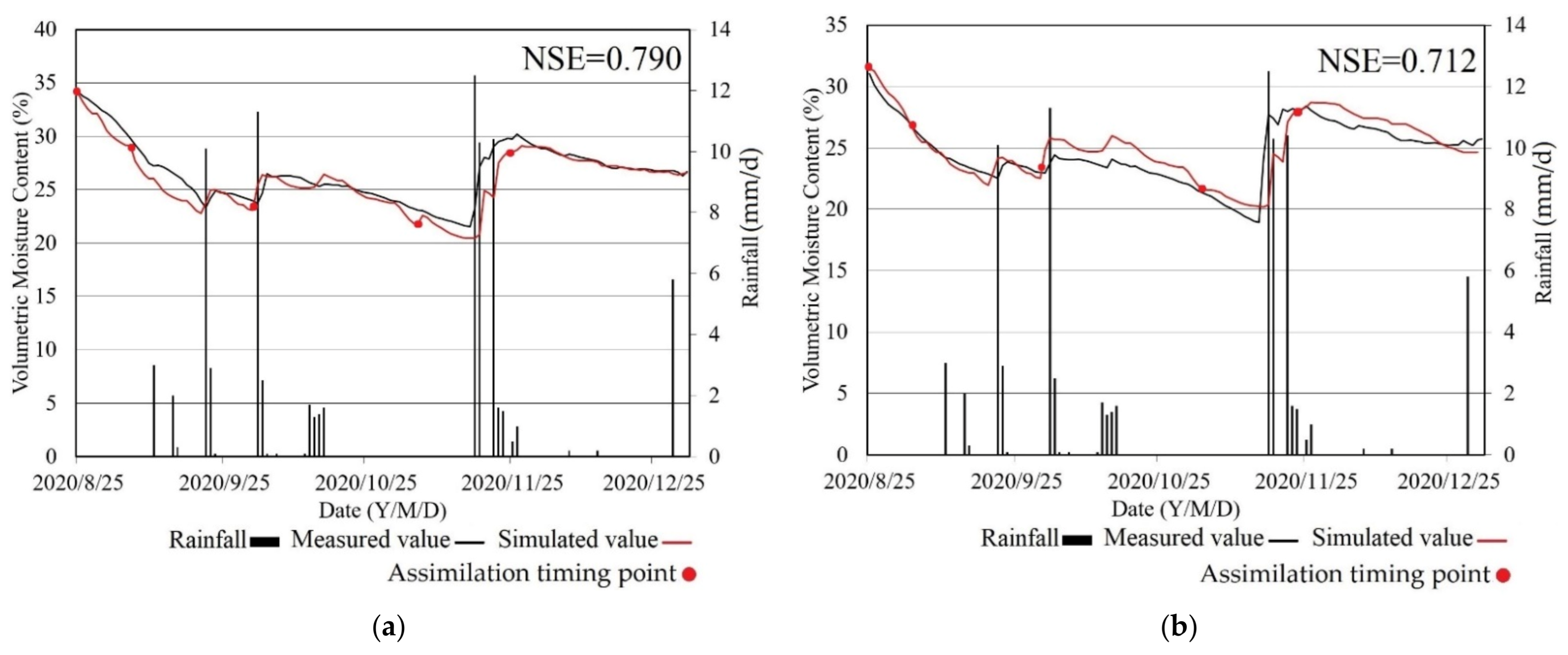
4.3. Accuracy Verification of the Agro-Hydrological Assimilation Model for Winter-Wheat Waterlogging Monitoring
4.4. The Soil Moisture Distribution Results by the Agro-Hydrological Assimilation Model
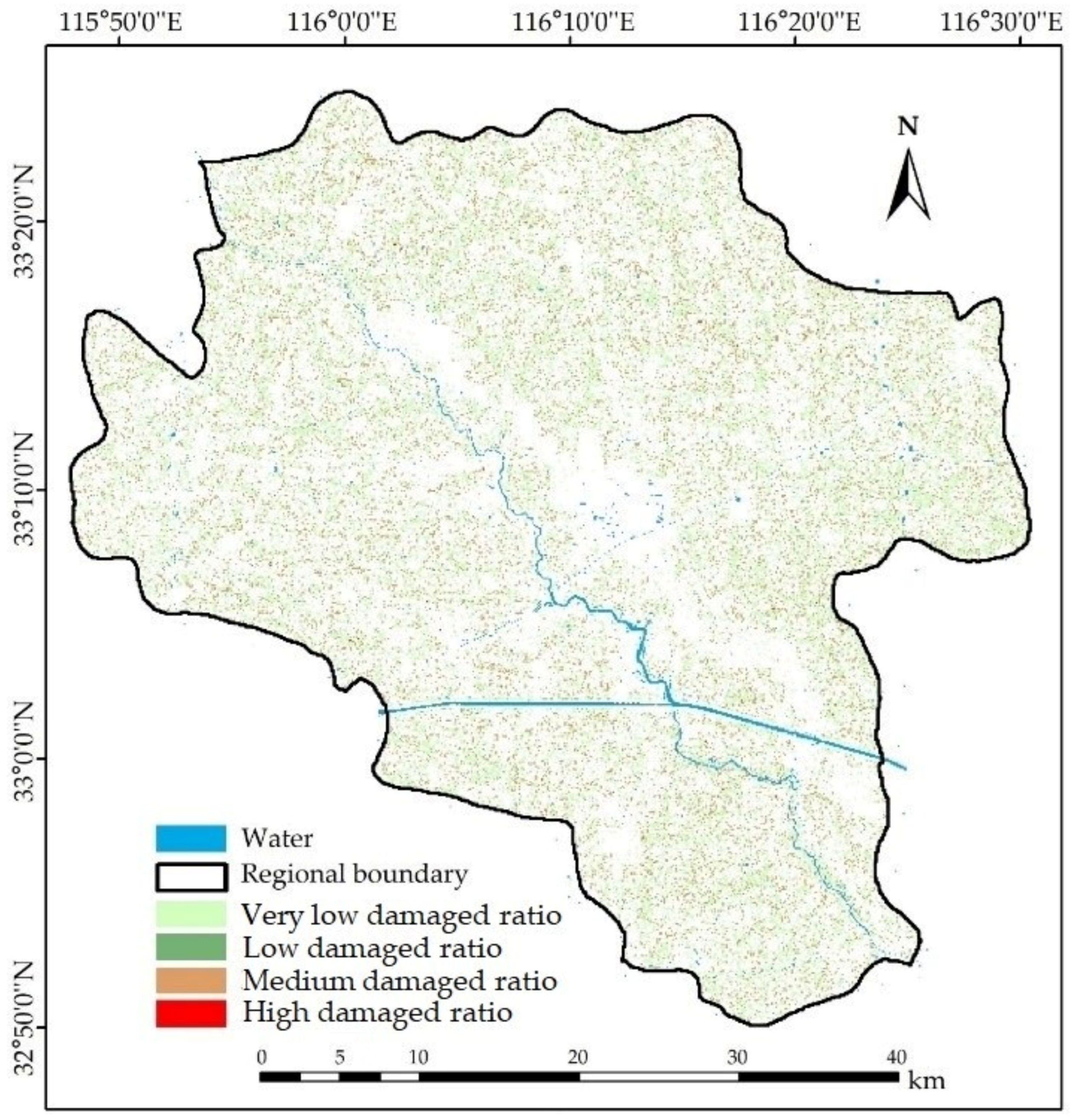
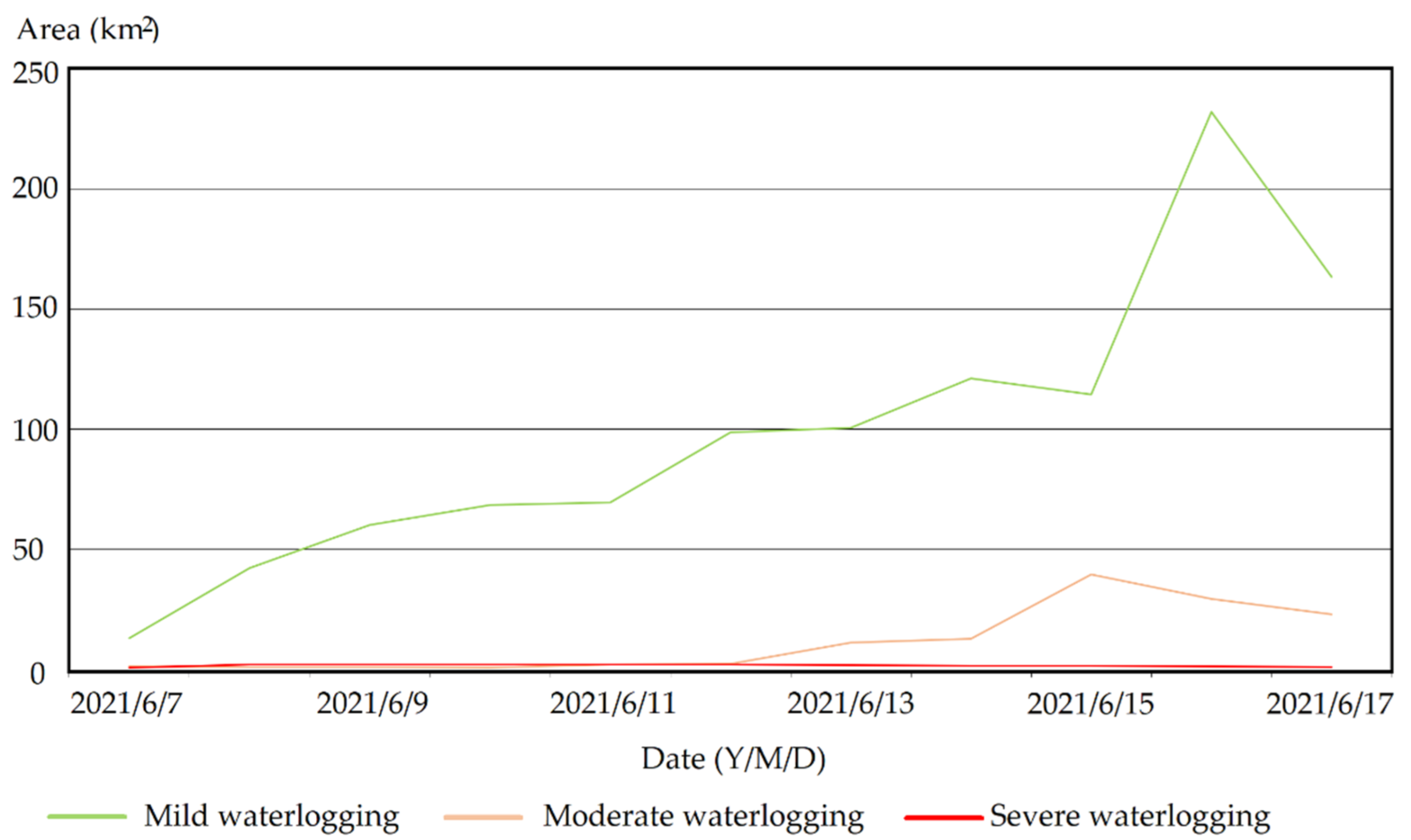
4.5. Monitoring Results of Damaged Ratio and Grade Distribution for Winter-Wheat Waterlgging
5. Discussion
5.1. Parameter Optimization Analysis of the DHSVM Model
5.2. Influence Factors Analysis on the Agro-Hydrological Assimilation Model for Winter-Wheat Waterlogging Monitoring
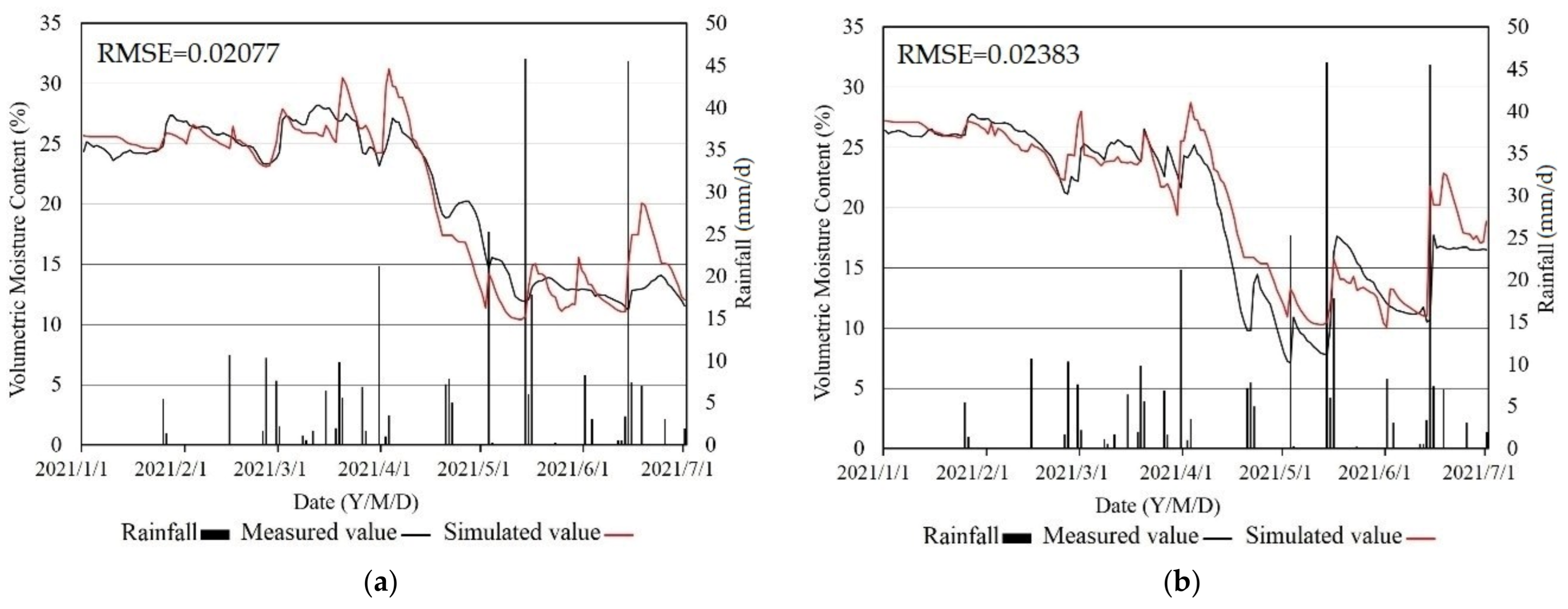
5.2.1. The Model Uncertainty Analysis
5.2.2. Influence Analysis of Assimilating Remote Sensing Inversion Data
5.3. Analysis of Waterlogging Damage Results in Lixin County
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, X. Risk Assessment of Water-Logged Disaster Expressed by the LST-EVI Space in Jianghan Plain. Master’s Thesis, Central China Normal University, Wuhan, China, 2016. [Google Scholar]
- Sreenivas, K.; Dwivedi, R.S.; Singh, A.N. Detection of sub-surface waterlogging using Terra-1 MODIS data. J. Indian Soc. Remote Sens. 2010, 38, 119–132. [Google Scholar] [CrossRef]
- Yu, G. Study on the ecological characteristics of waterlogging field in Jianghan Plain. Acta Ecol. Sin. 1993, 3, 252–260. [Google Scholar]
- Wang, Y.; Chu, D.; Hu, T. Research and Application of Key Technologies for Waterlogging Disaster Control in Huaihe Basin; Anhui & Huaihe River Institute of Hydraulic Research: Bengbu, China, 2011. [Google Scholar]
- Yang, F. Research on Monitoring Waterlogging Stress Level of Winter Wheat based on Hyperspectral Remote Sensing. Master’s Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2020. [Google Scholar]
- Veena, S.; Abdul, R.; Aimrun, W. Comparison of Field and SAR-Derived Descriptors in the Retrieval of Soil Moisture from Oil Palm Crops Using PALSAR-2. Remote Sens. 2021, 13, 4729. [Google Scholar]
- Zhang, L.; Zeng, Y.; Zhuang, R. In Situ Observation-Constrained Global Surface Soil Moisture Using Random Forest Model. Remote Sens. 2021, 31, 4893. [Google Scholar] [CrossRef]
- Uzair, A.; Arturo, A.; Stefano, M. A Review of Crop Water Stress Assessment Using Remote Sensing. Remote Sens. 2021, 13, 4155. [Google Scholar]
- Zhang, X.; Liu, H.; Yan, Y.; Tang, R.; Zhang, Y. Retrieval of Surface Soil Water Content Using Remote Sensing in Incorporation with Phenological Traits of Crops. J. Irrig. Drain. 2021, 40, 1–9. [Google Scholar]
- Liu, W.; Huang, J.; Wei, C. Mapping water-logging damage on winter wheat at parcel level using high spatial resolution satellite data. ISPRS J. Photogramm. Remote Sens. 2018, 142, 243–256. [Google Scholar] [CrossRef]
- Maurya, A.K.; Singh, D. Optimization of Model Parameters for Sm Estimation using Sentinel-1 Data with Efficient Analysis of Wheat Growth Cycle. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 4578–4581. [Google Scholar]
- Chatterjee, S.; Huang, J.; Hartemink, A.E. Establishing an Empirical Model for Surface Soil Moisture Retrieval at the U.S. Climate Reference Network Using Sentinel-1 Backscatter and Ancillary Data. Remote Sens. 2020, 12, 1242. [Google Scholar] [CrossRef] [Green Version]
- Montaldo, N.; Fois, L.; Corona, R. Soil Moisture Estimates in a Grass Field Using Sentinel-1 Radar Data and an Assimilation Approach. Remote Sens. 2021, 13, 3293. [Google Scholar] [CrossRef]
- Xiong, Q.; Hu, P.; Ma, Y. Extracting the spatial distribution information of crop sub-surface waterlogging using antecedent precipitation index and sentinel-1A SAR data. Trans. Chin. Soc. Agric. Eng. 2021, 37, 175–183. [Google Scholar]
- Ma, Y.; Xiong, Q.; Zhu, J.; Jiang, S. Early warning indexes determination of the crop injuries caused by waterlogging based on DHSVM model. J. Supercomput. 2020, 76, 2435–2448. [Google Scholar] [CrossRef]
- Singh, A.; Panda, S. Integrated Salt and Water Balance Modeling for the Management of Waterlogging and Salinization. I: Validation of SAHYSMOD. J. Irrig. Drain. Eng. 2012, 138, 955–963. [Google Scholar] [CrossRef]
- Singh, A.; Panda, S. Integrated Salt and Water Balance Modeling for the Management of Waterlogging and Salinization. II: Application of SAHYSMOD. J. Irrig. Drain. Eng. 2012, 138, 964–971. [Google Scholar] [CrossRef]
- Xiong, Q. Risk evaluation of sub-surface waterlogging of summer crops based on DHSVM model on county scale. Trans. Chin. Soc. Agric. Eng. 2015, 31, 177–183. [Google Scholar]
- Yu, F.; Li, H.; Gu, H. Assimilating ASAR Data for Estimating Soil Moisture Profile Using an Ensemble Kalman Filter. Chin. Geogr. Sci. 2013, 23, 666–679. [Google Scholar] [CrossRef] [Green Version]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System Hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Zhao, R. The Xinanjiang Model Applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Wigmosta, M.S.; Vail, L.W.; Lettenmaier, D.P. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Ferrant, S.; Bustillo, V.; Burel, E.; Salmon-Monviola, J.; Claverie, M.; Jarosz, N.; Yin, T.; Rivalland, V.; Dedieu, G.; Demarez, V.; et al. Extracting Soil Water Holding Capacity Parameters of a Distributed Agro-Hydrological Model from High Resolution Optical Satellite Observations Series. Remote Sens. 2016, 8, 154. [Google Scholar] [CrossRef] [Green Version]
- Brisson, N.; Mary, B.; Ripoche, D.; Jeuffroy, H.; Ruget, F.; Nicollaud, B.; Gate, P.; Devienne-Barret, F.; Antonioletti, R.; Durr, C.; et al. Stics: A generic model for the simulation of crops and their water and nitrogen balances. I. Theory and parameterization applied to wheat and corn. Agronomie 1998, 18, 311–346. [Google Scholar] [CrossRef]
- Ahsan, A.; Yaseen, M.; Yassin, C.; Malik, A.W.; Ghazi, A.R. Use of multispectral and thermal satellite imagery to determine crop water requirements using SEBAL, METRIC, and SWAP models in hot and hyper-arid Oman. Arab. J. Geosci. 2021, 14, 634–655. [Google Scholar]
- Crevoisier, D.; Popova, Z.; Maihol, J.C.; Ruelle, P. Assessment and simulation of water and nitrogen transfer under furrow irrigation. Agric. Water Manag. 2008, 95, 354–366. [Google Scholar] [CrossRef] [Green Version]
- Delphine, J.L.; Thierry, P.; Vischel, T.; Cohard, J.; Gascon, T.; Gibon, F.; Mialon, A.; Galle, S.; Peugeot, C.; Seguis, L. Assimilation of SMOS soil moisture into a distributed hydrological model and impacts on the water cycle variables over the Ouémé catchment in Benin. Hydrol. Earth Syst. Sci. Discuss. 2016, 20, 2827–2840. [Google Scholar]
- Zhu, H. Study and Application of Methods of Soil Moisture Content Data Assimilation Using Multi-Resource Data Serving for Agricultural Water Management Over Irrigation Area. Ph.D. Thesis, China Institute of Water Resources and Hydropower Research, Beijing, China, 3 June 2016. [Google Scholar]
- Yang, A. Study on Soil Moisture at Transitional Region between Oasis and Desert based on Remote Sensing and Hydrological model in the Weigan-Kuqa River Basin, Xinjiang. Ph.D. Thesis, Xinjiang University, Urumqi, China, 2 June 2017. [Google Scholar]
- Li, X.; Ma, H.; Ran, Y.; Wang, X.; Zhu, G.; Liu, F.; He, H.; Zhang, Z.; Huang, C. Terrestrial carbon cycle model-data fusion: Progress and challenges. Sci. China Earth Sci. 2021, 64, 1645–1657. [Google Scholar] [CrossRef]
- Li, X.; Huang, C.; Che, T.; Jin, R.; Wang, S.; Wang, J.; Gao, F.; Zhang, S.; Qiu, C. Progress and prospect of land surface data assimilation system in China. Prog. Nat. Sci. 2007, 17, 163–172. [Google Scholar]
- Rojas, R.W.; Willardson, L.S. Estimation of the allowable flooding time for surface drainage design. In Proceedings of the Twelfth Congress on Irrigation and Drainage Transaction, Fort Collins, CO, USA, 20 May 1984; pp. 493–505. [Google Scholar]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Cressman, G.P. An operational objective analysis system. Mon. Weather. Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Chen, D.; Wen, Z. Design of soil moisture sensor based on principle of frequency domain reflectometry. Electron. Meas. Technol. 2016, 39, 106–109. [Google Scholar]
- Matsushita, B.; Xu, M.; Chen, J.; Kameyama, S.; Tamura, M. Estimation of regional net primary productivity (NPP) using a process-based ecosystem model: How important is the accuracy of climate data? Ecol. Model. 2004, 178, 371–388. [Google Scholar] [CrossRef]
- Cuartas, L.A.; Tomasella, J.; Nobre, A.D.; Nobre, C.A.; Hodnett, M.G.; Waterloo, M.J.; Oliveira, S.M.; Randowa, R.C.; Trancoso, R.; Ferreira, M. Distributed hydrological modeling of a micro-scale rainforest watershed in Amazonia: Model evaluation and advances in calibration using the new HAND terrain model. J. Hydrol. 2012, 462, 15–27. [Google Scholar] [CrossRef]
- Yang, W.; Li, Q. Survey on particle swarm optimization algorithm. Strateg. Study CAE 2004, 6, 87–94. [Google Scholar]
- Banerjee, B.P.; Raval, S. A particle swarm optimization based approach to pre-tune programmable hyperspectral sensors. Remote Sens. 2021, 13, 3295. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A. Parameterization of vegetation backscatter in radar-based, soil moisture estimation. Remote Sens. Environ. 2001, 76, 130–137. [Google Scholar] [CrossRef]
- Baghdadi, N.; Hajj, M.E.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef] [Green Version]
- Jackson, T.J.; Schmugge, T.J. Vegetation effects on the microwave emission of soils. Remote Sens. Environ. 1991, 36, 203–212. [Google Scholar] [CrossRef]
- Shi, C. Reasearch of Drought Disaster Risk Map for Anhui Province. Master’s Thesis, Hefei University of Technology, Hefei, China, 1 April 2013. [Google Scholar]
- Barnes, S.L. A technique for maximizing details in numerical weather map analysis. J. Appl. Meteorol. 1964, 3, 396–409. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Nan, Z.; Yu, W.; Zhang, L. Calibrating a hydrological model by stratifying frozen ground types and seasons in a cold alpine basin. Water 2019, 11, 985. [Google Scholar] [CrossRef] [Green Version]
- Amorim, M.H.; Avelino, C.R.; Sara, Z.S. Influence of soil depth and spatial resolution on the performance of the DHSVM hydrological model in basins with low input data availability. J. S. Am. Earth Sci. 2021, 105, 102993. [Google Scholar]
- Schulz, S.; Rike, B.; Carlos, R.J.; Usman, M.; der Beek, T.; Merz, R.; Schüth, C. Estimating water balance components in irrigated agriculture using a combined approach of soil moisture and energy balance monitoring, and numerical modelling. Hydrol. Processes 2021, 35, 1–14. [Google Scholar] [CrossRef]
- Eekhout, J.; Millares, A.; Salvador, A.M.; García-Lorenzo, R.; Pérez-Cutillas, P.; Conesa-García, C.; de Vente, J. A process-based soil erosion model ensemble to assess model uncertainty in climate-change impact assessments. Land Degrad. Dev. 2021, 32, 2409–2422. [Google Scholar] [CrossRef]
- Yu, L. Study on Performances of Xin’anjiang Model in Forecasting Streamflow. Master’s Thesis, Huazhong University of Science & Technology, Wuhan, China, 2 June 2018. [Google Scholar]


| Phenological Stages | Time | C | D |
|---|---|---|---|
| sowing–tillering | Oct. 2020–Dec. 2020 | 0.103 | −0.025 |
| overwintering | Jan. 2021–Mar. 2021 | 0.668 | 0.020 |
| greening–maturity | Apr. 2021–Jun. 2021 | 0.125 | −0.008 |
| Parameter | First Order Sensitivity 1 | Total Sensitivity 2 |
|---|---|---|
| vegetation albedo | 0.80 | 0.90 |
| leaf area index | 0.24 | 0.65 |
| lateral conductivity | 0.08 | 0.51 |
| field capacity | 0.03 | 0.35 |
| wilting coefficient | 0.15 | 0.27 |
| minimum stomatal resistance | 0.02 | 0.25 |
| Manning coefficient | 0.02 | 0.09 |
| critical humidity | 0.01 | 0.05 |
| pore size distribution | 0.01 | 0.02 |
| maximum infiltration | 0.01 | 0.01 |
| bubbling pressure | 0.01 | 0.01 |
| Parameter | Unit | Range of Parameter | Calibration Value |
|---|---|---|---|
| vegetation albedo | - | 0.20–0.25 | 0.237 |
| leaf area index | m2/m2 | 0.5–10.0 | 5.38 |
| lateral conductivity | m/s | 10−5–10−2 | 5.2 × 10−3 |
| field capacity | m3/m3 | 0.25–0.41 | 0.34 |
| wilting coefficient | m3/m3 | 0.10–0.22 | 0.20 |
| minimum stomatal resistance | s/m | 200–500 | 266.84 |
| Spatial and Temporal Resolution Combination (m + h) | NSE |
|---|---|
| 90 m + 24 h | 0.68 |
| 90 m + 3 h | 0.73 |
| 30 m + 24 h | 0.45 |
| Damaged Ratio Level | Measure of Area (km2) | Percentage of County Area (%) |
|---|---|---|
| Very low damaged ratio | 392.45 | 19.57 |
| Low damaged ratio | 44.03 | 2.20 |
| Medium damaged ratio | 104.44 | 5.21 |
| High damaged ratio | 0.80 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Yuan, X.; Liu, H.; Gao, H.; Wang, X. Soil Moisture Estimation for Winter-Wheat Waterlogging Monitoring by Assimilating Remote Sensing Inversion Data into the Distributed Hydrology Soil Vegetation Model. Remote Sens. 2022, 14, 792. https://doi.org/10.3390/rs14030792
Zhang X, Yuan X, Liu H, Gao H, Wang X. Soil Moisture Estimation for Winter-Wheat Waterlogging Monitoring by Assimilating Remote Sensing Inversion Data into the Distributed Hydrology Soil Vegetation Model. Remote Sensing. 2022; 14(3):792. https://doi.org/10.3390/rs14030792
Chicago/Turabian StyleZhang, Xiaochun, Xu Yuan, Hairuo Liu, Hongsi Gao, and Xiugui Wang. 2022. "Soil Moisture Estimation for Winter-Wheat Waterlogging Monitoring by Assimilating Remote Sensing Inversion Data into the Distributed Hydrology Soil Vegetation Model" Remote Sensing 14, no. 3: 792. https://doi.org/10.3390/rs14030792
APA StyleZhang, X., Yuan, X., Liu, H., Gao, H., & Wang, X. (2022). Soil Moisture Estimation for Winter-Wheat Waterlogging Monitoring by Assimilating Remote Sensing Inversion Data into the Distributed Hydrology Soil Vegetation Model. Remote Sensing, 14(3), 792. https://doi.org/10.3390/rs14030792






