Inverted Algorithm of Groundwater Storage Anomalies by Combining the GNSS, GRACE/GRACE-FO, and GLDAS: A Case Study in the North China Plain
Abstract
1. Introduction
2. Materials and Methods
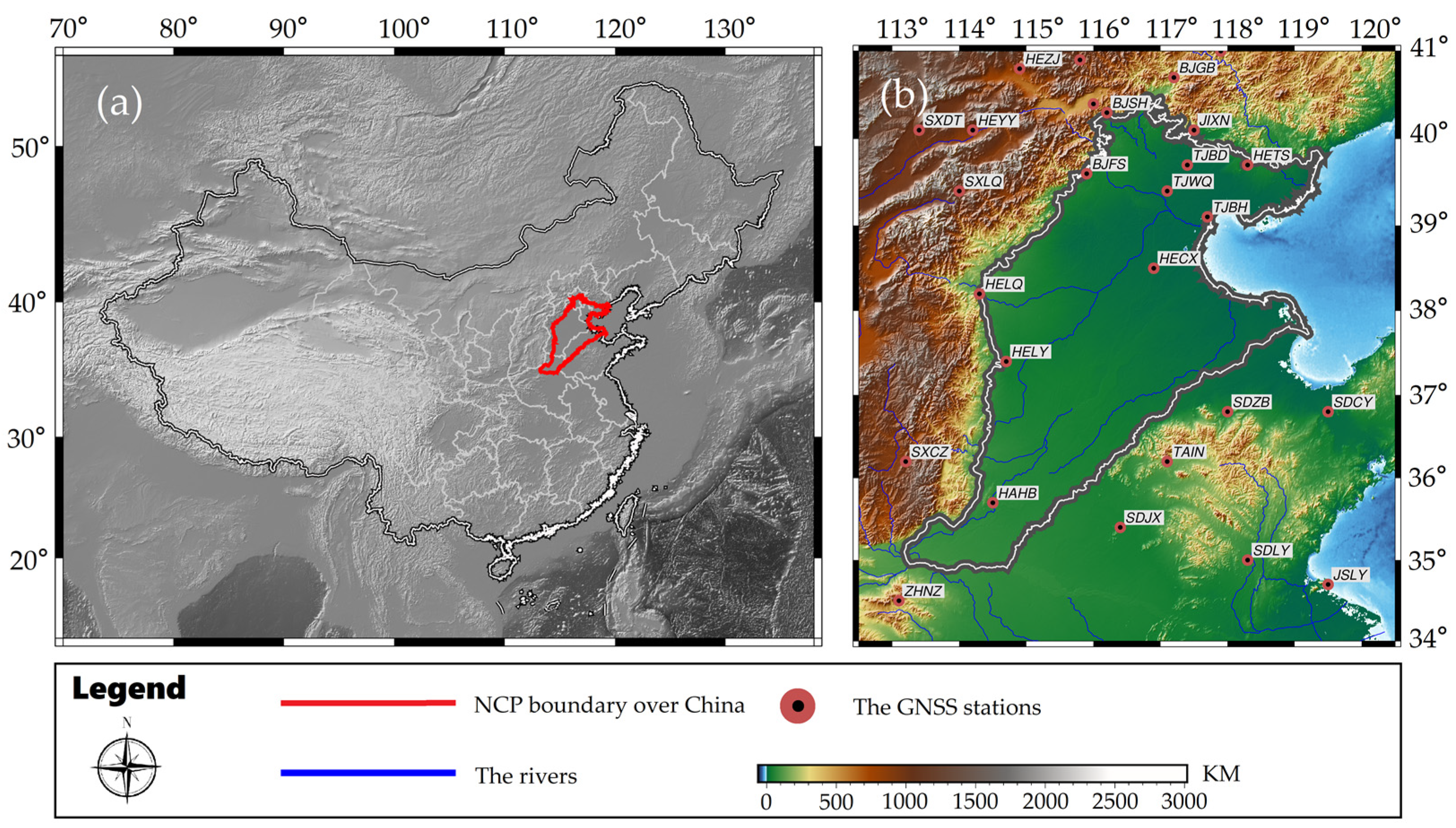
2.1. The Study Area
2.2. Data
2.2.1. GNSS Data
2.2.2. GRACE Mascon Dataset
2.2.3. GLDAS Dataset
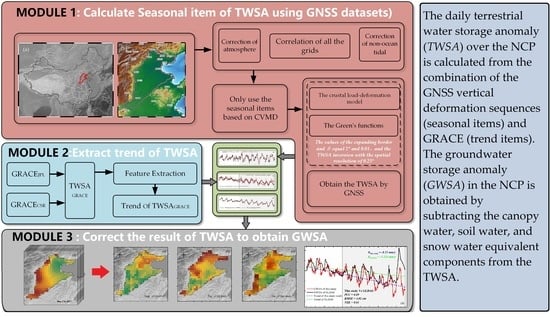
2.3. Method
2.3.1. Crustal Load Inversion Theory
2.3.2. Groundwater Storage Estimation
2.3.3. Groundwater Drought Index
| Grade | Classification | DSI Value |
|---|---|---|
| L1 | No drought | −0.8 < DSI |
| L2 | Mild drought | −1.3 < DSI ≤ −0.8 |
| L3 | Moderate drought | −1.60 < DSI ≤ −1.30 |
| L4 | Severe drought | −2.00 < DSI ≤ −1.60 |
| L5 | Extreme drought | DSI ≤ −2.00 |
2.3.4. Evaluation Index
3. Results
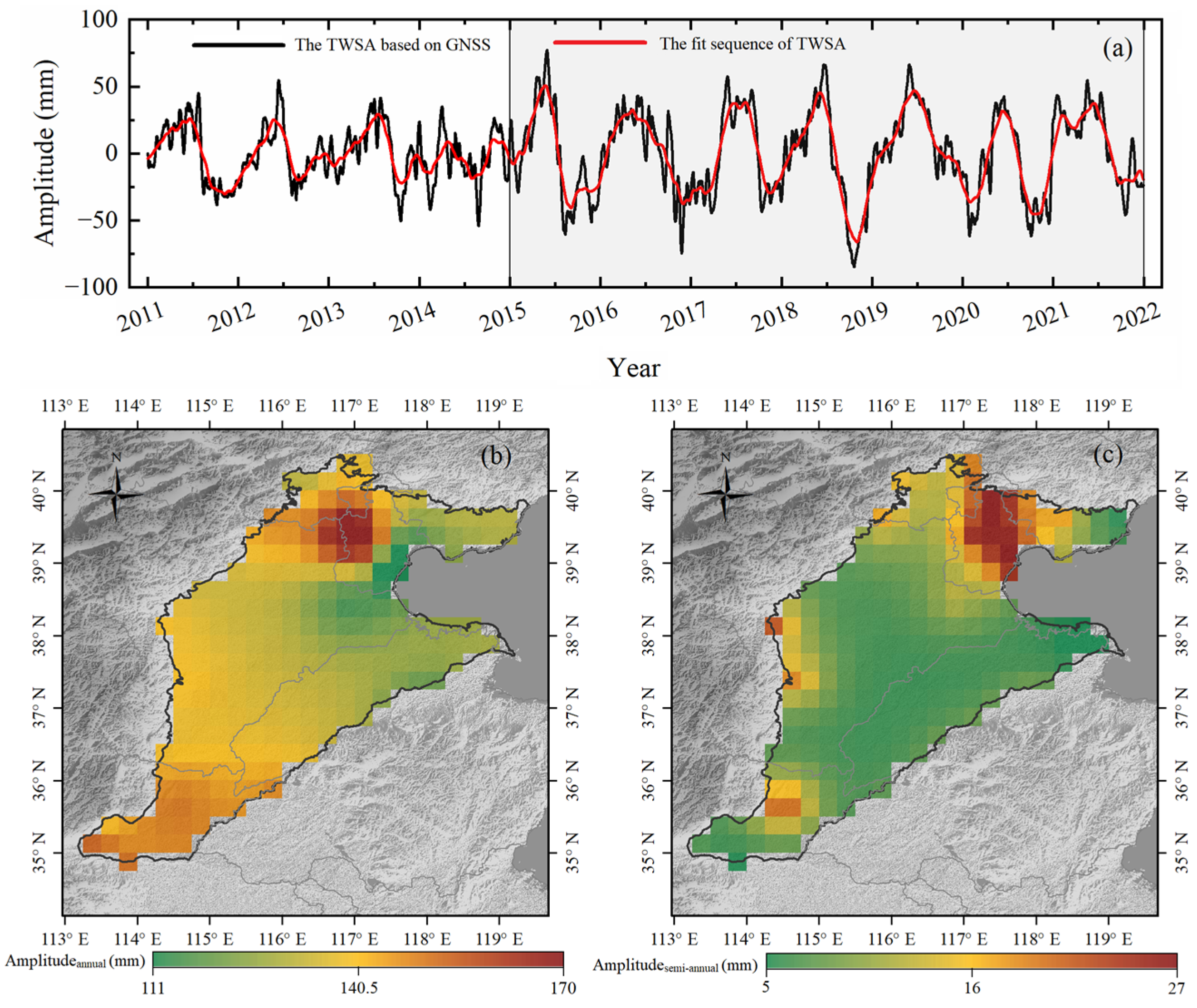
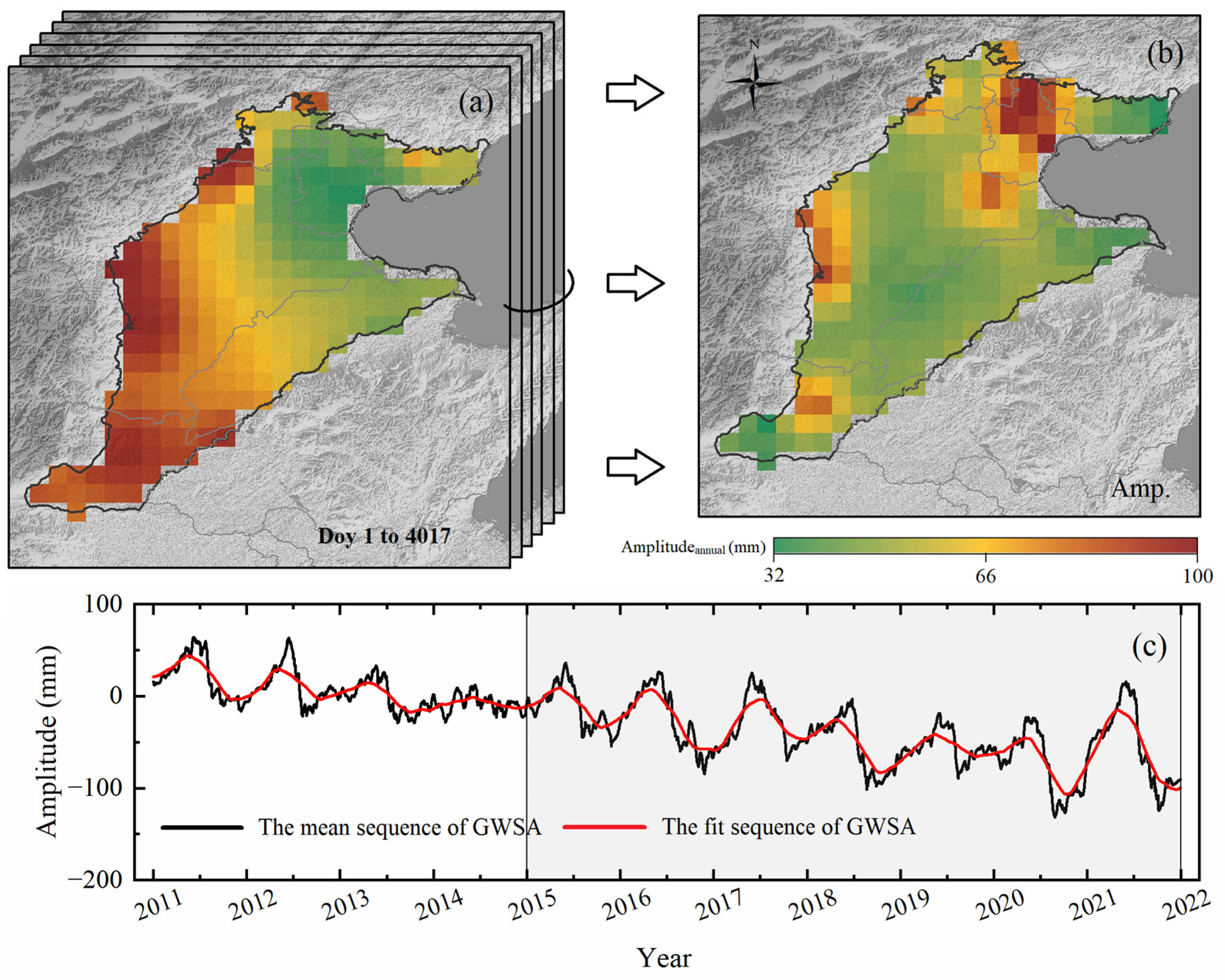
3.1. Inversion of TWSA Seasonal Features Based on GNSS
3.2. TWSA Trend-Feature Extraction Based on GRACE/GRACE-FO
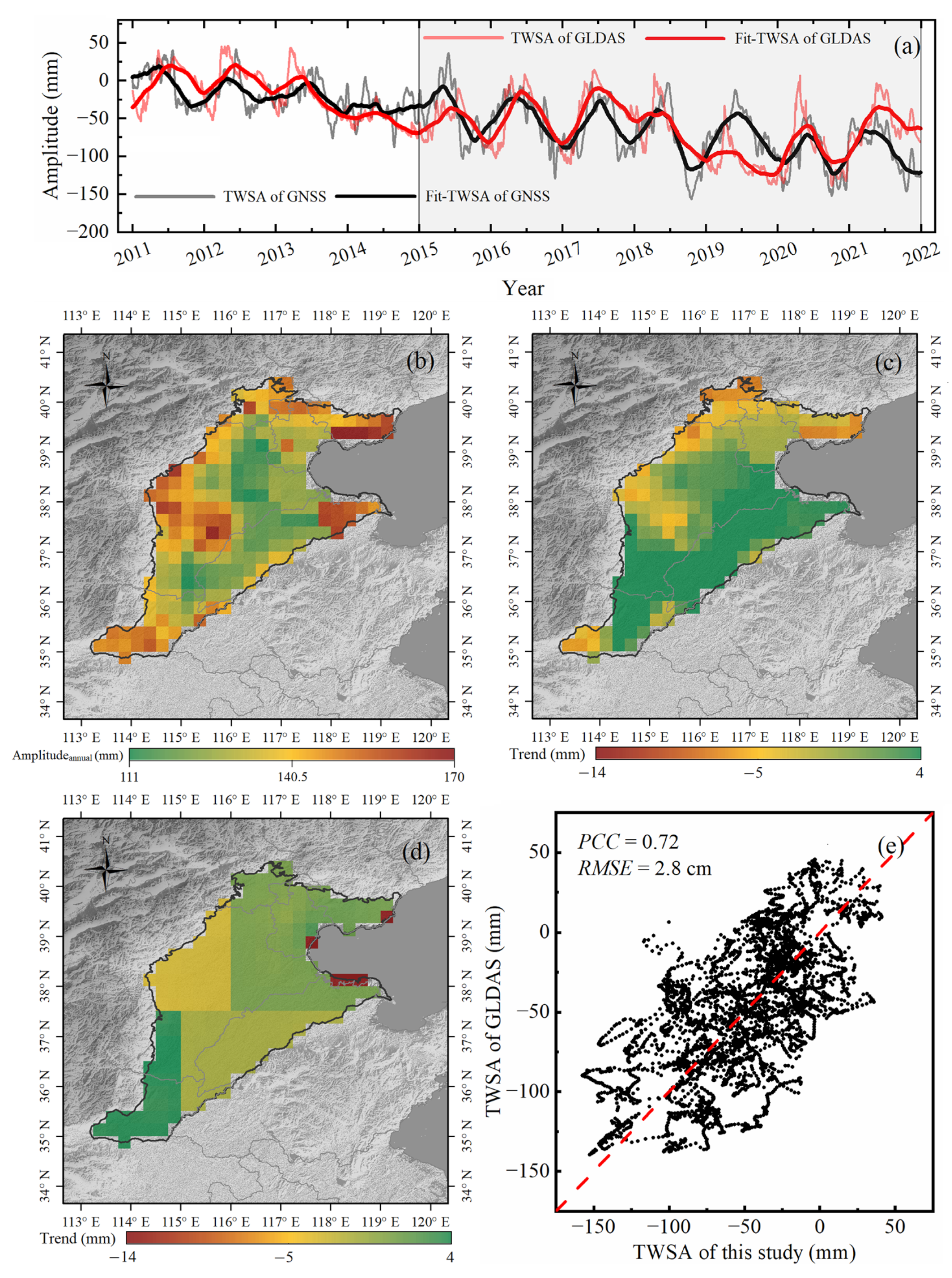
3.3. Inversion and Validation of GWSA
4. Discussion
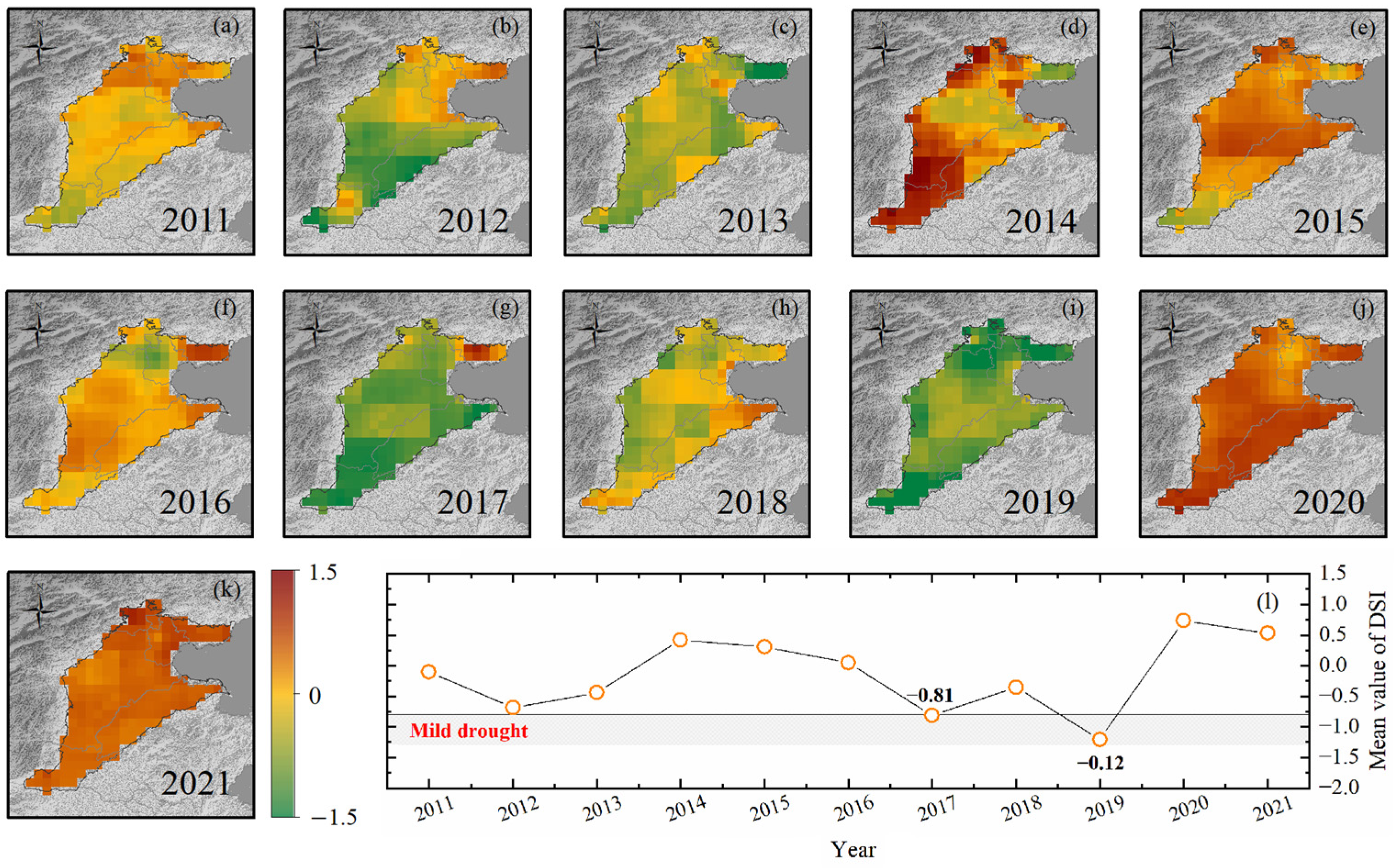
4.1. Analysis of Groundwater Drought Characteristics in the NCP
4.2. Impact of the South–North Water Diversion Project on GWSA
5. Conclusions
- (1)
- To take full advantage of the high spatiotemporal resolutions provided by GNSS data, as well as the ability of GRACE to accurately monitor ground water dynamics, the seasonal terms of TWSA in the NCP region were derived by using the GNSS vertical series, and the trend term of TWSA was determined by using GRACE mascon data. The GWSA was then calculated by subtracting values for canopy water, soil water, and snow water.
- (2)
- This study inverted the TWSA based on the 26 GNSS vertical sequences provided by CMONOC over NCP. The TWSA results shows that the TWSA amplitude is higher than that of 2011~2014, which is consistent with the timing of South–North Water Transfer Project. Meanwhile, the maximum annual amplitude of the TWSA result is 170 mm, which is higher than that of the maximum semiannual amplitude of TWSA. The results of TWSA sequences are the basis of the inversion for GWSA.
- (3)
- To verify the reliability of the inverted method by combining the GNSS, GRACE/GRACE-FO, and GLDAS, the experimental results were compared with the GWSA variables in the GLDAS datasets. The comparison results show that the amplitude peaks are located in the Beijing and Tianjin regions, and the spatial features of the trend terms show that the high anomalies are located in the north and south of the NCP, and the low anomalies are found in the middle of the NCP. The PCC, RMSE, and NSE values are 0.67, 4.01 cm, and 0.61, respectively, while the superimposed power spectra showed that the two sequences are consistent at low and medium frequencies. Therefore, the inversion methodology proposed in this study is a reliable way of determining regional GWSA.
- (4)
- Using the GWSA inversion results obtained in this study, we analyzed the groundwater drought and the impact of the South–North Water Transfer Project on groundwater storage in the NCP from 2011 to 2021. The most obvious groundwater drought year in the NCP was 2019, with a DSI value of −0.12, which was close to moderate drought conditions. Moreover, the DSI value reached −0.81 in 2017, which was indicative of mild drought conditions. The South–North Water Transfer Project officially opened for water transmission at the end of 2014, and the annual GWSA amplitude increased significantly compared with that before the opening of the South–North Water Transfer Project. This suggests that the demand for land water from industry and agriculture increased after the transfer. Additionally, there is a significant amplitude increase in the Tianjin and Hebei regions between 2015 and 2020, indicating that the demand for groundwater in this region is higher than in other regions. In conclusion, the South–North Water Transfer Project does have an impact on groundwater storage in Hebei Province.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in north China using the gravity recovery and climate experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhong, M.; Feng, W.; Zhang, Z.; Shen, Y.; Wu, D. Groundwater Depletion in the West Liaohe River Basin, China and Its Implications Revealed by GRACE and In Situ Measurements. Remote Sens. 2018, 10, 493. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Zhang, M.; Wang, J.; Han, S. Statistical downscaling of GRACE-derived groundwater storage using ET data in the north China plain. J. Geophys. Res. Atmos. 2018, 123, 5973–5987. [Google Scholar] [CrossRef]
- Davis, J.L.; Tamisiea, M.E.; Elosegui, P.; Mitrovica, J.X.; Hill, E.M. A statistical filtering approach for Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res.-Solid Earth 2008, 113, 1–14. [Google Scholar] [CrossRef]
- Pang, Y.; Zhang, H.; Cheng, H.; Shi, Y. Changes of crustal stress induces by groundwater over-puming in North China Plain. Chin. J. Geophy. 2016, 59, 1394–1402. [Google Scholar]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Zhang, C.; Wen, H.; Zhong, Y.; Zhu, Y.; Li, Z. Bridging terrestrial water storage anomaly during GRACE/GRACE-FO gap using SSA method: A case study in China. Sensors 2019, 19, 4144. [Google Scholar] [CrossRef]
- Zheng, W.; Hsu, H.; Zhong, M.; Yun, M. Requirements analysis for future satellite gravity mission improved-GRACE. Surv. Geophys. 2015, 36, 87–109. [Google Scholar] [CrossRef]
- Zheng, W.; Lu, X.; Hsu, H.; Shao, C.; Luo, J.; Wang, N. Simulation of the Earth’s gravitational field recovery from GRACE using the energy balance approach. Prog. Nat. Sci. 2005, 15, 596–601. [Google Scholar]
- Tangdamrongsub, N.; Ditmar, P.G.; Steele-Dunne, S.C.; Gunter, B.C.; Sutanudjaja, E.H. Assessing total water storage and identifying flood events over Tonlé Sap basin in Cambodia using GRACE and MODIS satellite observations combined with hydrological models. Remote Sens. Environ. 2016, 181, 162–173. [Google Scholar] [CrossRef]
- Tan, W.J.; Dong, D.A.; Chen, J.P.; Wu, B. Analysis of systematic differences from GPS-measured and GRACE-modeled deformation in Central Valley, California. Adv. Space Res. 2016, 57, 19–29. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.W.; Massoud, E.; Farr, T.G.; Lundgren, P.; Famiglietti, J.S. Monitoring groundwater change in California’s central valley using Sentinel-1 and GRACE observations. Geosciences 2019, 9, 436. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Jiao, J.J. Evaluation of groundwater storage variations in northern China using GRACE data. Geofluids 2017, 2017, 8254824. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, B.; Yao, Y.B.; Wu, W.W.; Meng, G.J.; Chen, Q. Geodetic and hydrological measurements reveal the recent acceleration of groundwater depletion in north China plain. J. Hydrol. 2019, 575, 1065–1072. [Google Scholar] [CrossRef]
- Li, W.Q.; Wang, W.; Zhang, C.Y.; Yang, Q.; Feng, W.; Liu, Y. Monitoring groundwater storage variations in the Guanzhong area using GRACE satellite gravity data. Chin. J. Geophys. 2018, 61, 67–75. [Google Scholar]
- Nie, N.; Zhang, W.; Zhang, Z.; Guo, H.; Ishwaran, N. Reconstructed terrestrial water storage change (ΔTWS) from 1948 to 2012 over the Amazon basin with the latest GRACE and GLDAS products. Water Resour. Manag. 2016, 30, 279–294. [Google Scholar] [CrossRef]
- Cui, L.L.; Song, Z.; Luo, Z.C.; Zhong, B.; Wang, X.L.; Zou, Z.B. Comparison of terrestrial water storage changes derived from GRACE/GRACE-FO and Swarm: A case study in the Amazon river basin. Water 2020, 12, 3128. [Google Scholar] [CrossRef]
- Flechtner, F.; Neumayer, K.H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.C.; Guntner, A. What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? Surv. Geophys. 2016, 37, 453–470. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhong, M.; Mao, Y.; Ji, B. Evaluation of Evapotranspiration for Exorheic Catchments of China during the GRACE Era: From a Water Balance Perspective. Remote Sens. 2020, 12, 1–23. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Fu, Y.N.; Freymueller, J.T.; Jensen, T. Seasonal hydrological loading in southern Alaska observed by GPS and GRACE. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H.; Yang, S.; Su, K. Inverted algorithm of terrestrial water-storage anomalies based on machine learning combined with load model and its application in southwest China. Remote Sens. 2021, 13, 3358. [Google Scholar] [CrossRef]
- Adusumilli, S.; Borsa, A.A.; Fish, M.A.; McMillan, H.K.; Silverii, F. A decade of water storage changes across the contiguous united states from GPS and satellite gravity. Geophys. Res. Lett. 2019, 46, 13006–13015. [Google Scholar] [CrossRef]
- Carlson, G.; Werth, S.; Shirzaei, M. Joint Inversion of GNSS and GRACE for Terrestrial Water Storage Change in California. J. Geophys. Res. Solid Earth 2022, 127, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Godah, W. Comparison of vertical deformation of the Earth_s surface obtained using GRACE_based GGMS and GNNS data _ a case study of South_Eastern Poland. Acta Geodyn. Geomater. 2020, 2, 169–176. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H. Feature extraction algorithm using a correlation coefficient combined with the VMD and its application to the GPS and GRACE. IEEE Access 2021, 9, 17507–17519. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H.; Wang, Q.; Chen, Z. Improving the inversion accuracy of terrestrial water storage anomaly by combining GNSS and LSTM algorithm and its application in mainland China. Remote Sens. 2022, 14, 535. [Google Scholar] [CrossRef]
- Wang, H.; Xiang, L.; Jia, L.; Jiang, L.; Wang, Z.; Bo, H.; Peng, G. Load love numbers and Green’s functions for elastic earth models PREM, iasp91, ak135, and modified models with refined crustal structure from Crust 2.0. Comput. Geosci. 2012, 49, 190–199. [Google Scholar] [CrossRef]
- Martens, H.R.; Rivera, L.; Simons, M. LoadDef: A python-based toolkit to model elastic deformation caused by surface mass loading on spherically symmetric bodies. Earth Space Sci. 2019, 6, 311–323. [Google Scholar] [CrossRef]
- Dill, R.; Klemann, V.; Martinec, Z.; Tesauro, M. Applying local Green’s functions to study the influence of the crustal structure on hydrological loading displacements. J. Geodyn. 2015, 88, 14–22. [Google Scholar] [CrossRef]
- Dach, R.; Böhm, J.; Lutz, S.; Steigenberger, P.; Beutler, G. Evaluation of the impact of atmospheric pressure loading modeling on GNSS data analysis. J. Geod. 2011, 85, 75–91. [Google Scholar] [CrossRef]
- Sheng, C.Z.; Gan, W.J.; Liang, S.M.; Chen, W.T.; Xiao, G.R. Identification and elimination of non-tectonic crustal deformation caused by land water from GPS time series in the western Yunnan province based on GRACE observations. Chin. J. Geophys. 2014, 57, 42–52. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y.B.; Fok, H.S.; Hu, Y.F.; Chen, Q. Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China. Sensors 2016, 16, 1526. [Google Scholar] [CrossRef]
- Xu, H.; Lu, T.; Montillet, J.P.; He, X. An improved adaptive IVMD-WPT-Based noise reduction algorithm on GPS height time series. Sensors 2021, 21, 8295. [Google Scholar] [CrossRef]
- Wu, S.G.; Li, Z.; Li, H.P.; Nie, G.G.; Liu, J.N.; He, Y.F. Application of an improved clustering approach on GPS height time series at CMONOC stations in southwestern China. Earth Planets Space 2021, 73, 233. [Google Scholar] [CrossRef]
- Jiang, Z.; Hsu, Y.-J.; Yuan, L.; Huang, D. Monitoring time-varying terrestrial water storage changes using daily GNSS measurements in Yunnan, southwest China. Remote Sens. Environ. 2021, 254, 112249–112266. [Google Scholar] [CrossRef]
- Ding, Y.H.; Huang, D.f.; Shi, Y.L.; Jiang, Z.S.; Chen, T. Determination of vertical surface displacements in Sichuan using GPS and GRACE measurements. Chin. J. Geophys. 2018, 61, 4777–4788. [Google Scholar]
- Liu, R.; Zou, R.; Li, J.; Zhang, C.; Zhao, B.; Zhang, Y. Vertical displacements driven by groundwater storage changes in the north China plain detected by GPS observations. Remote Sens. 2018, 10, 259. [Google Scholar] [CrossRef]
- Abdrakhmatov, K.Y.; Aldazhanov, S.A.; Hager, B.H.; Hamburger, M.W.; Herring, T.A.; Kalabaev, K.B.; Makarov, V.I.; Molnar, P.; Panasyuk, S.V.; Prilepin, M.T.; et al. Relatively recent construction of the Tien Shan inferred from GPS measurements of present-day crustal deformation rates. Nature 1996, 384, 450–453. [Google Scholar] [CrossRef]
- Sun, W.K.; Wang, Q.; Li, H.; Wang, Y.; Okubo, S. A reinvestigation of crustal thickness in the Tibetan Plateau using absolute gravity, GPS and GRACE data. Terr. Atmos. Ocean. Sci. 2011, 22, 109–119. [Google Scholar] [CrossRef]
- Sun, W.K.; Zhou, X. Advances, problems and prospects of modern geodesy applied in Tibetan geodynamic changes. Acta Geol. Sin. 2013, 87, 318–332. [Google Scholar] [CrossRef]
- Chen, C.; Wang, T.; Linsong, D.; Jin, S. Detecting seasonal and long-term vertical displacement in the north China plain using GRACE and GPS. Hydrol. Earth Syst. Sci. 2017, 21, 2905–2922. [Google Scholar]
- Long, D.; Yang, W.; Scanlon, B.R.; Zhao, J.; Liu, D.; Burek, P.; Pan, Y.; You, L.; Wada, Y. South-to-North water diversion stabilizing Beijing’s groundwater levels. Nat. Commun. 2020, 11, 3665–3675. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zheng, H. South-to-north Water Transfer Schemes for China. Int. J. Water Resour. Dev. 2002, 18, 453–471. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, B.; Wang, Q.; Yang, S. Noise analysis of continuous GPS coordinate time series for CMONOC. Adv. Space Res. 2012, 49, 943–956. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Mcclusky, S.C. GAMIT Reference Manual; Massachussetts Institute Technology: Cambridge, UK, 2010. [Google Scholar]
- Xiang, Y.F.; Yue, J.P.; Li, Z. Joint analysis of seasonal oscillations derived from GPS observations and hydrological loading for mainland China. Adv. Space Res. 2018, 62, 3148–3161. [Google Scholar] [CrossRef]
- Han, S.-C.; Shum, C.K.; Jekeli, C.; Kuo, C.-Y.; Wilson, C.; Seo, K.-W. Non-isotropic filtering of GRACE temporal gravity for geophysical signal enhancement. Geophys. J. Int. 2005, 163, 18–25. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Saito, M. Relationship Between Tidal and Load Love Numbers. J. Phys. Earth 1978, 26, 13–16. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 2011, 116, 1–14. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Li, Z.; Wang, S.-Y.; Hu, X. Ellipsoidal Correction in GRACE Surface Mass Change Estimation. J. Geophys. Res. Solid Earth 2017, 122, 9437–9460. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global GRACE Data Assimilation for Groundwater and Drought Monitoring: Advances and Challenges. Water Resour. Res. 2019, 55, 7564–7586. [Google Scholar] [CrossRef]
- Tesmer, V.; Steigenberger, P.; Dam, T.V.; Mayer-Guerr, T. Vertical deformations from homogeneously processed GRACE and global GPS long-term series. J. Geod. 2011, 85, 291–310. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Wang, X.; Chen, L.; Ai, Y.; Xu, T.; Jiang, M.; Yuan, L.; Gao, Y. Crustal structure and deformation beneath eastern and northeastern Tibet revealed by P-wave receiver functions. Earth Planet. Sci. Lett. 2018, 497, 69–79. [Google Scholar] [CrossRef]
- Wahr, J.; Khan, S.A.; Dam, T.V.; Liu, L.; Angelen, J.V.; Van, D.; Meertens, C.M. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J. Geophys. Res. Solid Earth 2013, 118, 1795–1806. [Google Scholar] [CrossRef]
- Springer, A.; Karegar, M.A.; Kusche, J.; Kurtz, W.; Kollet, S. Evidence of daily hydrological loading in GPS time series over Europe. J. Geod. 2019, 93, 2145–2153. [Google Scholar] [CrossRef]
- Wang, Z.; Ou, J. Determining the ridge parameter in a ridge estimation using L-curve method. Editor. Board Geomat. Inf. Sci. Wuhan Univ. 2004, 29, 235–238. [Google Scholar]
- Liesch, T.; Ohmer, M. Comparison of GRACE data and groundwater levels for the assessment of groundwater depletion in Jordan. Hydrogeol. J. 2016, 24, 1547–1563. [Google Scholar] [CrossRef]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; Bai, Q.; Zhao, J.; Ma, L.; Wang, L.; Du, M. Propagation dynamics from meteorological to groundwater drought and their possible influence factors. J. Hydrol. 2019, 578, 124102. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE) aguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Yu, J.; Tan, K.; Zhang, C.; Zhao, B.; Wang, D.; Li, Q. Present-day crustal movement of the Chinese mainland based on Global Navigation Satellite System data from 1998 to 2018. Adv. Space Res. 2019, 63, 840–856. [Google Scholar] [CrossRef]
- Gong, H.; Pan, Y.; Zheng, L.; Li, X.; Zhu, L.; Zhang, C.; Huang, Z.; Li, Z.; Wang, H.; Zhou, C. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef]
- Moiwo, J.P.; Tao, F.; Lu, W. Analysis of satellite-based and in situ hydro-climatic data depicts water storage depletion in North China Region. Hydrol. Process. 2013, 27, 1011–1020. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.F.; Li, X.; Zhou, D.; Zhao, W. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Li, P.; Zha, Y.; Shi, L.; Zhong, H. Identification of the terrestrial water storage change features in the North China Plain via independent component analysis. J. Hydrol. Reg. Stud. 2021, 38, 100955. [Google Scholar] [CrossRef]
- Zhang, C.; Duan, Q.; Yeh, P.J.-F.; Pan, Y.; Gong, H.; Moradkhani, H.; Gong, W.; Lei, X.; Liao, W.; Xu, L.; et al. Sub-regional groundwater storage recovery in North China Plain after the South-to-North water diversion project. J. Hydrol. 2021, 597, 126156. [Google Scholar] [CrossRef]


| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Reference frame | ITRF a 2008 | Flat Difference | Weighted least squares estimation + Kalman filtering |
| Height cutoff angle | 10° | Ionosphere | LC b portfolio observations |
| A priori troposphere | 0.5 m | Earth’s rotation parameters | Polar shift, UT1 c |
| Mapping functions | HGMF d, DGMF e | Inertial coordinate system | J2000.0 |
| Satellite phase center | IGS f ANTEX g Model | Phase movement | IAU h 1980 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Zheng, W.; Zhu, H.; Yin, W.; Xu, A.; Pan, F.; Wang, Q.; Zhao, Y. Inverted Algorithm of Groundwater Storage Anomalies by Combining the GNSS, GRACE/GRACE-FO, and GLDAS: A Case Study in the North China Plain. Remote Sens. 2022, 14, 5683. https://doi.org/10.3390/rs14225683
Shen Y, Zheng W, Zhu H, Yin W, Xu A, Pan F, Wang Q, Zhao Y. Inverted Algorithm of Groundwater Storage Anomalies by Combining the GNSS, GRACE/GRACE-FO, and GLDAS: A Case Study in the North China Plain. Remote Sensing. 2022; 14(22):5683. https://doi.org/10.3390/rs14225683
Chicago/Turabian StyleShen, Yifan, Wei Zheng, Huizhong Zhu, Wenjie Yin, Aigong Xu, Fei Pan, Qiang Wang, and Yelong Zhao. 2022. "Inverted Algorithm of Groundwater Storage Anomalies by Combining the GNSS, GRACE/GRACE-FO, and GLDAS: A Case Study in the North China Plain" Remote Sensing 14, no. 22: 5683. https://doi.org/10.3390/rs14225683
APA StyleShen, Y., Zheng, W., Zhu, H., Yin, W., Xu, A., Pan, F., Wang, Q., & Zhao, Y. (2022). Inverted Algorithm of Groundwater Storage Anomalies by Combining the GNSS, GRACE/GRACE-FO, and GLDAS: A Case Study in the North China Plain. Remote Sensing, 14(22), 5683. https://doi.org/10.3390/rs14225683