Cognitive Sparse Imaging Method for MIMO Radar under Wideband Interference
Abstract
1. Introduction
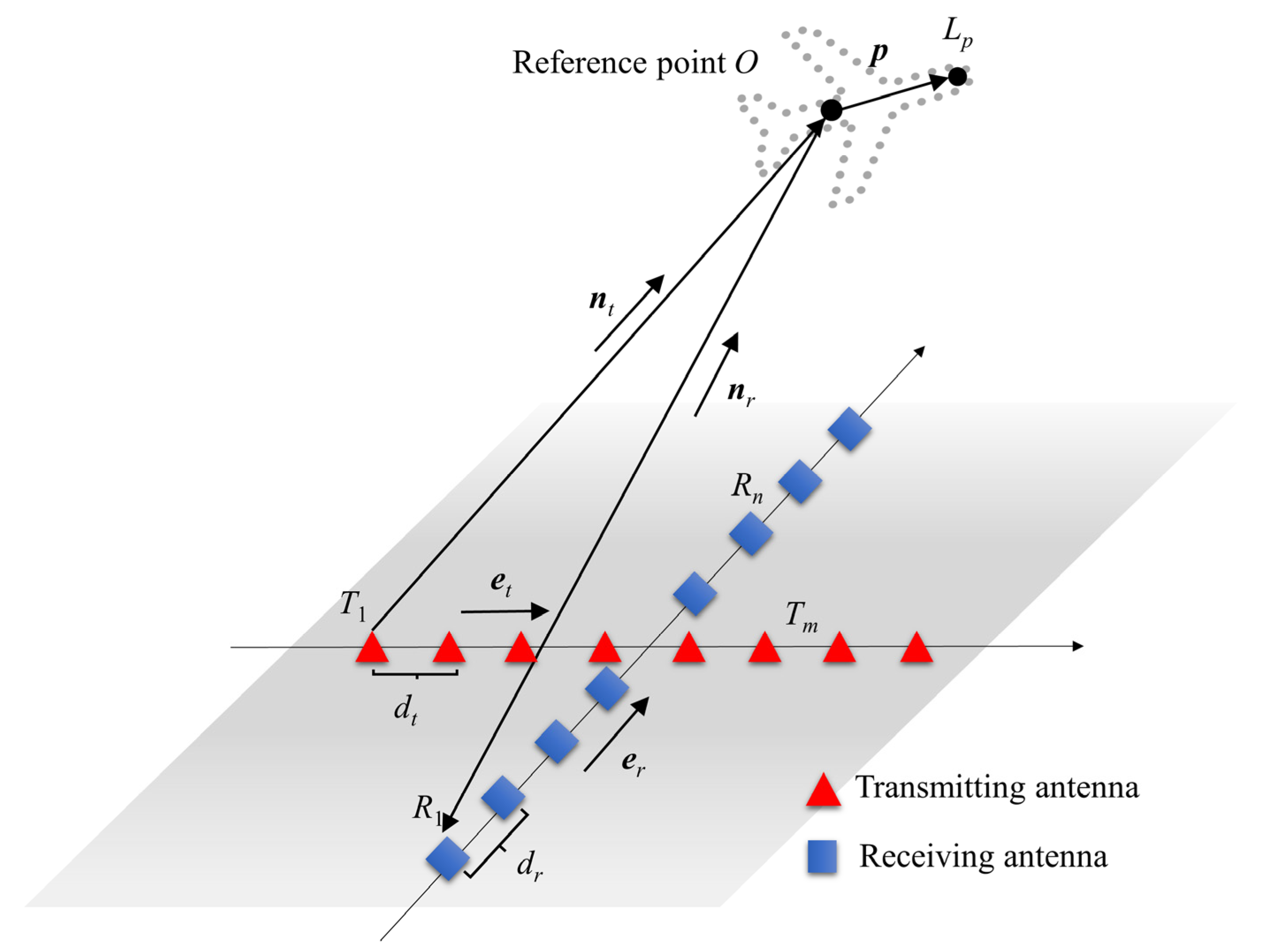
2. Theoretical Basics
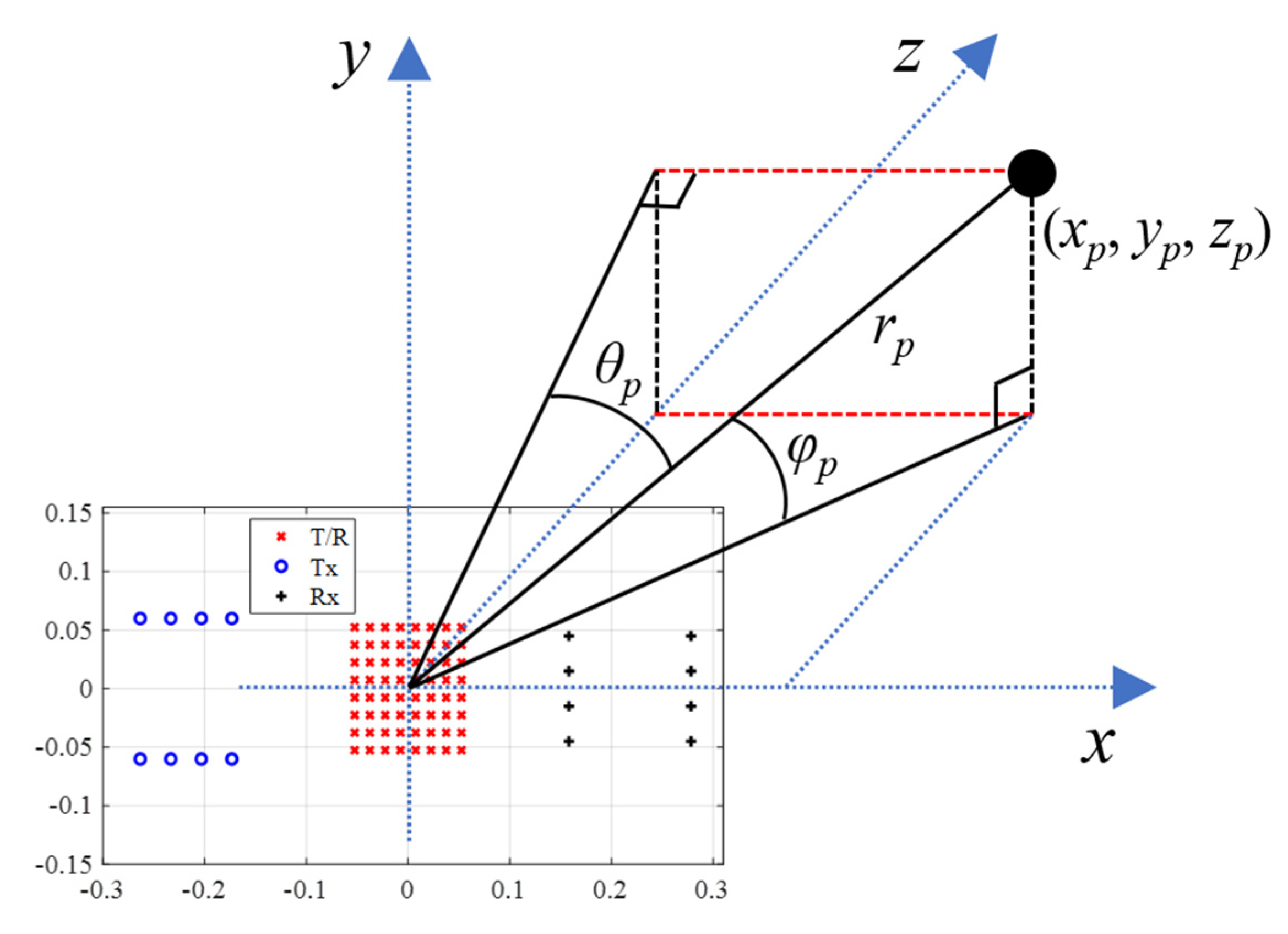
2.1. Signal Model
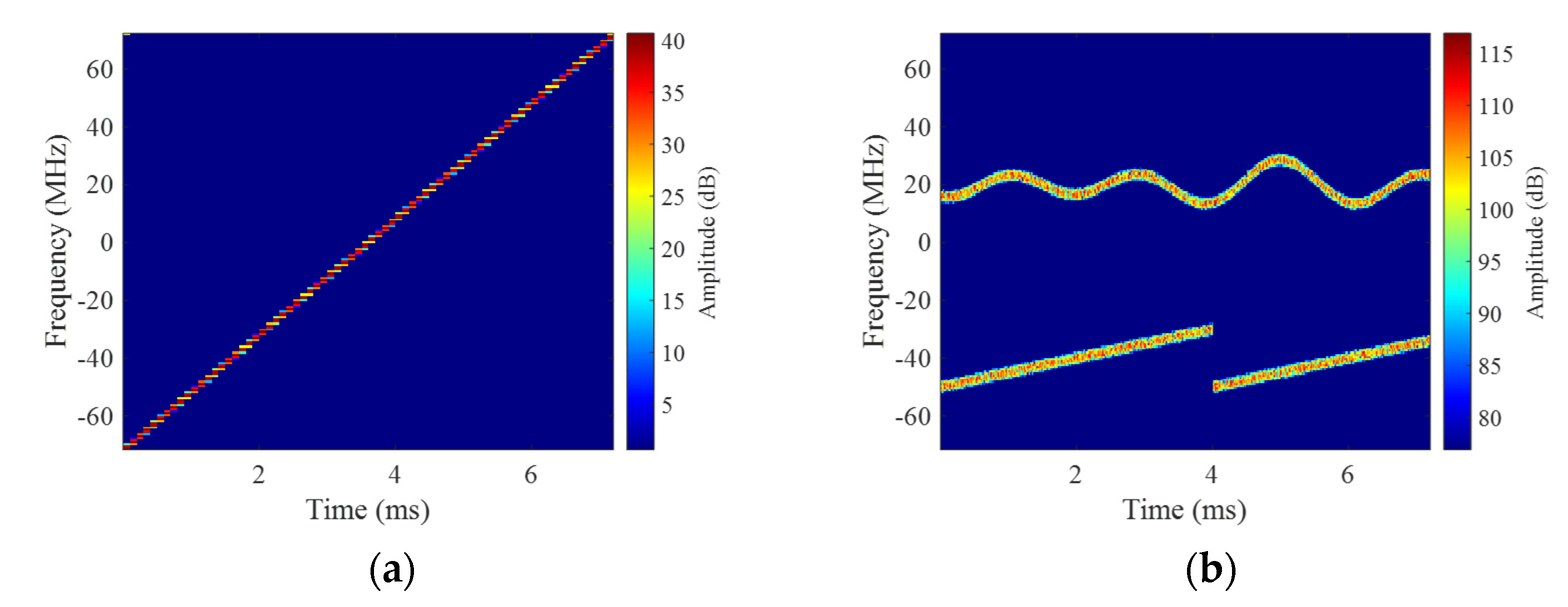
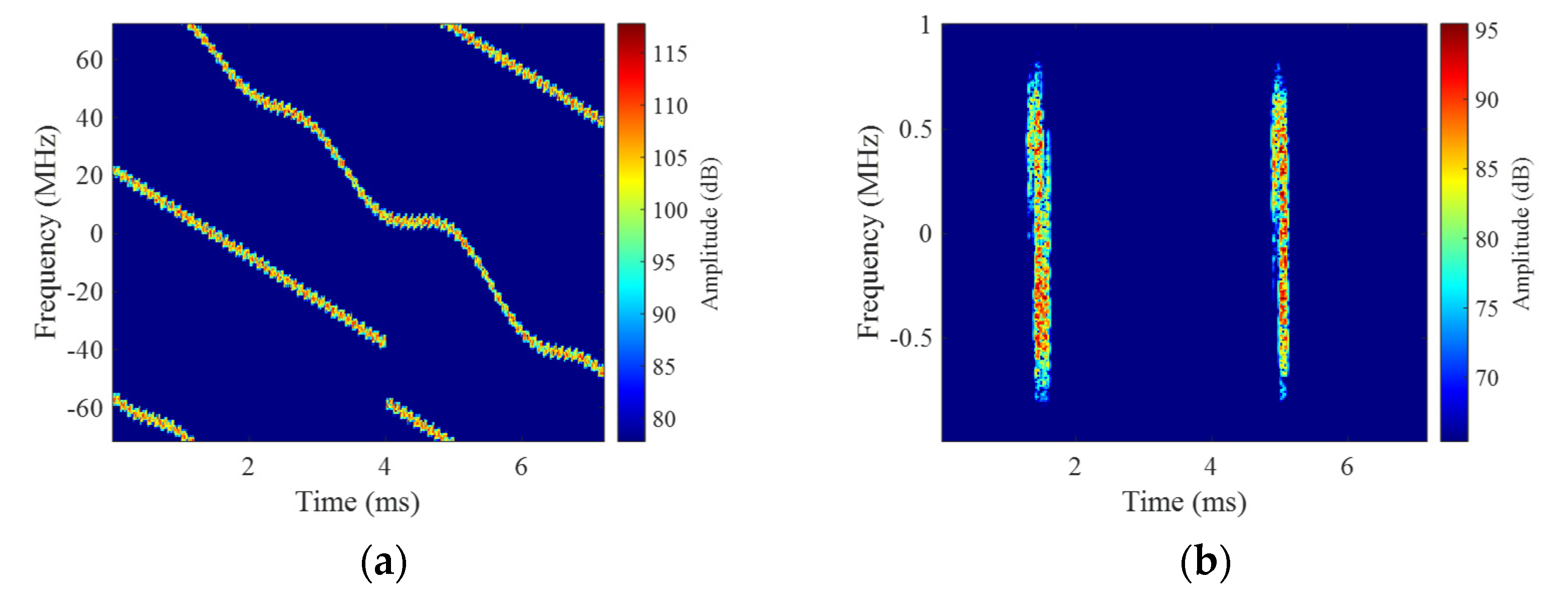
2.2. WBI Influences
2.3. Sparse Sampling (SS)
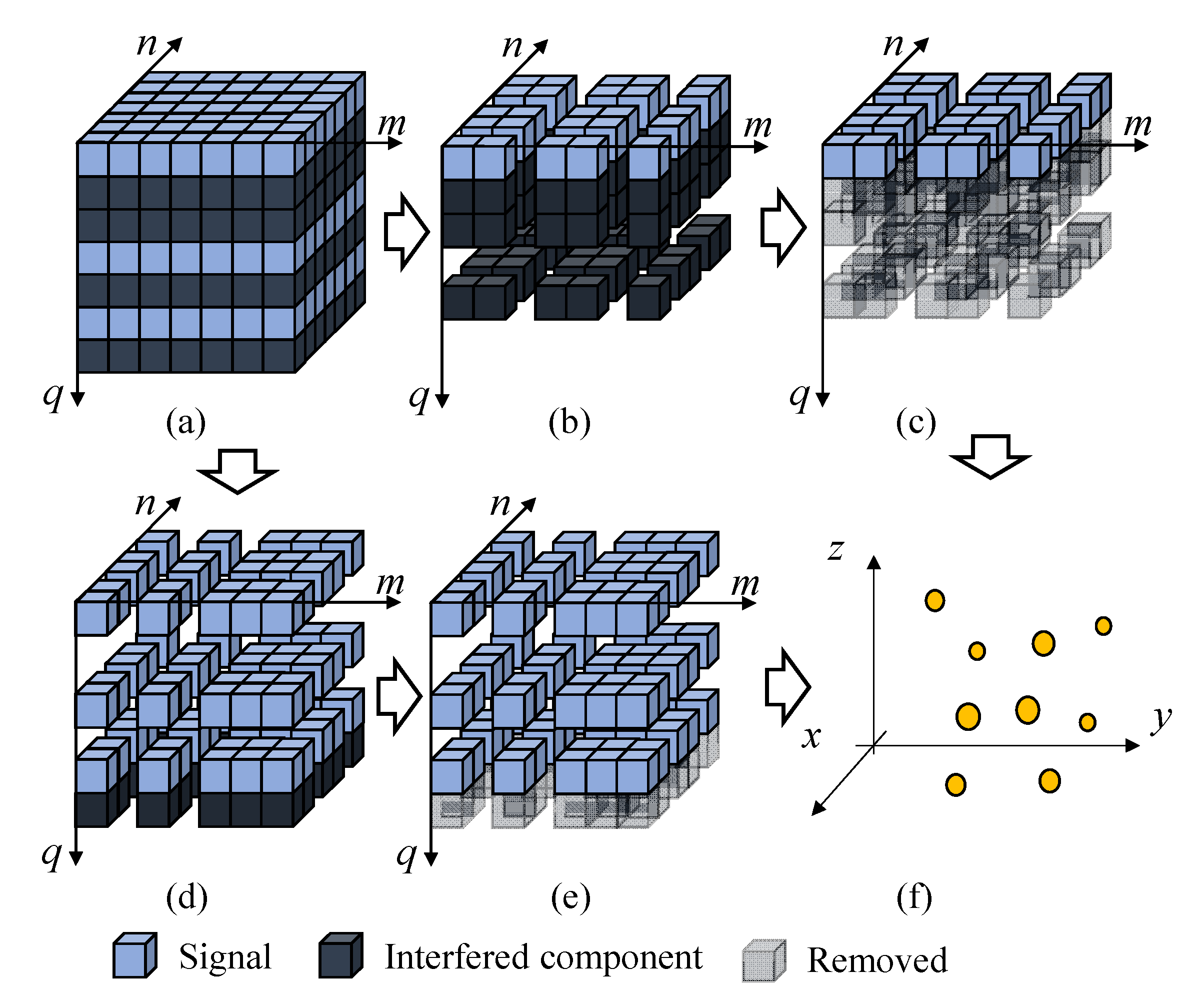
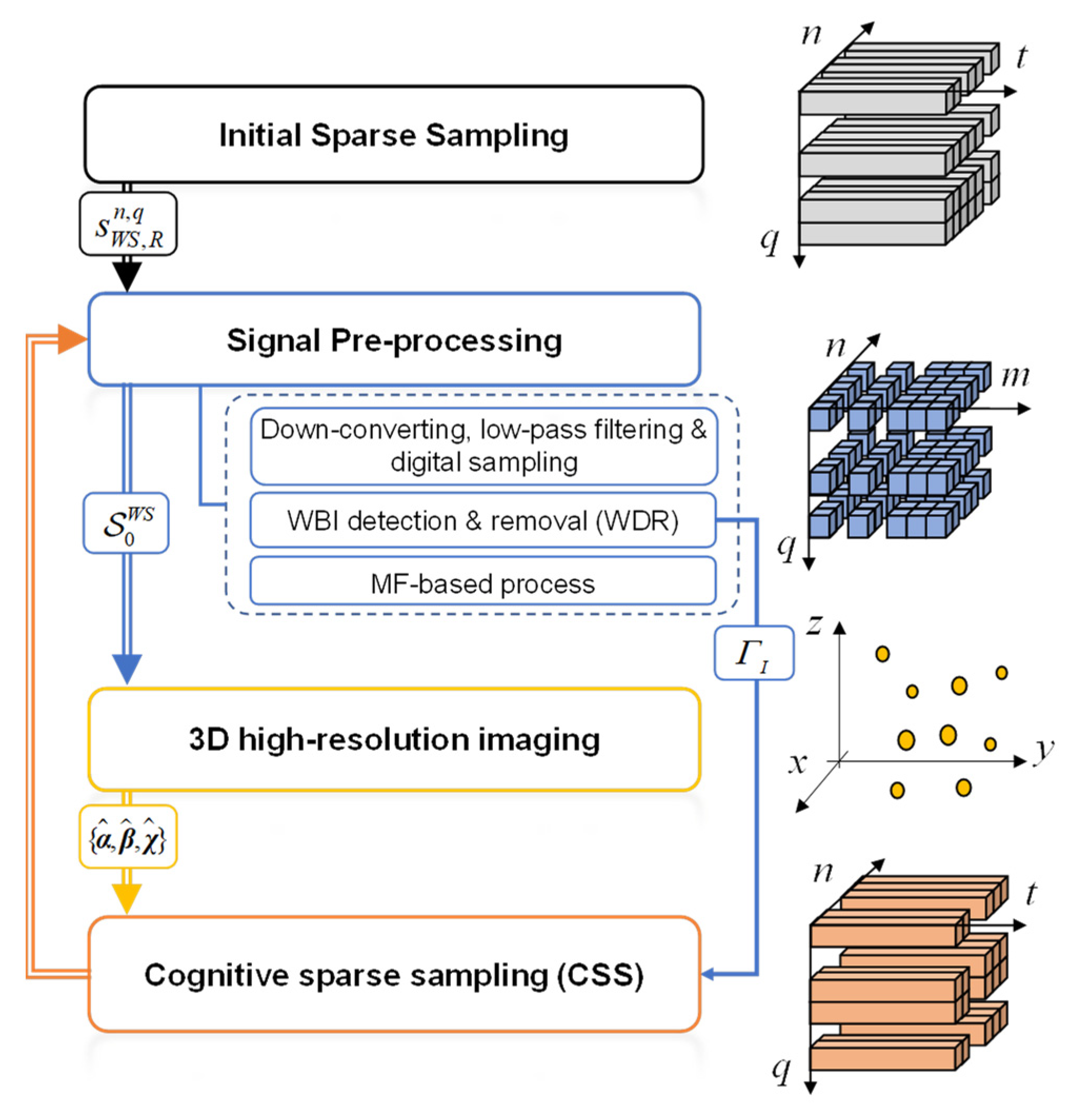
3. Cognitive Sparse Imaging Method
3.1. Cognitive Loop
3.1.1. Step 1: Initial Sparse Sampling
3.1.2. Step 2: Signal Pre-Processing
3.1.3. Step 3: 3D High-Resolution Imaging (HRI)
3.1.4. Step 4: Cognitive Sparse Sampling (CSS)
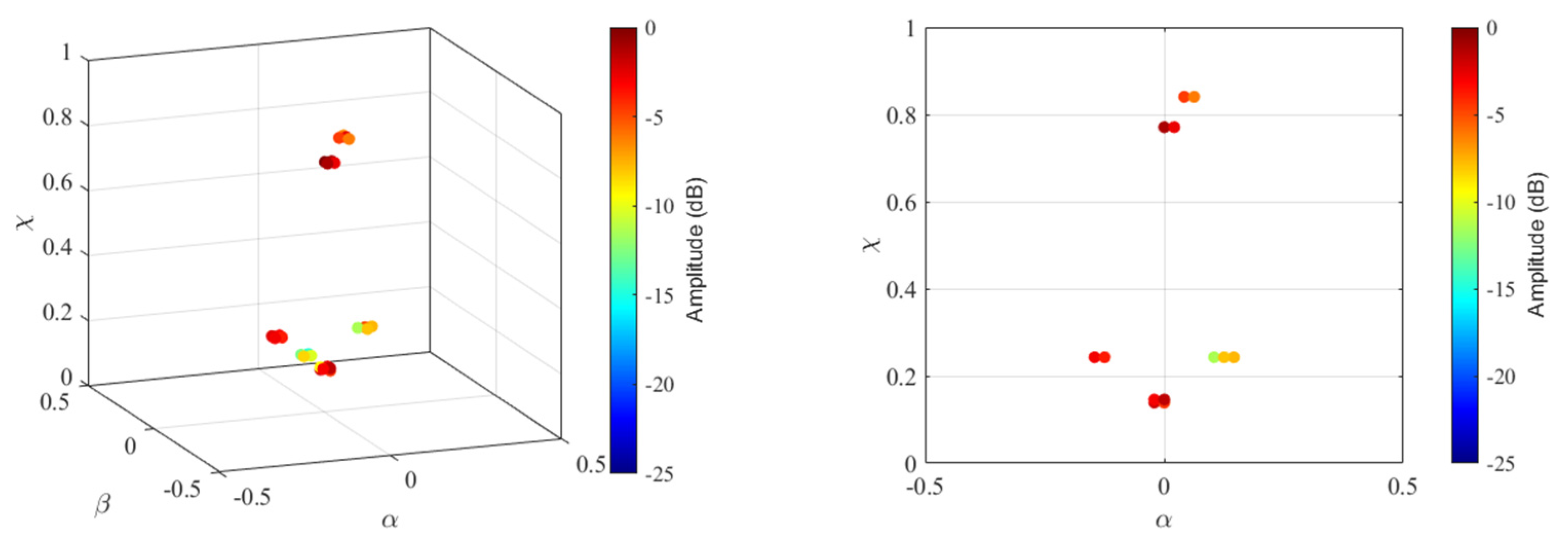
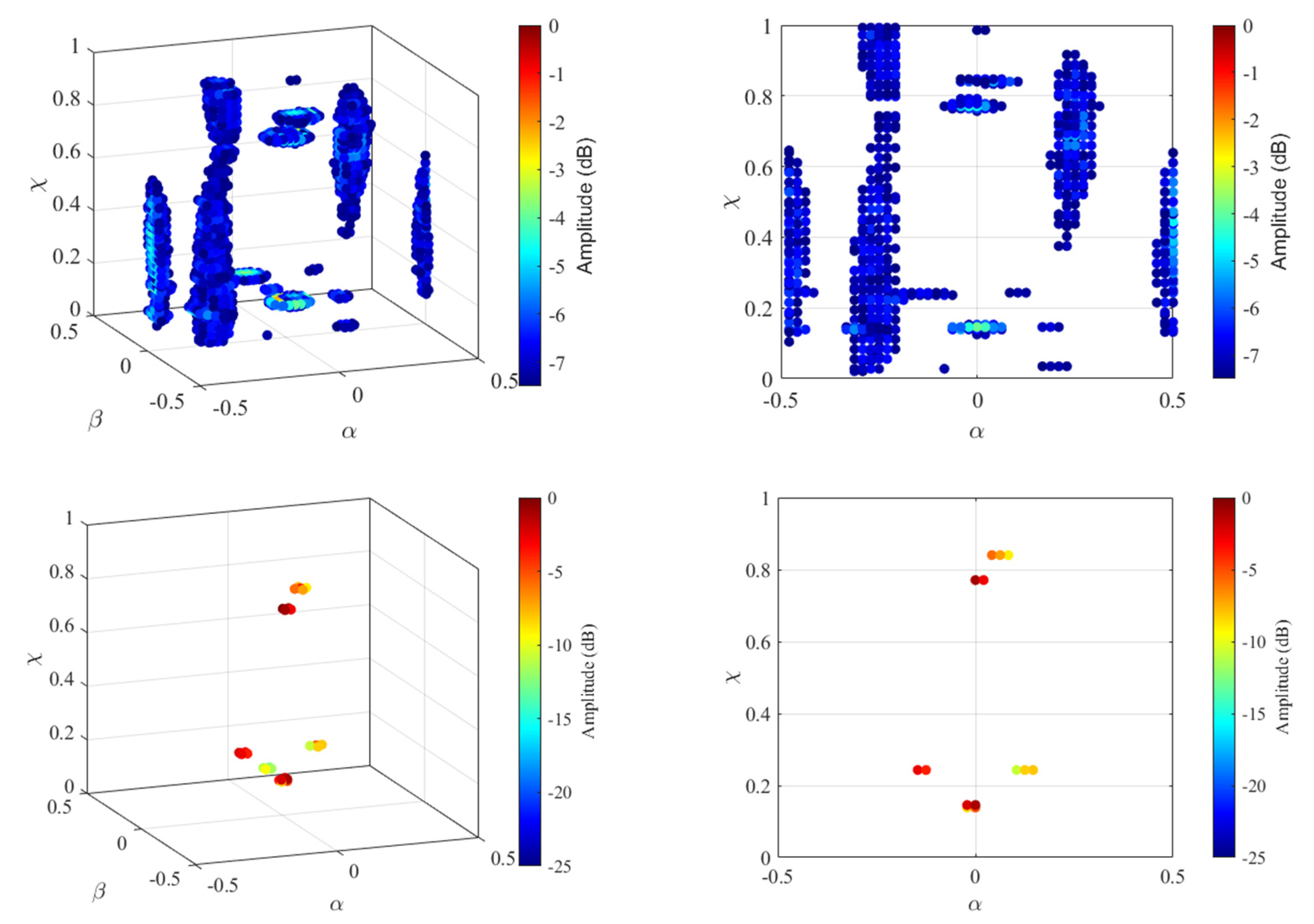
3.2. WDR Module
3.3. HRI Module
| Algorithms 1 Tensor-based SL0 (TSL0) algorithm |
| Input:, , , , iteration number W and H. Procedure: (1) Initialization: , a suitable decreasing sequence , the step size μ, and w = 1. (2) Let . (3) Minimize the cost function on the feasible set using H iterations of the steepest descent algorithm (followed by the projection onto the feasible set) as shown in the following and then go to (4). (3.1) Initialization ; (3.2) For : (3.2.1) ; (3.2.2) ; (3.2.3) . (4) Set and go to (5). (5) Let . If go back to (2), or else stop. Output: . |
3.4. CSS Module
| Algorithms 2 Greedy algorithm |
| Input:, , , , , , , , , and . Procedure: (1) Initialization: , , and . (2) Repetition: (2.1) If stop, or else continue; (2.2) Find the index satisfying: ; (2.3) and . Output: . |
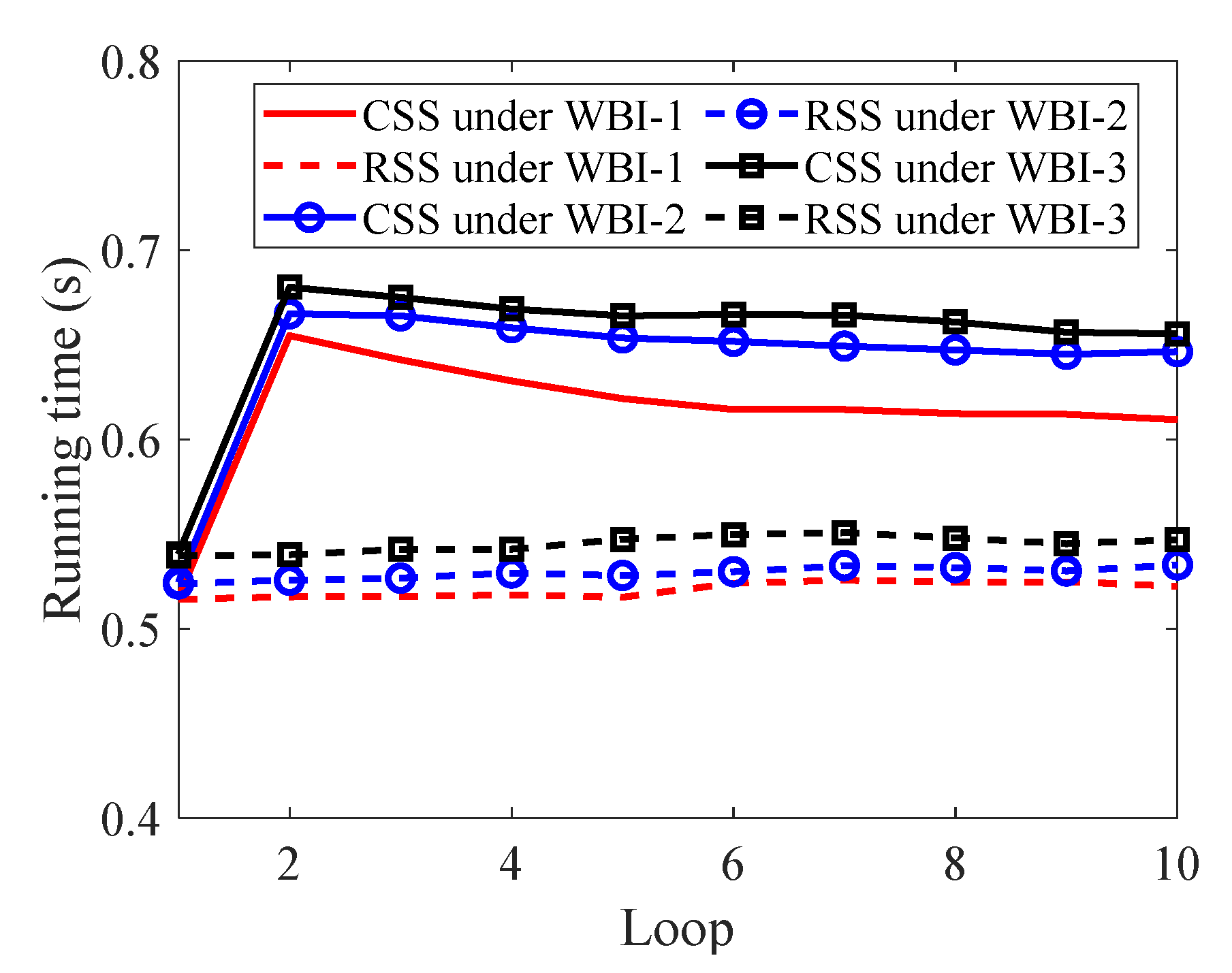
3.5. Complexity Analysis
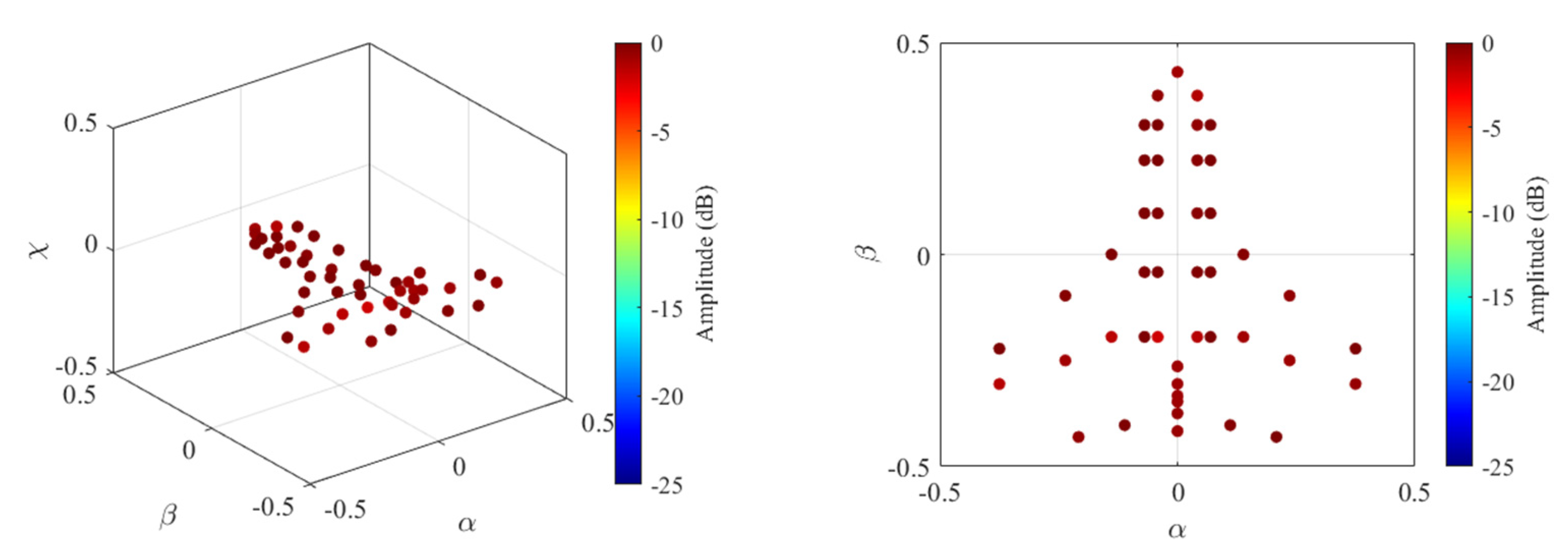
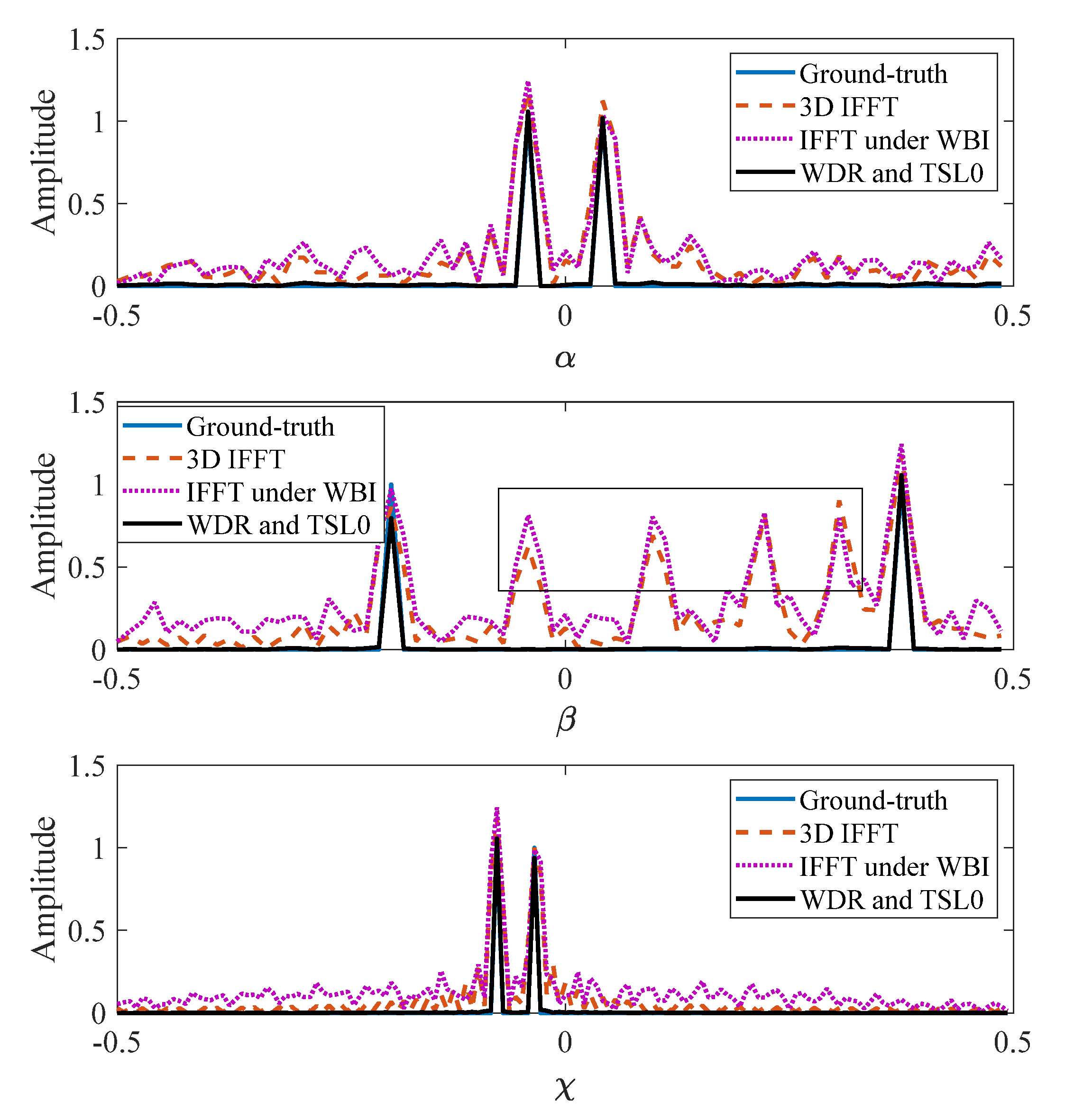
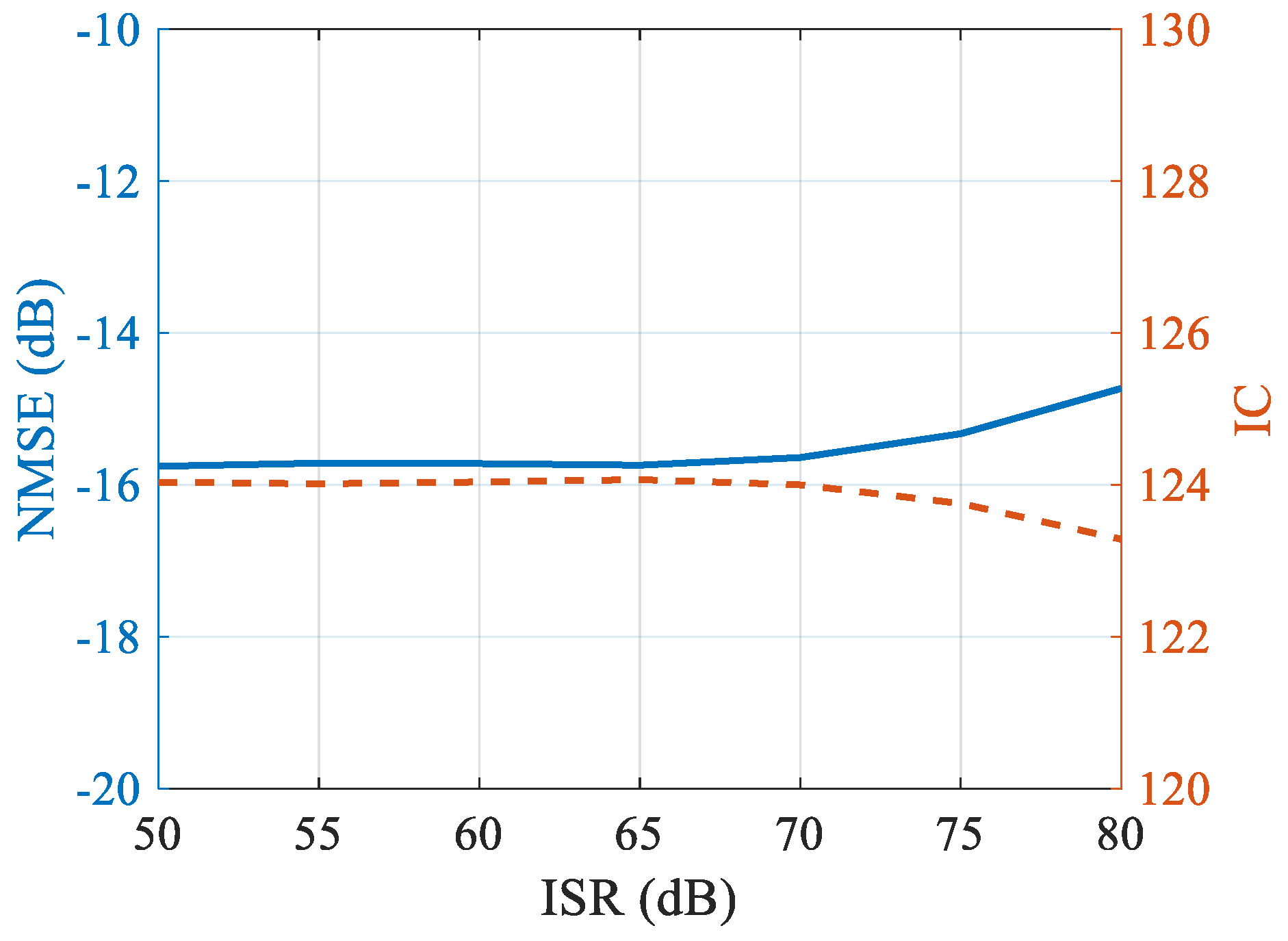
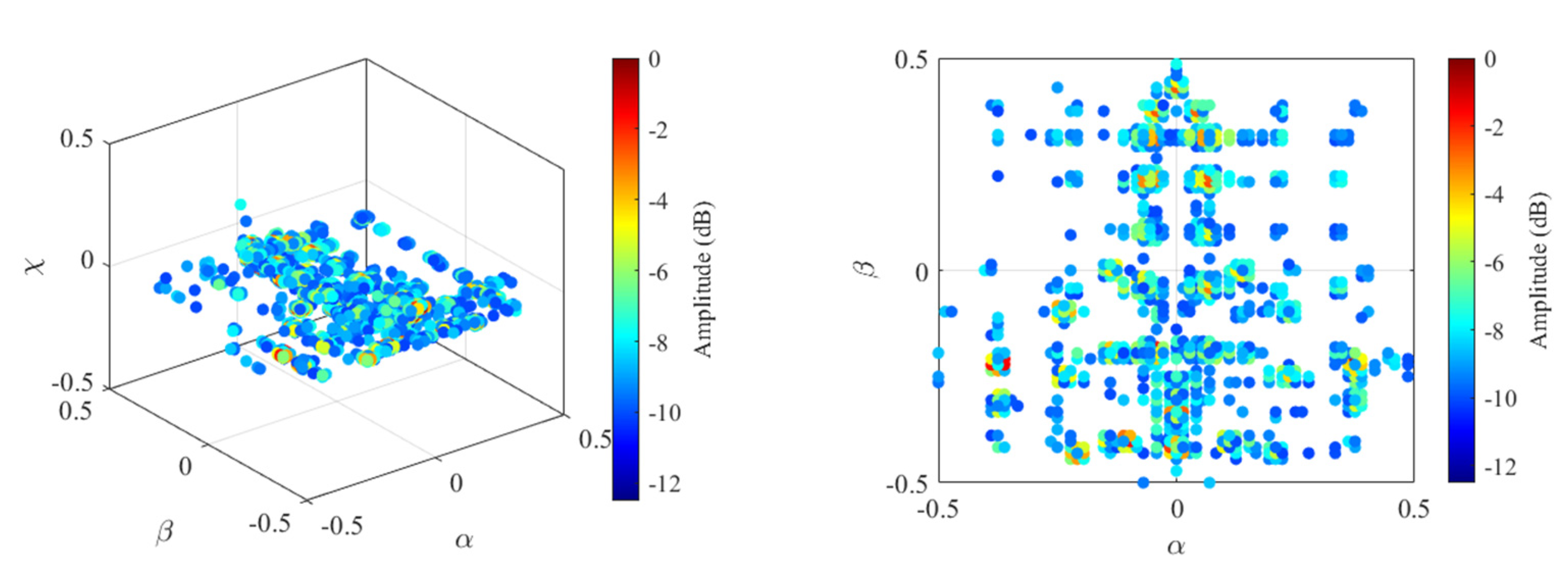
4. Simulation Results
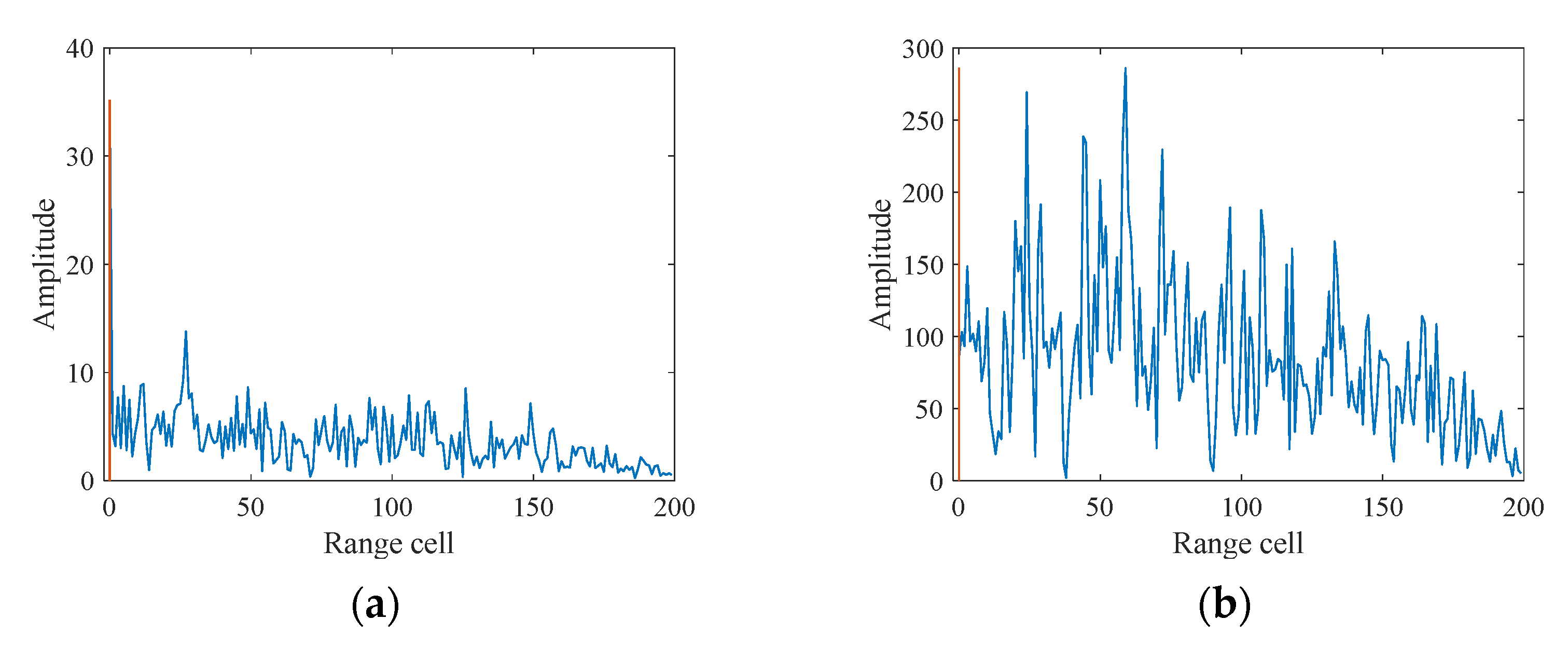
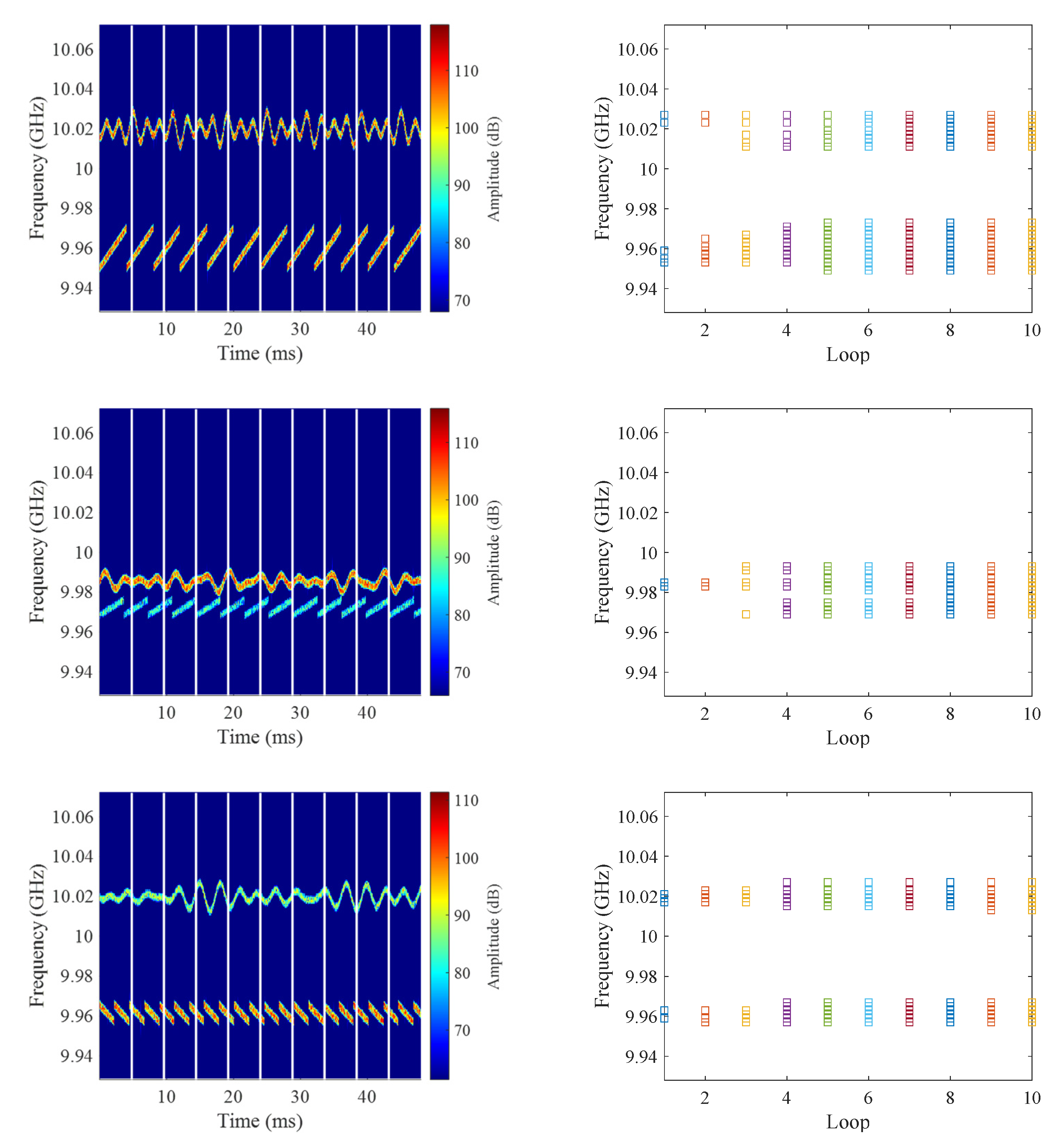
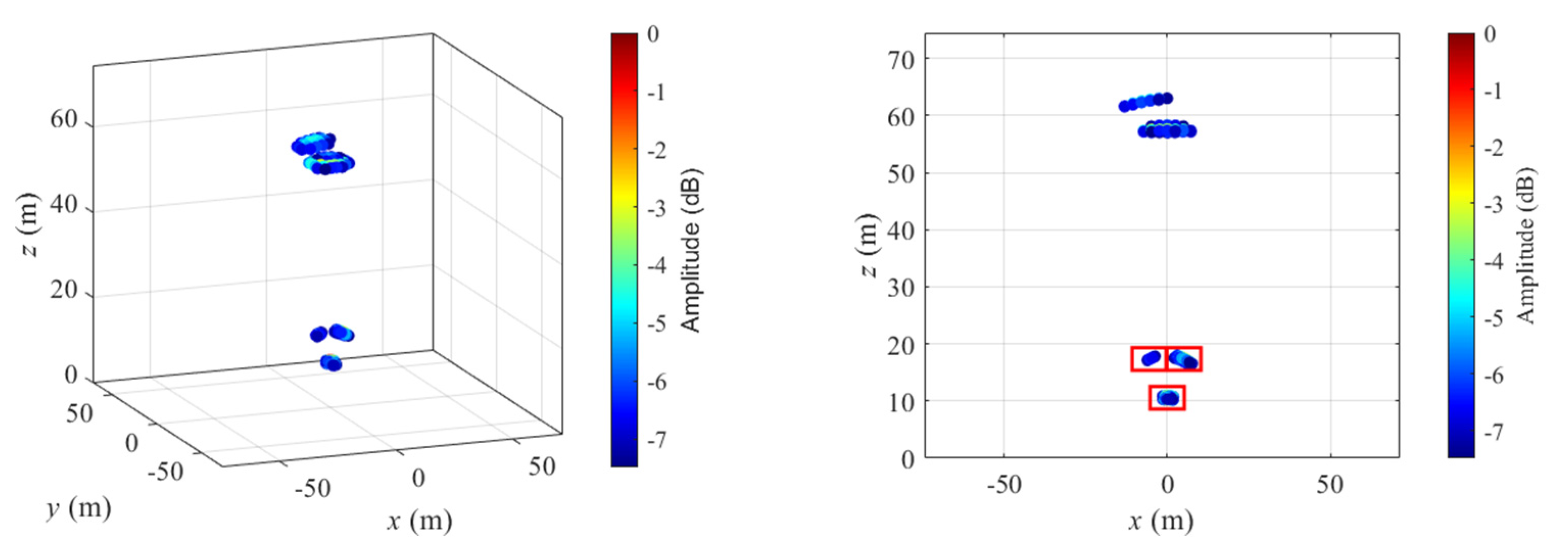
4.1. Imaging Results under WBI
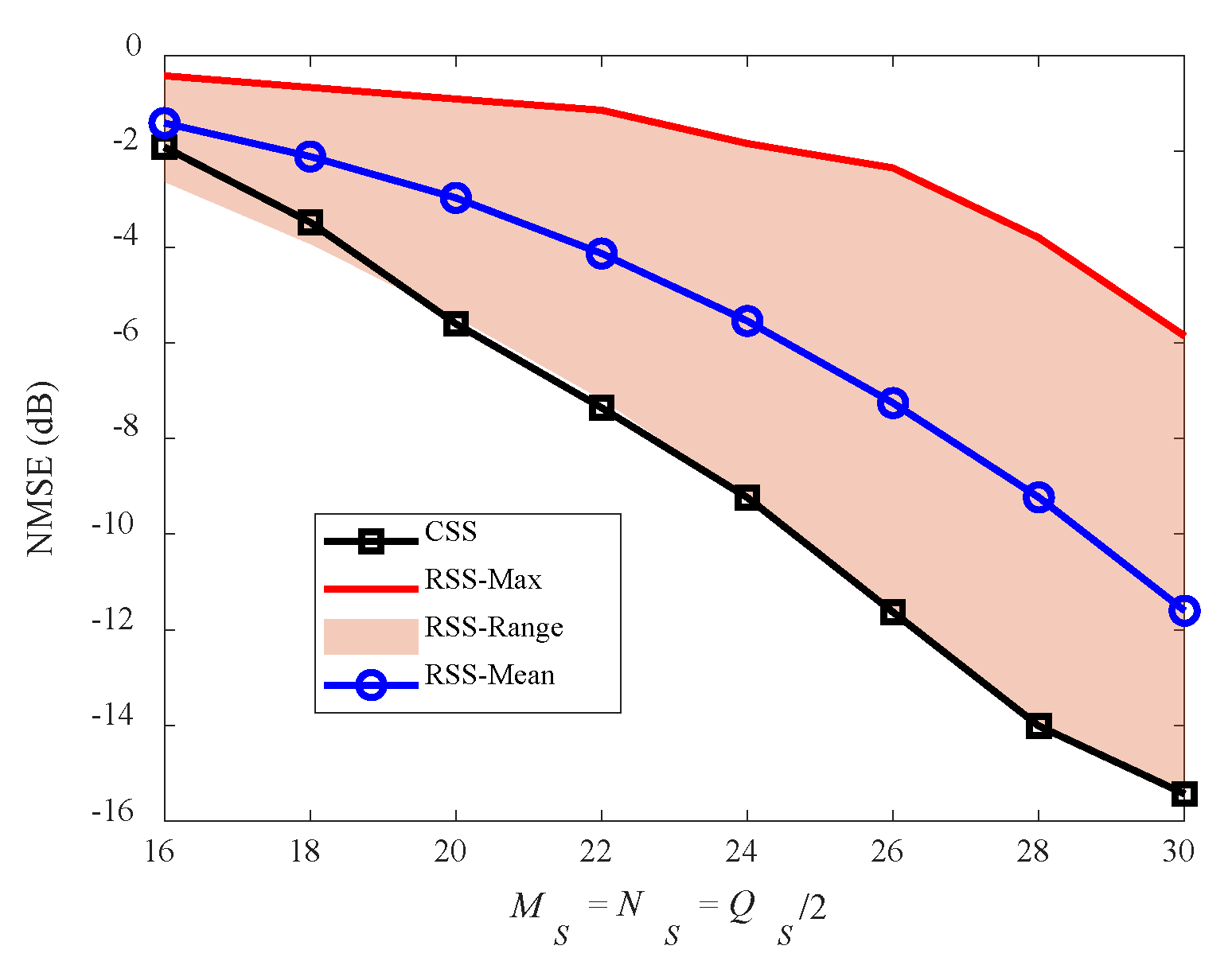
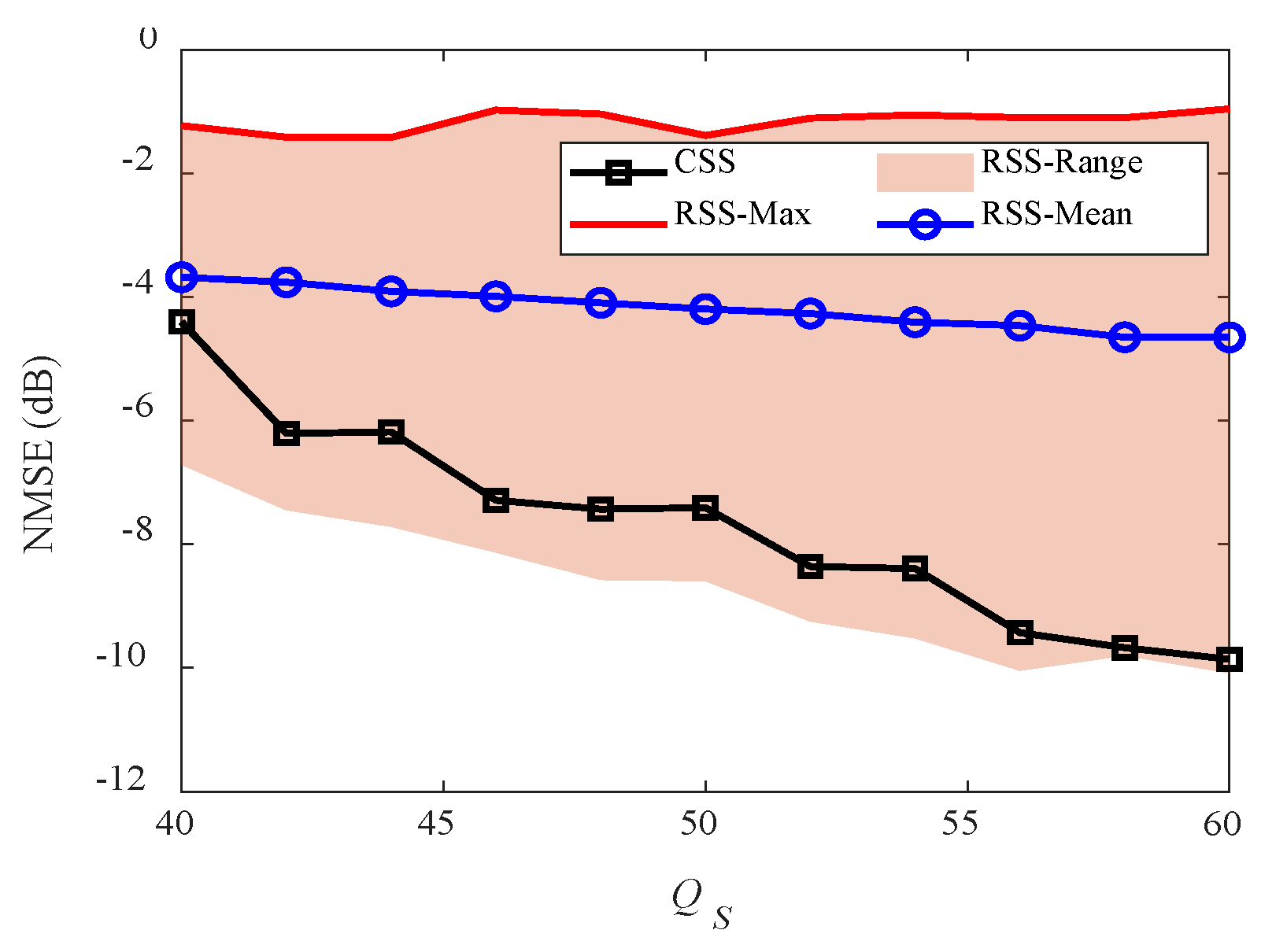
4.2. Imaging Results under SS
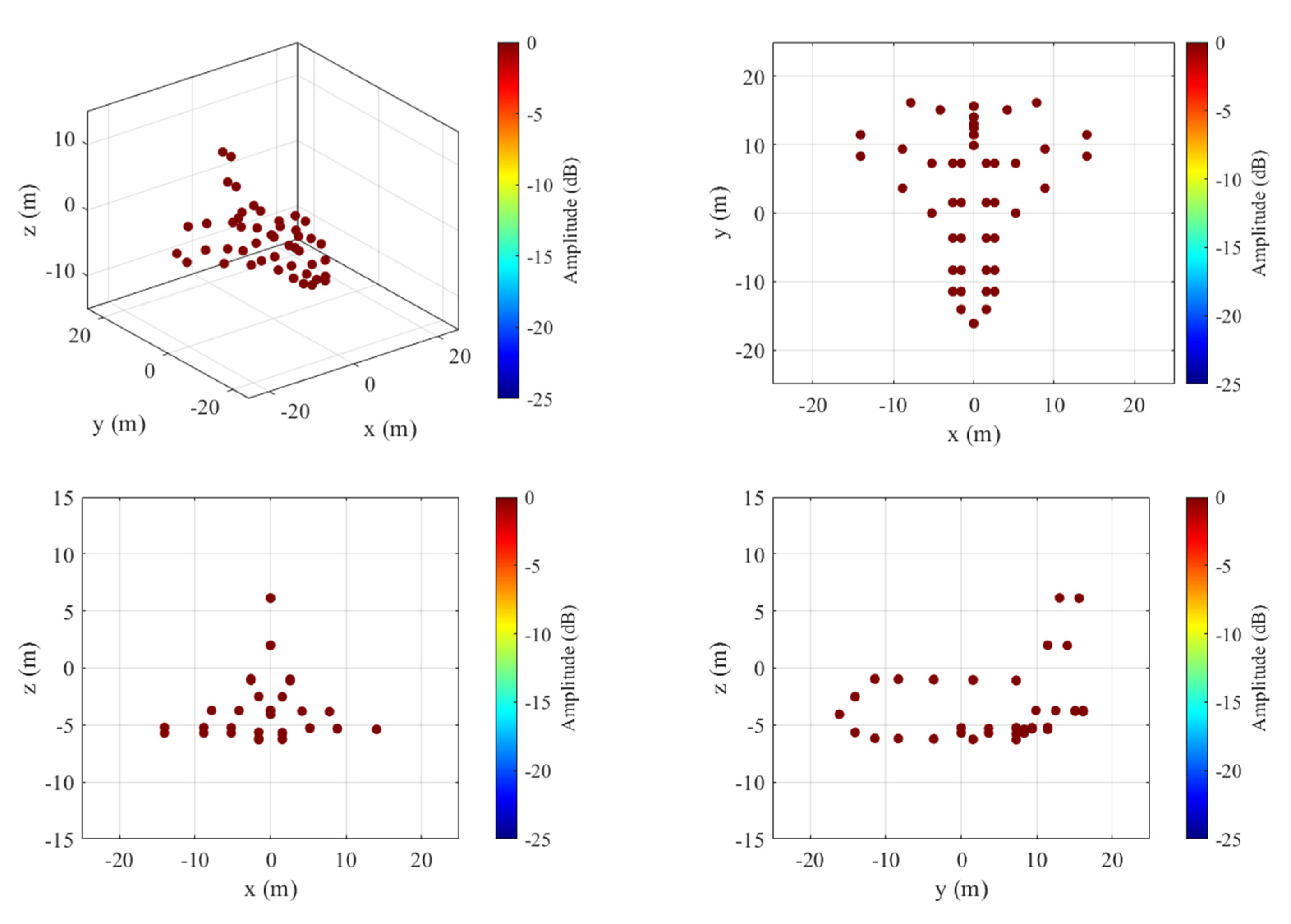
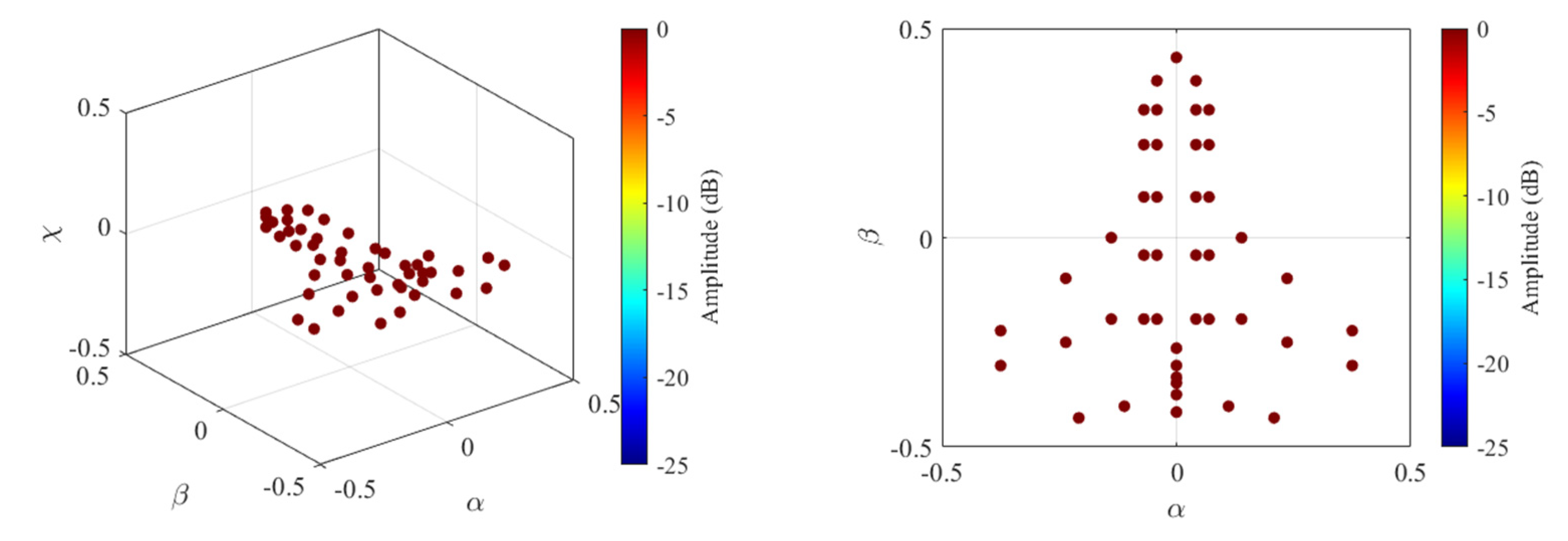
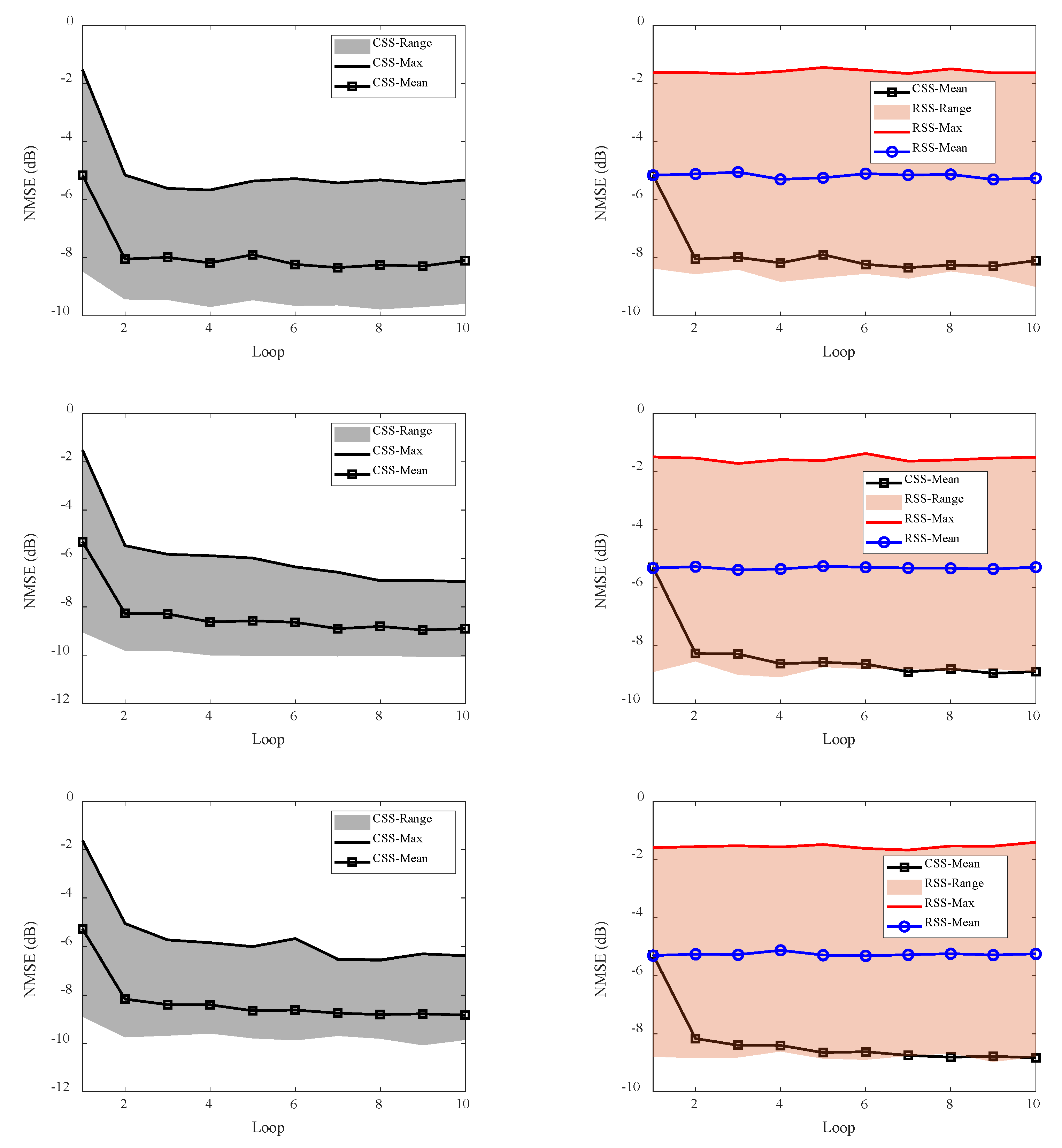
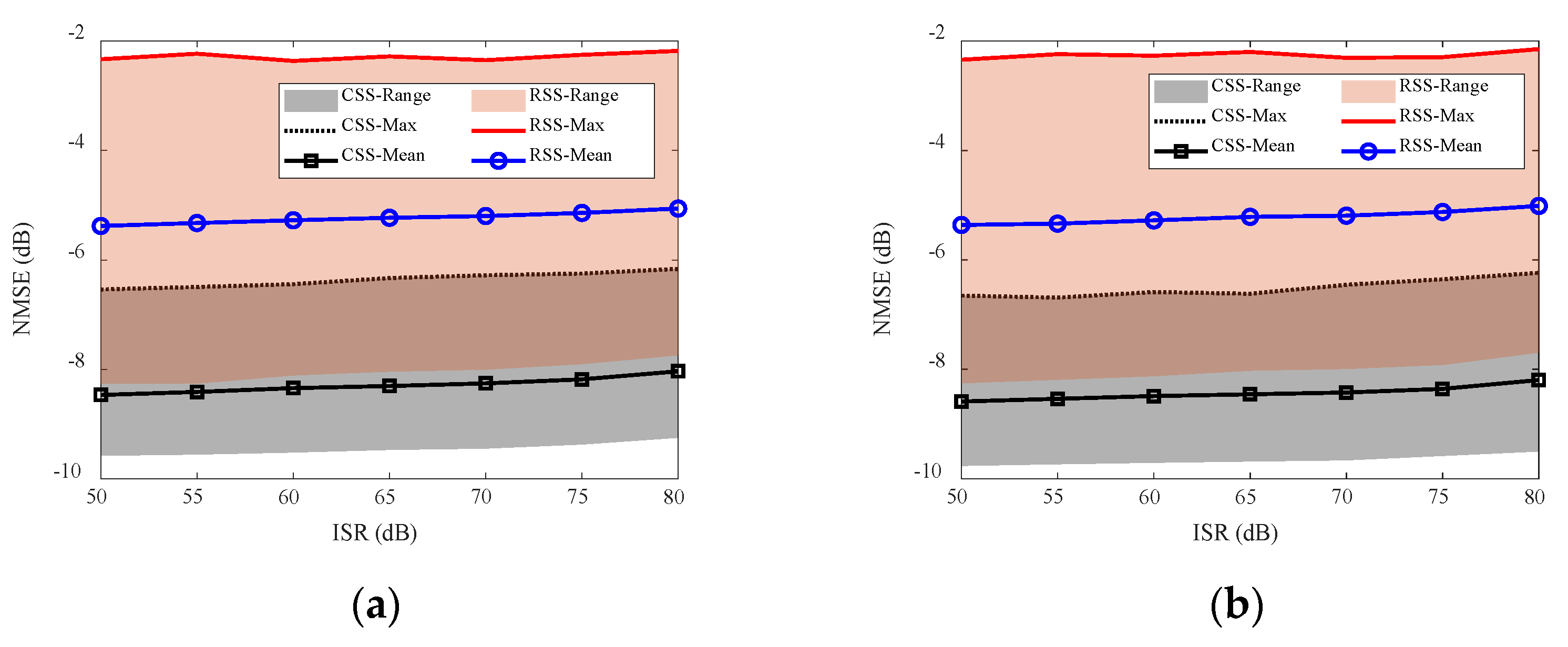
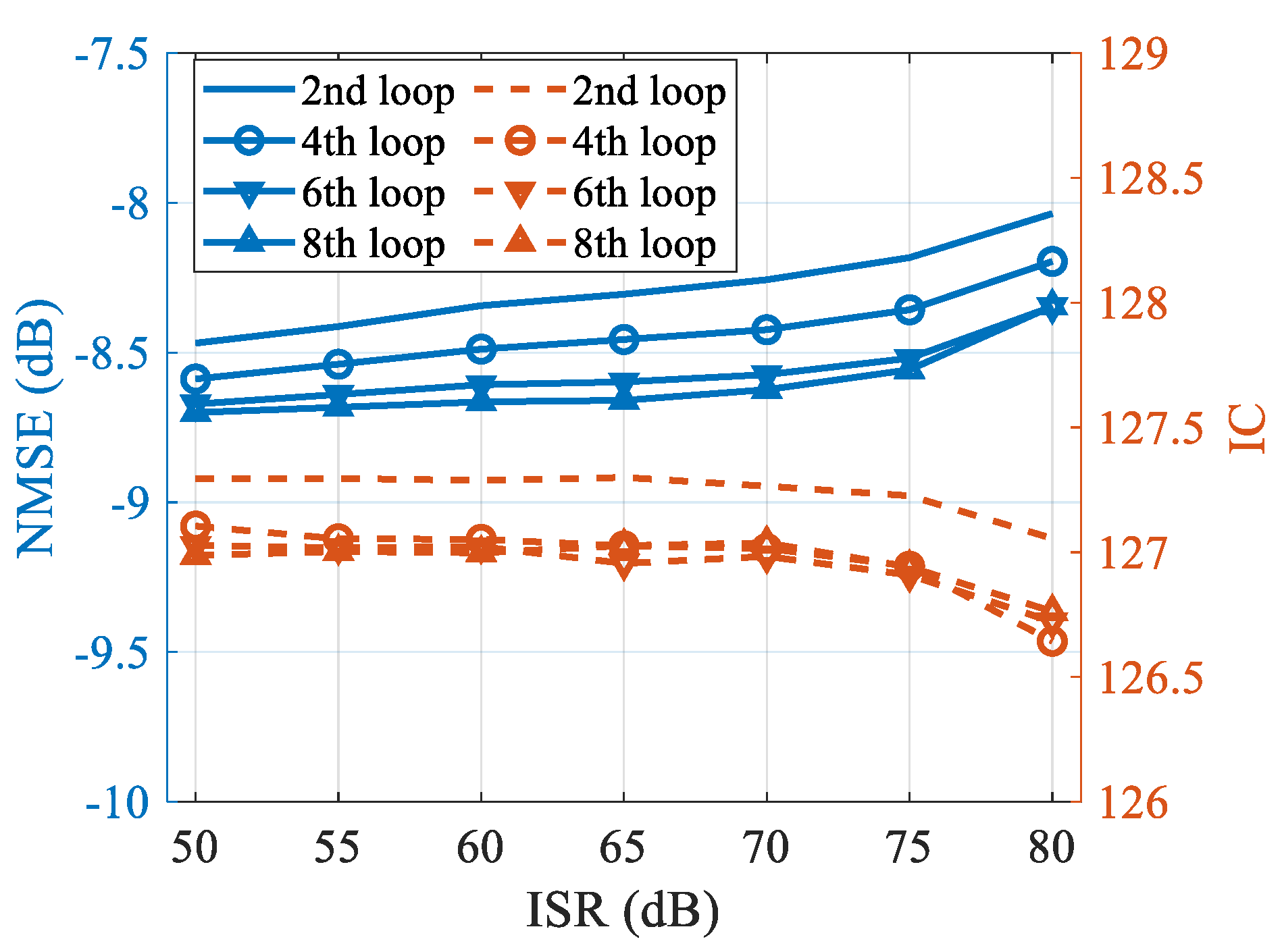
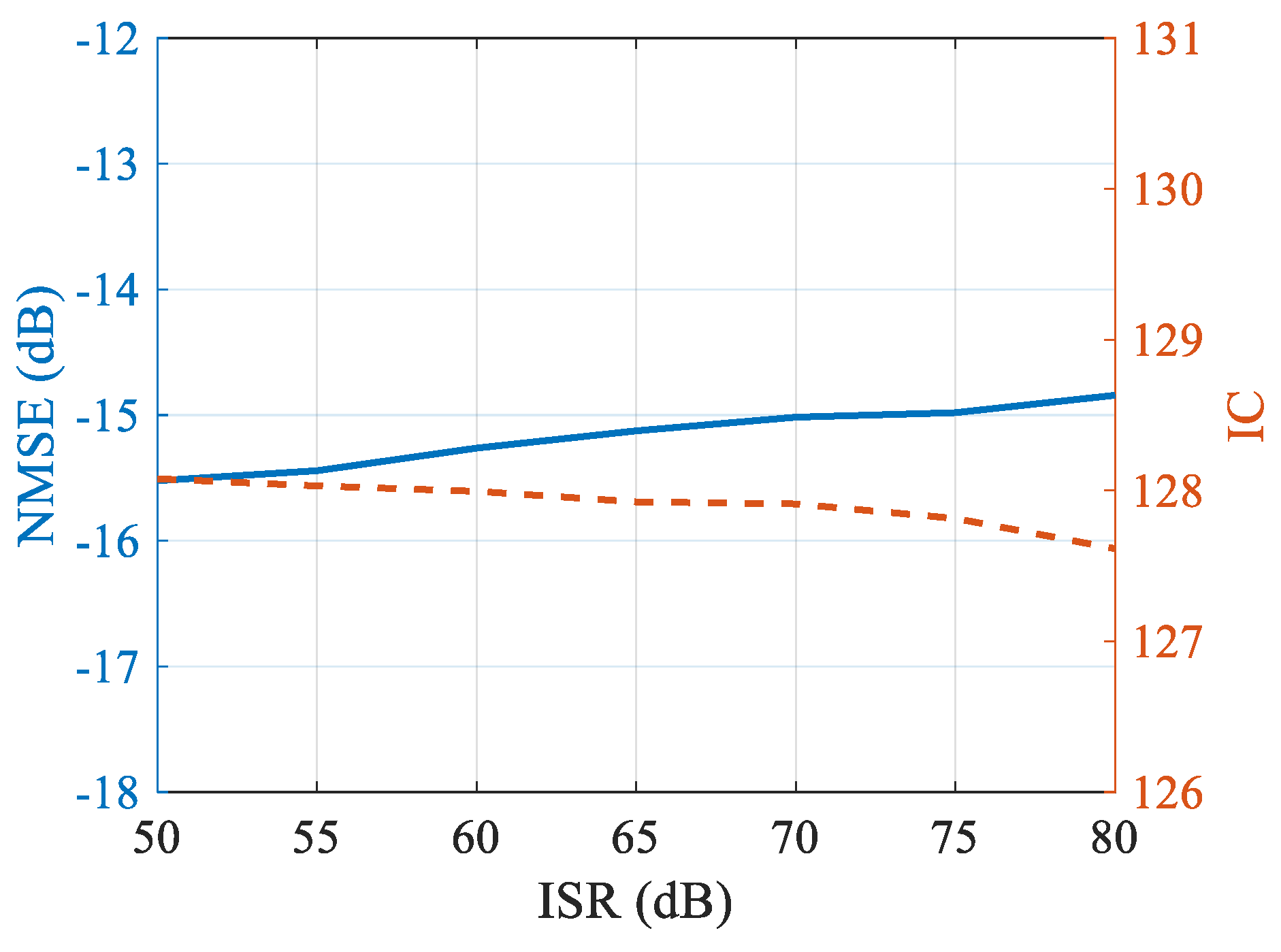
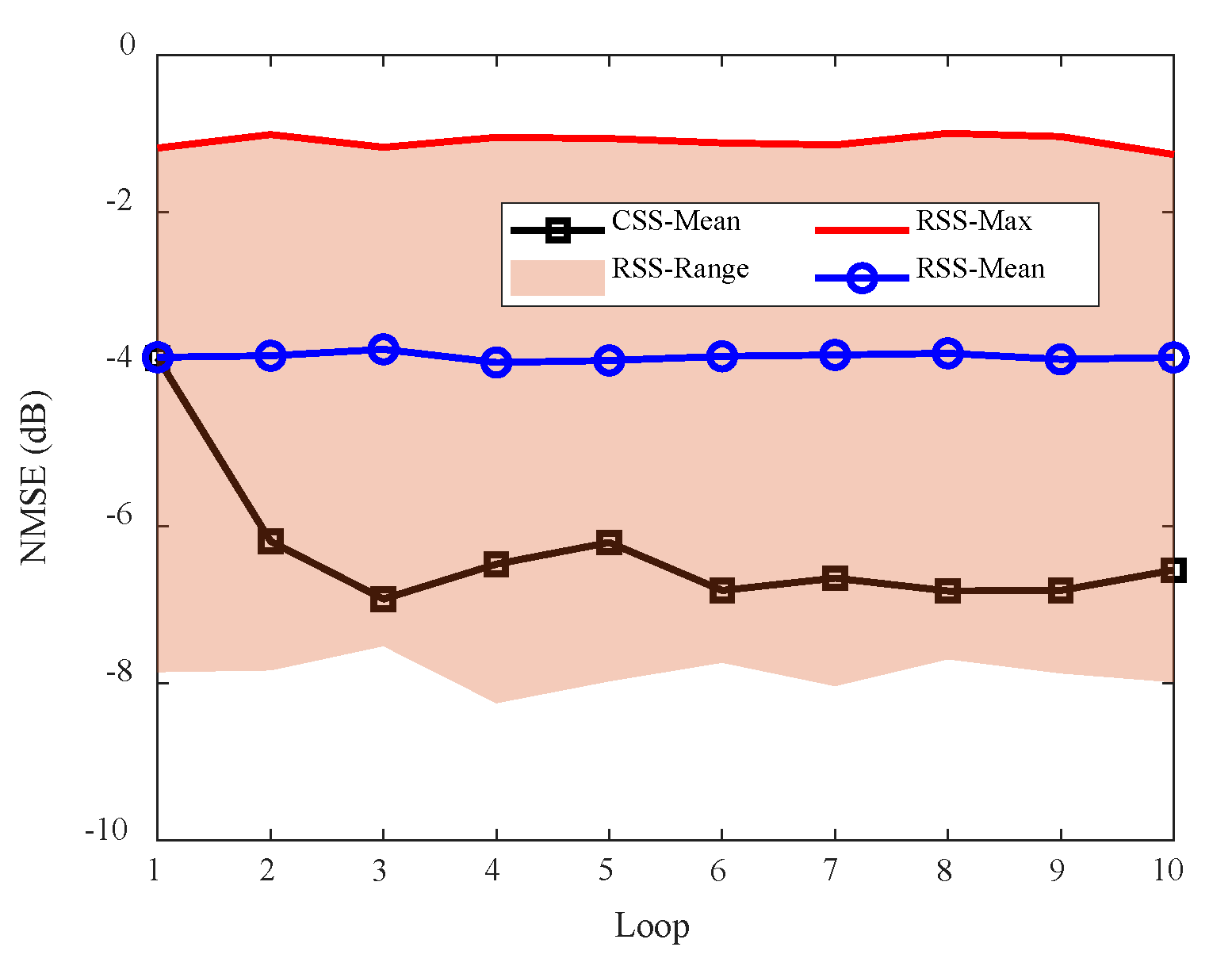
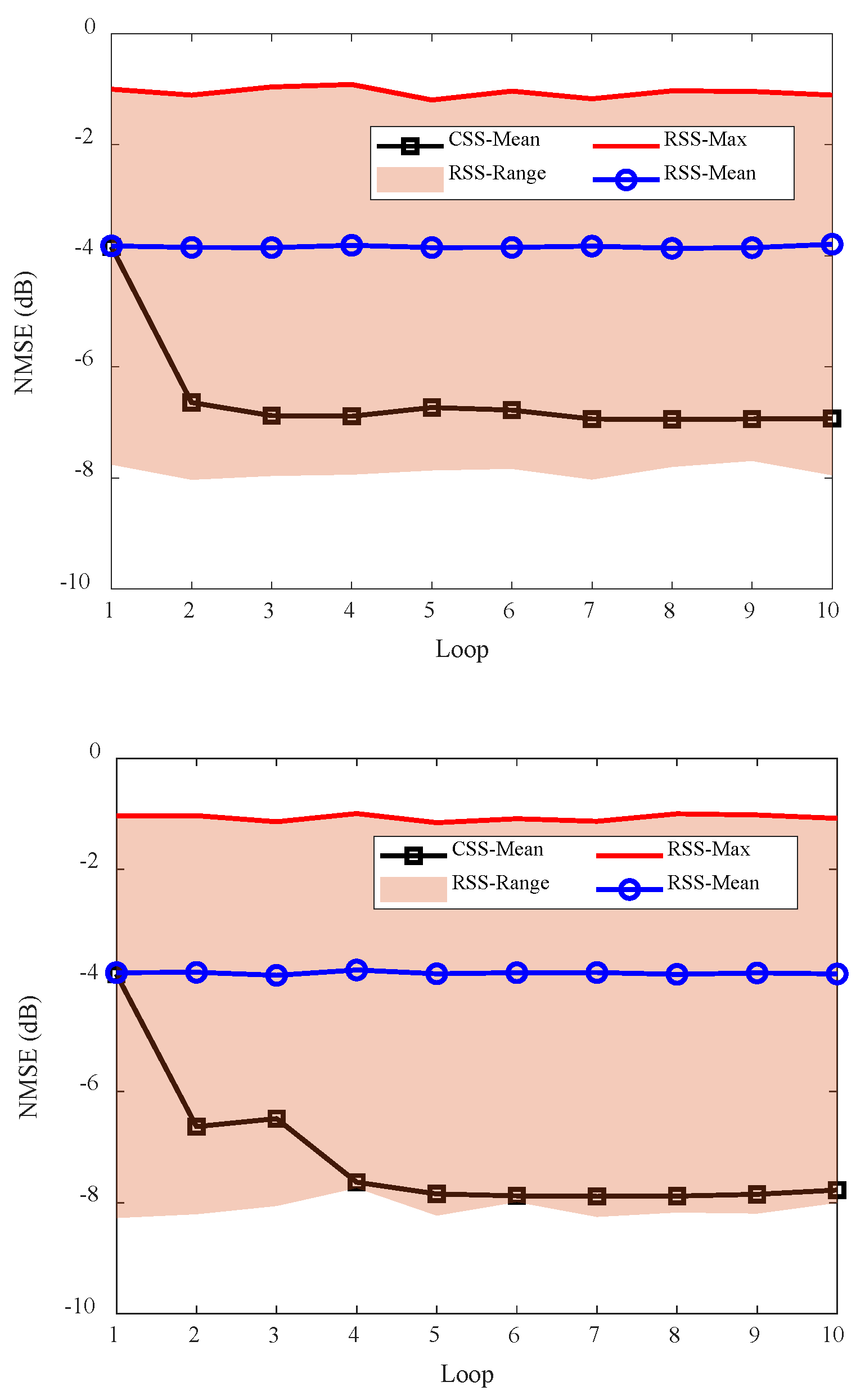
4.3. Cognitive Imaging under SS and WBI
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Duan, G.; Wang, D.; Ma, X.; Su, Y. Three-dimensional imaging via wideband MIMO radar system. IEEE Geosci. Remote Sens. Lett. 2010, 7, 445–449. [Google Scholar] [CrossRef]
- Hu, X.; Tong, N.; Guo, Y.; Ding, S. MIMO radar 3-D imaging based on multi-dimensional sparse recovery and signal support prior information. IEEE Sens. J. 2018, 18, 3152–3162. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Tran, T.D. Efficient and robust RFI extraction via sparse recovery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2104–2117. [Google Scholar] [CrossRef]
- Tao, M.; Su, J.; Huang, Y.; Wang, L. Mitigation of radio frequency interference in synthetic aperture radar data: Current status and future trends. Remote Sens. 2019, 11, 2438. [Google Scholar] [CrossRef]
- Rossi, M.; Haimovich, A.M.; Eldar, Y.C. Spatial compressive sensing for MIMO radar. IEEE Trans. Signal Process. 2013, 62, 419–430. [Google Scholar] [CrossRef]
- Hu, X.; Tong, N.; Wang, J.; Ding, S.; Zhao, X. Matrix completion-based MIMO radar imaging with sparse planar array. Signal Process. 2017, 131, 49–57. [Google Scholar] [CrossRef]
- Feng, W.; Friedt, J.-M.; Nico, G.; Sato, M. 3-D ground-based imaging radar based on C-band cross-MIMO array and tensor compressive sensing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1585–1589. [Google Scholar] [CrossRef]
- Cohen, D.; Eldar, Y.C.; Haimovich, A.M. SUMMeR: Sub-Nyquist MIMO radar. IEEE Trans. Signal Process. 2018, 66, 4315–4330. [Google Scholar] [CrossRef]
- Ding, S.; Tong, N.; Zhang, Y.; Hu, X.; Zhao, X. Cognitive antenna selection in MIMO imaging radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9829–9841. [Google Scholar] [CrossRef]
- Mishra, K.V.; Eldar, Y.C.; Shoshan, E.; Namer, M.; Meltsin, M. A cognitive sub-Nyquist MIMO radar prototype. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 937–955. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Z.; Wen, C.; Li, J.; Xia, X.; Hong, W. An efficient radio frequency interference mitigation algorithm in real synthetic aperture radar data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5224912. [Google Scholar] [CrossRef]
- Yang, Z.; Du, W.; Liu, Z.; Liao, G. WBI suppression for SAR using iterative adaptive method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1008–1014. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Li, J.; Hong, W.; Nehorai, A. A novel tensor technique for simultaneous narrowband and wideband interference suppression on single-channel SAR system. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9575–9588. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Li, J.; Chen, Z.; Yang, X. Reweighted tensor factorization method for SAR narrowband and wideband interference mitigation using smoothing multiview tensor model. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3298–3313. [Google Scholar] [CrossRef]
- Ding, Y.; Fan, W.; Tao, M.; Zhang, Z.; Wang, L.; Zhou, F.; Lu, B. Wideband interference mitigation for synthetic aperture radar based on the variational Bayesian method. Signal Process. 2022, 198, 108581. [Google Scholar] [CrossRef]
- Kirk, B.H.; Narayanan, R.M.; Gallagher, K.A.; Martone, A.F.; Sherbondy, K.D. Avoidance of time-varying radio frequency interference with software-defined cognitive radar. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1090–1107. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Meng, H.; Wang, X. Cognitive random stepped frequency radar with sparse recovery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 858–870. [Google Scholar] [CrossRef]
- Pu, T.; Tong, N.; Feng, W.; Wan, P.; Hu, X. MIMO radar sparse recovery imaging with wideband interference prediction. Remote Sens. 2022, 14, 3774. [Google Scholar] [CrossRef]
- Wan, P.; Feng, W.; Tong, N.; Hu, X.; Zheng, G. Wideband interference time–frequency feature prediction and its application to cognitive radar HRRP estimation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4025105. [Google Scholar] [CrossRef]
- Nemhauser, G.; Wolsey, L.; Fisher, M. An analysis of approximations for maximizing submodular set functions-I. Mathematical programming 1978, 14, 265–294. [Google Scholar] [CrossRef]
- Shamaiah, M.; Banerjee, S.; Vikalo, H. Greedy sensor selection: Leveraging submodularity. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010. [Google Scholar]
- Kovacevic, J.; Chebira, A. Life beyond bases: The advent of frames (Part I). IEEE Signal Process. Mag. 2007, 24, 86–104. [Google Scholar] [CrossRef]
- Ortiz-Jiménez, G.; Coutino, M.; Chepuri, S.P.; Leus, G. Sparse sampling for inverse problems with tensors. IEEE Trans. Signal Processing 2019, 67, 3272–3286. [Google Scholar] [CrossRef]
- Trunk, G.V. Range resolution of targets using automatic detectors. IEEE Trans. Aerosp. Electron. Syst. 1978, 14, 750–755. [Google Scholar] [CrossRef]
- Qiu, W.; Zhou, J.; Zhao, H.; Fu, Q. Fast sparse reconstruction algorithm for multidimensional signals. Electron. Lett. 2014, 50, 1583–1585. [Google Scholar] [CrossRef]
- Qiu, W.; Zhou, J.; Zhao, H.; Fu, Q. Three-dimensional sparse turntable microwave imaging based on compressive sensing. IEEE Geosci. Remote Sens. Lett. 2015, 12, 826–830. [Google Scholar] [CrossRef]
- Ding, S.; Tong, N.; Zhang, Y.; Hu, X.; Zhao, X. Cognitive MIMO imaging radar based on Doppler filtering waveform separation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6929–6944. [Google Scholar] [CrossRef]
- Hu, X.; Feng, C.; Wang, Y.; Guo, Y. Adaptive waveform optimization for MIMO radar imaging based on sparse recovery. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2898–2914. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chang, X.; Tan, W.; Hong, W. Generalized pseudopolar format algorithm for radar imaging with highly suboptimal aperture length. Sci. China Inf. Sci. 2015, 58, 1–5. [Google Scholar] [CrossRef]
- Ding, S.; Tong, N.; Feng, W.; Wan, P.; Zhang, Y. Three-dimensional decoupling imaging method for wideband two-dimensional multiple-input-multiple-output radar. IET Radar Sonar Navig. 2022, 16, 399–411. [Google Scholar] [CrossRef]
- Qiu, W.; Zhou, J.; Fu, Q. Tensor representation for three-dimensional radar target imaging with sparsely sampled data. IEEE Trans. Comput. Imaging 2020, 6, 263–275. [Google Scholar] [CrossRef]
- Das, A.; Kempe, D. Submodular meets spectral: Greedy algorithms for subset selection, sparse approximation and dictionary selection. In Proceedings of the 28th International Conference on International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Ranieri, J.; Chebira, A.; Vetterli, M. Near-optimal sensor placement for linear inverse problems. IEEE Trans. Signal Process. 2014, 62, 1135–1146. [Google Scholar] [CrossRef]
- Joshi, S.; Boyd, S. Sensor selection via convex optimization. IEEE Trans. Signal Process. 2009, 57, 451–462. [Google Scholar] [CrossRef]
- Feng, W.; Friedt, J.-M.; Wan, P. SDR-implemented ground-based interferometric radar for displacement measurement. IEEE Trans. Instrum. Meas. 2021, 70, 8502218. [Google Scholar] [CrossRef]
- Feng, W.; Friedt, J.-M.; Nico, G.; Wang, S.; Martin, G.; Sato, M. Passive bistatic ground-based synthetic aperture radar: Concept, system, and experiment results. Remote Sens. 2019, 11, 1753. [Google Scholar] [CrossRef]
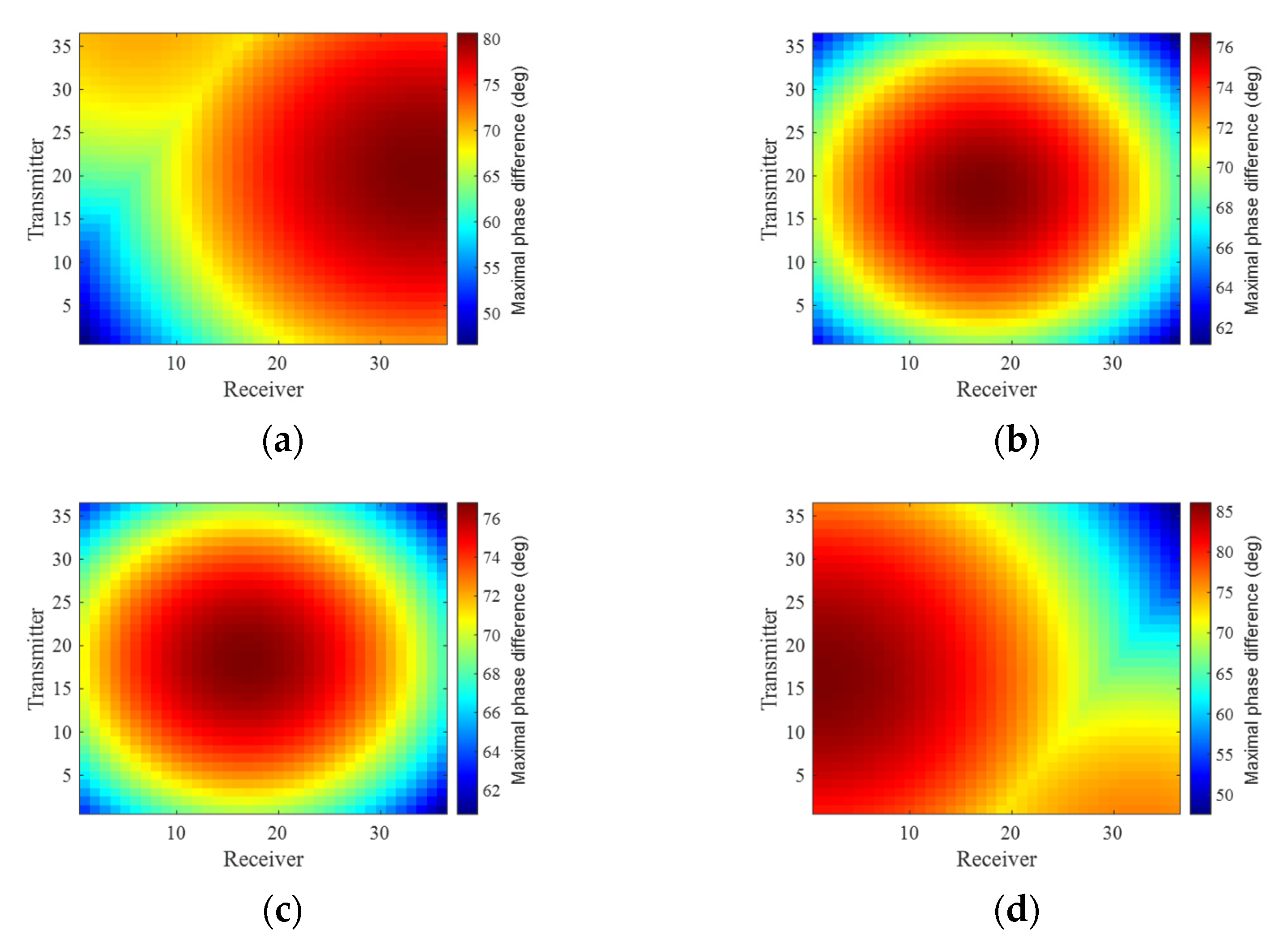
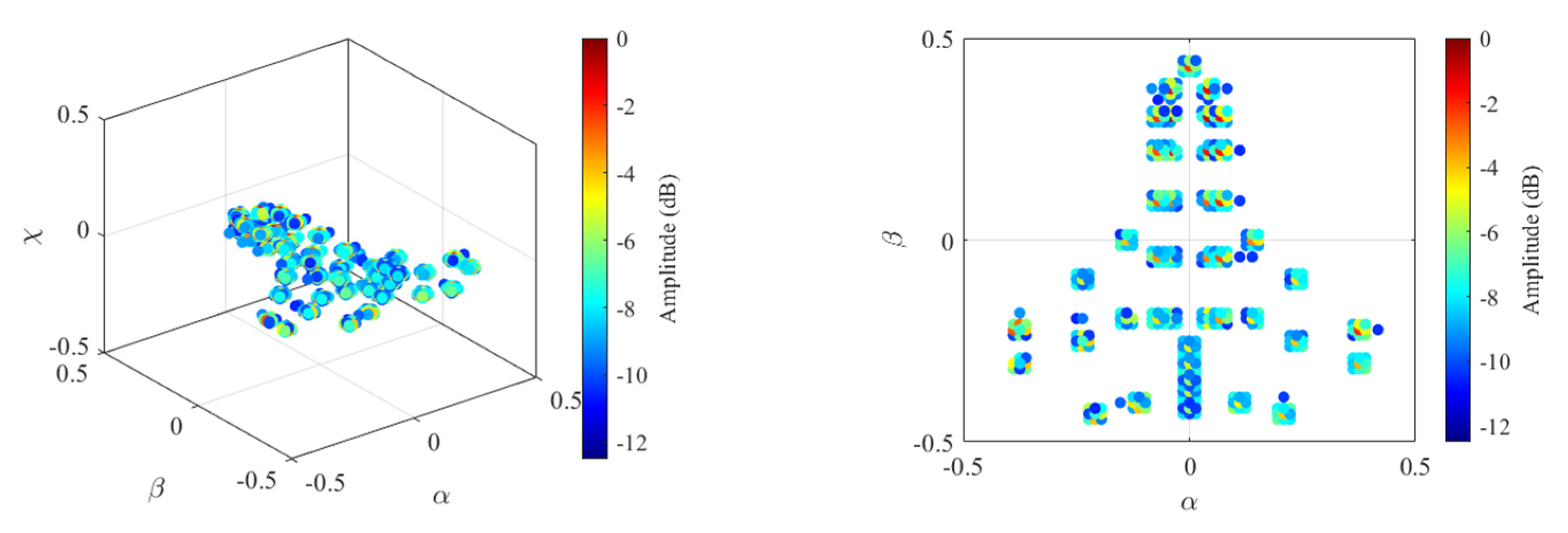
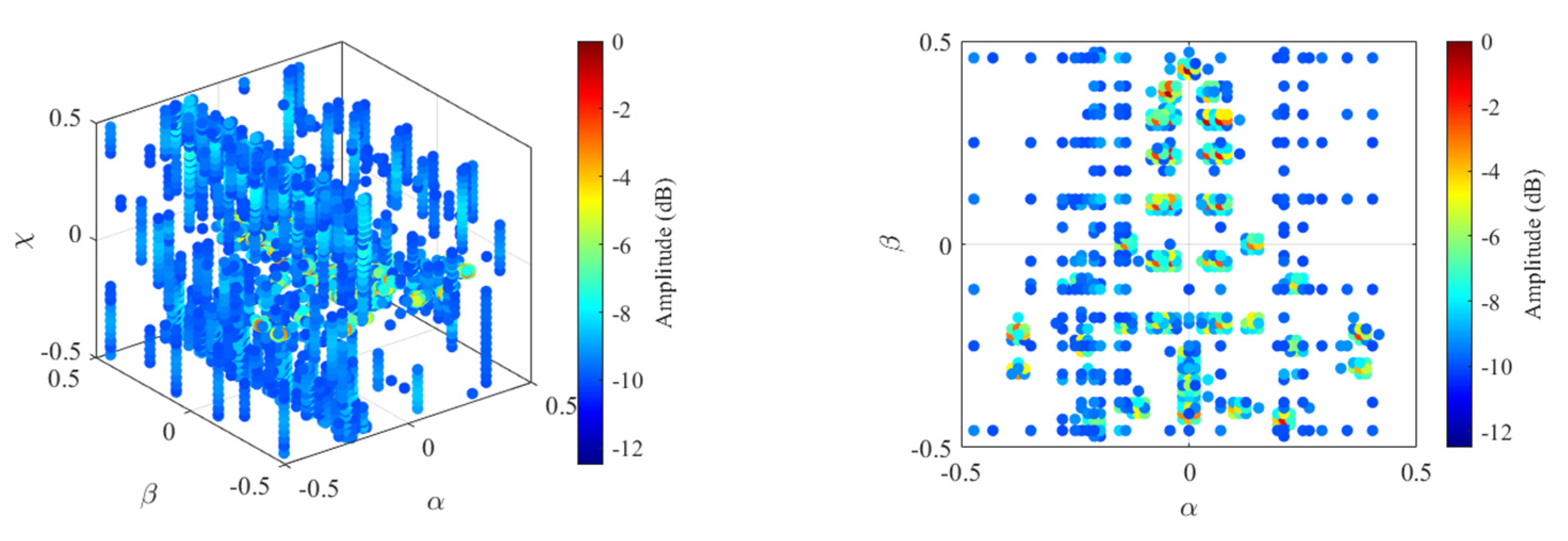
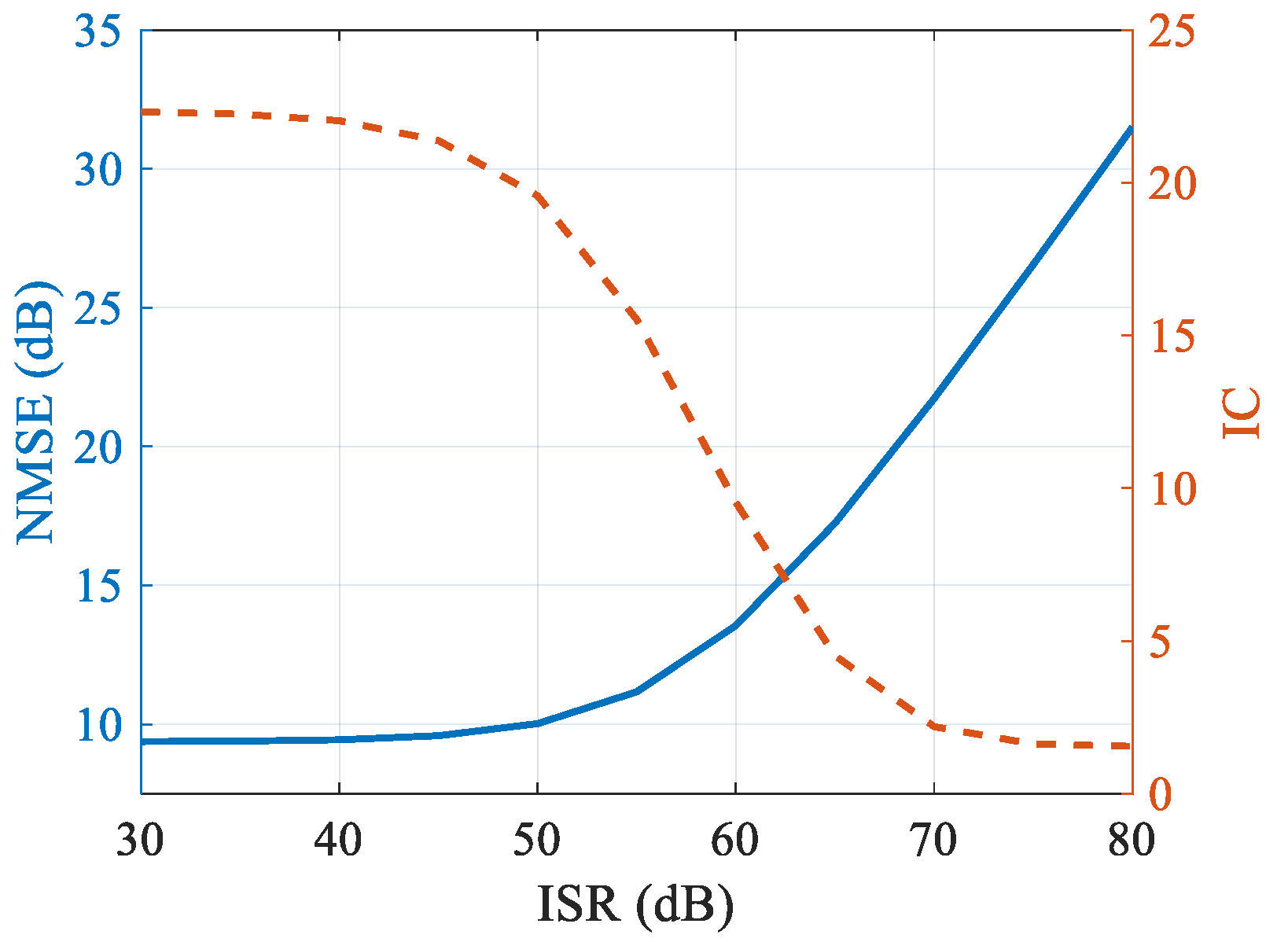

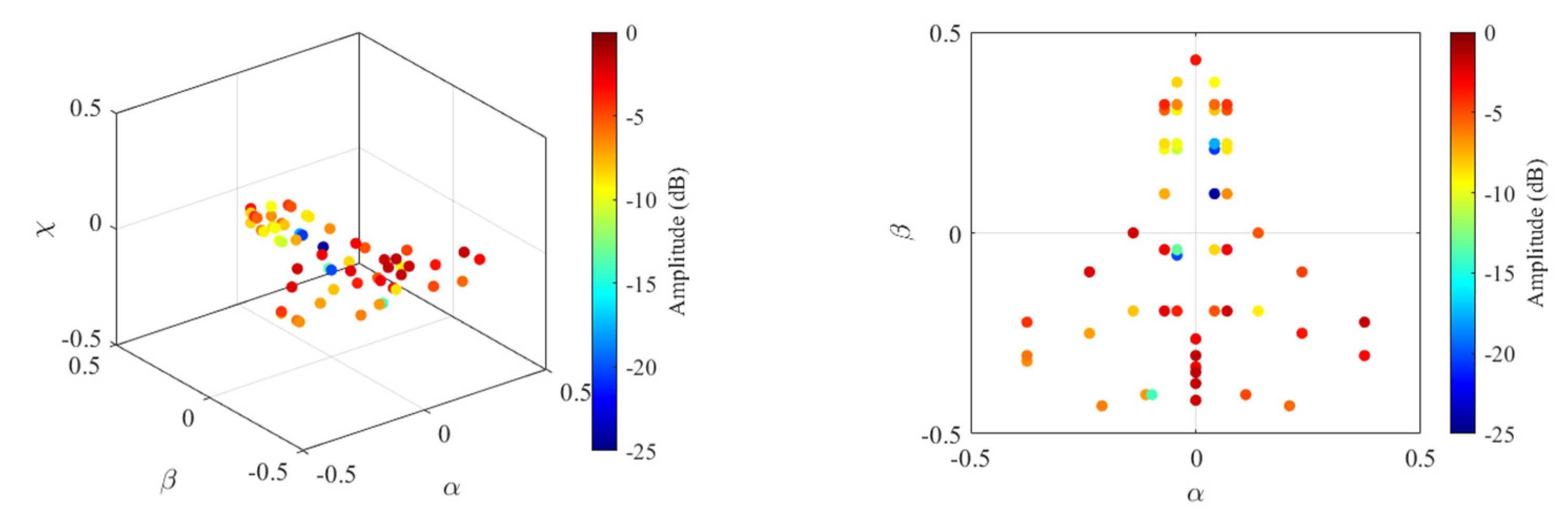
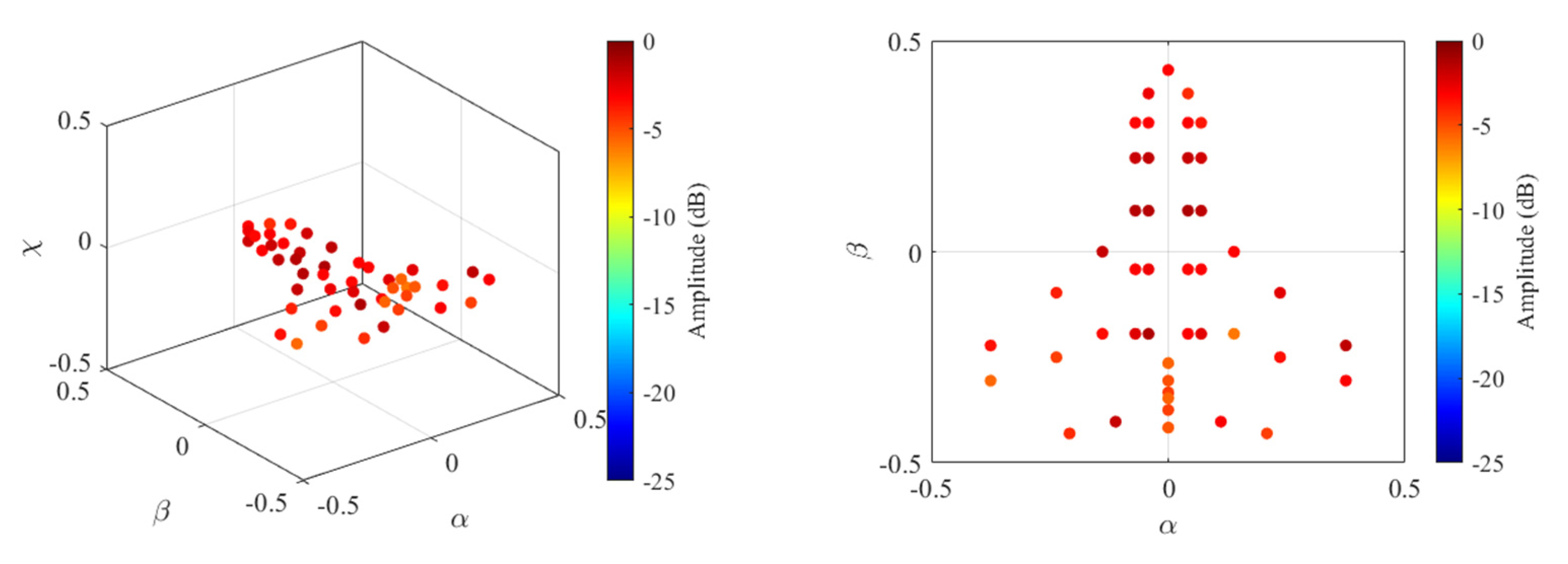




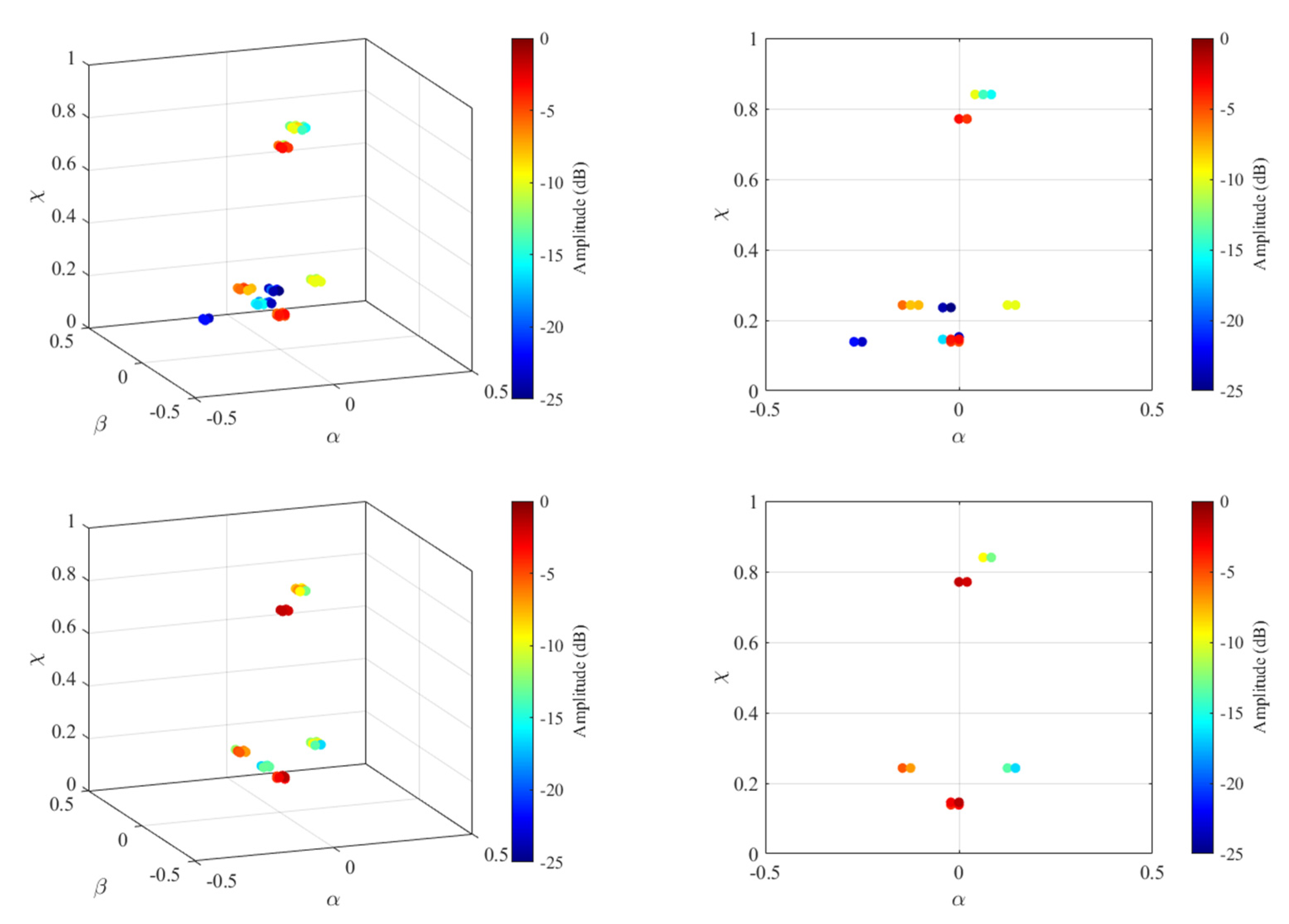
| Parameter | Value Range | Parameter | Value Range |
|---|---|---|---|
| fCM | ±[20, 40] MHz | G | [1, 2, 3] |
| TCM | [1, 4] ms | βg | [5, 10] × 103 |
| μ | ±[2, 5] MHz/ms | fg | [0.2, 0.5] kHz |
| fSM | ±[0, 20] MHz | φg | [0, 2π] |
| Loop | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Step | |||||||||||
| WDR | 0.82 | 0.82 | 0.83 | 0.83 | 0.82 | 0.82 | 0.83 | 0.83 | 0.83 | 0.85 | |
| MF | 58.65 | 59.69 | 60.06 | 61.51 | 59.79 | 66.35 | 67.23 | 67.29 | 67.12 | 64.99 | |
| HRI | 456.89 | 457.21 | 456.94 | 456.33 | 456.89 | 457.67 | 458.37 | 457.42 | 457.63 | 457.51 | |
| CSS | 0.03 | 137.08 | 124.26 | 112.32 | 103.97 | 91.03 | 89.40 | 88.18 | 87.67 | 87.11 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Wan, P.; Hu, X.; Guo, Y.; Zhu, H. Cognitive Sparse Imaging Method for MIMO Radar under Wideband Interference. Remote Sens. 2022, 14, 5294. https://doi.org/10.3390/rs14215294
Feng W, Wan P, Hu X, Guo Y, Zhu H. Cognitive Sparse Imaging Method for MIMO Radar under Wideband Interference. Remote Sensing. 2022; 14(21):5294. https://doi.org/10.3390/rs14215294
Chicago/Turabian StyleFeng, Weike, Pengcheng Wan, Xiaowei Hu, Yiduo Guo, and Hangui Zhu. 2022. "Cognitive Sparse Imaging Method for MIMO Radar under Wideband Interference" Remote Sensing 14, no. 21: 5294. https://doi.org/10.3390/rs14215294
APA StyleFeng, W., Wan, P., Hu, X., Guo, Y., & Zhu, H. (2022). Cognitive Sparse Imaging Method for MIMO Radar under Wideband Interference. Remote Sensing, 14(21), 5294. https://doi.org/10.3390/rs14215294






