Abstract
Medium-Earth-orbit (MEO) synthetic aperture radar (SAR) has the advantages of short revisit time and wide coverage, and thus is a potential tool for implementing ground moving target indication (GMTI) tasks. In the paper, aiming at MEO SAR’s problems of low signal-to-noise ratio and limited computation resource, an efficient imaging method is proposed for MEO multichannel SAR-GMTI systems with relatively low resolution. The proposed imaging method is designed with the consideration of both static scenes and ground moving targets, and it can simultaneously correct the range cell migrations of static scenes and multiple moving targets of no Doppler ambiguity. It needs only four Fourier transforms and twice phase multiplications, and thus is computationally efficient. Moreover, moving targets’ signal characteristics, including the azimuth and range displacements and along-track interferometric phase, in the SAR image obtained by the proposed imaging method are figured out. Experimental results validate the proposed imaging method and the theoretical analyses.
1. Introduction
Synthetic aperture radar (SAR) is an active microwave sensor that is able to obtain a high-resolution image of a scene, regardless of the weather and daylight [1,2]. Moreover, modern SAR usually has the operation mode of ground moving target indication (GMTI). SAR-GMTI systems can image the illustrated area and indicate ground moving targets in the SAR image simultaneously, and have played an important role in applications such as traffic monitoring and military reconnaissance [3,4,5,6,7].
With the development of satellite technology, GMTI with spaceborne SAR has attracted a lot of attentions in recent years [8,9,10]. Low-Earth-orbit (LEO) spaceborne SAR-GMTI has been widely studied. However, since the altitude of the orbit is relatively low, LEO SARs suffer the problems of long revisit time and limited coverage, which severely limits their applications in GMTI. To address this issue, many attentions have been paid to SARs with higher orbital altitude [11,12,13,14], such as medium-Earth-orbit (MEO) and geosynchronous-orbit (GEO) SARs. Compared with GEO SAR, MEO SAR has shorter synthetic aperture time, lower transmission cost and lower system complexity, and thus is more suitable for GMTI applications.
Many studies on MEO SAR have been conducted in recent years [15,16,17,18,19,20]. The observation performance of MEO SAR and the signal characteristics of static targets had been studied in [15]. In [16], the author studied the orbit design, coverage, and revisit time of MEO SAR, and concluded that MEO SAR had great value due to its advantages of wide coverage and short revisit time. In [17,18,19], the imaging of the stationary scene was studied, and several imaging algorithms that could address the 2-D spatial of the signal and the curvature of the radar track were proposed. However, studies on MEO SAR-GMTI are still rare.
The focusing of ground moving targets can improve the signal-to-clutter-noise ratio (SCNR), thus improving the GMTI performance of the system [21,22]. Particularly for MEO SAR, the high orbital altitude makes it suffer the problems of low signal-to-noise ratio (SNR) and limited computation resource. Therefore, it is essential to propose an imaging method with high computational efficiency for MEO SAR-GMTI systems to improve their performance. However, the existing imaging methods of MEO SAR [17,18,19] are designed only for the stationary scene and thus may not be suitable for SAR-GMTI systems. For example, [19] proposed an imaging algorithm based on a novel coordinate system. Since the imaging coordinate used in this algorithm depends on the Doppler parameters of the stationary scene, it cannot accurately correct the range cell migrations (RCMs) of moving targets.
In this paper, we propose an efficient imaging method suitable for the MEO SAR-GMTI system. This method is designed with the consideration of both the stationary scene and ground moving targets. It utilizes the fact that, in a 2-D frequency domain, the couplings between the range and azimuth of static targets and the moving targets of no Doppler ambiguity are approximately identical, and thus the RCMs of these targets can be corrected simultaneously via a phase multiplication. The proposed imaging method is very efficient because it needs only four Fourier transforms (FTs) and twice phase multiplications. Thus, the proposed imaging method is very suitable for MEO SAR, which suffers the problem of limited energy and computation resources.
The analysis and understanding of moving targets’ signal characteristics in the image domain are very important for the development of the GMTI method [23], e.g., the clutter suppression and motion parameter estimation methods. Therefore, one other objective of this paper is to reveal moving targets’ signal characteristics in the SAR image obtained by the proposed imaging method. Specifically, in the paper, the analytical expressions for the azimuth and range displacements and the along-track interferometric (ATI) phase of the target are derived, and their variation with the target’s parameters are investigated.
Note that the MEO SAR-GMTI system in this paper is assumed to have a relatively low resolution. The considerations are as follows: (1) A relatively low resolution can improve the SNR and reduce the data volume. This is important for MEO SAR, which suffers limited energy and computation resources and relatively high system complexity because of the increased orbital altitude; (2) For GMTI, a relatively low resolution can reduce the probability of Doppler ambiguity of moving targets.
The remainder of this paper is organized as follows. In Section 2, the target’s range equation model and 2-D spectrum for MEO multichannel SAR are derived. The proposed method is introduced in Section 3. The signal characteristics of the target in SAR image are analyzed in Section 4. In Section 5, experimental results are presented to verify the work of this paper. In Section 6, some discussions are presented. Finally, the paper is concluded in Section 7.
2. Signal Modelling
2.1. Range Equation Modelling
The MEO SAR geometrical model containing one moving target is illustrated in Figure 1, where OXYZ refers to the Earth-centered rotating (ECR) coordinate system. The origin of the ECR coordinate system coincides with the earth’s core, the OX axis points from the core of Earth to the prime meridian in the equatorial plane, the OZ axis points to the north pole, and the OY axis is determined by the right-hand rule. The target’s longitude and latitude at ta = 0 are assumed to be δlng and δlat, where ta is the azimuth slow time. Besides, vlng, alng, vlat and alat respectively represent the velocity along the longitude, acceleration along the longitude, velocity along the latitude, and acceleration along the latitude of the moving target. In addition, the radar’s beam centerline is assumed to cross the target at ta = 0.
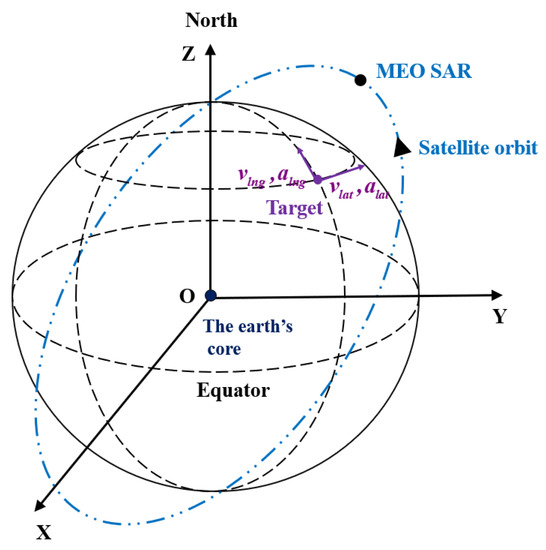
Figure 1.
MEO SAR geometry.
Based on the kinematics, the coordinates of the satellite in the ECR coordinate system can be expressed as [20]
with
where ω means the argument of perigee, f (ta) represents the satellite’s true anomaly, a indicates the orbit’s semi-major axis, and e represents the eccentricity, Ω is the right ascension of ascending node, θi defines the orbit’s inclination, and ΩG(ta) = ΩG0 + ωeta presents the Greenwich Hour Angle (GHA), where ωe refers to Earth’s rotational angular velocity, and ΩG0 indicates the GHA at ta = 0. The detailed derivation of (1) can be found in [20].
Based on Figure 1, the target’s coordinates in the ECR coordinate system are given by [20]
where Re refers to Earth’s radius.
Assuming that the MEO multichannel SAR has N channels in azimuth direction, and the distance between two adjacent channels is d, as shown in Figure 2. The dotted line in the figure represents the motion track of the satellite, and the azimuth axis of the antenna is parallel to the satellite’s velocity vector vs(ta) because of the zero-Doppler steering. Therefore, the position vector of the effective phase center of the nth (n = 1, 2, …, N) channel can be represented by rs,n(ta) = rs(ta) − (n − 1)d·vs(ta)/vs(ta), and the range from the target to the nth channel can be expressed as
where rt(ta) = [xt(ta) yt(ta) zt(ta)] and rs(ta) = [xs(ta) ys(ta) zs(ta)] are the position vectors of the moving target and the satellite, respectively, and |.| indicates modulo operation to the vector. In this paper, the bold letters represent vectors, and the letters of italic fonts represent the norms of vectors.
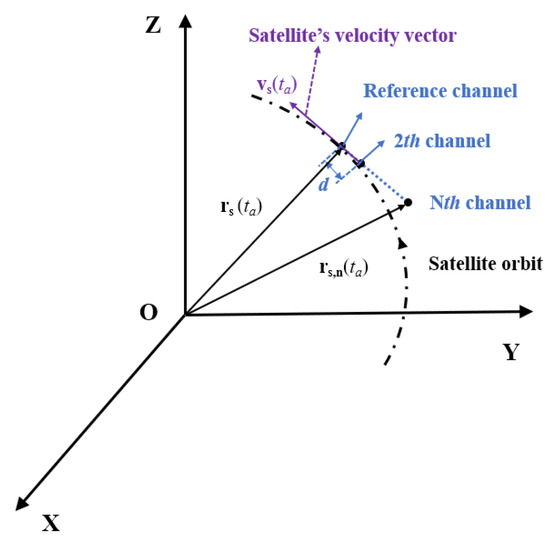
Figure 2.
MEO multichannel SAR geometry.
To facilitate the design of the GMTI method, the target’s range history is generally approximated by a Taylor series expansion around the time that the beam centerline crosses the target (i.e., ta = 0). In the case of MEO SAR, because of the obvious curve of the trajectory, a third-order Taylor series expansion should be adopted. By exploiting the vector projection and matrix differential, the cubic-approximated range equation for the multichannel system is given by [20]
with
where vs0 = |vs(0)| and vt0 = |vt(0)| are, respectively, the velocities of the radar and target at ta = 0. In addition, vtr and atr represent the target’s radial velocity and acceleration; vsr, asr and jsr are, respectively, the radial projections of the radar’s velocity, acceleration and jerk; vta and ata define the target’s along-track velocity and acceleration; asa is the radar’s acceleration. They can be expressed as [20]
where , , and are, respectively, the velocity, acceleration and jerk vectors of satellite at ta = 0; and indicate the velocity and acceleration vectors of the target at ta = 0.
2.2. Derivation of the Target’s 2-D Spectrum
Supposing that a chirp signal is transmitted, then the signal after demodulation and range compression can be expressed as [1]
where defines the function of range impulse response, indicates the azimuth window function, tr is the range time, c represents the velocity of light, and λ defines the wavelength. In the paper, the channels are assumed to be well calibrated.
Applying a FT to (19) in the range direction, the target signal in the range frequency domain can be obtained:
where fr is the range frequency, refers to the envelope of range spectrum, fc defines the carrier frequency.
The target’s 2-D spectrum can be obtained via taking a FT to (20) with respect to ta. Since there are quadratic and cubic terms of ta, the series reversion and the principle of stationary phase are used to solve the Fourier integral. The obtained expression for the target signal in the 2-D frequency domain is given by
with
where indicates the envelope of azimuth spectrum, fa defines the Doppler frequency, M represents the Doppler ambiguity number, PRF indicates the pulse repetition frequency.
To facilitate the design of the imaging method, θn (fr, fa) is decomposed via using power series expansions of and (keeping terms up to the third order), and also is rearranged according to the physical meaning. The decomposed and rearranged phase is given by
where represents echo delay, and indicate the residual quadratic and cubic range frequency modulation rates, respectively. Their expressions are as follows
3. Proposed Imaging Method
In this section, an efficient imaging method is proposed. The secondary range compression (SRC) and RCM correction (RCMC) are accomplished efficiently in the 2-D frequency domain via phase multiplications. In addition, the azimuth compression is implemented in the range Doppler domain. The main steps of this imaging method are introduced below. Note that the signal of the reference channel (i.e., n = 1) is taken as an example to describe the proposed method in this section.
3.1. Secondary Range Compression
It can be seen from (23) that there are still quadratic and cubic terms of range frequency after range compression. If these terms are not compensated, defocus will occur in the range direction. Therefore, the operation of SRC is implemented, and the filter is constructed as follows
with
where l10, l20 and l30 define the coefficients of the linear, quadratic, and cubic terms of range history of the static target located at the center of the illuminated scene.
Comparing (25) with (28) and (26) with (29), respectively, one can see that there is a residual phase error after SRC by (27), and it can be expressed as
This phase error is very small (about 10 −10) and much less than π/4, and thus it can be neglected. Therefore, the signal after SRC is given by
3.2. Range Cell Migration Correction
In order to improve the efficiency, a phase multiplication in 2-D frequency domain is used to accomplish RCMC. Based on (31), the RCM of target can be corrected by compensating the term containing fr. Therefore, the RCMC filter can be constructed as follows
By multiplying (32) into (31) and then performing inverse FT (IFT), one can obtain the range-Doppler domain signal as follows:
From the range envelope of (33), one can see that there is still a residual RCM, which can be expressed as
Considering –PRF/2 < fa < PRF/2, the maximum possible value of the residual RCM is given by
For the targets moving with such a radial velocity that there is no Doppler ambiguity (i.e., M = 0), will be smaller than half of a range resolution cell, and thus the residual RCM can be neglected. To validate this statement, numerical simulations are conducted. The MEO SAR parameters for simulations are presented in Table 1. The result is illustrated in Figure 3, which shows the of the targets with all possible velocities (note that, when there is no Doppler ambiguity, vtr will be less than about 10 m/s). As can be seen from Figure 3, the maximum value of is about 1.8 m. Therefore, will not exceed half the range resolution cell in the cases that the range resolution is not high.

Table 1.
Parameters of MEO SAR.
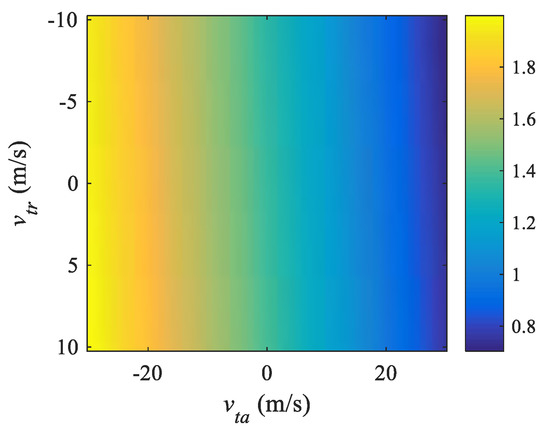
Figure 3.
Residual RCM of the target with all possible velocities (i.e., vtr and vta). The color indicates the value of , and the unit is m. The distance between the target and the scene center is set to be 7568.7 km. The accelerations are 0.1 m/s2.
The RCMC filter shown in (32) is constructed without any parameter of the target. Therefore, this filter can simultaneously correct the RCMs of static scenes and the multiple moving targets of no Doppler ambiguity. Note that after the RCM is corrected there will be no defocusing in the range direction after azimuth compression.
3.3. Azimuth Compression
To finely focus the static scene, we perform the azimuth compression in the range Doppler domain. Based on (33), the azimuth compression filter is constructed as follows
The target signal after azimuth compression is given by (the negligible residual RCM is omitted)
The focused SAR image can be obtained via applying an azimuth IFT to (37). From (37) it can be seen that, for static targets, they can be finely focused. For moving targets, since there are residual azimuth modulations, they will suffer from azimuth defocusing. It should be noted that, since the RCMs of the moving targets without Doppler ambiguity have been corrected, the range defocusing will not occur after azimuth compression. Therefore, the SCNR of the target can be improved, which will improve the GMTI performance of the system.
4. Property Analysis of Moving Target in the Complex Image Domain
Analyzing and understanding the moving targets’ characteristics in the SAR image is of great significance for moving target indication. However, it is difficult to derive the analytical expression of the target signal in complex image domain, because there is residual azimuth modulation after azimuth compression. In this section, some properties of the target signal in the image obtained by the proposed imaging method, e.g., the target’s range displacement, azimuth displacement, and ATI phase, are quantitatively analyzed.
4.1. Range Displacement
The target’s location in range is displaced from R0, which can be seen from the range envelope of (37). Thus, the target will suffer range displacement after focusing. Based on (37), the range displacement can be calculated as
Since the terms containing l3 are smaller than a range cell, they can be neglected. Therefore, rshift can be simplified as
where fb defines the target’s baseband Doppler center frequency, and it can be expressed as .
In order to reveal the relationship between the range displacement and the target’s parameters, the expressions of l2 and fb are substituted into (39), and rshift can be rewritten as
Note that, since is far smaller than , it is ignored.
From (39) one can see that the target’s range displacement is caused by its radial velocity, i.e., the range displacement will be equal to zero when the radial velocity is zero. Moreover, it is interesting that the range displacement is dependent on its baseband Doppler center frequency rather than the absolute Doppler center frequency. This property indicates that the range displacement is independent of Doppler ambiguity and will not be monotonically increasing with the target’s radial velocity. In addition, from (40) one can see that the range displacement is also related to the target’s radial acceleration, along-track velocity, and distance. However, it is very difficult to find out the variation of the range displacement with these parameters directly from (40). To address this issue, numerical simulations are conducted, with the results being presented in Figure 4.
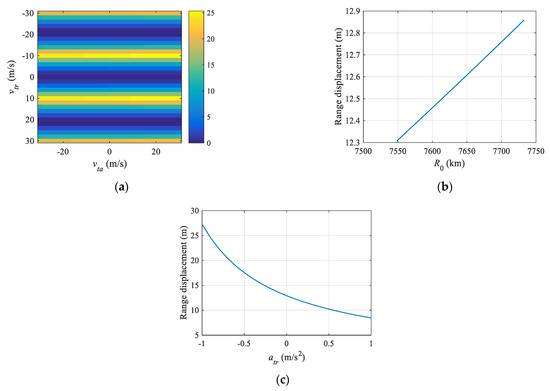
Figure 4.
Dependences of the range displacement on the parameters of the target. (a) rshift versus vtr and vta, where atr = 0.1 m/s2, ata = 0.2 m/s2, R0 = 7568.7 km; (b) rshift versus R0, the atr = 0.1 m/s2, ata = 0.2 m/s2, vtr = 7 m/s, vta = 15 m/s; (c) rshift versus atr, where ata = 0.2 m/s2, vtr = 7 m/s, vta = 15 m/s, R0 = 7568.7 km.
Figure 4a illustrates the variation of the range displacement with the velocities of the target. It can be seen that the range displacement varies with vtr periodically and gets the maximum value when the baseband Doppler center frequency equals to PRF/2. In addition, one can see that the range displacement is almost independent of vta. Figure 4b,c show the variation of the range displacement with the distance and radial acceleration of the target, respectively. It can be seen that the range displacement increases with R0 approximately linearly, and is inversely proportional to atr.
4.2. Azimuth Displacement
Besides the range displacement, the motion of the target will also lead to an azimuth offset in SAR image. According to (37) and the properties of FT, the target’s azimuth displacement can be expressed as
where vg is the velocity of the beam sweeping along the surface of earth.
Substituting the expressions of l1, l2 and l3 into (41), ashift can be rewritten as
Note that since the value of is much smaller than , it can be ignored.
From (42), one can see that the azimuth displacement is also caused by the target’s radial velocity and is dependent on the baseband Doppler center frequency rather than the absolute Doppler center frequency. Moreover, the azimuth displacement is also dependent on the target’s along-track velocity, accelerations, and distance. In order to reveal the variation of the range displacement with these parameters, numerical experiments are carried out, with the results presented in Figure 5.
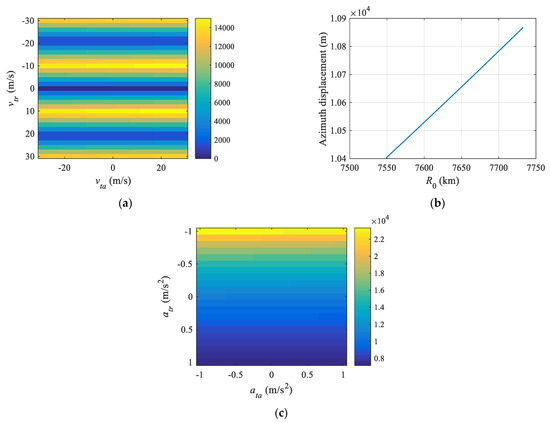
Figure 5.
Dependences of the azimuth displacement on the target’s parameters. (a) ashift versus vtr and vta, where atr = 0.1 m/s2, ata = 0.2 m/s2, R0 = 7568.7 km; (b) ashift versus R0, the atr = 0.1 m/s2, ata = 0.2 m/s2, vtr = 7 m/s, vta = 15 m/s; (c) ashift versus atr and ata, where vtr = 7 m/s, vta = 15 m/s, R0 = 7568.7 km.
From Figure 5a it can be seen that the azimuth displacement varies with vtr periodically and gets the maximum value when the baseband Doppler center frequency equals to PRF/2. In addition, one can see that the range displacement is almost independent of vta. The variation of the azimuth displacement with the target’s distance and accelerations are shown in Figure 5b,c. It can be seen that the range displacement increases with R0 approximately linearly. From Figure 5c one can see that the azimuth displacement is inversely proportional to atr and almost independent of ata.
4.3. Along-Track Interferometry Phase
ATI phase is a very important parameter in the SAR-GMTI field. It can be utilized to estimate the radial velocity of the target. In addition, moving targets can be detected according to the interference phase diagram.
Based on (37), the signal of the second channel after registration is:
According to (37) and (43), the interference phase between channel 1 and channel 2 can be expressed as
where * represents a conjugate operation on the signal.
Since the items containing d2α2, d3α3 and l3 are much smaller than other items, they can be ignored. Therefore, can be simplified to
In order to find out the variation of ATI phase with the target’s parameters, the expressions of α and l2 are substituted into (45). Then, the ATI phase can be rewritten as:
It can be seen from (46) that the ATI phase is also caused by the target’s radial velocity and is only dependent on the radial velocity when there is no Doppler ambiguity. For the cases where Doppler ambiguity is happening, in addition to the radial velocity the ATI phase depends also on the along-track velocity, radial acceleration and distance. To find out the variation of the ATI phase with these parameters, numerical experiments are carried out, with the results being presented in Figure 6. Figure 6a shows the relationship between the ATI phase and velocities. One can find out that the ATI phase is proportional to vtr, while the variation of the ATI phase with vta is very slight. In addition, the variation of ATI phase with the target’s distance and radial acceleration are shown in Figure 6b,c. One can see that the ATI phase is inversely proportional to R0, and that the ATI phase is proportional to atr when there is Doppler ambiguity.
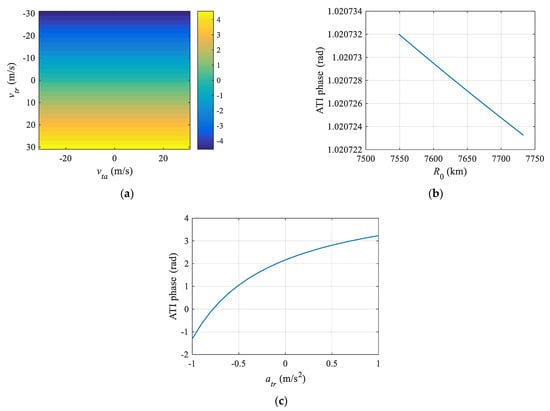
Figure 6.
Variations of the ATI phase with the parameters of the target. (a) ATI phase versus vtr and vta, where atr = 0.1 m/s2, ata = 0.2 m/s2, R0 = 7568.7 km; (b) ATI phase versus R0, where atr = 0.1 m/s2, ata = 0.2 m/s2, vtr = 7 m/s, vta = 15 m/s; (c) ATI phase versus atr, where ata = 0.1 m/s2, vta = 20 m/s, vtr = 15 m/s, R0 = 7568.7 km.
5. Experimental Results
In this section, numerical experiments are conducted to validate the proposed imaging method and the analysis presented in Section 4. The MEO SAR parameters used for simulation are given in Table 1. Five targets are simulated, including four moving targets and one stationary target. The parameters of these targets are given in Table 2.

Table 2.
Parameters of the targets.
The results of RCMC are presented in Figure 7. Comparing Figure 7a with Figure 7b, it is evident that the five targets’ RCMs are corrected at the same time. In addition, the residual RCMs of five targets are also calculated by (34), which are 0.42 m, 0.85 m, 0.53 m, 0 m, and 0.16 m. They are so much smaller than a range cell that can be ignored.
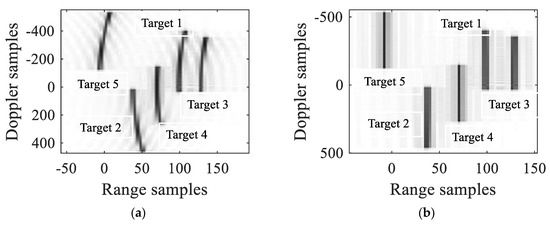
Figure 7.
RCMC results. (a) Five targets before RCMC; (b) Five targets after RCMC.
The azimuth compression results are given in Figure 8, from which it can be found out that the targets are focused simultaneously. Furthermore, it can be seen that the static target (target 4) is finely focused. In addition, the four moving targets are also well focused in range direction with defocusing only in the azimuth direction.
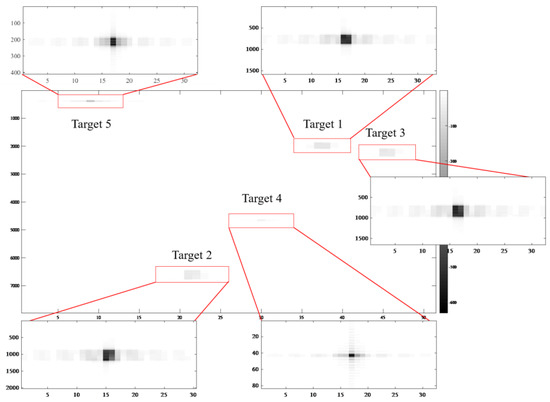
Figure 8.
SAR image of the five targets.
In order to verify the target’s signal characteristic analysis presented in Section 4, the range and azimuth displacements and the ATI phases of the four moving targets are measured, with the results shown in Table 3. Note that the measured displacements are calculated based on target’s position in the SAR image, and thus they can only be the integer multiples of the size of a pixel. From Table 3 it can be seen that the measured values are very close to the theoretical ones. The differences between the theoretical range displacements and the measured ones are all less than half of the range length of a pixel (i.e., 3.75 m), which indicates the measured values being exactly consistent with the theoretical ones. The differences between the theoretical azimuth displacements and measured ones are slightly larger. This could be caused by the residual cubic azimuth modulation (see Equation (37)) and azimuth defocusing.

Table 3.
Characteristic Measurement of Moving Targets.
6. Discussion
In Section 5, the results show that the proposed imaging method can correct the RCMs of the five targets simultaneously, and thus the static target can be finely focused and the moving targets can be focused with defocusing only in the azimuth direction. Moreover, the results presented in Table 3 show the measured azimuth and range displacements in the SAR image and ATI phases. It is seen that the measured values are very close to the theoretical ones and thus verify the theoretical analysis of the target’s properties in the SAR image. In this section, we will further present discussions on the computational complexity of the proposed imaging method, moving target refocusing, and link-budget determination.
6.1. Computational Complexity Analysis
One of the main advantages of the proposed imaging method is its high computational efficiency. In this subsection, its computational complexity is discussed and compared with that of the method proposed in [19].
For the proposed method, since the range compression, SRC, and RCMC can all be implemented via phase multiplications in the 2-D frequency domain, one can utilize a phase multiplication to accomplish these operations. Therefore, based on the analysis presented in Section 3, one can see that the proposed method needs only two azimuth FT/IFTs, two range FT/IFTs, and twice phase multiplications. The computational complexity can then be given by
where Na and Nr are the number of azimuth samples and range samples of the data, respectively.
The imaging method proposed in [19] requires four range FT/IFTs, two azimuth FT/IFTs, four phase multiplications, and one azimuth interpolation. Supposing that the length of sinc interpolation kernel is M (M is set to be 16 in [19]), the overall computational complexity of this method is then
From (47) and (48) one can see that the proposed method is more efficient, because there are no interpolation and less range FTs/IFTs and phase multiplications.
6.2. Moving Target Refocusing
Although moving targets suffer azimuth defocusing in the SAR image obtained by the proposed imaging method, we can refocus them after target detection and data extraction. Figure 9 presents a flowchart of moving target detection and refocusing. First, the DPCA processing is applied to the registered SAR images to cancel the clutter. Then, the detection and data extraction are implemented. Finally, the operation of refocusing is applied to the extracted target data.
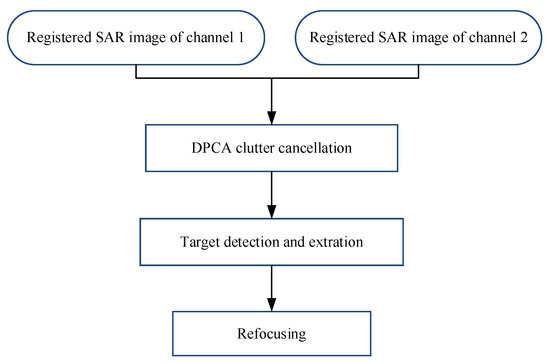
Figure 9.
Flowchart of moving target detection and refocusing.
A refocusing method exploiting the maximum contrast criterion is proposed below. Assuming that the inverse operations of azimuth compression and RCMC have been applied to the extracted data, then we can utilize the following method to refocus the target
with
where S (fr, fa) is the signal after range compression and SRC, IDFT2 (·) indicates 2-D IFT. In addition, , , and are the estimates of the coefficients of the range equation. They are estimated via the following maximum-contrast based way
with
where defines the spatial average, indicates the image contrast.
Figure 10 and Figure 11 present the refocusing results of target 1 and target 2. One can see that these two targets are all well focused.
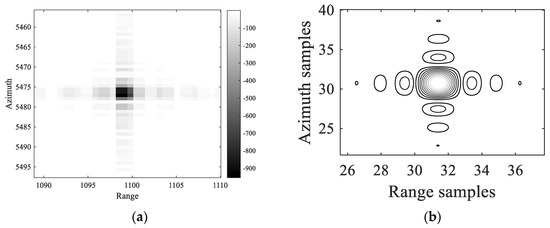
Figure 10.
Refocusing results of target 1. (a) SAR image of target 1; (b) Contour plot of target 1.
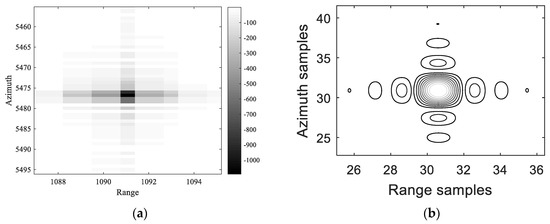
Figure 11.
Refocusing results of target 2. (a) SAR image of target 2; (b) Contour plot of target 2.
6.3. Link-Budget Determination
The high orbital altitude gives MEO SAR the advantages of short revisit time and wide coverage. However, it also requires radar having a high transmit power and large antenna area, because the signal energy decays rapidly with the distance. In the following, we will briefly discuss the relationships between the target’s SNR and radar’s transmit power and antenna area.
Since the MEO SAR considered in this paper is of relatively low resolution, the size of the ground moving target can be considered to be smaller than the area of a resolution cell. The SNR of the focused target can then be calculated as [1]
where Pave is the average transmit power, Gt is the gain of the transmitting antenna, Gr is the gain of the receiving antenna, σt is the target’s radar cross section (RCS), R0 is the distance from the target to the radar, K is the Boltzmann’s constant, T is the temperature of receiver, BT is the bandwidth of the transmitted signal, Fn is the receiver noise figure, Ls is the system losses, Ve is the effective velocity of satellite, ρr and ρa are the range and azimuth resolution, respectively.
We assume that the multichannel system has three channels in azimuth, and the whole antenna is used for transmission. The SNR per channel can then be expressed as
where ƞ is the antenna efficiency, A is the antenna area, and Ar = A/3 is the area of the receiving antenna per channel.
Based on (54), numerical experiments are conducted to investigate the relationship between the average transmit power, antenna area, and SNR. A target with an RCS of 2 m2 (≈small passenger car) is considered, and other parameters used in the experiments are given in Table 1 and Table 4. The experimental results are shown in Figure 12 and Figure 13. Figure 12 illustrates the dependence of SNR on the average transmit power and antenna area, with the color indicating the value of SNR (the unit is dB). In Figure 13, the required average transmit powers under various pairs of SNR and antenna area are plotted. From Figure 12 it can be seen that, in order to obtain satisfactory SNR, a relatively high transmit power and large antenna is required. In addition, as can be seen from Figure 13, when the antenna area is 180 m2 [24], for desired SNR of 10 dB, 20 dB, 30 dB, and 40 dB, the required average transmit powers are 21.08 dBW, 31.08 dBW, 41.08 dBW, and 51.08 dBW, respectively.

Table 4.
Parameters for radar equation.
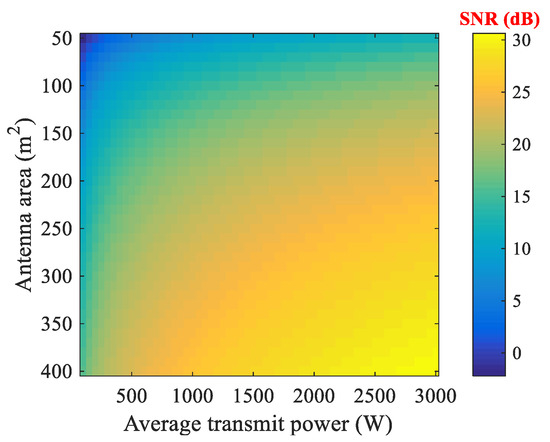
Figure 12.
Relationships between target’s SNR and radar’s average transmit power and antenna power.
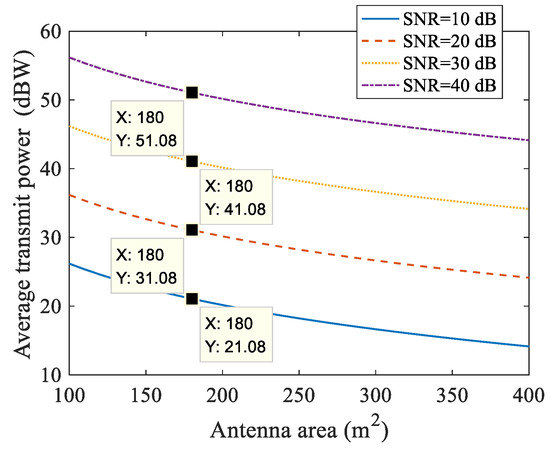
Figure 13.
Required average transmit powers under various pairs of SNR and antenna area.
7. Conclusions
This paper has proposed an efficient imaging method that can finely focus static scenes and coarsely focus the moving targets of no Doppler ambiguity at the same time. Based on the fact that, in the 2-D frequency domain, the couplings between the range and azimuth of static targets and the moving targets without Doppler ambiguity are approximately identical, the proposed method efficiently corrects the RCMs of these targets via a phase multiplication simultaneously. In addition, moving targets’ characteristics, including the range and azimuth displacements and ATI phases, in the SAR image focused by the proposed method have been analyzed. Furthermore, the dependence of these characteristics on the parameters of moving targets have been revealed. Experiments have been conducted to verify the proposed imaging method and theoretical analyses.
After moving targets have been efficiently and coarsely focused by the proposed method, their SCNRs will be improved. Therefore, the proposed method is very suitable for MEO SAR, which suffers from limited energy and computation resources due to the high orbital altitude. Moreover, the analysis of the target’s displacements and ATI phase in the SAR image will benefit the design of the GMTI method for MEO multichannel SAR.
Author Contributions
Y.L. wrote the manuscript, conducted the theoretical analyses, and verify the proposed method. T.H. conducted the theoretical derivations and experiments, and wrote the manuscript. C.C. proofed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was funded by the National Natural Science Foundation of China under Grant 62271398, and by the Postdoctoral Science Foundation of China under Grants BX20180261 and 2019M653739.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Zhang, B.J.; Xu, G.; Zhou, R.; Zhang, H.; Hong, W. Multi-Channel Back-Projection Algorithm for MMWave Automotive MIMO SAR Imaging with Doppler-Division Multiplexing. IEEE J. Sel. Top. Signal Process. 2022, 1–13. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zhang, X.D.; Yang, Q.; Xiao, Y.P.; An, H.Y.; Yang, H.G.; Wu, J.J.; Yang, J.Y. Hybrid SAR-ISAR Image Formation via Joint FrFT-WVD Processing for BFSAR Ship Target High-Resolution Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5215713. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, D.Y.; Wang, P.; Zhang, G.; Leung, H. Vision-Based Vehicle Detection for Video SAR Surveillance Using Low-Rank Plus Sparse Three-Term Decomposition. IEEE Trans. Veh. Technol. 2020, 69, 4711–4726. [Google Scholar] [CrossRef]
- Li, Z.Y.; Wu, J.J.; Liu, Z.T.; Huang, Y.L.; Yang, H.G.; Yang, J.Y. An Optimal 2-D Spectrum Matching Method for SAR Ground Moving Target Imaging. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5961–5974. [Google Scholar] [CrossRef]
- Ge, B.B.; An, D.X.; Chen, L.P.; Wang, W.; Feng, D.; Zhou, Z.M. Ground Moving Target Detection and Trajectory Reconstruction Methods for Multichannel Airborne Circular SAR. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2900–2915. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Xie, R.; Li, T. High-Order Phase Correction for Ground Moving Target Imaging in High-Squint SAR Mode. In Proceedings of the 2018 International Conference on Radar (RADAR), Brisbane, Australia, 27–31 August 2018; pp. 1–5. [Google Scholar]
- Baumgartner, S.V.; Krieger, G. Dual-Platform Large Along-Track Baseline GMTI. IEEE Trans. Geosci. Remote Sens. 2016, 3, 1554–1574. [Google Scholar] [CrossRef]
- Rousseau, L.P.; Gierull, C.H.; Chouinard, J.Y. First Results from an Experimental SCANSAR-GMTI Mode on RADARSAT-2. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 5068–5080. [Google Scholar] [CrossRef]
- Pastina, D.; Turin, F. Exploitation of the COSMO-SkyMed SAR System for GMTI Applications. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 966–979. [Google Scholar] [CrossRef]
- Dong, X.C.; Cui, C.; Li, Y.H.; Hu, C. Geosynchronous Spaceborne-Airborne Bistatic Moving Target Indication System: Performance Analysis and Configuration Design. Remote Sens. 2020, 12, 1810. [Google Scholar] [CrossRef]
- Xu, W.; Wei, Z.B.; Huang, P.P.; Tan, W.X.; Liu, B.; Gao, Z.Q.; Dong, Y.F. Azimuth Multichannel Reconstruction for Moving Targets in Geosynchronous Spaceborne–Airborne Bistatic SAR. Remote Sens. 2020, 12, 1703. [Google Scholar] [CrossRef]
- Dong, X.C.; Cui, C.; Tian, W.M.; Li, Y.H.; Mounir, M.; Hu, C. Moving Target Detection and Parameter Estimation via a Modified Imaging STAP with a Large Baseline in Multistatic GEO SAR. Remote Sens. 2021, 13, 346. [Google Scholar] [CrossRef]
- Bruno, D.; Hobbs, S.; Ottavianelli, G. Geosynchronous synthetic aperture radar. Acta Astronaut. 2006, 59, 149–156. [Google Scholar] [CrossRef]
- Huang, L.J. Imaging Algorithm for Medium-Earth-Orbit SAR. Ph.D. Thesis, Graduate University of Chinese Academy of Sciences, Beijing, China, 2011. [Google Scholar]
- Matar, J.; Rodriguez-Cassola, M.; Krieger, G.; López-Dekker, P.; Moreira, A. MEO SAR: System Concepts and Analysis. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1313–1324. [Google Scholar] [CrossRef]
- Chen, J.L.; Xing, M.D.; Sun, G.C.; Gao, Y.X.; Liu, W.K.; Guo, L.; Lan, Y. Focusing of medium-earth-orbit SAR using an ASE velocity model based on MOCO principle. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3963–3975. [Google Scholar] [CrossRef]
- Sun, G.C.; Liu, Y.B.; Xiang, J.X.; Liu, W.K.; Xing, M.D.; Chen, J.L. Spaceborne Synthetic Aperture Radar Imaging Algorithms: An overview. IEEE Mag. Geosci. Remote Sens. 2020, 10, 161–184. [Google Scholar] [CrossRef]
- Liu, W.K.; Sun, G.C.; Xing, M.D.; Li, H.; Bao, Z. Focusing of MEO SAR Data Based on Principle of Optimal Imaging Coordinate System. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5477–5489. [Google Scholar] [CrossRef]
- Li, Y.; Wang, T.; Huo, T.Y.; Nie, L.S. A Study on the Range Equation Modeling for Multichannel Medium-Earth-Orbit SAR-GMTI Systems. Remote Sens. 2021, 13, 2734. [Google Scholar] [CrossRef]
- Bacci, A.; Martorella, M.; Gray, D.A.; Berizzi, F. Space-Doppler Adaptive Processing for Radar Imaging of Moving Targets Masked by Ground Clutter. IET Radar Sonar Navig. 2015, 9, 712–726. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Xie, R. Ground Maneuvering Target Focusing via High-Order Phase Correction in High-Squint Synthetic Aperture Radar. Remote Sens. 2022, 14, 1514. [Google Scholar] [CrossRef]
- Xu, J.; Yu, Z.; Xia, B.; Xia, X.G.; Peng, Y.N.; Wang, Y.L. Ground Moving Target Signal Analysis in Complex Image Domain for Multichannel SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 538–552. [Google Scholar] [CrossRef]
- Matar, J.; López-Dekker, P.; Krieger, G. Potentials and Limitations of MEO SAR. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1035–1039. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).