Abstract
The main effects of the 10 June 2021 annular solar eclipse on GNSS position estimation accuracy are presented. The analysis is based on TEC measurements made by 2337 GNSS stations around the world. TEC perturbations were obtained by comparing results 2 days prior to and after the day of the event. For the analysis, global TEC maps were created using ordinary Kriging interpolation. From TEC changes, the apparent position variation was obtained using the post-processing kinematic precise point positioning with ambiguity resolution (PPP-AR) mode. We validated the TEC measurements by contrasting them with data from the Swarm-A satellite and four digiosondes in Central/South America. The TEC maps show a noticeable TEC depletion (<−60%) under the moon’s shadow. Important variations of TEC were also observed in both crests of the Equatorial Ionization Anomaly (EIA) region over the Caribbean and South America. The effects on GNSS precision were perceived not only close to the area of the eclipse but also as far as the west coast of South America (Chile) and North America (California). The number of stations with positioning errors of over 10 cm almost doubled during the event in these regions. The effects were sustained longer (∼10 h) than usually assumed.
1. Introduction
A solar eclipse is a natural phenomenon that occurs when the Moon moves in the way between the Sun and Earth, totally or partially blocking the Sun, casting a shadow over the Earth. Since the Sun is one of the major drivers of atmospheric effects, such as its ionization at high altitudes, its blocking produces several disturbances. The atmospheric effects of a solar eclipse have been the subject of extensive research, mainly in meteorological parameters, total column ozone, photochemistry, gravity waves, and ionospheric parameters [1]. Despite the large number of studies concerning eclipses, the event of a solar eclipse is still unique since it happens at different seasons, different times of the day, different locations, and under different synoptic and geomagnetic conditions [1,2,3]. In addition, with every new eclipse, the scientific community gains larger numbers and a variety of instruments, which allow us to revisit the proposed conclusions from previous eclipses.
The ionosphere is directly affected since this atmospheric layer is produced by solar radiation. The total electron content (TEC) is a measure of the electron density in the ionosphere integrated along the line of sight, thus, an indication of its ionization. TEC can be obtained using a radio link between a satellite and the ground. Nowadays, the most common system delivering TEC measurements is the Global Navigation Satellite Systems (GNSS), which requires TEC measurements to improve the precision of position estimation. TEC is expressed in TEC units (TECu), where . The perturbation of the ionosphere can be analyzed through the variations of TEC. The main parameters of the TEC variations during the eclipses are the delay value () relative to the maximum phase of the eclipse; its amplitude (A), which generally is a decrease; and the duration () of the perturbation [4]. Since the Moon’s shadow moves rapidly from west to east across the Earth at supersonic speed, the total eclipse lasts just a few minutes anywhere [5,6,7]. Previous works have reported the depletion of TEC after the onset of the partial solar eclipse and have presented values of A in percent (A[%]) that can reach up to −64% with from −30 to 180 min [8,9,10,11]. This delay has been interpreted as an indicator of the combined effect of the photochemical processes and plasma dynamics [1,12]. Some works have reported from 50 to 240 min [4,13]. However, some studies have reported even longer effects [14,15]. A historical summary of ionospheric responses to solar eclipses since 1920 can be found in the Appendix in Bravo et al. [16].
Recent studies have shown that the effects of a solar eclipse on the ionosphere are not only local but can affect other geographic regions outside the umbra/penumbra of the eclipse [15,17,18,19,20]. These effects may be due to transport between hemispheric magnetic conjugates, alteration of the equatorial fountain effect, generation of a disturbed dynamo, and/or Atmospheric Gravity Waves (AGWs) that generate Traveling Atmospheric Disturbances (TADs) and/or Traveling Ionospheric Disturbances (TIDs).
An annular solar eclipse took place on 10 June 2021. The first external contact (P1 time) and the last external contact (P4 time) of the solar eclipse were at 08:12:22 UT and 13:11:22 UT, respectively. The partial solar eclipse was seen from the following geographic regions: in parts of the eastern United States and northern Alaska, Canada and parts of the Caribbean, Europe, Asia, and northern Africa. The annular eclipse was visible from parts of northeastern Canada, Greenland, and the Arctic Ocean, passing through the North Pole, and ending in Russian territory. It maximum magnitude was 0.944: this is the fraction of the angular diameter of a celestial body being eclipsed. This magnitude value was reached at geographic coordinates 80.815°N, and 66.78°W, at 10:41:57 UT (Greatest Eclipse time, GE time, http://xjubier.free.fr/en/site_pages/solar_eclipses/ASE_2021_GoogleMapFull.html, last accessed on 15 June 2022). The paths at ground level and at 350 km of altitude of the annular eclipse are shown in Figure 1 (see Supplementary Materials, Video S1). Due to the specific geometry of each eclipse, the paths differ both geographically and temporally according to the height considered, which could be significant when analyzing them [21].
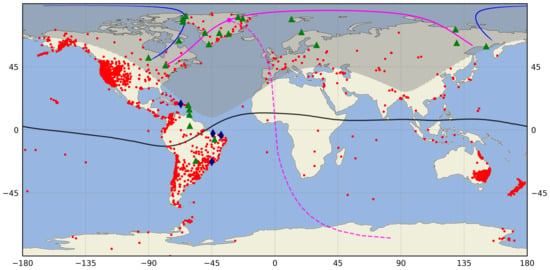
Figure 1.
Instruments used in present work: 2337 GNSS stations (red dots), 4 digisondes (blue rhombuses), and 24 selected GNSS stations (green triangles). The magnetic equator (black line) and the annular eclipse path at ground level (blue line) are shown. Eclipse obscuration mask from P1–P4 time (shaded region), the annular solar eclipse path (magenta line), the maximum obscuration (magenta dot) at 350 km altitude are presented. The magenta dashed line starts from the maximum obscuration of the solar eclipse to its conjugate location in the Southern Hemisphere.
Solar eclipses are rare events and, particularly, the 10 June 2021 event is an excellent opportunity to study the eclipse-induced effects on the polar ionosphere. Since the ionospheric variations can perturb GNSS, the eclipse can be used to study the positioning errors in these regions. There are some studies on the effects of the ionosphere during solar eclipses over the northern polar region. One of the first reported ones was the total solar eclipse that occurred on 9 March 1997 over Kazakhstan, Mongolia, eastern Siberia, and the Arctic Ocean ( to 180 min and A = −5 TECu) [4,22]. Another reported one is the total solar eclipse that occurred on 1 August 2008 over Canada, northern Greenland, the Arctic Ocean, central Russia, Mongolia, and China ( = −27 to 44 min, and A[%] = −40 to −11%) [10]. The most recent one is the eclipse that occurred on 20 March 2015 that covered the North Atlantic, Faroe Islands, and Svalbard (A[%] = −50 to −10%) [5,23]. This last one happened during the recovery phase of the most intense geomagnetic storm during Solar Cycle 24, the so-called St. Patrick’s Day Storm. Due to the limited availability of GNSS stations around the globe at the time of these previous studies, they were focused on a regional scale. The increasing number of accessible GNSS stations around the world allows a study on a global scale, facilitating the search of potential interactions between regions. This can show how spreadable GNSS disturbances are. In particular, the poles are of interest since several ionospheric disturbances can start from there during geomagnetic storms.
In GNSS receivers, TEC is estimated simultaneously from several satellites of the network, which serves to study the ionosphere. (e.g., [4,8,24], among many others). During the eclipses, the ionization decreases, producing a depletion in TEC. Although a decrease in electron concentration during a solar eclipse could produce an improvement in the positioning precision, it actually generates positional errors [25,26]. Few authors have analyzed the GNSS positioning errors caused by the influence of solar eclipses. The eclipses that occurred over Croatia on 11 August 1999 [27], over China on 22 July 2009 [28], and over the United States on 21 August 2017 [26] are some of the studies that analyzed GNSS positioning errors.
For the 1999 solar eclipse, Filjar, et al. [27] used a single frequency receiver located in the north of Croatia with ∼95% of maximum percentage of obscuration (MPO). In this work the authors did not relate ionospheric disturbances with positioning variations. The authors collected the horizontal positioning at the eclipse’s maximum obscuration time (MOT). They calculated an average positioning error of ∼34 m on horizontal Global Positioning System (GPS) accuracy for that time. These horizontal values could be due to the use of a single-frequency, the number of receiver channels, and the possible influence of Selective Availability (until May 2000).
Jia-Chun et al. [28] used eight GPS stations to study the TEC changes and their effect on the positioning during the 22 July 2009 solar eclipse. They possessed a real-time point positioning and real-time precision of single baselines. The measurements were affected by a geomagnetic storm (Dst peak = −80 nT and Kp-index = ), which made it difficult to separate the influence of the eclipse from the storm one.
In the case of the 2017 eclipse, Park et al. [26] computed and compared the rate of change of the TEC (ROT) with respect to the day before and the day after the eclipse; and with a time window of 3 h, from 16 UT. They determined the means of positioning errors at four GNSS stations (localized in Oregon, United States) within the path of the total solar eclipse which reached ∼32 cm. However, on reference days, the means of positioning errors were between 7–14 cm. The authors used the average length of the eight baselines, which was ∼270 km. On the eclipse day, the means of positioning results were −4 to 324% over the day before and the day after the eclipse. Yuan et al. [25] established the ionospheric eclipse factor method (IEFM) to model the ionospheric delay searching for the improvement of the GNSS positioning estimation. In this contest, the paper introduces the concept of the ionospheric eclipse factor method for the IPP for relatively precise separation of daytime from nighttime for the ionosphere. Although the ionospheric eclipse factor is not related to a solar eclipse as an astronomical phenomenon that occurs when the Moon obscures the Sun from Earth, this method could be used in future studies related to the impact of solar eclipses on GNSS positioning.
In our case, we obtain the apparent position variation using the post-processing kinematic precise point positioning (PPP) with ambiguity resolution (PPP-AR) mode. We chose this method because PPP demonstrates a high ability to improve position estimation. PPP is used for calculating the coordinates of a single receiver without the need for a reference station nearby as a control station. In addition, we can find some free PPP services available online [29]. PPP-AR is an enhanced version of the PPP technique that resolves the carrier phase ambiguities, improving the PPP accuracy [29,30,31]. Katsigianni et al. [30] recently presented a comparison between PPP and PPP-AR. In order to offer the community the possibility of evaluating our analysis, we used an online service. Thus, we selected the CSRS-PPP service for this work because it is one of the most commonly used PPP online services in the field. We also applied the common noise filter to more than 2300 GNSS stations, to correct the time series of the North, East, and Up components of the GNSS receivers, as described in [29].
The regular ionospheric effects of solar eclipses are not yet fully understood. Studies of the eclipse-induced effects on the ionosphere are important because they provide a better understanding of the processes that control the ionosphere and that can cause GNSS positioning errors. In the present paper, we present the impact of the 10 June 2021 annular solar eclipse on ionospheric variations that also cause errors in GNSS positioning. Therefore, we first analyze the ionospheric behavior at a global scale based on 2337 dual-frequency (DF) GNSS stations, Swarm-A satellite, and four ionospheric stations. We used GNSS stations distributed around the world since they will allow us to evaluate the effects beyond the northern polar region with a higher spatial resolution than ever before. Unlike previous studies about the GNSS positioning errors caused by the influence of solar eclipses, our study is focused on a global scale. This allowed us to find other locations in the world that could be affected by a perturbation in the north pole and how that perturbation propagates to those potential locations.
2. Materials and Methods
The methodology used in the 10 June 2021 annular eclipse is mainly based on the one described in Valdés-Abreu et al. [29]. However, in this work we incorporate the processing of ionospheric data from a Low Earth Orbit (LEO) satellite. The procedure of this work also includes the analysis of geophysical and geomagnetic conditions close to the date of the eclipse (10 June 2021). How we use this new set of data is detailed below.
2.1. Estimation of the Ionospheric Total Electron Content
The inherent space-time variability of the ionosphere can be observed through TEC that can be obtained using GNSS stations [32]. Then, GNSS measurements based on dual-frequency signals and , were used to obtain the vertical TEC (VTEC) data. The ground-based dual-frequency GNSS (DF-GNSS) receiver continually records two types of delay: the pseudoranges and the carrier phases of the two signals. The obtained data was used to estimate the slant TEC (STEC) and to calculate the VTEC. STEC and VTEC were calculated from Receiver Independent Exchange Format (RINEX) files by using the GPS-TEC analysis software (GPS-TEC program Ver 2.9.5, developed by Dr. Gopi Seemala, https://seemala.blogspot.com/2017/09/gps-tec-program-ver-295.html, last accessed on 17 April 2022) [24]. VTEC values were estimated with a satellite cut-off elevation angle of 30° at an altitude of 350 km to reduce possible errors. The TEC values were released every 30 s and were corrected for the satellite and receiver bias using the data obtained from the AIUB Data Center of Bern University in Switzerland (ftp://ftp.aiub.unibe.ch/CODE/, last accessed on 17 January 2022).
For the final selection of the RINEX files of each GNSS station, we took into account several aspects. First, we considered the quality of the files during the selected period of days (DoYs 159–163). Second, we verified that there were no errors or data-gap after TEC estimation and post-processing PPP-AR. This aspect is critical to relating TEC and/or ROTI with positioning variations. We used data from all available stations in the polar regions. We also tried to cover regions such as Africa, Australia, and Asia. The International GNSS Service (IGS) stations (http://www.igs.org, last accessed on 17 January 2022) [33]; the Chilean network of GNSS receivers operated by the National Seismological Center at University of Chile (CSN in Spanish); University NAVSTAR Consortium (UNAVCO); the Argentine Continuous Satellite Monitoring Network (RAMSAC in Spanish) [34]; the Brazilian Network for Continuous Monitoring of the Institute of Brazilian Geography and Statistics (IBGE in Portuguese); the Geoscience Australia; the Low-Latitude Ionospheric Sensor Network (LISN, http://lisn.igp.gob.pe/, accessed on 26 July 2021); and the African Geodetic Reference Frame (AFREF) provided RINEX files of 2337 GNSS stations that met the requirements we imposed (see Figure 1).
Additionally, the differential VTEC (DVTEC) in TECu and the percentage changes of DVTEC (DVTEC[%]) were used. These parameters are studied in the analysis of ionospheric irregularities, defined as the relative variation of VTEC, epoch by epoch, with respect to the mean value (in time) of as shown in Equations (1) and (2) [35].
where t represents the epoch, and is calculated by averaging the values of VTEC at the same time of the day, t, for the reference DoYs 159, 160, 162 and 163 which correspond to 2 days before and 2 days after the day of the eclipse (DoY 161).
According to the methodology [29], we used the ordinary Kriging interpolation method to produce the TEC maps at each ionospheric pierce point (IPP). With this method, we filled in the spatial gaps of the global ionosphere TEC maps, minimizing the effects of the inhomogeneous distribution of GNSS receivers. Before interpolating, we selected a spatial resolution of . Then, we employed the Kriging package implemented in Python (https://github.com/ERSSLE/ordinary_kriging, last accessed on 17 January 2022).
2.2. ROT and ROTI
In order to detect, investigate and characterize the occurrence of ionospheric irregularities, we have used the Rate of change of the TEC Index (ROTI). The ROT and ROTI values are usually expressed in TECu/min. ROTI is defined as the standard deviation of the rate of TEC (ROT), and it is estimated by dual-frequency GNSS data with the time interval of 5 min by using Equation (3) [29]:
where represents the temporal average. ROT is defined as the TEC variation rate of two successive epochs as stated in Equation (4) [29]:
where i indicates the observed satellite and t denotes the time of epoch. Hence, is the time interval between the subsequent epochs.
Depending on the ROTI value, the activity level can be classified in ranges such as: weak (if 0.25 ⩽ ROTI < 0.5); moderate (if 0.5 ⩽ ROTI < 1); and strong (if ROTI ⩾ 1), according to Liu et al. [36].
2.3. Low Earth Orbit Satellite Measurements and Ionospheric Data
Additionally, we analyze ionospheric measurements provided by a LEO satellite, the European Space Agency’s Swarm mission. This mission is a constellation of three LEO satellites that were successfully launched on 22 November 2013, and are still operating. This constellation is designed to provide measurements of the Earth’s magnetosphere and ionosphere, studying the impact of the solar wind on the dynamics of the upper atmosphere [37,38]. The Swarm-Alpha (A), Bravo (B), and Charlie (C) are three identical satellites that share the same design and payloads.
All three satellites were put into a circular near-polar orbit with a low eccentricity. Swarm-A/C pair have the same orbit configuration (inclination of 87.35°, altitude of ∼450 km, east–west separation of about 1–1.5° in longitude), while Swarm-B has a different one (inclination of 87.75°, altitude of ∼510 km). These satellites fly above the F-layer peak (the peak altitude of the ionospheric electron density). In addition, Swarm-A/C fly in tandem, while Swarm-B moves away from the couple Swarm-A/C by covering different local times [37,38].
The Swarm spacecraft were equipped with different payloads, including GPS receivers and Langmuir Probes (LP), among others. We considered the ionospheric VTEC values associated with the point where the link path between GPS and Swarm-A satellite pierces the spherical thin shell located 400 km above the Swarm-A orbit. We also used in-situ electron density () measurements by LP at ∼450 km [38,39] for each of the five selected DoYs in June 2021 (https://Earth.esa.int/web/guest/swarm/data-access, last accessed on 17 January 2022).
We used the Swarm Level 2 (L2) TEC (TECxTMS_2F) data product, which contains time series of slant and vertical (absolute and relative) TEC for each GPS satellite in view (at most eight due to instrumentation design). The cadence of the ionospheric TEC data is 1 Hz since it was changed from 10 s (0.1 Hz) to 1 s (1 Hz) on 14 July 2014 [38,40].
We also used the Swarm LP data, which is part of the EFI package (EFIX_LP_1B plasma data). LP provides measurements of in situ and electron temperature with a 2 Hz sampling rate [38,39].
2.4. Apparent Position Variation Using Kinematic Precise Point Positioning
The RINEX files of 2337 GNSS stations were processed using the Canadian Spatial Reference System (CSRS-PPP) online service (https://webapp.geod.nrcan.gc.ca/geod/tools-outils/ppp.php, last accessed on 6 January 2022) [41] with ambiguity resolution (PPP-AR) mode. The CSRS-PPP provides centimeter-level estimations with converged float solutions [41,42,43,44].
Usually, the CSRS-PPP report can provide a different reference start value for different days. To facilitate the evaluation of the apparent position variation time series, we process the data to have an equal reference for all the used data. At each of the 2337 stations, we applied the common noise filter to correct the time series of the North, East, and Up components, using the equation [29]:
where t is the epoch, is the corrected apparent position, is the apparent uncorrected position, and is the reference position. We use the average of AP, , from the same reference days mentioned in Equation (1) to calculate .
At each of the 2337 stations, the maximum error was obtained within the selected five days. Subsequently, the error of each station per component was classified by intervals, counting the percentage of the total number of stations that fell into each interval. In addition, a 3D position error was calculated as:
We use two threshold values. First, we selected threshold values for maximum 3D positioning error greater than or equal to 10 cm (3D ⩾ 10 cm) since according to data on quiet days, over 90% of the GNSS stations had 3D errors of less than 10 cm, while during ionospheric disturbances, only ∼40% kept this level of accuracy [29]. Second, we applied the Equation (6) to the horizontal and the vertical components presented in [29,30], obtaining the threshold of the 3D positioning error root mean square (3D-RMS) greater than or equal to 3 cm (3D-RMS ⩾ 3 cm).
2.5. Geomagnetic and Geophysical Conditions
The geomagnetic data downloaded from OMNIWeb Plus Data (https://omniweb.gsfc.nasa.gov, last accessed on 11 May 2022) for the 10 June 2021 annular solar eclipse indicates a period of low activity. Except in DoY 163, where it was between 3 and 6 UT, the estimated 3-hour planetary index (Kp) was ⩽. The disturbance storm time index (Dst) peak was >−17 nT, except after DoY 162 where a minimum of −37 nT was reached at 11 UT. The interplanetary magnetic field (IMF) Bz component in GSM coordinate peak was >−7.4 nT after DoY 162 and the solar wind speed (Vsw) was 330–520 km/s during 8–13 June 2021 (see Figure 2).
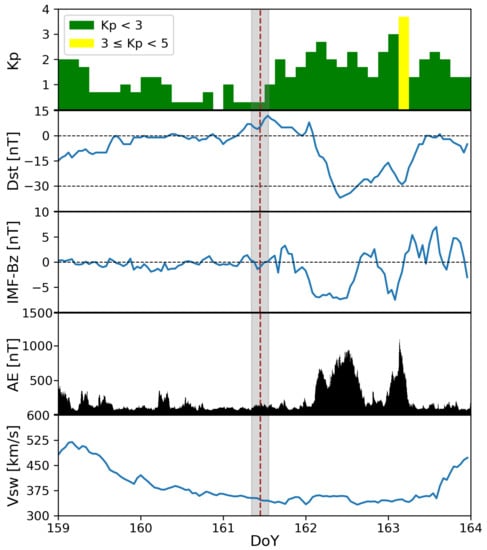
Figure 2.
Variations of 3-hourly Kp, Dst, IMF-Bz, AE, and Vsw indices that characterize the geomagnetic conditions on 8–13 June 2021. P1–P4 time (light grey bar) and GE time (red dashed line) are also represented.
The Auroral Electrojet index (AE) is a good proxy of the geomagnetic activity level at mid/high latitudes [29,45]. Following De Michelis et al. [46], we selected two distinct datasets corresponding, respectively, to geomagnetically quiet (AE < 50 nT) and active (AE > 300 nT) periods. Figure 2 also illustrates that the AE index was over 500 nT between 5 and 15 UT on DoY 162, and between 1 and 5 UT on DoY 163; so these time periods showed some activity in the auroral regions. Since these days are used by comparison with the day of the eclipse, these periods of time were treated with care to avoid interfering with the eclipse analysis.
Therefore, the geomagnetic conditions were generally quiet, except on DoY 162 where a weak geomagnetic storm took place between 8 and 16 UT. DoY 162 did not cause problems in the ionospheric TEC background to our results for the eclipse day. However, the geomagnetic activity the day after the eclipse had significant effects on GNSS positioning errors comparable to the positioning errors caused by the annular solar eclipse. These effects will be presented in more detail in the coming section.
Earthquake Occurrence
We also reviewed the occurrence of earthquakes (EQs) around the world, with a moment magnitude greater than 5 Mw and a depth of over 70 km on 8–13 June 2021. This review is important because EQs are sources of TEC disturbances and thus positioning errors. In the period analyzed, 15 moderate EQs of less than 5.7 Mw occurred (https://earthquake.usgs.gov, accessed on 17 January 2022). However, none of them produced noticeable effects on TEC or on the position estimation on the GNSS receivers during the analyzed period of days.
3. Results
In this section, we present the main results obtained after applying the methodology described in the previous section. The results obtained in this work can be divided into two main parts: (1) the analysis of the TEC maps that present the effects on the ionosphere at a global scale; and (2) the calculation of the positioning errors that these ionospheric effects generate.
3.1. Ionospheric Behavior and TEC Maps
From the data of each station, we can estimate the VTEC for each station during the selected period of days. By using the ordinary Kriging interpolation, as described in Section 2.1, it is possible to obtain VTEC maps. Figure 3 shows a summary of the TEC maps by contrasting the eclipse (VTECe) and control () days. We present some particular hours: 09.15 UT, 10.70 UT (GE time), 12.00 UT, 13.19 UT (P4 time), 13.72 UT (P4 time 0.5 h), and 17.66 UT. Figure 3 also shows the eclipse masks from 20% obscuration and with intervals of 20%, at 350 km altitude (white line). From these figures, it is possible to notice that the Greenland and South American sectors are two of the most affected in terms of VTEC depletion. VTECe in IPP and DVTEC[TECu] in Figure 3 use the Kriging interpolation method and are shown in equidistant cylindrical projection and Northern Hemisphere polar plots (see Supplementary Materials, Figure S1).
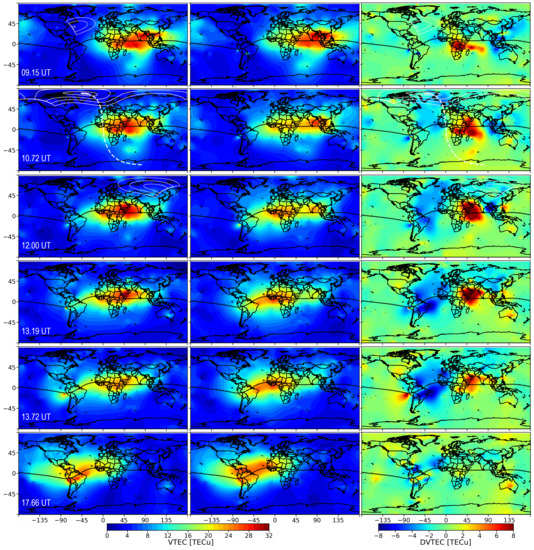
Figure 3.
Ionospheric TEC maps during the 10 June 2021 Annular Solar eclipse using the Kriging interpolation method. From left to right panels: VTECe, , and DVTEC[TECu]. From top to bottom panels: 09.15 UT, 10.70 UT (GE time), 12.00 UT, 13.19 UT (P4 time), 13.72 UT, and 17.66 UT. Eclipse obscuration masks from 20% obscuration and with intervals of 20%, at 350 km altitude (white line) are shown. The white dashed line starts from the maximum obscuration of the solar eclipse to its conjugate location in the Southern Hemisphere at 350 km altitude.
The 09.15 UT, 12.00 UT, and 13.72 UT maps were chosen in particular because they show the greatest apparent position variations during the eclipse time window. The 17.66 UT map was chosen because the ionosphere was roughly recovered by that time. For a better visualization of the eclipse effects, a third column has been incorporated where the VTEC differential in TEC units (DVTEC[TECu]) is shown.
DVTEC had values of around −20% (−2 TECu) over the oceanic sectors when the eclipse began (P1-time). However, at these locations, the GNSS receivers are scarce, which can cause less reliable interpolation. This value could be considered as part of the non-significant variations in DVTEC. A similar problem is identified over Central Africa, where there is a value of 50% (7 TECu), possibly also due to the few receivers in this area (see Figure 1). The anomalies in these areas were observed more than 5 h before the eclipse. We will focus mainly on changes generated over the continental areas of America and Europe, while the other areas will not be considered for this analysis.
When the ionospheric TEC effects due to eclipse have already begun, the 09.15 UT maps show a slight depletion of ( TECu) across eastern Canada under the shadow of the eclipse. At 10.70 UT (GE-time), these changes expand beyond the shadow area of the eclipse (see second row of Figure 3). The 10.70 UT maps show that ionospheric TEC depletion did not only occur across the obscuration region over the Northern Hemisphere. DVTEC[%] had values of around −60% (−4 to −2.5 TECu) over the South and East coasts of Greenland, ( TECu) eastern Canada, and around −50% (∼−3 TECu) over the Lesser Antilles.
The 12.00 UT, 13.19 UT, and 13.72 UT maps show DVTEC[%] had values of around −30% (−3 to −1.5 TECu) over Russia after GE time. Figure 3) also illustrates how the TEC disturbance moved from West to East over the Northern Hemisphere, following the path of the annular solar eclipse. At 12 UT, there is a recovery of the ionospheric TEC over Canada and Greenland regions, but DVTEC[%] had values of less than −50% in East coast of Greenland. Ionospheric TEC depletion had values of around −60% (∼−5 TECu) over the Lesser Antilles near the north crest of Equatorial Ionization Anomaly (EIA) and less than −30% (∼−5 TECu) appeared over South America near the south crest of EIA. The 13.19 UT and 13.72 UT maps show another slight recovery of the ionospheric TEC in the North Atlantic and Greenland, as well as a TEC depletion over Russia. Moreover, TEC depletion was accentuated in the EIA crests over South America, where DVTEC[%] had values of less than −60% (< TECu). It is shown that the effects lasted beyond the end of the eclipse.
The 17.66 UT maps present the global recovery of the ionosphere a few hours after the end of the eclipse. These maps show a slight DTEC[%] enhancement in the center of the EIA form ∼−16% to ∼10%. But the TEC depletion was ∼−20% (−5 to −3 TECu) in the EIA crest over South America. The TEC behavior in the EIA crests was maintained until after 19.66 UT.
On the other hand, DoY 162 had geomagnetic activity (see Section 2.5). Therefore, we checked if the DVTEC changes that we observed for the day of the eclipse were due to using DoY 162 as one of the reference days. We compute a new (, Equation (1)), and a new by averaging the VTEC values at the same time of the day, t, for the reference days, DoYs 159, 160, and 163. For each map, we used the map algebra (). The mean value ranged between −0.5 and 0.1 TECu, with a standard deviation of less than 0.7 TECu (see Supplementary Materials, Figure S2, Table S1). Therefore, geomagnetic activity during the DoY 162 did not cause problems in the background to our ionospheric TEC results for the eclipse day.
Ionospheric Behavior Using Swarm Satellite Measurements
We also present ionospheric behavior using Swarm-A measurements (see Figure 4). We illustrate VTEC at 850 km altitude on DoY 161 compared to DoY 159 during three ascending passes of the Swarm-A satellite (⩾45°S, see Figure 4 (upper panels)). We selected the three Swarm-A satellite passes that best fit the eclipse region and eclipse time window. The first satellite pass (∼8.50–9.20 UT) occurred after P1 time. The greatest ionospheric TEC degradation was −30°S–30°N (∼ TECu, ). The second pass (∼10.10–10.80 UT) was close to the GE time. As latitude increases, TEC decrease. The third satellite pass (∼11.70–12.40 UT) was performed prior to P4 time (∼ TECu, ). It is possible to see that TEC decrement was concentrated between 10 and 30°N (VTEC was close to ∼−1 TECu, and ∼−30%). Ionospheric TEC depletion was greatest in the 15–75°N region (∼ TECu, ).
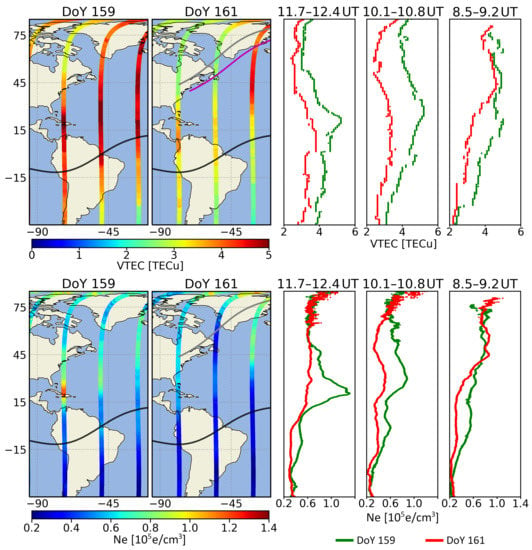
Figure 4.
Ionospheric behavior using Swarm-A measurements. (Upper panels) present ionospheric TEC data taken by Swarm-A satellite at 850 km (at 400 km above the Swarm-A). The TEC gathered through the satellite orbit is presented over an Earth map (left panel) and as a profile with data obtained in one of the comparison days (write panel). The three satellite passes are from 45°S to ∼90°N, from left to right, between ∼11.70–12.40, ∼10.10–10.80, and ∼8.50–9.20 UT during 2 days before eclipse day (DoY 159), and eclipse day (DoY 161). The annular eclipse path at 450 km (grey line) and 850 km altitude (magenta line) are also shown on DoY 161. VTEC on DoY 161 (red dots) compared to DoY 159 (green dots) between ∼11.70–12.40 UT, ∼10.10–10.80 UT, and ∼8.50–9.20 UT. (Bottom panels) depict Swarm-A in situ electron density () presented in the same way than the VTEC data.
3.2. ROTI and GNSS Precise Point Positioning Accuracy Maps
We estimated the ionospheric TEC, ROTI, and positioning for the full 5 days but only show 6 hours per day. On the eclipse day, we observe the largest positioning variations during this time window (around P1–P4 time, see Figure 5). This study focuses on the positioning accuracy of the stations during the 10 June 2021 annular solar eclipse, during the time between 8 and 14 UT. We estimated the PPP-AR using the CSRS-PPP service, as described in Section 2.4. Comparing the eclipse day with respect to the DoYs 159 and 160, we can see that the percentage of GNSS stations that exceeded maximum 3D positioning error ⩾10 cm and 3D-RMS ⩾3 cm (positioning thresholds) jumped from ∼180 (∼8%) to 333 (∼14%) and from ∼170 (∼7%) to 210 (∼9%), respectively. In addition, the ROTI threshold ⩾0.25 TECu/min was taken according to Liu et al. [36], and used in the methodology [29]. Figure 6 shows maximum 3D positioning errors, 3D-RMS of the apparent position, and ROTI maps, for each of the five selected DoYs.
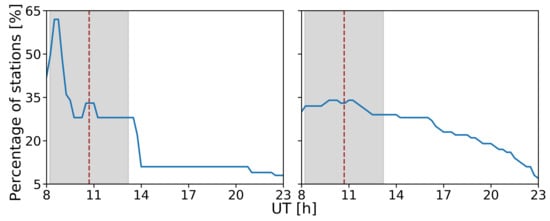
Figure 5.
Time variations of the percentage of stations with 3D positioning error greater than 10 cm on DoY 161. The (left panel) shows the 36 GNSS stations localized in Greenland. The (right panel) presents the 335 GNSS stations that are situated in South America.
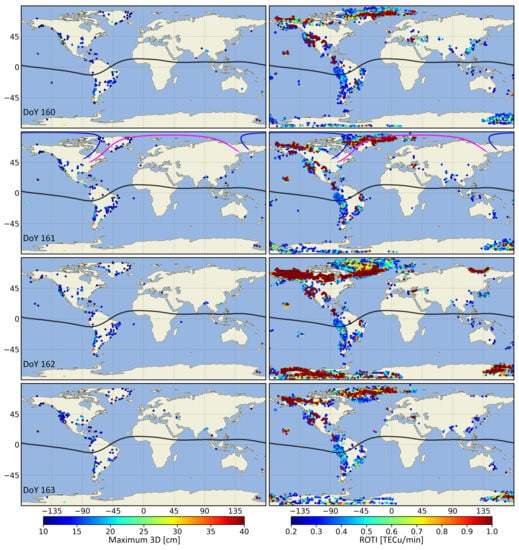
Figure 6.
Maximum 3D positioning errors ⩾10 cm (left panels); and ROTI ⩾0.25 TECu/min (right panels) between 8 and 14 UT. From top to bottom shows DoYs 160–163. Annular eclipse path at ground level (blue line), and at 350 km of altitude (magenta line) are also shown.
ROTI was calculated as described in Section 2.2 to study the relationship between the variation of TEC and the positioning error for the eclipse. The images in the Figure 6 (right panel) show five maps of ROTI, each representing the stations that had ROTI greater than 0.25 TECu/min. Each map represents a different day, but at the same time as that of the solar eclipse, DoYs 160–163 between 8 and 14 UT. We do not show the maps for DoY 159 because they are similar to those for DoY 160.
The TEC data (e.g., Figure 3) and the derived PPP-AR (see Figure 6 (left panels)), and Figure 7) show that there are two regions where the errors are more severe during the solar eclipse (DoY 161, between 8 and 14 UT). These regions are Greenland and South America. For this reason, we focused this study on these sectors.
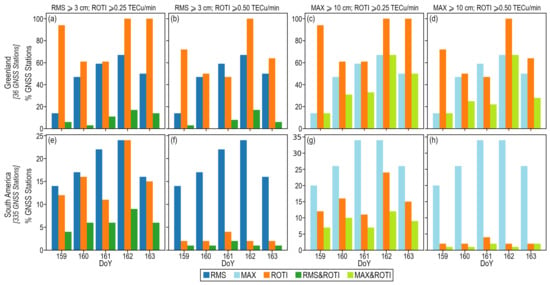
Figure 7.
Behavior of the maximum 3D positioning error, 3D-RMS, and ROTI in Greenland and South America sectors, where 36 GNSS stations are localized in Greenland (upper panels) and 335 GNSS stations are situated in South America (bottom panels). Percentage of GNSS stations where (a,b,e,f) 3D-RMS ⩾ 3 cm; (c,d,g,h) maximum 3D position ⩾ 10 cm; (a,c,e,g) ROTI ⩾ 0.25 TECu/min; and (b,d,f,h) ROTI ⩾ 0.50 TECu/min. Percentage of GNSS stations meeting 3D-RMS (blue bars); maximum 3D positioning error (light blue bars); ROTI (orange bars); 3D-RMS and ROTI (green bars); and maximum 3D positioning error and ROTI (light green bars) values.
In the Greenland and South America regions, we can find 36 (∼2%) and 335 (∼14%) of the 2337 total available GNSS stations, respectively. We determined the percentage of stations localized in both regions that had errors that fell at certain intervals during the time period of the annular eclipse (between 8 and 14 UT). Figure 7 shows the percentages of stations that meet the thresholds of maximum 3D positioning error, 3D-RMS, and ROTI. We determined the number of GNSS stations based on ROTI activity and positioning values (see Supplementary Materials, Tables S2–S4, where each column in these tables represents the percentage of stations with maximum 3D position error, 3D-RMS, and ROTI at certain intervals in the selected period).
Figure 5 shows in more detail the percentage of stations with maximum 3D errors ⩾10 cm on eclipse day. In Greenland, during the inicial period of the eclipse (∼P1 time), the percentage of stations with maximum 3D positioning error rises to 60%. Subsequently, the value remains at ∼28% until it increases to ∼33% between 10.5 and 11.25 UT (around GE time). The value then returns to ∼28% until 14 UT (after P4 time), when it drops to ∼11% of stations. In South America, the percentage of stations with maximum 3D positioning error had a maximum of ∼34% between 9.75 and 11.5 UT (around GE time). We also were able to observe a decrease in stations that exceeded the threshold maximum 3D positioning error from ∼28% to ∼22% between 16 and 17 UT.
3.3. Ionospheric Behavior and GNSS Positioning Errors by Region
To study the effects of the eclipse, we selected 24 stations from among the 2337 GNSS stations (see Figure 1). We chose five GNSS stations close to the annular solar eclipse (KMOR, KAGZ, MARG, IQAL, PICL). There were six GNSS stations located in the partial eclipse region (CN00, TRO1, SVTL, TIXI, MAG0, YAKT). Furthermore, we used five stations located in the Caribbean and South America (LMMF, BOAV, PIFL, MSBL). The sunrise (in PICL and CN00 stations) and the sunset (in MAG0 and YAKT stations) happened during the eclipse time window at ground level but did not take place at the ionospheric height of 350 km. More details about the GNSS stations and eclipse conditions (with respect to the ionospheric height of 350 km) can be found in Table 1.

Table 1.
Detail about the GNSS stations analyzed, their location, eclipse condition, magnitude and change in VTEC at each station. Eclipse characteristics (time and maximum obscuration) for the 24 selected GNSS stations. Further, we have also estimated eclipse conditions at the ionospheric height of 350 km by the method suggested by Verhulst et al. [21]. Ionosphere, 3D eclipse, and 3D non-eclipse values are between 8 and 14 UT. In 3D non-eclipse: MAX refers to the maximum 3D positioning error of the reference days, and we calculate RMS by taking all the values of the reference days between 8 and 14 UT.
Figure 8 presents the results of ionospheric TEC of 12 stations from among the 24 selected GNSS stations for the eclipse day (VTECe), the reference days (), and the final results of DVTEC [%]. The vertical blue shaded region between P1 time and P4 time, with GE time (brown dotted line). The vertical yellow shaded region between C1 time and C4 time, with MOT (black dotted line). Each plot is shown between 5 and 23 UT. The maximum reduction values of TEC for each station are indicated in Table 1 ( = 1 to 288 min, and A[%]= −65 to −27%). This eclipse occurred during the morning at most of the selected stations but took place in the afternoon at five stations (NYA1, TRO1, SVTL, TIXI, MAG0, YAKT). The Sun’s activity became stronger around noon and the clear TEC reduction during the eclipse can be observed. The stations that are near the path of the annular eclipse at 350 km altitude and the east coast of Greenland reached lower values of DVTEC [%] ∼−55% than the stations with the annular eclipse at the surface level DVTEC [%] ∼−40%.
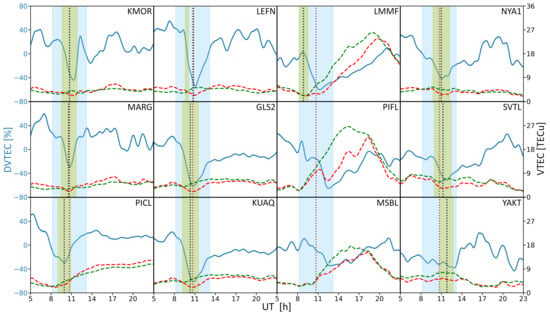
Figure 8.
The behavior of the ionospheric TEC during the 10 June 2021 Annular Solar Eclipse in 12 of the 24 selected GNSS stations. DVTEC[%] (blue line), VTECe (red dashed line) and (green dashed line). The GNSS stations are ordered by latitude and then by longitude. P1–P4 time is represented by the light blue bar, C1–C4 time by the yellow bar, MOT by black dotted line, and GE time by the red dotted line.
Figure 8 shows the ionospheric TEC changes for 12 of the 24 GNSS stations presented in Table 1. The TEC disturbance lasted longer at the GNSS stations located in South America and the Lesser Antilles (CN00, LMMF, CN57, BOAV, PIFL, MSBL). In these GNSS stations, the ionospheric effect caused by the eclipse started at ∼8.5–9 UT and ended ∼18–21 UT ( > 10 h). The ionospheric response is similar in BOAV and MSBL stations where A[%] ∼−30%. In MAG0, TIXI, and YAKT stations, we observe a TEC depletion during the eclipse time window, but it is not as noticeable as in the other cases.
Additionally, the number of GNSS stations according to ROTI activity was: 5 strong (BLAS, PIFL, LEFN, NYA1, and MARG stations), 2 moderate (KMOR and KAGZ stations) and 17 without activity (see Table 1).
In the same way, we presented the results of PPP-AR of 24 DF-GNSS stations during eclipse day. The time series were corrected for the common noise filter of the East, North, and Up components. The stations had variations in position within the time window of the eclipse (between 8 and 14 UT). The station with the highest positioning errors in the East, North, and Up components was PIFL stations. KAGA, GLS2, SENU, and MSBL stations also showed position variations between 5 and 8 UT.
Equation (6) is used to obtain the 3D results. Then, the maximum 3D positioning error and 3D-RMS values (between 8 and 14 UT) for each station are indicated in Table 1. We note that the GNSS stations can be separated according to the percentage of maximum 3D positioning error and 3D-RMS, with respect to the maximum values of reference days.
In the case of maximum 3D positioning error, four stations presented values below 0% (MARG, ALGO, CN00, and LMMF); eight 0–25% (KAGZ, IQAL, BLAS, BOAV, NYA1, SVTL, MAG0, and YAKT); seven GNSS stations were between 25 and 50%; three stations were 60–70% (GLS2, KUAQ, and SENU); and two stations > 100% (PIFL and TRO1).
On the other hand, for 3D-RMS in a percentage, 1 station was < 0% (CN00); 11 stations were 0–25% (KAGZ, MARG, LEFN, BLAS, KAGA, GLS2, KUAQ, NYA1, SVTL, TIXI, and YAKT); 7 stations were 25–50% (KMOR, IQAL, ALGO, LMMF, CN57, PIFL, and MSBL); 3 stations were 75–100% (SENU, PICL, and BOAV); and 2 stations > 100% (TRO1 and MAG0).
A Case Study
We will describe in more detail the results obtained with PIFL GNSS station (6.79°S, 43.04°W). PILF had the largest ionospheric disturbances and GNSS positioning errors (see Table 1). TEC depletion had values around −65% (−11.8 TECu) at 110 min after GE time (see Figure 8). Figure 9 presents the ionospheric behavior (ROT, ROTI) and kinematic DF-GNSS PPP-AR mode during DoYs 160–163 between 5 and 23 UT. We do not show DoY 159 because it does not differ significantly from DoY 160.
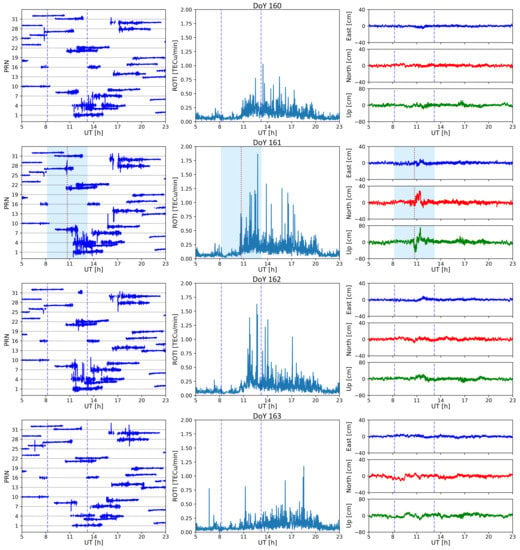
Figure 9.
Ionospheric behavior and apparent position variation of the PIFL GNSS station. From top to bottom show DoYs 160–163. ROT (TECu/m) (left panels), ROTI (TECu/m) (middle panels), DF-GNSS PPP-AR (cm): East [cm] (blue line), North [cm] (red line), and Up [cm] (green line) (right panels). P1–P4 time on non-eclipse day (blue dashed lines), P1–P4 time on eclipse day (light blue bar), GE time (red dotted line).
Figure 9 (left, middle panels) illustrates examples of GPS ROT and GPS ROTI variations along with all visible GPS satellites. On eclipse day, we can observe a |ROT| > 1.5 TEC/min in eight Pseudo Random Noises (PRN-4, 7, 8, 9, 14, 27, 28, 30). The |ROT| value was exceeded by 3–4 PRNs during the reference DoYs 159, 160, and 163. In contrast, the |ROT| was exceeded by seven PRNs on DoY 162 (see Figure 9 (left panels)). On DoY 161 between 10.66 and 17.39 UT (6.73 h), we could note 22 and 8 ROTI values >0.5 and >1 TECu/min, respectively (see Figure 9 (middle panels)). The ROTI peak was 1.9 TECu/min at 12.75 UT, estimated from the PRN-4. On this day, nine PRNs (PRN-4, 7, 8, 9, 10, 14, 27, 28, 30) presented a moderate and/or strong ROTI activity. Regarding DoYs 159, 160, 162 and 163, we observed 12, 8, 20 and 6 values with moderate and/or strong ROTI activity. Then, this station showed strong TEC activity during each of the five DoYs. The ROTI value was higher on eclipse day 1.9 TECu/min at 12.76 UT (∼25 min after P4 time).
Figure 9 (right panels) show the apparent position variation of kinematic DF-GNSS PPP-AR mode in the East, North, and Up components for the PIFL GNSS station. These time series has been corrected for the common noise filter. On DoY 161, the apparent peak ground displacement in the East, North, and Up components were 18, 40, and 119.8 cm, respectively. Moreover, the maximum 3D positioning error ⩾10 cm ∼9.80 UT by ∼3.30 h. The Up, North, and East components are ordered from highest to lowest errors. Then, positioning errors in the three components and their results were clear during the eclipse time window (after GE time), relative to the reference days.
4. Discussion
In this section, we discuss the main findings regarding the 10 June 2021 annular solar eclipse. The main goal is to study the positioning errors of GNSS receivers caused by this solar eclipse. In order to verify our findings, we compare our ionospheric values with results presented for other solar eclipses over the northern polar region (9 March 1997 [4,22]; 1 August 2008 [10]; and 20 March 2015 [5,23]).
There are several free-to-use software available for single-station TEC estimation methods [47,48]. We selected GPS-TEC software because it is a widely used method by the scientific community to study phenomena such as geomagnetic storms [29] and solar eclipses [49], among others. GPS-TEC software is fundamentally based on the assumption that ionospheric density depends on altitude to determine VTEC from STEC.
4.1. Ionospheric Behavior
The present analysis aims to show, as best as currently possible, the effects that the solar eclipse generates both in the ionosphere under the moon’s shadow as well as in the global ionosphere. The relevance of this event is that there are few of them that occur in polar regions, in this case, in the Arctic.
We have used interpolated global maps from TEC and we have calculated the difference between eclipse and reference days. The results of the TEC maps show a significant reduction under the moon’s shadow, except at the CN00 station that has similar behavior to the LMMF, CN57, BOAV, and MSBL stations (see Figure 3 and Figure 8, Table 1); the GNSS stations located in the region of the eclipse reaching a maximum of = 1 to 288 min, A peak ∼−5 TECu, A[%] = −61 to −27%. Table 1 details these parameters for GNSS stations of some selected regions (see Figure 1). The values of these parameters agree with those obtained for the solar eclipses of 9 March 1997 solar eclipse [4,22], 1 August 2008 [10], and 20 March 2015 [5,23].
TEC depletion was not as pronounced in the MAG0, TIXI, and YAKT stations (A[%] = −38 to −30%) compared to others GNSS stations (A[%] = −61 to −40%) with a similar percentage of obscuration (∼88%). This could be due to the fact that the sunset in MAG0, TIXI, and YAKT stations happened during the time-window of the eclipse at ground level. Moreover, the other stations were closer to the greatest eclipse (see Figure 1 and Figure 8, Table 1).
In addition to the decrease of TEC in the ionosphere under the Moon’s shadow, we have observed interesting and significant effects far from that region. This is the case of a significant decrease in TEC that seems to move southward from the shadow, passing through the North Atlantic, and remaining stationary for several hours over the Caribbean and the north of Brazil, at the stations CN00, LMMF, CN57, BOAV, PIFL, MSBL (see Figure 3 and Figure 8, and Table 1). The delay value relative to GE time was between ∼30 and ∼168 min, A peak ∼−11 TECu, A[%] = −65 to −28%, T > 10 h. This area coincides with the location of the crests of EIA. The TEC variations were more intense north and south of the magnetic equator, where they were similar to those obtained at the GNSS stations located in the eclipse region.
On the other hand, applying , we observed that the mean was between −0.5 and 0.1 TECu; and standard deviation was less than 0.7 TECu. Therefore, TEC changes due to the weak geomagnetic activity during the DoY 162, did not cause problems in the ionospheric TEC background to our presented results for the eclipse day (see Supplementary Materials, Figure S2, Table S1).
In order to verify the negative disturbance in TEC on EIA crests, we have compared them with ionosonde observations of the sector involved (Figure 10). The Ramey (RA, 18.5°N, 67.1°W) station on the Caribbean side, and Sao Luis (SL, 2.6°S, 44.2°W), Fortaleza (FZ, 3.9°S, 38°W) and Cachoeira Paulista (CP, 22.7°S, 45.0°W) stations on the Brazil side were selected. The geographic locations of these stations are indicated with blue rhombuses in Figure 1. The data is obtained from the Digital Ionogram Data Base (http://giro.uml.edu/didbase/scaled.php, accessed on 4 August 2021) [50].
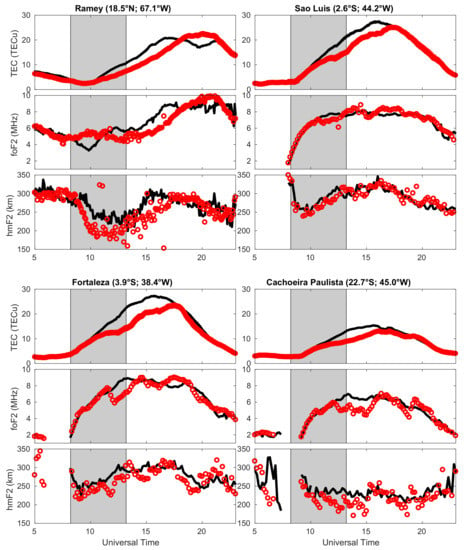
Figure 10.
Comparison between TEC differences and differences in the critical frequency of the plasma (foF2) and its height (hmF2). Observations (red circles), reference variation (black line), and P1–P4 time (shaded interval) are shown.
As a result, Figure 10 shows coherence between TEC and the critical frequency of the plasma (foF2) of each station. That is, the electron concentration after the eclipse maximum (∼11 UT) decreases (red circles) with respect to the reference curve (black line) calculated as indicated in Section 2.1. These same changes can be seen in the height of maximum electron concentration (hmF2). The decrease in foF2 and hmF2 is notorious at stations near the anomaly’s crest (RA, FZ, CP); however, it is not very significant in the stations at the magnetic equator (SL). Moreover, similar ionospheric effects were seen in distant regions in the moon’s shadow [16,17,18,19,20,51,52,53,54,55,56]. Differences between foF2 and TEC may be due to the fact that foF2 was the result of the original autoscaled records, and also that TEC was calculated from a spatial average.
A possible explanation for this phenomenon is that the eclipse could alter the thermospheric neutral wind regime and thus generate a ionospheric disturbance dynamo, which could be observed at the equator as a counter-electrojet. This counter-electrojet could be observed in the vertical drift of the plasma, for instance, the one measured by the Jicamarca incoherent radar. However, there are no measurements at Jicamarca for this period. Another way to observe is to calculate the difference in the horizontal component between an equatorial magnetometer and another in low latitude [57], or in the temporal variation of the same horizontal component of an equatorial magnetometer. In this case, neither the difference between Jicamarca (12.0°S, 76.8°W, I = 1°)—Piura (5.2°S, 80.6°W, I = 11°; available at http://lisn.igp.gob.pe/, last accessed on 22 May 2022), in the west coast of South America, nor the variation of the magnetometer of Kourou (5.2°N, 52.7°W; I = 13°; available at https://intermagnet.github.io, last accessed on 22 May 2022), in the east coast of South America shows significant variations during the eclipse day with respect to the other days (figure not shown), which rejects this hypothesis. Another possible explanation could be that due to the fact that the partial eclipse begins at low latitudes (see Supplementary Materials, Video S1) the electron concentration never reaches normal values again. An eclipse also can cause effects on a global scale. Because the eclipse-induced abrupt cooling of the atmosphere can result in an instantaneous temperature shift and pressure differential, triggering AGWs, and associated TADs and/or TIDs. However, a detailed investigation of these causes is out of the scope of the current paper [17].
On the other hand, ionospheric effects in the magnetic conjugate of the eclipse (end of the white line in Figure 3, at 10.70 UT) are not possible to observe due to the lack of receivers in this region (see Figure 1).
On DoY 161, there was low ROTI activity in the western region of the United States of America, compared to the reference DoYs. The decrease in the percentage of GNSS stations in South America with weak ROTI activities caused the increase of stations without activity up to 89%. Then, the number of stations with strong ROTI activity only increased from 1% to 3% in this sector. However, the behavior of the ROTI activity in Greenland was less than the reference days (see Figure 6 and Figure 7; Supplementary Materials, Table S4).
The behavior of ionospheric TEC and ROTI shows that electrons were less active in the ionosphere during the solar eclipse (see Table 1, and Figure 3, Figure 4, Figure 6, Figure 7 and Figure 8 and Figure 10). The behavior of the ROTI in the eclipse region was consistent with that indicated by Park et al. [26]. They found a significant reduction in the ROT during the eclipse. Furthermore, eclipse day was the least ROTI active in Greenland because we were able to observe a clear reduction in ROTI values compared to the other four DoYs (see Figure 6 (left panels), Figure 7 (upper panels)).
On the other hand, as a consequence of the geomagnetic activity (AE-index > 500 nT) in the polar regions from 5–15 UT on DoY 162; we can see an increase in ROTI activity (ROTI ⩾ 0.25 TECu/min) that starts at the northern polar region, propagating later the increment toward the equator (∼N), which agrees with previous studies [29,58,59] (see Figure 6 (left panels)). In South America, the percentage of stations with ROTI activity increased from ∼12% to 24% (see Figure 6 (left panels), Figure 7 (upper panels), and Supplementary Materials, Table S4).
The results obtained with the GNSS stations at 350 km (see Figure 3 and Figure 8) were consistent with the ionospheric TEC behavior at 400 km above the Swarm-A (see Figure 4). At P1 time, we observe a TEC depletion (∼ TECu, ) in the central Atlantic region, where the eclipse started and its conjugate. The greatest TEC reduction (∼ TECu, ) occurred at GE time (see Figure 4 (upper panels)). This TEC value was similar to that reported by Cherniak and Zakharenkova (−2 to −1.5 TECu) [60]. From Figure 4 (buttom panels), we were also able to show that the disturbance remained in the North and South American regions (TEC ∼−30%) even though the eclipse was already over the northern European and Asian regions. Moreover, we can observe a close similarity in the behavior of in situ Ne and VTEC (see Figure 4). Furthermore, the results of ionospheric plasma depletion using Swarm-A LP were consistent with the findings presented in [60].
4.2. Ionospheric Impacts on GNSS Positioning Errors
The manner in which we present the positioning errors in this work was through the statistics of perturbed stations around the world and, in particular, in the Greenland and South American sectors.
On the eclipse day, we could see a slight increase in the percentage of GNSS stations around the world that exceeded both positioning thresholds compared to previous days. The main increment suffered by the maximum 3D positioning error goes from ∼8% to ∼14%. Then, Greenland and the southern sector of America were within the regions that presented GNSS stations with the highest positioning errors during the eclipse time window. This positioning behavior in both regions was consistent with the global ionospheric TEC changes.
Contrary to what happens with the activity of electrons, the percentage of stations that exceed both positioning-error thresholds was greater on DoY 161 compared to DoYs 159, 160, and 163 (see Figure 6 and Figure 7 (upper panels)). We could see similar behavior in both cases of the 3D-RMS and ROTI activity relationships (RMS&ROTI). The eclipse day was the second DoY with the highest percentage of stations that exceeded the positioning-error thresholds. The effects of the eclipse day were only exceeded by DoY 162 due to weak geomagnetic activity (AE-index >500 nT) in the polar regions from 5 UT to 15 UT. In South America, the behavior of maximum 3D positioning error ⩾10 cm (34%) and 3D-RMS ⩾3 cm (22%) on day 161 was similar to day 162. In Greenland, these parameters were also similar on days 161 and 162, where maximum 3D positioning error ⩾10 cm was >55% and 3D-RMS ⩾ 3 cm was ∼17%. However, the effects on positioning on DoY 162 were slightly higher (see Figure 6 and Figure 7 (bottom panels)).
Our RMS position values for the quiet days were in accordance with those from previous results [29,30]. They showed that the precision of the post-processing kinematic PPP-AR method was ⩽0.8 and ⩽2 cm for the horizontal and vertical components, respectively. Moreover, our 3D-RMS results in percentage (⩽3 cm = −4 to 225%) are consistent with the −4 to 324% presented by Park et al. [26].
Unlike previous studies [61,62,63,64], the results presented by Valdés-Abreu et al. [29], suggested that positioning errors also occur, regardless of whether the ROTI has rapid variations, with or without ROTI activity, in this type of DF-GNSS stations with the use of PPP-AR. Moreover, our results confirm that ionospheric disturbance sources can cause degradation of the GNSS accuracy (maximum 3D positioning error ⩾ 10 cm and 3D-RMS ⩾ 3 cm) when ROTI ⩾ 0.25 TECu/min, ROTI ⩾ 0.5 TECu/min, and without ROTI activity (see Table 1, and Figure 6, Figure 7, Figure 8 and Figure 9). In addition, not all GNSS stations that had ROTI activity presented position errors.
Further, the ROTI activity–positioning variation relationship would have been met if two necessary conditions had been observed on each day in Figure 7. First, the positioning bars (RMS and MAX) had to be greater than or equal to the ROTI activity bar. This condition ensures that any ROTI activity causes variations in GNSS positioning. Second, the positioning ROTI bars (RMS&ROTI and MAX&ROTI) had to be the same or similar to the ROTI activity bar.
In most GNSS stations, we can observe the positioning errors were around the beginning of the TEC reduction (∼P1 time), the TEC peak (∼MOT and GE time), and/or in the final phase of the TEC recovery (see Figure 8). Then, we can see from one to more than three time slots with positioning errors. In general, after P1 time, the behavior of the stations with maximum 3D positioning error ⩾10 cm is similar to the DVTEC [%] of the stations located in Greenland (see Figure 8 (left, center left panels), Figure 5 (left panels)) and South America (see Figure 8 (center right panels), Figure 5 (right panel)). For example, in the Greenland region, the ionospheric TEC depletion was significant until ∼14 UT, and the recovery also could be observed in the rapid decrease from 28% to 11% of stations that exceeded the threshold of maximum 3D positioning error ∼14 UT, where the persistence of the positioning errors provoked by the 10 June 2021 annular eclipse lasted ∼6 h. Although the TEC depletion in sectors of South America could be observed until ∼19–21 UT, a ionospheric TEC enhancement was observed around 16–17 UT, similar to the behavior of the GNSS stations with a maximum 3D positioning error greater than the threshold of 10 cm (from 28% to 22% between 16 and 17 UT). Therefore, the persistence of the positioning errors provoked by the 10 June 2021 annular eclipse lasted ∼10 h.
The annular eclipse in Greenland caused significant TEC changes (∼), although with low ROTI activity. However, the GNSS positioning errors are similar to those caused during a weak geomagnetic storm with high auroral activity.
From Table 1, Figure 8 and Figure 9, we see that the stations (PIFL, TRO1, GLS2, KUAQ, SENU) presented maximum 3D position errors >60%, also had A[%] 49%, but without ROTI activity (<0.25 TECu/min). PIFL station was the only one with ROTI activity over the 5-day period under consideration. Additionally, not all the stations that had A[%] 49% got maximum 3D erros >60% (BLAS, LEFN, IQAL, SVTL, LMMF, and CN57 stations). The LMMF station presented A[%] = −61%, but maximum 3D position errors = −8%, and ROTI = 0.2 TECu/min. Although the BLAS and LEFN stations had strong ROTI activity and the IQAL station had weak ROTI activity, the percentage of maximum 3D positioning error in these stations was between 24% and 31%.
Thus, the results suggest that when maximum 3D errors >60%, with respect to the maximum of the reference days, we can find A[%] 49%, but not the opposite. The results also reinforce the idea that ROTI activity is not a necessary condition to affect GNSS accuracy. We were not able to estimate the ionospheric effects on GNSS positioning in the magnetic conjugate region of MPO of the solar eclipse, due to the lack of GNSS stations in this region.
Our study showed that the ionospheric TEC disturbances due to the solar eclipse in the polar regions can produce disturbances in low and medium latitudes. Ionospheric changes can cause GNSS positioning errors. The estimation of these errors is critical in teleoperated and autonomous (ground, maritime, and aerial) applications and other high-precision activities. For example, mining, agriculture, and fishing are all key economic activities in Chile that are considering the use of more teleoperated or autonomous systems. If the positioning error in the GNSS receivers spikes in vehicles in these industries, it could impose a serious risk to people and infrastructure. For open-pit mines, a high error can generate a failure in the estimation of the terrace on which a vehicle is located, with the consequent risk of falling. Halting autonomous operations during some events such as eclipses can reduce potential risks, but they can be complex for these industries. Stopping the operation for even a short period of time, such as an hour, could be prohibitively expensive. Therefore, forecasting the impact should be precise in location and duration.
5. Conclusions
In this work, we analyzed the ionospheric behavior during the 10 June 2021 annular solar eclipse and its impact on DF-GNSS PPP-AR accuracy. We use a large global GNSS network located around the planet to estimate the effects on positioning. This solar eclipse had a trajectory over the northern polar region. We used global ionospheric TEC maps with data gathered by ground-based GNSS stations.
The TEC maps show a noticeable depletion under the moon’s shadow, reaching A[%] < −60%. Furthermore, a significant TEC decrease (A[%] < −60%) can also be observed far from the ionosphere under the moon’s shadow in regions close to the crests of the EIA over the Caribbean and South America, with a duration or T over 10 h. Then, percentages of the ionospheric TEC over the Caribbean and South America were similar to those obtained for GNSS stations located in the region of the eclipse. Our study also confirms that there are cases and places where the disturbance can last much longer than previously expected.
We show that TEC enhancement caused by geomagnetic activity on the day after the eclipse did not cause problems in the ionospheric TEC background to our presented results for the eclipse day. We also validated the ionospheric variations estimated with GNSS receivers through measurements from other instruments such as the Swarm-A satellite (VTEC and in situ Ne), and four ionosondes (TEC, foF2, and hmF2). The ionospheric behavior clearly demonstrates that electrons are less active in that layer during the solar eclipse. Furthermore, our results are consistent with ionospheric effects reported in similar previous solar eclipses.
This study not only analyzes the eclipse’s day but also compares the effects of the ionosphere and its impact on the positioning precision with those over 2 days previous and 2 days after the day of the eclipse. The day of the eclipse was the day with the second highest percentage of stations that exceeded the selected positioning thresholds (maximum 3D positioning error ⩾ 10 cm, 3D-RMS ⩾ 3 cm), only surpassed by the day after, which had geomagnetic activity. The data analysis shows that the eclipse had a significant effect on GNSS precision for a long time (∼10 h). The Greenland and South America sectors are within the regions that presented GNSS stations with the highest positioning errors during the eclipse time window. Moreover, both regions had the greatest ionospheric TEC decrease (∼−60%).
The ROTI variations were not relevant. Thus, the results reinforce the idea that ROTI activity is not a necessary condition to affect DF-GNSS PPP-AR accuracy. Additionally, the results suggest that when maximum 3D errors are larger than 60%, the A[%] is much less than −49%. However, the opposite is not necessarily true.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs14133119/s1, Video S1: Eclipse obscuration mask from P1 to P4 time at 350 km altitude. Figure S1: Ionospheric TEC maps during the 10 June 2021 Annular Solar Eclipse: the world and Northern Hemisphere polar plots. Figure S2: DVTEC[TECu] maps using the Kriging interpolation method to the eclipse day. Table S1: Mean and standard deviation for each map of Figure S2. Table S2: 3D-RMS in Greenland and South America. Table S3: Maximum 3D positioning error in Greenland and South America. Table S4: ROTI in Greenland and South America.
Author Contributions
Conceptualization, J.C.V.-A., M.A.D. and M.B.; methodology, J.C.V.-A. and M.A.D.; software, J.C.V.-A., M.B. and Y.S.-S.; validation, J.C.V.-A., M.A.D., M.B., J.C.B. and Y.S.-S.; formal analysis, J.C.V.-A., M.B. and Y.S.-S.; investigation, J.C.V.-A., M.A.D., M.B., J.C.B. and Y.S.-S.; resources, J.C.V.-A., M.A.D., M.B., J.C.B. and Y.S.-S.; data curation, J.C.V.-A., M.B. and Y.S.-S.; writing—original draft preparation, J.C.V.-A., M.B. and Y.S.-S.; writing—review and editing, M.A.D. and J.C.B.; visualization, J.C.V.-A., M.A.D. and Y.S.-S.; supervision, M.A.D. and J.C.B.; project administration, M.A.D.; funding acquisition, M.A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Air Force Office of Scientific Research under award numbers FA9550-18-1-0249. This work was also partially funded by the ANID-FONDECYT 1211144 and the National Agency for Research and Development (ANID)/Scholarship Program/Doctorado Nacional/2018–21181599 (CONICYT Doctoral Grant Number 21181599). M.B. thanks the support of ANID-FONDECYT Regular 1211144 and FONDECYT Postdoctorado 3180742. J.C.B. was also supported by ANID PIA (ACT192169) and supported by Fondecyt project (Nº1200779 ANID, Chile).
Data Availability Statement
The RINEX files were obtained from: IGS stations; the Chilean network of GNSS receivers operated by CSN; UNAVCO; RAMSAC; Brazilian Network for Continuous Monitoring of IBGE; the Geoscience Australia; LISN; and AFREF. The satellite and receiver bias the data were obtained from AIUB Data Center of Bern University in Switzerland. The geomagnetic data were downloaded from: WDC for Geomagnetism, Kyoto; and OMNIWeb Plus Data Documentation. EQ data were available in the USGS Comprehensive Catalog of Earthquakes. The ionospheric TEC and LP measurements of in situ electron density data provided by ESA Swarm mission.
Acknowledgments
The authors would sincerely thank Miguel Martínez-Ledesma from Universidad de Concepción for his advice on plotting the eclipse obscuration mask.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Kumar, S.; Singh, A. Changes in total electron content (TEC) during the annular solar eclipse of 15 January 2010. Adv. Space Res. 2012, 49, 75–82. [Google Scholar] [CrossRef]
- Founda, D.; Melas, D.; Lykoudis, S.; Lisaridis, I.; Gerasopoulos, E.; Kouvarakis, G.; Petrakis, M.; Zerefos, C. The effect of the total solar eclipse of 29 March 2006 on meteorological variables in Greece. Atmos. Chem. Phys. 2007, 7, 5543–5553. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.K.; Singh, R.; Veenadhari, B.; Singh, A. Response of low latitude D-region ionosphere to the total solar eclipse of 22 July 2009 deduced from ELF/VLF analysis. Adv. Space Res. 2012, 50, 1352–1361. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Astafyeva, E.I.; Demyanov, V.V.; Edemskiy, I.K.; Gavrilyuk, N.S.; Ishin, A.B.; Kosogorov, E.A.; Leonovich, L.A.; Lesyuta, O.S.; Palamartchouk, K.S.; et al. A review of GPS/GLONASS studies of the ionospheric response to natural and anthropogenic processes and phenomena. J. Space Weather Space Clim. 2013, 3, A27. [Google Scholar] [CrossRef] [Green Version]
- Hoque, M.M.; Wenzel, D.; Jakowski, N.; Gerzen, T.; Berdermann, J.; Wilken, V.; Kriegel, M.; Sato, H.; Borries, C.; Minkwitz, D. Ionospheric response over Europe during the solar eclipse of March 20, 2015. J. Space Weather Space Clim. 2016, 6, A36. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.Y.; Liu, J.Y.; Lin, C.C.H.; Lin, C.Y.; Shen, M.H.; Chen, C.H.; Chen, C.H.; Chou, M.Y. Ionospheric bow wave induced by the moon shadow ship over the continent of United States on 21 August 2017. Geophys. Res. Lett. 2018, 45, 538–544. [Google Scholar] [CrossRef]
- Paul, A.; Das, T.; Ray, S.; Das, A.; Bhowmick, D.; DasGupta, A. Response of the equatorial ionosphere to the total solar eclipse of 22 July 2009 and annular eclipse of 15 January 2010 as observed from a network of stations situated in the Indian longitude sector. Ann. Geophys. 2011, 29, 1955–1965. [Google Scholar] [CrossRef]
- An-hua, C.; Sheng-Bing, Y.; Ji-Sheng, X. Ionospheric responses to a total solar eclipse deduced by the GPS beacon observations. Wuhan Univ. J. Nat. Sci. 1999, 4, 439–444. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Lesyuta, O.S. Ionospheric response to the total solar eclipse of 21 June 2001. arXiv 2002, arXiv:0201047. [Google Scholar]
- Momani, M.A.; Yatim, B.; Mohd Ali, M.A. Ionospheric and geomagnetic response to the total solar eclipse on 1 August 2008 over Northern Hemisphere. J. Geophys. Res. Space Phys. 2010, 115, A8. [Google Scholar] [CrossRef] [Green Version]
- Panda, S.K.; Gedam, S.; Rajaram, G.; Sripathi, S.; Bhaskar, A. Impact of 15 Jan 2010 annular solar eclipse on the equatorial and low latitude ionosphere over Indian region from Magnetometer, Ionosonde and GPS observations. arXiv 2015, arXiv:1506.05245. [Google Scholar]
- Sharma, S.; Dashora, N.; Galav, P.; Pandey, R. Total solar eclipse of 22 July 2009: Its impact on the total electron content and ionospheric electron density in the Indian zone. J. Atmos. Sol. Terr. Phys. 2010, 72, 1387–1392. [Google Scholar] [CrossRef]
- Tsai, H.; Liu, J. Ionospheric total electron content response to solar eclipses. J. Geophys. Res. Space Phys. 1999, 104, 12657–12668. [Google Scholar] [CrossRef]
- Farges, T.; Le Pichon, A.; Blanc, E.; Perez, S.; Alcoverro, B. Response of the lower atmosphere and the ionosphere to the eclipse of 11 August 1999. J. Atmos. Sol. Terr. Phys. 2003, 65, 717–726. [Google Scholar] [CrossRef]
- Lei, J.; Dang, T.; Wang, W.; Burns, A.; Zhang, B.; Le, H. Long-Lasting Response of the Global Thermosphere and Ionosphere to the 21 August 2017 Solar Eclipse. J. Geophys. Res. Space Phys. 2018, 123, 4309–4316. [Google Scholar] [CrossRef]
- Bravo, M.; Martínez-Ledesma, M.; Foppiano, A.; Urra, B.; Ovalle, E.; Villalobos, C.; Souza, J.; Carrasco, E.; Muñoz, P.R.; Tamblay, L.; et al. First Report of an Eclipse From Chilean Ionosonde Observations: Comparison with Total Electron Content Estimations and the Modeled Maximum Electron Concentration and Its Height. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027923. [Google Scholar] [CrossRef]
- Aa, E.; Zhang, S.R.; Shen, H.; Liu, S.; Li, J. Local and conjugate ionospheric total electron content variation during the 21 June 2020 solar eclipse. Adv. Space Res. 2021, 68, 3435–3454. [Google Scholar] [CrossRef]
- He, L.; Heki, K.; Wu, L. Three-Dimensional and Trans-Hemispheric Changes in Ionospheric Electron Density Caused by the Great Solar Eclipse in North America on 21 August 2017. Geophys. Res. Lett. 2018, 45, 10933–10940. [Google Scholar] [CrossRef] [Green Version]
- Le, H.; Liu, L.; Yue, X.; Wan, W. The ionospheric behavior in conjugate hemispheres during the 3 October 2005 solar eclipse. Ann. Geophys. 2009, 27, 179–184. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.R.; Erickson, P.J.; Vierinen, J.; Aa, E.; Rideout, W.; Coster, A.J.; Goncharenko, L.P. Conjugate Ionospheric Perturbation During the 2017 Solar Eclipse. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028531. [Google Scholar] [CrossRef]
- Verhulst, T.G.W.; Stankov, S.M. Height Dependency of Solar Eclipse Effects: The Ionospheric Perspective. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028088. [Google Scholar] [CrossRef]
- Afraimovich, E.; Kosogorov, E.; Lesyuta, O. Effects of the 11 August 1999 total solar eclipse as deduced from total electron content measurements at the GPS network. J. Atmos. Sol. Terr. Phys. 2002, 64, 1933–1941. [Google Scholar] [CrossRef] [Green Version]
- Stankov, S.M.; Bergeot, N.; Berghmans, D.; Bolsée, D.; Bruyninx, C.; Chevalier, J.M.; Clette, F.; De Backer, H.; De Keyser, J.; D’Huys, E.; et al. Multi-instrument observations of the solar eclipse on 20 March 2015 and its effects on the ionosphere over Belgium and Europe. J. Space Weather Space Clim. 2017, 7, A19. [Google Scholar] [CrossRef]
- Seemala, G.K.; Valladares, C.E. Statistics of total electron content depletions observed over the South American continent for the year 2008. Radio Sci. 2011, 46, 1–14. [Google Scholar] [CrossRef]
- Yuan, Y.; Tscherning, C.; Knudsen, P.; Xu, G.; Ou, J. The ionospheric eclipse factor method (IEFM) and its application to determining the ionospheric delay for GPS. J. Geod. 2008, 82, 1–8. [Google Scholar] [CrossRef]
- Park, J.; Shahbazi, A.; Kim, S.K.; Oberg, R. Ionospheric Response to the Total Solar Eclipse of 21 August 2017, and Its Impact on GNSS Positioning. J. Surv. Eng. 2019, 145, 05019001. [Google Scholar] [CrossRef]
- Filjar, R. Horizontal GPS positioning accuracy during the 1999 solar eclipse. J. Navig. 2001, 54, 293–296. [Google Scholar] [CrossRef]
- Jia-Chun, A.; Ze-Min, W.; Dong-Chen, E.; Wei, S. Ionospheric Behavior During the Solar Eclipse of 22 July 2009 and Its Effect on Positioning. Chin. J. Geophys. 2010, 53, 731–739. [Google Scholar] [CrossRef]
- Valdés-Abreu, J.C.; Díaz, M.A.; Báez, J.C.; Stable-Sánchez, Y. Effects of the 12 May 2021 Geomagnetic Storm on Georeferencing Precision. Remote Sens. 2022, 14, 38. [Google Scholar] [CrossRef]
- Katsigianni, G.; Loyer, S.; Perosanz, F. PPP and PPP-AR Kinematic Post-Processed Performance of GPS-Only, Galileo-Only and Multi-GNSS. Remote Sens. 2019, 11, 2477. [Google Scholar] [CrossRef] [Green Version]
- Abou-Galala, M.; Rabah, M.; Kaloop, M.; Zidan, Z.M. Assessment of the accuracy and convergence period of Precise Point Positioning. Alex. Eng. J. 2018, 57, 1721–1726. [Google Scholar] [CrossRef]
- Turel, N.; Arikan, F. Probability density function estimation for characterizing hourly variability of ionospheric total electron content. Radio Sci. 2010, 45, 1–10. [Google Scholar] [CrossRef]
- Dow, J.; Neilan, R.; Rizos, C. The International GNSS Service in a Changing Landscape of Global Navigation Satellite Systems. J. Geod. 2008, 83, 191–198. [Google Scholar] [CrossRef]
- Piñón, D.; Gomez, D.; Smalley, B.; Cimbaro, S.; Lauría, E.; Bevis, M. The History, State, and Future of the Argentine Continuous Satellite Monitoring Network and Its Contributions to Geodesy in Latin America. Seismol. Res. Lett. 2018, 89, 475–482. [Google Scholar] [CrossRef] [Green Version]
- Tsidu, G.M.; Abraha, G. Moderate geomagnetic storms of 22–25 January 2012 and their influences on the wave components in ionosphere and upper stratosphere-mesosphere regions. Adv. Space Res. 2014, 54, 1793–1812. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, Y.; Tan, B.; Li, M. Observational Analysis of Variation Characteristics of GPS-Based TEC Fluctuation over China. ISPRS Int. J. Geo-Inf. 2016, 5, 237. [Google Scholar] [CrossRef] [Green Version]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Pignalberi, A. TITIPy: A Python tool for the calculation and mapping of topside ionosphere turbulence indices. Comput. Geosci. 2021, 148, 104675. [Google Scholar] [CrossRef]
- Swarm L1b Product Definition. 2018. Available online: https://earth.esa.int/eogateway/documents/20142/37627/swarm-level-1b-product-definition-specification.pdf/12995649-fbcb-6ae2-5302-2269fecf5a08 (accessed on 15 March 2022).
- Swarm L2 TEC Product Description. 2017. Available online: https://earth.esa.int/eogateway/documents/20142/37627/swarm-level-2-tec-product-description.pdf/8fe7fa04-6b4f-86a7-5e4c-99bb280ccc7e (accessed on 15 March 2022).
- Abdallah, A.; Saifeldin, A.; Abomariam, A.; Ali, R. Efficiency of using GNSS-PPP for digital elevation model (DEM) production. Artif. Satell. 2020, 55, 17–28. [Google Scholar] [CrossRef]
- Alkan, R.M.; Erol, S.; Ozulu, I.M.; Ilci, V. Accuracy comparison of post-processed PPP and real-time absolute positioning techniques. Geomat. Nat. Hazards Risk 2020, 11, 178–190. [Google Scholar] [CrossRef]
- Yigit, C.O. Experimental assessment of post-processed kinematic Precise Point Positioning method for structural health monitoring. Geomat. Nat. Hazards Risk 2016, 7, 360–383. [Google Scholar] [CrossRef] [Green Version]
- Mendez Astudillo, J.; Lau, L.; Tang, Y.T.; Moore, T. Analysing the Zenith Tropospheric Delay Estimates in On-line Precise Point Positioning (PPP) Services and PPP Software Packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef] [Green Version]
- Davis, T.N.; Sugiura, M. Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 1966, 71, 785–801. [Google Scholar] [CrossRef] [Green Version]
- De Michelis, P.; Consolini, G.; Pignalberi, A.; Tozzi, R.; Coco, I.; Giannattasio, F.; Pezzopane, M.; Balasis, G. Looking for a proxy of the ionospheric turbulence with Swarm data. Sci. Rep. 2021, 11, 6183. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Kiselev, A.V.; Zhivetiev, I.V.; Edemskiy, I.K.; Syrovatskii, S.V.; Maletckii, B.M.; Vesnin, A.M. SIMuRG: System for ionosphere monitoring and research from GNSS. GPS Solut. 2020, 24, 69. [Google Scholar] [CrossRef]
- Pignalberi, A.; Pietrella, M.; Pezzopane, M.; Habarulema, J. Investigating different vTEC calibration methods for data assimilation in ionospheric empirical models. Adv. Space Res. 2021, 68, 2138–2151. [Google Scholar] [CrossRef]
- Kundu, S.; Chowdhury, S.; Palit, S.; Mondal, S.K.; Sasmal, S. Variation of ionospheric plasma density during the annular solar eclipse on 26 December 2019. Astrophys. Space Sci. 2022, 367, 44. [Google Scholar] [CrossRef]
- Reinisch, B.; Galkin, I. Global Ionospheric Radio Observatory (GIRO). Earth Planets Space 2011, 63, 377–381. [Google Scholar] [CrossRef] [Green Version]
- Dang, T.; Lei, J.; Wang, W.; Zhang, B.; Burns, A.; Le, H.; Wu, Q.; Ruan, H.; Dou, X.; Wan, W. Global Responses of the Coupled Thermosphere and Ionosphere System to the August 2017 Great American Solar Eclipse. J. Geophys. Res. 2018, 123, 7040–7050. [Google Scholar] [CrossRef]
- Huba, J.D.; Drob, D. SAMI3 prediction of the impact of the 21 August 2017 total solar eclipse on the ionosphere/plasmasphere system. Geophys. Res. Lett. 2017, 44, 5928–5935. [Google Scholar] [CrossRef]
- Jonah, O.F.; Goncharenko, L.; Erickson, P.J.; Zhang, S.; Coster, A.; Chau, J.L.; de Paula, E.R.; Rideout, W. Anomalous Behavior of the Equatorial Ionization Anomaly During the 2 July 2019 Solar Eclipse. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027909. [Google Scholar] [CrossRef]
- Martínez-Ledesma, M.; Bravo, M.; Urra, B.; Souza, J.; Foppiano, A. Prediction of the Ionospheric Response to the 14 December 2020 Total Solar Eclipse Using SUPIM-INPE. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028625. [Google Scholar] [CrossRef]
- Sergeenko, N. Irregular Phenomena in Magnetically Conjugate Regions of the F2 Layer of the Ionosphere. Geomagn. Aeron. 2018, 58, 823–830. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Dandenault, P.B.; Galkin, I.A.; Hamel, R.; Richards, P.G. Investigation of the Electron Density Variation During the 21 August 2017 Solar Eclipse. Geophys. Res. Lett. 2018, 45, 1253–1261. [Google Scholar] [CrossRef]
- Anderson, D.; Anghel, A.; Chau, J.; Veliz, O. Daytime vertical E × B drift velocities inferred from ground-based magnetometer observations at low latitudes. Space Weather 2004, 2, S11001. [Google Scholar] [CrossRef] [Green Version]
- Kotulak, K.; Krankowski, A.; Froń, A.; Flisek, P.; Wang, N.; Li, Z.; Błaszkiewicz, L. Sub-Auroral and Mid-Latitude GNSS ROTI Performance during Solar Cycle 24 Geomagnetic Disturbed Periods: Towards Storm’s Early Sensing. Sensors 2021, 21, 4325. [Google Scholar] [CrossRef]
- Kotulak, K.; Zakharenkova, I.; Krankowski, A.; Cherniak, I.; Wang, N.; Fron, A. Climatology Characteristics of Ionospheric Irregularities Described with GNSS ROTI. Remote Sens. 2020, 12, 2634. [Google Scholar] [CrossRef]
- Cherniak, I.; Zakharenkova, I. Ionospheric Total Electron Content Response to the Great American Solar Eclipse of 21 August 2017. Geophys. Res. Lett. 2018, 45, 1199–1208. [Google Scholar] [CrossRef]
- Shagimuratov, I.; Chernouss, S.; Despirak, I.; Filatov, M.; Efishov, I.; Tepenitsyna, N.Y. Occurrence of TEC fluctuations and GPS positioning errors at different longitudes during auroral disturbances. Sun Geosph. 2018, 13, 89–94. [Google Scholar] [CrossRef]
- Poniatowski, M.; Nykiel, G. Degradation of Kinematic PPP of GNSS Stations in Central Europe Caused by Medium-Scale Traveling Ionospheric Disturbances during the St. Patrick’s Day 2015 Geomagnetic Storm. Remote Sens. 2020, 12, 3582. [Google Scholar] [CrossRef]
- Luo, X.; Gu, S.; Lou, Y.; Xiong, C.; Chen, B.; Jin, X. Assessing the performance of GPS precise point positioning under different geomagnetic storm conditions during solar cycle 24. Sensors 2018, 18, 1784. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Mrak, S.; Morton, Y.J. Geomagnetic Storm Induced Mid-latitude Ionospheric Plasma Irregularities and Their Implications for GPS Positioning over North America: A Case Study. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 234–238. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).