Testing the Robust Yield Estimation Method for Winter Wheat, Corn, Rapeseed, and Sunflower with Different Vegetation Indices and Meteorological Data
Abstract
:1. Introduction
2. Study Area and Database Used
2.1. Study Area and Crop Information
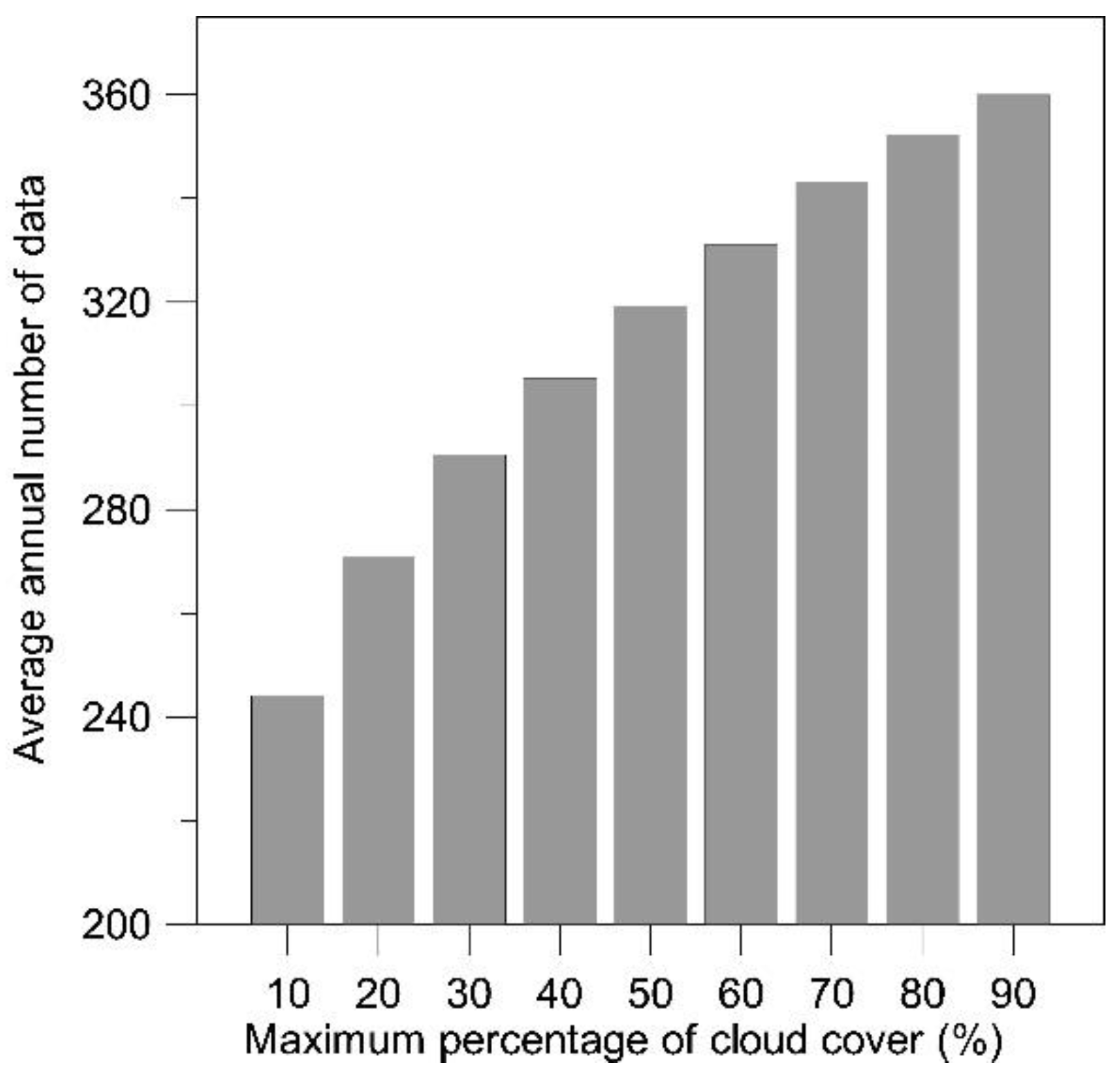
2.2. Remote Sensing and Land Cover Database
2.3. Vegetation Indices
2.4. Meteorological and Soil Water Content Data
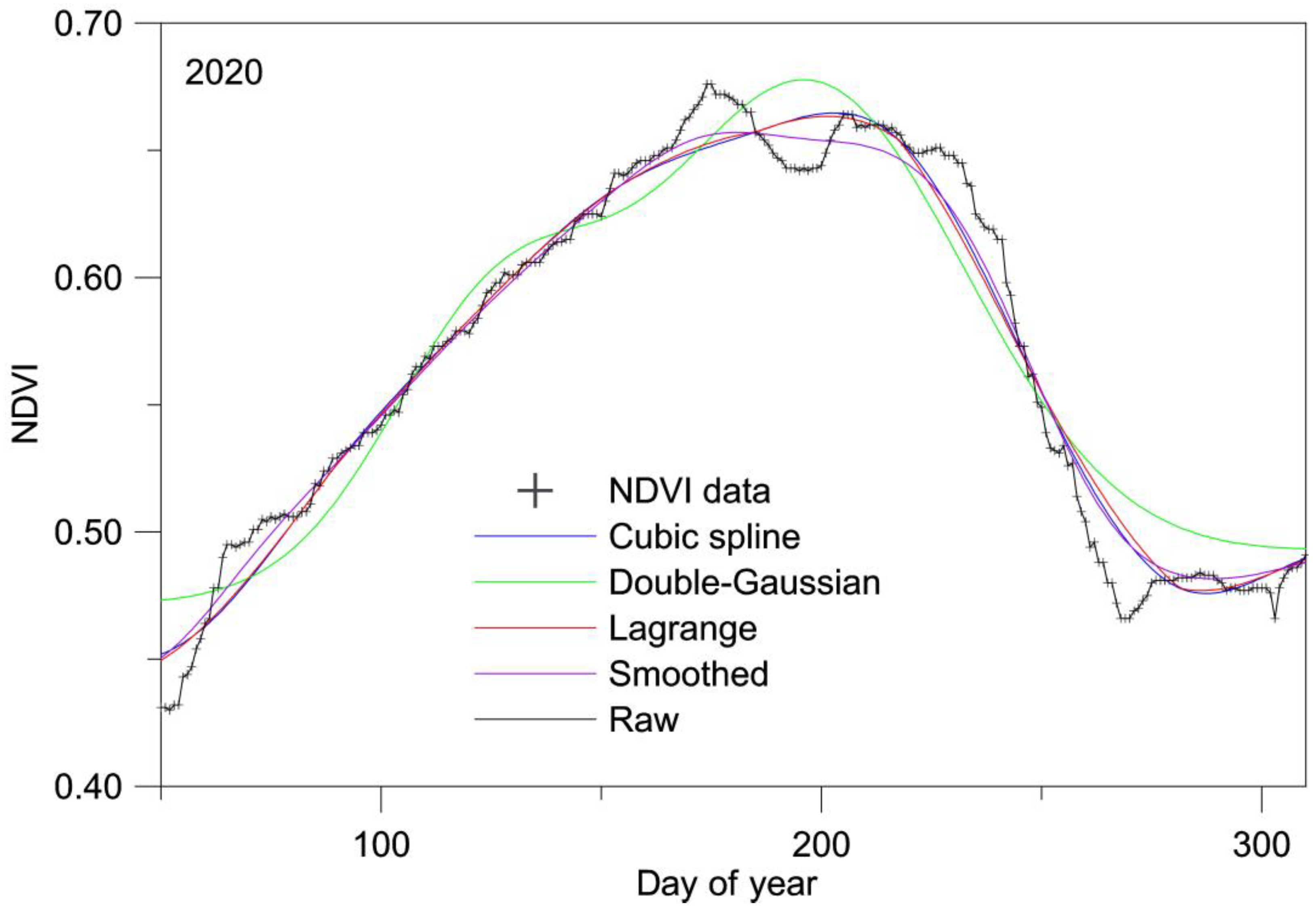
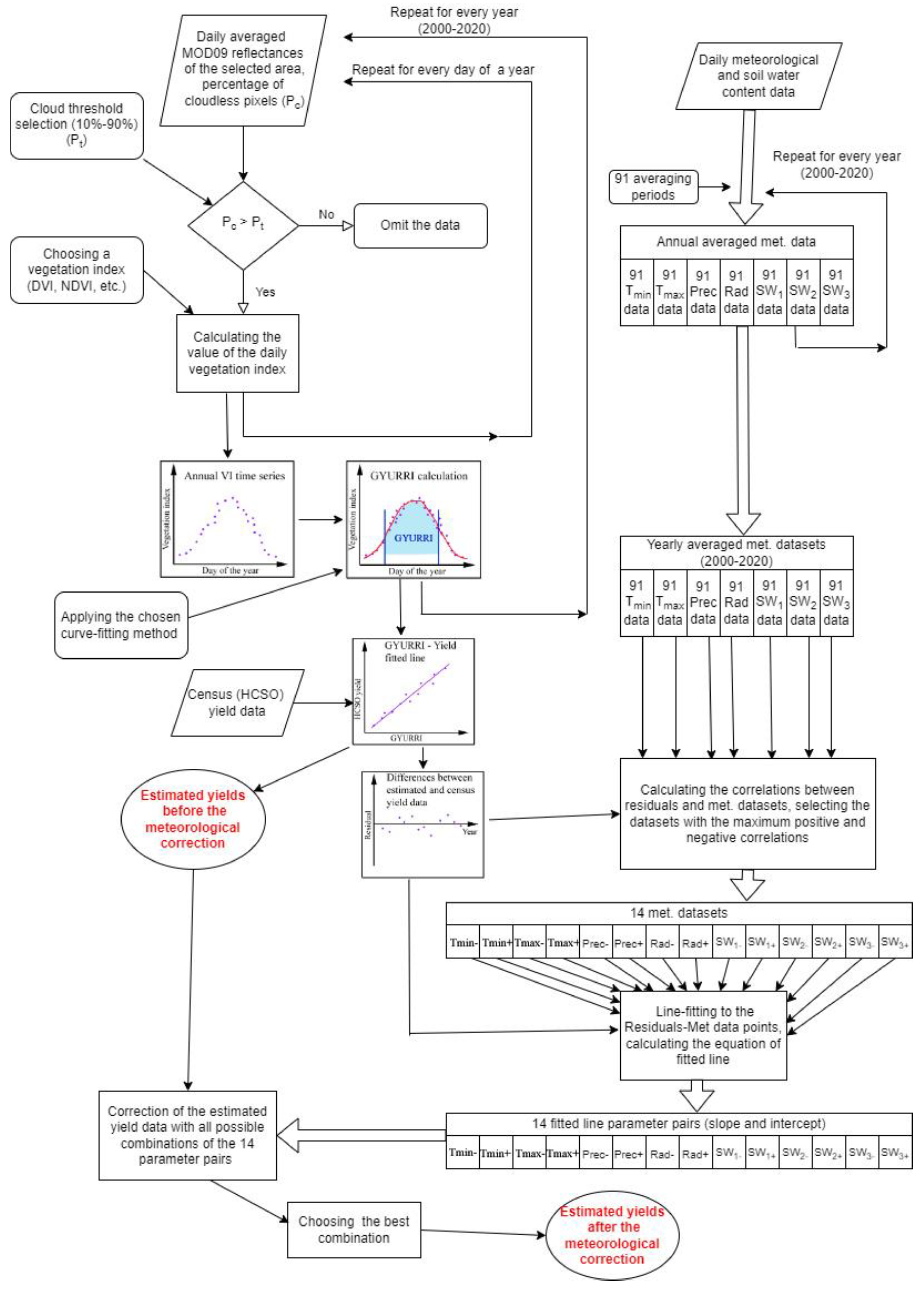
3. Methodology
4. Results
4.1. Corn, Country Level
4.2. Winter Wheat, Country Level
4.3. Sunflower and Rapeseed, Country Level
4.4. Data Series of 19 Counties
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khamala, E. Review of the Available Remote Sensing Tools, Products, Methodologies and Data to Improve Crop Production Forecasts; FAO: Rome, Italy, 2017; ISBN 978-92-5-109840-0. [Google Scholar]
- Khanal, S.; Kushal, K.C.; Fulton, J.P.; Shearer, S.; Ozkan, E. Remote sensing in agriculture—Accomplishments, limitations, and opportunities. Remote Sens. 2020, 12, 3783. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in Remote Sensing of Agriculture: Context Description, Existing Operational Monitoring Systems and Major Information Needs. Remote Sens. 2013, 5, 948–981. [Google Scholar] [CrossRef] [Green Version]
- Basso, B.; Cammarano, D.; Carfagna, E. Review of Crop Yield Forecasting Methods and Early Warning Systems. In Proceedings of the First Meeting of the Scientific Advisory Committee of the Global Strategy to Improve Agricultural and Rural Statistics; FAO: Rome, Italy, 2013; pp. 15–31. [Google Scholar]
- Wiegand, C.L.; Richardson, A.J.; Kanemasu, E.T. Leaf Area Index estimates for wheat from Landsat and their implications for evapotranspiration and crop modeling. Agron. J. 1979, 71, 336–342. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Yitayew, M.; Slack, D.C.; Hatchinson, C.F.; Huete, A.; Petersen, M.S. Estimating crop yields and production by integrating the FAO crop specific water data and ground-based ancillary data. Int. J. Remote Sens. 2010, 21, 3487–3508. [Google Scholar] [CrossRef]
- Curnel, Y.; de Wit, A.J.W.; Duvellier, G.; Defourny, P. Potential Performances of Remotely Sensed LAI Assimilation in WOFOST Model Based on an OSS Experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Nearing, G.S.; Crow, W.T.; Thorp, K.R.; Moran, M.S.; Reichle, R.H.; Gupta, H.V. Assimilating remote sensing observations of leaf area index and soil moisture for wheat yield estimates: An observing system simulation experiment. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the Leaf Area Index from Landsat TM and MODIS data into the WOFOST Model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Kasampalis, D.; Alexandridis, T.; Deva, C.; Challinor, A.; Moshou, D.; Zalidis, G. Contribution of remote sensing on crop models: A review. J. Imaging 2018, 4, 52. [Google Scholar] [CrossRef] [Green Version]
- Maselli, F.; Conese, C.; Petkov, L.; Gilabert, M.A. Use of NOAA–AVHRR NDVI data for environmental monitoring of crop forecasting in the Sahel. Preliminary results. Int. J. Remote Sens. 1992, 13, 2743–2749. [Google Scholar] [CrossRef]
- Hamar, D.; Ferencz, C.; Lichtenberger, J.; Tarcsai, G.; Ferencz-Árkos, I. Yield Estimation for Corn and Wheat in the Hungarian Great Plain Using Landsat MSS Data. Int. J. Remote Sens. 1996, 17, 1689–1699. [Google Scholar] [CrossRef]
- Schut, A.G.T.; Stephens, D.J.; Stovold, R.G.H.; Adams, M.; Craig, R.L. Improved wheat yield and production forecasting with a moisture stress index, AVHRR and MODIS data. Crop. Pasture Sci. 2009, 60, 60–70. [Google Scholar] [CrossRef]
- López-Lozano, R.; Duveiller, G.; Seguini, L.; Meroni, M.; García-Condado, S.; Hooker, J.; Leo, O.; Baruth, B. Towards regional grain yield forecasting with 1km-resolution EO biophysical products: Strengths and limitations at Pan-European level. Agric. For. Meteorol. 2015, 206, 12–32. [Google Scholar] [CrossRef]
- Kern, A.; Barcza, Z.; Marjanovic, H.; Árendás, T.; Fodor, N.; Bónis, P.; Bognár, P.; Lichtenberger, J. Statistical modelling of crop yield in Central Europe using climate data and remote sensing vegetation indices. Agric. For. Meteorol. 2018, 260–261, 300–320. [Google Scholar] [CrossRef]
- Hayes, M.J.; Decker, W.L. Using NOAA AVHRR Data to Estimate Maize Production in the United States Corn Belt. Int. J. Remote Sens. 1996, 17, 3189–3200. [Google Scholar] [CrossRef]
- Shao, Y.; Campbell, J.B.; Taff, G.N.; Zheng, B. An analysis of cropland mask choice and ancillary data for annual corn yield forecasting using MODIS data. Int. J. Appl. Earth Obs. 2015, 38, 78–87. [Google Scholar] [CrossRef]
- Bognár, P.; Kern, A.; Pásztor, S.; Lichtenberger, J.; Koronczay, D.; Ferencz, C. Yield estimation and forecasting for winter wheat in Hungary using time series of MODIS data. Int. J. Remote Sens. 2017, 38, 3394–3414. [Google Scholar] [CrossRef] [Green Version]
- Nagy, A.; Fehér, J.; Tamás, J. Wheat and maize yield forecasting for the Tisza river catchment using MODIS NDVI time series and reported crop statistics. Comput. Electron. Agric. 2018, 151, 41–49. [Google Scholar] [CrossRef]
- Kogan, F.; Kussul, N.; Adamenko, T.; Skakun, S.; Kravchenko, O.; Kryvobok, O.; Shelestov, A.; Kolotii, A.; Kussul, O.; Lavrenyuk, A. Winter wheat yield forecasting in Ukraine based on earth observation, meteorological data and biophysical models. Int. J. Appl. Earth Obs. 2013, 23, 192–203. [Google Scholar] [CrossRef]
- Kouadio, L.; Newlands, N.K.; Davidson, A.; Zhang, Y.; Chipanshi, A. Assessing the performance of MODIS NDVI and EVI for seasonal crop yield forecasting at the ecodistrict scale. Remote Sens. 2014, 6, 10193–10214. [Google Scholar] [CrossRef] [Green Version]
- Bognár, P.; Ferencz, C.S.; Pásztor, S.; Molnár, G.; Timár, G.; Hamar, D.; Lichtenberger, J.; Székely, B.; Steinbach, P.; Ferencz, O. Yield forecasting for wheat and corn in Hungary by satellite remote sensing. Int. J. Remote Sens. 2011, 32, 4749–4758. [Google Scholar] [CrossRef]
- Kamir, E.; Waldner, F.; Hochman, Z. Estimating wheat yields in Australia using climate records, satellite image time series and machine learning methods. ISPRS J. Photogramm. 2020, 160, 124–135. [Google Scholar] [CrossRef]
- Ren, S.; Guo, B.; Wu, X.; Zhang, L.; Ji, M.; Wang, J. Winter wheat planted area monitoring and yield modeling using MODIS data in Huang-Huai-Hai Plain, China. Comput. Electron. Agric. 2021, 182, 106049. [Google Scholar] [CrossRef]
- Kastens, J.H.; Kastens, T.L.; Kastens, D.L.A.; Price, K.P.; Martinko, E.A.; Lee, R. Image masking for crop yield forecasting using AVHRR NDVI time series imagery. Remote Sens. Environ. 2005, 99, 341–356. [Google Scholar] [CrossRef]
- Demirpolat, C.; Leloğlu, U.M. Barley yield estimation with Sentinel-2 vegetation indices. In Proceedings of the 26th IEEE Signal. Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Prasad, A.K.; Singh, R.P.; Tare, V.; Kafatos, M. Use of vegetation index and meteorological parameters for the prediction of crop yield in India. Int. J. Remote Sens. 2007, 28, 5207–5235. [Google Scholar] [CrossRef]
- Mosleh, M.K.; Hassan, Q.K.; Chowdhury, E.H. Application of remote sensing in mapping rice area and forecasting its production: A review. Sensors 2015, 15, 769–791. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, M.S. Assessment of millet yields and production in Northern Burkina Faso using integrated NDVI from the AVHRR. Int. J. Remote Sens. 1992, 13, 3431–3442. [Google Scholar] [CrossRef]
- Mounkaila, Y.; Garba, I.; Moussa, B. Yield prediction under associated millet and cowpea crops in the Sahelian zone. Afr. J. Agric. Res. 2019, 14, 1613–1620. [Google Scholar] [CrossRef]
- Esquerdo, J.; Zullo, J.; Antunes, J.F.G. Use of NDVI/AVHRR time-series profiles for soybean crop monitoring in Brazil. Int. J. Remote Sens. 2011, 32, 3711–3727. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Schwalbert, R.A.; Amado, T.; Corassa, G.; Pott, L.P.; Prasad, P.V.; Ciampatti, I.A. Satellite-based soybean forecast: Integrating machine learning and weather data for improving crop yield prediction in southern Brazil. Agric. For. Meteorol. 2020, 284, 107886. [Google Scholar] [CrossRef]
- Kogan, F.N.; Salazar, L.; Roytman, L. Forecasting crop production using Satellite-based vegetation health indices in Kansas, USA. Int. J. Remote Sens. 2012, 33, 2798–2814. [Google Scholar] [CrossRef]
- Ferencz, C.; Bognár, P.; Lichtenberger, J.; Hamar, D.; Tarcsai, G.; Timár, G.; Molnár, G.; Pásztor, S.; Steinbach, P.; Székely, B.; et al. Crop yield estimation by satellite remote sensing. Int. J. Remote Sens. 2004, 25, 4113–4149. [Google Scholar] [CrossRef]
- Mkhabela, M.S.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agric. For. Meteorol. 2011, 151, 385–393. [Google Scholar] [CrossRef]
- White, J.; Berg, A.; Champagne, C.; Zhang, Y.; Chipanshi, A.; Daneshfar, B. Improving crop yield forecasts with satellite-based soil moisture estimates: An example for township level canola yield forecasts over the Canadian Prairies. Int. J. Appl. Earth Obs. 2020, 89, 102092. [Google Scholar] [CrossRef]
- Vallentin, C.; Harfenmeister, K.; Itzerott, S.; Kleinschmit, B.; Conrad, C.; Spengler, D. Suitability of satellite remote sensing data for yield estimation in northeast Germany. Precis. Agric. 2021, 23, 52–82. [Google Scholar] [CrossRef]
- Anderson, M.C.; Cornelio, A.; Zolin, P.C.; Sentelhas, C.R.; Hain, K.; Semmens, M.T.; Yilmaz, F.; Gao, J.; Otkin, A.; Tetrault, R. The Evaporative Stress Index as an Indicator of Agricultural Drought in Brazil: An Assessment Based on Crop Yield Impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Rahman, A.; Khan, K.; Krakauer, N.Y.; Roytman, L.; Kogan, F. Using AVHRR-based vegetation health indices for estimation of potato yield in Bangladesh. J. Civ. Environ. Eng. 2012, 2, 111. [Google Scholar] [CrossRef] [Green Version]
- Salvador, P.; Gómez, D.; Sanz, J.; Casanova, J.L. Estimation of potato yield using satellite data at a municipal level: A machine learning approach. ISPRS Int. J. Geo-Inf. 2020, 9, 343. [Google Scholar] [CrossRef]
- Fieuzal, R.; Sicre, C.M.; Baup, F. Estimation of Sunflower Yield Using a Simplified Agrometeorological Model Controlled by Optical and SAR Satellite Data. IEEE J. Sel. Top. Appl. 2017, 10, 5412–5422. [Google Scholar] [CrossRef]
- Narin, O.G.; Abdikan, S. Monitoring of phenological stage and yield estimation of sunflower plant using Sentinel-2 satellite images. Geocarto Int. 2020, 37, 1378–1392. [Google Scholar] [CrossRef]
- Boken, V.K.; Hoogenboom, G.; Williams, J.H.; Diarra, B.; Dione, S.; Easson, G.L. Monitoring peanut contamination in Mali (Africa) using AVHRR satellite data and a crop simulation model. Int. J. Remote Sens. 2008, 29, 117–129. [Google Scholar] [CrossRef]
- Santos, J.A.; Malheiro, A.C.; Karremann, M.K.; Pinto, J.G. Statistical modelling of grapevine yield in the Port wine region under present and future climate conditions. Int. J. Biometeorol. 2011, 55, 119–131. [Google Scholar] [CrossRef]
- Waine, T.W.; Simms, D.M.; Taylor, J.C.; Juniper, G.R. Towards improving the accuracy of opium yield estimates with remote sensing. Int. J. Remote Sens. 2014, 35, 6292–6309. [Google Scholar] [CrossRef]
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens. 2013, 5, 1704–1733. [Google Scholar] [CrossRef] [Green Version]
- Panek, E.; Gozdowski, D.; Stępień, M.; Samborski, S.; Ruciński, D.; Buszke, B. Within-field relationships between satellite-derived vegetation indices, grain yield and spike number of winter wheat and triticale. Agronomy 2020, 10, 1842. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Mróz, M.; Sobieraj, A. Comparison of several vegetation indices calculated on the basis of a seasonal SPOT XS time series, and their suitability for land cover and agricultural crop identification. Techn. Sc. 2004, 7, 40–66. [Google Scholar]
- Payero, J.O.; Neale, C.M.U.; Wright, J.L. Comparison of eleven vegetation indices for estimating plant height of alfalfa and grass. Appl. Eng. Agric. 2004, 20, 385–393. [Google Scholar] [CrossRef] [Green Version]
- Vina, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef] [Green Version]
- Towers, P.C.; Strever, A.; Poblete-Echeverria, C. Comparison of vegetation indices for leaf area index estimation in vertical shoot positioned vine canopies with and without Grenbiule hail-protection netting. Remote Sens. 2019, 11, 1073. [Google Scholar] [CrossRef] [Green Version]
- Hatfield, J.L.; Boote, K.J.; Kimball, B.A.; Ziska, L.H.; Izaurralde, R.C.; Ort, D.; Thomson, A.M.; Wolfe, D. Climate impacts on agriculture: Implications for crop production. Agron. J. 2011, 103, 351–370. [Google Scholar] [CrossRef] [Green Version]
- Siebert, S.; Webber, H.; Rezael, E.E. Weather impacts on crop yields—Searching for simple answers to a complex problem. Environ. Res. Lett. 2017, 22, 81001. [Google Scholar] [CrossRef] [Green Version]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for the early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. 2008, 10, 438–452. [Google Scholar] [CrossRef] [Green Version]
- Franch, B.; Vermote, E.F.; Becker-Reshef, I.; Claverie, M.; Huang, J.; Zhang, J.; Justice, C.; Sobrino, A.J. Improving the timeliness of winter wheat production forecast in the United States of America, Ukraine and China using MODIS data and NCAR growing degree day information. Remote Sens. Environ. 2015, 161, 131–148. [Google Scholar] [CrossRef]
- Vannotten, A.; Gobin, A. Estimating farm wheat yields from NDVI and meteorological data. Agronomy 2021, 11, 946. [Google Scholar] [CrossRef]
- Schaaf, C.; Wang, Z. MCD43A4 MODIS/Terra + Aqua BRDF/Albedo Nadir BRDF Adjusted Ref Daily L3 Global—500 m V006. NASA EOSDIS Land Processes DAAC. Available online: https://lpdaac.usgs.gov/products/mcd43a4v006/ (accessed on 14 March 2021).
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Rouse, J.W.; Haas, R.W.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the vernal advancement and retrogradation (Green wave effect) of natural vegetation. In Proceedings of the NASA/GSFCT Type III Final Report, Greenbelt, MD, USA, 1974; Available online: https://ntrs.nasa.gov/api/citations/19730017588/downloads/19730017588.pdf (accessed on 5 May 2022).
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships between NDVI, canopy structure, and photosynthesis in three Californian vegetation types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Clevers, J.P.W. The derivation of a simplified reflectance model for the estimation of Leaf Area Index. Remote Sens. Environ. 1988, 25, 53–69. [Google Scholar] [CrossRef]
- Clevers, J.P.W. Application of WDVI in estimating LAI at the generative stage of barley. ISPRS J. Photogramm. 1991, 46, 37–47. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Xu, D.; Guo, X. A study of soil line simulation from Landsat images in mixed grassland. Remote Sens. 2013, 5, 4533–4550. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Dempewolf, J.; Adusei, B.; Becker-Reshef, I.; Hansen, M.; Potapov, P.; Khan, A.; Barker, B. Wheat yield forecasting for Punjab Province from vegetation index time series and historic crop statistics. Remote Sens. 2014, 6, 9653–9675. [Google Scholar] [CrossRef] [Green Version]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to topographic effects: A case study in high-density cypress forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant. Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Somvanshi, S.S.; Kumari, M. Comparitive analysis of different vegetation indices with respect to atmospheric particulate pollution using sentinel data. Appl. Comput. Geosci. 2020, 7, 100032. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S.A. Modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D. Atmospherically Resistant Vegetation Index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Pinty, B.; Verstraete, M.M. GEMI: A non-linear index to monitor global vegetation from satellites. Plant. Ecol. 1992, 101, 15–20. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Pavlova, A. The application of remote sensing data for wheat yield production. In Economic and Social Development, Proceedings of the 55th International Scientific Conference on Economic and Social Development, 18–19 June 2020; Baku, A.B., Ismaylov, A., Aliyev, K., Benazic, M., Eds.; Varazdin Development and Entrepreneurship Agency: Varazdin, Croatia; University North: Koprivnica, Croatia; Azerbaijan State University of Economics: Baku, Azerbaijan; Faculty of Management University of Warsaw: Warsaw, Poland; Faculty of Law, Economics and Social Sciences Sale—Mohammed V University: Rabat, Morocco; Polytechnic of Medimurje in Cakovec: Cakovec, Croatia, 2020; pp. 326–332. [Google Scholar]
- Gitelson, A.; Kaufman, Y.; Merzlyak, M. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Lymburner, L.; Beggs, P.J.; Jacobson, C.R. Estimation of canopy-average surface-specific leaf area using Landsat TM data. Photogramm. Eng. Remote Sens. 2000, 66, 183–191. [Google Scholar]
- Jin, S.; Sader, S.A. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ. 2005, 94, 364–372. [Google Scholar] [CrossRef]
- Karnieli, A.; Kaufman, Y.J.; Remer, L.; Wald, A. AFRI—Aerosol free vegetation index. Remote Sens. Environ. 2001, 77, 10–21. [Google Scholar] [CrossRef]
- Ben-Ze’ev, E.; Karnieli, A.; Agam, N.; Kaufman, Y.; Holben, B. Assessing vegetation condition in presence of biomass burning smoke by applying the Aerosol-free Vegetation Index (AFRI) on MODIS images. Int. J. Remote Sens. 2006, 27, 3203–3221. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, A.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Muñoz-Marí, J.; García-Haro, F.J.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef]
- Dobor, L.; Barcza, Z.; Hlásny, T.; Havasi, Á.; Horváth, F.; Ittzés, P.; Bartholy, J. Bridging the gap between climate models and impact studies: The FORESEE Database. Geosci. Data J. 2014, 2, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Thornton, P.E.; Hasenauer, H.; White, M.A. Simultaneous estimation of daily solar radiation and humidity from observed temperature and precipitation: An application over complex terrain in Austria. Agric. For. Meteorol. 2020, 104, 255–271. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Kogan, F.; Ciolkosz, A.; Gruszczynska, M.; Kowalik, W. Modelling of crop growth conditions and crop yield in Poland using AVHRR-Based indices. Int. J. Remote Sens. 2002, 23, 1109–1123. [Google Scholar] [CrossRef]
- Schlenker, W.; Lobell, D.B. Robust negative impacts of climate change on African agriculture. Environ. Res. Lett. 2010, 5, 14010. [Google Scholar] [CrossRef]
- Gornott, C.; Wechsung, F. Statistical regression models for assessing climate impacts on crop yields: A validation study for winter wheat and silage maize in Germany. Agric. For. Meteorol. 2016, 217, 89–100. [Google Scholar] [CrossRef]
- Pinke, Z.; Lövei, G.L. Increasing temperature cuts back crop yields in Hungary over the last 90 years. Glob. Chang. Biol. 2017, 23, 5426–5435. [Google Scholar] [CrossRef]
- Lobell, D.B.; Field, C.B. Global scale climate-crop yield relationships and the impacts of recent warming. Environ. Res. Lett. 2007, 2, 014002. [Google Scholar] [CrossRef]
- Schauberger, B.; Gornott, C.; Wechsung, F. Global evaluation of a semiempirical model for yield anomalies and application to within-season yield forecasting. Glob. Chang. Biol. 2017, 23, 4750–4764. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, R.; Liu, T.; Xu, K. Crop yield prediction based on agrometeorological indexes and remote sensing data. Remote Sens. 2021, 13, 2016. [Google Scholar] [CrossRef]
- Bojanowski, J.; Sikora, S.; Musial, J.P.; Wozniak, E.; Dabrowska-Zielinska, K.; Slesinski, P.; Milewski, T.; Laczynski, A. Integration of Sentinel-3 and MODIS vegetation indices with ERA-5 agro-meteorological indicators for operational crop yield forecasting. Remote Sens. 2022, 14, 1238. [Google Scholar] [CrossRef]

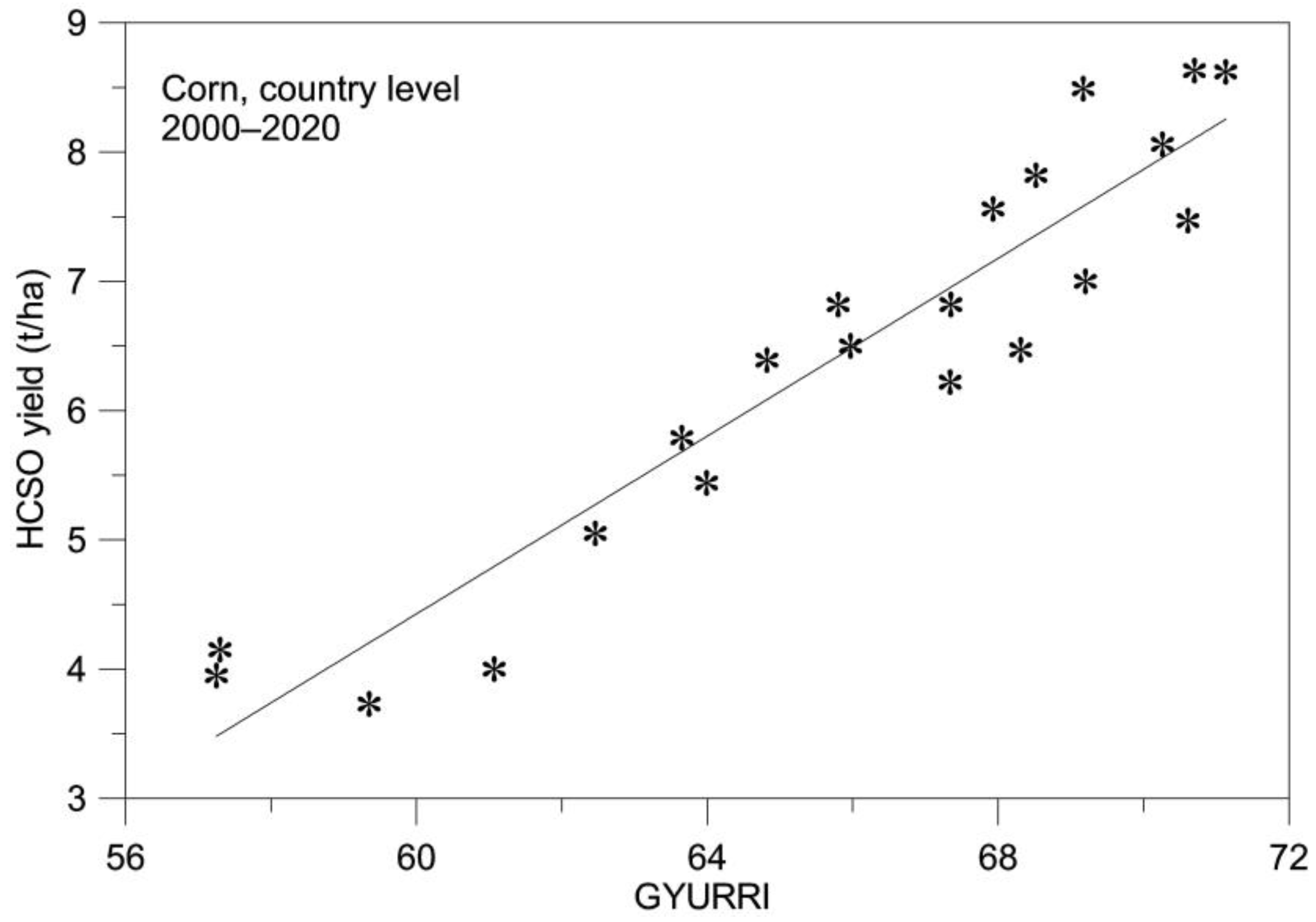
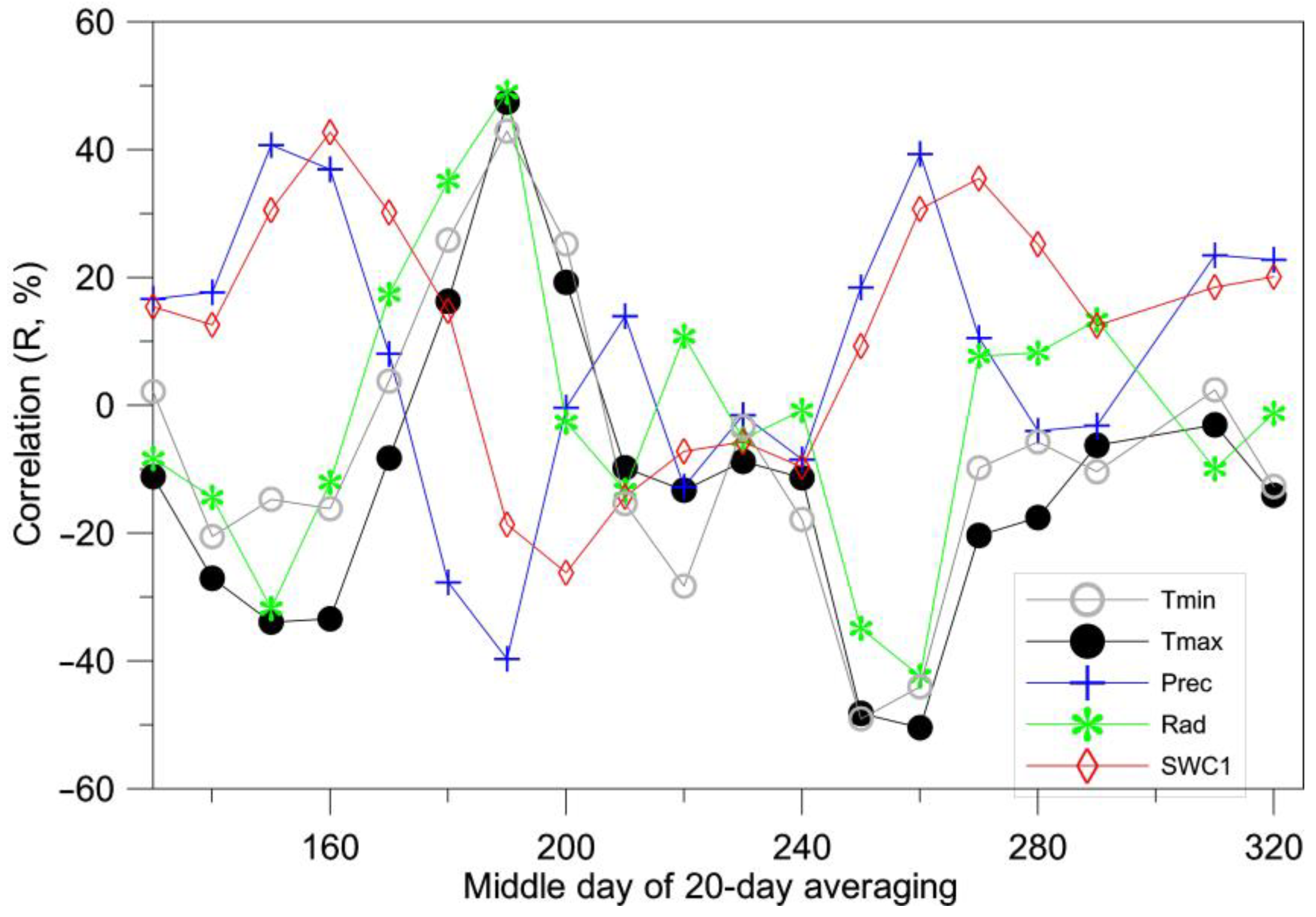
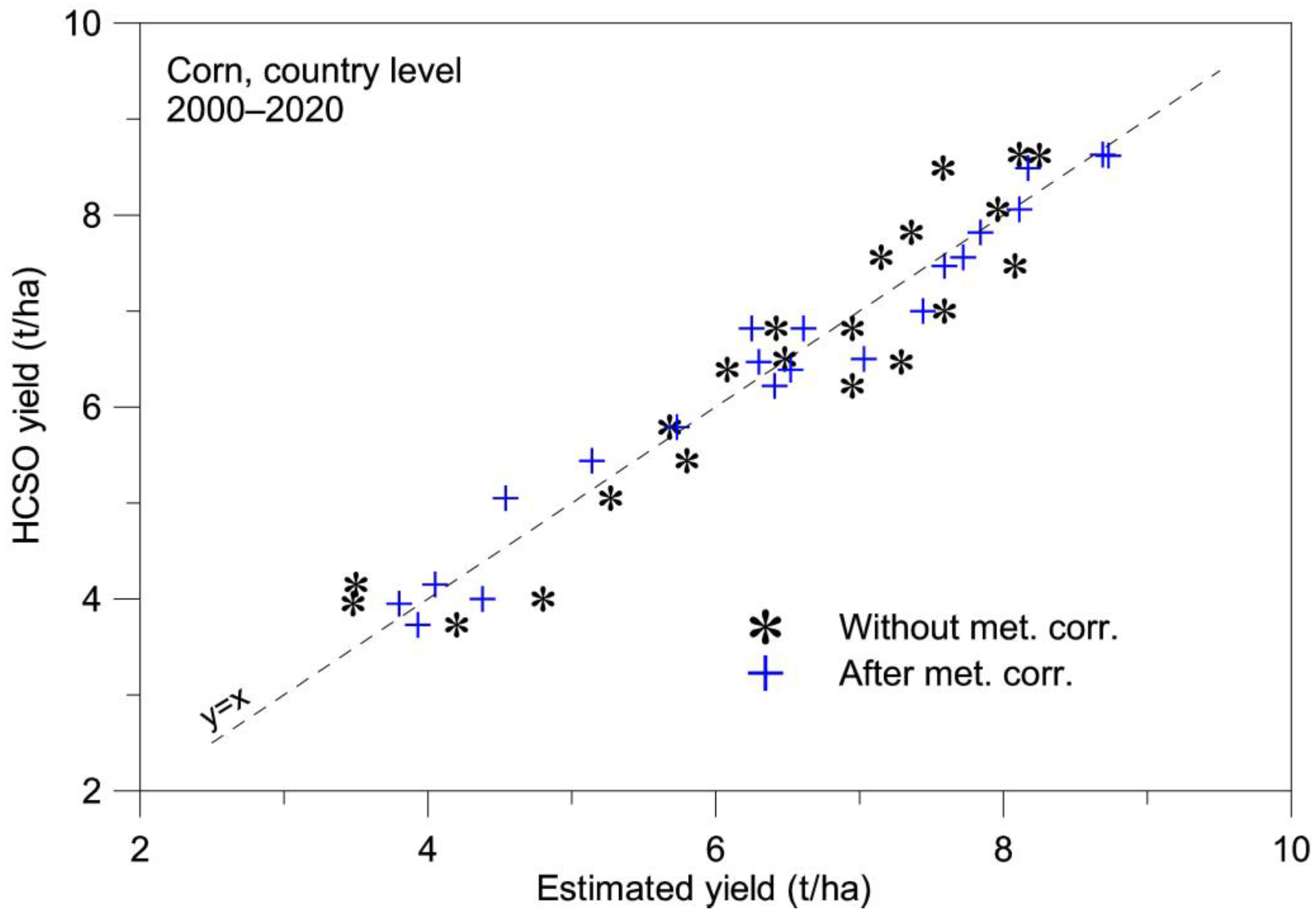
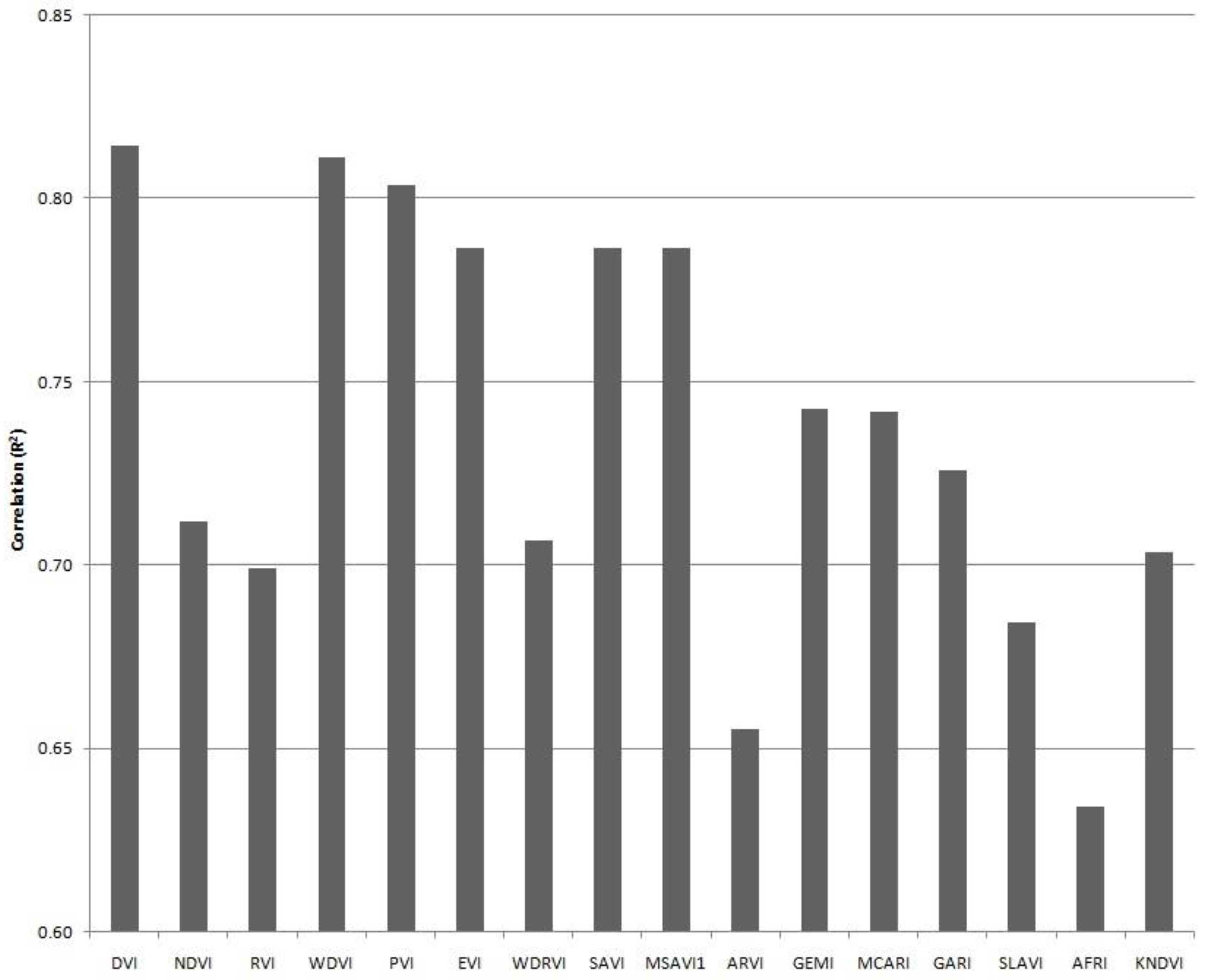

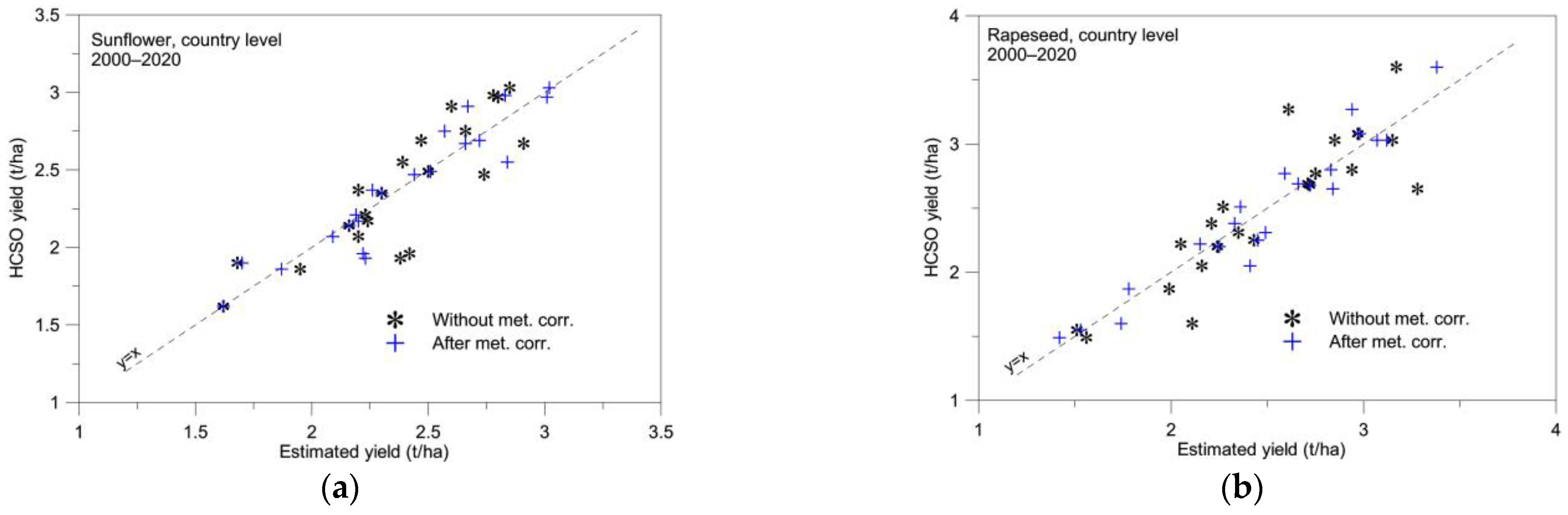
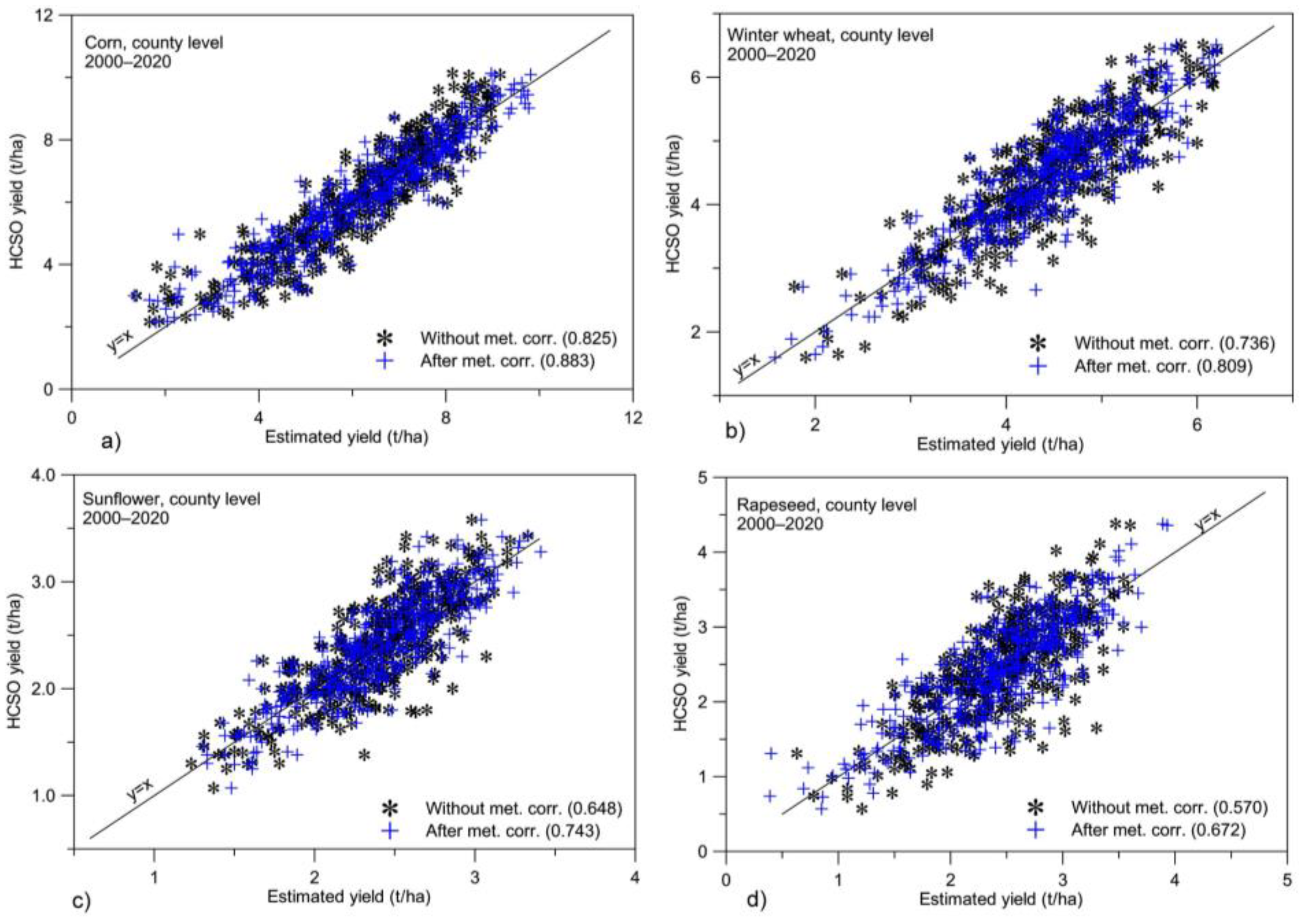
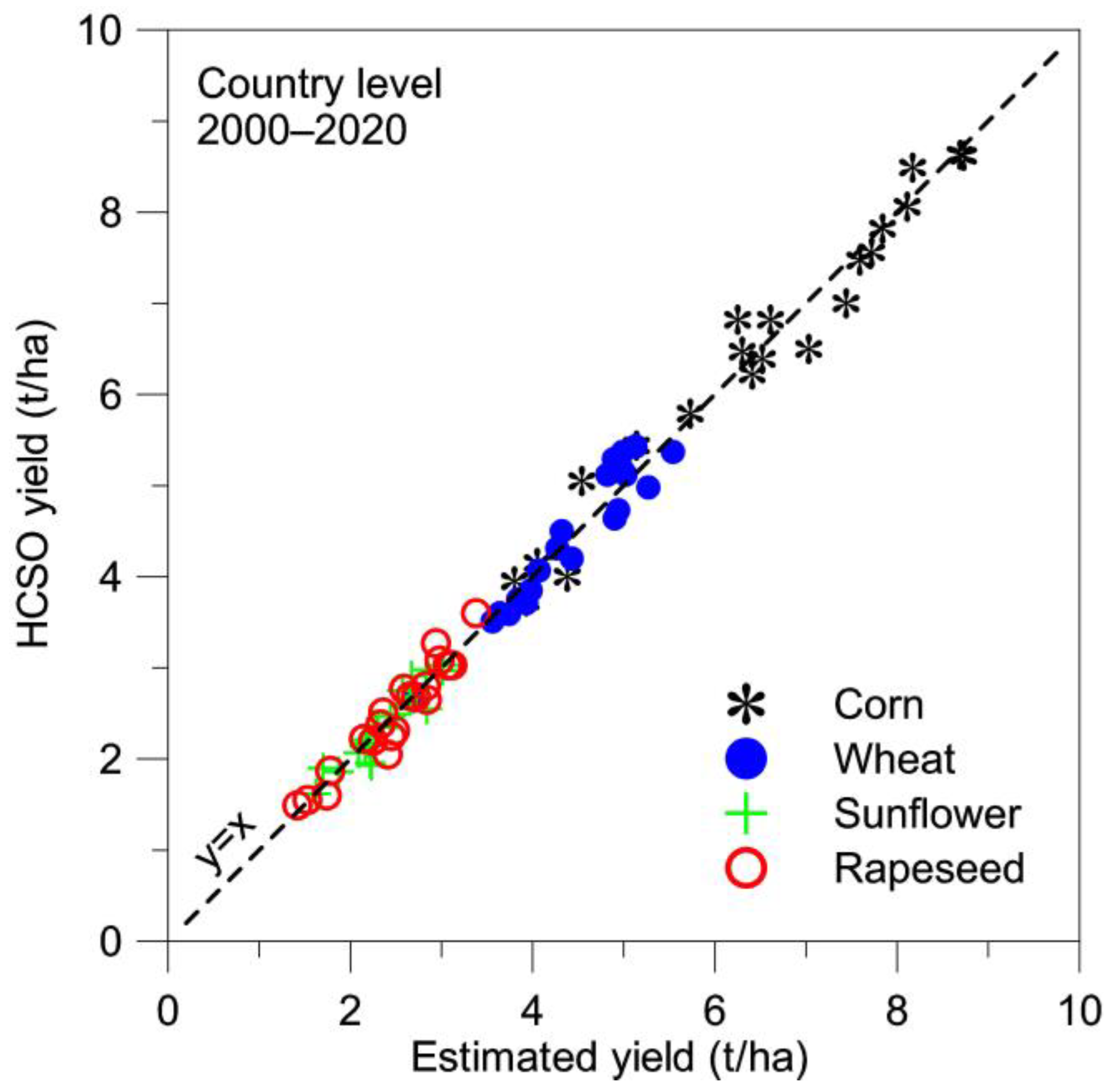
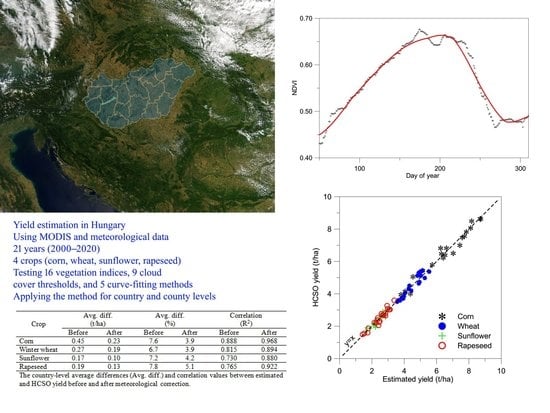
| Crop | Avg. Diff. (t/ha) | Avg. Diff. (%) | Correlation (R2) | |||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| Corn | 0.60 | 0.48 | 11.1 | 9.0 | 0.825 | 0.883 |
| Winter wheat | 0.38 | 0.32 | 9.2 | 7.6 | 0.736 | 0.809 |
| Sunflower | 0.22 | 0.19 | 9.6 | 8.3 | 0.648 | 0.743 |
| Rapeseed | 0.35 | 0.31 | 16.7 | 14.4 | 0.570 | 0.672 |
| Crop | Avg. Diff. (t/ha) | Avg. Diff. (%) | Correlation (R2) | |||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| Corn | 0.45 | 0.23 | 7.6 | 3.9 | 0.888 | 0.968 |
| Winter wheat | 0.27 | 0.19 | 6.7 | 3.9 | 0.815 | 0.894 |
| Sunflower | 0.17 | 0.10 | 7.2 | 4.2 | 0.730 | 0.880 |
| Rapeseed | 0.19 | 0.13 | 7.8 | 5.1 | 0.765 | 0.922 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bognár, P.; Kern, A.; Pásztor, S.; Steinbach, P.; Lichtenberger, J. Testing the Robust Yield Estimation Method for Winter Wheat, Corn, Rapeseed, and Sunflower with Different Vegetation Indices and Meteorological Data. Remote Sens. 2022, 14, 2860. https://doi.org/10.3390/rs14122860
Bognár P, Kern A, Pásztor S, Steinbach P, Lichtenberger J. Testing the Robust Yield Estimation Method for Winter Wheat, Corn, Rapeseed, and Sunflower with Different Vegetation Indices and Meteorological Data. Remote Sensing. 2022; 14(12):2860. https://doi.org/10.3390/rs14122860
Chicago/Turabian StyleBognár, Péter, Anikó Kern, Szilárd Pásztor, Péter Steinbach, and János Lichtenberger. 2022. "Testing the Robust Yield Estimation Method for Winter Wheat, Corn, Rapeseed, and Sunflower with Different Vegetation Indices and Meteorological Data" Remote Sensing 14, no. 12: 2860. https://doi.org/10.3390/rs14122860
APA StyleBognár, P., Kern, A., Pásztor, S., Steinbach, P., & Lichtenberger, J. (2022). Testing the Robust Yield Estimation Method for Winter Wheat, Corn, Rapeseed, and Sunflower with Different Vegetation Indices and Meteorological Data. Remote Sensing, 14(12), 2860. https://doi.org/10.3390/rs14122860